Abstract
Because of their improved properties, FRP composites are vastly used in the strengthening of aged concrete infrastructures. However, it has been observed that their performance is highly compromised when exposed to high temperatures, as expected during fire incidents, which critically affects FRP–concrete bond behavior, hence affecting the overall efficiency of the strengthening system. This paper critically presents the available literature concerning the degradation of bond strength between FRP systems with concrete substrates due to increased temperatures. Both analytical and numerical bond–slip models developed for the prediction of bond strength degradation under such conditions are reviewed. A generally confirmed fact is that exposure to high temperatures, especially those reaching glass transition temperature (Tg) for epoxy adhesives, leads to bond degradation. Therefore, cement mortar-bonded CFRP textiles display better performance in fire endurance. This present paper also utilizes machine learning algorithms for the prediction of bond strength under elevated temperatures based on an experimental database of 37 beams. The nonlinear relationships and variable interactions in the developed model provide a reliable method for the estimation of bond strength with reduced extensive experimental testing, where the critical role of temperature in bond behavior is identified. This paper emphasizes the use of advanced predictive models to ensure the durability and safety of FRP-strengthened concrete structures in thermally challenging environments.
1. Introduction
FRP composites have been considerably used in the strengthening and retrofitting of concrete structures in the last four decades because of their high strength-to-weight ratio, resistance to corrosion, and ease of application. However, high temperatures can negatively affect the bond between FRP and concrete, which is essential for effective load transfer. This becomes particularly concerning in cases of fire or high-temperature exposure, which is a norm in many parts of the world [,,,,,,,,,,].
FRP materials typically contain a polymer matrix reinforced by fibers, which could be carbon, glass, or aramid. The mechanical properties of these composites, which include tensile strength and stiffness, highly depend on the type of fibers used and the quality of the bonding agent. Adhesive epoxy resin is one of the most commonly used bonding agents in FRP–concrete systems. However, epoxy adhesives show high-temperature sensitivity, which leads to degradation in bond performance when exposed to high temperatures [,,,,,]. The critical temperature point corresponds to the glass transition temperature (Tg) of adhesives. Beyond this temperature point, a huge softening will occur in the bond, leading to significant deterioration in the integrity and mechanical properties of the FRP–concrete bond [].
High temperatures can cause a variety of adverse effects on FRP–concrete joints, including mechanical property deterioration, thermal incompatibility stresses due to different coefficients of thermal expansion between FRP and concrete, and chemical decomposition of both the polymer matrix and the adhesive. In this regard, the bond strength may be considerably reduced with strong possibilities of debonding or delamination of the FRP system, leading to a loss of the carried structural load and hence compromising the FRP-reinforced concrete elements’ structural integrity [,,,,,,,,,,,,,].
To date, the literature has broadly covered the higher temperature effect on FRP–concrete bond behavior. It is reported that an increase in temperature reduces the efficiency of the bond, especially when the temperature is higher than the Tg of the adhesive [,,,,]. On the other hand, some investigations were carried out using other adhesives, which are much less dependent on temperature in comparison with epoxy-based adhesives. The mechanism of bond deterioration can be more complicated than described herein. The contact plane between the epoxy and cement pastes or concrete substrate is called the interface. From a macroscopic point of view, the interface separates the two materials. Although this interface is evident at higher length scales, recent work has illustrated that a transition or interphase region exists between the bulk epoxy and the bulk cement paste or concrete substrate. This zone is created by the penetration of the low-viscosity epoxy into the porous network of the cementitious substrate with the selective reaction between the amine-based hardener and cement hydrates. It is believed that this selective reaction creates a deficit of amines near the interface. Correspondingly, the cross-linking density for the epoxy near the contact plane with the substrate is probably lower than for bulk epoxy. It is hypothesized to be adjacent to an amine-rich region, with a lower degree of cure that makes the interface more susceptible to environmental conditions [].
Several potential scenarios could occur at the FRP–concrete joint when exposed to elevated temperatures. Higher temperatures have the ability to lower concrete’s modulus of elasticity, tensile strength, and compressive strength. This may impact the concrete substrate’s capacity to transfer stresses to the FRP system efficiently. In the same vein, the FRP’s tensile strength, modulus of elasticity, and ultimate strain can deteriorate at high temperatures [,,,,,,]. Moreover, when exposed to temperature changes, the different coefficients of the thermal expansion of concrete and FRP can result in the development of thermal incompatibility stresses at the bond interface. The strengthening system bond’s integrity could be affected by debonding or microcracking at the interface by these residual stresses [,,]. In addition, high temperatures have the potential to start chemical reactions and breakdown processes in the FRP materials and bonding adhesive; the thermal degradation of both the polymer matrix and adhesive layer can result in mechanical property loss and compromised bond performance and thus lessen the bond’s capacity to transfer stresses between the FRP and the concrete substrate efficiently [,,,]. In the event of a fire, the behavior of the FRP-to-concrete bond may significantly deteriorate because of the quick temperature rise and exposure to high temperatures [,,,,]. The specific FRP system, concrete composition, temperature range, and exposure duration can all affect the degradation mechanisms and changes in bond strength. Comprehending these impacts is essential for evaluating the durability and long-term performance of FRP-strengthened concrete members exposed to high temperatures or fire situations. Additionally, the reported results may differ because of variations in experimental setups and test methods, particularly the specific temperature ranges. Table 1 summarizes the effect of the temperature range on the FRP–concrete bond [,,,,,,,,,,,,,,,,,,].

Table 1.
Temperature range effect.
This paper intends to review the literature on the degradation in FRP–concrete joint bond strength under elevated temperature conditions. Various experimental, analytical, and numerical efforts were briefed to explain the bond–slip relationship in such conditions. Furthermore, machine learning (ML) algorithms were utilized to predict bond strength using a dataset that includes a wide range of FRP–concrete systems under varying temperatures and material properties. The ML model provides a reliable and efficient assessment of bond performance, reducing reliance upon comprehensive experimental testing.
2. Previous Work
Previous studies in the literature have discussed bond performance using a variety of experimental, numerical and mathematical techniques, and experimental procedures including pull-off tests, beam tests, single-lap shear tests, and double-lap shear tests, as well as analytical and numerical modeling approaches [,,,,,,]. The following sections illustrate remarkable studies and their results that investigate the bond–slip relationships under elevated temperatures for FRP systems bonded with both epoxy adhesives and recently developed cementitious adhesives.
2.1. The Behavior of FRP Bonded with Epoxy Adhesives
Gamag et al. [] investigated the bond behavior of carbon fiber-reinforced polymer (CFRP) plates bonded to concrete substrates at elevated temperatures experimentally and numerically. Two series of single-shear tests were carried out on CFRP-strengthened concrete specimens. The first series consisted of 11 non-insulated specimens to verify critical temperatures, temperature distributions, and influencing factors. The second series had two insulated specimens to study the effects of insulation on heat transfer. Varying bond lengths (75–175 mm) were investigated, and a 50 mm thick layer of insulation was applied to the insulated specimens. The non-insulated specimens were loaded to half the ultimate load of the same bond length at ambient temperature. Afterward, the oven temperature was increased to 10 °C/min until failure, and the temperatures were recorded using thermocouples. The insulated specimens were subjected to a three-step temperature increase (up to 1200 °C) without any load. Furthermore, finite element models were developed using Strand 7 to predict heat transfer in both series of specimens. The numerical model was validated against the experimental results, showing good agreement in predicting temperature distributions within the epoxy layer. However, the bond between CFRP and concrete was lost in the non-insulated specimens when the average epoxy temperature reached 70–81 °C (experimental) or 70–76 °C (numerical).
Aguiar et al. [] highlighted the importance of selecting adhesives whose Tg was well above expected service temperatures. Insulating materials were used to keep the temperature of the epoxy below Tg, which is a practical means of bond protection. However, even with insulation, bond failure can occur under certain temperatures, such as those that occur during fire exposure. Three insulation materials—rock wool, expanded polystyrene, and foamed polyurethane—were tested by encasing 100 mm concrete cubes strengthened with CFRP in a 30 mm thick layer of insulation. Temperatures were measured in the epoxy adhesive and insulation surface until stabilization after exposing specimens to a temperature of 60 °C. The foamed polyurethane showed the best insulating performance among the three materials tested. It was able to maintain the bonding epoxy temperature well below the glass transition temperature (Tg) of 62 °C. The authors concluded that the epoxy adhesives used for CFRP–concrete bonding were very sensitive to high temperatures; rapid deterioration was reported above 60 °C (near the Tg). This temperature can be reached even under solar exposure in warm environments. Therefore, careful epoxy selection with a Tg well above the maximum service temperature is recommended. However, applying protective insulation like foamed polyurethane can be an effective solution to prevent excessive temperature rise in the epoxy layer during exposures to fire.
Firmo et al. [] performed double-lap shear tests to study the bond behavior of CFRP-strengthened RC elements at elevated temperatures. The experimental investigation involved double-lap shear testing in both the steady state (series S1) and the transient (series S2) state on concrete blocks reinforced with CFRP strips externally attached with epoxy adhesive. Two varieties of specimens, with and without mechanical anchoring on the CFRP strip extremities, were evaluated in series S1. The specimens were heated to 20 °C, 55 °C, 90 °C, and 120 °C. The specimens in series S2 were heated to failure after being loaded to 25%, 50%, or 75% of their ambient temperature strength. The axial strain readings were used to construct the shear stress (τ) vs. slip (s) curves (bond–slip models). The process outlined in Ferracutti et al. [] adhered to the slip at a general point (x), with xi ≤ x > xi+1, and ξ = xm − x was derived by integrating the strain distribution beginning from the bottom strain gauge (Equations (1) and (2)) next to the CFRP free-end, x = xm, where s(xm) is the slip measured by the bottom LVDT as follows:
From the difference between the axial strains measured at such a pair of readings (εi+1 − εi), the elastic modulus of the CFRP strip (Ep) for the test temperature, its cross-section (Ap), and width (bp), one can easily obtain the average shear stress between two adjacent strain gauges (Equation (3)) as follows:
The obtained results for specimens without mechanical anchorage demonstrate that as the temperature rises, the strain distributions along the bonded length change significantly, approaching linearity because of the softening of the epoxy adhesive. Moreover, the effective bond length increases, and the stiffness and the maximum shear stress of the bond–slip relationships suffer significant reductions. The failure mode shifts from cohesive (at ambient temperature) to adhesive (at elevated temperature), and the overall stiffness and strength of the CFRP–concrete interface decrease significantly, with the bond strength reduction in the transient tests being comparable to that observed on the steady-state conditions.
Gamag et al. [] investigated the bond durability between CFRP laminates and concrete under different combined effects including cyclic temperatures from 20 to 50 °C, a constant low humidity of 30% RH, and sustained loading levels from 0 to 50% of the ultimate load. The preliminary tests showed that the effective bond length was in the range of 100–150 mm for the materials and configuration used. After 1800 h of conditioning, the maximum bond strength reduction was 22% for the unstressed specimens and 15% for those under the 50% sustained load. A further decrease in strength was very minimal up to 2250 h; therefore, the degradation at this point was considered to have plateaued. Under the 25–35% sustained load, the bond strength reduction after 2250 h was only 8%. However, the greater 50% sustained loads accounted for more considerable strength decreases after 2250 h of about 14–15% since the high stresses had poor effects on the concrete-primer interface, resulting in interface failure modes. In comparison with the unstressed and low-load specimens that failed through concrete rupture near the interface, the high-sustained-load specimens failed by debonding along the concrete–primer interface. It showed nonlinear descending bond stress–slip response curves whose peak bond stresses decreased with increasing levels of the sustained load applied because of the degradation in the bond.
Few studies are available in the literature for other types of FRPs. Zhou et al. [] investigated the thermal stability and durability of aramid fiber-reinforced polymer (AFRP), basalt fiber-reinforced polymer (BFRP), and CFRP bonded to concrete under elevated temperatures. The specimens were subjected to a temperature regime, controlled from ambient up to 300 °C. After exposure, the bond strength at the FRP–concrete interface was tested by a pull-off test. The microstructural changes that took place at the interface and their chemical composition were analyzed using Scanning Electron Microscopy (SEM) and Energy Dispersive Spectroscopy (EDS), respectively, to give a comprehensive understanding of the degradation mechanisms involved in the degradation process. The results showed that the CFRP sustained relatively high temperatures up to 200 °C, beyond which a high drop was noted. In contrast, AFRP and BFRP showed a drastic drop in bonding strength at lower temperatures. Microstructural observations showed that in the case of the CFRP samples, there was very little change in the interface structure up to 200 °C. In the cases of the AFRP and BFRP samples, matrix degradation was appreciable with fiber debonding starting as low as 150 °C. The SEM images showed that micro-cracks and delamination at the interfaces were more prominent in AFRP and BFRP compared with CFRP. Zhou et al. [] observed a higher degree of micro-cracks and interface delamination with AFRP and BFRP, while such a phenomenon was not found with CFRP as shown in Figure 1. For the 25 °C scenario, one SEM with different magnifications showed that the epoxy was intact, and the surface of the fibers was smooth. For the 300 °C scenarios, various defects, including microcracks and fiber exposure, were observed. The epoxy broke into small pieces of fragments and particles, and small fragments and particles were randomly distributed at the surface of the fibers. In the meantime, a gap between the epoxy and the fiber was observed, implying the separation between the epoxy and fibers. Their study also pointed out some crucial tasks involving the formation of advanced epoxy adhesives with better formulations and the development of FRP systems that are more thermally stable to improve the high-temperature performance of AFRP and BFRP.

Figure 1.
SEM images of the fracture surface of (a) AFRP-S-25; (b) AFRP-S-300; (c) BFRP-S-25; (d) BFRP-S-300; (e) CFRP-S-25; and (f) CFRP-S-300 [].
Recently, Kalyni et al. [] studied the behavior of CFRP, GFRP, and stainless-steel wire mesh (SSWM), along with the behavior of two types of epoxy adhesives (Sikadur 30 LP and Sikadur 330) at elevated temperatures. Concretely, the main results of the tests were that both CFRP and GFRP had huge losses in tensile strength beyond 200 °C. In contrast, SSWM depicted a small drop in tensile strength of only 5–8% up until the temperature of 500 °C. For the epoxy adhesives, Sikadur 330 had a fairly large weight loss and degradation above 200 °C, whereas Sikadur 30 LP showed better performance and therefore seemed to be more suitable for high-temperature applications. Their study concluded that SSWM, in combination with Sikadur 30 LP, offers an excellent solution to raise the strengthening of concrete structures exposed to elevated temperatures through improved thermal resistance.
2.2. The Behavior of FRP Bonded with Cementitious Adhesives
Hashemi et al. [] proposed a study that investigated the flexural performance of (RC) beams strengthened with (CFRP) textiles using cement-based adhesives at high temperatures. The control RC beam sustained the service load up to 876 °C before failure by steel yielding, similar to ambient conditions. Their study concluded that epoxy adhesive performed poorly, with CFRP debonding at relatively low temperatures around 400 °C. The epoxy-bonded CFRP beams failed at 428–496 °C because of explosive concrete spalling and CFRP debonding, while the cement-based mortar-bonded CFRP textile failed at 846–855 °C, nearly the same as the control RC beam but at a 40% higher service load, indicating the CFRP contribution. Moreover, it was mentioned that the presence of anchorage did not significantly improve the high-temperature performance, as failure was initiated by debonding at high-moment mid-span regions, as shown in Figure 2.

Figure 2.
CFRP debonding at mid-span [].
A developed innovative insulating cementitious adhesive was investigated by Widanage C et al. [], known as modified Engineered Cementitious Composite (ECC), which is used to bond CFRP fabrics to concrete surfaces. This novel ECC is modified with locally sourced materials, including fly ash, silica sand, and polyethylene terephthalate (PET) fibers, to enhance thermal insulation properties compared with traditional epoxy adhesives. The adhesive was formulated using a mix of ordinary Portland cement, silica sand, class F fly ash, water, and PET fibers, achieving a specific mix proportion of cement to fly ash to silica sand to water of 1:1.2:0.8:0.85 by weight, with PET fibers comprising 2% of the cement volume. This composition yielded a PET-ECC with notably low thermal conductivity, ranging between 0.145 and 0.180 W/mK. The application process involved two 5 mm thick layers of PET-ECC, one layer for bonding the CFRP to the concrete and a second layer over the CFRP for additional insulation. The PET-ECC demonstrated significant material properties, including a compressive strength of 16.97 MPa, tensile strength of 1.47 MPa, and flexural strength of 5.34 MPa at 28 days, which surpassed the performance of ECCs incorporating polyvinyl alcohol (PVA) fibers from previous studies. Regarding bond characteristics, the PET-ECC exhibited an effective bond length of 125 mm with a bond strength of 224.9 MPa in its unmodified form. Furthermore, the bond strength was significantly enhanced to 570.28 MPa when river sand was bonded to the CFRP with epoxy before the application of the PET-ECC. Concrete columns reinforced with the PET-ECC/CFRP system showed a 34% increase in strength, although this was less than the 147% increase observed with epoxy bonding. The findings suggested that the insulating PET-ECC adhesive held considerable potential for improving CFRP strengthening of concrete structures, with further optimization needed to enhance the bond between concrete and PET-ECC.
Wang et al. [] discussed the residual bond performance of CFRP reinforcements bonded to concrete interfaces using both epoxy and cement-based adhesives after exposure to elevated temperatures. In their research, twelve groups of concrete beams strengthened with CFRP sheets and grids using different adhesives, epoxy resin, and two cement-based adhesives, that is, a polymer cement mortar and an engineered cementitious composite, were tested. These samples were tested under temperatures from 20 °C to 600 °C for three-point monotonic bending. The key findings of their study were as follows. Firstly, the beams changed from debonding, with a thin layer of concrete substrate at lower temperatures, to debonding near the fiber–adhesive interface and the tearing of CFRP grids from the ECC matrix at higher temperatures. Secondly, for beams strengthened with cement-bonded CFRP grids, peak loads were found to be at least 50% higher when compared with an epoxy bond, thus performing better under increased temperatures. Thirdly, the results showed that high temperature caused severe degradation of mechanical performances for the epoxy-bonded system, more so above the glass transition temperature (Tg) of the epoxy resin. Finally, compared with the epoxy systems, the cement-based systems, mainly for those using PCM, maintained higher residual bond strengths after thermal exposure. Thus, PCM was considered a more efficient adhesive for fire-resistant CFRP strengthening.
3. Proposed Bond–Slip Models
Dai et al. [] proposed a bond–slip model based on single-lap shear tests of FRP laminates externally bonded to concrete at elevated temperatures up to 120 °C, accounting for thermal degradation and residual stresses. The nonlinear temperature-dependent local bond–slip model was developed for FRP-to-concrete interfaces based on a thorough investigation of previously published experimental data in the literature consisting of 79 tests. The investigated temperatures ranged from 4 °C to 180 °C. This model is an extension of the bond–slip model with two parameters that were first proposed for FRP-to-concrete contacts at room temperature by Dai et al. []. Regression analysis of available test data at elevated temperatures was used to determine the following important parameters used in the bond–slip model: the interfacial brittleness index B (a shape parameter for the bond–slip curve) and the interfacial fracture energy Gf (i.e., the area beneath the bond–slip curve). The model is illustrated by Equations (4) and (5).
where τ is the bond stress at location x, δ is the slip, is the ultimate load, , are the elastic modulus of the FRP laminate and concrete, tp and bp are the thickness and the width of the laminate, and tc and bc are the thickness and the width of the concrete prism.
Once the value Gf is known, the value of B was obtained from least-squares regression analysis of the experimental relationship between the pull-out load and the local slip at the loaded end or from stain distribution curves that were reported in most of the studies. The strains were measured at different load levels (Pi, i = 1, …, m) at n number strain gauge locations on the FRP laminate. The predicted theoretical strain was calculated by Equation (6).
where , L is the bond length, and is the temperature variation.
The interfacial brittleness index B also showed a decreasing trend, but the decrease was almost complete before reaching the glass transition temperature. It was demonstrated that the interfacial fracture energy Gf was initially almost constant but began to decrease as the temperature approached the glass transition temperature.
Arruda et al. [] proposed a numerical model to simulate the bond behavior between concrete and externally bonded CFRP laminates at elevated temperatures. The numerical model was based on the cohesive zone model (CZM) approach and was implemented using the finite element method.
The bond stress–slip relationship was defined by the following bilinear traction-separation law (Equation (7)):
where τ is the bond stress, τmax is the maximum bond stress, δ is the slip, δ0 is the slip corresponding to τmax, and δf is the slip at complete debonding.
The maximum bond stress τmax at elevated temperatures was modeled using the following exponential decay function (Equation (8)):
where τmax(T) is the maximum bond stress at temperature T, τmax(20 °C) is the maximum bond stress at 20 °C, and αT is an empirical parameter determined from experimental data.
The fracture energy Gf, which represents the area under the traction-separation curve, was also modeled as a function of temperature (Equation (9)) as follows:
where Gf(T) is the fracture energy at temperature T, Gf(20 °C) is the fracture energy at 20 °C, and αG is an empirical parameter determined from experimental data.
Their study validated the numerical model using experimental data from double-shear pull-out tests at different temperatures. The model showed good agreement with the experimental results, capturing the reduction in bond strength and bond stiffness at elevated temperatures. Bond–slip laws were proposed for both near-surface mounted (NSM) and externally bonded reinforcement (EBR) strengthening techniques. It exhibited consistent reductions in stiffness and maximum shear stress with increasing temperature, aligning closely with experimental findings. Stiffness reductions with temperature were similar for both techniques and correlated with the variation experienced by the adhesive storage modulus. This confirmed a strong dependence of CFRP-concrete interface stiffness on adhesive behavior at elevated temperatures.
The maximum shear stress reduction with temperature was lower for the NSM specimens compared with their EBR counterparts. However, it remained notably above the corresponding values of the adhesive storage modulus, indicating considerable bond performance even after the glass transition process. Residual bond performance in NSM may also have been attributed to friction forces at interfaces. Moreover, the proposed bond–slip laws showed excellent agreement between the numerical results and experimental data, accurately simulating observed failure modes. A linear elastic model could be adopted for concrete at elevated temperatures to reduce computational costs. These laws, calibrated for typical FRP strengthening systems, applied to similar systems used in their study. They were also successfully applied to simulate the fire resistance behavior of CFRP-strengthened RC beams, demonstrating accurate prediction of midspan deflection evolution and debonding instant.
Leone et al. [] investigated the effect of elevated service temperatures (up to 60 °C) on the bond behavior of externally bonded FRP systems to concrete. The researchers conducted double-shear pull-out tests and proposed a bond stress-slip model based on their experimental data. Their model is illustrated in Equation (10).
where τ is the bond stress, τmax is the maximum bond stress, s is the slip, s0 is the slip corresponding to τmax, and α and β are empirical parameters determined experimentally.
Their study found that both the maximum bond stress and the bond stiffness decreased with increasing temperature, and the proposed model accurately captured the bond stress–slip behavior at different temperatures.
A simplified analytical solution was proposed by Dong et al. [] to derive a two-parameter bond–slip relationship in joints with the help of parameters calculated from the strength and stiffness of the CFRP–concrete interface. In their paper, simplified formulas were developed to predict the peak load and the load–slip relationship, considering the impacts of bond length and free-end slip. Regression analysis of the existing test data indicated that the normalized bond property at high temperature was a function of the temperature difference between service temperature and glass transition temperature of the adhesive, Tg. Because of some scatter, the model proposed in the bonding strength with temperature had fairly good agreement with experimental data. Their paper confirmed the previous findings that there is a dramatic reduction in bond strength. The bond–slip relationship is given by Equation (11).
where A and B are key parameters that govern the shape of the bond–slip curve. Additionally, the proposed temperature-dependent bond strength model is represented by Equation (12):
where ηt is the variation coefficient of the bond strength, τmax(T) is the maximum bond stress at temperature T, and τmax(20 °C) is the maximum bond stress at temperature 20 °C.
Jia D et al. [] proposed a closed-form analytical solution for predicting the full-range deformation behavior of FRP–concrete bonded joints under different thermal conditions. Whereas available studies relate to local bond slip and changes in properties with temperature, Jia’s study dealt with the first comprehensive thermal stress analysis to isolate and quantify, analytically, the effects of interfacial thermal stress from intrinsic changes in material properties due to temperature variation. This distinction was predicted to permit a more precise understanding of the bond behavior and the interfacial fracture energy of FRP–concrete joints (Equations (13)–(15)).
where D, n1, and n2 are constants defined by boundary conditions and material properties. Load capacity prediction is described in Equation (16) as follows:
The obtained analytical solutions were validated in great detail with corresponding experimental and numerical values. Moreover, the versatility of the analytical solution was illustrated through its application to different types of bonded joints, such as those involving steel, rock, or masonry substrates, making it applicable to a wide range of structural contexts.
Another recent bond–slip model proposed by [] was characterized by three stages as follows: the initial elastic, the nonlinear inelastic, and the final ultimate failure stage. In the initial elastic stage, the ultimate slip was within the elastic portion of the curve. This linear relationship characterized the early behavior of the bond plane when the CFRP and concrete are initially loaded. As the applied load increased, the bond behavior entered a non-linear inelastic stage. At this stage, the bond stress continued to increase at a decreasing rate because of the degradation in bond strength and stiffness. The non-linear model was expressed as a function of bond stress (τ), similar to previous models, with the slip corresponding to the peak bond stress as a key factor. Additionally, the parameter “n” was used to control the shape of the bond-slip curve (refer to Equations (17)–(20)).
where
Similar to previous proposed models, the coefficients A and B were determined through a curve fitting of experimental data.
The complicated interactions at the interface and the reducing bond degradation with increasing slip were determined with this equation. Ultimately, at the bond critical state, an appreciable fall in the bond strength that finally led to the failure of the bond system was reached. The model conceptualized this as the assumption that at a slip greater than the ultimate slip, a complete failure of load transfer occurred between the CFRP and concrete. This was the point at which the bond failed. The constants were influenced by material properties as well as bonding configurations. This non-linearity in the model allowed flexibility and accuracy features, which can describe the behavior of the bond and capture the full range of bond responses due to initial loading to failure. Such a very wide, generic theoretical framework as presented before is of key interest not just for design but for the analysis of CFRP-strengthened concrete structures, whose predictability and safety must be guaranteed under service in any kind of environment.
Recently, a study by Wang Y. et al. [] provided analytical solutions considering the thermal effects on CFRP-to-concrete/steel interface debonding response under thermomechanical loading. The proposed solution accounted for arbitrary bond lengths and interfacial friction. These two aspects were not included in previous models. The basic assumptions on which the analysis was based concerned uniform thermal expansion, and shear deformation at the interface, and it used a bond–slip trilinear model, which included the whole debonding process, as shown in the proposed Equations (21) and (22).
Numerical results were presented to validate the proposed solution using experimental data and demonstrate the efficiency of the proposed solution as a coupled thermal–mechanical tool to capture the thermal effects of debonding. These effects were highly dependent on the bond length, and, in both tests and analyses, their magnitudes increased with increased thickness and rigidity of the CFRP. The effective bond length concept introduced a change in the effective length with a change in temperature. The proposed load–slip presented in Equation (23).
Table 2 provides a comprehensive overview of the key bond-slip models, including their key features, advantages, and potential shortcomings.

Table 2.
Summary of the key bond–slip models in the literature.
4. Machine Learning Models
Many individuals in the field of engineering have embraced the use of machine learning (ML) models for a range of purposes. One significant advantage of employing ML models is their ability to simplify and streamline tasks. In this context, a Random Forest ML model was applied to forecast the bond strength of beams. The effectiveness of ML has proven to be remarkable in enhancing the accuracy and expediting the prediction process through an efficient methodology. The dataset used to train the machine learning model was gathered from various studies, as detailed in Table A1 (Appendix A). The sources of the data were a compilation of research works focus [,,,,].
The dataset contains key variables such as the modulus of elasticity of the FRP (Ef) in GPa, width of the FRP sheet (bf) in mm, thickness of the FRP sheet (tf) in mm, glass transition temperature Tg (°C), test temperature in °C, and bonded length (L) in mm. The data is listed in Appendix A. These variables were selected because of their established influence on bond strength in FRP-reinforced beams. Examining the distribution of these variables through accompanying count plots (Figure 3) reveals the diversity within the data. The figure shows variations in the mentioned properties. Moreover, Figure 4 shows the correlation matrix, which illustrates the interconnections between these variables and the target variable, the bond strength (τmax). Interestingly, the thickness and glass transition temperature exhibit high positive correlations with the target variable, while the elastic modulus and the width show significant negative correlations. These insights guided the selection of features for inclusion in the machine learning model. All those correlations were considered for the regression model created in this research, which had an R of 0.86. Developing the model required normalization and division into training and testing sets. Additionally, cross-validation with five folds was implemented on the dataset because of its small size, which ensures robust model performance. Random Forest, an interpretable machine learning technique, was utilized to analyze and quantify the connection between input features and bond strength. Several algorithms were considered, but Random Forest was selected for its robustness and ability to handle complex relationships between features while avoiding overfitting, especially with smaller datasets. The model was built using the default hyperparameters of the Random Forest Regressor, which includes 100 estimators and no restrictions on tree depth. No explicit hyperparameter tuning was applied in this case. The model underwent training and validation to guarantee accuracy across various data representations. Cross-validation with five folds was used to ensure robust model performance, as the dataset was small. This method ensured that the model’s performance was validated across multiple data subsets, leading to reliable and generalized results. The comparison between the predicted and actual values of both the training and testing datasets can be seen in Figure 5, which shows how the current model performs. The final model achieved an R of 0.86, demonstrating high predictive accuracy. This comparison shows that the Random Forest model generalizes well, supporting its effectiveness in predicting bond strength accurately.
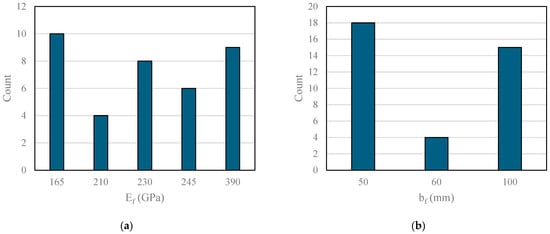
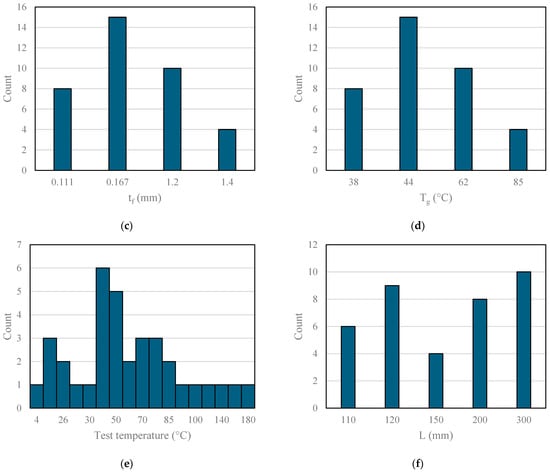
Figure 3.
Distribution of the collected data including the following: (a) Ef (GPa); (b) bf (mm); (c) tf (mm); (d) Tg (°C); (e) test temperature (°C); and (f) L (mm).
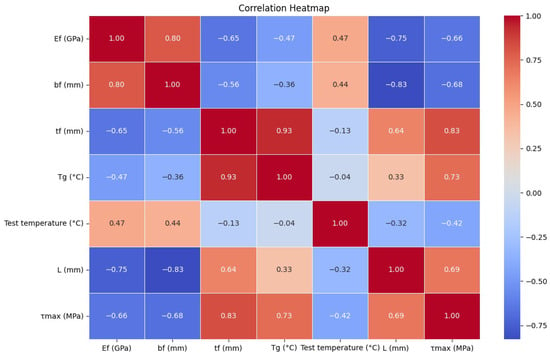
Figure 4.
Correlation matrix.
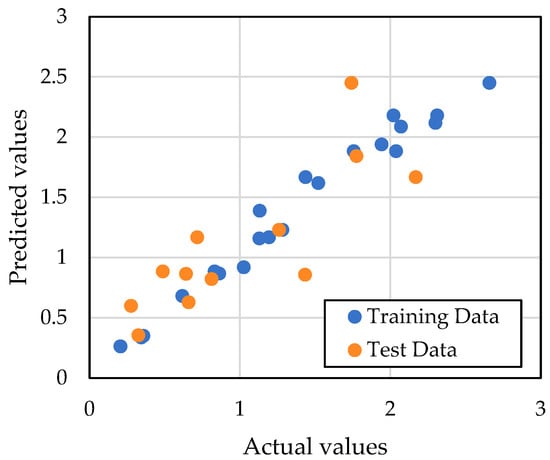
Figure 5.
Predicted versus actual values of the training and test data in the Random Forest ML model.
Apart from constructing the model, a detailed study was conducted to assess the model’s abilities under certain conditions. This investigation focused on changing test temperatures between 20 and 300 °C while keeping all factors constant. A research study was conducted with an FRP sheet length of 200 mm and a base width of 50 mm. This study examined how the bond strength (τmax) is affected by varying test temperatures. The findings are shown in Figure 6 as test temperature versus bond strength. This figure shows how bond strength is affected by changes in test temperature. The graphs illustrate the connection between increasing test temperatures and the corresponding predicted bond strength, showcasing the model’s ability to replicate real-world scenarios and optimize material properties and testing procedures. By leveraging an efficient machine learning model for predicting and streamlining bond strength estimates, it becomes clear that the accuracy of estimating bond strength can be significantly improved with data and enhanced machine learning models that can capture diverse trends among variables. This highlights an opportunity for research that could benefit from leveraging machine learning technology, leading to precise and dependable predictions in upcoming studies.
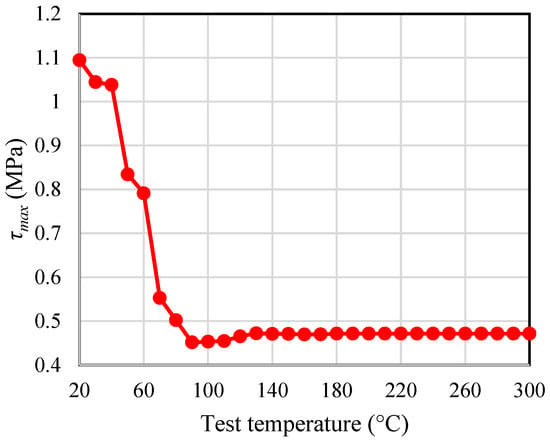
Figure 6.
Parametric study results: L = 200 mm and bf = 50.
5. Conclusions and Gaps in the Literature
This literature review demonstrated the effects of elevated temperatures on bond behavior between FRP materials and concrete substrates. It was verified that exposure to high temperatures could greatly decrease the bond strength, especially above the epoxy adhesive glass transition temperature. However, it has been reported that cement-based bonding adhesives have proved better than normal epoxy adhesives under raised temperatures, which are able to retain higher residual bond strengths. Such deterioration of the FRP–concrete bond at high temperatures may be attributed to a number of factors, which include differential thermal expansion coefficients, thermal incompatibility stresses, and chemical decomposition of the polymer matrix and adhesive. Moreover, the application of a machine learning model to predict the bond strength of FRP-reinforced concrete beams at elevated temperatures showed great potential. The R-squared was 0.86; hence, the predictive ability was great. The model captured the interaction effects of different input parameters on bond strength efficiently enough in this complex relationship. This approach is a promising alternative to extensive experimental testing. Thus, it may eventually reduce the time and effort required to estimate bond strength under different temperature conditions in future studies.
Despite the extensive research conducted on the bond behavior of FRP-–concrete systems under high temperatures, significant gaps in knowledge persist. The following are some of these gaps:
- There are limited models for the FRP–concrete bond behavior under high temperatures. The development and validation of an extensive bond–slip model under high temperatures incorporating temperature-dependent properties of FRPs and adhesives are needed.
- The work performed in the literature is insufficient regarding the long-term performance and life of adhesives at elevated temperatures.
- In most of the previous works, researchers focus on specific scenarios or materials; the vast majority of the experimental campaigns are conducted for CFRP-strengthened beams. This has created an evident lack of general experimental research works covering a wide range of other FRP materials. It would be useful to have detailed studies concerning different types of FRP and adhesives so that their particular behavior under high-temperature conditions could be understood and appropriate materials could be selected for a whole range of applications.
- Some studies consider thermal effects on mechanical properties but, generally, no deep discussions concerning micro-mechanisms of bond failure are performed. Researching the micro-mechanisms of bond failure under thermal stress with state-of-the-art imaging and analytical techniques is desirable.
- Regarding real-world application scenarios, most studies are conducted under a highly controlled laboratory setup, accounting just for mere simulation in real applications. Real case application scenarios should be established and validated by case studies, followed by model adjustment as per the results.
6. Recommendations
- Identify advanced tools for analysis that will be used to investigate microstructural change and failure mechanisms of FRP–concrete bonds under elevated temperatures, such as digital image correlation, scanning electron microscopy, and X-ray diffraction.
- Field studies, inclusive of real-life case studies of the application of FRPs in concrete structures in elevated temperature conditions, could become very instrumental with valuable insights and important empirical data for consideration in the refinement of theoretical models and results of experiments.
- Newer developments in materials, such as nanocomposites or advanced epoxy formulations, have huge potential for improving the durability of FRP composites at higher temperatures. In contrast, additional research work is still needed to develop models for the prediction of service life with accuracy by considering multiple factors of bond degradation in real-world conditions.
- Standard test methods and guidelines should be developed for adoption in the evaluation of the bond performance of FRP–concrete systems at elevated temperatures. This will help provide consistency and reliability in research findings on the derived values for practical applications.
Author Contributions
Conceptualization, A.S. and R.H.; methodology, A.S. and R.H.; software, H.S.; validation, A.S. and M.A.; formal analysis, H.S.; investigation, A.S. and H.S.; resources, R.H. and J.A.; data curation, A.S.; writing—original draft preparation, A.S.; writing—review and editing, M.A.; visualization, A.S. and H.S.; supervision, R.H. and J.A.; project administration, R.H. and J.A.; funding acquisition, R.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within this article.
Acknowledgments
This research was funded by the American University of Sharjah and Riad T. Sadek Endowed Chair in Civil Engineering. The support is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Collected data.
Table A1.
Collected data.
| Specimen Code * | Ef (GPa) | bf (mm) | tf (mm) | Tg (°C) | Test Temperature (°C) | L (mm) | τmax (MPa) |
|---|---|---|---|---|---|---|---|
| B1-20 | 165 | 50 | 1.2 | 62 | 20 | 300 | 1.757 |
| B1-40 | 165 | 50 | 1.2 | 62 | 40 | 300 | 1.7416 |
| B1-50 | 165 | 50 | 1.2 | 62 | 50 | 300 | 2.3115 |
| B1-70 | 165 | 50 | 1.2 | 62 | 70 | 300 | 2.1695 |
| B1-80 | 165 | 50 | 1.2 | 62 | 80 | 300 | 1.7753 |
| B2-20 | 165 | 50 | 1.2 | 62 | 20 | 300 | 2.0382 |
| B2-40 | 165 | 50 | 1.2 | 62 | 40 | 300 | 2.6586 |
| B2-50 | 165 | 50 | 1.2 | 62 | 50 | 300 | 2.0212 |
| B2-70 | 165 | 50 | 1.2 | 62 | 70 | 300 | 1.4361 |
| B2-90 | 165 | 50 | 1.2 | 62 | 90 | 300 | 1.1315 |
| O-26 | 230 | 50 | 0.111 | 38 | 26 | 200 | 1.2606 |
| O-30 | 230 | 50 | 0.111 | 38 | 30 | 200 | 1.1301 |
| O-40 | 230 | 50 | 0.111 | 38 | 40 | 200 | 0.7165 |
| O-50 | 230 | 50 | 0.111 | 38 | 50 | 200 | 0.4874 |
| T-26 | 230 | 50 | 0.111 | 38 | 26 | 200 | 1.283 |
| T-40 | 230 | 50 | 0.111 | 38 | 40 | 200 | 1.194 |
| T-50 | 230 | 50 | 0.111 | 38 | 50 | 200 | 0.8323 |
| T-60 | 230 | 50 | 0.111 | 38 | 60 | 200 | 0.6427 |
| T-SL20 | 210 | 60 | 1.4 | 85 | 20 | 150 | 1.5213 |
| T-SL70 | 210 | 60 | 1.4 | 85 | 70 | 150 | 1.9423 |
| T-SL80 | 210 | 60 | 1.4 | 85 | 80 | 150 | 2.0705 |
| T-SL85 | 210 | 60 | 1.4 | 85 | 85 | 150 | 2.2996 |
| CS-4 | 390 | 100 | 0.167 | 44 | 4 | 120 | 1.0261 |
| CS-40 | 390 | 100 | 0.167 | 44 | 40 | 120 | 1.4335 |
| CS-60 | 390 | 100 | 0.167 | 44 | 60 | 120 | 0.6594 |
| CS-80 | 390 | 100 | 0.167 | 44 | 80 | 120 | 0.3251 |
| CS-100 | 390 | 100 | 0.167 | 44 | 100 | 120 | 0.345 |
| CS-120 | 390 | 100 | 0.167 | 44 | 120 | 120 | 0.3593 |
| CS-140 | 390 | 100 | 0.167 | 44 | 140 | 120 | 0.3478 |
| CS-160 | 390 | 100 | 0.167 | 44 | 160 | 120 | 0.342 |
| CS-180 | 390 | 100 | 0.167 | 44 | 180 | 120 | 0.3506 |
| ZS-27 | 245 | 100 | 0.167 | 44 | 27 | 110 | 0.8627 |
| ZS-40 | 245 | 100 | 0.167 | 44 | 40 | 110 | 0.8121 |
| ZS-50 | 245 | 100 | 0.167 | 44 | 50 | 110 | 0.6178 |
| ZS-65 | 245 | 100 | 0.167 | 44 | 65 | 110 | 0.2769 |
| ZS-85 | 245 | 100 | 0.167 | 44 | 85 | 110 | 0.2061 |
| ZS-110 | 245 | 100 | 0.167 | 44 | 110 | 110 | 0.2076 |
* Note: Specimen B1-# and B2-# were offered by Klamer [], respectively, for ordinary concrete specimens and high-strength concrete specimens. Specimen O-# and T-# were offered by Wu Zhishen [], respectively, for ordinary epoxy specimens and Thermo-resistance epoxy specimens. Specimen T-SL# was offered by Camate [], CS-# was offered by Cai [], and ZS-# was offered by Zhao [].
References
- Ferracuti, B.; Savoia, M.; Mazzotti, C. Interface law for FRP-concrete delamination. Compos. Struct. 2007, 80, 523–531. [Google Scholar] [CrossRef]
- Shier, G. Flexural Behaviour of Fibre Reinforced Polymer Strengthened Reinforced Concrete Beams at Elevated Temperatures; Library and Archives Canada = Bibliothèque et Archives Canada: Ottawa, ON, Canada, 2014. [Google Scholar]
- Correia, J.R.; Gomes, M.M.; Pires, J.M.; Branco, F.A. Mechanical behaviour of pultruded glass fibre reinforced polymer composites at elevated temperature: Experiments and model assessment. Compos. Struct. 2013, 98, 303–313. [Google Scholar] [CrossRef]
- Bazli, M.; Abolfazli, M. Mechanical properties of fibre reinforced polymers under elevated temperatures: An overview. Polymers 2020, 12, 2066. [Google Scholar] [CrossRef]
- Sharifianjazi, F.; Zeydi, P.; Bazli, M.; Esmaeilkhanian, A.; Rahmani, R.; Bazli, L.; Khaksar, S. Fibre-Reinforced Polymer Reinforced Concrete Members under Elevated Temperatures: A Review on Structural Performance. Polymers 2022, 14, 472. [Google Scholar] [CrossRef]
- Haddad, R.H.; Al-Rousan, R.; Almasry, A. Bond-slip behavior between carbon fiber reinforced polymer sheets and heat-damaged concrete. Compos. B Eng. 2013, 45, 1049–1060. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Assad, M.A.; Abdalla, J.A.; Naser, M.Z. Finite element modeling of reinforced concrete beams externally bonded with PET-FRP laminates. Comput. Concr. 2024, 33, 163–173. [Google Scholar] [CrossRef]
- Hawileh, R.; Abdalla, J.; Thomas, B.S.; Bahurudeen, P.H.D.B.; Jittin, V.; Syed, K.I.; Kabeer, A.; Hadi, M.; Abu-Obeidah, A. Influence of Synthesized Nanomaterials on the Strength and Durability of Cementitious Composites; Manuscript Draft-Powered by Editorial Manager® and ProduXion Manager® from Aries Systems Corporation; Aries Systems Corporation: North Andover, MA, USA, 2023. [Google Scholar]
- Hawileh, R.A.; Abu-Obeidah, A.; Abdalla, J.A.; Al-Tamimi, A. Temperature effect on the mechanical properties of carbon, glass and carbon-glass FRP laminates. Constr. Build. Mater. 2015, 75, 342–348. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Rasheed, H.A.; Abdalla, J.A.; Al-Tamimi, A.K. Behavior of reinforced concrete beams strengthened with externally bonded hybrid fiber reinforced polymer systems. Mater. Des. 2014, 53, 972–982. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Abdalla, J.A.; Hasan, S.S.; Ziyada, M.B.; Abu-Obeidah, A. Models for predicting elastic modulus and tensile strength of carbon, basalt and hybrid carbon-basalt FRP laminates at elevated temperatures. Constr. Build. Mater. 2016, 114, 364–373. [Google Scholar] [CrossRef]
- Firmo, J.P.; Correia, J.R.; Pitta, D.; Tiago, C.; Arruda, M.R.T. Experimental characterization of the bond between externally bonded reinforcement (EBR) CFRP strips and concrete at elevated temperatures. Cem. Concr. Compos. 2015, 60, 44–54. [Google Scholar] [CrossRef]
- Firmo, J.P.; Roquette, M.G.; Correia, J.R.; Azevedo, A.S. Influence of elevated temperatures on epoxy adhesive used in CFRP strengthening systems for civil engineering applications. Int. J. Adhes. Adhes. 2019, 93, 102333. [Google Scholar] [CrossRef]
- Zhang, Y.; Vassilopoulos, A.P.; Keller, T. Effects of low and high temperatures on tensile behavior of adhesively-bonded GFRP joints. Compos. Struct. 2010, 92, 1631–1639. [Google Scholar] [CrossRef]
- Di Tommaso, A.; Neubauer, U.; Pantuso, A.; Rostasy, F.S. Behavior of Adhesively Bonded Concrete-CFRP Joints at Low and High Temperatures. Mech. Compos. Mater. 2001, 37, 327–338. [Google Scholar] [CrossRef]
- Biscaia, H.C. The influence of temperature variations on adhesively bonded structures: A non-linear theoretical perspective. Int. J. Non-Linear Mech. 2019, 113, 67–85. [Google Scholar] [CrossRef]
- Jadooe, A.; Al-Mahaidi, R.; Abdouka, K. Bond Behavior between NSM CFRP Strips and Concrete Exposed to Elevated Temperature Using Cement-Based and Epoxy Adhesives. J. Compos. Constr. 2017, 21, 04017033. [Google Scholar] [CrossRef]
- Arruda, M.R.T.; Firmo, J.P.; Correia, J.R.; Tiago, C. Numerical modelling of the bond between concrete and CFRP laminates at elevated temperatures. Eng. Struct. 2016, 110, 233–243. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W.; Liu, C.; Li, N. Bond Performance of CFRP/Steel Double Strap Joint at Elevated Temperatures. Sustainability 2022, 14, 15537. [Google Scholar] [CrossRef]
- Gamage, J.C.P.H.; Al-Mahaidi, R.; Wong, M.B. Bond characteristics of CFRP plated concrete members under elevated temperatures. Compos. Struct. 2006, 75, 199–205. [Google Scholar] [CrossRef]
- Ferrier, E.; Rabinovitch, O.; Michel, L. Mechanical behavior of concrete–resin/adhesive–FRP structural assemblies under low and high temperatures. Constr. Build. Mater. 2016, 127, 1017–1028. [Google Scholar] [CrossRef]
- He, J.; Xian, G.; Zhang, Y.X. Effect of moderately elevated temperatures on bond behaviour of CFRP-to-steel bonded joints using different adhesives. Constr. Build. Mater. 2020, 241, 118057. [Google Scholar] [CrossRef]
- Ahmed, A.; Rahman, M.Z.; Ou, Y.; Liu, S.; Mobasher, B.; Guo, S.; Zhu, D. A review on the tensile behavior of fiber-reinforced polymer composites under varying strain rates and temperatures. Constr. Build. Mater. 2021, 294, 123565. [Google Scholar] [CrossRef]
- Foster, S.K.; Bisby, L.A. High Temperature Residual Properties of Externally-Bonded FRP Systems. In Proceedings of the 7th International Symposium on Fiber Reinforced Polymer Reinforcement for Reinforced Concrete Structures (FRPRCS-7), Kansas City, MO, USA, 6–9 November 2005. [Google Scholar]
- Li, Y.; Liu, X.; Wu, M. Mechanical properties of FRP-strengthened concrete at elevated temperature. Constr. Build. Mater. 2017, 134, 424–432. [Google Scholar] [CrossRef]
- Mikami, C.; Wu, H.C.; Elarbi, A. Effect of hot temperature on pull-off strength of FRP bonded concrete. Constr. Build. Mater. 2015, 91, 180–186. [Google Scholar] [CrossRef]
- Dai, J.-G.; Gao, W.Y.; Teng, J.G. Bond-slip model for FRP laminates externally bonded to concrete at elevated temperature. J. Compos. Constr. 2013, 17, 217–228. [Google Scholar] [CrossRef]
- Al-Shawaf, A.; Al-Mahaidi, R.; Zhao, X.L. Effect of elevated temperature on bond behaviour of high modulus CFRP/steel double-strap joints. Aust. J. Struct. Eng. 2009, 10, 63–74. [Google Scholar] [CrossRef]
- Zhou, A.; Qiu, Q.; Chow, C.L.; Lau, D. Interfacial performance of aramid, basalt and carbon fiber reinforced polymer bonded concrete exposed to high temperature. Compos. Part A Appl. Sci. Manuf. 2020, 131, 105802. [Google Scholar] [CrossRef]
- Selvaratnam, A.; Gamage, J.C.P.H. A Review on Thermo-mechanical Behaviour of CFRP-Concrete Composites at Elevated Temperature and Available Insulation Systems. Lect. Notes Civ. Eng. 2021, 94, 533–541. [Google Scholar] [CrossRef]
- Assad, M.; Hawileh, R.A.; Abdalla, J.A. Modeling the behavior of CFRP-strengthened RC slabs under fire exposure. Procedia Struct. Integr. 2022, 42, 1668–1675. [Google Scholar] [CrossRef]
- Gao, W.Y.; Teng, J.G.; Asce, M.; Dai, J.-G. Effect of Temperature Variation on the Full-Range Behavior of FRP-to-Concrete Bonded Joints. J. Compos. Constr. 2012, 16, 671–683. [Google Scholar] [CrossRef]
- Moussa, O.; Vassilopoulos, A.P.; De Castro, J.; Keller, T. Time-temperature dependence of thermomechanical recovery of cold-curing structural adhesives. Int. J. Adhes. Adhes. 2012, 35, 94–101. [Google Scholar] [CrossRef]
- Tatar, J.; Milev, S. Durability of externally bonded fiber-reinforced polymer composites in concrete structures: A critical review. Polymers 2021, 13, 765. [Google Scholar] [CrossRef] [PubMed]
- Firmo, J.P.; Correia, J.R.; França, P. Fire behaviour of reinforced concrete beams strengthened with CFRP laminates: Protection systems with insulation of the anchorage zones. Compos. B Eng. 2012, 43, 1545–1556. [Google Scholar] [CrossRef]
- Firmo, J.P.; Correia, J.R.; Bisby, L.A. Fire behaviour of FRP-strengthened reinforced concrete structural elements: A state-of-the-art review. Compos. B Eng. 2015, 80, 198–216. [Google Scholar] [CrossRef]
- Chowdhury, E.U.; Eedson, R.; Bisby, L.A.; Green, M.F.; Benichou, N. Mechanical Characterization of Fibre Reinforced Polymers Materials at High Temperature. Fire Technol. 2011, 47, 1063–1080. [Google Scholar] [CrossRef]
- Selvaratnam, A.; Arachchi, K.A.D.Y.T.K.; Gamage, J.C.P.H.; Attanayake, V. Investigation on an effective bond arrangement of insulated CFRP-strengthened flexural members for improved thermo-mechanical performance. Case Stud. Constr. Mater. 2021, 14, e00544. [Google Scholar] [CrossRef]
- Liu, K. Analytical study on bond characterization of hybrid-bonded FRP to concrete interfaces. Appl. Mech. Mater. 2013, 405–408, 2528–2533. [Google Scholar] [CrossRef]
- Yu, B.; Kodur, V.K.R. Effect of high temperature on bond strength of near-surface mounted FRP reinforcement. Compos. Struct. 2014, 110, 88–97. [Google Scholar] [CrossRef]
- Dai, J.; Ueda, T.; Sato, Y. Development of the Nonlinear Bond Stress–Slip Model of Fiber Reinforced Plastics Sheet–Concrete Interfaces with a Simple Method. J. Compos. Constr. 2005, 9, 52–62. [Google Scholar] [CrossRef]
- Blontrock, H.; Taerwe, L.; Vanwalleghem, H. Bond testing of externally glued FRP laminates at elevated temperatures. In Proceedings Bond in Concrete-From Research to Standards; Ghent University: Ghent, Belgium, 2002; pp. 648–654. [Google Scholar]
- Guo, D.; Liu, Y.L.; Gao, W.Y.; Dai, J.G. Bond behavior of CFRP-to-steel bonded joints at different service temperatures: Experimental study and FE modeling. Constr. Build. Mater. 2023, 362, 129836. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Naser, M.; Zaidan, W.; Rasheed, H.A. Modeling of insulated CFRP-strengthened reinforced concrete T-beam exposed to fire. Eng. Struct. 2009, 31, 3072–3079. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Bisby, L.A. Evaluation of Fire Endurance of Concrete Slabs Reinforced with Fiber-Reinforced Polymer Bars. J. Struct. Eng. 2005, 131, 34–43. [Google Scholar] [CrossRef]
- Bhatt, P.P.; Kodur, V.K.R.; Shakya, A.M.; Alkhrdaji, T. Performance of insulated FRP-strengthened concrete flexural members under fire conditions. Front. Struct. Civ. Eng. 2021, 15, 177–193. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, G.; Zhang, L.; Zhang, J.; Hui, D. Experimental study on the fire resistance of RC beams strengthened with near-surface-mounted high-Tg BFRP bars. Compos. B Eng. 2014, 60, 680–687. [Google Scholar] [CrossRef]
- Saafi, M. Effect of Fire on FRP Reinforced Concrete Members. Compos. Struct. 2002, 58, 11–20. [Google Scholar] [CrossRef]
- Maraveas, C.; Miamis, K.; Vrakas, A.A. Fiber-reinforced polymer-strengthened/reinforced concrete structures exposed to fire: A review. Struct. Eng. Int. J. Int. Assoc. Bridge Struct. Eng. (IABSE) 2012, 22, 500–513. [Google Scholar] [CrossRef]
- Chowdhury, E.U.; Bisby, L.A.; Green, M.F.; Kodur, V.K.R.; Asce, F. Residual Behavior of Fire-Exposed Reinforced Concrete Beams Prestrengthened in Flexure with Fiber-Reinforced Polymer Sheets. J. Compos. Constr. 2008, 12, 61–68. [Google Scholar] [CrossRef]
- Ahmed, A.; Kodur, V.K.R. Effect of bond degradation on fire resistance of FRP-strengthened reinforced concrete beams. Compos. B Eng. 2011, 42, 226–237. [Google Scholar] [CrossRef]
- Li, J.; Gravina, R.J.; Smith, S.T.; Visintin, P. Bond strength and bond stress-slip analysis of FRP bar to concrete incorporating environmental durability. Constr. Build. Mater. 2020, 261, 119860. [Google Scholar] [CrossRef]
- Dong, K.; Hu, K.; Gao, W. Fire behavior of full-scale CFRP-strengthened RC beams protected with different insulation systems. J. Asian Archit. Build. Eng. 2016, 15, 581–588. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond-slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Chang, Y.F.; Chen, Y.H.; Sheu, M.S.; Yao, G.C. Residual stress-strain relationship for concrete after exposure to high temperatures. Cem. Concr. Res. 2006, 36, 1999–2005. [Google Scholar] [CrossRef]
- Wang, K.; Young, B.; Smith, S.T. Mechanical properties of pultruded carbon fibre-reinforced polymer (CFRP) plates at elevated temperatures. Eng. Struct. 2011, 33, 2154–2161. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, J.G.; Wang, M.; Chen, L.; Zhang, F.; Xu, Q. Residual bond strengths of epoxy and cement-bonded CFRP reinforcements to concrete interfaces after elevated temperature exposure. Fire Saf. J. 2021, 124, 103393. [Google Scholar] [CrossRef]
- Chandrathilaka, E.R.K.; Gamage, J.C.P.H.; Fawzia, S. Numerical modelling of bond shear stress slip behavior of CFRP/steel composites cured and tested at elevated temperature. Compos. Struct. 2019, 212, 1–10. [Google Scholar] [CrossRef]
- Biscaia, H.C.; Chastre, C.; Viegas, A.; Franco, N. Numerical modelling of the effects of elevated service temperatures on the debonding process of FRP-to-concrete bonded joints. Compos. B Eng. 2015, 70, 64–79. [Google Scholar] [CrossRef]
- Krzywoń, R. Behavior of EBR FRP Strengthened Beams Exposed to Elevated Temperature. Procedia Eng. 2017, 193, 297–304. [Google Scholar] [CrossRef]
- Pellegrino, C.; Tinazzi, D.; Modena, C. Experimental Study on Bond Behavior between Concrete and FRP Reinforcement. J. Compos. Constr. 2008, 12, 180–189. [Google Scholar] [CrossRef]
- Aguiar, J.B.; Camões, A.; Vaz, N.F. Effect of temperature on RC elements strengthened with CFRP. Mater. Struct./Mater. Constr. 2008, 41, 1133–1142. [Google Scholar] [CrossRef]
- Gamage, J.C.P.H.; Al-Mahaidi, R.; Wong, B.; Ariyachandra, M.R.E.F. Bond characteristics of CFRP-strengthened concrete members subjected to cyclic temperature and mechanical stress at low humidity. Compos. Struct. 2017, 160, 1051–1059. [Google Scholar] [CrossRef]
- Zhou, H.; Torres, J.P.; Fernando, D.; Law, A.; Emberley, R. The bond behaviour of CFRP-to-steel bonded joints with varying bond properties at elevated temperatures. Eng. Struct. 2019, 183, 1121–1133. [Google Scholar] [CrossRef]
- Kalyani, V.J.; Joshi, D.D.; Patel, P.V. Study of the behaviour of FRP materials and epoxy adhesives under elevated temperature. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]
- Hashemi, S.; Al-Mahaidi, R. Flexural performance of CFRP textile-retrofitted RC beams using cement-based adhesives at high temperature. Constr. Build. Mater. 2012, 28, 791–797. [Google Scholar] [CrossRef]
- Widanage, C.; Gamage, J.C.P.H.; De Silva, G.I.P. Bond characteristics of CFRP strengthened concrete members bonded using Modified Engineered Cementitious Composite. Case Stud. Constr. Mater. 2021, 15, e00766. [Google Scholar] [CrossRef]
- Leone, M.; Matthys, S.; Aiello, M.A. Effect of elevated service temperature on bond between FRP EBR systems and concrete. Compos. B Eng. 2009, 40, 85–93. [Google Scholar] [CrossRef]
- Dong, K.; Hu, K. Development of bond strength model for CFRP-to-concrete joints at high temperatures. Compos. B Eng. 2016, 95, 264–271. [Google Scholar] [CrossRef]
- Mofrad, M.H.; Mostofinejad, D.; Hosseini, A. A generic non-linear bond-slip model for CFRP composites bonded to concrete substrate using EBR and EBROG techniques. Compos. Struct. 2019, 220, 31–44. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wu, Z.M.; Liu, H.B.; Zhang, Q.M.; Yang, S.T.; Li, Y.C. Influence of thermal effects on debonding response of CFRP-to-concrete/steel interfaces under thermal and mechanical loads: An analytical solution. Compos. Struct. 2023, 303, 116333. [Google Scholar] [CrossRef]
- Klamer, E.L.; Hordijk, D.A.; Janssen, H.J.M. The Influence of Temperature on the Debonding of Externally Bonded CFRP. Spec. Issue ACI 2005, 23, 1551–1570. [Google Scholar]
- Wu, Z.S.; Iwashita, K.; Yagashiro, S.; Ishikawa, T.; Hamaguchi, Y. Temperature effect on bonding and debonding behavior b tween FRP sheets and concrete. J. Soc. Mater. Sci. 2005, 54, 474–480. [Google Scholar] [CrossRef]
- Camata, G.; Pasquini, F.; Spacone, E. High temperature flexural strengthening with externally bonded FRP reinforcement. In Proceedings of the 8th International Symposium on Fiber Reinforced Polymer (FRP) Reinforcement for Concrete Structures (FRP8RCS), Patras, Greece, 16–18 July 2007; pp. 1–10. [Google Scholar]
- Hu, K.X.; Lu, F.; Cai, Z.H. Researches on mechanical property of CFRP-concrete interface at elevated temperatures. J. Tongji Univ. 2009, 37, 1592–1597. [Google Scholar]
- Hu, K.X.; Peng, D.P.; Zhao, C.X. Influence of temperature on the bond-slip behavior of CFRP-concrete interface. J. Disaster Prev. Mitig. Eng. 2012, 32, 45–49. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).