A Sequence-Based Hybrid Ensemble Approach for Estimating Trail Pavement Roughness Using Smartphone and Bicycle Data
Abstract
1. Introduction
1.1. Background
1.2. Related Works
1.3. Ensemble Machine Learning Models
2. Materials and Methods
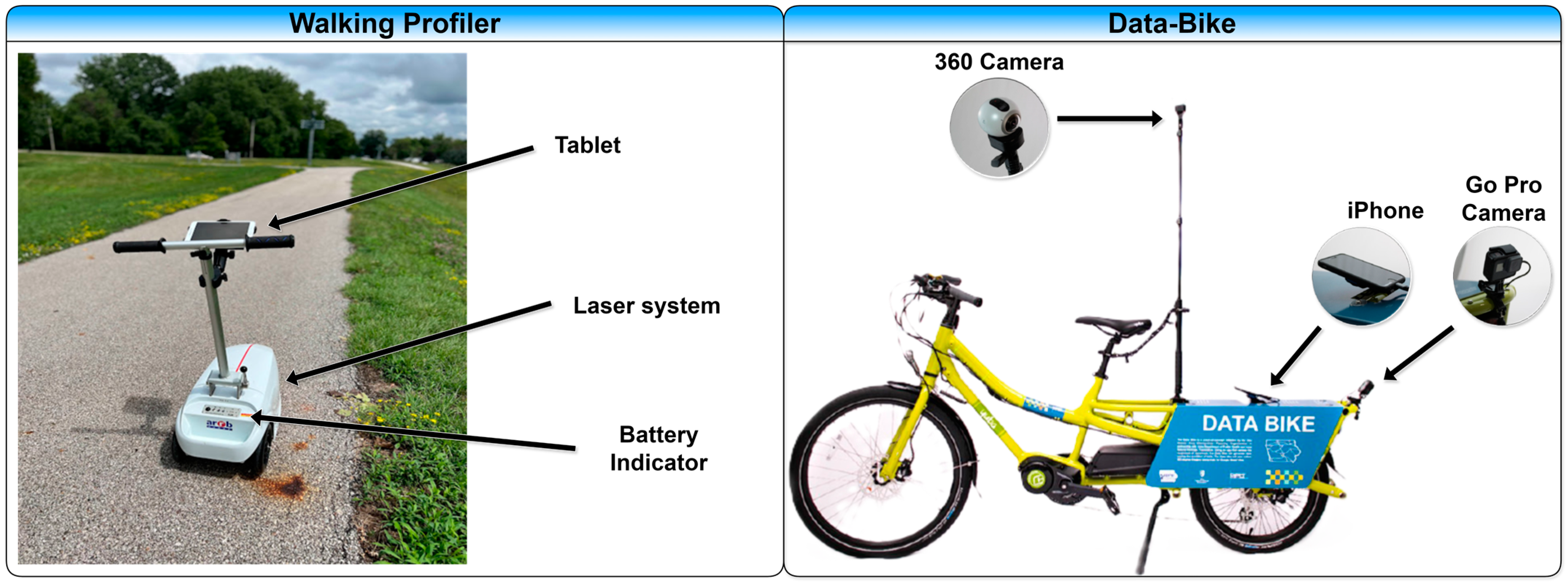
2.1. Data Collection
2.2. Numerical Double Integration Method
2.3. Whole-Body Vibration Method
2.4. Hybrid Ensemble Machine Learning Method
2.5. Evaluating and Comparing Terms
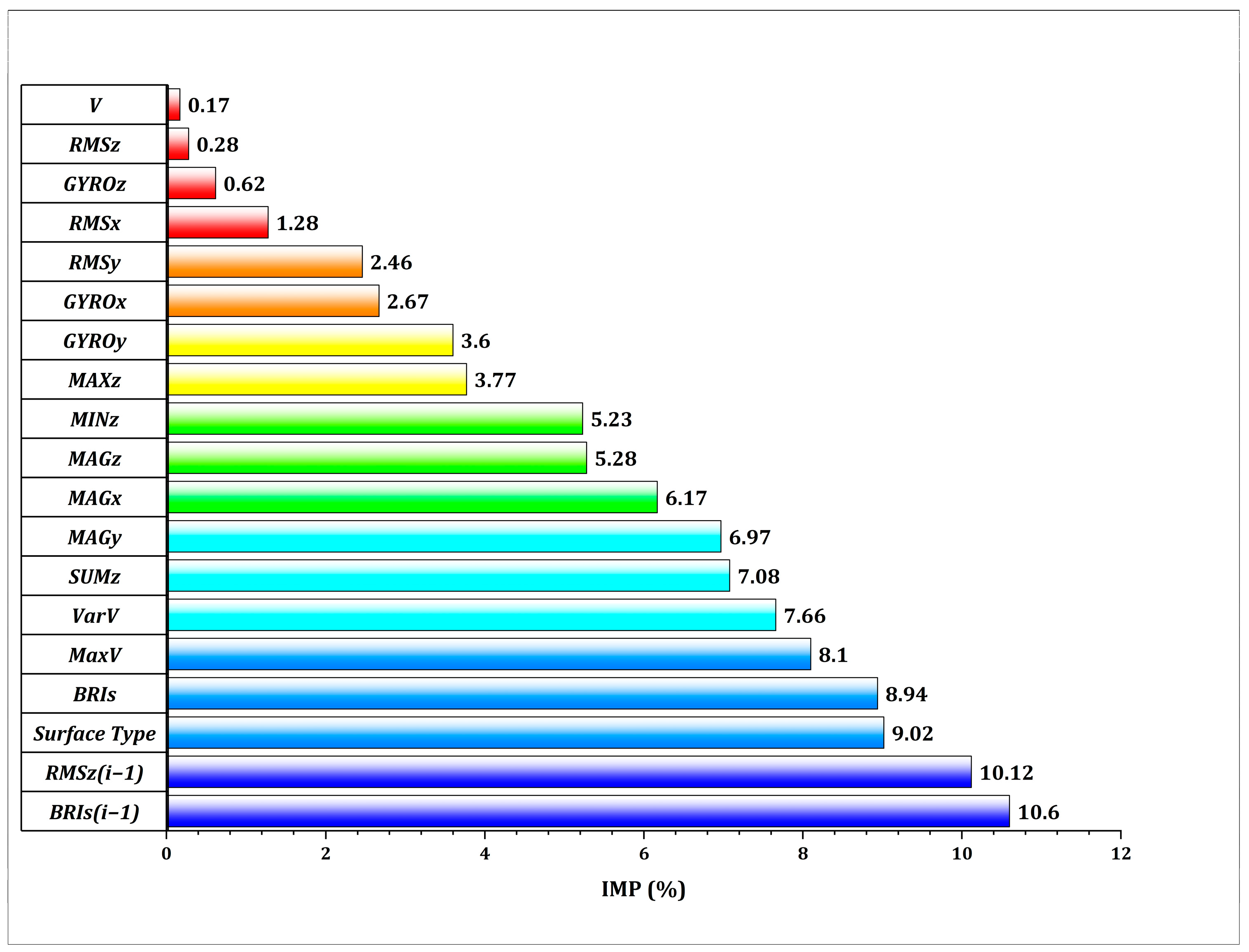
2.6. Sensitivity Analysis
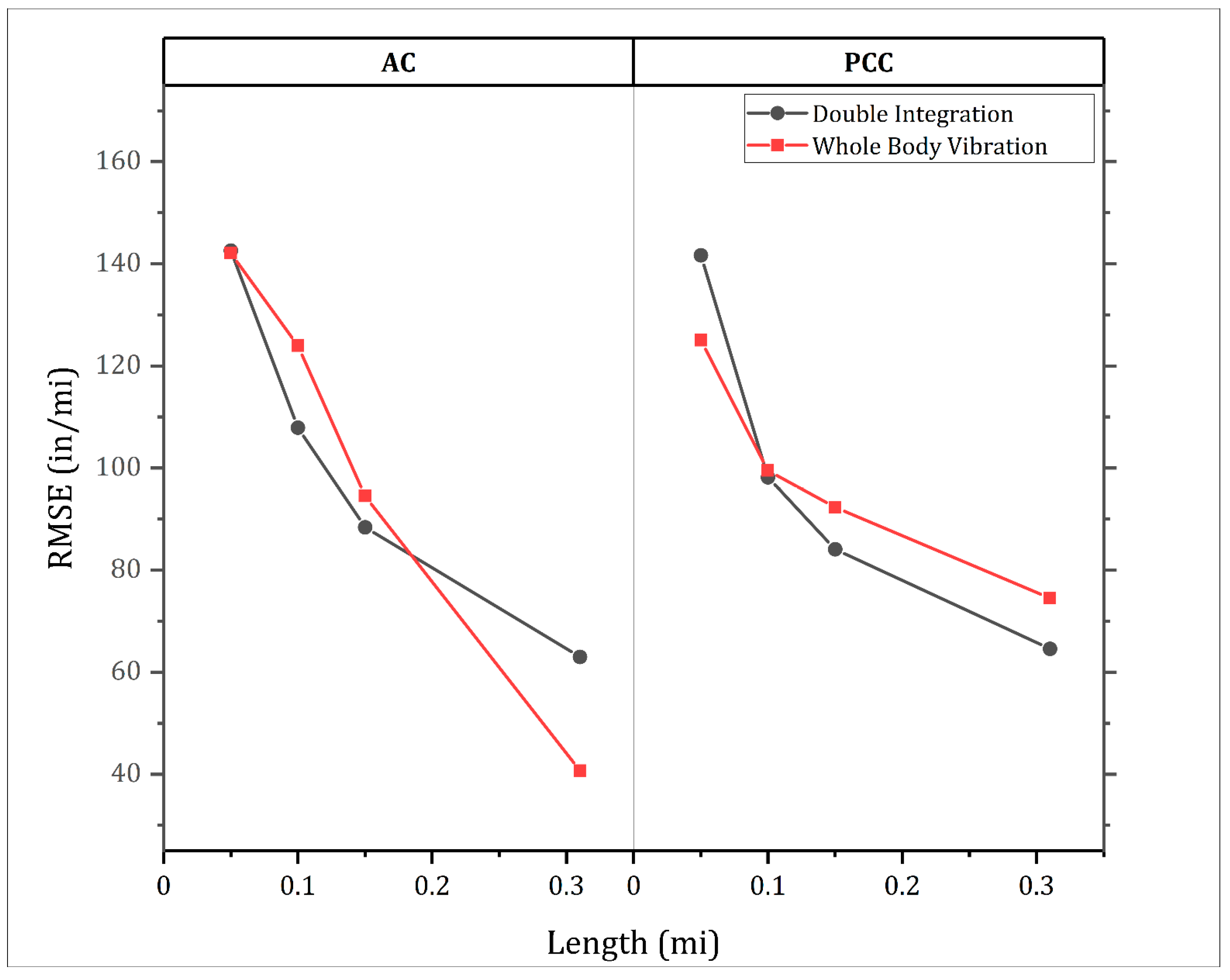
3. Results for Double Integration and Vibration-Based Methods
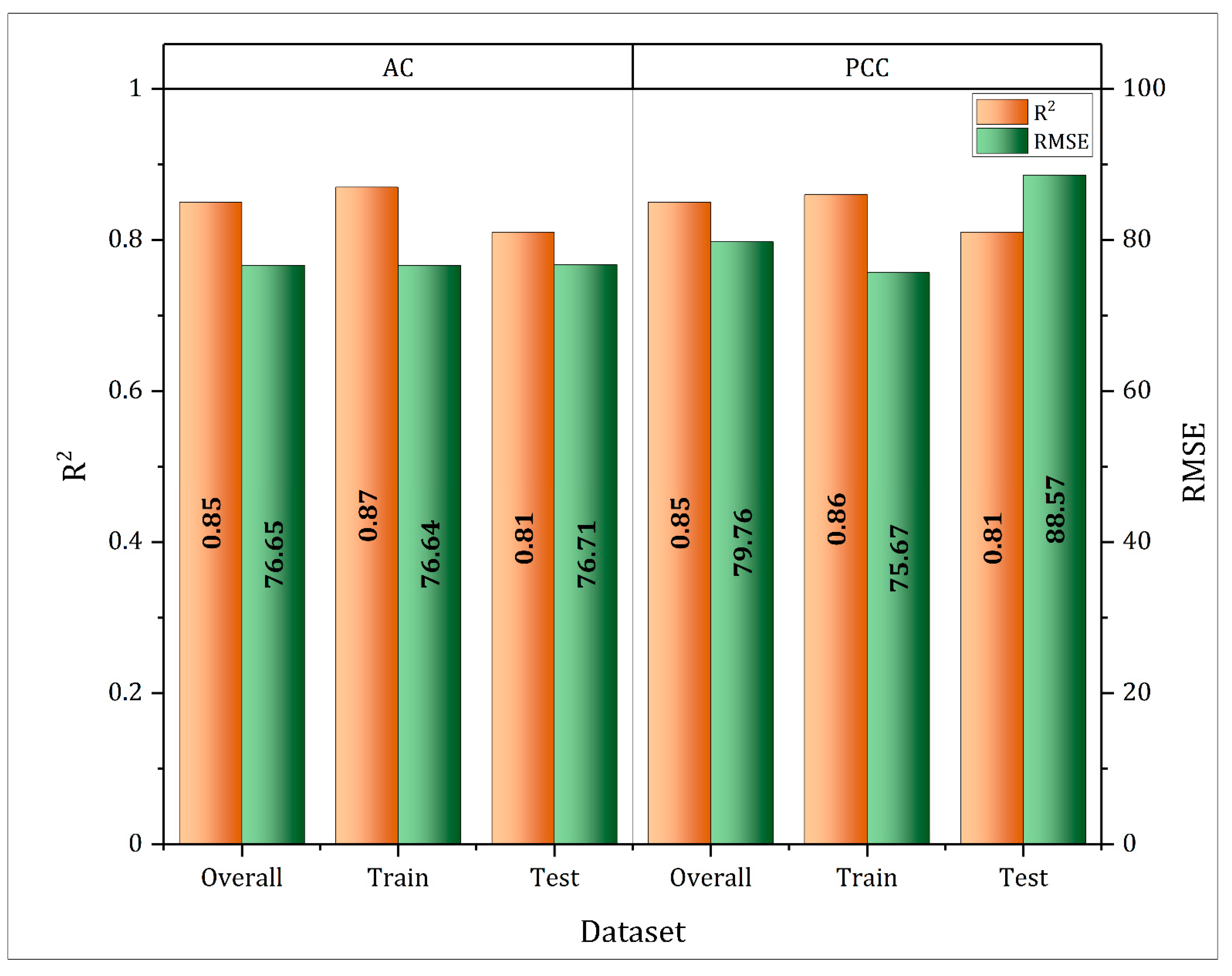
4. Results for the Hybrid Ensemble Model
4.1. Base Models
4.2. Hybrid Sequence-Based Model
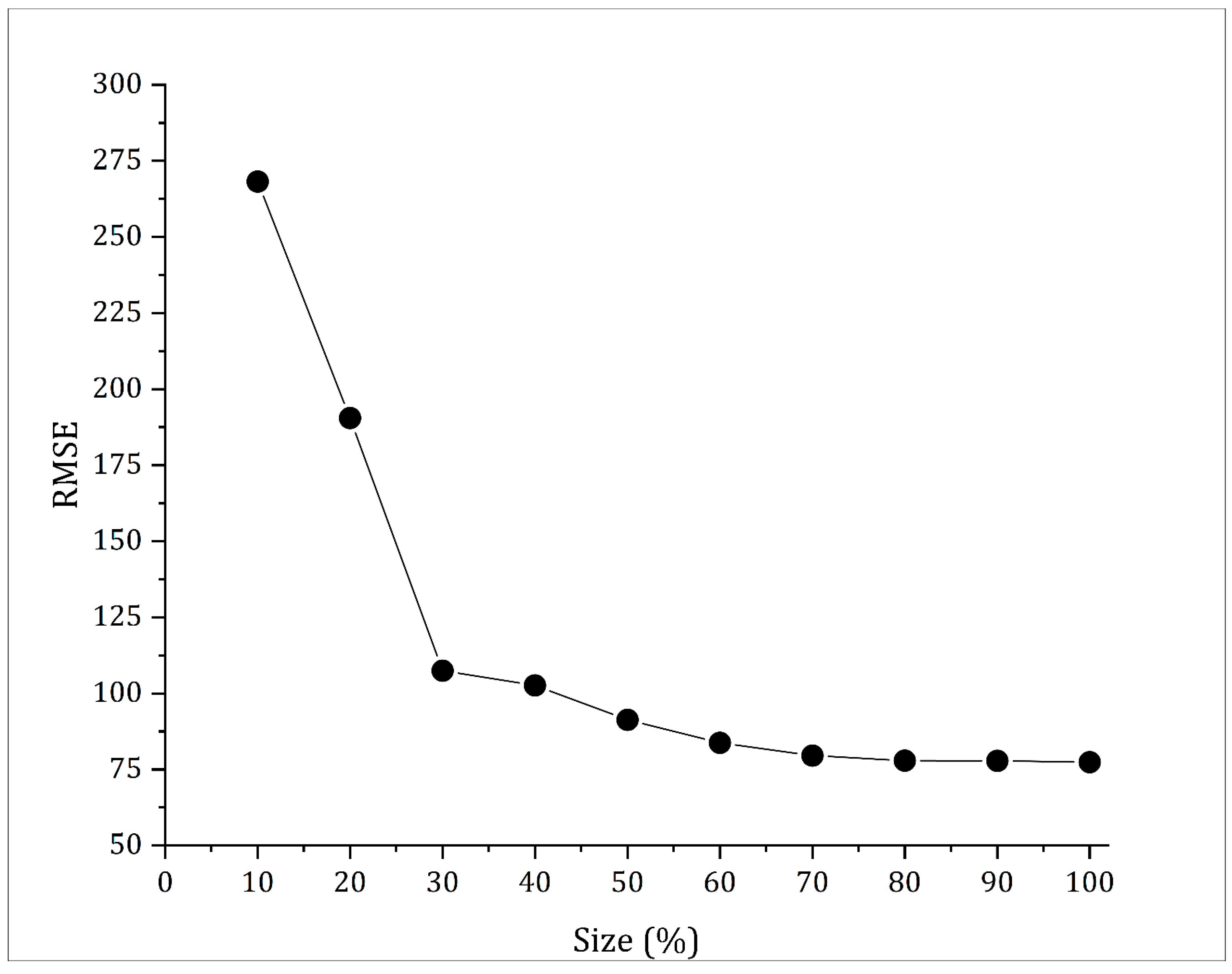
4.3. Sensitivity Analysis Result
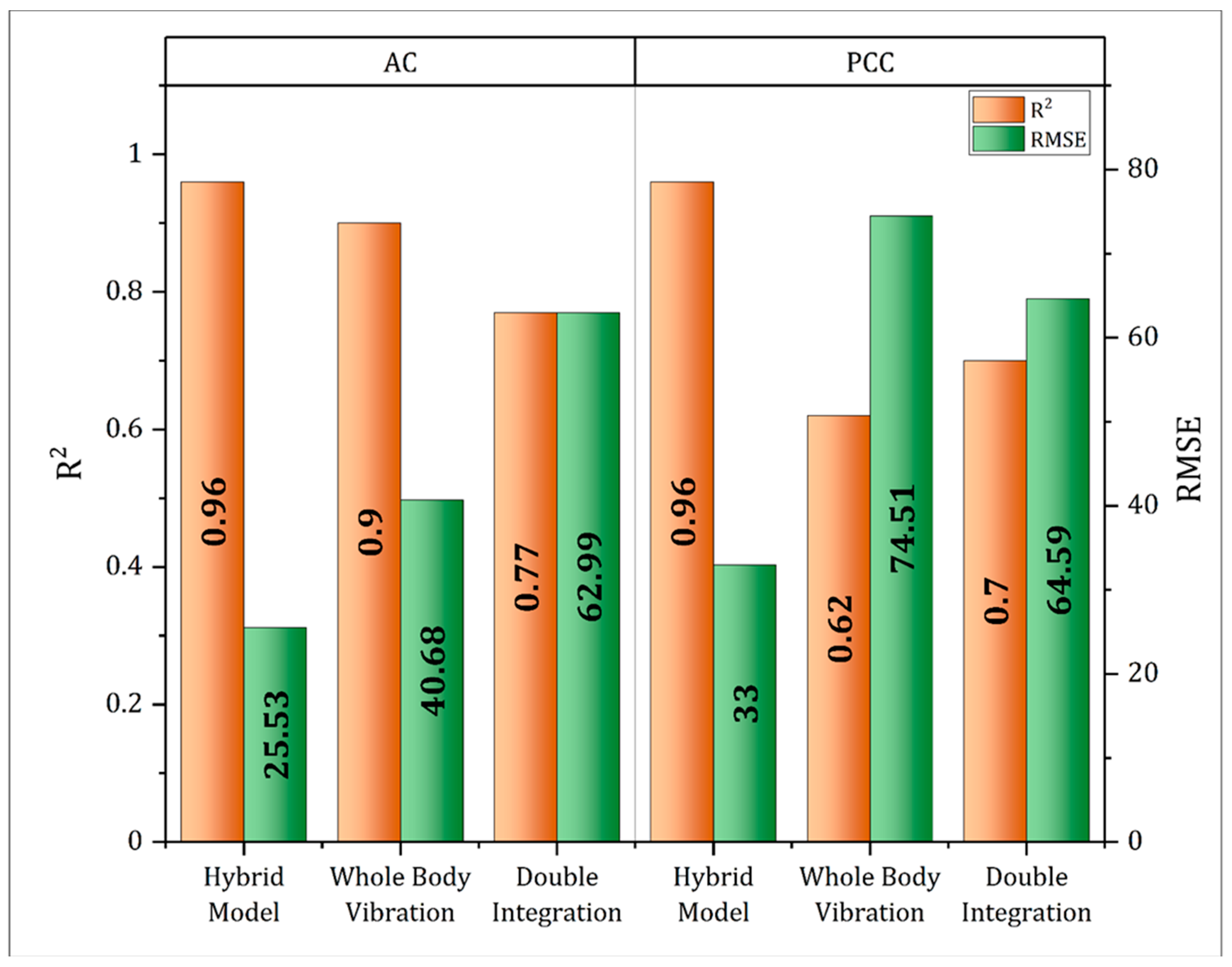
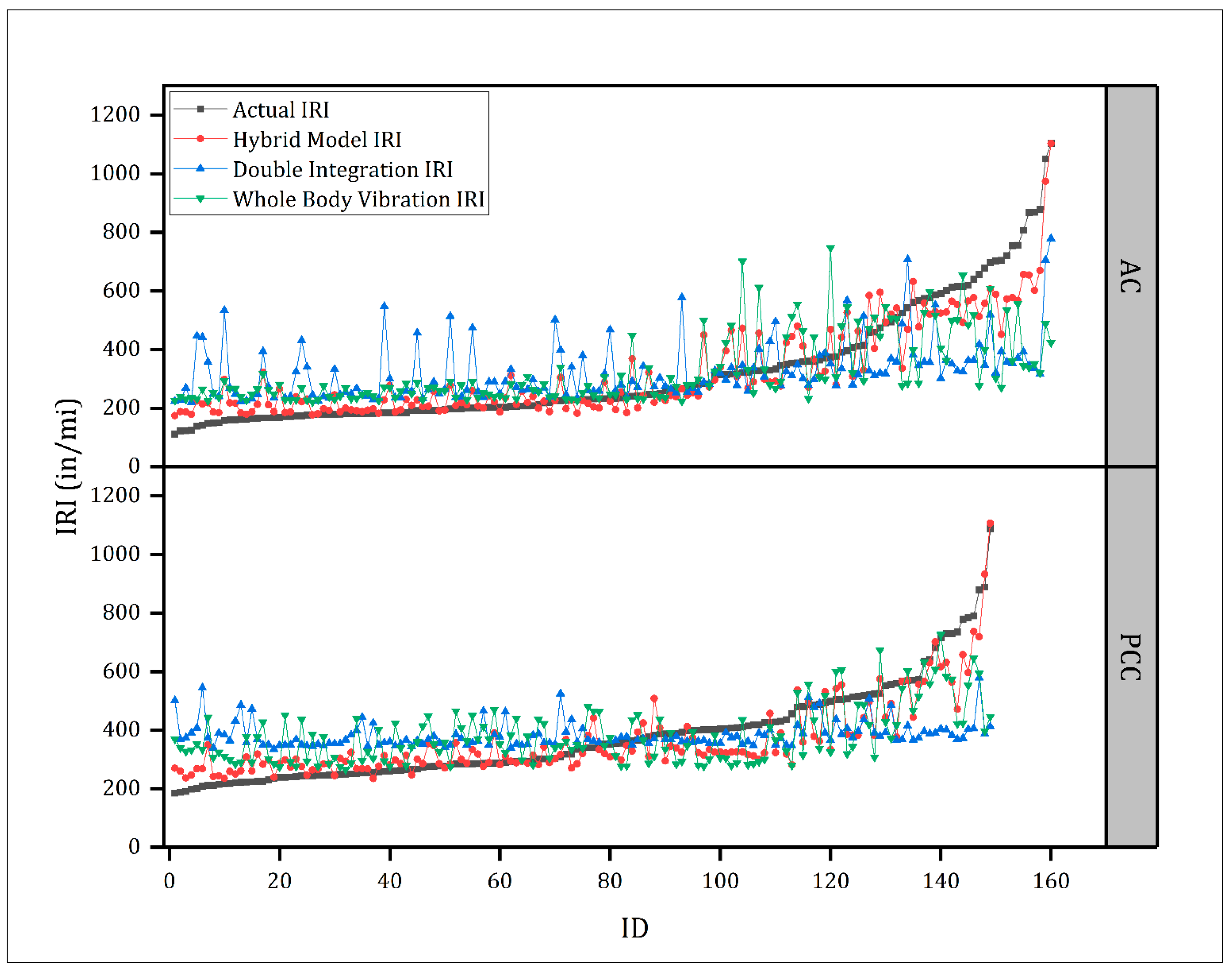
5. Comparison between the Proposed Methods
5.1. Segment Length: 0.31 mi (499 m)
5.2. Segment Length: 0.031 mi (50 m)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, W.; Dong, Y.; Ren, X.; Han, H.; Jung, Y. Development and Application of Riding Profiler for Roughness Evaluation on Bicycle Riding Surfaces. Sens. Mater. 2022, 34, 2709. [Google Scholar] [CrossRef]
- IOWA DOT Iowa Department of Transportation (DOT)—IOWA BIKES INTERACTIVE MAP. Available online: https://iowadot.gov/iowabikes/bikemap/home.aspx (accessed on 25 December 2022).
- AASHTO. Guide for the Development of Bicycle Facilities, 4th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2012. [Google Scholar]
- Landis, B.W.; Petritsch, T.A.; Huang, H.F.; Do, A.H. Characteristics of Emerging Road and Trail Users and Their Safety. Transp. Res. Rec. J. Transp. Res. Board 2004, 1878, 131–139. [Google Scholar] [CrossRef]
- Landis, B.W.; Vattikuti, V.R.; Brannick, M.T. Real-Time Human Perceptions: Toward a Bicycle Level of Service. Transp. Res. Rec. J. Transp. Res. Board 1997, 1578, 119–126. [Google Scholar] [CrossRef]
- Bíl, M.; Andrášik, R.; Kubeček, J. How Comfortable Are Your Cycling Tracks? A New Method for Objective Bicycle Vibration Measurement. Transp. Res. Part C Emerg. Technol. 2015, 56, 415–425. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Smadi, O. How Prediction Accuracy Can Affect the Decision-Making Process in Pavement Management System. Infrastructures 2021, 6, 28. [Google Scholar] [CrossRef]
- Al-Suleiman (Obaidat), T.I.; Alatoom, Y.I. Development of Pavement Roughness Regression Models Based on Smartphone Measurements. J. Eng. Des. Technol. 2022, 22, 1136–1157. [Google Scholar] [CrossRef]
- Sayers, M.W. The International Road Roughness Experiment: Establishing Correlation and a Calibration Standard for Measurements; University of Michigan, Ann Arbor, Transportation Research Institute: Ann Arbor, MI, USA, 1986. [Google Scholar]
- Sayers, M.W. On the Calculation of International Roughness Index from Longitudinal Road Profile. Transp. Res. Rec. 1995. Available online: https://trid.trb.org/View/452992 (accessed on 4 October 2024).
- Thigpen, C.G.; Li, H.; Handy, S.L.; Harvey, J. Modeling the Impact of Pavement Roughness on Bicycle Ride Quality. Transp. Res. Rec. J. Transp. Res. Board 2015, 2520, 67–77. [Google Scholar] [CrossRef]
- Larsson, M.; Niska, A.; Erlingsson, S.; Tunholm, M.; Andrén, P. Condition Assessment of Cycle Path Texture and Evenness Using a Bicycle Measurement Trailer. Int. J. Pavement Eng. 2023, 24, 2262085. [Google Scholar] [CrossRef]
- Rizelioğlu, M.; Yazıcı, M. New Approach to Determining the Roughness of Bicycle Roads. Transp. Res. Rec. J. Transp. Res. Board 2023, 2678, 781–793. [Google Scholar] [CrossRef]
- Wage, O.; Feuerhake, U.; Koetsier, C.; Ponick, A.; Schild, N.; Beening, T.; Dare, S. Ride Vibrations: Towards Comfort-Based Bicycle Navigation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLIII-B4-2020, 367–373. [Google Scholar] [CrossRef]
- Niska, A.M.; Sjogren, L.; Weber, C.; De Jong, T.; Fyhri, A. Determination of Riding Comfort on Cycleways Using a Smartphone App. SSRN Electron. J. 2022. [Google Scholar] [CrossRef]
- Zang, K.; Shen, J.; Huang, H.; Wan, M.; Shi, J. Assessing and Mapping of Road Surface Roughness Based on GPS and Accelerometer Sensors on Bicycle-Mounted Smartphones. Sensors 2018, 18, 914. [Google Scholar] [CrossRef] [PubMed]
- Alatoom, Y.I.; Obaidat, T.I. Measurement of Street Pavement Roughness in Urban Areas Using Smartphone. Int. J. Pavement Res. Technol. 2022, 15, 1003–1020. [Google Scholar] [CrossRef]
- Janani, L.; Doley, R.; Sunitha, V.; Mathew, S. Precision Enhancement of Smartphone Sensor-Based Pavement Roughness Estimation by Standardizing Host Vehicle Speed. Can. J. Civ. Eng. 2022, 49, 716–730. [Google Scholar] [CrossRef]
- Sandamal, R.M.K.; Pasindu, H.R. Applicability of Smartphone-Based Roughness Data for Rural Road Pavement Condition Evaluation. Int. J. Pavement Eng. 2022, 23, 663–672. [Google Scholar] [CrossRef]
- Yang, X.; Hu, L.; Ahmed, H.U.; Bridgelall, R.; Huang, Y. Calibration of Smartphone Sensors to Evaluate the Ride Quality of Paved and Unpaved Roads. Int. J. Pavement Eng. 2022, 23, 1529–1539. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, H.; Xu, S.; Lv, W. Pavement Roughness Evaluation Method Based on the Theoretical Relationship between Acceleration Measured by Smartphone and IRI. Int. J. Pavement Eng. 2022, 23, 3082–3098. [Google Scholar] [CrossRef]
- Shtayat, A.; Moridpour, S.; Best, B.; Shahriar Rumi, M. Using a Smartphone Software and a Regular Bicycle to Monitor Pavement Health Statues. In Proceedings of the 2020 2nd International Conference on Robotics Systems and Vehicle Technology; Xiamen, China, 3–5 December 2020, Association for Computing Machinery: New York, NY, USA, 2020; pp. 121–126. [Google Scholar]
- Cafiso, S.; di Graziano, A.; Marchetta, V.; Pappalardo, G. Urban Road Pavements Monitoring and Assessment Using Bike and E-Scooter as Probe Vehicles. Case Stud. Constr. Mater. 2022, 16, e00889. [Google Scholar] [CrossRef]
- Titov, W.; Schlegel, T. Monitoring Road Surface Conditions for Bicycles—Using Mobile Device Sensor Data from Crowd Sourcing. Proceedings of the 5th International Conference, MobiTAS 2023, 25th HCI International Conference, HCII 2023, Copenhagen, Denmark, 23–28 July 2023, Krömker, H., Ed.; Springer International Publishing: Cham, Switzerland, 2019; 340–356. [Google Scholar]
- Aleadelat, W.; Aledealat, K.; Ksaibati, K. Estimating Pavement Roughness Using a Low-Cost Depth Camera. Int. J. Pavement Eng. 2022, 23, 4923–4930. [Google Scholar] [CrossRef]
- Mahmoudzadeh, A.; Golroo, A.; Jahanshahi, M.R.; Firoozi Yeganeh, S. Estimating Pavement Roughness by Fusing Color and Depth Data Obtained from an Inexpensive RGB-D Sensor. Sensors 2019, 19, 1655. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble Learning. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: Boston, MA, USA, 2012; pp. 1–34. ISBN 978-1-4419-9326-7. [Google Scholar]
- Brownlee, J. A Gentle Introduction to Ensemble Learning Algorithms. Available online: https://machinelearningmastery.com/tour-of-ensemble-learning-algorithms/ (accessed on 13 December 2022).
- Ustuner, M.; Balik Sanli, F. Polarimetric Target Decompositions and Light Gradient Boosting Machine for Crop Classification: A Comparative Evaluation. ISPRS Int. J. Geoinf. 2019, 8, 97. [Google Scholar] [CrossRef]
- Kadiyala, A.; Kumar, A. Applications of Python to Evaluate the Performance of Bagging Methods. Environ. Prog. Sustain. Energy 2018, 37, 1555–1559. [Google Scholar] [CrossRef]
- Alatoom, Y.I.; Al-Hamdan, A.B. A Comparative Study Between Different Machine Learning Algorithms for Estimating the Vehicular Delay at Signalized Intersections. J. Soft Comput. Civ. Eng. 2024, 123–160. Available online: https://www.jsoftcivil.com/article_196451.html (accessed on 4 October 2024).
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost Tree-Based Ensemble Classification and Spectral Band Selection for Ecotope Mapping Using Airborne Hyperspectral Imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Yao, P.; Liu, Z.; Wang, Z.; Bu, S. Fault Signal Classification Using Adaptive Boosting Algorithm. Electron. Electr. Eng. 2012, 18, 97–100. [Google Scholar] [CrossRef]
- Acula, D.D. Classification of Disaster Risks in the Philippines Using Adaptive Boosting Algorithm with Decision Trees and Support Vector Machine as Based Estimators. J. Model. Simul. Mater. 2021, 4, 7–18. [Google Scholar] [CrossRef]
- Mayr, A.; Binder, H.; Gefeller, O.; Schmid, M. The Evolution of Boosting Algorithms. Methods Inf. Med. 2014, 53, 419–427. [Google Scholar] [CrossRef]
- Sharma, A.; Sachdeva, S.N.; Aggarwal, P. Predicting IRI Using Machine Learning Techniques. Int. J. Pavement Res. Technol. 2023, 16, 128–137. [Google Scholar] [CrossRef]
- Bral, S.; Kumar, P.P.; Chopra, T. Prediction of International Roughness Index Using CatBooster and Shap Values. Int. J. Pavement Res. Technol. 2022, 17, 518–533. [Google Scholar] [CrossRef]
- Guo, R.; Fu, D.; Sollazzo, G. An Ensemble Learning Model for Asphalt Pavement Performance Prediction Based on Gradient Boosting Decision Tree. Int. J. Pavement Eng. 2022, 23, 3633–3646. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, J.; Cao, D.; Yao, H. Cost-Effective Assessment of in-Service Asphalt Pavement Condition Based on Random Forests and Regression Analysis. Constr. Build. Mater. 2022, 330, 127219. [Google Scholar] [CrossRef]
- Chou, C.-P.; Siao, G.-J.; Chen, A.-C.; Lee, C.-C. Algorithm for Estimating International Roughness Index by Response-Based Measuring Device. J. Transp. Eng. Part B Pavements 2020, 146, 04020031. [Google Scholar] [CrossRef]
- Haque, M.A. BaselineRemoval. GitHub Repository. 2022. Available online: https://github.com/StatguyUser/BaselineRemoval (accessed on 4 October 2024).
- ISO 2631-1; Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements, 2nd ed. International Organization for Standardization: Geneva, Switzerland, 1997.
- Zeng, H.; Park, H.; Fontaine, M.D.; Smith, B.L.; McGhee, K.K. Identifying Deficient Pavement Sections by Means of an Improved Acceleration-Based Metric. Transp. Res. Rec. J. Transp. Res. Board 2015, 2523, 133–142. [Google Scholar] [CrossRef]
- Ahlin, K.; Granlund, N.O.J. Relating Road Roughness and Vehicle Speeds to Human Whole Body Vibration and Exposure Limits. Int. J. Pavement Eng. 2002, 3, 207–216. [Google Scholar] [CrossRef]
- Loprencipe, G.; Zoccali, P.; Cantisani, G. Effects of Vehicular Speed on the Assessment of Pavement Road Roughness. Appl. Sci. 2019, 9, 1783. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Z.; Ruth, J. Modeling Indirect Statistics of Surface Roughness. J. Transp. Eng. 2001, 127, 105–111. [Google Scholar] [CrossRef]
- Múčka, P. International Roughness Index Specifications around the World. Road Mater. Pavement Des. 2017, 18, 929–965. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Uddin, W.; Hudson, W.; Elkins, G. Surface-Smoothness Evaluation and Specifications for Flexible Pavements. In Surface Characteristics of Roadways: International Research and Technologies; ASTM International: West Conshohocken, PA, USA, 1990; pp. 224–236. [Google Scholar]
- Blum, J.R.; Greencorn, D.G.; Cooperstock, J.R. Smartphone Sensor Reliability for Augmented Reality Applications. In Proceedings of the Mobile and Ubiquitous Systems: Computing, Networking, and Services; Melbourne, VIC, Australia, 14–17 November 2023, Zheng, K., Li, M., Jiang, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 127–138. [Google Scholar]
- Merry, K.; Bettinger, P. Smartphone GPS Accuracy Study in an Urban Environment. PLoS ONE 2019, 14, e0219890. [Google Scholar] [CrossRef]
- Liashchynskyi, P.; Liashchynskyi, P. Grid Search, Random Search, Genetic Algorithm: A Big Comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Sharp, T. An Introduction to Support Vector Regression (SVR). Available online: https://towardsdatascience.com/an-introduction-to-support-vector-regression-svr-a3ebc1672c2 (accessed on 13 December 2022).
- Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)?—Arguments against Avoiding RMSE in the Literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Saltelli, A.; Sobol’, I.M. About the Use of Rank Transformation in Sensitivity Analysis of Model Output. Reliab. Eng. Syst. Safety 1995, 50, 225–239. [Google Scholar] [CrossRef]
- Zhang, P. A Novel Feature Selection Method Based on Global Sensitivity Analysis with Application in Machine Learning-Based Prediction Model. Appl. Soft Comput. 2019, 85, 105859. [Google Scholar] [CrossRef]
- Mrzygłód, B.; Hawryluk, M.; Janik, M.; Olejarczyk-Wożeńska, I. Sensitivity Analysis of the Artificial Neural Networks in a System for Durability Prediction of Forging Tools to Forgings Made of C45 Steel. Int. J. Adv. Manuf. Technol. 2020, 109, 1385–1395. [Google Scholar] [CrossRef]
- Alatoom, Y.I.; Al-Suleiman (Obaidat), T.I. Development of Pavement Roughness Models Using Artificial Neural Network (ANN). Int. J. Pavement Eng. 2022, 23, 4622–4637. [Google Scholar] [CrossRef]
- Ehsani, M.; Hamidian, P.; Hajikarimi, P.; Moghadas Nejad, F. Optimized Prediction Models for Faulting Failure of Jointed Plain Concrete Pavement Using the Metaheuristic Optimization Algorithms. Constr. Build. Mater. 2023, 364, 129948. [Google Scholar] [CrossRef]
- Bisconsini, D.R.; Pegorini, V.; Casanova, D.; de Oliveira, R.A.; Farias, B.A.; Júnior, J.L.F. Intervening Factors in Pavement Roughness Assessment with Smartphones: Quantifying the Effects and Proposing Mitigation. J. Transp. Eng. Part B Pavements 2021, 147, 04021051. [Google Scholar] [CrossRef]
- Jia, X.; Huang, B.; Zhu, D.; Dong, Q.; Woods, M. Influence of Measurement Variability of International Roughness Index on Uncertainty of Network-Level Pavement Evaluation. J. Transp. Eng. Part B Pavements 2018, 144, 04018007. [Google Scholar] [CrossRef]






| Method | Trail Material | Model Equation | Evaluation | |
|---|---|---|---|---|
| Double Integration | AC | (19) | R2 = 0.77, RMSE = 62.99 | |
| PCC | (20) | R2 = 0.70, RMSE = 64.59 | ||
| Vibration-Based | AC | (21) | R2 = 0.90, RMSE = 40.68 | |
| PCC | (22) | R2 = 0.62, RMSE = 74.51 | ||
| Model | Hyperparameters | Training Results | Testing Results |
|---|---|---|---|
| Random forest | Trees = 500 Depth of trees = 4 Subset split limit = 4 | R2 = 0.80, RMSE = 85.53 | R2 = 0.73, RMSE = 91.06 |
| Adaptive boosting | Number of estimators = 5 Learning rate = 0.1 Random generator = 1000 Loss = ‘Square’ | R2 = 0.95, RMSE = 41.10 | R2 = 0.66, RMSE = 102.59 |
| Gradient boosting | Number of estimators = 5 Learning rate = 0.15 Depth of trees = 3 Random generator = 1000 | R2 = 0.79, RMSE = 88.90 | R2 = 0.71, RMSE = 93.74 |
| Model | Submodel | Hyperparameters | Training Results | Testing Results |
|---|---|---|---|---|
| Hybrid model | Sequence-based | Trees = 400 Depth of trees = 4 Subset split limit = 4 | R2 = 0.85, RMSE = 76.16 | R2 = 0.80, RMSE = 77.42 |
| SVR | C =1 ε = 0.5 Kernel = Polynomial |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alatoom, Y.I.; Zihan, Z.U.; Nlenanya, I.; Al-Hamdan, A.B.; Smadi, O. A Sequence-Based Hybrid Ensemble Approach for Estimating Trail Pavement Roughness Using Smartphone and Bicycle Data. Infrastructures 2024, 9, 179. https://doi.org/10.3390/infrastructures9100179
Alatoom YI, Zihan ZU, Nlenanya I, Al-Hamdan AB, Smadi O. A Sequence-Based Hybrid Ensemble Approach for Estimating Trail Pavement Roughness Using Smartphone and Bicycle Data. Infrastructures. 2024; 9(10):179. https://doi.org/10.3390/infrastructures9100179
Chicago/Turabian StyleAlatoom, Yazan Ibrahim, Zia U. Zihan, Inya Nlenanya, Abdallah B. Al-Hamdan, and Omar Smadi. 2024. "A Sequence-Based Hybrid Ensemble Approach for Estimating Trail Pavement Roughness Using Smartphone and Bicycle Data" Infrastructures 9, no. 10: 179. https://doi.org/10.3390/infrastructures9100179
APA StyleAlatoom, Y. I., Zihan, Z. U., Nlenanya, I., Al-Hamdan, A. B., & Smadi, O. (2024). A Sequence-Based Hybrid Ensemble Approach for Estimating Trail Pavement Roughness Using Smartphone and Bicycle Data. Infrastructures, 9(10), 179. https://doi.org/10.3390/infrastructures9100179







