A Comparative Study of Pavement Roughness Prediction Models under Different Climatic Conditions

Abstract

Predicting the International Roughness Index (IRI) is crucial for maintaining road quality and ensuring the safety and comfort of road users. Accurate IRI predictions help in the timely identification of road sections that require maintenance, thus preventing further deterioration and reducing overall maintenance costs. This study aims to develop robust predictive models for the IRI using advanced machine learning techniques across different climatic conditions. Data were sourced from the Ministry of Energy and Infrastructure in the UAE for localized conditions coupled with the Long-Term Pavement Performance (LTPP) database for comparison and validation purposes. This study evaluates several machine learning models, including regression trees, support vector machines (SVMs), ensemble trees, Gaussian process regression (GPR), artificial neural networks (ANNs), and kernel-based methods. Among the models tested, GPR, particularly with rational quadratic specifications, consistently demonstrated superior performance with the lowest Root Mean Square Error (RMSE) and highest R-squared values across all datasets. Sensitivity analysis identified age, total pavement thickness, precipitation, temperature, and Annual Average Daily Truck Traffic (AADTT) as key factors influencing the IRI. The results indicate that pavement age and higher traffic loads significantly increase roughness, while thicker pavements contribute to smoother surfaces. Climatic factors such as temperature and precipitation showed varying impacts depending on the regional conditions. The developed models provide a powerful tool for predicting pavement roughness, enabling more accurate maintenance planning and resource allocation. The findings highlight the necessity of tailoring pavement management practices to specific environmental and traffic conditions to enhance road quality and longevity. This research offers a comprehensive framework for understanding and predicting pavement performance, with implications for infrastructure management both locally and worldwide.

1. Introduction

The International Roughness Index (IRI) is a globally recognized standard for measuring pavement smoothness and ride quality [1]. Developed by the World Bank in the 1980s, the IRI quantifies the longitudinal profile of a road surface by calculating the vertical displacement of a vehicle’s suspension system over a standardized distance [2]. Typically expressed in meters per kilometer (m/km) or inches per mile (in/mi), the IRI provides a numerical value that reflects the roughness of a pavement. Lower IRI values indicate smoother roads, while higher values denote rougher surfaces [3]. This metric is crucial for understanding and comparing the performance of different pavement sections, making it an essential tool for engineers and road authorities worldwide [4].

The IRI plays a pivotal role in pavement management by serving as a key indicator of pavement condition. Regular measurement of the IRI helps in monitoring the deterioration of road surfaces, enabling timely maintenance and rehabilitation interventions [5]. By identifying areas with high roughness, road agencies can prioritize repairs, thereby extending the lifespan of pavements and optimizing the use of maintenance budgets. Additionally, maintaining low IRI values is critical for enhancing the safety and comfort of road users [6]. Smoother roads reduce vehicle wear and tear, lower fuel consumption, and minimize the risk of accidents caused by poor road conditions. Furthermore, the IRI is often used in performance-based contracts and funding allocation, making it a vital metric for achieving sustainable and cost-effective pavement management practices [7].

The UAE’s harsh environmental conditions present significant challenges for maintaining flexible pavements. Extreme air temperatures, which can exceed 50 °C (122 °F) in the summer, cause stiffness degradation of the asphalt concrete (AC) layers associated with thermal expansion and contraction in pavement materials, leading to cracking and rutting [8]. Additionally, the region experiences frequent sandstorms that deposit fine particles on road surfaces, increasing abrasion and wear. These sandstorms also reduce visibility and pose hazards for drivers, further complicating maintenance efforts [9]. Heavy traffic, especially from commercial vehicles, exacerbates the stress on pavements, accelerating deterioration. The combination of these factors creates a challenging environment for preserving pavement smoothness and achieving low IRI values [10]. Flexible pavements in the UAE face numerous issues that demand constant attention. Frequent maintenance is necessary due to the rapid wear and tear from environmental and traffic-related stresses [11]. Premature deterioration, such as cracking, rutting, raveling, and potholes, is common, necessitating regular inspections and repairs. These issues not only increase maintenance costs but also disrupt traffic flow and pose safety risks. Additionally, the accumulation of sand on road surfaces can reduce traction and increase the likelihood of skidding accidents [12]. These local issues increase the degradation of surface smoothness, thereby increasing the necessity for more frequent IRI measurements. This typically results in higher costs and potential traffic disruptions. To address these challenges more efficiently, the development of cost-effective IRI predictive models tailored to local conditions presents a promising alternative [13].

Machine learning (ML) is a subset of artificial intelligence (AI) that focuses on developing algorithms and statistical models that enable computers to learn from and make predictions or decisions based on data [14,15,16,17]. In pavement engineering, ML offers significant potential benefits by enhancing the ability to analyze vast amounts of data and identify patterns that might not be apparent through traditional methods. By leveraging ML, engineers can develop more accurate models for predicting pavement conditions, leading to improved decision-making and resource allocation [18]. ML can handle complex, non-linear relationships within data, making it particularly effective in predicting various pavement performance indicators such as the IRI, pavement distress, and deterioration rates [19].

Machine learning has been increasingly applied in pavement management with promising results [20,21]. For example, ML algorithms have been used to predict pavement distress, such as cracking, rutting, and potholes, based on historical data and environmental factors [22]. These predictive models help road agencies anticipate and address issues before they become severe, thereby extending the life of pavement assets [23]. Additionally, ML has been employed to optimize maintenance schedules by identifying the most critical sections of roadways that require immediate attention, ensuring efficient use of maintenance budgets [24]. Furthermore, ML techniques have been utilized in improving pavement design by analyzing data from previous projects to refine material selection, structural design, and construction practices. Overall, the integration of ML in pavement engineering facilitates more proactive and cost-effective pavement management strategies, leading to enhanced road safety and performance [25].

Traditional methods for predicting the IRI often rely on empirical models and linear regression techniques that can be limited in their accuracy and adaptability [26]. These methods typically require simplified assumptions and may not fully capture the complex, non-linear relationships between various factors affecting pavement roughness. As a result, predictions may be less accurate and less responsive to changes in environmental or traffic conditions ML offers a more robust alternative by leveraging advanced algorithms capable of handling large datasets and uncovering intricate patterns within the data [27]. ML models can continuously learn and improve over time, providing more precise and timely predictions. This data-driven approach enables better planning and optimization of maintenance activities, ultimately leading to more efficient resource allocation and improved pavement performance [28]. ML models for IRI prediction can utilize a diverse range of data sources to enhance their accuracy and reliability [29]. Historical IRI measurements are fundamental for training and validating the models, providing a baseline understanding of pavement performance over time. Traffic data, including vehicle types, volumes, and loadings, are crucial as they directly impact pavement wear and tear [30]. Climatic conditions, such as temperature fluctuations, precipitation levels, and humidity, are also important as they influence the pavement’s structural integrity and surface characteristics. Additionally, data on material properties, including the type of asphalt or concrete used, layer thicknesses, and the presence of additives, can significantly affect the pavement’s response to external stresses. By integrating these diverse data types, ML models can provide comprehensive and nuanced predictions of the IRI, enabling more proactive and effective pavement management strategies [31,32].

This study aims to develop a predictive model for the International Roughness Index (IRI) of flexible pavements using advanced machine learning (ML) techniques, with a specific focus on addressing the unique environmental and traffic conditions in the UAE. While previous studies have predominantly relied on data from the Long-Term Pavement Performance (LTPP) database, they often generalize findings that may not be fully applicable to local contexts. To bridge this gap, our research combines data sourced from the Ministry of Energy and Infrastructure (MOEI) in the UAE with data from the LTPP. The MOEI data will provide region-specific insights, while the LTPP dataset will be used for broader comparisons and validation purposes due to its extensive and well-established global coverage. By leveraging ML techniques such as regression decision trees, support vector machines (SVMs), Gaussian process regression (GPR), ensemble trees, artificial neural networks (ANNs), and kernel-based approaches, this study aims to develop a robust, accurate model for predicting the IRI. The ultimate goal is to optimize pavement maintenance and management practices, improving the longevity and performance of road infrastructure in the UAE.

Table 1. Historical IRI prediction efforts for flexible pavements.

Model Variables	Modeling Procedure	IRI0	Data Source	N	Metrics
Abdelaziz et al. (2020) [33]	MLR	✓	LTPP	2439	$R^2$ = 0.57
Abdelaziz et al. (2020) [33]	ANN	✓	LTPP	2439	$R^2$ = 0.75
ARA (2008) [34]	MLR	✓	LTPP	1926	$R^2$ = 0.56
Jaafar and Fahmi (2016) [35]	MLR	✓	LTPP	34	$R^2$ = 0.26
Jaafar and Fahmi (2016) [35]	ANN	✓	LTPP	34	$R^2$ = 0.90
Mazari and Rodriguez (2016) [36]	ANN, GEP	✓	LTPP	98	$R^2$ = 0.98, RMSE = 0.078 m/km
Zeiada et al. (2020) [37]	ANN	✓	LTTP	115	$R^2$ = 0.87, RMSE = 0.16
Dong et al. (2019) [38]	LSTM-BPNN	✓	LTPP	2243	$R^2$ = 0.87, RMSE = 0.242
Choi and Do (2019) [39]	RNN	-	RPM *	1880	$R^2$ = 0.873, RMSE = 0.14
Marcelino et al. (2021) [40]	RFA	-	LTPP	27	$R^2$ = 0.93
Marcelino et al. (2020) [41]	TLA	-	LTPP + PRA *	2890	$R^2$ = 0.786
Yamany et al. (2020) [42]	RPR	-	LTPP	1159	$R^2$ = 0.48, RMSE = 0.3 m/km
Yamany et al. (2020) [42]	ANN	-	LTPP	1159	$R^2$ = 0.71, RMSE = 0.26 m/km
Gong et al. (2018) [43]	RFR	✓	LTPP	11,000	$R^2$ = 0.95, RMSE = 0.26 m/km
Hossain et al. (2019) [44]	ANN	-	LTPP	NA	RMSE = 0.027
Ziari et al. (2016) [45]	ANNs	-	LTPP	205	$R^2$ = 0.95, RMSE = 0.19
Patrick and Soliman (2019) [46]	MLR	-	LTPP	135	$R^2$ = 0.75, RMSE = 0.25
Rifai et al. (2015) [47]	DM	✓	IIRMS *	165	$R^2$ > 0.70
Zhou et al. (2021) [48]	RNN	✓	LTTP	854	$R^2$ = 0.93
Guo et al. (2021) [49]	GBDT	✓	LTPP	1781	$R^2$ = 0.90
Alatoom and Al-Suleiman (2021) [50]	ANN	✓	GAM *	204	$R^2$ = 0.86, RMSE = 0.37

* RPM = Road Pavement Monitoring, PRA = Portuguese Road Administration, IIRMS = Integrated Indonesia Road Management System, and GAM = Amman Greater Municipality.

highlights the historical efforts to predict the IRI for flexible pavements, revealing a significant research gap: most previous studies utilized data from the LTPP database. These studies, such as those employing linear regression, ANNs, and SVMs, demonstrated varying degrees of accuracy but often lacked applicability to specific regional conditions like those in the UAE.

This research contributes by developing three distinct predictive models for the IRI, each tailored to specific climatic conditions. The first model, using data from 233 sections in the LTPP database, captures global climatic diversity. The second model, based on 136 sections of the LTPP, focuses on warm climates. The third model leverages localized data from the MOEI, specifically targeting the UAE’s unique environmental and traffic conditions. This approach ensures the development of contextually relevant models, facilitating more effective pavement management locally and providing insights that could be applied worldwide.

2. Research Scope

This study develops and compares three predictive models for the International Roughness Index (IRI) of flexible pavements under different climatic conditions: one for global climates using data from the LTPP database, another for warm climates, and a third tailored to the UAE using local data from the Ministry of Energy and Infrastructure (MOEI). The process involves data collection and preprocessing, followed by the application of machine learning techniques such as regression trees, SVMs, GPR, ensemble trees, and ANNs to build the models. The models are validated, compared, and assessed through feature importance analysis to identify key factors influencing the IRI, and sensitivity analysis to ensure model robustness. This comprehensive approach aims to improve pavement management practices in different climatic contexts, particularly in the UAE.

3. Methodology

This research aims to develop predictive models for assessing asphalt pavement performance, specifically focusing on the IRI, across different climatic conditions. This study develops three predictive models: one using global climate data from the LTPP database, another using warm-climate data from the LTPP, and a third using localized data from the UAE’s federal highway network.

For the global and warm-climate models, data were sourced from the LTPP database, including parameters such as road section specifics, structural characteristics, traffic loading data, and IRI measurements. The global model includes 233 sections representing a wide range of climatic conditions, while the warm-climate model focuses on 136 sections from warmer regions. For the UAE model, data were sourced from the MOEI, covering major highways such as E55, E11, E88, E311, and E18, which serve the northern emirates including Fujairah, Ras Al Khaimah, Sharjah, Umm Al Quwain, and Ajman. These highways experience heavy traffic loads, making them more susceptible to deterioration compared to other road types in the UAE, thus necessitating precise and reliable IRI predictions to optimize maintenance and management efforts. Additional climatic data, such as temperature and humidity, were obtained from the UAE’s National Center of Meteorology.

The methodology, detailed in Figure 1, encompasses several stages from initial data acquisition to the final model validation, ensuring a comprehensive approach to developing and validating the predictive IRI models for each climatic scenario.

Table 2. Summary of obtained data.

Data Type	Data Attribute
Structure	Age, years
	L2 Thickness, mm
	L3 Thickness, mm
	L4 Thickness, mm
	Total Thickness, mm
Traffic	Annual Average Daily Truck Traffic (AADTT)
Climate	Annual Average Temperature, C
	Annual Average Precipitation, mm
	Max Humidity, %
	Min Humidity, %
Performance	IRI, m/km

shows the inputs and outputs for the three predictive models developed in this study. The models utilize various data attributes categorized into structure, traffic, climate, and performance parameters. These inputs are essential for predicting the IRI across different climatic conditions.

Before applying the machine learning models, several data preprocessing steps were undertaken to ensure the datasets from both the LTPP and UAE were clean, consistent, and suitable for analysis. As the selected variables from both datasets had complete observations, there were no missing values, eliminating the need for imputation. However, we addressed potential data issues by identifying and removing outliers in continuous variables such as pavement age, IRI, and AADTT using the interquartile range (IQR) method. This was essential to prevent skewed predictions caused by extreme values. Since some machine learning models, such as SVMs and ANNs, are sensitive to the scale of input features, all numerical data (e.g., pavement thickness, traffic load, and climate variables) were normalized using min–max scaling to ensure that all features were within a range of 0 to 1, which also improved model convergence during training. Categorical variables, such as climate zone and layer type, were transformed into numerical data using one-hot encoding, ensuring that the machine learning algorithms could process these non-numeric variables effectively without introducing unintended ordinal relationships. Instead of splitting the data into training and testing sets, we applied 10-fold cross-validation to assess the performance and generalizability of the models. This method provided a robust approach by ensuring that each part of the data was used for both training and validation, reducing the risk of overfitting. Finally, while the UAE dataset had some underrepresented road sections or conditions, we applied data balancing techniques, such as oversampling of minority classes and undersampling of majority classes, to avoid bias in the models and improve their predictive accuracy. These preprocessing steps were crucial for ensuring that the machine learning models could reliably predict pavement roughness under different climatic conditions.

3.1. Statistical Analysis

Statistical analysis is a crucial step in understanding the underlying relationships between the various variables in our dataset and the IRI. This study employs descriptive statistics to summarize the main characteristics of the dataset, including measures such as mean, standard deviation, and skewness. These statistics provide insights into the distribution and central tendencies of the input variables (e.g., pavement age, layer thickness, AADTT, temperature, precipitation) and the output variable (IRI).

Furthermore, a correlation analysis is conducted to identify the strength and direction of linear relationships between the input variables and the IRI. A correlation matrix is developed to visualize these relationships, with particular attention given to variables that exhibit strong positive or negative correlations with the IRI. This step helps in the initial selection of variables that are likely to have a significant impact on pavement roughness, thus guiding the subsequent machine learning model development.

3.2. Feature Importance

Feature importance analysis is an essential component of this study, as it helps identify the most significant variables influencing the IRI and provides insights into the impact of each variable across different datasets. Unlike cases with high-dimensional data, we chose not to remove less important features because our dataset consisted of only 10 input variables, a manageable number that did not require reduction. Instead, the focus was on understanding how each variable contributed to the prediction of the IRI across different climatic conditions. To assess feature importance, we employed a random forest model, known for its robustness in ranking variables based on their predictive power. The random forest algorithm, trained using 95 decision trees (a number optimized for accuracy and efficiency), allowed us to evaluate the relative influence of factors such as structural attributes (e.g., layer thicknesses), traffic data (AADTT), and climatic conditions (e.g., temperature and precipitation) on the IRI. This analysis helped us interpret the results by highlighting the most influential features, which provided valuable insights into the behavior of the models without requiring feature reduction.

The feature importance was calculated using the “Out-of-Bag Permuted Predictor Delta Error” method, integrated within the random forest model. This method assesses the increase in the prediction error of the model when the values of a specific feature are randomly permuted while all other features remain unchanged. A larger increase in error indicates that the feature is more important for the model’s predictions.

The resulting feature importance scores were then sorted in descending order to rank the variables according to their influence on the IRI. The following steps were taken to display and interpret the feature importance:

• Sorting and Displaying Importance: The calculated importance scores were sorted, and the corresponding variables were ranked from most to least important. This sorting allowed for a clear identification of the key factors that drive pavement roughness.
• Visualization: A bar plot was generated to visually represent the importance of each feature. The plot displayed the sorted feature importance scores, with the x-axis representing the feature names and the y-axis showing the importance scores. The features were labeled and rotated for clarity, and the plot was titled “Random Forest Feature Importance” to reflect its content.

The feature importance analysis revealed that certain variables had a significantly higher impact on the IRI than others. For instance, variables related to traffic load, such as AADTT, were among the most influential factors. Structural features, particularly the thickness of pavement layers, also showed a strong correlation with the IRI, highlighting the importance of proper pavement design in maintaining road smoothness. Climatic conditions like temperature and precipitation, while still important, had a more variable impact depending on the specific climatic scenario being modeled.

This analysis not only informed the selection of input variables for subsequent machine learning models but also provided insights into the relative significance of different factors affecting pavement roughness. These insights can be used to prioritize areas for further research and guide practical decisions in pavement management and maintenance.

3.3. Machine Learning Models

This study employs a range of machine learning models to predict the IRI under varying climatic conditions. The models include regression decision trees, SVMs, ensemble trees, GPR, and ANNs. Each model is selected based on its ability to handle the non-linear relationships and high-dimensional data inherent in pavement performance prediction.

1. Regression Decision Trees: These models are used for their simplicity and interpretability. They work by recursively partitioning the dataset into subsets based on the values of input variables, resulting in a tree-like model of decisions. Different configurations, such as fine, medium, and coarse trees, are tested to optimize performance.

2. Support Vector Machines (SVMs): SVM models are employed due to their effectiveness in high-dimensional spaces and their ability to handle both linear and non-linear relationships. Various kernel functions, including linear, quadratic, cubic, and Gaussian, are used to capture the complex patterns in the data.

3. Ensemble Trees: Ensemble methods, such as Boosted trees and Bagged trees, combine the predictions of multiple decision trees to improve accuracy. Boosted trees sequentially adjust the model to correct errors from previous iterations, while Bagged trees reduce variance by averaging predictions from multiple independent trees.

4. Gaussian Process Regression (GPR): GPR is chosen for its probabilistic approach, providing not only predictions but also uncertainty estimates. Different kernel functions, including squared exponential, Matern, and rational quadratic, are explored to capture the underlying data distributions.

5. Artificial Neural Networks (ANNs): ANN models are included for their ability to learn complex, non-linear patterns from large datasets. Various network architectures, including narrow, medium, wide, bilayered, and trilayered networks, are tested to identify the optimal configuration for IRI prediction.

To evaluate the performance of the machine learning models, several key metrics are employed, including Root Mean Square Error (RMSE), R-squared ($R^2$), Mean Squared Error (MSE), and Mean Absolute Error (MAE). These metrics provide a comprehensive assessment of model accuracy and robustness.

RMSE is a standard way to measure the error of a model in predicting quantitative data. It is the square root of the average of the squared differences between predicted and observed values.

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}} {\sum }_{i=1}^N(y_i-{{\widehat{y}}_i)}^2}$$

where

$y_i$ is the actual value.

${\widehat{y}}_i$ is the predicted value.

N is the number of observations.

R-squared is a statistical measure that represents the proportion of the variance for the dependent variable that is explained by the independent variables in the model. It provides an indication of the goodness of fit.

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^N(y_i-{{\widehat{y}}_i)}^2}{\sum _{i=1}^N(y_i-{\overline{y})}^2}}$$

where

$\overline{y}$ is the mean of the actual value.

MSE is the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value.

$$\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{N}} \sum _{i=1}^N(y_i-{{\widehat{y}}_i)}^2$$

MSE is useful for comparing different models, as a lower MSE indicates a better fit.

MAE measures the average magnitude of the errors in a set of predictions, without considering their direction. It is the average of the absolute differences between predicted and actual values.

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{N}} \sum _{i=1}^N|y_i-{\widehat{y}}_i|$$

MAE is easier to interpret than RMSE because it gives a clear view of the average error.

The machine learning models used in this study were carefully tuned using specific hyperparameters to optimize their performance, based on the regression learner application in MATLAB 2022a.

Table 3. Hyperparameter settings for machine learning models [51].

Model Type	Specifications	Hyperparameters
Linear Regression	Linear	Terms: Linear; Robust option: Off
	Robust Linear	Terms: Linear; Robust option: On
Regression tree	Fine	Minimum leaf size: 4; Surrogate decision splits: Off
	Medium	Minimum leaf size: 12; Surrogate decision splits: Off
	Coarse	Minimum leaf size: 36; Surrogate decision splits: Off
Support vector machine	Linear SVM	Kernel function: Linear; Kernel scale: Automatic; Box constraint: Automatic; Epsilon: Auto; Standardize data: Yes
	Quadratic SVM	Kernel function: Quadratic; Kernel scale: Automatic; Box constraint: Automatic; Epsilon: Auto; Standardize data: Yes
	Cubic SVM	Kernel function: Cubic; Kernel scale: Automatic; Box constraint: Automatic; Epsilon: Auto; Standardize data: Yes
	Fine Gaussian	Kernel function: Gaussian; Kernel scale: 1.1; Box constraint: Automatic; Epsilon: Auto; Standardize data: Yes
	Medium Gaussian	Kernel function: Gaussian; Kernel scale: 4.5; Box constraint: Automatic; Epsilon: Auto; Standardize data: Yes
	Coarse Gaussian	Kernel function: Gaussian; Kernel scale: 18; Box constraint: Automatic; Epsilon: Auto; Standardize data: Yes
Ensemble trees	Boosted Trees	Minimum leaf size: 8; Number of learners: 30; Learning rate: 0.1
	Bagged Trees	Minimum leaf size: 8; Number of learners: 30
Gaussian process regression	Squared Exponential GPR	Basis function: Constant; Kernel function: Squared Exponential; Use isotropic kernel: Yes; Kernel scale: Automatic; Signal standard deviation: Automatic; Sigma: Automatic; Standardize data: Yes; Optimize numeric parameters: Yes
	Matern 5/2 GPR	Basis function: Constant; Kernel function: Matern 5/2; Use isotropic kernel: Yes; Kernel scale: Automatic; Signal standard deviation: Automatic; Sigma: Automatic; Standardize data: Yes; Optimize numeric parameters: Yes
	Exponential GPR	Basis function: Constant; Kernel function: Exponential; Use isotropic kernel: Yes; Kernel scale: Automatic; Signal standard deviation: Automatic; Sigma: Automatic; Standardize data: Yes; Optimize numeric parameters: Yes
	Rational Quadratic GPR	Basis function: Constant; Kernel function: Rational Quadratic; Use isotropic kernel: Yes; Kernel scale: Automatic; Signal standard deviation: Automatic; Sigma: Automatic; Standardize data: Yes; Optimize numeric parameters: Yes
Artificial neural network	Narrow Neural Network	Number of fully connected layers: 1; First layer size: 10; Activation: ReLU; Iteration limit: 1000; Regularization strength (Lambda): 0; Standardize data: Yes
	Medium Neural Network	Number of fully connected layers: 1; First layer size: 25; Activation: ReLU; Iteration limit: 1000; Regularization strength (Lambda): 0; Standardize data: Yes
	Wide Neural Network	Number of fully connected layers: 1; First layer size: 100; Activation: ReLU; Iteration limit: 1000; Regularization strength (Lambda): 0; Standardize data: Yes
	Bilayered Neural Network	Number of fully connected layers: 2; First layer size: 10; Second layer size: 10; Activation: ReLU; Iteration limit: 1000; Regularization strength (Lambda): 0; Standardize data: Yes
	Trilayered Neural Network	Number of fully connected layers: 3; First layer size: 10; Second layer size: 10; Third layer size: 10; Activation: ReLU; Iteration limit: 1000; Regularization strength (Lambda): 0; Standardize data: Yes
Kernel	SVM Kernel	Learner: SVM; Number of expansion dimensions: Auto; Regularization strength (Lambda): Auto; Kernel scale: Auto; Epsilon: Auto; Iteration limit: 1000
	Least Squares Regression Kernel	Learner: Least Squares Kernel; Number of expansion dimensions: Auto; Regularization strength (Lambda): Auto; Kernel scale: Auto; Iteration limit: 1000

summarizes the hyperparameter settings for each model. The selection of these hyperparameters was guided by MATLAB’s built-in optimization features, which streamline model configuration and ensure a systematic approach to improving performance.

For instance, in SVM models, various kernel functions (linear, quadratic, cubic, Gaussian) were tested to capture different patterns in the data, as MATLAB’s regression learner provides an efficient way to experiment with these kernels. The hyperparameters for SVM models, such as kernel scale and box constraint, were chosen based on automatic tuning by MATLAB, which optimizes them to minimize the prediction error. Similarly, GPR models were tested with different kernel functions (e.g., squared exponential, Matern 5/2, rational quadratic) to find the best fit for the data’s underlying variability, with MATLAB automatically adjusting signal standard deviation and kernel scale for optimal performance.

For ensemble trees, hyperparameters like the number of learners and learning rates in Boosted trees were selected through MATLAB’s cross-validation and grid search process, ensuring the models are neither overfitted nor underfitted. The regression trees (fine, medium, coarse) and artificial neural networks (narrow, medium, wide) were similarly configured using MATLAB’s recommended settings for leaf size, layer size, and iteration limits based on model accuracy and computational efficiency.

In all cases, hyperparameters were tuned using a combination of empirical testing, prior studies, and MATLAB’s internal optimization functions, ensuring robust and reliable model performance while minimizing the potential for overfitting. These choices were specifically made to align with the strengths of MATLAB 2022a’s regression learner application, which provides a structured and powerful environment for optimizing machine learning models.

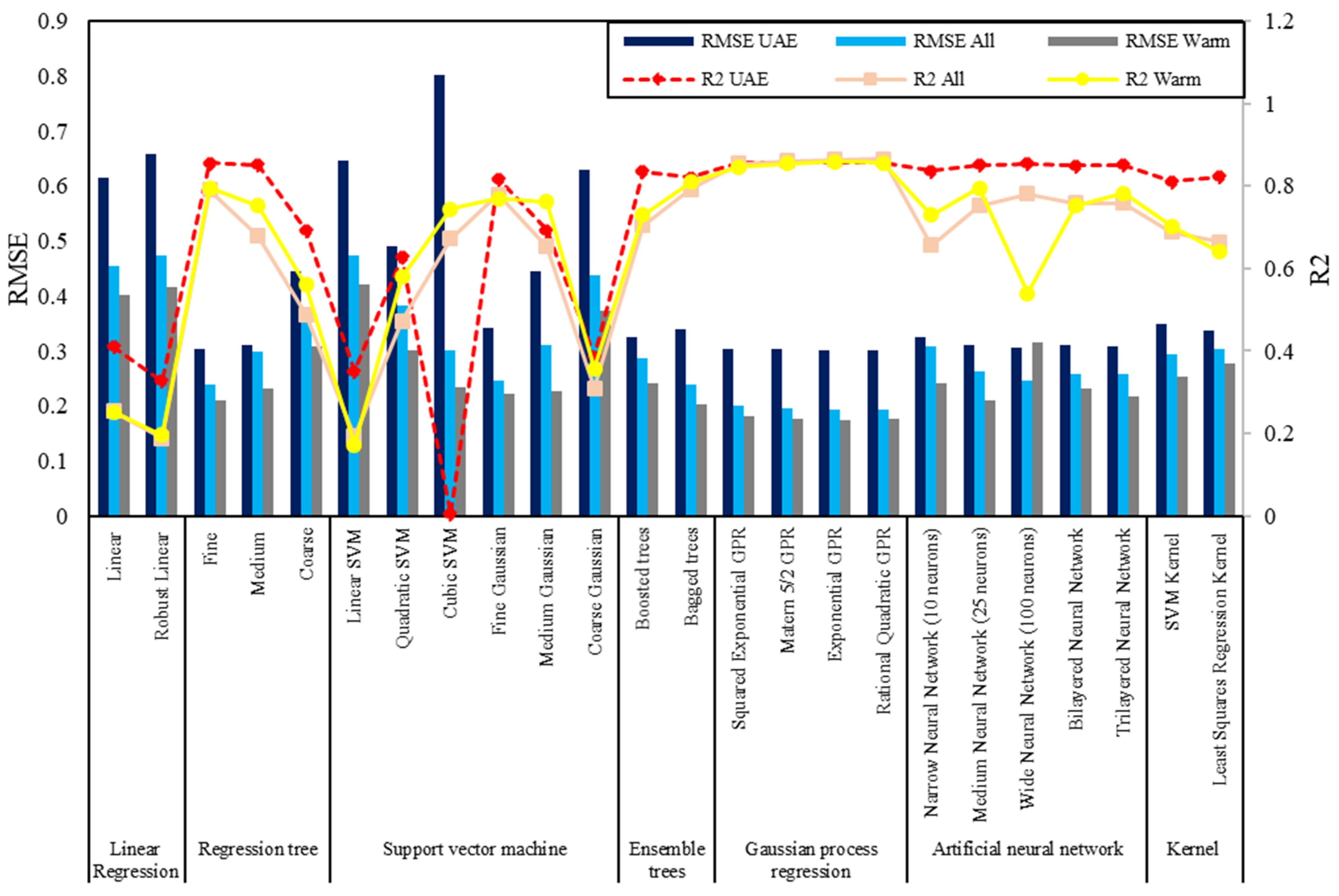
After training the models, their performance was evaluated using the performance measures (RMSE, R2, MSE, and MAE). Cross-validation techniques were employed to ensure the models were generalizable and performed well on unseen data. The models with the lowest error rates and highest R2 values were selected as the best-performing models for each climatic scenario.

4. Results and Discussions

4.1. Statistical Analysis

Table 4. Descriptive statistics for UAE MOEI dataset.

Variable	Mean	SD	Minimum	Q1	Median	Q3	Maximum	Skewness
Age (years)	4.83	2.54	1.00	2.00	5.50	7.00	8.00	−0.36
L2 Thickness (mm)	134.65	176.30	0.00	0.00	0.00	300.00	450.00	0.78
L3 Thickness (mm)	239.10	42.56	100.00	230.00	250.00	250.00	330.00	−0.20
L4 Thickness (mm)	150.28	52.17	40.00	120.00	180.00	180.00	200.00	−1.42
Total Thickness (mm)	524.04	137.74	320.00	430.00	480.00	680.00	780.00	0.45
AADTT	5110.00	6995.00	459.00	989.00	2402.00	5320.00	29,650.00	2.09
Temperature (°C)	26.96	0.55	9.73	26.40	26.91	27.35	27.92	0.46
Precipitation (mm)	87.92	25.13	46.50	59.30	103.55	106.90	107.70	−0.75
Humidity max (%)	75.50	2.22	73.00	74.00	74.50	78.00	79.00	0.55
Humidity min (%)	28.00	2.00	26.00	26.00	28.00	28.00	32.00	1.00
IRI (m/km)	1.31	0.85	0.01	0.84	1.04	1.38	6.82	1.89

outlines the descriptive statistics for the UAE model, using localized data from the MOEI. These data includes pavement age (mean 4.83 years), L2 thickness (mean 134.65 mm), L3 thickness (mean 239.10 mm), L4 thickness (mean 150.28 mm), total thickness (mean 524.04 mm), AADTT (mean 5110.00), temperature (mean 26.96 °C), precipitation (mean 87.92 mm), max humidity (mean 75.50%), min humidity (mean 28.00%), and the IRI (mean 1.31 m/km).

Table 5. Descriptive statistics for all-climate LTPP.

Variable	Mean	SD	Minimum	Q1	Median	Q3	Maximum	Skewness
Age (years)	14.23	10.21	0.00	7.00	12.00	19.00	51.00	1.10
L2 Thickness (mm)	244.81	169.58	81.00	152.00	203.00	305.00	1219.00	3.20
L3 Thickness (mm)	145.39	86.59	10.00	86.50	122.00	203.00	538.00	1.14
L4 Thickness (mm)	83.56	63.27	5.00	30.00	76.00	114.00	297.00	0.89
Total Thickness (mm)	473.76	226.13	178.00	320.00	424.50	544.00	1532.00	2.32
AADTT	727.10	723.30	0.00	248.00	638.00	1112.00	11,707.00	5.63
Temperature (°C)	15.95	5.43	−1.10	11.60	16.90	20.00	24.80	−0.39
Precipitation (mm)	1070.30	477.20	53.60	845.20	1039.60	1325.40	3708.80	0.78
Humidity max (%)	113.56	6.36	92.00	110.00	114.00	118.00	137.00	−0.40
Humidity min (%)	19.70	10.77	2.00	12.00	19.00	27.00	51.00	0.30
IRI (m/km)	1.24	0.54	0.56	0.84	1.08	1.51	4.45	1.63

presents the descriptive statistics for the “all-climate” model using data extracted from the LTPP database. The data include variables such as pavement age (mean 14.23 years), Layer 2 (L2) thickness (mean 244.81 mm), L3 thickness (mean 145.39 mm), L4 thickness (mean 83.56 mm), total thickness (mean 473.76 mm), AADTT (mean 727.10), temperature (mean 15.95 °C), precipitation (mean 1070.30 mm), max humidity (mean 113.56%), min humidity (mean 19.70%), and the IRI (mean 1.24 m/km). Finally,

Table 6. Descriptive statistics for warm-climate LTPP.

Variable	Mean	SD	Minimum	Q1	Median	Q3	Maximum	Skewness
Age (years)	13.37	9.53	0.00	6.50	11.00	18.00	51.00	1.23
L2 Thickness (mm)	215.11	90.17	86.00	152.00	203.00	292.00	572.00	0.69
L3 Thickness (mm)	135.27	88.99	10.00	84.00	107.00	175.00	538.00	1.52
L4 Thickness (mm)	76.42	59.40	5.00	23.00	59.00	110.00	297.00	0.88
Total Thickness (mm)	426.80	140.06	199.00	310.00	402.00	509.00	811.00	0.65
AADTT	722.50	563.50	1.00	270.00	785.00	1054.00	4080.00	1.77
Temperature (°C)	18.65	3.33	7.60	16.70	17.70	22.80	24.80	0.03
Precipitation (mm)	1084.30	480.00	53.60	880.30	1039.60	1258.20	3708.80	1.20
Humidity max (%)	112.62	6.65	92.00	110.00	113.00	117.00	137.00	−0.31
Humidity min (%)	19.55	11.32	2.00	12.00	19.00	28.50	51.00	0.48
IRI (m/km)	1.16	0.49	0.56	0.80	1.02	1.37	3.76	1.49

provides descriptive statistics for the “warm-climate” model, also using LTPP data but focusing on warmer regions. The variables include pavement age (mean 13.37 years), L2 thickness (mean 215.11 mm), L3 thickness (mean 135.27 mm), L4 thickness (mean 76.42 mm), total thickness (mean 426.80 mm), AADTT (mean 722.50), temperature (mean 18.65 °C), precipitation (mean 1084.30 mm), max humidity (mean 112.62%), min humidity (mean 19.55%), and the IRI (mean 1.16 m/km). These tables collectively provide a comprehensive overview of the data utilized in developing and validating the predictive models for the IRI across different climatic conditions.

Figure 2a illustrates the histogram of the IRI values for the UAE dataset. The distribution is more tightly clustered, with the IRI values mostly ranging from 0.8 to 1.5 m per kilometer and a peak frequency around an IRI of 1.0 to 1.2 m per kilometer. This indicates that the majority of pavements in the UAE dataset maintain relatively high roughness levels, with fewer sections exhibiting extreme roughness compared to the LTPP datasets. Figure 2b shows the histogram of the IRI values for the all-climate LTPP dataset. The distribution indicates that the IRI values predominantly range between 0.6 and 1.8 m per kilometer, with a peak frequency around 0.8 to 1.0 m per kilometer. This suggests that most pavements in the all-climate dataset maintain relatively low roughness levels, though there is a noticeable tail extending towards higher IRI values up to 4.2 m per kilometer. Figure 2c presents the histogram of the IRI values for the warm-climate LTPP dataset. Similar to the all-climate LTPP dataset, the IRI values are mostly concentrated between 0.5 and 1.5 m per kilometer, with an IRI peak around 0.8 to 1.0 m per kilometer. The warm-climate dataset also shows a tail extending towards higher IRI values, but the overall distribution indicates smoother pavement conditions compared to the all-climate dataset. Collectively, these histograms highlight the variations in pavement roughness across different climatic conditions and emphasize the need for tailored predictive models to accurately assess and manage pavement performance.

The correlation heatmap matrix for the UAE dataset (Figure 3a) presents unique insights tailored to the specific environmental and traffic conditions of the region. The IRI shows a significant positive correlation with AADTT (0.44), indicating that higher traffic volumes, particularly from heavy trucks, are a primary contributor to pavement roughness in the UAE. The negative correlation between the IRI and maximum humidity (−0.30) suggests that higher humidity levels may contribute to smoother pavement surfaces, possibly due to reduced material degradation in moist conditions. The age of the pavement also shows a positive correlation with the IRI (0.35), aligning with the trend observed in other datasets. However, the correlations between structural layer thicknesses and the IRI are generally weaker in the UAE dataset, implying that factors such as traffic and climate play a more dominant role in influencing pavement roughness. The matrix highlights the distinctive factors affecting pavement performance in the UAE, emphasizing the need for localized predictive models.

The correlation heatmap matrix for the all-climate LTPP dataset (Figure 3b) visually represents the relationships between various structural, traffic, climate, and performance parameters, offering a comprehensive overview of how these factors interact and influence pavement roughness. Heatmaps are essential tools for identifying patterns of correlation between variables, allowing researchers to quickly discern which factors may have a significant impact on outcomes like the IRI. In this analysis, the IRI shows a moderate positive correlation with pavement age (0.18), suggesting that as pavements age, their roughness tends to increase. On the other hand, the IRI is negatively correlated with temperature (−0.33) and total thickness (−0.06), indicating that higher temperatures and thicker pavements are generally associated with smoother road surfaces. The heatmap also reveals strong positive correlations between L2 thickness and total thickness (0.85), as well as L3 thickness and total thickness (0.60), underscoring the interdependence of different structural layers in the pavement’s overall integrity. Additionally, a negative correlation between temperature and maximum humidity (−0.36) highlights the inverse relationship often observed between these climatic factors. Overall, the heatmap provides valuable insights into the complex interactions between the various variables that influence pavement roughness across different climatic conditions, helping to inform better decision-making in pavement design and maintenance.

The correlation heatmap matrix for the warm-climate LTPP dataset (Figure 3c) reveals distinct patterns in the relationships between the variables. The IRI shows a stronger positive correlation with pavement age (0.33) compared to the all-climate dataset, indicating a more pronounced impact of aging on pavement roughness in warm climates. This could be mainly due to oxidative aging of the pavement surface and surface distorting due to high temperatures. The correlation between the IRI and AADTT is also more significant (−0.30), suggesting that higher truck traffic volumes contribute to increased pavement roughness. Interestingly, the correlation between the IRI and temperature remains negative (−0.27), consistent with the all-climate data, but the magnitude is slightly reduced. Total thickness is positively correlated with both L2 thickness (0.54) and L3 thickness (0.73), underscoring the critical role of these layers in determining overall pavement structure. Additionally, temperature and minimum humidity exhibit a strong positive correlation (0.50), highlighting the climatic interplay in warm regions. This matrix underscores the specific factors that influence pavement performance under warm climatic conditions.

4.2. Feature Importance

The random forest analysis for the UAE dataset (Figure 4a) reveals that AADTT is the most significant predictor of the IRI, with a high importance value of 5.30. This finding suggests that heavy truck traffic contributes significantly to pavement roughness in the UAE, potentially due to the lack of strict traffic load enforcement, which may lead to heavier trucks operating on the roads and causing greater wear and tear. The insight gained from the importance of AADTT has practical implications for targeting traffic management and enforcement as key areas to reduce pavement degradation. Age, with an importance value of 1.77, is the second most influential variable, reinforcing the understanding that older pavements accumulate more damage over time, leading to increased roughness. The high importance values for L3 thickness (1.73) and total thickness (1.62) underscore the critical role of structural integrity in maintaining pavement quality. Additionally, maximum humidity (1.46) and temperature (1.40) highlight the influence of environmental factors on pavement performance, indicating that weather conditions should be accounted for in maintenance planning. These insights from the feature importance analysis enable better resource allocation by focusing on the most impactful variables, such as traffic load and structural integrity, to mitigate the IRI.

In the all-climate LTPP dataset (Figure 4b), the analysis identifies age as the most critical factor influencing the IRI, with an importance value of 0.93, suggesting that as pavements age, their roughness increases due to the cumulative effects of traffic and environmental stress. This reinforces the importance of timely pavement maintenance and rehabilitation in extending pavement life. Temperature, with an importance value of 0.79, further emphasizes the significant impact of climatic conditions on pavement performance, indicating that pavements in regions with extreme temperatures may require more frequent interventions. Other notable variables, such as L4 thickness (0.74) and maximum humidity (0.66), highlight the combined effect of structural integrity and environmental factors on the IRI. AADTT, with a value of 0.65, underscores the role of traffic load in contributing to pavement roughness. These insights help in interpreting the model results by demonstrating the relative importance of pavement age, climate, and structural factors in predicting the IRI across diverse climatic regions, allowing for tailored pavement management strategies.

For the warm-climate LTPP dataset (Figure 4c), precipitation emerges as the most influential variable, with an importance value of 0.51, indicating that rainfall has a significant effect on pavement roughness in warm climates. This insight can be attributed to the interaction between high temperatures and precipitation, which accelerates pavement deterioration through thermal expansion and moisture infiltration. This finding highlights the need for more robust pavement designs and drainage systems in regions experiencing warm climates with significant rainfall. L4 thickness (0.51) and temperature (0.48) also play critical roles, indicating that both structural integrity and climatic conditions should be prioritized when developing maintenance plans for warm climates. The analysis also shows the importance of variables such as L3 thickness (0.46) and AADTT (0.31), reflecting the combined impact of traffic and pavement structure on the IRI. These insights help interpret the results by providing a clear understanding of how climatic conditions and pavement structure interact to influence roughness, enabling more informed decisions regarding pavement design and maintenance in warm climates. The comparison between the UAE and warm-climate datasets illustrates both similarities and differences in the factors influencing the IRI, emphasizing the importance of tailoring pavement management strategies to specific regional conditions and traffic patterns.

4.3. Machine Learning Models

The results of various machine learning models applied to the MOEI UAE dataset, as summarized in

Table 7. Machine learning results, MOEI UAE dataset.

Model Type	Specifications	Performance
		RMSE	R-Squared	MSE	MAE	Training Time
Linear Regression	Linear	0.616	0.410	0.380	0.440	17.644
	Robust Linear	0.658	0.327	0.433	0.418	4.554
Regression tree	Fine	0.304	0.856	0.092	0.201	4.362
	Medium	0.310	0.851	0.096	0.205	3.556
	Coarse	0.445	0.693	0.198	0.279	1.919
Support vector machine	Linear SVM	0.646	0.352	0.417	0.413	10.511
	Quadratic SVM	0.490	0.627	0.240	0.289	174.561
	Cubic SVM	0.801	0.004	0.641	0.372	824.149
	Fine Gaussian	0.342	0.818	0.117	0.211	8.542
	Medium Gaussian	0.445	0.693	0.198	0.275	13.033
	Coarse Gaussian	0.629	0.386	0.395	0.404	9.054
Ensemble trees	Boosted trees	0.326	0.835	0.106	0.222	18.353
	Bagged trees	0.339	0.821	0.115	0.231	15.576
Gaussian process regression	Squared Exponential GPR	0.303	0.857	0.092	0.200	733.986
	Matern 5/2 GPR	0.303	0.858	0.092	0.199	324.221
	Exponential GPR	0.302	0.858	0.091	0.200	445.445
	Rational Quadratic GPR	0.302	0.858	0.091	0.199	915.255
Artificial neural network	Narrow Neural Network (10 neurons)	0.324	0.837	0.105	0.212	458.939
	Medium Neural Network (25 neurons)	0.310	0.851	0.096	0.203	491.946
	Wide Neural Network (100 neurons)	0.306	0.854	0.094	0.200	590.943
	Bilayered Neural Network	0.311	0.849	0.097	0.204	614.054
	Trilayered Neural Network	0.309	0.852	0.095	0.202	644.994
Kernel	SVM Kernel	0.348	0.812	0.121	0.206	669.984
	Least Squares Regression Kernel	0.338	0.823	0.114	0.222	674.501

, reveal distinct differences in the predictive capabilities of the models, reflecting the complexity and variability of the data. Regression tree models, particularly the Fine Regression Tree (RMSE = 0.304, R² = 0.856), and ensemble methods like Boosted trees (RMSE = 0.326, R² = 0.835) performed well, capturing non-linear relationships effectively. Gaussian process regression (GPR) models, especially the Exponential and Rational Quadratic GPR (RMSE = 0.302, R² = 0.858), also achieved strong results but at a high computational cost, which may limit their use in real-time applications. In contrast, simpler models like linear regression (RMSE = 0.616, R² = 0.410) and Robust Linear Regression (RMSE = 0.658, R² = 0.327) showed moderate performance, while more complex models like the Cubic SVM (RMSE = 0.801, R² = 0.004) performed poorly, indicating the risk of using overly complex algorithms unsuitable for the data. Artificial neural networks (ANN) also showed strong predictive capabilities, with the Wide Neural Network (RMSE = 0.306, R² = 0.854) being one of the best-performing models, though longer training times were required. Overall, the study demonstrates the superior performance of regression trees, ensemble methods, and GPR models, but emphasizes the need to balance predictive accuracy with computational efficiency. Ensemble models like Boosted trees offer a good compromise, providing high accuracy with lower computational demands compared to GPR models.

The results of the machine learning models applied to the all-climate LTPP dataset, as presented in

Table 8. Machine learning results, all-climate LTPP.

Model Type	Specifications	Performance
		RMSE	R-Squared	MSE	MAE	Training Time
Linear Regression	Linear	0.454	0.254	0.206	0.336	10.602
	Robust Linear	0.474	0.188	0.225	0.329	2.110
Regression tree	Fine	0.240	0.791	0.058	0.130	0.937
	Medium	0.298	0.679	0.089	0.186	0.939
	Coarse	0.376	0.489	0.141	0.246	2.428
Support vector machine	Linear SVM	0.473	0.193	0.223	0.325	1.636
	Quadratic SVM	0.382	0.473	0.146	0.245	6.507
	Cubic SVM	0.301	0.672	0.091	0.171	9.308
	Fine Gaussian	0.246	0.780	0.061	0.128	1.811
	Medium Gaussian	0.310	0.653	0.096	0.174	2.586
	Coarse Gaussian	0.437	0.309	0.191	0.297	1.840
Ensemble trees	Boosted trees	0.286	0.704	0.082	0.184	5.249
	Bagged trees	0.240	0.792	0.057	0.141	9.937
Gaussian process regression	Squared Exponential GPR	0.201	0.854	0.040	0.109	55.090
	Matern 5/2 GPR	0.196	0.861	0.039	0.105	74.855
	Exponential GPR	0.194	0.864	0.038	0.101	69.931
	Rational Quadratic GPR	0.194	0.865	0.037	0.102	121.048
Artificial neural network	Narrow Neural Network (10 neurons)	0.308	0.657	0.095	0.205	62.215
	Medium Neural Network (25 neurons)	0.262	0.753	0.068	0.167	76.051
	Wide Neural Network (100 neurons)	0.246	0.781	0.061	0.139	96.266
	Bilayered Neural Network	0.258	0.759	0.067	0.163	84.251
	Trilayered Neural Network	0.258	0.759	0.067	0.160	91.318
Kernel	SVM Kernel	0.294	0.688	0.086	0.166	94.235
	Least Squares Regression Kernel	0.304	0.665	0.093	0.201	93.114

, exhibit varying levels of effectiveness in predicting pavement roughness, with clear distinctions in performance based on the model type and its specifications. Linear models like linear regression (RMSE = 0.454, R² = 0.254) and Robust Linear (RMSE = 0.474, R² = 0.188) performed poorly, indicating their inability to capture the dataset’s complexity. In contrast, regression tree models, especially the Fine Regression Tree (RMSE = 0.240, R² = 0.791), performed significantly better by effectively modeling non-linear relationships. SVM models also varied, with Fine Gaussian SVM (RMSE = 0.246, R² = 0.780) performing well, while Coarse Gaussian SVM (RMSE = 0.437, R² = 0.309) struggled. Ensemble methods, particularly Bagged trees (RMSE = 0.240, R² = 0.792), were robust and competitive. GPR models, like Exponential and Rational Quadratic GPR, were the top performers (RMSE = 0.194, R² = 0.865), offering precise predictions but with high computational costs. ANN models, such as the Wide Neural Network (RMSE = 0.246, R² = 0.781), also performed well, although with longer training times. Kernel methods showed reasonable performance but required substantial computational resources. Overall, GPR and Regression Tree models were the most effective, with ensemble methods like Bagged trees offering strong, reliable performance.

The results of the machine learning models applied to the warm-climate LTPP dataset, as summarized in

Table 9. Machine learning results, warm-climate LTPP.

Model Type	Specifications	Performance
		RMSE	R-Squared	MSE	MAE	Training Time
Linear Regression	Linear	0.402	0.252	0.161	0.302	21.113
	Robust Linear	0.416	0.196	0.173	0.293	6.805
Regression tree	Fine	0.210	0.796	0.044	0.119	6.267
	Medium	0.231	0.753	0.053	0.148	7.910
	Coarse	0.308	0.561	0.095	0.204	3.568
Support vector machine	Linear SVM	0.422	0.173	0.178	0.292	5.259
	Quadratic SVM	0.301	0.579	0.091	0.200	8.087
	Cubic SVM	0.235	0.744	0.055	0.131	25.096
	Fine Gaussian	0.223	0.769	0.050	0.123	4.490
	Medium Gaussian	0.227	0.761	0.052	0.131	1.484
	Coarse Gaussian	0.372	0.358	0.138	0.258	3.284
Ensemble trees	Boosted trees	0.241	0.730	0.058	0.156	8.385
	Bagged trees	0.202	0.810	0.041	0.122	15.369
Gaussian process regression	Squared Exponential GPR	0.182	0.847	0.033	0.102	40.485
	Matern 5/2 GPR	0.177	0.854	0.031	0.099	53.022
	Exponential GPR	0.174	0.860	0.030	0.096	59.051
	Rational Quadratic GPR	0.176	0.856	0.031	0.097	109.904
Artificial neural network	Narrow Neural Network (10 neurons)	0.241	0.730	0.058	0.160	64.305
	Medium Neural Network (25 neurons)	0.210	0.795	0.044	0.127	73.978
	Wide Neural Network (100 neurons)	0.315	0.539	0.099	0.149	102.781
	Bilayered Neural Network	0.231	0.753	0.053	0.144	87.926
	Trilayered Neural Network	0.217	0.782	0.047	0.131	99.376
Kernel	SVM Kernel	0.253	0.703	0.064	0.147	102.738
	Least Squares Regression Kernel	0.278	0.640	0.078	0.188	100.550

, reveal significant differences in model performance, reflecting the unique challenges posed by warm climates in predicting pavement roughness. Linear models, such as Linear Regression (RMSE = 0.402, R² = 0.252) and Robust Linear (RMSE = 0.416, R² = 0.196), struggled to capture the complexity of the dataset. In contrast, Regression Trees performed well, especially the Fine Regression Tree (RMSE = 0.210, R² = 0.796), which effectively modeled non-linear interactions. SVM models also varied, with Fine Gaussian SVM (RMSE = 0.223, R² = 0.769) performing strongly, while Coarse Gaussian SVM (RMSE = 0.372, R² = 0.358) performed poorly. Ensemble models, particularly Bagged trees (RMSE = 0.202, R² = 0.810), emerged as top performers, underscoring their robustness. GPR models, such as Exponential GPR (RMSE = 0.174, R² = 0.860), were the best overall performers but required high computational resources. ANNs also showed strong predictive power, with the Medium Neural Network (RMSE = 0.210, R² = 0.795) performing well, though over-parameterization in the Wide Neural Network resulted in poorer performance. Kernel methods provided moderate results but were computationally intensive. Overall, GPR and ensemble methods were the best suited for handling the complexities of the warm-climate dataset.

When comparing the results from the MOEI UAE dataset and the warm-climate LTPP dataset, several interesting contrasts and similarities emerge that highlight the influence of regional climatic conditions and data characteristics on model performance. The GPR models consistently outperformed other models in both datasets, with the Exponential GPR achieving an RMSE of 0.174 and an R² of 0.860 in the warm-climate LTPP dataset compared to an RMSE of 0.194 and an R² of 0.864 in the MOEI UAE dataset. This suggests that GPR’s ability to model complex, non-linear relationships and provide uncertainty estimates makes it particularly well suited for diverse climatic conditions. However, while ensemble tree models like Bagged trees performed exceptionally well in both datasets, achieving RMSEs of 0.202 and 0.240 in the warm-climate LTPP and MOEI UAE datasets, respectively, the performance in the MOEI UAE dataset was slightly lower, which may be due to the unique traffic and structural characteristics in the UAE that introduce additional variability. Additionally, SVM models showed stronger performance in the warm-climate LTPP dataset, particularly with the Fine Gaussian SVM achieving an RMSE of 0.223 and an R² of 0.769, compared to the MOEI UAE dataset where the same model had a slightly higher RMSE of 0.342 and a lower R² of 0.818. This difference might reflect the more complex interaction between climatic factors and pavement performance in the UAE, where high temperatures and traffic loads play a more dominant role. Overall, while both datasets benefited from advanced machine learning models, the specific climatic and regional factors inherent to the UAE introduced additional challenges, requiring careful model selection and tuning to achieve optimal performance.

Figure 5 presents a graphical comparison of the performance of various machine learning models evaluated using the UAE, warm-climate, and all-climate datasets. The models are assessed based on their Root Mean Square Error (RMSE) and R-squared (R²) values. The RMSE values are represented by bars, with dark blue indicating the UAE dataset, light blue for all-climate conditions, and gray for warm climates. R² values are illustrated by lines, with red representing the UAE, peach for all climates, and yellow for warm climates. The figure highlights the variation in model performance across different datasets, with models such as Gaussian process regression (exponential and rational quadratic kernels) and ensemble methods like Boosted trees and Bagged trees achieving superior performance, as evidenced by lower RMSE values and higher R² scores. Conversely, models such as Cubic SVM and Coarse Gaussian demonstrate weaker performance, characterized by higher RMSE and lower R² values. This visual representation provides a clear and intuitive comparison, underscoring the relative effectiveness of each model in predicting pavement roughness under different climatic conditions.

Figure 6 illustrates the comparison between measured and predicted IRI values for three different datasets: (a) all-climate LTPP, (b) warm-climate LTPP, and (c) UAE. In Figure 6a, the scatter plot for the all-climate LTPP dataset shows a strong correlation between the measured and predicted IRI values, indicating high model accuracy, as evidenced by the clustering of data points along the 45-degree line. Figure 6b for the warm-climate LTPP dataset also demonstrates a good fit, with most data points closely following the 45-degree line, suggesting reliable predictions by the model under warm climatic conditions. In contrast, Figure 6c for the UAE dataset exhibits a wider spread of data points around the line of equality, indicating some deviations between measured and predicted values. This suggests that while the model performs well overall, there is greater variability in the predictions for the UAE dataset, likely due to the unique environmental and traffic conditions in the region. These visualizations confirm the effectiveness of the developed models in predicting pavement roughness, with particularly strong performance noted in the all-climate and warm-climate scenarios.

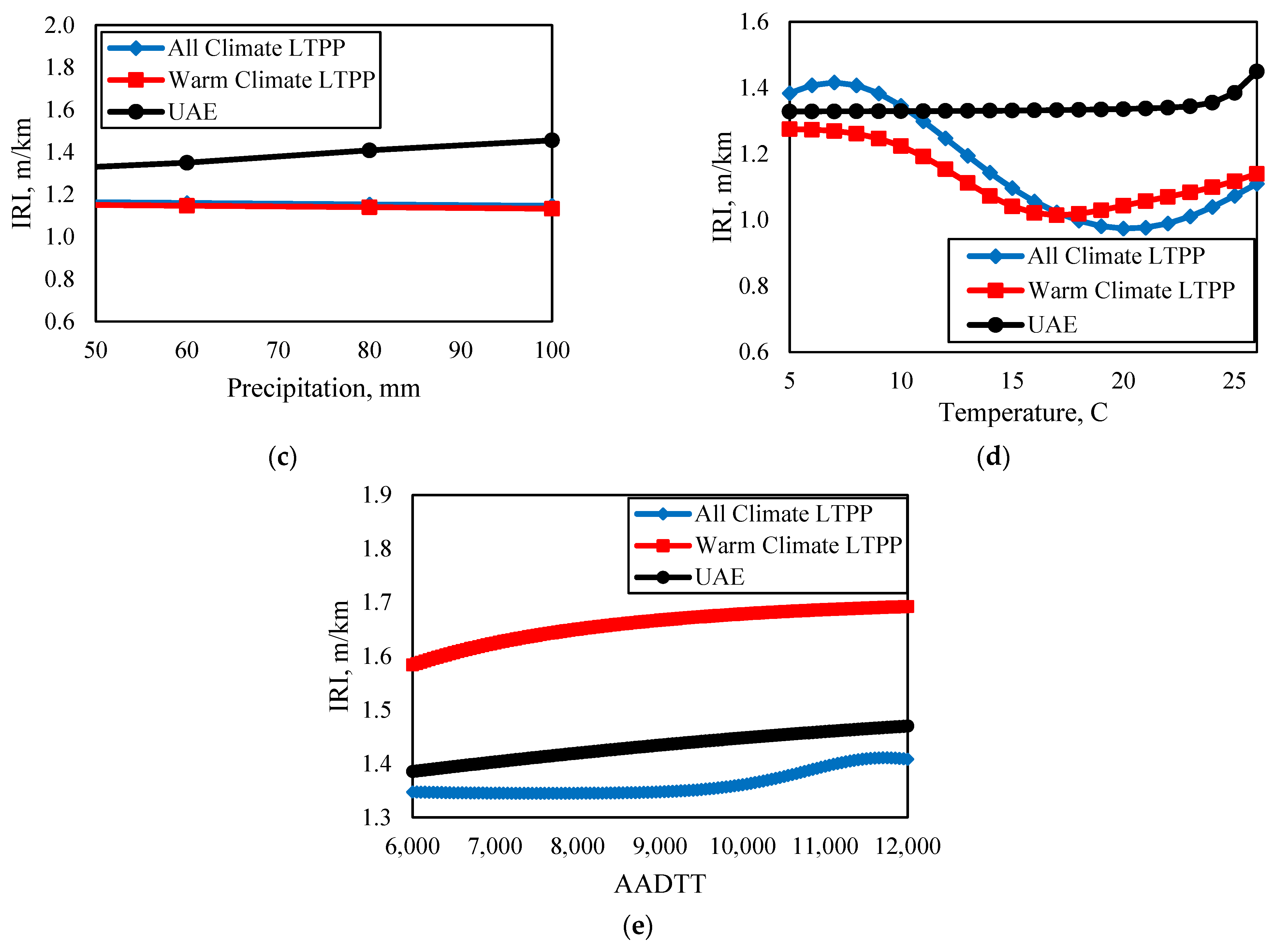
5. Sensitivity Analysis

Figure 7 presents the sensitivity analysis results for the most influential variables affecting pavement performance: (a) age, (b) total thickness, (c) precipitation, (d) temperature, and (e) AADTT. In these analyses, each variable was evaluated while keeping all other variables fixed at their mean values to isolate the effect of each individual factor on the IRI. It is worth noting that the range for all independent variables was set to avoid extrapolations with the three dataset scenarios.

In Figure 7a, the impact of pavement age on the IRI is shown across all datasets. The analysis indicates that older pavements tend to have higher roughness levels. This trend is most pronounced in the all-climate LTPP dataset, suggesting that aging effects are more significant in diverse climatic conditions. The warm-climate LTPP and UAE datasets also show an increase in the IRI with age, but the increase is more severe with the UAE dataset, which may reflect the adverse impact of harsh climate conditions associated with heavy truck traffic.

Figure 7b examines the influence of total pavement thickness on the IRI. An increase in total thickness generally results in an increase in the IRI across all datasets, to a certain total thickness level, after which any further increases in the total thickness results in a positive improvement in the surface roughness by decreasing the IRI. This peak point could be considered as the critical total pavement thickness, whereas increases in this total thickness will start to have a positive impact on the pavement roughness. This can be interpreted where a thicker pavement experiences less fatigue cracking and structural rutting, yet it could experience more rutting coming from the surface layer. The balance between these different distresses can define the critical total pavement thickness. For both the LTPP all-climate dataset and the warm-climate LTPP dataset, the critical total pavement thickness values are found relatively similar (800 mm and 700 mm, respectively). The UAE dataset shows a critical total pavement thickness of 450 mm, which is relatively lower than both LTPP datasets. This outcome reflects different pavement engineering practices and consequent relative impacts of the design factors on the IRI in the UAE compared to the LTPP dataset located mainly in the USA.

In Figure 7c, the relationship between precipitation and the IRI is analyzed considering the UAE precipitation range to avoid extrapolation since it is relatively low compared to the LTPP dataset. For both the all-climate LTPP and warm-climate LTPP datasets, the impact of higher precipitation levels on the IRI seems very minimal, acknowledging that the investigated precipitation range has a very low value compared to extreme precipitation levels across the USA. Interestingly, the UAE dataset demonstrates more sensitivity to precipitation, indicating that local pavements are expected to get worse as rainfall increases.

Figure 7d illustrates the relationship between temperature and the IRI for different datasets. At lower temperatures, there appears to be minimal impact of temperature on IRI values for all datasets. In the all-climate and warm-climate LTTP datasets, temperature increases from 10 to 20 °C seem to slightly decrease IRI values, potentially due to reduced thermal and fatigue cracking in more moderate conditions without significant concerns about rutting. However, as temperatures rise above 20 °C, the IRI begins to increase, likely due to a worse rutting performance under higher temperatures. The UAE dataset exhibits a somewhat different trend, with temperature showing no impact on the IRI until around 23 °C, beyond which further temperature increases result in a noticeable rise in the IRI. This could be attributed to the unique climate and pavement conditions in the UAE, where higher temperatures exacerbate pavement roughness.

Finally, Figure 7e illustrates the effect of AADTT on the IRI across different datasets. As expected, increased truck traffic correlates with higher IRI values in all datasets, highlighting the adverse impact of traffic loading on pavement deterioration. Notably, the warm-climate LTPP dataset shows the steepest rise in the IRI with increasing AADTT, suggesting that pavements in consistently warm climates are more susceptible to damage from heavy truck traffic. The UAE dataset also shows a noticeable increase in the IRI with AADTT, although the slope is less steep than in the warm-climate LTPP dataset, indicating that while heavy traffic does contribute to pavement roughness in the UAE, the effect is somewhat mitigated compared to other regions. The all-climate LTPP dataset exhibits the most gradual increase in the IRI with AADTT, suggesting that in more varied climatic conditions, the impact of heavy truck traffic on pavement deterioration is less severe, potentially due to less adverse effect on moderate climate regions, which are part of the all-climate LTPP dataset.

6. Conclusions

This study developed and evaluated predictive models for the IRI using advanced ML techniques across different climatic conditions. By leveraging data from the LTPP database for diverse and warm climates, and localized data from the MOEI in the UAE, the study provides a comprehensive analysis of pavement performance under varying environmental and traffic conditions. The following conclusions can be drawn from the conducted analysis:

• This study reveals that certain factors play a crucial role in influencing the IRI across different climatic conditions. The most significant factors identified include pavement age, layer thickness, AADTT, temperature, and precipitation. These factors consistently showed high importance across the different models, highlighting their critical impact on pavement performance.
• The correlation analysis showed that traffic-related variables, particularly AADTT, have a strong positive correlation with the IRI, indicating that higher traffic volumes, especially from heavy trucks, significantly contribute to pavement roughness. Climatic factors such as temperature and humidity also exhibited important correlations, with higher temperatures generally associated with smoother pavements due to reduced freeze–thaw cycles, whereas humidity showed a more variable impact depending on the specific regional conditions.
• The machine learning models employed in this study demonstrated varying levels of effectiveness in predicting the IRI. GPR models, particularly those with exponential and rational quadratic kernels, consistently outperformed other models across all datasets, achieving the lowest RMSE and highest R² values. Regression trees, especially the Fine Regression Tree, also showed strong performance, particularly in non-linear data contexts. Ensemble methods, such as Bagged and Boosted trees, provided a robust alternative with high predictive accuracy and lower computational demands compared to GPR models. SVMs and ANNs showed moderate success, with their effectiveness largely dependent on the chosen kernel or network configuration.
• The sensitivity analysis provided specific insights into the influence of various factors on the IRI, confirming the findings from the feature importance rankings. It emphasized the significant impact of traffic loading, particularly AADTT, which was found to be a critical factor in increasing pavement roughness, especially in regions with high heavy truck traffic. The analysis also highlighted the role of structural integrity, with layer thicknesses playing a crucial role in maintaining smoother pavements. Climatic conditions, particularly temperature and precipitation, were shown to have varying impacts depending on the specific regional context. For instance, higher temperatures generally led to a reduced IRI in cooler climates, while in consistently warm regions, the effect was less pronounced. These findings underscore the necessity of tailoring pavement management strategies to the specific environmental and traffic conditions of each region. By doing so, infrastructure managers can ensure more accurate predictions and implement more effective maintenance plans that address the unique challenges posed by different climatic and traffic scenarios.

7. Limitations and Future Research

One key limitation of this study is the basic hyperparameter tuning applied, as more advanced techniques like Bayesian optimization or AutoML could have further improved model performance by automatically selecting optimal configurations. Future work should explore these methods to enhance both accuracy and efficiency.

Another area for improvement is the development of hybrid models that combine the strengths of different algorithms, such as GPR and ensemble methods, to improve predictive accuracy while balancing computational costs.

Additionally, the expansion of datasets is necessary to enhance the generalizability of the models. Future studies should incorporate data from more diverse regions and climates to improve model robustness and applicability across various environmental and traffic conditions.