Prediction of the Response of Masonry Walls under Blast Loading Using Artificial Neural Networks

Abstract

A methodology to predict key aspects of the structural response of masonry walls under blast loading using artificial neural networks (ANN) is presented in this paper. The failure patterns of masonry walls due to in and out-of-plane loading are complex due to the potential opening and sliding of the mortar joint interfaces between the masonry stones. To capture this response, advanced computational models can be developed requiring a significant amount of resources and computational effort. The article uses an advanced non-linear finite element model to capture the failure response of masonry walls under blast loads, introducing unilateral contact-friction laws between stones and damage mechanics laws for the stones. Parametric finite simulations are automatically conducted using commercial finite element software linked with MATLAB R2019a and Python. A dataset is then created and used to train an artificial neural network. The trained neural network is able to predict the out-of-plane response of the masonry wall for random properties of the blast load (standoff distance and weight). The results indicate that the accuracy of the proposed framework is satisfactory. A comparison of the computational time needed for a single finite element simulation and for a prediction of the out-of-plane response of the wall by the trained neural network highlights the benefits of the proposed machine learning approach in terms of computational time and resources. Therefore, the proposed approach can be used to substitute time consuming explicit dynamic finite element simulations and used as a reliable tool in the fast prediction of the masonry response under blast actions.

1. Introduction

Masonry is commonly used in the construction of non-structural and structural walls in residential and commercial buildings in developing and developed countries. The behavior of masonry walls when subjected to in-plane and out-of-plane actions has been investigated for the past decades. Blast loading may lead to the collapse of such buildings. Researchers such as Hao [1], Davidson et al. [2], Knock et al. [3], and Masi et al. [4] conducted laboratory and field blast tests to develop empirical relations of masonry wall damage and blast loading conditions. There is, however, limited data on field tests for walls subjected to blast loading and that is mainly due to safety and cost considerations. Numeral analysis of walls has then become popular and has been proven to provide reliable results. According to Hao [1], the numerical approach generally simplifies the masonry wall to a single degree-of-freedom (SDOF), and from this simplification the wall’s response under blast loading is calculated by investigating the dynamic responses of the SDOF system. The model’s definition is said to influence the computational time each model will take to generate the set of results. In their study, Dorn et al. [5] were able to reduce the computational time and computer memory by assuming the bricks to be rigid and only subjecting the mortar to failure.

As part of the ongoing effort of reducing the computational cost, Pande et al. [6] and Pietruszczak et al. [7] derived the corresponding elastic moduli for brick masonry from the elastic properties of individual components and assumed the masonry material as an orthotropic elastic-brittle material. Research on numerical modelling of masonry under dynamic excitations or blast loading, also integrating micro- and macro-modelling approaches, has garnered increasing interest in recent years. The motivation for this study emanates from the international drive to better understand the behavior of masonry walls under out-of-plane and in-plane loading, in the context of data-driven mechanics. Therefore, the main goal of this paper is to extend existing knowledge by introducing machine learning techniques in predicting the response of masonry walls under different blast loading and standoff distances.

First, parametric explicit dynamic simulations are conducted for a masonry wall, adopting varying blast weight and stand-off distances. The out-of-plane deflection is used as output in the generated dataset. The wall is simulated within non-linear finite element analysis. Unilateral contact and friction laws are introduced to capture discrete damage (opening-sliding) in the interfaces between masonry blocks. A concrete damage plasticity model is also used to capture tensile and compressive damage to the bricks. Explicit dynamic simulations are done using commercial finite element software.

To run and automatically control the parametric finite element simulations, MATLAB R2019a and Python scripts are developed. Once the datasets are developed, ANNs are used to train and test the data. The error is recorded, and tests to random input values are conducted to highlight the efficiency of the method.

The paper is structured as follows: In Section 2 of this article, the relevant literature review is presented. In Section 3.1, failure modes of masonry walls are provided and modeling approaches that can be used to capture these modes are briefly discussed. This part includes, among others, information on the geometry of the walls, the material constitutive description, and details of the blast load simulation. In Section 3.2, the blast wave propagation is discussed. Section 3.3 and Section 3.4 provide an overview of artificial neural networks and the architecture of the adopted network. Section 3.5 and Section 3.6 detail the adopted methodology and the finite element models which are used for the development of the dataset. In Section 3.7, the details of the finite element model are presented. In Section 3.8 and Section 3.9, the contact mechanics and the wall’s response are provided. In Section 4 and Section 5, results and discussions derived from the proposed network are provided. Lastly, in Section 6, the conclusions of this investigation are presented.

2. Literature Review

Literature findings on the topic of blast actions on masonry walls are discussed in this section. Su et al. [8] performed a numerical investigation of unreinforced masonry walls subjected to blast loads. In their study, a distinctive model, in which mortar and brick units of masonry are discretized individually was used to model the performance of masonry and the contact between the masonry. On the other hand, Ishfaq et al. [9] numerically studied the out-of-plane behavior of confined dry-stacked masonry walls under blast loading. Their study considered four different test cases using a charge weight of 4 k, 8 kg, 12 kg, and 19 kg of Wabox explosive.

Masi et al. [4] investigated the dynamic behavior of non-standard curvilinear masonry geometries under blast loading using the discrete element method. This approach allowed the consideration of detailed mechanical and geometrical properties of masonry. One of the important findings from their study was that masonry joints with zero dilatancy result in greater out-of-plane deformations and decreased membrane deformations. Additionally, it was discovered that cohesion and tensile strength have very little bearing on the structural reaction. Investigating the effect of material properties on the blast response of walls is of utmost importance. Anas et al. [10] conducted an experimental study on clay-brick and concrete block unreinforced walls. Their study highlighted that the effect of brick strength and mortar had an insignificant role to play on the maximum mid-span deflection under reflected pressures that are above 2 MPa. The same study concluded that increasing the Young’s modulus of masonry is an effective way of reducing the maximum mid-span deflection.

A study by Zhang et al. [11] investigated the dynamic behavior of a clay-brick masonry wall under a blast weight of 21.5 kg TNT at 4.0 m standoff and 50.8 kg TNT at 5.5 m standoff. According to the study findings presented in this paper, the thickness of the wall and its boundary connection with the frame have a major impact on how blast resistance is developed. This study further concluded that the reaction and damage pattern of walls exposed to medium- and far-range explosions are significantly influenced by the wall’s boundary constraints, length, breadth, thickness, and other dimensional parameters.

Similarly, Thango et al. [12] investigated the failure response of masonry walls subjected to blast loading using nonlinear finite element analysis. This investigation aimed in highlighting potential collapse mechanisms by testing different blast load parameters, namely, the weight of the explosive and the standoff distance between the source of the explosion and the structure. Explosive weights of 100 kg TNT, 200 kg TNT and 1150 kg TNT were considered with the varying standoff distances which included distances such as 20 m, 50 m, and 100 m. Additionally, Thango et al. [12], investigated the influence of an opening (window) on the wall and the results highlighted that the present of an opening may reduce the effect of the blast action by decreasing the out-of-plane response of the structure.

Recently, the rapid advances in data processing techniques and the emergence of different artificial intelligence approaches have led to the development of different applications for masonry walls. According to Jasmine et al. [13] and Thai [14], Machine Learning (ML) is a major subfield of artificial intelligence (AI) that deals with the study, design, and development of algorithms that can learn from the data itself and make predictions using the learned data. Additionally, machine learning methods use programmed algorithms to optimize a performance standard based on previously accumulated data [15]. There are different types of machine learning algorithms, which have been adopted in applications related to structural engineering, such as Artificial Neural Networks (ANN), Support Vector Machines, Nearest Neighbors and Random Forests. These methods can deal with a significant large amount of data. Data for such studies is acquired in situ or using numerical models.

Friaa et al. [16] used ANNs to predict the elastic membrane and bending constants of the equivalent Love–Kirchhoff plate of hollow concrete blocks masonry wall. Drosopoulos and Stavroulakis [17] used the ML approach in multi-scale computational homogenization to obtain the masonry wall’s non-linear response. In Cascardi et al. [18] an analytical model for predicting the shear strength of Fiber Reinforced Mortars (FRM) masonry by using the ANN approach is proposed and proven to be able to predict the shear strength of the FRM walls.

Zhang et al. [19] adopted ANN techniques to predict the cracking patterns of masonry wallets that are subjected to vertical loading. Also, studies by Zhou et al. [20] aimed to use ANN to predict the failure of a wall panel subjected to lateral loading using laboratory data. In the study conducted by Plevris and Asteris [21], ANN was applied to approximate the failure surface of a brittle anisotropic material. In their study, the ANN was trained using the available experimental data.

Chomacki et al. [22] used ML methods to predict the damage of the residential houses that are exposed to the industrial environment of mines. In their study, four machine learning methods were considered, namely, the Probabilistic Neural Network, Support Vector Machine, Naive Bayes Classification and Bayesian Belief Network. Amongst the four methods, it was highlighted that the selection of the Bayesian Belief Network was the most effective approach. This raised the importance of ML methods for efficient structural or damage assessments and design activities.

In the study conducted by Remennikov et al. [23], an ANN was used to predict the effectiveness of blast wall barriers. Experimental data sets for a wide range of scaled wall heights and a large area of scaled space behind the wall were adopted to train and validate the ANN. A total of 285 measurements were used in their study and the cross-validation techniques were adopted in which the training set was employed to decide the connection weight, whereas the validation set was used to evaluate the performance of the model. This study highlighted the feasibility of using ANN for fast prediction of barrier wall’s response against blast loading.

Bewick et al. [24] developed a neural-network model-based engineering tool to estimate the peak pressure, impulse, time of arrival, and time of duration of blast loads on buildings protected by simple barriers. Their study used 91 experimental datasets in which 81 simulations were used to train the network and the other 10 simulations were used to verify and validate the accuracy of the network. It was highlighted that due to the dispersion of the available training data, the model had a constrained range of application even though it demonstrated strong correlation with the data. This study showed the development of an ANN methodology for a range of values for the variables of charge weight, charge to barrier standoff, barrier to structure standoff, barrier height, and location on the structure face as well as roof loads. This work also highlighted that given sufficient data and training, neural networks can provide efficient solutions to nonlinear problems to any degree of accuracy.

A study conducted by Huang et al. [25] used a dataset of 76 explosion observations to develop a machine learning model that will be able to predict the damage scale of buildings subjected to a fertilizer plant explosion. This study evaluated three machine learning models which included k-Nearest Neighbour, ANN, and gradient boosting (a sub technique of decision trees). The input parameters in this study included the building category, building structure, wall surface material, distance from the blast centre, year built, and the shockwave overpressure. It was concluded that the gradient boosting and the ANN models offered better prediction accuracy. The importance of ML models was highlighted in this work as being a tool that can assist government decision makers, architects, and engineers in selecting the most resilient structure design and material for buildings.

Salem et al. [26] used 100 experimental data for blast performance of a masonry wall. In their study, four different ML models were tested and assessed. The models were developed using linear, polynomial, and random forest regressions, and an artificial neural network. Comparing the different models, it was concluded that the artificial neural network was the most reliable model. This study highlighted the ANN’s ability to generate the blast curves (P-I curves) faster than traditional methods. The P-I diagram produced is thought to be a quicker and less expensive method for further resilience evaluations.

Khaleghi et al. [27] utilized the ANN to examine how unreinforced masonry walls responded to in-plane loading. This study examined how a wall’s reduced ability to support weight may result in structural deterioration. A number of 49 different configurations were considered and a set of designed experiments were used to generate numerical simulations for dataset creation. The ability of ANNs to precisely forecast the initial stiffness and loss in load capacity resulting from unreinforced masonry wall piercing was determined by this study. The peak load and initial stiffness were used as the inputs of the ANN.

Existing prediction techniques, such as numerical methods, call for a solid foundation in computer modeling, as well as a significant investment in time and resources. Similarly, analytical models are dependent on assumptions based on the complex pattern of the structural configuration. The ability to predict damage patterns has recently made data-driven approaches more popular. Comparative studies have been done to evaluate the accuracy of machine learning approaches. The study conducted by Chopra et al. [28] proved that neural networks had the highest predictive accuracy.

Various researchers have developed ANN models to predict masonry wall response mainly considering in-plane actions. The behaviour of masonry has been numerically and experimentally studied by many researchers but to the authors’ best knowledge there have not been many attempts to apply ML techniques for the prediction of masonry response under blast loading. Thus, although studies highlighting conventional, finite element analysis solutions on masonry response against blast actions can be found on literature, it seems that less studies are identified, introducing machine learning techniques to investigate blast actions. This article aims to contribute to this area by proposing a machine learning formulation that can be adopted to predict fast and accurately the response of masonry walls under blast actions.

3. Material and Methods

3.1. Failure Mechanisms of Masonry

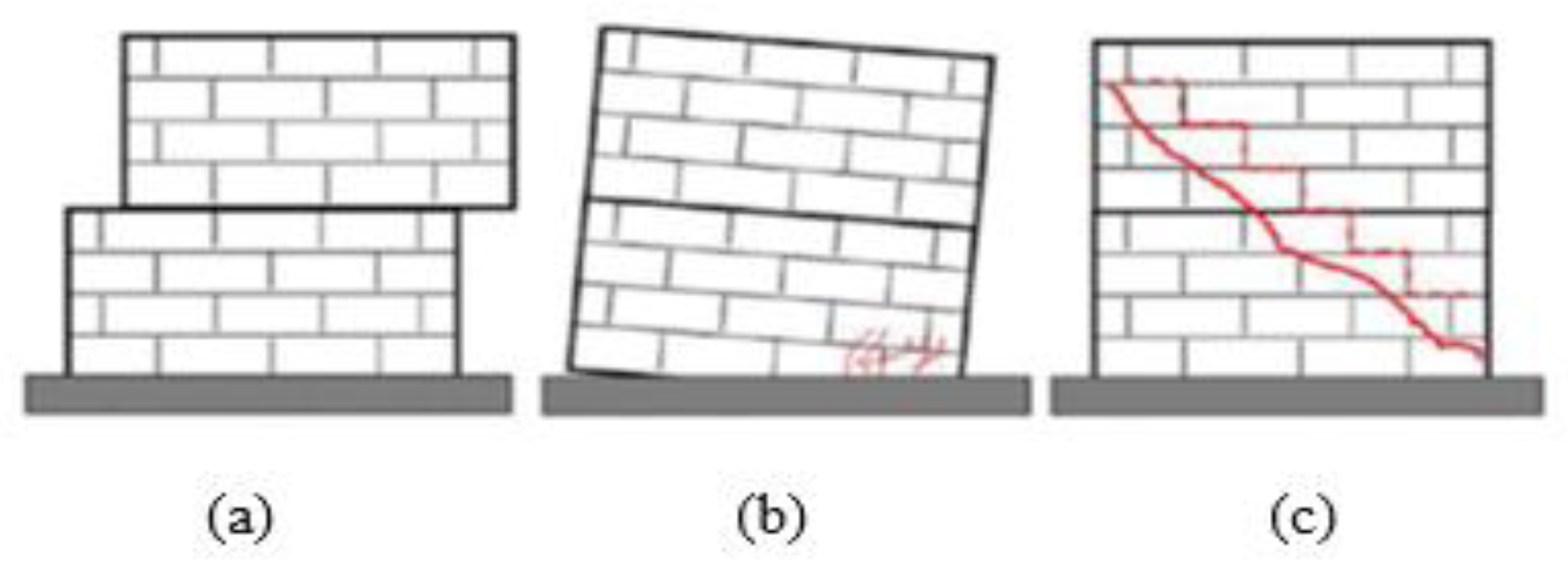
Typically, load-bearing masonry wall panels exposed to in-plane lateral and vertical loads will exhibit either flexural or shear behavior, each with a distinct set of related failure mechanisms. Figure 1 below depicts the failure modes for walls that are subjected to in-plane loading.

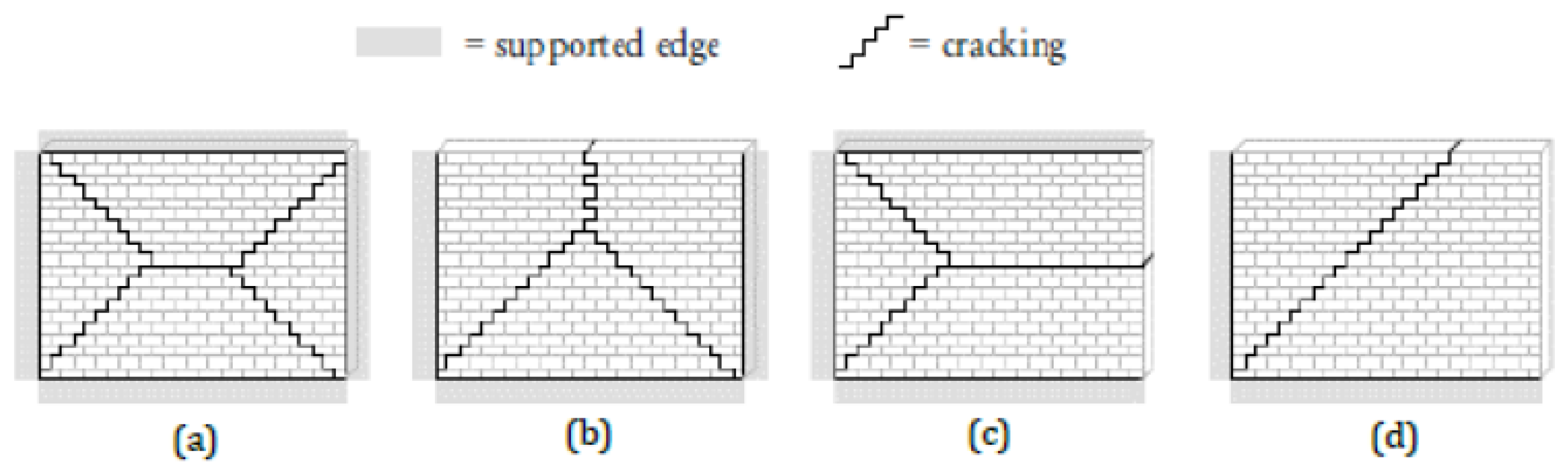
Due to the residual tensile strength of the brickwork material, the behavior caused by an out-of-plane stress, such as an explosion, shares some similarities with flexural behavior [29]. Walls that are subjected to out-of-plane loading such as blast loading, will often have the orientation of the internal stresses within the wall and the resulting crack pattern developed is dictated by the boundary conditions or the position of its supported edges. Figure 2 shows the various types of wall support shapes and the associated out-of-plane flexure cracking patterns.

3.2. Wave Propagation

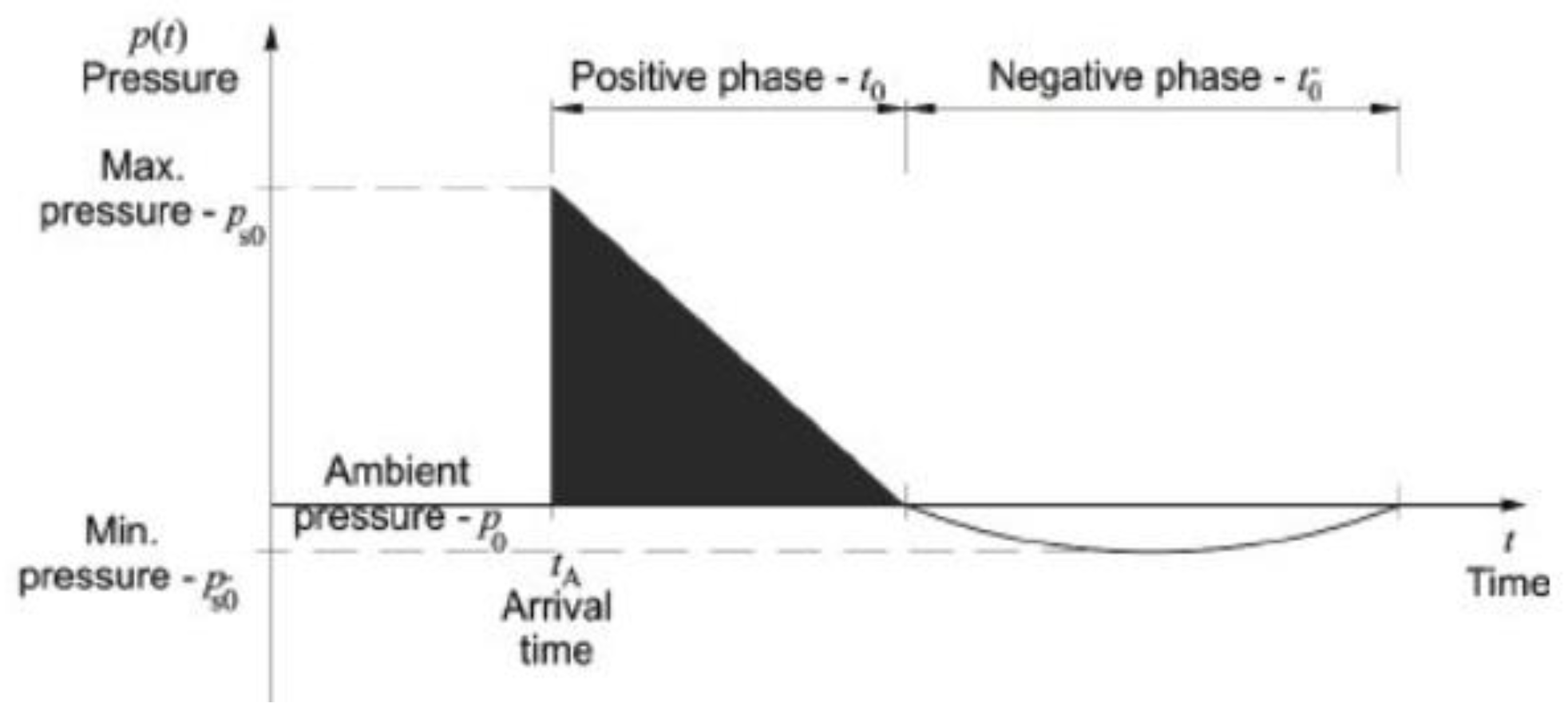
In a blast, wave propagation describes how energy from an explosion spreads out and impacts nearby structures. Mining activities that entail blasting have been considered as case study for this paper. When an explosion happens, a shock wave is produced that travels through the air quickly, causing a significant rise in pressure and temperature [31]. Various researchers have argued that a shock wave can cause significant damage to buildings, especially if they are near the blast.

According to Baumgart [32], the strength and direction of the shock wave depend on various factors, including the size and type of the explosive device, the distance between the explosion and the building, and the near terrain. When designing buildings for blast resistance, it is important to consider how the shock wave will propagate through the structure, and to design walls, floors, and roofs that can withstand the pressure and forces generated by the blast. Low-cost rural houses are unlikely to have its design or construction taking into account such loading. Figure 3 depicts the typical blast wave propagation curve.

When a shock wave hits a structure, reflection occurs, which is described by the reflection coefficient c_r:

$$C_r=\frac{p_{ref}}{p_{inc}}.$$

(1)

where p_ref is the reflected pressure and p_inc the incident pressure, respectively. Understanding the wave propagation curve is critical in analysing the blast loading on structures. To determine the magnitude of peak overpressure, two major factors are utilized: the charge weight and the standoff distance.

3.3. An Overview of Neural Network

Artificial Neural Network (ANN) is a machine learning technique composed of a system of interconnected neurons [14,34]. ANN is built on a collection of connected nodes known as artificial neurons, which are basically the prototypical neurons found in the genetic animal brain. Furthermore, using learning algorithms, the interconnected nodes can have the ability to recognize the hidden patterns and correlations in the given raw data and can even cluster and classify it over some time through the learning process [35].

The networks consist of neurons which are basic units in this operating system. Each artificial neuron, or node, is connected to others and has a corresponding weight and threshold. The development process of the model includes data collection and training the data set. Training data is used by neural networks to develop their accuracy over time. Since many of the links between inputs and outputs in real life are non-linear and complex, it is crucial that ANNs be able to learn and represent non-linear and complex interactions, hence the training and aiming of high accuracy levels of output received.

According to Asteris et al. [36], ANNs are information-processing models arranged for a specific application through a training process. Once the network is well trained, a specific output is obtained from specified input data. The common advantage of ANN is that it can learn from experience, so that it is possible to train the network to recognise certain patterns to improve its performance or better understand or predict the modes of failure in structures.

There are different types of neural networks. They are often classified depending on their structure, data flow, neurons used and their density, layers, and their depth activation filters. These types include Convolutional Neural Network, Multilayer Perceptron, Radial Basis Functional Neural Network, Feedforward Neural Network, and Modular Neural Network.

3.4. The Architecture of an Artificial Neural Network

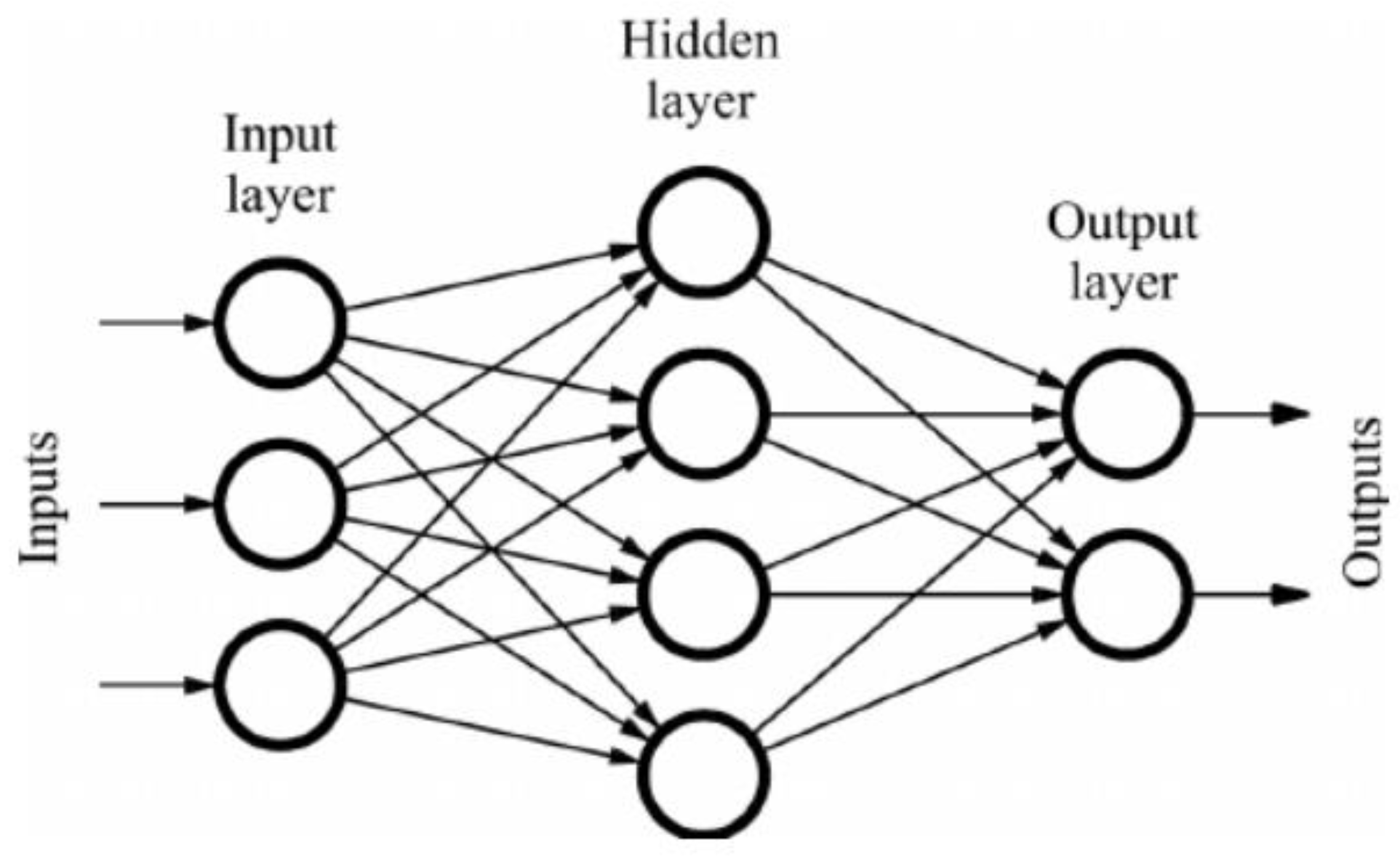
In this paper, the feedforward backpropagation neural network developed in MATLAB R2019a is used. The feedforward ANN’s structure has three forms of layers, namely input, hidden, and output layers. They are mostly used in pattern generation, pattern recognition, and classification. A feedforward neural network has the capability to correlate vector inputs with vector outputs, provided that the parameters involved have been suitably calculated [37]. Predictions are formed during the feedforward phase of an ANN based on the values in the input nodes and the weights. This is relevant to this study, where the out of plane deflection of the masonry wall is intended to be recognised or predicted by the trained ANN. Figure 4 and Figure 5 show a typical ANN and its layers.

As shown in Figure 5, the neurons are connected by synapses, and the signals travel in one way, i.e., from input to output only in the Feedforward Neural Network. In this ANN type, there is no feedback or loops, and the output of any layer does not affect that same layer in such networks.

According to Liu [38] the neural network can be single-layer or multilayer, although after training, a neural network with a single hidden layer and a single output node can approximate nearly any functional relationship. This paper adopted a single hidden layer neural network due to few input and output parameters. The number of hidden-layer neurons affects the calculation accuracy as well as the learning efficiency. The choice on the number of hidden-layer neurons also considered the crucial observation made by Qi [39], where fewer hidden-layer neurons lead to underfitting, while several hidden-layers lead to the reduction of learning efficiency and results in an overfitting issue.

The ANN model consists of three layers, namely, the input layer, hidden layer, and output layer. The input layer accepts inputs in a variety of programming-provided forms, while the hidden layer, which is commonly known as the secreted-up layer, is positioned in between the input and output layers. In this framework, the ANN model performs all the calculations to discover covered up highlights and designs. Lastly, the output layer contains the final values from the input that has gone through an arrangement of changes utilizing the hidden layer, which at last comes about in a yield that is passed on utilizing this layer.

Following the above definition of layers, ANN takes the input and computes the weighted sum of the inputs and includes a bias. This computation is represented in the form of a transfer function.

A single layer in a feedforward neural network can be described using Equation (2) below:

$$y_i=f_{\left(i\right)}\left(W_{\left(i\right)}.y_{\left(i-1\right)}+b_{\left(i\right)}\right),i=\mathrm{1,2}\dots \dots ,n_{layers}$$

(2)

where y is the output vector of the ith layer, W and b are weight and bias vectors, and f is the activation function. Adopting the supervised learning method, the error function may be determined using the mean squared error defined as given by the Equation (3) below:

$$MSE=\frac{1}{n}\sum _{j=1}^n(Y_j{-{Y^{*}}_j)}^2$$

(3)

where n is the number of output nodes, Y is the network output, and Y* is the actual expected value.

The performance of the ANN is further evaluated using the correlation coefficient (R). The R-value is calculated using Equation (4) below:

$$R=\frac{{\sum }_{i=1}^n\left(m_i-\overline{m}\right)(p_i-\overline{p})}{\sqrt{{\sum }_{i=1}^n{\left(m_i-\overline{m}\right)}^2}{\sum }_{i=1}^n{\left(p_i-\overline{p}\right)}^2}$$

(4)

where $m_i$ represents experimental or numerical data values, $p_i$ represents predicted values, n is the number of samples, and $\overline{m}$ and $\overline{p}$ are the mean values of m and p, respectively.

3.5. Adopted Methodology

In the present study, numerically generated data from commercial finite element software was used. This data consisted of 95 numerical simulations/samples. The data comprised of input parameters, namely, standoff distance, and blast weight/charge. The output parameter is the out-of-plane displacement at the centre of the wall. This study utilised a multi-layered feed-forward neural network to examine data that was generated numerically and a Python script to modify the input variables without opening the finite element software. Using the MATLAB R2019a/SIMULINK tool, a neural network model was developed.

The stage of data gathering and processing entails transforming the chosen data into a comprehensible format so that the machine learning analysis may quickly access and use the data. This involves formatting, cleaning, and sampling the data. Considering the standoff distance, the authors concluded that standoff distances that were greater than 100 m had less damage on the wall though some in-plane failure was noticed. The dataset therefore focused mainly on parameters that had significant in-plane and out-of-plane response. The datasets were classified into three categories: learning, verification, and evaluation. Splitting of data was such that the learning sample comprised 80% of the dataset, and 20% used for verification and evaluation. The dataset consisted of simulations using blast weights ranging from 100 kg TNT to 1700 kg TNT with varying standoff distances. The flowchart of the artificial neural network is shown in Figure 6 below.

Table 1. Neural network parameters.

Network	Hidden Layer	Hidden Neurons	Output Nodes	Training Function	Learning Function
Feed Forward	1	10	1	Trainlm	Tansig-Purelin

lists the network parameters for the proposed model. Ten hidden layer neurons and one output neuron make up the network. The training function adopted in the training network is the Levenberg–Marquardt backpropagation (TRAINLM).

3.6. Finite Element Model for Data Simulation

This study adopted the approach of simplified micro modelling, which did not model the mortar thickness (zero thickness is assumed). Instead, the contact law adopted replicated the effect of mortar between the bricks. The masonry units are represented by continuum elements, while between masonry units normal and tangential contact surfaces are introduced to represent the mortar layer. Using commercial finite element software, the interface between the blocks was defined as surface-to-surface contact with zero tensile resistance. Since the tensile strength of the mortar is very low, this is an appropriate assumption as indicated also by a number of studies [12]. The dimensions of each masonry unit considered in this paper are 390 mm × 140 mm × 190 mm. This solid structural concrete masonry unit size is commonly used in low-cost housing. Figure 7 below shows the dimensions of the wall. It is noted that the numerical model used in this article to generate the dataset, that will then be used to train the artificial neural network, has been validated in [12], by comparing the results of this model with the literature.

3.7. Details of the Finite Element Model

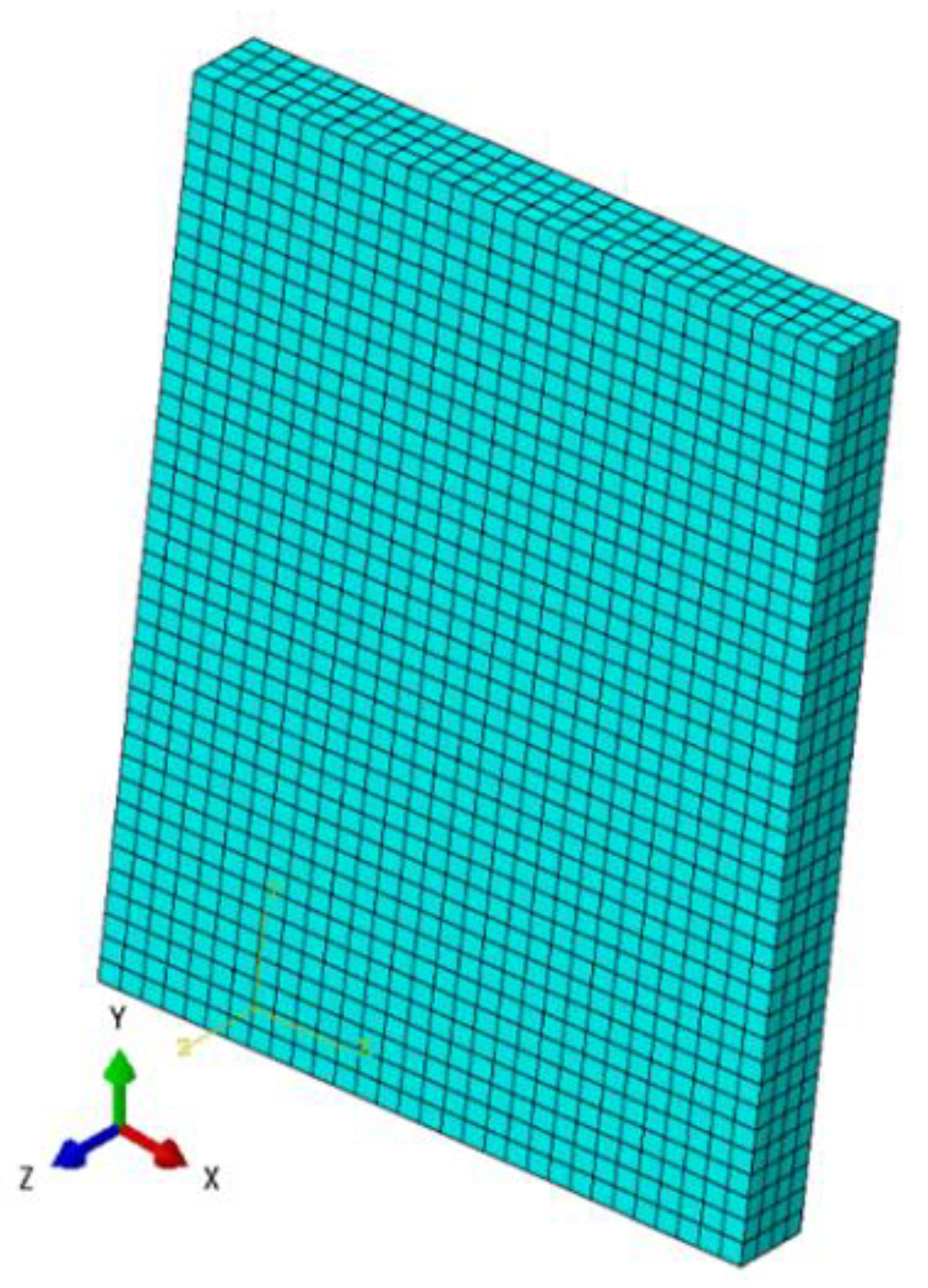
Figure 8 below shows the mesh which was adopted in the finite element model. Three-dimensional, eight-node linear brick elements were used, with the element side equal to 40 mm. A total number of 4800 elements was used for the model.

The boundary conditions of the wall were fixed in three translational degrees of freedom, according to the coordinate system shown in Figure 8. Thango et al. [12] in their study assumed the restraining effect on the top side of the walls in the Z direction as attributed to the assumption that an upper slab or roof will provide the restraint in that direction. A similar assumption was adopted for this study.

The loading of the model was applied in two load steps. In an initial, pre-existing step a vertical pressure of 0.25 MPa is applied to the top side of the structure. In the first load step, a horizontal shear (in-plane) displacement of 10 mm is applied to the top side of the walls. In the second load step, the blast loading is applied.

3.8. Contact Mechanics and Material Properties

Material models were developed to examine the structural behavior of the unreinforced masonry wall. The Concrete Damage Plasticity (CDP) law was used for the analysis to capture damage occurring in the material. CDP is a constitutive model used to simulate the failure behaviour of concrete under loading and unloading conditions.

Figure 9 below shows the compressive and tensile stress–strain curves that were used in this study to define the compressive and tensile failure response of the masonry units on the numerical models.

The uniaxial tensile damage and uniaxial compressive damage parameters were developed using the post-failure stress as a function of cracking strain. The cracking strain is equal to the total strain minus the elastic strain of the undamaged material [40]. The inelastic strains are calculated using Equation (5) below:

$${\epsilon }_{in}={\epsilon }_t-{\epsilon }_{el}$$

(5)

where ${\epsilon }_{in}$ represents the inelastic strain, ε_t denotes the “total strain”, and ε_el denotes the “elastic strain”. According to [37], the damage parameter that is utilised to capture the failure at peak load is shown below in Equation (6):

$$d_c=1-\raisebox{1ex}{${\sigma }_c$}\!\left/ \!\raisebox{-1ex}{${\sigma }_c^{\prime }$}\right.$$

(6)

where d_c represents the damage parameter in compression, while ${\sigma }_c$ is the compressive strength of masonry unit after the peak stress. The ultimate compressive strength of masonry is denoted by ${\sigma }_c^{\prime }$.

Equation (7) is used to calculate the plastic strain:

$${\epsilon }_c^{pl}={\epsilon }_c^{in}-\frac{d_c}{1-d_c}.\frac{{\sigma }_c}{E_0}$$

(7)

In terms of the tensile behaviour, the strain is calculated using Equation (8), which is obtained from the ultimate value of the tensile stress:

$${\epsilon }_{cr}={\epsilon }_t-{\epsilon }_{el}$$

(8)

where ${\epsilon }_{cr}$ represents the cracking strain. The damage parameter and the plastic strain are calculated using Equations (9) and (10) below:

$$d_c=1-\raisebox{1ex}{${\sigma }_t$}\!\left/ \!\raisebox{-1ex}{${\sigma }_t^{\prime }$}\right.$$

(9)

$${\epsilon }_t^{pl}={\epsilon }_t^{in}-\frac{d_t}{1-d_t}.\frac{{\sigma }_t}{E_0}$$

(10)

Some additional material properties adopted within the concrete damage plasticity law are provided in

Table 2. Mechanical properties of masonry unit and mortar [41].

Plasticity Parameter	Value
Dilation angle	30
Eccentricity parameter	0.1
Bi and unidirectional compressive strength ratio	1.16
Stress ratio in tensile meridian	0.67
Viscosity parameter	0.001

and

Table 3. Material properties [41].

Material	Modulus of Elasticity [MPa]	Poisson’s Ratio	Tensile Strength [MPa]	Compressive Strength [MPa]
Masonry Unit	15,500	0.15	1.05	10.5

.

3.9. Wall’s Response

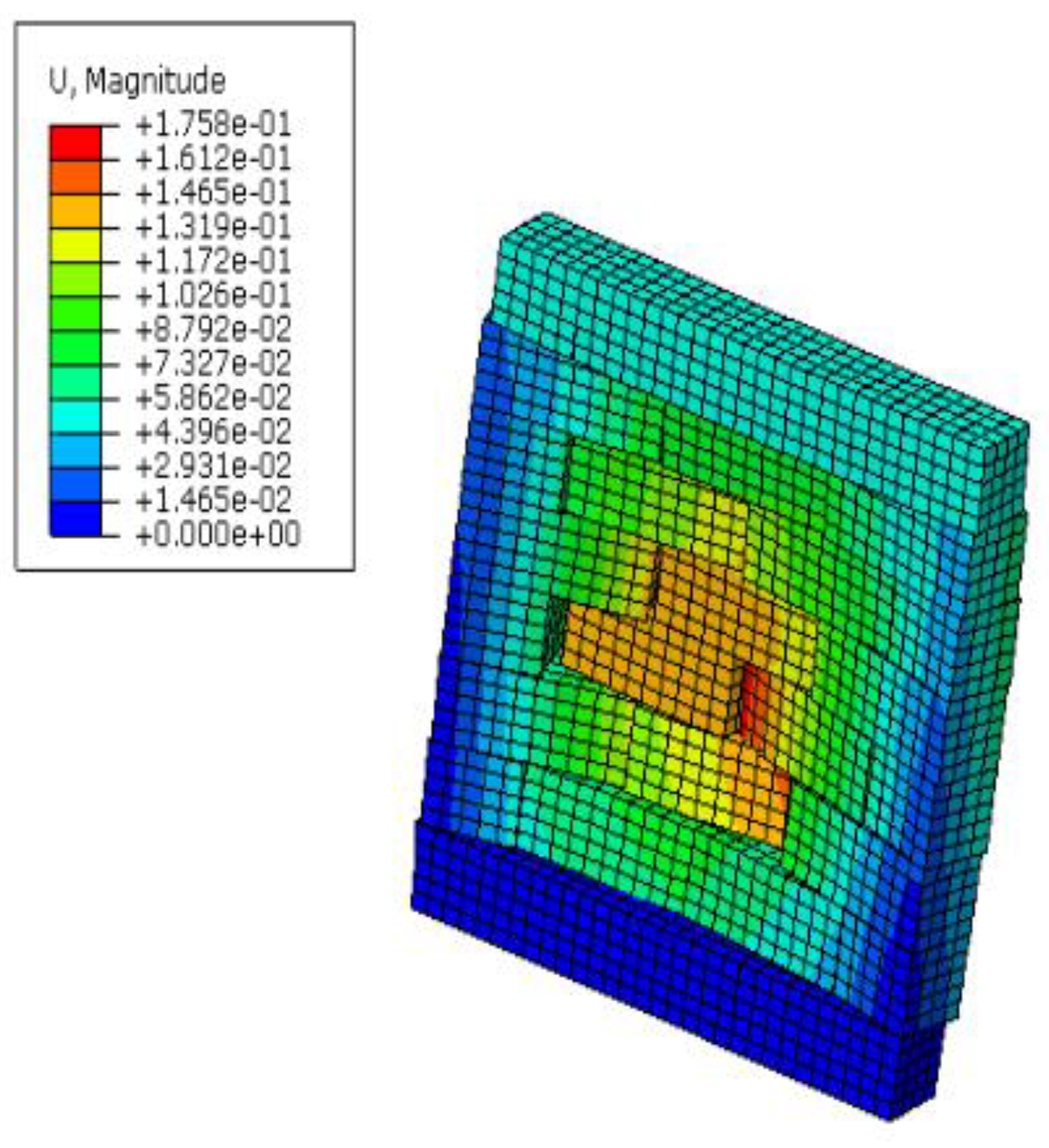
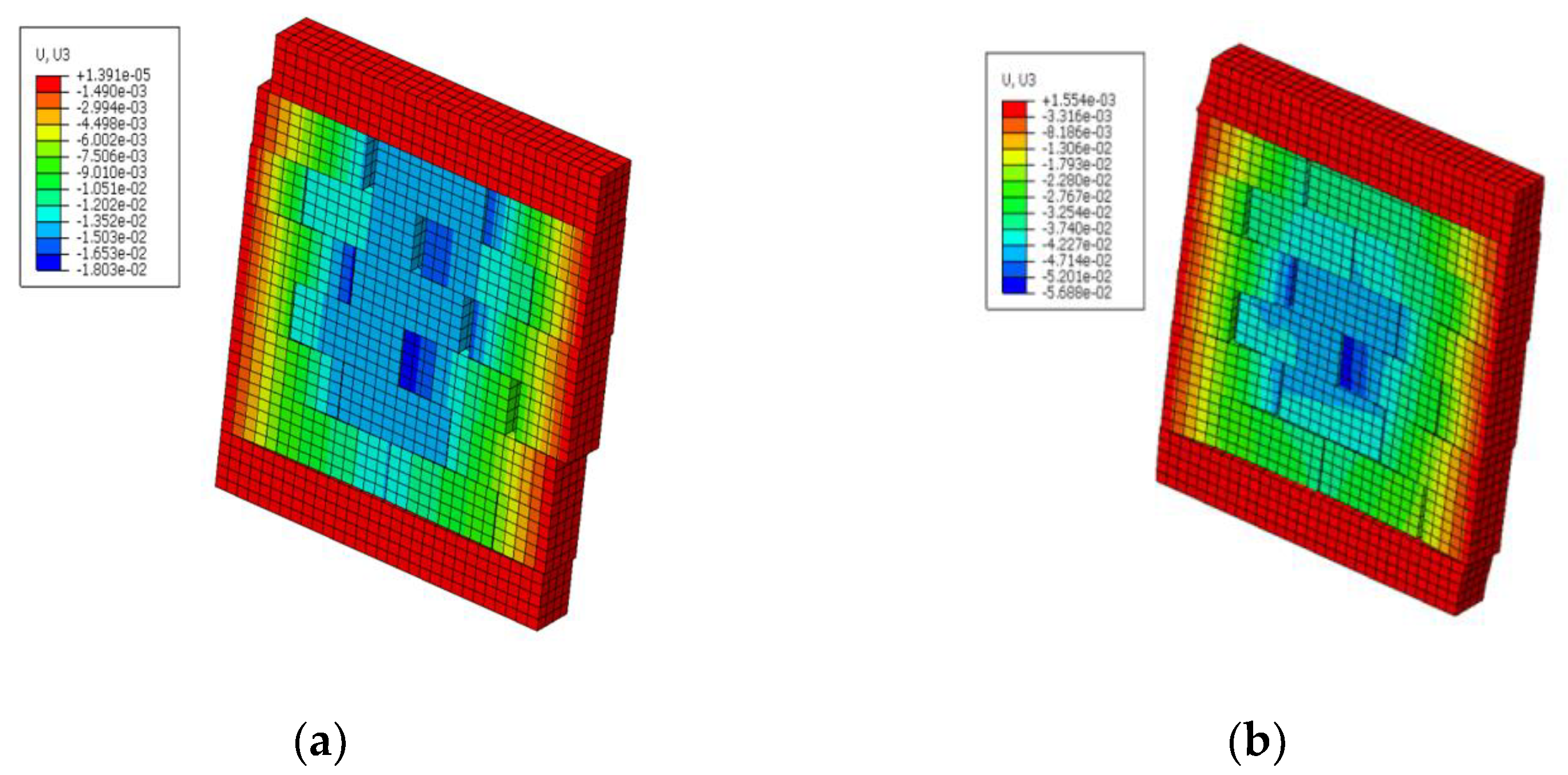
Figure 10 below shows the typical response of the masonry wall under blast loading. This was generated using finite element analysis as part of the dataset creation process. This is similar to Figure 2, which depicted modes of failure under in-plane and out-of-plane loading, thus validating the model.

4. Results

4.1. Out-of-Plane Response

The performance and training accuracy of the developed ANN is discussed in this section. The model consisted of two input variables, namely, the blast weight in terms of kg TNT and the standoff distance in metres. The trained ANN is aimed at predicted the in-plane and out-of-plane deformation of the chosen node or location on the wall. The mid-section of the wall was chosen. Using MATLAB R2019a/finite element analysis interface, 95 numerical simulations were generated. The choice of the number of datasets was based on the sample size from the available literature such as the Gaopale [42] where a total of 104 blasting datasets was provided by Orapa Diamond mine for their study to apply ANN to predict blast-induced ground vibration. The authors used 95 simulations as the first trial.

It may be inferred from an analysis of the results collected during the training, testing, and validation phases that ANN models are sufficiently competent to distinguish between input and output variables while making predictions that are relatively accurate. To investigate the training accuracy of the proposed ANN model, results on regression plots and the training state of the designed ANN were investigated. As per the plots below, the performance of the model for training, testing and validation were found to be acceptable. These acceptable correlation results confirm the relationship between model output values vs. the actual target deflection values. Figure 11 shows the simulation process. As can be seen in Figure below, the data division that was chosen for this model is random and this data sampling method prevents the data modelling process from being bias towards different possible data characteristics. The performance evaluation parameter (mean squared error, MSE) is also known as mean square deviation. The MSE is calculated as the average of the squared alterations between the predicted value and the actual values in the model. A value close to zero as the MSE is generally considered acceptable. In ANN, a gradient is used to measure how much the output of a function changes if there are adjustments in the inputs [43]. In this case, for the gradient descent algorithm to reach the local minimum, the learning rate was set to an appropriate value of 0.0338, which was considered as neither too low nor too high. Validation check is employed to terminate the learning of the ANN and the amount of validation checks will depend on how many times the neural network is iterated. The Mu value is utilized to control the weights of the neurons during the training, specifically on the updating process. The algorithms and progress parameters are further shown in Figure 12.

The coaching efficiency graph in Figure 12 demonstrates unequivocally that the ANN’s learning capacity is appropriate. The plot for performance of training includes the gradient, momentum parameter and validation check which are then plotted against the number of epochs.

Figure 13 depicts the decreasing trend of MSE for the test, training, and verification sets. When the number of iterations reached 19, the MSE of the verification set dropped to the minimum value of 0.000068441, thus achieving the reliable training effect. When the number of iterations got to 19, the training reached the highest number of failures and was stopped.

The distribution of the errors made by the neural network on the testing instances is displayed in error histograms. The histogram displays the difference between the anticipated values and the desired values. According to Mtsweni [44], after the training phase, the error histogram is a useful tool for assessing the accuracy of error distributions based on ANN predictions. Figure 14 shows a normal distribution centred at zero for each output variable, and this confirms the decent performance and good error distributions of the developed ANN model.

Figure 15 summarizes the regression plots at the end of the training phase. The predictive performance of the wall deflection under the blast load obtained from the ANN framework is shown in Figure 15, where the coefficient of correlation (R) during training, validation, testing, and combination of three phases were recorded as 0.96737, 0.97981, 0.95596, and 0.96381, respectively. In a similar study conducted by [22], the overall coefficient of correlation (R) that was obtained for a dataset of 478 cases was 94.77%. These are comparable to the proposed study, which has proven to offer acceptable prediction with a reasonable number of number of datasets. In the study conducted by [38], the correlation coefficient for validation of dataset was 0.98011 which is comparable to the present study (R = 0.97981) and to the overall R = 0.99037, which is comparable to R = 0.96381. This validated the training method that was adopted for this study. One of the common checks is that the data must fall on a 45-degree line where the network outputs equal the targets for a perfect fit. As can be seen in the figure below, most data fall along the 45-degree line, and this indicates that the fit by regression is acceptable for all data sets.

To confirm the feasibility of using the above-proposed model in the fast prediction of masonry wall’s response, a random value of blast weight was chosen, and standoff distances varied but did not contain any of the distances used as part of training the model. Figure 16 below shows the plot of z-displacement vs. standoff distances for some of the simulations that were used for the training and validation of the model. The randomly selected blast weight showed good prediction, as can be seen on the graph. Firstly, it can be observed that the proposed ANN is able to show the relationship between the displacement and the standoff distance. The damage severity reduces with the increased blast weight. The proposed ANN can be adopted in predicting the masonry wall’s response.

Additional random predictions were also performed. These are presented in

Table 4. Out-of-plane response prediction.

Blast Weight (kg TNT)	Standoff Distance (m)	Actual Out-of-Plane (m)	Predicted Out-of-Plane(m)	Percentage Error	FEA TIME (cpu Time)	Ann Time
120	43	−1.32 × 10−2	−1.24 × 10−2	6.4%	1915.2 s	6.5 s
160	26	−3.99 × 10−2	−4.01 × 10−2	0.4%	1926.6 s	6.5 s

below.

Figure 17 depicts the out-of-plane deflection of explosive weights 120 kg and 160 kg that were used for random prediction.

4.2. Effect of Blast Weight/Standoff Distance

In order to analyse the effect of blast weight and standoff distance, Figure 18 clearly shows that the out-of-plane response is greatly influenced by the explosive weight and the standoff distance. This can be seen by an increasing exponential graph. On the other hand, Figure 19 depicts the relationship between the ratio of the explosive weight and the distance vs. in-plane deflection. From this figure it can be concluded that there is no direct relationship between the two variables, however, it can be highlighted that a higher ratio leads to less in-plane deflection which is the opposite of the results presented in Figure 18. Thus, a higher explosive weight at a closer standoff distance results in more out-of-plane and less in-plane deflection.

5. Discussion

Machine learning has gained popularity in the field of structural engineering. Researchers have conducted research on the prediction of masonry wall response, but the majority focuses on the in-plane loading. Upon reviewing literature, it was found that limited efforts are found in machine learning for blast loading. In this study, an innovative approach was adopted to predict the response of masonry under blast loading. Additionally, this study utilized the unilateral contact-friction and damage mechanics laws, which are adopted to capture masonry’s failure modes, and these are strongly non-linear, and this increases the computation cost for one numerical simulation. This article proposed a scheme that uses machine learning techniques that can be adopted, to predict parameters of the mechanical response of the wall under blast actions, by drastically reducing computational cost. This is achieved by training and then using an artificial neural network.

The generation of datasets in this study entailed varying the blast weights and the standoff distance. The present study utilized the wall definition and properties from the study that was conducted by Thango et al. [12]. Other researchers such as Zhang et al. [8,9,11] highlighted the influence of standoff distance and the size of the explosive weight on the response of masonry wall. 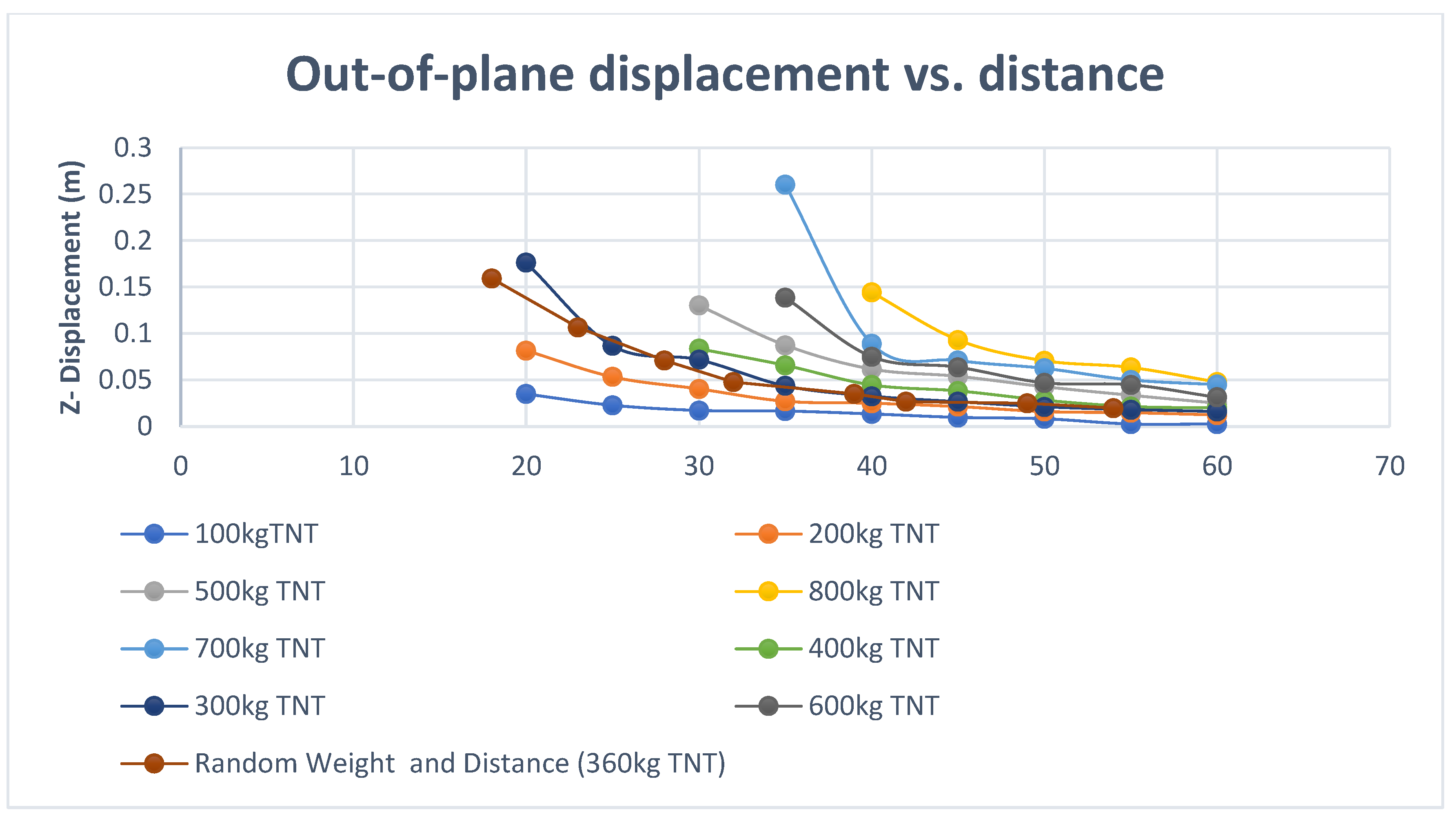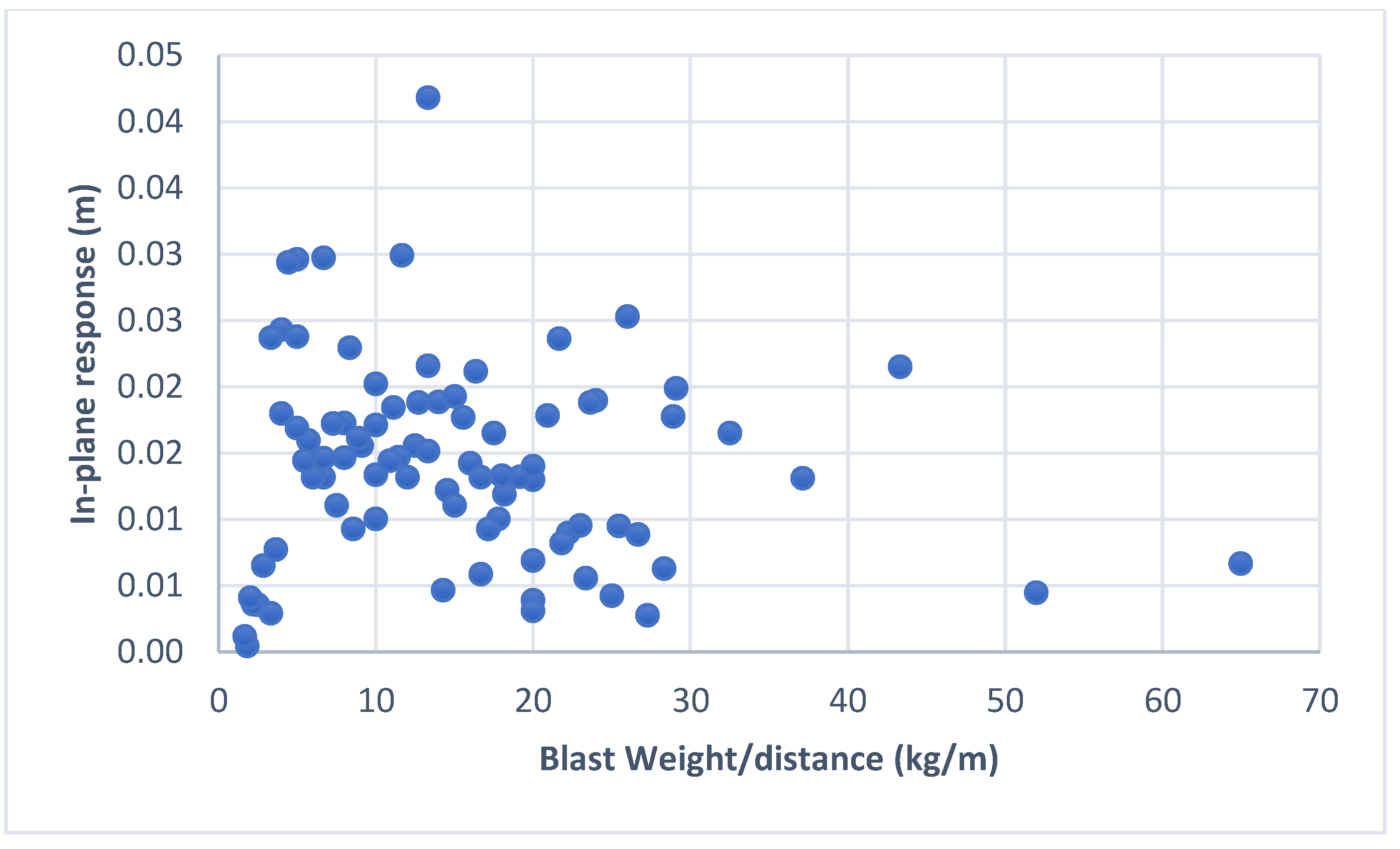With reference to Figure 18, it can be seen that the out-of-plane response is greatly influenced by the explosive weight and standoff distance. Figure 16 also shows for majority of explosive weights, a closer standoff distance will lead to higher out-of-plane deflection.

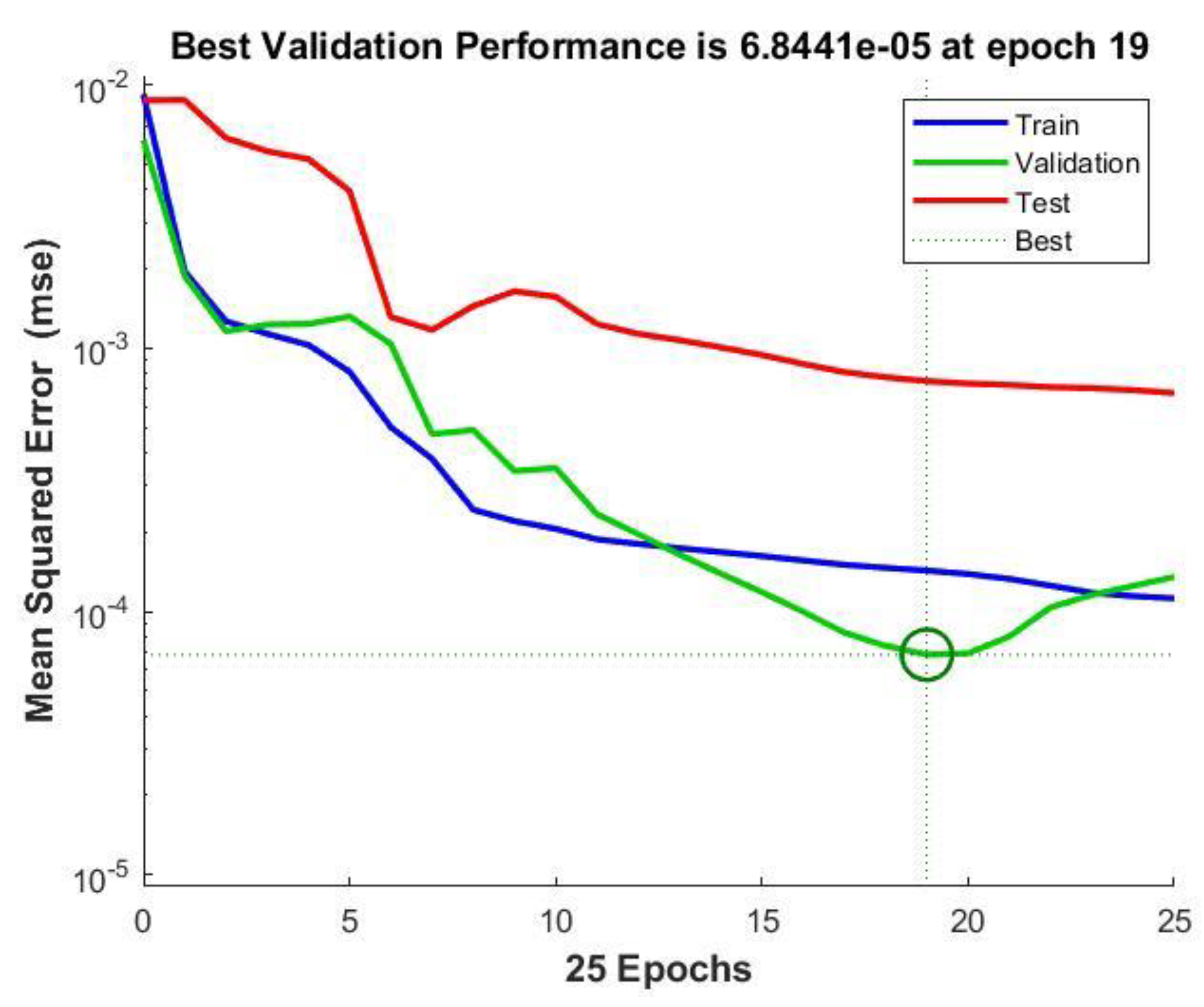
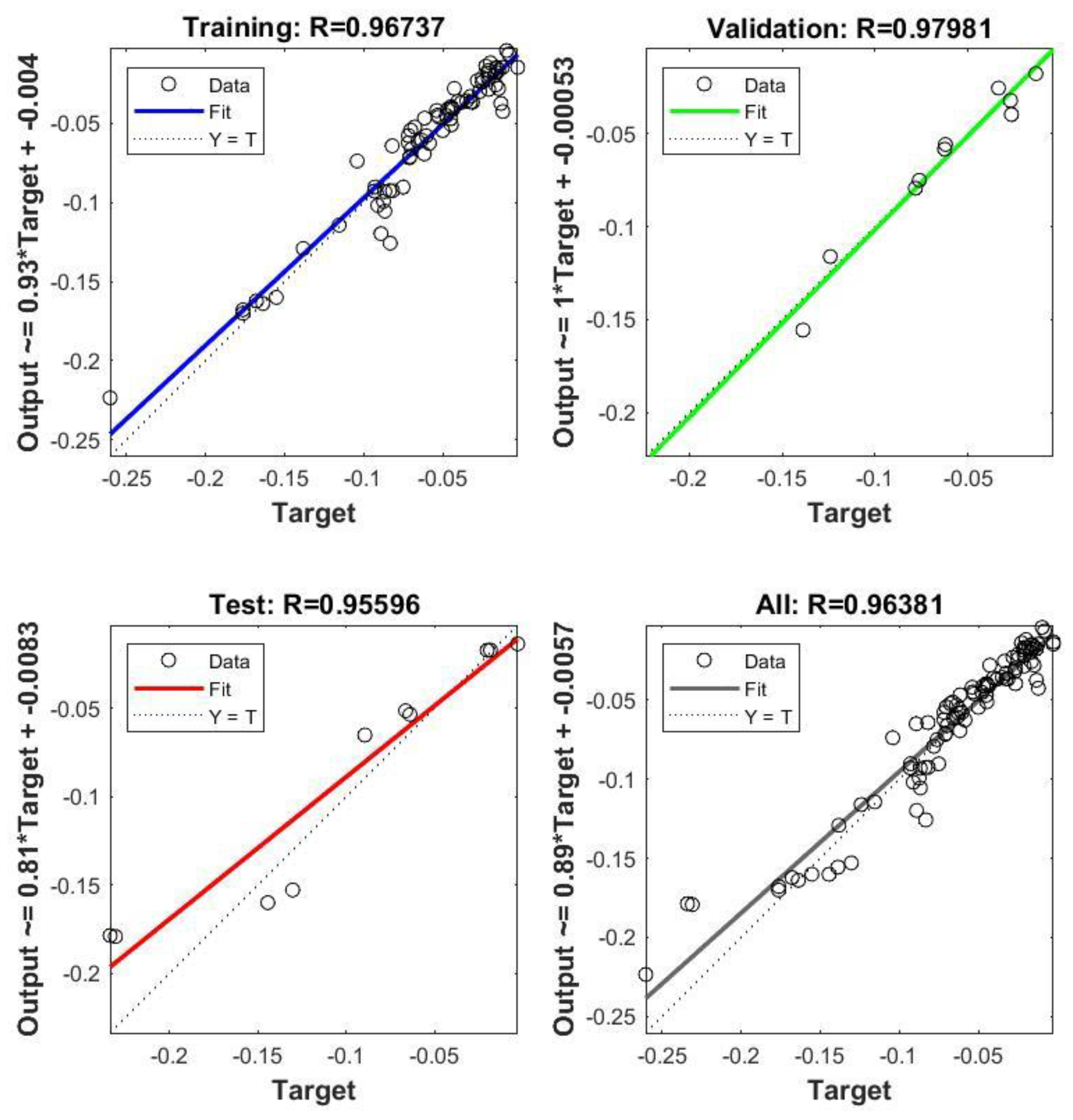
In this study, the accuracy of the proposed ANN framework was evaluated using the coefficient of correlation (R) during training, validation, and testing. Generally, acceptable results offer an R value close to one which shows the model’s ability to predict the output given a set of data (input). An overall value of 0.96381 which indicated that the fit by regression is acceptable. The studies conducted by [22] and [38] obtained similar regression results using the quantity of datasets that were compared to the proposed study.

According to Table 4, it has been found that the proposed model is highly capable of predicting deflection given the random input values (blast weight and standoff distance). In addition to that, the proposed model is able to offer results within seconds which is one of the advantages that this model will contribute as part of the practical applications in structural engineering.

6. Conclusions

In this article, a machine learning approach is proposed to predict the structural response of masonry walls under blast actions. First, a non-linear finite element model is used to provide the failure response of masonry, considering unilateral contact-friction interfaces between masonry stones and a damage mechanics law. Then, parametric simulations are conducted to generate a dataset that is finally used to train an artificial neural network.

Solution of the non-linear finite element model is computationally expensive, in terms of the computational time and resources needed, even for one simulation. This is attributed to the non-linear constitutive descriptions, which are adopted to capture the real failure response of the wall, including the discrete failure mode between masonry stones and continuum failure in the mass of stones.

Therefore, the article aims to provide an efficient machine learning tool that can be used for a first, fast prediction of the out-of-plane deflection of masonry walls under blast loads. In particular, after the generation of the dataset from parametric non-linear finite element simulations, training of the artificial neural network is implemented. As shown in the article, the trained neural network is then able to provide a fast prediction of the response of the masonry wall due to random blast properties (blast weight and standoff distance), avoiding time consuming numerical simulations and heavy computational cost.

The accuracy of the trained artificial neural network is satisfactory, as given by relevant regression plots. Tests to random input variables (not included in the dataset used to train the artificial neural network) also depict a satisfactory accuracy, as compared to finite element analysis.

In addition, the proposed process is able to automatically generate parametric finite element simulations to create the dataset using Python and MATLAB R2019a scripts in collaboration with commercial finite element software.

The study can be extended and overcome current limitations by introducing in the machine learning scheme random geometries of the masonry wall, while also considering the random sizes and patterns of the masonry stones. The influence of modelling the mortar joint between stones, using for instance cohesive zone laws, is another future investigation. Finally, numerical solutions can be evaluated on advanced materials that can be used to protect masonry walls under blast actions. For instance, auxetic materials, with negative Poisson’s ratio can be numerically tested by developing proper finite element models [45,46].