Soft Computing to Predict Earthquake-Induced Soil Liquefaction via CPT Results

Abstract

Earthquake-induced soil liquefaction (EISL) can cause significant damage to structures, facilities, and vital urban arteries. Thus, the accurate prediction of EISL is a challenge for geotechnical engineers in mitigating irreparable loss to buildings and human lives. This research aims to propose a binary classification model based on the hybrid method of a wavelet neural network (WNN) and particle swarm optimization (PSO) to predict EISL based on cone penetration test (CPT) results. To this end, a well-known dataset consisting of 109 datapoints has been used. The developed WNN-PSO model can predict liquefaction with an overall accuracy of 99.09% based on seven input variables, including total vertical stress (${\sigma }_v$), effective vertical stress (${\sigma }_v^{\prime }$), mean grain size (D₅₀), normalized peak horizontal acceleration at ground surface (α_max), cone resistance (q_c), cyclic stress ratio (CSR), and earthquake magnitude (M_w). The results show that the proposed WNN-PSO model has superior performance against other computational intelligence models. The results of sensitivity analysis using the neighborhood component analysis (NCA) method reveal that among the seven input variables, q_c has the highest degree of importance and M_w has the lowest degree of importance in predicting EISL.

1. Introduction

Natural disasters, such as earthquakes, have long been associated with risks to human life and environmental degradation. Earthquake-induced soil liquefaction (EISL) is one of the most important geotechnical phenomena, and occurs in loose, saturated, and non-dense sandy soils during an earthquake. This phenomenon causes the pore water pressure to increase due to the soil’s tendency to decrease in volume, and as a result, it reduces the effective stress in the soil. In this case, the shear resistance of the soil is greatly reduced and approaches almost zero, and finally, the granular materials in the soil transform from solid to liquid [1,2]. Several factors can affect the occurrence of EISL, including the intensity and magnitude of the earthquake, the type and mechanical characteristics of local soil, unit weights, relative density, fine content, mean particle diameters, the void ratio, and the initial confining pressure during the earthquake [1,3,4,5,6]. The EISL can cause significant damage to structures, facilities, and vital urban arteries. It can also cause loss of life and geographical disasters, such as the rising of underground facilities, subsidence of buildings, landslides, and loss of life [7]. Therefore, predicting the EISL potential is a basic and essential step in designing structures to reduce earthquake damage. Although the phenomenon of EISL has been known for a long time, it has been widely studied by geotechnical engineers due to the massive destruction of several strong earthquakes such as the Niigata 1964, Kocaeli 1999, Chi-Chi 1999, Baja California 2010, Tohoku 2011, and Bushehr 2013 [1,8,9,10,11,12,13].

In general, the prediction of liquefaction is a difficult and complicated task due to the complicated mechanism of soil liquefaction and its relationship with numerous influencing factors. Therefore, many researchers have proposed several methods in the last three decades. Traditional techniques for estimating the liquefaction resistance of soils include statistical methods and laboratory tests, including the cyclic simple shear test, the cyclic triaxial test, and the cyclic torsional test, which are not only expensive and time-consuming [14], but also have several limitations [15]. For example, the insufficient accuracy of statistical methods [16] and the dependence of laboratory methods on sampling and testing methods have led to unreliability [17].

Recently, field test methods based on the cone penetration test (CPT) [7,9,18,19,20,21,22,23,24], standard penetration test (SPT) [6,7,14,17,25,26,27,28,29,30], and shear wave velocity (V_S) [17,31] test have become the most widely used approaches to predict EISL. SPT has limitations in cohesive soils and coarse-grained soils, and it provides discrete datapoints rather than continuous profiling. The shear wave test involves sending shear waves into the ground and measuring their travel time and velocity. This test requires specialized equipment and expertise and is typically conducted in conjunction with other site investigations. In summary, while both CPT and SPT can provide valuable information for assessing liquefaction potential, CPT is generally considered the more accurate and reliable due to its continuous profiling and direct measurement of soil resistance. The shear wave test provides additional insights into the dynamic properties of soils and can be used in conjunction with other tests for a comprehensive liquefaction assessment. However, the CPT has attracted more attention from many geotechnical researchers in the last 20 years since it is consistent, faster, and repeatable [7,9,19,20,21,22,23,24].

With the development of soft computing techniques, many scholars have tried to develop these models for solving science and engineering problems [2,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. These techniques such as artificial neural networks (ANN), fuzzy neural inference system (Neuro-Fuzzy), and the support vector machine (SVM) have also been proposed to predict EISL using in situ test data. Goh investigated the feasibility of using various ANN models such as a backpropagation (BP) neural network and probabilistic neural network (PNN) to assess the liquefaction potential based on historical cases [46,47]. A general regression neural network (GRNN) model has been developed by Hanna et al. [16] to determine the occurrence of EISL using the field test data from the earthquakes in Taiwan and Turkey. Rezania et al. [24] presented an evolutionary polynomial regression (EPR) to estimate the EISL potential of sands based on the CPT data. Kayadelen developed two models based on genetic expression programming (GEP) and adaptive neuro-fuzzy inference system (ANFIS) to estimate the safety factor for the liquefaction of soils using the data from the earthquakes in Turkey and Taiwan [48]. Muduli and Das proposed a classification approach based on multi-gene genetic programming (MGGP) to evaluate soil liquefaction using a large CPT dataset [22]. Samui developed an SVM model to predict the EISL based on actual CPT data from the 1999 Chi-Chi earthquake [19]. Ardakani and Kohestani investigated the potential of the decision tree (C4.5) algorithm for estimating EISL using CPT test results [23]. Xue and Xiao developed two hybrid SVM classifiers based on the genetic algorithm (GA) and grid search (GS) to estimate the potential of soil liquefaction based on the CPT data from five significant earthquakes [9]. Xue and Liu used two optimization algorithms, namely particle swarm optimization (PSO) and GA, to select the optimal parameters and prediction accuracy of the backpropagation (BP) neural network model using the CPT data from eight earthquakes between 1964 and 1983 to forecast the EISL susceptibility of soil [21]. Kurnaz and Kaya predicted the potential of soil liquefaction using an ensemble model based on a group method of data handling neural network based on CPT data [14]. Rahbarzadeh and Azadi used a fuzzy support vector machine (FSVM) classification method optimized with a hybrid PSO and GA to improve the prediction of soil liquefaction using CPT data [20]. Mahmood et al. proposed a hybrid approach based on a Bayesian belief network (BBN) to predict the potential of EISL using CPT data [49]. Zhang and Wang presented a hybrid classifier ensemble by integrating different base classifiers including BP, SVM, RF, multiple linear regression (MLR), naive Bayes (NB), k-nearest neighborhoods (KNN), and logistic regression (LR) to improve the prediction accuracy of soil liquefaction. GA was also applied to tune the hyperparameters and weights of all classifiers [7]. Cai et al. developed a least squares support vector machine (LSSVM) and a radial basis function neural network (RBFNN) optimized by differential evolution (DE), GA, and grey wolf optimization (GWO) to assess the liquefaction potential based on CPT test results [50]. The results showed that LSSVM-GWO and RBFNN-GWO outperformed the other classifiers.

Examining computational intelligence models developed to predict EISL shows that some of these models have not reached sufficient accuracy and have been under-fitted or over-fitted in the training process. On the other hand, regarding developing computational intelligence models for predicting EISL, due to the complexity of the developed models, the final model or computer code for predicting EISL using CPT test results has not been provided. The lack of clear presentation of these models renders these methods unusable in practice for engineers. Therefore, it seems necessary to develop a computational intelligence method that, in addition to high accuracy, can be expressed and implemented in a simple and straightforward manner, in order to predict EISL via CPT test results.

This study proposed a hybrid intelligent method based on WNN and PSO to predict the potential of EISL based on the CPT results. PSO is employed to train WNN to increase its accuracy in predicting the liquefaction potential. The developed WNN-PSO model’s accuracy was compared to other computational intelligence methods (e.g., ANN and SVM). To the best of the authors’ knowledge, this is the first time that WNN architecture is used to predict EISL based on CPT test data. Based on the discussion above, the application of the WNN-PSO model may be more accurate in estimating EISL. Additionally, in this study, the MATLAB function for the simulation of the optimized WNN model is provided, which renders geotechnical engineers or researchers able to estimate EISL via CPT results.

2. Methods

2.1. Wavelet Neural Networks

ANNs are statistical methods based on the structure of the brain to determine complicated relationships between inputs and outputs [16]. One of the primary merits of ANNs over traditional statistical approaches is that they can learn with no prior knowledge about the relationships between independent and dependent variables [51]. ANNs have successfully been employed to solve several geotechnical problems [14,16,47,50,52,53,54].

The WNN, proposed in 1992 by Zhang and Benveniste [55], is an advanced hybrid version of the ANN and wavelet transform [56], which employs the wavelet function as the activation function, as a substitute for the sigmoid activation function.

Three types of layers, including the input layer, the hidden layer, and the output layer, construct the architecture of WNN. Figure 1 shows the topology of the wavelet neural network in this study.

In Figure 1, $X=$ ${\left[x_1, x_2,\dots ,x_n\right]}^T$ is the vector of the input variables, $y$ is the predicted value (output), $w_{ij}(\mathrm{i}=1,\dots ,\mathrm{n};\mathrm{j}=1,\dots ,\mathrm{m})$ is the weight of hidden layer, $w_j(\mathrm{j}=1,\dots ,\mathrm{m})$ is the weight of output layer, and ${\psi }^{d_j,{\tau }_j}(j=1,\dots ,m)$ is the daughter wavelet function.

In order to compute the output value of WNN, for each hidden neuron (e.g., jth neuron) the connecting weights $W=\left[w_{1j}, w_{2j},\dots ,w_{nj}\right]$ between the inputs and the jth wavelet neuron are firstly multiplied (dot product) by the vector of neuron inputs $X=$ ${\left[x_1, x_2,\dots ,x_n\right]}^T$ to represent the importance of the inputs and then all of the weighted inputs are algebraically added by the summation block to compute the input value of the jth neuron in the hidden layer (i.e., ${net}_j$). After that, the output of the jth neuron in the hidden layer is calculated as follows [57]:

$${\psi }^{d_j,{\mathsf{\tau }}_j}\left({net}_j\right)=\psi \left(\frac{{net}_j-{\tau }_j}{d_j}\right)$$

(1)

where $\psi$ is the wavelet function, $d_j$ is the value of dilation for neuron j, and ${\tau }_j$ is the value of translation for neuron j in the hidden layer. The most common wavelet functions are listed in

Table 1. Wavelet function used in the WNN.

Wavelet Function	Equation
Morlet	$\psi \left(t\right)=cos\left(1.75t\right)exp\left(-\frac{t^2}{2}\right)$
Meyer (approximate formula)	$\psi \left(t\right)=35t^4-84t^5+70t^6-20t^7$
Gaussian	$\psi \left(t\right)=\frac{1}{\sqrt{2\pi }}exp\left(-\frac{t^2}{2}\right)$
Mexican hat	$\psi \left(t\right)=c\left(1-t^2\right)exp\left(-\frac{t^2}{2}\right), c=\frac{2}{\sqrt{3}}{\pi }^{\frac{-1}{4}}$
Shannon	$\psi \left(t\right)=\frac{sin\pi \left(t-\frac{1}{2}\right)-sin2\pi \left(t-\frac{1}{2}\right)}{\pi \left(t-\frac{1}{2}\right)}$
GGW	$\psi \left(t\right)=sin\left(3t\right)+sin\left(0.3t\right)+sin\left(0.03t\right)$

.

The output $y$ in the output layer is then calculated as Equation (2):

$$y=Heaviside\left(\sum _{j=1}^m{w}_j{\psi }^{d_j,{\mathsf{\tau }}_j}\left({net}_j\right)\right)$$

(2)

where Heaviside is represented in Figure 2. The Heaviside step function used to transfer the output $y$ to either 0 or 1. In this study, 1 indicates the occurrence of EISL and 0 indicates the non-occurrence of EISL.

2.2. Particle Swarm Optimization

PSO was proposed by Eberhart and Kennedy and is one of several nature-inspired algorithms [58]. It has been successfully applied in many realistic and scientific problems. PSO was inspired by the observation of swarm behaviors. Each solution in PSO is only one particle in the search space. All particles have two vectors, i.e., position vector and velocity vector, which represent the particle’s state in the search space. Each particle $\mathrm{i}$ has a position in the $\mathrm{d}$-dimensional space of the problem, which is represented by $X_i=\left[x_i^1, x_i^2,\dots ,x_i^D\right]$. The velocity vector of the ith particle is represented by $V_i=\left[v_i^1, v_i^2,\dots ,v_i^D\right]$. In each iteration t, the position and velocity vectors of the ith particle are updated by Equations (3) and (4):

$$V_i\left(t+1\right)=w.V_i\left(t\right)+c_1{r}_1\left({pbest}_i\left(t\right)-X_i\left(t\right)\right)+c_2{r}_2\left(gbest\left(t\right)-X_i\left(t\right)\right)$$

(3)

$$X_i\left(t+1\right)=X_i\left(t\right)+V_i\left(t+1\right)$$

(4)

where ${pbest}_i$ is the personal best position experienced by the particle, and $gbest$ is the global best position (best-so-far) of all particles in the whole swarm. $r_1$ and $r_2$ are two random numbers in the range $\left[\mathrm{0,1}\right]$. $c_1$ and $c_2$ are acceleration coefficients which control the tradeoff between exploration and exploitation. $w$ is the inertia weight. Shi and Eberhart showed that a higher $w$ helps exploration while a smaller $w$ helps exploitation [59]. The flowchart of PSO is illustrated in Figure 3.

2.3. Hybridization of WNN with PSO

In this section, a hybrid model of WNN and PSO is described. In the present study, the PSO algorithm was used to train the WNN and select optimal input weights, dilations, and transformations of the hidden neurons, and the input weights of the output neuron. The objective function used to select these parameters is the accuracy of the WNN. The accuracy is calculated by Equation (5):

$$Accuracy \left(\%\right)=\left(\frac{Number of Corrected Predictions}{Total Data}\right)\times 100$$

(5)

In order to be compatible and to be able to compare the results of WNN-PSO with soft computing methods implemented in previous researches, 74 datapoints from 109 total data were considered as the training set (68%) and 35 datapoints from 109 datapoints were considered as the testing set (32%). The previous research also considered these two fractions for training and testing sets. In the next step, the PSO parameters including the number of populations, inertia weight, acceleration coefficients, the maximum iteration, and the lower and upper bound of design variables (w_ij, w_j, d, τ) are set for the training procedure. Then, the values of the weights, dilations, and translations of the WNN are randomly initialized. The WNN is trained by these values and the accuracy of the WNN is computed by Equation (5). In the PSO loop, PSO tries to find and update the optimal values of weights, dilations, and translations. These steps continue until the maximum iteration is reached. The procedure for developing the proposed WNN-PSO model to predict the EISL potential is depicted in Figure 4.

3. Dataset Description

The dataset used in this study was obtained from Goh [47]. It includes 109 CPT datapoints with a broad range of parameters from five extreme earthquakes between 1964 to 1983. The majority of these records come from locations that have flat terrain and consist of sand or silty sand deposits. The CPT data include 79 case records from China based on the Tangshan earthquake, 16 from Japan based on the Niigata and Nihonkaichubu earthquakes, nine from the USA based on the Imperial Valley earthquake, and five from Romania based on the Vrancea earthquake. Out of 109 records, the occurrence of EISL is reported in 74 records, and the non-occurrence of EISL is reported in 35 records. The dataset has been provided in Appendix A. Sensitivity to EISL depends on seismic and soil parameters. Based on the previous research, the evaluating indices, including total vertical stress (${\sigma }_v$), mean grain size (D₅₀), effective vertical stress (${\sigma }_v^{\prime }$), cone resistance (q_c), cyclic stress ratio (CSR), normalized peak horizontal acceleration at ground surface (α_max), and earthquake magnitude (M_w) have been considered for the assessment of the EISL potential.

Table 2. Seismic and soil properties of the desired dataset.

Description	Symbol	Range
Cone resistance (MPa)	qc	[1, 31.4]
Effective vertical stress (kPa)	${\sigma }_v^{\prime }$	[6, 122]
Total vertical stress (kPa)	${\sigma }_v$	[17, 249]
Average grain size (mm)	D50	[0.06, 0.67]
Earthquake magnitude	Mw	[6.6, 7.8]
Cyclic Stress Ratio	CSR	[0.11, 0.64]
Normalized peak horizontal acceleration at ground surface	αmax	[0.1, 0.8]

indicates the seismic and soil properties of the desired dataset.

Table 3. Statistical descriptions of the training, the testing, and the overall sets.

Variables	Min	Max	Mean	Median	SD
	The Training Set
qc	1	31.40	7.11	5.55	6.08
${\sigma }_v$	6	122	59.68	54	28.69
${\sigma }_v^{\prime }$	17	249	99.05	88	61.68
D50	0.06	0.67	0.23	0.17	0.17
Mw	6.6	7.8	7.63	7.8	0.35
CSR	0.06	0.90	0.29	0.23	0.16
amax	0.10	0.80	0.32	0.23	0.21
	The Testing Set
qc	1.03	18.94	6.02	4.24	4.63
${\sigma }_v$	22	102	57.46	57	18.39
${\sigma }_v^{\prime }$	23	162	79.60	76	32.75
D50	0.13	0.32	0.20	0.19	0.05
Mw	7.20	7.80	7.71	7.80	0.21
CSR	0.09	0.41	0.18	0.16	0.05
amax	0.20	0.22	0.20	0.20	0.01
	The Overall
qc	1	31.40	6.76	5	5.66
${\sigma }_v$	6	122	58.96	55	25.77
${\sigma }_v^{\prime }$	17	249	92.81	76	54.70
D50	0.06	0.67	0.22	0.17	0.14
Mw	6.60	7.80	7.64	7.80	0.35
CSR	0.06	0.90	0.25	0.21	0.15
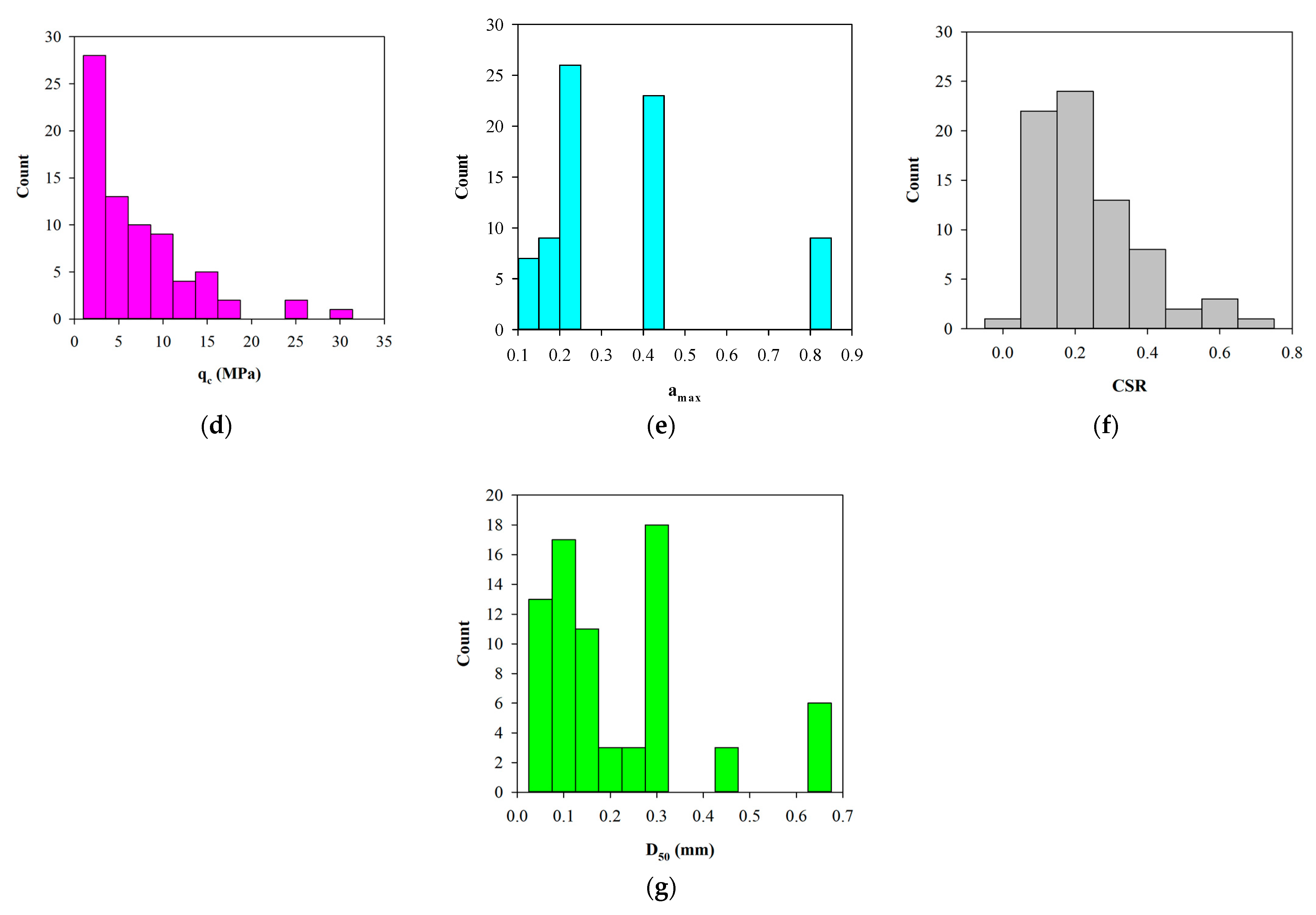
amax	0.10	0.80	0.28	0.20	0.18

shows the statistical descriptions of the data, including the minimum, maximum, mean, median, and standard deviation (SD) of each input variable for the training set, the testing set, and the overall data. A frequency histogram for input variables has been depicted in Figure 5.

Before training, the data were normalized as follows:

$$u=\frac{v-v_{min}}{v_{max}-v_{min}}$$

(6)

where $v$ is the original value of the input parameter, and $v_{min}$ and $v_{max}$ are the minimum and the maximum values of the input parameter.

4. Developing WNN-PSO Model for the Assessment of Liquefaction

In this study, a program was developed in the MATLAB environment to train and test the WNN-PSO model.

4.1. The Parameter Settings

In the proposed model, the control parameters affecting the wavelet neural network training using the PSO algorithm are the number of the initial population, inertia weight, acceleration coefficients, the lower and upper bounds of the design variables, and the stop criterion, which is the maximum allowable iterations.

Table 4. The parameter setting of the WNN-PSO model.

Control Parameters	Symbol	Value
Number of initial populations	nPop	200
Maximum iteration	MaxIt	1000
Inertia weight	$w$	0.1
Acceleration coefficient	$c_1$	0.25
Acceleration coefficient	$c_2$	0.25
Lower bound of variables	VarMin	−10
Upper bound of variables	VarMax	+10

reported the settings of the control parameters of the WNN-PSO model.

4.2. The Optimal Architecture of WNN-PSO

In this study, the WNN model with one hidden layer has sufficient accuracy. The number of hidden neurons is determined by trial-and-error process. To this end, various architectures with different numbers of hidden neurons from 1 to 20 were used to train and test the networks. The most optimal structure of the WNN was determined to be 7-2-1, which indicates seven input neurons, two hidden neurons, and one output neuron.

Moreover, six different wavelet functions including Shannon, GGW, Gaussian, Mexican hat, Meyer, and Morlet were examined as the wavelet function in the hidden layer. The optimal architecture of the WNN-PSO model with these wavelet functions was tested to choose the best wavelet function for the model. Each model using each wavelet activation function was run 10 times separately, and the best model for each wavelet function was selected as the candidate model.

The performance accuracy (%) of each wavelet function for the training set, the testing set, and the overall data are presented in

Table 5. The performance accuracy of each wavelet function in the WNN-PSO.

Wavelet Function	Accuracy (%)
	Train	Test	Overall
Shannon	97.37	100	98.16
GGW	97.37	96.97	97.25
Gaussian	97.37	100	98.16
Mexican Hat	97.37	96.97	97.25
Meyer	97.37	96.97	97.25
Morlet	98.68	100	99.09

. According to the results, the Morlet wavelet function has the highest accuracy of 98.68%, 100%, and 99.09% for the training set, the testing set, and the overall, respectively. Therefore, the Morlet function was selected as the wavelet function in the optimal model. The MATLAB function for simulating the optimal WNN model has been represented in the Appendix B.

4.3. Performance of WNN-PSO Model

This section discussed the performance of the optimal WNN model and the effectiveness of the WNN-PSO model for the assessment of EISL. The best WNN model was obtained with the architecture of 7-2-1 and the Morlet wavelet function.

Figure 6 depicts the confusion matrix to test the performance of the optimal WNN model. A confusion matrix, widely used in binary classification, is a performance measurement consisting of four different combinations of predicted and actual values, which are true positive (TP), false positive (FP), true negative (TN), and false negative (FN). Here, TP represents that EISL has occurred and was correctly estimated. FP denotes that non-EISL is incorrectly estimated as EISL. TN means that non-EISL has not occurred and it was correctly estimated. FN denotes that EISL is incorrectly estimated as non-EISL.

The performance of the WNN-PSO model was evaluated by several performance metrics, such as accuracy, precision, sensitivity, and specificity derived from the confusion matrix. These performance metrics are the most widely used metrics for binary classification [60].

Table 6. The performance metrics with formulas.

Metrics	Formulation
Precision	$\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}$
Sensitivity	$\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$
Specificity	$\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}}$
Accuracy	$\frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}}$

shows the formulas for these evaluation metrics.

Figure 7 illustrates the confusion matrix of the optimal WNN model for the training and testing sets using the CPT data. From the 74 records in the training set (Figure 7a), 73 records were correctly predicted (TP = 51 and TN = 22), and 1 record was wrongly predicted (FN = 1 and FP = 0). As shown in Figure 7b, all 35 records in the testing set were correctly predicted (TP = 23 and TN = 12). Moreover, the performance metrics of the proposed WNN-PSO model for the training, the testing, and all data are represented in

Table 7. The performance metrics of the proposed WNN-PSO model.

Performance Metrics	Train	Test	Overall
Precision	100	100	100
Sensitivity	98.08	100	98.67
Specificity	96	100	97.14
Accuracy	98.68	100	99.09

.

5. Comparison with Other Soft Computing Models

The performance accuracy of the optimal WNN model was compared with other models to evaluate the capabilities of the hybrid WNN-PSO method. To this end, six available models, including ANN [47], decision trees [23], PSO-SVM [18], GS-SVM and GA-SVM [9], and PSO-GA-SVM [20] were employed. These models also used 67% of the data (74 values) for the training set and 33% of data (35 values) for the testing set.

The performance accuracy of using the optimal WNN model based on the CPT data to predict the EISL was compared with the models mentioned in

Table 8. The accuracy comparison of the WNN-PSO model with the other methods.

Method	Performance Accuracy (%)
	Train	Test	Overall
ANN [47]	100.00	85.70	95.41
C4.5 [23]	95.90	97.10	96.30
GA-SVM [9]	97.29	97.14	97.25
GS-SVM [9]	91.89	94.29	92.66
PSO-SVM [18]	-	-	96.50
PSO-GA-SVM [20]	-	-	99.09
WNN-PSO (This study)	98.68	100	99.09

. Prediction results show that the classification accuracy of the proposed WNN-PSO method surpasses that of the other methods. As shown in Table 8, the accuracy of the WNN-PSO for the training set is 98.68%, which is higher than the success rates of GS-SVM (91.89%), GA-SVM (97.29%), ANN (98.60%), and the C4.5 decision tree (95.90%). The classification accuracy of the WNN-PSO for the testing set (100%) is also higher than those of the GS-SVM (94.29%), GA-SVM (97.14%), ANN (94.30%), and the C4.5 decision tree (97.10%). These results showed that the proposed WNN-PSO outperformed the other methods in the training and testing phases. Moreover, the overall accuracy of WNN-PSO for the whole CPT dataset is 99.09%, which is better than those of GS-SVM (92.66%), GA-SVM (97.25%), ANN (97.20%), and the C4.5 decision tree (96.30%). Although the overall accuracy of the WNN-PSO is equal to that of the PSO-GA-SVM (99.09%), the WNN-PSO method provides a simpler model due to the low number of neurons in the hidden layer. It is worth noting that the PSO-GA-SVM model has not been provided by researchers [20] and so it cannot be employed for further predictions. On the other hand, in this research the MATLAB code for predicting EISL is represented, which can be used by geotechnical engineers in practice.

6. Sensitivity Analysis

After developing the soft computing model, it is possible to determine the degree of importance of each of the input variables on the output of the model by means of sensitivity analysis. It is essential to carry out different analyses on the proposed model to validate and test the robustness of the model for unknown data. Sensitivity analysis determines the degree of importance of the input variables on the output of the model. In this study, the neighborhood component analysis (NCA) [61] algorithm was utilized to determine the degree of importance of input variables on the prediction of EISL potential. Let $S=\left\{\left(x_i,y_j\right),i=1,\dots ,n;j=\mathrm{0,1}\right\}$ as the training set with $n$ records for two-class classification problem, where $x_i\in R_p$ are the feature vectors and $y_j$ are the labels of classes. The objective of NCA is to train a classifier $f:R_p\to \left\{\mathrm{0,1}\right\}$ which obtains a feature vector and predicts the proper label $y$ for $x$. Build a randomized classifier which (1) selects randomly a reference point for $x$ as $Ref\left(x\right)$, and (2) labels $x$ based on the label of $Ref\left(x\right)$. A possibility exists that an input variable $x_i$ in the NCA algorithms is related to the class $y_j$. The distance between two records is obtained by Equation (7):

$$d_w=\sum _{r=1}^p{w}_r^2\left|x_{ir}-x_{jr}\right|$$

(7)

where $w_r$ is the weight of the input variable.

The reference points (x) in the input vector are obtained by Equation (8):

$$P\left(Ref\left(x\right)=x_i\left|S\right.\right)=\frac{k\left(d_w\left(x,x_i\right)\right)}{{\sum }_{j=1}^{N}k\left(d_w\left(x,x_i\right)\right)}$$

(8)

The probability of selecting $x_j$ as the reference point for $x_i$ is obtained by Equation (9):

$$p_{ij}=P\left(Ref\left(x_i\right)=x_j\left|S\right.\right)=\frac{k\left(d_w\left(x_i,x_j\right)\right)}{{\sum }_{j=1 j\ne i}^{N}k\left(d_w\left(x_i,x_j\right)\right)}$$

(9)

Herein, k corresponds to the kernel function ($k\left(z\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{z}{\sigma })$) and $\sigma$ is the width of kernel function whereas the correct classification possibility of the real class is calculated by Equation (10).

$$p_i=\sum _j{y}_{ij}{p}_{ij}$$

(10)

where $y_{ij}=1$ if and only if $y_i$ = $y_j$, otherwise $y_{ij}=0.$

The results of the sensitivity analysis using NCA is illustrated in Figure 8.

The results of sensitivity analysis using the NCA method reveals that among the seven input variables, the cone resistance (q_c) has the highest degree of importance and earthquake magnitude (M_w) has the lowest degree of importance in predicting EISL. Other input variables in terms of importance to predicting the EISL based on the CPT results after qc include mean grain size (D₅₀), total vertical stress (${\sigma }_v$), cyclic stress ratio (CSR), effective vertical stress (${\sigma }_v^{\prime }$), and normalized peak horizontal acceleration at ground surface (α_max), respectively.

7. Limitations and Future Studies

One of the limitations of the computational intelligence model developed in this research and other research related to predicting EISL via CPT data is the use of a limited dataset for training and testing the model. It should also be noted that most computational intelligence models have appropriate accuracy and reliability only in the range of inputs used for training the model, and if the input data are not within the range of training data, the developed model should not be used for extrapolation.

For future research, it is suggested that first the dataset related to EISL prediction based on CPT data be expanded and then the method proposed in this research be employed to provide a model with higher generalizability for practical applications. Additionally, the hybrid WNN-PSO method which is proposed in this research can be used to predict liquefaction based on the results of other field tests (e.g., SPT or shear wave velocity).

8. Conclusions

Because of the numerous damages and disasters caused by earthquakes, predicting seismic liquefaction is an important task in geotechnical engineering. In this paper, a hybrid WNN-PSO was developed to predict the occurrence of liquefaction based on the seven input variables, including total vertical stress (${\sigma }_v$), effective vertical stress (${\sigma }_v^{\prime }$), normalized peak horizontal acceleration at ground surface (α_max), cone resistance (q_c), mean grain size (D₅₀), cyclic stress ratio (CSR), and earthquake magnitude (M_w). In the developed model, the PSO algorithm was used to train the wavelet neural network and find the optimal values of weights, dilation, and translation parameters. A reliable CPT dataset including 109 datapoints was employed for the training of the WNN. In order to find the optimal wavelet neural network topology to predict seismic liquefaction, different numbers of neurons in the hidden layer as well as different wavelet functions (e.g., Morlet, Gaussian, Mexican hat, GGW, Meyer, Shannon) in the hidden layer were investigated. The optimal architecture of the WNN was determined as 7-2-1, which shows that the optimal WNN has seven neurons in the input layer, two neurons in the hidden layer with the Morlet wavelet function and one neuron in the output layer with a Heaviside transfer function. Several performance indicators for binary classification models, including accuracy, precision, sensitivity, and specificity, were used to evaluate the performance of the WNN-PSO model. These indices are equal to 98.68%, 100%, 99.08%, and 96% for the training set, equal to 100%, 100%, 100%, and 100% for the testing set; and also equal to 99.09%, 100%, 98.67%, and 97.14% for the total data, respectively. A comparison of the results obtained by the proposed WNN-PSO model with those obtained by the other methods (e.g., ANN, SVM, and C4.5) showed that the proposed model has superior classification performance in predicting the nonlinear relationship between the seismic and soil parameters and the liquefaction potential. The results of sensitivity analysis using the NCA method showed that the qc has the highest degree of importance and Mw has the lowest degree of importance in predicting EISL.