Prediction of Fatalities at Northern Indian Railways’ Road–Rail Level Crossings Using Machine Learning Algorithms
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Selection of Study Area and Data Collection
3.2. Primary Investigation of the Accident Data of Northern Railways
Descriptive Statistics of the Variable
3.3. Model Development and Analysis
3.3.1. Models
- I.
- Logistic regression;
- II.
- Artificial neural network.
Logistic Regression
Artificial Neural Networks
3.3.2. Preparation of Model Data
4. Result
4.1. Result of Logistic Regression Model
Logistic Regression Model Validation
4.2. Results of the ANN Model
4.2.1. Area under Curve (AUC) from ROC Curve
4.2.2. Sensitivity Analysis for the ANN Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Welcome to Indian Railway Passenger Reservation Enquiry. Available online: https://www.indianrail.gov.in/enquiry/StaticPages/StaticEnquiry.jsp?StaticPage=index.html (accessed on 25 September 2022).
- Annual Statistical Statement 2018–19—Indian Railway. Available online: https://indianrailways.gov.in/railwayboard/view_section.jsp?lang=0&id=0,1,304,366,554 (accessed on 10 October 2022).
- Accidental Deaths & Suicides in India (ADSI)|National Crime Records Bureau. Available online: https://ncrb.gov.in/en/accidental-deaths-suicides-india-adsi (accessed on 22 October 2022).
- Road Accidents in India. Available online: https://www.statista.com/topics/5982/road-accidents-in-india/ (accessed on 1 November 2022).
- Clifton, K.J.; Kreamer-Fults, K. An Examination of the Environmental Attributes Associated with Pedestrian–Vehicular Crashes near Public Schools. Accid. Anal. Prev. 2007, 39, 708–715. [Google Scholar] [CrossRef] [PubMed]
- Dai, D. Identifying Clusters and Risk Factors of Injuries in Pedestrian–Vehicle Crashes in a GIS Environment. J. Transp. Geogr. 2012, 24, 206–214. [Google Scholar] [CrossRef]
- Mrema, I.J.; Dida, M.A. A Survey of Road Accident Reporting and Driver’s Behavior Awareness Systems: The Case of Tanzania. Eng. Technol. Appl. Sci. Res. 2020, 10, 6009–6015. [Google Scholar] [CrossRef]
- Mohan, D.; Tsimhoni, O.; Sivak, M.; Flannagan, M.J. Road Safety in India: Challenges and Opportunities; University of Michigan, Ann Arbor, Transportation Research Institute: Ann Arbor, MI, USA, 2009. [Google Scholar]
- Mohan, D.; Tiwari, G.; Mukherjee, S. Urban traffic safety assessment: A case study of six Indian cities. IATSS Res. 2016, 39, 95–101. [Google Scholar] [CrossRef]
- Muley, D.; Kharbeche, M.; Alhajyaseen, W.; Al-Salem, M. Pedestrians’ crossing behavior at marked crosswalks on channelized right-turn lanes at intersections. Procedia Comp. Sci. 2017, 109, 233–240. [Google Scholar] [CrossRef]
- Railroad Accidents: Common Causes, Statistics and Prevention. Available online: https://www.sidgilreath.com/learn/railroad-accidents-causes.html (accessed on 10 January 2023).
- Madigan, R.; Golightly, D.; Madders, R. Application of Human Factors Analysis and Classification System (HFACS) to UK Rail Safety of the Line Incidents. Accid. Anal. Prev. 2016, 97, 122–131. [Google Scholar] [CrossRef]
- Das, S.; Kong, X.; Lavrenz, S.M.; Wu, L.; Jalayer, M. Fatal Crashes at Highway Rail Grade Crossings: A U.S. Based Study. Int. J. Transp. Sci. Technol. 2022, 11, 107–117. [Google Scholar] [CrossRef]
- Salmon, P.M.; Read, G.J.M.; Stanton, N.A.; Lenné, M.G. The Crash at Kerang: Investigating Systemic and Psychological Factors Leading to Unintentional Non-Compliance at Rail Level Crossings. Accid. Anal. Prev. 2013, 50, 1278–1288. [Google Scholar] [CrossRef]
- Khattak, A.; Tung, L.-W. Severity of Pedestrian Crashes at Highway-Rail Grade Crossings. J. Transp. Res. Forum 2015, 54, 91–100. [Google Scholar] [CrossRef]
- Liu, J.; Khattak, A.J.; Richards, S.H.; Nambisan, S. What Are the Differences in Driver Injury Outcomes at Highway-Rail Grade Crossings? Untangling the Role of Pre-Crash Behaviours. Accid. Anal. Prev. 2015, 85, 157–169. [Google Scholar] [CrossRef]
- Larue, G.S.; Naweed, A.; Rodwell, D. The Road User, the Pedestrian, and Me: Investigating the Interactions, Errors, and Escalating Risks of Users of Fully Protected Level Crossings. Saf. Sci. 2018, 110, 80–88. [Google Scholar] [CrossRef]
- Keramati, A.; Lu, P.; Tolliver, D.; Wang, X. Geometric Effect Analysis of Highway-Rail Grade Crossing Safety Performance. Accid. Anal. Prev. 2020, 138, 105470. [Google Scholar] [CrossRef] [PubMed]
- Moodie, E.E.M. A Review of: “An Introduction to Generalized Linear Models, Third Edition, by A. J. Dobson and A. G. Barnett”. J. Biopharm. Stat. 2009, 19, 307. [Google Scholar] [CrossRef]
- Xu, C.; Tarko, A.P.; Wang, W.; Liu, P. Predicting Crash Likelihood and Severity on Freeways with Real-Time Loop Detector Data. Accid. Anal. Prev. 2013, 57, 30–39. [Google Scholar] [CrossRef] [PubMed]
- Sohn, S.Y.; Shin, H. Pattern Recognition for Road Traffic Accident Severity in Korea. Ergonomics 2001, 44, 107–117. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Lord, D.; Zhang, Y. Predicting Motor Vehicle Collisions Using Bayesian Neural Network Models: An Empirical Analysis. Accid. Anal. Prev. 2007, 39, 922–933. [Google Scholar] [CrossRef]
- Najjar, Y.M.; Stokes, R.W.; Russell, E.R. Setting Speed Limits on Kansas Two-Lane Highways: Neuronet Approach. Transp. Res. Rec. 2000, 1708, 20–27. [Google Scholar] [CrossRef]
- Ali, G.A.; Bakheit, C.S. Comparative analysis and prediction of traffic accidents in Sudan using artificial neural networks and statistical methods. In Proceedings of the 30th South African Transport Conference, Centurion, South Africa, 11–14 July 2011; Document Transformation Technologies: Centurion, South Africa, 2011; pp. 202–214. [Google Scholar]
- Delen, D.; Sharda, R.; Bessonov, M. Identifying Significant Predictors of Injury Severity in Traffic Accidents Using a Series of Artificial Neural Networks. Accid. Anal. Prev. 2006, 38, 434–444. [Google Scholar] [CrossRef]
- Jadaan, K.S.; Al-Fayyad, M.; Gammoh, H.F. Prediction of Road Traffic Accidents in Jordan Using Artificial Neural Network (ANN). J. Traffic Logist. Eng. 2014, 2, 92–94. [Google Scholar] [CrossRef]
- Alkheder, S.; Taamneh, M.; Taamneh, S. Severity Prediction of Traffic Accident Using an Artificial Neural Network. J. Forecast. 2016, 36, 100–108. [Google Scholar] [CrossRef]
- Sameen, M.; Pradhan, B. Severity Prediction of Traffic Accidents with Recurrent Neural Networks. Appl. Sci. 2017, 7, 476–492. [Google Scholar] [CrossRef]
- García de Soto, B.; Bumbacher, A.; Deublein, M.; Adey, B.T. Predicting Road Traffic Accidents Using Artificial Neural Network Models. Infrastruct. Asset Manag. 2018, 5, 132–144. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, L.; Ma, H.; Wang, H.; Wan, S. Parallel LSTM-Based Regional Integrated Energy System Multienergy Source-Load Information Interactive Energy Prediction. Complexity 2019, 2019, 7414318. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Mamlook, R.E.A.; Almuflih, A.S. Evaluating the Impact of External Support on Green Building Construction Cost: A Hybrid Mathematical and Machine Learning Prediction Approach. Buildings 2022, 12, 1256. [Google Scholar] [CrossRef]
- Singh, P.; Pasha, J.; Moses, R.; Sobanjo, J.; Ozguven, E.E.; Dulebenets, M.A. Development of Exact and Heuristic Optimization Methods for Safety Improvement Projects at Level Crossings under Conflicting Objectives. Reliab. Eng. Syst. Saf. 2022, 220, 108296. [Google Scholar] [CrossRef]
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Mamlook, R.E.A.; Almuflih, A.S.; Almakayeel, N. Machine Learning-Based Model for Predicting the Shear Strength of Slender Reinforced Concrete Beams without Stirrups. Buildings 2022, 12, 1166. [Google Scholar] [CrossRef]
- Zheng, S.; Lyu, Z.; Foong, L.K. Early Prediction of Cooling Load in Energy-Efficient Buildings through Novel Optimizer of Shuffled Complex Evolution. Eng. Comput. 2020, 38, 105–119. [Google Scholar] [CrossRef]
- Zhu, W.; Ma, C.; Zhao, X.; Wang, M.; Heidari, A.A.; Chen, H.; Li, C. Evaluation of Sino Foreign Cooperative Education Project Using Orthogonal Sine Cosine Optimized Kernel Extreme Learning Machine. IEEE Access 2020, 8, 61107–61123. [Google Scholar] [CrossRef]
- Liu, G.; Jia, W.; Wang, M.; Heidari, A.A.; Chen, H.; Luo, Y.; Li, C. Predicting Cervical Hyperextension Injury: A Covariance Guided Sine Cosine Support Vector Machine. IEEE Access 2020, 8, 46895–46908. [Google Scholar] [CrossRef]
- Kozłowski, E.; Borucka, A.; Świderski, A.; Skoczyński, P. Classification Trees in the Assessment of the Road–Railway Accidents Mortality. Energies 2021, 14, 3462. [Google Scholar] [CrossRef]
- Tang, H.; Xu, Y.; Lin, A.; Heidari, A.A.; Wang, M.; Chen, H.; Luo, Y.; Li, C. Predicting Green Consumption Behaviors of Students Using Efficient Firefly Grey Wolf-Assisted K-Nearest Neighbor Classifiers. IEEE Access 2020, 8, 35546–35562. [Google Scholar] [CrossRef]
- Shehadeh, A.; Alshboul, O.; Al Mamlook, R.E.; Hamedat, O. Machine Learning Models for Predicting the Residual Value of Heavy Construction Equipment: An Evaluation of Modified Decision Tree, LightGBM, and XGBoost Regression. Autom. Constr. 2021, 129, 103827. [Google Scholar] [CrossRef]
- Map. Available online: https://nr.indianrailways.gov.in/view_section.jsp?lang=0&id=0,1,285 (accessed on 22 January 2023).
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis; Springer: New York, NY, USA, 2010; pp. 215–221. [Google Scholar]
- Singh, G.; Pal, M.; Yadav, Y.; Singla, T. Deep Neural Network-Based Predictive Modelling of Road Accidents. Neural Comput. Appl. 2020, 32, 12417–12426. [Google Scholar] [CrossRef]
- Ziegel, E.R.; Menard, S. Applied Logistic Regression Analysis. Technometrics 1996, 38, 192. [Google Scholar] [CrossRef]
- Schumm, W.R.; Stevens, J. Applied Multivariate Statistics for the Social Sciences. Am. Stat. 1993, 47, 155. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Stanley, L. Applied Logistic Regression; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Fawcett, T. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Garson, G.D. Interpreting neural-network connection weights. AI Expert 1991, 6, 46–51. [Google Scholar]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Predicting Settlement of Shallow Foundations Using Neural Networks. J. Geotech. Geoenviron. Eng. 2002, 128, 785–793. [Google Scholar] [CrossRef]
- Jones, B.; Janssen, L.; Mannering, F. Analysis of the Frequency and Duration of Freeway Accidents in Seattle. Accid. Anal. Prev. 1991, 23, 239–255. [Google Scholar] [CrossRef]
- Miaou, S.-P. The Relationship between Truck Accidents and Geometric Design of Road Sections: Poisson versus Negative Binomial Regressions. Accid. Anal. Prev. 1994, 26, 471–482. [Google Scholar] [CrossRef]
- Pulugurtha, S.S.; Sambhara, V.R. Pedestrian Crash Estimation Models for Signalized Intersections. Accid. Anal. Prev. 2011, 43, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, A.; Mukherjee, D.; Mitra, S. Development of Pedestrian Crash Prediction Model for a Developing Country Using Artificial Neural Network. Int. J. Inj. Control Saf. Promot. 2019, 26, 283–293. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, D.; Mitra, S. Impact of Road Infrastructure Land Use and Traffic Operational Characteristics on Pedestrian Fatality Risk: A Case Study of Kolkata, India. Transp. Dev. Econ. 2019, 5, 6. [Google Scholar] [CrossRef]
- Priyadarshini, P.; Mitra, S. Investigating Pedestrian Risk Factors Leading to Pedestrian Fatalities in Kolkata City Roads. Transp. Dev. Econ. 2017, 4, 1. [Google Scholar] [CrossRef]
- Soleimani, S.; Mousa, S.R.; Codjoe, J.; Leitner, M. A Comprehensive Railroad-Highway Grade Crossing Consolidation Model: A Machine Learning Approach. Accid. Anal. Prev. 2019, 128, 65–77. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, S.; Mohammadi, A.; Chen, J.; Leitner, M. Mining the highway-rail grade crossing crash data: A text mining approach. In Proceedings of the 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16 December 2019; pp. 1063–1068. [Google Scholar]

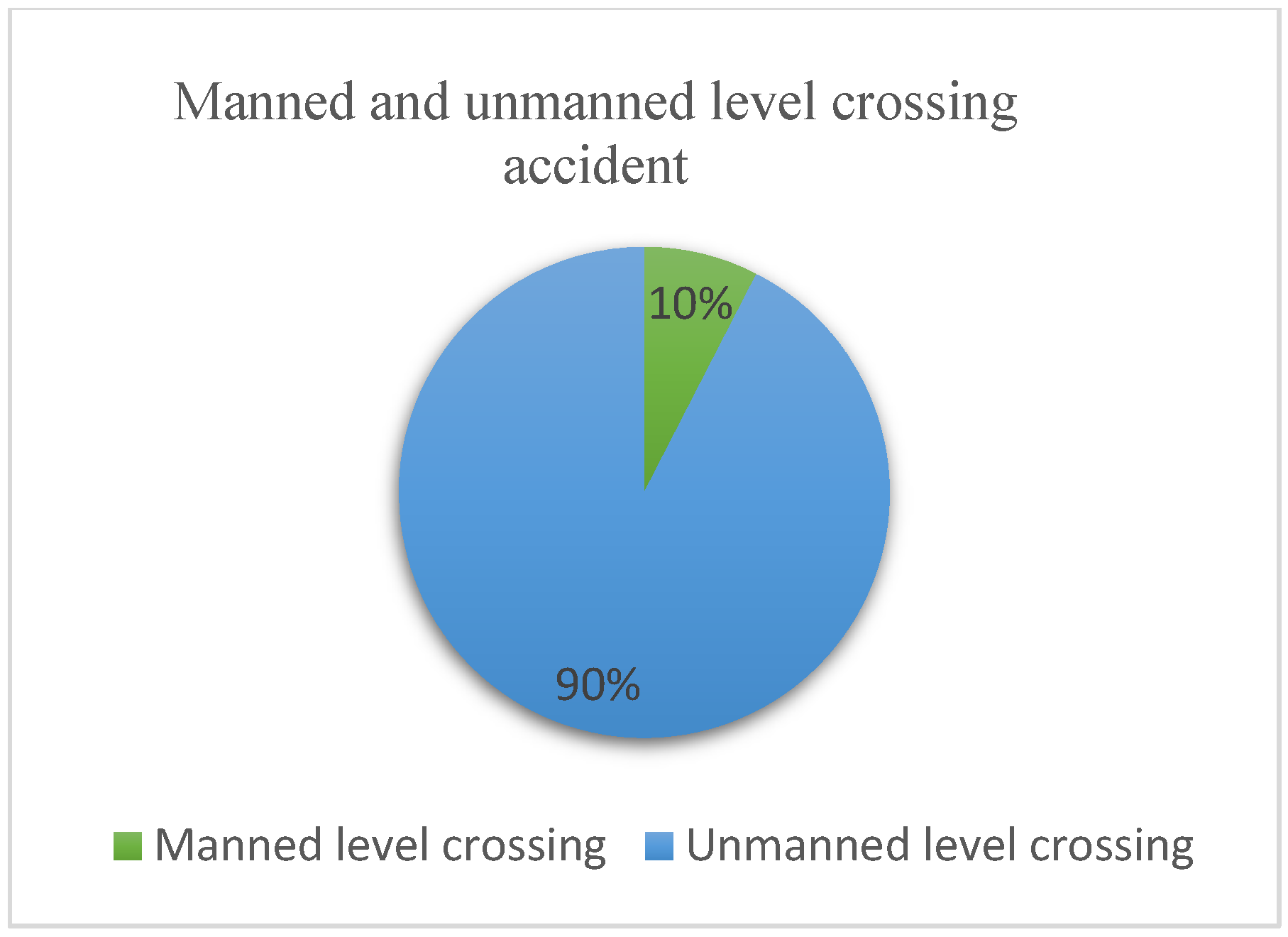
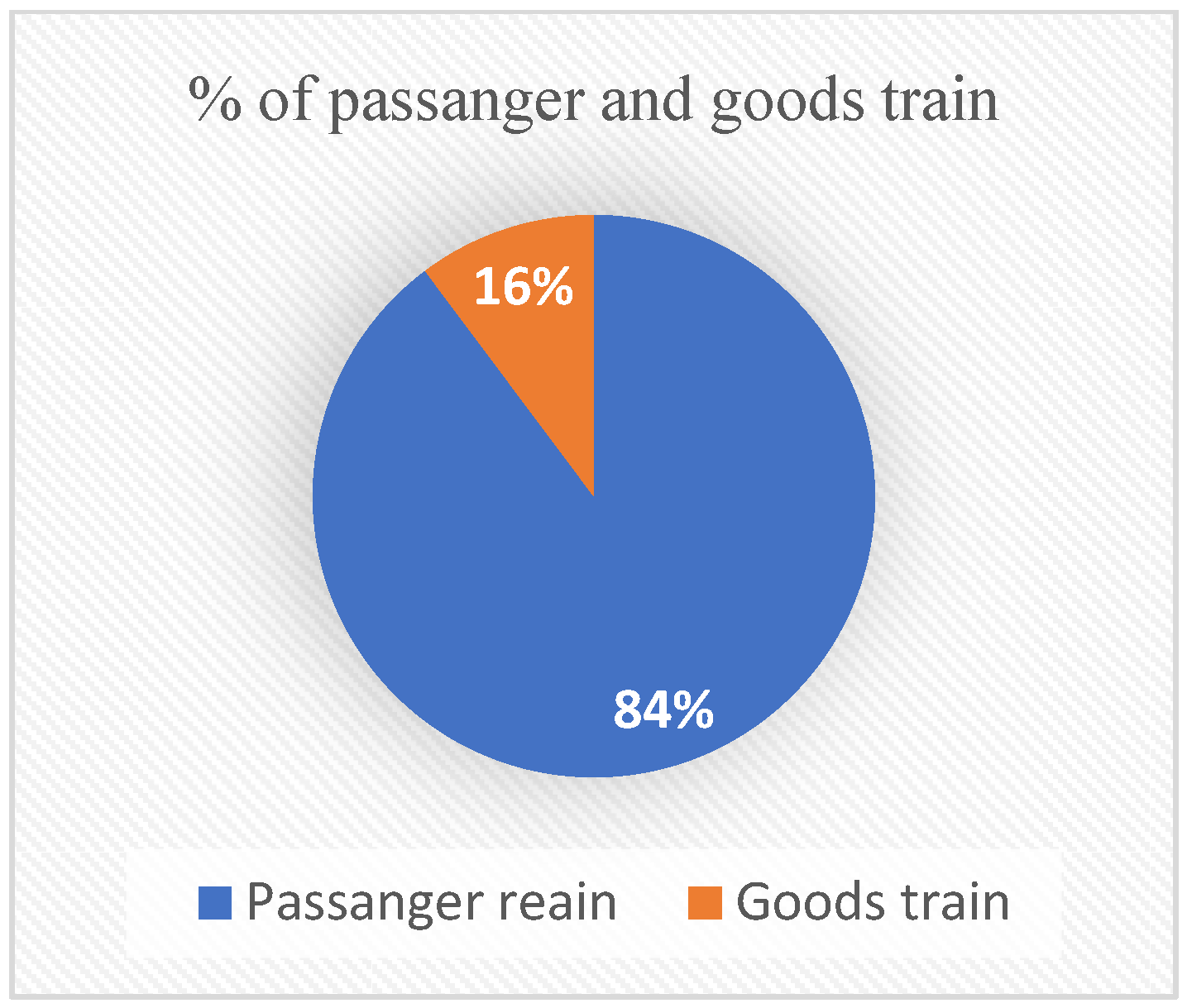
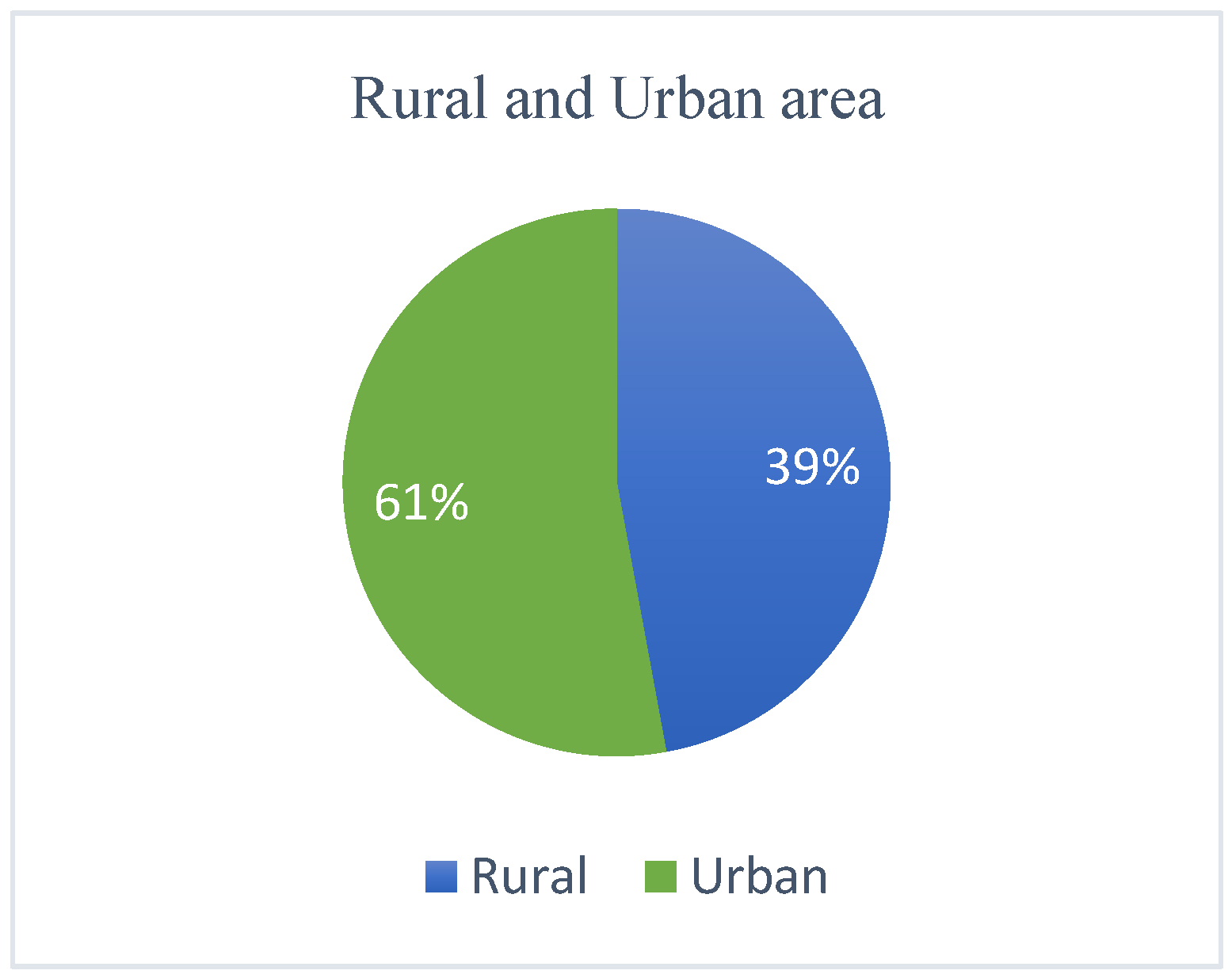
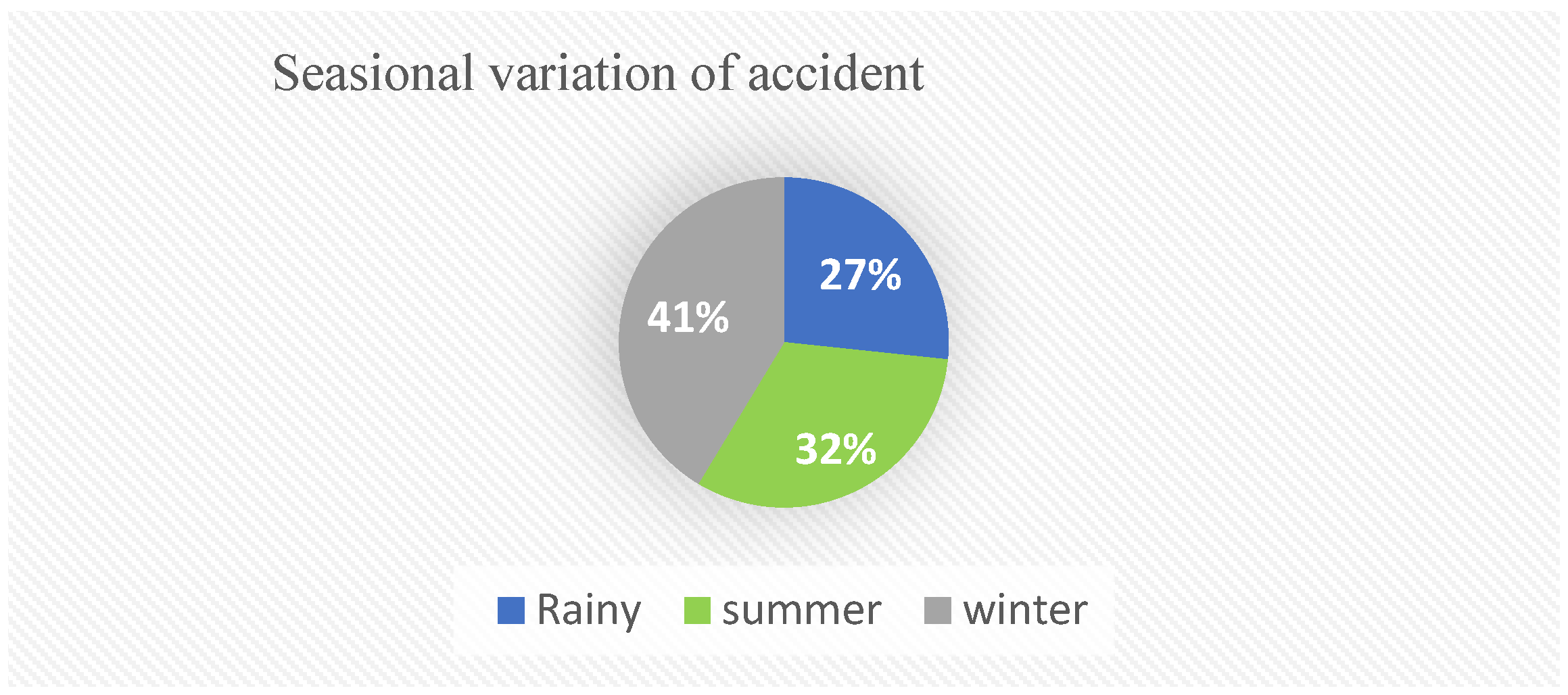
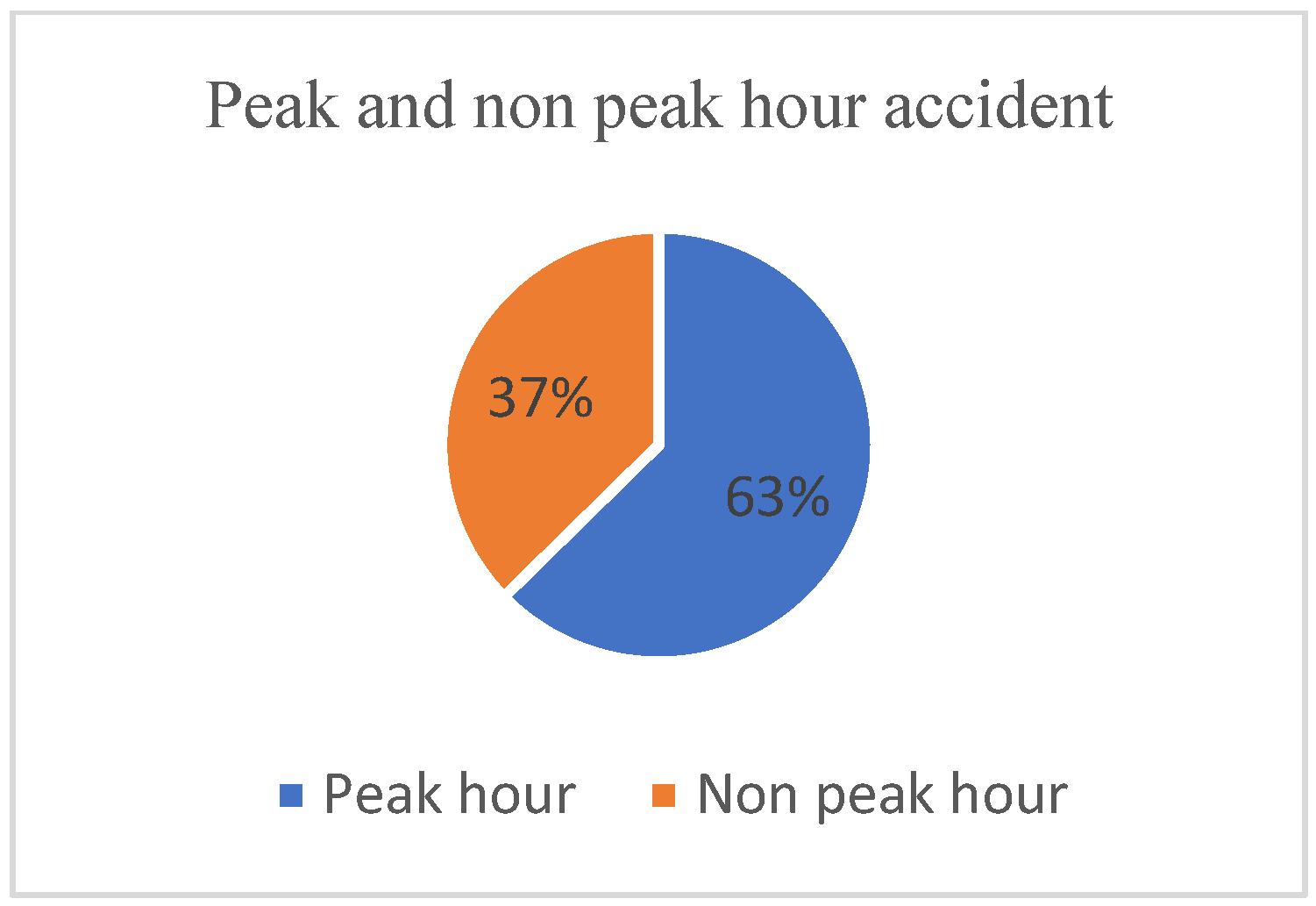
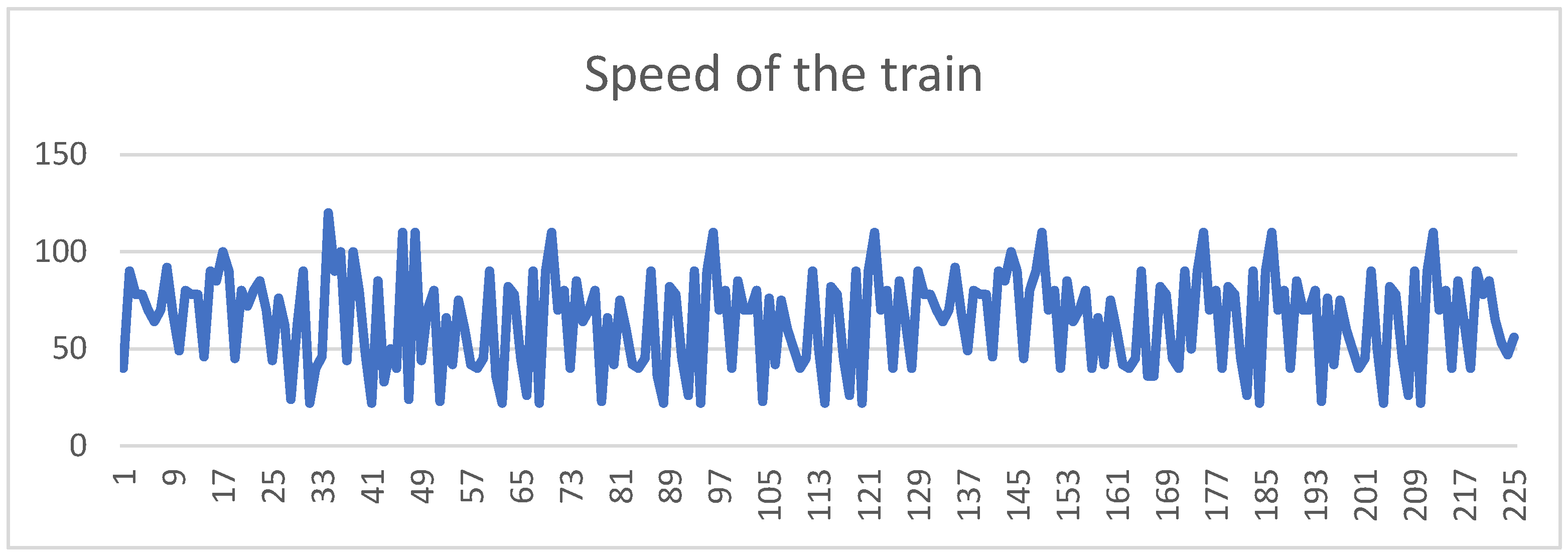
| S. No. | Date of Accident | Brief Description | Casualties | Reason | ||
|---|---|---|---|---|---|---|
| Killed | Major Injuries | Minor Injuries | ||||
| 1 | 21 January 2014—01:35 | Train No.12,485 Up Nanded-Sri Ganganagar Express left Pakki at 01:23 hr towards Abohar. While the train was approaching Manned Level Crossing Gate No A/47-A (Engineering, Interlocked Gate) between Pakki and Abohar stations, one Car (No. PB-10DW-7202, Toyota Etios Liva), after hitting the closed boom of MLC Gate No. A-47/A, dashed against the train engine, thus causing the death of 02 car occupants. The car driver was unhurt. | 2 | 0 | 0 | Negligent driving by a road vehicle driver who did not stop at the closed gate. |
| 2 | 9 December 2012—18:48 | Maruti car no- PB-08W-1789 was stuck with train no-54,621 at manned level crossing gate no-A-82 between the Dasua–Khudda Kurala part of the Pathankot–Jalandhar section. | 2 | 0 | 1 | L-xing Gate A-82, before granting a line clear to train No-54,621 to Station Master/Khuda Kurala (due to which the gate remained in an open condition), resulted in an accident. |
| Descriptive Statistics | ||||||
|---|---|---|---|---|---|---|
| Variable | N | Min. | Max. | Mean | Std. Deviation | Variance |
| Rural or urban area (AUR) | 225 | 0 | 1 | 0.64 | 0.480 | 0.230 |
| Fatal and non-fatal accidents (AFN) | 225 | 0 | 1 | 0.631 | 0.483 | 0.234 |
| No. of railway track (TN) | 225 | 0 | 1 | 0.61 | 0.488 | 0.238 |
| Day and night (TDN) | 225 | 0 | 1 | 0.573 | 0.495 | 0.246 |
| Weather (WDW) | 225 | 0 | 1 | 0.587 | 0.497 | 0.244 |
| Manned and unmanned level crossings (LCMU) | 225 | 0 | 1 | 0.827 | 0.380 | 0.144 |
| Surface type (SBC) | 225 | 0 | 1 | 0.462 | 0.499 | 0.250 |
| Average speed (V) | 225 | 22.0 | 120.0 | 64.9 | 23.9 | 571.0 |
| Type of train (TPG) | 225 | 0 | 1 | 0.740 | 0.438 | 0.192 |
| Vehicle type (VCN) | 225 | 0 | 1 | 0.710 | 0.464 | 0.235 |
| Road geometry (GCS) | 225 | 0 | 1 | 0.524 | 0.505 | 0.251 |
| Warning device (WIN) | 225 | 0 | 1 | 0.58 | 0.495 | 0.551 |
| Weekend and weekdays (WWWD) | 225 | 0 | 1 | 0.267 | 0.443 | 0.196 |
| Peak and non-peak hours (HPN) | 225 | 0 | 1 | 0.360 | 0.481 | 0.231 |
| Gauge of track (GBM) | 225 | 0 | 1 | 0.733 | 0.434 | 0.0197 |
| Negligence of driver or gateman (NGD) | 225 | 0 | 1 | 0.667 | 0.472 | 0.223 |
| Variable | Abbreviation of Variables | Measure of Variable | Coded Value |
|---|---|---|---|
| Rural or urban area | AUR | Nominal | 0 = Rural area, 1 = urban area |
| Fatal/non-fatal accidents | AFN | Nominal | 0 = Non-fatal, 1 = Fatal |
| No. of railway track | TN | Nominal | 0 = One track, 1 = For two-track |
| Day and night | TDN | Nominal | 0 = Day time, 1 = Night time |
| Weather | WDW | Nominal | 0 = Dry weather, 1 = Wet weather |
| Manned and unmanned level crossings | LCMU | Nominal | 0 = Manned level crossing, 1 = Unmanned level crossing |
| Road surface type | SCE | Nominal | 0 = Concrete, 1 = Earthen |
| Average speed | V | Nominal | 0 = less than 50, 1 = greater than 50 |
| Type of train | TPG | Nominal | 0 = Passenger train, 1 = Goods train |
| Vehicle type | VLH | Nominal | 0 = Light vehicle, 1 = Heavy vehicle |
| Road geometry | GCS | Nominal | 0 = Curve, 1 = Straight |
| Warning device | WIN | Nominal | 0 = Not installed properly, 1 = Installed properly |
| Weekend and weekdays | WWWD | Nominal | 0 = Weekend, 1 = Weekdays |
| Peak and non-peak hours | HPN | Nominal | 0 = Non peak hour, 1 = Peak hour |
| Gauge of track | GBM | Nominal | 0 = Meter gauge, 1 = Broad gauge |
| Negligence of driver or gateman | NGD | Nominal | 0 = Gateman, 1 = Driver |
| Variable | Estimates | S.E. | Wald | df | p-Value |
|---|---|---|---|---|---|
| Rural or urban area | 8.941 | 2.525 | 12.541 | 1 | 0.000 |
| No. of railway track | 6.794 | 2.526 | 7.234 | 1 | 0.007 |
| Day and night | 3.823 | 1.492 | 6.567 | 1 | 0.010 |
| Weather | 3.067 | 1.720 | 3.179 | 1 | 0.045 |
| Manned and unmanned level crossings | −1.233 | 1.594 | 0.599 | 1 | 0.042 |
| Road surface type | −1.185 | 1.309 | 0.820 | 1 | 0.365 |
| Average speed | 0.237 | 0.068 | 12.156 | 1 | 0.000 |
| Type of train | −1.725 | 1.928 | 0.800 | 1 | 0.371 |
| Vehicle type | −0.716 | 0.587 | 1.487 | 1 | 0.223 |
| Road geometry | −0.640 | 1.351 | 0.225 | 1 | 0.047 |
| Warning device | 2.320 | 1.235 | 3.531 | 1 | 0.048 |
| Weekend and weekdays | 4.119 | 2.213 | 3.464 | 1 | 0.063 |
| Peak and non-peak hours | 0.744 | 1.354 | 0.301 | 1 | 0.583 |
| Gauge of track | 0.271 | 1.400 | 0.117 | 1 | 0.847 |
| Negligence of driver or gateman | −0.444 | 1.295 | 0.037 | 1 | 0.032 |
| Interceptions | −27.037 | 9.381 | 8.306 | 1 | 0.004 |
| Model | Confusion Matrices | Accuracy | Sensitivity | Specificity | AUC | ||
|---|---|---|---|---|---|---|---|
| Non-fatal | Fatal | ||||||
| Logistic regression | Non-fatal | 80 | 3 | 0.96 | 0.98 | 0.09 | 0.94 |
| Fatal | 2 | 140 | |||||
| Model | Activation Function | Confusion Matrices | Accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | ||||||
| MLP Model | Input t Layer | Output Layer | Fatal | Non Fatal | Fatal | Non Fatal | |||
| Hyperbolic Sigmoid Tangent | Fatal | 98 | 0 | 44 | 0 | 100 | 100 | ||
| Non-fatal | 2 | 62 | 1 | 18 | 96.9 | 94.7 | |||
| Variable | TR | AUR | SSW | DDN | LCMU | WWWD | V | WYN | GCS | HPN | NDR | GBM | SCE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RI | 6.1 | 7.2 | 6.3 | 8.2 | 9.7 | 4.0 | 32.1 | 5.4 | 4.6 | 9.4 | 4.3 | 1.2 | 1.5 |
| Rank | 7 | 5 | 6 | 3 | 2 | 11 | 1 | 8 | 9 | 4 | 10 | 13 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chhotu, A.K.; Suman, S.K. Prediction of Fatalities at Northern Indian Railways’ Road–Rail Level Crossings Using Machine Learning Algorithms. Infrastructures 2023, 8, 101. https://doi.org/10.3390/infrastructures8060101
Chhotu AK, Suman SK. Prediction of Fatalities at Northern Indian Railways’ Road–Rail Level Crossings Using Machine Learning Algorithms. Infrastructures. 2023; 8(6):101. https://doi.org/10.3390/infrastructures8060101
Chicago/Turabian StyleChhotu, Anil Kumar, and Sanjeev Kumar Suman. 2023. "Prediction of Fatalities at Northern Indian Railways’ Road–Rail Level Crossings Using Machine Learning Algorithms" Infrastructures 8, no. 6: 101. https://doi.org/10.3390/infrastructures8060101
APA StyleChhotu, A. K., & Suman, S. K. (2023). Prediction of Fatalities at Northern Indian Railways’ Road–Rail Level Crossings Using Machine Learning Algorithms. Infrastructures, 8(6), 101. https://doi.org/10.3390/infrastructures8060101









