Abstract
The aging of reinforced concrete structures is one of the biggest concerns in civil engineering today since billions of dollars are spent annually on deck repairs and replacements. This study focuses on the rehabilitation of reinforced concrete box girders used in bridge construction. Bridge rehabilitation with a new concrete overlay possesses many challenges that involve cracking and debonding of the overlay caused by the restraining effect of the substrate. This effect leads to the development of tension stresses in the overlay, compression stresses in the substrate, and shear stresses at the interface. In order to mitigate this type of cracking and to ensure a desirable monolithic structural behavior of the rehabilitated bridge, a long-term assessment of the free shrinkage strains acting in the overlay is necessary. This study conducts a two-dimension finite element analysis of a reinforced concrete box girder bridge to evaluate humidity and free shrinkage strain profiles at different times. The humidity gradient between the overlay and the substrate generates differential volume changes between substrate and overlay. The substrate deformations are negligible, while the overlay is subjected to high shrinkage; 78% of the ultimate shrinkage strain is reached after 3 years, indicating a high susceptibility to cracking.
1. Introduction
The issue of aging reinforced concrete structures is one of the biggest concerns in civil engineering today, particularly because the majority of structures built in the 1960s and 1970s have already exceeded their designed service life [1]. According to the National Bridge Inventory 2022 data of the U.S. Department of Transportation [2], 42,966 bridges in the United States (around 7% of the total number of bridges) are listed as “poor” bridges and 301,394 bridges (around 48% of the total number of bridges) are categorized as “fair”. Exposure to aggressive environmental conditions, use of deicing salts in cold weather countries, and truck impacts increase the aging of bridge decks, which leads to cracking of the concrete surfaces and debonding and corrosion of the embedded reinforcement [3]. Among the different types of bridges, concrete box girder bridges need to be studied carefully, since they generally require more deck rehabilitation works [4]. Usually, repairs of deteriorated bridge decks involve replacing the deck with a new concrete overlay; more than USD 5 billion are spent annually in the United States for bridge deck repairs and replacements [5]. However, this method of bridge repair involves two main risks: debonding and cracking of the overlay [6,7]. The interface between new and old concrete behaves as a restraint to the free shrinkage strains of the overlay, leading to the development of tension stresses in the overlay, compression and bending stresses in the substrate, and shear stresses across the interface at the free ends of the member [8]. Furthermore, concrete overlays have shown to be sensitive to moisture loss [9] from the layer of new concrete.
Various experimental tests and theoretical models have been developed in the past to predict the behavior of reinforced concrete bridges rehabilitated with overlays. Lange and Shin [10] carried out experimental measurements and developed a finite element model (FEM) to describe early age stresses and debonding in bonded concrete overlays in high-performance concrete (HPC) and fiber-reinforced concrete (FRC). Beushausen and Alexander [7] then performed tests on composite specimens to have a better understanding of the failure mechanisms of bonded overlays, which are cracking and debonding, and tensile relaxation effects were also described. They later developed an analytical model based on localized strain at the interface to design bonded overlays subjected to shrinkage restraint [11]. Furthermore, Orta and Bartlett carried out a one-dimensional finite element analysis (FEA) to assess free shrinkage strains [8] and stresses due to the restrained shrinkage [12] in a rectangular cross-section, which was modeled as an infinite wide slab. The test-to-predicted ratio of the results agreed with experimental results found in the literature.
Even if the literature about concrete overlays in reinforced concrete bridges is quite extensive, studies about concrete overlays in box girder bridges are scarce. The research on a concrete segmental box girder, the H-3 Windward Viaduct at Oahu, Hawaii, conducted by Tang [13], consisted of a 2D FEM combined with field and experimental tests to identify the main influencing factors for delamination and to establish the appropriate procedures for repairs. Moreover, the rehabilitation of the deteriorated deck of post-tensioned concrete box girder bridges by ultra-high-performance concrete (UHPC) overlays was studied by a 3D FEA performed by Zhang and Chai [4]; an analytical model was then developed by Zhang and Chai [14] to study deck rehabilitation by UHPC overlays, which involves the balancing load concept and the age-adjusted effective modulus method (AEMM).
Although extensive research including various experimental tests and theoretical models have been carried out in the past to predict the behavior of reinforced concrete bridges rehabilitated with overlays, prior studies are generally limited to rectangular cross-sections and one-dimensional finite element analysis [7,8,11,12], or they involve the rehabilitation of the deteriorated deck of post-tensioned concrete box girder bridges by HPC or FRC overlays [10] or by UHPC [4,14]. Moreover, previous researches generally focus on the evaluation of restrained stresses and little attention is given to the humidity and free shrinkage strain profiles (except for the investigation developed by [8,12], but it is concerned with only rectangular cross-sections).
This study is therefore set out to determine the humidity and the free shrinkage strain profiles of a reinforced concrete box girder bridge rehabilitated with a new concrete overlay of the same characteristic compressive strength; the FEA is performed in two dimensions in Matlab. The high percentage of unsound bridges repaired with overlays shows that much uncertainty still exists about this type of rehabilitation work; therefore, an accurate evaluation of the non-linear free shrinkage strain distribution is necessary to assess the magnitude of strains involved and the likelihood of failure by cracking or debonding of the repair.
2. Materials and Methods
2.1. Geometry and Mesh Size
The study assesses the humidity profiles and free shrinkage strains of the concrete box girder bridge 2100-2 with a 61 m span detailed in [15]. The original bridge presented a 225 mm deck. It was assumed that in order to repair the damaged deck, 150 mm was removed from the top of the bridge and substituted with a 250 mm overlay, as shown in Figure 1. A 10 mm extra layer has been added to the cross-section in order to be able to use Dirichlet boundary conditions. A two-dimensional FEA based on three-node constant strain triangles (CSTs) is carried out in Matlab [16]. The cross-section along with the finite element mesh is shown in Figure 1. The length of the edges of the finite elements is roughly 50 mm. The horizontal line in the deck represents the boundary between the new concrete overlay and the existing cross-section of the box girder. The mesh has been enlarged in the cross-section for a better visualization; the actual mesh size is displayed in the focus.
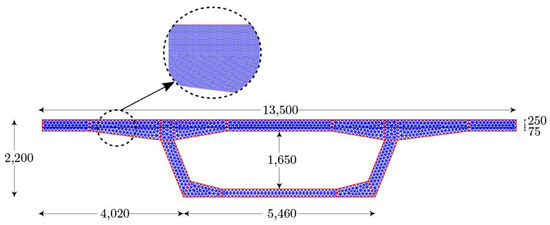
Figure 1.
Finite element mesh of the girder cross-section; dimensions in mm.
The longitudinal reinforcement and prestressed tendons of the girder are assumed to have no effect in this study since the steel reinforcement area does not seem to be an influential parameter in the computation of shrinkage strains [17].
2.2. Humidity Profiles
The moisture diffusion that occurs after the casting of the overlay on the existing substrate is the first phenomenon that needs to be described to be able to evaluate the free shrinkage strains of the repaired box girder bridge.
With the purpose of evaluating the humidity profiles at all nodes in time, the governing differential equation is shown in Equation (1):
where h is the internal relative humidity, , is the drying humidity, and is the autogenous humidity. The change in drying humidity is the moisture loss due to the evaporation of water towards the outer environment. On the other hand, the change in autogenous humidity is due to the chemical process of cement hydration after the initial setting without taking into account any volume reduction caused by load, thermal, or moisture effects; this process is also called self-desiccation of the hardened structure. It consists in consumption of capillary water by hydration reaction [18,19].
To compute the rate of change in drying humidity, Fick’s Second Law of Diffusion (Equation (2)) has been chosen and expressed as
In Equation (2), denotes the diffusivity of the concrete (mm2/day) as a function of , is the number of curing days, and is the Heaviside unit step function. Since the diffusion coefficient D is a function of the internal drying humidity, Equation (2) is a non-linear differential equation and iterations are needed to calculate its solution. D can be estimated with Equation (3):
where represents the ratio ( is the minimum diffusivity at and is the maximum diffusivity at ) and controls the diffusion at low humidities; is the relative pore humidity at and characterizes the location of the drop in the versus plot defining the humidity in the middle of the transition between low and high diffusivity. Lastly, defines the spread of the drop when [20,21]. In this study, the parameter values in Equation (3) were taken as ; ; following the recommendations given in [8], while the maximum diffusivity at , , is evaluated with Equation (4) [21]:
where mm2/day, MPa, and MPa. The characteristic compressive strength of the concrete is , and represents the mean compressive strength of the specimen at 28 days, which is taken in this research to be equal to 38 MPa.
Figure 2 presents a comparison between the diffusion coefficient evaluated in [20] and the one estimated in the current analysis in a node at midspan at mid-depth of the overlay; even with slightly different values of , the curves are consistent with each other.
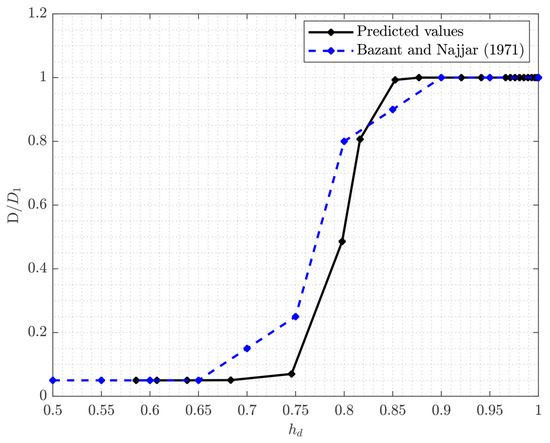
Figure 2.
Diffusion coefficient ratio as a function of the drying humidity : comparison between published research [20] and this study.
The autogenous humidity in Equation (1) is computed with Equation (5):
where , , and are empirically derived coefficients, which represent the ultimate long-term humidity loss due to autogenous shrinkage, the rate of the humidity change, and the dependence of autogenous humidity with time [8], respectively. During the curing time, the evaluation of the autogenous shrinkage is neglected since only the strains developed after the final setting time of the concrete are deemed to be of importance. Moreover, since it has been experimentally proved that the effective curing time is shorter than the actual one, autogenous shrinkage is assumed to occur just after two-thirds of this time. Therefore, the general assumptions of this research are that for the first two-thirds of the four-day curing period, no shrinkage occurs, then only autogenous shrinkage occurs for the remaining curing time. After the curing period ends, both drying and autogenous shrinkage occur [8].
2.2.1. Initial Drying Humidity Profile
An initial assumed humidity is assigned to all nodes; nodes of the freshly cast overlay are assumed to have a humidity equal to 1, while internal nodes are assumed to be equal to 0.55. A humidity value equal to 1 is necessary to describe nodes in the saturation period, as experimentally observed by Zhang et al. 2010 [22]; on the other hand, nodes within the substrate have an initial humidity equal to 0.55 given the results of the one-dimensional finite element analysis described at the end of this section. The nodes belonging to the edges are exposed to the environmental humidity, which is considered to be 0.5 on the outside of the box. Since this study mainly focuses on the long-term behavior of a repaired bridge, the year-round random fluctuation of environmental humidity has been neglected. The nodes on the inside edges of the box are assumed to have an initial drying humidity of 0.6 [23]. This value has been examined by performing a one-dimensional finite element transient analysis for the same box girder without overlay along the 61 m span of the bridge and by reading the drying humidity value at mid-span after a selected number of years. The entire girder is assumed to be freshly cast; hence, the initial drying humidity is taken to be equal to 1 for all internal nodes and 0.9 for the first and the last node. The bridge is subdivided into elements 4 cm in length. An extra segment was added at the beginning of the bridge, and another at the end in order to take into consideration the humidity gradient between the freshly cast surface of the bridge and the environmental humidity. The drying humidity value at midspan predicted after 2 years with Equation (2) is about 0.55; after 3 years, the value decreases to 0.52. Assuming repairs to the deck are performed quite early, it is plausible to use an initial humidity value for the substrate of 0.55 at the time of the repairs and a humidity boundary condition value for the nodes along the internal edges of the box girder equal to 0.6, considering that condensation effects were neglected in the one-dimensional analysis.
2.2.2. Drying Humidity: Solution Method
In the calculation of Equation (1), first, the drying humidity is solved with Equation (2), and then the autogenous humidity is added to the results. In the first loop, the diffusivity coefficient D is calculated with Equation (3) using the initial assumed values of drying humidity. Then for each finite element, the average value of D among the three nodes of the triangle is estimated and considered in the calculation of the element stiffness matrix presented in Equation (6), where D is the diffusion coefficient (see Equation (3)), is the element area, and J is the Jacobian matrix. The element mass matrix is calculated with Equation (7), where is the mass density, then the global stiffness and mass matrices are assembled using element connectivity information [24].
Considering only the drying humidity, Equation (2) becomes:
The finite element formulation of the governing moisture diffusion equation, Equation (8), is carried out using Galerkin’s weighted residual approach, which leads to Equation (9):
where is the global capacitance matrix, is the rate of change of the nodal drying humidity vector, is the moisture content global stiffness matrix, and is the nodal drying humidity vector. The time derivatives in Equation (9) are then further approximated using an implicit scheme with a backward difference approximation for the time term because of its unconditional stability [25], which leads to the following equation:
Since D is non-linear, the solution of Equation (10) follows an iterative procedure. The iterations are repeated until the ratio between the norm of the difference of drying humidities of the last two subsequent iterations and the norm of the drying humidities of the last iteration is smaller than a chosen tolerance (). More details of the solution method are presented in [16].
2.3. Free Shrinkage Strains
Free shrinkage strains, , depend on the pore water content, which may be expressed as a function of the internal relative humidity, . Because of the occurrence of evaporation, the water content changes significantly if it is expressed as a percentage, and therefore, in order to have better accuracy on the results, the free shrinkage strains are considered to depend on the internal humidity of the pore rather than the amount of water [26].
The rate of change of the total free shrinkage strain is evaluated with Equation (11) [26]:
where is the ultimate (maximum) long-term shrinkage strain for a theoretical internal humidity of zero, is a parameter that shows the dependence of the shrinkage strain on the aging, and represents the rate of humidity change.
The value is taken to be equal to , as estimated in [8]. The ultimate free shrinkage strain, , is evaluated with Equation (12) [27]:
The parameters and are taken to be equal to 1 and 1.2, respectively, assuming a type I cement, and sealed or normally cured concrete in air with initial protection against drying; is the mean compressive strength of concrete (38 MPa), w is the water content, and c is the content of cement, taken as 350 kg/m3. The magnitudes of and are 680 and 882 , respectively.
In Equation (13), is a parameter that represents the age dependence of the elastic modulus. It is evaluated with Equation (14), which expresses the ratio between the elastic modulus evaluated at the end of the curing time and the elastic modulus at the equivalent hydration period [26]:
In Equation (14), the elastic modulus at time is calculated as [27]:
where is taken as according to [28].
It must be taken into account that shrinkage strain, besides being a function of the humidity, is subjected to aging effects as well. Aging, caused by hydration, increases the stiffness of the solid microstructure, which is inversely proportional to the shrinkage strain. For low values of humidity, the rate of hydration of cement particles is close to zero; therefore, there is no aging. Hence, the equivalent hydration period has been introduced in order to properly model the shrinkage strain taking into consideration the aging effects. It is evaluated with Equation (17) [26]:
with t equal to the number of days from the casting of the concrete until the moment in which is calculated.
The parameter represents the rate of hydration and it is taken as shown in Equation (18):
with parameter as experimentally proved (as reported by [26]). Continuing with the analysis of the variables in Equation (13), is an empirical function of the internal humidity, which is evaluated with Equations (19)–(21) [27]:
Autogenous shrinkage is significant in high-strength concretes, in which, because of the low water-to-cement ratio, there is a smaller source of internal water that can replace the water consumed by chemical shrinkage during hydration; therefore, the risk of development of autogenous shrinkage is higher. For normal concretes, such as the one considered in this study, the autogenous shrinkage could be considered negligible [29]. However, in order to have a more precise analysis, this research includes the effect of the autogenous shrinkage by taking into consideration the total humidity, which includes the drying humidity and the autogenous humidity, in Equation (11).
3. Results
3.1. Humidity Profiles
The changes in drying humidity and autogenous humidity of a node at midspan at mid-depth of the overlay are shown in Figure 3; the time is represented in the horizontal axis in a natural logarithmic scale. In the first days after casting the concrete, the drying humidity is equal to 1; after the curing period of 4 days, drying shrinkage starts to occur, and a gradual decrease in the humidity can be noticed until it reaches the value of 0.59 after 50 years. Regarding the change in autogenous humidity, for the first two-thirds of the four-day curing period, there is no autogenous shrinkage; after this time, autogenous shrinkage starts to occur and a gradual decrease in the humidity can be noticed until it reaches the value of 0.9 after just about 100 days, staying the same until the end of the analysis.
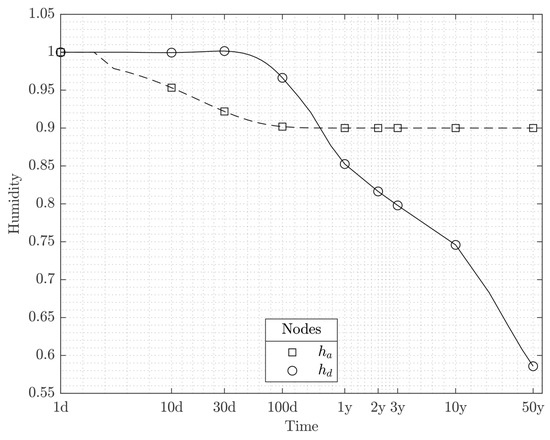
Figure 3.
Drying and autogenous humidity values for a node at midspan at mid-depth of the overlay.
The final humidity profiles are evaluated by summing the changes in humidity caused by drying and autogenous shrinkage between time steps. The humidity profiles at different times are shown in Figure 4. Initially, the humidity of the older parts of the cross-section is assumed to be 0.55; with time, this humidity decreases to a value closer to that of the environmental humidity (0.5). Similarly, at the beginning, the humidity of the freshly cast overlay is equal to 1, then as the years pass, it reaches a value slightly inferior to that of the external environmental humidity.
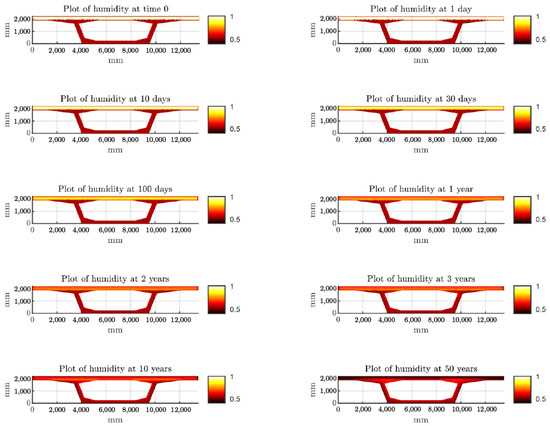
Figure 4.
Humidity profiles of the box girder bridge cross-section at different times.
Figure 5 presents a focused graph on the internal humidity content inside the overlay. This figure shows the behavior of nine nodes located in the deck; the horizontal axis shows the humidity magnitude and the vertical axis shows the ratio between the y coordinate of the nodes and the total height of the cross-section, . The horizontal line at represents the boundary of the overlay. The first node from the top belongs to the dummy layer; therefore, its magnitude always stays the same and it is equal to the environmental humidity. Nodes 2 to 7 (counting from the top) are located in the overlay; their humidity levels go from the initial value of 1 to the final values after 50 years in the 0.43 to 0.51 range. The behavior of the eighth node from the top is of particular interest since the node is located in the bridge deck but outside the overlay. Initially, its humidity is equal to 0.55, then because of the moisture loss in the overlay and the consequent water migration, it reaches an increased humidity value of 0.78 after 100 days. After this time, there is a reversal trend and the humidity decreases until it reaches the value of 0.61, close to its initial value of 0.55. Lastly, the ninth node belongs to the internal edge of the cross-section and its value is constant and equal to 0.6, which was set as a boundary condition.

Figure 5.
Humidity profiles in the bridge deck at midspan. The horizontal line shows the position of the overlay.
Considering the humidity profiles along a web of the box girder in Figure 6, the humidity begins at 0.50 at the left edge (boundary condition of external humidity), 0.55 inside the web, and 0.60 at the right edge. The nodes closer to the external environment tend to reach the 0.5 value, while the ones closer to the hole of the box girder bridge reach values closer to the assumed boundary condition for the internal edge of 0.6.

Figure 6.
Humidity profiles across the box girder bridge web.
The average value of the humidity in the entire cross-section is 0.60 after 10 years and 0.53 after 50 years, a value close to the assumed environmental humidity of 0.5. The analyzed cross-section presents a marked difference between the behavior of the overlay and that of the substrate. The freshly cast overlay starts with a humidity equal to 1, while the substrate is equal to 0.55. After 10 years, the predicted average value of the humidity is 0.62 in the overlay and 0.59 in the substrate; hence, the moisture content in the overlay is just 4.2% higher than in the section below. However, after 50 years, a higher moisture loss is recorded in the overlay, which reaches an average humidity value of 0.48, while the 0.57 average humidity value for the substrate is still close to the predicted value for this section after 10 years. This 17% difference in humidity between the overlay and the substrate after 50 years is due to the drying process which, even if it is governed by a very low diffusion coefficient at these humidities, keeps occurring. After this time, having reached equilibrium, the humidity stays constant. The effects of the autogenous shrinkage end earlier, around the 4-month mark; at this time, the autogenous humidity reaches its final value of 0.9.
3.2. Free Shrinkage Strain Profiles
The normalized free shrinkage strain profiles for selected nodes along one web of the box girder bridge at different times are shown in Figure 7; the horizontal axis shows the values of the normalized free shrinkage strains and the vertical axis shows the ratio between the y coordinate of the nodes and the total height of the cross-section, . The horizontal line at represents the overlay boundary and the horizontal line at represents the beginning of the deck thickness.
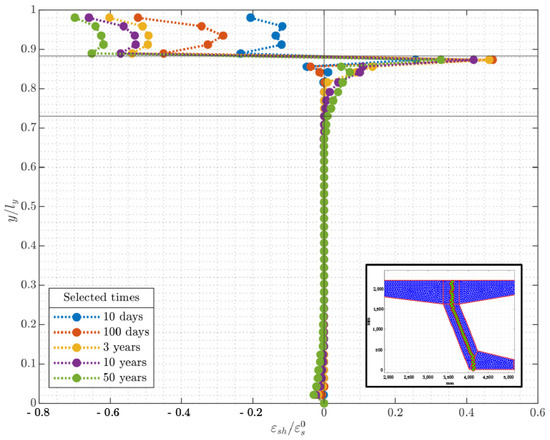
Figure 7.
Normalized free shrinkage profiles at discrete times along one web of the box girder bridge.
The overlay presents increasing compressive strains, while there is swelling at the interface between the new and old concrete.
Figure 8 shows the normalized shrinkage strain results for the entire cross-section at different selected times. The different behavior of the overlay with respect to the substrate is clearly recorded; there is a noticeable increase in shrinkage strain in the overlay with time, which increases the possibility of repair failure.
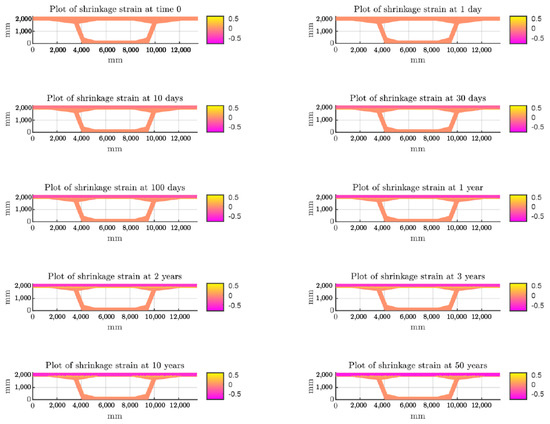
Figure 8.
Normalized free shrinkage strain results of the box girder bridge cross-section at different time steps.
A significant shrinkage strain gradient is recorded in the overlay; the section at the top and the one closer to the interface with the substrate show high levels of strain, while the intermediate region experiences shrinkage of a smaller magnitude. As a matter of fact, the average compressive strain recorded in the overlay is 0.38 after 100 days and 0.65 after 50 years, while the maximum predicted compressive strains are about 0.55 after 100 days, 0.60 after 3 years, and 0.70 after 50 years. An increase in shrinkage strain can be observed with time, although at a slower rate. Taking into account the swelling in the substrate close to the interface with the new concrete layer, the average value calculated after 100 days is about 0.051 and it reaches 0.041 after 50 years. The maximum recorded swellings are 0.47 after 100 days, 0.53 after 6 months, 0.46 after 3 years, and 0.33 after 50 years, showing an initial increase and then, after 1 year, a decrease in magnitude.
These values have been compared with values reported in the literature for overlays of different thicknesses used to repair a bridge of rectangular cross-section with a 700 mm height [8]. Even if the analyzed bridge presents a more slender box girder cross-section and the analysis is performed in two dimensions, the results prove to be consistent; the values are in the same range, the shrinkage strain in the overlay increases with time, and the swelling in the substrate at the interface with the overlay tends to decrease after some years.
4. Discussion
4.1. Humidity Profiles: Discussion of the Results
This study carries out a 2D FEA of a box girder bridge in order to evaluate the humidity profiles at different time steps after the bridge is repaired with a new concrete overlay. An approximate one-dimensional finite element analysis was previously performed to corroborate the value of the relative humidity inside the box found in [23], which is used in the 2D FEM as a boundary condition for the internal edges. The predicted humidity profiles are consistent with the humidity profiles of the one-dimensional analysis of a bridge with a rectangular cross-section and a new concrete overlay performed by [8]. The non-linearity of the humidity in the overlay is evident and the results show that there is always a difference in moisture content between the overlay and the substrate. For the first 10 years, the overlay has a higher moisture content than the substrate, but because of the continuous moisture loss, the final predicted humidity in the overlay after 50 years is actually slightly lower than that predicted for the substrate. This internal humidity gradient must be taken into account because it influences the drying shrinkage and increases the tensile stresses, which may result in surface cracks [30].
The computed results shown in Figure 5 indicate that the rate of humidity change decreases with time. For example, at the mid-depth of the overlay, the rate of change is 0.28/year (from 1.0 to 0.72) for the first year and 0.02/year (from 0.72 to 0.70) for the second year. The behavior of the humidity profiles in time suggests that the substrate and the first layers of the top act like a sealant for the migration of water, preventing the process of water evaporation and promoting the growth in strength and stiffness into the core of the overlay. This raises the concern that future shrinkage strains will act upon a larger modulus of elasticity, causing larger tensile stresses, and they need to be compared with the corresponding strength to compute the probability of cracking.
Moreover, Figure 6 shows that in about 10 years, equilibrium is almost observed, and in 50 years, full equilibrium is reached. Thus, it is expected that an analysis of about 10 years suffices for practical applications and standard designs conducted in engineering firms.
4.2. Free Shrinkage Strains: Discussion of the Results
After the evaluation of the humidity profiles, the free shrinkage strain distribution across the box girder bridge cross-section is assessed. The rate of change of free shrinkage strain is considered to be a function of the rate of humidity change, considering both drying humidity and autogenous humidity. The shrinkage profiles derived from the finite element analysis agree with results from [8]. Shrinkage strains are recorded in the overlay and there is swelling in the substrate at the interface with the new layer; the maximum swelling, 469 , is recorded after 6 months from casting. The non-linearity of the humidity profile creates a shrinkage strain differential across the overlay depth; the largest values are computed at the top and bottom faces of the overlay, while a more gradual distribution is recorded at the overlay mid-depth. The computation of shrinkage strains increases with time. After 100 days, the maximum shrinkage strain in the overlay is nearly 485 (71.5% of ); 78% of the ultimate free shrinkage strain, , is reached after 3 years and 91% after 50 years. These values suggest that the overlay might be very susceptible to cracking.
The behavior of humidity and shrinkage is not quite the same in terms of the rate of change. At the beginning, say 10 days, the change in relative humidity is about 0.05 (Figure 5), whereas the change in shrinkage strains is 0.2 = 176 , which is a significant magnitude of shrinkage (Figure 7). If this strain is restrained at this very short age of the overlay, the probability of cracking might be significant, since at 10 days, the strength of the concrete is low. On the other hand, at late ages, say 10 to 50 years, the internal humidity is still changing (see Figure 4) for 10 and 50 years, while for shrinkage strains, the change is not significantly different (see Figure 8) for 10 to 50 years. This analysis confirms that for practical applications or standard designs, an analysis of about 10 years seems to be adequate, leading to a reduction in computational work for the prediction of stresses, probability of cracking, or displacements due to restrained shrinkage of new concrete overlays.
5. Conclusions
In this investigation, a two-dimension finite element analysis of a reinforced concrete box girder bridge was conducted to evaluate the internal humidity and free shrinkage strain profiles at different times. The following conclusions are drawn.
- The humidity gradient between the overlay and the substrate generates differential volume changes between them. The substrate deformations are negligible while the overlay is subjected to high shrinkage strains.
- The internal humidity gradient must be considered because it influences the drying shrinkage and it may result in increased tensile stress, which may lead to early age cracking.
- The predicted free shrinkage strain values suggest that the overlay might be quite susceptible to cracking.
- The computation of shrinkage strains increases with time, and after 50 years, full equilibrium is reached; however, an analysis of about 10 years seems to be appropriate for practical applications and standard designs conducted in engineering firms, leading to a reduction in computational work for the prediction of stresses, probability of cracking, or displacements due to restrained shrinkage of new concrete overlays.
6. Future Work
An assessment of the tensile stresses acting in the overlay that takes into account the effects of creep relaxation is needed to have a precise description of the long-term performance of the bridge girder. Moreover, since this research is performed on a box girder bridge of certain size and dimensions and deterministic values of the main variables for the internal distribution of the relative humidity (concrete diffusivity, environmental humidity, etc.) are used, future works should include a probabilistic analysis in order to take into consideration the inherent randomness of these variables.
Author Contributions
Conceptualization, L.O.; Methodology, M.G.P.; Formal analysis, M.G.P.; Investigation, M.G.P.; Writing—original draft, M.G.P.; Writing—review and editing, L.O.; Supervision, L.O. All authors have read and agreed to the published version of the manuscript.
Funding
We gratefully acknowledge financial support from the National Council on Science and Technology (CONACyT) of Mexico and from Tecnologico de Monterrey.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors would like to thank G. Faraone for the support and technical input.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lukovic, M.; Ye, G.; Van Breugel, K. Reliable concrete repair: A critical review. In Proceedings of the 14th International Conference Structural Faults and Repair, Edinburgh, UK, 3–5 July 2012. [Google Scholar]
- Federal Highway Administration. Bridge Condition by Highway System 2022. U.S. Department of Transportation. Available online: https://www.fhwa.dot.gov/bridge/nbi/no10/condition22.cfm (accessed on 15 May 2023).
- Parmiani, M.G.; Orta, L. Reliability Assessment of a Continuous Bridge Beam with Exposed Reinforcement. Eng. Struct. 2022, 262, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, Y.H. Numerical analysis of bridge deck rehabilitation by ultra-high-performance concrete (UHPC) overlay. Structures 2021, 33, 4791–4802. [Google Scholar] [CrossRef]
- Gucunski, N.; Imani, A.; Romero, F.; Nazarian, S.; Yuan, D.; Wiggenhauser, H.; Shokouhi, P.; Taffe, A.; Kutrubes, D. Nondestructive Testing to Identify Concrete Bridge Deck Deterioration; Transportation Research Board: Washington, DC, USA, 2012. [Google Scholar]
- Silfwerbrand, J.L. 8—Bonded concrete overlays for repairing concrete structures. In Failure, Distress and Repair of Concrete Structures; Delatte, N., Ed.; Woodhead Publishing Series in Civil and Structural Engineering; Woodhead Publishing: Sawston, UK, 2009; pp. 208–243. [Google Scholar] [CrossRef]
- Beushausen, H.; Alexander, M.G. Failure mechanisms and tensile relaxation of bonded concrete overlays subjected to differential shrinkage. Cem. Concr. Res. 2006, 36, 1908–1914. [Google Scholar] [CrossRef]
- Orta, L.; Bartlett, F.M. Free shrinkage strains in concrete overlays. ACI Mater. J. 2014, 111, 263–271. [Google Scholar] [CrossRef]
- Delatte, N.J.; Scott Williamson, M.; Fowler, D.W. Bond strength development with maturity of high-earlystrength bonded concrete overlays. ACI Struct. J. 2000, 97, 201–207. [Google Scholar] [CrossRef]
- Lange, D.A.; Shin, H.C. Early age stresses and debonding in bonded concrete overlays. Transp. Res. Rec. 2001, 1778, 174–181. [Google Scholar] [CrossRef]
- Beushausen, H.; Alexander, M.G. Localised strain and stress in bonded concrete overlays subjected to differential shrinkage. Mater. Struct. Mater. Constr. 2007, 40, 189–199. [Google Scholar] [CrossRef]
- Orta, L.; Bartlett, F.M. Stresses due to restrained shrinkage in concrete deck overlays. ACI Mater. J. 2014, 111, 701–710. [Google Scholar] [CrossRef]
- Tang, F. Overlay for Concrete Segmental Box-Girder Bridges. J. Bridge Eng. 2000, 5, 311–321. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, Y.H. An Analytical Model to Evaluate Short- and Long-Term Performances of Post-Tensioned Concrete Box-Girder Bridges Rehabilitated by an Ultrahigh-Performance Concrete Overlay. J. Bridge Eng. 2023, 28. [Google Scholar] [CrossRef]
- AASHTO. Segmental Box Girder Standards for Span-by-Span and Balanced Cantilever Construction; Technical Report, AASHTO-PCI-ASBI; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1997. [Google Scholar]
- Parmiani, M.G. Evaluation of Aging and Repaired Reinforced Concrete Structures. Ph.D. Thesis, Tecnologico de Monterrey, Monterrey, Mexico, 2023. [Google Scholar]
- Orta, L.; Bartlett, F.M. Sensitivity analysis of restrained shrinkage stresses of concrete deck overlays. Eng. Struct. 2020, 210, 110396. [Google Scholar] [CrossRef]
- Neville, A. Properties of Concrete, 5th ed.; Pearson: London, UK, 2012. [Google Scholar]
- Tazawa, E.I. (Ed.) Autogenous Shrinkage of Concrete: Proceedings of the International Workshop Organized by JCI, Hiroshima June 13–14, 1998; Taylor & Francis: Oxfordshire, UK, 1999; pp. 1–411. [Google Scholar]
- Bažant, Z.P.; Najjar, L.J. Drying of concrete as a nonlinear diffusion problem. Cem. Concr. Res. 1971, 1, 461–473. [Google Scholar] [CrossRef]
- CEB-FIP. CEB-FIP Model Code 1990: Design Code; Thomas Telford: Lausanne, Switzerland, 1993. [Google Scholar]
- Zhang, J.; Dongwei, H.; Wei, S. Experimental study on the relationship between shrinkage and interior humidity of concrete at early age. Mag. Concr. Res. 2010, 62, 191–199. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Křístek, V.; Vitek, J.L. Drying and Cracking Effects in Box-Girder Bridge Segment. J. Struct. Eng. 1992, 118, 305–321. [Google Scholar] [CrossRef]
- Chandrupatla, T.; Belegundu, A. Introduction to Finite Elements in Engineering, 4th ed.; Pearson: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Hughes, T. Unconditionally stable algorithms for nonlinear heat conduction. Comput. Methods Appl. Mech. Eng. 1977, 10, 135–139. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Chern, J.C. Concrete creep at variable humidity: Constitutive law and mechanism. Mater. Constr. 1985, 18, 1–20. [Google Scholar] [CrossRef]
- Bazant, Z.; Baweja, S. Creep and shrinkage prediction model for analysis and design of concrete structures: Model 83. In Adam Neville Simposium: Creep and Shrinkage—Structural Design Effects; Al-Manaseer, A., Ed.; American Concrete Institute: Farmington Hills, MI, USA, 2000; pp. 1–83. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Wu, L.; Farzadnia, N.; Shi, C.; Zhang, Z.; Wang, H. Autogenous shrinkage of high performance concrete: A review. Constr. Build. Mater. 2017, 149, 62–75. [Google Scholar] [CrossRef]
- Grasley, Z.C.; Lange, D.A. Modeling drying shrinkage stress gradients in concrete. Cem. Concr. Aggreg. 2004, 26, 1–13. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).