Abstract
Prestressed concrete bridges built between 1960 and 1990 no longer meet today’s requirements due to loads and increasing mileage of higher loads that have increased since the bridges were designed. Prestressed concrete bridges are representative of Germany’s existing bridges. In order to deal with the large number of ageing bridges, recalculations and measurements for control as well as bridge monitoring are an important means of support. For both, it is important to find features that are damage-sensitive as well as robust against measurement noise, vehicle parameters (dynamics, geometry, weight, etc.) and environmental influences (temperature, wind, etc.). In this paper, we present features for damage detection based on the influence line, which are investigated with respect to the above requirements by using the analytical solution of the Euler–Bernoulli beam and more complex numerical bridge simulations. In this context, we restrict ourselves to the damage caused by bending stress. The features are calculated on the basis of single vehicle crossings over the bridge for the strain in the longitudinal direction as well as for the deflection of the bridge at different sensor positions. The ratio-based features are compared with raw data and natural frequencies in a classification. Additionally, the sensor positioning is considered. The investigations shows that the ratio-based integrated influence lines are equivalent to or better than the modal parameters, especially when noise and temperature changes are taken into account.
1. Introduction
Bridges are an important part of a country’s infrastructure []. Most bridges in Germany were built between the mid-1960s and the mid-1980s []. During this time, prestressed concrete bridges were primarily built. A total of 70% of the existing bridges are prestressed concrete bridges. In recent years, this type of bridge has been found to be in a state of sudden, chronic failure. Examples include the Salzbachtal bridge of the A66 motorway, which was closed due to a support failure [,] and the Rahmede bridge of the A45 motorway, which was closed due to structural damage [,]. Both bridges have to be rebuilt and will be out of operation for years. The failure of bridges results in very high costs []. In the near future, many bridges will have to be replaced []. The reason for this involves the current loads for which the bridges were not designed []. This is because the mileage and the permitted vehicle load have increased since their initial planning. For this reason, bridge monitoring plays an important role in supporting the maintenance of the bridges.
In this work, we only consider damage caused by bending stress because this is one of the more common damage types. Therefore, we analyse features for bridge-condition assessment based on the influence line where the vehicle parameters, such as the number of axles, the load, and the speed, are unknown. The influence line is the characteristic strain, curvature, or displacement signal at a fixed reference point that results for a single load moving over the structure. We examine the displacement and the curvature as well as the strain influence line. On real structures, for example, a radar device can be used to measure the displacement []. The advantage of radar devices is that they are mobile and can measure without contact. Thus, radar devices can measure several bridges without much installation effort. A radar measures the displacement in line of sight [,]. The displacement in line of sight needs to be transformed into deflection of the bridge []. Refs. [,] used corner reflectors mounted under the bridge where the displacement is measured.
Alternatively, strain gauges or long-/short-fibre Bragg grating sensors (FBG) can measure the strain. The features we have studied are calculated based on measured single vehicle crossings. We define a single crossing as a crossing of just one vehicle over the bridge. The extraction of single crossings from a measured signal can be done with specially developed algorithms such as the dynamic time warping [] algorithm or with specially trained convolutional neural networks [].
1.1. Related Work and Open Questions
In this section, we give an overview of the related work on features based on influence lines that are meant to detect bending damage in bridges. Mostly, features based on the modal parameters are used for condition assessment of bridges []. These are the damping, the natural frequency, and the modes or the derivatives of the modes (curvature modes). The disadvantages of the modal parameters are that they are not damage-sensitive enough to environmental influences and also that they do not take nonlinear behaviour into account [,]. In addition, when determining the curvature modes during the derivation, the influence of noise is amplified, so that the calculated curvature mode is unusable. For the determination of the modes, a dense sensor network is also required. The sensors usually have to be permanently installed for this purpose.
In contrast to the modal parameters as features for the condition assessment which are mostly calculated from crossing collectives, features based on single vehicle crossings can also be extracted. For example, features based on the influence line have been investigated more recently. The measured strain signal or displacement signal at a fixed sensor position is composed of several shifted, superpositioned influence lines for a crossing of a vehicle with several axles. For the reconstruction of the strain and displacement signal by influence line, as many shifted and weighted influence lines are required as the vehicle has axles. The amplitude of the individual influence lines is adapted to the axle load. Normally, the influence lines for individual structures are determined by using the analytical bending beam based on the Euler–Bernoulli theory []. Because of the relationship between strain and curvature , the strain is assumed to be proportional to the curvature with a constant z []. Therefore, we treat the strain and curvature as the same information. Features based on the curvature influence line or strain influence line are, for example, features that describe the influence line []: change of influence line, Girder distribution factor, and dynamic amplification factor. With the three features mentioned, the change of the features over time to the undamaged state (reference state) is measured. A deviation from the reference state is used for damage detection. However, the disadvantages of these features are that the correct influence line must first be calculated for the bridge to be examined, and that these features depend strongly on the temperature as well as on the vehicle parameters (axle load, number of axles, spring stiffness) and the lane deviation.
Then there are three features based on the fibre Bragg grating (FBG) sensors. This type of sensor reflect the strains of the bridge in the longitudinal direction at several points. We use the notation that [] uses for the features. The first feature uses the maximum of the influence lines within each gauges and is called the macrostrain influence line response envelope (MIE) [,]. The second features are the integrals of the macrostrain influence line response (IMIL) [,,], and the second-order difference of macrostrain influence line response (SODM) corresponds to the third feature [,]. The advantage of all three features is that they do not require a reference state to detect damage and that with all three it is possible to localise the damage. In case of damage, this is noticeable as discontinuity in the feature. The mentioned features have the disadvantage that they require a very dense sensor network and the application has so far been investigated on strains from simple bending beam simulations by using the FEM []. Due to the required sensor type for this feature [], this feature is not always feasible.
Two further features based on the strain of single vehicles crossings are the max/min ratio and the ratio of the integral of the positive part to the integral of the negative part within a signal []. However, these features are limited to two-span bridges with continuous girders.
There are few studied features based on the displacement influence line. The features’ change in the displacement influence lines (CDIL), change in the rotation of displacement influence lines (CRDIL), as well as the change in the curvature of displacement influence lines (CCDIL) compare the influence line between the current state and the reference state []. Discontinuities in the difference over the crossing duration indicate damage. CDIL is not damage-sensitive, and CRDIL/CCDIL use derivatives, which should become unusable when dynamics or noise occur. In addition, investigations of the features have so far been limited to FEM bending beam simulations and laboratory measurements. The features also have the disadvantage that they require exactly the same vehicle for the creation of the reference state and for the state to be inspected later. There is generally a need for research on features based on the influence line and especially on features based on the displacement influence line. The Grey relational coefficient (GRC) method in [] is comparable to CCDIL and has the same requirements and disadvantages. GRC uses the second-order derivative of the displacement influence line. The feature displacement-based index (DBI) requires also a reference state, which does not have to be from the same vehicle, but DBI needs many displacement sensors along the beam [].
Recent work investigates features that use the ratio of signals at different positions [,,]. The advantage with these features is that the load, as well as the speed, of the vehicle is reduced, and thus the vehicle parameters are not needed for damage assessment. While [] performs a principal component analysis after the calculation, [,] do without a principal component analysis and use the features directly for condition assessment. In [,], static vehicle crossings over beams/bridges were investigated.
In this paper, we first introduce the new features based on the influence line, make basic statements about the detectability of damage and consider sensor positioning in the stepped Euler–Bernoulli beam. The stepped Euler–Bernoulli beam is introduced in Section 1.2. Then, we introduce the features based on the influence line in Section 2. On the stepped Euler–Bernoulli beam we compare in Section 2.1 the changes in influence line between damaged and undamaged beam with the changes in natural frequencies and modes. The integral-based features are investigated in Section 2.2. In Section 3, we compare features based on the influence line from finite-element method (FEM) simulations in a classification that also takes the influence of temperature into account. Compared to most studies in the literature, we consider the dynamics of the vehicles and the bridge in our simulations. The vehicle parameters are varied from crossing to crossing, and we investigate the robustness against noise as well as an optimal sensor positioning.
1.2. Stepped Euler–Bernoulli Beam
In the analytical investigation in Section 2.1 and Section 2.2, we use the stepped Euler–Bernoulli beam. We modelled the stepped Euler–Bernoulli beam according to [] based on the Euler–Bernoulli theory. Our resulting Matlab implementation of the stepped Euler–Bernoulli beam can be found in []. In this work, we always consider a two-span beam as shown in Figure 1 which has the length L. A continuous beam is statically indeterminate, and its behaviour is closer to that of real structures than a single-span beam. In this work, the middle support is always in the middle of the beam ().
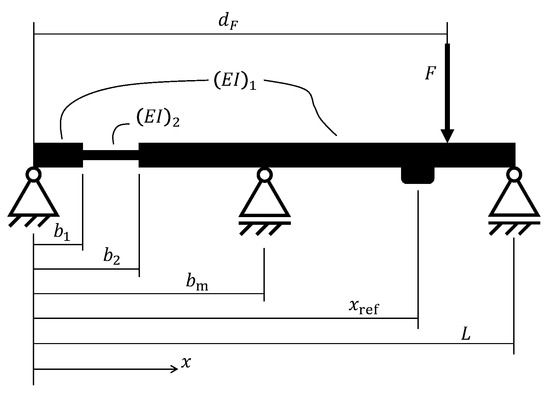
Figure 1.
Structure of the analytical Euler–Bernoulli beam.
Singularity functions can be used to change the bending stiffness in the beam, where E is the elastic modulus and I is the second moment of area. In the ranges and , the bending stiffness is applied. By changing the bending stiffness between and , damage can be modelled. We express the damage with
For a damage, must hold. The middle damage position is expressed with
and the damage width with
The load F is applied at the position . The influence line is calculated as the resulting course of displacement w or curvature at a fixed reference point , while the load F moves across the beam from to . The displacement w at the location over all positions of the load is called the displacement influence line
Similarly, the curvature influence line
is defined for the curvature . Thus, the influence lines are a simplification of the temporal course of the displacement and the curvature at the sensor during a vehicle crossing under neglect of the additionally occurring dynamic. In the following, we use the variable for simplification if we mean the curvature influence line and the displacement influence line equally.
Figure 2a shows an example of the curvature influence line , and Figure 2b shows the displacement influence line for the reference point . The damage for the damaged case is at %. The damage midpoint is at , and the damage width is . The load is . The influence line consists of .
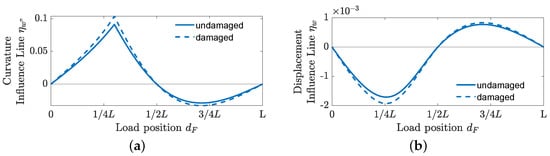
Figure 2.
Example influence lines with reference point for the undamaged and damaged bending beam. Change in bending stiffness is at % between and . (a) Curvature influence line at . (b) Displacement influence line at .
We simulate the bridge in a simplified way with the analytical Euler–Bernoulli bending beam. In reality, the material properties of the bridge are not homogeneous. In addition, the prestressing of the bridge is left out. The moving load F is applied statically. This neglects the dynamics of the vehicles and the bridge. Furthermore, the lane deviation of the vehicle is not taken into account for the bending beam.
In the next section, we present selected features based on the influence line.
2. Features Based on Influence Line
In this section, we present the features to be investigated, which have already been considered in [] on the stepped Euler–Bernoulli bending beam in a damage classification.
By forming the ratio from features based on the influence line at different positions, invariance to the load F and the velocity can be achieved [,,]. In the following, seven ratio-based features are presented, which are calculated from signals at two different positions. The first five features are M features, which are composed of two individual values. The M features can only be applied to the full extent to influence lines of two-span continuous beams.
Refs. [,] use the ratio of maximum value to maximum value between two influence lines of the same crossing at different reference points and
where and , respectively, are the sample numbers at which the influence lines and reach their maxima.
The second M feature variant
gives the ratio between maximum value of the influence line in reference point and minimum value of the influence line in reference point , where is the sample number at which influence line has its minimum [,].
The third feature is the ratio between the signal and the signal at the time
where the time , is the time at which the signal i has its maximum [,].
The fourth M feature variant
is the ratio between the signal i and the signal j at time , where the time corresponds to the time at which the signal i has its minimum [,].
The last M feature variant is the ratio of the minimum value of the influence line at reference point , and the minimum value of the influence line at reference point []
The R features and extensions of the R feature were the best features in the comparison in []. When considering the R feature, all available samples, and thus all available information, are used. The R feature is slightly modified to [] by omitting the magnitude of the influence line. The feature
is calculated from the quotient of the integrated influence line at reference point i and the integrated influence line at reference point j [,]. The value of the R feature is constant for different loads F, because the load F is reduced during the quotient formation. If damage occurs, the R value for the damaged beam deviates from the R value for the undamaged beam. The advantage of the R feature is that the integral suppresses possible measurement noise.
The dimension of the R feature can be extended by dividing the time signal into sections and forming the quotient between the individual sections []
In the next two sections, we motivate the use of features based on the influence line and present a basic investigation of detectability and sensor positioning.
2.1. Motivation for Features Based on Influence Line
Based on the stepped Euler–Bernoulli beam, we want to make a first estimation of the potential of features based on the influence line for damage detection. For a better evaluation, we compare the influence line with modal parameters in the following. The modal parameters describe the vibration behaviour of a structure and are mostly used for the assessment []. We follow [] in calculating the modal parameters using the stepped Euler–Bernoulli beam. These features are determined based on a time window in which several crossings have taken place, using mainly accelerometers. The modal parameters include
- the natural frequency f,
- the modes (displacement), and
- the curvature modes (curvature of the modes).
For the calculation of the modal parameters we discretise the beam with elements. The nodes are located between the elements. Thus, the beam consists of nodes. The displacement is determined at the nodes. The damage width is always . We consider 191 damage positions where the centre of damage moves from to . The bending stiffness change is always %, where the elastic modulus E is changed. The second moment of area I remains constant so that the cross-section in the beam remains constant, and thus no change in mass takes place. The density is . The damage chosen here is very small and would probably be covered by the noise and environmental influences in a real measurement environment. We only want to allow a relative assessment of the curvature influence line and displacement influence line here and assume that the relative comparison is maintained for higher damage scenarios.
First, we consider the changes in the modal parameters. Figure 3 summarises the results for the modal parameters. The first three modes (, and ) are shown in Figure 3a for the undamaged case. Here, the amplitude is plotted along the longitudinal beam direction x. The modes are mass normalised. In Figure 3b–d, the relative difference is plotted as a function of the damage location . The relative difference of the hth natural frequency is calculated with
where is the hth natural frequency for the undamaged case and is the hth natural frequency for the damaged case. The largest relative difference for a selected natural frequency can be expected at the location where the damage location is close to the largest magnitude deflection of the associated mode . For example, the first mode in Figure 3a has its absolute maximum in and . This means that damage close to both points leads to a larger relative difference . For the first natural frequency, the relative difference can go up to −0.1011% in Figure 3b for damage in . However, this also means that damage in the nodal points of the amplitude of the mode (zeros in ) will remain undetected. For example, damage at the both outer supports remains undetected, since none of the first three modes has a large deflection here. This also applies to the modes and curvature modes . The largest relative difference in Figure 3b for the second natural frequency can be up to −0.1658% in . For the third natural frequency, the relative difference in Figure 3b can go up to −0.0987% at damage points , , and .
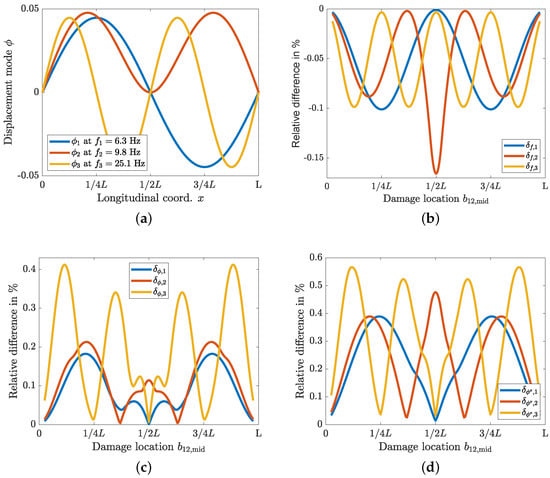
Figure 3.
Modal parameters and relative difference between damaged and undamaged beams for different damage positions on the x-axis. (a) Thefirst three modes (displacement) , and for the undamaged beam. (b) Relative difference in natural frequencies of the damaged beam compared to the undamaged beam. (c) Relative difference of the modes of the damaged beam compared to the undamaged beam. (d) Relative difference of the second derivative of the modes of the damaged beam compared to the undamaged beam.
Since the modes for the damaged case are qualitatively the same as the modes for the undamaged case, the integral of the mode changes and curvature mode changes are compared. Furthermore, the modes with odd index, such as and in Figure 3a, are rotationally symmetric in the middle support (). Therefore, the absolute values are used. The relative integral difference of the hth mode is calculated with
where is the kth node of the hth mode for the undamaged case and is the kth of the hth mode for the damaged case. The maximum relative integral difference for the first mode is 0.1824% in Figure 3c, for the second mode 0.2130% and for the third mode 0.4122%. With the modes, the relative difference compared to the natural frequencies could be increased.
The hth curvature mode is the second derivative of the hth mode with respect to the longitudinal coordinate x. The equation for the relative integral difference of the hth curvature mode is given by
where is the kth node of the hth curvature mode for the undamaged case and is the kth of the hth curvature mode for the damaged case. The maximum relative difference in Figure 3d for the first curvature mode can go up to 0.3889%, second curvature mode up to 0.4762% and third curvature mode up to 0.5661%. When comparing the modes with the curvature modes , it is noticeable that the double derivative can be used to increase the relative difference between the damaged and undamaged states.
Next, we consider the relative difference for the influence lines in Figure 4. The influence line additionally depends on the reference point. Therefore, in Figure 4a,b, besides the middle damage position on the abscissa, the reference point is also plotted on the ordinate. The colouring reflects the relative difference. The integrated absolute influence line is also used for the influence lines and the course of the undamaged influence line corresponds qualitatively to the course of the damaged influence line. The relative difference of the influence lines
is calculated by using the influence line for the damaged beam and the undamaged beam . The relative difference for the curvature influence line is given by , and the relative difference for the displacement influence line is given by . We have set the limits of the colour bar in Figure 4a to the limits of the colour bar in Figure 4b, as otherwise no evaluation for Figure 4a would be possible for sensor positions that lie outside the damage position (diagonal).
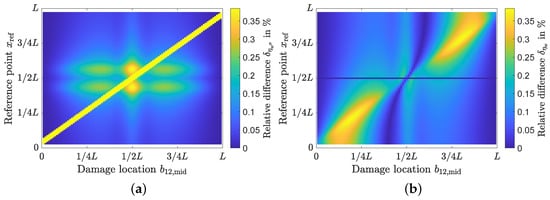
Figure 4.
Relative difference between damaged and undamaged beams for different sensor positions and damage positions. (a) Relative difference between damaged and undamaged beams for the curvature influence line . The relative difference is coloured, and the limits are adjusted to the relative difference for displacement in Figure 4b. In the diagonal there is a maximum relative difference of 2.0395%. (b) Relative difference between damaged and undamaged beam for the displacement influence line.
The largest relative difference for the curvature influence line in Figure 4a is found in the diagonal. In this case the reference point is within the damage position and . The relative difference here is between 1.7738% and 2.0395%. At reference point and , a larger relative difference is detectable for almost all damage positions . Outside the diagonal and outside the middle support, the relative difference goes up to 0.2642%. Damage in the middle support () is noticeable in almost all reference points .
The largest relative difference of the displacement influence line in Figure 4b is in a curved diagonal. The band of the diagonal is wider than for the curvature influence line, and it is sufficient if the reference point is close to the damage location . On the diagonal, the relative difference is between 0.1229% and 0.3838%. Between the diagonal with the high relative difference and the middle support runs a second diagonal that shows a very low relative difference .
A damage near the middle support () is detectable by almost all reference points . Since there is no displacement in the middle support, the relative difference here is zero.
While the natural frequencies (maximum relative difference is −0.1658%) can be determined with a few sensors, this is not true for the natural modes and curvature natural modes . For the modes (maximum relative difference is 0.4122%) and curvature eigenmodes (maximum relative difference is 0.5661%), several sensors are necessary to describe the modes and curvature modes sufficiently for damage detection. The highest relative difference can be achieved with the curvature influence line (maximum relative difference is 2.0395%). In comparison, the displacement influence line achieves a relative difference of 0.3838%. Thus, it is expected that features based on the influence line are equally sensitive for damage detection compared to the modal parameters, but a smaller number of sensors is required. The advantage for real measurements is that the influence lines do not have to be identified from the measurement signal. The features based on the influence line can be used on the basis of the measured unprocessed signals that correspond to superposed influence lines. In contrast, the modal parameters must first be determined in order to use features based on the modal parameters, which introduces further uncertainties.
2.2. Features Based on Integrated Influence Line
The R feature in Equation (11) is composed of two integrals and at two different reference points. We examine the integral in more detail below. By using the analytical solution for the stepped Euler–Bernoulli beam, the integral of the displacement influence line can be expressed in simplified form:
The same type of equation can be achieved for the curvature influence line. The equation shows that the undamaged component and the damaged component are additive. The damage severity is mainly expressed by . From Equation (17), it can be seen that when a ratio is formed—for example the R feature—the load F is reduced. Furthermore, the bending stiffness is reduced. If the bending stiffness is assumed to depend on the temperature, then the temperature influence is thus reduced.
In Figure 5, the contour for the relative difference of the integral of the curvature influence line and in Figure 6 the contour for the difference of the integral of the displacement influence line for different damage positions () is shown. The relative integral difference is calculated with
from the integral of the damaged beam and the integral of the undamaged beam . The damage position is plotted on the abscissa and the reference point is plotted on the ordinate. The integral difference is shown in colour. The minimum and maximum on the colour scale for the integral difference have been truncated to allow evaluation. This is because the integral difference for the curvature influence line goes to infinity in and in . The integral difference of the displacement influence line goes to infinity in . For better orientation, the area in the contour images with a change close to 0% is shown in grey. The grey areas thus indicate combinations of damage location and sensor position , which are difficult to detect because the integral difference in this area is near zero. As the damage width increases, the damage middle begins and ends shifted. This unaccounted region is white at the left and right edges (compare Figure 5b for smallest damage width with Figure 5d for largest damage width).
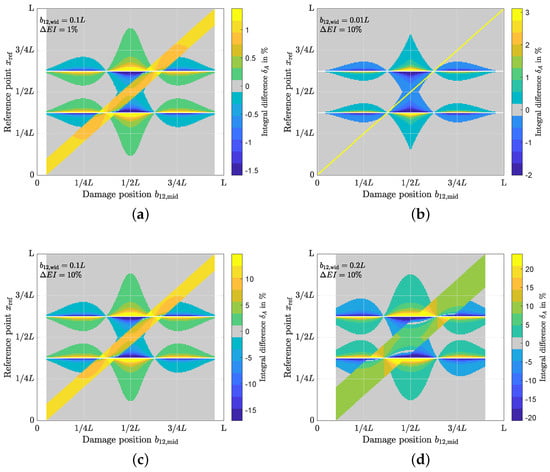
Figure 5.
Contour plots for the relative integral difference of the curvature influence line . The relative integral difference is shown in colour. The damage location is plotted on the abscissa and the reference point is plotted on the ordinate. (a) and . (b) and ; (c) und ; (d) und .
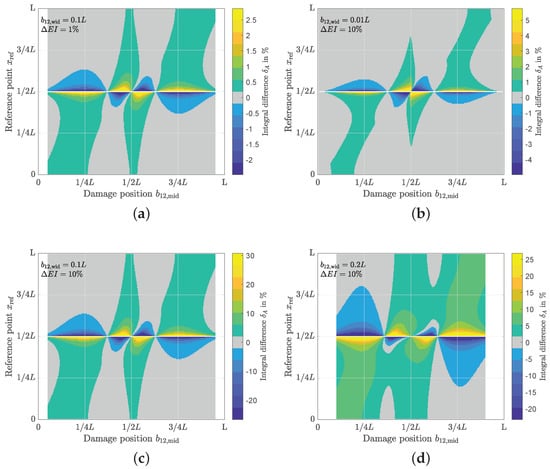
Figure 6.
Contour plots for the relative integral difference of the displacement influence line . The relative integral difference is shown in colour. The damage location is plotted on the abscissa and the reference point is plotted on the ordinate. (a) and ; (b) and . (c) and . (d) and .
A high integral difference can be found when the reference point is inside the damage position (between and ). The diagonal band in Figure 5 reflects this case. This band is as wide as the damage width (compare Figure 5b → Figure 6c → Figure 5d).
However, the highest integral difference can be found for reference points near the positions and . At these reference points, —the integral of the curvature influence line—takes the value zero, since the integral of the influence line to the left of the support () is equal to the integral to the right of the middle support (). As soon as damage occurs, the relative integral difference within the curvature influence line shifts and damage becomes clearly visible. In or in , damage can be detected in almost any position (). These locations are of great interest when choosing sensor positioning. Damage in the middle of the beam could be detected by many reference points, except reference points too close to the outer supports (ends of the beam). Only reference points close to the outer supports can detect damage located at the outer supports. In general, it is difficult to detect damage near the outer supports because they are pinned in this example. There is no moment in pinned supports and therefore no curvature that can be measured. In reality, in bridges there is no perfect pinned support, so there is a certain amount of fixed support []. In general, the contour (detectable area) does not change when the damage severity changes (compare Figure 5a with Figure 6c). However, as the damage severity increases, the relative integral difference increases. If the damage width changes, then the contour also changes (compare Figure 5b with Figure 6c and Figure 5d). Depending on the damage width, there are damage positions that would not be detected by any reference point except reference points that are within the damage. This range shifts from for damage width to for damage width .
The relative integral difference of the displacement influence line goes to infinity for the reference point in the middle support because the displacement in this area goes to zero. Figure 6 indicates that the displacement influence line reference points near the support are very sensitive to damage. However, displacements near supports are small and thus lead to an unfavourable signal-to-noise ratio (SNR).
For the relative integral difference of the displacement influence line, almost all damage positions are best detected by reference points close to the support. Otherwise, it is true for the relative integral difference of the displacement influence line that damage is best detected when the reference point is close to the damage location. The reference point does not necessarily have to lie within the damage location, as it is the case for the curvature influence line. However, no such high integral difference is noticeable as for the curvature influence line. Furthermore, if the reference point lies within the damage, the integral difference is comparatively low. Damage near the middle of the beam in Figure 6 can be detected by almost all reference points. The contour hardly changes as the damage severity increases (see Figure 6a → Figure 6c). However, the integral difference increases with increasing damage severity . As the damage width varies, the contour changes (Figure 6b–d). However, there are damage positions that cannot be detected by reference points if the damage width is too small (in the examined examples ). This damage position that remains invisible moves from for to for . As the damage width increases, more damage positions can be better detected from reference points in the same field. Damage positions in the range between and can partly be better detected by reference points in the right field. These are the places where the diagonal with the high integral difference values does not pass through as in Figure 5 for the curvature influence line. If the damage is in the right field () and not directly in the centre of the field or near the middle support, the damage will not be detected by a reference point in the left support in this example.
If the reference point is inside the damage location, the curvature influence line performs better. Furthermore, the reference point in and in seems to be well-suited for the curvature influence line as a damage-sensitive reference point by making any damage visible. For the displacement influence line, a reference point close to the middle support is suitable to cover all damage positions, whereby the signal-to-noise ratio (SNR) has to be taken into account here, as the displacement close to the support goes to zero. While reference points near the outer supports with the displacement influence line can detect damage up to and beyond as well as in the middle of the beam, reference points near the support using the curvature influence line can only detect damage if the reference point is in the damage location.
In this section, we have theoretically investigated the integral of the influence line (R feature). From this investigation we conclude that not all reference points are suitable for a condition assessment. Furthermore, we were able to show damage positions where no change in the integral difference is visible. For condition assessment with the curvature influence line, reference points must be provided at these positions. With the displacement influence line, these locations cannot be made visible to any reference point. These locations remain undetected when forming the R feature.
In the next section, we apply the ratio-based features to FEM simulations and discuss their suitability for damage detection.
3. Results and Discussion for Ratio-Based Features at FEM Simulations
The R feature has so far only been applied to static simulations in the literature. In this section, we analyse the R feature based on FEM simulations that take dynamics into account. In the Section 3.1, we explain the setup of the FEM simulations. In Section 3.2, we investigate the features in a general damage classification. Here, the classification model should distinguish between the undamaged state of the bridge (0-0) and two damage sates (damage class 1-5 and 2-3).This investigation is conducted at a temperature for the bridge of 20 °C. A major disadvantage of most of the features in the literature is the dependence on the temperature change and the lane deviation. Therefore, in Section 3.3, the classification models trained in Section 3.2 are used to classify undamaged bridges at different temperatures. The classification algorithm does not know the temperature and vehicle parameters and lane deviation. The evaluation based on the FEM simulations is a good estimation of the features for a real application.
3.1. Setup of the FEM Simulation
For the numerical investigation, we have chosen the bridge in Dietersdorf near Coburg of the federal road 303 in Bavaria/Germany in Figure 7a as an example. The FEM model in Figure 7 was created with the FEM program SOFiSTiK. The bridge is a two-span prestressed concrete bridge, as can be seen in Figure 7b. The bridge has one lane per direction for both directions of traffic. The bridge has a total length of 57 m and a width of 13.6 m. Figure 7c shows that the structure consists of five T-shaped precast concrete beams (girder). The two spans are connected by the deck, but the girders are not. The bridge consists of shell elements, which have six degrees of freedom. The asphalt layer was modelled as a separate layer.
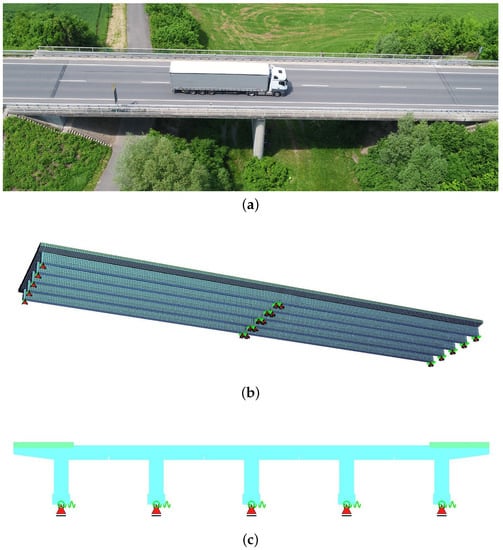
Figure 7.
FEM model of the bridge in Dietersdorf near Coburg in Bavaria. The used FEM programme is SOFiSTiK. (a) View from above on the example bridge in Dietersdorf on 9 July 2021. (b) Isometric view of the bridge from below. The girders of the bridge are not connected to each other. (c) Cross-section of the bridge.
We have simulated several vehicle crossings over the bridge. The FEM simulations include crossings of different vehicle types with different vehicle parameters. We varied the vehicles’ parameters with regard to speed, number of axles, mass per axle, axle spacing and thus vehicle length, vehicle width, spring stiffness, and damping of the axles, as well as lane deviation. These parameters were varied randomly in the individual simulations based on the normal distribution. In each simulation, the vehicles cross on the southern lane in the eastbound direction. By lane deviation we mean the deviation from the centre of the lane. The lane remains constant throughout the crossing on the bridge. A simulation consists of 1000 samples and has the duration of 10 s. The crossing duration goes from 2.34 s for the fastest simulated vehicle to 7.96 s for the slowest vehicle. On average, a simulated crossing takes 4.08 s. The temperature is 20 °C for all simulations. We consider another dataset with 100 crossings at different temperatures for the temperature independence study created in Section 3.3. We present this data set in Section 3.3.
The layout of the bridge in Figure 8 shows the positions of the nodes or elements from the FEM simulations with the corresponding names. In the following, we refer to a node or element as a sensor or sensor position. The letters represent the girder in each case.
- SS: South–south girder,
- S: South girder,
- M: Middle girder,
- N: North girder, and
- NN: North–north girder.
At all 70 sensor positions in Figure 8, we took the strain in x direction and the displacement in z direction at the bottom of the webs from the FEM simulation. The strain in the x direction is the strain in longitudinal direction and the displacement in the z direction represents the deflection of the bridge. We assume the sensor positions of the displacement to be constant because there are corner reflectors attached under the example bridge at which the displacement is measured.
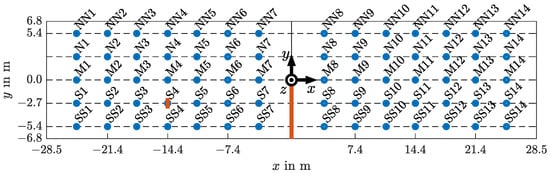
Figure 8.
Bridge floor plan with node and element positions (blue points) of the simulated crossings for the Dietersdorf bridge and their names. The dotted lines indicate the beams. At the blue points, the strain in the x direction and the displacement in the z direction is available. The measurement direction corresponds to the coordinate system in the centre of the picture. The damage locations are marked in red.
Class 0-0 represents the undamaged case. For damage 1–5, we removed elements in the southern deck between and at above the middle support (in Figure 8 between S7 and S8) and for damage class 2-3, we removed three elements from the web in the Western middle of the field in the S girder (in Figure 8 near S4). The removal of the elements leads for class 1-5 to a change of the first natural frequency by −0.04 Hz, of the second natural frequency by −0.09 Hz and of the third natural frequency by −0.03 Hz compared to the undamaged state (00). Damage class 1-5 leads to a change of the first natural frequency by −0.01 Hz, of the second natural frequency by −0.03 Hz, and of the third natural frequency by −0.01 Hz compared to the undamaged state (0-0).
We examine the robustness of the features against noise. Therefore, we generate the noise artificially by adding normally distributed random numbers to the signal []. Usually, the signal-to-noise ratio (SNR) is calculated from the ratio between the root mean square value of the signal and the root mean square value of the noise []. We use the absolute maximum of the strain or displacement signal. This yields to higher SNR values. The SNR is determined for all sensor positions for all crossings with
where is the signal of the strain or displacement signal, at a sensor position during the vehicle crossing and is the standard deviation of the random numbers. Table 1 summarises the SNR for strain in the x direction and Table 2 for displacement in the z direction. Three levels of noise are investigated in this study: Without Noise, Noise Level 1, and Noise Level 2. There are no entries in the column without noise in Table 1 and Table 2 because no noise was considered here and thus the SNR is infinite. For the strain in the x direction in Table 1, random numbers in the column Noise Level 1 with a standard deviation were added to the signal and in the column Noise Level 2 random numbers with a standard deviation of were added. Similarly, for the displacement in the z direction in Table 2 in column Noise Level 1 random numbers with a standard deviation were added and in column Noise Level 2 random numbers with a standard deviation of were added to the signal.

Table 1.
Table with signal-to-noise ratio for strain in x direction for different elements.

Table 2.
Table with signal-to-noise ratio for displacement in the z direction for different nodes.
In Table 1 and Table 2, respectively, we give the smallest SNR (min) and the largest SNR (max) as well as the median SNR (median). The smallest SNR (min) results from the crossing for the lightest vehicle and the largest SNR (max) from the crossing for the heaviest vehicle. The median SNR (median) results from the vehicle that represents the median value in the weight distribution of the simulated vehicles. For Noise Level 2, the smallest SNR is negative. This means that here the standard deviation of the noise is greater than the absolute maximum of the signal. Such a signal makes damage detection difficult. The tables show that the SNR depends on the position. The SNR is smaller for positions close to the support (S1 and S7) than for positions in the middle of the field (S3, S4, and S5). We have only calculated the SNR for the undamaged case. From the large difference between the highest SNR and the smallest SNR, the wide range of the weight of the simulated vehicles can be concluded. The range of vehicle weight used in the simulations lies between 0.8 t and 51.7 t. The difference between the largest SNR and the smallest SNR is about the same for the strain in the x direction in Table 1 as for the displacement in the z direction in Table 2. This results from the linear relationship between the load and the strain or displacement. The SNR was chosen so that the same value results for sensor point S4 for strain in x in direction, as well as for displacement in z direction. We did not filter the data after adding the noise, except for the M feature.
The selected sample in Figure 9 represents the crossing of the vehicle whose weight corresponds to the median value in the weight distribution of all simulated vehicles. This selected crossing represents the median in Table 1 and Table 2 for the SNR. The selected vehicle in Figure 9 corresponds to an articulated truck with a total of four axles. The vehicle in the example has a weight of 17.7 t, a length of 16.3 m, and a vehicle width of 2.16 m. The vehicle crosses the bridge at a speed of 55 km/h.
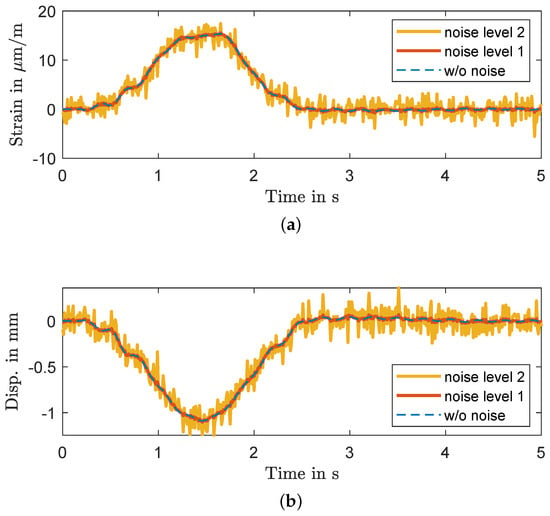
Figure 9.
Exemplary crossing with the first 5 s for different noise levels. The selected crossing represents the median with 17.7 t. This means that half of the simulated crossings have worse SNR and half of the simulated crossings have greater SNR. (a) Strain in x direction for sensor position S4. (b) Displacement in z direction for sensor position S4.
The presented features from Section 2 are applied here to the FEM simulations. In addition to the features presented in Section 2, we consider the feature “raw” data and the natural frequencies f of the decay process. The raw feature denotes the complete unprocessed time series of the signal at a sensor position. Since the crossing duration varies from crossing to crossing in the simulations, the signal for the raw feature is interpolated with 400 samples per crossing. This step is necessary for the classification algorithm, as it requires a constant length of the input signal for each crossing. For the feature natural frequencies f, we take the first four natural frequencies from the decay of the bridge after the vehicle has left the bridge. The raw features and the first four natural frequencies f shall serve as reference.
Before calculating the M features, we filtered the strain signal and the displacement signal after adding the noise with a low-pass filter with a cutoff frequency below the first natural frequency of the bridge. This is an acausal finite impulse response (FIR) filter with order 20 and a cutoff frequency of 0.3 Hz. The low-pass filtering reduces the influence of noise and dynamics. This improves the accuracy up to 20 percentage points for the M features. However, filtering for the raw feature would worsen the classification results. The R features barely change the accuracy after filtering.
For the evaluation of the features, we have chosen the metric
An accuracy of 100% is a “perfect” classification, which means that the classification model has correctly classified the whole test dataset. An accuracy of 33.3% means that the classification model makes a random classification. For a comparison of the features based on the damage classification, we consider an accuracy % as a very good classification and an % as a usable classification. An unusable classification is thus an accuracy under 85%. The general damage classification in Section 3.2 and the investigation on the influence of the temperature deviation in Section 3.3 are formulated as classification problems. Thus, the problem at hand corresponds to supervised learning. In Section 3.2 and in Section 3.3 we use bagged tree algorithm as the classification algorithm []. Preliminary investigations have shown that with the bagged tree classification algorithm all features perform well. In particular, the raw feature benefits from the use of the bagged tree classification algorithm. For M and R features, other classification algorithms are suitable, such as K-nearest neighbor, naïve Bayes or support vector machine. We create a separate classification model for all features and all sensor pairs as well as all noise levels. In addition, we generate a model for each feature and each noise level by using all sensors or all-sensor pairs. A sensor pair consists of two sensors. This results in 2415 sensor pair combinations per feature. This yields to two sets of 79,728 classification models (one set for the strain in the x direction and one for the displacement in the z direction).
3.2. General Damage Classification
We trained the bagged tree classifier with 389 crossings per damage class (0-0, 1-5, 2-3) and tested with 100 crossings per damage class. This corresponds approximately to a training–test ratio of 80% to 20% and a total of 1467 simulated crossings.
Table 3 gives the results for the features based on the strain in the x direction and Table 4 gives the results for the features based on the displacement in the z direction (deflection of the bridge). Six rows are given for each feature. The first five rows list the classification models with the sensor pairs that achieved the highest accuracy. The sixth row shows the result for the use of all available sensors or sensor pairs. The columns contain the results for the features calculated by using the three noise levels described in Table 1 for the strain in the x direction and in Table 2 for the displacement in the z direction.

Table 3.
Results for the five sensor pairs of each feature with the highest accuracy (Acc.) calculated based on strain in the x direction. The bottom six rows show the result for using all features. In the first column, the results for a Without Noise signal are given. The standard deviation of the noise and the corresponding SNR for the noise levels can be taken from Table 1.

Table 4.
Results for the five sensor pairs of each feature with the highest accuracy (Acc.) calculated based on displacement in the z direction. The bottom six rows show the result for using all features. In the first column, the results for a Without Noise signal are given. The standard deviation of the noise and the corresponding SNR for the noise levels can be taken from Table 2.
By using the raw feature in the first six rows as an example based on the strain in the x direction in Table 3, we explain the structure of the tables. The first five rows contain the classification models with the five sensor pairs for the raw feature that achieved the highest accuracy (Acc.) of the 2415 trained sensor pairs. In the sixth row, all sensors for the raw feature are used. The best sensor pair (S4,S8) for the raw feature without noise (column Without Noise) consists of sensors S4 and S8 with an accuracy of 99.3%. The fifth-highest accuracy is achieved by the sensor pair (S4,S7) with an accuracy of 98.3% in the fifth row. Considering the low noise level in column Noise Level 1, the sensor pair (S4,S7) is the best feature with an accuracy of 98.7%. At the highest noise level in column Noise Level 2, the sensor pair (S4,S7) is again the best sensor pair for the raw feature with an accuracy of 89.0%. In the last column—Acc. (heavy)—of each noise level, the accuracy for the 50% heaviest simulated vehicles of the test data set is given. For Acc. (heavy), it should be noted that the training data set is the same as for Acc., and therefore light vehicles were also taken into account during training. The accuracy for the heaviest 50% vehicles reflects the SNR range between median and maximum in Table 1 and Table 2, respectively. If only the 50% heaviest vehicles in the test dataset are considered, the accuracy for the sensor pair (S4,S7) for Noise Level 2 increases to 96.0%. This structure for the raw characteristic applies for all other features. In the last feature row (the last six rows) “all” features were used. In the first five rows, the best five sensor pairs are given. A sensor pair of the feature all consists of 820 dimensions. The last line contains the results for all sensor combinations, which corresponds to training with 69,685 dimensions for one noise level.
3.2.1. Strain in x Direction
First, we consider the results for the features based on strain in the x direction in Table 3. The raw feature calculated based on the Without Noise signal performs similarly well as based on the Noise Level 1 signal. With a Without Noise and Noise Level 1 signal, a very good classification can be achieved with the raw feature. However, the classification model for all sensors with an accuracy of 89.7% shows a significantly worse result than for single sensor pairs. This can be attributed to overfitting, where the classification model performs poorly on the unknown test dataset. The problem of overfitting is solved as soon as the noise in Noise Level 1 is taken into account. Here, the classification model with an accuracy of 99.0% performs significantly better than the classification model based on the Without Noise signal. As soon as the noise increases, the accuracy decreases. The highest accuracy using the raw feature with 89.0% for Noise Level 2 can be achieved with the sensor pair (S4,S7), whereas the accuracy for the third best sensor pair (S4,M7) drops to 79.7%. In order for the classification to provide usable results for Noise Level 2 signals, it is recommended that one consider only heavy vehicles in the classification (compare the results in the Acc. (heavy) column). Then the classification results are in the usable range with (%). Thus, the accuracy can be improved by 4.7 to 12.3 percentage points. For the raw feature, sensor position S4 performs relatively well. The selected five best sensor pairs consist of sensors that are located in the lane over which the vehicles drive in the simulation (sensor pairs consist exclusively of sensors in the girders M, S, and SS).
With the feature natural frequencies of the decay f, a very good classification ( can be achieved only for the Without Noise signals. Here, a sensor close to the support is preferred for the Western field (NN7, M7, N7, NN7, and S7). As soon as noise is present in the signal, the accuracy drops sharply, so that the classification models are unusable. For Noise Level 1 the best sensor pair (M11,NN2) has an accuracy of 66.3% and for the sensor pair (NN6,NN12) for Noise Level 2 an accuracy of 42.7%. Reducing the test dataset to the heaviest 50% vehicles does not improve the classification results. For the feature natural frequency f, it is important to have a sensor in each of the two fields. This can be explained by the fact that both spans of the bridge are not implemented as continuous beams and rather show the behaviour of two single-span bridges.
As expected, using all of the “all” features (last six rows in Table 3) leads to the best results. For the Without Noise and Noise Level 1 signals, several sensor pairs lead to a perfect classification. Moreover, for “all” features the combination with the sensor S4 is mostly advantageous, whereas for the Without Noise and Noise Level 1 signal SS3, SS4, and S3 allow a perfect classification. The accuracy for Noise Level 2 is between 91.7% and 95.3%. For the fourth-best sensor pair, the accuracy drops by four percentage points. Using the heaviest 50% vehicles and all sensors, a perfect classification (%) can be achieved for Noise Level 2 for the best three sensor pairs.
Four out of five M features based on the strain in the x direction achieve a very good to perfect classification for the best sensor pair for the Without Noise signal. The feature performs best for the Without Noise and Noise Level 1 signal. Here, a perfect classification is possible for the Without Noise and Noise Level 1 signal. is better than the raw reference feature for the Without Noise and Noise Level 1 signal. For Noise Level 2, all M features are unusable, because they have an accuracy below 85%. Moreover, reducing the test dataset to the heaviest 50% vehicles does not bring a significant improvement for the M features. If all sensor pairs are considered for the M features (last row for the individual M features), then , and are always better than all sensors for the raw feature. The strain signal contains mainly positive rather than negative values for each sensor. Therefore, the features that use the maximum (max in the feature name) should perform better. For the M feature, improvements can only be expected if only heavy vehicles are considered already during training.
The best individual features are variations of the R feature. All R feature variations achieve perfect classification for different sensor pairs based on the Without Noise and Noise Level 1 signals. All R feature variations can achieve a usable classification based on the Noise Level 2 signal (%). For Noise Level 2 the R and features, respectively, perform best. With the reduction of the test dataset to the heaviest vehicles, all R features can increase the accuracy. By using all sensor pairs, the R feature can achieve almost perfect classification for Noise Level 2.
For M and R features, it can be stated that the best five sensor pairs are mostly composed of sensors located in the same girder or in the neighbouring girder. Further investigation shows that sensor pairs consisting of one girder are more independent of lane deviation. All features (R, M- and raw features as well as “all”), except the natural frequency of the decay f, prefer a combination with sensor S4. Damage 2–3 is located in vicinity of S4. The damage 1–5 is detected by different sensors.
3.2.2. Displacement in z Direction
Next, we examine the results for the features based on the displacement in the z direction in Table 4. With the raw feature, a very good classification cannot be performed already based on the Without Noise signal. When taking all sensors into account, the accuracy is even worse. The results for the raw feature based on the displacement in the x direction are partly far below the results for the strain in the z direction, especially when noise is added. There is also no sensor pair that is represented across all noise levels. While the sensors SS7, S7, and N7 are preferred on the basis of the Without Noise signal, no pattern is apparent for Noise Level 1 and Noise Level 2. The reduction of the test dataset to the 50% heaviest vehicles (Acc. (heavy)) does not make sense for all sensor pairs for the Without Noise and Noise Level 1 signal. For Noise Level 2, all sensor pairs for the reduced test set with the 50% heaviest vehicles (Acc. (heavy)) get better.
The results for the f feature based on displacement in the z direction are in a comparable range to the results for the f feature based on strain in the x direction. Again, the classification models are unusable as soon as noise is present in the signal. With the reduction of the test dataset to the heaviest 50% vehicles, a small improvement for Noise Level 1 of the accuracy can be observed. However, the results are still in the unusable range. It can also be observed that the best sensor pairs are composed of one sensor from both fields. For the Without Noise signal, sensor pairs where one sensor lies in the M-girder perform best.
As for the strain in x direction, also for the displacement in z direction the classification models with all features (“all”) perform best. For the Without Noise and Noise Level 1 signals, a very good classification is possible. Reducing the test dataset to the heaviest 50% vehicles leads to an improvement in all Noise Levels. Thus, a perfect classification for the Without Noise and Noise Level 1 signal case can be achieved for single sensor pairs. The use of all sensor pairs makes sense for Noise Level 2 as well as a reduction of the test dataset to the heaviest 50% vehicles. Again, the S4 sensor is the most common among the top five sensors at all Noise Levels, especially for Noise Level 1 and Noise Level 2 signals.
The only M feature based on the displacement in the z direction for a Without Noise signal that allows a usable classification is the feature with an accuracy of 86.7% to 92.3% for the best five sensor pairs. For Noise Level 1 and Noise Level 2, no M feature achieves an accuracy for a usable classification. In general, reducing the test dataset to the heaviest 50% vehicles for the M feature based on the displacement in the z direction does not yield to significant improvement for single sensor pairs. However, M features perform significantly better when all sensor pairs are used. By using all sensor pairs, the best M feature is again the feature. Here, the feature still achieves a perfect classification with all sensor pairs for Noise Level 1. When using all sensor pairs, the feature and the feature perform better than the feature. This results from the course of the displacement signal, which mainly contains more negative values than positive ones. For the displacement in z direction, all sensor pairs always perform better for the M features than the raw features. However, for Noise Level 2, a usable classification with all sensor pairs is no longer possible.
In addition, with the displacement in the z direction, the variations of the R features are the best single features. With the R and features, perfect classification is possible for the Without Noise signal and very good classification for Noise Level 1 for a single sensor pair. For Noise Level 2, no single sensor pair achieves a usable classification. If all sensor pairs are considered, the best R feature variation is the R feature with 90.3% for Noise Level 2. The accuracy can be further increased for this case by considering only heavy vehicles. In general, reducing the test dataset to the heaviest 50% vehicles mainly improves the classification quality. In addition, the R features based on displacement in the z direction are worse from the result than the R features based on strain in the x direction. The best five sensor pairs for R feature variations are mostly composed of sensors of the S-girder for the Without Noise and Noise Level 1 signals. The sensors S3 and S4 for the Without Noise and Noise Level 1 signals are almost always represented in the sensor pair.
The tendency for the best five M and R features, respectively, to consist of sensor pairs lying within a girder is more apparent for displacement in the z direction than for strain in the x direction.
We conclude from the results in Table 3 and Table 4 that with both quantities (strain in the x direction as well as displacement in z direction) a damage detection is possible, with strain in the x direction performing better than displacement in the z direction for a similar SNR. The worst feature for both quantities is the natural frequencies f from the decay of the bridge after the vehicle has left the bridge. Surprisingly, the natural frequency is already not robust against noise at Noise Level 1.
The unprocessed signal (raw feature) is a very good reference because this has a high accuracy compared to the natural frequency f. We observe the best results when considering all sensors and sensor pairs, whereby the accuracy difference for the displacement in z direction is smaller than that for the strain in the x direction.
If the noise is not too high (Without Noise and Noise Level 1), single M features for a sensor pair are better than the raw feature. With increasing noise, more dimensions (sensors/sensor pairs) are needed. Thus, classification models with M features using all sensor pairs perform better than raw features that can use all sensor pairs.
The best single features we investigated were variations of the R feature. For strain in the x direction, the best feature is and for displacement in the x direction, the best feature is . The classification model can be built for the R feature with all available crossings. For later testing, we recommend using only heavy vehicles, as these lead to a higher accuracy.
For the M- and R features, sensor pairs that are located within a girder or in the neighbouring girder usually perform best. Further investigations show that M and R features consisting of sensor pairs from a girder or neighbouring girder are more independent of the lane deviation. In most cases, the M and R features consist of a sensor in the middle of the field (S3 or S4) and near the support (S7,S8,S9).
3.3. Influence of Temperature Deviation
In this section we investigate the temperature dependence. For this, we look at how the best five sensor pairs from the general classification in Section 3.2 cope with temperature differences. For the training dataset in Section 3.2, only crossings at a temperature of 20 °C were considered, and all three damage classes are known to the algorithm. For the test in this section, we use the temperature test data set consisting of
- 20 crossings at −10 °C,
- 20 crossings at −5 °C,
- 20 crossings at 0 °C,
- 20 crossings at 10 °C, and
- 20 crossings at 30 °C,
- which thus contains a total of 100 crossings. These crossings were all made for undamaged class (0-0).
3.3.1. Strain in x Direction
We have arranged the sensor pairs for the strain in the x direction in Table 5 in the same way as in Table 3. This applies analogously to the arrangement of the sensor pairs in Table 6 for the displacement in the z direction, where the sensor pairs are arranged as in Table 4. That means in Table 5 and Table 6 the sensor pairs that achieve the highest accuracy on the temperature test dataset are not mentioned. First, the strain in x direction is again treated in Table 5 for the temperature test dataset. The raw feature performs better on average for Noise Level 1 than for the Without Noise signal. This means that the classification algorithm has poor transferability to a temperature change. Training with noisy signal makes the classification algorithms more robust and prevents overfitting, so that an undamaged bridge with unknown temperatures can be classified correctly when trained in test. For sensor pair (S4,S8) an accuracy of 83.0% can be achieved. If the sensor S7 is used instead of S8, an accuracy of 100.0% can be achieved for the sensor pair (S4,S7). While the sensor pair (S4,S7) is in the same field, the sensor pair (S4,S8) is in different fields. In Noise Level 1, with the raw feature, a very good classification for the temperature test dataset can be achieved. In Noise Level 2, with the reduction of the dataset to the 50% heaviest vehicles (Acc. (heavy)) a usable classification can be performed.


The feature natural frequencies of the decay process f can be badly transferred to deviating temperatures after training with only one known constant temperature. The accuracy is below 50.0% for almost all classification models.
Moreover, for the temperature test dataset, the use of all features leads to the highest accuracy. For all signals, a very good to perfect classification can be achieved. With Noise Level 2 signals, an accuracy above 89% can be achieved. The accuracy can be increased by reducing the dataset to the heaviest vehicles.
The best M feature variation feature from Section 3.2 also performs best in the temperature test. This provides a perfect classification for the Without Noise and Noise Level 1 signal. No single sensor pair for the M feature achieves a usable classification (accuracy greater than 85%) for Noise Level 2. In general, all M features perform better when all sensor pairs are used.
The best individual features are again variations of the R feature. For the Without Noise and Noise Level 1 signals, perfect classification is achievable with single-sensor pairs for all R features. For the R and feature, sensor pairs perform better where the sensors are within a girder. The best feature for a sensor pair here is the R feature. The use of all sensor pairs is especially recommended for Noise Level 2 signals for all R features. This way, all R feature variations can achieve a very good to perfect classification. Furthermore, it is recommended to reduce the dataset to the heaviest 50% vehicles to increase the accuracy.
Again, for M and R features, it is noticeable that the sensor pairs with the highest accuracy are composed of sensors that lie within a girder or in the neighbouring girder.
3.3.2. Displacement in the z Direction
Next, we examine the results for the features based on the displacement in the z direction in Table 6 for the temperature test dataset. With the raw feature, no perfect classification can be performed based on the Without Noise signal. Considering all sensors, the accuracy even falls compared to the use of single-sensor pairs. This is an indication of the poor ability to generalise the classification model. For Noise Level 1 and Noise Level 2, all classification models with the raw feature are unusable (accuracy below 85%). In addition, the use of all sensors and the restriction to the heaviest 50% vehicles does not lead to any improvement.
Although better results can be obtained for the natural frequency of the decay f with the displacement in the z direction on the basis of the Without Noise signal than for the strain in the x direction, all results are in the unusable range (accuracy below 85%).
The classification models for “all” features of the displacement in the z direction yield to very good to perfect classification. For Noise Level 1 and Noise Level 2, all features perform best. For Without Noise and Noise Level 1 signals, a perfect classification can be achieved for the sensor pair (S4,S11) while the sensor pair (S4,S10) and (S4,S12) achieve an accuracy of 98.0%. For Noise Level 2, no usable classification can be achieved for a single-sensor pair. The reduction of the dataset to the heaviest vehicles leads to an improvement of the classification, but still no usable classification can be achieved. Only the use of all sensors and sensor pairs results in a usable classification with an accuracy of 89.0% for the complete test dataset and 96.0% for the test dataset reduced to the heaviest vehicles.
No M feature creates a usable classification for a single-sensor pair for the complete temperature test set based on the displacement in the z direction. Only with a reduction of the test dataset to the heaviest vehicles can a usable classification be achieved for the feature for the sensor pair (M2,M9) and (M7,M14) and for the feature for the sensor pair (SS5,SS8). By using all sensor pairs for the Without Noise signal, a very good to perfect classification can be achieved for the and features. For an accuracy of 90.0% can be achieved. For Noise Level 1 and Noise Level 2 the results for classification with a single sensor pair are unusable. , and achieve an accuracy greater than 90% for the Noise Level 1 signal for all sensor pairs. For Noise Level 2, no usable classification can be achieved even with all sensors and sensor pairs.
The R features are again the best single features. The best feature for single sensor pairs among the R feature variations is the R feature for the Without Noise and Noise Level 1 signal. This achieves a perfect classification for the Without Noise signal and a usable classification for Noise Level 1 for four out of five sensor pairs. The second-best feature is the feature, which also achieves a perfect classification for the Without Noise signal and an accuracy of 89.0% for Noise Level 1. A usable classification for Noise Level 2 is only possible with the R feature when using all sensor pairs. If in addition only heavy vehicles were considered in the test, a very good classification with an accuracy of 96.0% is possible.
The tendency for the best five M and R features, respectively, to consist of sensors that lie within a girder is also apparent for the temperature test data set for the displacement in the z direction.
From the results in Table 5 and Table 6 for the temperature test dataset, it follows that both signal types (strain in the x-direction as well as displacement in the z-direction) show robustness to temperature changes, whereby the strain in the x-direction again performs better than the displacement in the z-direction for a similar SNR. For Noise Level 2 with displacement in the z direction, no usable classification can be carried out with any feature for a single-sensor pair. Here, several sensors or sensor pairs are necessary, as well as crossings of heavy vehicles. The R feature is the only single feature for the displacement in z direction for Noise Level 2, which allows a very good classification.
The natural frequencies f from the decay of the bridge can distinguish poorly between an undamaged bridge with deviating temperature from damage.
Moreover, for the temperature test dataset, the best single features are R feature variations. The best single feature for the strain in the x direction is the R feature. This is followed by the and features. For the R feature at Noise Level 2, all sensor pairs must be used. If all sensor pairs are used, the M features perform very well. For the application, it can be seen from this section that R features are robust to temperature for some sensor pairs. In particular, M and R features perform best when the sensors of the sensor pairs are located within a girder or in the neighbouring girder.
3.4. Summary of the FEM Simulation
We have summarised the main findings from Section 3.2 and Section 3.3 in Table 7. In the column Feature, the previously studied features are listed, with the M feature variations and the R feature variations combined in one row, respectively, because the behaviour of each variation is similar. We considered the categories independence against vehicle weight, independence against temperature, robustness against noise, independence against vehicle speed and sampling rate, respectively, and transferability to anomaly detection, which are are located in the second to sixth columns. The first three categories are self-explanatory. The different vehicle speeds and sampling rates result in signals of different lengths, which leads to different dimensions of the features per crossing. For the investigated classifiers a constant dimension is necessary; therefore the signal for the raw feature was always interpolated to 400 sampling points, and this leads to uncertainties. Under the category transferability to anomaly detection, we understand how easy it is to create a reference state for the undamaged case and then measure the deviation from the reference state in the monitoring phase. The features in the individual categories were ranked between good, neutral, and poor performance.

Table 7.
Summary of the classification results with respect to the suitability of the features for anomaly detection on real structures.
The raw feature is poorly suited for anomaly detection due to the different signal lengths per crossing, and it cannot define a reference state without further considerations. Since the “all” feature uses the raw feature, it is also less suitable. The natural frequencies of the decay f performed poorly with noise as well as crossings with other temperatures. The only criticism of the M feature variations is that they perform poorly based on signals with noise. The R feature variations perform best. These are independent against vehicle weight, vehicle speed, and temperature variation, and robust against noise. It is also easy to determine a reference condition for the undamaged case and to measure later the deviation from the reference state.
4. Conclusions
In this work, we have investigated ratio-based features (so-called M and R features) for the curvature and strain influence lines, as well as the displacement influence line. We compared features based on the influence line on the stepped Euler–Bernoulli beam with modal parameters. Then, we investigated the sensor positioning for features by using the integral of the influence line on the stepped Euler–Bernoulli beam. This was followed by comparing the ratio-based features with the raw signal and natural frequencies of the bridge decay on FEM simulations in a damage classification. As a result, a statement can be made about the most suitable sensor position. In addition, we investigated the independence of the features against a temperature change.
In general, features based on the influence line have a high potential for condition assessment. This has been demonstrated for both longitudinal strain and deflection by using damage classification based on complex FEM simulations in this work. Features based on deflection generally perform slightly worse than features based on longitudinal strain for the same SNR.
The best results were achieved by using all features (raw signal, natural frequencies f, M, and R feature variations). A damage classification is not feasible for a later application on real bridges in this form, because not all damage cases are known to perform a classification. For a later implementation for the application, an anomaly detection, as presented in [], is recommended. For an anomaly detection, the natural frequency f, M, and R feature variations are best suited because the vehicle geometry (number of axles, dynamics, axle load, etc.), as well as the speed, is irrelevant or reduced, and thus a low-dimensional feature space is possible for anomaly detection.
The best individual features in our study were R feature variations. These achieved the highest accuracy compared to other single features. The R feature variations are robust to noise and show very good robustness to different temperatures. It can be concluded that sensor pairs for the R feature variations perform best when the sensors are located within a girder. Furthermore, it makes sense to perform damage classification, and thus anomaly detection only on the basis of heavy vehicles.
The best sensor positioning in the stepped Euler–Bernoulli beam for using the displacement influence line would be near the support. However, it is important to consider the SNR, as the deflection near the support is smaller and therefore noise can overlay the signal. Damage near the centre support can again be seen in all sensor positions in the displacement influence line. However, there are damage positions that cannot be detected by the displacement in the Euler–Bernoulli beam. With the curvature influence line, damage can be best detected when the sensor is within the damage. However, there are also sensor positions in the curvature influence line in which all damage locations can be detected.
In our investigation on FEM simulations, a perfect damage classification could be carried out. This means that two sensors are sufficient to distinguish between the two types of damage. The location of the damage in the first case was in the deck above the middle support of the longitudinal direction of the bridge and should be detectable by all sensors according to the findings from the investigation on the Euler–Bernoulli beam in Section 2.2. The second case of damage is in the middle of the field. Thus, one of the sensors of a sensor pair was in the direct neighbourhood of the second damage case.
For further investigations, we recommend considering more damage locations and damage severities, as well as other types of damage, such as smeared cracking in the asphalt layer or smaller damage severities. Although the FEM simulations are closer to reality than the bending beam, future work must investigate how well the features, especially the ratio-based integrated features, can be transferred to reality. The first investigations could be made on real beams in the laboratory, for example.
Author Contributions
Conceptualization, A.D., M.V., S.H. and J.M. (Jörg Matthes); methodology, A.D., S.H. and J.M. (Jörg Matthes); software, A.D.; validation, A.D.; formal analysis, A.D., M.V. and J.M. (Jörg Matthes); investigation, A.D., O.S. and J.M. (Jacob Müller); resources, A.D., M.V. and J.M. (Jörg Matthes); data curation, A.D., O.S. and J.M. (Jacob Müller); writing—original draft preparation, A.D.; writing—review and editing, A.D., M.V., O.S., J.M., S.H. and J.M. (Jörg Matthes); visualization, A.D., O.S. and J.M. (Jacob Müller); supervision, S.H. and J.M. (Jörg Matthes); project administration, A.D. and J.M. (Jörg Matthes); funding acquisition, S.H. and J.M. (Jörg Matthes). All authors have read and agreed to the published version of the manuscript.
Funding
This work is part of the ZEBBRA project, which was funded by the Federal Ministry of Education and Research under the funding number 13N14709. We also acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
We would like to thank our partner in Karlsruhe ci-tec, as well as the cooperation with Matthias Arnold, Sina Keller, and Chris Michel.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schwab, K. The Global Competitiveness Report 2018; The World Economic Forum: Geneve, Switzerland, 2018. [Google Scholar]
- Federal Highway Research Institute. Brückenstatistik—Brücken an Bundesfernstraßen—Altersstruktur nach Brückenflächen. 2021. Available online: https://www.bast.de/DE/Statistik/Bruecken/Brueckenstatistik.html (accessed on 30 November 2022).
- Lauer, F. Hohe Kosten durch Ausfall der Salzbachtalbrücke; IHK Wiesbaden: Wiesbaden, Germany, 2021; Available online: https://www.ihk-wiesbaden.de/presse/pressemeldungen/-hohe-kosten-durch-ausfall-der-salzbachtalbruecke-5359948 (accessed on 1 February 2022).
- Arndt, M. Komplexe Gründung der Salzbachtalbrücke—Entwurf und Durchführung einer Probepfahlbelastung. In Proceedings of the Internationale Arbeitstagung Brücken und Ingenieurbau 2018, Potsdam, Germany, 24–26 April 2018. [Google Scholar]
- Giewald, J.; Harlos, L. A45 bei Lüdenscheid Gesperrt: Das Ist der Aktuelle Stand zu Sperrung und Neubau der Brücke. ADAC Website. Available online: https://www.adac.de/der-adac/regionalclubs/nrw/verkehr-sicherheit/a45-sperrung-gesperrt/ (accessed on 1 May 2022).
- Schlenga, S. Bericht der Autobahn GmbH. Autobahn GmbH Website. Available online: https://www.autobahn.de/die-autobahn/aktuelles/detail/a45-untersuchungen-an-der-rahmede-laufen (accessed on 1 May 2022).
- Schlenga, S. Autobahn Westfalen: Brückenneubau an der A45 läuft seit Jahren mit Hochdruck. Autobahn GmbH Website. Available online: https://www.autobahn.de/die-autobahn/aktuelles/detail/autobahn-westfalen-brueckenneubau-an-der-a45-laeuft-seit-jahren-mit-hochdruck (accessed on 1 May 2022).
- Keller, S.; Michel, C.; Schneider, O.; Müller, J.; Arnold, M.; Döring, A.; Hoyer, M.; Hinz, S.; Keller, H.B. Überwachung von Brückeninfrastrukturen: Neuer Ansatz von konventionellen und berührungslosen Sensoren. Brückenbauwerke 2020, 3, 22–29. [Google Scholar]
- Michel, C.; Keller, S. Advancing Ground-Based Radar Processing for Bridge Infrastructure Monitoring. Sensors 2021, 21, 2172. [Google Scholar] [CrossRef] [PubMed]
- Salvador, S.; Chan, P. Toward accurate dynamic time warping in linear time and space. Intell. Data Anal. 2007, 11, 561–580. [Google Scholar] [CrossRef]
- Arnold, M.; Hoyer, M.; Keller, S. Convolutional Neural Networks for Detecting Bridge Crossing Events with Ground-Based Interferometric Radar Data. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2021, 1, 31–38. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Cawley, P. Structural health monitoring: Closing the gap between research and industrial deployment. Struct. Health Monit. 2018, 17, 1225–1244. [Google Scholar] [CrossRef]
- Rainieri, C. Operational Modal Analysis of Civil Engineering Structures: An Introduction and Guide for Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Moses, F. Weigh-in-motion system using instrumented bridges. Transp. Eng. J. ASCE 1979, 105, 233–249. [Google Scholar] [CrossRef]
- Spura, C. Technische Mechanik 2. Elastostatik: Nach Fest Kommt ab; Springer: Wiesbaden, Germany, 2019. [Google Scholar]
- Žnidarič, A.; Kalin, J. Using bridge weigh-in-motion systems to monitor single-span bridge influence lines. J. Civ. Struct. Health Monit. 2020, 10, 743–756. [Google Scholar] [CrossRef]
- Chen, S.-Z.; Feng, D.-C.; Han, W.-S. Comparative Study of Damage Detection Methods Based on Long-Gauge FBG for Highway Bridges. Sensors 2020, 20, 3623. [Google Scholar] [CrossRef]
- Wu, B.; Wu, G.; Yang, C.; He, Y. Damage identification and bearing capacity evaluation of bridges based on distributed long-gauge strain envelope line under moving vehicle loads. J. Intell. Mater. Syst. Struct. 2016, 27, 17. [Google Scholar] [CrossRef]
- Hong, W.; Cao, Y.; Wu, Z. Strain-Based Damage-Assessment Method for Bridges under Moving Vehicular Loads Using Long-Gauge Strain Sensing. J. Bridge Eng. 2016, 21, 10. [Google Scholar] [CrossRef]
- Wu, B.; Wu, G.; Lu, H.; Feng, D.-C. Stiffness monitoring and damage assessment of bridges under moving vehicular loads using spatially-distributed optical fiber sensors. Smart Mater. Struct. 2017, 26, 3. [Google Scholar] [CrossRef]
- Chen, S.; Wu, G.; Wu, B. Simultaneous identification method of damage and vehicle parameters on bridges utilizing long-gauge strain influence line under moving vehicle loads. Sens. Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 2017, 2017, 10168. [Google Scholar]
- Waibel, P.; Scherer, O.; Keller, H.B.; Müller, J.; Schneider, O.; Keller, S. A strain sensor based monitoring and damage detection system for a two-span beam bridge. In Bridge Maintenance, Safety, Management, Life-Cycle Sustainability and Innovations; CRC Press: Boca Raton, FL, USA, 2018; pp. 1627–1634. [Google Scholar]
- Štimac Grandić, I.; Grandic, D.; Bjelanović, A. Comparison of techniques for damage identification based on influence line approach. Mach. Technol. Mater. 2011, 7, 53–57. [Google Scholar]
- Štimac Grandić, I.; Grandic, D. Estimation of damage severity using sparse static measurement. J. Civ. Eng. Manag. 2015, 23, 213–221. [Google Scholar] [CrossRef]
- Ha, T.M.; Fukada, S. Nondestructive damage detection in deteriorated girders using changes in nodal displacement. J. Civ. Struct. Health Monit. 2017, 7, 385–403. [Google Scholar] [CrossRef]
- Döring, A.; Waibel, P.; Matthes, J.; Scherer, O.; Keller, H.B.; Keller, S.; Müller, J.; Schneider, O. Ratio-based features for data-driven bridge monitoring and damage detection. In Bridge Maintenance, Safety, Management, Life-Cycle Sustainability and Innovations; CRC Press: Boca Raton, FL, USA, 2021; pp. 2532–2541. [Google Scholar]
- Döring, A.; Vogelbacher, P.; Schneider, O.; Müller, J.; Hinz, S.; Matthes, J. Ratio-based features for bridge damage detection based on displacement influence line and curvature influence line. In Bridge Maintenance, Safety, Management, Life-Cycle Sustainability and Innovations; hlCRC Press: Boca Raton, FL, USA, 2022; pp. 2010–2018. [Google Scholar]
- Jansen, A.; Geißler, K. Ausreißererkennung zur Strukturüberwachung von Bestandsbrücken durch Bauwerksmonitoring mit vier Signalmerkmalen. Brückenkolloquium 2020, 4, 313–322. [Google Scholar]
- Cheng, P.; Davila, C.; Hou, G. Static, Vibration Analysis and Sensitivity Analysis of Stepped Beams Using Singularity Functions. J. Struct. 2014, 2014, 234085. [Google Scholar] [CrossRef]
- Döring, A. Stepped-Euler-Bernoulli-Beam for Matlab. 2022. Available online: https://zenodo.org/record/6675982#.ZCbf9XZBxPY (accessed on 21 June 2022).
- Coppi, F.; Gentile, C.; Ricci, P.P. A Software Tool for Processing the Displacement Time Series Extracted from Raw Radar Data. AIP Conf. Proc. 2010, 1253, 190–201. [Google Scholar]
- Mertins, A. Signaltheorie—Grundlagen der Signalbeschreibung, Filterbänke, Wavelets, Zeit-Frequenz-Analyse, Parameter und Signalschätzung, 4th ed.; Springer: Wiesbaden, Germany, 2020. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).