Application and Experimental Validation of Seven-Degree-of-Freedom Beam Element for Girder Bridges during Deck Construction
Abstract
1. Introduction
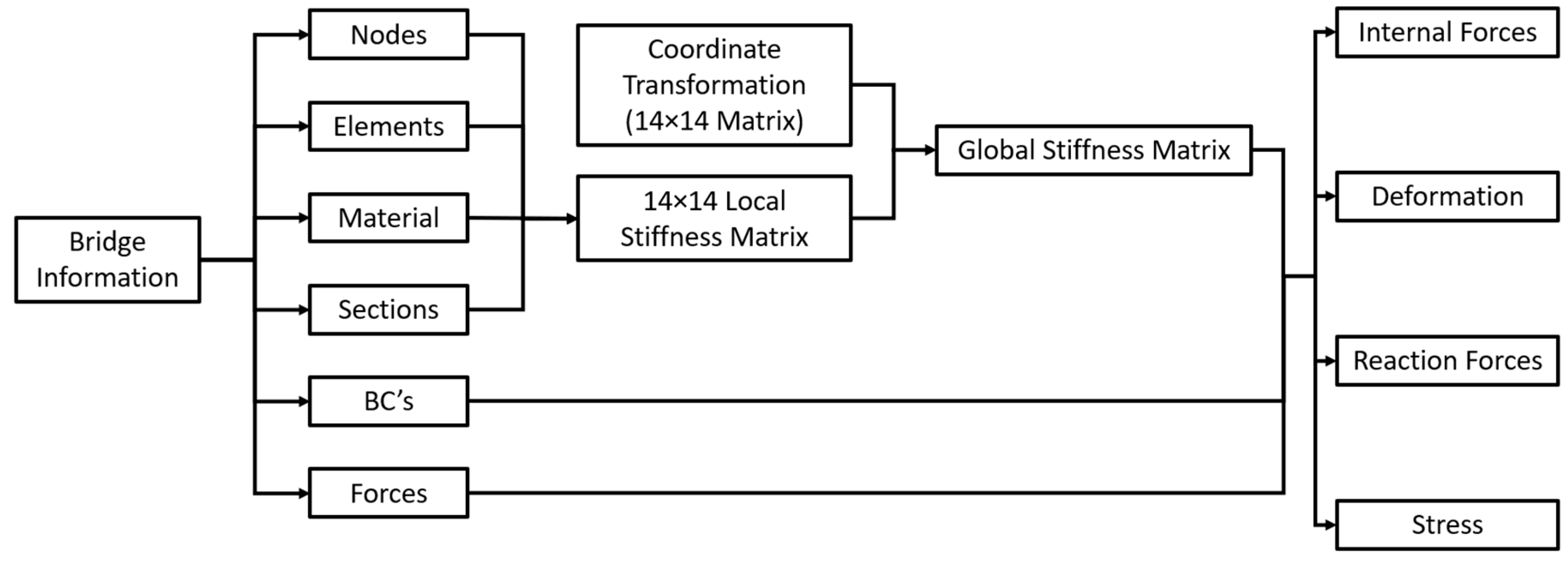
2. The 7-DOF Beam Element
2.1. Deformation and Kinematics of 7-DOF Beam Element
2.2. Potential Energy and Stiffness Matrix
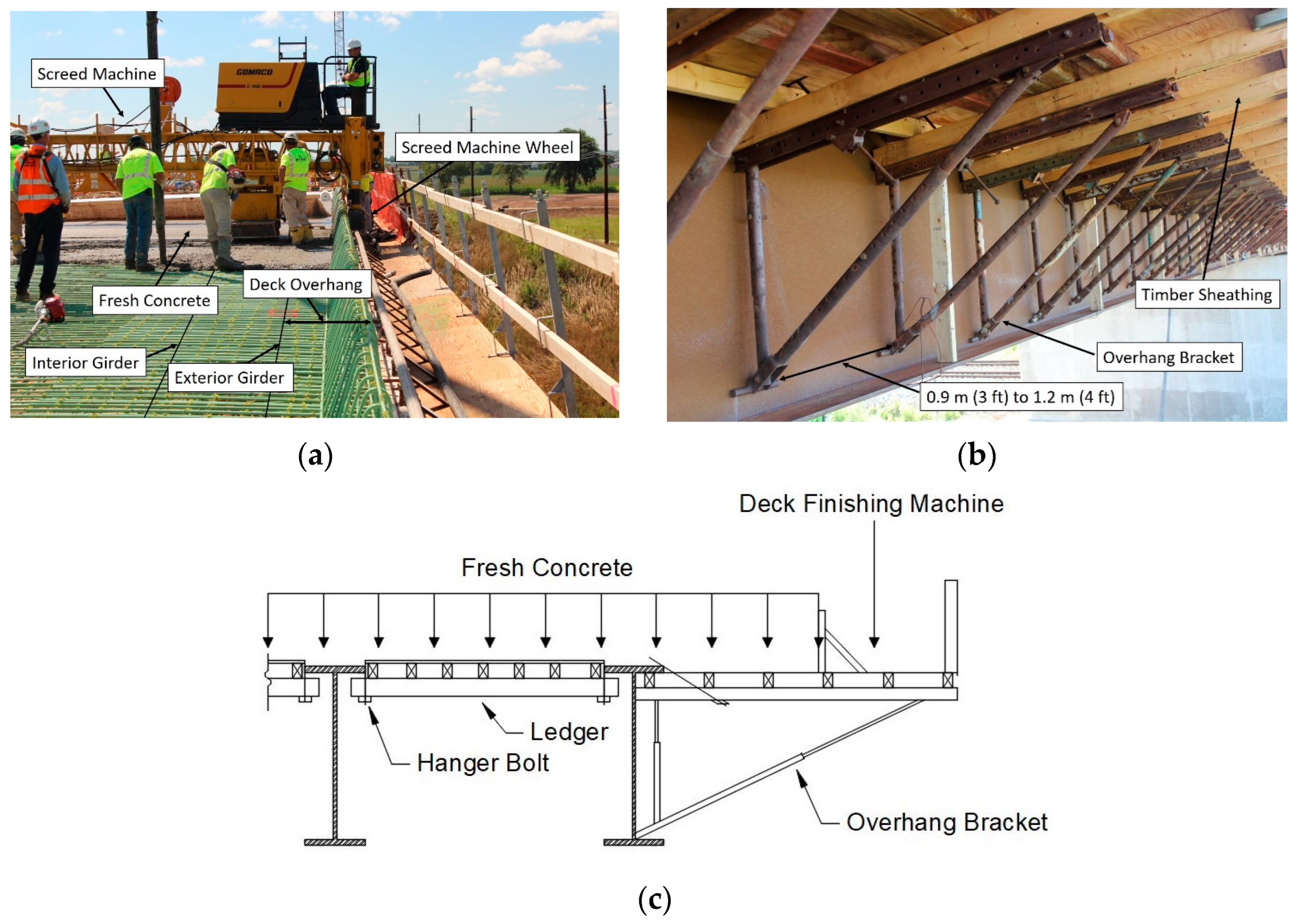
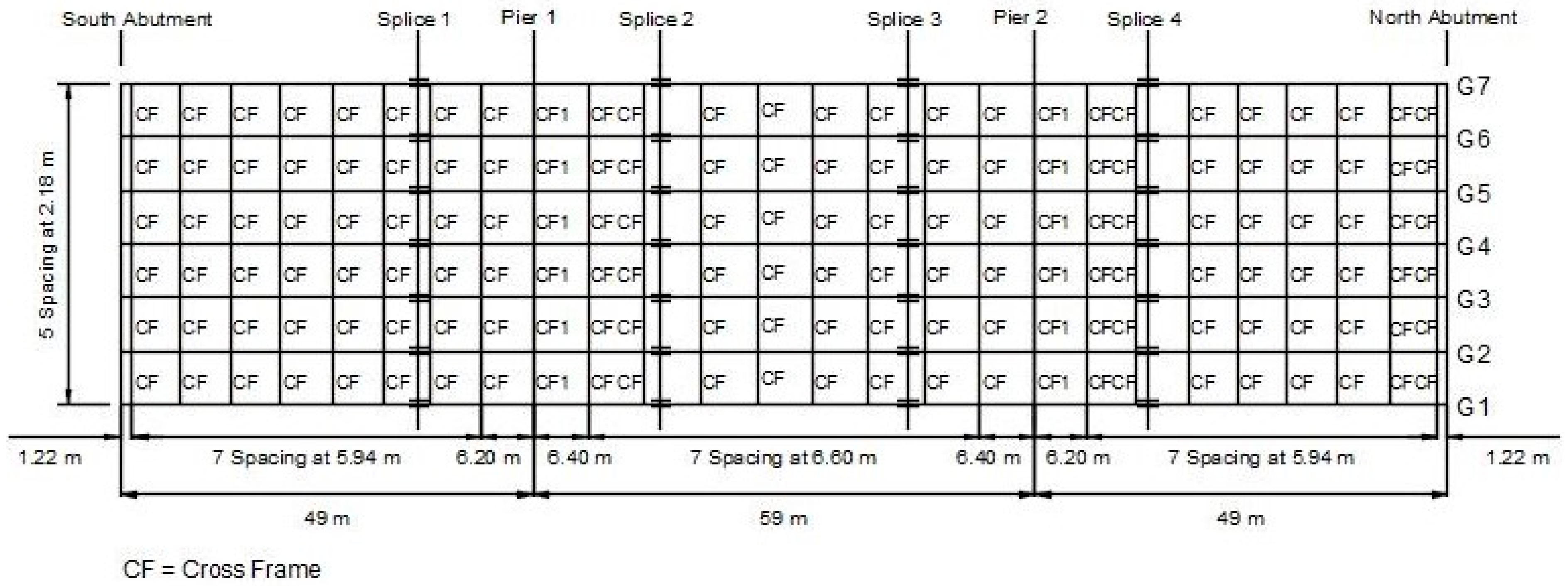
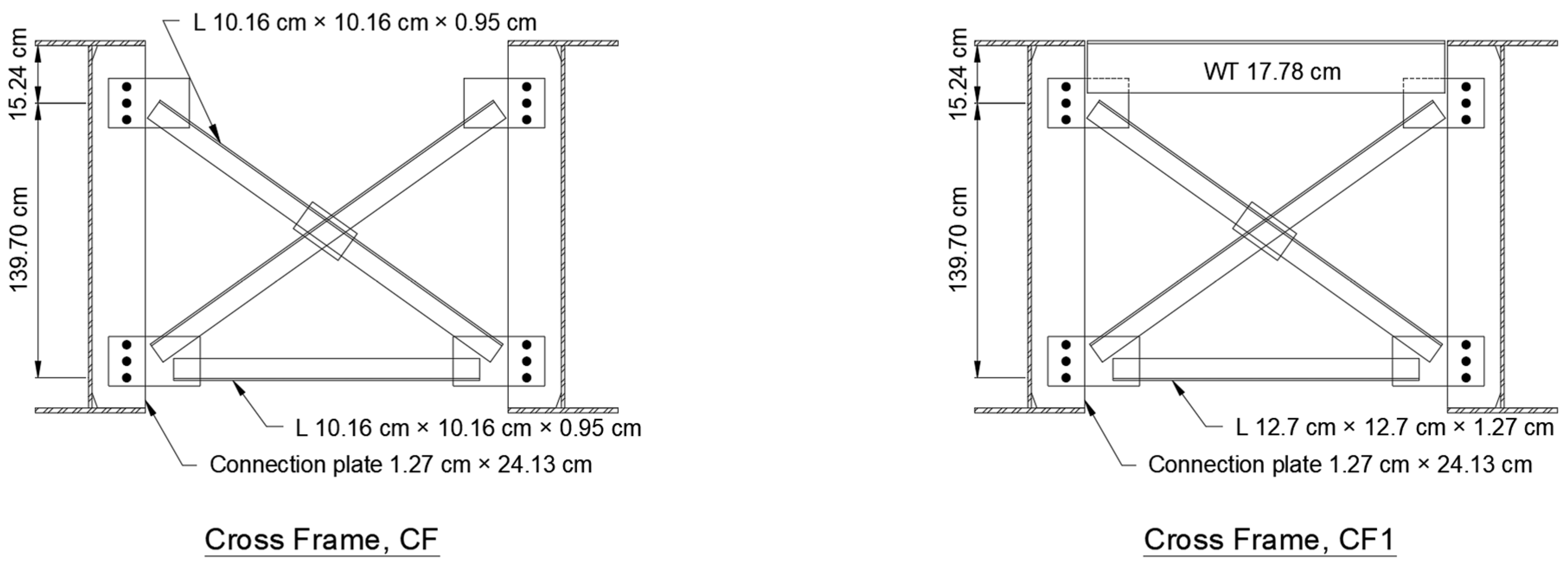
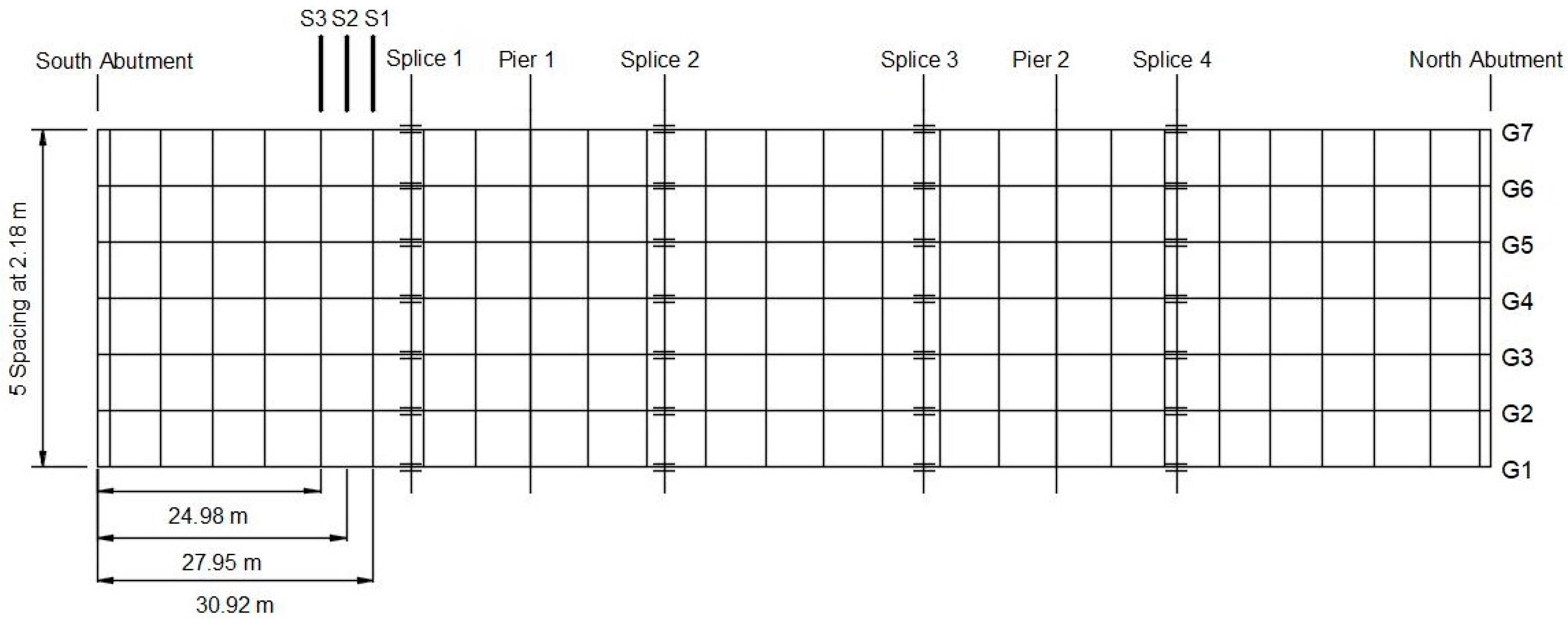
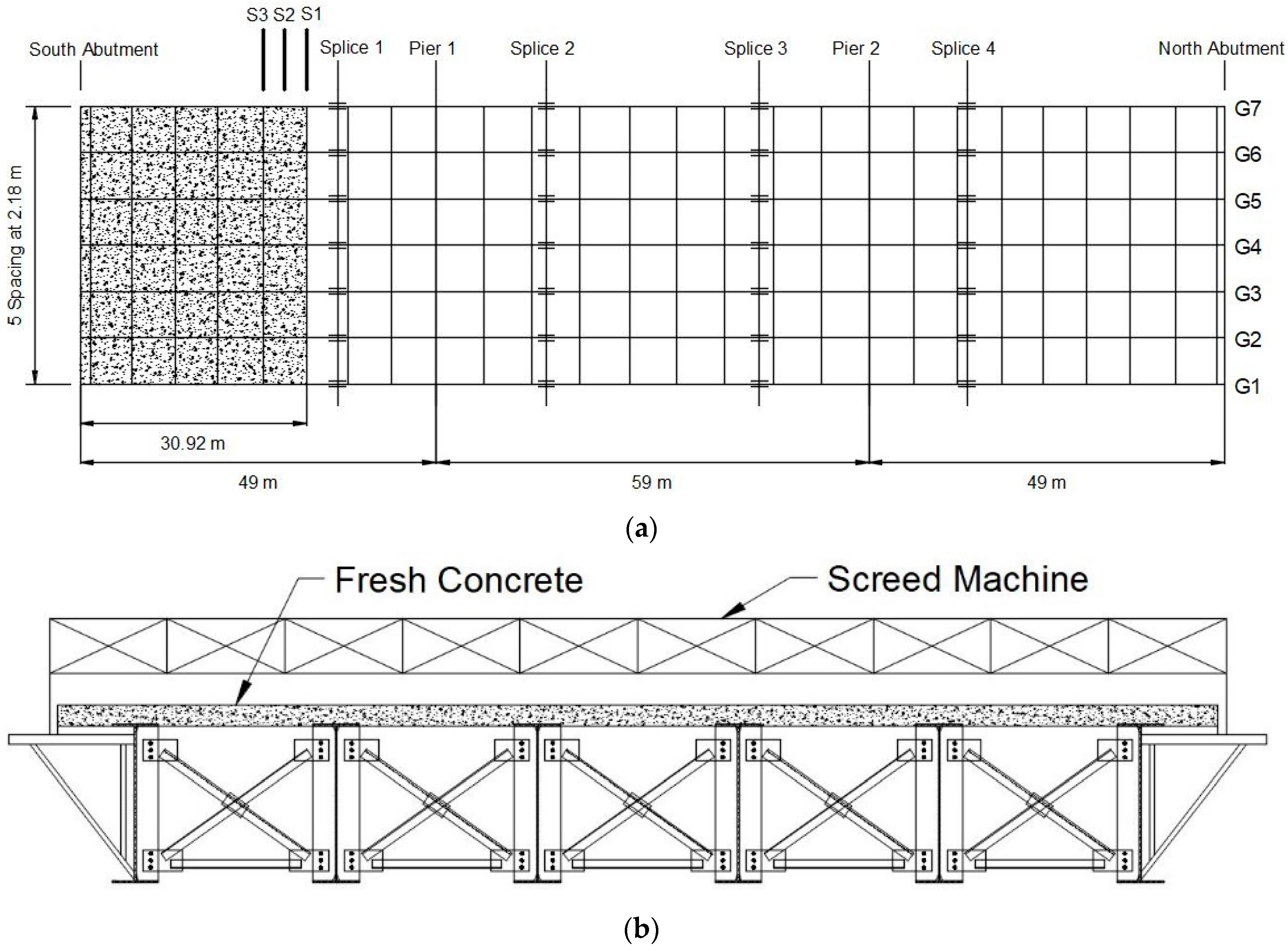
3. Field Bridge Experiment
3.1. Bridge Instrumentation
3.2. Experimental Results
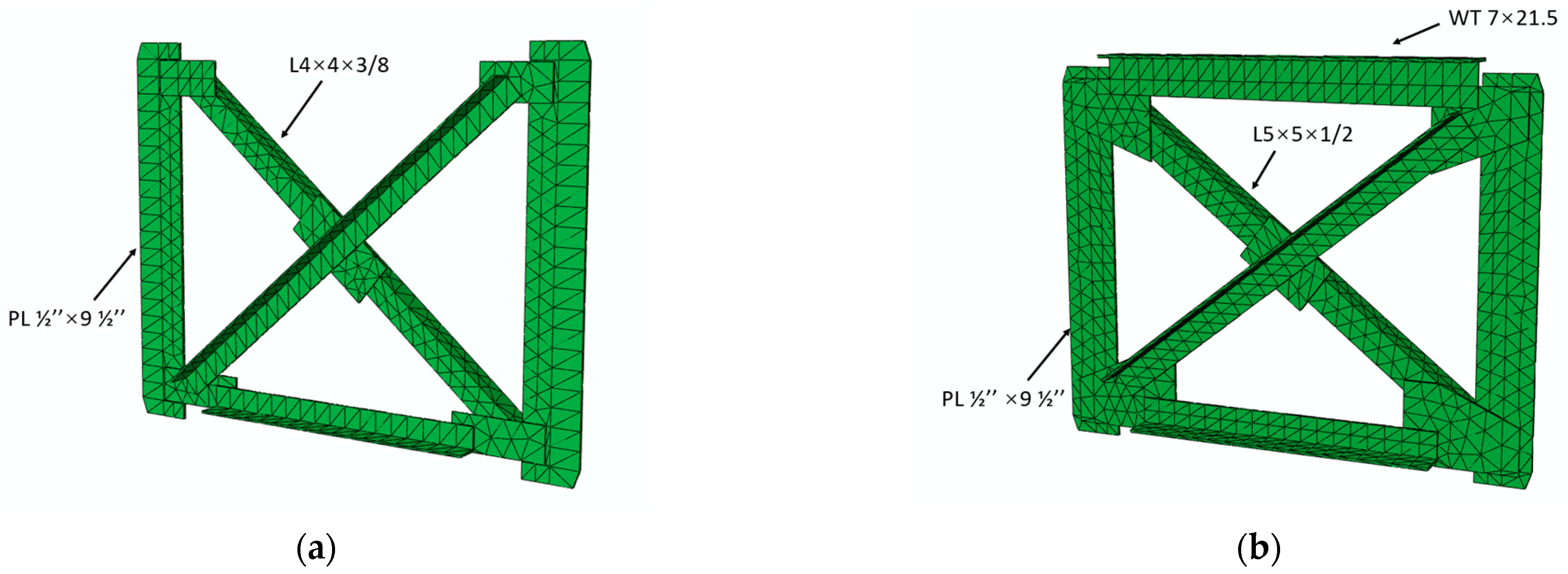
4. Numerical Modeling
5. Results
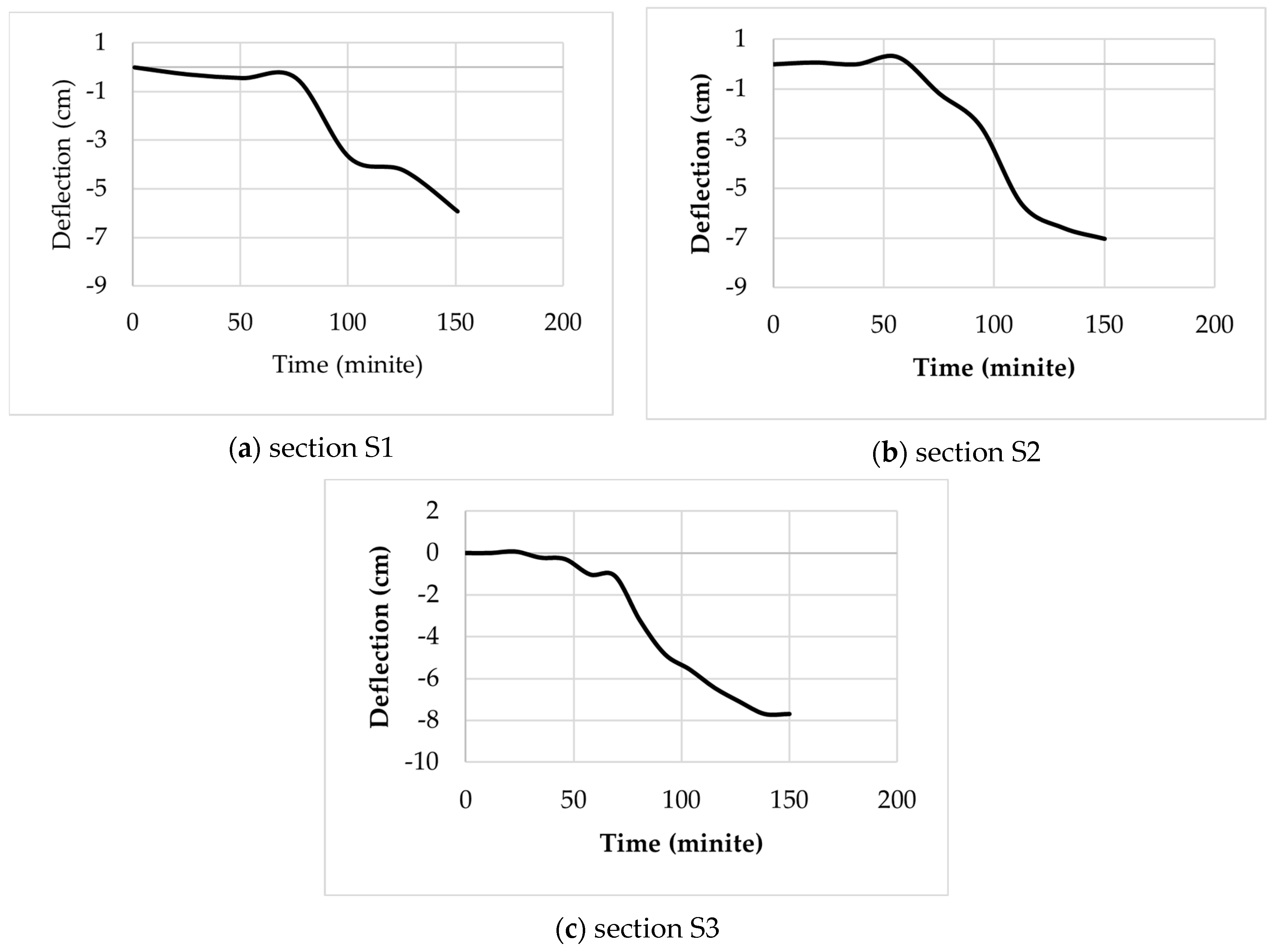
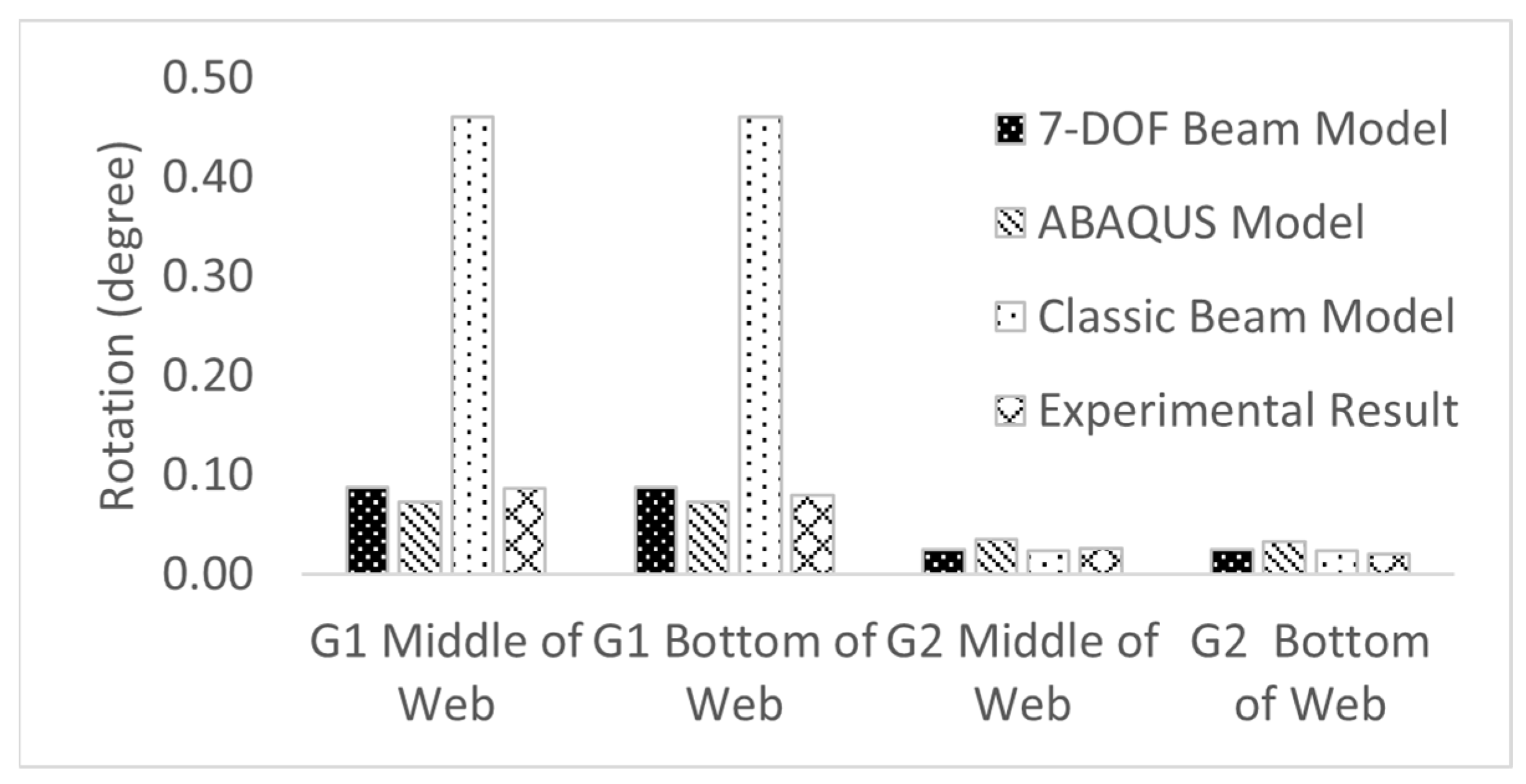
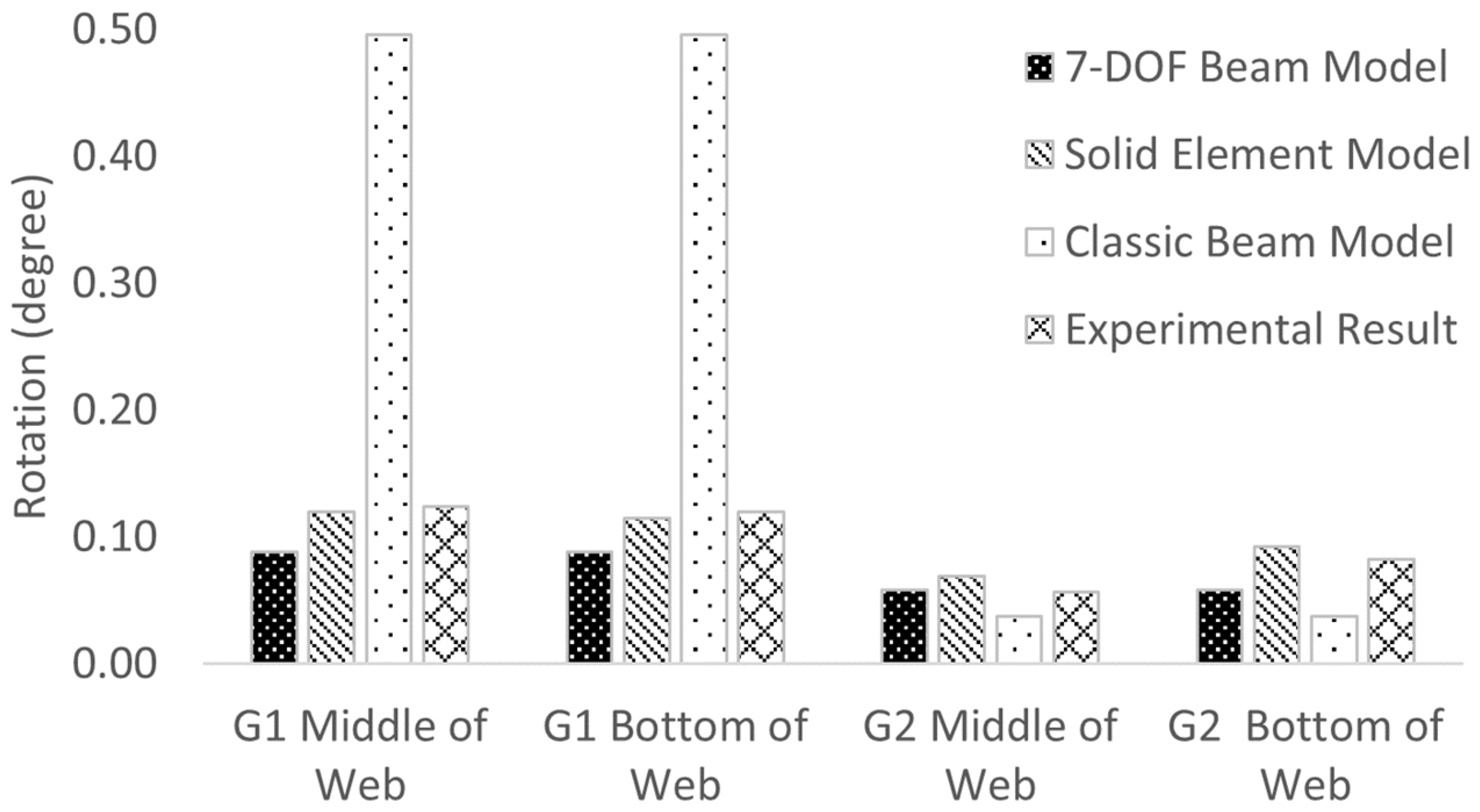
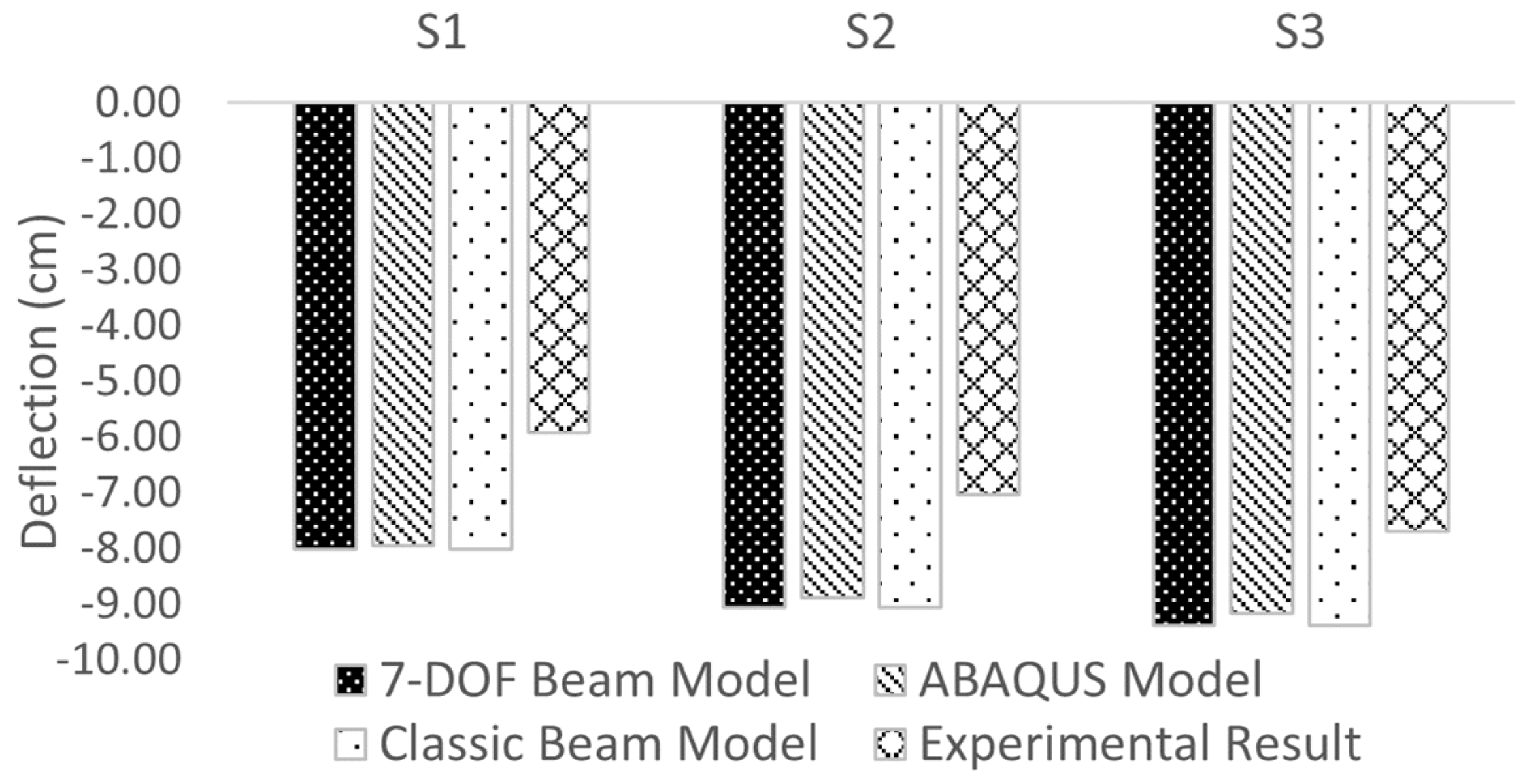
5.1. Rotation and Deflection
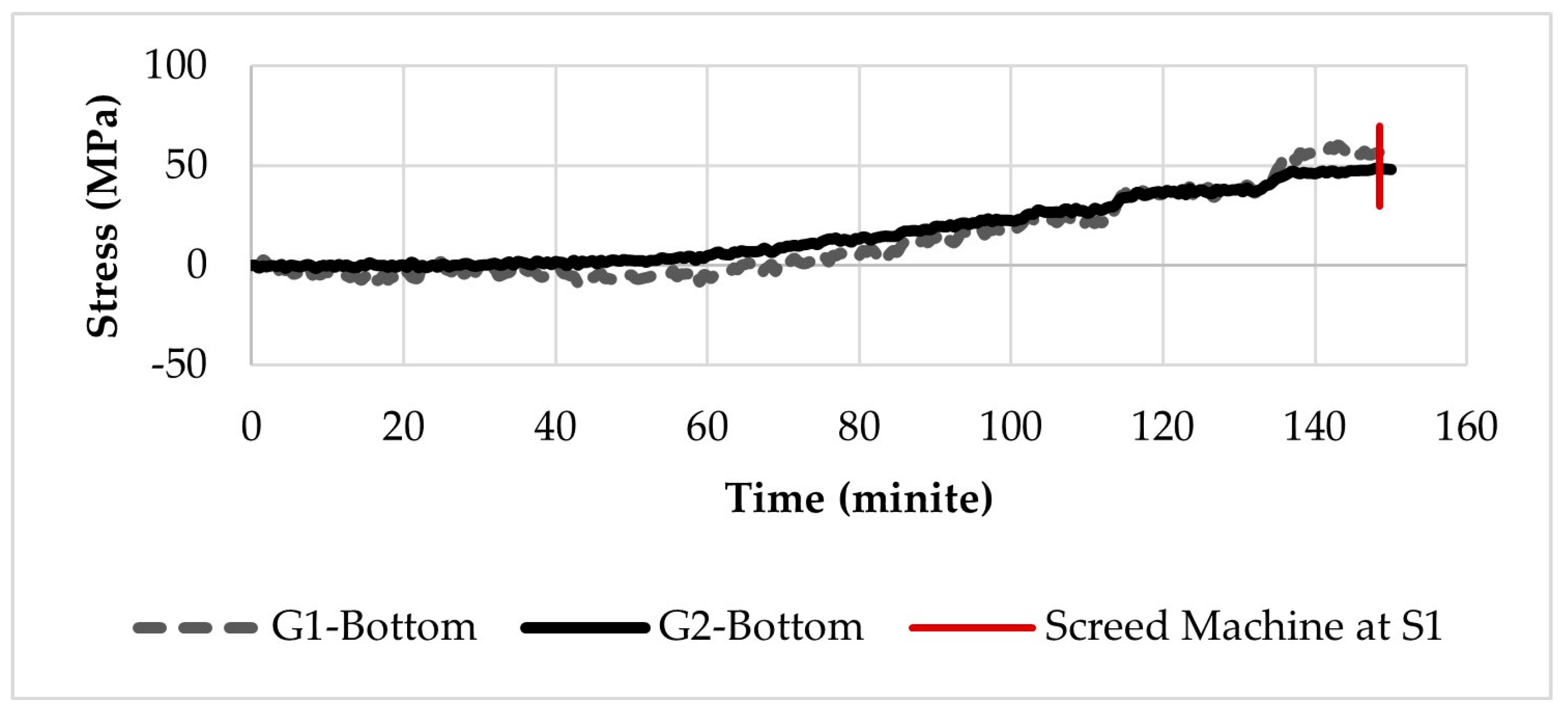
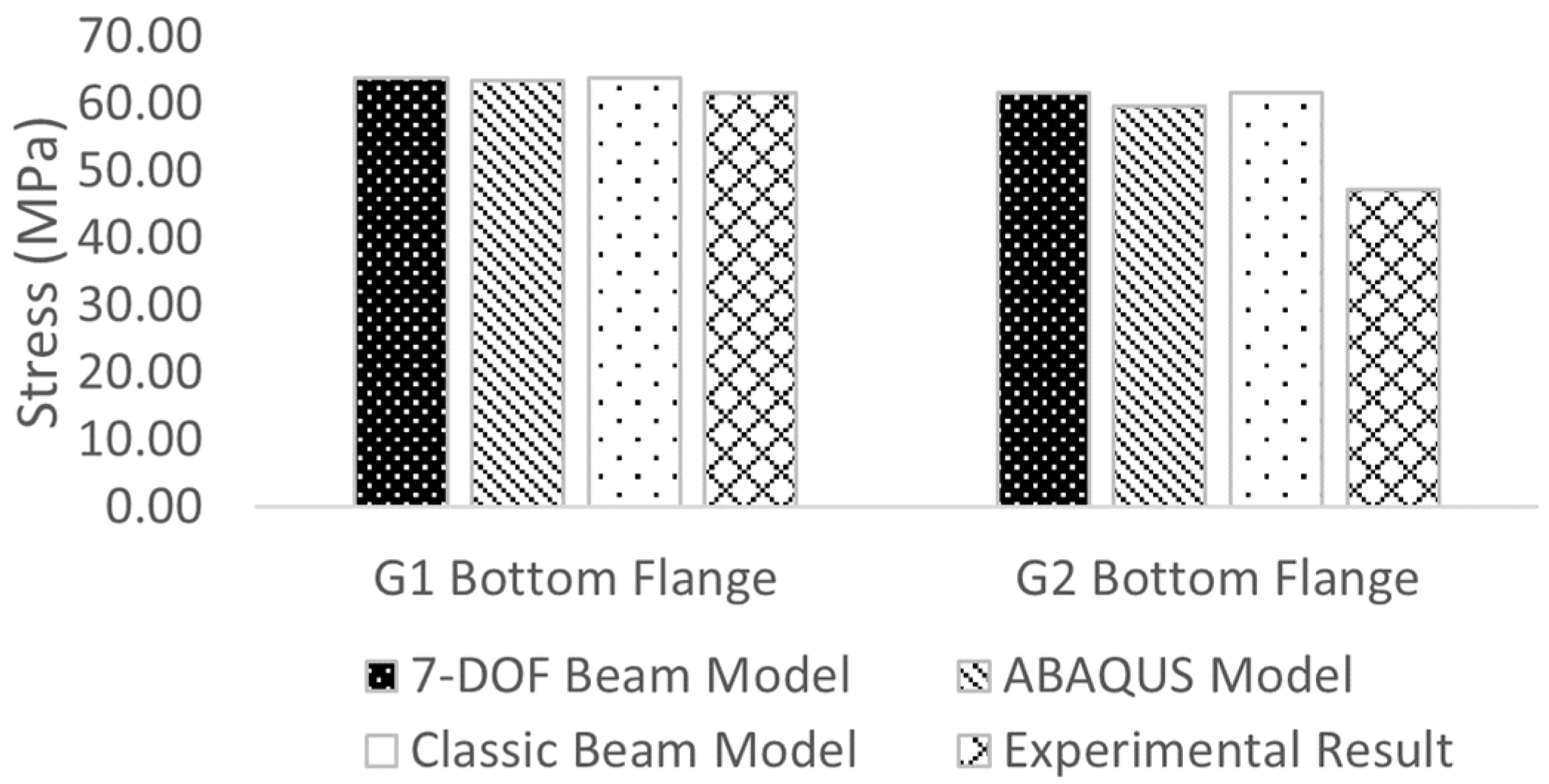
5.2. Stress
6. Discussion
7. Conclusions
- (a)
- The 7-DOF beam element can accurately evaluate the torsional behaviors of bridge girders under construction load. The results were validated using the results from the solid element model and experimental data.
- (b)
- In terms of stress and vertical deflection, the 7-DOF beam element had the same behavior as the other numerical methods. However, according to the strain equations for the 7-DOF beam, the warping effect can lead to re-distribution of the stress on the cross-section, especially when the torsional moment applied to the structure is significant.
- (c)
- The classical beam element that is widely used in commercial software packages failed to compute the transverse rotation of bridge girders when the torsional moment was applied. The transverse rotation based on the results from the classical beam element was often larger than experimental data due to the lack consideration of warping stiffness during the torsional analysis.
- (d)
- With similar accuracy, the 7-DOF element model requires less modeling effort and computing time compared with the solid element model. For the experimental bridge in this study, the size of global stiffness matrix reduced to 1% when switching the solid element model to the 7-DOF beam element model.
- (e)
- Unlike the solid and shell element models, with which it is difficult to determine the internal forces directly, the 7-DOF beam element can compute the internal force of cross-sections along the bridge girder for design purposes.
- (f)
- The 7-DOF beam element model does not require changes in the nodal and element information of the classical beam element model. Therefore, it is possible to convert a classical beam element model into the 7-DOF beam element without much effort.
- (g)
- The numerical analysis using the 7-DOF beam element can be an alternative approach to the solid element and shell element for bridge analysis, especially when detailed information on stress distribution on the cross-section is not required and internal forces need to be generated.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, S.; Helwig, T.; Klingner, R.; Engelhardt, M.; Fasl, J. Impact of Overhang Construction on Girder Design; University of Texas at Austin: Austin, TX, USA, 2009. [Google Scholar]
- Hui, L.; Hraib, F.; Gillis, B.; Vicente, M.; Hindi, R. A Simplified Method to Minimize Exterior Girder Rotation of Steel Bridges during Deck Construction. Eng. Struct. 2019, 183, 84–93. [Google Scholar] [CrossRef]
- Hui, L.; Hraib, F.; Vicente, M.; Hindi, R. Effectiveness of Exterior-Beam Rotation-Prevention Systems for Bridge Deck Construction—Phase II; Illinois Center for Transportation: Springfield, IL, USA, 2019. [Google Scholar]
- Ashiquzzaman, M.; Hui, L.; Schmeltz, J.; Merino, C.; Bozkurt, B.; Ibrahim, A.; Lindquist, W.; Hindi, R. Effectiveness of Exterior Beam Rotation Prevention Systems for Bridge Deck Construction; Illinois Center for Transportation: Springfield, IL, USA, 2016. [Google Scholar]
- Ashiquzzaman, M.; Calvo, C.M.; Hui, L.; Ibrahim, A.; Lindquist, W.; Hindi, R. Effectiveness of Different Bracing Systems to Prevent Exterior Girder Rotation during Bridge Deck Construction. Eng. Struct. 2017, 142, 272–289. [Google Scholar] [CrossRef]
- Ashiquzzaman, M.; Hui, L.; Ibrahim, A.; Lindquist, W.; Thomson, M.; Hindi, R. Effect of Inconsistent Diaphragms on Exterior Girder Rotation During Overhang Deck Construction. Structures 2016, 8, 25–34. [Google Scholar] [CrossRef]
- Ashiquzzaman, M.; Hui, L.; Hindi, R.; Ibrahim, A.; Lindquist, W. Validation of Field Exterior Girder Rotation in Non-Skewed Bridge Due to Construction Loads with FE Analysis. In Maintenance, Monitoring, Safety, Risk and Resilience of Bridges and Bridge Networks; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Fasl, J.D. The Influence of Overhang Construction on Girder Design; University of Texas at Austin: Austin, TX, USA, 2008. [Google Scholar]
- Shokouhian, M.; Shi, Y. Flexural Strength of Hybrid Steel I-Beams Based on Slenderness. Eng. Struct. 2015, 93, 114–128. [Google Scholar] [CrossRef]
- Winkler, R.; Kindmann, R.; Knobloch, M. Lateral Torsional Buckling Behaviour of Steel Beams—On the Influence of the Structural System. Structures 2017, 11, 178–188. [Google Scholar] [CrossRef]
- Gupta, V.K.; Okui, Y.; Nagai, M. Development of Web Slenderness Limits for Composite I-Girders Accounting for Initial Bending Moment. Struct. Eng./Earthq. Eng. 2006, 23, 229s–239s. [Google Scholar] [CrossRef]
- Jáger, B.; Dunai, L.; Kövesdi, B. Lateral-Torsional Buckling Strength of Corrugated Web Girders—Experimental Study. Structures 2022, 43, 1275–1290. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials. AASHTO LRFD Bridge Design Specifications; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- American Association of State Highway and Transportation Officials. Guidelines for Steel Girder Bridge Analysis, G13.1-2019; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2019. [Google Scholar]
- Vlasov, V.Z. Thin-Walled Elastic Beams; National Technical Information Service: Haifa, Israel, 1984.
- Jönsson, J. Distortional Theory of Thin-Walled Beams. Thin-Walled Struct. 1999, 33, 269–303. [Google Scholar] [CrossRef]
- Kim, N.-I.; Kim, M.-Y. Exact Dynamic/Static Stiffness Matrices of Non-Symmetric Thin-Walled Beams Considering Coupled Shear Deformation Effects. Thin-Walled Struct. 2005, 43, 701–734. [Google Scholar] [CrossRef]
- Pavazza, R. Torsion of Thin-Walled Beams of Open Cross-Section with Influence of Shear. Int. J. Mech. Sci. 2005, 47, 1099–1122. [Google Scholar] [CrossRef]
- Roberts, T.M.; Al-Ubaidi, H. Influence of Shear Deformation on Restrained Torsional Warping of Pultruded FRP Bars of Open Cross-Section. Thin-Walled Struct. 2001, 39, 395–414. [Google Scholar] [CrossRef]
- Sapountzakis, E.J.; Mokos, V.G. Warping Shear Stresses in Nonuniform Torsion of Composite Bars by BEM. Comput. Methods Appl. Mech. Eng. 2003, 192, 4337–4353. [Google Scholar] [CrossRef]
- Prokić, A. Thin-Walled Beams with Open and Closed Cross-Sections. Comput. Struct. 1993, 47, 1065–1070. [Google Scholar] [CrossRef]
- Gruttmann, F.; Sauer, R.; Wagner, W. Shear Stresses in Prismatic Beams with Arbitrary Cross-Sections. Int. J. Numer. Meth. Engng. 1999, 45, 865–889. [Google Scholar] [CrossRef]
- Mentrasti, L. Torsion of Box Girders with Deformable Cross Sections. J. Eng. Mech. 1991, 117, 2179–2200. [Google Scholar] [CrossRef]
- Zhang, S.H.; Lyons, L.P.R. A Thin-Walled Box Beam Finite Element for Curved Bridge Analysis. Comput. Struct. 1984, 18, 1035–1046. [Google Scholar] [CrossRef]
- Cambronero-Barrientos, F.; Díaz-del-Valle, J.; Martínez-Martínez, J.-A. Beam Element for Thin-Walled Beams with Torsion, Distortion, and Shear Lag. Eng. Struct. 2017, 143, 571–588. [Google Scholar] [CrossRef]
- Dassault Systèmes. Abaqus Analysis User’s Manual (6.14); Dassault Systèmes: Vélizy-Villacoublay, France, 2014. [Google Scholar]
- Thompson, M.K.; Thompson, J.M. ANSYS Mechanical APDL for Finite Element Analysis; Elsevier Science: San Diego, CA, USA, 2017; ISBN 978-0-12-813110-7. [Google Scholar]
- ADINA R&D Inc. ADINA User’s Manual; ADINA R&D Inc.: Watertown, MA, USA, 2012. [Google Scholar]
- Murín, J.; Kutiš, V. An Effective Finite Element for Torsion of Constant Cross-Sections Including Warping with Secondary Torsion Moment Deformation Effect. Eng. Struct. 2008, 30, 2716–2723. [Google Scholar] [CrossRef]
- Sabat, L.; Kundu, C.K. Flexural-Torsional Analysis of Steel Beam Structures Using ANSYS. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Li, X.; Wan, S.; Mo, Y.L.; Shen, K.; Zhou, T.; Nian, Y. An Improved Method for Analyzing Shear Lag in Thin-Walled Box-Section Beam with Arbitrary Width of Cantilever Flange. Thin-Walled Struct. 2019, 140, 222–235. [Google Scholar] [CrossRef]
- Sapountzakis, E.J.; Mokos, V.G. 3-D Beam Element of Composite Cross Section Including Warping and Shear Deformation Effects. Comput. Struct. 2007, 85, 102–116. [Google Scholar] [CrossRef]
- Yau, J.D.; Kuo, S.-R. Geometrical Stiffness of Thin-Walled I-Beam Element Based on Rigid-Beam Assemblage Concept. J. Mech. 2012, 28, 97–106. [Google Scholar] [CrossRef][Green Version]
- Bernuzzi, C.; Simoncelli, M. The Transformation Matrix in the 7DOFs Beam Formulation. Thin-Walled Struct. 2023, 190, 110951. [Google Scholar] [CrossRef]
- Ramaprasad, S.; Dattaguru, B.; Singh, G. Exact Solutions for Thin-Walled Composite Open Section Beams Using a Unified State Space Coupled Field Formulation. Mech. Based Des. Struct. Mach. 2023, 51, 5983–6007. [Google Scholar] [CrossRef]
- Lebastard, M.; Couchaux, M.; Bureau, A.; Hjiaj, M. Lateral-Torsional Buckling of Beams with Warping Restraints at Supports. ce/papers 2021, 4, 2262–2270. [Google Scholar] [CrossRef]
- Lebastard, M.; Couchaux, M.; Santana, M.V.B.; Bureau, A.; Hjiaj, M. Elastic Lateral-Torsional Buckling of Beams with Warping Restraints at Supports. J. Constr. Steel Res. 2022, 197, 107410. [Google Scholar] [CrossRef]
- Justín, M.; Juraj, H.; Mehdi, A.; Vladimír, K.; Juraj, P.; Stephan, K. Extension of the FGM Beam Finite Element by Warping Torsion. Strojnícky Časopis J. Mech. Eng. 2019, 69, 57–76. [Google Scholar] [CrossRef]
- Piotrowski, R.; Szychowski, A.; Vičan, J. Elastic Critical Resistance of the Simple Beam Grillage Resulting from the Lateral Torsional Buckling Condition: FEM Modelling and Analytical Considerations. Materials 2023, 16, 1346. [Google Scholar] [CrossRef] [PubMed]
- Burlon, A.; Failla, G.; Arena, F. Exact Stochastic Analysis of Coupled Bending–Torsion Beams with in-Span Supports and Masses. Probabilistic Eng. Mech. 2018, 54, 53–64. [Google Scholar] [CrossRef]
- Megson, T.H.G. Torsion of Solid Sections. In Aircraft Structures for Engineering Students; Elsevier: Amsterdam, The Netherlands, 2022; pp. 75–95. ISBN 978-0-12-822868-5. [Google Scholar]
- Mohammadi, E.; Hosseini, S.S.; Rohanimanesh, M.S. Elastic Lateral-Torsional Buckling Strength and Torsional Bracing Stiffness Requirement for Monosymmetric I-Beams. Thin-Walled Struct. 2016, 104, 116–125. [Google Scholar] [CrossRef]
- Roddis, W.M.K.; Kriesten, M.; Liu, Z. Torsional Analysis for Exterior Girders; University of Kansas Center for Research, Inc.: Lawrence, KS, USA, 1999; 128p. [Google Scholar]
- Cook, R.D. Concepts and Applications of Finite Element Analysis, 4th ed.; Wiley: New York, NY, USA, 2001; ISBN 978-0-471-35605-9. [Google Scholar]









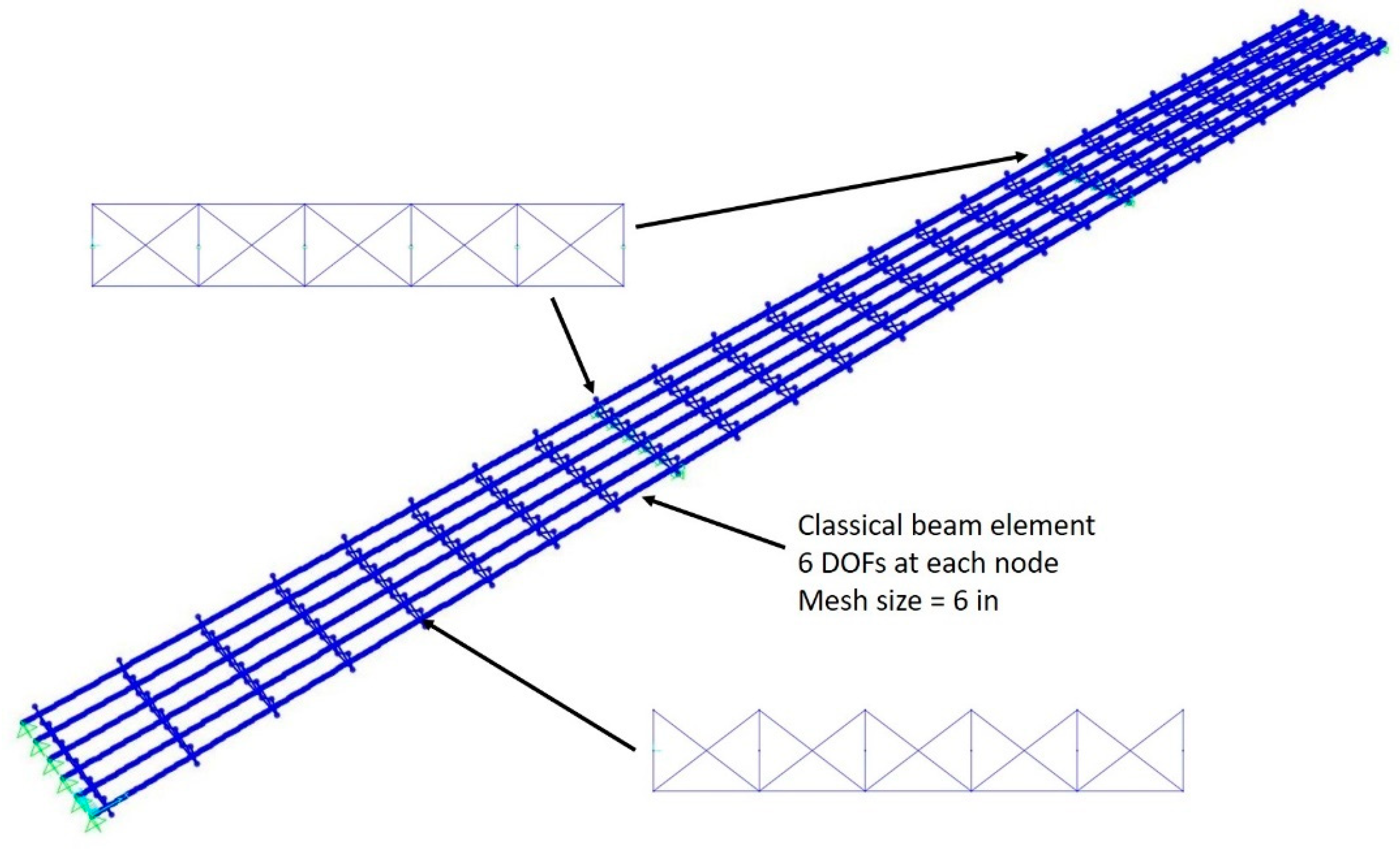


| Solid Element Model (SEM) | Classical Beam Element Model | 7-DOF Beam Element Model | |
|---|---|---|---|
| Number of Nodes | 1,348,288 | 6640 (0.49% of the nodes of SEM) | 6640 (0.49% of the nodes of SEM) |
| Number of Elements | 690,152 | 7164 (1.04% of the nodes of SEM) | 7164 (1.04% of the nodes of SEM) |
| DOF at Each Node | 3 | 6 | 7 |
| Global Stiffness Matrix Size | 4,044,864 | 39,840 (0.98% of the nodes of SEM) | 46,480 (1.15% of the nodes of SEM) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hui, L.; Ashiquzzaman, M.; Hindi, R. Application and Experimental Validation of Seven-Degree-of-Freedom Beam Element for Girder Bridges during Deck Construction. Infrastructures 2023, 8, 175. https://doi.org/10.3390/infrastructures8120175
Hui L, Ashiquzzaman M, Hindi R. Application and Experimental Validation of Seven-Degree-of-Freedom Beam Element for Girder Bridges during Deck Construction. Infrastructures. 2023; 8(12):175. https://doi.org/10.3390/infrastructures8120175
Chicago/Turabian StyleHui, Li, Md Ashiquzzaman, and Riyadh Hindi. 2023. "Application and Experimental Validation of Seven-Degree-of-Freedom Beam Element for Girder Bridges during Deck Construction" Infrastructures 8, no. 12: 175. https://doi.org/10.3390/infrastructures8120175
APA StyleHui, L., Ashiquzzaman, M., & Hindi, R. (2023). Application and Experimental Validation of Seven-Degree-of-Freedom Beam Element for Girder Bridges during Deck Construction. Infrastructures, 8(12), 175. https://doi.org/10.3390/infrastructures8120175





