Multi-Parametric Delineation Approach for Homogeneous Sectioning of Asphalt Pavements ^†

Abstract

The demand for preserving existing roadway infrastructure has been increasing to regulate expensive reconstruction activities. The maintenance of homogeneous road sections is one of the approaches to economize the overall management of pavement systems. The existing homogeneous delineation methods consider one or two parameters for segmenting the pavements based on similar characteristics, which are found to be a repetitive process. Also, there is a need to consider multiple parameters that represent the functional, structural, and traffic characteristics in segmentation process. Therefore, the objective of this study was to develop a multi-parameter-based delineation approach (MPDA) to segment the pavements into subsections with similar features considering functional, structural, and traffic characteristics. Deflection bowl parameters, unified pavement health index (functional performance metric), surface layer modulus, and traffic reported in terms of AADT were employed for developing a multi-parametric delineation index (MPDI). A total of 1781 datapoints covering 26 road sections in the State of Andhra Pradesh, India, were used. The C-charts method-based segmentation for MPDI was applied to obtain the homogeneous sections. The devised approach was found to be efficient in segmenting the pavements as well as robust in selecting suitable maintenance strategies for each group of the homogeneous sections. Further, the segmentation processes were automated for easier implementation by the agencies.

1. Introduction

Roadway maintenance and rehabilitation is critical toward sustaining the economy of any nation. In 2021, the roadway network in the United States of America (USA) was ranked with a ‘D’ grade by the American Society of Civil Engineers (ASCE) [1]. The report stated that 40% of the major roads and highways in the USA are in poor and mediocre condition and need to be maintained immediately. According to the International Transport Forum, France has spent EUR 2 billion on the maintenance of roadway infrastructure, which was found to be the highest amongst 63 participating countries, while the spending details were not available for India [2]. With the growing importance to preserve the existing pavement infrastructure, the Government of India initiated asset recycling processes to monitor and manage pavements to cater to the traffic needs during their remaining service lives [3].

In order to plan a maintenance intervention, it is essential to collect present pavement condition and predict future performance. The present pavement condition encompasses both structural and functional behavior of the roadways affected by prevailing traffic conditions. Also, it is essential to segment the pavements based on similar characteristics so as to suggest an optimum maintenance intervention at the project level. The existing homogeneous sectioning methods include the cumulative difference approach (CDA), absolute difference approach (ADA) [4,5,6,7], Bayesian algorithm [8], cumulative sum [9], quality control charts [10], and minimization of sum of squared error approach [11], all of which consider single pavement performance parameter at an instant of time for delineating the pavement sections.

Statistically, delineation is similar to the estimation of change points in a process. The CDA used for homogeneous sectioning was first introduced in the American Association of State Highway and Transportation Officials (AASHTO) guide for the Design of Pavement Structures [12], which was then used and implemented by the roadway agencies in Europe, Asia, and Africa [5,13]. Ping et al. [14] developed a statistical analysis software to automate the pavement sectioning process using CDA. However, the approach was found to be weak in classifying the non-substantial changes in the readings, which resulted in a higher number of delineated sections than actual. With this major drawback, the approach was preferred only for road sections whose length was considerably less than 2 km for segmentation. In contrast, the ADA, which was developed and used in Germany [5] was preferred for road sections whose length was noticeably high as the approach smoothened the borders of the homogeneous sections. Further, the Bayesian algorithmic approach developed and widely used in Europe was found to be sensitive to minor changes in the data points, leading to a “higher” number of segments that were practically not feasible for implementation. In another study, the classification and regression trees (CART) approach was reported as a better method in comparison with the other statistical change-point estimation algorithms such as multiple regression, generalized linear models, maximum likelihood estimation, and exponential smoothing methods [4].

Gendy and Shalaby [10] used quality control charts to identify the drastic changes in the roadway conditions, which were considered as change points in the process control, i.e., pavement condition. The dynamic process of determination of outliers made this approach suitable for segmenting both short and long measurement series of roadway stretches. Further, Tejeda and Echaveguren [9] reviewed the change-point-based segmentation methods and concluded that the effect of outlier data should be taken into account for segmentation. Researchers developed a leverage method-based segmentation approach to delineate the skid resistance data of asphalt pavement sections. In another study, Cafiso and Graziano [11] developed a minimization of sum of squared error approach to detect change points in the pavement condition data such as rutting, roughness, or skid resistance. The results showed that the defined approach recognized many change points that were identified using the Bayesian approach. Likewise, Zhao et al. [15] considered pavement layer thickness data collected using ground penetrating radar for typical pavement segmentation based on the thickness and material characteristics. Ahmed and David [16] developed an affinity propagation clustering technique for pavement segmentation based on only condition data. Similarly, Biswas and Kuna [17] used a pruned exact linear time algorithm for pavement delineation based on deflection.

Other researchers [18] reviewed the existing delineation methods explicitly based on pavement surface deflection data measured using a falling weight deflectometer (FWD). Further, the investigators developed a segmentation approach accounting for the mean and local variations in the deflection. In another study, Donev and Hoffmann [19] considered rutting, surface defects, and alligator cracking in sectioning the pavements based on similar characteristics for project-level maintenance applications. More so, the researchers stated that homogenous segmentation was not an appropriate option for project-level maintenance interventions. However, the outcomes were found to be suitable for short measurement series and presented a methodology that may not be suitable for application elsewhere, especially in emerging economies [20]. The existing homogeneous segmentation methods such as CDA used by the roadway agencies in the USA and Canada, ADA used in Germany, and Bayesian approach used in Europe used single parameters for homogeneous sectioning. Further, in some of the studies, homogenous sectioning was reported as a radical approach for project-level maintenance interventions. Importantly, should there be budgetary constraints in some regions [21], a homogeneous section length of 10 m will be practically difficult to adopt and perform any maintenance intervention.

Further, artificial intelligence (AI) techniques were used for pavement delineation, which reduced the tedious analysis process when using a single parameter for segmentation. However, the use of AI techniques for segmentation using multiple parameters was yet to be verified [22]. A recent study tested the performance of the C-charts method in segmenting the roadway sections that utilized two parameters: IRI and rutting [6]. It was found that the bi-parametric approach developed in the study was efficient in the segmentation process compared to the traditional methods. In another study, researchers used clustering techniques for homogeneous segmentation [23]. However, there is a need to explore the interaction of the other parameters such as deflection and traffic data in the pavement segmentation process.

It is noteworthy that the previous studies only used one pavement condition parameter such as rutting, deflection, or roughness measured in terms of rut depth, international roughness index (IRI), skid resistance, or cracking at one time to segment the pavement sections. Later, the procedure was repeated for the remaining parameters to obtain the optimum homogenous segmentation, which was found to be monotonous, resulting in a rigorous analysis of the results, and tedious, consequential of obtaining erroneous results if the analyses were to be delayed. Therefore, there is a need to develop a multi-parametric-based sectioning approach, where multiple parameters can be considered simultaneously for sectioning. Thus, the objective of this research study was to develop a multi-parameter-based delineation approach (MPDA) to segment the pavements into subsections with similar features encompassing functional, structural, and traffic characteristics. It is envisioned that the developed approach would certainly reduce the analysis costs and duration while also helping the decision-making authorities in identifying the optimum homogeneous sections at the project level.

2. Multi-Parametric Delineation Approach Framework

C-charts are amongst the statistical quality control methods widely used to monitor the defects in the production process as well as for several engineering applications. The C-charts method was basically used for the data, which was obtained in a count-type fashion. Since homogeneous sectioning was performed for different pavement performance parameters that were measured at regular intervals, the data were presumed to be in a count-type arrangement. The results of the C-charts-based pavement homogeneous segmentation were better than the other segmentation methods [9]. With the merits of the C-charts-based segmentation approach over classical homogeneous sectioning methods presented in Eddula, Peraka, and Biligiri [6], the C-charts-based method was used to perform homogeneous segmentation, with consideration given to multiple pavement characteristics. A series of tasks were performed to develop the MPDA for the homogeneous sectioning of roads. The framework for the development of MPDA is presented in Figure 1. These tasks were grouped into three categories, and the corresponding set of operations performed under each category is explained below:

• Metric formulation: a procedure was formulated to identify the parameters for homogeneous sectioning, pre-processing of data, formulation of a multi-parametric delineation index (MPDI) as a function of the identified parameters for sectioning, and calculation of the control limits for MPDI, which included mean, standard deviation, and the upper control limit (UCL) and the lower control limit (LCL) from the entire dataset.
• C-charts-based MPDA: a process that was adopted to construct C-charts for MPDI for each road section in the dataset, which could identify the outlier data and help segment the sections between the outliers as homogeneous sections.
• Validation: a method was followed that used the CDA segmentation with roughness and rutting, while also earmarking the homogeneous sections with roughness and rutting using the C-charts method, and finally the results of these methods were compared (CDA and C-charts) against the MPDA results.

3. Multi-Parametric Delineation Index

In general, it is crucial to identify the various factors to undertake the homogeneous segmentation process in pavements. In this study, multiple parameters were considered as a single entity to segment the pavement network. The necessity of segmenting the pavements that have the most similar characteristics formed the basis for the selection of multiple parameters for segmentation. The pavement deflection bowl parameters such as peak deflection, base layer index (BLI), middle layer index (MLI), and lower layer index (LLI) [24], being representative of the structural integrity of the pavement system, were chosen, and a metric called unified pavement health index (UPHI) [25] was selected as developed by the authors that indicated the functional condition of the pavements based on the current distress levels on a scale of 0 to 100. In addition to these, higher traffic volumes that increase the rate of deterioration were also selected along with the modulus corresponding to the structural capacity of the pavement system. The following parameters were found to be significantly connected with pavement deterioration.

• Pavement condition reported in terms of UPHI;
• Pavement peak deflection;
• BLI, MLI, and LLI;
• Traffic reported as annual average daily traffic (AADT);
• Modulus of elasticity of the surface layer (E).

3.1. Dataset and Pre-Processing

Andhra Pradesh Road Development Corporation (APRDC), India, a nodal agency in the State of Andhra Pradesh, India, has been performing several studies pertaining to traffic, trial-pit, deflection, and distress condition data collection on most of the road sections across thirteen districts in the State. APRDC conducted deflection studies on two road sections in each district of the State. The road section data concerning deflections, functional condition, and traffic was used for this study. The following pre-processing steps were performed on the dataset to formulate the MPDI for each of the road segments:

• Computation of UPHI for each segment of the road sections from the extent of the current distress and severity levels, as detailed by the authors in [25];
• Calculation of mean deflections, BLI, MLI, and LLI from deflection data;
• Assessment of E from deflection readings.

FWD was used to capture pavement deflection at every 300 m interval over the entire roadway stretch. A set of three trials was performed at each location with the aim to obtain optimum deflections at the test location. The deflections were measured at nine radial distances from the loading position. In total, deflections were measured at 1781 locations across 26 roadway sections covering 265.2 lane km. A seating load of 40 kN was applied during the deflection measurements at the loading position and at a distance of 200, 300, 450, 600, 900, 1200, 1500, and 1800 mm away from the loading position reported as D0, D1, D2, D3, D4, D5, D6, D7, and D8, respectively. As a first step, the mean values for each deflection were calculated for the three trials. From these deflections, BLI, MLI, and LLI were estimated using Equations (1) through (3). A schematic representation of the FWD load application process and the deflection bowl parameters used in the study are shown in Figure 2.

BLI = D0 − D2

(1)

MLI = D2 − D4

(2)

LLI = D4 − D5

(3)

Based on the condition data, distresses were reported for every 10 m interval. A deep neural network (DNN) was developed to compute UPHI for each 10 m segment. Later, the UPHI values were averaged for 300 m long sections to obtain a single data frame for both surface deflections as well as UPHI. The modulus of elasticity E of the surface layer at each deflection measurement location was calculated using KGPBACK^TM software [13]. Pavement layer thickness details of the road sections, FWD seating load, contact pressure, deflection measurements at all radial distances, Poisson’s ratios, and ranges for layer moduli were given as inputs to the application, while back-calculated layer moduli of surface, base layers, and subgrade were estimated. Finally, a data frame with all the parameters (UPHI, D0, BLI, MLI, LLI, AADT, and E) was created.

3.2. MPDI Formulation

The pavement system parameters selected for the study were characteristics of different dimensions. UPHI represented the functional condition of the pavement; peak deflection, BLI, MLI, and LLI indicated the structural integrity of the pavement system; modulus of elasticity provided the measure of the remaining service life of the pavement; and traffic exemplified the load that the pavement was bound to take a while it was in service. The dimensionless parameter called MPDI was formulated with the normalized values of all these parameters, as in Equation (4). Note that the normalized parameters were added to account for the individual contribution of each of the parameters during homogeneous sectioning.

$${MPDI}_i=\frac{{UPHI}_i}{{\mu }_{UPHI}}+\frac{{DO}_i}{{\mu }_{D0}}+\frac{{BLI}_i}{{\mu }_{BLI}}+\frac{{MLI}_i}{{\mu }_{MLI}}+\frac{{LLI}_i}{{\mu }_{LLI}}+\frac{{AADT}_i}{{\mu }_{AADT}}+\frac{E_i}{{\mu }_E}$$

(4)

where i = datapoint; μ_UPHI = mean UPHI of the entire dataset (1781 datapoints); μ_BLI = mean BLI, µm; μ_MLI = mean MLI, µm; μ_LLI = mean LLI, µm; μ_AADT = mean AADT; and μ_E = mean back-calculated elasticity modulus of surface layer, MPa.

Usually, the control limits measure process stability, while sigma levels (standard deviations) measure process capability [26,27]. Further, the control limits identify an unexpected variation in the quality control process. The conventional three-standard deviations used for identifying the control limits has been classically determined and applied in various research studies [28], while other researchers [29,30] have also used two standard deviations to recognize the warning limits without compromising on the quality of the established control limits and process capability. Thus, in this study, the control limits of the MPDI accounted for two standard deviations to rationally ascertain the homogeneous segments and the overall process stability, as presented in

Table 1. Control limits for MPDI.

Mean (μ)	Standard Deviation (s)	UCL (μ + 2 s)	LCL (μ − 2 s)
7	2.1992	14.3683	2.6016

. Note that the mean UPHI, D0, BLI, MLI, LLI, AADT, and E of the whole dataset were 75.27, 379.58, 222.79, 80.44, 16.91, 2832, and 2068.02, respectively.

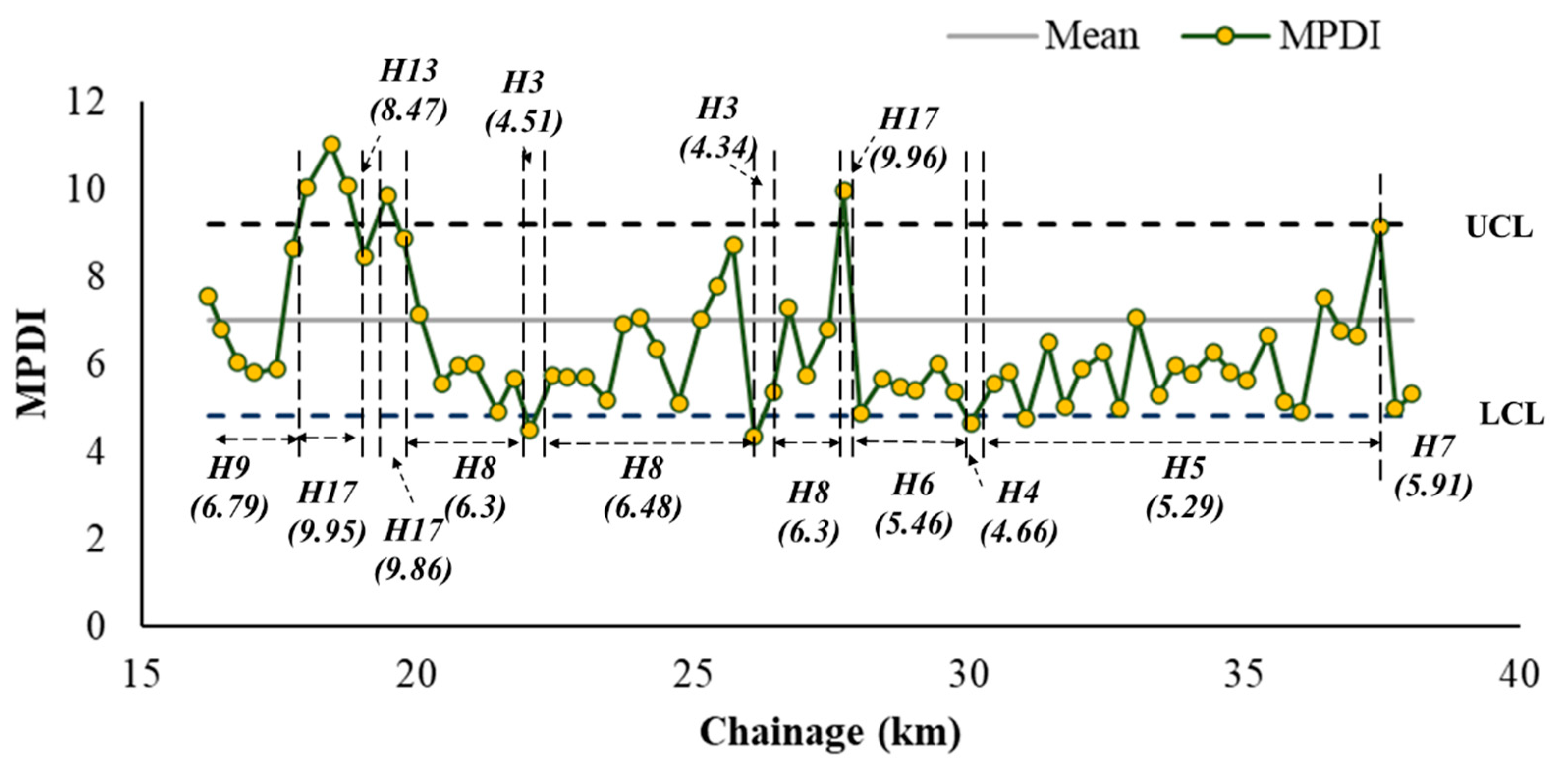
4. C-Charts Method-Based MPDA

In a recent study [6], the C-charts method was selected for segmenting the pavements based on similar MPDI values. Using the control limits presented in Table 1, C-charts for MPDI were constructed for the whole dataset covering 1781 data points. The points that crossed the UCL and LCL (Table 1) were recorded as outliers. Section boundaries were introduced to the chart when the curve crossed either UCL or LCL. The data points that were present between any two section boundaries were regarded as “homogeneous segments”. It was observed that the lowest mean MPDI was 3, while the highest was 17.8. Based on the mean MPDI of the homogeneous segments, 37 homogeneous section types were defined and summarized, as in

Table 2. Homogeneous section classification based on mean MPDI.

Mean MPDI	Homogeneous Section Classification	Mean MPDI	Homogeneous Section Classification	Mean MPDI	Homogeneous Section Classification
3.0–3.4	H0	8.2–8.6	H13	13.0–13.4	H25
3.4–3.8	H1	8.6–9.0	H14	13.4–13.8	H26
3.8–4.2	H2	9.0–9.4	H15	13.8–14.2	H27
4.2–4.6	H3	9.4–9.8	H16	14.2–14.6	H28
4.6–5.0	H4	9.8–10.2	H17	14.6–15.0	H29
5.0–5.4	H5	10.2–10.6	H18	15.0–15.4	H30
5.4–5.8	H6	10.6–11.0	H19	15.4–15.8	H31
5.8–6.2	H7	11.0–11.4	H20	15.8–16.2	H32
6.2–6.6	H8	11.4–11.8	H21	16.2–16.8	H33
6.6–7.0	H9	11.8–12.2	H22	16.8–17.0	H34
7.0–7.4	H10	12.2–12.6	H23	17.0–17.4	H35
7.4–7.8	H11	12.6–13.0	H24	17.4–17.8	H36
7.8–8.2	H12

. For example, the section that had a mean MPDI of 6.5 would be classified as a homogeneous section category “H8”. The homogeneous sections for the entire 26 road sections of the dataset were thus established. The homogeneous sections of the road section and C-charts for the MPDI in the State of Andhra Pradesh between chainages 22.41 and 28.71 km are shown in Figure 3. The control limits for MPDI, segmented portions, homogeneous section categories, and mean MPDI are also marked on the plots. For example, H8 (6.55) in the plot basically represents the segment belonging to the homogeneous section category “H8” with a mean MPDI of 6.55. A similar approach was followed for the remaining 25 road sections in the State.

From the results, it was observed that the highest MPDI represented the poor performance of a section, and vice versa. Further, the lowest value of the mean MPDI revealed that there was less variation in the study variables from the overall pavement normalized mean values, which indicated that the segment was indeed homogeneous and needed preventive maintenance. Higher values of mean MPDI indicated that the section had a huge deviation in the study variables from the mean, and required a critical maintenance intervention. Essentially, MPDI-based pavement maintenance selection scale was defined, which will provide insights to the roadway practitioners to select appropriate maintenance interventions for the designated homogeneous sections.

Table 3. Categorization of MPDI for maintenance treatment selection.

Mean MPDI	Maintenance Intervention	Indication
<4	Preventive maintenance	P_M_I
4 to 7	Corrective maintenance	C_M_I
7 to 10	Minor rehabilitation	Mi_R_M_I
10 to 14	Major rehabilitation	Ma_R_M_I
>14	Reconstruction	R_M_I

depicts the categorization of MPDI required for selecting the maintenance treatment.

In the entire dataset of 26 road sections, a total of 389 homogeneous sections belonging to 34 homogeneous section categories were identified. Amongst all the sections, 57.58% of them would need corrective maintenance, while 25.96% would require minor rehabilitation. The minimum length of the homogeneous section was found to be 300 m (<500 m), which was appropriate for project-level maintenance applications, as also reported by Jannat et al. [31].

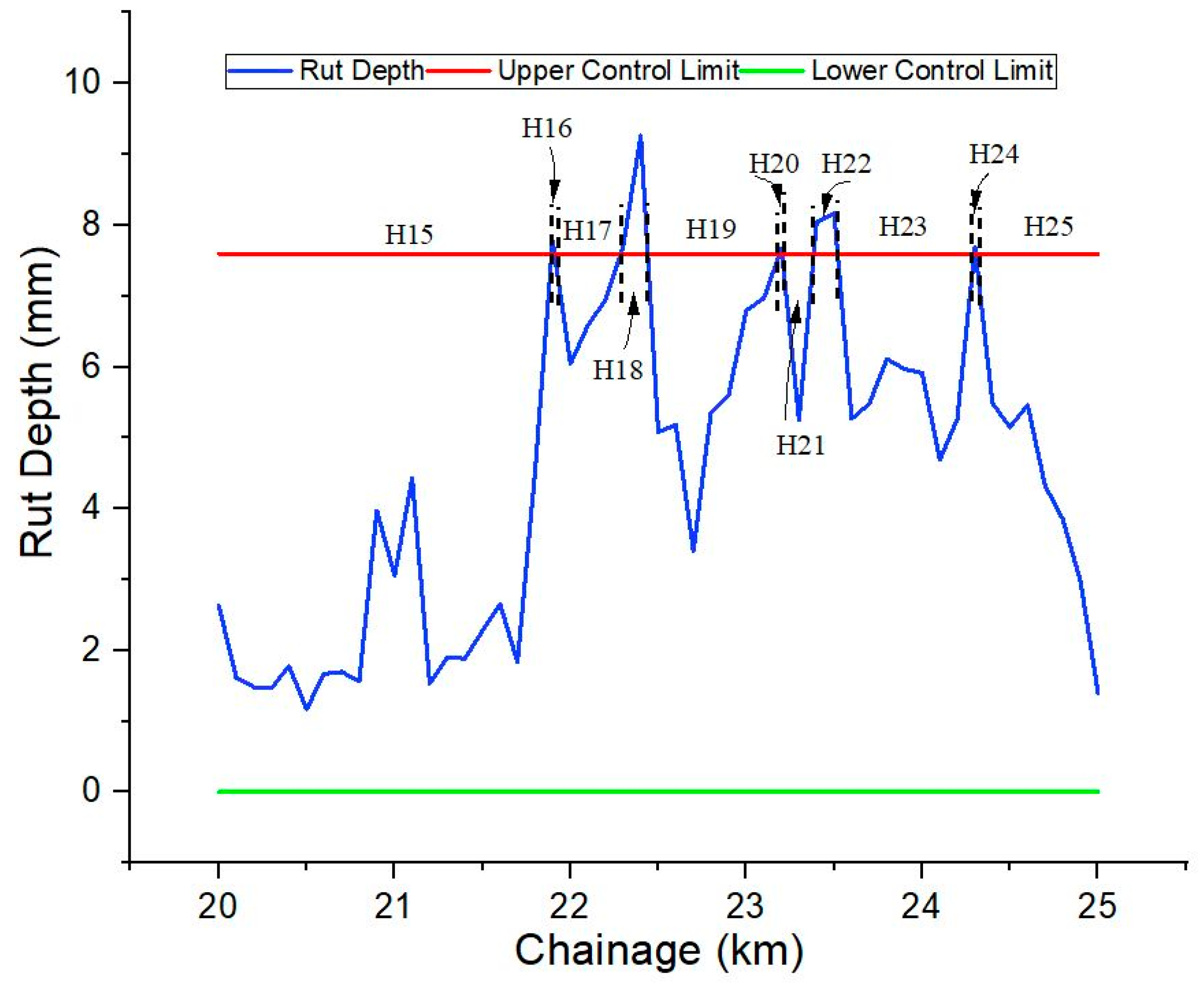
5. Comparison of MPDI with CDA and C-Charts Methods

In order to validate the developed approach, it was essential to compare the results obtained from MPDA with those approaches recorded in the literature. CDA and C-charts methods were used by many roadway agencies such as in India, the USA, and Canada. Therefore, a comparison of the results obtained from MPDA with CDA and C-charts methods represents the merits of the developed approach. For this purpose, the data of a road section between Bellary and Gundlapally was used, which helped draw CDA and C-charts for rutting and roughness individually. The results of the CDA approach for the road section between 20 and 25 km are shown in Figure 4 and Figure 5 for IRI and rutting, respectively. Further, the results of the C-Charts for rutting are displayed in Figure 6, and the segmentation results of MPDA method for the same section are presented in Figure 7. From these Figures, it could be inferred that the homogeneous sections obtained using CDA and C-charts methods for IRI and rutting were different from the MPDA-based segmentation developed in this study. It is very important to note that the MPDA considered UPHI, which is a good indicator of IRI and rutting for segmentation that resulted in rational segmentation compared to CDA and C-charts approaches. Thus, this method could be comfortably adopted for delineating the pavements for project-level maintenance activities.

6. Automation of MPDA Method for Sectioning

The manual estimations of MPDI and the interpretation of the results will actually be laborious when dealing with large amount of data such as in this study. Automating the entire approach would practically reduce the time required for providing timely solutions to the agencies for making appropriate decisions as well as recommending maintenance interventions. With this objective, a Python code was written on the Spyder platform, and the data operations were performed through automation, which included estimations of UPHI, BLI, MLI, LLI, and E for the given road segments. The pseudo-code for the algorithm is shown in Figure 8, and the entire process had five components:

• Estimations of normalized values of D0, BLI, MLI, and LLI from deflection readings (D0, D1, …, D8), and seating load;
• Measurements of E from the normalized deflection readings;
• Calculations of UPHI based on pavement condition;
• Development of MPDI for each segment;
• Segmentation of pavement sections based on mean MPDI using C-charts.

As shown in Figure 8, the inputs and outputs of each component were marked with respect to the components. The first component of the program calculated the normalized deflection bowl parameters from the FWD readings. The inputs and outputs are represented as I_1 and O_1, respectively. Next, a DNN was developed as a second component to calculate E from the normalized deflection bowl parameters obtained as output from component 1 (O_1). Note that the DNN developed by the authors to compute UPHI from the surface distresses [25] was used as a third component. Next, MPDI was computed using O_1, O_2, and O_3 and used as the input for segmentation.

6.1. Computation of Normalized Deflection Bowl Parameters

The following libraries were used to perform the tasks (Figure 8) to segment the given road section into homogeneous sections and suggest a maintenance strategy: Keras, matplotlib, statistics, pandas, and sci-kit learn. The first algorithm was written using the pandas and sci-kit learn libraries in Python. The deflection readings obtained from the FWD test were used as inputs to obtain normalized deflection bowl parameters as output (O_1). The procedure followed to develop the DNN architecture for computing E from deflection bowl parameters is described next.

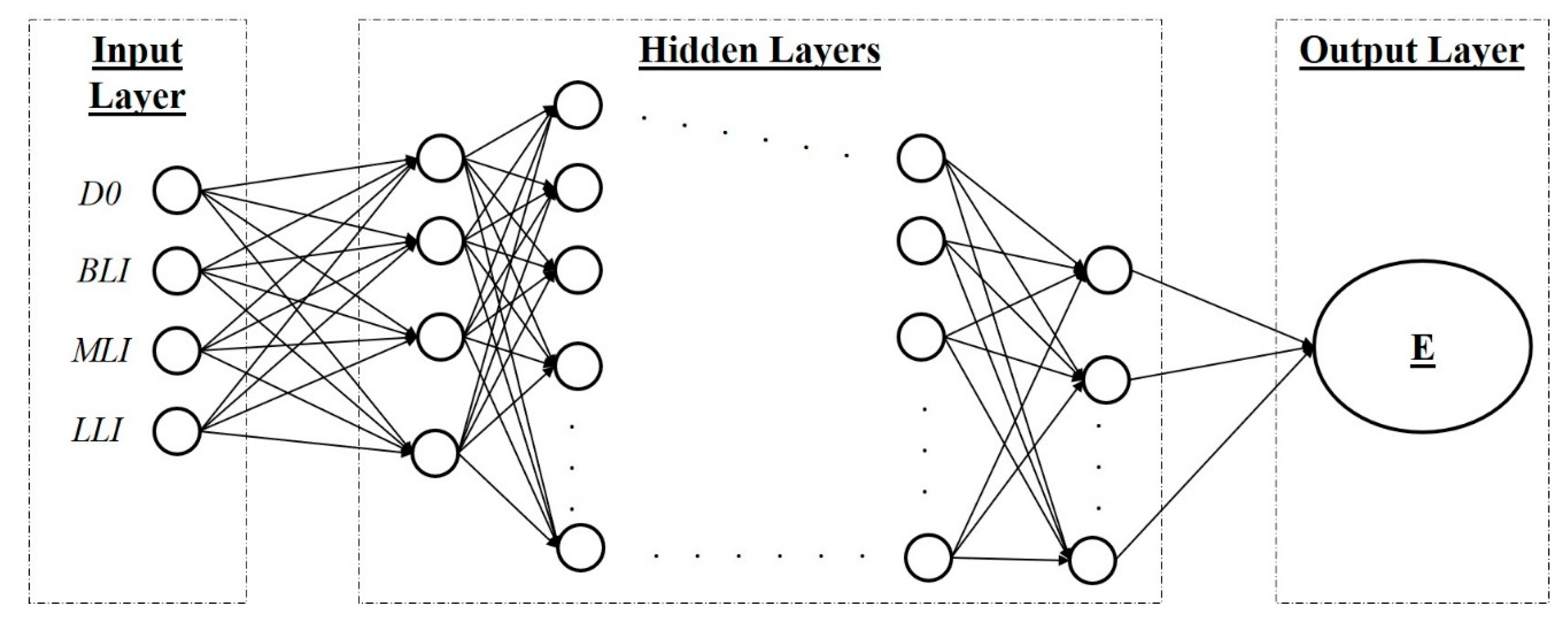
6.2. DNN Architecture for Estimating Surface Layer Modulus

A DNN architecture was adopted to predict E values from the deflection bowl parameters and seating load. A schematic representation of the DNN architecture for computing E is shown in Figure 9. As presented in Figure 8, D0, BLI, MLI, and LLI were given as inputs to the DNN, which had several hidden layers with neurons that recursively establish a relationship between inputs and output, E. The Keras and tensorflow libraries in Python were used to develop the DNN architecture. In order to obtain the optimum network architecture in terms of number of hidden layers and number of neurons in each hidden layer, the kerastuner function was used. The following settings for hyperparameters were considered:

• Learning rate: 0.01, 0.001, 0.0001, 0.00001, 0.005, 0.0005;
• Activation function for hidden layers: ReLU, linear, Leaky ReLU;
• Maximum number of hidden layers: 100;
• Minimum number of hidden layers: 1;
• Maximum number of neurons in each hidden layer: 20;
• Minimum number of neurons in each hidden layer: 2;
• Loss function: Mean squared error (MSE);
• Performance estimator: coefficient of determination (R²).

The Kerastuner program computed MSE and R² for each combination of the hyperparameters. The program identified the following settings of the hyperparameters as optimum for estimating the surface layer modulus:

• Learning rate: 0.001;
• Activation function for hidden layers: ReLU;
• Number of hidden layers: 4;
• Number of neurons in each hidden layer: 4, 14, 9, 5.

The DNN architecture to estimate E value was then developed based on the aforementioned optimum hyperparameters. A total of 1781 data points were used to train and test the computational efficiency of the network. Note that 80% of the data points were used for training and validating the network, and the remaining data points were used for testing the network performance. During training, the network achieved an MSE of 34.33 and an R² of 68.43%, while MSE and R² during testing were found to be 36.54 and 67.67%, respectively. The low values of the results could be attributed to the use of a smaller number of data points in the dataset. The output of the architecture (O_2) was used to compute the MPDI.

6.3. Evaluation of UPHI from Surface Distresses

The authors developed a parameter called UPHI to represent the current distress level of the asphalt pavements on a scale of 0 to 100 [25]. The surface distresses and roughness were considered in the computation of the UPHI value. A DNN architecture was developed to compute UPHI from the distress extents and severities. The DNN architecture was used in this study to assess the functional condition of the pavement. The results of the DNN architecture were reported as UPHI values measured at 10 m intervals (O_3).

6.4. Homogeneous Sectioning Using MPDA

The outputs from the three aforementioned modules were averaged for 300 m intervals to compute the MPDI. In addition to these outputs, traffic reported in terms of AADT was also included to calculate MPDI, as given in Equation (4). The mean and standard deviation of MPDI were measured to compute lower and upper control limits. For the road section, the MPDI values were compared with LCL and UCL to find homogeneous sections. For each homogeneous section, the mean MPDI was computed, an appropriate homogeneous section class was assigned, and a maintenance strategy was suggested.

6.5. Research Significance

The MPDA method of pavement segmentation developed in the study accounted for multiple parameters to delineate the pavements based on similar characteristics. The salient features of the method are as follows:

• Seven diverse parameters were considered for segmenting the pavements that have significant similar characteristics: peak deflection, BLI, MLI, LLI, UPHI, AADT, and E;
• Segmentation interval was dependent on the sample test length of the FWD studies;
• The developed Python code automatically segmented the sections from the input data;
• The developed sectioning approach is anticipated to help researchers and roadway management systems personnel in delineating the pavements based on most similar characteristics with a roadway network. The MPDI-based categorization will assist the decision makers in selecting the most feasible maintenance interventions for the project-level roadway systems. However, the minimum test length required for FWD measurements was 50 m, and hence, the system was not capable of predicting the homogeneous sections less than 50 m road length, which is one of the limitations of the study. However, the study could be extended by including the moduli of base and subgrade layers for segmentation purposes in future.

7. Conclusions and Recommendations

The delineation process developed in this study considered multiple parameters for segmentation of asphalt pavements to accord maintenance activities. The major conclusions and recommendations are as follows:

• Multiple parameters for segmentation: the parameters were found to be significantly interlinked with pavement deterioration and the corresponding structural and functional characteristics. Thus, a dimensionless parameter called MPDI was formulated with the normalized values of all these parameters for segmentation, which could be used to predict the deterioration pattern of the pavement sections.
• MPDI-based categorization for maintenance treatment selection: MPDI-based pavement maintenance selection scale was defined, which will provide insights to the roadway practitioners to select appropriate maintenance interventions for the designated homogeneous sections.
• Automation of the delineation process: the DNN developed in this study would serve as a one-stop solution for pavement segmentation, which will potentially help the practitioners for project-level maintenance applications.
• Recommendations and future scope: The multi-parametric delineation approach developed in this research study considered seven parameters in order to obtain the homogeneous roadway segments using the C-charts-based approach. However, other pavement characteristics must also be incorporated in future for better segmentation and validated using the proposed method.