Abstract
The development of reliability theory has led to the setting of tasks requiring consideration of the efficiency and functional safety of technical objects of transport over the life cycle. The paper demonstrates the possibility of using the universal laws of elastic wave theory to describe natural phenomena occurring in complex dynamic systems, on the examples of solving issues arising in the interaction of rolling stock and the railway track. The accounting of the time component and the ability of elastic waves to propagate energy in time and space allowed considering any interaction process as a chain of processes, incidence-reflection-refraction of force impulses of interaction. Understanding the physics of dynamic processes that occur in objects while performing their intended functions allows developers to improve objects in such a way as to minimize their life cycle cost and maximize their ability to perform their intended functions under different operating conditions. In addition, it allows the expansion of existing methods and approaches to diagnostics of dynamic transport systems. All this is a base for making it possible to develop an innovative and effective tool for engineers and scientists to assess the impact of technosphere transport objects on human habitats.
1. Introduction
The high theoretical level of development of physics leads to the fact that mathematical methods are very widely used in it, and many provisions are derived from the basic ones. At the same time, as part of natural science, physics is an experimental science. The experiment serves in it both as the initial base, supplying the factual material, and as a method of verifying one or another consequence of the theory. The conditions for using the mathematical apparatus and the methodology of the experiment depend on the task conditions. So, until the seventies of the last century, the main task was to determine the possibility of using an object for certain operating conditions, and technical and economic indicators evaluated the efficiency of using objects. The technical indicators are based on a first-limit state assessment considering the loss of load-bearing capacity or steadiness (strength, stability, and endurance). Therefore, the methods of modeling and conducting experiments correspond to the definition of these criteria, using the provisions of the theory of elasticity. There are many issues could be solved by such approach, for example, when designing suspensions for carriages running at regular and high-speed speed [1], for research and analysis of the stressed-strained state of metal corrugated structures of railroad tracks [2], to evaluate value changes of critical buckling loads, different time instants after loading the structure as well as different relative humidity [3], for simulations of aerodynamic characteristics braking performance [4], to model an induction motor for vehicles [5], for solving engineering problems such as the soil elasticity unevenness [6], for the simulation of dynamic vehicle/track interaction [7], to develop coupled matrix formulations to characterize the dynamic interaction between the vehicle, track, and tunnel [8], for the investigation of vertical vehicle-track interaction [9], for the development a methodology of computational and experimental investigation of strength and fatigue life of bodies of road vehicles for mass passenger transport [10], to study the applicability of low vibration track heavy-haul railway tunnels [11], for the simulation of the wheel-rail contact [12], etc.
The main problem with the theory of elasticity is the absence of a time component, as there are no dependencies that, on the timescale, connect the duration of the effect of force, deformation, or stress. For such conditions, it is sufficient to consider the dynamic process as a quasi-dynamic one since the main evaluation parameters are the values of the maximum possible stresses, strains, loads, and accelerations that appear in objects during operation. Examples include decisions on the following: investigation the influence of wheel flat on wheel-rail dynamic interaction [13], reduction subgrade surface stress [14,15], detection the effects of the different kinds of load and how the corresponding strains are affected by the boundary conditions [16], assessment the effects of different track and loading configurations on vertical wheel load measurements [17], analysis of the dynamic impact of a rail vehicle on various types of a railway infrastructure [18], determination of temperature stresses [19], track condition monitoring [20], investigation the possibility of improving the ride quality of a two-axle railway vehicle with a single-stage suspension [21], assessment the impact of dynamic actions resulting from impact loads [22], studying the dynamic wheel–rail forces under the presence of track irregularities [23], wear investigation of railway wheel running surface [24], investigations of influence of flexibility parameters of wheels and wheelset on the railway bogie dynamics [25], design strategy on the articulation of a freight wagon [26], permanent deformation prediction [27], railway vehicle modeling [28], exploring the impact of structural deformations on the wheel-rail contact [29], detailed creep force analysis at wheel-rail interaction [30], investigation the impact of dynamic track vertical irregularity on the values of wheel-rail contact forces of a passing vehicle was [31], modeling and simulation of two degrees of freedom rail vehicle [32], simulating track longitudinal forces and the rail creep phenomenon [33], development of passive protection devices for a power head of a high-speed multiple unit train at its collisions [34].
The same values of stresses and strains are also measured in experiments as follows: to calculate the blocked forces at the connection points between the secondary suspension elements and the car body [35], to characterize the vehicle-track interaction [36], for wheel-rail contact dynamics simulation [37], to investigate the influence of different braking systems on the braking process of railway passenger vehicles [38], for analysis based on the results from static strength calculation of the wagon body [39], for the calibration of a numerical model of a freight railway wagon [40], for the track condition monitoring based on the bogie and car body acceleration measurements [41], for investigation on the rail residual stress distribution and its influence on the bending fatigue resistance of rails [42], and to discuss the problem of the correctness of the unification of experimental data by axes and points of measurement [43].
According to technical indicators, various options are determined for comparison, and according to economic indicators, the costs for each option are calculated, and, in fact, they are decisive in terms of the efficiency of using the facility. Instances include decisions on the following issues: effective planning and optimization of rail transport operations [44], exploring progressive and irreversible transformations on the surface of material due to the interaction of contact between two materials [45], analysis possibilities of integration of the national railway transport sector into global railway networks [46] and railway passenger flows [47], successful transport process optimization [48], transport systems efficiency [49], estimation the role of road infrastructure in the context of the critical infrastructure system [50] and the environmental impact of a battery-electric vehicles [51], solution for the sustainability of transport and mobility [52], improving the efficiency of transport companies entrepreneurial activities [53], analysis the residual values of selected vehicle models [54] and the optimal sleeper spacing [55], assessment civil infrastructure resilience as follows: state-of-the-art on transportation network systems [56], increasing the energy efficiency of the railway system [57].
Since the seventies of the last century, a direction has been widely developed that studies the property of an object to keep in time within the established limits the values of all parameters characterizing the ability to perform the required functions under specified conditions of use, maintenance, storage, and transportation (dependability). This direction forms new requirements for the question of the efficiency of the use of the object [58,59]. They are based on an assessment of the first limit state and studies of the second limit state as follows: unfit for normal operation (deflections, deformations, crack opening values). The accounting of the second limiting state allows moving on to the definition of states in which the object does not meet the operating conditions and its operation is inappropriate based on risk assessment. Thus, the effectiveness of the use of objects is evaluated by a set of parameters for ensuring the functional safety of the use of an object during its life cycle and techno-economic indicators. Therefore, the modern requirements of the object utilization strategy are aimed at the stable operation of the object while minimizing costs and maximizing the functional safety of using the object by ensuring the parameters of reliability, availability, maintainability, and safety (RAMS) during its life cycle. This is observed when solving problems for a holistic assessment of track condition when planning maintenance activities [60], for railway track monitoring using acceleration measurements from sensors installed on a passenger train [61], to pay attention to the impact of the transition process on the system reliability of the traction drive system [62], for evaluating the influence of the most relevant geometric, mechanical and aerodynamic vehicle properties in the risk of derailment caused by crosswinds [63], for evaluation of the justifiability of modernization of rail vehicles as a method for improving the efficiency regarding a reduction of operation and maintenance costs [64], to develop distributed simulation and testing environment capable of linking information among virtual and physical components [65], evaluates the energy intensity of passenger car [66], for predicting the technical condition of a vehicle [67], for application of the monitoring system to a rail freight vehicle [68], to analyses the impact of the vehicle-track dynamic interactions [69], for modeling of the lifecycle of the railway track elements [70], for selection of noise-protective measures in accordance with the sanitary noise regulations for a specific receptive facility [71], to estimate octave spectra of sound levels in relation to distance from the source [72], to reduce the carbon dioxide emissions of the train [73], to achieve high multitonal sound absorption at specific design frequencies and their multiple harmonics [74], for identifying vertical wheel-rail force waveform from monitoring data of rail dynamic responses [75], for monitoring the operational condition of a running vehicle [76], to examine the effects of different vehicles on track deterioration and consequent maintenance costs [77], to determine of possibility of the track geometry from the motion of a wheel set [78], identifying the type of sensors that can be adopted in a wayside monitoring system for wheel flat detection, as well as their optimal position [79], for the perspective of vehicle automation equipment and simulators of different application domains [80], for analysis the ways of descriptions of the dynamic parameters impulse impact of the rail vehicle [81], to assess the resilience of road network infrastructures [82], to improve rail system development and operation by employing artificial intelligence [83], about alternative ways of transporting goods from remote industrial zones [84], for rail track degradation prediction [85], to identify and quantify the direct sustainable effects resulting from the improved road infrastructure in the local urban-port transport system [86], for simultaneous state and parameter estimation of a land vehicle [87], to locate trains on the railway network [88], the possibilities of applying the big data concept in the railway transportation industry [89], to economically justify railway track infrastructure conditions [90], for risk assessment for construction of urban rail transit projects [91], to study the process of transferring forces in the interaction of the rolling stock and the railway track [92], for operational investigation of rolling stock derailment [93], for improving the reliability and availability of railway systems and of substantially reducing maintenance costs [94], for the health assessment of wheelset bearings of high-speed trains [95], problems management of efficiency of use of production and technological potential of rolling stock of rail transport [96], to model wheel-rail normal contact in vehicle dynamics simulation [97], for ensuring perspectives of sustainable transport infrastructure [98], for criticality analysis the different failure modes of the running gear and their effect on rail infrastructure [99], for life cycle assessment of a railway tracks substructures [100], for risk management plan for technical facility operation [101], for data-driven predictive maintenance scheduling policies for railways [102], for discussing the problem of the maintenance conditions of the railway track [103], for predictive maintenance of railway track, as follows: implications in geotechnical engineering [104], for dynamic analysis by demonstrating the effect that different ways of dealing with faulty signals have on delays and propagation of delays [105], for reliability and availability assessment of railway locomotive bogies under correlated failures [106], for modeling railway ballasted track settlement [107], for evaluation of the cost of intelligent upgrades of transportation infrastructure for intelligent connected vehicles [108], for smart railway maintenance systems [109], for railway track maintenance planning [110], for analysis of driver assistance systems in rail vehicles [111], for work on advances in high-speed rail vehicle tilt control design enabled [112],to design a means of transport using a suspended railway track [113], to improve the driving stationarity of suspension-type small rail vehicles and enhance ride comfort [114], for predicting rail damage in railway switches and crossings [115], to overcome the problems existing in traditional track inspection and ensure efficient and safe detection [116], for damage detection of railway tracks by a two-axle test vehicle [117], for handling performance analysis of vehicle system [118].
Consequently, it became necessary to describe the fundamental provisions of physics by mathematical methods that allow studying the course of dynamic processes in order to form the conditions for the functionally safe operation of objects. The problem was that there was no tool for analytical modeling of physical processes inside the objects of simulation in time. Understanding that power effects in objects are transmitted by waves can be seen in many works, for instance, to identify the acoustic signature of railway vehicles [119], for simulating the vehicle-soil-track interaction phenomenon [120], to investigate the properties of elastic waves propagating in the periodic ballasted track [121], for improving the time-frequency representation for signals dedicated to structural diagnostics [122], for the application of embedded track in metro systems [123], to study the effects of wheel-rail impacts on the fatigue damage of the fastening clips at the rail joints of a high-speed railway [124], for evaluating the reliability of the dynamic performance of the vehicle [125], for the prediction of the influences of rail irregularities on the wheel/rail dynamic force [126], for studying the cause of train-induced ground vibration [127], for investigating issue of predictive maintenance by detecting possible structural failure or defects the third rail [128], to assess derailment risks [129], for simulation studies of the oscillatory behavior of road and rail vehicles [130], for advanced remote condition monitoring of railway infrastructure and rolling stock [131], for random-vibration-based on-board railway vehicle and track monitoring [132]. However, the provisions of the elastic wave theory have not been used to analytically describe the propagation of dynamic processes in space and time. Therefore, it was difficult to study the relationship and influence of these processes on the functionally safe state of the object in time. To overcome the problem of the absence of a time component in the analytical description of dynamic processes, it appeared necessary to use the elastic wave theory. Thus, a mathematical apparatus for simulating physical processes over time to determine the parameters of deformability based on mathematical modeling of the operation of a railway track under the influence of rolling stock [70,133,134] was developed.
The originality of this article is the justification and demonstration of the following positions:
- -
- Using the elastic wave theory makes it possible to overcome five main drawbacks of the elasticity theory;
- -
- Opportunity to describe any process of interaction as a chain of processes, incidence-reflection-refraction of force impulses;
- -
- The wording of the basic law of mechanics and the description of the characteristics of the impulse of action have been expanded.
All this is the base for making it possible to develop an innovative and effective tool for engineers and scientists to assess the impact of technosphere objects on human habitats.
This study is divided into four parts. The first part deals with the background, novelty, and aim of the study. The second part is concerned with the methodologies used for this study. The third part presents the findings of this study. The final part draws upon the entire study, tying up the various methodologies and results of this study to present the discussion and implications of the findings of this research.
2. Materials and Methods
The elastic wave theory makes it possible to describe the processes of transfer of a force impulse in all mediums that an object’s material can consist of (gaseous, liquid, and solid), and also has the laws of propagation over time in these mediums. Elastic waves have properties based on an object’s physical, mechanical, and geometric characteristics, describing the transformation of physical quantities inside and during the transition from one to another when modeling dynamic processes.
Based on the elasticity theory and propagation of elastic waves, a method has been developed for determining the processes that lead to a change over time in local values of deformations and displacements inside elements [70,81,92,133,134]. The main advantage of the proposed modeling method is the use of the ability of elastic waves to propagate the energy of force actions (impulses) in space and time.
Since the theory of elastic waves is universal, further for visualization, the following are presented:
- -
- -
- Determination of wave propagation velocity, Formula (1);
- -
- Dependences for determining the magnitude of wave amplitudes, Formulas (2)–(7);
- -
- Record of Newton’s second law for the relationship between external and internal forces, Formula (8).where —the Young modulus or the modulus of elasticity;—Poisson’s ratio;—are the transverse and longitudinal wave propagation speeds in a particular medium.
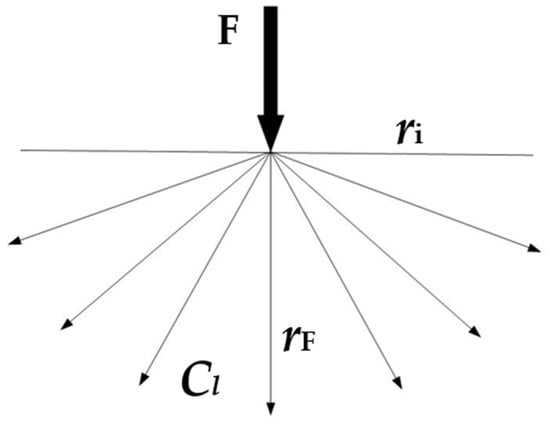
Figure 1.
Directions of the longitudinal waves.
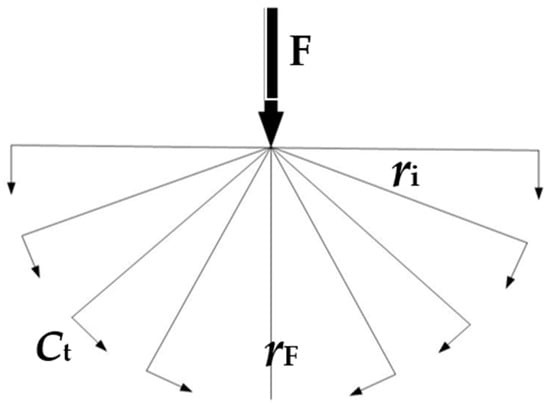
Figure 2.
Directions of the transverse waves.
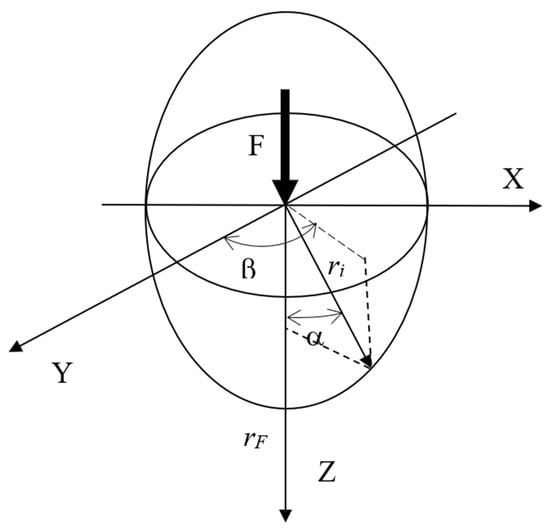
Figure 3.
The force field ellipsoid is generated by the pulse.
All the energy of the force action moves material particles by means of longitudinal waves in the direction of wave propagation . In the direction perpendicular to the direction of wave propagation , particles move only due to transverse waves. Particles are set in motion by two types of waves, in accordance with the wave propagation speed and the impact time and amplitude of the impact on each material particle in all other directions of wave propagation . The processes of reflection and refraction of waves depend on the geometry of objects and their connections in the structure, on the density of the material, and the speed of wave propagation.
where —are the amplitudes of waves of incidence, refraction, and reflection, respectively;
—is the impedance (resistance of medium);
—is the speed of the wave.
where —the influence of external load;
—forces of elasticity and friction of the medium;
—is the reaction of the external medium.
The ratios of amplitudes of the wave process at the incidence of longitudinal wave are defined as follows:
where —longitudinal wave;
—transverse wave;
—refracted longitudinal wave with refraction angle ;
—transverse refracted wave with refraction angle ;
ρa—density upper medium;
ρb—density lower medium
The ratios of amplitudes of the wave process at the incidence of transverse waves of vertical polarization are determined as follows:
The ratios of amplitudes of the wave process at the incidence of transverse waves of horizontal polarization are determined as follows:
where —is the impulse external force acting on the object;
—is the momentum of the force field acting inside the object;
—is the mass of the object, absorbing the influence of an external impulse by means of a force field pulse, which is formed on the basis of a superposition of force waves;
—impulse;
—the density of the material through which the wave propagates;
—concentration, the number of molecules per unit volume;
—the mass of one particle;
—the material density of the object;
—the object’s volume, absorbing the influence of an external impulse by means of a force field pulse, which is formed on the basis of a superposition of force waves;
—the velocity of particles exposed to the force field that is dependent on the transverse and longitudinal wave propagation speeds in a particular medium.
The basis of modeling when using the elastic wave theory is the presence of wave processes caused by both external and internal oscillations. In this case, vibrations mean the movement of the particles of an object under the action of force waves of both incident, reflected, and refracted wave processes.
According to the elastic wave theory, all vibrations excited by the contact of surfaces that by this moment were not in contact or resumed their contact due to a break propagate as spherical waves. They characterize the main direction of propagation of the wave process from the place of new or renewed contact of the surfaces and are responsible for the contact and local strain concentrations.
All vibrations excited by the contact of the surfaces, which have touched and have contact connections at this moment, are propagated by quasi-spherical waves. They characterize the main direction of propagation of the wave process from the point of contact of the surfaces and are responsible for the inhomogeneity of the oscillation. However, one spherical incidence wave, carrying longitudinal and transverse modes, causes the following four quasi-spherical refracted waves: two longitudinal and two transverse. Each of them is inhomogeneous since it has a clear dependence on the change in characteristics, propagating along its “own” direction at a certain speed, and bears the consequences of the propagation of adjacent refracted waves, which have their own speeds and directions of propagation.
Since the superposition of waves over time occurs in the process of propagation, it characterizes the inhomogeneity of the entire oscillation. Consequently, at each point of the object structure at a certain time of action, either homogeneous spherical and (or) inhomogeneous quasi-spherical waves will be observed. Thus, oscillations propagated by waves in time cannot be predicted based on the approximation used by numerical calculation methods since each particle of an object will have an oscillation trajectory depending both on the law of change of the force impulse and on the geometry of the object. There are periods of time when the particles of the object directly perceive and transform force effects in accordance with the propagation time of the process of force waves in the object. Additionally, the time when the particles of the object are displaced due to deformations and displacements of other particles of the object located behind them in the direction of the force waves.
In other words, both elements of structure and particles of objects can work “actively” (transforming force effects) and “passively” (without the direct influence of force effects on them) [103,134]. The law of change of the force impulse characterizes the deformations and displacements associated with the action of the applied external force when performing “active” work. The geometry of the object characterizes the “passive” work. Thus, different particles of an object have different trajectories of oscillations in time and hence different local concentrations of force waves in time, which makes it possible to predict the places where fatigue processes and defects appear under certain operating conditions and characteristics of the structure and material of the object.
The use of the elastic wave theory allow us to proceed to the consideration of systems that were previously considered open systems since it becomes possible to use the law of conservation of momentum (p = const) both for individual objects and for their parts.
The method allows determining the distribution of influence energy in space and time depending on physical, mechanical, and geometric parameters of the modeling object (time and rate of movement of material particles in the direction of propagation of waves). In this way, the deformation processes occurring in the simulation object under the action of dynamic pulses over time are determined, resulting in the assessment of the object’s reliability, availability, maintainability, and safety under various operating conditions.
Below are examples of applications of the proposed method in the simulation of dynamic processes in order to study the influence of the dynamics of processes on the efficiency of the use of the object.
3. Results
3.1. Expansion of the Capabilities of the Mathematical Apparatus to Describe the Dynamics of the Process in Determining the Issues of Facility Efficiency
Using the elastic wave theory in the proposed method makes it possible to overcome the following five main drawbacks of the elasticity theory:
- The main limitation of the elasticity theory is the absence of a time component. There are no dependencies in the timescale that connect the duration of the action of force, deformation, or stress. The laws of elastic wave propagation over time in different mediums and during the transition from one medium to another completely negate this limitation.
- In the theory of stresses, internal forces are studied that arise in solid deformable materials or objects as a result of physical influences on them. With an external physical impact, the distances between the internal points of the material (material particles) change, resulting in internal forces that represent the macroscopic interaction between atoms or molecules. The method of sections and the connection axiom are used to describe internal forces in stress theory. Internal forces can change during the transition from one particle to another; therefore, the stress state in the object is generally inhomogeneous (as well as the deformed state). However, deformations can be measured, but stresses cannot because deformations are physically measured to measure stresses. Consequently, the stress theory is axiomatic, and stress is an artificial measure of the internal forces arising in the object. By their physical nature, stresses are pressures caused by a force field inside an object. The calculated amplitudes of the oscillations of the particles under the influence of force waves allow for determining the deformations at the points of the sensor established. Thus, it is possible to directly correlate the quantities measured in the experiment and actually occurring in the objects of measurement. Understanding the dynamic processes within an object allows the selection of equipment for recording specific types of pulses and interpreting and analyzing the recorded signals in terms of noise.
- In the theory of deformations, the kinematics of a continuous medium is considered regardless of physical influences. Stress theory studies the internal forces generated in the object or in the material as a result of physical pressure. Neither the deformation theory nor the stress theory took into account the specific properties of the material to describe the process of propagation of force influences within objects. Even with numerical modeling methods such as finite element methods, the partitioning of the inner mesh is independent of the material properties. The laws of elastic wave propagation over time in various mediums allow considering changes occurring inside objects under the influence of force fields over time. This makes it possible to modify the object’s geometric and elastic characteristics to specific operating conditions, taking into account the deformability processes within the objects.
- The behavior of specific materials and structures of objects, as well as the relationships between them, under different influences, are given to the studied models by defining ratios. In order to construct defining ratios, experiments are carried out on the physical influence on samples of objects. From the processing of these experiments, a specific type of dependency and the values of the constants of the constituent dependencies are set. Such experiments are called set-up experiments, and dependency constants are called material constants. Both experiments and constants are applicable only for the conditions under consideration and present actual physical processes in separate correlated aspects, the physical nature of which is not taken into account. The laws of elastic wave propagation are universal because they eliminate the following limitations:
- Applications of different mathematical apparatus for problems of mechanics in Newtonian, relativistic, and ultra-relativistic areas. It is believed that momentum increases only by increasing velocity in Newtonian mechanics, as the change in mass can be ignored. In the ultra-relativistic area, the object’s velocity is practically unchanged, and the momentum increases only due to the increase in mass. It is considered in the relativistic area that the increase in momentum is due to an increase in both the velocity and mass. In this case, the speed increases more slowly than in Newtonian mechanics, precisely because of the increase in the mass of the object being accelerated. Elastic wave theory allows the consideration of momentum propagation problems in any mechanics area (see Formula (8)), as the time accounting for the propagation of force waves in an object, automatically considers the change in mass over time and changes in the velocity of the deformation process within the object in time.
- The need to divide the energy spent on the dynamics of the process into types, as well as the concepts that characterize the dynamics of the process into types. For example, the process of moving an object in mechanics is characterized by the following two types of energy: kinetic and potential. The first describes the movement process in terms of velocity change and the second in terms of coordinate changes. This artificial separation of the energy used in the movement process is related to the history of technical calculations, which led to the existence of several systems of measures at a certain stage, as follows: physical and technical. In the physical system of measures, the basic unit of measurement is the mass, and force is a derivative unit, the value of which is obtained by multiplying the basic unit of mass by the dimension of the acceleration. In a technical system of measures, mass is a derivative of the unit obtained by dividing the basic unit of force by the acceleration dimension. However, since any amount of force involved in the experiment is easier to attach or measure than to determine the mass involved in the experiment in dynamic processes, the technical calculations and logic of their development are invisibly based on the technical system of measurement, where equivalent/effective mass values are used.
For the same reason, there is a division of the concepts of the collision into «elastic» and «inelastic». It is believed that any collision is completely inelastic if the objects after the collision move at the same speed, forming one new object. Only the sum of the momentum of the colliding objects is retained, but the sum of their kinetic energy is not conserved. An elastic is called a collision in which the sum of the momentum and the sum of the kinetic energy of colliding objects are stored. By definition, kinetic energy is the difference between total and internal energy. The theory of elasticity does not allow calculating what part of the energy of colliding objects is absorbed by them during an interaction; that is, how much the internal energy of the objects of interaction has changed. The internal energy of the object is equal to the rest energy of the particles of which the object is composed, plus the total kinetic energy of these particles and the potential energy of the fields that interact with these particles. As already mentioned, there are the following two types of spherical volumetric waves: longitudinal and transverse. Longitudinal waves have the following many names: irrotational, expansion waves, P-waves, compression-discharge waves, and dilatation waves. Transverse waves are also called equivolume waves, distortion waves, shear waves, and S-waves. However, regardless of the name, longitudinal waves cause material particles to move along the propagation direction of the force field by changing the distances between the particles, compacting, or decompressing the propagation medium, freeing up space for particle displacement under the influence of transverse waves in the direction perpendicular to the propagation of the force field. Thus, longitudinal waves characterize the total kinetic energy of particles, and transverse waves represent the potential energy of the fields that carry out the interaction of these particles. In this case, depending on the nature of the interaction between particles (atoms, molecules, Brownian particles, particles of a fraction of granular medium—any particles that are considered in the model), the potential energy of the forces of attraction of particles is accompanied by friction forces that arise when particles come into contact and prevent their mutual movement. Since the amount of energy that is transferred by a wave is proportional to the square of the amplitude. This allows us to characterize what part of the energy is spent on deformability inside objects (reflection process) and what part of the energy is transferred to another object as an external impulse (refraction process). Thus, the theory of elastic waves does not require a separate division and describes the process of interaction as a chain of processes of incidence-reflection-refraction of force impulses.
- 5.
- The theory of elasticity perfectly describes the material of objects using the concept of a material continuum but completely excludes the possibility of studying the behavior of internal forces. Knowledge of internal force change mechanisms is used, for example, to create high- or low-damping materials for mechanical applications in various fields of technology. In addition, this knowledge will help select the charge for a specific type of wall in explosive wall breaking, which is an important operation used by firefighters or special forces as a method of gaining immediate access to a structure in an emergency as a direct replacement for conventional breaking methods. Even when studying the internal state in the elasticity of anisotropic materials, the macroscopic behavior of materials is considered, that is, the atomic or molecular structure is not considered. In the proposed method, local volumes and material density, which vary over time due to force waves, must be taken into account when calculating the amplitude. Therefore, it is necessary to take into account the influence of a change in the distance between particles on the interaction forces of particles in order to determine the probability of the occurrence of irreversible deformation or the impossibility of deformation, as well as the probability of a defect and a change in the structure of the material. Thus, the application of the first law of thermodynamics and the extended use of material properties in the calculation makes it possible to develop modeling in this direction, linking the macro- and microscopic behavior of materials.
3.2. Influence of Characteristics of an Impulse on the Dynamics of the Process in the Study of Facility Efficiency
The use of the elastic wave theory in the proposed method makes it possible to describe and evaluate the influence of the pulse characteristics on the dynamics of the process due to the following facts:
- In the proposed method, impulses are considered as a measure of any action of different physical quantities on an object over time at which there is an exchange of energy over time. The action of the impulse on the object has clear time characteristics of beginning and end of action, that is, duration of action. This makes it possible to determine the additional characteristics of the pulse as follows: at the time of transmission of the pulse. Therefore, the influence of any physical quantity, when cyclically acting in a dynamic process, is characterized by the following two types of frequencies:
- 3.
- The frequency (or frequencies) of pulse transmission acting on a specific contact site. It is characterized by its action duration;
- 4.
- The frequency of pulse repetition (repetition rate) in a certain cross-section. It is characterized by the time through which the repetition of the action occurs.
This provides a clear separation between single and repetitive impulses, leading to increased simulation capabilities. For example, when considering the impact on the rail of a rolling stock wheel (force pulse) moving at a constant speed, the same rail cross-section is subjected to different force pulses from different wheels because each wheel has different impact characteristics at the time of passage, namely, the following:- 5.
- The amplitude of the force impulse is determined as it is an oscillation superposition of the wagon, bogie, damping system, and railway track structure state;
- 6.
- The direction of the pulse depends on the position of the bogie relative to the railway track axis;
- 7.
- The number, area, and location of rail/wheel contacts depend on the position of the wheelset relative to the track axis.
In addition, the uneven distribution of bogies on the rolling stock also introduces heterogeneity into the cycle impact of the wheels on the same rail cross-section. Thus, to consider the impact of the wheels on the rail cross-section over time, it was possible to describe the smooth passing of the wheel over the cross-section by moving the rail/wheel contacts along the rail over time along a particular trajectory. As an example, Figure 4 demonstrates the oscillation amplitude of the track structure under the wheel passage with speeds of 70, 90, and 110 km/h above the rail cross-section with the central position of the wheelset.
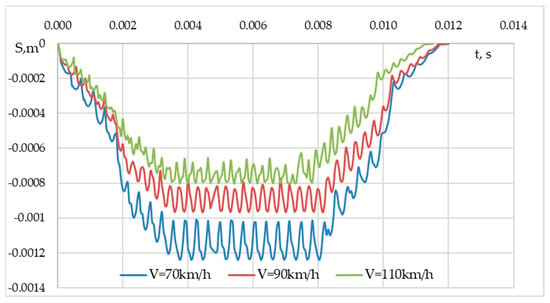
Figure 4.
Oscillation amplitudes of the track structure cross-section under the wheel passage over time.
At each rail/wheel contact area, the force will change according to the following law:
where —is the maximum value that the force gains in the intersection;
—frequency of transferring load pulse (frequency of excitation of intersections of the rails) and with the aggregate action area. A range of parameters of this oscillation along the length of the track depends on the motion speed and position of the wheelset in a track;
—is the time;
—varies from 0 to , and during this time, depending on the speed, the wheel goes through the entire cycle of impact on the track: the pressure appears, gradually increases to the maximum, and goes out.
Figure 5 shows the oscillation of the track structure cross-section over time when a single force pulse is applied to the rail/wheel contact area, depending on the contact time of the wheel with the rail when a passage of the wheel at speeds of 70, 90, and 110 km/h.
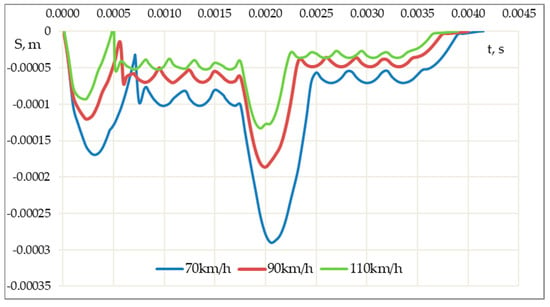
Figure 5.
The dependence of oscillation amplitudes of the track structure cross-section over time under the single force impulse affects a single contact area.
Figure 4 and Figure 5 clearly demonstrate that, under the influence of a force pulse having a sine wave law, the amplitudes of oscillations of the cross-section of the track have a complex form. The amplitudes of oscillations under a single force impulse are determined by the superposition of the oscillations of the elements over time (Figure 5). The amplitudes of oscillations during the passage of the wheel are determined by the superposition of oscillations of elements of the track structure from various contact areas over time (Figure 4).
- 2.
- Since there is an energy exchange that occurs during the action of an impulse, one of its characteristics is the law of change of the acting physical quantity over time. This value characterizes the intensity of the effect of the force impulse per unit time during the force action. For example, according to Hooke’s law, the force acting on an object causes directly proportional deformations or displacements. When a force acts on an object, the latter will do work equal to the product of the force and the displacement. The action of a constant force per unit time on an object, regardless of the time of its impact, is characterized by the same value of the amount of motion per unit of time, which serves as a potential for performing the same amount of work on the object per unit of time. This means that it transfers the same amount of energy per unit time during the action of the force. So, impulses of constant forces transfer a constant amount of energy per unit of time and force the object to have a permanent deformation under their influence, that is, behave according to the laws of statics from the moment equilibrium is established. Or, if the object does not interact with other objects, it will move in a straight line and uniformly with the speed established in this medium. If the force has a variable value over time, then the impulses of variable forces cause the exchange of a variable amount of energy per unit of time during the duration of the force impulse. When describing impacts, the amplitude of the force impulse characterizes the impact force in mechanical systems or loudness in music. Additionally, the intensity of the impact allows you to describe such characteristics of the impact as “legato”, “staccato” and sound density in music, or “soft”, “hard/sharp” impact, and flow density per unit time in mechanical systems.
Therefore, the possibility of using time when describing the impact of the impulse on any object, enables expanding the use of the formulation «the time derivative of the momentum is the force» to the «law of change of the force pulse over acting time, characterizing the intensity of influence per unit time (moment), determines the total amount of motion over acting time (the total monument), characterizing the amount of energy on performance of work per unit time (moment)». This formulation removes the limitations that existed in describing momentum in Newtonian and relativistic areas of mechanics. When considering the movement of an object in Newtonian mechanics, it follows from the relation that with the long-term action of a constant force on an object, the speed of its movement can increase indefinitely. However, since the dependence —describes the momentum, mass, and speed at time t, a more correct notation should be and is the total momentum of the system transferred to the object by the force in time t, thereby . Thus, the time-unlimited impact of a constant force on an object at each moment of time is characterized by equal quantities of motion (monument) equal to , while the object is given equal amounts of energy in each moment of time, for setting in motion the same amount of masses , which either move with the same (steady-state/fixed) speed , or lead to the same (steady-state/fixed) deformability at each moment of the action of this force impulse.
- 3.
- Unlike modern equipment, previously used instruments used in the study of oscillations were very inertial. Such instruments respond only to a change in the average energy value over a period of time significantly exceeding the oscillation period. In this case, knowledge of the spectrum was sufficient, as it could be used to determine the energy of each harmonic and thus determine the average energy of the total oscillation. This is why spectral decomposition plays an extremely important role in the study of oscillations. However, knowledge of the spectrum of some non-sinusoidal oscillations makes it impossible to determine the shape of this oscillation and build its graph. In addition, the energies of harmonics depend only on the amplitude and frequency, and do not depend on the phase of the oscillations. When recording vibrations, it is impossible to divide them into the incident and reflected processes, so it is necessary to understand the energy of which the oscillating process is recorded. An introduction to the calculation of the time characteristic allows evaluating what oscillatory processes were recorded at the time of recording.
- 4.
- The introduction of the time component allows describing and comparing changes in the values of different vectors in time and space. Additionally, the use of the properties of elastic longitudinal and transverse waves makes it possible to consider changes in the values of vectors without observing mechanical equilibrium. This enables considering the change in impulses depending on specific conditions, which expands the possibilities of applying an impulse not only to a specific object but also outside the object. So, for example, suppose that the initial impulse of force was a uniformly distributed pressure moving through the air by the propagation of longitudinal waves from a source located at a distance . Figure 6 shows an example of changing the parameters of the impact of the primary force impulse on a rectangular object located perpendicular to the incident flow of the force impulse. Upon reaching the object, the amplitude of the incident waves will be equal to . The values of the amplitudes of reflection and refraction will be calculated using Formulas (2) and (3). It is supposed that the object is a solid shell with air inside. Since the force impulse falls perpendicular to the incident surface, the reflection and refraction waves will have equal amplitudes over the entire loaded surface of the object. Thus, the law of impact of a force impulse applied to an object remained completely identical to the original one in form but with a smaller impact.
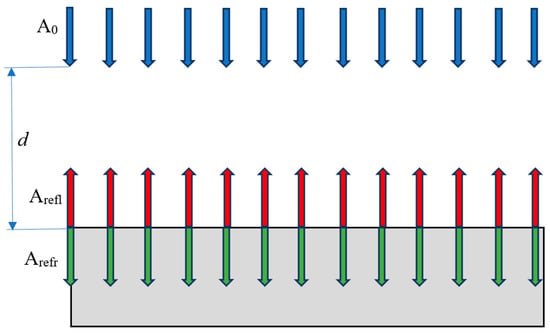 Figure 6. Changes in the parameters of the impact of the primary impulse of force when falling on a rectangular object.
Figure 6. Changes in the parameters of the impact of the primary impulse of force when falling on a rectangular object.
The fall of the primary impulse of a rectangular force on a triangular object is shown in Figure 7. As the waves of the incidence move at the same speed, they will reach the lateral faces of the object at different times, and the incident amplitudes will have values in the interval . The amplitudes of the reflection and refraction waves for the vertex and lateral faces, respectively, will be calculated by Formulas (2) and (3), and by Formula (5). The amplitudes of the reflection and refraction waves along the lateral faces of the triangle will have different values. Thus, the law of action of a rectangular force pulse applied to an object of triangular shape differs from the primary force pulse both in form and in impact values, but the law of changing the force impulse in time remains the same as that of the original one.
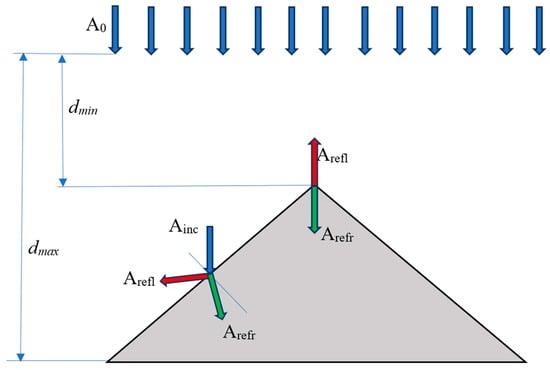
Figure 7.
Changes in the parameters of the impact of the primary impulse of force when falling on a triangular object.
Therefore, when considering the application of a constant load to a triangular object, it is necessary to take into account both the difference in the application of the load over time and the uneven impact of the load. Neglect of these characteristics is possible when the source is located at a sufficiently large distance from the object (when the value of the difference between the incidence amplitudes can be neglected), as well as when the speeds of movement before and inside the object do not have a significant difference (when refractive and reflective processes within an object do not affect its lateral faces). Consideration of the above characteristics can be used both in the selection of streamlined forms, for example in aviation, to reduce the pressure of air masses on the structure, and in the construction of structures requiring protection against a blast wave, noise, or water flow, because the proposed method allows analysis of phenomena in boundary layers, under different conditions of influence of momentum and shapes of objects, in time.
- 5.
- There are the following three types of deformability:
- Deformability of manerial—the ability of a material to respond to impulses from physical factors;
- Deformability of elements—the ability of elements, as products from a certain material with a certain geometry, to react to mechanical impulses;
- Deformability of the structure—total deformability of its elements, in which the elements of the structure can not only change shape, dimensions, and volume but also move due to deformability of other elements that make up the structure.
Typically, there is no stand-alone object that is experiencing a dynamic process. Consequently, all three types of deformability should be considered in the simulation of facilities in order to study the effectiveness of their use under specific operating conditions. As already mentioned, the presence of waves is determined by the characteristics of the material. It is known that longitudinal waves propagate in liquid and gaseous mediums, and both longitudinal and transverse waves propagate in solid mediums, but only longitudinal waves can propagate, as, for example, in wooden products. The constant speed of waves in materials in any direction of propagation and the universalism of wave propagation, depending on the geometry of the object and its physical and mechanical characteristics, make it possible to calculate local changes in density and volume in any location of the object. To consider the energy transfer between the elements, consider the contact pair of the rail-pad with the characteristics shown in Table 1.

Table 1.
Physical-mechanical characteristics the contact pair of the rail-pad.
The angles characterizing the process of transmission of power waves for the contact pair rail-pad are given in Table 2.

Table 2.
Characteristics of the angles of the wave process in the contact pair of the rail-pad for the first option.
The results presented in Table 2 demonstrate the collection ability of the pad. According to the results, when the force spectrum falls on the gasket surface at angles from 100 to 800, the gasket accumulates this spectrum, narrowing its flux to 0.68–6.58 for longitudinal waves and 0.340–3.510 for transverse waves.
When using the data for the second option, the impact of the external force spectrum on the gasket will increase by an average of 4.2 times for longitudinal waves and 1.37 times for transverse waves.
This result demonstrates the possibility of taking into account the influence of changes in both the geometry of the object and the characteristics of its material on the process of deformability under the influence of various forces.
The results in Table 3 show how many times the amplitudes of reflected and refracted waves change relative to the amplitudes of the incident waves (see Formulas (5)–(7)). As you know, the wave energy is proportional to the square of the amplitude. This aspect reflects the ability to control the energy spectra of reflection and energy absorption of an object depending on the geometry of the object and the characteristics of its material.

Table 3.
Coefficients of reflection and refraction of the wave process in a contact pair of rails with pads.
In addition, the collision of the processes of incidence and reflection leads to a local concentration of particles inside the objects, as well as to the release of heat in proportion to the amount of deformation not realized in each direction. The proposed method does not require consideration of the equality of thermodynamic parameters and the thermodynamic probability of the state of the system, since the time component and the regularity of the incidence-reflection chain make it possible to consider the course of irreversible processes over time. All of this enables the use of the first law of thermodynamics for modeling all types of deformability processes when studying the effectiveness of research objects by changing objects’ geometric and physical-mechanical characteristics for certain operating conditions.
4. Discussion, Conclusions and Future Recommendation
Mankind is surrounded by a huge number of objects, the work of which is associated with the flow of dynamic processes. The study of these processes allows for expanding knowledge about the physical changes occurring in them. Understanding the physics of dynamic processes that occur in objects while performing their intended functions allows developers to improve objects in such a way as to minimize their life cycle cost and maximize their ability to perform their intended functions. Thus, the conflicting requirements of a manufacturer who wants to reduce the cost of creating a product while providing the buyer with a product that reliably and safely performs its functions are satisfied.
Previously, the main conditions for ensuring the operability of facilities were the conditions of loss of bearing capacity or unsuitability for operation, while the criteria were strength, stability, and endurance. At the present stage, all facilities fulfill these conditions. Therefore, it became necessary to study the conditions of unsuitability for the normal operation of the facility, that is, the conditions for its technical, economic, and safe use.
The change in the approach in which facilities are assessed has led to new requirements, the results of which, for example, for rail transport, have been reflected in such instruments as the following: «Specification and demonstration of reliability, availability, maintainability and safety (RAMS)» and «Dependability management».
Changing the requirements provides for the formation of a system for assessing the state of facilities during their operation. To do this, it is necessary to study the effects of changes in the characteristics of materials and geometric deviations of objects that occur during operation on the ability to perform intended functions. In most cases, releasing a new object and verifying that it works in practice is very costly. Consequently, developers need to use mathematical models that allow simulating the dynamic processes that will occur with the object during the actual operation. Modeling of dynamic processes allows you to design, evaluate, and predict the behavior of objects during their life cycle, that is, from the beginning of design to disposal. Thus, one of the methods for modeling dynamic processes based on the theory of elastic waves is proposed in the paper.
The proposed calculation method is aimed at solving such issues as the following:
- The description of physical processes in the most approximate way to the course of natural phenomena. For this purpose, the time component is taken into account when describing the transmission of impulses by elastic waves. This description of the dynamics of the process regulates the pattern of natural phenomena, the sequence of which determines the cause-and-effect relationship, giving an answer to the question of what consequences will arise from the influence of physical impulses in the future. Without knowledge of the mechanism of cause-and-effect relationships, it is impossible to determine risk in a universal way. A person, in many cases, assesses the risks of various actions subconsciously. If we look at a person’s ordinary life, we will see that he automatically uses the importance of taking into account the duration of exposure in his life. For example, someone decided to make a new dish. In preparation for the realization of his wish, he is sure to learn the duration of necessary operations when cooking, for instance, meat, as follows: the duration of marinating in a particular sauce, the duration of baking or extinguishing a dish of a particular type of meat, set weight and under certain temperature and/or power conditions. Or if someone decides to dye fabric or remove a stain on clothes at home, he will certainly be aware of exactly what (reagent) and what (type of fabric) will be affected and how long its effect is needed. When someone chooses shoes for a hike, he necessarily decides for himself how much he is willing to pay for the comfortable and guaranteed performance of these shoes for the duration of the hike (a certain period of time) under the specific operating conditions of the shoes. A person, in many cases, assesses the risks of various actions regardless of paying attention.
However, if we consider these moments from the point of view of the theory of elasticity used to model dynamic processes, we will find that in this theory, the time of action of forces, deformations, or stresses does not affect the result. That is, it does not matter how long the impact lasts; it is important that it be fully perceived by the object. In ordinary life, this means that whether they crush your foot for 5 min or 5 days is not important; it is important that your foot withstands it. There is no reason to think that informing a person that the impact on his foot is perceived by his shoes and what he is standing on will alleviate the fate of the person. Additionally, the question remains unanswered as to what consequences will arise as a result of this mode of exposure in the future, as follows: will the foot be able to function? Thus, the proposed method of using the elastic wave theory for impulse transmission provides an opportunity to expand approaches to predicting and assessing the occurrence of risk in various objects under various operating conditions. Since any effect can be represented as a vector of changes in the amount of energy in time at any point of the simulation object, depending on the physical, mechanical, and geometric parameters of the simulation object, the proposed method allows combining the influence of mechanical, temperature, electromagnetic, and hydrodynamic influences into a single calculation.
- 2.
- Ensuring the functional security of the technosphere objects of the human habitat. Throughout its existence, mankind has been constantly creating and modifying artificial technological and technical objects to meet its socio-economic needs both in the engineering field (factories, transport infrastructure, mechanisms, etc.) and in everyday life (vehicles, household appliances, medical equipment, etc.). The operation of the technosphere objects in the human habitat affects both the ecological envelope of the Earth and the health of the person himself.The wave process can have a variety of physical natures as follows: mechanical, chemical, electromagnetic, gravitational, spin, probability density, etc. Therefore, a universal tool is needed to study the influence of technosphere objects on both people’s lives and the environment. The proposed method uses universal properties and laws of elastic wave propagation for different materials and object geometries. This allows analytical simulation of the behavior of the object under the influence of various impulses. Development of this direction in the future will allow answering such questions as the following:
- What actual changes in the characteristics of the object itself can occur during the period of operation;
- What maintenance is required by the facility under any operating conditions;
- Whether the object is able to safely perform the intended functions for the total period of operation;
- Whether the object is able to give the required level of economic efficiency of use, that is, whether the object is competitive in the market.
Thus, the proposed method uses a new approach to describe dynamic processes by pulses propagating as elastic waves over time. It provides engineers and scientists with an innovative and effective tool to modify technosphere objects and assess the impact of technosphere transport objects on human habitats.
Author Contributions
Conceptualization, I.B., A.S., I.O.O., T.C. and L.N.; methodology, I.B., A.S., I.O.O., T.C. and L.N.; software, I.B., A.S., I.O.O., T.C. and L.N.; validation, I.B., A.S., I.O.O., T.C. and L.N.; formal analysis, I.B., A.S., I.O.O., T.C. and L.N.; resources, I.B., A.S., I.O.O., T.C. and L.N.; data curation, I.B., A.S., I.O.O., T.C. and L.N.; writing—original draft preparation, I.B., A.S., I.O.O., T.C. and L.N.; writing—review and editing, I.B., A.S., I.O.O., T.C. and L.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Erhova, N.; Bondarenko, I.; Shibko, O.; Velmagina, N. Development of the procedure for verifying the feasibility of designing an active suspension system for transport carriages. East.-Eur. J. Enterp. Technol. 2018, 3, 53–63. [Google Scholar] [CrossRef]
- Kovalchuk, V.; Luchko, J.; Bondarenko, I.; Markul, R.; Parneta, B. Research and analysis of the stressed-strained state of metal corrugated structures of railroad tracks. East.-Eur. J. Enterp. Technol. 2016, 6, 4–9. [Google Scholar] [CrossRef]
- Magalhães, K.M.M.; Brasil, R.M.L.R.F.; Wahrhaftig, A.M.; Siqueira, G.H.; Bondarenko, I.; Neduzha, L. Influence of Atmospheric Humidity on the Critical Buckling Load of Reinforced Concrete Columns. Int. J. Struct. Stab. Dyn. 2022, 22, 2250011. [Google Scholar] [CrossRef]
- Radulović, S.; Milković, D.; Raković, M.; Simić, G.; Kostić, A. Influence of the head wind on determining brake performance of Zacns tank wagon. Acta Polytech. Hung. 2022, 19, 81–98. [Google Scholar]
- Goolak, S.; Gubarevych, O.; Yermolenko, E.; Slobodyanyuk, M.; Gorobchenko, O. Mathematical modeling of an induction motor for vehicles. East. -Eur. J. Enterp. Technol. 2020, 2, 25–34. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Y.; Li, Z.; Shi, C.; Yu, Z. Three-dimensional vehicle-ballasted track-subgrade interaction: Model construction and numerical analysis. Appl. Math. Model. 2020, 86, 424–445. [Google Scholar] [CrossRef]
- Fan, D.; Sebès, M.; Qazi, A.; Bourgeois, S.; Chollet, H.; Pozzolini, C. A new dynamic vehicle/track interaction method with a finite element track model. In Proceedings of the Second International Conference on Rail Transportation (ICRT), Chengdu, China, 5–6 July 2021. [Google Scholar]
- Xu, L.; Zhai, W. Vehicle–track–tunnel dynamic interaction: A finite/infinite element modelling method. Railw. Eng. Sci. 2021, 29, 109–126. [Google Scholar] [CrossRef]
- Meacci, M.; Meli, E.; Pugi, L.; Rindi, A. Development and Validation of a Vertical Vehicle-Track Interaction Model. In Proceedings of the First International Conference on Rail Transportation, Chengdu, China, 10–12 July 2017. [Google Scholar] [CrossRef]
- Kepka, M.; Václavík, J.; Chvojan, J. Fatigue life of a bus structure in normal operation and in accelerated testing on special tracks. Procedia Struct. Integr. 2019, 17, 44–50. [Google Scholar] [CrossRef]
- Zeng, Z.; Xiao, Y.; Wang, W.; Huang, X.; Du, X.; Liu, L.; Victor, J.; Xie, Z.; Yuan, Y.; Wang, J. The Influence of Track Structure Parameters on the Dynamic Response Sensitivity of Heavy Haul Train-LVT System. Appl. Sci. 2021, 11, 11830. [Google Scholar] [CrossRef]
- Escalona, J.L.; Aceituno, J.F.; Urda, P.; Balling, O. Railway multibody simulation with the knife-edge-equivalent wheel–rail constraint equations. Multibody Syst. Dyn. 2020, 48, 373–402. [Google Scholar] [CrossRef]
- Spiroiu, M.A.; Camil, C. Wheel flat effect on wheel-rail dynamic interaction. In IOP Conference Series Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 444, p. 042002. [Google Scholar] [CrossRef]
- Guo, Y.; Shi, C.; Zhao, C.; Markine, V.; Jing, G. Numerical Analysis of Train-Track-Subgrade Dynamic Performance with Tire-Derived Aggregate in Ballast Layer. Constr. Build. Mater. 2022, 336, 127599. [Google Scholar] [CrossRef]
- Qi, Y.; Indraratna, B.; Ngo, T.; Ferreira, F.B. Advancements in Geo-Inclusions for Ballasted Track: Constitutive Modelling and Numerical Analysis. Sustainability 2021, 13, 9048. [Google Scholar] [CrossRef]
- Bruner, M.; Cortis, D.; Malavasi, G. Rail Strain under Different Loads and Conditions as a Source of Information for Operation. In Proceedings of the Third International Conference on Railway Technology: Research, Development and Maintenance, Cagliari, Italy, 5–8 April 2016. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Johnson, D.K.; Mishra, D.; Bruzek, R. Effect of Track Configuration and Loading Conditions on Vertical Wheel Load Measurements using the Differential Shear Approach. Transp. Res. Rec. 2019, 2673, 279–288. [Google Scholar] [CrossRef]
- Idczak, W.; Lewandrowski, T.; Pokropski, D.; Rudnicki, T.; Trzmiel, J. Dynamic Impact of a Rail Vehicle on a Rail Infrastructure with Particular Focus on the Phenomenon of Threshold Effect. Energies 2022, 15, 2119. [Google Scholar] [CrossRef]
- Mirković, N.; Brajović, L.; Popović, Z.; Todorović, G.; Lazarević, L.; Petrović, M. Determination of temperature stresses in CWR based on measured rail surface temperatures. Constr. Build. Mater. 2021, 284, 122713. [Google Scholar] [CrossRef]
- Weston, P.; Roberts, C.; Yeo, G.; Stewart, E. Perspectives on railway track geometry condition monitoring from in-service railway vehicles. Veh. Syst. Dyn. 2015, 53, 1063–1091. [Google Scholar] [CrossRef]
- Jiang, J.Z.; Matamoros, A.; Zolotas, A.; Goodall, R.M.; Smith, M.C. Passive suspensions for ride quality improvement of two-axle railway vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2013, 229, 315–329. [Google Scholar] [CrossRef]
- Jukowski, M.; Śledziewski, K.; Hypki, M. Assessment of the impact of vibrations on the track surfacefrom impact loads. In Proceedings of the MATEC Web of Conferences, Moscow, Russia, 4–7 August 2019; Volume 252, p. 01007. [Google Scholar] [CrossRef]
- Naeimi, M.; Zakeri, J.A.; Shadfar, M.; Esmaeili, M. 3D dynamic model of the railway wagon to obtain the wheel-rail forces under track irregularities. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2015, 229, 357–369. [Google Scholar] [CrossRef]
- Drozdziel, P.G.; Stastniak, P.; Smetanka, L. Computer aided simulation analysis for wear investigation of railway wheel running surface. Diagnostyka 2019, 20, 63–68. [Google Scholar] [CrossRef]
- Konowrocki, R.; Walczak, S. Influence of Flexibility Parameters of Wheels and Wheelset on the Railway Bogie Dynamics: Experimental and Theoretical Investigations. Mach. Dyn. Res. 2017, 41, 128–142. [Google Scholar]
- Sunbuloglu, E.; Bozdag, E. A design strategy on the talbot type articulation of a freight wagon. WIT Trans. Built Environ. 2018, 181, 145–156. [Google Scholar] [CrossRef]
- Xiao, Y.; Tutumluer, E. Performance Checks for Unbound Aggregate Base Permanent Deformation Prediction Models under Dynamic Stress States Induced by Moving Wheel Loading. Procedia Eng. 2016, 143, 979–990. [Google Scholar] [CrossRef]
- Sharma, R.C.; Sharmab, S.K.; Pallic, S. Rail Vehicle Modelling and Simulation using Lagrangian Method. Veh. Struct. Syst. 2018, 10, 188–194. [Google Scholar] [CrossRef]
- Kaiser, I.; Poll, G.; Vinolas, J. Modelling the impact of structural flexibility of wheelsets and rails on the wheel-rail contact and the wear. Wear 2020, 504–505, 203445. [Google Scholar] [CrossRef]
- Sharma, R.C.; Palli, S. Analysis of creep force and its sensitivity on stability and vertical-lateral ride for railway vehicle. Int. J. Veh. Noise Vib. 2016, 12, 60. [Google Scholar] [CrossRef]
- Dusza, M. Rail vehicle model motion analysis on curved track with vertical irregularity. WUT J. Transp. Eng. 2020, 130, 75–84. [Google Scholar] [CrossRef]
- Pehlivan, F.; Mizrak, C.; Esen, I. Modeling and Validation of 2-DOF Rail Vehicle Model Based on Electro–Mechanical Analogy Theory Using Theoretical and Experimental Methods. Eng. Technol. Appl. Sci. Res. 2018, 8, 3603–3608. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, Y.Q.; Spiryagin, M.; Cole, C. Railway track longitudinal force model. Veh. Syst. Dyn. 2019, 59, 155–170. [Google Scholar] [CrossRef]
- Sobolevska, M.; Horobets, D.; Syrota, S. 2020. Development of passive protection devices for a power head of a high-speed multiple unit train at its collisions. IOP Conf. Ser. Mater. Sci. Eng. 2020, 985, 012016. [Google Scholar] [CrossRef]
- Liu, X.; Thompson, D.; Squicciarini, G.; Rissmann, M.; Bouvet, P.; Xie, G.; Martínez-Casas, J.; Carballeira, J.; Arteaga, I.L.; Garralaga, M.A.; et al. Measurements and modelling of dynamic stiffness of a railway vehicle primary suspension element and its use in a structure-borne noise transmission model. Appl. Acoust. 2021, 182, 108232. [Google Scholar] [CrossRef]
- Xu, L.; Xin, L.; Yu, Z.; Zhu, Z. Construction of a dynamic model for the interaction between the versatile tracks and a vehicle. Eng. Struct. 2020, 206, 110067. [Google Scholar] [CrossRef]
- Sichani, M.S.; Enblom, R.; Berg, M. A fast wheel–rail contact model for application to damage analysis in vehicle dynamics simulation. Wear 2016, 366–367, 123–130. [Google Scholar] [CrossRef]
- Cruceanu, C.; Crǎciun, C. Aspects regarding braking process of passenger trains with different braking systems in composition. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 042012. [Google Scholar] [CrossRef]
- Stoilov, V.; Simić, G.; Purgić, S.; Milković, D.; Slavchev, S.; Radulović, S.; Maznichki, V. Comparative analysis of the results of theoretical and experimental studies of freight wagon Sdggmrss-twin. IOP Conf. Ser. Mater. Sci. Eng. 2019, 664, 012026. [Google Scholar] [CrossRef]
- Silva, R.; Ribeiro, D.; Bragança, C.; Costa, C.; Arêde, A.; Calçada, R. Model Updating of a Freight Wagon Based on Dynamic Tests under Different Loading Scenarios. Appl. Sci. 2021, 11, 10691. [Google Scholar] [CrossRef]
- Wei, X.; Liu, F.; Jia, L. Urban rail track condition monitoring based on in-service vehicle acceleration measurements. Measurement 2016, 80, 217–228. [Google Scholar] [CrossRef]
- Kang, C.; Wenner, M.; Marx, S. Experimental investigation on the rail residual stress distribution and its influence on the bending fatigue resistance of rails. Constr. Build. Mater. 2021, 284, 122856. [Google Scholar] [CrossRef]
- Bondarenko, I.; Keršys, R.; Neduzha, L. Analysis of problem related to experimental data processing in the study of the crew’s influence on the track. In Proceedings of the 26th International Conference Transport Means, Kaunas, Lithuania, 5–7 October 2022; pp. 1–6. [Google Scholar]
- Borucka, A.; Mazurkiewicz, D.; Łagowska, E. Mathematical modelling as an element of planning rail transport strategies. Transport 2021, 36, 354–363. [Google Scholar] [CrossRef]
- Aimé, L.S.; Lebon, F.; Saulot, A. Thermomechanical modelling of the tribological surface transformations in the railroad network (white etching layer). Mech. Mater. 2020, 151, 103636. [Google Scholar] [CrossRef]
- Jarašūnienė, A.; Sinkevičius, G.; Čižiūnienė, K.; Čereška, A. Adaptation of the Management Model of Internationalization Processes in the Development of Railway Transport Activities. Sustainability 2020, 12, 6248. [Google Scholar] [CrossRef]
- Milenkovic, M.; Svadlenka, L.; Melichar, V.; Bojovic, N.; Avramović, Z. SARIMA modelling approach for railway passenger flow forecasting. Transport 2018, 33, 1113–1120. [Google Scholar] [CrossRef]
- Stopka, O.; Zitrický, V.; Abramović, B.; Marinov, M.; Ricci, S. Innovative Technologies for Sustainable Passenger Transport. J. Adv. Transp. 2019, 2019, 4197246. [Google Scholar] [CrossRef]
- Severino, A.; Martseniuk, L.; Curto, S.; Neduzha, L. Routes Planning Models for Railway Transport Systems in Relation to Passengers’ Demand. Sustainability 2021, 13, 8686. [Google Scholar] [CrossRef]
- Rehak, D.; Patrman, D.; Foltin, P.; Dvořák, Z.; Skrickij, V. Negative impacts from disruption of road infrastructure element performance on dependent subsystems: Methodological framework. Transport 2021, 36, 510–524. [Google Scholar] [CrossRef]
- Pipitone, E.; Caltabellotta, S.; Occhipinti, L. A Life Cycle Environmental Impact Comparison between Traditional, Hybrid, and Electric Vehicles in the European Context. Sustainability 2021, 13, 10992. [Google Scholar] [CrossRef]
- Mikušová, N.; Fedorko, G.; Molnár, V.; Hlatká, M.; Kampf, R.; Sirková, V. Possibility of a Solution of the Sustainability of Transport and Mobility with the Application of Discrete Computer Simulation—A Case Study. Sustainability 2021, 13, 9816. [Google Scholar] [CrossRef]
- Vojtek, M.; Kendra, M.; Zitrický, V.; Široký, J. Mathematical approaches for improving the eflciency of railway transport. Open Eng. 2020, 10, 57–63. [Google Scholar] [CrossRef]
- Wróblewski, P.; Lewicki, W. A Method of Analyzing the Residual Values of Low-Emission Vehicles Based on a Selected Expert Method Taking into Account Stochastic Operational Parameters. Energies 2021, 14, 6859. [Google Scholar] [CrossRef]
- Sañudo, O.R.; Pombo, J.; Ricci, S.; Miranda, M. The importance of sleepers spacing in railways. Constr. Build. Mater. 2021, 300, 124326. [Google Scholar] [CrossRef]
- Twumasi-Boakye, R.; Sobanjo, J. Civil infrastructure resilience: State-of-the-art on transportation network systems. Transp. A Transp. Sci. 2019, 15, 455–484. [Google Scholar] [CrossRef]
- Frilli, A.; Meli, R.; Nocciolini, D.; Pugi, L.; Rindi, A.; Romani, B.; Ceraolo, M.; Lutzemberger, G. The Tesys Rail Project: Innovative Models to Enhance the Energy Sustainability of Railway Systems. Int. J. Railw. Technol. 2017, 6, 1–28. [Google Scholar] [CrossRef]
- Rausand, M.; Høyland, A. System Reliability Theory: Models, Statistical Methods, and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003; 672p, ISBN 978-0-471-47133-2. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, P.; Agarwal, A. RAMS of HVAC for Rolling Stock Application. Int. J. Eng. Tech. Res. 2021, 10, 157. [Google Scholar]
- Loidolt, M.; Marschnig, S. Evaluating Short-Wave Effects in Railway Track Using the Rail Surface Signal. Appl. Sci. 2022, 12, 2529. [Google Scholar] [CrossRef]
- Malekjafarian, A.; OBrien, E.J.; Quirke, P.; Cantero, D.; Golpayegani, F. Railway Track Loss-of-Stiffness Detection Using Bogie Filtered Displacement Data Measured on a Passing Train. Infrastructures 2021, 6, 93. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, J.; Liu, C.; Wang, J.; Yao, D. Dynamic Characteristics of a Traction Drive System in High-Speed Train Based on Electromechanical Coupling Modeling under Variable Conditions. Energies 2022, 15, 1202. [Google Scholar] [CrossRef]
- Heleno, R.; Montenegro, P.A.; Carvalho, H.; Ribeiro, D.; Calcada, R.; Baker, C.J. Influence of the railway vehicle properties in the running safety against crosswinds. J. Wind Eng. Ind. Aerodyn. 2021, 217, 104732. [Google Scholar] [CrossRef]
- Tułecki, A.; Szkoda, M. Ecology, energy efficiency and resource efficiency as the objectives of rail vehicles renewal. Transp. Res. Procedia 2017, 25, 386–406. [Google Scholar] [CrossRef]
- Alfonso, J.; Rodriguez, J.M.; Salazar, J.C.; Orús, J.; Schreiber, V.; Ivanov, V.; Augsburg, K.; Molina, J.V.; Sakka, M.A.; Castellano, J.A. Distributed simulation and testing for the design of a smart suspension. SAE Int. J. Connect. Autom. Veh. 2020, 3, 129–138. [Google Scholar] [CrossRef]
- Kendra, M.; Skrúcaný, T.; Synák, F.; Škorupa, M.; Grenčík, J. Energy intensity of railway and road passenger transport and its breaking point according to vehicle capacity usage. In Proceedings of the 7th Transport Research Arena TRA, Vienna, Austria, 16–19 April 2018; pp. 1–10. [Google Scholar] [CrossRef]
- Babyak, M.; Keršys, R.; Neduzha, L. Improving the dependability evaluation technique of a transport vehicle. In Proceedings of the International Conference Transport Means, Kaunas, Lithuania, 30 September–2 October 2020; pp. 646–651. [Google Scholar]
- Bosso, N.; Gugliotta, A.; Magelli, M.; Zampieri, N. Monitoring of railway freight vehicles using onboard systems. Procedia Struct. Integr. 2019, 24, 692–705. [Google Scholar] [CrossRef]
- Komorski, P.; Nowakowski, T.; Firlik, B.; Szymański, G.M. Analysis of wheel and track irregularities impact on the vibroacoustic signals emission in rail vehicles. In Proceedings of the 25th International Congress on Sound and Vibration ICSV25, Hiroshima, Japan, 8–12 July 2018. [Google Scholar]
- Bondarenko, I. Modeling for establishment of evaluation conditions of functional safety of the railway track. East. -Eur. J. Enterp. Technol. 2016, 1, 4–10. [Google Scholar] [CrossRef][Green Version]
- Zelenko, Y.; Zelenko, D.; Neduzha, L. Contemporary principles for solving the problem in noise reduction from railway rolling stock. IOP Conf. Ser. Mater. Sci. Eng. 2020, 985, 012015. [Google Scholar] [CrossRef]
- Komorski, P.; Szymański, G.M.; Nowakowski, T. Development of the urban rail vehicle acoustic model. Appl. Acoust. 2022, 195, 108807. [Google Scholar] [CrossRef]
- Harrison, T.; Midgley, W.; Goodall, R.M.; Ward, C.P. Development and control of a rail vehicle model to reduce energy consumption and carbon dioxide emissions. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 1237–1248. [Google Scholar] [CrossRef]
- Boccaccio, M.; Fierro, G.P.M.; Bucciarelli, F.; Meo, M. Multi-tonal subwavelength metamaterial for absorption and amplification of acoustic and ultrasonic waves. Eng. Res. Express 2021, 3, 025024. [Google Scholar] [CrossRef]
- Liu, Q.; Lei, X.; Rose, J.G.; Chen, H.P.; Feng, Q.; Luo, X. Vertical wheel-rail force waveform identification using wavenumber domain method. Mech. Syst. Signal Process. 2021, 159, 107784. [Google Scholar] [CrossRef]
- Velletrani, F.; Licciardello, R.; Bruner, M. Intelligent Wheelsets for the trains of the future: The role of in-service wheel-rail force measurement. Ing. Ferrov. 2020, 10, 701. [Google Scholar]
- Iwnicki, S.D.; Grassie, S.L.; Kik, W. Track Settlement Prediction Using Computer Simulation Tools. Vehicle System Dynamics. In The Dynamics of Vehicles on Roads and on Tracks; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- True, H.; Christiansen, L.E.; Plesner, A.L.; Ammitzbøll, A.L.; Dahl, B.J. Why is it so difficult to determine the lateral Position of the Rails by a Measurement of the Motion of an Axle on a moving Vehicle? In Proceedings of the First International Conference on Rail Transportation, Chengdu, China, 10–12 July 2017.
- Mosleh, A.; Montenegro, P.A.; Costa, P.A.; Calçada, R. Railway Vehicle Wheel Flat Detection with Multiple Records Using Spectral Kurtosis Analysis. Appl. Sci. 2021, 11, 4002. [Google Scholar] [CrossRef]
- Enjalbert, S.; Gandini, L.M.; Pereda-Baños, A.; Ricci, S.; Frédéric, V. Human–Machine Interface in Transport Systems: An Industrial Overview for More Extended Rail Applications. Machines 2021, 9. [Google Scholar] [CrossRef]
- Bondarenko, I.; Keršys, R.; Neduzha, L. Studying of Dynamic Parameters Impulse Impact of the Vehicle Taking into Account the Track Stiffness Variations. In Proceedings of the 25th International Conference Transport Means, Kaunas, Lithuania, 6–8 October 2021; pp. 684–689. [Google Scholar]
- Borghetti, F.; Petrenj, B.; Trucco, P.; Marchionni, G.; Ponti, M.; Calabrese, V. Multi-level approach to assessing the resilience of road network infrastructure. Int. J. Crit. Infrastruct. 2021, 17, 97. [Google Scholar] [CrossRef]
- Ngo, D.; Parkinson, H.; Bamford, G.; Bamford, J.; Rayson, P. Opportunities for resilient rail system development using natural language processing. In Proceedings of the Conference: 7th Transport Research Arena TRA 2018, Vienna, Austria, 16–19 April 2018. [Google Scholar] [CrossRef]
- Knapcikova, L.; Konings, R. European railway infrastructure: A review. Acta Logist.-Int. Sci. J. About Logist. 2018, 5, 71–77. [Google Scholar] [CrossRef]
- Falamarzi, A.; Moridpour, S.; Nazem, M. A reviewof rail track degradation prediction models. Aust. J. Civ. Eng. 2019, 17, 152–166. [Google Scholar] [CrossRef]
- Bernacki, D.; Lis, C. Exploring the sustainable effects of urban-port road system reconstruction. Energies 2021, 14, 6512. [Google Scholar] [CrossRef]
- Scholte, W.J.; Marco, V.R.; Nijmeijer, H. Experimental Validation of Vehicle Velocity, Attitude and IMU Bias Estimation. IFAC-Pap. 2019, 52, 118–123. [Google Scholar] [CrossRef]
- Olaby, O.; Hamadache, M.; Soper, D.; Winship, P.; Dixon, R. Development of a Novel Railway Positioning System Using RFID Technology. Sensors 2022, 22, 2401. [Google Scholar] [CrossRef]
- Galar, D.; Seneviratne, D.; Kumar, U. Big Data in Railway O&M: A Dependability Approach. In Research Anthology on Big Data Analytics, Architectures, and Applications; IGI Global: Hershey, PA, USA, 2022. [Google Scholar] [CrossRef]
- Sasidharan, M.; Burrow, M.P.N.; Ghataora, G.S.; Marathu, R. A risk-informed decision support tool for the strategic asset management of railway track infrastructure. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 236, 183–197. [Google Scholar] [CrossRef]
- Yan, H.; Gao, C.; Elzarka, H.; Mostafa, K.; Tang, W. Risk assessment for construction of urban rail transit projects. Saf. Sci. 2019, 118, 583–594. [Google Scholar] [CrossRef]
- Bondarenko, I.; Lunys, O.; Neduzha, L.; Keršys, R. Dynamic Track Irregularities Modeling when Studying Rolling Stock Dynamics. In Proceedings of the 23rd International Conference Transport Means, Palanga, Lithuania, 2–4 October 2019; pp. 1014–1019. [Google Scholar]
- Domin, R.; Domin, Y.; Chernyak, G.; Nozhenko, V. Method of operational investigation of rolling stock derailment. Transp. Syst. Technol. 2021, 37, 173–186. [Google Scholar] [CrossRef]
- Nandan, S.; Trivedi, R.; Kant, S.; Ahmad, J.; Maniraj, M. Design, Analysis and Prototype Development of Railway Wagons on Different Loading Conditions. Int. J. Eng. Appl. Sci. Technol. 2020, 4, 122–129. [Google Scholar] [CrossRef]
- Liu, Z.; Kang, J.; Zhao, X.; Zuo, M.J.; Qin, Y.; Jia, L. Modelling of the Safe Region Based on Support Vector Data Description for Health Assessment of Wheelset Bearings. Appl. Math. Model. 2019, 73, 19–29. [Google Scholar] [CrossRef]
- Kulbovskyi, I.; Holub, H.; Andonova, S.; Saiapina, I.; Tkachuk, M. Model and methods of management of efficiency of use of production and technological potential of rolling stock of rail transport. Transp. Syst. Technol. 2021, 38, 232–238. [Google Scholar] [CrossRef]
- Sichani, M.S.; Enblom, R.; Berg, M. A novel method to model wheel–rail normal contact in vehicle dynamics simulation. Veh. Syst. Dyn. 2014, 52, 1752–1764. [Google Scholar] [CrossRef]
- Liu, W.; Xiong, W. Rethinking the Transport Infrastructure-Led Development Model. Sustainability 2022, 14, 407. [Google Scholar] [CrossRef]
- Poveda-Reyes, S.; Rizzetto, L.; Triti, C.; Shi, D.; García-Jiménez, E.; Molero, G.M.; Santarremigia, F.E. Risk evaluation of failures of the running gear with effects on rail infrastructure. Eng. Fail. Anal. 2021, 128, 105613. [Google Scholar] [CrossRef]
- Pons, J.J.; Sanchis, I.V.; Franco, R.I.; Yepes, V. Life cycle assessment of a railway tracks substructures: Comparison of ballast and ballastless rail tracks. Environ. Impact Assess. Rev. 2020, 85, 106444. [Google Scholar] [CrossRef]
- Procházková, D.; Prochazka, J. Risk Management Plan for Technical Facility Operation. In Proceedings of the 31st European Safety and Reliability Conference, Angers, France, 19–23 September 2021. [Google Scholar] [CrossRef]
- Gerum, P.C.L.; Altay, A.; Baykal-Gürsoy, M. Data-driven Predictive Maintenance Scheduling Policies for Railways. Transp. Res. Part C Emerg. Technol. 2019, 107, 137–154. [Google Scholar] [CrossRef]
- Bondarenko, I.; Keršys, A.; Neduzha, L. Assessment of the Railway Track Deformability Behaviour as the Parameter of Operational Availability Function. In Proceedings of the 25th International Conference Transport Means, Kaunas, Lithuania, 6–8 October 2021; pp. 644–648. [Google Scholar]
- Xie, J.; Huang, J.; Zeng, C.; Jiang, S.-H.; Podlich, N. Systematic Literature Review on Data-Driven Modelsfor Predictive Maintenance of Railway Track: Implications in Geotechnical Engineering. Geosciences 2020, 10, 425. [Google Scholar] [CrossRef]
- Kamburjan, E.; Hähnle, R. Formal modeling and analysis of railway operations with active objects. Sci. Comput. Program. 2018, 166, 167–193. [Google Scholar] [CrossRef]
- Leite, M.; Costa, M.A.; Alves, T.; Infante, V.; Andrade, A.R. Reliability and availability assessment of railway locomotive bogies under correlated failures. Eng. Fail. Anal. 2022, 135, 106104. [Google Scholar] [CrossRef]
- Grossoni, I.; Powrie, W.; Zervos, A.; Bezin, Y.; Pen, L.P. Modelling railway ballasted track settlement in vehicle-track interaction analysis. Transp. Geotech. 2021, 26, 100433. [Google Scholar] [CrossRef]
- Liu, Z.; Song, H.; Tan, H.; Hao, H.; Zhao, F. Evaluation of the Cost of Intelligent Upgrades of Transportation Infrastructure for Intelligent Connected Vehicles. J. Adv. Transp. 2022, 2022, 5841373. [Google Scholar] [CrossRef]
- Rahimi, M.; Liu, H.; Cardenas, I.D.; Starr, A.; Hall, A.; Anderson, R. A Review on Technologies for Localisation and Navigation in Autonomous Railway Maintenance Systems. Sensors 2022, 22, 4185. [Google Scholar] [CrossRef] [PubMed]
- Sedghi, M.; Kauppila, O.; Bergquist, B.; Vanhatalo, E.; Kulahci, M. A taxonomy of railway track maintenance planning and scheduling: A review and research trends. Reliab. Eng. Syst. Saf. 2021, 215, 107827. [Google Scholar] [CrossRef]
- Maciej, A.; Ryszard, S.; Kinga, S.; Mateusz, N. Analysis of driver assistance systems in rail vehicles. Pojazdy Szyn. 2020, 4, 25–32. [Google Scholar] [CrossRef]
- Zolotas, A.; Hassan, F. Impact of Fractional Order Methods on Optimized Tilt Control for Rail Vehicles. Fract. Calc. Appl. Anal. 2017, 20, 765–789. [Google Scholar] [CrossRef]
- Kuźma, K.; Pyrek, K.; Kocik, W.; Kalinowski, P.; Kamiński, P. Individual rail transport and the conception of a means of transport using a suspended railway track. Min.-Inform. Autom. Electr. Eng. 2019, 3, 47. [Google Scholar] [CrossRef]
- Liu, B.; Yue, H.; Lin, J.; Wu, X.; Shi, Z. Analysis and Optimization of Driving Attitude and Oscillation Characteristics of Suspension-Type Small Rail Vehicles. Shock Vib. 2020, 2020, 8894597. [Google Scholar] [CrossRef]
- Pillai, N.; Shih, J.Y.; Roberts, C. Evaluation of Numerical Simulation Approaches for Simulating Train-Track Interactions and Predicting Rail Damage in Railway Switches and Crossings (S&Cs). Infrastructures 2021, 6, 63. [Google Scholar] [CrossRef]
- Chang, C.; Ling, L.; Chen, S.; Zhai, W.; Wang, K.; Wang, G. Dynamic performance evaluation of an inspection wagon for urban railway tracks. Measurement 2020, 170, 108704. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wang, Z.L.; Shi, K.; Xu, H.; Mo, X.Q.; Wu, Y.T. Two-axle test vehicle for damage detection for railway tracks modeled as simply supported beams with elastic foundation. Eng. Struct. 2020, 319, 110908. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, J.; Yang, S.; Li, Z. Study on improvement of LuGre dynamical model and its application in vehicle handling dynamics. J. Mech. Sci. Technol. 2019, 33, 545–558. [Google Scholar] [CrossRef]
- Polak, K.; Korzeb, J. Acoustic Signature and Impact of High-Speed Railway Vehicles in the Vicinity of Transport Routes. Energies 2022, 15, 3244. [Google Scholar] [CrossRef]
- Lesgidis, N.; Sextos, A.; Moschen, L.; Gomez, J.S.G.; Pistone, E. Rigorous vehicle-soil-track simulation of high-speed rail through optimization-based model order reduction. Transp. Geotech. 2020, 23, 100350. [Google Scholar] [CrossRef]
- Liang, Y.; Feng, Q.; Lu, J.; Guo, W.; Yang, Z. A Double-Rail Phononic Crystal Model for the Ballasted Track. International J. Struct. Stab. Dyn. 2022, 22, 2250066. [Google Scholar] [CrossRef]
- Minda, A.; Lucian, P.; Burtea, D.G.; Gillich, G.R. Smoothing the Time-Frequency Representations to Improve the Diagnosis for Engineering Structures. Annals of the “Constantin Brancusi” University of Targu Jiu, Engineering Series. No. 1/2021. Available online: https://www.utgjiu.ro/rev_ing/pdf/2021-1/01_Andrea%20Amalia%20Minda_SMOOTHING%20THE%20TIME-FREQUENCY%20REPRESENTATIONS%20TO%20IMPROVE%20THE%20DIAGNOSIS%20FOR%20ENGINEERING%20STRUCTURES.pdf (accessed on 1 August 2022).
- Han, J.; He, Y.; Wang, J.; Xiao, X. Simulation and experimental study on vibration and acoustic characteristics of a continuous supported embedded track. Appl. Acoust. 2021, 180, 108103. [Google Scholar] [CrossRef]
- Xiao, J.; Yan, Z.; Shi, J.; Ma, D. Effects of Wheel-Rail Impact on the Fatigue Performance of Fastening Clips in Rail Joint Area of High-Speed Railway. KSCE J. Civ. Eng. 2022, 26, 120–130. [Google Scholar] [CrossRef]
- Xu, L.; Zhai, W.M. A novel model for determining the amplitude-wavelength limits of track irregularities accompanied by a reliability assessment in railway vehicle-track dynamics. Mech. Syst. Signal Process. 2017, 86, 260–277. [Google Scholar] [CrossRef]
- Sadeghi, J.; Khajehdezfuly, A.; Esmaeili, M.; Poorveis, D. Investigation of rail irregularity effects on wheel/rail dynamic force in slab track: Comparison of two and three dimensional models. J. Sound Vib. 2016, 374, 228–244. [Google Scholar] [CrossRef]
- Auersch, L. Different Types of Continuous Track Irregularities as Sources of Train-Induced Ground Vibration and the Importance of the Random Variation of the Track Support. Appl. Sci. 2022, 12, 1463. [Google Scholar] [CrossRef]
- Paudel, M.; Lim, L.; Yap, F.; Kho, K. Vibration Analysis of the Third Rail Structure of a Mass Rapid Transit System with Structural Defects. Appl. Sci. 2021, 11, 8410. [Google Scholar] [CrossRef]
- Costa, M.A.; Costa, J.N.; Andrade, A.R.; Ambrósio, J. Combining wavelet analysis of track irregularities and vehicle dynamics simulations to assess derailment risks. Int. J. Veh. Mech. Mobil. 2022, 1–27. [Google Scholar] [CrossRef]
- Sekulic, D.; Dedović, V.; Mladenović, D.M. General oscillatory model of vehicles for passenger transport. In Proceedings of the Second International Conference on Traffic and Transport Engineering (ICTTE), Belgrade, Serbia, 27–28 November 2014. [Google Scholar]
- Papaelias, M.; Amini, A.; Culwick, R.; Heesom, J.; Huang, Z.; Junior, V.L.J.; Kaenwunruen, S.; Kerkyras, S.; Kongpuang, M.; Marquez, F.P.G.; et al. Advanced remote condition monitoring of railway infrastructure and rolling stock. In Proceedings of the 1st International Conference on Welding & Non Destructive Testing, Athens, Greece, 22–23 October 2018. [Google Scholar]
- Vlachospyros, G.; Iliopoulos, I.A.; Kritikakos, K.; Kaliorakis, N.; Fassois, S.D.; Sakellariou, J.S.; Deloukas, A.; Leoutsakos, G.; Giannakis, C.; Chronopoulos, E.; et al. The MAIANDROS System for Random-Vibration-Based On-Board Railway Vehicle and Track Monitoring. In Proceedings of the ASME 2021 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, Online, 17–19 August 2021. [Google Scholar] [CrossRef]
- Bondarenko, I. Development of algorithm for calculating dynamic processes of railroad track deformability work. East. -Eur. J. Enterp. Technol. 2016, 6, 28–36. [Google Scholar] [CrossRef][Green Version]
- Bondarenko, I. Advantages of applying elastic waves theory in solving dynamic problems. Publ. House “Balt. Publ.” 2022, 328–352. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).