Mountain Roads’ Geometric Design: Methodological Proposal for Hairpin Bend Design/Retrofitting

Abstract

Mountainous roads often have to overcome considerable differences in height, which is why hairpin bends find a valid and common use. Despite this, there is a lack of specific international standards. Given the absence of a national standard governing the mountain roads’ design, in Italy, as in many other countries, the Swiss standard SNV 640198a is generally applied. This standard does not guarantee the correct geometric design of hairpin bends for Italian vehicle fleets and fleets according to the Directive 2002/7/EC. In this paper, the authors have developed a new methodology based on the Swiss standard upgrade, which is applicable internationally. Starting from hairpin bends’ geometric layouts provided by SNV 640198a and from related considerations, respectively, to the gyration formulae use and to swept path analysis’ simulations, they developed new planimetric layouts compatible with the vehicle fleet and with the cross-sectional dimensions of Italian roads. In this way, a generally valid methodology applicable to any international context was defined. In particular, the study allowed the definition of new geometric layouts to be used in hairpin bend design/retrofitting when it is necessary to guarantee the simultaneous entry into the bend of a 12 m long bus, and a car travelling in the opposite direction. Finally, the proposed methodology was applied to a mountain road case study in the Lucanian Dolomites area; an area of great tourist, cultural and environmental interest in southern Italy.

1. Introduction

Mountain roads crossing orographically difficult terrain are often used to connect the valley road with centers of population located on the slopes. In order to limit the longitudinal slope and the occupation area, they require that road axis direction to be reversed (even repeatedly); so, they are characterized by very small vertex angles, i.e., angles at the center greater than 180°.

The design of a bend positioned inside straights would not be able to guarantee the minimum requirements due to its limited length. In order to minimize earth works and limit the use of major retaining structures such as walls and/or bulkheads, hairpin bends with very small radii (generally between 6 and 15 m) are used so that the planimetric distance between the downstream and upstream branches is sufficiently small. On mountain roads, driver behavior and speed are influenced by the road characteristics but also by generally unfavorable visibility conditions [1]. Hairpin bends are always travelled at very low speeds (usually less than 20 km/h) [2] (p. 48), [3] (p. 40), so vehicle stability issues related to the effects of centrifugal force and lateral jerk are marginal. For this reason, their dimensioning is not based on dynamic considerations but on geometric ones. Such considerations are aimed at guaranteeing visibility conditions and the safe entry and/or crossing of two vehicles travelling in opposite directions [4]. 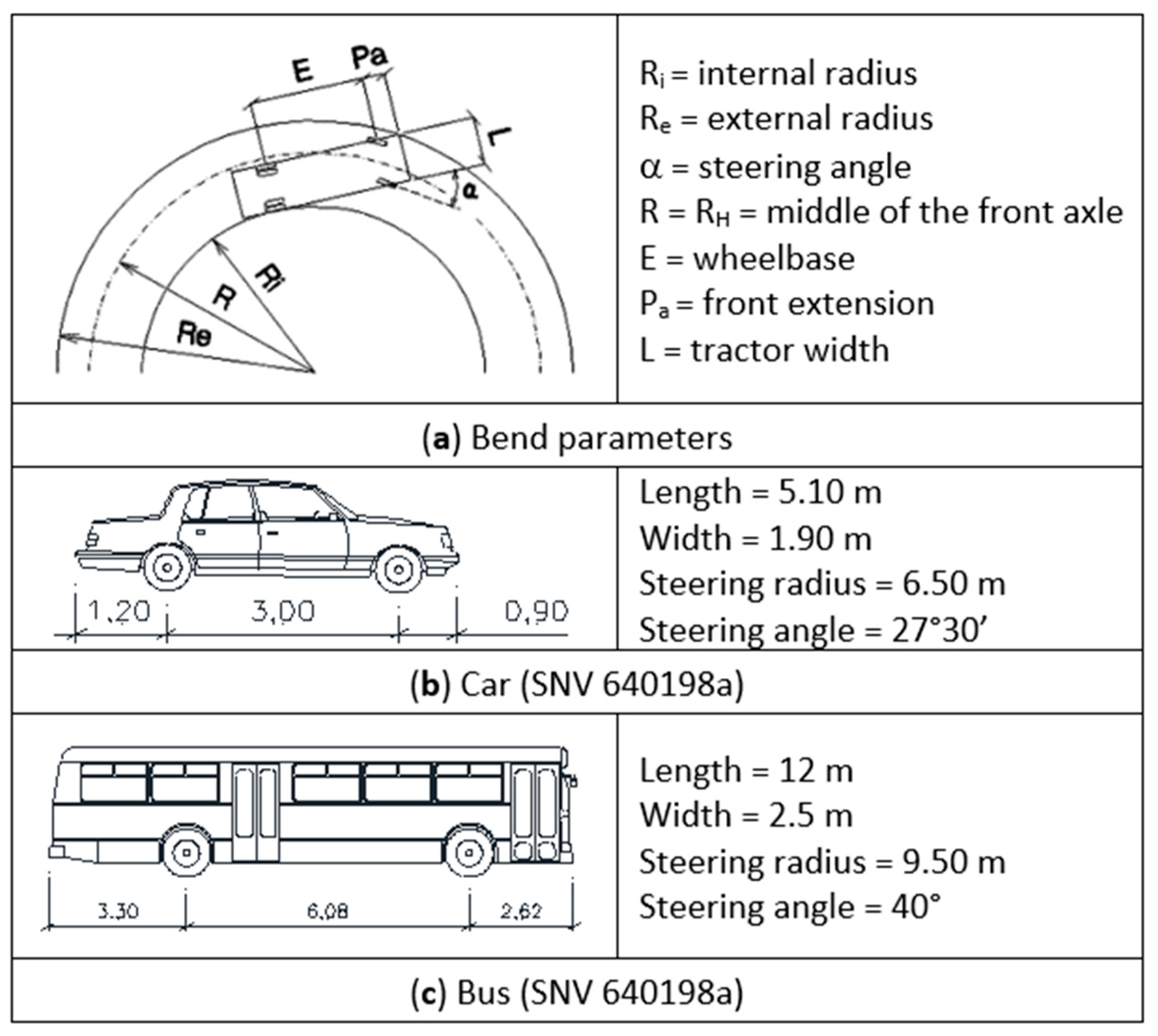Planimetrically, the geometric elements of hairpin bends can be limited to circular arcs (with the possible inclusion of short straight lines), excluding transition (i.e., clothoids), whose usefulness is somewhat reduced [5] (p. 66). An appropriate carriageway widening must be foreseen, considering that road vehicles travelling around a bend occupy a wider section than when travelling in a straight line, and that this width increases as the bend radius decreases and the vehicle wheelbase increases [6] (p. 144). The SÉTRA (Service d’Études Techniques des Routes et Autoroutes), for example, states that when, on curves with a radius of less than 200 m, heavy vehicle traffic reaches a certain importance (heavy vehicle high percentage), a 50/R widening must be provided so that semi-trailer trucks can pass them without leaving their lane [7] (p. 17).

It also states that, in case of hairpin bends, the effectiveness of this minimum value (50/R) must be verified by more precise turning studies (i.e., by means of swept path analysis simulations). The French standards follow the same approach, but with a greater detail level. These standards provide bend widening (E) values using the formula E = 3.5 + (K/R), with K equal to 25 for bends with a radius greater than 10 m and equal to 30 for bends with a radius between 5 and 10 m [8] (p. 100).

The widening values can be obtained by applying more complex analytical formulae (gyration formulae) [6] that take into account further variables in addition to the bend radius (R), specifically, the vehicle’s wheelbase, the vehicle’s width (tractor width), the distance between the steering axle and its front end (front extension) and the vehicle’s steering angle (Figure 1). If further issues, such as longitudinal profile, superelevation and pavement surface characteristics are taken into account, it can be understood that the design of road bends is not a banal task. Despite this, the international dissemination of scientific studies, guidelines and regulations is extremely lacking. Some rare examples of national regulations can be found in France [8] and Switzerland [9].

Even in Italy, despite the extensive diffusion of mountainous and hilly territories, the current regulations [10] do not directly address the hairpin bend designs and/or retrofitting. The Swiss standard SNV 640198a [9], which provides different solutions depending on the geometric parameters’ variation, design vehicles’ dimensional/typological characteristics and carriageway cross-section dimension, is frequently applied. However, it must be emphasized that such solutions may not be fully effective in the Italian context or in other international contexts that are characterized by their own vehicle fleets and a different hierarchical road classification.

Both in the case of ex novo and retrofitting design, the objective is to achieve the simultaneous entry into the bend of two vehicles travelling in opposite directions. Such vehicles, under minimal conditions, consist of a 12 m long bus and a passenger car. Since hairpin bends are generally located in mountainous areas characterized by considerable tourist, cultural and environmental interest and are often travelled by buses, it seems reasonable to provide the above-mentioned minimum condition and thus exclude other less frequent situations, such as, for example, the crossing of two buses. The authors, in order to overcome the application limits of SNV 640198a, have revised, with the appropriate modifications, the planimetric hairpin bends’ layouts provided by standards through an approach based on the vehicle clearance bands’ evaluation on bends and subsequent validation using swept path analysis techniques. These new layouts are proposed as operational tools to be used for the design/retrofitting of hairpin bends in Italy, defining overall a new methodological approach valid in any international context. Furthermore, the paper proposes a case study related to the research project interest area in which this work was carried out [11,12].

2. Swiss Standard SNV 640198a

The SNV 640198a [9] is used for the design of road hairpins compatible with Swiss roads’ geometric characteristics and vehicle fleets. This research refers to “lacet” type hairpins [9,13] characterized by a road section consisting of two traffic lanes of 2.85 m each, while the considered vehicles are passenger car and bus. The entry mode into the bends of such two-axle vehicles and their main dimensional parameters are shown in Figure 1a–c, respectively. The gyration formulae that link the geometric parameters shown in Figure 1a are contained in the Annex to SNV 640198a [13] and are, in any case, available in the literature [14].

In addition, the simultaneous bend entry of two vehicles with two axles travelling in opposite directions is of great importance. On the basis of these considerations, it seems reasonable that hairpin bends (existing or newly constructed) can at least guarantee the simultaneous entry of a bus and a passenger car (a very frequent situation). Obviously, satisfying this minimum requirement does not guarantee the safe crossing of two buses (a less likely situation). This would only be possible by increasing hairpin bend geometric dimensions, i.e., by adopting more expensive solutions that are not always justifiable and/or feasible.

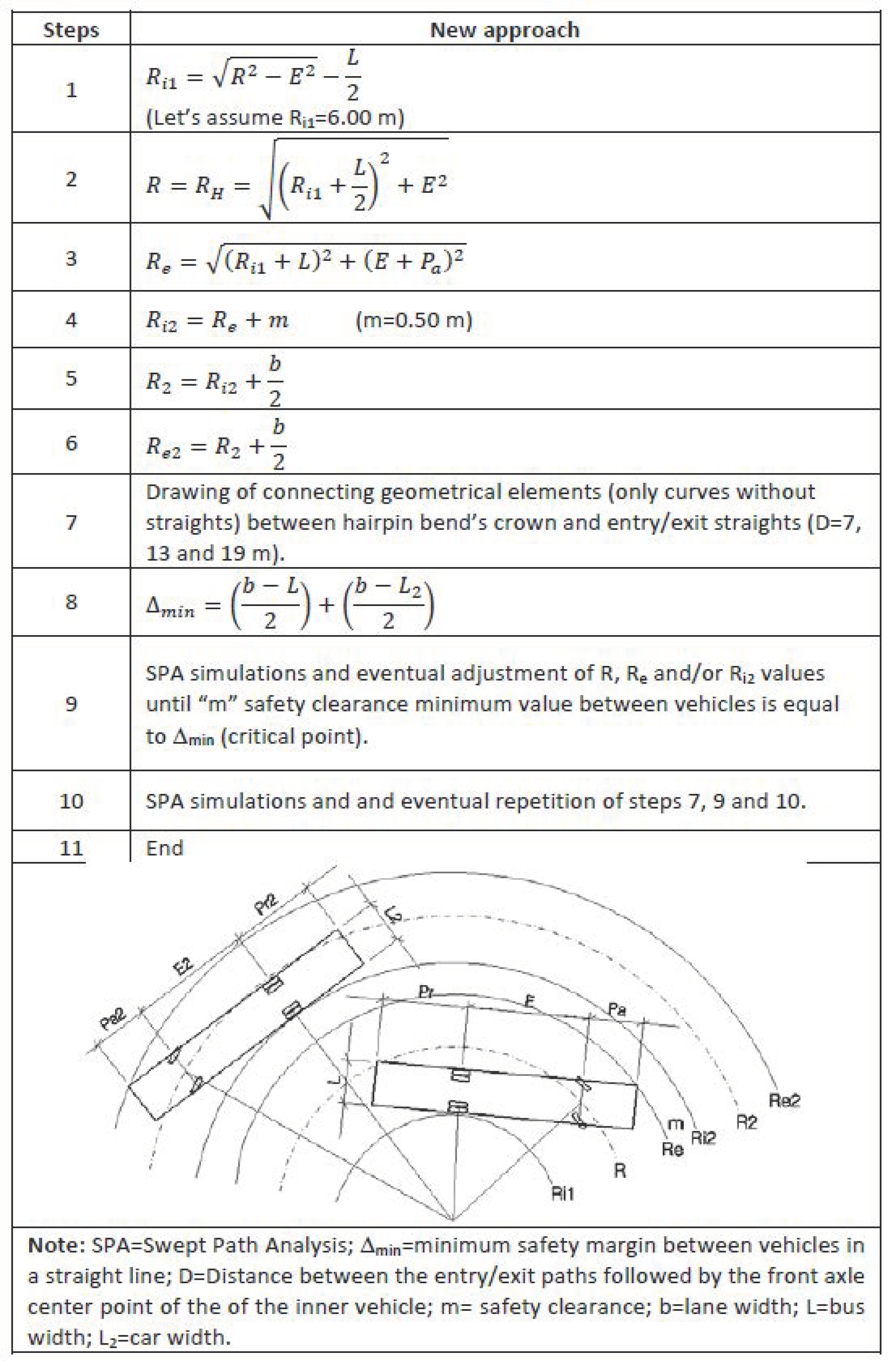
Figure 2 shows the planimetric layout and the corresponding gyration formulas used by Swiss standard for preliminary hairpin bends dimensioning in case of the simultaneous crossing between two two-axle vehicles [13].

A minimum clearance gap (m) must always be ensured between crossing vehicles along the bend, and this gap must be at least 0.5 m. To ensure traffic safety, an appropriate distance (D) must be provided between the entry/exit paths followed by the center point of the inside vehicle front axle. The Swiss standard considers three reference values called minimum, intermediate and maximum, equal to 5, 13 and 19 m, respectively [9,13].

The Swiss standard [9] uses a continuous geometry consisting of a succession of circular curves and short straight lines in the geometric design of hairpin bends. This requires a preliminary hairpin bend circular crown calculation by gyration formulae and a subsequent general verification with swept path analysis simulations [9,13].

The operational phases are described below (Figure 2):

• assignment of an inner radius value (R_i1 = 6.05 m);
• gyration formulae application in the heaviest hypothesis of a car (Figure 1b) on the outside lane and a bus (Figure 1c) on the inside lane. The safety clearance gap (m) between the two vehicles is initially set at 0.54 m;
• hairpin bend circular crown dimensioning using gyration formulae (R = R_H = 9.50 m, R_e = 12.20 m, R_i2 = 12.74 m, R₂ = 14.01 m, R_e2 = R_a = 15.15 m);
• layout’s completion with circular junction arcs and possible short straight lines. Compatibility verification by swept path analysis simulations and implementation of possible corrections (e.g., minimum safety clearance gap increasing) aimed at guaranteeing the correct inscription of vehicles.

3. Italian Regulatory Framework

The Italian regulatory framework does not directly address the mountain roads issue. There are only a few prescriptions concerning the hairpin bends use within limited traffic volume road types [10]. The setting of a road within such typologies makes it possible to take advantage of particular derogations, although the same regulations suggest adopting the general design criteria valid for ordinary roads. In Italy, in the absence of specific standards, for the design of hairpin bends, the prescriptions established by the in-force regulations are adopted [10] for extra-urban roads in category C (subcategories C1 and C2) and F (subcategories F1 and F2) [4].

Usually, the adopted road’s cross-section for new hairpin bend designs is F2 (consisting of two 3.25 m lanes and two 1.00 m shoulders, for a total width of 8.50 m). The one found in almost all existing hairpin bends, and which should therefore be used for their eventual geometric retrofitting, is the A2 type, defined in CNR technical bulletin 31/73 [15]. This cross-section, consisting of two 2.75 m lanes and two 0.75 m shoulders, for a total width of 7.0 m, corresponds to B type as indicated in CNR technical bulletin 78/80 [16]. In few cases, there is the type VI section, consisting of two 3.00 m wide lanes and two 1.00 m shoulders, for a total width of 8.0 m [16].

For the vehicles’ geometric characteristics, the current regulations [17,18,19,20] establish that the two-axle bus’s maximum length is 13.50 m.

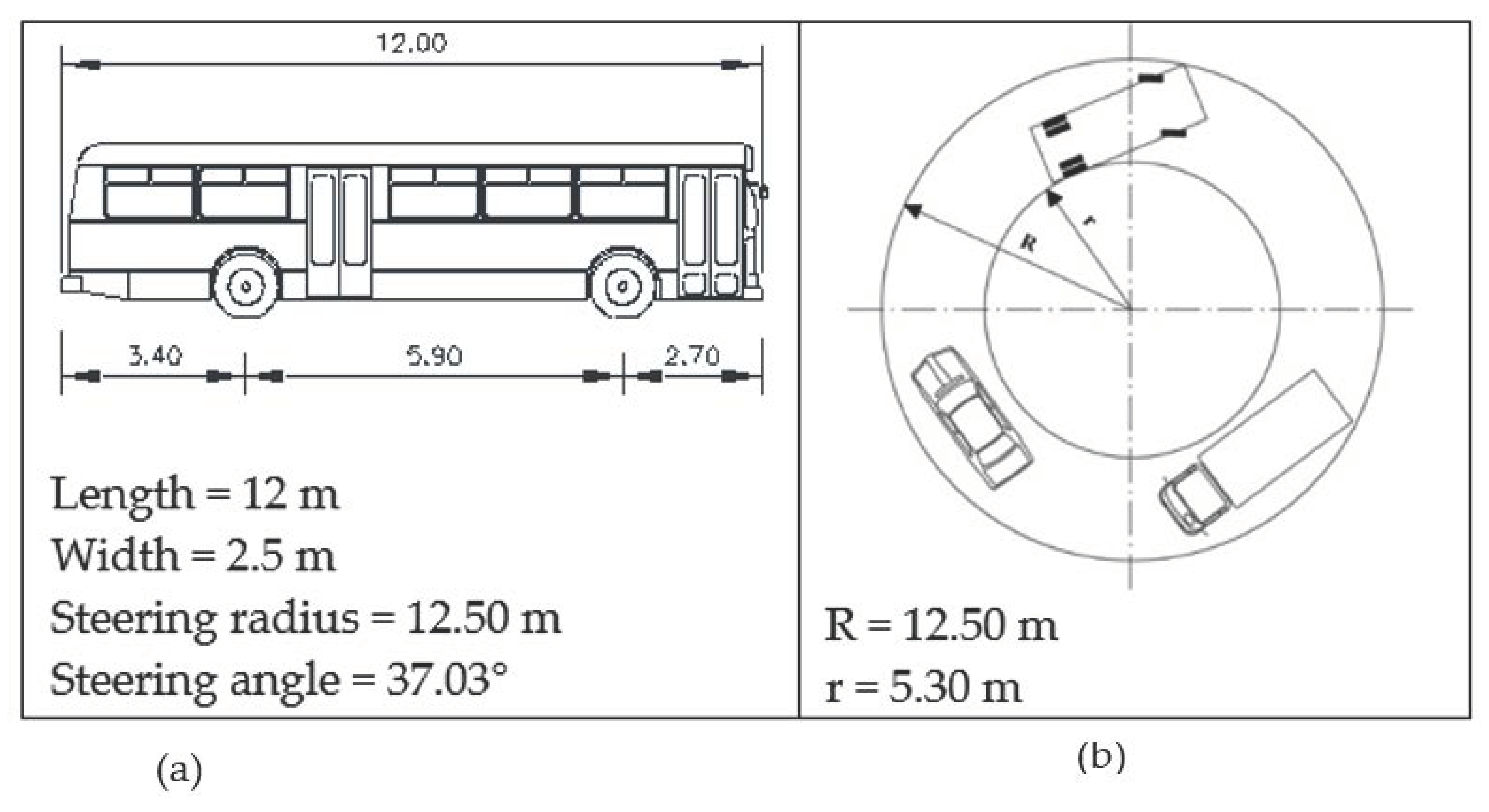
This indication is also valid in the Swiss context, since article 65 of [21] provides the same indication. However, the two-axle buses common throughout Europe rarely reach this maximum length, which is “reserved” by the major manufacturers for three-axle buses. For this reason, the authors consider the indication provided by the Swiss standard to assume a maximum length of 12.00 m to be correct. Rare examples of two-axle buses with lengths between 12.50 m and 13.30 m are never used on mountain roads due to their difficulty in driving on bends.

Therefore, the 12.00 m Italian bus is adopted, the dimensional specifications of which are shown in Figure 3a. For the car, the authors propose to retain the same Swiss vehicle (Figure 1b), given its greater dimensions. According to the Italian regulatory framework [19] transposing Directive 2002/7/2002 [20], each vehicle must be able to inscribe itself in a circular crown (encumbrance strip) of outer radius 12.50 m and inner radius 5.30 m (Figure 3b).

4. Hairpin Bend Design and Geometric Retrofitting: A New Approach

As already stated, the hairpin bend design in the Italian context is constrained by certain mandatory conditions. These conditions concern both characteristics of the vehicle fleet and type of roads. In Italy, the use of the Swiss standard SNV 640198a, although justified by an obvious deficiency in the national regulatory framework, cannot be considered decisive because the standard has been calibrated on the operating conditions in force in Swiss territory.

For this, the authors propose adopting some improvements and (at the same time) adapting it to the Italian context.

The study is conducted on two-lane hairpin bends with reference to the operating condition characterized by the crossing of a 12 m long bus in the inside lane and a car in the outside lane. The cross-section of the reference road is the F2 type [10] (6.50 m carriageway, i.e., lane modulus of 3.25 m).

Compared to Swiss standard solutions, the authors consider not using the short straight inserted between the basic geometric elements, i.e., between the circular bends making up the circular crown of the hairpin bends and the entry/exit branches. These straight sections should allow vehicles exiting a bend to regain their “vertical” alignment before entering a new bend to be taken in the opposite direction. However, they are too short to fulfil this function (shorter than the length of the bus); authors consider their elimination to be justified. This contributes to simplifying the geometric layouts without, however, reducing safety and ride comfort in view of the low transit speeds typical of mountain roads.

Since kinematic and dynamic problems are negligible, superelevation can be implemented in a transition zone of reduced length, typically not less than 15 m [3] (p. 40). This zone starts at the beginning of the hairpin circular crown and develops along the connecting circular arch that precedes or follows it. Therefore, the proposed new layouts have been dimensioned with transition zone lengths always exceeding 15 m. In any case, even if this length had been less than the minimum, the superelevation could have started/ended on the entry/exit straight [4]. It is important to note that the low travel speeds (less than 20 km/h) do not condition the constructing method of superelevation, which can be carried out, indifferently, with the rotation of the carriageway with respect to the inner edge, the outer edge or the center line. The choice will depend only on geometric/constructive considerations. An operational steps summary of the new design approach is shown in Figure 4.

Initially, an appropriate value is assigned to the internal radius R_i1. Considering that the minimum value set by the standard [18,19,20,22] is 5.30 m (Figure 3b), R_i1 = 6.00 m is set (Figure 4, step 1). Subsequently, the gyration formulas for the study hypothesis are applied, i.e., car (Figure 1b) on the outer lane and bus (Figure 3a) on the inner lane. This makes it possible to calculate the inner radius values (R = R_H = 9.35 m) and outer radius (R_e = 12.09 m) in full accordance with the Swiss standard (Figure 4, steps 2 and 3). The safety clearance gap (m) between vehicles is initially set equal to 0.50 m (Figure 4, step 4), while the values of the R₂ and R_e2 are identified with the curvature radii (centerline and outer edge) of the outer traffic lane having a width of b = 3.25 m (Figure 4, steps 5 and 6). In contrast to the approach defined by [9], which determines the R₂ and R_e2 values with the gyration formulae use (Figure 2, steps 5 and 6), this approach is more conservative because it guarantees better inscribability of the vehicles in the bends, especially in the crossing phase.

Having proportioned the hairpin bend circular crown (Figure 4, steps 1 ÷ 6), it is necessary to design its connection with the inlet/outlet straight sections. On the basis of the considerations developed previously (Section 1 and Section 4), the authors believe that this task can be assigned to the circular bends alone and therefore do not contemplate the use of further connecting geometric elements such as straight and/or clothoids.

An important aspect to consider is the choice of spacing values (D) between the entry/exit lanes of the hairpin bends (Section 2). Compared to the Swiss standard (D = 5, 13 and 19 m), the authors suggest increasing the minimum value from 5 to 7 m. This choice is justified by a general improvement in driving conditions and, above all, by a more effective vehicle “realignment” on the entry/exit lanes, as shown by the swept path analysis simulations conducted (Figure 4, step 7).

The next step involves verifying the hairpin bend performance by means of swept path analysis simulations and its geometric calibration in the event of criticality. In particular, the Swiss standard suggests calibrating the safety clearance gap (m) assumed in the initial phase (Figure 2, step 4) and repeating steps 4÷8 until a satisfactory solution is obtained that allows the geometric process to be completed (Figure 2, step 9). It should be noted that the new safety clearance gap (m) to be assigned must be the smallest among those that allow for the elimination of the encountered criticalities. This procedure does not generate an optimal solution because it does not always guarantee that a safety clearance gap between vehicles of a value at least equal to that present in the straight is respected.

It is proposed to calculate this value, called Δ_min (Figure 4, step 8), and to impose it as the minimum safety clearance gap at the “critical point”, i.e., on the bend at the point of maximum vehicle proximity (Figure 5). This requires analyzing the vehicles’ driving trajectories [23] and remodeling (if necessary) the geometric variables (Figure 4, step 9). In this way, the safety clearance gap between vehicles travelling along the circular crown of the bend is always between a minimum and a maximum value that varies from case to case.

Subsequently, further swept path analysis simulations are carried out and, after assessing the effectiveness of the obtained layout, any geometric modifications are made (Figure 4, step 10). Finally, steps 7, 9 and 10 are repeated until a satisfactory solution is obtained that ends the geometrical process (Figure 4, step 11).

Figure 6 shows the hairpin bends’ geometric layouts (D = 7, 13 and 19 m) obtained with the described procedure. These layouts guarantee the design vehicle’s safe crossing, as shown by the results of the swept path analysis simulations carried out by the Autodesk Vehicle Tracking^® software [23].

Figure 7 shows the bus steering diagrams obtained using the same software with a travel speed of 5 km/h. The critical conditions of maximum steering occur on reduced path length percentages (18.7, 16.3 and 9.8%) in the cases of D = 7, 13 and 19 m, respectively. It also follows that for the solution with maximum spacing between the entry/exit straights (D = 19 m), the steering diagram is sufficiently regular, and this is compatible with a comfortable driving condition.

So, it was possible to define the hairpin bends’ optimum geometries under the indicated operating conditions.

The main hairpin bends’ geometric design parameters (D= 7, 13 and 19 m) both in designing the new F2 roads, and in retrofitting existing roads, are shown in Figure 8. In the latter case, the procedure followed by the authors is identical to that described for the new roads’ design. The only difference is the road class which, as explained in Section 3, is the A2 type.

5. Case Study

This research was developed within the project “MitiGO” (Mitigation of Natural Hazards for Safety and Mobility in the Mountain Areas of Southern Italy) MIUR PON R&I 2014–2020 Program (project MitiGo, ARS01_00964) [11]. “MitiGo” is an industrial research and experimental development project in the specialization area Smart, Secure and Inclusive Communities of the PNR 2015–2020, co-financed by the European Union–ERDF, PON Research and Innovation 2014–2020. One of the research lines of “MitiGo” involves the existing road audit in the project study area. This area is located in Basilicata (southern Italy) in Lucanian Dolomites [12]. This territory is characterized by great tourist, cultural and environmental interest and by the presence of a mountain road network rich in hairpin bends. The problem of the geometric and functional roads’ audit was addressed by applying the methodology presented in this paper.

This section proposes a developed methodology application for the geometric retrofitting of an existing hairpin bend with A2 type road cross-section, identified in the reference area of the MIUR PON R&I 2014–2020 Research Program.

Initially, the “Lucanian Dolomites quadrilateral” rural road network was studied. This territory is a mountainous area of great touristic, cultural and environmental interest, located in the municipalities of Pietrapertosa, Castelmezzano, Albano di Lucania and Campomaggiore (Basilicata Region, Potenza Province) [12] (Figure 9a).

The study highlighted the presence of very winding road axes, rich in hairpin bends, affected, for substantial portions, by landslide phenomena. Within the network, the provincial road SP13 connecting the E847-Basentana road and the municipality of Campomaggiore was examined. It is characterized by an overall planimetric development of approximately 7.4 km and by the presence of 16 hairpin bends (Figure 9a–c).

This road belongs to the A2 type defined in Section 3, which made it possible to carry out an initial geometric effectiveness check limited to the circular hairpin bends’ crown with the aim of assessing the possibility of safe crossing of the design car and bus (Figure 1b and Figure 3a). A preliminary comparison was made between the actual conditions found and the minimum geometry that guarantees safety conditions, as shown in Figure 8 (R_i = 6.00 m, R_e2 = 15.94 m for D = 7.00 m, R_e2 = 15.64 m for D = 13.00 m and D = 19.00 m). The circular design crown (Figure 9d) was therefore overlaid on each of the 16 bends, making it osculatory along the internal circular curve of radius R_i (Figure 9c,e).

The obtained results highlighted circular crown geometric criticalities that can be found in all the hairpin bends. For example, in hairpin bend n. 3, the crown under-sizing was evident (Figure 9f), so the simultaneous entry of a 12 m long bus and car into the bend was not guaranteed. Therefore, the hairpin bend study was extended by evaluating the space D between the entry/exit lanes, which was found close to the maximum value, as defined in Section 4, i.e., D = 19.00 m.

The reference layout (Figure 8) was overlaid on the hairpin bend, taking care to make the inner circle of radius 6.00 m osculatory to the corresponding inner edge of the traffic lane (Figure 10a). It can be seen that the hairpin circular crow requires a geometric adjustment in order to meet the expected operating conditions, i.e., the safe crossing of bus and car.

The outer radius of the circular crown needs to be increased and the “lower” entrance/exit branch needs to be connected to the existing road (Figure 10b).

The new hairpin bend layout was defined and its geometric set-up is shown in Figure 10c,d. The new layout effectiveness was subsequently verified by swept path analysis simulations carried out with Autodesk Vehicle Tracking^® software [23]. The obtained results (Figure 10e,f) confirmed that the modified hairpin bend guarantees the optimal bend entry of a car and a 12 m long bus travelling in opposite directions. In particular, the simulations show that the safety clearance gap between vehicles in the hairpin bend crown is always higher than the minimum safety clearance (Δ_min = 0.55 m) as discussed in Section 4 (Figure 4 and Figure 8, step 8).

Figure 10g shows the bus steering diagram for a travel speed of 5 km/h. It can be seen that the critical condition of maximum steering occurs over a rather small percentage of path development (5.37%) and that the diagram itself is sufficiently regular.

For the entrance/exit branches, the hairpin bend retrofitting does not require any changes in routing and/or off-site works. These works only concern the circular crown. An outward widening along the bend vertex of 1.55 m is necessary. This produces an overall increase in the paved area of approximately 125 m² (Figure 10h).

The refitting execution is compatible with the orographic/topographic site layout. The presence of a retaining wall in the area highlighted in Figure 10h does not allow for easy implementation of the required geometry, which would require retaining the structure, partial demolition and repositioning (Figure 10i) with an inevitable increase in costs.

Furthermore, widening the crown requires additional retaining structures to contain the roadway widening. In general, and even more so in cases like this, it is always necessary to develop a prior benefit/cost analysis aimed at verifying the economic feasibility in relation to the increase in functionality, safety and environmental sustainability of the planned works [24,25,26].

6. Discussion

The proposed methodology makes it possible to carry out the design and, above all, the geometric retrofitting of hairpin bends. This methodology is justified by the lack of standards and guidelines in the international context and by the widespread tendency in all countries without a specific regulatory framework to “borrow” the rare standards in force in other countries. Internationally (including Italy), the Swiss standard SNV640198a, described in detail in Section 2, is widely used. The proposed methodology refers to a specific but very frequent configuration, i.e., the simultaneous entry into a bend of a 12 m long bus and a passenger car proceeding in the opposite direction. However, the methodology is entirely general because it can similarly be applied to any type of vehicle and any type of road. The theoretical applications of gyration formulae and their subsequent experimental validation by means of swept path analysis techniques make it possible to take into account all the problem variables (vehicles and hairpin bends’ geometric dimensions, roads typologies, vehicle kinematics, safety clearance gap and vehicle design speeds, etc.). The large number of variables involved justifies the methodology “complexity”. To summarize, in the case of a new hairpin design, the methodology can be traced back to the following four stages:

• circular crown pre-dimensioning and geometric verification by gyration formulas and swept path analysis simulations;
• hairpin entry/exit branches pre-dimensioning and geometrical verification according to the road’s hierarchical class and the route layout;
• constant–radius junction curves’ pre-dimensioning for the connection between the circular crown and the entry/exit branches;
• implementation of swept path analysis simulations for the geometric verification of the planned hairpin bend.

In case of existing roads’ retrofitting, the proposed methodology makes it possible to identify, by means of a safety review process, the hairpin bend’s geometric criticalities and subsequently to design the necessary adjustments. As shown in the case study (Section 5), it is possible to adapt any road type with different carriageway dimensions. In fact, the hairpin bend layouts (Figure 6) can be reworked for any carriageway width and applied in the geometric retrofit design. However, it must be clearly noted that the hairpin bend design/retrofitting does not end with the geometry, but it is necessary to solve difficult problems with respect to the longitudinal profile, superelevation, retaining structures, etc. Some indications concerning the superelevation management have already been given in Section 4. The case study is representative of how the retaining structure’s presence conditions the hairpin retrofit process. In fact, the construction of expensive retaining works always makes it necessary to develop accurate benefit/cost analyses to verify the economic sustainability of the intervention.

7. Conclusions

Mountain roads are characterized by the presence of particular planimetric curves called hairpin bends. In this paper, the authors, starting from the issues that emerged within the MIUR PON R&I 2014–2020 Program project, describe the main characteristics of these curves, highlight the differences with the planimetric bends used in ordinary roads and provide a contribution to their design/geometrical retrofitting. This need is justified by the international lack of guidelines and standards that address the problem in a complete and exhaustive manner. One of the rare normative references used is the Swiss standard SNV 640198a. On the basis of this standard, a generally valid methodological approach was developed to construct hairpin bends’ new planimetric layouts that can be used internationally. The implemented methodology was developed with a mixed analytical and experimental approach by means of swept path analysis simulations.

Taking the Italian context as a reference, the methodology has been applied to the development of new geometric layouts that provide a valid contribution to the design/geometrical retrofitting of hairpin bends, when it is necessary to guarantee the simultaneous entry into the bend of a 12 m long bus and a car travelling in the opposite direction.

Finally, with regard to the problem of the geometric retrofitting of existing hairpin bends, the authors proposed the application of the new methodology to a case study of a hairpin bend identified in the area of the Lucanian Dolomites.