Predicting Pavement Condition Index Using Fuzzy Logic Technique
Abstract
:1. Introduction and Related Work
1.1. Fuzzy Logic Approach
1.2. Fuzzy Rule-Based System
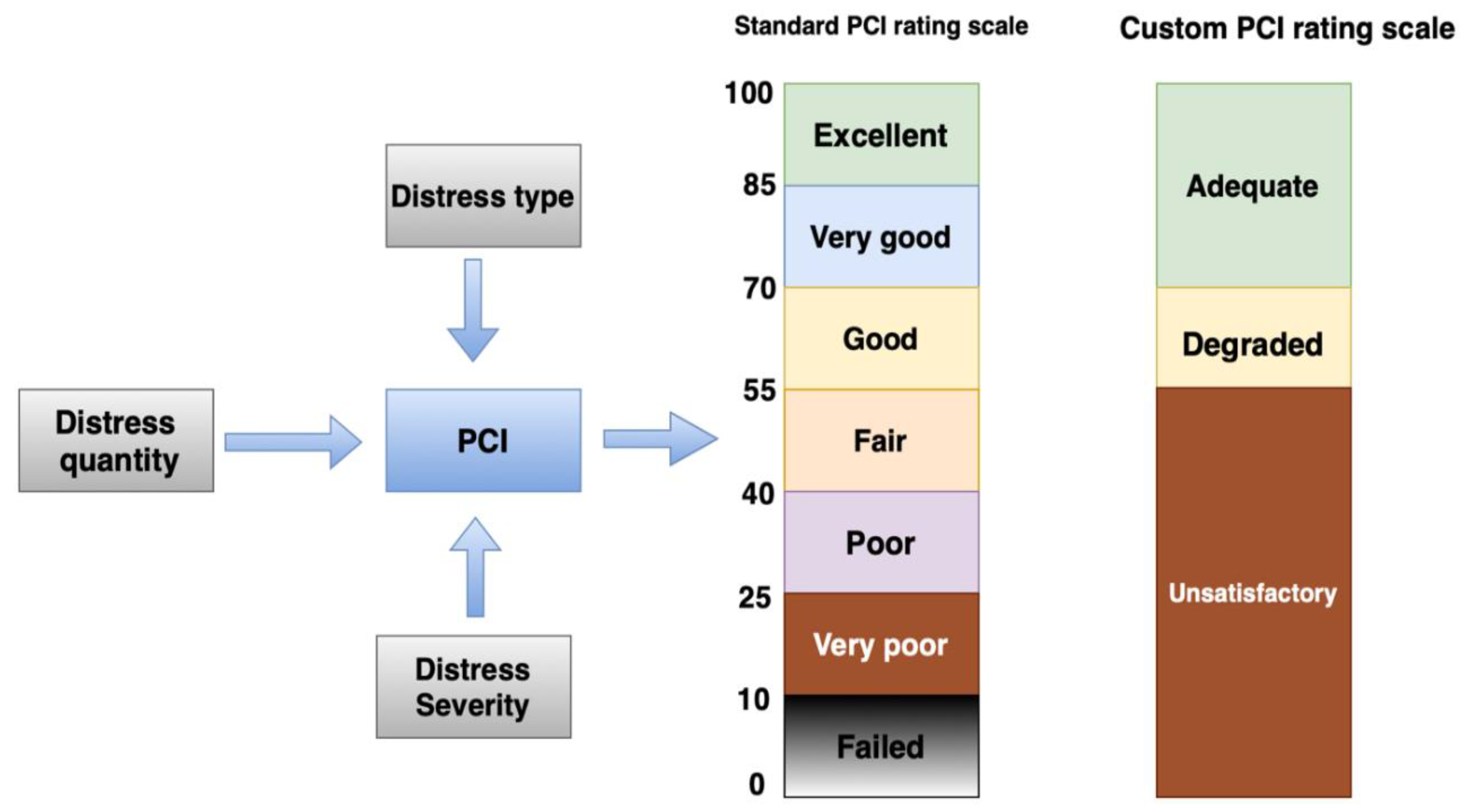
2. Research Objective
Methodology and Data Collection
3. Fuzzy Inference System (FIS) and Membership Function
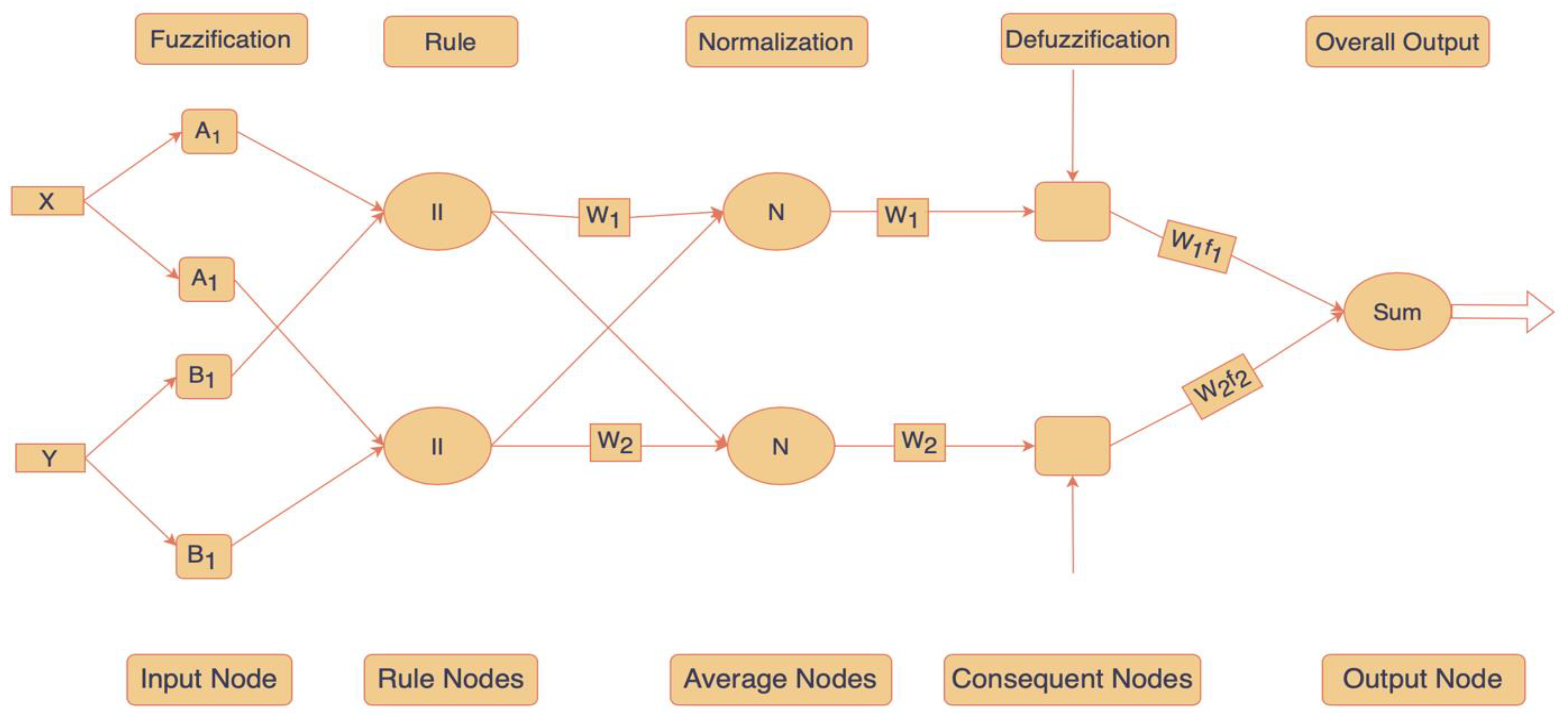
4. Mathematical Development
4.1. Model Formulation
4.2. Data Pre-Processing and Fuzzification
4.3. Fuzzy Rule Generation
4.4. Defuzzification Methods
- 1.
- Centroid method
- 2.
- Bisector Method
- 3.
- Largest of Maximum
- 4.
- Smallest of Maximum
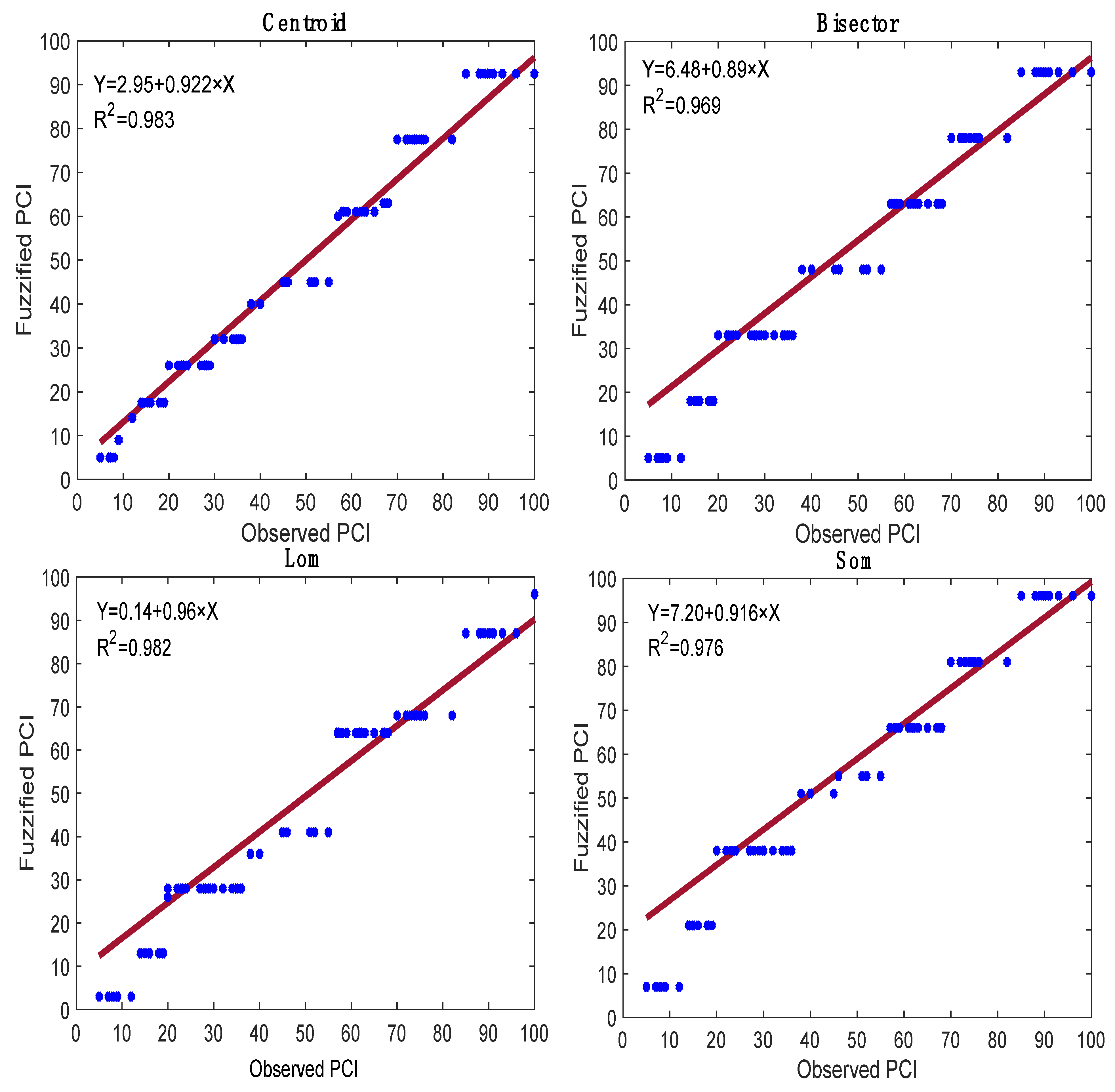
4.5. Evaluation of Model’s Performance
5. Results and Discussions
5.1. Fuzzy Inference Systems’ Configurations for 120 Sections
- Centroid method: The value was 97.3%, while the RMSE and MAE values were 5.28% and 4.617%.
- Bisector method: The value was 96.3%, while the RMSE and MAE values were 5.916% and 5.367%.
- Lom method: The value was 95.4%, while the RMSE and MAE values were 8.096% and 6.185%.
- Som method: The value was 95.8%, while the RMSE and MAE values were 6.696% and 5.567%.
- The results showed the Centroid method gives a more accurate result ( = 97.3%, RMSE = 5.28%, and MAE = 4.617%) compared to other techniques.
- The results showed the Lom method gives the lowest accurate result ( = 95.4%, RMSE = 8.096%, and MAE = 6.185%) compared to other techniques.
5.2. Fuzzy Inference Systems’ Configurations for 150 Sections
- Centroid method: The value was 98.3%, while the RMSE and MAE values were 4.957% and 4.243%.
- Bisector method: The value was 96.9%, while the RMSE and MAE values were 5.499% and 5.347%.
- Lom method: The value was 98.2%, while the RMSE and MAE values were 5.042% and 4.487%.
- Som method: The value was 97.6%, while the RMSE and MAE values were 5.465% and 4.92%.
- The results showed the Centroid method gives a more accurate result ( = 98.3%, RMSE = 4.957%, and MAE = 4.243%) compared to other techniques.
- The results showed the Bisector method gives the lowest accurate result ( = 96.9%, RMSE = 5.449%, and MAE = 5.347%) compared to other techniques.
5.3. Sensitivity Analysis
5.4. Comparison and Validation of the Models
- Centroid method: The results of the statistical measures of 150 sections were improved by 1.03%, 6.12%, and 8.10% compared to 120 sections for , RMSE, and MAE, respectively.
- Bisector method: The results of the statistical measures of 150 sections were improved by 0.62%, 7.01%, and 0.372% compared to 120 sections for , RMSE, and MAE, respectively.
- Lom method: The results of the statistical measures of 150 sections were improved by 2.85%,37.72%, and 27.45% compared to 120 sections for , RMSE, and MAE, respectively.
- Som method: The results of the statistical measures of 150 sections were improved by 1.84%,18.38%, and 11.6% compared to 120 sections for , RMSE, and MAE, respectively.
- The results show the Centroid method of 150 sections gave a more accurate result ( = 98.3%, RMSE = 4.957%, and MAE = 4.243%) compared to other techniques.
6. Conclusions
- This technique has a crucial advantage because it generates rules from large-scale distress data in a short time, especially when robust distress data are required, and the distress classification has become more consistent.
- As the FIS technique uses linguistic variables, this technique enables pavement engineers to identify pavement conditions and enhance decision-making processes, reduces human involvement in decision-making processes, and provides consistency to the process.
- Rutting and transverse cracking have the most influence on the FPCI calculation. Longitudinal cracking and fatigue cracking have some influence on the model, while patching, bleeding, and ravelling had only minor effects on the FPCI calculation.
- According to the results, the differences between the observed data and results from fuzzy logic system techniques were acceptable within allowed limits. The results also indicate that the models became more accurate as the number of road sections increased.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shahin, M.Y. Pavement Management for Airports, Roads, and Parking Lots; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Fwa, T.F. The Handbook of Highway Engineering; CRC Press: Boca Raton, FL, USA, 2006; pp. 19–25. [Google Scholar]
- Shahin, M.Y. Pavement Management for Airports, Roads, and Parking Lots, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Ahmed, N.G.; Awda, G.J.; Saleh, S.E. Development of pavement condition index model for flexible pavement in Baghdad city. J. Eng. 2008, 14, 2120–2135. [Google Scholar]
- Mousa, E.; El-Badawy, S.; Azam, A. Effect of reclaimed asphalt pavement in granular base layers on predicted pavement performance in Egypt. Innov. Inf. Solut. 2020, 5, 57. [Google Scholar] [CrossRef]
- Ali, A.; Dhasmana, H.; Hossain, K.; Hussein, A. Modeling Pavement Performance Indices in Harsh Climate Regions. J. Transp. Eng. Part B Pavements 2021, 147, 04021049. [Google Scholar] [CrossRef]
- Sagheer, A.M.; Al Kubaisy, Y.A.; Awad, H.A. Diagnosis of Flexible Pavement Road Deterioration by Using Expert System. Iraqi J. Civ. Eng. 2008, 12, 1–25. [Google Scholar]
- Piryonesi, S.M.; El-Diraby, T. Using Data Analytics for Cost-Effective Prediction of Road Conditions: Case of the Pavement Condition; Rep. No. FHWA-HRT-18-065; Federal Highway Administration: Washington, DC, USA, 2018. [Google Scholar]
- Sony, S.; Laventure, S.; Sadhu, A. A literature review of next-generation smart sensing technology in structural health monitoring. Struct. Control Health Monit. 2019, 26, e2321. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T. A machine-learning solution for quantifying the impact of climate change on roads. In Proceedings of the CSCE Annual Conf. Montreal: Canadian Society for Civil Engineering, Montreal, QC, Canada, 12–15 June 2019. [Google Scholar]
- Kırba, Ş.U.; Karaşahin, M. Performance models for hot mix asphalt pavements in urban roads. Constr. Build. Mater. 2016, 116, 281–288. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T.E. Data analytics in asset management: Cost-effective prediction of the pavement condition index. J. Infrastruct. Syst. 2020, 26, 04019036. [Google Scholar] [CrossRef]
- Piryonesi, S.M.; El-Diraby, T.E. Role of data analytics in infrastructure asset management: Overcoming data size and quality problems. J. Transp. Eng. Part B. Pavement 2020, 146, 04020022. [Google Scholar] [CrossRef]
- Imam, R.; Murad, Y.; Asi, I.; Shatnawi, A. Predicting pavement condition index from international roughness index using gene expression programming. Innov. Infrastruct. Solut. 2021, 6, 139. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 38, 656–657. [Google Scholar] [CrossRef] [Green Version]
- Moazami, D.; Behbahani, H.; Muniandy, R. Pavement rehabilitation and maintenance prioritization of urban roads using fuzzy logic. Expert Syst. Appl. 2011, 38, 12869–12879. [Google Scholar] [CrossRef]
- Mahmood, M.S. Pavement section classification by using fuzzy rule-based system. In Proceedings of the Research and the Researcher 4th Annual Research Practice Course Conference, Nottingham, UK, 17 May 2013; pp. 58–63. [Google Scholar]
- Mahmood, M.S. Network-Level Maintenance Decisions for Flexible Pavement Using a Soft Computing-Based Framework. Ph.D. Thesis, Highway and Airport Engineering, Nottingham Trent University, Nottingham, UK, 2015. [Google Scholar]
- Jeong, H.; Kim, H.; Kim, K.; Kim, H. Prediction of flexible pavement deterioration in relation to climate change using fuzzy logic. J. Infrastruct. Syst. 2017, 23, 04017008. [Google Scholar] [CrossRef]
- Karashahin, M.; Terzi, S. Performance model for asphalt concrete pavement based on the fuzzy logic approach. Transport 2014, 29, 18–27. [Google Scholar] [CrossRef] [Green Version]
- Mamdani, E.H. Application of fuzzy algorithms for control of simple dynamic plants. Proc. IEEE 1976, 121, 1585–1588. [Google Scholar] [CrossRef]
- Artificial intelligence-based decision support technologies in pavement management. Comput. Aided Civ. Infrastruct. Eng. 2001, 16, 143–157. [CrossRef]
- Zadeh, L.A. Probability Theory and Fuzzy Logic; Computer Science Division Department of EECS UC: Berkeley, CA, USA, 2003. [Google Scholar]
- Zadeh, L.A. Fuzzy sets, information and control. Inf. Technol. 1965, 8, 338–353. [Google Scholar]
- Wang, K.; Liu, F. Fuzzy set-based and performance-oriented pavement network optimization system. J. Infrastruct. Syst. 1997, 3, 154–159. [Google Scholar] [CrossRef]
- Isik, H.; Arslan, S. The design of ultrasonic therapy device via fuzzy logic. Expert Syst. App 2011, 38, 7342–7348. [Google Scholar] [CrossRef]
- Kusan, H.; Aytekin, O.; Ozdemir, I. The use of fuzzy logic in predicting house selling price. Expert Syst. Appl. 2010, 37, 1808–1813. [Google Scholar] [CrossRef]
- Hainin, R.; Reshi, W.F.; Niroumand, H. The Importance of Stone Mastic Asphalt in Construction. Electron. J. Geotech. Eng. 2012, 17, 49–56. [Google Scholar]
- STM International. ASTM D6433-18 Standard Practice for Roads and Parking Lots Pavement Condition Index Surveys; STM: West Conshohocken, PA, USA, 2018. [Google Scholar] [CrossRef]
- Mehran, K. Takagi-sugeno fuzzy modeling for process control. Ind. Autom. Robot. Artif. Intell. 2008, 262, 1–31. [Google Scholar]
- Sugeno, M. An introductory survey of fuzzy control. Inf. Sci. 1985, 36, 59–83. [Google Scholar] [CrossRef]
- Bunce, J.A. Effect of boundary layer conductance on the response of stomata to humidity. Plant Cell Environ. 2000, 8, 55–57. [Google Scholar] [CrossRef]



| Parameters | Unit | Min Statistic | Maxi Statistic | Mean Statistic | Mean Std. Error | Std Statistic |
|---|---|---|---|---|---|---|
| PCI | - | 5.00 | 100.00 | 59.07 | 2.78 | 32.34 |
| Rutting | (mm) | 0.0 | 135.9 | 23.6 | 3.1 | 37.7 |
| Fatigue Cracking | () | 0.00 | 377.90 | 38.59 | 6.58 | 76.48 |
| Block Cracking | () | 0.00 | 557.60 | 5.80 | 4.30 | 50.01 |
| Longitudinal Cracking | () | 0.00 | 325.60 | 66.88 | 7.77 | 90.29 |
| Transverse Cracking | () | 0.00 | 192.30 | 30.63 | 3.74 | 43.50 |
| Patching | ( | 0.00 | 45.80 | 1.52 | 0.67 | 7.73 |
| Potholes | (Number) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Bleeding | () | 0.00 | 350.80 | 18.95 | 6.12 | 70.32 |
| Ravelling | () | 0.00 | 564.30 | 44.98 | 10.62 | 122.05 |
| Distress of Type | Category | Number of MF | Description |
|---|---|---|---|
| Rutting | Input | 3 | Extremely important |
| Fatigue Cracking | Input | 3 | Relatively important |
| Block Cracking | Input | 3 | Relatively important |
| Longitudinal Cracking | Input | 3 | Important |
| Transverse Cracking | Input | 3 | Important |
| Patching | Input | 3 | Moderately important |
| Potholes | Input | 3 | Moderately important |
| Ravelling | Input | 3 | Relatively important |
| Bleeding | Input | 3 | Relatively important |
| PCI | Output | 7 | Extremely important |
| Rule No. | Distress Type (Input) | FPCI (Output) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Rutting | Fatigue Cracking | Block Cracking | Longitudinal Cracking | Trans Cracking | Patching | Potholes | Bleeding | Ravelling | ||
| 1 | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Excellent |
| 2 | Minimal | Minimal | Minimal | Moderate | Minimal | Minimal | Minimal | Minimal | Minimal | Excellent |
| 3 | Minimal | Minimal | Minimal | Severe | Minimal | Minimal | Minimal | Minimal | Moderate | Very Good |
| 4 | Minimal | Minimal | Minimal | Minimal | Severe | Minimal | Minimal | Minimal | Minimal | Good |
| 5 | Minimal | Severe | Minimal | Moderate | Minimal | Minimal | Minimal | Minimal | Minimal | Good |
| 6 | Minimal | Moderate | Minimal | Minimal | Severe | Minimal | Minimal | Minimal | Minimal | Good |
| 7 | Minimal | Moderate | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Good |
| 8 | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Moderate | Good |
| 9 | Minimal | Moderate | Minimal | Moderate | Severe | Minimal | Minimal | Moderate | Minimal | Good |
| 10 | Minimal | Moderate | Minimal | Moderate | Minimal | Minimal | Minimal | Minimal | Severe | Fair |
| 11 | Minimal | Minimal | Minimal | Moderate | Moderate | Minimal | Minimal | Minimal | Minimal | Fair |
| 12 | Moderate | Severe | Minimal | Minimal | Minimal | Minimal | Minimal | Moderate | Minimal | Fair |
| 13 | Moderate | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Minimal | Severe | Poor |
| 14 | Minimal | Severe | Minimal | Minimal | Moderate | Minimal | Minimal | Minimal | Minimal | Poor |
| 15 | Moderate | Moderate | Minimal | Minimal | Minimal | Moderate | Minimal | Minimal | Minimal | Poor |
| 16 | Minimal | Minimal | Minimal | Moderate | Severe | Minimal | Minimal | Minimal | Minimal | Poor |
| 17 | Minimal | Minimal | Minimal | Moderate | Moderate | Minimal | Minimal | Minimal | Minimal | Very Poor |
| 18 | Moderate | Moderate | Minimal | Minimal | Moderate | Minimal | Minimal | Moderate | Minimal | Very Poor |
| 19 | Moderate | Moderate | Minimal | Moderate | Severe | Minimal | Minimal | Moderate | Moderate | Very Poor |
| 20 | Minimal | Minimal | Minimal | Minimal | Moderate | Minimal | Minimal | Minimal | Severe | Very Poor |
| 21 | Minimal | Severe | Minimal | Severe | Severe | Minimal | Minimal | Moderate | Minimal | Very Poor |
| 22 | Moderate | Moderate | Minimal | Moderate | Moderate | Minimal | Minimal | Minimal | Moderate | Very Poor |
| 23 | Minimal | Minimal | Minimal | Severe | Severe | Minimal | Minimal | Minimal | Minimal | Very Poor |
| 24 | Minimal | Moderate | Minimal | Minimal | Moderate | Minimal | Minimal | Minimal | Minimal | Failed |
| 25 | Moderate | Severe | Minimal | Moderate | Severe | Minimal | Minimal | Minimal | Minimal | Failed |
| 26 | Severe | Moderate | Minimal | Moderate | Severe | Minimal | Minimal | Minimal | Minimal | Failed |
| 27 | Severe | Severe | Minimal | Moderate | Moderate | Minimal | Minimal | Moderate | Minimal | Failed |
| Inference | Number of Sections | Defuzzification | Statistical Measures | ||
|---|---|---|---|---|---|
| RMSE | MAE | ||||
| Mamdani (Triangular) | 120 | Centroid | 97.3 | 5.28 | 4.617 |
| Bisector | 96.3 | 5.916 | 5.367 | ||
| Lom | 95.4 | 8.096 | 6.185 | ||
| Som | 95.8 | 6.696 | 5.567 | ||
| Inference | Number of Sections | Defuzzification | Statistical Measures | ||
|---|---|---|---|---|---|
| RMSE | MAE | ||||
| Mamdani (Triangular) | 150 | Centroid | 98.3 | 4.957 | 4.243 |
| Bisector | 96.9 | 5.499 | 5.347 | ||
| Lom | 98.2 | 5.042 | 4.487 | ||
| Som | 97.6 | 5.465 | 4.92 | ||
| Independent Variable | ||
|---|---|---|
| 120 Sections | 150 Sections | |
| Rutting | 45.1 | 46.5 |
| Fatigue | 27.9 | 28.4 |
| Block Cracking | 0. 1 | 0. 2 |
| Longitudinal Cracking | 26.6 | 26.6 |
| Transverse Cracking | 35.5 | 39.9 |
| Patching | 5.1 | 0.6 |
| Potholes | - | - |
| Bleeding | 9.6 | 7.2 |
| Ravelling | 6.5 | 7.1 |
| Inference | Number of Sections | Defuzzification | Statistical Measures | Improvement (%) | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | ||||
| Mamdani (Triangular) | 120 | Centroid | 97.3 | 5.28 | 4.617 | - | - | - |
| Bisector | 96.3 | 5.916 | 5.367 | - | - | - | ||
| Lom | 95.4 | 8.096 | 6.185 | - | - | - | ||
| Som | 95.8 | 6.696 | 5.567 | - | - | - | ||
| 150 | Centroid | 98.3 | 4.957 | 4.243 | +1.03 | +6.12 | +8.10 | |
| Bisector | 96.9 | 5.499 | 5.347 | +0.62 | +7.01 | +0.372 | ||
| Lom | 98.2 | 5.042 | 4.487 | +2.85 | +37.72 | +27.45 | ||
| Som | 97.6 | 5.465 | 4.92 | +1.84 | +18.38 | +11.6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.; Heneash, U.; Hussein, A.; Eskebi, M. Predicting Pavement Condition Index Using Fuzzy Logic Technique. Infrastructures 2022, 7, 91. https://doi.org/10.3390/infrastructures7070091
Ali A, Heneash U, Hussein A, Eskebi M. Predicting Pavement Condition Index Using Fuzzy Logic Technique. Infrastructures. 2022; 7(7):91. https://doi.org/10.3390/infrastructures7070091
Chicago/Turabian StyleAli, Abdualmtalab, Usama Heneash, Amgad Hussein, and Mohamed Eskebi. 2022. "Predicting Pavement Condition Index Using Fuzzy Logic Technique" Infrastructures 7, no. 7: 91. https://doi.org/10.3390/infrastructures7070091
APA StyleAli, A., Heneash, U., Hussein, A., & Eskebi, M. (2022). Predicting Pavement Condition Index Using Fuzzy Logic Technique. Infrastructures, 7(7), 91. https://doi.org/10.3390/infrastructures7070091






