Application of a Non-Invasive Technique for the Preservation of a Fortified Masonry Tower
Abstract
:1. Introduction
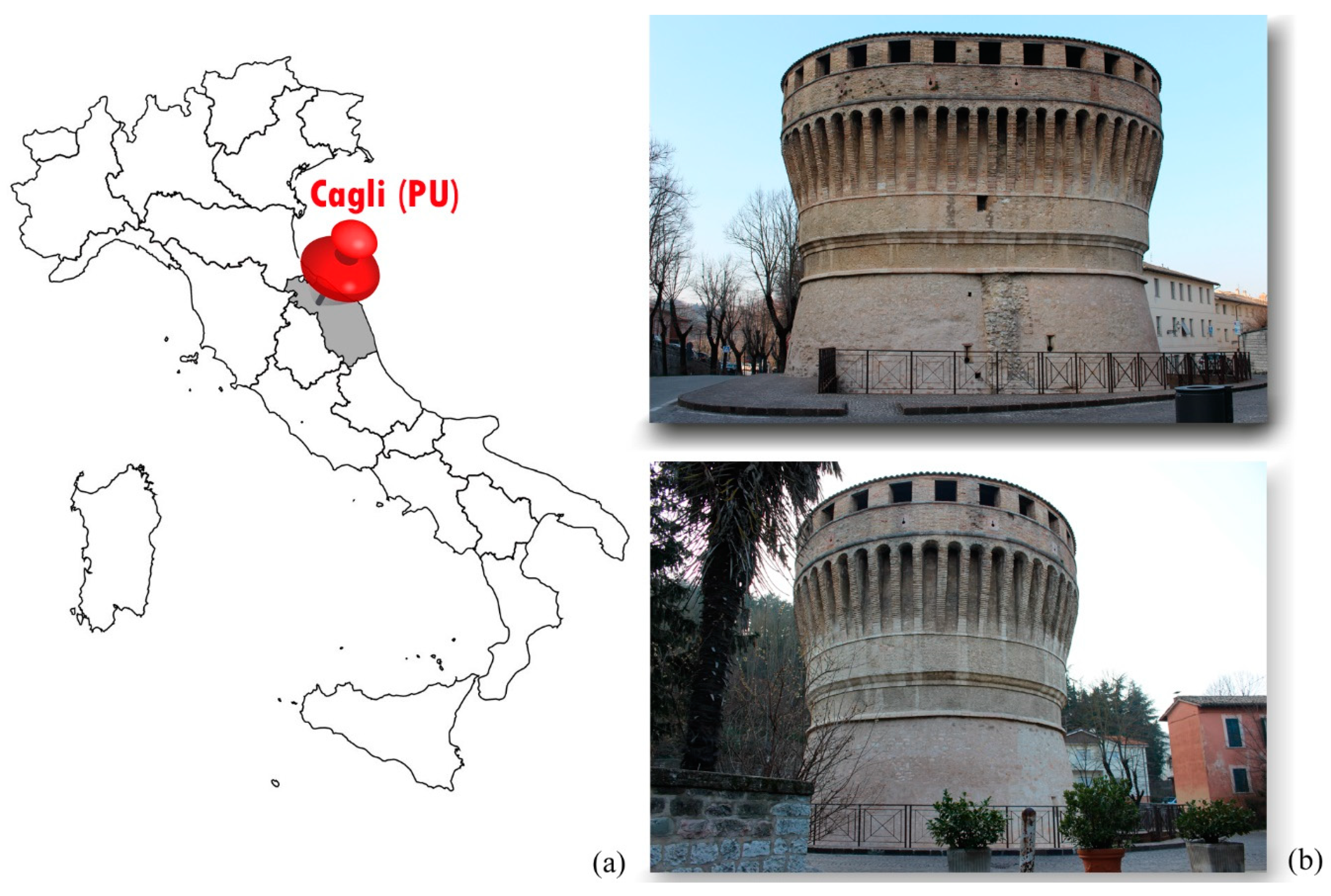
2. The Fortified Tower of Cagli
2.1. Historical Survey
2.2. Geometrical Survey
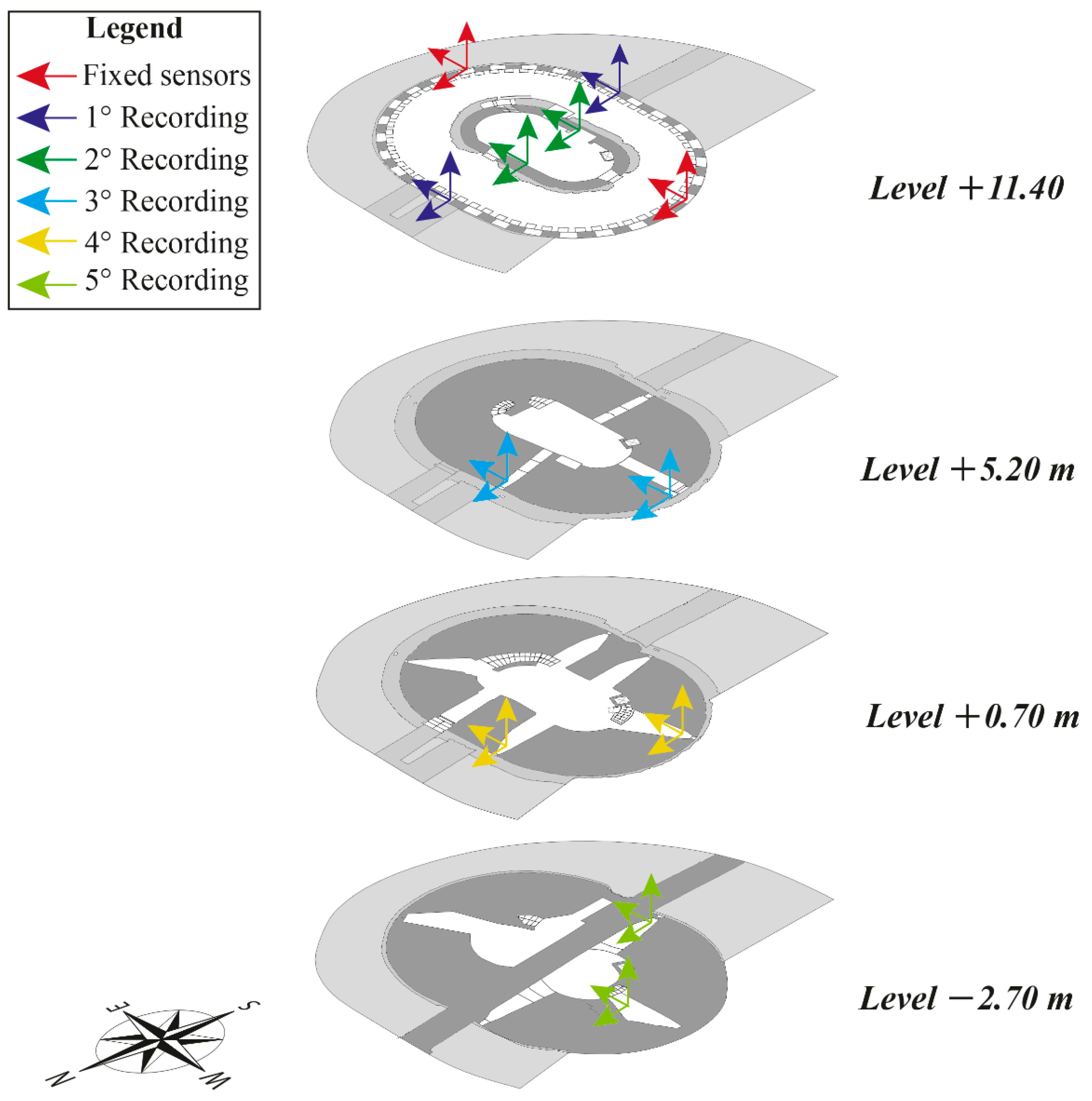
3. Ambient Vibration Tests
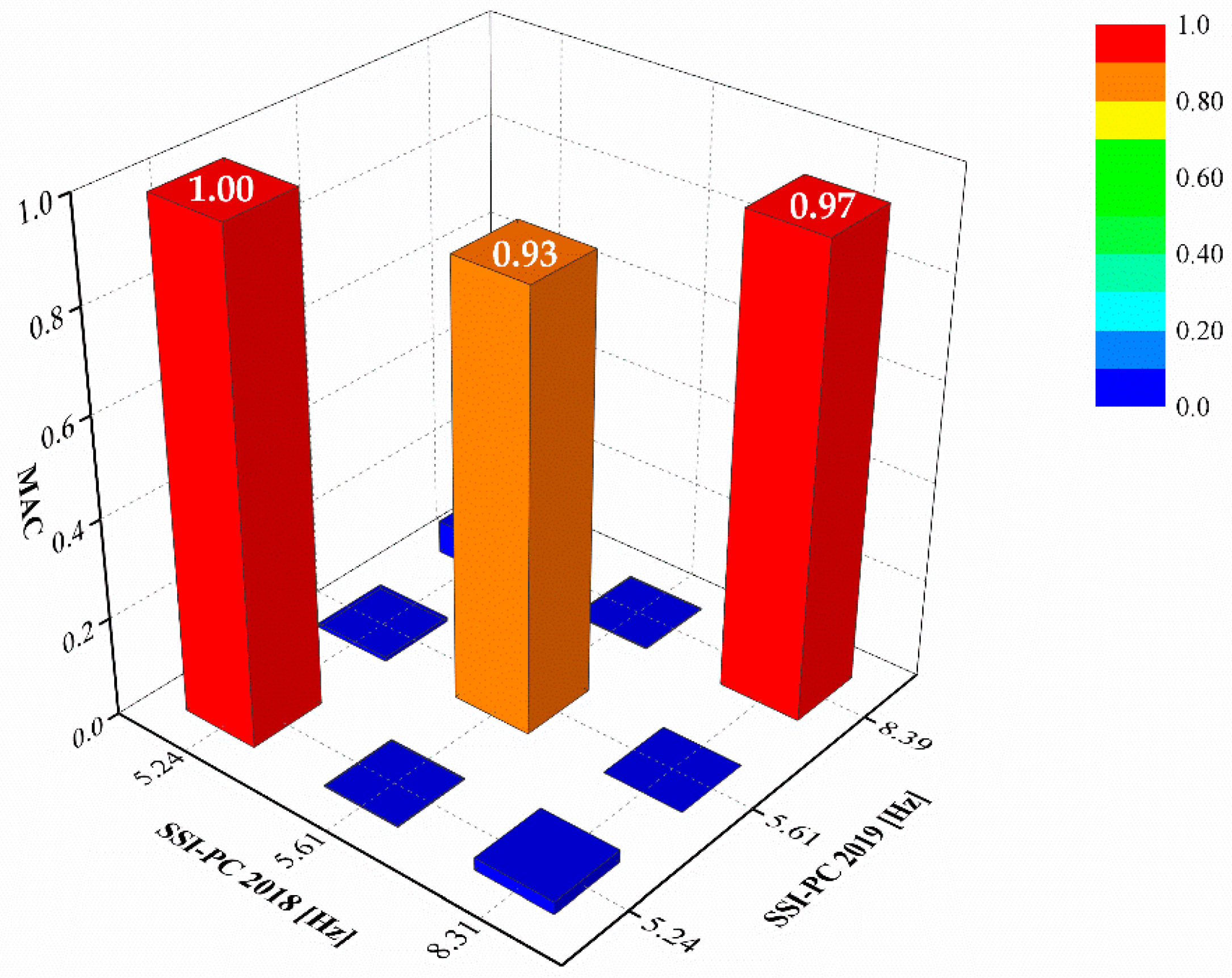
4. Operation Modal Analysis
5. Numerical Model and Model Updating
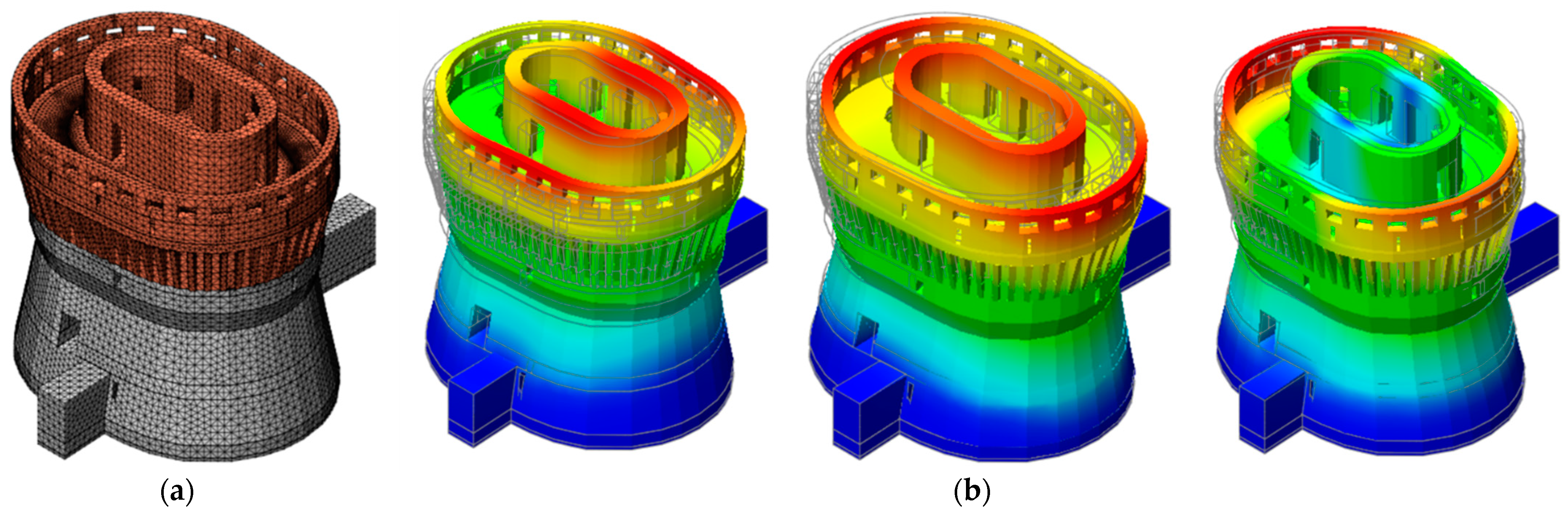
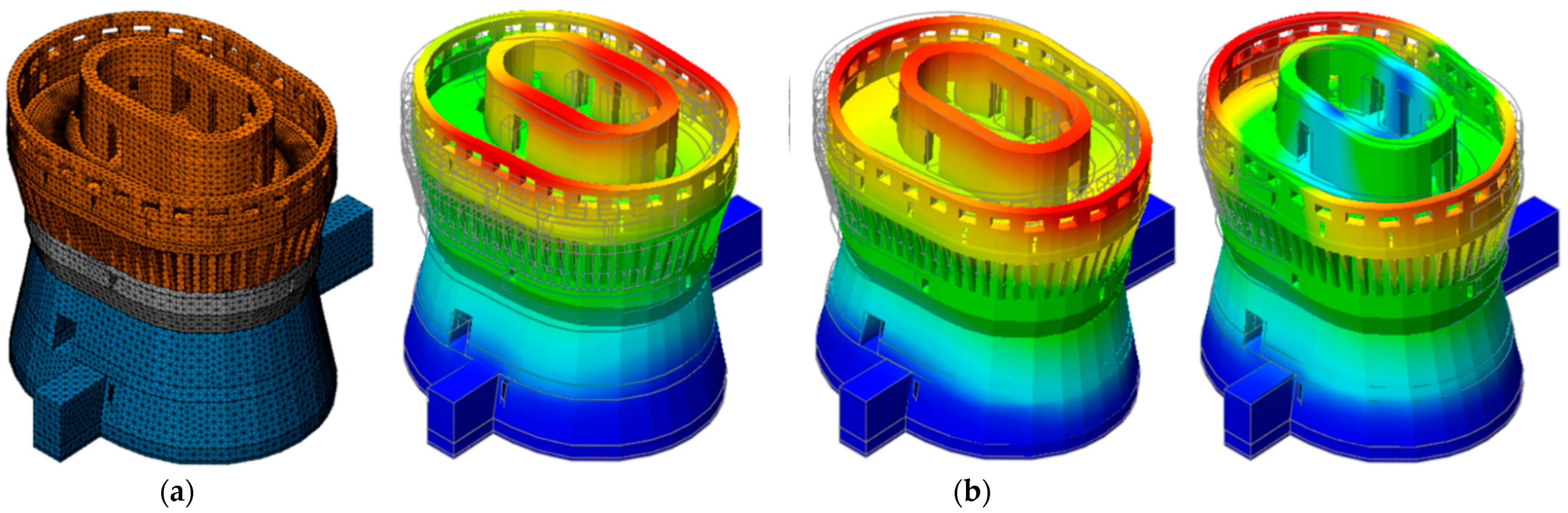
5.1. The Finite Element Model
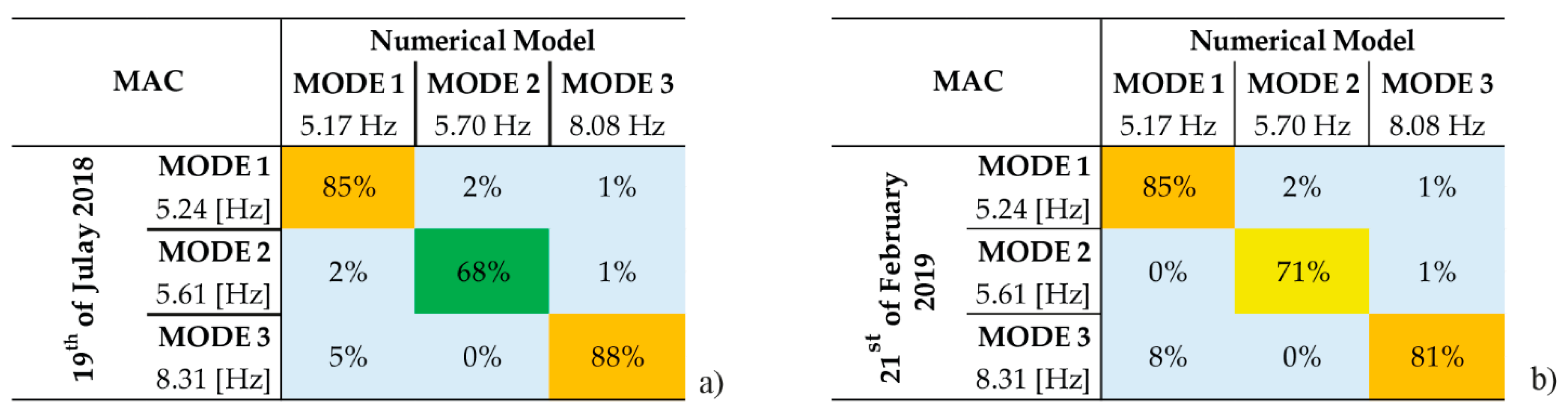
5.2. Model Updating
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. A review of numerical models for masonry structures. In Numerical Modeling of Masonry and Historical Structures; Elsevier: Amsterdam, The Netherlands, 2019; pp. 3–53. [Google Scholar]
- Lourenço, P.B.; Mendes, N.; Ramos, L.F.; Oliveira, D.V. Analysis of Masonry Structures Without Box Behavior. Int. J. Archit. Herit. 2011, 5, 369–382. [Google Scholar] [CrossRef]
- Clementi, F. Failure Analysis of Apennine Masonry Churches Severely Damaged during the 2016 Central Italy Seismic Sequence. Buildings 2021, 11, 58. [Google Scholar] [CrossRef]
- Zizi, M.; Corlito, V.; Lourenço, P.B.; De Matteis, G. Seismic vulnerability of masonry churches in Abruzzi region, Italy. Structures 2021, 32, 662–680. [Google Scholar] [CrossRef]
- Giordano, E.; Clementi, F.; Nespeca, A.; Lenci, S. Damage Assessment by Numerical Modeling of Sant’Agostino’s Sanctuary in Offida During the Central Italy 2016–2017 Seismic Sequence. Front. Built Environ. 2019, 4, 87. [Google Scholar] [CrossRef] [Green Version]
- Formisano, A.; Di Lorenzo, G.; Krstevska, L.; Landolfo, R. Fem Model Calibration of Experimental Environmental Vibration Tests on Two Churches Hit by L’Aquila Earthquake. Int. J. Archit. Herit. 2021, 15, 113–131. [Google Scholar] [CrossRef]
- Rots, J.G. Smeared and discrete representations of localized fracture. Int. J. Fract. 1991, 51, 45–59. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Ferrante, A.; Loverdos, D.; Clementi, F.; Milani, G.; Formisano, A.; Lenci, S.; Sarhosis, V. Discontinuous approaches for nonlinear dynamic analyses of an ancient masonry tower. Eng. Struct. 2021, 230, 111626. [Google Scholar] [CrossRef]
- Ferrante, A.; Schiavoni, M.; Bianconi, F.; Milani, G.; Clementi, F. Influence of Stereotomy on Discrete Approaches Applied to an Ancient Church in Muccia, Italy. J. Eng. Mech. 2021, 147, 04021103. [Google Scholar] [CrossRef]
- Beatini, V.; Royer-Carfagni, G.; Tasora, A. A non-smooth-contact-dynamics analysis of Brunelleschi’s cupola: An octagonal vault or a circular dome? Meccanica 2019, 54, 525–547. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.A. A computer model for simulating progressive large-scale movements in blocky rock systems. In Proceedings of the Symposio of the International Society of Rock Mechanics, Nancy, France, 4–6 October 1971. [Google Scholar]
- Moreau, J.J. Unilateral Contact and Dry Friction in Finite Freedom Dynamics. In Nonsmooth Mechanics and Applications; Springer: Vienna, Austria, 1988; pp. 1–82. [Google Scholar]
- Jean, M. The non-smooth contact dynamics method. Comput. Methods Appl. Mech. Eng. 1999, 177, 235–257. [Google Scholar] [CrossRef] [Green Version]
- Ferrante, A.; Giordano, E.; Clementi, F.; Milani, G.; Formisano, A. FE vs. DE Modeling for the Nonlinear Dynamics of a Historic Church in Central Italy. Geosciences 2021, 11, 189. [Google Scholar] [CrossRef]
- Mendes, N.; Lourenço, P.B. Seismic assessment of historic masonry structures: Out-of-plane effects. In Numerical Modeling of Masonry and Historical Structures; Elsevier: Amsterdam, The Netherlands, 2019; pp. 141–162. [Google Scholar]
- Malena, M.; Portioli, F.; Gagliardo, R.; Tomaselli, G.; Cascini, L.; de Felice, G. Collapse mechanism analysis of historic masonry structures subjected to lateral loads: A comparison between continuous and discrete models. Comput. Struct. 2019, 220, 14–31. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, F.; Lin, Q.; Li, Q. Application of Sensing Technology in the Protection of Architectural Heritage: A Review. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 28–30 June 2021; pp. 654–658. [Google Scholar]
- De Stefano, A.; Matta, E.; Clemente, P. Structural health monitoring of historical heritage in Italy: Some relevant experiences. J. Civ. Struct. Heal. Monit. 2016, 6, 83–106. [Google Scholar] [CrossRef]
- Giordano, P.F.; Ubertini, F.; Cavalagli, N.; Kita, A.; Masciotta, M.G. Four years of structural health monitoring of the San Pietro bell tower in Perugia, Italy: Two years before the earthquake versus two years after. Int. J. Mason. Res. Innov. 2020, 5, 445. [Google Scholar] [CrossRef]
- Pallarés, F.J.; Betti, M.; Bartoli, G.; Pallarés, L. Structural health monitoring (SHM) and Nondestructive testing (NDT) of slender masonry structures: A practical review. Constr. Build. Mater. 2021, 297, 123768. [Google Scholar] [CrossRef]
- Giordano, E.; Mendes, N.; Masciotta, M.G.; Clementi, F.; Sadeghi, N.H.; Silva, R.A.; Oliveira, D.V. Expeditious damage index for arched structures based on dynamic identification testing. Constr. Build. Mater. 2020, 265, 120236. [Google Scholar] [CrossRef]
- Cawley, P.; Adams, R.D. The location of defects in structures from measurements of natural frequencies. J. Strain Anal. Eng. Des. 1979, 14, 49–57. [Google Scholar] [CrossRef]
- Pepi, C.; Cavalagli, N.; Gusella, V.; Gioffrè, M. Damage detection via modal analysis of masonry structures using shaking table tests. Earthq. Eng. Struct. Dyn. 2021, 50, 2077–2097. [Google Scholar] [CrossRef]
- Giordano, E.; Bertolesi, E.; Clementi, F.; Buitrago, M.; Adam, J.M.; Ivorra, S. Unreinforced and TRM-Reinforced Masonry Building Subjected to Pseudodynamic Excitations: Numerical and Experimental Insights. J. Eng. Mech. 2021, 147, 04021107. [Google Scholar] [CrossRef]
- Gentile, C.; Guidobaldi, M.; Saisi, A. One-year dynamic monitoring of a historic tower: Damage detection under changing environment. Meccanica 2016, 51, 2873–2889. [Google Scholar] [CrossRef] [Green Version]
- Kita, A.; Cavalagli, N.; Ubertini, F. Temperature effects on static and dynamic behavior of Consoli Palace in Gubbio, Italy. Mech. Syst. Signal Processing 2019, 120, 180–202. [Google Scholar] [CrossRef]
- Venanzi, I.; Kita, A.; Cavalagli, N.; Ierimonti, L.; Ubertini, F. Earthquake-induced damage localization in an historic masonry tower through long-term dynamic monitoring and FE model calibration. Bull. Earthq. Eng. 2020, 18, 2247–2274. [Google Scholar] [CrossRef]
- Clementi, F.; Pierdicca, A.; Milani, G.; Gazzani, V.; Poiani, M.; Lenci, S. Numerical model upgrading of ancient bell towers monitored with a wired sensors network. In Proceedings of the 10th International Masonry Conference (IMC_10), Milano, Italy, 9–11 July 2018; Milani, G., Taliercio, A., Garrity, S., Eds.; pp. 1–11. [Google Scholar]
- Standoli, G.; Salachoris, G.P.; Masciotta, M.G.; Clementi, F. Modal-based FE model updating via genetic algorithms: Exploiting artificial intelligence to build realistic numerical models of historical structures. Constr. Build. Mater. 2021, 303, 124393. [Google Scholar] [CrossRef]
- Bianconi, F.; Salachoris, G.P.; Clementi, F.; Lenci, S. A Genetic Algorithm Procedure for the Automatic Updating of FEM Based on Ambient Vibration Tests. Sensors 2020, 20, 3315. [Google Scholar] [CrossRef]
- Altunişik, A.C.; Okur, F.Y.; Genç, A.F.; Günaydin, M.; Adanur, S. Automated Model Updating of Historical Masonry Structures Based on Ambient Vibration Measurements. J. Perform. Constr. Facil. 2018, 32, 04017126. [Google Scholar] [CrossRef]
- Bakir, P.G.; Reynders, E.; Roeck, G. De An improved finite element model updating method by the global optimization technique ‘Coupled Local Minimizers’. Comput. Struct. 2008, 86, 1339–1352. [Google Scholar] [CrossRef]
- Levin, R.I.; Lieven, N.A.J. Dynamic finite element model updating using simulated annealing and genetic algorithms. Mech. Syst. Signal Processing 1998, 12, 91–120. [Google Scholar] [CrossRef] [Green Version]
- ARTeMIS Modal Structural Vibration Solutions A/S. 2021. Available online: https://svibs.com/ (accessed on 25 January 2022).
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification from ambient responses using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441. [Google Scholar] [CrossRef] [Green Version]
- Systems, M.; Leuven, K.U.; Peeters, B.; De Roeck, G. Reference-Based Stochastic Subspace Identification for Output-Only Modal Analysis. Mech. Syst. Signal Processing 1999, 13, 855–878. [Google Scholar] [CrossRef] [Green Version]
- Ewins, D.J. Modal Testing: Theory and Practice; Research Studies Press: Hertfordshire, UK, 1984. [Google Scholar]
- Midas FEA Analysis and Algorithm Manual. 2016. Available online: https://www.midasoft.com/ (accessed on 25 January 2022).
- GU Serie Generale, n. 42 del 20-02-2018—Suppl. Ordinario n. 8; Decreto Ministeriale 17/01/2018—Aggiornamento delle “Norme Tecniche per le Costruzioni”; Ministero delle Infrastrutture e dei Trasporti: Rome, Italy, 2018; pp. 1–198. (In Italian) [Google Scholar]
- GU Serie Generale, n. 35 del 11-02-2019—Suppl. Ordinario n. 5; Circolare 21 gennaio 2019 n. 7 C.S.LL.PP—Istruzioni per l’applicazione dell’Aggiornamento delle “Norme Tecniche per le Costruzioni” di cui al D.M. 17/01/2018; Ministero delle Infrastrutture e dei Trasporti: Rome, Italy, 2019; pp. 1–337. (In Italian) [Google Scholar]

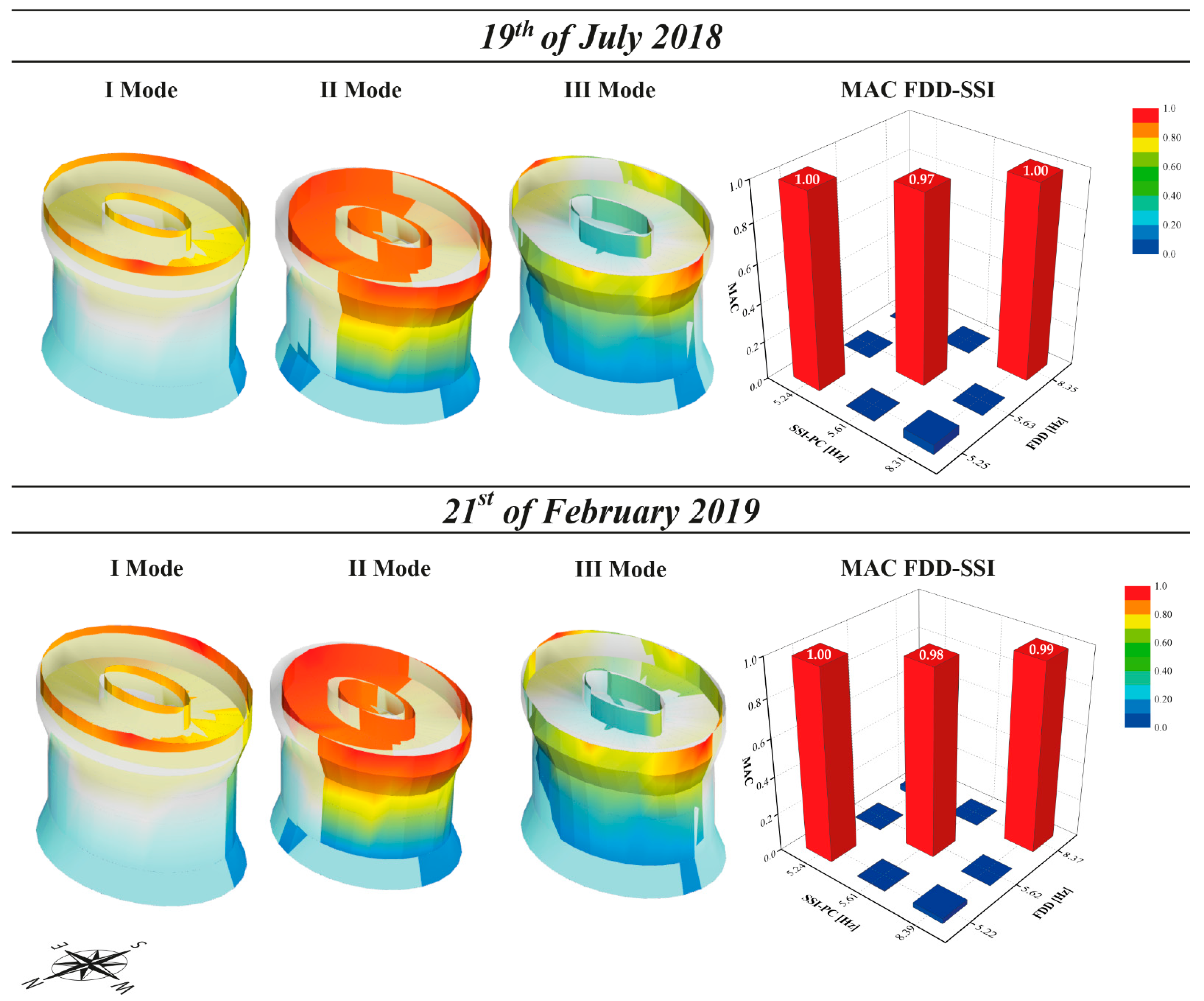
| 19 July 2018 | |||||
| SSI-PC | FDD | ||||
| Mode | Frequencies [Hz] | Complexity [%] | Damping [%] | Frequencies [Hz] | Complexity [%] |
| I | 5.24 | 0.20 | 0.94 | 5.22 (0.4%) | 0.70 |
| II | 5.61 | 4.59 | 1.37 | 5.62 (0.2%) | 3.18 |
| III | 8.31 | 0.63 | 0.51 | 8.30 (0.1%) | 1.04 |
| 21 February 2019 | |||||
| SSI-PC | FDD | ||||
| Mode | Frequencies [Hz] | Complexity [%] | Damping [%] | Frequencies [Hz] | Complexity [%] |
| I | 5.24 | 0.09 | 1.04 | 5.22 (0.4%) | 0.40 |
| II | 5.61 | 1.46 | 1.36 | 5.63 (0.2%) | 4.75 |
| III | 8.39 | 0.33 | 0.55 | 8.40 (0.1%) | 2.23 |
| Material | Elastic Modulus [MPa] | Poisson’s Ratio [-] | Density [kN/m3] |
|---|---|---|---|
| Full bricks and lime mortar | 1500 | 0.4 | 18 |
| Cut stones with good bonding | 1740 | 0.4 | 21 |
| Mode | fnum [Hz] | MAC 2018 | Numerical Modal Shapes | |
|---|---|---|---|---|
| I | 5.05 | 4.00% | 0.83 | Translational on North direction |
| II | 5.56 | 0.89% | 0.68 | Translational on East direction |
| III | 7.90 | 4.93% | 0.88 | Torsional |
| Mode | fnum [Hz] | MAC 2018 | Numerical Modal Shapes | |
|---|---|---|---|---|
| I | 5.17 | 1.34% | 0.85 | Translational on North direction |
| II | 5.70 | 1.60% | 0.68 | Translational on East direction |
| III | 8.08 | 2.77% | 0.88 | Torsional |
| Mode | fnum [Hz] | MAC 2019 | Numerical Modal Shapes | |
|---|---|---|---|---|
| I | 5.17 | 1.34% | 0.85 | Translational on North direction |
| II | 5.70 | 1.60% | 0.71 | Translational on East direction |
| III | 8.08 | 3.69% | 0.81 | Torsional |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giordano, E.; Marcheggiani, L.; Formisano, A.; Clementi, F. Application of a Non-Invasive Technique for the Preservation of a Fortified Masonry Tower. Infrastructures 2022, 7, 30. https://doi.org/10.3390/infrastructures7030030
Giordano E, Marcheggiani L, Formisano A, Clementi F. Application of a Non-Invasive Technique for the Preservation of a Fortified Masonry Tower. Infrastructures. 2022; 7(3):30. https://doi.org/10.3390/infrastructures7030030
Chicago/Turabian StyleGiordano, Ersilia, Laura Marcheggiani, Antonio Formisano, and Francesco Clementi. 2022. "Application of a Non-Invasive Technique for the Preservation of a Fortified Masonry Tower" Infrastructures 7, no. 3: 30. https://doi.org/10.3390/infrastructures7030030
APA StyleGiordano, E., Marcheggiani, L., Formisano, A., & Clementi, F. (2022). Application of a Non-Invasive Technique for the Preservation of a Fortified Masonry Tower. Infrastructures, 7(3), 30. https://doi.org/10.3390/infrastructures7030030








