Design of an Active Damping System for Vibration Control of Wind Turbine Towers
Abstract
:1. Introduction
- A grid search on the timing of an internal or external electrical system fault combined to gusty wind conditions with respect to IEC61400 standards;
- Theoretical design of an active damping system including the TRD and a control algorithm to reduce the vibrations of wind turbine towers;
- Evaluation of the proposed damping system in an extreme load event triggered by the loss of electrical network connection while the turbine is producing power;
- Investigations and discussions on the use of TRD for damping wind turbine vibrations; a comparison between TRD and other types of damping system used in the wind industry.
2. Twin Rotor Damper (TRD)
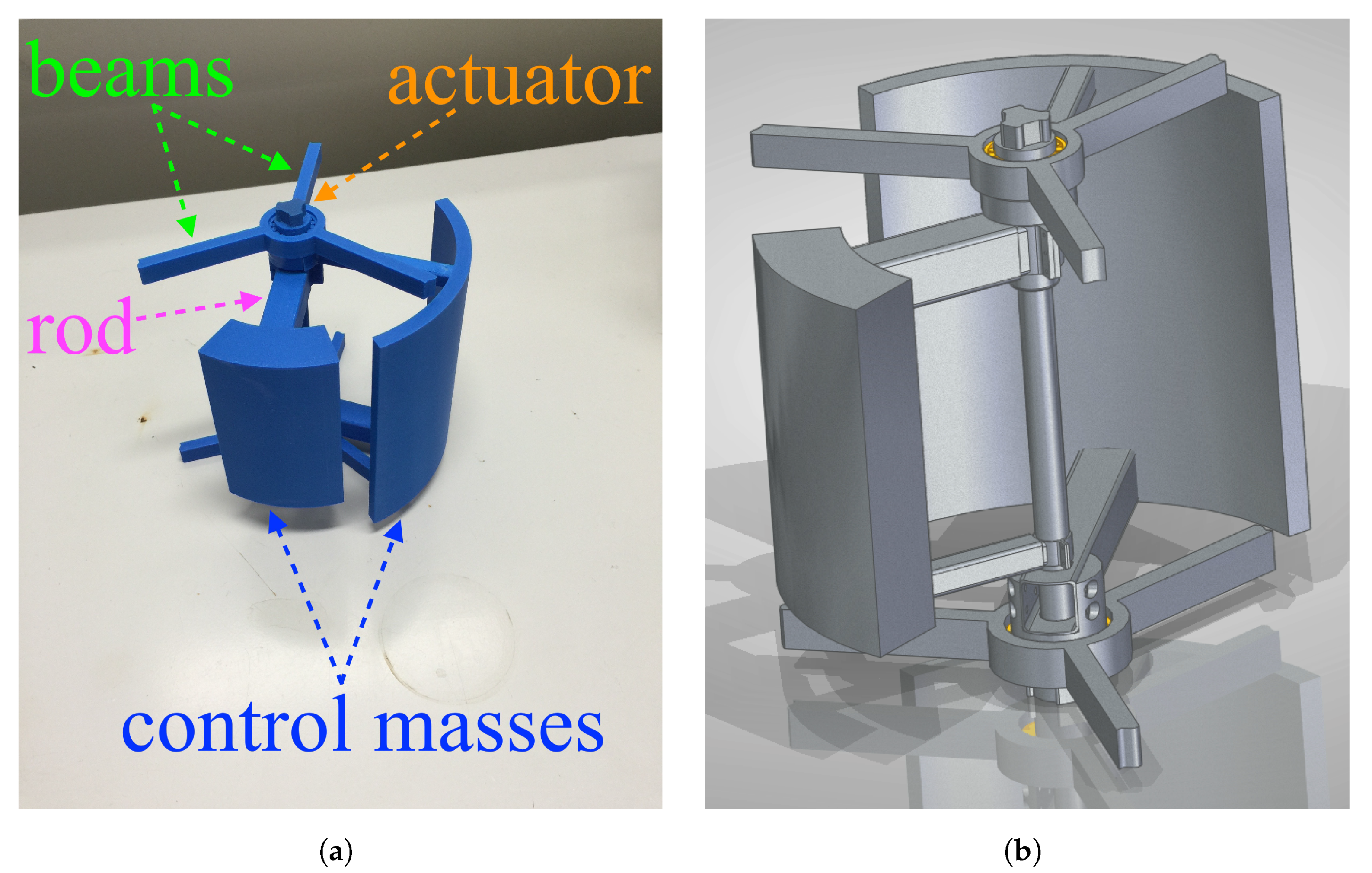
2.1. Theory and Layout
2.2. Single Degree of Freedom (SDOF) Oscillator
| excitation force normalized by | |
| TRD control force normalized by | |
| control mass ratio | |
| natural angular frequency of the system | |
| damping ratio of the system. |
2.3. Phasing the TRD with the SDOF Oscillator
2.3.1. Theory
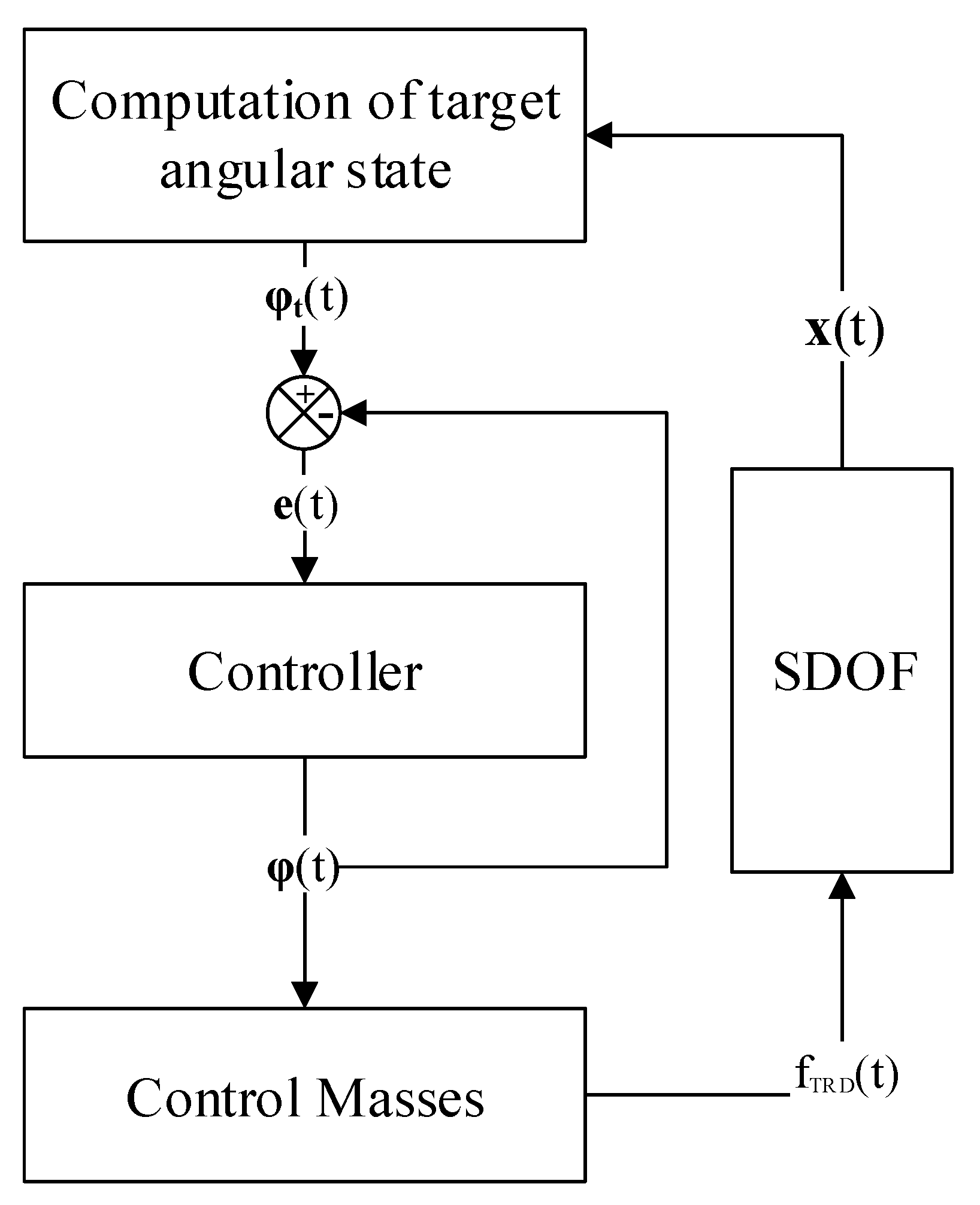
2.3.2. Observer Design
2.3.3. Controller Design
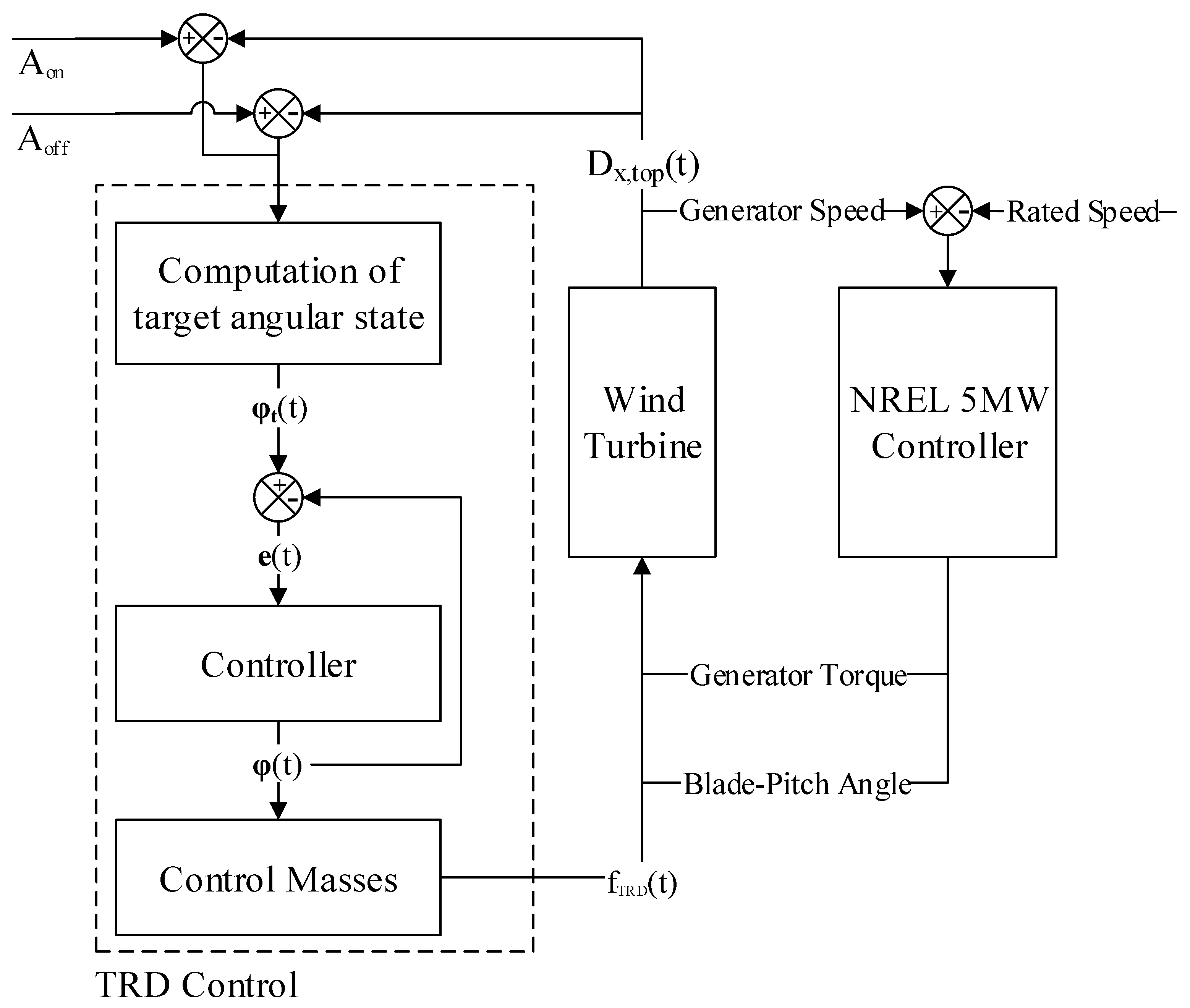
3. Design of a Damping System with the TRD for Wind Turbine
3.1. NREL 5MW Reference Wind Turbine with FAST Simulation Tools
3.2. Design Load Case
3.2.1. Wind Condition: Extreme Operating Gust (EOG)
| = wind speed at hub height (). | |
| based on the wind turbine class specified by designer () |
| z | = height above ground level () |
| = wind turbine hub height (). |
| = annual extreme wind speed () | |
| = wind speed at hub height () | |
| = standard deviation of wind speed | |
| D | = diameter of the rotor () |
| = longitudinal turbulence scale parameter (). |
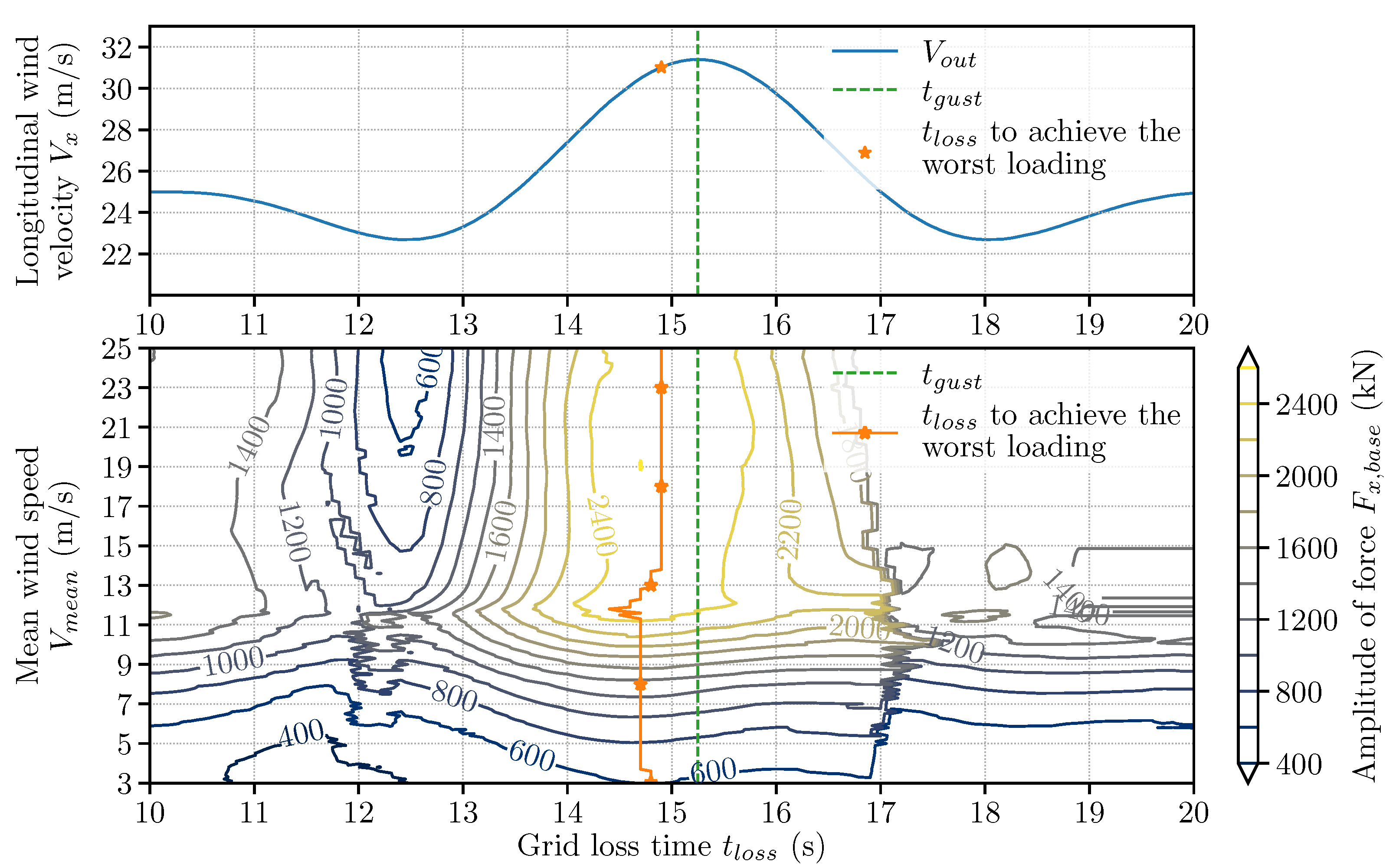
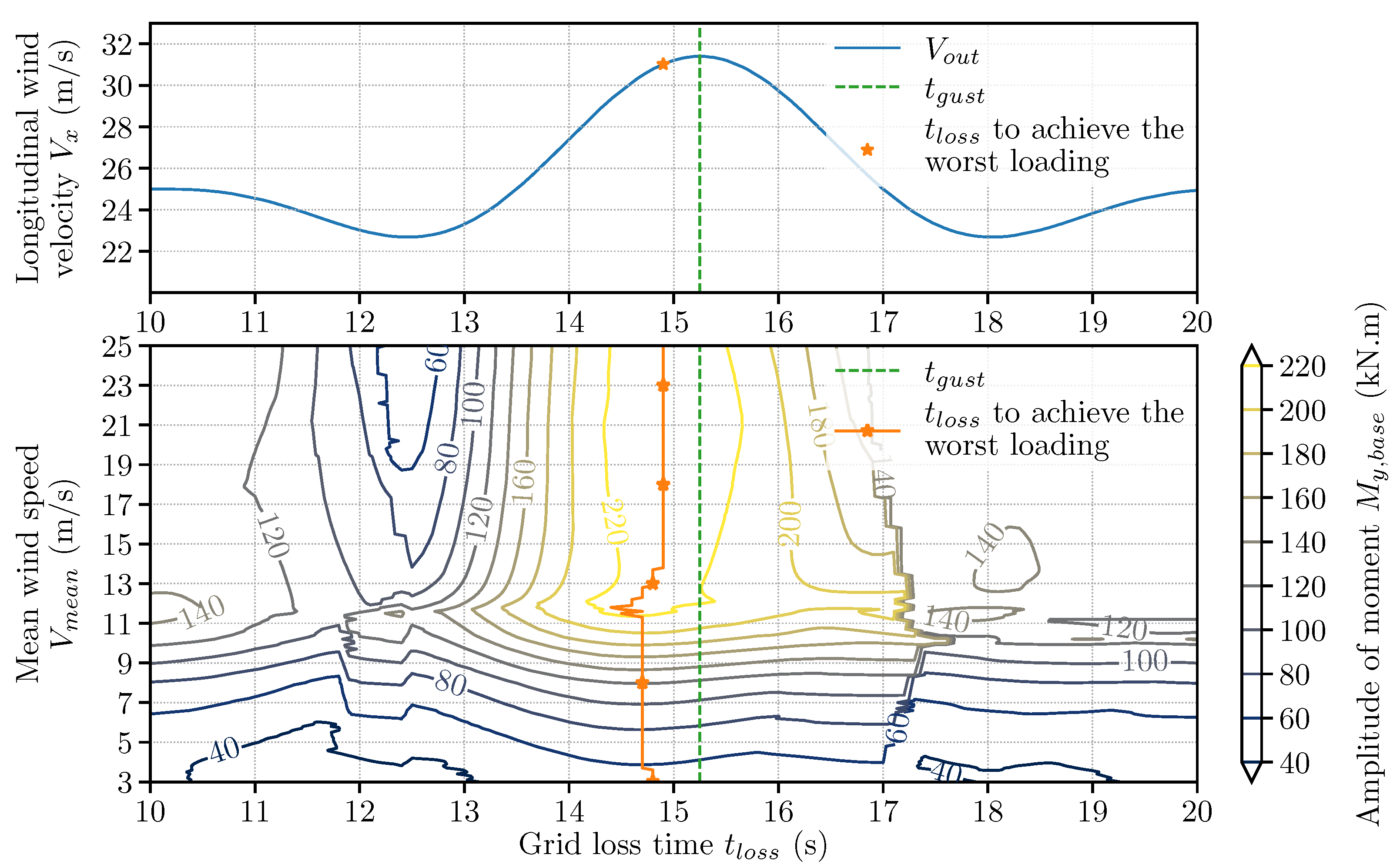
3.2.2. Operating Condition: Grid Loss
3.3. Numerical Setup of FAST with TRD
| Algorithm 1. ON/OFF control of the TRD for the wind turbine tower. |
 |
4. Results and Discussion
4.1. EOG with Grid Loss
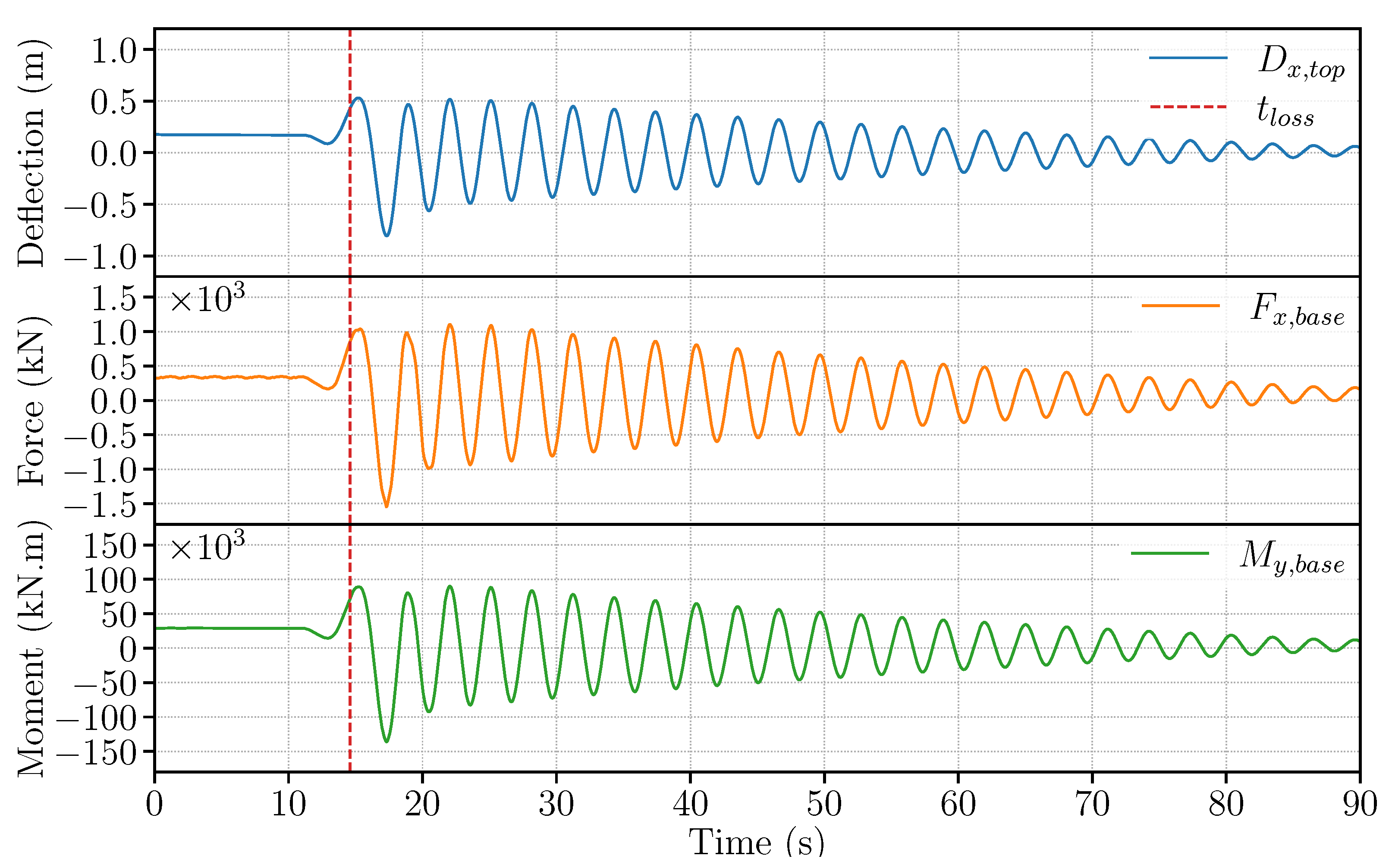
4.1.1. Evaluation of System Performance without Damper
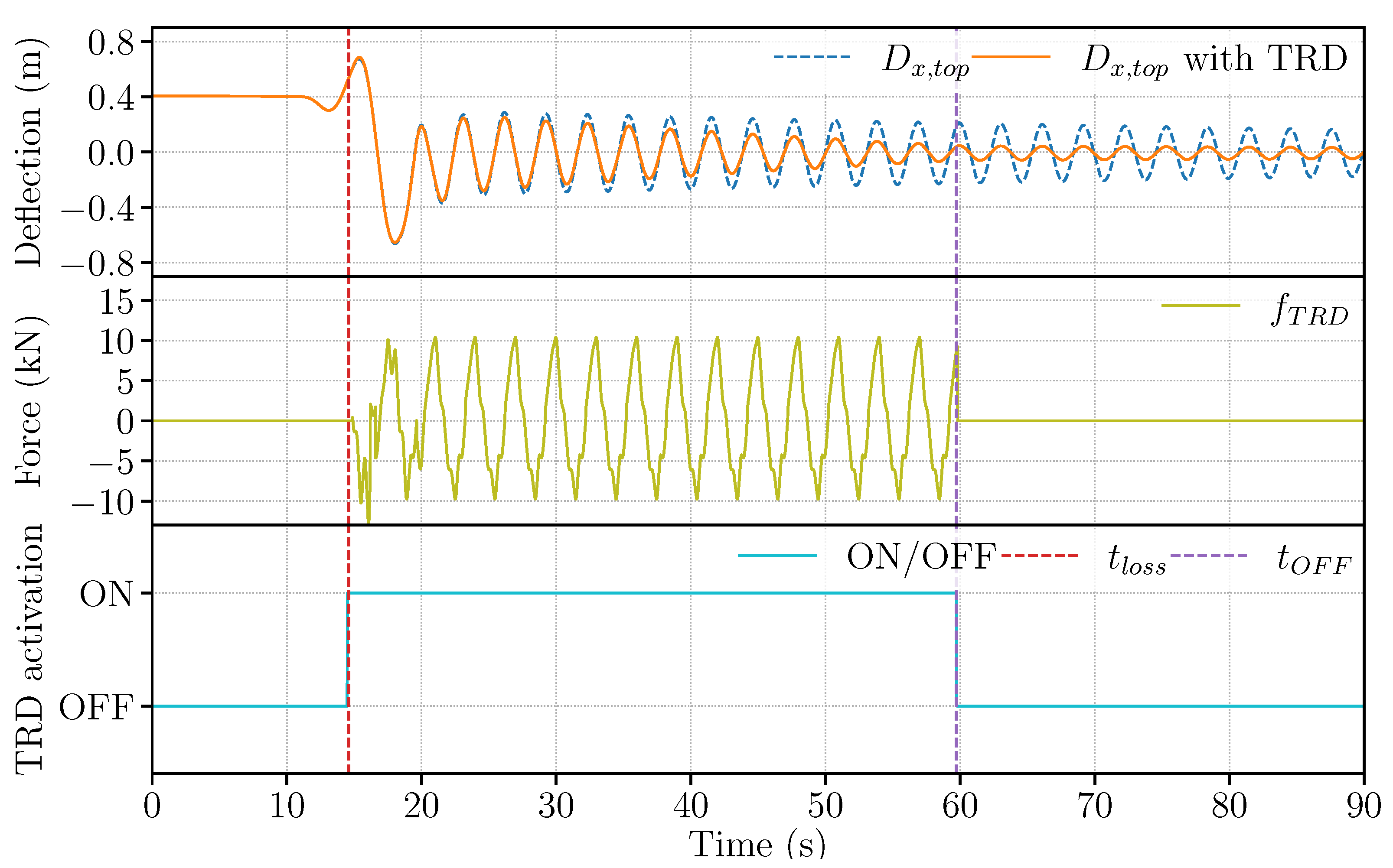
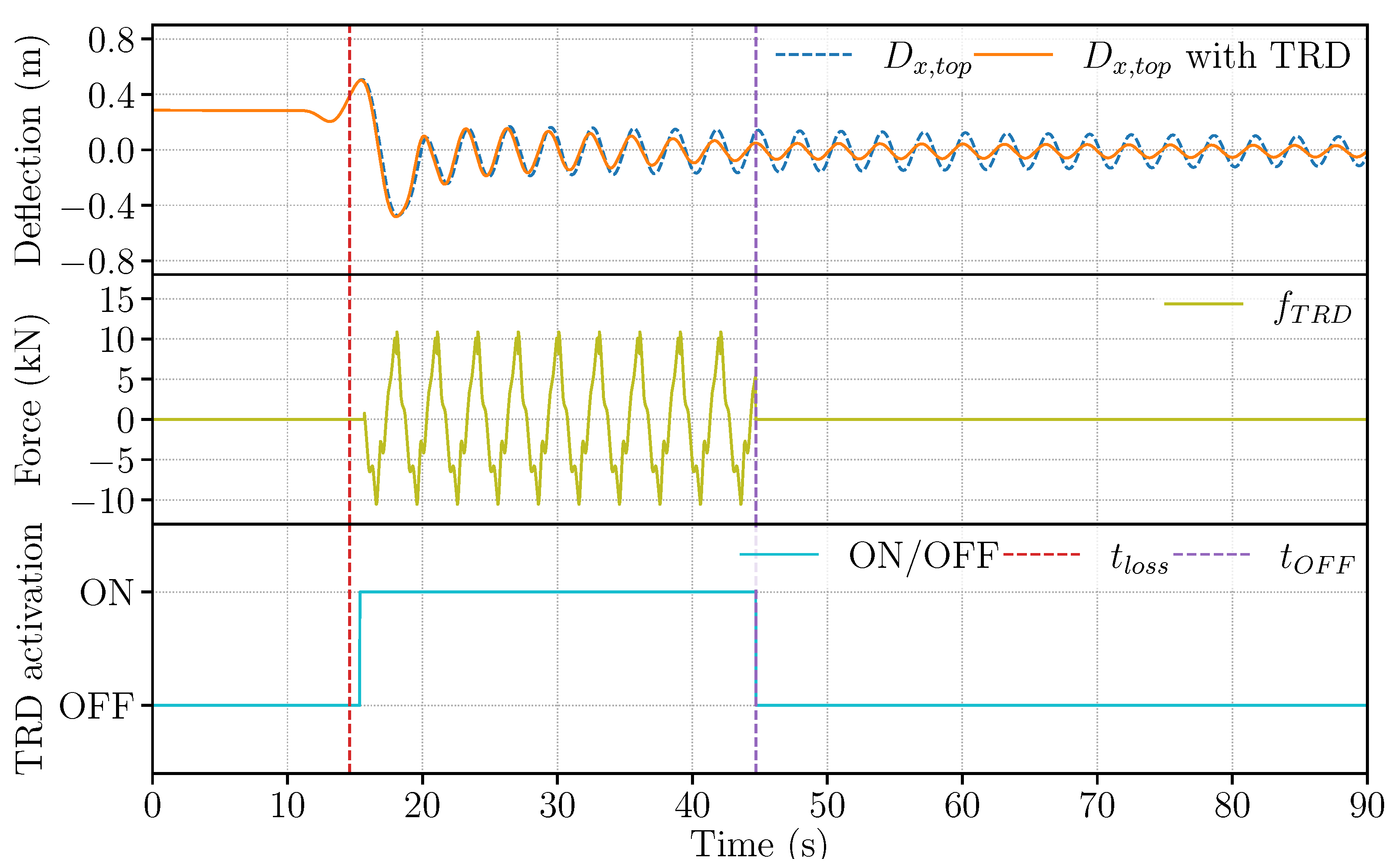
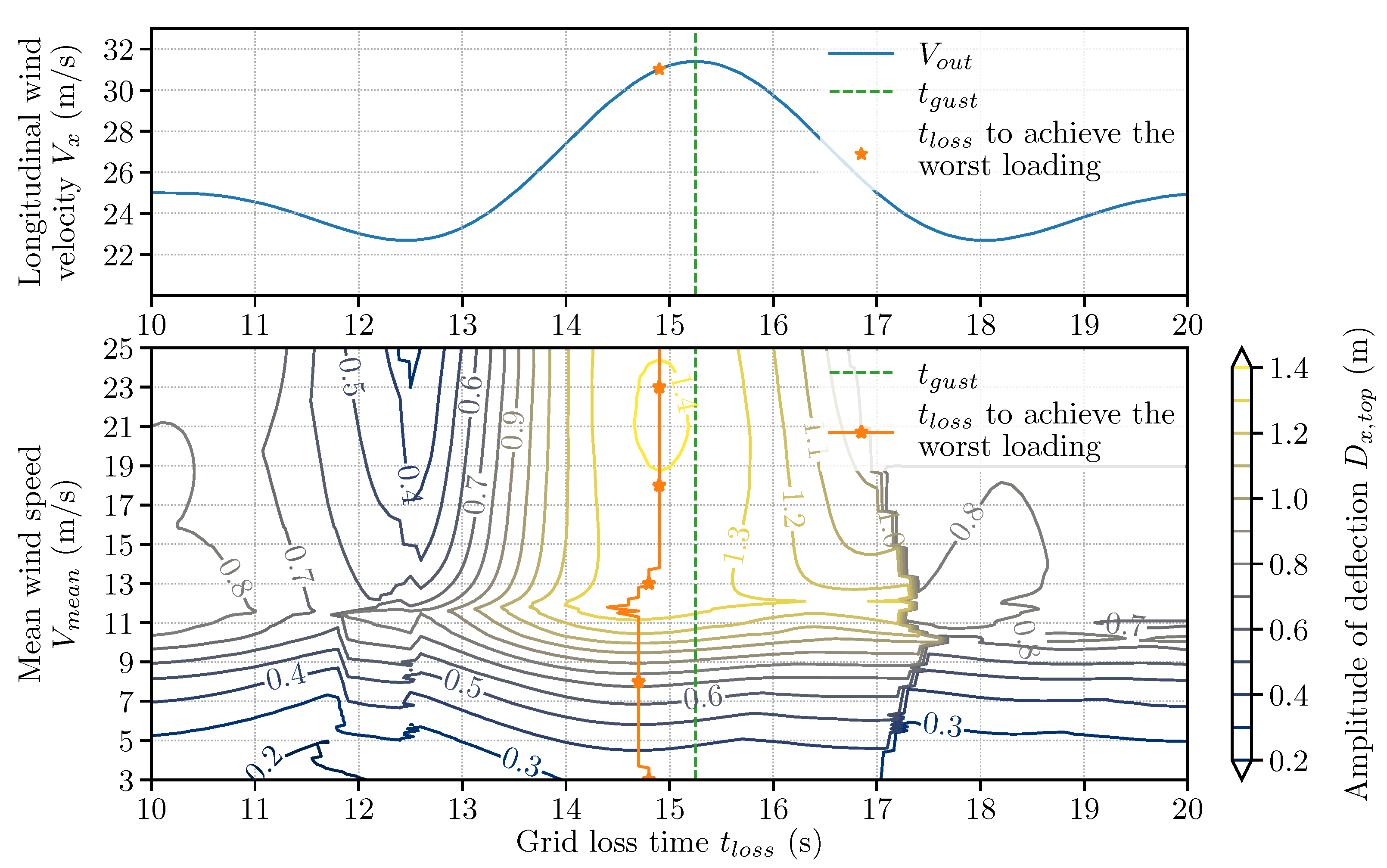
4.1.2. Grid Loss Timing
4.1.3. Discussions
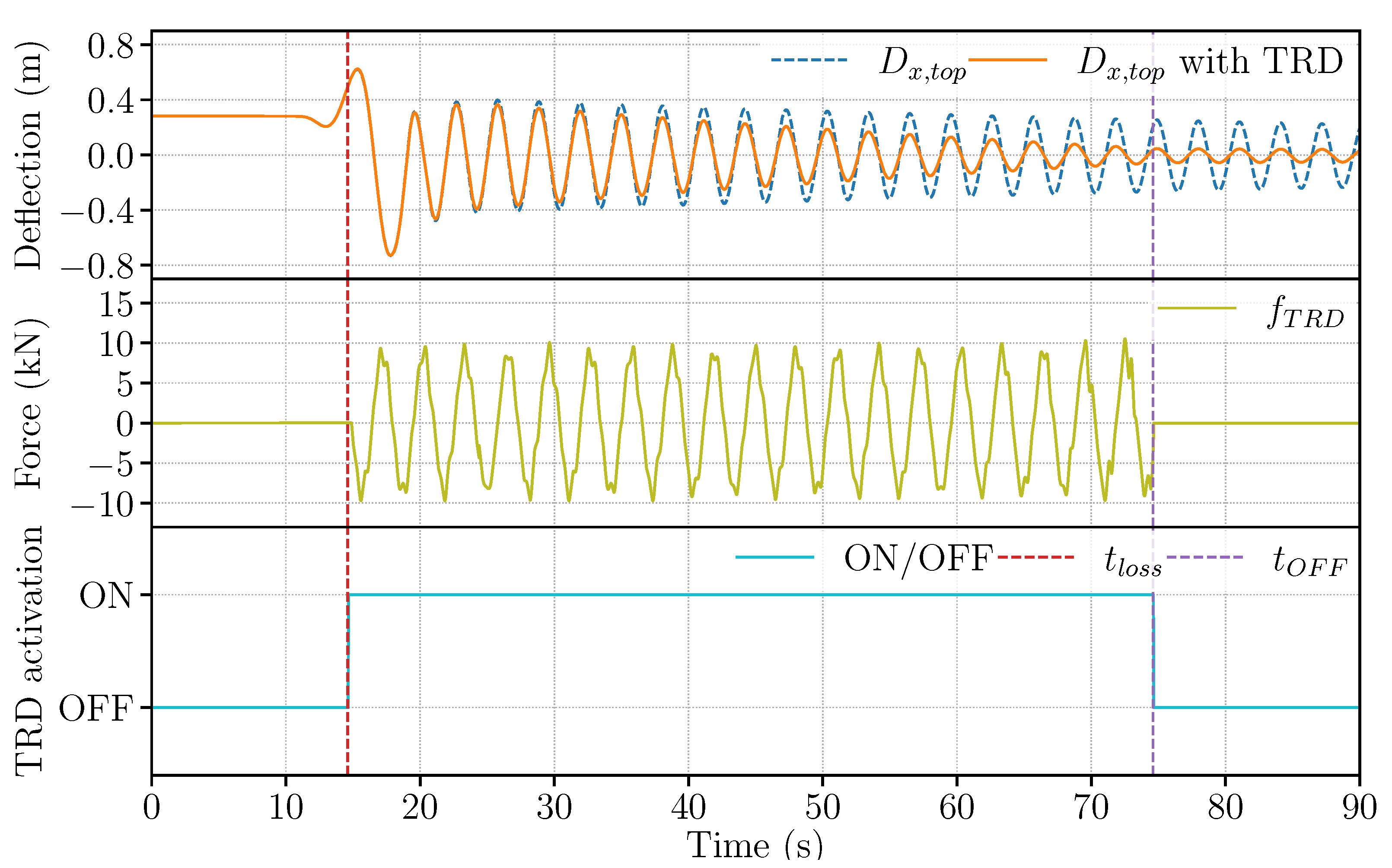
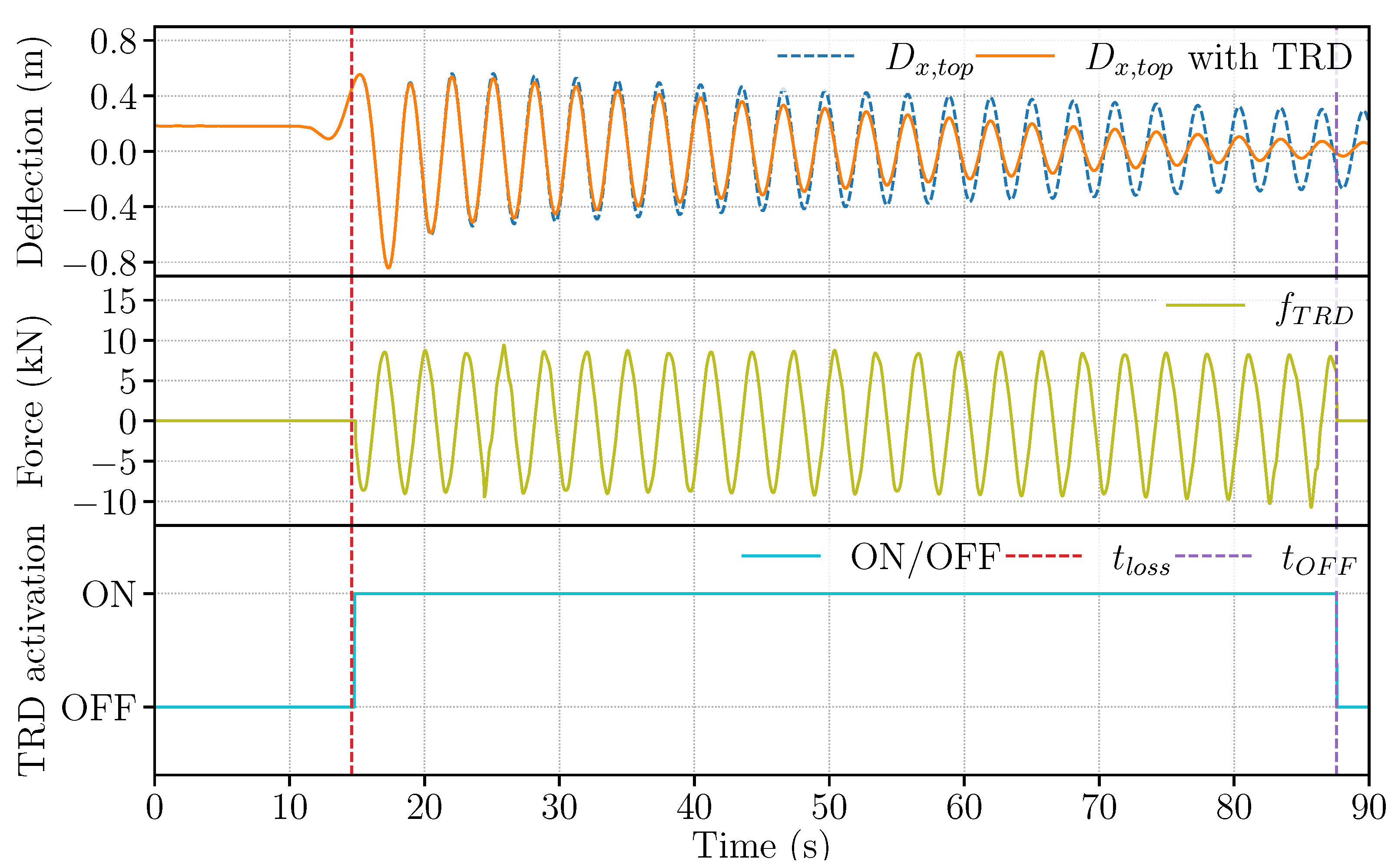
4.2. Evaluation of TRD Performance
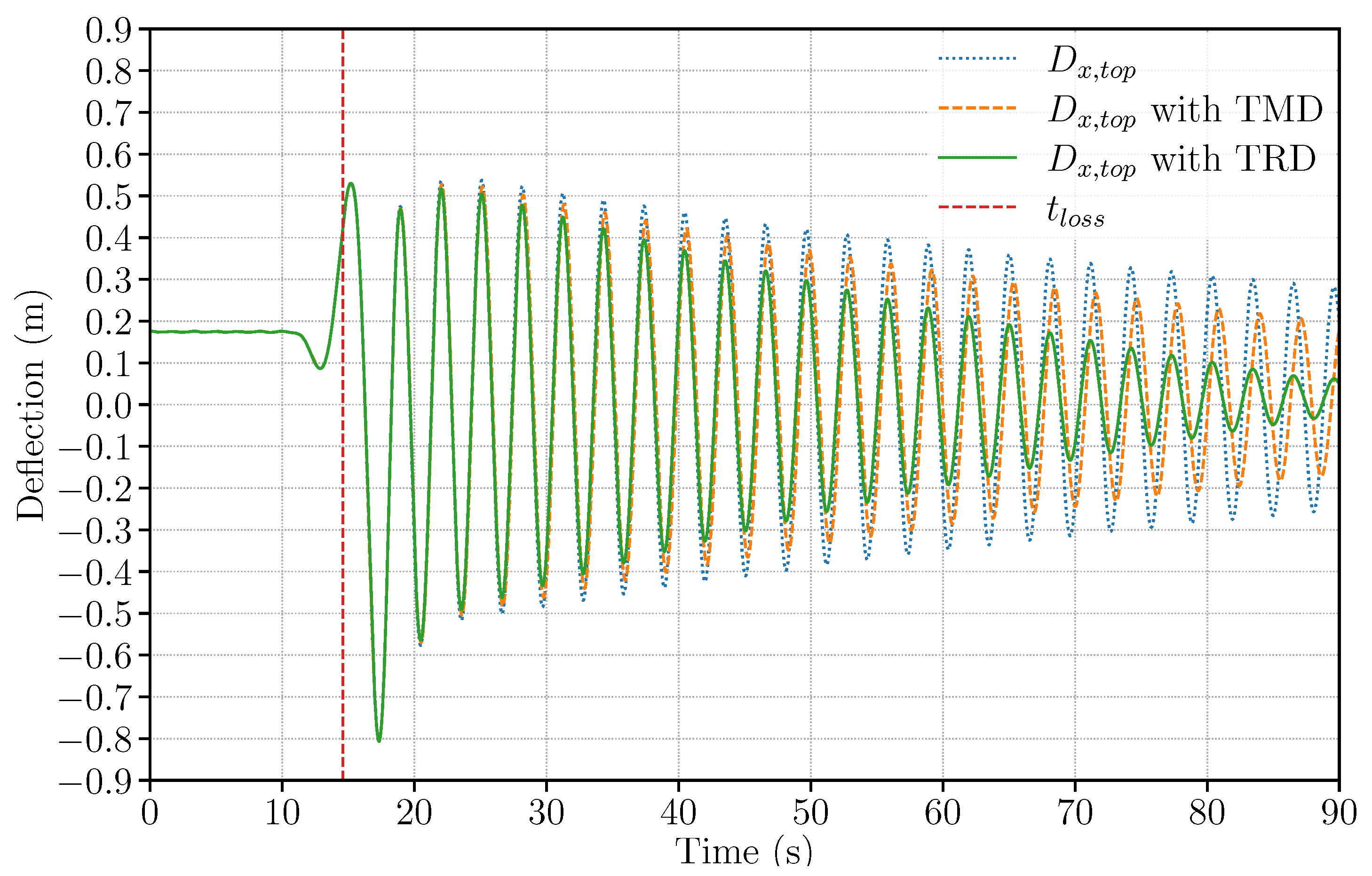
4.2.1. Results
4.2.2. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DLC | Design Load Case |
| EOG | Extreme Operating Gust |
| HAWT | Horizontal-Axis Wind Turbine |
| NREL | National Renewable Energy Laboratory |
| FAST | Fatigue, Aerodynamic, Structure and Turbulence codes |
| TRD | Twin Rotor Damper |
| TMD | Tuned Mass Damper |
| SDOF | Single Degree Of Freedom |
| PAC | Pitch Angle Control |
Appendix A
Appendix A.1
| Component | Property | Value |
|---|---|---|
| Blade | Variable-speed collective pitch control | - |
| Number of blades | 3 | |
| Mass | ||
| Rotor | Rotor mass | 110 |
| Cut-in wind speed | / | |
| Rated wind speed | / | |
| Cut-out wind speed | / | |
| Hub and nacelle | Hub mass | |
| Hub height | ||
| Elevation of yaw bearing above ground | ||
| Nacelle mass | 240 | |
| Drivetrain | High-speed multiple-stage gearbox | - |
| High-speed shaft brake time | ||
| Tower | Mass | |
| Density | 8500 / | |
| Young’s modulus | 210 | |
| Shear modulus | ||
| Poisson’s radio | 0.3 | |
| 1st full-system natural frequency (tower fore-aft) | ||
| Structural damping ratio under all modes | 1.00% |
Appendix A.2
References
- Mohammadi, E.; Fadaeinedjad, R.; Moschopoulos, G. Implementation of internal model based control and individual pitch control to reduce fatigue loads and tower vibrations in wind turbines. J. Sound Vib. 2018, 421, 132–152. [Google Scholar] [CrossRef]
- Lio, W.H.; Jones, B.L.; Rossiter, J.A. Estimation and Control of Wind Turbine Tower Vibrations Based on Individual Blade-Pitch Strategies. IEEE Trans. Control Syst. Technol. 2019, 27, 1820–1828. [Google Scholar] [CrossRef] [Green Version]
- Fitzgerald, B.; Staino, A.; Basu, B. Wavelet-based individual blade pitch control for vibration control of wind turbine blades. Struct. Control Health Monit. 2019, 26, e2284. [Google Scholar] [CrossRef] [Green Version]
- Weber, F.; Feltrin, G.; Huth, O. Guidelines for Structural Control; Technical Report March, Swiss Federal Laboratories for Materials Science and Technology (EMPA); Structural Engineering Research Laboratory: Dubendorf, Switzerland, 2006. [Google Scholar]
- Weber, F. Semi-active vibration absorber based on real-time controlled MR damper. Mech. Syst. Signal Process. 2014, 46, 272–288. [Google Scholar] [CrossRef]
- Shi, L.; Wang, Y.; Liao, M.; Jiang, Y. Approach and Application of Semi-Blind Source Separation for Aero-Engine Vibration Signals Using ICA-R; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1215, p. 12030. [Google Scholar] [CrossRef]
- Kaveh, A.; Javadi, S.M.; Mahdipour Moghanni, R. Optimal structural control of tall buildings using tuned mass dampers via chaotic optimization algorithm. Structures 2020, 28, 2704–2713. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Soria, J.M.; Díaz, I.M.; Guillen-González, F. A common framework for the robust design of tuned mass damper techniques to mitigate pedestrian-induced vibrations in lively footbridges. Structures 2021, 34, 1276–1290. [Google Scholar] [CrossRef]
- Jin, C.; Chung, W.C.; Kwon, D.S.; Kim, M.H. Optimization of tuned mass damper for seismic control of submerged floating tunnel. Eng. Struct. 2021, 241, 112460. [Google Scholar] [CrossRef]
- Si, Y.; Karimi, H.R.; Gao, H. Modelling and optimization of a passive structural control design for a spar-type floating wind turbine. Eng. Struct. 2014, 69, 168–182. [Google Scholar] [CrossRef]
- Tong, X.; Zhao, X.; Karcanias, A. Passive vibration control of an offshore floating hydrostatic wind turbine model. Wind Energy 2018, 21, 697–714. [Google Scholar] [CrossRef] [Green Version]
- Stewart, G.; Lackner, M. Offshore wind turbine load reduction employing optimal passive tuned mass damping systems. IEEE Trans. Control Syst. Technol. 2013, 21, 1090–1104. [Google Scholar] [CrossRef]
- Li, C.; Zhuang, T.; Zhou, S.; Xiao, Y.; Hu, G. Passive vibration control of a semi-submersible floating offshore wind turbine. Appl. Sci. 2017, 7, 509. [Google Scholar] [CrossRef] [Green Version]
- Murtagh, P.J.; Ghosh, A.; Basu, B.; Broderick, B.M. Passive control of wind turbine vibrations including blade/tower interaction and rotationally sampled turbulence. Wind Energy 2008, 11, 305–317. [Google Scholar] [CrossRef]
- Yu, W.; Lemmer, F.; Cheng, P.W. Performance of a passive tuned liquid column damper for floating wind turbines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering-OMAE. American Society of Mechanical Engineers Digital Collection, Glasgow, UK, 9–14 June 2019; Volume 10. [Google Scholar] [CrossRef]
- Prasad, B.B.; Duvigneau, F.; Woschke, E.; Juhre, D. Wind turbine blade and generator test specimen for evaluating a passive vibration reduction concept based on granular materials. In Proceedings of the ISMA 2020-International Conference on Noise and Vibration Engineering and USD 2020-International Conference on Uncertainty in Structural Dynamics, Leuven, Belgium, 7–9 September 2020; pp. 3525–3539. [Google Scholar]
- Fitzgerald, B.; Basu, B. Cable connected active tuned mass dampers for control of in-plane vibrations of wind turbine blades. J. Sound Vib. 2014, 333, 5980–6004. [Google Scholar] [CrossRef]
- Coudurier, C.; Lepreux, O.; Petit, N. Passive and semi-active control of an offshore floating wind turbine using a tuned liquid column damper. IFAC-PapersOnLine 2015, 28, 241–247. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Xing, Z.; Zhang, C. Active vibration control strategy based on expert PID pitch control of variable speed wind turbine. In Proceedings of the 11th International Conference on Electrical Machines and Systems, ICEMS 2008, Wuhan, China, 17–20 October 2008; pp. 635–639. [Google Scholar]
- Gambier, A.; Nazaruddin, Y.Y. Collective Pitch Control with Active Tower Damping of a Wind Turbine by Using a Nonlinear PID Approach; IFAC-PapersOnLine; Elsevier: Amsterdam, The Netherlands, 2018; Volume 51, pp. 238–243. [Google Scholar] [CrossRef]
- Lara, M.; Garrido, J.; Vázquez, F. Adaptive pi control and active tower damping compensation of a wind turbine. Renew. Energy Power Qual. J. 2020, 18, 339–344. [Google Scholar] [CrossRef]
- Bai, H. Machine Learning Assisted Probabilistic Prediction of Long-Term Fatigue Damage and Vibration Reduction of Wind Turbine Tower Using Active Damping System. Ph.D. Thesis, INSA Rouen Normandie, Rouen, France, 2021. [Google Scholar]
- Gambier, A. Simultaneous design of pitch control and active tower damping of a wind turbine by using multi-objective optimization. In Proceedings of the 1st Annual IEEE Conference on Control Technology and Applications, CCTA 2017, Hawaii, HI, USA, 26–29 August 2017; Volume 2017, pp. 1679–1684. [Google Scholar] [CrossRef]
- Preumont, A.; Seto, K. Active Control of Structures; Wiley Online Library: Hoboken, NJ, USA, 2008; pp. 1–296. [Google Scholar] [CrossRef] [Green Version]
- Scheller, J. Power-Efficient Active Structural Vibration Control by Twin Rotor dampers. Ph.D. Thesis, Hamburg University of Technology, Hamburg, Germany, 2014. [Google Scholar]
- Korkmaz, S. A review of active structural control: Challenges for engineering informatics. Comput. Struct. 2011, 89, 2113–2132. [Google Scholar] [CrossRef]
- Rodríguez Tsouroukdissian, A.; Carcangiu, C.E.; Pineda, I.; Fischer, T.; Kuhnle, B.; Scheu, M.; Martin, M. Wind Turbine Structural Damping Control for Tower Load Reduction; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Berlin, Germany, 2011; Volume 4, pp. 141–153. [Google Scholar] [CrossRef]
- Starossek, U. Device for Vibration Control of a Structure. Patent No. US9169894B2, 20 May 2015. [Google Scholar]
- Bäumer, R.; Starossek, U. Active vibration control using centrifugal forces created by eccentrically rotating masses. J. Vib. Acoust. 2016, 138, 041018. [Google Scholar] [CrossRef]
- Bäumer, R.; Terrill, R.; Wollnack, S.; Werner, H.; Starossek, U. Twin rotor damper for the damping of stochastically forced vibrations using a power-efficient control algorithm. J. Sound Vib. 2018, 413, 308–331. [Google Scholar] [CrossRef]
- Durbin, J.; Koopman, S.J. Time Series Analysis by State Space Methods; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 8th ed.; Pearson: London, UK, 2019. [Google Scholar]
- Bäumer, R. Active Vibration Control Using the Centrifugal Forces of Eccentrically Rotating Masses. Ph.D. Thesis, Hamburg University of Technology, Hamburg, Germany, 2017. [Google Scholar]
- Bäumer, R.; Starossek, U.; Scheller, J. Continuous state feedback control for twin rotor damper. In Proceedings of the International Conference on Structural Dynamic, EURODYN, Porto, Portugal, 30 June–2 July 2014; Volume 2014, pp. 1647–1654. [Google Scholar]
- International Electrotechnical Commission (IEC). Wind Turbines-Part1: Design Requirements; IHS Markit: London, UK, 2005. [Google Scholar]
- Jimack, P.K.; Topping, B.H.V. An overview of parallel dynamic loadbalancing for parallel adaptive computational mechanics codes. In Parallel and Distributed Processing for Computational Mechanics: Systems and Tools; Saxe-Coburg Publications: Kippen, UK, 1999; pp. 350–369. [Google Scholar]
- Larsen, T.J.; Hansen, A.M. How 2 HAWC2, the User’s Manual; DTU Wind Energy: Roskilde, Denmark, 2007. [Google Scholar]
- Bottasso, C.L.; Croce, A. Cp-Lambda a Code for Performance, Loads, Aeroelasticity by Multi-Body Dynamics Analyis; Technical Report; Technical University of Munich (TUM): München, Germany, 2016. [Google Scholar]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2005; p. 143. [Google Scholar]
- Jonkman, J.M.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report February; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar] [CrossRef] [Green Version]
- Bak, C.; Zahle, F.; Bitsche, R.; Yde, A.; Henriksen, L.C.; Natarajan, A.; Hansen, M.H. Description of the DTU 10 MW Reference Wind Turbine; Technical Report July; Technical University of Denmark: Lyngby, Denmark, 2013. [Google Scholar] [CrossRef]
- Di Paolo, M.; Nuzzo, I.; Caterino, N.; Georgakis, C.T. A friction-based passive control technique to mitigate wind induced structural demand to wind turbines. Eng. Struct. 2021, 232, 111744. [Google Scholar] [CrossRef]
- Arcigni, F.; Abhinav, K.A.; Collu, M.; Venturini, M. Analysis of tripod supported offshore wind turbines under conditions of marine growth. Ocean Eng. 2021, 220, 108441. [Google Scholar] [CrossRef]
- Lee, H.M.; Kwon, O.J. Performance improvement of horizontal axis wind turbines by aerodynamic shape optimization including aeroealstic deformation. Renew. Energy 2020, 147, 2128–2140. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Movahhedi, M. Power improvement of NREL 5-MW wind turbine using multi-DBD plasma actuators. Energy D 2017, 146, 96–106. [Google Scholar] [CrossRef]
- Kooijman, H.; Lindenburg, C.; Winkelaar, D.; van der Hooft, E. DOWEC 6 MW PRE-DESIGN Aero-Elastic Modelling of the DOWEC 6 MWpre-Design in PHATAS; Technical Report; Energy Research Centre of the Netherlands: Petten, The Netherlands, 2003. [Google Scholar]
- Frost, W.; Long, B.H.; Turner, R.E. Engineering Handbook on the Atmospheric Environmental Guidelines for Use in Wind Turbine Generator Development; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1978. [Google Scholar]
- Lackner, M.A.; Rotea, M.A. Passive structural control of offshore wind turbines. Wind Energy 2011, 14, 373–388. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations; Dover: Garden City, NY, USA, 1985; p. 342. [Google Scholar]
- Bäumer, R.; Wollnack, S.; Scheller, J.; Starossek, U.; Werner, H. Twin rotor damper applied to the damping of non-harmonic vibrations. In Proceedings of the International Conference on Structural Dynamic, EURODYN, Porto, Portugal, 30 June–2 July 2014; Volume 2014, pp. 1655–1661. [Google Scholar]



| Property | Value |
|---|---|
| Total mass of control masses | |
| Radius of TRD | |
| Position of TRD (in tower-base coordinate system) | (0.00, 0.00, 87.60) |
| Working mode | Mode 1: continuous rotation |
| Threshold of vibration-amplitude | |
| Threshold of vibration-amplitude |
| Mean Wind Speed () | Grid Loss Time () | ||
|---|---|---|---|
| ( /) | 14.9 | 14.9 | 14.9 |
| ( /) | 14.8 | 14.8 | 14.8 |
| ( /) | 14.6 | 14.6 | 14.6 |
| ( /) | 14.7 | 14.7 | 14.7 |
| Property | Value |
|---|---|
| Mass | 2 |
| Position of TMD (in tower-base coordinate system) | (0.00, 0.00, 87.60) |
| Damped natural angular frequency | / |
| Stiffness | 8245 / |
| Viscous damping | 252 /(/) |
Deflection (m) | without damper | 0.54 | 0.44 | 0.33 | 0.20 | |
| with TMD | 0.39 (−27.78%) | 0.35 (−20.45%) | 0.27 (−18.18%) | 0.18 (−10.0%) | ||
| with TRD | 0.09 (−83.33%) | 0.08 (−81.82%) | 0.08 (−75.76%) | 0.08 (−60.00%) | ||
Force (kN) | without damper | 1084 | 898 | 656 | 408 | |
| with TMD | 761 (−29.80%) | 696 (−22.49%) | 548 (−16.46%) | 367 (−10.05%) | ||
| with TRD | 195 (−82.01%) | 179 (−80.07%) | 161 (−75.46%) | 159 (−61.03%) | ||
Moment (kN.m) | without damper | |||||
| with TMD | (−29.64%) | (−21.84%) | (−17.29%) | (−9.20%) | ||
| with TRD | (−82.52%) | (−80.00%) | (−75.58%) | (−60.63%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, H.; Aoues, Y.; Cherfils, J.-M.; Lemosse, D. Design of an Active Damping System for Vibration Control of Wind Turbine Towers. Infrastructures 2021, 6, 162. https://doi.org/10.3390/infrastructures6110162
Bai H, Aoues Y, Cherfils J-M, Lemosse D. Design of an Active Damping System for Vibration Control of Wind Turbine Towers. Infrastructures. 2021; 6(11):162. https://doi.org/10.3390/infrastructures6110162
Chicago/Turabian StyleBai, Hao, Younes Aoues, Jean-Marc Cherfils, and Didier Lemosse. 2021. "Design of an Active Damping System for Vibration Control of Wind Turbine Towers" Infrastructures 6, no. 11: 162. https://doi.org/10.3390/infrastructures6110162
APA StyleBai, H., Aoues, Y., Cherfils, J.-M., & Lemosse, D. (2021). Design of an Active Damping System for Vibration Control of Wind Turbine Towers. Infrastructures, 6(11), 162. https://doi.org/10.3390/infrastructures6110162