Energy Balance in Wastewater Systems with Energy Recovery: A Portuguese Case Study
Abstract
:1. Introduction
2. Methodology
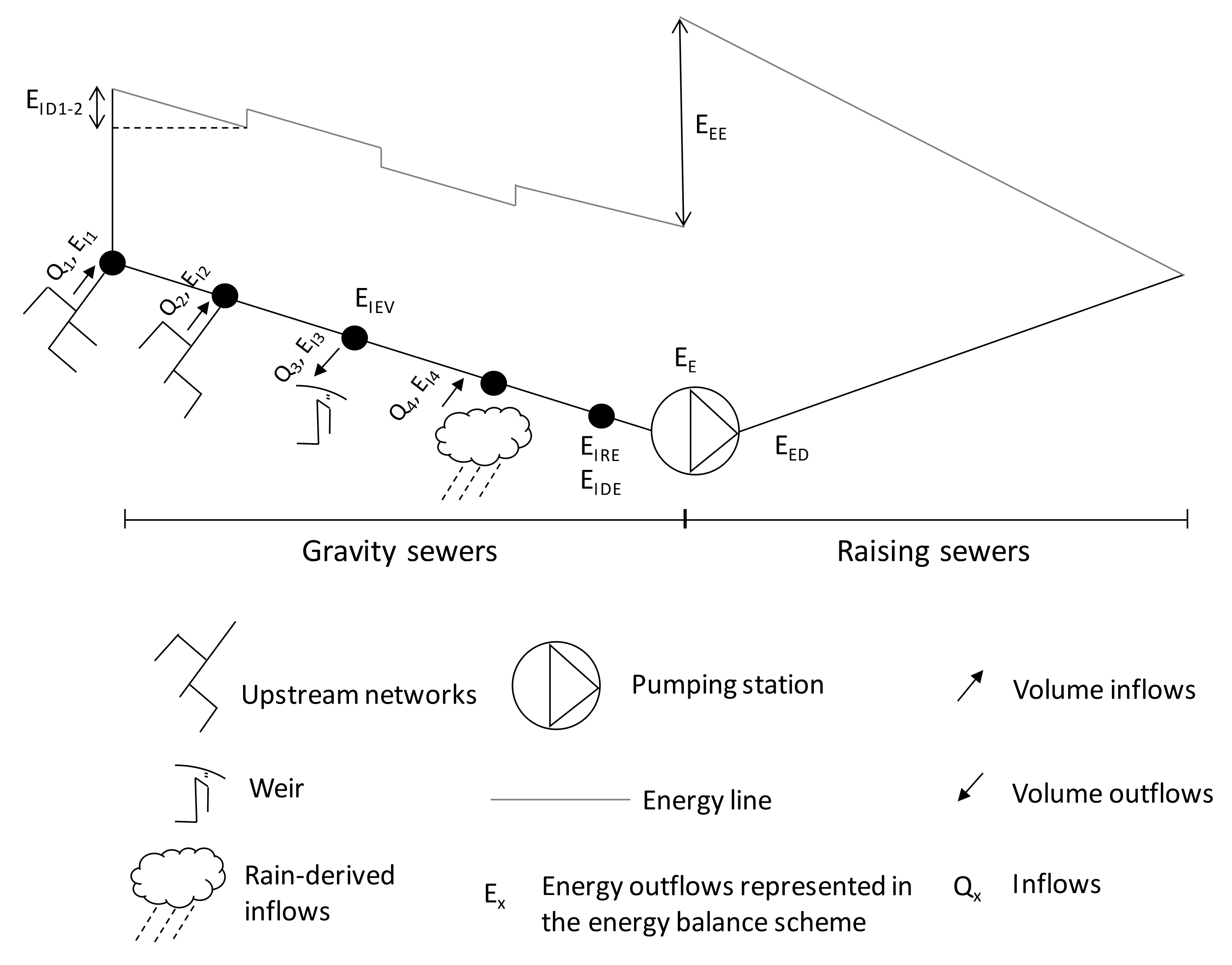
2.1. Energy Balance for Wastewater Systems
2.2. Micro-Level Assessment Description and Formulation
2.3. Energy Recovery and Economic Viability
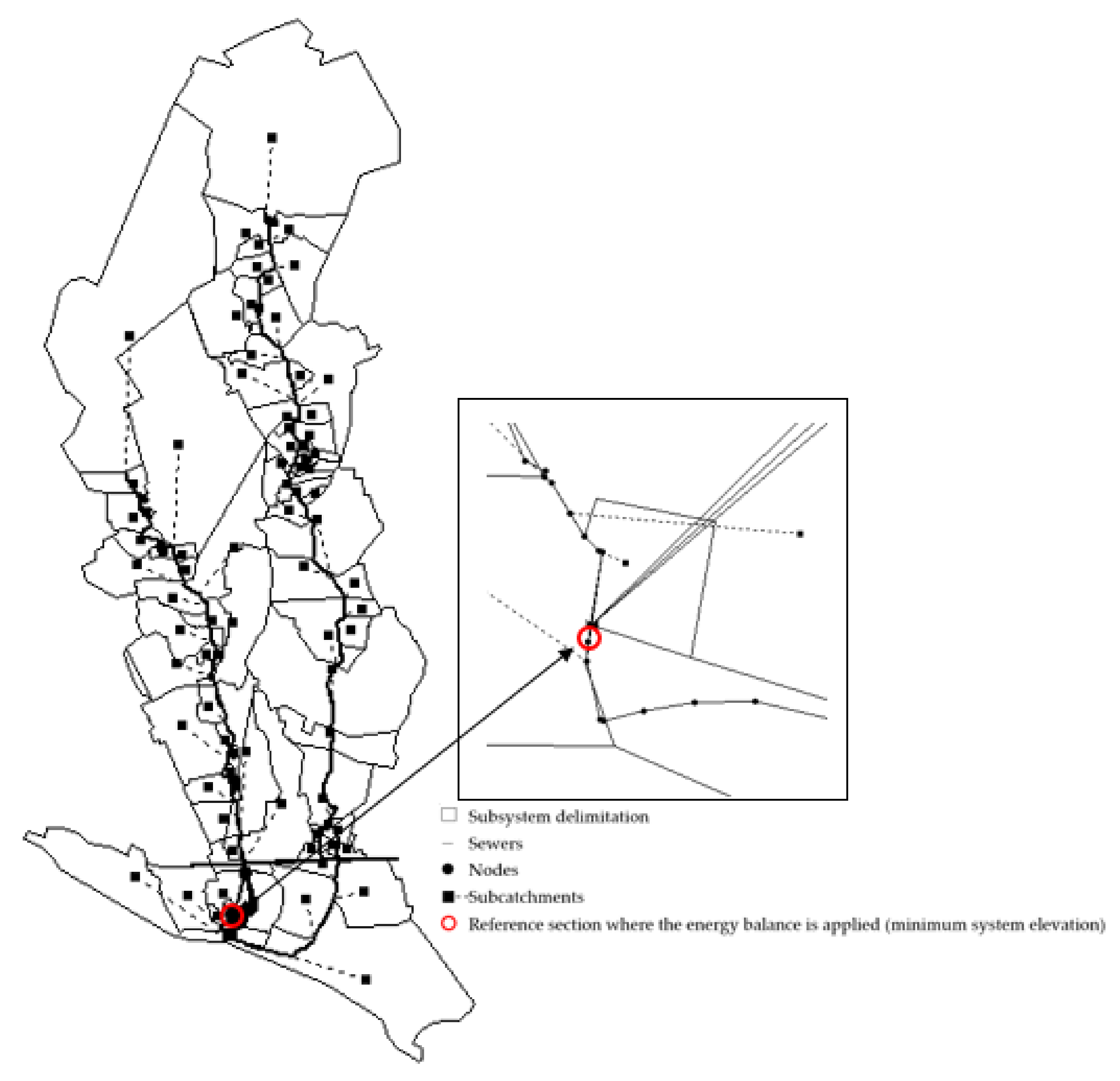
3. Case Study
4. Results and Discussion
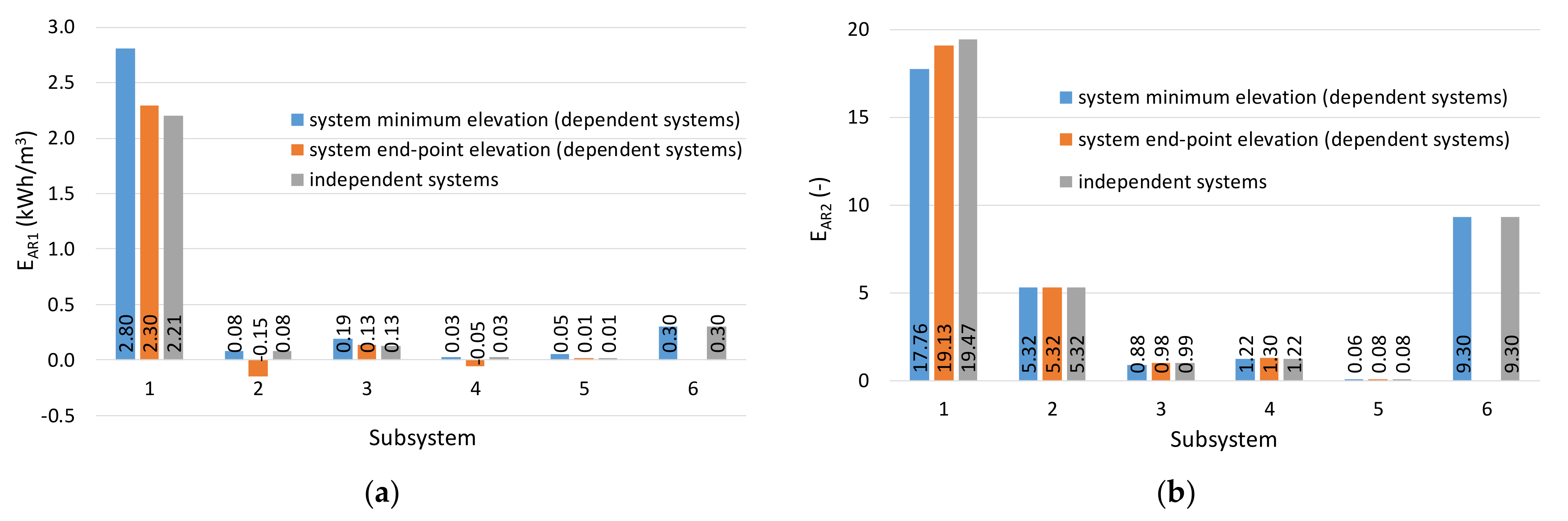
4.1. Micro-Level Assessment Application
4.2. Reference Elevation Analysis
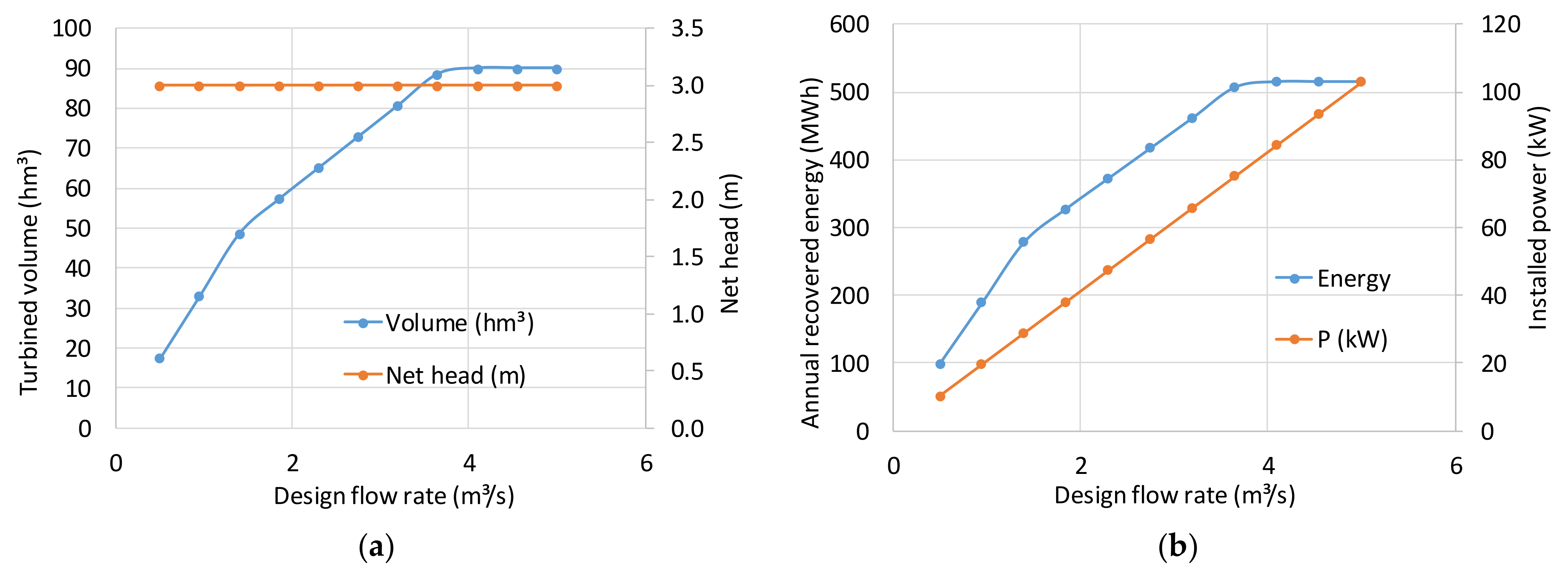
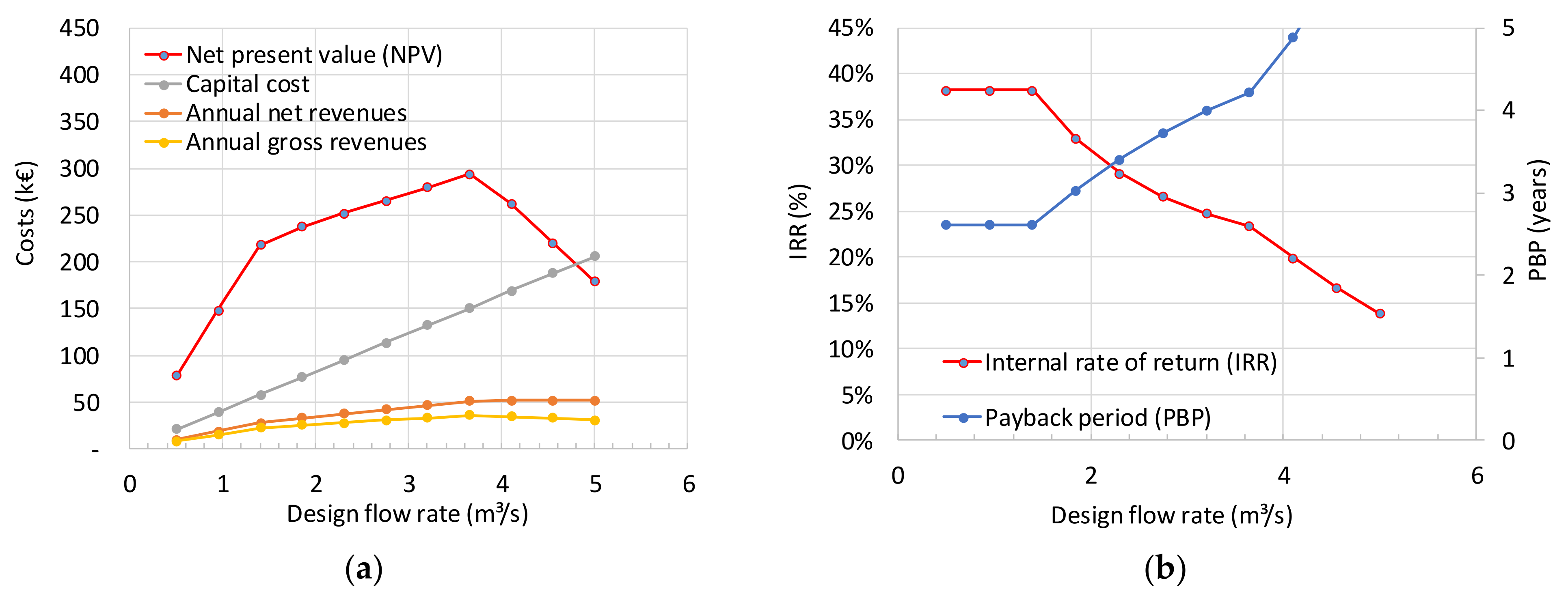
4.3. Energy Recovery Curves Application and Economic Viability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ENERGY INFLOWS | ENERGY OUTFLOWS | |||||||
|---|---|---|---|---|---|---|---|---|
| Total energy used for system processes (transport and treatment), ET = 2857 MWh (100%) | Total inflow intrinsic energy (associated with the gravity flow), EI = 2759 MWh (96.5%) | Inflow intrinsic energy associated with authorized or due inflows, EIAI = 2759 MWh (96.5%) | Total inflow intrinsic energy, EI = 2,759,184 MWh (96.5%) | System downstream energy, EIDE = 184 MWh (6.4%) | ||||
| Recovered energy (micro hydropower), EIRE = 0 (0%) | ||||||||
| Dissipated energy, EID = 2574 MWh (90.1%) | …due to inefficiencies in energy recovery equipment (e.g., turbines), EIDT = 0 (0%) | |||||||
| …due to pipe friction and local head losses (e.g., junctions, bends, valves, screens), EIDL = 2575 MWh (90.1%) | ||||||||
| Inflow intrinsic energy associated with undue inflows, EIUI = 0 (0%) | ||||||||
| Energy associated with exceedance volumes, EIEV = 0 (0%) | …not connected to an energy consuming component, E′IEV = 0 (0%) | |||||||
| …potentially inflowing to an energy consuming component, E″IEV = 0 (0%) | ||||||||
| External energy (electrical), EE = 99 MWh (3.5%) | External energy associated with authorized or due inflows, EEAI = 99 MWh (3.5%) | External energy, EE = 99 MWh (3.5%) | Elevation associated energy, EEE = 29 MWh (1.0%) | |||||
| Dissipated energy, EED = 70 MWh (2.5%) | …due to inefficiencies (in electromechanical equipment, e.g., pumps), EEDE = 69.5 MWh (2.47%) | |||||||
| External energy associated with undue inflows, EEUI = 0 (0%) | ||||||||
| …due to pipe friction and local head losses (e.g., junctions, bends, valves, screens), EEDL = 0.5 MWh (0.03%) | ||||||||
| ENERGY INFLOWS | ENERGY OUTFLOWS | |||||||
|---|---|---|---|---|---|---|---|---|
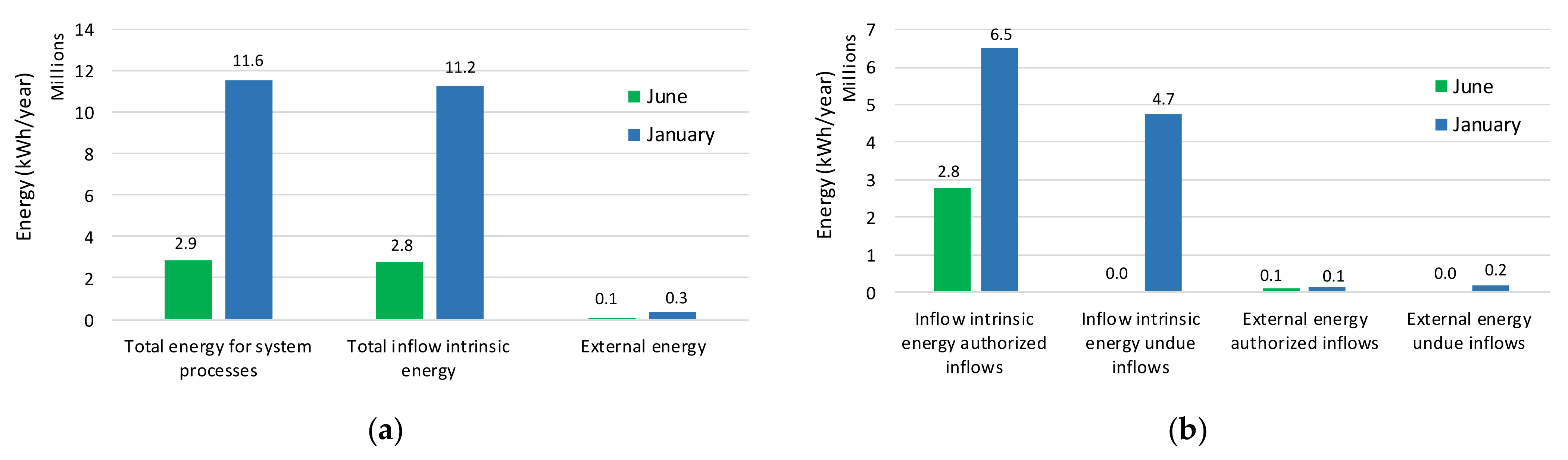
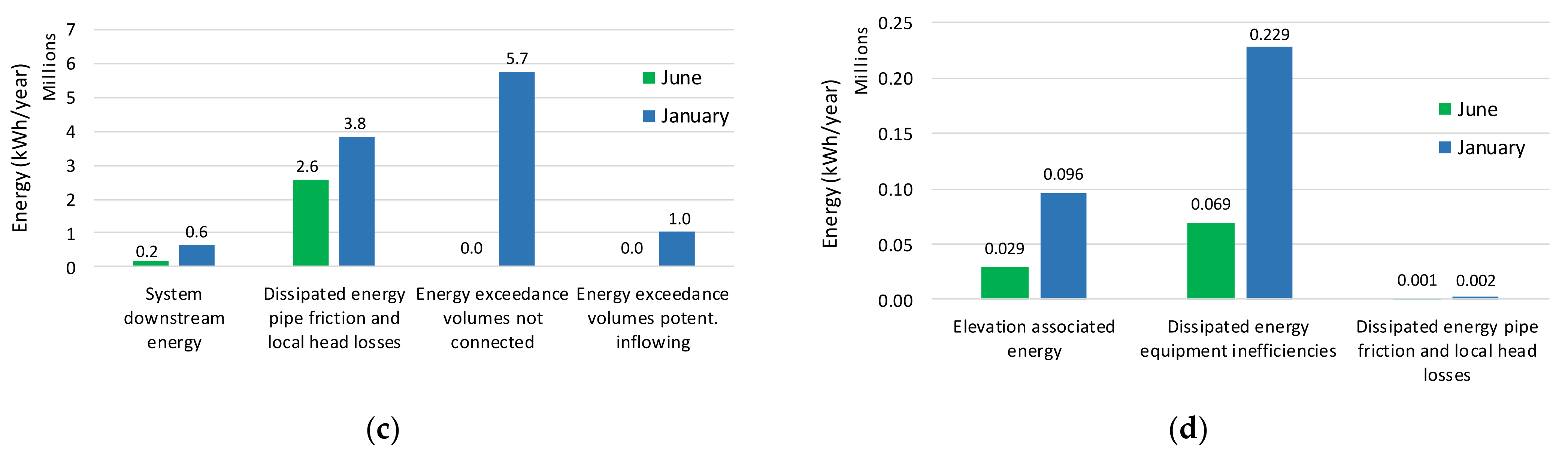
| Total energy used for system processes (transport and treatment), ET = 11,566 MWh (100%) | Total inflow intrinsic energy (associated with the gravity flow), EI = 11,239 MWh (97.2%) | Inflow intrinsic energy associated with authorized or due inflows, EIAI = 6504 MWh (56.2%) | Total inflow intrinsic energy, EI = 11,239,224 MWh (97.2%) | System downstream energy, EIDE = 645 MWh (5.6%) | ||||
| Recovered energy (micro hydropower), EIRE = 0 (0%) | ||||||||
| Dissipated energy, EID = 3828 MWh (33.1%) | …due to inefficiencies in energy recovery equipment (e.g., turbines), EIDT = 0 (0%) | |||||||
| …due to pipe friction and local head losses (e.g., junctions, bends, valves, screens), EIDT = 3828 MWh (33.1%) | ||||||||
| Inflow intrinsic energy associated with undue inflows, EIUI = 4735 MWh (40.9%) | ||||||||
| Energy associated with exceedance volumes, EIEV = 6766 MWh (58.5%) | …not connected to an energy consuming component, E′IEV = 5736 MWh (49.6%) | |||||||
| …potentially inflowing to an energy consuming component, E″IEV = 1030 MWh (8.9%) | ||||||||
| External energy (electrical), EE = 327 MWh (2.8%) | External energy associated with authorized or due inflows, EEAI = 133 MWh (1.1%) | External energy, EE = 327 MWh (2.8%) | Elevation associated energy, EEE = 96 MWh (0.8%) | |||||
| Dissipated energy, EED = 231 MWh (2.0%) | …due to inefficiencies (in electromechanical equipment, e.g., pumps), EEDE = 229 MWh (1.98%) | |||||||
| External energy associated with undue inflows, EEUI = 194 MWh (1.7%) | ||||||||
| …due to pipe friction and local head losses (e.g., junctions, bends, valves, screens), EEDL = 2 MWh (0.02%) | ||||||||
References
- Lingireddy, S.; Wood, J. Improved operation of water distribution systems using variable-speed pumps. J. Energy Eng. 1998, 124, 90–103. [Google Scholar] [CrossRef]
- U.S. Department of Energy—USDE. Energy Demands on Water Resources. Rep. to Congress on the Interdependency of Energy and Water. U.S. Department of Energy: Washington, DC, USA, 2006. [Google Scholar]
- Frijns, J.; Hofman, J.; Nederlof, M. The potential for (waste)water as energy carrier. Energy Convers. Manag. 2013, 65, 357–363. [Google Scholar] [CrossRef]
- Wilson, L.; Lichinga, K.N.; Kilindu, A.B.; Masse, A.A. Water utilities’ improvement: The need for water and energy management techniques and skills. Water Cycle 2021, 2, 32–37. [Google Scholar] [CrossRef]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. A comprehensive and well tested energy balance for water supply systems. Urban Water J. 2017, 14, 853–861. [Google Scholar] [CrossRef]
- Williams, A.A.; Smith, N.P.A.; Bird, C.; Howard, M. Pumps as Turbines and Induction Motors as Generators for Energy Recovery in Water Supply Systems. Water Environ. J. 1998, 12, 175–178. [Google Scholar] [CrossRef]
- Fecarotta, O.; McNabola, A. Optimal Location of Pump as Turbines (PATs) in Water Distribution Networks to Recover Energy and Reduce Leakage. Water Resour. Manag. 2017, 31, 5043–5059. [Google Scholar] [CrossRef]
- ISO. Energy Audits—Requirements with Guidance for Use; ISO 50002:2014(E); International Organizational for Standardization: Geneve, Switzerland, 2014. [Google Scholar]
- Duarte, P.; Alegre, H.; Covas, D. Avaliação do Desempenho Energético em Sistemas de Abastecimento de Água. VIII Seminário Ibero-americano; SEREA: Lisbon, Portugal, 2008. (In Portuguese) [Google Scholar]
- Cabrera, E.; Pardo, M.A.; Cobacho, R.; Cabrera, E., Jr. Energy audit of water networks. J. Water Resour. Plan. Manag. 2010, 136, 669–677. [Google Scholar] [CrossRef]
- Mamade, A.; Loureiro, D.; Alegre, H.; Covas, D. Top-Down and Bottom-Up Approaches for Water-Energy Balance in Portuguese Supply Systems. Water 2018, 10, 577. [Google Scholar] [CrossRef] [Green Version]
- Mamade, A. Enhancement of Water and Energy Efficiency in Water Supply Systems. PhD. Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2019. [Google Scholar]
- Monteiro, L.; Delgado, J.; Covas, D. Improved Assessment of Energy Recovery Potential in Water Supply Systems with High Demand Variation. Water 2018, 10, 773. [Google Scholar] [CrossRef] [Green Version]
- Delgado, J.; Ferreira, J.P.; Covas, D.I.C.; Avellan, F. Variable speed operation of centrifugal pumps running as turbines. Experimental investigation. Renew. Energy 2019, 142, 437–450. [Google Scholar] [CrossRef]
- Jain, S.V.; Patel, R.N. Investigations on pump running in turbine mode: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2014, 30, 841–868. [Google Scholar] [CrossRef]
- Nowak, O.; Enderle, P.; Varbanov, P. Ways to optimize the energy balance of municipal wastewater systems: Lessons learned from Austrian applications. J. Clean. Prod. 2015, 88, 125–131. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Williams, A.P. Energy recovery in the water industry: An assessment of the potential for micro-hydropower. Water Environ. J. 2014, 28, 294–304. [Google Scholar] [CrossRef]
- Gallagher, J.; Harris, I.M.; Packwood, A.J.; McNabola, A.; Williams, A.P. A strategic assessment of micro-hydropower in the UK and Irish water industry: Identifying technical and economic constraints. Renew. Energy 2015, 81, 808–815. [Google Scholar] [CrossRef]
- Su, P.-A.; Karney, B. Micro hydroelectric energy recovery in municipal water systems: A case study for Vancouver. Urban Water J. 2015, 12, 678–690. [Google Scholar] [CrossRef]
- Oliveira, P.F.; Martins, N.; Fontes, P.; Covas, D. Hydroenergy Harvesting Assessment: The Case Study of Alviela River. Water 2021, 13, 1764. [Google Scholar] [CrossRef]
- Berger, V.; Niemann, A.; Frehmann, T.; Brockmann, H. Advanced energy recovery strategies for wastewater treatment plants and sewer systems using small hydropower. Water Util. J. 2013, 5, 15–24. [Google Scholar]
- Pereira, H. Hydroenergy Recovery in Urban Water Systems: The Case Study of Alcântara wastewater Treatment Plant. Master’s Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2018. [Google Scholar]
- Jorge, C.; Almeida, M.C.; Covas, D. A novel energy balance tailored for wastewater systems. Urban Water 2021. (Under Review). [Google Scholar]
- Fernandes, E. Avaliação da Eficiência Hídrica e Energética em Aproveitamentos Hidroagrícolas: Contributo Para o Diagnóstico Setorial e Estudo de Soluções de Intervenção. Master’s Thesis, Instituto Superior Técnico, Lisbon, Portugal, 2020. (In Portuguese). [Google Scholar]
- Almeida, M.C.; Cardoso, M.A. Infrastructure Asset Management of Wastewater and Rainwater Services; Technical Guide n.17; ERSAR: Lisbon, Portugal; LNEC: Lisbon, Portugal; IST: Lisbon, Portugal, 2010; ISBN 978-989-8360-05-2. (In Portuguese) [Google Scholar]
- Castro, R. Uma Introdução às Energias Renováveis: Eólica, Fotovoltaica e Minihídrica, 3rd ed.; IST Press: Palo Alto, CA, USA, 2018. (In Portuguese) [Google Scholar]
- Jorge, C.; Almeida, M.C.; Covas, D. Impacto de afluências indevidas no consumo energético em instalações elevatórias em sistemas de drenagem urbana. Revi. Águas Resíduos 2021, IV, 29–40. (In Portuguese) [Google Scholar] [CrossRef]
- Souza, E.V.; Covas, D.I.C.; Soares, A.K. Novel standardized energy auditing scheme in water supply systems. In Proceedings of the 11th International Conference on Computing and Control in the Water Industry, Exeter, UK, 5–7 September 2011. [Google Scholar]
- Feliciano, J.; Almeida, R.; Santos, A.; Ganhão, A.; Covas, D.; Alegre, H. Energy efficiency in water distribution systems—A path to an ideal network—AGS experience. Water Sci. Technol. Water Supply 2014, 14, 708–716. [Google Scholar] [CrossRef]
- Lenzi, C.; Bragalli, C.; Bolognesi, A.; Artina, S. From energy balance to energy efficiency indicators including water losses. Water Sci. Technol. Water Supply 2013, 13, 889–895. [Google Scholar] [CrossRef]
- Carriço, N.; Covas, D.I.C.; Alegre, H.; Almeida, M.C. How to assess the effectiveness of energy management processes in water supply systems. J. Water Supply Res. Technol.—AQUA 2014, 63, 342. [Google Scholar] [CrossRef]
- Simmons, S.; Dellinger, G.; Lyons, M.; Terfous, A.; Ghenaim, A.; Lubitz, W.D. Effects of Inclination Angle on Archimedes Screw Generator Power Production with Constant Head. J. Hydraul. Eng. 2021, 147, 04021001. [Google Scholar] [CrossRef]
- YoosefDoost, A.; Lubitz, W.D. Archimedes Screw Turbines: A Sustainable Development Solution for Green and Renewable Energy Generation—A Review of Potential and Design Procedures. Sustainability 2020, 12, 7352. [Google Scholar] [CrossRef]
- Lashofer, A.; Hawle, W.; Kaltenberger, F.; Pelikan, B. Die Wasserkraftschnecke—Praxis, Prüfstand und Potenzial. Osterr. Wasser- Abfallwirtsch. 2013, 65, 339–347. [Google Scholar] [CrossRef]

| ENERGY INFLOWS | ENERGY OUTFLOWS | |||||||
|---|---|---|---|---|---|---|---|---|
| Total energy used for system processes (transport and treatment), ET | Total inflow intrinsic energy (associated with gravity flow), EI | Inflow intrinsic energy associated with authorized or due inflows, EIAI | Total inflow intrinsic energy, EI | System downstream energy, EIDE | ||||
| Recovered energy (e.g., micro-hydropower), EIRE | ||||||||
| Dissipated energy, EID | …due to inefficiencies in energy recovery equipment (e.g., turbines), EIDT | |||||||
| …due to pipe friction and local head losses (e.g., junctions, bends, valves, screens), EIDL | ||||||||
| Inflow intrinsic energy associated with undue inflows, EIUI | Energy associated with exceedance volumes, EIEV | …not connected to an energy-consuming component, E′IEV | ||||||
| …potentially inflowing to an energy-consuming component, E″IEV | ||||||||
| External energy (electrical), EE | External energy associated with authorized or due inflows, EEAI | External energy, EE | Elevation associated energy, EEE | |||||
| Dissipated energy, EED | …due to inefficiencies in electromechanical equipment (e.g., pumps), EEDE | |||||||
| External energy associated with undue inflows, EEUI | ||||||||
| …due to pipe friction and local head losses (e.g., junctions, bends, valves, screens), EEDL | ||||||||
| Hydraulic head | (1) | |
| Total energy used for system processes | (2) | |
| Total inflow intrinsic energy | (3) | |
| External energy | (4) | |
| Recovered energy | (5) | |
| Dissipated energy due to pipe friction and local head losses | (6) | |
| Dissipated energy due to inefficiencies in energy recovery equipment | (7) | |
| Total dissipated energy associated with inflow intrinsic energy | (8) | |
| Elevation associated energy | (9) | |
| Dissipated energy due to inefficiencies in electromechanical equipment | (10) | |
| Total dissipated energy associated with external energy | (11) |
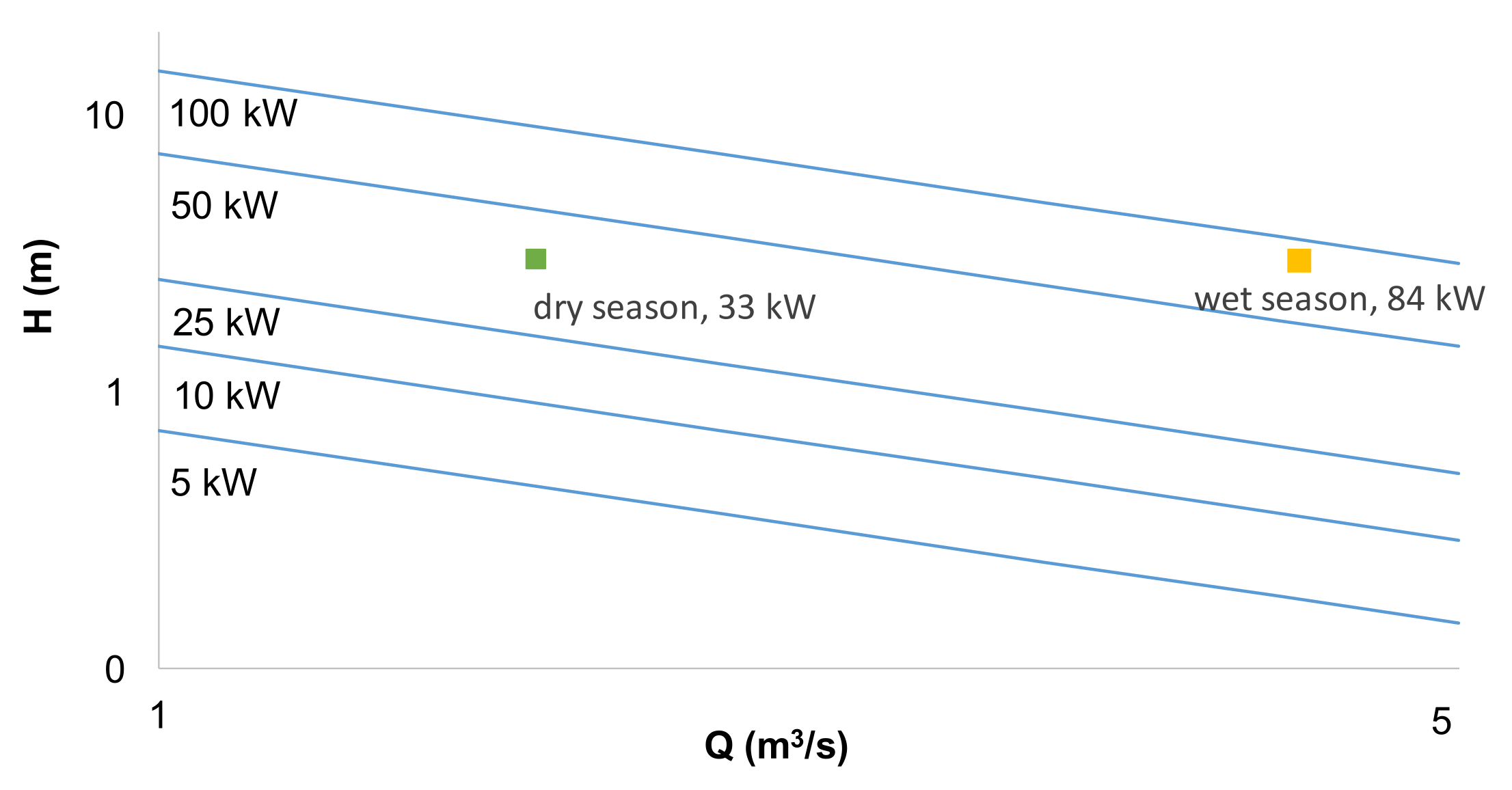
| Head, H (m) | Season | Average Flow Rate, Q (m3/s) | Hydraulic Power (kW) |
|---|---|---|---|
| 3 | Dry | 1.6 | 47 |
| Wet | 4.1 | 121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jorge, C.; Almeida, M.d.C.; Covas, D. Energy Balance in Wastewater Systems with Energy Recovery: A Portuguese Case Study. Infrastructures 2021, 6, 141. https://doi.org/10.3390/infrastructures6100141
Jorge C, Almeida MdC, Covas D. Energy Balance in Wastewater Systems with Energy Recovery: A Portuguese Case Study. Infrastructures. 2021; 6(10):141. https://doi.org/10.3390/infrastructures6100141
Chicago/Turabian StyleJorge, Catarina, Maria do Céu Almeida, and Dídia Covas. 2021. "Energy Balance in Wastewater Systems with Energy Recovery: A Portuguese Case Study" Infrastructures 6, no. 10: 141. https://doi.org/10.3390/infrastructures6100141
APA StyleJorge, C., Almeida, M. d. C., & Covas, D. (2021). Energy Balance in Wastewater Systems with Energy Recovery: A Portuguese Case Study. Infrastructures, 6(10), 141. https://doi.org/10.3390/infrastructures6100141







