Separate Track Impact Factor Application Depending on Track Types through Correlative Analysis with Track Support Stiffness
Abstract
1. Introduction
2. Theoretical Discussion and Review
2.1. Spring Coefficient and TSS Calculation Methods
- : the stiffness of the rail pad (kN/mm),
- : the stiffness of the sleeper (because of the compressibility of wood in the rail-seat region and sleeper bending) (kN/mm),
- : the stiffness of the ballast layer (kN/mm),
- : the stiffness of the subgrade (kN/mm), and
- : the stiffness of the ballasted track structure (kN/mm).
- : the stiffness of the pad (kN/mm),
- : the stiffness of the resilience (if applicable) (kN/mm),
- : the stiffness of the sleeper (if applicable) (kN/mm),
- : the stiffness of the ballast-less slab (kN/mm),
- : the stiffness of the subgrade (kN/mm),
- : the stiffness of the ballast-less slab track structure (kN/mm).
- E: modulus of elasticity (GPa),
- I: moment of inertia (mm4),
- d: distance of the sleepers (mm),
- : stiffness of the track structure (kN/mm),
- : track support stiffness (kN/mm).
- when V ≤ 60 km/h, DAF = 1+
- when passenger train speed is 60 < V < 300 km/h,
- when freight train speed is 60 < V < 160 km/h,
- Q: Static wheel load (kN),
- : Effective wheel load (kN),
- : Dynamic wheel load (kN).
2.2. Performance Criteria for Track Dynamic Stability
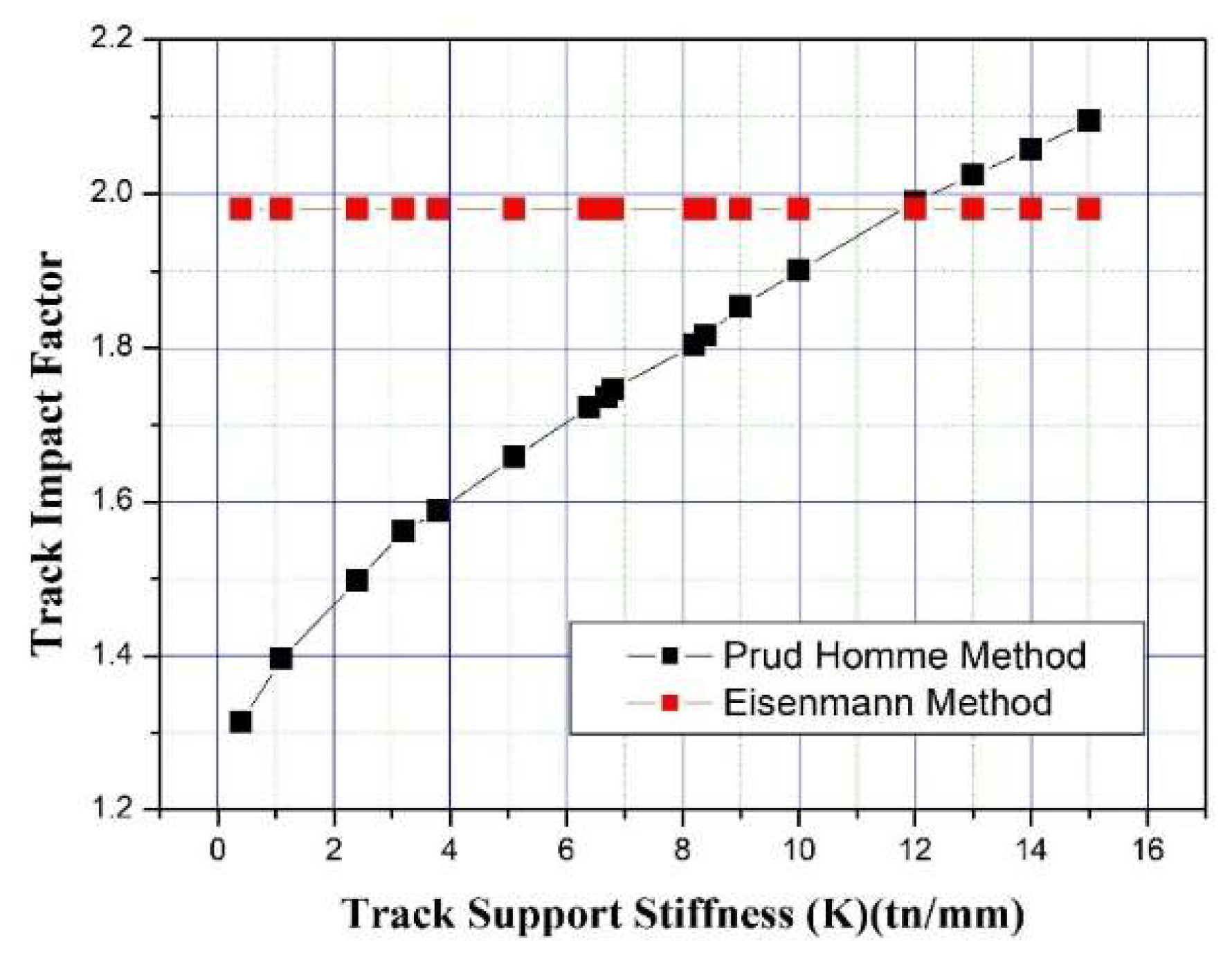
2.2.1. TIF Calculation Specifications
2.2.2. Theoretical Derivation Method and Trackside Measurement Method Comparison for TSS
- : is the trackside measurement based track support stiffness (kN/mm);
- : is dynamic wheel load (maximum value derived from trackside measurement) (kN);
- : is rail vertical displacement (maximum value derived from trackside measurement (mm).
3. Trackside Measurement Method (Materials and Specification)
3.1. Trackside Measurement Method
3.2. Trackside Measurement Equipment
3.2.1. Equipment Installation and Trackside Measurement Conditions
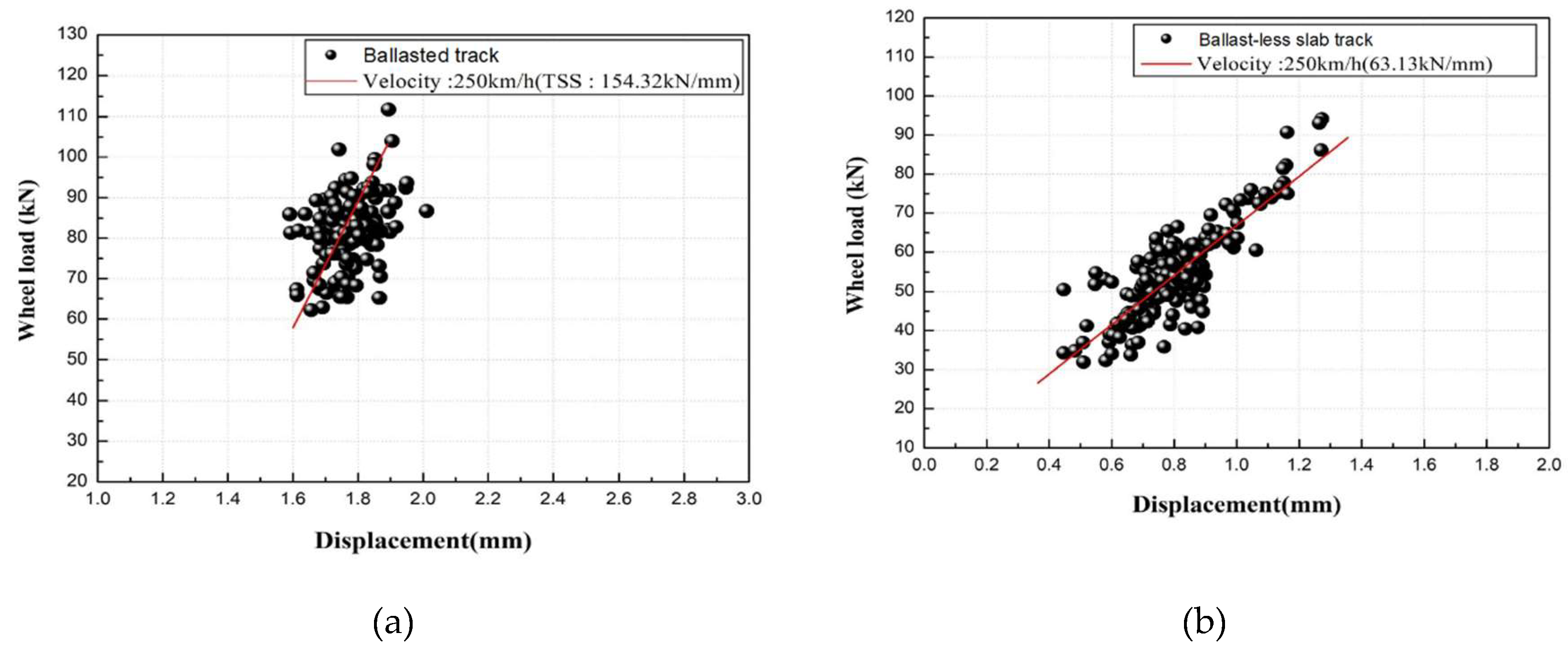
3.2.2. Dynamic Wheel Load Calculation Using Shear Strain Data
4. Trackside Measurement Results and Analysis
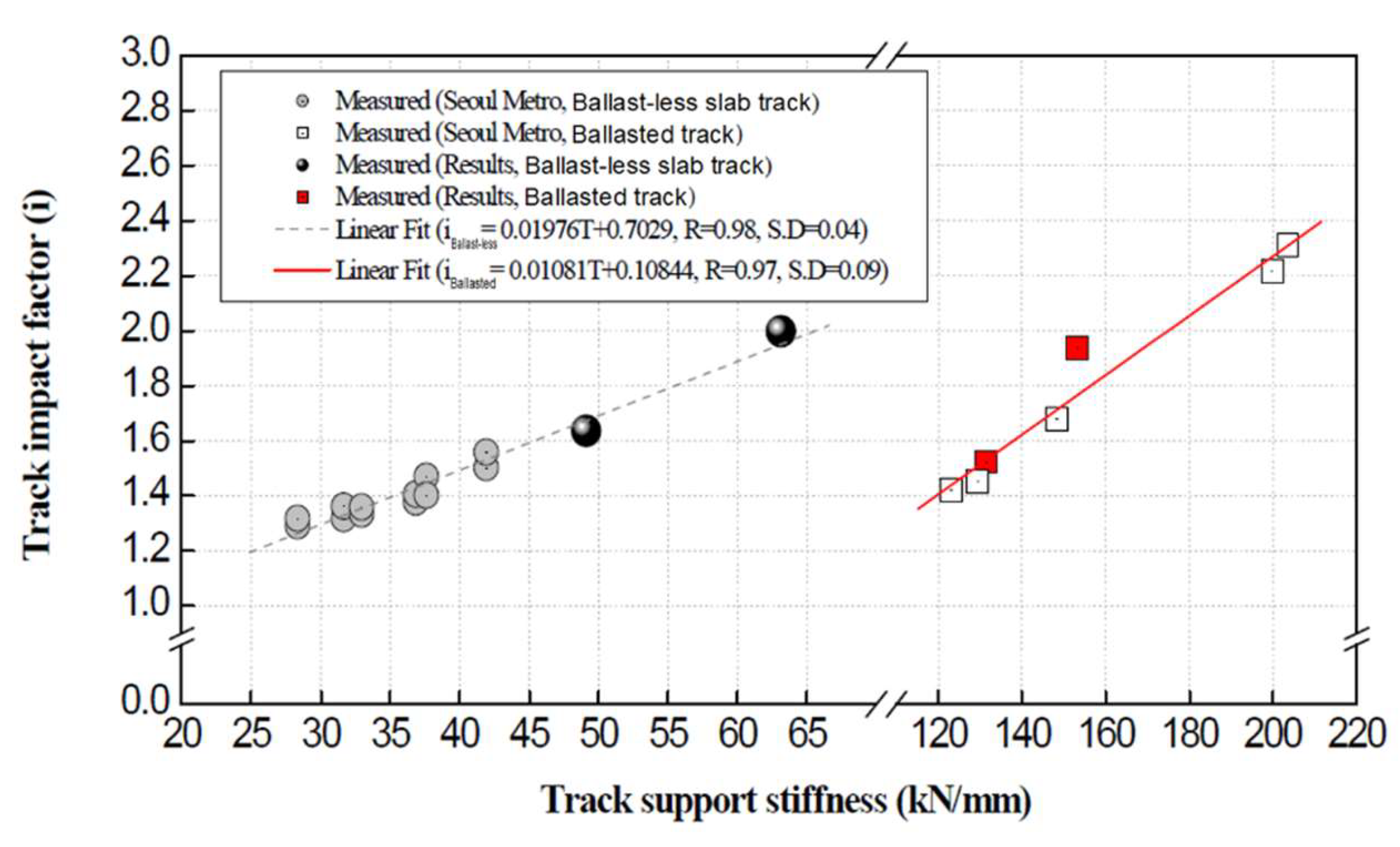
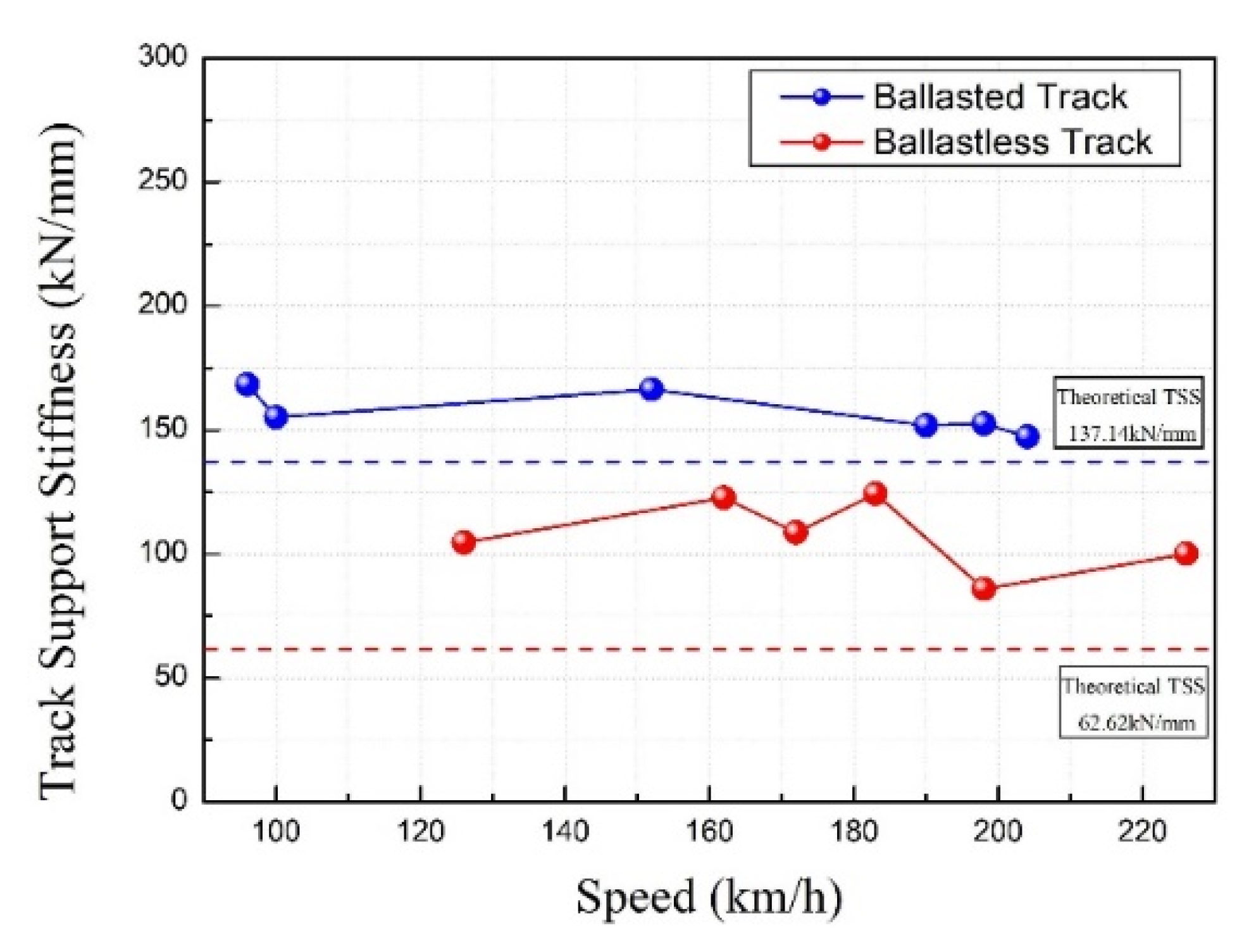
4.1. Result of TSS
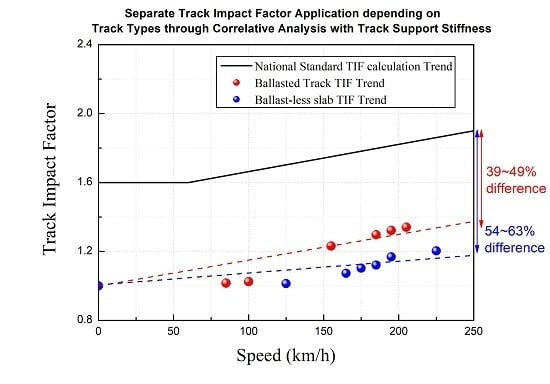
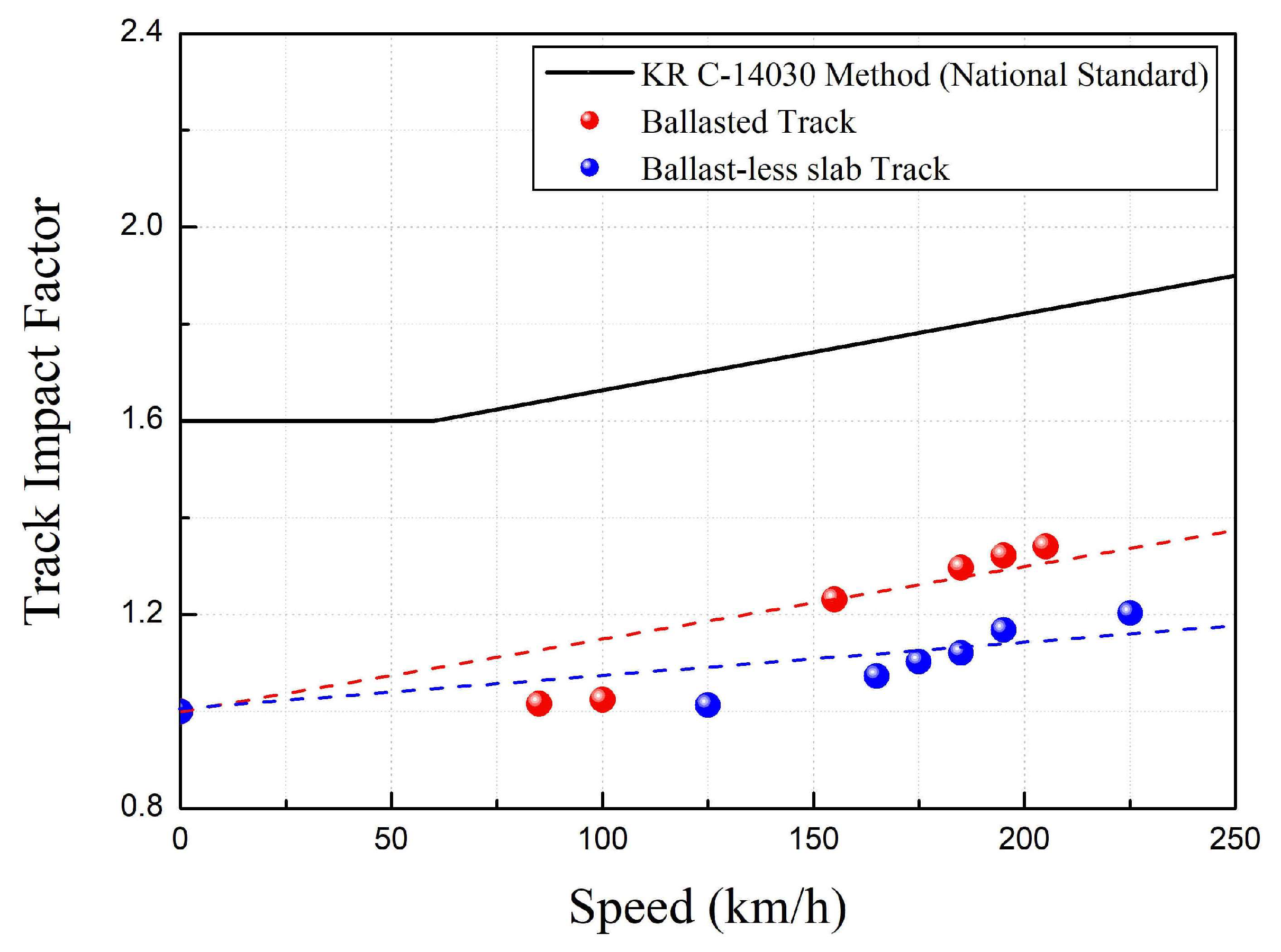
4.2. TiF Comparison between Track Types
- Korea Railroad Authority’s Track Design Standard (KR-C 14030);
- TIF(DAF) using the trackside measured data in Ballasted track;
- TIF(DAF) using the trackside measured data in Ballast-less slab track.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ISO | International Standard Organization |
| TIF | Track Impact Factor |
| TSS | Track Support Stiffness |
| DAF | Dynamic Amplitude Factor |
| KR-C | Korea Railroad Authority’s Track Design Standard |
| LVDT | Linear Variable Differential Transformers |
References
- Puzavac, L.; Popović, Z.; Lazarević, L. Influence of Track Stiffness on Track Behaviour Under Vertical Load. PROMET Traffic Transp. 2012, 24. [Google Scholar] [CrossRef]
- Priest, J.A.; Powrie, W. Determination of Dynamic Track Modulus from Measurement of Track Velocity during Train Passage. J. Geotech. Geoenviron. Eng. 2009, 135, 1732–1740. [Google Scholar] [CrossRef]
- Giannakos, K. Stiffness Coefficient in the Transition Zone Between Ballasted and Ballastless Track and Its Influence on Formation Stressing. Int. Conf. Recent Adv. Geotech. Earthq. Eng. Soil Dyn. 2010, 50, 1–11. [Google Scholar]
- Lucia, B.; Gallego, I.; Sanchez-Cambronero, S.; Rivas, A. Importance of Vertical Rail Track Stiffness on Dynamic Overloading: Limitations of the Eisenmann Formulation. 360 Revista de alta Velocidad, June 2018; 301–311. [Google Scholar]
- Van Dyk, B.J.; Edwards, J.R.; Dersch, M.S.; Ruppert, C.J.; Barkan, C.P. Evaluation of dynamic and impact wheel load factors and their application in design processes. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 231, 33–43. [Google Scholar] [CrossRef]
- Kim, M.C.; Park, Y.G.; Lim, H.J.; Park, S.H.; Ryu, J.Y. A study on the condition assessment of ballasted tracks of various substructure types of in-service railway line. In Proceedings of the 2013 Autumn Conference of Korean Society for Railway, Korea, Pyeongchang, Korea, 23–25 May 2013; pp. 178–186. [Google Scholar]
- Jenkins, H.H.; Stephenson, J.E.; Clayton, G.A.; Morland, G.W.; Lyon, D. The effect of track and vehicle parameters on wheel/rail vertical dynamic forces. Railw. Eng. J. 1974, 3, 2–16. [Google Scholar]
- Köllő, S.A.; Puskas, A.; Köllő, G. Ballasted Track versus Ballastless Track. Key Eng. Mater. 2015, 660, 219–224. [Google Scholar] [CrossRef]
- Shin, D.U.; Park, Y.G. Analysis of noise reduction effect of concrete slab by the sound absorption block in urban railway. Spring Acad. Conf. J. Korean Soc. Railw. 2017. Available online: https://dbpia.co.kr/journal/articleDetail?nodeId=NODE07266383 (accessed on 17 December 2019).
- Kim, J.W.; Lee, D.J.; Lee, J.H.; Kang, Y.S.; Park, Y.G. Urban railway track structure must be redefined based on the maintenance of orbital research. Autumn Acad. Conf. J. Korean Soc. Railw. 2013, 1155–1162. Available online: https://dbpia.co.kr/journal/articleDetail?nodeId=NODE02282150 (accessed on 15 December 2019).
- LEE, S.H. A Study for Correlation of Track Support Stiffness and Track Impact Factor according by Track Structures. Ph.D. Thesis, Seoul National University of Science and Technology, Seoul, Korea, 2018. [Google Scholar]
- Nimbalkar, S.; Indraratna, B. Improved Performance of Ballasted Rail Track Using Geosynthetics and Rubber Shockmat. J. Geotech. Geoenviron. Eng. 2016, 142, 4016031. [Google Scholar] [CrossRef]
- Doyle, N.F. Railway Track Design: A Review of Current Practice. BHP Melbourne Research 300 Laboratories; Bureau of Transport Economics: Canberra, Australia, 1980.
- Roberto, S.; Valeri, M.; João, P. Study on different solutions to reduce the dynamic impacts in transition zones for high-speed rail. J. Theor. Appl. Vib. Acoust. 2017, 3, 199–222. [Google Scholar] [CrossRef]
- Korea Railroad Authority’s Track Design Standard (2018) KR-C 14030, Ballast Track Structure. Daejeon, Korea; pp. 22–25. Available online: https://www.kr.or.kr/boardCnts/view.do?boardID=1000009&boardSeq=1113233&lev=0&m=041101 (accessed on 19 December 2019).
- Konstantinos, G.; Spyridon, T. Transition Zone between Ballastless and Ballasted Track: Influence of Changing Stiffness on Acting Forces, Procedia—Social and Behavioral Sciences; Elsevier: Amsterdam, The Netherlands, 2012; Volume 48, pp. 3548–3557. [Google Scholar]
- Noh, G.T.; Lim, H.J.; Lee, J.Y.; Park, Y.G. Evaluation of Track Support Stiffness and Track Impact factor for Ballast and Concrete Type Tracks. J. Korean Soc. Railw. 2019, 21, 389–395. [Google Scholar] [CrossRef]
- Kim, J.W.; Kim, M.C.; Park, Y.G. An Experimental Study on the Evaluation of Track Impact factor on the Various Track Type in Urban Transit. Autumn Acad. Conf. J. Korean Soc. Railw. 2011, 382–399. [Google Scholar]
- Henrik, L. Transition Zones between Ballasted and Ballastless Tracks, Lunds University. 2014. Available online: http://lup.lub.lu.se/luur/download?func=downloadFile&recordOId=4498421&fileOId=8961741 (accessed on 9 January 2020).
- Nyström, P.; Prokopov, A. Spårkonstruktioner för 320 km/h—Övergångskonstruktioner, Borlänge; Trafikverket: Stockholm, Sweden, 2011.
- Kerr, A.D. On the determination of the rail support modulus k. Int. J. Solids Struct. 2000, 37, 4335–4351. [Google Scholar] [CrossRef]
- Bisadi Mehrdad, Ma Quincy, Beskhyroun Sherif. Evaluation of the Dynamic Amplification Factor for Railway Bridges Subjected to a Series of Moving Mass. In Proceedings of the 5th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015. [CrossRef]
- Jenks, C.W. Design of Track Transitions; Transportation Research Board: Washington, DC, USA, 2006. [Google Scholar]
- Lee, D.W.; Park, Y.G.; Choi, J.Y. A Study on the Evaluation of Track Support Stiffness on the Various Track Type in Urban Transit. J. Korean Soc. Railw. 2011, 14, 262–270. [Google Scholar] [CrossRef][Green Version]


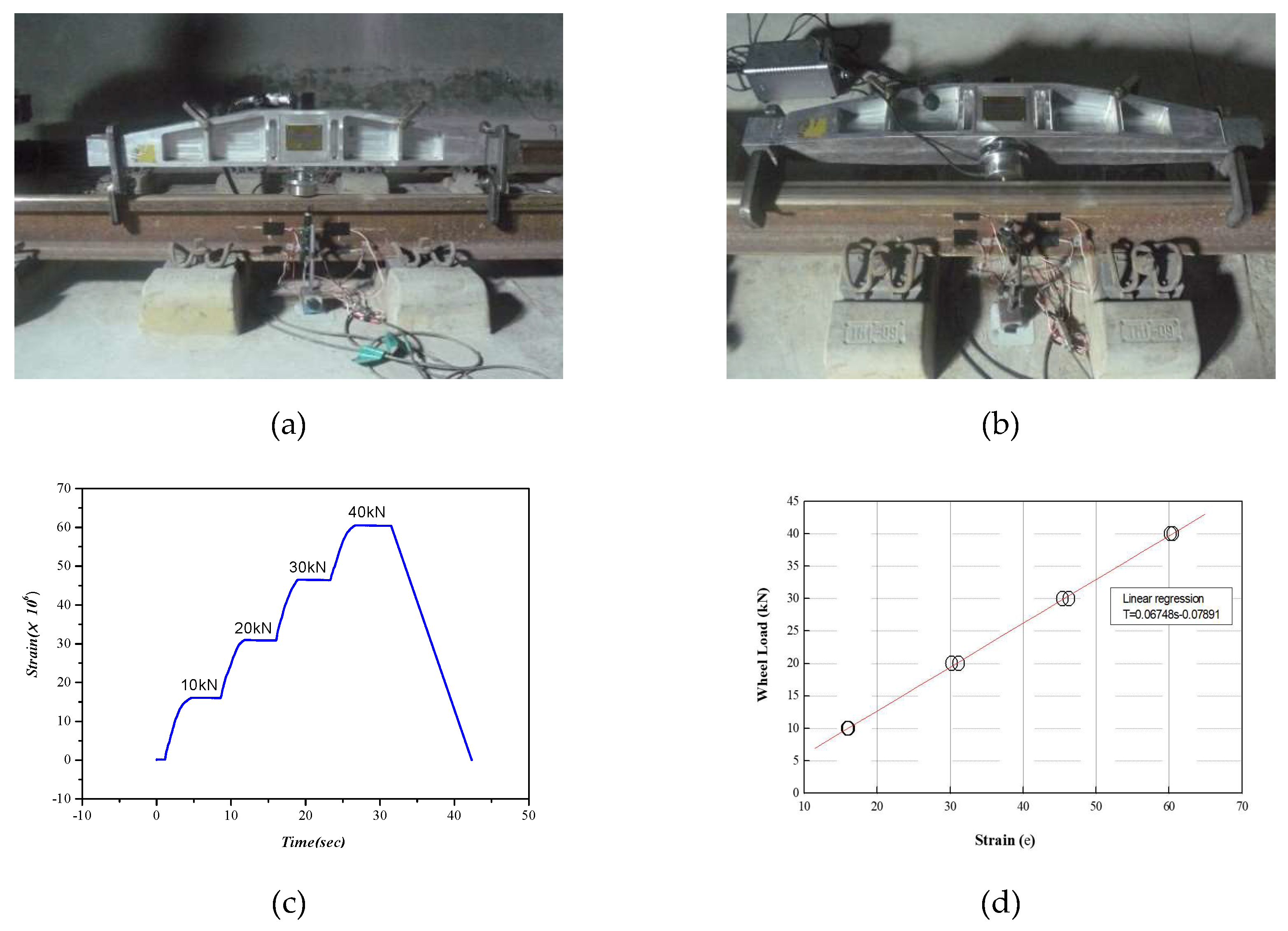
| Dynamic Factor | Expression for ø | Vehicle Parameters Included | Track Parameters Included | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train Speed | Wheel Diameter | Static Wheel Load | Unsprung Mass | Vehicle Center of Gravity | Locomotive Maintenance Condition | Track Modulus | Track Stiffness at Rail Joint | Track Joint Dip Angle | Cant Deficiency in Curves | Curve Radius | Track Maintenance Condition | ||
| Talbot | ● | ● | |||||||||||
| Indian Railways | ● | ● | |||||||||||
| Eisenmann | ● | ● | |||||||||||
| ORE/Birmann | ● | ● | ● | ● | ● | ● | |||||||
| German Railways | ● | ||||||||||||
| British Railways | ● | ● | ● | ● | ● | ||||||||
| South African Railways | ● | ● | |||||||||||
| Clarke | ● | ● | ● | ||||||||||
| WMATA | ● | ||||||||||||
| Sadeghi | ● | ||||||||||||
| AREMA C30 | ● | ||||||||||||
| Track Types | Track Geometry (Lines) | Structure Type | Fastening System | Track Condition (Φ) |
|---|---|---|---|---|
| Ballasted | Straight line | Earthwork Tunnel | E-clip (ballasted) | 0.2 |
| Ballast-less (slab) | Straight line | Bridge, Tunnel | System300 (Ballast-less slab) | 0.2 |
| Train Vehicle Type | KTX-Sancheon (10 Cars & 1 Vehicle) |
|---|---|
| Design wheel load (Static load) (kN) Gauge (mm) | 85 |
| 1435 | |
| Max. design speed (km/h) | 330 |
| Max. operation speed (km/h) | 250/305 |
| Category | Type | Model | Measurement Item |
|---|---|---|---|
| Sensor | 2 axis-strain gauge | FCA-5-11-1L | Vert./Lateral wheel load |
| 1 axis-strain gauge | FLA-5-11-1L | Bending stress in rail | |
| LVDT (Linear variable differential transformer) | CDP-10 (10 mm) | Vert./lateral displ. of rail | |
| Measurement instrument | Data acquisition device for dynamic responses | MGC Plus | |
| SDA-810 (8 ch) | |||
| Bridge box | DB-120 (1 ch, 8 ch) |
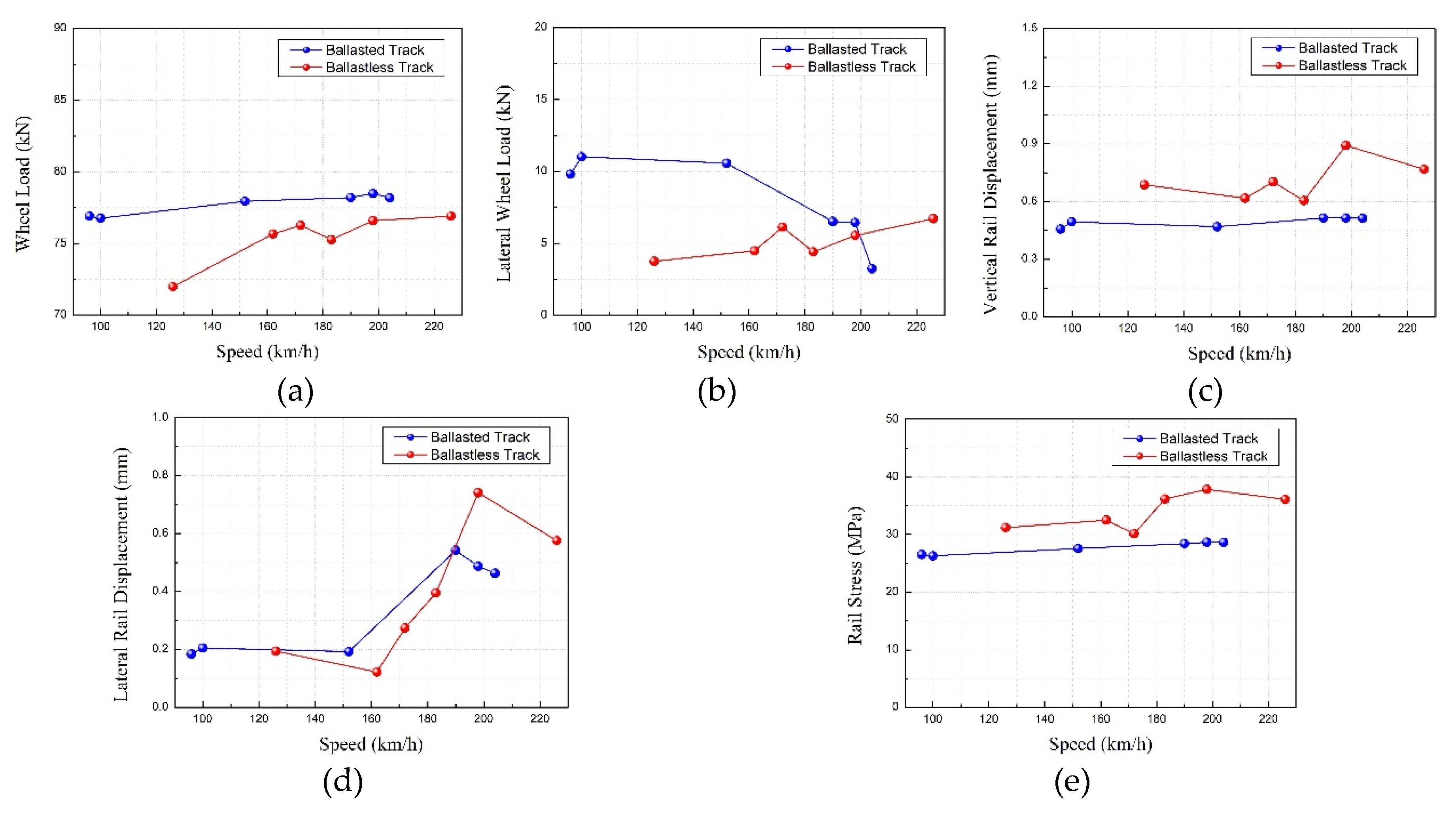
| Ballasted Track | |||||
|---|---|---|---|---|---|
| Speed (km/h) | Wheel Load (kN) | Lateral Wheel Load (kN) | Vertical Rail Displacement (mm) | Lateral Rail Displacement (mm) | Rail Stress (MPa) |
| 80–90 | 76.936 | 9.823 | 0.457 | 0.184 | 26.529 |
| 90–110 | 76.767 | 11.021 | 0.495 | 0.205 | 26.298 |
| 150–160 | 77.950 | 10.563 | 0.469 | 0.192 | 27.581 |
| 180–190 | 78.200 | 6.524 | 0.515 | 0.542 | 28.429 |
| 190–200 | 78.483 | 6.454 | 0.514 | 0.487 | 28.675 |
| 200–210 | 78.179 | 3.252 | 0.531 | 0.463 | 28.649 |
| Ballast-Less Slab Track | |||||
|---|---|---|---|---|---|
| Speed (km/h) | Wheel Load (kN) | Lateral Wheel Load (kN) | Vertical Rail Displacement (mm) | Lateral Rail Displacement (mm) | Rail Stress (MPa) |
| 120–130 | 71.980 | 3.759 | 0.687 | 0.194 | 31.210 |
| 160–170 | 75.663 | 4.486 | 0.617 | 0.122 | 32.494 |
| 170–180 | 76.263 | 6.137 | 0.702 | 0.274 | 30.141 |
| 180–190 | 76.268 | 4.416 | 0.605 | 0.122 | 36.178 |
| 190–200 | 75.268 | 5.546 | 0.892 | 0.741 | 37.851 |
| 220–230 | 76.906 | 6.726 | 0.768 | 0.575 | 36.107 |
| Track Structure | Rail Supporting Point Spring Coefficient (kN/mm m) | Theoretical TSS (kN/mm) | Field Measurement | Ratio between Theoretical and Measurement | |
|---|---|---|---|---|---|
| Speed (km/h) | TSS (kN/mm) | ||||
| Ballasted | 85.71 | 137.14 | 80–90 | 168.325 | 1.227 |
| 90–110 | 155.222 | 1.132 | |||
| 150–160 | 166.365 | 1.213 | |||
| 180–190 | 151.857 | 1.107 | |||
| 190–200 | 152.607 | 1.113 | |||
| 200–210 | 147.230 | 1.074 | |||
| Ballast-less slab | 39.14 | 62.62 | 120–130 | 107.715 | 1.720 |
| 160–170 | 122.664 | 1.959 | |||
| 170–180 | 108.669 | 1.735 | |||
| 180–190 | 124.386 | 1.986 | |||
| 190–200 | 85.901 | 1.372 | |||
| 220–230 | 100.091 | 1.598 | |||
| Track Structure | Speed (km/h) | Measured Max. Wheel Load (kN) | KR C-14030 TIF | TIF Calculation Using Measured Data | Ratio between KR C-14030 and Measured Data TIF | Note |
|---|---|---|---|---|---|---|
| Ballasted | 80–90 | 103.487 | 1.639 | 1.015 | 0.619 | Static Wheel load 85 kN |
| 90–110 | 104.520 | 1.663 | 1.025 | 0.616 | ||
| 150–160 | 107.141 | 1.750 | 1.050 | 0.600 | ||
| 180–190 | 112.240 | 1.797 | 1.100 | 0.612 | ||
| 190–200 | 117.380 | 1.813 | 1.151 | 0.635 | ||
| 200–210 | 116.624 | 1.829 | 1.143 | 0.625 | ||
| Ballast-less slab | 120–130 | 103.376 | 1.703 | 1.013 | 0.595 | Static Wheel load 85 kN |
| 160–170 | 109.396 | 1.766 | 1.073 | 0.608 | ||
| 170–180 | 112.516 | 1.782 | 1.103 | 0.619 | ||
| 180–190 | 114.322 | 1.797 | 1.121 | 0.624 | ||
| 190–200 | 119.113 | 1.813 | 1.168 | 0.644 | ||
| 220–230 | 122.687 | 1.861 | 1.203 | 0.646 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-I.; Oh, K.-H.; Park, Y.-G. Separate Track Impact Factor Application Depending on Track Types through Correlative Analysis with Track Support Stiffness. Infrastructures 2020, 5, 17. https://doi.org/10.3390/infrastructures5020017
Lee J-I, Oh K-H, Park Y-G. Separate Track Impact Factor Application Depending on Track Types through Correlative Analysis with Track Support Stiffness. Infrastructures. 2020; 5(2):17. https://doi.org/10.3390/infrastructures5020017
Chicago/Turabian StyleLee, Jae-Ik, Kyu-Hwan Oh, and Yong-Gul Park. 2020. "Separate Track Impact Factor Application Depending on Track Types through Correlative Analysis with Track Support Stiffness" Infrastructures 5, no. 2: 17. https://doi.org/10.3390/infrastructures5020017
APA StyleLee, J.-I., Oh, K.-H., & Park, Y.-G. (2020). Separate Track Impact Factor Application Depending on Track Types through Correlative Analysis with Track Support Stiffness. Infrastructures, 5(2), 17. https://doi.org/10.3390/infrastructures5020017