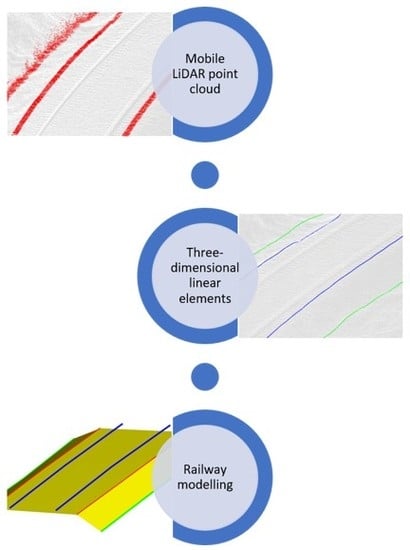
Automated Three-Dimensional Linear Elements Extraction from Mobile LiDAR Point Clouds in Railway Environments
Abstract
1. Introduction
2. Materials and Methods
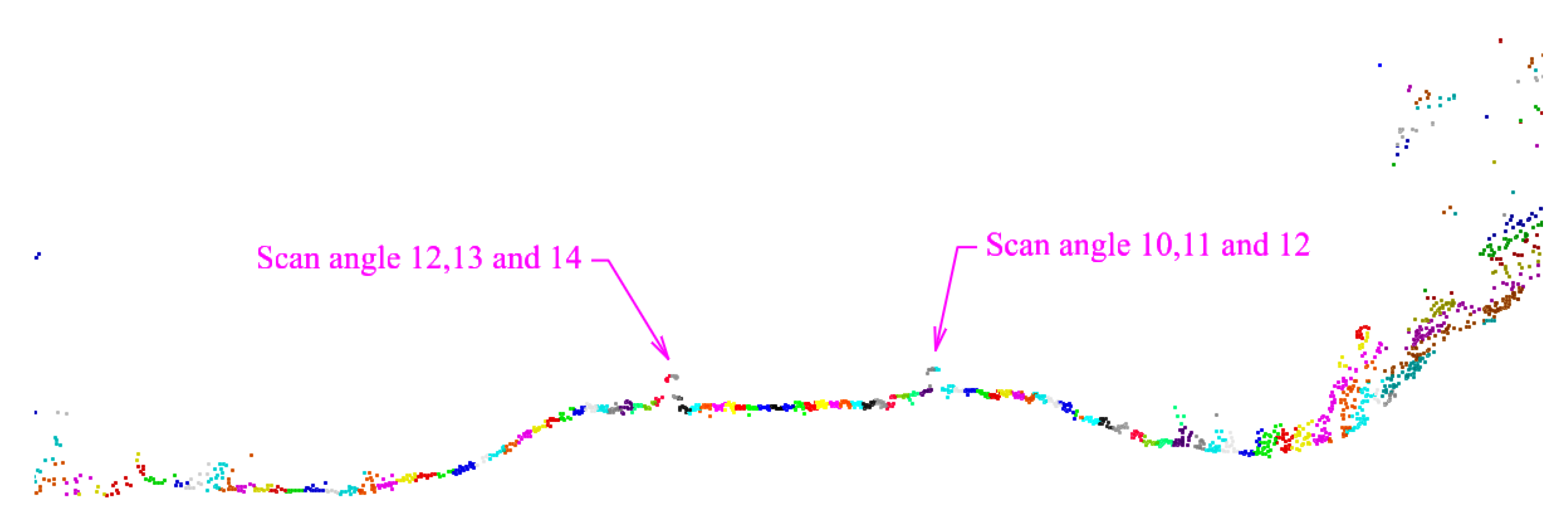
2.1. MLS Working Principles and Storing Standard Files Format
2.2. Proposed Methodology
- Input: Restricted scan angle classified cloud points
- For each point P
- ○
- If Distance2D (P, Pprev) < D then go to Jump:
- ○
- For each point P1
- ▪
- If Distance2D (P, P1) < R then
- ▪
- PointsList add P1
- ▪
- End if
- ○
- Next
- ○
- Vertex = Average (PointList (X, Y, Z))
- ○
- VertexList add Vertice
- ○
- Clear PointList
- ○
- Jump
- ○
- Set Pprev = P
- Next
- Polyline = Vertexlist
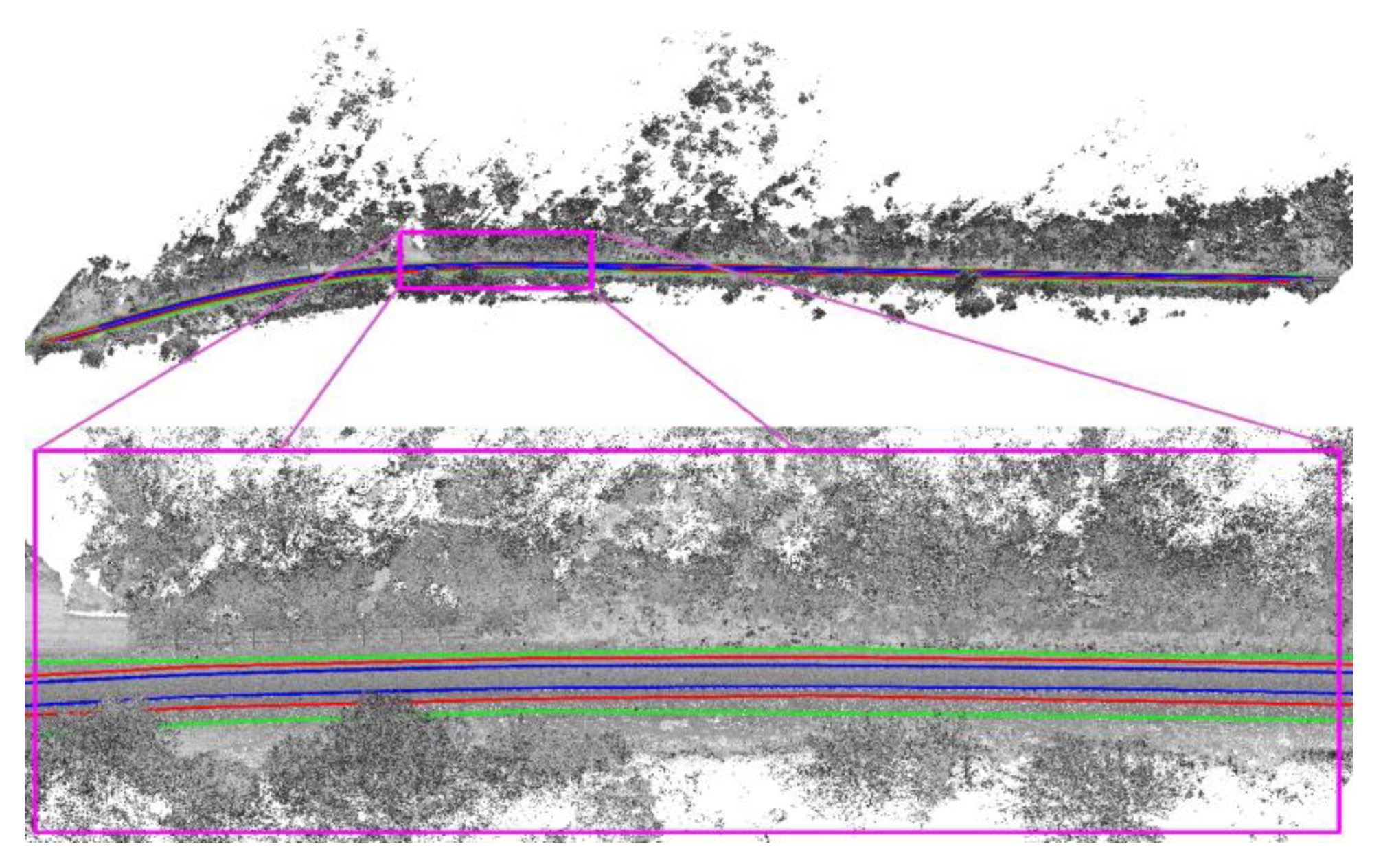
2.3. Rail Tracks Centre Lines
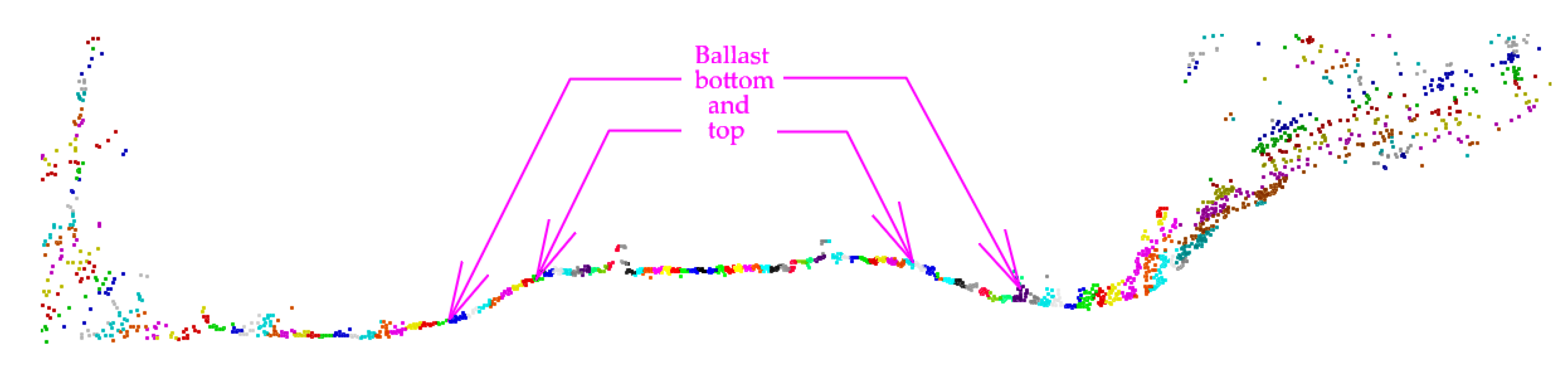
2.4. Ballast Top and Bottom Break-Lines
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mikrut, S.; Kohut, P.; Pyka, K.; Tokarczyk, R.; Barszcz, T.; Uhl, T. Mobile laser scanning systems for measuring the clearance gauge of railways: State of play, testing and outlook. Sensors 2016, 16, 683. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Guo, J.; Chiang, Y. Monitoring tunnel profile by means of multi-epoch dispersed 3-D LiDAR point clouds. Tunn. Undergr. Space Technol. 2013, 33, 186–192. [Google Scholar] [CrossRef]
- Xie, X.; Lu, X. Development of a 3D Modelling Algorithm for Tunnel Deformation Monitoring Based on Terrestrial Laser Scanning. Undergr. Space 2107, 2, 16–29. [Google Scholar] [CrossRef]
- Gawronek, P.; Makuch, M. TLS Measurement during Static Load Testing of a Railway Bridge. ISPRS Int. J. Geo Inf. 2019, 8, 44. [Google Scholar] [CrossRef]
- Taheri Andani, M.; Mohammed, A.; Jain, A.; Ahmadian, M. Application of LIDAR technology for rail surface monitoring and quality indexing. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2018, 232, 1398–1406. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, Q.; Mao, Q.; Zou, Q. A 3D Laser Profiling System for Rail Surface Defect Detection. Sensors 2017, 17, 1791. [Google Scholar] [CrossRef]
- Pastucha, E. Catenary System Detection, Localization and Classification Using Mobile Scanning Data. Remote Sens. 2016, 8, 801. [Google Scholar] [CrossRef]
- Rodríguez-Cuenca, B.; García-Cortés, S.; Ordóñez, C.; Alonso, M.C. Automatic detection and classification of pole-like objects in urban point cloud data using an anomaly detection algorithm. Remote Sens. 2015, 7, 12680–12703. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Zai, D.W. Automated Extraction of 3D Trees from Mobile LiDAR Point Clouds. ISPRS Int. Arch. Photogramm. 2014, 40, 629. [Google Scholar] [CrossRef]
- Gargoum, S.; El-Basyouny, K.; Sabbagh, J.; Froese, K. Automated Highway Sign Extraction Using Lidar Data. Transp. Res. Rec. J. Transp. Res. Board 2017, 2643, 1–8. [Google Scholar] [CrossRef]
- Zhu, L.; Hyyppä, J. The Use of Airborne and Mobile Laser Scanning for Modelling Railway Environments in 3D. Remote Sens. 2014, 6, 3075–3100. [Google Scholar] [CrossRef]
- Zhu, L.; Hyyppa, J.; Kukko, A.; Kaartinen, H.; Chen, R. Photorealistic 3D city modeling from mobile laser scanning data. Remote Sens. 2011, 3, 1406–1426. [Google Scholar] [CrossRef]
- The Use of Mobile Laser Scanning Data and Unmanned Aerial Vehicle Images for 3D Model Reconstruction. Available online: http://www.int-arch-photogramm-remote-sens-spatial-inf-sci.net/XL-1-W2/419/2013/isprsarchives-XL-1-W2-419-2013.pdf (accessed on 21 June 2019).
- Hyyppa, J.; Hyyppa, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Axelsson, P. DEM generation from laser scanner data using adaptive TIN models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 110–117. [Google Scholar]
- Che, E.; Jung, J.; Olsen, M.J. Object Recognition, Segmentation, and Classification of Mobile Laser Scanning Point Clouds: A State-of-the-Art Review. Sensors 2019, 19, 810. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Fang, L. Automated extraction of 3-D railway tracks from mobile laser scanning point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4750–4761. [Google Scholar] [CrossRef]
- Stein, D.; Spindler, M.; Kuper, J.; Lauer, M. Rail detection using lidar sensors. Int. J. Sustain. Dev. Plan. 2016, 11, 65–78. [Google Scholar] [CrossRef]
- Arastounia, M.; Oude Elberink, S. Application of Template Matching for Improving Classification of Urban Railroad Point Clouds. Sensors 2016, 16, 2112. [Google Scholar] [CrossRef]
- Arastounia, M. An Enhanced Algorithm for Concurrent Recognition of Rail Tracks and Power Cables from Terrestrial and Airborne LiDAR Point Clouds. Infrastructures 2017, 2, 8. [Google Scholar] [CrossRef]
- Jung, J.; Chen, L.; Sohn, G.; Luo, C.; Won, J. Multi-Range Conditional Random Field for Classifying Railway Electrification System Objects Using Mobile Laser Scanning Data. Remote Sens. 2016, 8, 1008. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, T.; Tang, J.; Song, W.; Zhang, Y.; Chen, L. A Fast Algorithm for Rail Extraction Using Mobile Laser Scanning Data. Remote Sens. 2018, 10, 1998. [Google Scholar] [CrossRef]
- Niina, Y.; Honma, R.; Honma, Y.; Kondo, K.; Tsuji, K.; Hiramatsu, T.; Oketani, E. Automatic rail extraction and celarance check with a point cloud captured by mls in a railway. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 767–771. [Google Scholar] [CrossRef]
- Oude Elberink, S.; Khoshelham, K.; Arastounia, M.; Diaz Benito, D. Rail Track Detection and Modelling in Mobile Laser Scanner Data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, II-5/W2, 223–228. [Google Scholar]
- Elberink, S.O.; Khoshelham, K. Automatic Extraction of Railroad Centerlines from Mobile Laser Scanning Data. Remote Sens. 2015, 7, 5565–5583. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, C.; Yang, Z.; Chen, Y.; Li, J. Automatic railway power line extraction using mobile laser scanning data. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B5, 615–619. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, Q.; Liu, L.; Zheng, D.Y.; Li, C.K.; Lim, K. Supervised Classification of Power Lines from Airborne LiDAR Data in Urban Areas. Remote Sens. 2017, 9, 771. [Google Scholar] [CrossRef]
- Zarembski, A.M.; Grissom, G.T.; Euston, T.L. On the Use of Ballast Inspection Technology for the Management of Track Substructure. Transp. Infrastruct. Geotechnol. 2014, 1, 83–109. [Google Scholar] [CrossRef]
- Bensalah, M.; Elouadi, A.; Mharzi, H. Integrating BIM in railway projects: Review & perspectives for Morocco & Mena. Int. J. Recent Sci. Res. 2018, 9, 23398–23403. [Google Scholar]
- Nuttens, T.; De Breuck, V.; Cattor, R.; Decock, K.; Hemeryk, I. Using Bim models for the design of large rail infrastructure projects: Key factors for a successful implementation. Int. J. Sustain. Dev. Plan. 2018, 13, 73–83. [Google Scholar] [CrossRef]
- LASer (LAS) File Format Exchange Activities. Available online: https://www.asprs.org/divisions-committees/lidar-division/laser-las-file-format-exchange-activities (accessed on 22 June 2019).
- LAS Specification 1.4—R14. Available online: http://www.asprs.org/wp-content/uploads/2019/03/LAS_1_4_r14.pdf (accessed on 22 June 2019).
- Douglas, D.; Peucker, T. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cust. Cartogr. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y.; Li, J. Two-step adaptive extraction method for ground points and breaklines from lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Zarembski, A.M.; Grissom, G.T.; Euston, T.L. Use of Ballast Inspection Technology for the Prioritization, Planning and Management of Ballast Delivery and Placement. In Proceedings of the American Railway Engineering Association Annual Conference, Indianapolis, IN, USA, 29 September 2013. [Google Scholar]
- Ciotlaus, M.; Kollo, G. Ballast bed cleaning and recycling—Influence on stability of continuously welded rail track. Procedia Manuf. 2108, 22, 294–300. [Google Scholar] [CrossRef]













| Characteristics | Values |
|---|---|
| Scan frequency | 200 Hz |
| Laser pulse repetition rate | Up to 300 Hz |
| Minimum distance | 1.5 m |
| Points relative precision | 0.005 m |
| Extracted Line | Completeness (%) | Correctness (%) | Quality (%) |
|---|---|---|---|
| Left bottom ballast | 82.0 | 81.6 | 69.2 |
| Left top ballast | 85.8 | 85.4 | 74.8 |
| Right bottom ballast | 80.6 | 80.4 | 67.3 |
| Right top ballast | 82.9 | 82.5 | 70.5 |
| Left rail | 98.7 | 98.9 | 97.7 |
| Right rail | 99.3 | 99.3 | 98.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gézero, L.; Antunes, C. Automated Three-Dimensional Linear Elements Extraction from Mobile LiDAR Point Clouds in Railway Environments. Infrastructures 2019, 4, 46. https://doi.org/10.3390/infrastructures4030046
Gézero L, Antunes C. Automated Three-Dimensional Linear Elements Extraction from Mobile LiDAR Point Clouds in Railway Environments. Infrastructures. 2019; 4(3):46. https://doi.org/10.3390/infrastructures4030046
Chicago/Turabian StyleGézero, Luis, and Carlos Antunes. 2019. "Automated Three-Dimensional Linear Elements Extraction from Mobile LiDAR Point Clouds in Railway Environments" Infrastructures 4, no. 3: 46. https://doi.org/10.3390/infrastructures4030046
APA StyleGézero, L., & Antunes, C. (2019). Automated Three-Dimensional Linear Elements Extraction from Mobile LiDAR Point Clouds in Railway Environments. Infrastructures, 4(3), 46. https://doi.org/10.3390/infrastructures4030046