Probabilistic Identification of Seismic Response Mechanism in a Class of Similar Arch Dams
Abstract
1. Introduction
2. Probabilistic Analysis and Seismic Intensity Levels
2.1. ICOLD Recommendations
- Operating Basis Earthquake (OBE) represents the SIL at the dam site for which only minor (easily repairable) damage is acceptable, and the dam should remain functional. OBE corresponds to the return period of 145 years (50% probability of exceedance in 100 years).
- Safety Evaluation Earthquake (SEE) represents the SIL at the dam site for which a dam must be able to resist without uncontrolled release of the reservoir water. The SEE ground motion can be obtained from a probabilistic seismic hazard analysis (PSHA) and/or a deterministic seismic hazard analysis (DSHA). For large and high consequence dams, SEE is defined as:
- -
- Maximum Credible Earthquake (MCE): produces the largest expected ground motion at the dam site and is estimated based on DSHA. According to ICOLD [15], the ground motion parameters should be estimated at the 84th percentile level.
- -
- Maximum Design Earthquake (MDE): corresponds to return period of 10,000 years (1% probability of exceedance in 100 years) and is estimated based on PSHA.
Note that for moderate consequence dams, the SEE ground motion parameters should be estimated at the 50 to 84th percentile level (based on DSHA) and need not have a smaller than (based on PSHA). For low consequence dams, the SEE ground motion parameters should be estimated at the 50th percentile level (based on DSHA) and need not have a smaller than (based on PSHA).
- The three components of the spectrum-matched acceleration time histories must be statistically independent. One cannot scale one of the acceleration components and use in other direction.
- The duration of strong ground shaking shall be selected in such a way that aftershocks are also covered.
- For the safety check of a dam, at least three different earthquakes shall be considered for the SEE ground motion.
2.2. ATC Recommendations
- Generate a seismic hazard curve, vs. , for the dam site.
- Compute seismic intensity range which covers the dam response from no (or negligible) damage to collapse. As a recommendation, the minimum and maximum spectral acceleration can be assumed as: , and , where corresponds to years.
- Split the range into equal intervals; calculate and record in each interval; identify the midpoint spectral acceleration in each interval and the corresponding . For 2D model of gravity dams, is recommended to be 8; while for 3D arch dams it may be reduced to 4.
- Develop a target response spectrum, , based on data collected from each midpoint. Three types of response spectra are acceptable: (1) uniform hazard spectra, (2) conditional mean spectra, and (3) conditional spectra.
- For each target response spectrum, select and scale suites of n ground motion triplets as follows:
- -
- Select a candidate suite of ground motion triplets from available recorded motions (e.g., PEER [20]).
- -
- For each ground motion triplet, construct the geomean spectrum for the horizontal components over a period range of as , where and can be selected as 0.2 and 2.0, respectively. is the fundamental period of dam-reservoir-foundation system.
- -
- Compare and , and select those ground motion horizontal pairs which are similar in shape to the target response spectrum within the period range of .
- -
- Amplitude-scale all three components of each ground motion triplet by the ratio of .
3. Criteria for Performance Evaluation
3.1. Linear Analysis
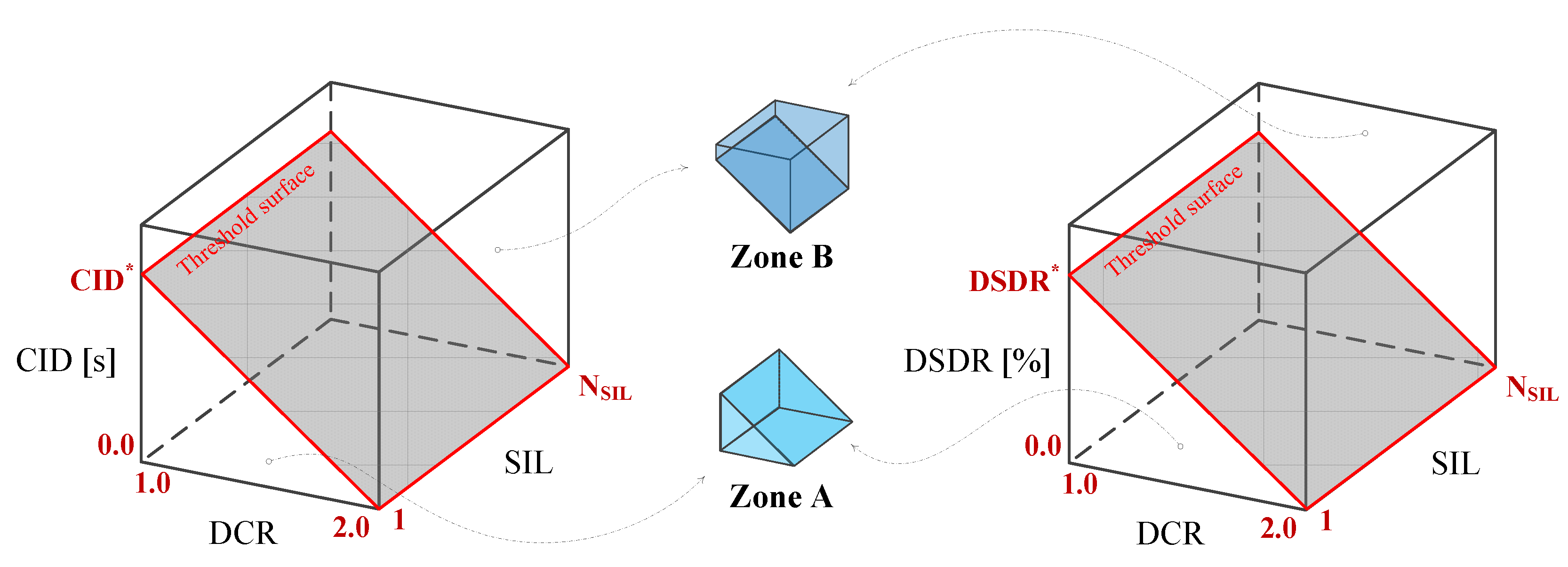
- Demand Capacity Ratio (DCR): This local index refers to the ratio of the calculated stresses or strains in a dam body to the tensile strength of mass concrete or its equivalent strain.
- Cumulative Inelastic Duration (CID): This local index refers to the total duration of stress (or strain) excursions above a stress (or strain) level associated with a certain DCR.
- Damage Spatial Distribution Ratio (DSDR): This global index refers to the ratio of the overstressed (or overstrained) region to total dam area at the specific DCR.
- If DCR ≤ 1.0 for all N, the dam response is in linear elastic range. No (or minor) damage is expected.
- If 1.0 < DCR < 2.0, the dam response is in nonlinear phase. The status of the critical nodes should be checked as follows:
- -
- If even one of the critical nodes (completely or partially) exceeds the threshold surface, being in zone B, significant damage is expected. In this condition, performing detailed nonlinear analysis is required.
- -
- If all the critical nodes are in zone A, application of the linear elastic procedure is allowed only if the DSDR does not exceed the threshold, zone A (of right plot).
- -
- If all the critical nodes fall below the threshold curve in CID–DCR plot (i.e., zone A), but DSDR exceeds the threshold in DSDR–DCR plot (i.e., zone B), severe damage is expected in the dam body. Performing detailed nonlinear analysis is required.
- If DCR ≥ 2.0, severe damage (at least localized damage) is expected. If it is accompanied by considerable spatial extension, zone B in the right plot, global damage is also expected. In this case, performing detailed nonlinear analysis is required.
3.2. Nonlinear Analysis
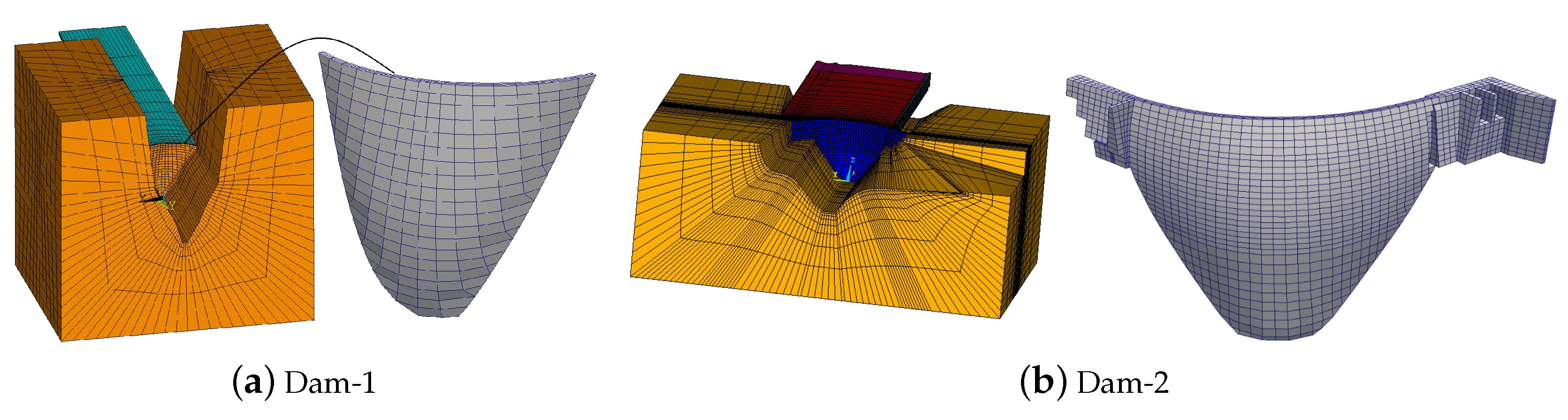
4. Case Study Dams
5. Results and Discussions
5.1. Statistical Response Comparison
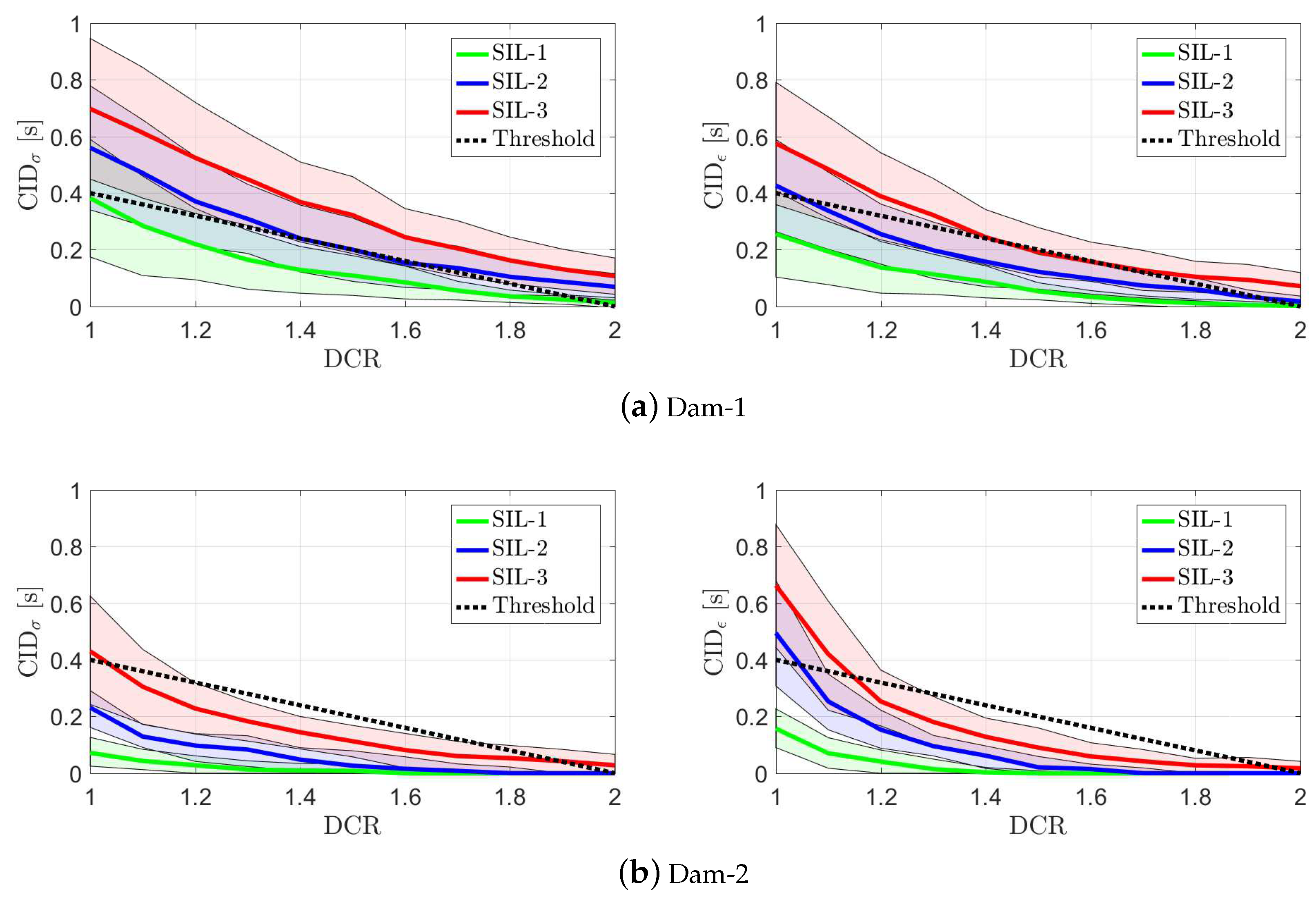
- The stress-based and strain-based CID–DCR metrics are not identical. In fact, the stress-based CID–DCR metric shows higher CID values for Dam-1, while the opposite is true for Dam-2.
- According to the stress-based criteria, SIL-2 and SIL-3 exceed the threshold in Dam-1, while SIL-3 exceeds the threshold only at DCR = 1 and 2 in Dam-2.
- The strain-based CID–DCR curves for both dams share more similarities. In both cases, the mean curve exceeds the threshold extensively for SIL-3, partially for SIL-2 (only DCR = 1), and never for SIL-1.
- Moreover, the curves associated with Dam-2 decay faster than the curves belonging to Dam-1. This means that the localized damage risk at higher DCR values is lower for Dam-2.
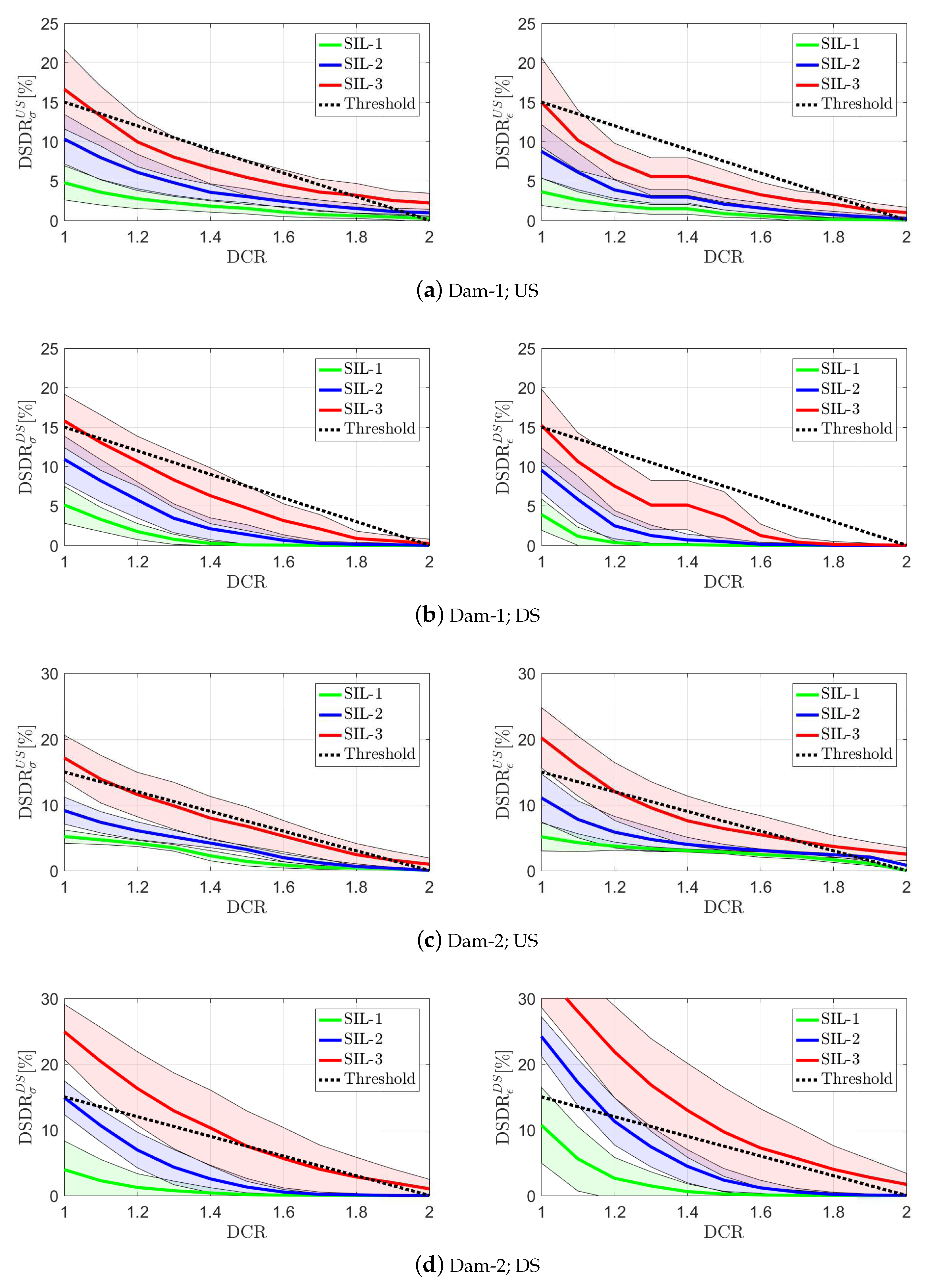
- The stress-based and strain-based responses have a similar pattern for Dam-1, while they are different for Dam-2.
- In Dam-2, the strain-based DSRD is higher than stress-based one for lower DCR values.
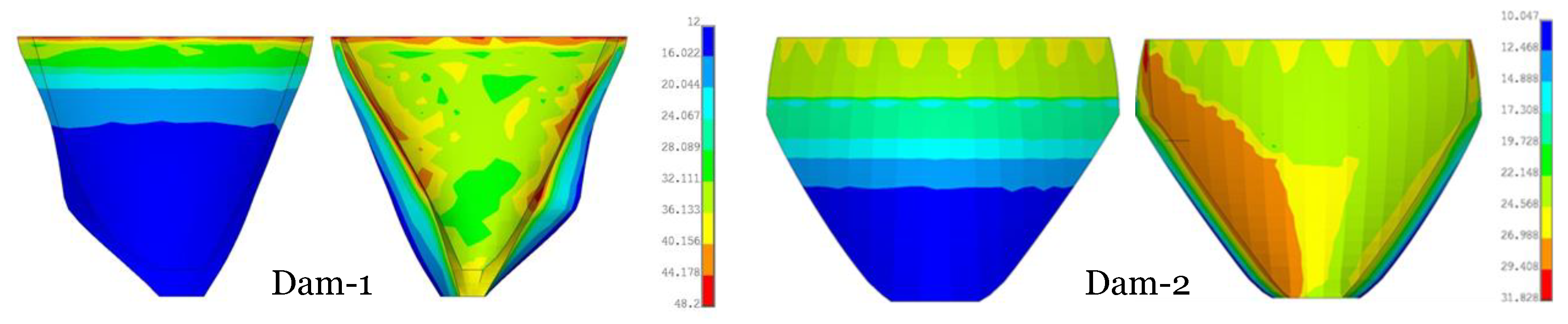
- For Dam-1, the US face is a bit more critical than DS one. However, Dam-2 has a different mechanism and the DSDR in DS is much higher.
- In Dam-1, only SIL-3 exceeds the threshold at DCR = 1. In Dam-2, both SIL-3 and SIL-2 exceed the threshold at several DCRs (especially at the DS face).
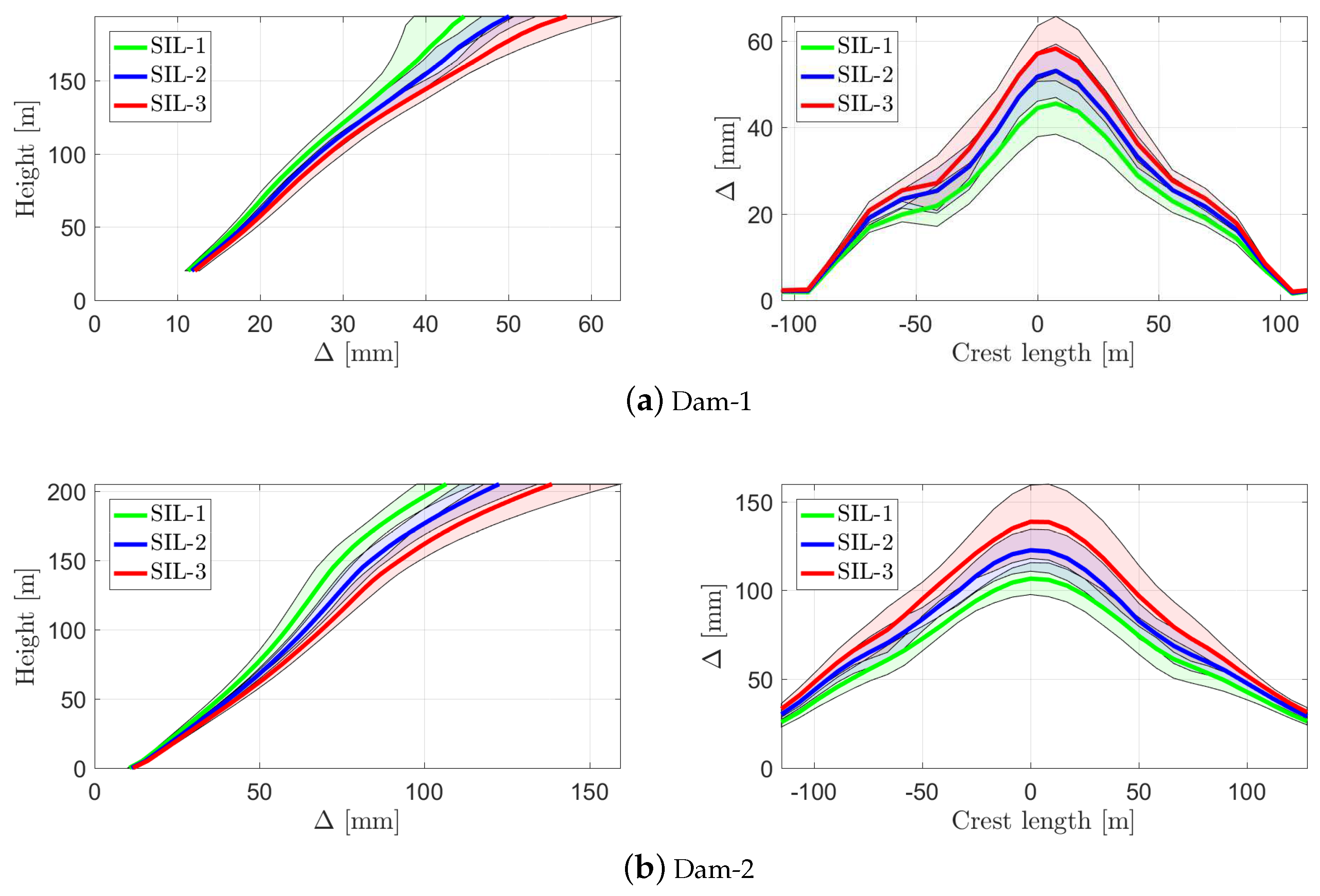
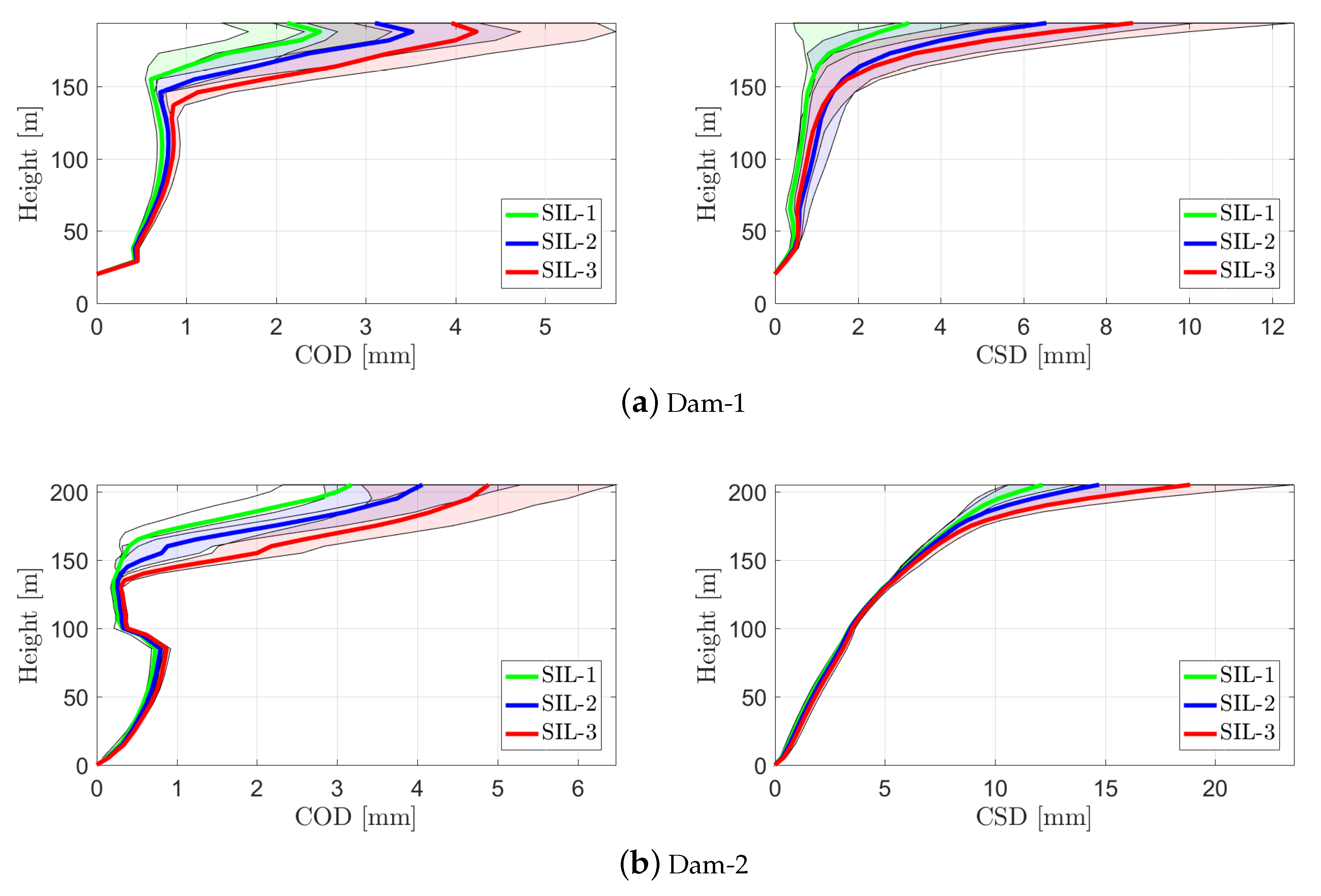
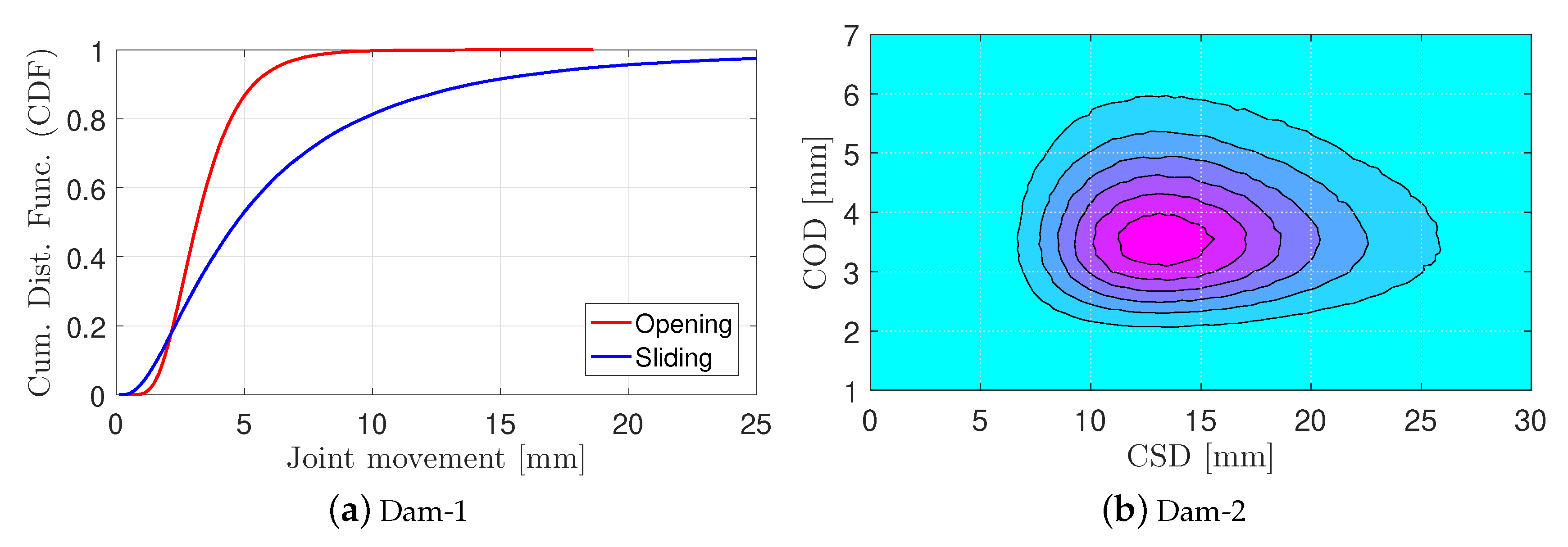
- In general, the mean CSD is twice and three times the COD for Dam-1 and Dam-2, respectively.
- In general, joint opening is more critical than joint sliding (since the water can penetrate inside the joint and increases the pressure on the inner walls). The COD appears to be well-controlled in both dams.
- The CODs in both dams are very similar: limited to no more than 1 mm for the first 150 m of height. Moreover, there is practically no difference between three SILs up to height 150 m. The major joint opening occurs at the top 50 m (i.e., upper quarter of dam).
- On the other hand, the joint sliding has a more smoothed behavior along the height (especially for Dam-2). Again, the most critical zone is the upper quarter of dam height.
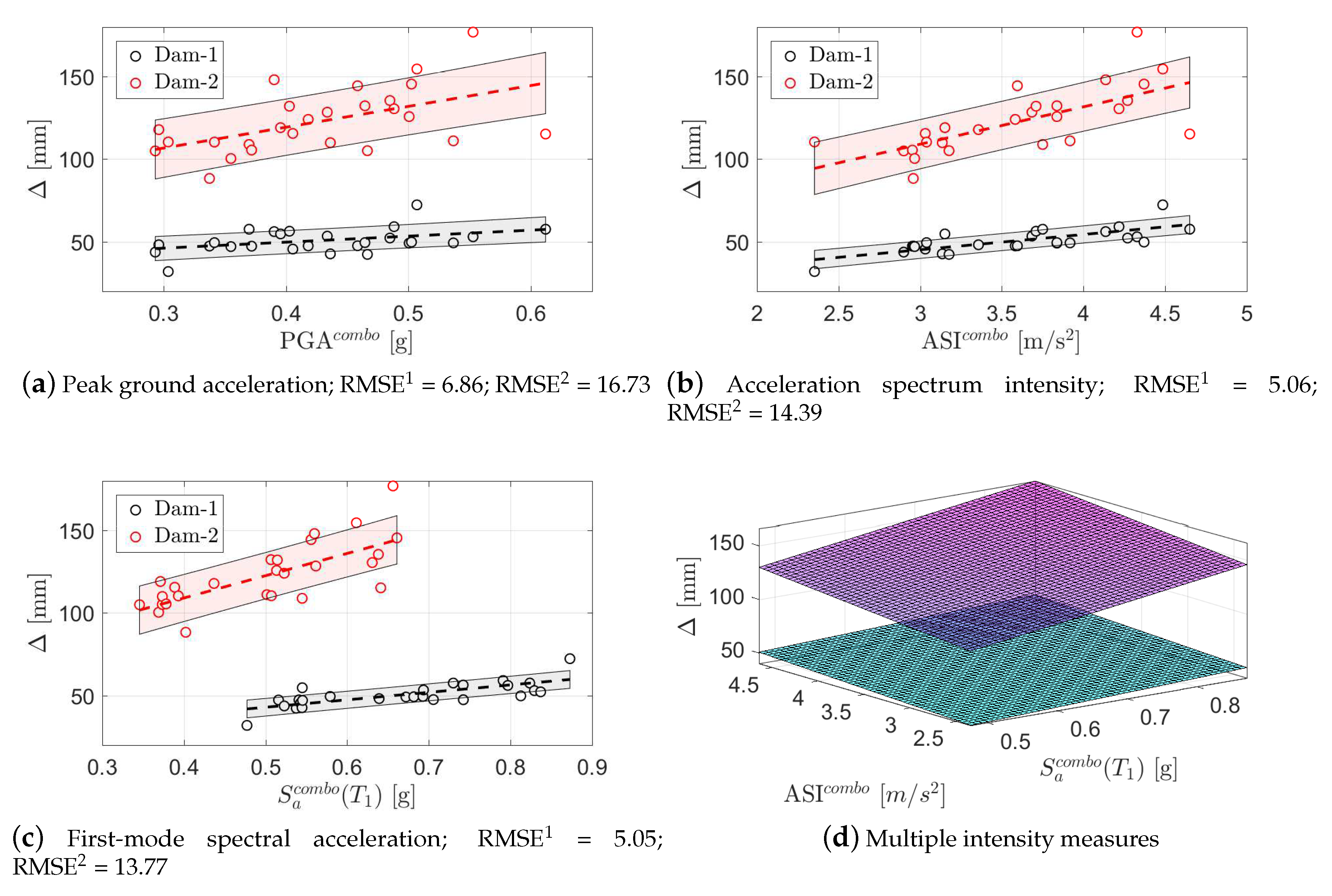
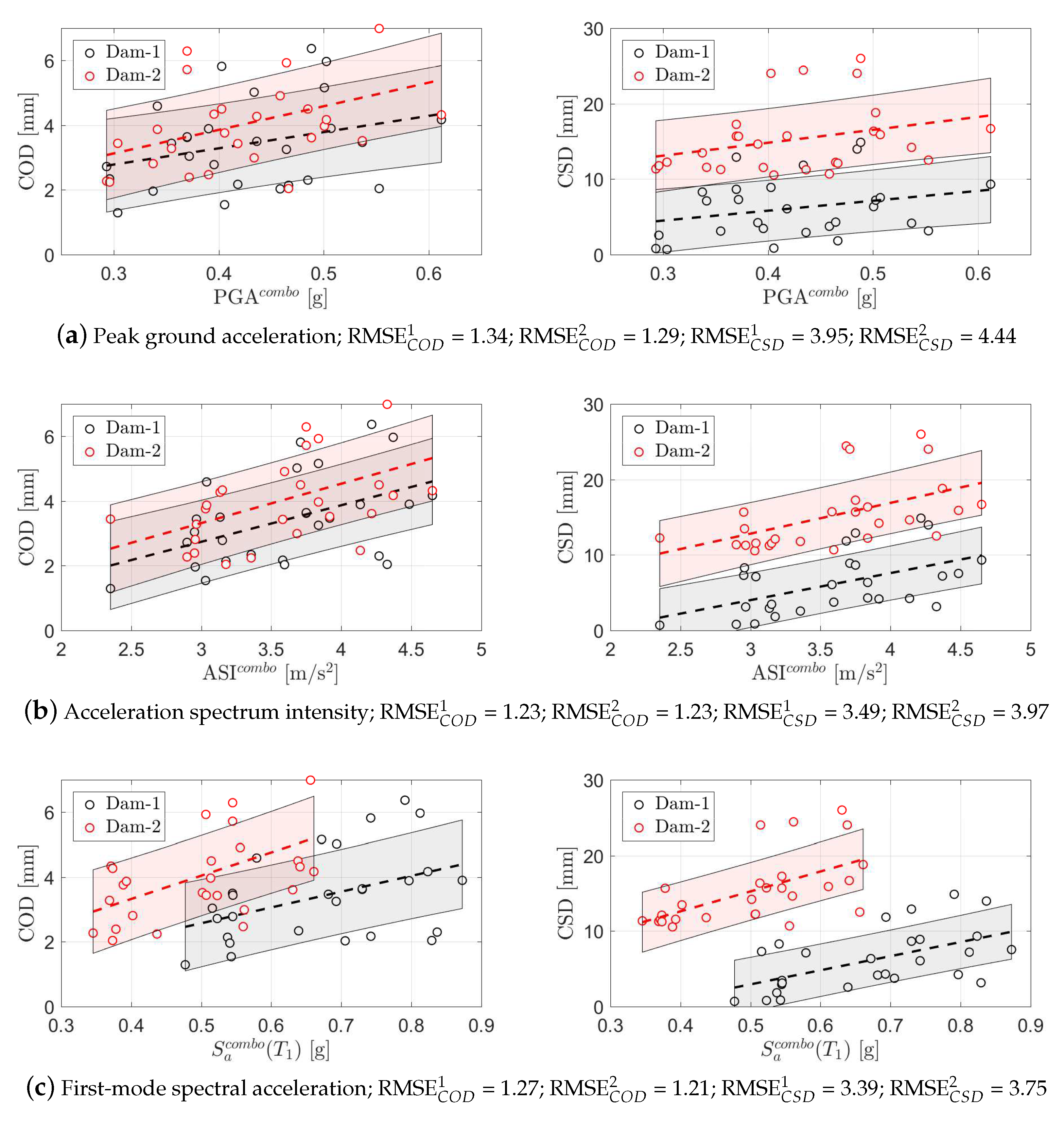
5.2. Probabilistic Response Correlation
- The confidence interval for Dam-2 is larger than Dam-1.
- The slope of the curve in Dam-2 is higher than Dam-1, which shows more correlation between the input and output parameters.
- In order to increase the accuracy of the PSDM, it is possible to develop a multiple IM model, See Figure 9d. Although one may apply a polynomial with different degrees, a planer one is selected in this paper. It is already found that higher order models over-fit the results Hariri-Ardebili et al. [24]. In this plot the upper plane belong to Dam-2.
| Algorithm 1 Generating correlated EDPs from initial finite number of simulations |
Inputs:X ▹ EDP matrix, where k is the number of different EDPs. Output:
|
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Detailed DSDR Plots
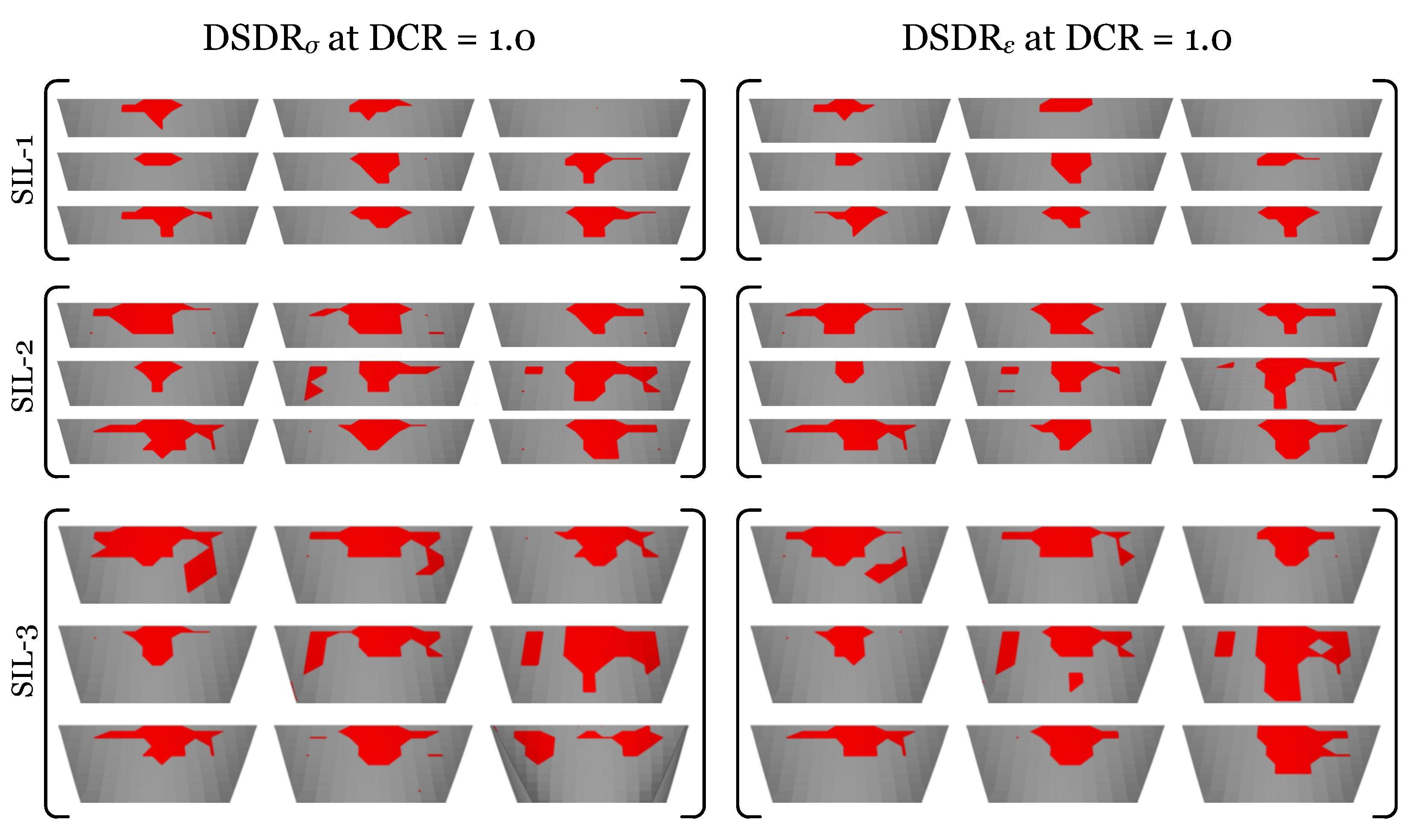
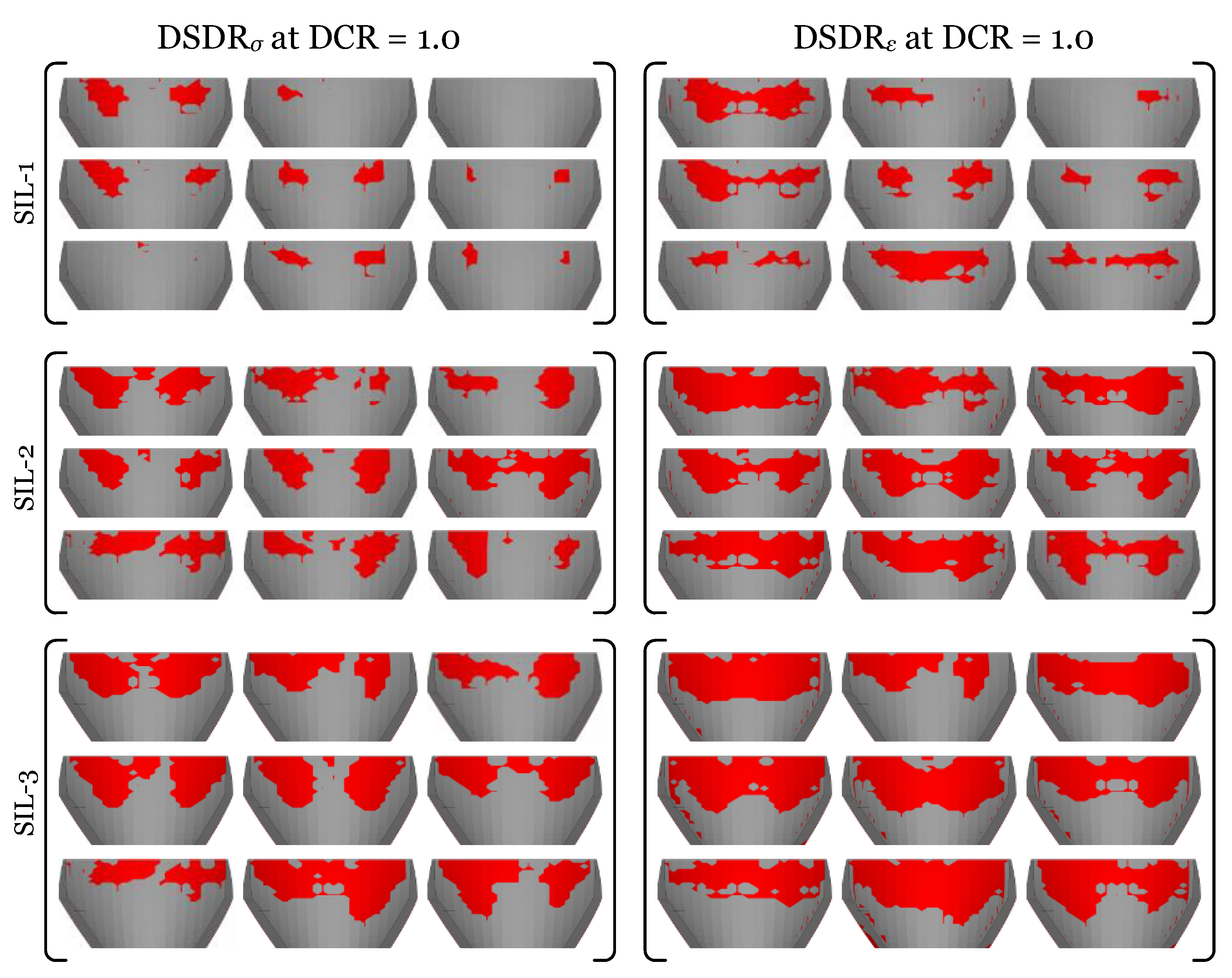
References
- Bowles, D.S.; Anderson, L.R.; Glover, T.F. A role for risk assessment in dam safety management. In Proceedings of the 3rd International Conference HYDROPOWER, Trondheim, Norway, 30 June–2 July 1997; Volume 97. [Google Scholar]
- Hartford, D.; Baecher, G. Risk and Uncertainty in Dam Safety; Technical Report; Thomas Telford, Ltd.: London, UK, 2004. [Google Scholar]
- Hariri-Ardebili, M.A.; Nuss, L.K. Seismic risk prioritization of a large portfolio of dams: Revisited. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Bretas, E.; Batista, A.; Lemos, J.; Léger, P. Seismic analysis of gravity dams: A comparative study using a progressive methodology. In Proceedings of the EURODYN 2014-9th International Conference on Structural Dynamics, Porto, Portugal, 30 June–2 July 2014. [Google Scholar]
- USACE-USBR. Best Practices in Dam And Levee Safety Risk Analysis; Technical Report; A Joint Publication by U.S. Department of the Interior, Bureau of Reclamation, and U.S. Army Corps of Engineers: Denver, CO, USA, 2015.
- Canadian Dam Association (CDA). Dam Safety Guidelines; Technical Report; Canadian Dam Association: Edmonton, AB, Canada, 2007. [Google Scholar]
- ICOLD. Bulletin on Risk Assessment in Dam Safety Management; Technical Report; International Commission on Large Dams: Paris, France, 2005. [Google Scholar]
- NSW. Risk Management Policy Framework for Dam Safety; Technical Report; New South Wales Government Dams Safety Committee: New South Wales, Australia, 2006.
- Italian Technical Code for dams. Guidelines for Seismic Safety Reassessment of Existing Dams in Italy; Technical Report; Dipartimento per I Servizi Tecnici Nazionali: Roma, Italy, 2001. [Google Scholar]
- ASDSO. State and Federal Oversight of Dam Safety Must be Improved; Magazine of Association of State Dam Safety Officials (ASDSO): Lexington, KY, USA, 2011. [Google Scholar]
- McCann, M.W., Jr. Seismic Risk of a Co-located Portfolio of Dams–Effects of Correlation and Uncertainty. In Proceedings of the 3rd International Week on Risk Analysis, Dam Safety, Dam Security, and Critical Infrastructure Management, Polytechnic University of Valencia, Valencia, Spain, 17–18 October 2011; pp. 1–6. [Google Scholar]
- Malm, R.; Gasch, T.; Eriksson, D.; Hassanzadeh, M. Probabilistic Analyses of Crack Propagation in Concrete Dams: Part 1; Elforsk: Stockholm, Sweden, 2013. [Google Scholar]
- Cornell, C. Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 1968, 58, 1583–1606. [Google Scholar]
- Hariri-Ardebili, M.A. Concrete Dams: From Failure Modes to Seismic Fragility. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I.A., Patelli, E., Au, I.S.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–26. [Google Scholar]
- ICOLD. Selecting Seismic Parameters for Large Dams, Guidelines, Bulletin 148 (Revision of Bulletin 72); Technical Report; International Commission on Large Dams: Paris, France, 2010. [Google Scholar]
- Wieland, M. Features of seismic hazard in large dam projects and strong motion monitoring of large dams. Front. Archit. Civ. Eng. China 2010, 4, 56–64. [Google Scholar] [CrossRef]
- Wieland, M. Seismic hazard and seismic design and safety aspects of large dam projects. In Perspectives on European Earthquake Engineering and Seismology; Springer: Berlin/Heidelberg, Germany, 2014; pp. 627–650. [Google Scholar]
- Wieland, M. ICOLD’s revised seismic design and performance criteria for large storage dams. In Proceedings of the AFRICA 2013—Water Storage and Hydropower Development for Africa, Addis Ababa, Ethiopia, 16–18 April 2013. [Google Scholar]
- Applied Technology Council. Seismic Performance Assessment of Buildings: Methodology; Technical Report ATC-58-1; Federal Emergency Management Agency: Redwood City, CA, USA, 2012; Volume 1.
- PEER. Ground Motion Database. 2017. Available online: http://ngawest2.berkeley.edu/ (accessed on 15 June 2017).
- Saouma, V.; Porter, K.; Nuss, L.; Hariri-Ardebili, M. Performance Based Engineering Design Guidelines for Concrete Dams; Technical Report; Enerjisa: Istanbul, Turkey, 2012. [Google Scholar]
- Ghanaat, Y. Failure modes approach to safety evaluation of dams. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- USACE. Earthquake Design and Evaluation of Concrete Hydraulic Structures; Technical Report EM 1110-2-6053; Department of the Army, U.S. Army Corps of Engineers: Washington, DC, USA, 2007. [Google Scholar]
- Hariri-Ardebili, M.A.; Saouma, V.; Porter, K.A. Quantification of seismic potential failure modes in concrete dams. Earthq. Eng. Struct. Dyn. 2016, 45, 979–997. [Google Scholar] [CrossRef]
- Bayraktar, A.; Türker, T.; Akköse, M.; Ateş, Ş. The effect of reservoir length on seismic performance of gravity dams to near-and far-fault ground motions. Nat. Hazards 2010, 52, 257–275. [Google Scholar] [CrossRef]
- Valamanesh, V.; Estekanchi, H.; Vafai, A.; Ghaemian, M. Application of the endurance time method in seismic analysis of concrete gravity dams. Sci. Iran. 2011, 18, 326–337. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, S.; Wang, C.; Yu, M. Seismic performance evaluation of dam-reservoir-foundation systems to near-fault ground motions. Nat. Hazards 2014, 72, 651–674. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Zhou, W.; Zhou, C. Integrated duration effects on seismic performance of concrete gravity dams using linear and nonlinear evaluation methods. Soil Dyn. Earthq. Eng. 2015, 79, 223–236. [Google Scholar] [CrossRef]
- Yilmazturk, S.M.; Arici, Y.; Binici, B. Seismic assessment of a monolithic RCC gravity dam including three dimensional dam–foundation–reservoir interaction. Eng. Struct. 2015, 100, 137–148. [Google Scholar] [CrossRef]
- Bezzi, A.M.A.; Fontana, C.; Fiorani, A.; Masciotta, S.; Pietrangeli, S.; Visconti, V.E. Evaluation of Dam Performance Under Seismic Loads with Linear Time History Analysis, Case Study Grand Ethiopian Renaissance Rcc Main Dam; HYDRO: London, UK, 2017. [Google Scholar]
- Zacchei, E.; Molina, J.L. Artificial accelerograms to estimate damage of dams by using failure criteria. Sci. Iran. 2018. [Google Scholar] [CrossRef]
- Bybordiani, M.; Arıcı, Y. Effectiveness of motion scaling procedures for the seismic assessment of concrete gravity dams for near field motions. Struct. Infrastruct. Eng. 2018, 14, 1339–1354. [Google Scholar] [CrossRef]
- Malm, R. Guideline for FE Analyses Of Concrete Dams; Technical Report, Energiforsk: Malmo, Sweden, 2016. [Google Scholar]
- Zhang, Y.; Chen, G.; Zheng, L.; Li, Y.; Zhuang, X. Effects of geometries on three-dimensional slope stability. Can. Geotech. J. 2013, 50, 233–249. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Quantitative failure metric for gravity dams. Earthq. Eng. Struct. Dyn. 2015, 44, 461–480. [Google Scholar] [CrossRef]
- Ansari, M.I.; Agarwal, P. Categorization of Damage Index of Concrete Gravity Dam for the Health Monitoring after Earthquake. J. Earthq. Eng. 2016, 20, 1222–1238. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Furgani, L.; Meghella, M.; Saouma, V.E. A new class of seismic damage and performance indices for arch dams via ETA method. Eng. Struct. 2016, 110, 145–160. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Kianoush, M.R. Integrative seismic safety evaluation of a high concrete arch dam. Soil Dyn. Earthq. Eng. 2014, 67, 85–101. [Google Scholar] [CrossRef]
- Mirzabozorg, H.; Hariri-Ardebili, M.; Heshmati, M.; Seyed-Kolbadi, S. Structural safety evaluation of Karun III Dam and calibration of its finite element model using instrumentation and site observation. Case Stud. Struct. Eng. 2014, 1, 6–12. [Google Scholar] [CrossRef][Green Version]
- ANSYS. ANSYS Software Reference Manuals, Release Notes, Mechanical Apdl, Elements Reference, Commands Reference and Theory Reference, Version Release 11; ANSYS: Berkeley, CA, USA, 2007. [Google Scholar]
- Hariri-Ardebili, M.A.; Seyed-Kolbadi, S.M. Seismic cracking and instability of concrete dams: Smeared crack approach. Eng. Fail. Anal. 2015, 52, 45–60. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.; Boodagh, P. Taguchi design-based seismic reliability analysis of geostructures. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2018, 13, 34–52. [Google Scholar] [CrossRef]
- Yang, T.; Moehle, J.; Stojadinovic, B.; DerKiureghian, A. Seismic Performance Evaluation of Facilities: Methodology and Implementation. Asce Struct. Eng. 2009, 135, 1146–1154. [Google Scholar] [CrossRef]
- Vicente, D.; San Mauro, J.; Salazar, F.; Baena, C. An Interactive Tool for Automatic Predimensioning and Numerical Modeling of Arch Dams. Math. Probl. Eng. 2017, 2017, 9856938. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hariri-Ardebili, M.A.; Heshmati, M.; Boodagh, P.; Salamon, J.W. Probabilistic Identification of Seismic Response Mechanism in a Class of Similar Arch Dams. Infrastructures 2019, 4, 44. https://doi.org/10.3390/infrastructures4030044
Hariri-Ardebili MA, Heshmati M, Boodagh P, Salamon JW. Probabilistic Identification of Seismic Response Mechanism in a Class of Similar Arch Dams. Infrastructures. 2019; 4(3):44. https://doi.org/10.3390/infrastructures4030044
Chicago/Turabian StyleHariri-Ardebili, M. A., M. Heshmati, P. Boodagh, and J. W. Salamon. 2019. "Probabilistic Identification of Seismic Response Mechanism in a Class of Similar Arch Dams" Infrastructures 4, no. 3: 44. https://doi.org/10.3390/infrastructures4030044
APA StyleHariri-Ardebili, M. A., Heshmati, M., Boodagh, P., & Salamon, J. W. (2019). Probabilistic Identification of Seismic Response Mechanism in a Class of Similar Arch Dams. Infrastructures, 4(3), 44. https://doi.org/10.3390/infrastructures4030044





