Force Performance Analysis of Pile Behavior of the Lateral Load
Abstract
:1. Introduction
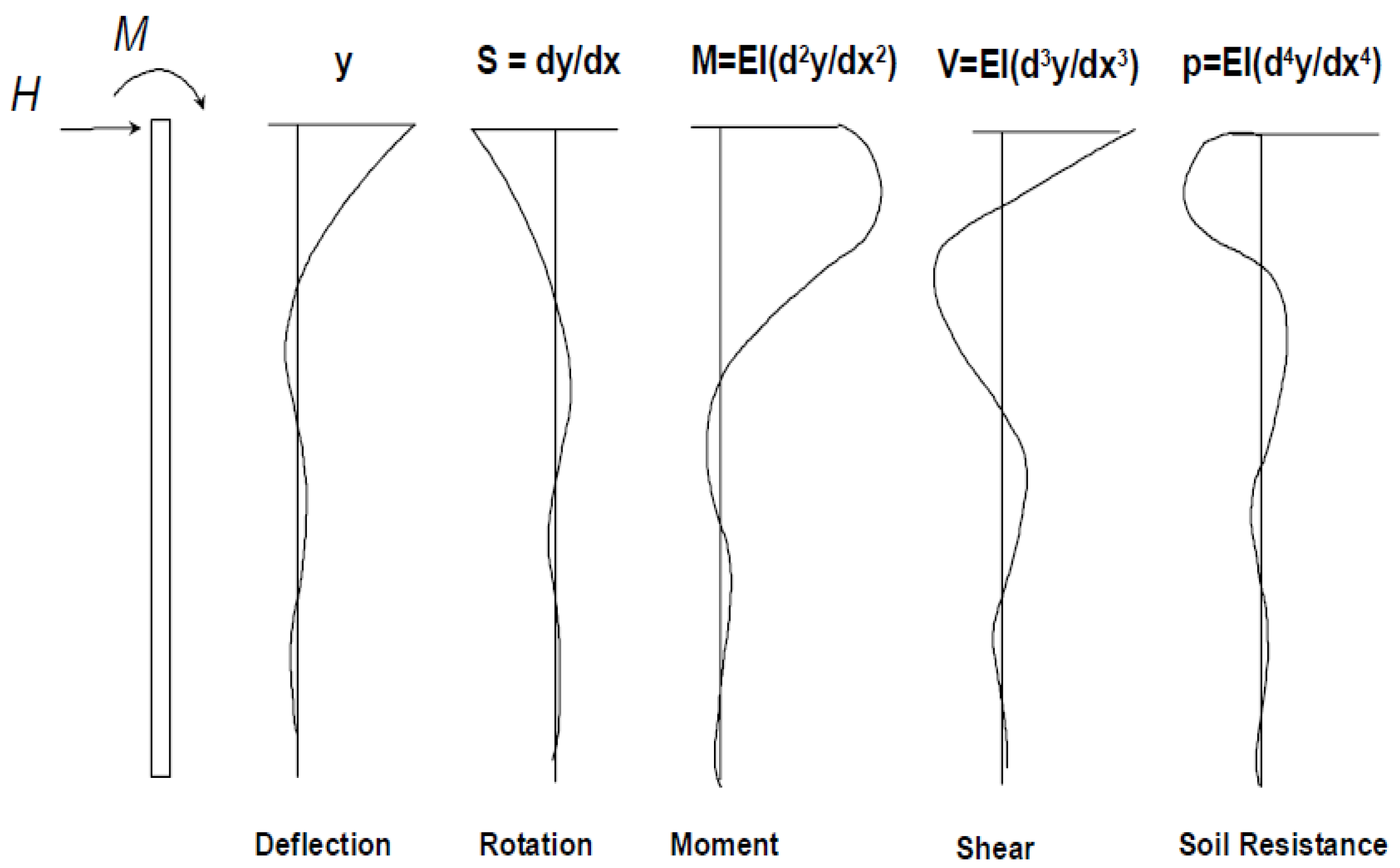
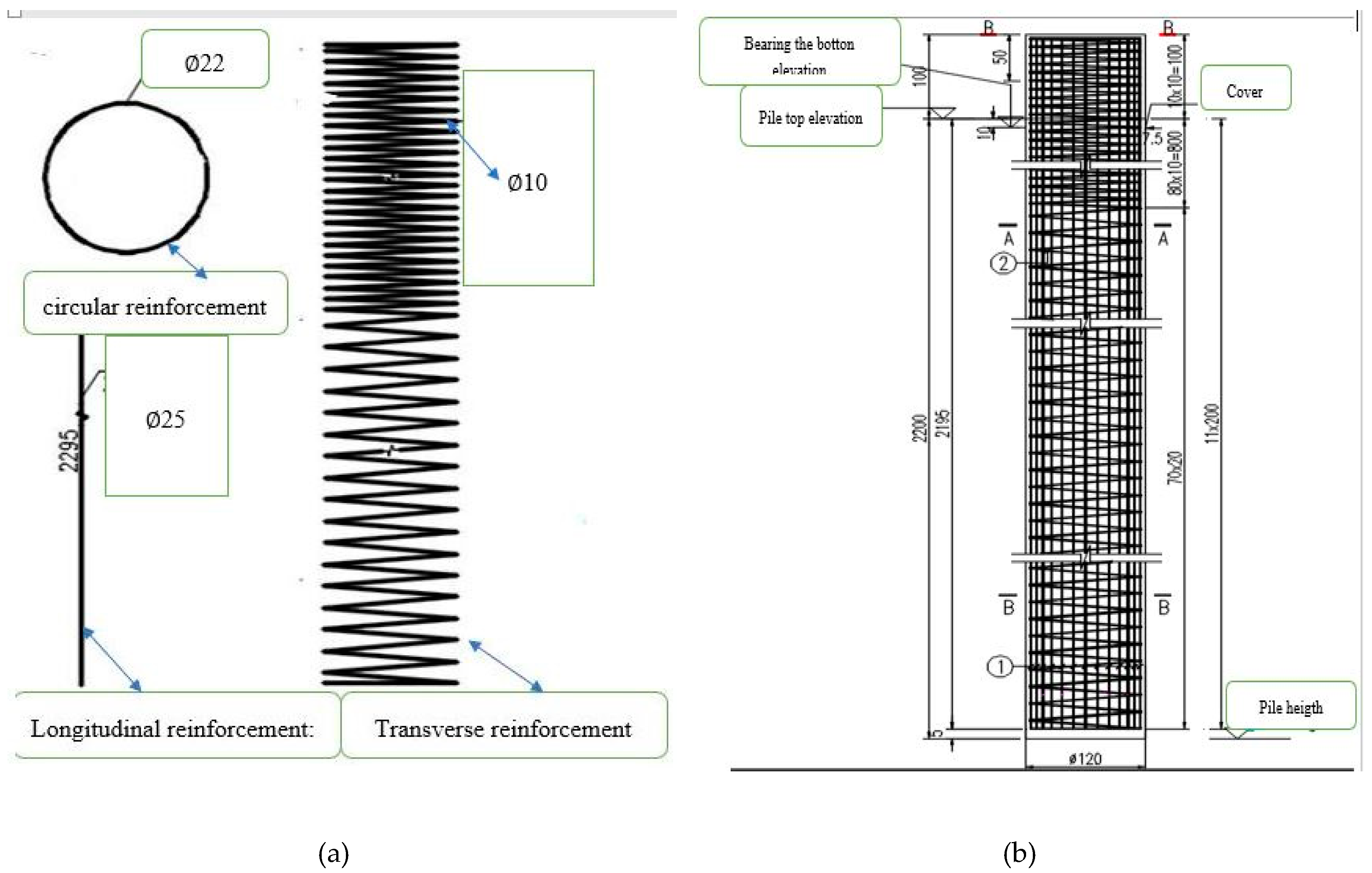
2. Basic Theory of Reinforcement Concrete Pile on a Lateral Load
- y = deflection of the pile
- S = slope of the deflected pile
- M = moment of the pile
- V = Shear
- P = Soil reaction
- Ep = elasticity modulus
- Ip = moment of inertia of the pile
- QA = load
- z = depth below the pile top
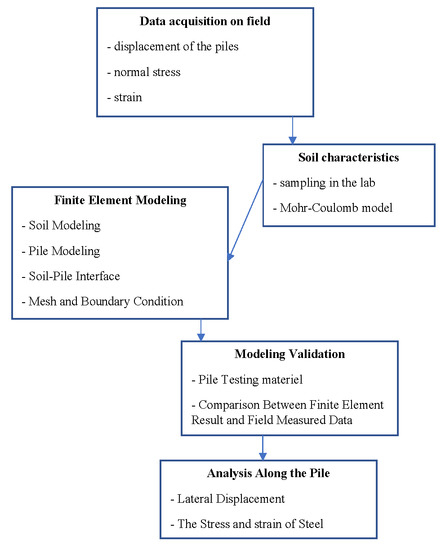
3. Finite Element Modeling (FEM)
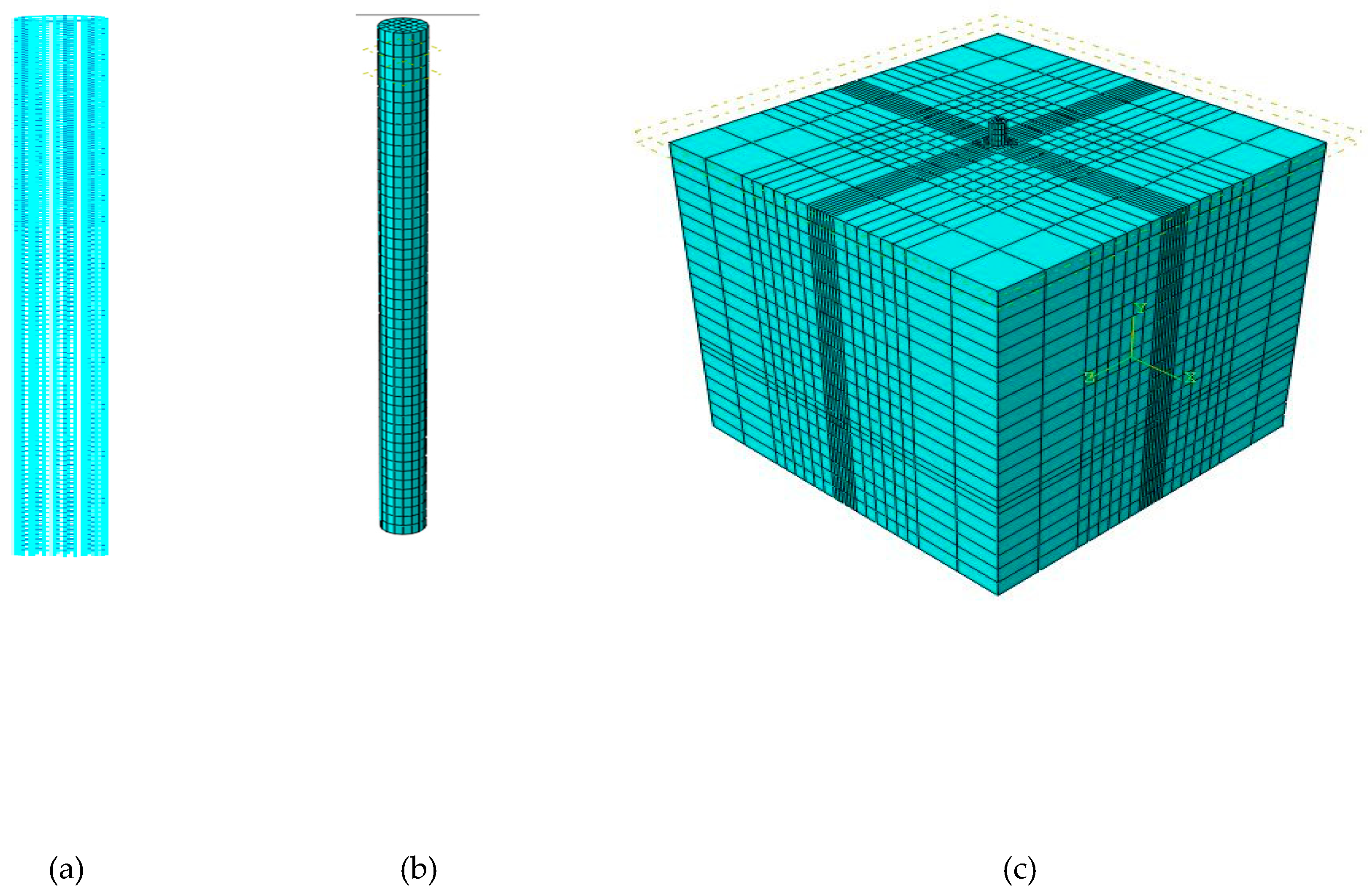
3.1. Soil Finite Element Modeling
3.2. Single Pile Finite Element Modeling
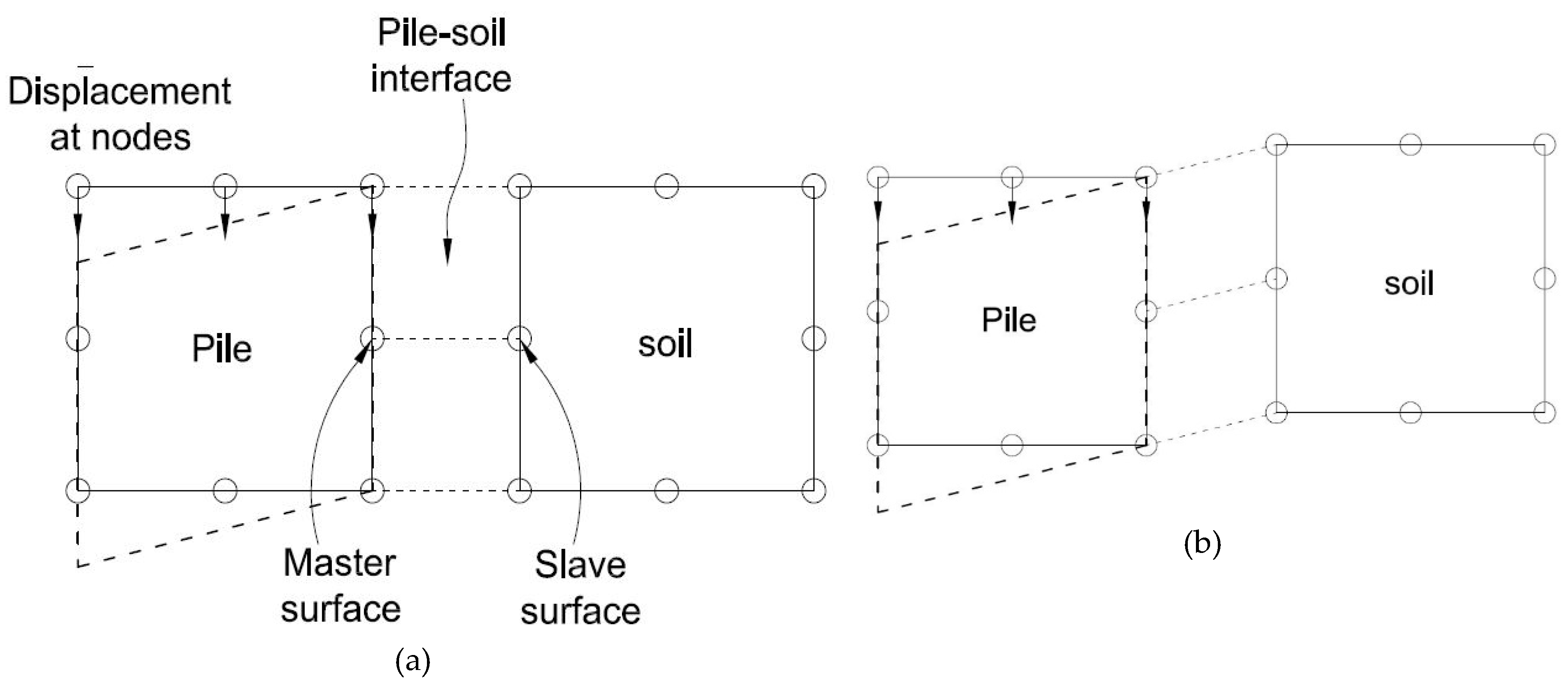
3.3. Soil-Pile Interface
3.4. Mesh and Boundary Condition
4. Finite Element Modeling Validation by Field Lateral Loaded Pile Test
4.1. Field Lateral Loaded Pile Testing
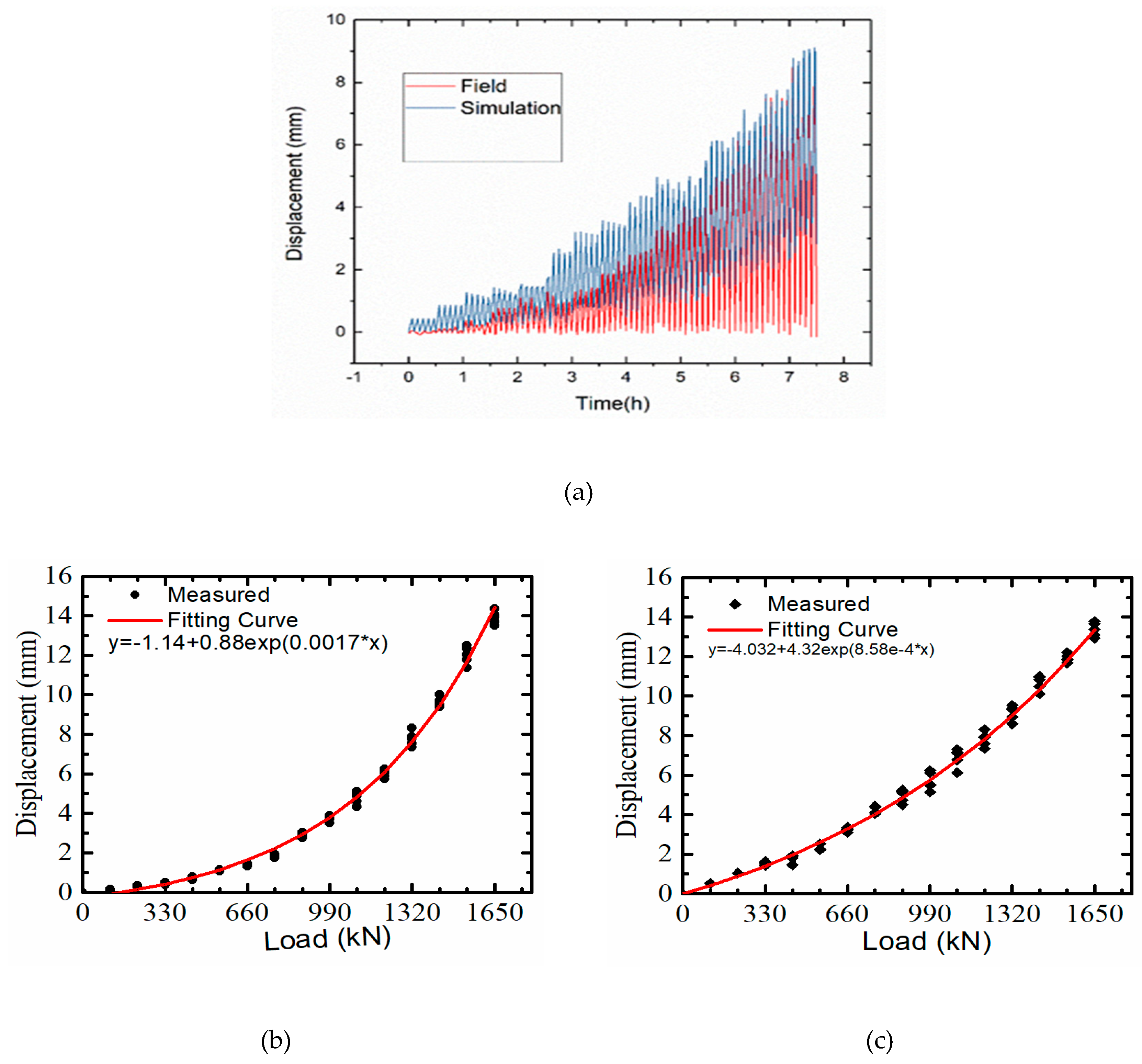
4.2. Comparison Between Finte Element Result and Field Measured Data
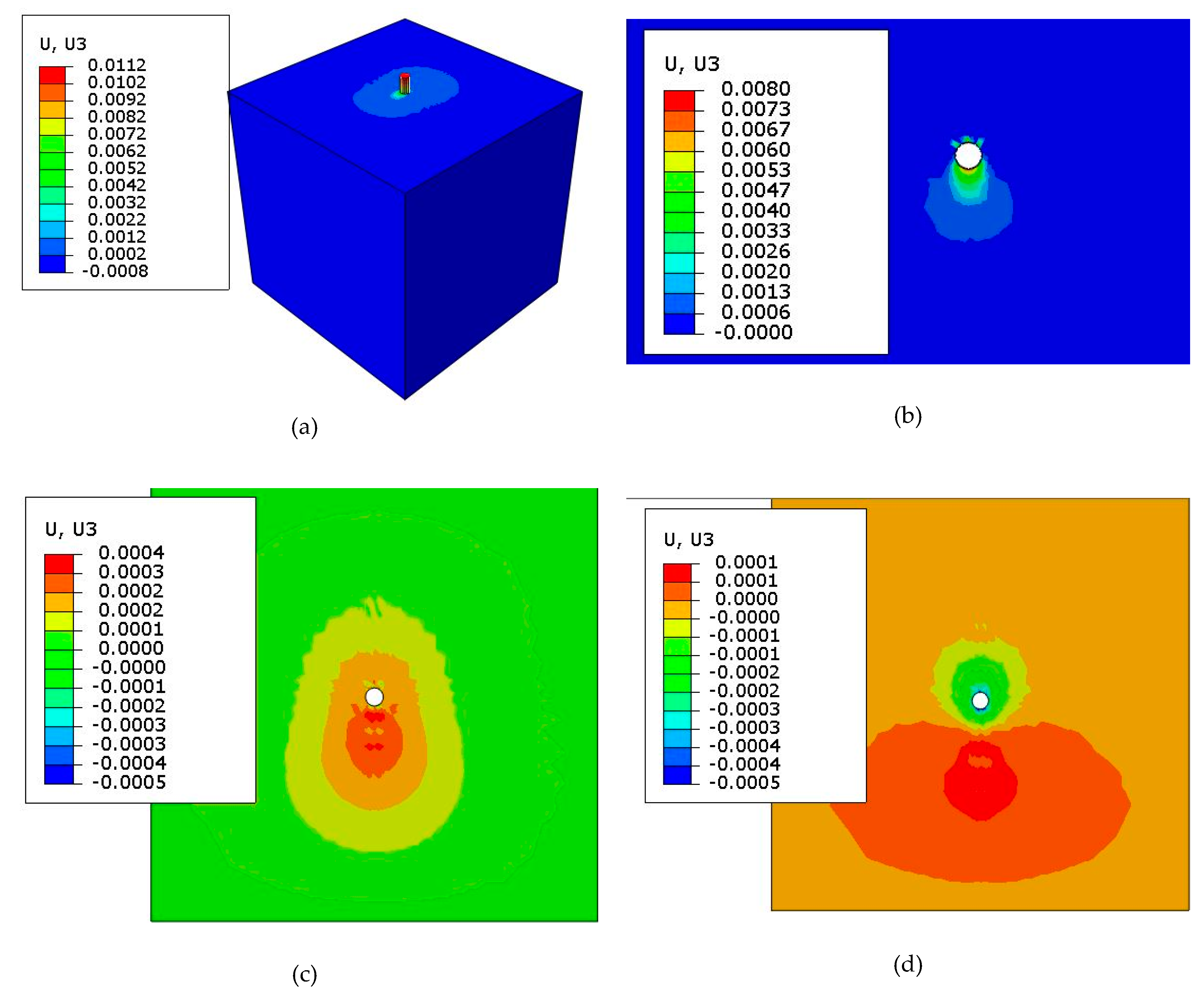
5. Numerical Results and Analysis
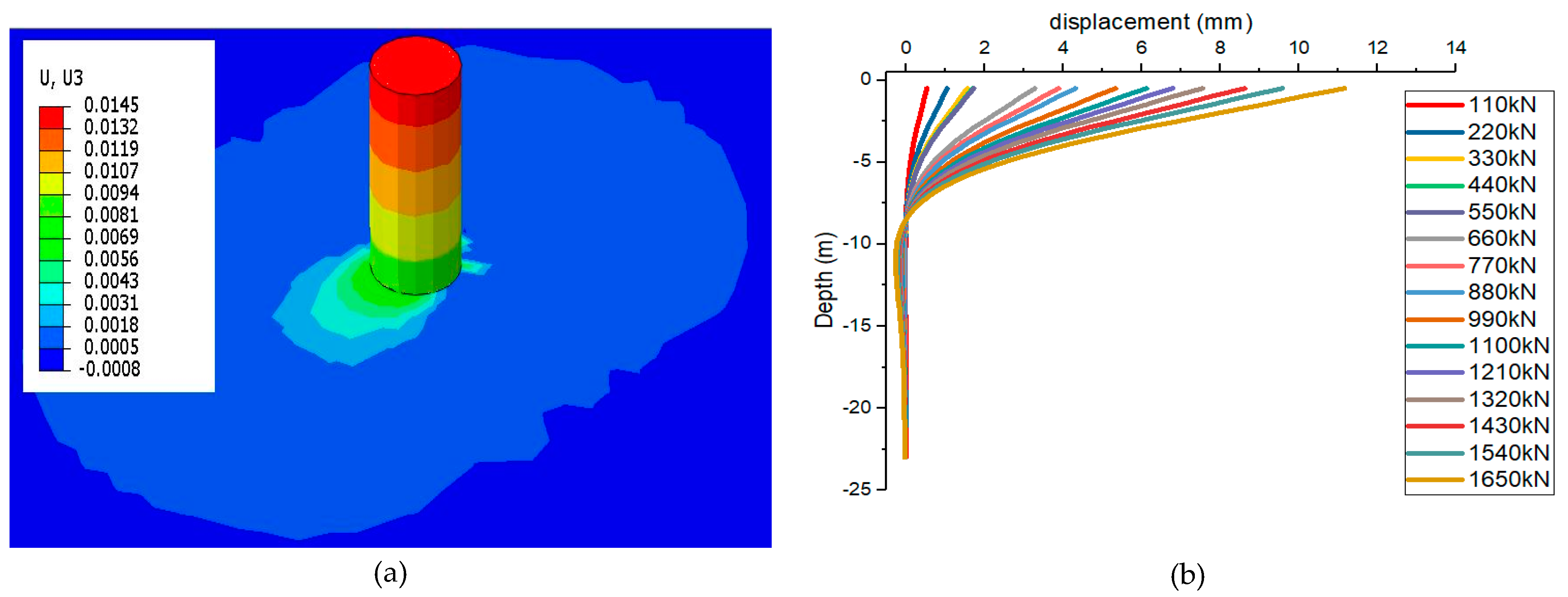
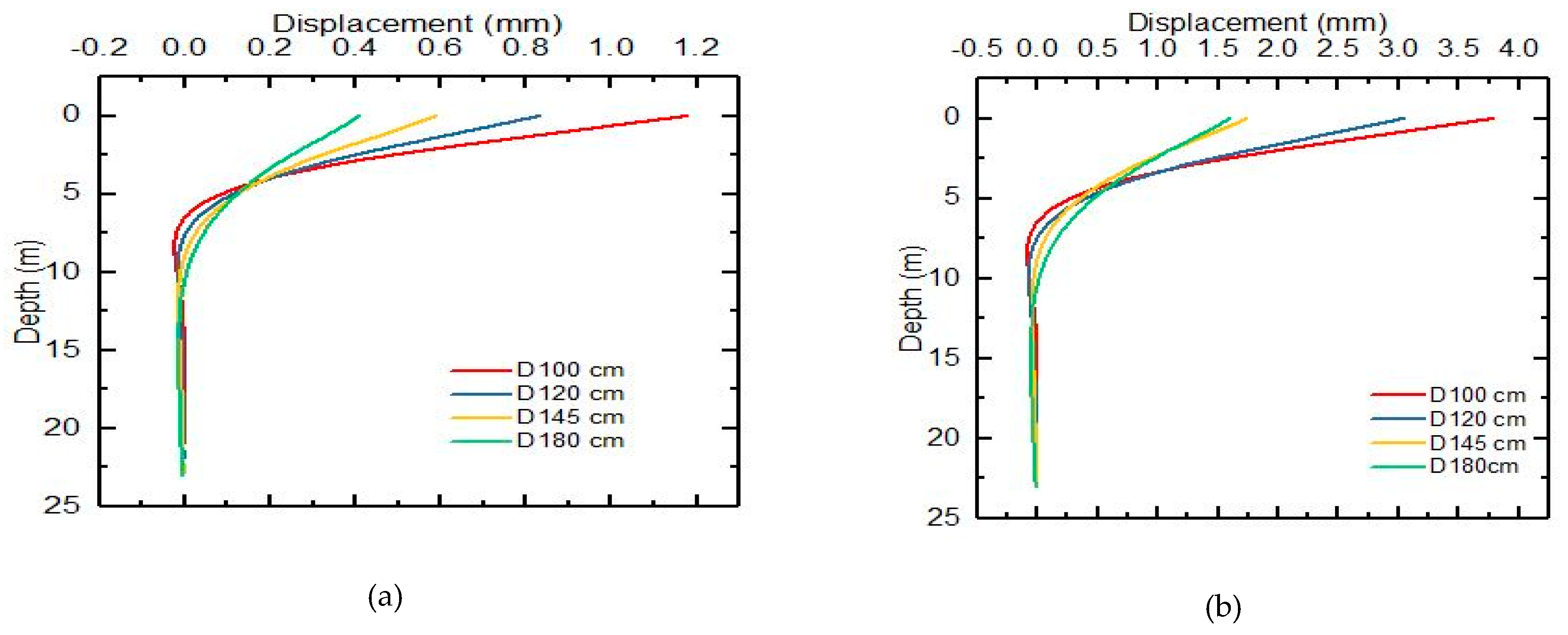
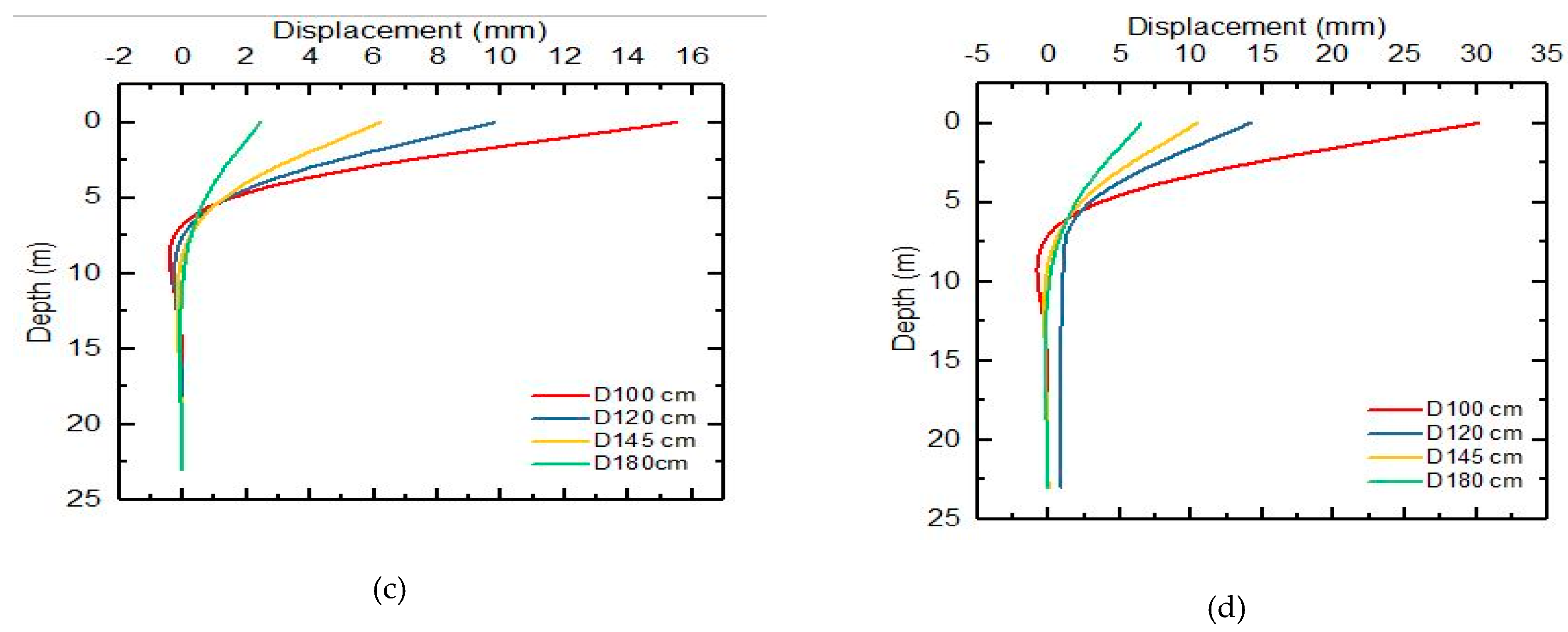
5.1. Lateral Displacement Along the Pile
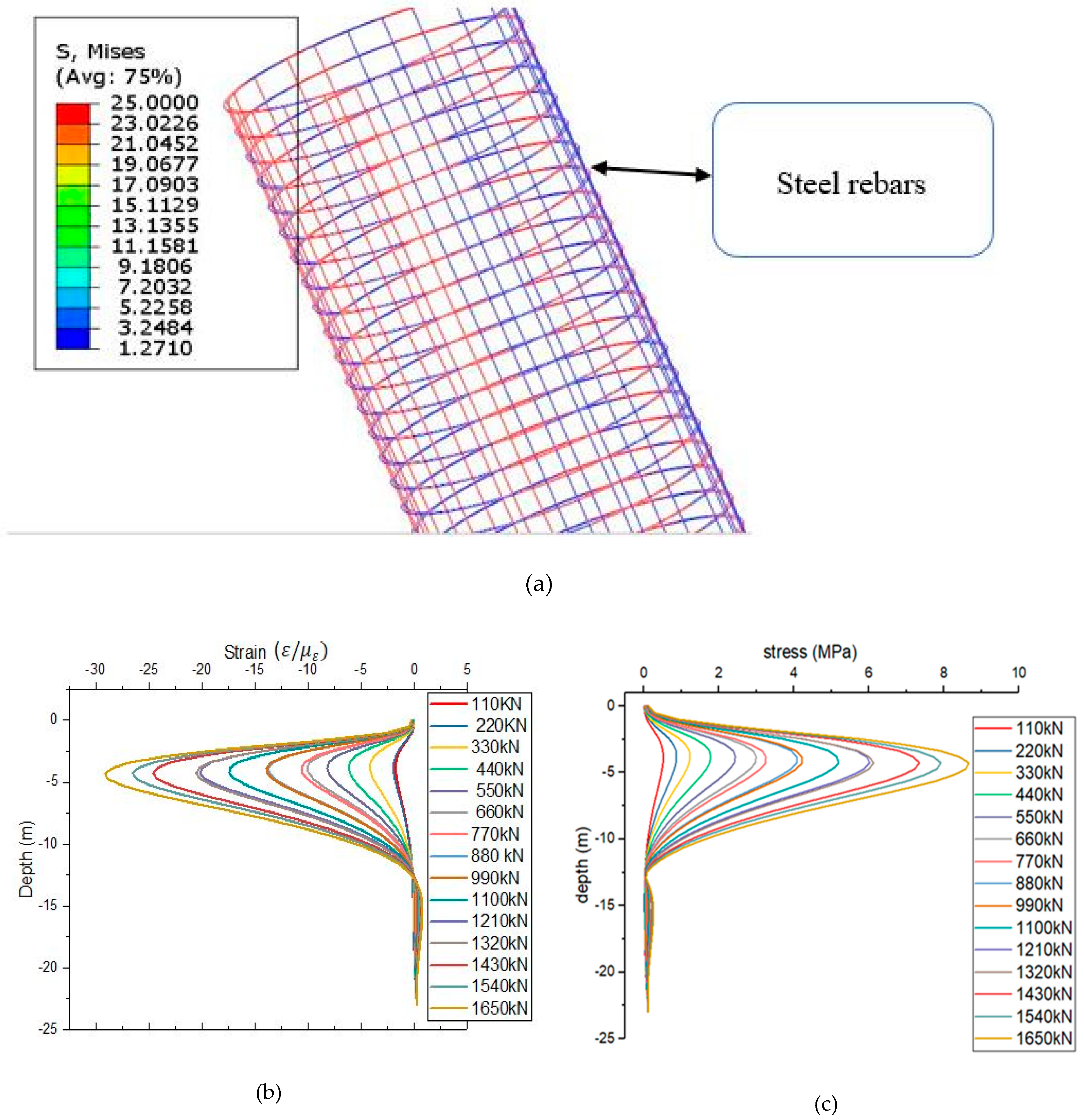
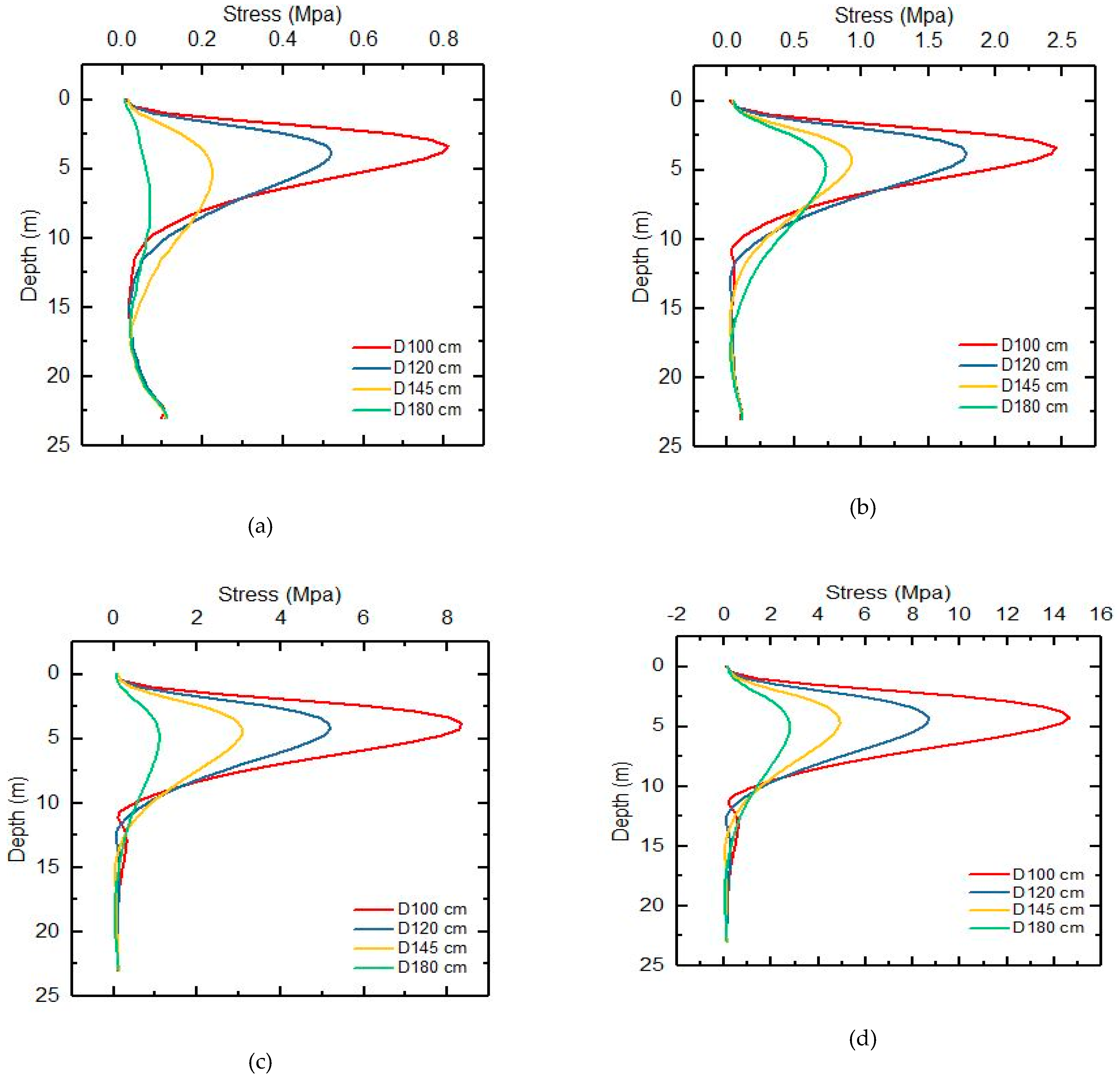
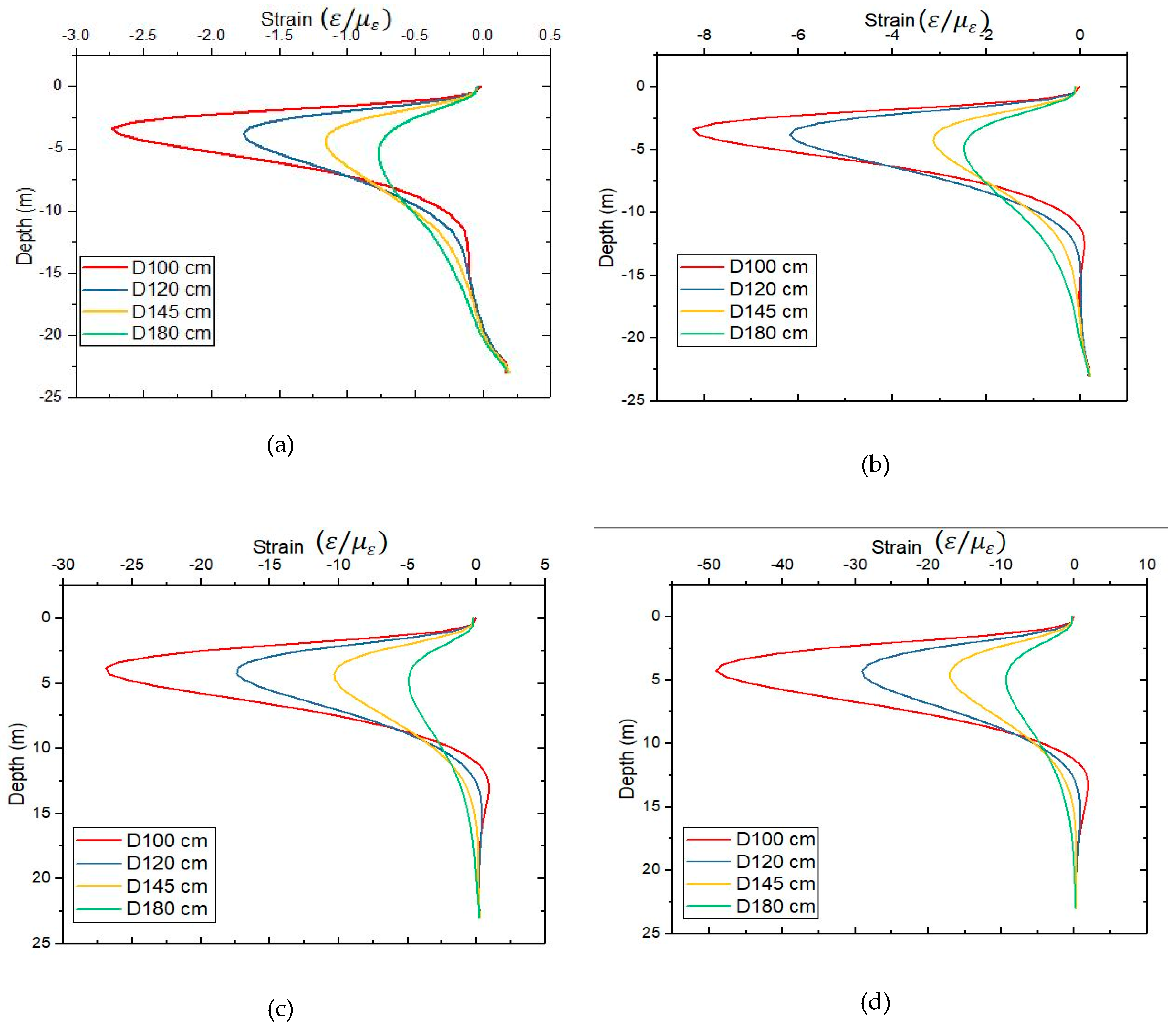
5.2. The Stress and strain of Steel Along the Pile
5.3. Effect of Reinforced Concrete Pile Diameter
- Inversely proportional to diameter (the larger the diameter, the smaller the stress).
- Proportional to the horizontal displacement of the piles (the higher the stress, the greater the horizontal displacement to the pile increases).
- Proportional and opposite direction to the strain (more the stress increases and the more the strain increases, but the direction is negative).
6. Conclusions
- The comparison between the FE simulation result and the field measurement, reveals that at the beginning of the experiment (applied load stage), the displacement of the pile from the field is smaller than the simulation. When the load increases the displacement of the field, and the simulation is almost followed, when the lateral load reached its maximum value of 1,650,000 N the displacement of the field is about 9, 67 mm, while that of the simulation is 9, 62 mm, this great advocate agreement between the FE model and the Field measure.
- The analysis of the influence of the lateral loads level applied on the RCP head shows that the deformation of the soil varies depending on the soil layer. Moreover, it was constant that at a depth of 6m there are the displacement zeros by applying different lateral loads on the pile head (110,000 N to 1,650,000 N).
- It can be concluded that taking a point on the head of the pile, the maximum displacement of the field was 14.74 mm and the displacement of the simulation was 14.79 mm, either 0.05 mm, less than 1 % difference, which is acceptable for validating the simulation.
- It can be noted that taking into account the field and the simulation, the maximum stress and strain on the pile body is at a depth of 5 m and point where the stress and strain are returning to 0 at a depth of 13 m; it can also be noted that stress and strain have opposite directions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kourkoulis, R.; Gelagoti, F.; Anastasopoulos, I.; Gazetas, G. Slope Stabilizing Piles and Pile-Groups: Parametric Study and Design Insights. J. Geotech. Geoenviron. Eng. 2011, 137, 663–677. [Google Scholar] [CrossRef]
- Di Laora, R.; Maiorano, R.M.S.; Aversa, S. Ultimate Lateral Load Of Slope-Stabilising Piles. Geotech. Lett. 2017, 7, 2045–2543. [Google Scholar] [CrossRef]
- Mujah, D.; Ahmad, F.; Hazarika, H.; Watanabe, N. The Design Method of Slope Stabilizing Piles: A Review. Int. J. Curr. Eng. Technol. 2013, 3, 224–229. [Google Scholar]
- Jain, A.; Gupta, T.; Sharma, R.K. Measurement and Repair Techniques of Corroded Underwater Piles: An Overview. Int. J. Eng. Res. Appl. 2016, 6, 19–27. [Google Scholar]
- Cai, Y.; Tu, B.; Yu, J.; Zhu, Y.; Zhou, J. Numerical Simulation Study on Lateral Displacement of Pile Foundation and Construction Process Under Stacking Loads. Complexity 2018, 2018, 2128383. [Google Scholar] [CrossRef]
- Mardfekri, M.; Gardoni, P.; Roesset, J.M. Modeling Laterally Loaded Single Piles Accounting for Nonlinear Soil-Pile Interactions. J. Eng. 2013, 2013, 243179. [Google Scholar] [CrossRef]
- Kavitha, P.; Venkatesh, M.M.; Sundaravadivelu, R. Soil-Structure Interaction Analysis of a Dry Dock. Aquat. Procedia 2015, 4, 287–294. [Google Scholar] [CrossRef]
- Salman, F.A.; Mohammed, M.M.; Shirazi, S.M.; Jameel, M. Reinforcement in Concrete Piles Embedded in Sand. Int. J. Phys. Sci. 2010, 5, 2259–2271. [Google Scholar]
- Hashem-Ali, S.F. Analytical Methods for Predicting Load-Displacement Behaviour of Piles; Durham E-Theses, Durham University: Durham, UK, 2014. [Google Scholar]
- Sections, C. Analysis Methods for Laterally Loaded Pile Groups Using an Advanced Modeling of Reinforced Concrete Sections. Materials 2018, 11, 300. [Google Scholar]
- Kontoni, D.-P.; Farghaly, A. 3d Fem Analysis of a Pile-Supported Riverine Platform under Environmental Loads Incorporating Soil-Pile Interaction. Computation 2018, 6, 8. [Google Scholar] [CrossRef]
- Cui, K.; Feng, J.; Zhu, C. A Study on the Mechanisms of Interaction between Deep Foundation Pits and The Pile Foundations of Adjacent Skewed Arches as Well as Methods for Deformation Control. Complexity 2018, 2018, 6535123. [Google Scholar] [CrossRef]
- Abdel-Rahman, K.; Achmus, M. Numerical Modelling of Combined Axial and Lateral Loading of Vertical Piles. In Numerical Methods in Geotechnical Engineering, Proceedings of the 6th Eur. Conferences, Denver, CO, USA, 5–8 August 2000; American Society of Civil Engineers: New York, NY, USA, 2006; pp. 575–581. [Google Scholar]
- Kim, B.T.; Yoon, G.L. Laboratory Modeling of Laterally Loaded Pile Groups in Sand. KSCE J. Civ. Eng. 2011, 15, 65–75. [Google Scholar] [CrossRef]
- Shaia, H.A.; Abbas, S.A. Three-Dimensional Analysis Response of Pile Subjected to Oblique Loads. Int. J. Sci. Eng. Res. 2015, 6, 508–511. [Google Scholar]
- Abdel-Mohti, A.; Khodair, Y. Analytical Investigation of Pile-Soil Interaction in Sand under Axial and Lateral Loads. Int. J. Adv. Struct. Eng. 2014, 6, 54. [Google Scholar] [CrossRef]
- Phanikanth, V.S.; Choudhury, D.; Reddy, G.R. Response of Single Pile under Lateral Loads in Cohesionless Soils. Electron. J. Geotech. Eng. 2010, 15, 813–830. [Google Scholar]
- Fuentes, J.L.; Gamble, W.L. Design, Manufacture, and Installation of Concrete Piles; ACI 543r-00; ACI Committee: Bismarck, ND, USA, 2005; pp. 1–49. [Google Scholar]
- Schall, J.D.; Price, G.R. National Cooperative Highway Research Program: Report 515, 2004.
- Kanakeswararao, T.; Ganesh, B. “Analysis of Pile Foundation Subjected to Lateral and Vertical Loads,”. Int. J. Eng. Trends Technol. no. 2. 2017, 113–127. [Google Scholar] [CrossRef]
- Niyaz, A.A.; Junaid, A.; Shafeeque, A.; Mohd, B.; Sadique, A.; Noor, K.A. Pile-Soil Interaction by Finite. pp. 2016–2017. Available online: https://pdfs.semanticscholar.org/1077/2e22206003382ea499c3e7978211343be406.pdf (accessed on 28 March 2019).
- Balendra, S. Numerical Modeling of Dynamic Soil-Pile-Structure Interaction. MSc Thesis, Department of Civil and Environmental Engineering, Washington State University, Washington, DC, USA, December 2005. [Google Scholar]
- Salman, F.A.; Fattah, M.Y.; Mohammed, M.M.; Hashim, R. Numerical Investigation on Reinforcement Requirement for Piles Embedded in Clay. Sci. Res. Essays 2010, 5, 2731–2741. [Google Scholar]
- Brown, D.A.; O’Neill, M.W.; Hoit, M.; Mcvay, M.; el Naggar, M.H.; Chakraborty, S. Static and Dynamic Lateral Loading of Pile Groups. Natl. Coop. Highw. Res. Progr. 2001, 461, 50. [Google Scholar]
- Rasmussen, L.; Wolf, K.; Bo, L.; Rasmussen, K.L. A Literature Study on the Effects of Cyclic Lateral Loading of Monopiles in Cohesionless Soils; Aalborg University: Aalborg, Denmark, 2013. [Google Scholar]
- Favaretti, C. Towards Next Generation P-Y Relationships: Part 1 Report Part 1: State of Practice–State of the Art; University of California: Irvine, CA, USA, 2018. [Google Scholar]
- Wrana, B. Pile Load Capacity–Calculation Methods. Stud. Geotech. Mech. 2015, 37, 4. [Google Scholar] [CrossRef]
- Ashour, M.; Norris, G. Pile Group Program for Full Material Modeling and Progressive Failure; The Final Report; California Department of Transportation: Sacramento, CA, USA, 2008. [Google Scholar]
- Dodds, A.; Martin, G. Modeling Pile Behavior in Large Pile Groups under Lateral Loading. 2007. Available online: https://www.researchgate.net/profile/Cihan_Akdag/publication/265592075_AN_INVESTIGATION_OF_THE_BEHAVIOR_OF_FIBER_REINFORCED_CONCRETE_PILES_UNDER_LATERAL_LOADING /links/5412eb840cf2788c4b3587e7/AN-INVESTIGATION-OF-THE-BEHAVIOR-OF-FIBER-REINFORCED-CONCRETE-PILES-UNDER-LATERAL-LOADING.pdf (accessed on 28 March 2019).
- Graduate School of Natural and Applied Sciences an Investigation of the Behavior of Fiber Reinforced Concrete Piles under an Investigation of The Behavior Of. 2011.
- Johnson, K.; Lemcke, P.; Karunasena, W.; Sivakugan, N. Modelling the Load E Deformation Response of Deep Foundations under Oblique Loading. Environ. Model. Softw. 2006, 21, 1375–1380. [Google Scholar] [CrossRef]
- Hazzar, L.; Hussien, M.N.; Karray, M. Influence of Vertical Loads on Lateral Response of Pile Foundations in Sands and Clays. J. Rock Mech. Geotech. Eng. 2017, 9, 291–304. [Google Scholar] [CrossRef]
- Rahemi, N. Numerical Investigation on Lateral Deflection of Single Pile under Static and Dynamic Loading. Master’s Thesis, Eastern Mediterranean University, Famagusta, Turkey, 2012. [Google Scholar]
- Bahloul, D.; Moussai2, B. Three-Dimensional Analysis of Laterally Loaded Barrette Foundation Using Plaxis 3d. Tanda Kardinal Pemeriksaan Eksternal Jenasah Diduga Tenggelam Dari Data Bagian Ilmu Kedokt. Forensik Rsup Sanglah Bali Tahun 2012–2014. 2015, 4, pp. 29–42. Available online: http://www.eventscribe.com/2016/CECAR7/assets/pdf/326516.pdf (accessed on 28 March 2019).
- El Naggar, M.H.; Bentley, K.J. Dynamic Analysis for Laterally Loaded Piles and Dynamic P-Y Curves. Can. Geotech. J. 2000, 37, 1166–1183. [Google Scholar] [CrossRef]
- Bentley, K.J.; el Naggar, M.H. Numerical Analysis of Kinematic Response of Single Piles. Can. Geotech. J. 2000, 37, 1368–1382. [Google Scholar] [CrossRef]
- Heidari, M.; Jahanandish, M.; el Naggar, H.; Ghahramani, A. Nonlinear Cyclic Behavior of Laterally Loaded Pile in Cohesive Soil. Can. Geotech. J. 2014, 51, 129–143. [Google Scholar] [CrossRef]
- Rahmani, A.; Taiebat, M.; Finn, W.; Ventura, C. “Evaluation of p-y Curves Used in Practice for Seismic Analysis of Soil-Pile Interaction,”. GeoCongress 2012, vol. 10.1061/97, no. May. 1780–1788. [Google Scholar]
- Zhan, Y.G.; Wang, H.; Liu, F.C. Modeling Vertical Bearing Capacity of Pile Foundation by Using Abaqus. Electron. J. Geotech. Eng. 2012, 17, 1855–1865. [Google Scholar]
- Qu, H. Hysteresis Analysis on Beam-Column Connection of Concrete-Filled Steel Tubular Structure under Cyclic Loading. Trans. Tech. Publ. Switz. Mater. 2012, 517, 376–381. [Google Scholar] [CrossRef]
- Najafgholipour, M.A.; Dehghan, S.; Dooshabi, A.; Niroomandi, A. Finite Element Analysis of Reinforced Concrete Beam-Column Connections With Governing Joint Shear Failure Mode. Lat. Am. J. Solids Struct. 2017, 14, 1200–1225. [Google Scholar] [CrossRef]
- Voyiadjis, G.; Taqieddin, Z. Elastic-Plastic and Damage Model for Concrete Materials: Part I-Theoretical Formulation. Int. J. Struct. Chang. Solids 2009, 1, 31–59. [Google Scholar]
- Asadi, M. Experimental Test and Finite Element Modelling of Pedestrian. Test, No. Figure 1. 2010; 60876. [Google Scholar]
- Maheshwari, B.K.; Truman, K.Z.; el Naggar, M.H.; Gould, P.L. Three-Dimensional Finite Element Nonlinear Dynamic Analysis of Pile Groups for Lateral Transient and Seismic Excitations. Can. Geotech. J. 2004, 41, 118–133. Available online: https://scholar.google.com/scholar?q=Parameterised+Finite+Element+Modelling+of+RC+Beam+Shear+Failure&hl=fr&as_sdt=0&as_vis=1&oi=scholart (accessed on 28 March 2019). [CrossRef]
- Budge, S. Design And Analysis of Driven Pile Foundations for Lateral Capacity of Single Piles.
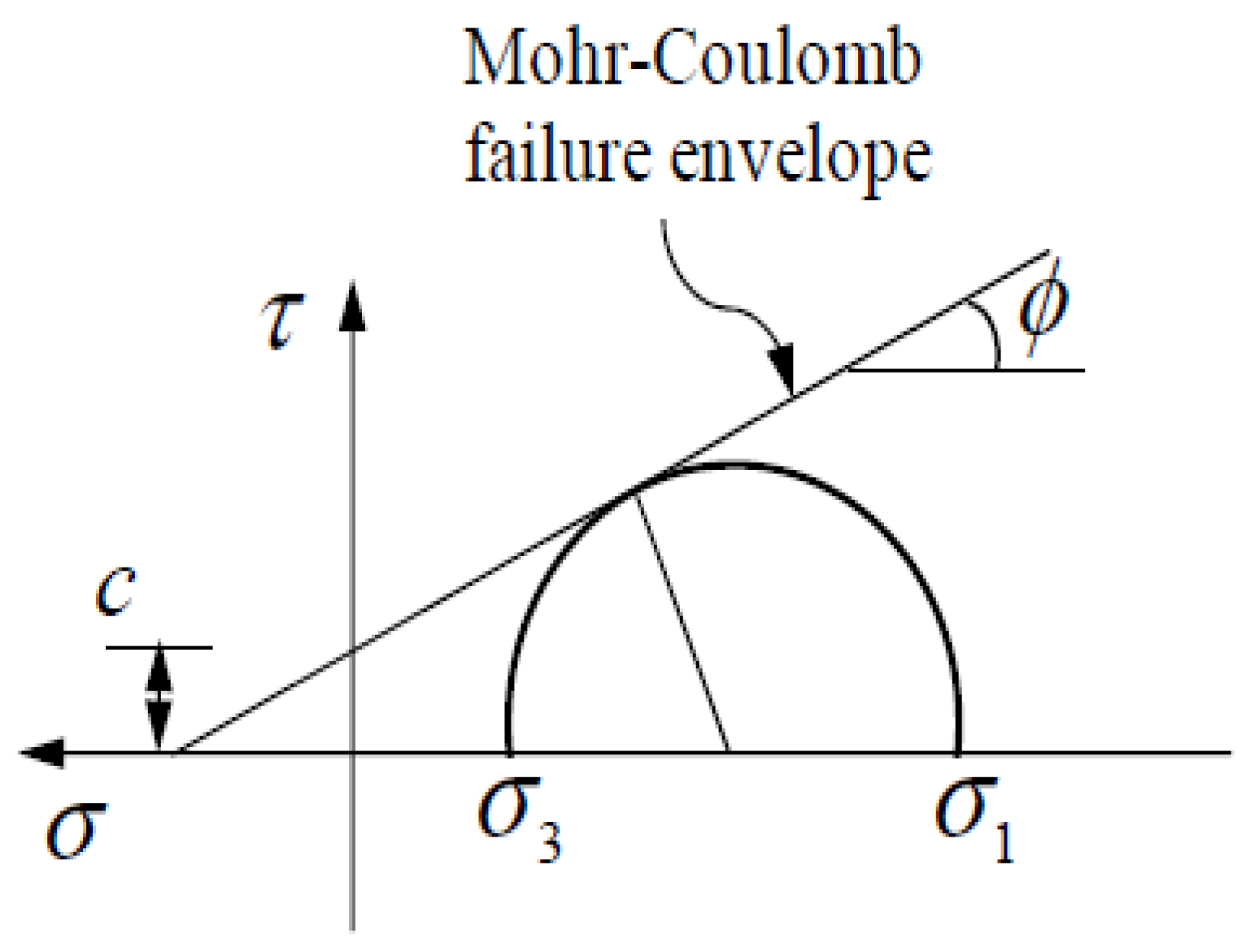

| Soil | Elasticity | Mohr-Coulomb | |||||
|---|---|---|---|---|---|---|---|
| Quality | Layer Thickness | Young’s Modulus (Pa) | Poison Ratio | Density (kg/m3) | Friction Angle (°) | Cohesion (KPa) | |
| Heavy weathered sandstone | top | 6.5 | 76.80 × 10 e6 | 0.25 | 1650 | 25.32 | 34 |
| Second | 3.1 | 56.50 × 10 e6 | 0.25 | 1850 | 28.30 | 2.57 | |
| third | 3.2 | 96.70 × 10 e6 | 0.25 | 1690 | 23.18 | 2.2 | |
| fourth | 0.8 | 57.80 × 10 e6 | 0.25 | 1675 | 26.77 | 2.8 | |
| Metamorphic siltstone mudstone | fifth | 8.4 | 64.20 × 10 e6 | 0.25 | 1600 | 22.24 | 4.6 |
| Pile Concrete | ||
|---|---|---|
| Density | 2500 | |
| Elastic | Young’s Modulus (Pa) | Poisson’s Ratio |
| 30•1010 | 0.3 | |
| Steel for the Pile | |||||
|---|---|---|---|---|---|
| Density (kg/m3) | 7800 | ||||
| Elastic | Young’s Modulus (Pa) | Poisson´s Ratio | |||
| 21e11 | 0.2 | ||||
| Concrete damage plasticity | Dilatation Angle (°) | Eccentricity | fbo/fco | k | Viscosity parameter |
| 31 | 0.1 | 1.16 | 0.6677 | 0 | |
| Properties Chosen for Model | Alternative Option | |
|---|---|---|
| Interaction | Mechanical contact<surface to surface> | <Node to surface> |
| Theory model | Frictional behavior contacts by Mohr-coulomb theory | Various |
| Sliding formulation | Small sliding | Finite sliding |
| Interaction properties | ||
| Tangential behavior | ||
| Friction formation | Penalty friction | Various |
| Friction coefficient (–) | 0.75 | 0.5 |
| Shear stress limit | No | Option limit can be set |
| Elastic slip, Absolute distance [m] | 0.001 | 0.0005 |
| Normal behavior, hard contact with penalty constraint method | ||
| Separation after contact | Allowed | Not allowed |
| Tie contact for the tip of the pile | Assigned |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssouf, T.; Yu, T.; Abdramane, D.; Cyriaque, A.O.; Youssouf, D. Force Performance Analysis of Pile Behavior of the Lateral Load. Infrastructures 2019, 4, 13. https://doi.org/10.3390/infrastructures4020013
Youssouf T, Yu T, Abdramane D, Cyriaque AO, Youssouf D. Force Performance Analysis of Pile Behavior of the Lateral Load. Infrastructures. 2019; 4(2):13. https://doi.org/10.3390/infrastructures4020013
Chicago/Turabian StyleYoussouf, Touré, Tianlai Yu, Dembélé Abdramane, Assogba Ogoubi Cyriaque, and Diakité Youssouf. 2019. "Force Performance Analysis of Pile Behavior of the Lateral Load" Infrastructures 4, no. 2: 13. https://doi.org/10.3390/infrastructures4020013
APA StyleYoussouf, T., Yu, T., Abdramane, D., Cyriaque, A. O., & Youssouf, D. (2019). Force Performance Analysis of Pile Behavior of the Lateral Load. Infrastructures, 4(2), 13. https://doi.org/10.3390/infrastructures4020013