Framework for Flexural Rigidity Estimation in Euler-Bernoulli Beams Using Deformation Influence Lines

Abstract

Structural degradation is an inevitable part of a structure’s service life. Detecting structural impairments and assessing their nature is a significant challenge. Degradations reduce structural system stiffness and subsequently affect system deformations. An appropriate structural health index that is able to capture these changes in deformation and relate them to a structural system stiffness may help engineers to adequately rate structural condition. This paper outlines a theoretical framework for the utilization of static deformation influence lines for estimating the flexural rigidity of Euler-Bernoulli beams. In the proposed technique, the relationship between the second derivative of the deformation influence line and the flexural rigidity for both statically determinate and indeterminate beam structures is presented. The proposed method provides a flexural rigidity estimate (FRE) over the entire span that is based on a single measurement location and estimates both the location and severity of impairments, regardless of the location of the measurement or the damaged zones. Noisy analytical simulations are presented with noise levels of 0%, 0.5%, 1%, 2%, 3%, and 4%; in all cases the modeled damage is quantified and localized using the FRE. A laboratory experiment is also presented that validates the theoretical framework.

1. Introduction

Detecting, classifying, and mitigating structural impairments are significant challenges for structural engineers, inspectors, and owners. The field of structural health monitoring (SHM) has developed to address these challenges associated with aging infrastructure [1,2,3,4,5,6,7,8,9]. Rytter outlines criteria for classification of SHM algorithms into four levels based on their output information [2]. At the simplest level (level-1), the SHM algorithm should provide a general indication of damage, while in levels 2–4 additional information regarding damage location, severity, and remaining service life of the structure will be provided, respectively. Algorithms utilizing appropriate structural health indices may increase the SHM classification level and aid engineers in adequately rating structural condition. Appropriate indices include the following essential features [10,11,12,13]:

• sensitivity to impairment,
• foundation in mechanical theory,
• consistency in the evaluation technique, and
• efficacy and efficiency of the technique in practice.

Many damage scenarios reduce a structural system’s stiffness; these stiffness degradations affect system deformations and lead to structural impairment [14,15]. Significant advancements in state of the art of deformation estimations (e.g., camera-based systems) and their increasing applications present opportunities for monitoring frameworks that utilize deformation data streams [16,17,18]. This paper presents an index and technique for locating and quantifying reductions in flexural rigidity along a beam structure, by analyzing deformation influence lines at a single location on the beam.

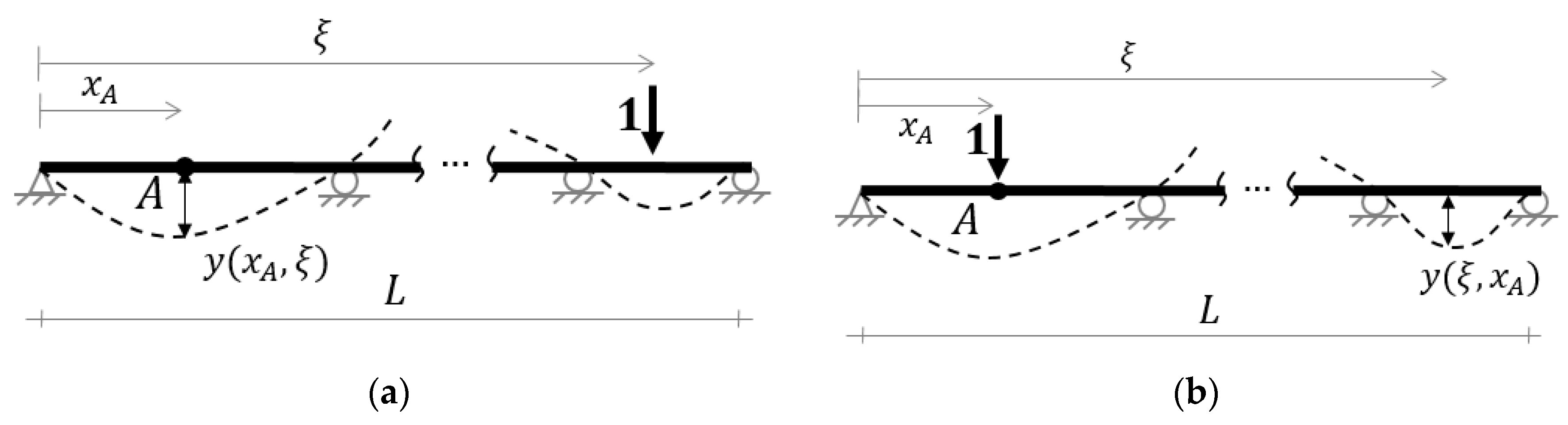
2. Influence Lines for Euler-Bernoulli Beam Evaluation

An influence line function represents the magnitude of a desired response (e.g., strain, shear, moment, deflection, rotation) at a fixed point on a structural system that is caused by a static load pattern placed anywhere on the structure. If the load pattern is limited to a single unit load, the influence line is called a Unit Influence Line (UIL). The UIL technique has been implemented widely in bridge engineering design and load rating.

A system’s static response influence lines are comprehensive evaluation indices that contain many of the previously outlined features that are rich in diagnostic content [10,11,12,19,20,21]. Several studies utilizing an influence line approach for bridge evaluation and monitoring are outlined in the literature. A great portion utilized the internal responses, such as strain [11,12,19,22,23] or stress influence lines [20,24]. Others use global deformation influence lines [10,21,25]. Changes in flexural rigidity anywhere along a span will manifest in global deformation influence lines at any other point on the beam, regardless of the determinacy of the system.

The preliminary efforts of employing deformation influence lines as a bridge condition index gathered measurements from diagnostic crawl-speed tests and derived the unit load influence line using numerical decomposition [10,21,25]. Turer utilized two methods to show that a conceptual relation between flexibility and deformation influence coefficients exists [10].

Over the last decade, some studies have proposed a method to locate damage by analyzing the absolute differences between the curvature of deflection influence lines for intact and damaged beam structures [26,27,28,29,30]. These studies provide influence-line-based methods to detect and localize damage that is a critical step in monitoring and evaluating a structure.

This paper presents a theoretical framework for using static global response in gravity-carrying components of beam structures for impairment detection. Utilizing the second derivative of the static deformation influence line as an impairment index, the proposed technique presents a robust method of characterizing both the location and the severity of impairments in beam structures based on deformation data streams.

3. Flexural Rigidity Estimation (FRE)

3.1. Derivation for FRE

A straight beam with linear elastic material and two-dimensional linear geometric behavior is illustrated in Figure 1a. A unit force is applied on this beam at distance $\xi$ from the left support location. The vertical deflection, $y\left(x,\xi \right),$ (dashed lines in Figure 1a) is a function of the location of the unit load, $\xi ,$ and varies with the position along the beam. The first argument in the function $y\left(x,\xi \right)$ represents the monitoring location along the beam. The second argument is the location of the unit load. If the first argument varies and the second is fixed, then $y$ is a deflection function when the unit load is fixed; if the opposite is true, then $y$ is a DIL of the fixed first argument.

The vertical deflection influence line (DIL) of an arbitrary point $A$ located at distance $x_A$ from the left support, $y\left(x_A,\xi \right),$ is defined as the deflection of the beam at point $A$ as a unit load located at $\xi$ traverses the span, i.e., ($0<\xi <L$).

According to Maxwell’s theorem of reciprocal displacement, the deflection at point $A$ due to a unit load acting at distance $\xi$ (i.e., $y\left(x_A,\xi \right)$) is equal to the beam deflection at distance $\xi$ when the unit load is acting at point $A$ (i.e.,$y\left(\xi ,x_A\right)$). So, using Maxwell’s theorem gives:

$$y\left(x_A,\xi \right)=y\left(\xi ,x_A\right)$$

(1)

If $\xi$ varies from $0$ to $L$, the left side of Equation (1) is the DIL of point $A$, and the right side of Equation (1) represents the beam’s deflected shape when a unit load is applied at point $A$. This is illustrated in Figure 1b.

Assuming that both sides of Equation (1) are twice differentiable, differentiating both sides of Equation (1) twice with respect to $\xi$ yields:

$$\frac{{\partial }^{2}y\left(x_A,\xi \right)}{\partial {\xi }^2}=\frac{{\partial }^{2}y\left(\xi ,x_A\right)}{\partial {\xi }^2}$$

(2)

The left side of Equation (1) may be acquired practically by collecting deflection data at point $A$ as a unit load traverses the structure and differentiating twice.

The right side of Equation (1) represents the deflected shape of the beam when a unit load is located at $x_A$; therefore, the right side of Equation (2) is the beam curvature when a unit load is applied at distance $x_A$. If Euler-Bernoulli behavior is considered, then the right side of Equation (2) can be related to internal moment and flexural rigidity:

$$\frac{{\partial }^{2}y\left(x_A,\xi \right)}{\partial {\xi }^2}=\frac{{\partial }^{2}y\left(\xi ,x_A\right)}{\partial {\xi }^2}=\frac{m\left(\xi \right)}{EI\left(\xi \right)}$$

(3)

In Equation (3), $EI\left(\xi \right)$ is the current beam flexural rigidity at $\xi$ and may be a variable function along the beam. Moreover, the moment $m\left(\xi \right)$ is the internal moment when a unit load is acting at point $A$.

By using Maxwell’s reciprocal theorem and the same procedure, it can be shown that Equation (3) is also valid for the rotation influence line (RIL). In the case of using the RIL instead of the DIL (i.e., $\theta \left(x_A,\xi \right)$ instead of $y\left(x_A,\xi \right)$), the moment $m\left(\xi \right)$ in Equation (3) equals the internal moment when a unit moment is acting at the point $A$.

For simplification and generalization, the term $y\left(x_A,\xi \right)$ (or $\theta \left(x_A,\xi \right)$) is replaced with $u_A\left(\xi \right)$. Equation (3) becomes:

$$u_A^{″}\left(\xi \right)=\frac{m\left(\xi \right)}{EI\left(\xi \right)}$$

(4)

Practically, $EI\left(\xi \right)$ will never be equal to zero in Equation (4). So, in regions that $m\left(\xi \right)$ is zero, $u_A^{″}\left(\xi \right)$ becomes zero and in regions that $m\left(\xi \right)$ is not equal to zero, Equation (4) yields:

$$EI\left(\xi \right)=\frac{m\left(\xi \right)}{u_A^{″}\left(\xi \right)}$$

(5)

Equation (5) is the Flexural Rigidity Estimate (FRE), which provides $EI\left(\xi \right)$, the beam’s flexural rigidity at location $\xi$ as a function of a known internal moment $m\left(\xi \right)$ and the second derivative of a measured $DIL$ or $RIL$, $u_A^{″}\left(\xi \right)$.

By comparing the nominal flexural rigidity ($E{I}_0$) with the FRE calculated from Equation (5), the location and quantity of the impairment to the flexural rigidity can be estimated.

3.2. Alternate Derivation for FRE

The deflection of point $A$ in Figure 1 as a function of a traversing unit load,$u_A\left(\xi \right)$, can be calculated using the flexural equation for virtual work.

In the case of linear geometry, elastic material behavior, and negligible shear deformations, the small flexural deflection $u_A\left(\xi \right)$, under the effects of a unit load at distance $\xi$ is expressed as:

$$u_A\left(\xi \right)={{\displaystyle \int }}_0^L\frac{M\left(x,\xi \right)·m\left(x\right)}{EI\left(x\right)}dx$$

(6)

In Equation (6), the moment $M\left(x,\xi \right)$ is the beam internal moment caused by an externally applied load (i.e., the moving unit load) and $m\left(x\right)$ is the internal moment caused by a virtual unit load applied at point $A$. The moment $m\left(x\right)$ is a function of location $x_A$, but independent of variable $\xi$.

The moment $M\left(x,\xi \right)$ in Equation (6) is the only parameter on the right side that is a function of $\xi$. Both $m\left(x\right)$ and $EI\left(x\right)$ remain constant as a unit load traverses the beam. Hence, the first and second derivatives of $u_A\left(\xi \right)$ with respect to $\xi$ are equal to Equations (7) and (8), respectively.

$$\frac{d{u}_A}{d\xi }=u_A^{\prime }\left(\xi \right)={{\displaystyle \int }}_0^L\frac{\frac{\partial M\left(x,\xi \right)}{\partial \xi }·m\left(x\right)}{EI\left(x\right)}dx$$

(7)

$$\frac{d^2{u}_A}{d{\xi }^2}=u_A^{″}\left(\xi \right)={{\displaystyle \int }}_0^L\frac{\frac{{\partial }^{2}M\left(x,\xi \right)}{\partial {\xi }^2}·m\left(x\right)}{EI\left(x\right)}dx$$

(8)

The moment $M\left(x,\xi \right)$ in Equation (6) is the internal moment influence line at point $x$. According to the Muller-Breslau principle, the influence line for this internal moment is the scaled deflected shape of a beam with released moment resistance that is subject to a virtual displacement at a frictionless hinge. This modified beam with an internal hinge is depicted in Figure 2. In other words, the moment $M\left(x,\xi \right)$ is equal to:

$$M\left(x,\xi \right)=\frac{1}{{\mathsf{\alpha }}_{\mathrm{x}}}{y}_{M.B.}\left(\xi \right)$$

(9)

In Equation (9), $y_{M.B.}\left(\xi \right)$ and ${\mathsf{\alpha }}_{\mathrm{x}}$ are the deflection curve and angular displacement at $x$ of the modified beam under the effects of a virtual displacement, as illustrated in Figure 2. The second derivative of moment $M$. with respect to $\xi$. is equal to:

$$\frac{{\partial }^{2}M\left(x,\xi \right)}{\partial {\xi }^2}=\frac{1}{{\mathsf{\alpha }}_{\mathrm{x}}}\frac{d^2{y}_{M.B.}}{d{\xi }^2}$$

(10)

The right side of Equation (10) is related to the curvature of the modified beam that is subject to a small virtual displacement, as shown in Figure 2. For the case of a statically determinate beam, the moment influence line is linear, so the curvature of the deflected shape of the modified beam must be zero except for at the location of the hinge, where the curvature is infinite. Hence, the right side of Equation (10) is equal to:

$$\frac{1}{{\mathsf{\alpha }}_{\mathrm{x}}}\frac{d^2{y}_{M.B.}}{d{\xi }^2}=\{\begin{array}{cc}0& \xi \ne x\\ \infty & \xi =x\end{array}$$

(11)

The right side of Equation (11) is the Dirac delta function centered at $\xi =x$. Substituting Equations (10) and (11) into Equation (8) gives:

$$u_A^{″}\left(\xi \right)={{\displaystyle \int }}_0^L\frac{\delta \left(x-\xi \right)·m\left(x\right)}{EI\left(x\right)}dx$$

(12)

According to the properties of the Dirac delta function, when $0<\xi <L$, Equation (12) yields:

$$u_A^{″}\left(\xi \right)=\frac{m\left(\xi \right)}{EI\left(\xi \right)}$$

(13)

This is the same as Equation (4). Superposition is used when applying the framework to statically indeterminate structures as shown in the following section.

4. Calculation of Moment $\mathit{m}\left(\mathit{\xi }\right)$

Equation (5) can be used to detect the status of a beam’s flexural rigidity. In practice, the influence line is extracted by solving an inverse problem. First, the desired response (e.g., vertical deflection or rotation) of a specific location is recorded. Then, by synchronizing the recorded measurement with the location of moving loads (e.g., vehicular loads) and solving an inverse problem, the influence line,$u_A\left(\xi \right)$, of a unit load can be extracted [10,11,12,19,21,22,23].

The second derivative of $u_A\left(\xi \right)$ can be estimated numerically. The moment $m\left(\xi \right)$ in Equation (5) must be calculated or estimated. The moment $m\left(\xi \right)$ will be independent of a system’s flexural stiffness if the system is statically determinate; conversely, the moment $m\left(\xi \right)$ will be dependent upon a system’s flexural stiffness if the system is statically indeterminate. The methods for calculating and estimating the moment $m\left(\xi \right)$ are as follows.

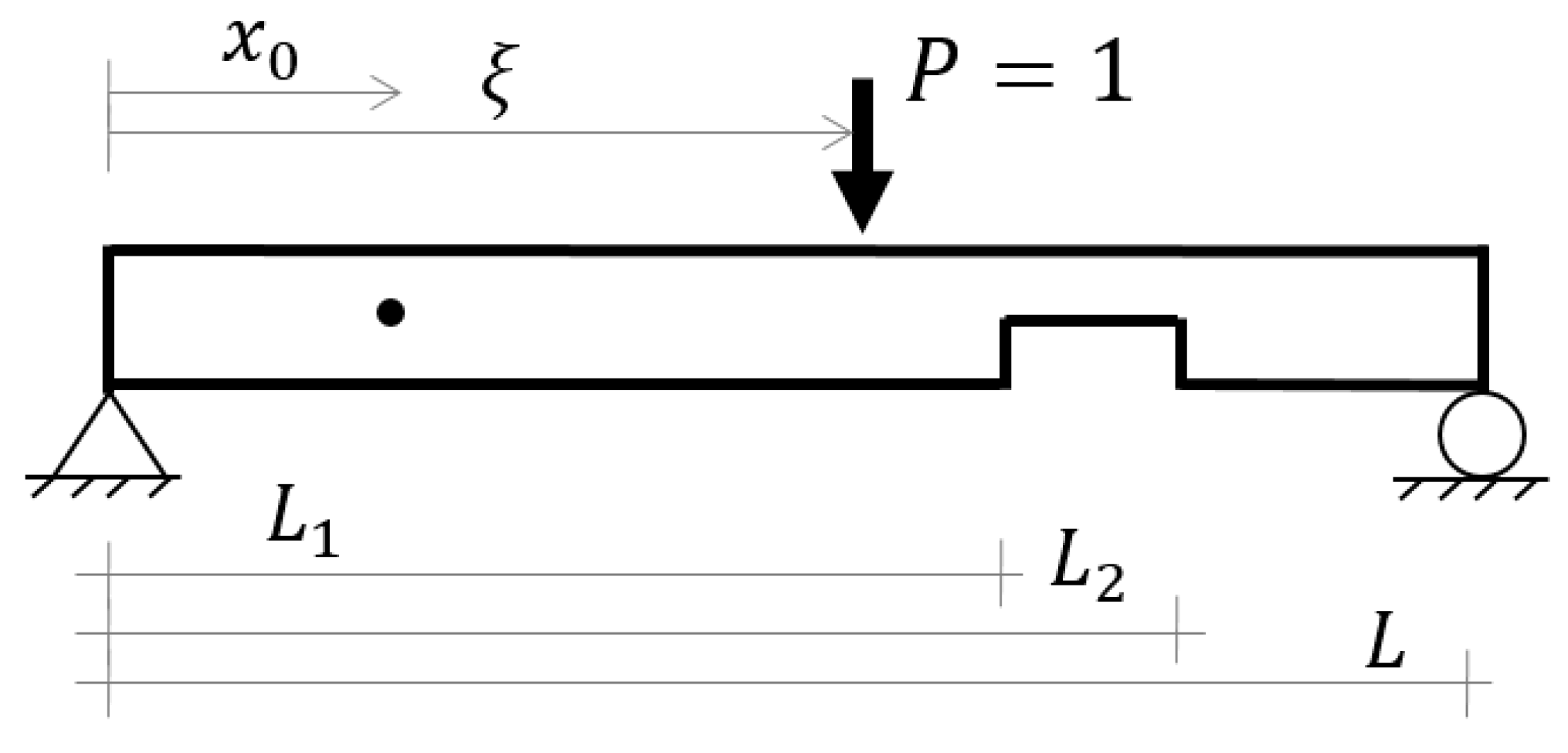
4.1. Statically Determinate Systems

In a statically determinate system, $m\left(\xi \right)$ is not a function of beam flexural stiffness, but is a function of the location ($x_A$) and the type of recorded deformation. Hence, no additional information is required to calculate the $m\left(\xi \right)$ diagram.

In the case of using a DIL:

$$m\left(\xi \right)=\{\begin{array}{cc}\frac{\xi \left(L-x_A\right)}{L}& \xi \le x_A\\ \frac{x_A\left(L-\xi \right)}{L}& \xi >x_A\end{array}$$

(14)

In the case of using a RIL:

$$m\left(\xi \right)=\{\begin{array}{cc}\frac{\xi }{L}& \xi \le x_A\\ \frac{\xi }{L}-1& \xi >x_A\end{array}$$

(15)

4.2. Statically Indeterminate Systems

In a statically indeterminate system (e.g., continuous multi-span beam), the moment $m\left(\xi \right)$ is a function of the system’s flexural stiffness. Hence, calculation of the moment $m\left(\xi \right)$ requires additional information. Two techniques are described to calculate and estimate the moment $m\left(\xi \right)$ for both $DIL$ and $RIL$.

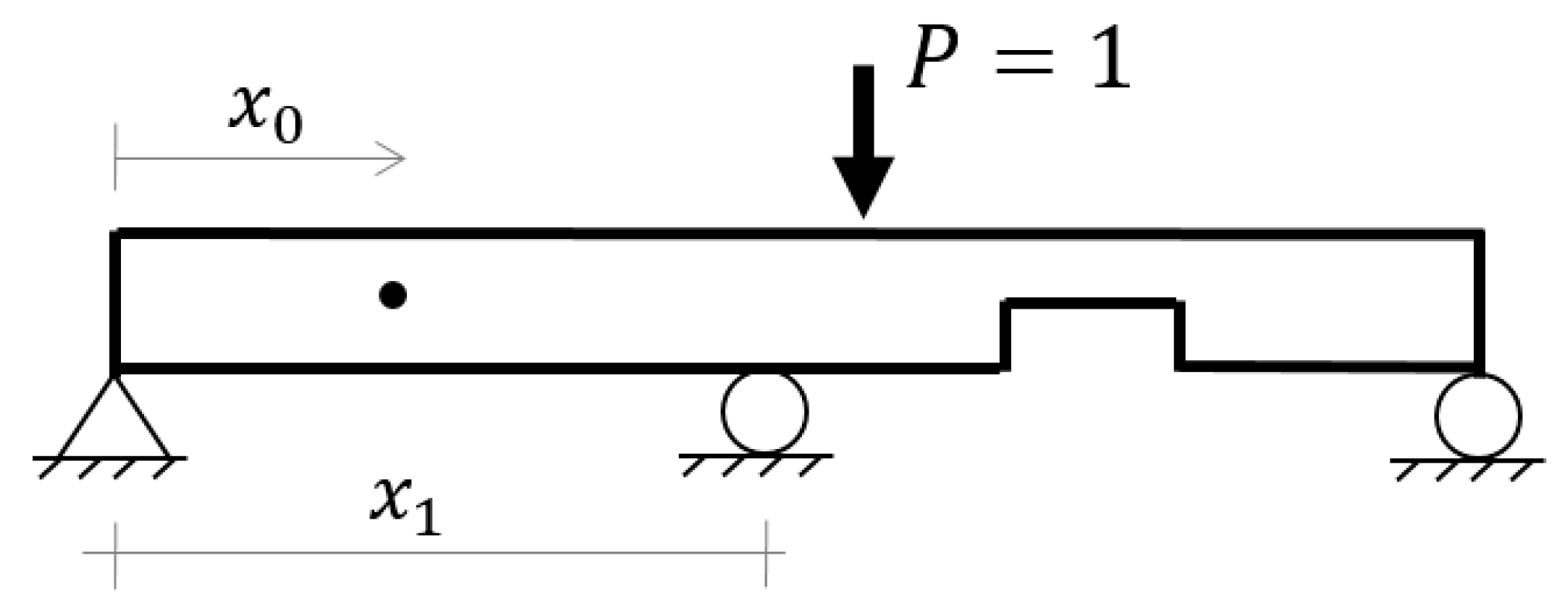
4.2.1. Deflection Influence Line (DIL)

In the case of using a DIL, the moment $m\left(\xi \right)$ will be the diagram of the moment that is created by a unit load that is applied at distance $x_A$. In a linear system, the response of a statically indeterminate or continuous beam with a degree of indeterminacy (DOI, i.e., the number of interior vertical support reactions) can be calculated by the superposition of $DOI+1$ number of statically determinate systems (i.e., simply supported beams). For this purpose, each vertical support (support $i$) is replaced by a vertical reaction $R_i$. The moment that $m\left(\xi \right)$ of the continuous beam is calculated by the superposition of moment of these $DOI+1$ statically determinate simply supported beams:

$$m\left(\xi \right)=m_{UL}\left(\xi \right)+{\displaystyle \sum }_{i=1}^{DOI}{R}_i{m}_i\left(\xi \right)$$

(16)

In Equation (16), $m_{UL}\left(\xi \right)$ is the moment that is caused by a unit load applied at a distance $x_0$ on a simply supported beam. Moment $m_i\left(\xi \right)$ is the moment that is caused by a unit load that is applied on the simply supported beam at location of the interior support $i$. If $x_i$ serves as the location of interior support,$i$, the equations for $m_{UL}$ and $m_i$ are as follows:

$$m_{UL}\left(\xi \right)=\{\begin{array}{cc}\frac{\xi \left(L-x_A\right)}{L}& \xi \le x_A\\ \frac{x_A\left(L-\xi \right)}{L}& \xi >x_A\end{array}$$

(17)

$$m_i\left(\xi \right)=\{\begin{array}{cc}\frac{\xi \left(L-x_i\right)}{L}& \xi \le x_i\\ \frac{x_i\left(L-\xi \right)}{L}& \xi >x_i\end{array}$$

(18)

Moreover, in Equation (16), reaction $R_i$ is the reaction of interior support $i$ when a unit load is applied on a continuous beam at distance $\xi =x_A$. These reactions are unknown and additional information is required.

To get this additional information, assume that a strain gage is attached to an adequate cross-section location at each support location on the continuous beam. By having knowledge about the status of the flexural rigidity on interior support locations, the internal moment at each support location can be calculated by converting the recorded strains.

Thus, when the moving unit load is located at a distance $\xi =x_A$, the moment at each support can be measured by using these strain gages. These measured moments constitute the moment $m\left(\xi \right)$ at each support location (i.e.,$m\left(x_1\right),m\left(x_2\right),\dots ,m\left(x_{DOI}\right)$). So,

$${\left[\begin{array}{c}m\left(x_1\right)\\ ⋮\\ m\left(x_{DOI}\right)\end{array}\right]}_{DOI\times 1}={\left[\begin{array}{c}{m}_{UL}\left(x_1\right)\\ ⋮\\ m_{UL}\left(x_{DOI}\right)\end{array}\right]}_{DOI\times 1}+{\left[\begin{array}{ccc}{m}_1\left(x_1\right)& \dots & m_{DOI}\left(x_1\right)\\ ⋮& \ddots & ⋮\\ m_1\left(x_{DOI}\right)& \dots & m_{DOI}\left(x_{DOI}\right)\end{array}\right]}_{DOI\times DOI}\times {\left[\begin{array}{c}{R}_1\\ ⋮\\ R_{DOI}\end{array}\right]}_{DOI\times 1}$$

(19)

Or, in matrix format:

$$\tilde{m}={\tilde{m}}_{UL}+\left[\begin{array}{cc}\begin{array}{cc}{\tilde{m}}_1& {\tilde{m}}_2\end{array}& \begin{array}{cc}\dots & {\tilde{m}}_{DOI}\end{array}\end{array}\right]\times {\tilde{R}}_i$$

(20)

As can be seen in Equation (20), the measured moments give $DOI$ number of equations with $DOI$ number of unknowns ($R_i$). By solving Equation (20), the unknowns $R_i$ can be solved as:

$${\tilde{R}}_i={\left[\begin{array}{cc}\begin{array}{cc}{\tilde{m}}_1& {\tilde{m}}_2\end{array}& \begin{array}{cc}\dots & {\tilde{m}}_{DOI}\end{array}\end{array}\right]}^{-1}\times \left(\tilde{m}-{\tilde{m}}_{UL}\right)$$

(21)

Therefore, when a DIL is measured, the general diagram of moment $m\left(\xi \right)$ of the continuous beam can constructed by substituting the resultant $R_i$ from Equation (21) in Equation (16).

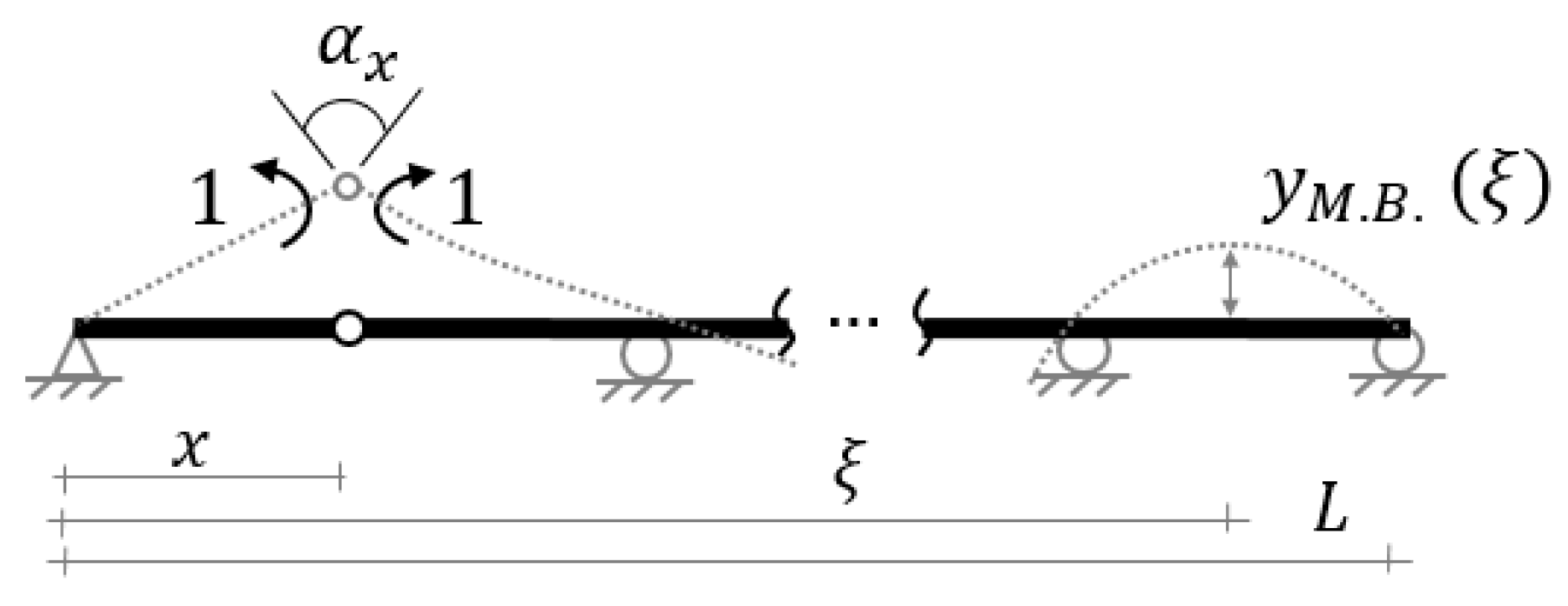
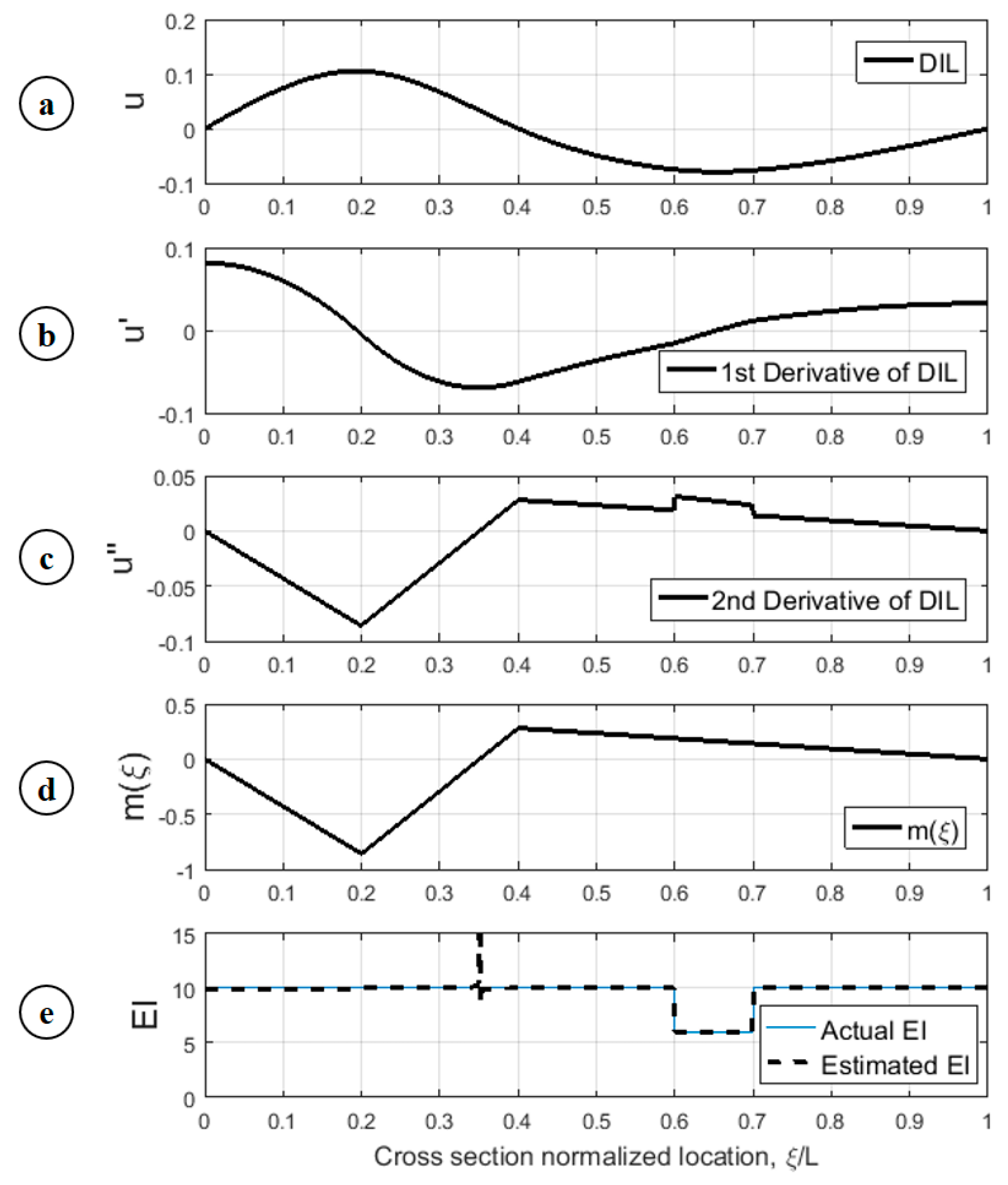
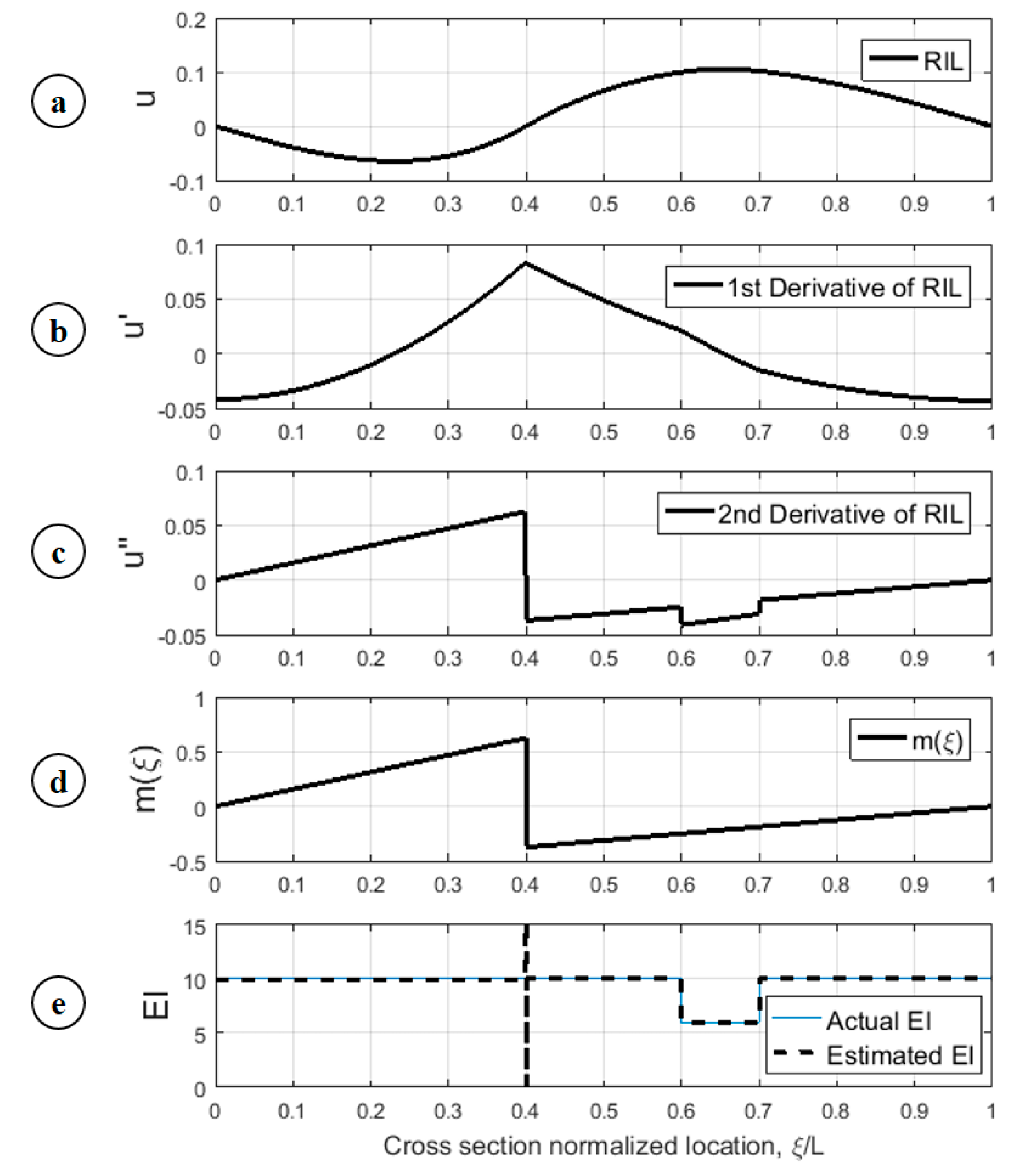
4.2.2. Rotation Influence Line (RIL)

In the case of measuring the RIL, the moment $m\left(\xi \right)$ is the moment that is caused by a concentrated unit moment at measurement location ($x_A$). The influence line is constructed using a unit point load; the technique proposed for using a deflection influence line is not applicable here, and the measured moments (i.e.,$m\left(x_1\right),m\left(x_2\right),\dots ,m\left(x_{DOI}\right)$) must be preprocessed.

The first derivative of the deflection influence line can be explained using Equation (22):

$$\frac{du}{d\xi }=\underset{\mathsf{\Delta }\xi \to 0}{\lim }\frac{u\left(\xi +\mathsf{\Delta }\xi \right)-u\left(\xi \right)}{\mathsf{\Delta }\xi }$$

(22)

The right side of Equation (22) can be expanded to:

$$u^{\prime }=\underset{\mathsf{\Delta }\xi \to 0}{\lim }\frac{u\left(\xi +\mathsf{\Delta }\xi \right)}{\mathsf{\Delta }\xi }-\frac{u\left(\xi \right)}{\mathsf{\Delta }\xi }$$

(23)

According to the definition of the deflection influence line, $u\left(\xi \right)$ is the beam deformation at a location $x_0$ when a unit load is applied at a distance $\xi$. So, in Equation (22), the terms $\frac{u\left(\xi +\mathsf{\Delta }\xi \right)}{\mathsf{\Delta }\xi }$ and $\frac{u\left(\xi \right)}{\mathsf{\Delta }\xi }$ are the beam deformations at location $x_0$ when a moving load with intensity equal to $\frac{1}{\mathsf{\Delta }\xi }$ is applied at distances $\xi +\mathsf{\Delta }\xi$ and $\xi$, respectively. By using the principle of superposition, $u\prime$ in Equation (22) is the beam deformation under the effects of two concentrated loads that are applied in opposite directions. These concentrated loads can be replaced by a couple with intensity equal to:

$$M=\frac{1}{\mathsf{\Delta }\xi }\times \mathsf{\Delta }\xi =1$$

(24)

As $\mathsf{\Delta }\xi$ approaches zero, the location of this couple approaches $\xi$. This means that $u\prime \left(\xi \right)$ is the beam deformation at location $x_0$ that is caused by a positive unit moment applied at location $\xi$. The first derivative of the deformation influence line under the effects of a moving unit load can be interpreted as the deformation influence line under the effects of a moving unit moment.

In a similar manner, the first derivative of the recorded moment measurement at each interior support location can be assumed as interior support moment under the effects of moving unit moment. By taking the first derivative of the recorded moment at each interior support location, the moment $m\left(\xi \right)$ at each support location (i.e.,$m\left(x_1\right),m\left(x_2\right),\dots ,m\left(x_{DOI}\right)$) is determined. In this section, $m_i\left(\xi \right)$ has the same definition used in Equation (18). By gathering this information, Equation (4) still can be utilized to calculate the diagram of moment $m\left(\xi \right)$.

5. Analytical Illustrations of the Method

5.1. Example I—Statically Determinate System

Figure 3 depicts a simply supported beam with a reduction in flexural rigidity from $E{I}_0$ (nominal rigidity) to $\beta E{I}_0$ ($0<\beta <1$) between locations $L_1$ and $L_2$. The deflection influence line of the beam at location $x_0$ is available from recorded deflection data.

Using the arbitrary values that are listed in

Table 1. Value of Constant Parameters in Example-1 and Example-2.

Parameter	Value	Unit
$E{I}_0$	$10$	$\mathrm{Force}/{\mathrm{Length}}^2$
$\beta$	$0.6$	-
$L$	$10$	$\mathrm{Length}$
$x_0$	$2$	$\mathrm{Length}$
$L_1$	$6$	$\mathrm{Length}$
$L_2$	$7$	$\mathrm{Length}$

, a finite element (FE) model is created to solve the defined problem. By using this FE model, the DIL is calculated. In this solution, the beam is divided into 1500 elements, with flexural stiffness and two degrees of freedom at each node.

The resultant DIL and its first and second derivatives are plotted in Figure 4a–c, respectively. In practice, the resultant DIL is a series of points. Hence, to get the first and second derivatives, numerical methods should be utilized. To get the second derivative in this example, the second order central difference method (CDM) with three points is implemented.

Moreover, the piecewise equation of moment $m$, the resultant moment that is caused by a unit point load applied at distance $x_0$ on a simply supported beam, is equal to Equation (14).

By substituting the calculated second derivative and Equation (14) into Equation (5), the beam’s flexural rigidity can be calculated. The resultant flexural rigidity is illustrated in Figure 4d.

As can be seen in Figure 4, the proposed formula is robust enough to give the exact diagram of flexural rigidity. The differences between this plot and the flexural rigidity diagram obtained from nominal conditions give the location and magnitude of damages along the beam.

5.2. Example II—Statically Indeterminate Systems

Figure 5 illustrates a statically indeterminate system similar to the one in Example I but with an additional interior support located at $x_1=4$.

5.2.1. Using Deflection Influence Line (DIL)

In this section, the DIL is implemented to solve the damage detection problem in Example 2. Like Example 1, the resultant DIL and its first and second derivatives are plotted in Figure 6a–c using a FE model and the CDM. The moment, $m\left(\xi \right),$ is a function of the system’s flexural rigidity in indeterminate systems, and its calculation requires additional information. To obtain this additional information, a strain gage is attached to the cross-section at the interior support location. If the status of the flexural rigidity at this cross-section is already known, the measured strains at this cross-section can be converted to internal moment at this location.

The moment is calculated from strain that occurs when the moving unit load is located at distance $\xi =x_A$. This moment is substituted into Equation (21). The resultant $R_1$ is then substituted into Equation (16) and the general function of moment $m\left(\xi \right)$ in this two-span continuous beam is constructed. Using this procedure, the diagram of moment $m\left(\xi \right)$ is plotted in Figure 6d.

By using Equation (4), the resultant calculated beam flexural rigidity is presented in Figure 6e. As can be seen from Figure 6e, the proposed formula was able to predict the flexural rigidity correctly, aside from a small region between locations $x=3.3$ and $x=3.7$ where the flexural rigidity curve diverges.

As stated previously, the proposed formula in Equation (5) is acceptable when the terms $u″\left(\xi \right)$ or $m\left(\xi \right)$ are not equal to zero. The ratio of $m\left(\xi \right)/u^{″}\left(\xi \right)$ is unstable around zero points of $m\left(\xi \right)$. Due to the implementation of numerical methods in the calculation of the second derivative, the magnitudes of $u″$ are not precise enough to give the correct answers near zero values. Consequently, flexural rigidity is not precisely predicted where $m\left(\xi \right)$ approaches zero.

5.2.2. Using Rotation Influence Line (RIL)

If the beam rotation influence line at an interior support is used, then the $m\left(\xi \right)$ diagram will have a jump at the location of the interior support. The function $m\left(\xi \right)$ is not defined at this point, and the location of this jump is the only point at which the corresponding flexural rigidity cannot be calculated using Equation (5). However, according to the procedure defined in Section 5.2.1, it is required that the status of beam cross-section on interior support locations be investigated in order to implement the proposed method in a statically-indeterminate system. Therefore, the only cross-section that could not be monitored by using the RIL is already diagnosed.

In other words, by using the RIL, the theoretical solution for the flexural rigidity of all cross-sections can be accurately assessed. If the central difference method is used for calculating the second derivative, then using the beam RIL at an interior support location is recommended rather than the DIL.

The resultant diagrams for Example 2 when the RIL is utilized are given in Figure 7. As can be seen in Figure 7e, the RIL was able to correctly predict the flexural rigidity of all cross-sections.

6. Application

In practice, measurements can be noisy, and the finite difference method may not produce a suitable second derivative for noisy data. One approach for addressing this challenge is to use a parametric approximation of the measurements. This section introduces an algorithm to overcome the obstacles of noisy measurements and its application to a series of numerical and experimental results.

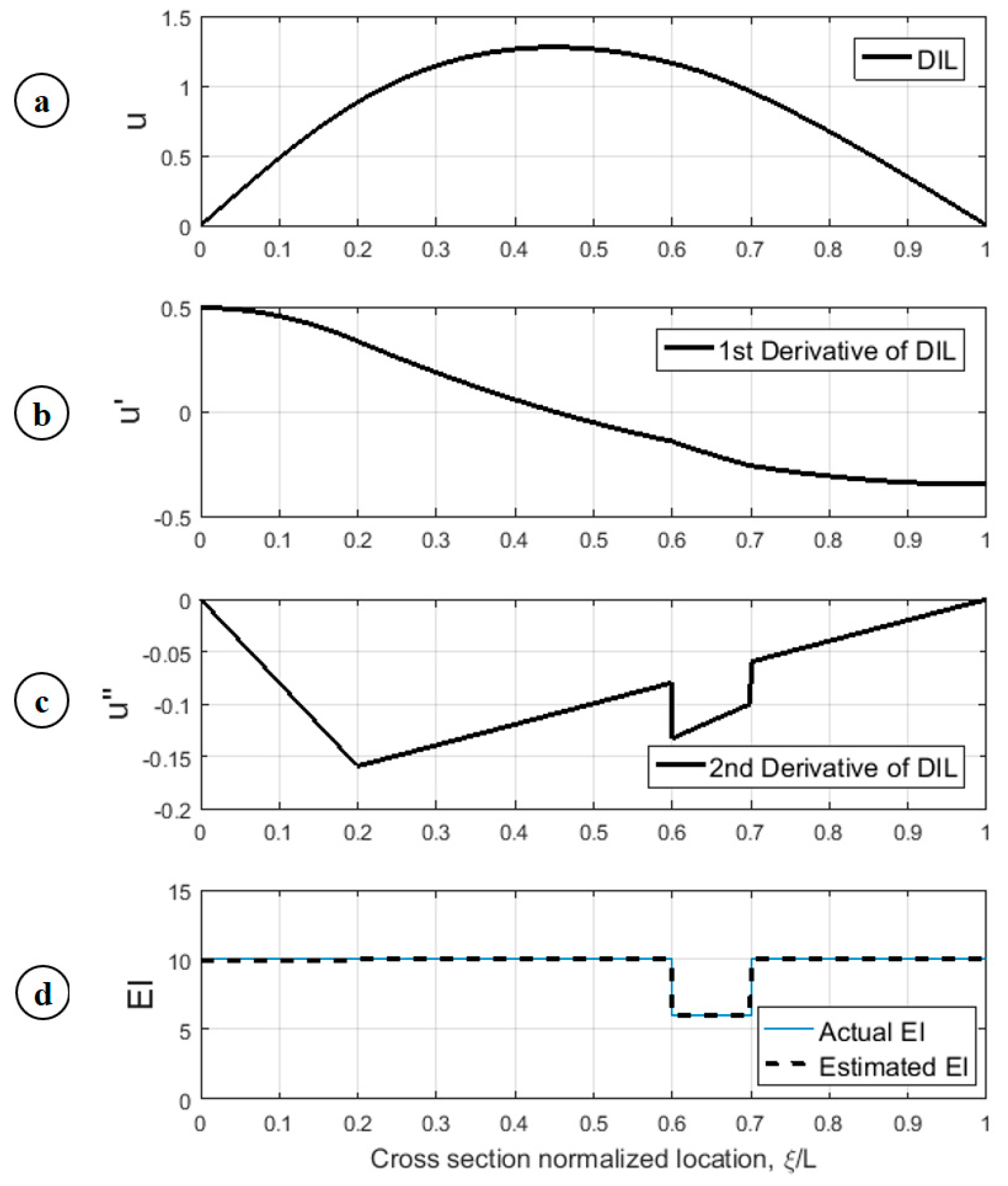
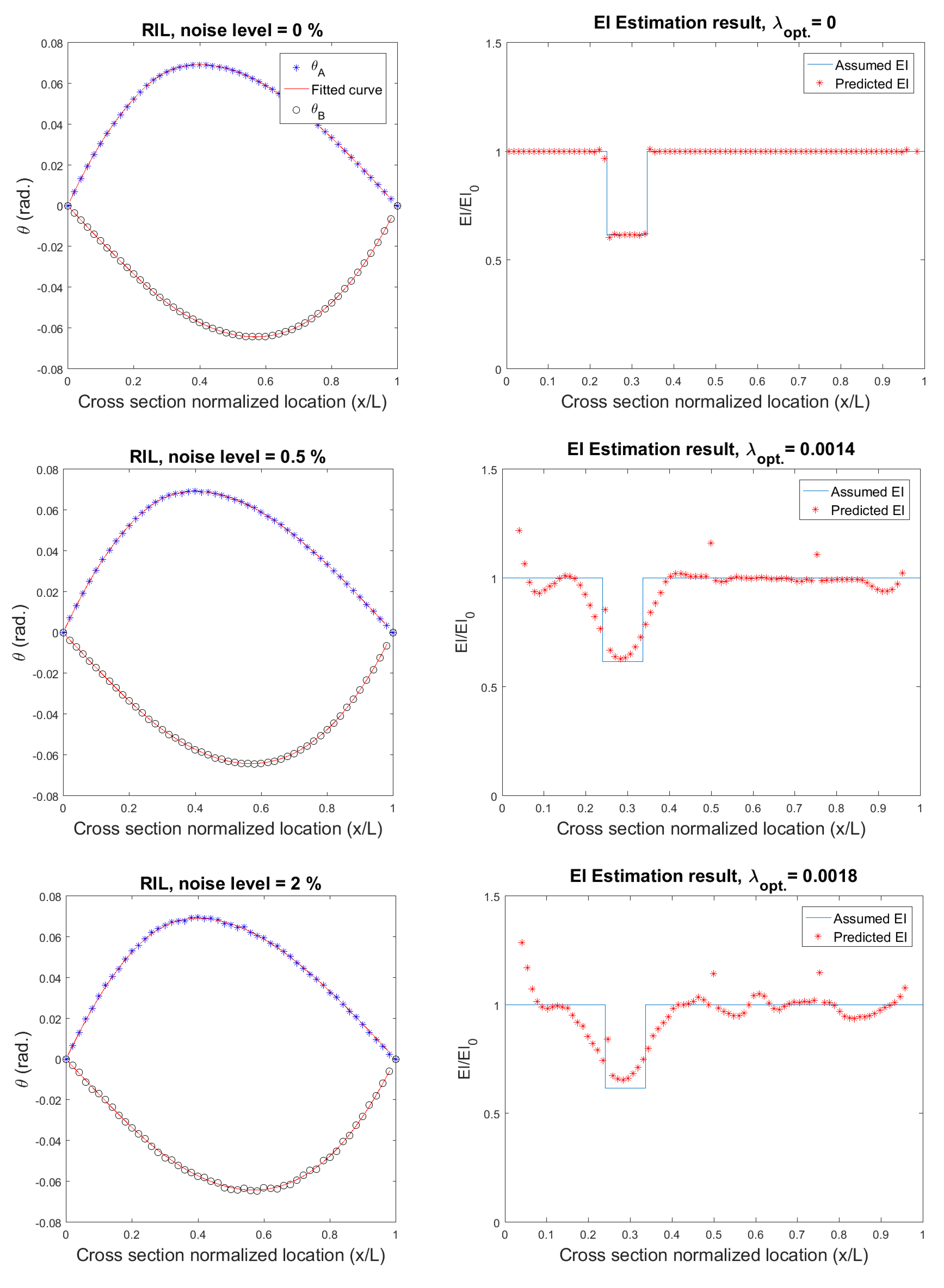
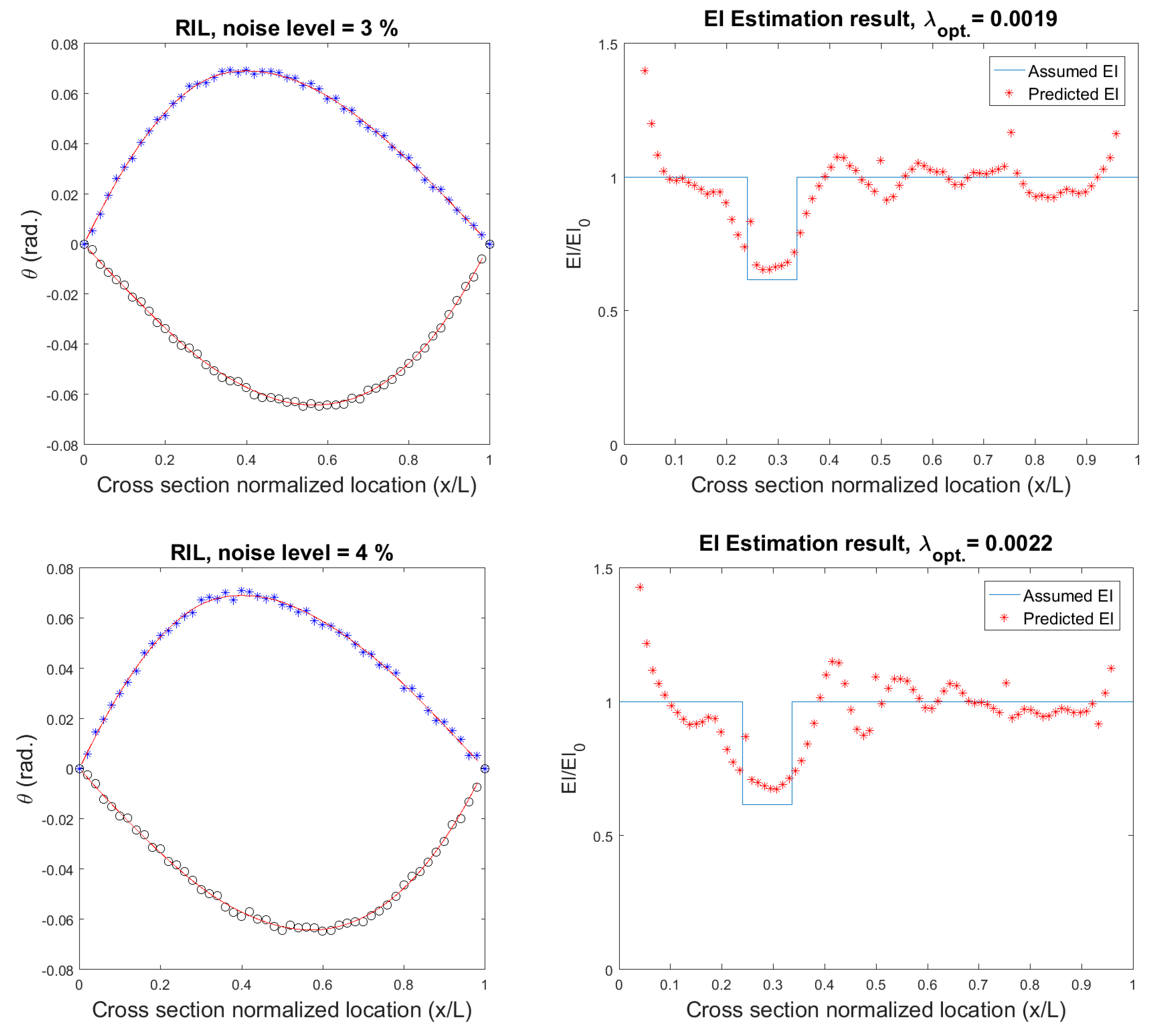
6.1. Algorithm for Addressing Noisy Measurements

The approach seeks to fit a smooth parametric function to the measured noisy influence line. After curve fitting, an estimation of the second derivative of the influence line is constructed using this approximated function. The fitted function should be continuous and smooth while closely estimating the numerical values at each measurement.

A piecewise quadratic spline is considered as the parametric function. This function consists of NS number of quadratic continuous functions and is defined as Equation (25).

$$U_{fit}\left(x\right)=\{\begin{array}{cc}{\alpha }_{1,1}{x}^2+{\alpha }_{1,2}x+{\alpha }_{1,3}& x_0\le x<x_1\\ {\alpha }_{2,1}{x}^2+{\alpha }_{2,2}x+{\alpha }_{2,3}& x_1\le x<x_2\\ ⋮& ⋮\\ {\alpha }_{NS,1}{x}^2+{\alpha }_{NS,2}x+{\alpha }_{NS,3}& x_{NS-1}\le x<x_{NS}\end{array}$$

(25)

This piecewise function should be constrained as follows:

• It will become zero at the location of each support.
• The value of the function and its first derivative would become equal at both the left- and right-hand boundaries of the considered pieces.

The problem of fitting a smooth curve can be defined as Equation (26).

$$\underset{{\alpha }_{i,j}}{\min }\frac{1}{2}{\displaystyle \sum }_{i=1}^{\mathrm{ND}}{\parallel U_{fit}\left(X_s{}_i\right)-Y_s{}_i\parallel }^2+\frac{1}{2}\lambda {\displaystyle \sum }_{i=1}^{\mathrm{NS}}{\displaystyle \sum }_{j=1}^3{\parallel {\alpha }_{i,j}\parallel }^2$$

(26)

In Equation (26), the first term fits the curve to the measurements, while the second term, called the regularization term, smooths the resultant fitted curve. The value of the parameter $\lambda$ makes a balance, which should be optimized [31].

This optimization problem can be simplified as a constrained linear least-squares problem, which may be solved by the robust lsqlin function implemented in the MATLAB programming software. The constraints and the objective function are defined as linear equations in the format ${\mathrm{A}}_{\mathrm{cts}}\mathrm{X}={\mathrm{b}}_{\mathrm{cts}}$ and ${\mathrm{A}}_{\mathrm{obj}}\mathrm{X}={\mathrm{b}}_{\mathrm{obj}}$, respectively, where vector $\mathrm{X}$ is the vector of unknowns. Appendix A presents the method for calculating these matrices. Resultant matrices $A_{obj},b_{obj},A_{cts},$ and $b_{cts}$ are input into the lsqlin function using the “Interior-Point” algorithm [32].

The regularization parameter $\lambda$ should be optimized to balance fitting the measurement points with obtaining a smooth curve. The L-curve method is utilized for this optimization problem; the log-log plot of the residual of each term of the objective function for different values of parameter $\lambda$ is plotted. The resultant plot will have an L-shape. The value corresponding to the corner of this curve is the optimal point. This optimal value of $\lambda$ makes a balance between a smooth curve and a well-fitted curve [31].

Even after fitting a smooth curve to noisy data, some estimation error will remain in the calculation of the second derivative. The FRE is more sensitive to the second derivative calculation error in regions with small values from the unit moment curve; this occurs because the second derivative approaches small values in the denominator of Equation (5). To overcome this challenge, multiple measurements of influence line were recorded, and a weighted average of the results was used.

6.2. Application on a Numerical Model

To demonstrate the robustness of the proposed method, the approach is applied on a series of analytical models. Analytical models closely simulate the experimental test that was conducted in Section 6.3. For this purpose, a simply supported beam with a geometrical imperfection near the middle of the span is considered, as shown in Figure 8. Any normalized flexural rigidity value presented in this paper is achieved by using the constant parameter ${\mathrm{EI}}_0=\mathrm{1,268,322.8}(\mathrm{N}$-${\mathrm{mm}}^2)$, representing the intact flexural rigidity defined in Figure 8.

The RIL at both ends is calculated using finite element method. Equation (27) is used to create noisy RIL data:

$${\mathrm{U}}_{\mathrm{noisy}}={\mathrm{U}}_{\mathrm{noise}-\mathrm{free}}+\mathsf{\epsilon }·\mathrm{rms}\left({\mathrm{U}}_{\mathrm{noise}-\mathrm{free}}\right)·\mathrm{r}$$

(27)

In Equation (27), the parameter $\epsilon$ is the noise level, $\mathrm{rms}\left({\mathrm{U}}_{\mathrm{noise}-\mathrm{free}}\right)$ is the root-mean-squared of noise-free data, and vector $\mathrm{r}$ is a normal random vector. Vector $\mathrm{r}$ has a unit standard deviation, a mean equal to zero, and the same vector length as the ${\mathrm{U}}_{\mathrm{noise}-\mathrm{free}}$ vector. In this paper, calculated RILs are polluted with noise levels $\epsilon$ equal to 0.5%, 1%, 2%, 3%, and 4%. The 4% noise level is significantly higher than the noise level that is observed in the experiment presented in Section 6.3 and illustrates that the FRE is robust to this level.

Utilizing the proposed parametric approximation, the piecewise function is fitted to the artificial noisy measurements and the second derivative of the fitted curve is calculated. The resultant second derivatives are input into a weighted average equation:

$$\begin{array}{lll}& & E{I}_{ave.}=\frac{m_{{\theta }_A}\left(\xi \right)}{{\theta }_A^{″}\left(\xi \right)}·f_A+\frac{m_{{\theta }_B}\left(\xi \right)}{{\theta }_B^{″}\left(\xi \right)}·f_B,\\ \mathrm{where}& & \\ & & f_A={\left(\frac{L-\xi }{L}\right)}^2\mathrm{and}{f}_B={\left(\frac{\xi }{L}\right)}^2\end{array}$$

(28)

Equation (28) gives the weighted average of the calculated flexural rigidity from each RIL. Weights are selected in a way that calculated values for flexural rigidity are mostly affected by the resultant values from the closer RIL.

Figure 9 presents the results of the fitted curve of the support RILs at both ends (${\theta }_A$ of support A is closer to damaged region, in this example). The results of FRE are shown for different noise levels. Even in higher noise levels, the method gives acceptable results regarding flexural rigidity estimation.

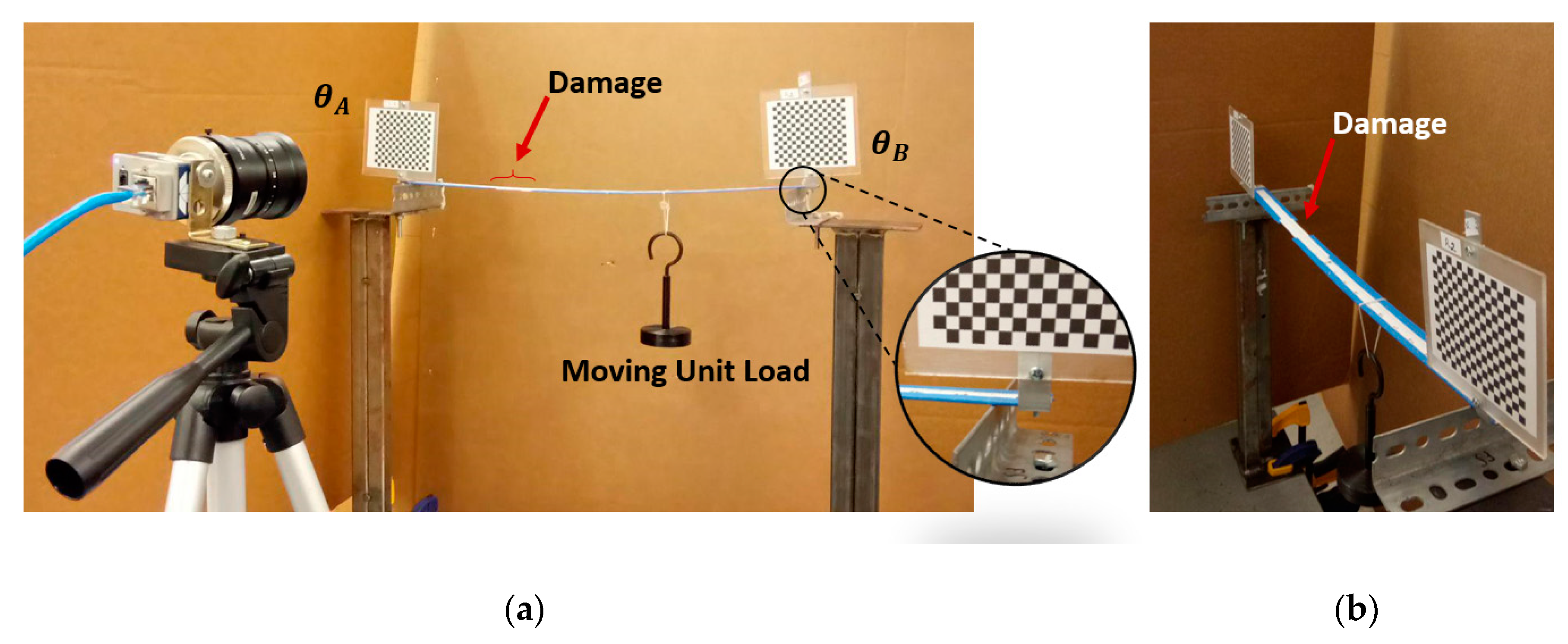
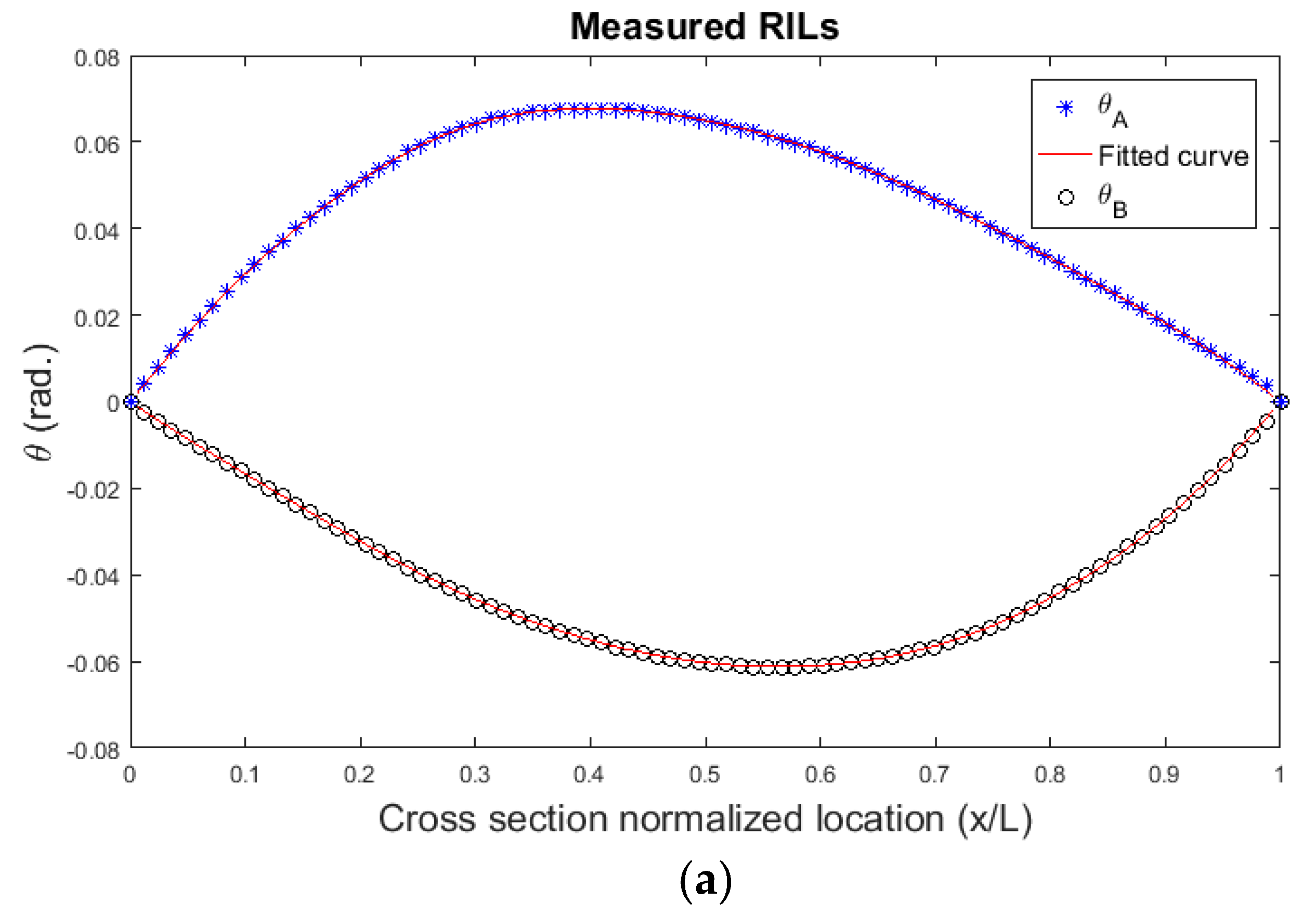
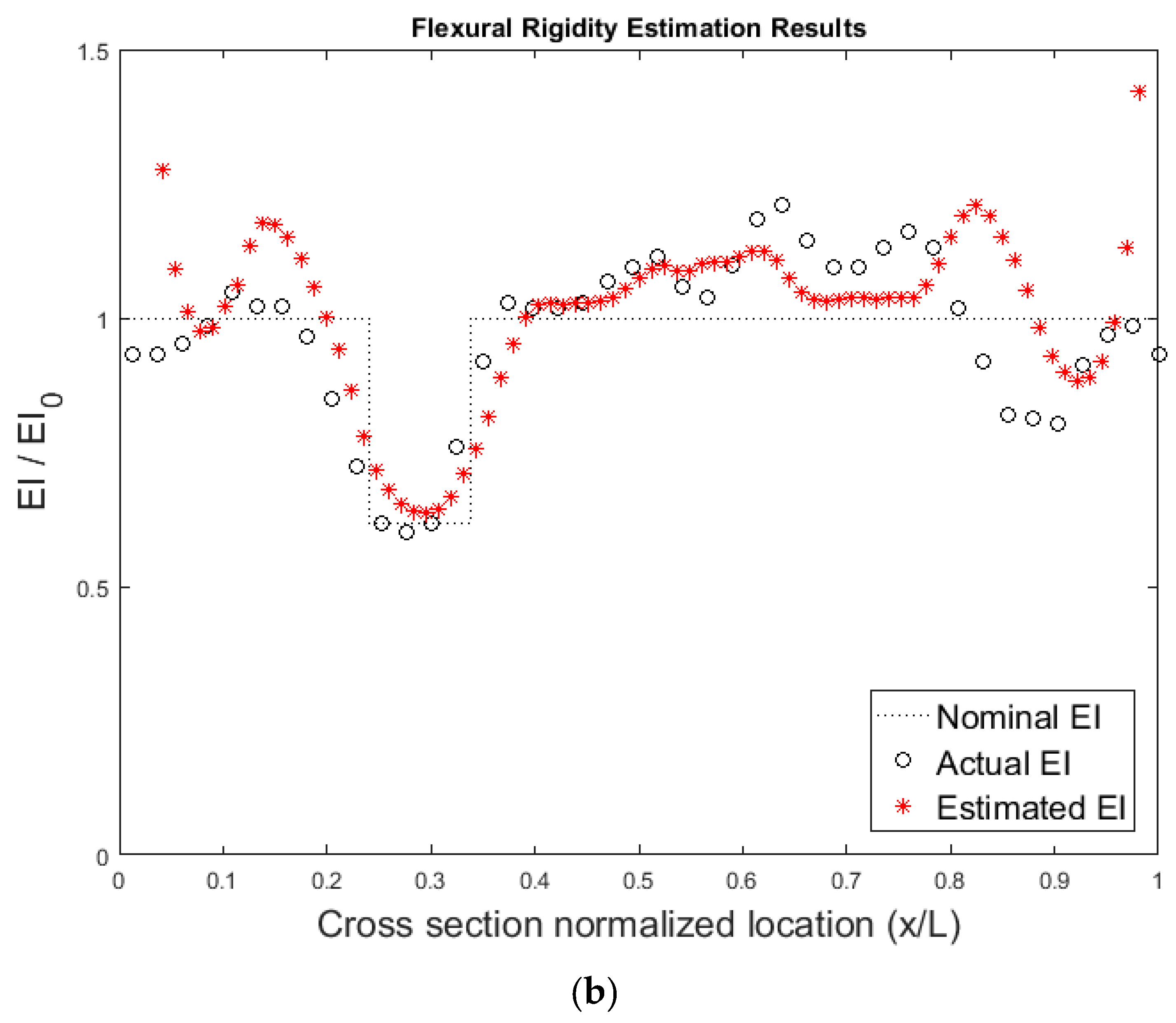
6.3. Application on a Real World System

A rectangular steel specimen with 1.5 mm nominal thickness and 25.4 mm nominal width is supported on the edge of an L-shape bracket in a simply supported manner, as illustrated in the Figure 10. A geometrical damage is created on this specimen by reducing the cross-section at the specified location in Figure 8. The geometry of this simply supported beam and considered nominal values for this experiment is illustrated in Figure 8.

The unit RIL was created by measuring rotations at both supports, caused by passing a hanging load of 0.5 kg weight over the beam span with the resolution of 6 mm distance (i.e., totally 81 measurements). Measurements were conducted in a static manner.

The rotation measurements are conducted by using a machine vision algorithm that is implemented in MATLAB and a robust camera calibration method that tracks the checkerboards that are attached to the ends of this beam. A camera with a resolution of $2592\times 2048$ pixels, a 75 mm lens, and $15\times 16$ checkerboards with $4.8\times 4.8$ mm squares are utilized for this experiment setup. The RILs at the ends of this simply supported beam are calculated by tracking the movements of the checkerboards corners while the load is moved along the beam span. Zeinali et al. [33] present the details of this robust measurement method. One advantage of a camera-based displacement estimation is that the location of the load is simultaneously estimated.

A quadratic piecewise function with 82 pieces and ${\lambda }_{opt}=0.0018$ is utilized for the curve fitting. Figure 11a shows the results of RIL measurements and curve fitting to these measurements. By taking the second derivative of the resultant fitted curves and substituting into Equation (28), the flexural rigidity of the specimen is estimated, and results are plotted in Figure 11b and labeled “Estimated EI”.

The geometry of this variable rectangular cross-section was measured using calipers with 1/100 mm accuracy at 5 mm increments. Assuming $\mathrm{E}=200\mathrm{GPa}$ and using the measured geometry, the flexural rigidity of this beam was calculated and plotted and labeled as “Actual EI” in Figure 11b. The nominal and actual flexural rigidities shown in Figure 11b differ due to small deviations in the specimen’s cross-section. Actual EI values are the reference values to which the estimated EI values from FRE results are compared.

Even in the presence of measurement noise and geometric deviations in intact sections of the specimen, the FRE method can quantify and localize the damage as a 40% reduction from 0.25 L to 0.34 L. Variations in the actual EI result from imperfections in the specimen; small variations in specimen thickness along the length can result in large departures from the nominal EI values. This result suggests that the FRE method can detect multiple reductions in EI that is caused by multiple damage locations.

7. Summary

This paper outlines a theoretical framework for the utilization of deformation influence lines calculated from a moving unit load for impairment detection on Euler-Bernoulli beams. The relationship between the second derivative of the deformation influence line (DIL or RIL) and the flexural rigidity of a beam is shown as the FRE equation. This novel formulation allows for both the location and quantification of damage directly from deformation data streams (i.e., deflection and rotation). Analytical and experimental studies have been presented to validate the FRE equation.

One of the common challenges that is outlined in the literature regarding influence-line-driven impairment detection is that increases in distance between the measurement and the damage location decrease these methods’ robustness; the FRE method overcomes these challenges and provides an estimate of flexural rigidity over the entire span based on a single measurement location. Comparing results from the FRE equation and the intact beam flexural rigidity curve gives the advantages of both localization and quantification of impairments, regardless of the locations of the measurements or the damaged zones.

The FRE formula is suitable for both statically determinate and indeterminate structures. Indeterminate structures require additional information in the form of an additional measurement of internal deformations for each degree of indeterminacy. All necessary expressions for integration of this additional information into the FRE formula are derived in explicit forms. Such forms may be useful for applications such as model updating.