Comparative Analysis of Triangulation Libraries for Modeling Large Point Clouds from Land and Their Infrastructures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Evaluated Libraries
2.1.1. LASTools
2.1.2. Fade2.5D
2.1.3. Triangle
2.1.4. CGAL
2.1.5. gDel3D
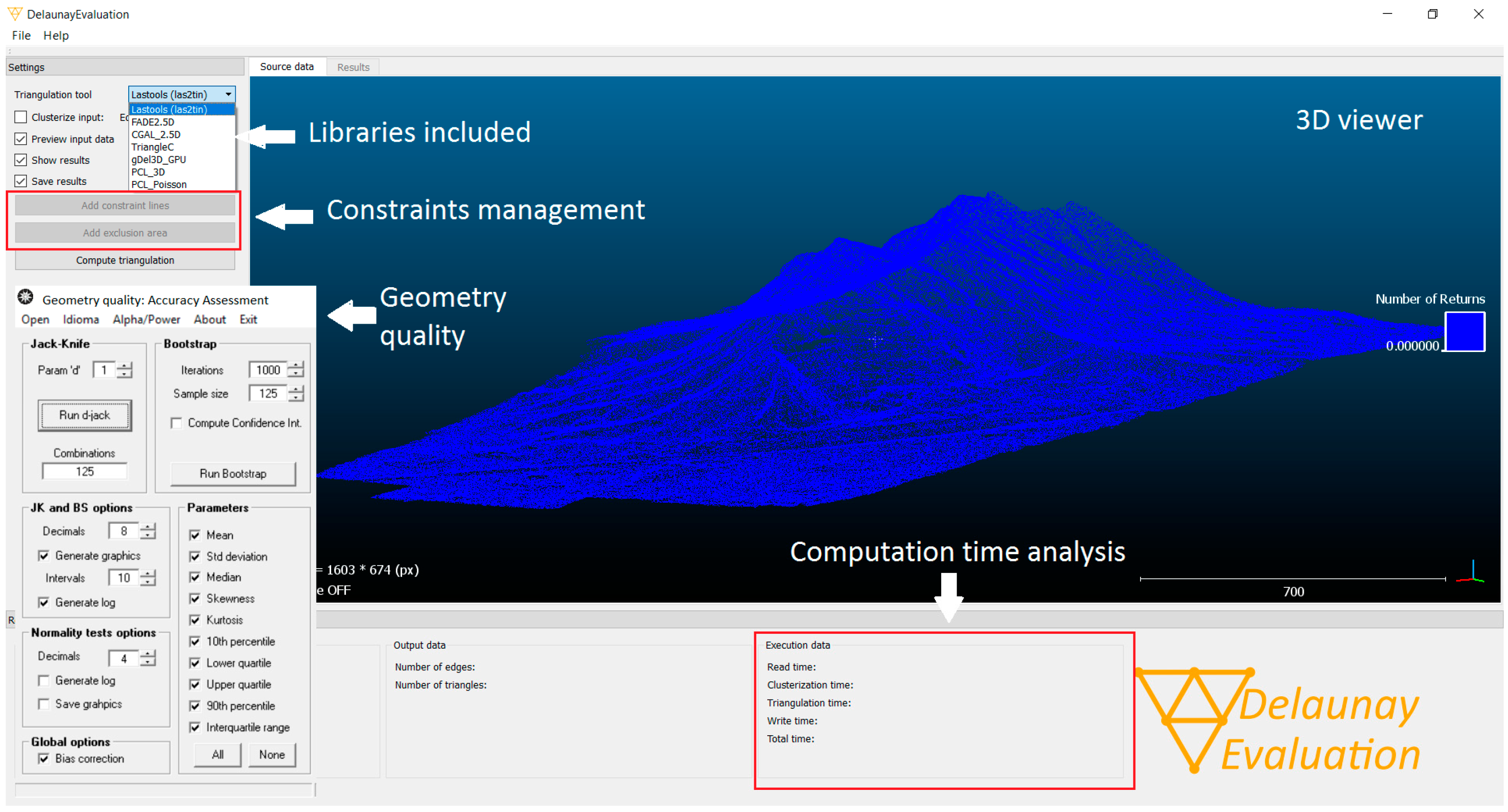
2.2. In-House Software
3. Results
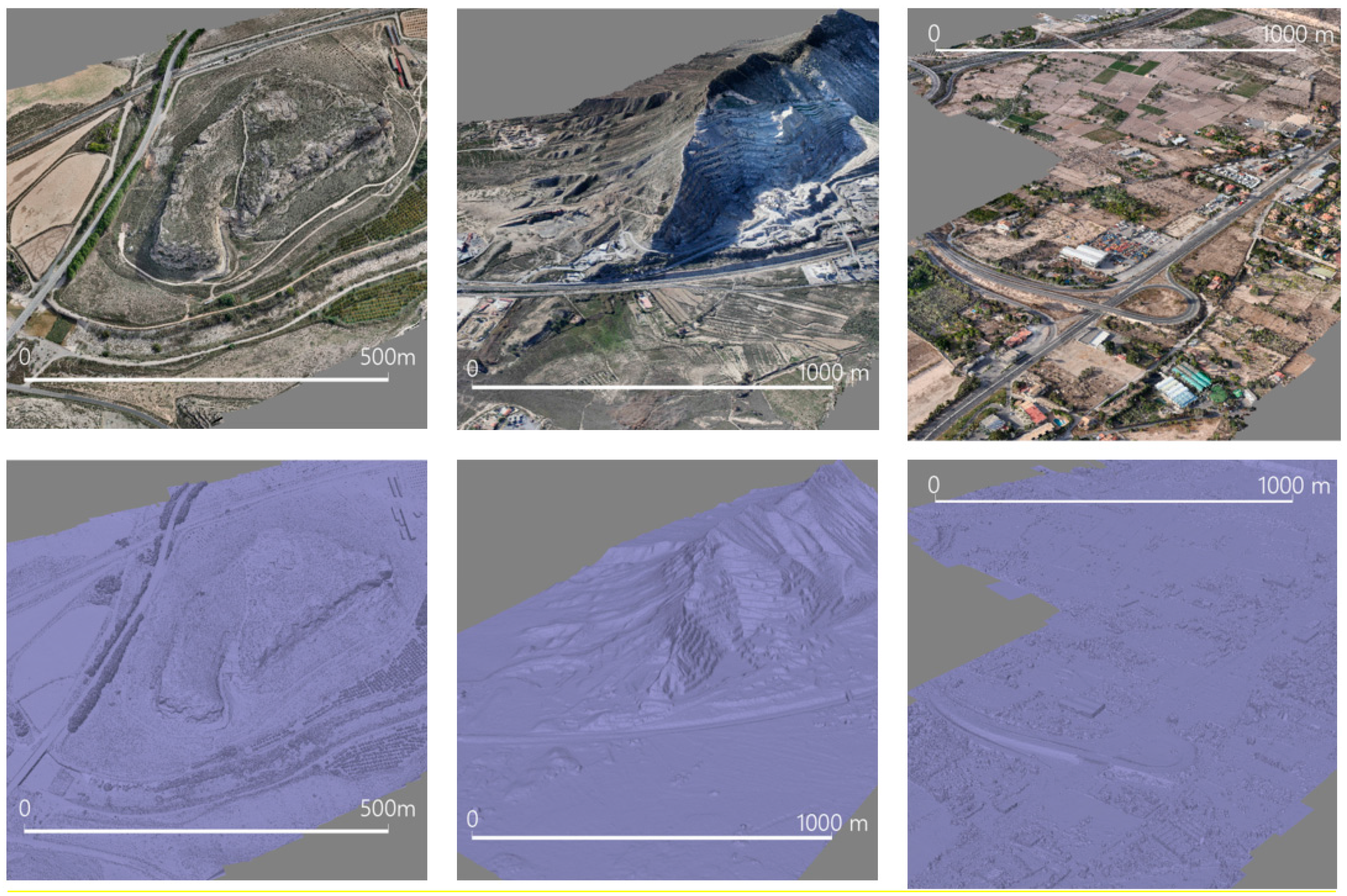
3.1. Study Cases Description
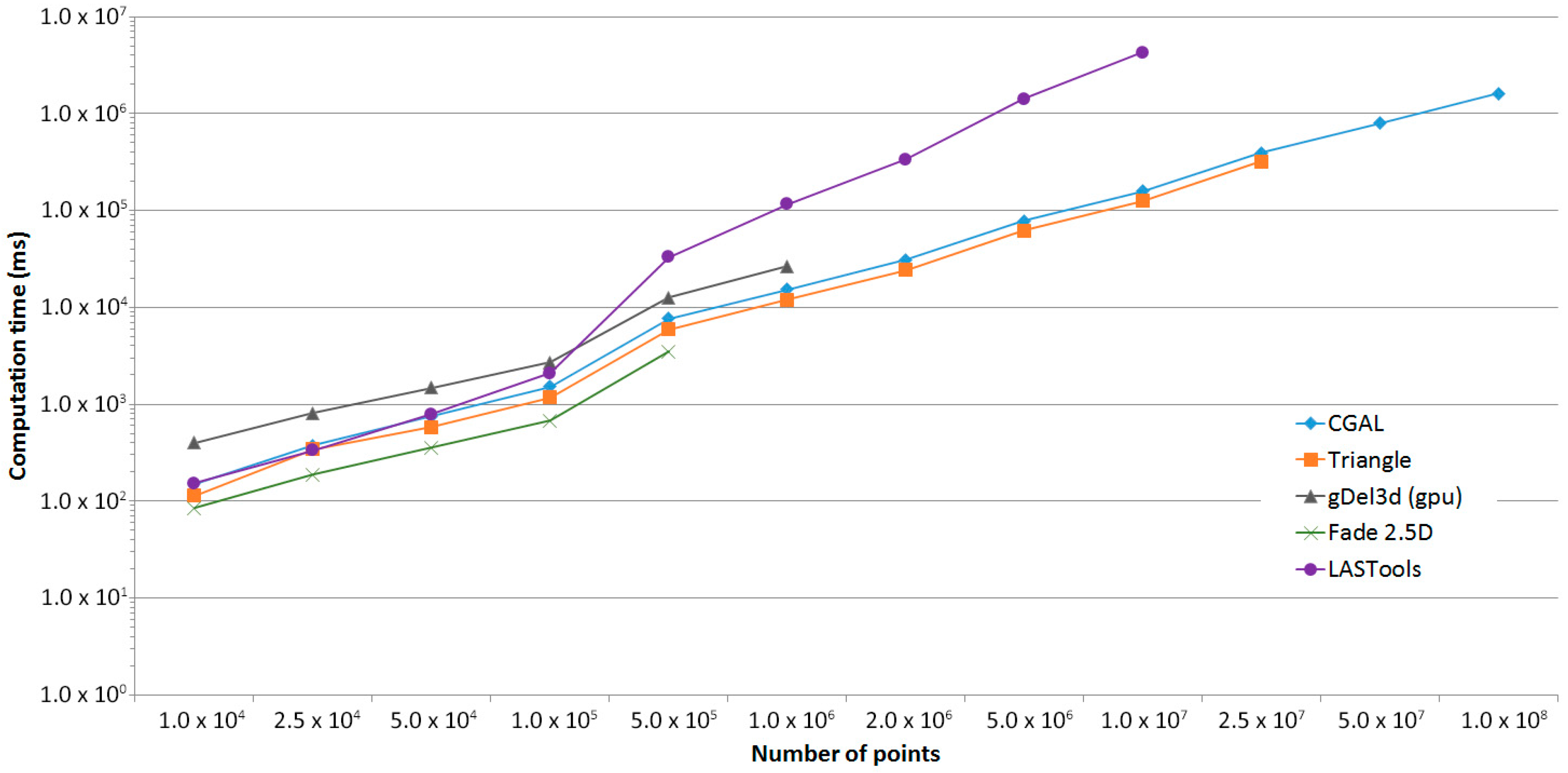
3.2. Computational Performance Analysis
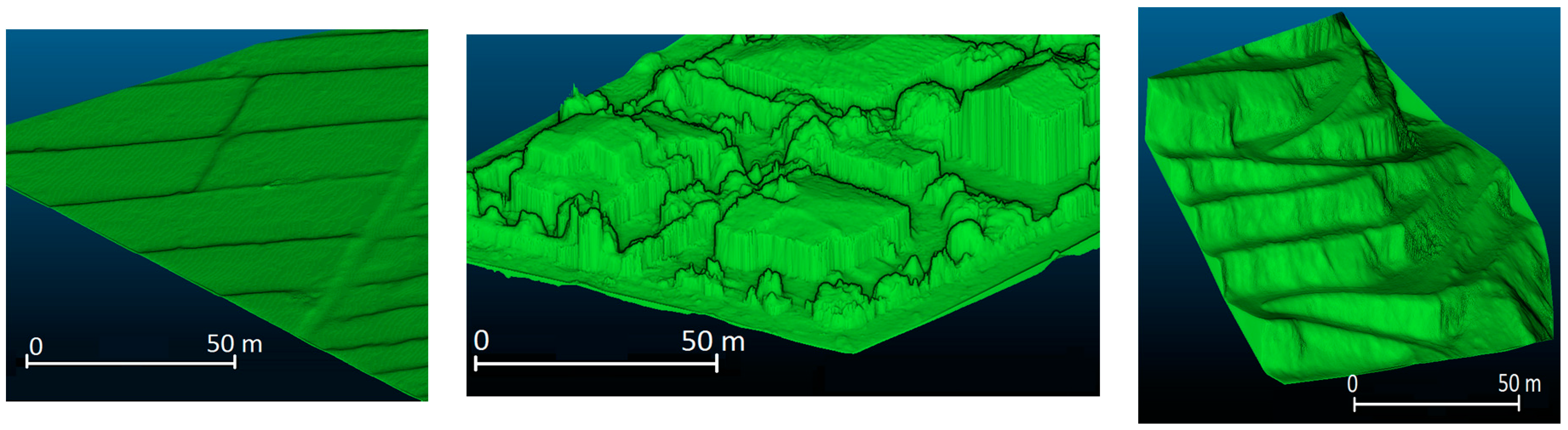
3.3. Geometry Quality Analysis
- Plain sample. Involves two areas of flat terrain with small natural obstacles corresponding to the study cases Zone 3 - Road and Zone 2 - Quarry.
- Buildings/walls sample. Encompasses two areas of buildings or the presence of vertical walls, which were drawn from the study cases Zone 3 - Road and Zone 1 - Archaeology, respectively.
- Slope sample. Involves two areas of steep terrain with considerable slope that were extracted from the study cases Zone 1 - Archaeology and Zone 2 - Quarry.
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, J.; Dowman, I.; Li, S.; Li, Z.; Madden, M.; Mills, J.; Paparoditis, N.; Rottensteiner, F.; Sester, M.; Toth, C.; et al. Information from imagery: ISPRS scientific vision and research agenda. ISPRS J. Photogramm. Remote Sens. 2016, 115, 3–21. [Google Scholar] [CrossRef]
- Vosselman, G.; Maas, H.-G. Airborne and Terrestrial Laser Scanning; Whittles: Dunbeath, UK, 2010; Volume 318. [Google Scholar]
- González, R.; Llamas, C.; Sánchez, M. Hyperspectral sensors integration in a RPAS investigation aerial platform. Aerosp. Sci. Technol. 2016, 58, 217–224. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Kraus, K. Photogrammetry: Geometry from Images and Laser Scans; Walter de Gruyter: Berlin, Germany, 2007. [Google Scholar]
- Egels, Y.; Kasser, M. Digital Photogrammetry; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Herrero-Huerta, M.; Felipe-García, B.; Belmar-Lizarán, S.; Hernández-López, D.; Rodríguez-Gonzálvez, P.; González-Aguilera, D. Dense canopy height model from a low-cost photogrammetric platform and LiDAR data. Trees 2016, 30, 1287–1301. [Google Scholar] [CrossRef]
- Haala, N.; Kada, M. An update on automatic 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2010, 65, 570–580. [Google Scholar] [CrossRef]
- Tang, X.; Liu, Y.; Zhang, J.; Kainz, W. Advances in Spatio-Temporal Analysis; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Bryan, B.A. High-performance computing tools for the integrated assessment and modelling of social-ecological systems. Environ. Model. Softw. 2013, 39, 295–303. [Google Scholar] [CrossRef]
- Yastikli, N.; Cetin, Z. Classification of LiDAR data with point based classification methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B3, 441–445. [Google Scholar] [CrossRef]
- González-Aguilera, D.; López-Fernández, L.; Rodriguez-Gonzalvez, P.; Guerrero, D.; Hernandez-Lopez, D.; Remondino, F.; Menna, F.; Nocerino, E.; Toschi, I.; Ballabeni, A.; et al. Development of an all-purpose free photogrammetric tool. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B6, 31–38. [Google Scholar] [CrossRef]
- Peucker, T.K.; Fowler, R.J.; Little, J.J.; Mark, D.M. The triangulated irregular network. In Proceedings of the Digital Terrain Models Symposium, St. Louis, MO, USA, 9–11 May 1978; pp. 96–103.
- Blandford, D.K.; Blelloch, G.E.; Cardoze, D.E.; Kadow, C. Compact representations of simplicial meshes in two and three dimensions. Int. J. Comput. Geom. Appl. 2005, 15, 3–24. [Google Scholar] [CrossRef]
- Blelloch, G.E.; Miller, G.L.; Hardwick, J.C.; Talmor, D. Design and implementation of a practical parallel Delaunay algorithm. Algorithmica 1999, 24, 243–269. [Google Scholar] [CrossRef]
- Chen, M.-B.; Chuang, T.-R.; Wu, J.-J. Parallel divide-and-conquer scheme for 2D Delaunay triangulation. Concurr. Comput. Pract. Exp. 2006, 18, 1595–1612. [Google Scholar] [CrossRef]
- Yoon, S.-E.; Lindstrom, P.; Pascucci, V.; Manocha, D. Cache-oblivious mesh layouts. In Proceedings of ACM SIGGRAPH 2005, Los Angeles, CA, USA, 31 July–4 August 2005; pp. 886–893.
- Isenburg, M.; Liu, Y.; Shewchuk, J.; Snoeyink, J. Streaming computation of Delaunay triangulations. In Proceedings of ACM SIGGRAPH 2006, Boston, MA, USA, 30 July–3 August 2006; pp. 1049–1056.
- Vitter, J.S. External memory algorithms and data structures: Dealing with massive data. ACM Comput. Surv. 2001, 33, 209–271. [Google Scholar] [CrossRef]
- Tu, T. A Scalable Database Approach to Computing Delaunay Triangulations. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2008. [Google Scholar]
- Isenburg, M.; Lindstrom, P. Streaming meshes. In Proceedings of the 16th IEEE Visualization Conference VIS 05, Minneapolis, MN, USA, 23–28 October 2005; pp. 231–238.
- Allègre, R.; Chaine, R.; Akkouche, S. A streaming algorithm for surface reconstruction. In Proceedings of the Symposium on Geometry Processing, Barcelona, Spain, 4–6 July 2007; pp. 79–88.
- Agarwal, P.K.; Arge, L.; Yi, K. I/O-Efficient Construction of Constrained Delaunay Triangulations. In Algorithms—ESA 2005, Proceedings of the 13th Annual European Symposium, Palma de Mallorca, Spain, 3–6 October 2005; Brodal, G.S., Leonardi, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 355–366. [Google Scholar]
- Isenburg, M. LAStools—Efficient Tools for LiDAR Processing. Available online: https://rapidlasso.com/lastools/ (accessed on 27 October 2016).
- Fade2.5D. Available online: http://www.geom.at/fade2d/html/ (accessed on 27 October 2016).
- Shewchuk, J.R. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. In Applied Computational Geometry towards Geometric Engineering, Proceedings of the FCRC’96 Workshop, WACG’96, Philadelphia, PA, USA, 27–28 May 1996; Selected Papers; Lin, M.C., Manocha, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 203–222. [Google Scholar]
- Shewchuk, J.R. Delaunay refinement algorithms for triangular mesh generation. Comput. Geom. 2002, 22, 21–74. [Google Scholar] [CrossRef]
- Triangle. Available online: http://www.cs.cmu.edu/~quake/triangle.html (accessed on 27 October 2016).
- Ruppert, J. A Delaunay refinement algorithm for quality 2-dimensional mesh generation. J. Algorithms 1995, 18, 548–585. [Google Scholar] [CrossRef]
- Lawson, C. Software for C1 surface interpolation. In Mathematical Software III; Rice, J.R., Ed.; Academic Press: New York, NY, USA, 1977; pp. 161–194. [Google Scholar]
- Yvinec, M. CGAL User and Reference Manual. CGAL 4.9—2D Triangulation; 2016. Available online: https://doc.cgal.org/latest/Triangulation_2/index.html (accessed on 29 December 2016).
- CGAL. Available online: http://www.cgal.org/ (accessed on 27 October 2016).
- Boissonnat, J.-D.; Devillers, O.; Pion, S.; Teillaud, M.; Yvinec, M. Triangulations in CGAL. Comput. Geom. 2002, 22, 5–19. [Google Scholar] [CrossRef]
- Ye, S.; Daniels, K. Hierarchical Delaunay Triangulation for Meshing. In Experimental Algorithms, Proceedings of the 10th International Symposium, SEA 2011, Kolimpari, Chania, Crete, Greece, 5–7 May 2011; Pardalos, P.M., Rebennack, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 54–64. [Google Scholar]
- Nanjappa, A. Delaunay Triangulation in R3 on the GPU. Ph.D. Dissertation, Visvesvaraya Technological University, Belgaum, India, 2012. [Google Scholar]
- Cao, T.-T.; Nanjappa, A.; Gao, M.; Tan, T.-S. A GPU accelerated algorithm for 3D Delaunay triangulation. In Proceedings of the 18th Meeting of the ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, San Francisco, CA, USA, 14–16 March 2014; pp. 47–54.
- gDEL3D. Available online: http://www.comp.nus.edu.sg/~tants/gdel3d.html (accessed on 27 October 2016).
- Shewchuk, R. Star splaying: An algorithm for repairing Delaunay triangulations and convex hulls. In Proceedings of the Twenty-First Annual Symposium on Computational Geometry, Pisa, Italy, 6–8 June 2005; pp. 237–246.
- Trimple Inpho. DTMaster. Available online: http://www.trimble.com/imaging/inpho.aspx (accessed on 27 October 2016).
- Rodríguez-Gonzálvez, P.; González-Aguilera, D.; Hernández-López, D.; González-Jorge, H. Accuracy assessment of airborne laser scanner dataset by means of parametric and non-parametric statistical methods. IET Sci. Meas. Technol. 2015, 9, 505–513. [Google Scholar] [CrossRef]


| Library | Gaussian Estimators | Robust Estimators | ||||
|---|---|---|---|---|---|---|
| Mean (m) | Standard Deviation (m) | Median (m) | P90–P10 (m) | P97.5–P2.5 (m) | ||
| “Buildings/walls” sample | CGAL | 0.0313 | ±0.5575 | 0.0000 | 0.4697 | 2.4175 |
| Fade2.5D | 0.0313 | ±0.5575 | 0.0000 | 0.4696 | 2.4175 | |
| LASTools | 0.0312 | ±0.5575 | 0.0000 | 0.4695 | 2.4176 | |
| Triangle | 0.0312 | ±0.5575 | 0.0000 | 0.4696 | 2.4176 | |
| “Plain” sample | CGAL | −0.0018 | ±0.0469 | 0.0000 | 0.0088 | 0.1336 |
| Fade2.5D | −0.0018 | ±0.0469 | 0.0000 | 0.0088 | 0.1335 | |
| LASTools | −0.0018 | ±0.0469 | 0.0000 | 0.0088 | 0.1335 | |
| Triangle | −0.0018 | ±0.0469 | 0.0000 | 0.0088 | 0.1336 | |
| “Slope” sample | CGAL | −0.0016 | ±0.0855 | 0.0000 | 0.0506 | 0.3159 |
| Fade2.5D | −0.0016 | ±0.0855 | 0.0000 | 0.0506 | 0.3159 | |
| LASTools | −0.0016 | ±0.0855 | 0.0000 | 0.0506 | 0.3159 | |
| Triangle | −0.0016 | ±0.0855 | 0.0000 | 0.0506 | 0.3159 | |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez-Fernandez, L.; Rodriguez-Gonzalvez, P.; Hernandez-Lopez, D.; Ortega-Terol, D.; Gonzalez-Aguilera, D. Comparative Analysis of Triangulation Libraries for Modeling Large Point Clouds from Land and Their Infrastructures. Infrastructures 2017, 2, 1. https://doi.org/10.3390/infrastructures2010001
Lopez-Fernandez L, Rodriguez-Gonzalvez P, Hernandez-Lopez D, Ortega-Terol D, Gonzalez-Aguilera D. Comparative Analysis of Triangulation Libraries for Modeling Large Point Clouds from Land and Their Infrastructures. Infrastructures. 2017; 2(1):1. https://doi.org/10.3390/infrastructures2010001
Chicago/Turabian StyleLopez-Fernandez, Luis, Pablo Rodriguez-Gonzalvez, David Hernandez-Lopez, Damian Ortega-Terol, and Diego Gonzalez-Aguilera. 2017. "Comparative Analysis of Triangulation Libraries for Modeling Large Point Clouds from Land and Their Infrastructures" Infrastructures 2, no. 1: 1. https://doi.org/10.3390/infrastructures2010001
APA StyleLopez-Fernandez, L., Rodriguez-Gonzalvez, P., Hernandez-Lopez, D., Ortega-Terol, D., & Gonzalez-Aguilera, D. (2017). Comparative Analysis of Triangulation Libraries for Modeling Large Point Clouds from Land and Their Infrastructures. Infrastructures, 2(1), 1. https://doi.org/10.3390/infrastructures2010001








