Static Loading Tests and Finite Element Analysis of Phosphogypsum Steel Truss Concrete Slabs
Abstract
1. Introduction
2. Experimental Overview
2.1. Material Properties and Specimen Design
2.2. Test Program and What to Measure
3. Experimental Observations and Result Analysis
3.1. Experimental Observations
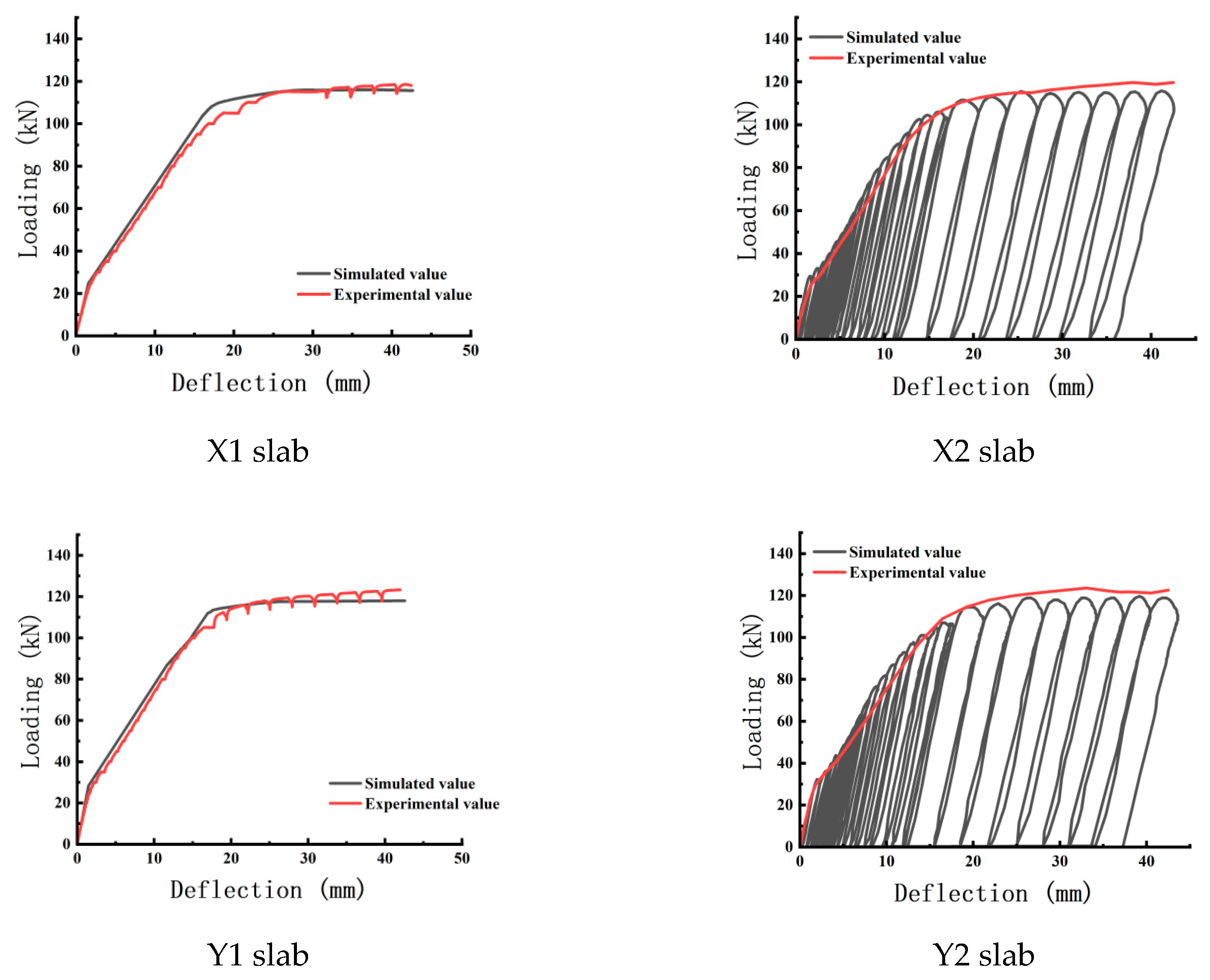
3.2. Test and Simulated Load Deflection Curves
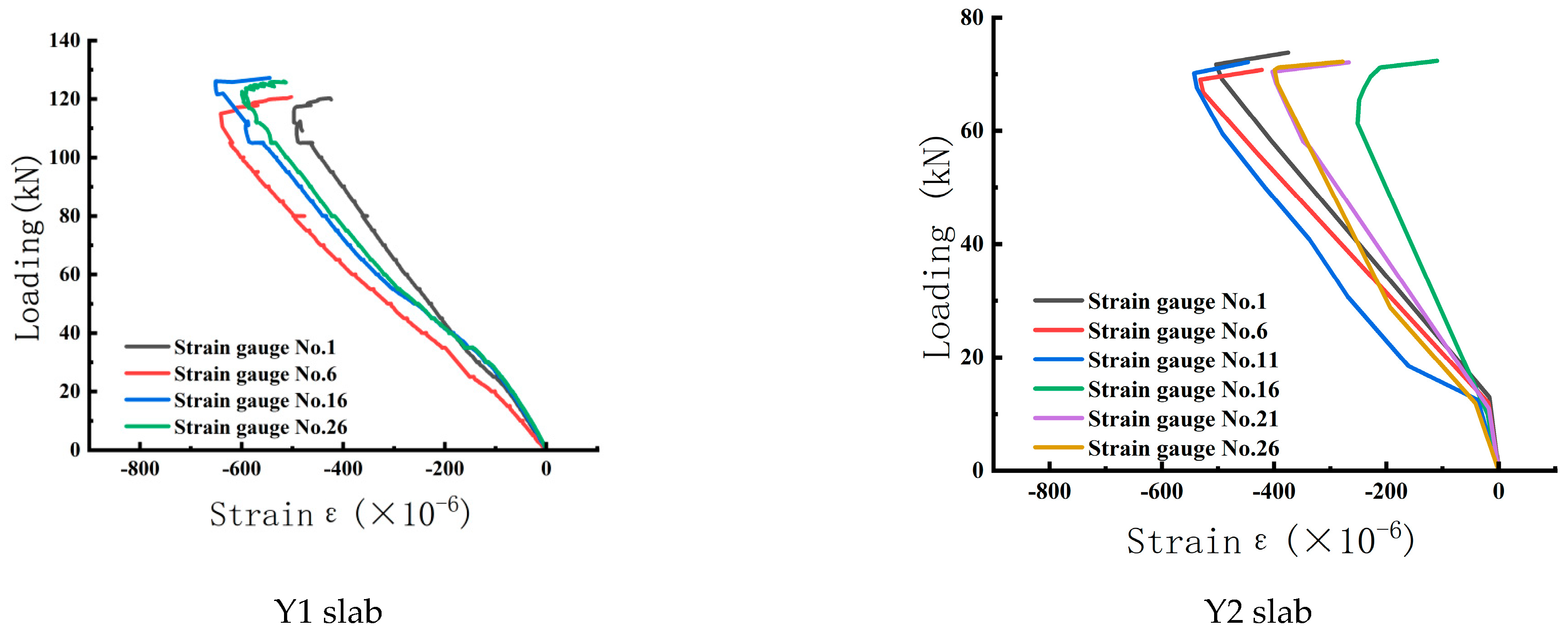
3.3. Load Strain Curves of Reinforcing Steel
4. Finite Element Analysis
4.1. Steel Model
4.2. Concrete Model
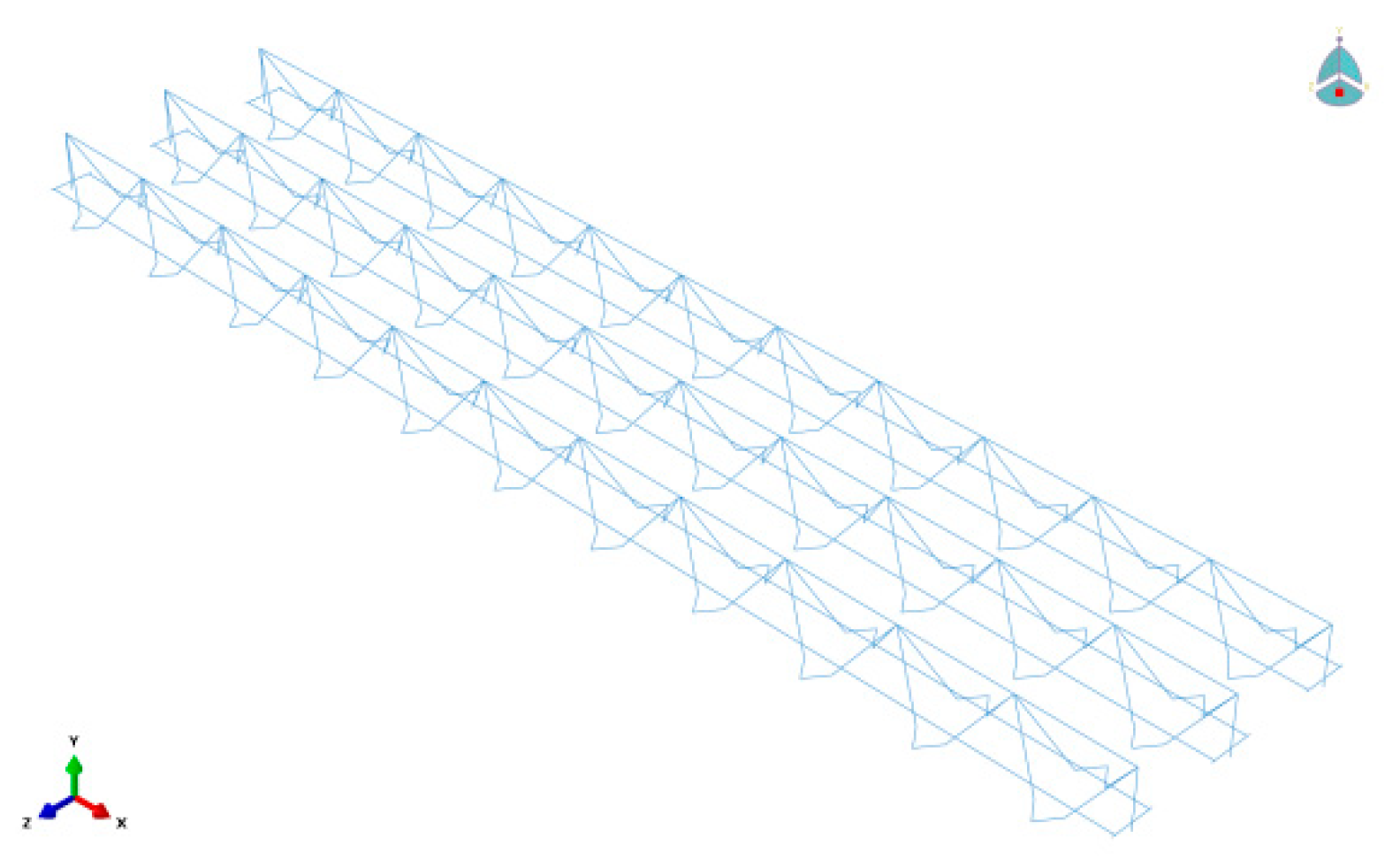
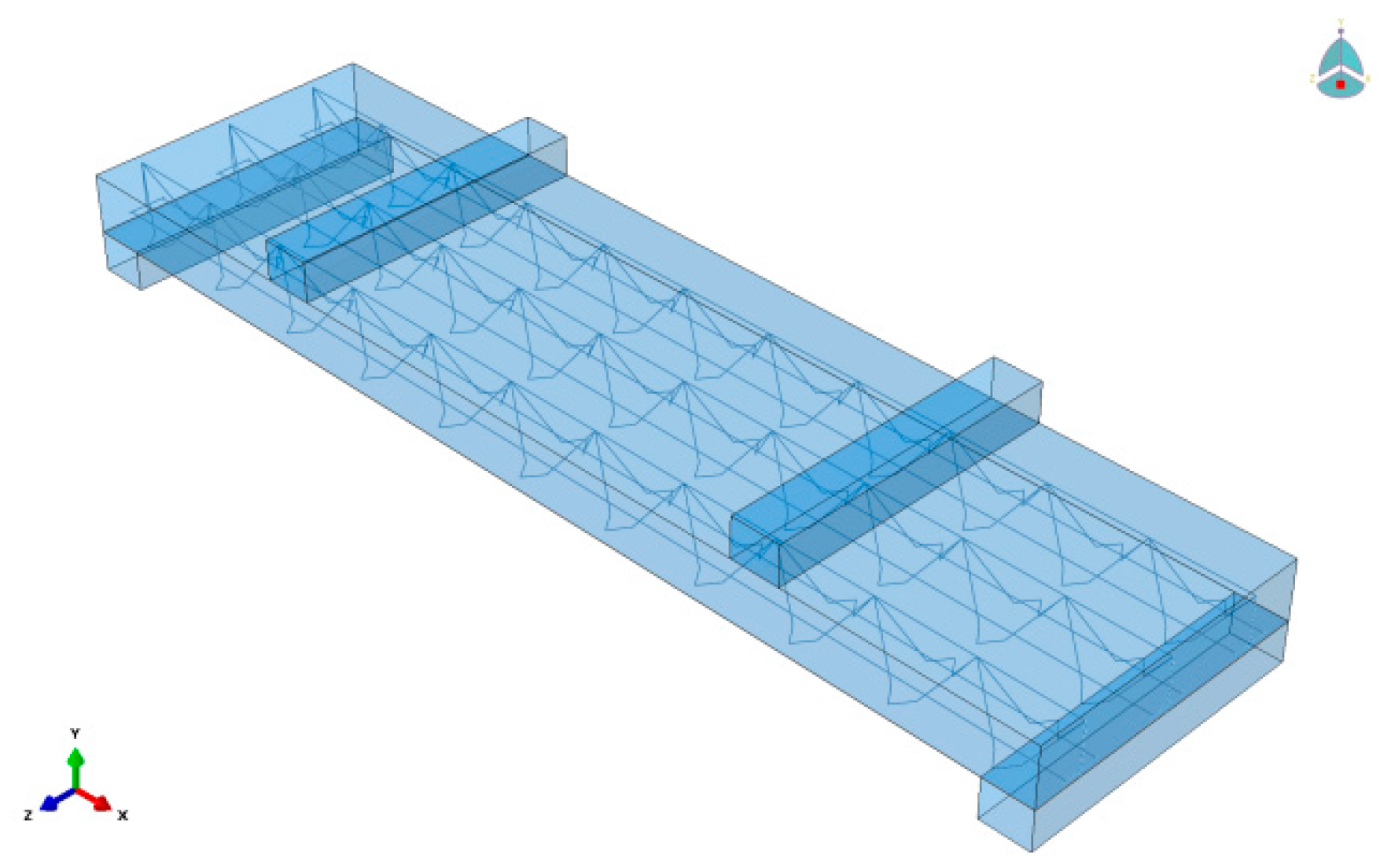
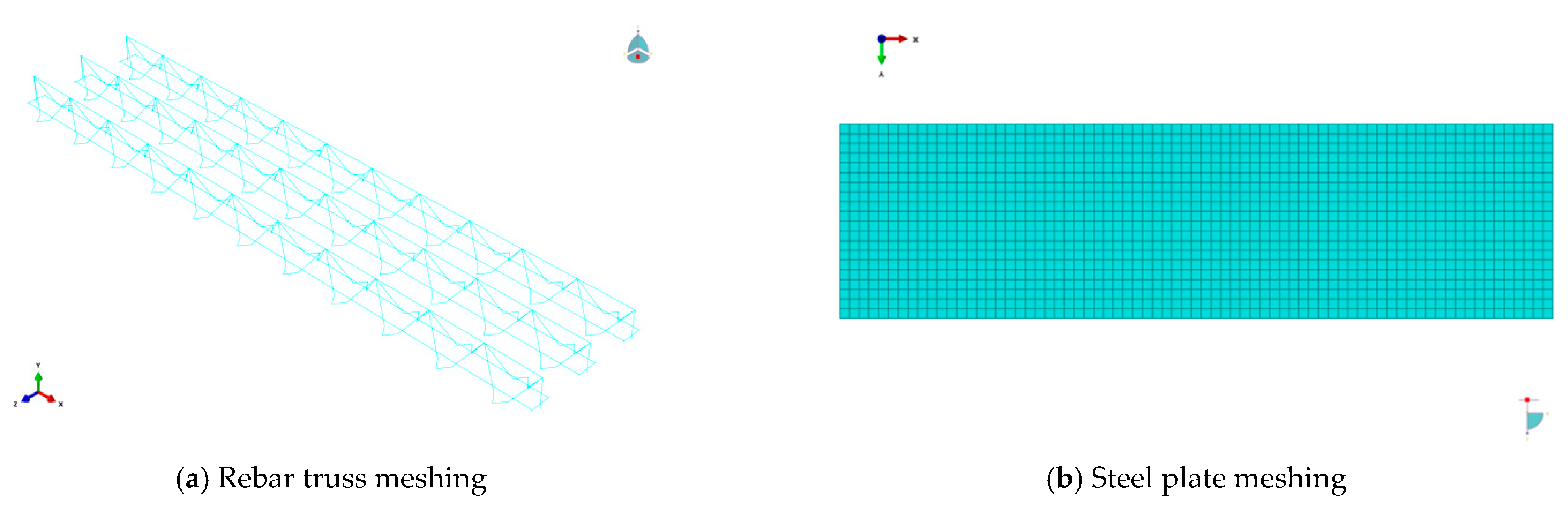
4.3. Grid Division and Mutual Setting of Roles
4.4. Comparison of Load-Deflection Curves
4.5. Analysis of Finite Element Simulation Contour Plots
5. Conclusions
- 1.
- Ultimate Capacity Preservation: The incorporation of 2% PG content resulted in statistically insignificant reductions in key mechanical properties, with the compressive strength decreasing by 4.3%, flexural capacity by 2.6%, and elastic modulus by 1.2%. These minimal reductions demonstrate that the fundamental structural integrity and ultimate load-bearing capacity remain substantially uncompromised, confirming the structural viability of PG concrete for primary load-bearing applications in building construction.
- 2.
- Pronounced Effect on Serviceability Performance: A more notable influence was observed on parameters governing serviceability limit states. The 10–12% reduction in cracking load suggests that PG incorporation affects the microstructural integrity at early loading stages, leading to earlier crack initiation. However, the strong correlation (R2 = 0.89) between pre-yield stiffness and concrete strength implies that the overall deformation behavior post cracking remains predictable and controlled.
- 3.
- Robustness of Numerical Modeling: The finite element model developed in ABAQUS2023 demonstrated a high degree of accuracy in simulating the structural response, with a 90% correlation in load-deflection curves and an 82% similarity in failure modes. The discrepancies observed (primarily in crack propagation and ultimate load prediction, with <12% deviation) are largely attributable to the idealized modeling of the PG concrete interface and the simplified assumptions in the concrete damage plasticity parameters. This highlights the model’s utility for design-stage prediction while underscoring the need for more sophisticated material constitutive laws to capture localized failure mechanisms accurately.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jalali, J.; Gaudin, P.; Capiaux, H.; Ammar, E.; Lebeau, T. Fate and transport of metal trace elements from phosphogypsum piles in Tunisia and their impact on soil bacteria and wild plants. Ecotoxicol. Environ. Saf. 2019, 174, 12–25. [Google Scholar] [CrossRef] [PubMed]
- Lütke, S.F.; Oliveira, M.L.S.; Silva, L.F.O.; Cadaval, T.R.S.; Dotto, G.L. Nanominerals assemblages and hazardous elements assessment in phosphogypsum from an abandoned phosphate fertilizer industry. Chemosphere 2020, 256, 127138. [Google Scholar] [CrossRef] [PubMed]
- Meskini, S.; Mechnou, I.; Benmansour, M.; Remmal, T.; Samdi, A. Environmental investigation on the use of a phosphogypsum-based road material: Radiological and leaching assessment. J. Environ. Manag. 2023, 345, 118597. [Google Scholar] [CrossRef] [PubMed]
- Baolin, K.; Qin, Z.; Xianhai, L.; Zhihui, S. Adsorption and solidification of cadmium by calcium sulfate dihydrate (gypsum) in an aqueous environment: A dispersion-corrected DFT and ab initio molecular dynamics study. Phys. Chem. Chem. Phys. 2022, 24, 9521–9533. [Google Scholar] [CrossRef]
- Wu, F.; Ren, Y.; Qu, G.; Liu, S.; Chen, B.; Liu, X.; Zhao, C.; Li, J. Utilization path of bulk industrial solid waste: A review on the multi-directional resource utilization path of phosphogypsum. J. Environ. Manag. 2022, 313, 114957. [Google Scholar] [CrossRef]
- Bilal, E.; Bellefqih, H.; Bourgier, V.; Mazouz, H.; Dumitraş, D.-G.; Bard, F.; Laborde, M.; Caspar, J.P.; Guilhot, B.; Iatan, E.-L.; et al. Phosphogypsum circular economy considerations: A critical review from more than 65 storage sites worldwide. J. Clean. Prod. 2023, 414, 137561. [Google Scholar] [CrossRef]
- Garbaya, H.; Jraba, A.; Khadimallah, M.A.; Elaloui, E. The Development of a New Phosphogypsum-Based Construction Material: A Study of the Physicochemical, Mechanical and Thermal Characteristics. Materials 2021, 14, 7369. [Google Scholar] [CrossRef]
- Shuhua, L.; Lu, W.; Baoying, Y. Effect of modified phosphogypsum on the hydration properties of the phosphogypsumbased supersulfated cement. Construct. Build. Mater. 2019, 214, 9–16. [Google Scholar]
- Meng, W.; Dong, Y. Mechanical properties and chemical microscopic characteristics of all-solid-waste composite cementitious materials prepared from phosphogypsum and granulated blast furnace slag. Mater. Today Commun. 2024, 41, 110809. [Google Scholar] [CrossRef]
- Akfas, F.; Elghali, A.; Aboulaich, A.; Munoz, M.; Benzaazoua, M.; Bodinier, J.L. Exploring the potential reuse of phosphogypsum: A waste or a resource? Sci. Total Environ. 2024, 908, 168196. [Google Scholar] [CrossRef]
- Wang, Z.; Shui, Z.; Sun, T.; Li, X.; Zhang, M. Recycling utilization of phosphogypsum in eco excess-sulphate cement: Synergistic effects of metakaolin and slag additives on hydration, strength and microstructure. J. Clean. Prod. 2022, 358, 131901. [Google Scholar] [CrossRef]
- Chernysh, Y.; Yakhnenko, O.; Chubur, V.; Roubik, H. Phosphogypsum recycling: A review of environmental issues, current trends, and prospects. Appl. Sci. 2021, 11, 1575. [Google Scholar] [CrossRef]
- Romero-Hermida, M.I.; Borrero-López, A.M.; Alejandre, F.J.; Flores-Alés, V.; Santos, A.; Franco, J.M.; Esquivias, L. Phosphogypsum waste lime as a promising substitute of commercial limes: A rheological approach. Cem. Concr. Compos. 2019, 95, 205–216. [Google Scholar] [CrossRef]
- Kutymbek, N.; Musabekov, K.; Yestayev, K.; Yessengeldiyeva, P.; Omarova, G. Evaluating the efficacy of phosphogypsum as a soil amendment for enhancing fertility in compacted gray-earth soils of Kazakhstan during comprehensive land reclamation. Int. J. Des. Nat. Ecodyn. 2023, 18, 529–536. [Google Scholar] [CrossRef]
- Xiang, H.; Dong, C.; Wu, H.; Hu, X.; Gao, B.; Fan, Z.; Wan, J.; Ma, Y.; Guan, H. Study on Harmless Treatment and Performance of Phosphogypsum-Based Inorganic Cementing Material. Infrastructures 2025, 10, 196. [Google Scholar] [CrossRef]
- Ennaciri, Y.; Bettach, M.; El Alaoui-Belghiti, H. Phosphogypsum conversion into calcium fluoride and sodium sulfate. Ann. Chim.-Sci. Matér. 2020, 44, 407–412. [Google Scholar] [CrossRef]
- Gawatre, D.W. Advantages of Waste–Phosphogypsum in Concrete. Int. J. Sci. Res. 2013, 2, 2. [Google Scholar] [CrossRef]
- Al Qadi, A.N.S.; Khedaywi, T.S.; Haddad, M.A.; AlRababa’ah, O.A. Investigating the effect of olive husk ash on the properties of asphalt concrete mixture. Ann. Chim.-Sci. Matér. 2021, 45, 11–15. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, X.; Pan, H.; Yang, X.; Zhang, X.; Lyu, Y.; Liao, W.; Shui, W.; Wu, J.; Xu, M.; et al. Investigating effects of phosphogypsum disposal practices on the environmental performance of phosphate fertilizer production using emergy analysis and carbon emission amounting: A case study from China. J. Clean. Prod. 2023, 409, 137248. [Google Scholar] [CrossRef]
- Chen, G.; Yao, N.; Ye, Y.C.; Fu, F.H.; Hu, N.Y.; Zhang, Z. Influence of partial cement substitution by ground blast furnace slag on the mechanical properties of phosphogypsum cemented backfill. Environ. Sci. Pollut. Res. 2023, 30, 102972–102985. [Google Scholar] [CrossRef]
- Wei, P.; Zeng, H.; Yang, J.; Zhang, H.; Chu, H.; Zhang, F.; Jiang, L. Preparation and properties of vegetation-compatible concrete using phosphogypsum. Concrete 2024, 1, 169–173. [Google Scholar]
- Kuang, Y.; Li, J.; Ding, Q.; Wang, J.; Shi, J.; Xie, P. Influence of cement on foam concrete with high-content phosphogypsum. New Build. Mater. 2023, 50, 145–149. [Google Scholar]
- Calderon-Morales, B.R.S.; García-Martínez, A.; Pineda, P.; García-Tenorio, R. Valorization of phosphogypsum in cement-based materials: Limits and potential in eco-efficient construction. J. Build. Eng. 2021, 44, 102506. [Google Scholar] [CrossRef]
- Koвaлeв, Я.H.; Яглoв, B.H.; Чиcтoвa, T.A.; Гиpинcкий, B.B. Пpимeнeниe φocφoгипca в дopoжнoм cтpoитeльcтвe. Hayкa Texникa 2021, 6, 493–498. [Google Scholar]
- Vybranets, Y.; Vikhot, S. Spatial calculation of metal truss structure in joint work with reinforced concrete slab. In Proceedings of the International Scientific Conference EcoComfort and Current Issues of Civil Engineering, Lviv, Ukraine, 14–16 September 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- De Seixas Leal, L.A.A.; De Miranda Batista, E.J.S.C. Composite floor system with cold-formed trussed beams and prefabricated concrete slab: Selected and extended contribution of SDSS 2019. Steel Constr. 2020, 13, 12–21. [Google Scholar] [CrossRef]
- Gholamhoseni, A. Experimental and finite element study of ultimate strength of continuous composite concrete slabs with steel decking. Int. J. Adv. Struct. Eng. 2018, 10, 85–97. [Google Scholar] [CrossRef]
- Zhang, H.; Geng, Y.; Wang, Y.; Wang, Q. Long-term behavior of continuous composite slabs made with 100% fine and coarse recycled aggregate. Eng. Struct. 2020, 212, 110464. [Google Scholar] [CrossRef]
- Arrayago, I.; Ferrer, M.; Marimon, F.; Real, E.; Mirambell, E. Experimental investigation on ferritic stainless steel composite slabs. Eng. Struct. 2018, 174, 538–547. [Google Scholar] [CrossRef]
- Francavilla, B.; Latour, M.; Rizzano, G. Experimental and numerical analyses of steel-concrete composite floors. Open Civ. Eng. J. 2020, 14, 163. [Google Scholar] [CrossRef]
- Uy, B.; Bradford, M.A. Composite action of structural steel beams and precast concrete slabs for the flexural strength limit state. Aust. J. Struct. Eng. 2007, 7, 123–133. [Google Scholar] [CrossRef]
- Jin, X. Performance optimization of recycled aggregate concrete with basalt fibers using Box-Behnken response surface methodology. Brick Tile 2024, 4, 39–43. [Google Scholar] [CrossRef]
- Shen, W.; Liu, Y.; Wu, M.; Zhang, D.; Du, X.; Zhao, D.; Xu, G.; Zhang, B.; Xiong, X. Ecological carbonated steel slag pervious concrete prepared as a key material of sponge city. J. Clean. Prod. 2020, 256, 120244. [Google Scholar] [CrossRef]
- Sha, L.; Zhang, A. Static Load Test and Finite Element Analysis of Phosphogypsum Concrete Composite Slabs. Buildings 2025, 15, 1122. [Google Scholar] [CrossRef]

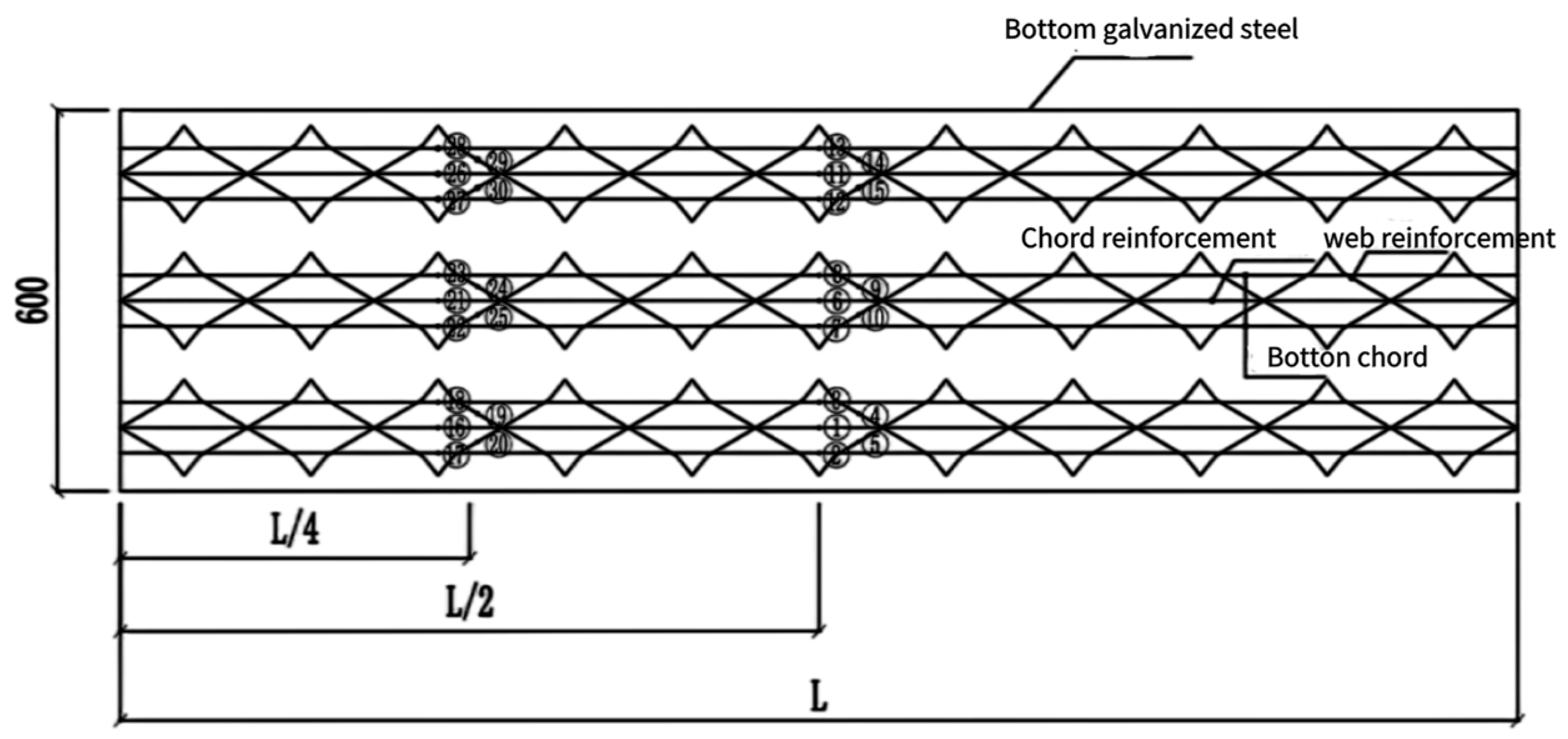
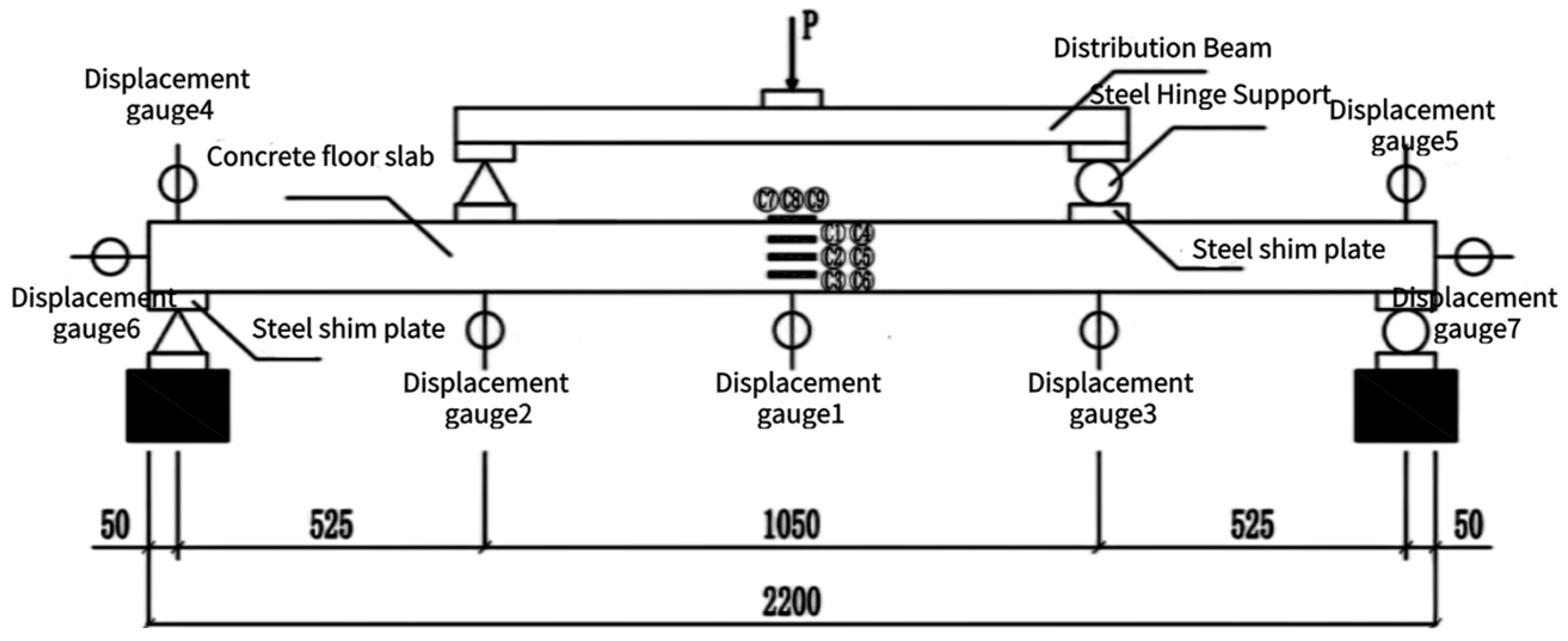


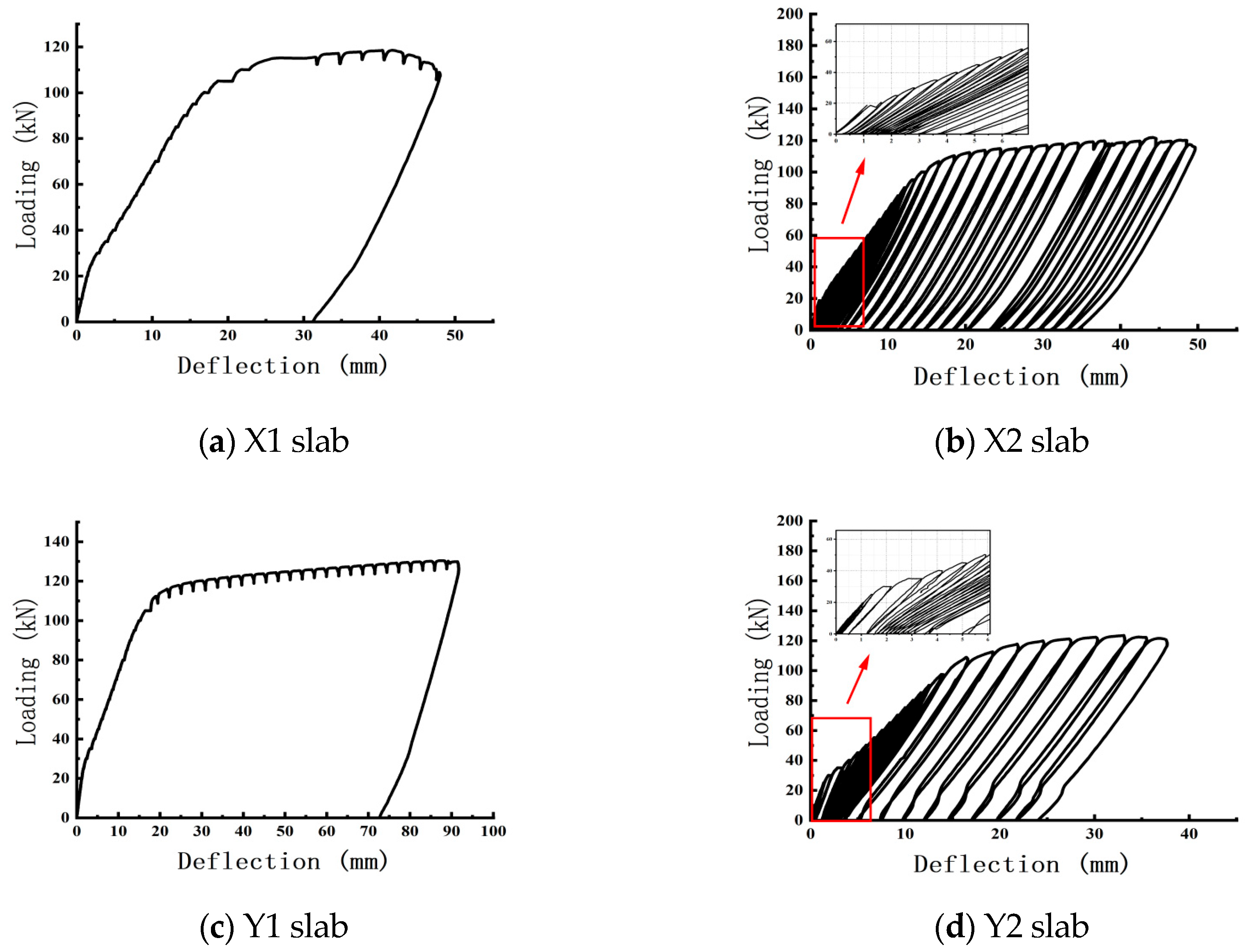
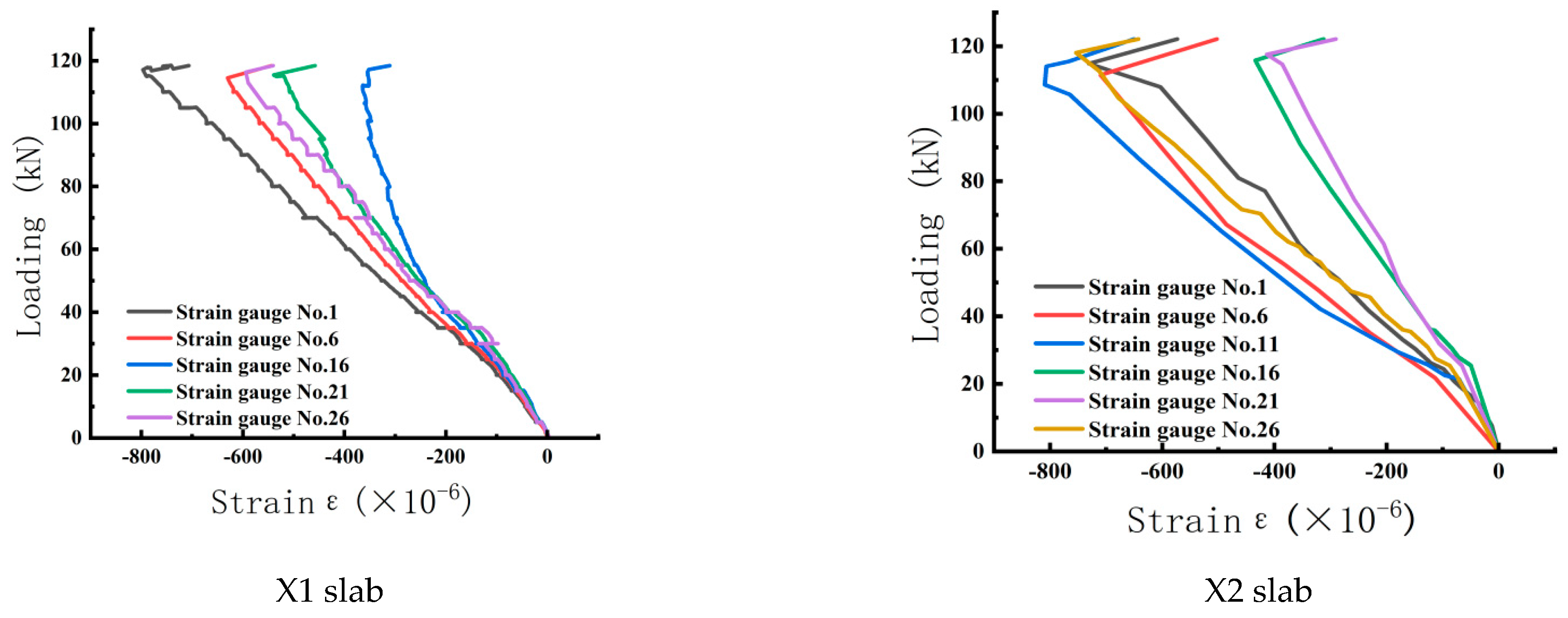



| Slab Number | Concrete Grade | Truss Height/mm | Top Chord, Web, Bottom Chord Diameter/mm | Phosphogypsum Dosage | Loading Method |
|---|---|---|---|---|---|
| X1 | C40 | 90 | 10, 5, 10 | 0 | Monotonic loading |
| X2 | C40 | 90 | 10, 5, 10 | 0 | Repeated loading |
| Y1 | C40 | 90 | 10, 5, 10 | 2% | Monotonic loading |
| Y2 | C40 | 90 | 10, 5, 10 | 2% | Repeated loading |
| Plate Number | Cracking Load | Normal Use Limit Load | Yield Load | Ultimate Load | ||||
|---|---|---|---|---|---|---|---|---|
| X1 | 23.54 | 18.68 | 70.26 | 55.76 | 95.20 | 75.56 | 118.45 | 94.01 |
| X2 | 24.96 | 19.81 | 80.08 | 63.56 | 94.57 | 75.06 | 119.58 | 94.90 |
| Y1 | 25.40 | 20.16 | 77.08 | 61.17 | 94.78 | 75.22 | 123.30 | 97.86 |
| Y2 | 24.86 | 19.73 | 77.22 | 61.29 | 97.11 | 77.07 | 121.81 | 96.67 |
| Plate Number | Cracking Load (kN/mm) | Normal Use Limit Load (kN/mm) | Yield Load (kN/mm) | Ultimate Load (kN/mm) | ||||
|---|---|---|---|---|---|---|---|---|
| Flexure | Stiffness | Flexure | Stiffness | Flexure | Stiffness | Flexure | Stiffness | |
| X1 | 1.71 | 13.77 | 10.50 | 6.69 | 15.44 | 6.17 | 42.00 | 2.82 |
| X2 | 1.63 | 15.31 | 10.50 | 7.63 | 12.97 | 7.29 | 42.00 | 2.85 |
| Y1 | 1.69 | 15.03 | 10.50 | 7.34 | 14.19 | 6.68 | 42.00 | 2.94 |
| Y2 | 1.39 | 17.88 | 10.50 | 7.35 | 13.84 | 7.02 | 42.00 | 2.90 |
| Plate Number | Cracking Load (kN) | Use Limit Load (kN) | Yield Load (kN) | Ultimate Load (kN) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test Value | Simulated Value | Error | Test Value | Simulated Value | Error | Test Value | Simulated Value | Error | Test Value | Simulated Value | Error | |
| X1 | 23.54 | 24.78 | 5.27 | 70.26 | 76.80 | 9.31 | 95.20 | 107.94 | 13.38 | 118.45 | 115.58 | 2.42 |
| X2 | 24.96 | 28.32 | 13.46 | 80.08 | 82.13 | 2.63 | 94.57 | 101.45 | 7.27 | 119.58 | 116.61 | 2.48 |
| Y1 | 25.40 | 28.17 | 10.90 | 77.08 | 79.65 | 3.33 | 94.78 | 112.48 | 18.67 | 123.30 | 118.75 | 3.69 |
| Y2 | 24.86 | 28.56 | 14.88 | 77.22 | 83.35 | 7.93 | 97.11 | 105.33 | 8.46 | 121.81 | 118.25 | 2.92 |
| Plate Number | Cracking Load Deflection (mm) | Yield Load Deflection (mm) | ||||
|---|---|---|---|---|---|---|
| Test Value | Simulated Value | Error | Test Value | Simulated Value | Error | |
| X1 | 1.71 | 1.57 | 8.19 | 15.44 | 17.08 | 10.62 |
| X2 | 1.63 | 1.74 | 6.75 | 12.97 | 15.41 | 18.81 |
| Y1 | 1.69 | 1.76 | 4.14 | 14.19 | 17.13 | 20.71 |
| Y2 | 1.39 | 1.46 | 5.04 | 13.84 | 15.68 | 13.29 |
| Plate Number | Cracking Load Stiffness | Service Limit Load Stiffness | Yield Load Stiffness | Ultimate Load Stiffness | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test Value | Simulated Value | Error | Test Value | Simulated Value | Error | Test Value | Simulated Value | Error | Test Value | Simulated Value | Error | |
| X1 | 13.77 | 15.78 | 14.62 | 6.69 | 7.31 | 9.33 | 6.17 | 6.32 | 2.43 | 2.82 | 2.75 | 2.41 |
| Y2 | 6.46 | 7.30 | 12.98 | 3.59 | 3.62 | 0.94 | 3.29 | 3.45 | 4.81 | 1.38 | 1.33 | 3.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Sha, L.; Fang, J. Static Loading Tests and Finite Element Analysis of Phosphogypsum Steel Truss Concrete Slabs. Infrastructures 2025, 10, 250. https://doi.org/10.3390/infrastructures10090250
Zhang A, Sha L, Fang J. Static Loading Tests and Finite Element Analysis of Phosphogypsum Steel Truss Concrete Slabs. Infrastructures. 2025; 10(9):250. https://doi.org/10.3390/infrastructures10090250
Chicago/Turabian StyleZhang, Ao, Lirong Sha, and Juan Fang. 2025. "Static Loading Tests and Finite Element Analysis of Phosphogypsum Steel Truss Concrete Slabs" Infrastructures 10, no. 9: 250. https://doi.org/10.3390/infrastructures10090250
APA StyleZhang, A., Sha, L., & Fang, J. (2025). Static Loading Tests and Finite Element Analysis of Phosphogypsum Steel Truss Concrete Slabs. Infrastructures, 10(9), 250. https://doi.org/10.3390/infrastructures10090250






