Mechanical Response Mechanism and Acoustic Emission Evolution Characteristics of Deep Porous Sandstone
Abstract
1. Introduction
2. Experimental Procedures
2.1. Specimen Preparation
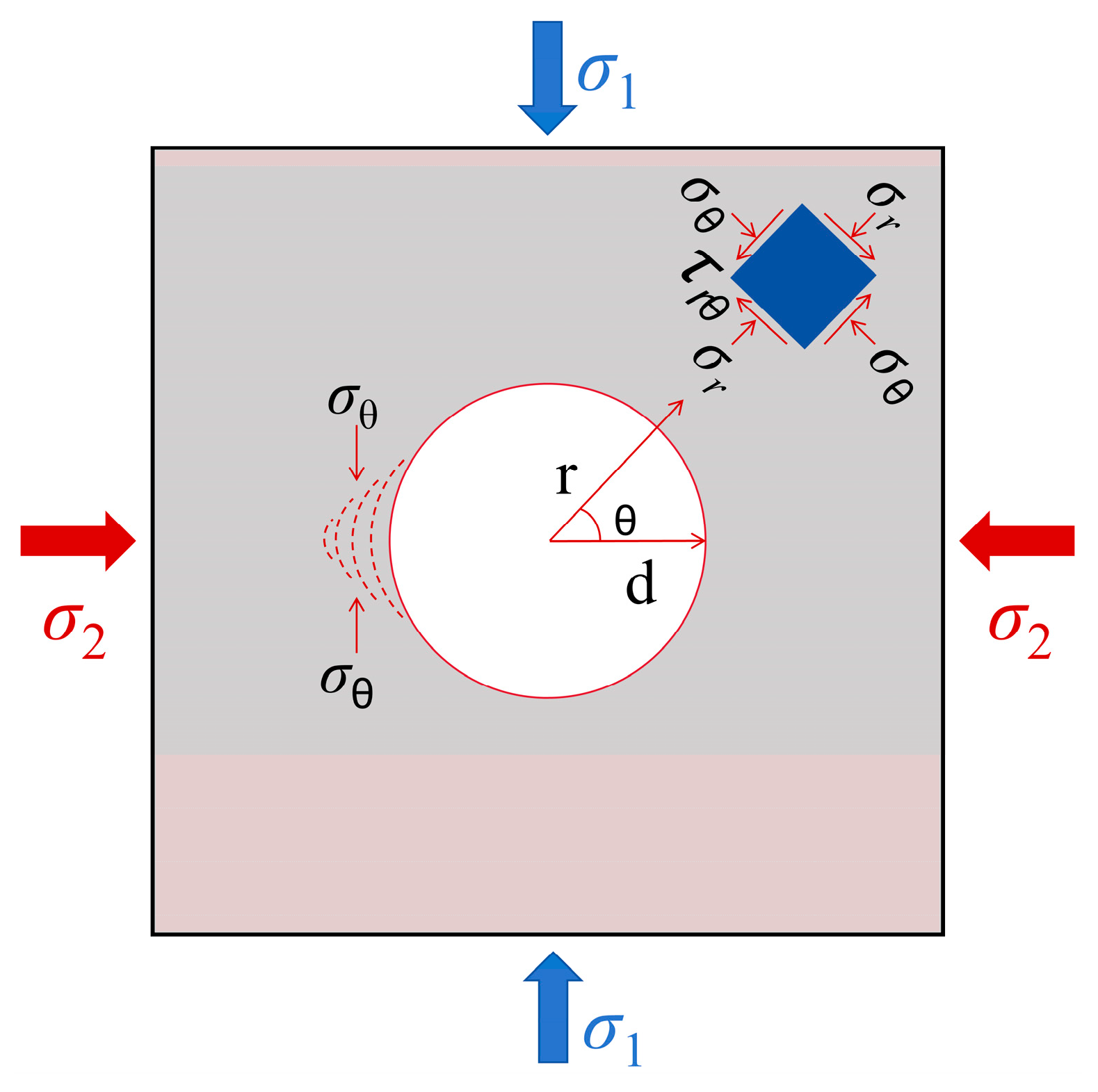
2.2. Testing System and Experimental Scheme
3. Analysis of Test Results
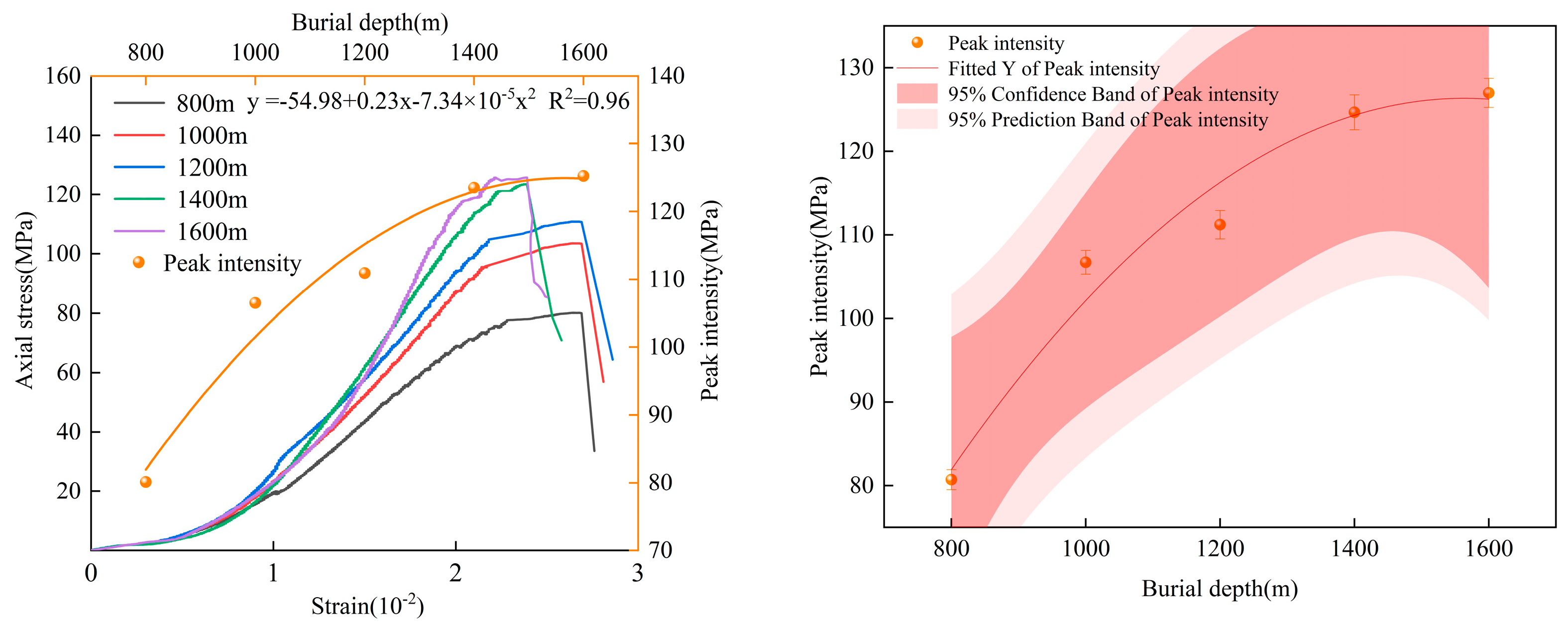
3.1. Mechanical Characteristics Analysis
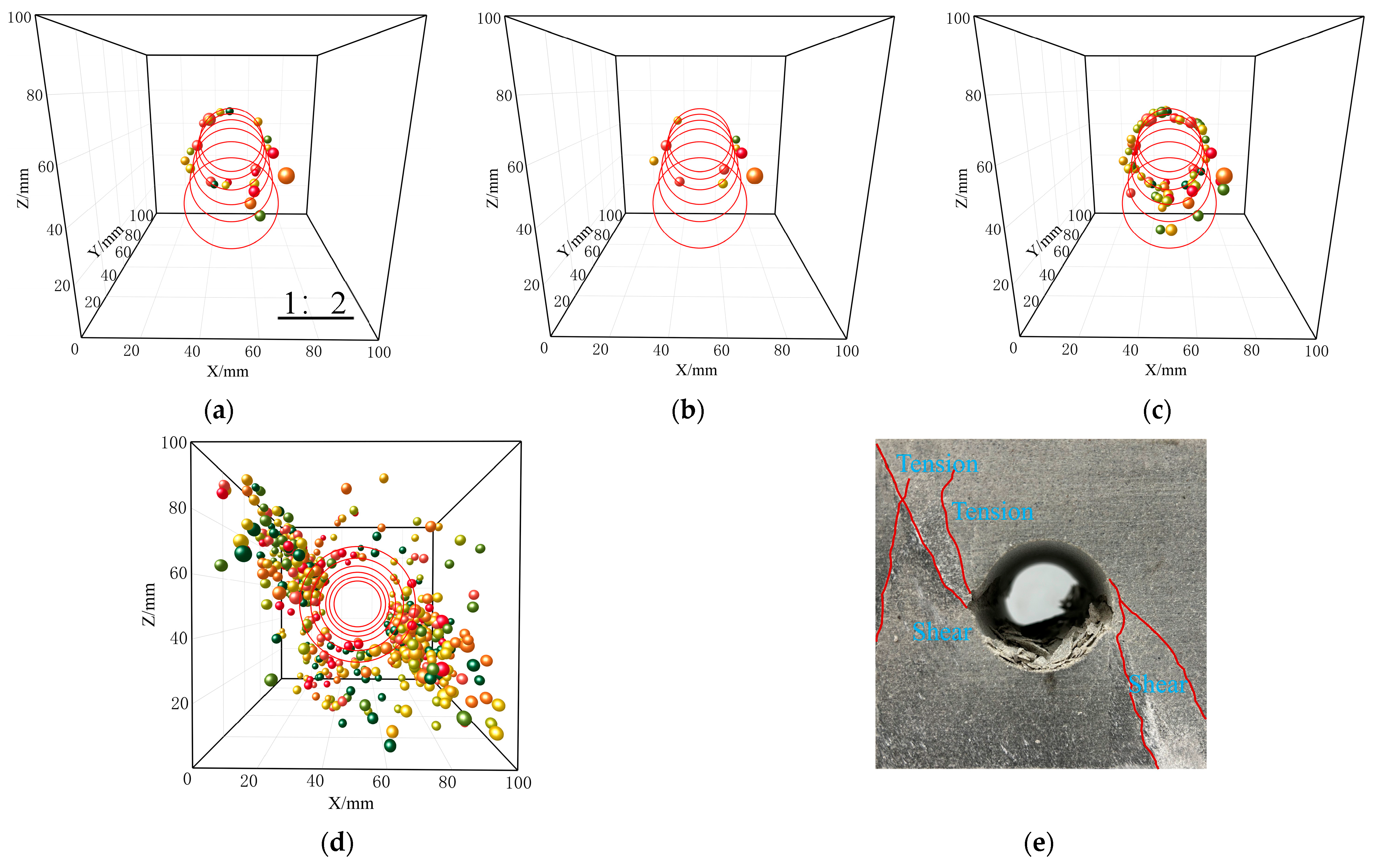
3.2. Analysis of Specimen Failure Characteristics
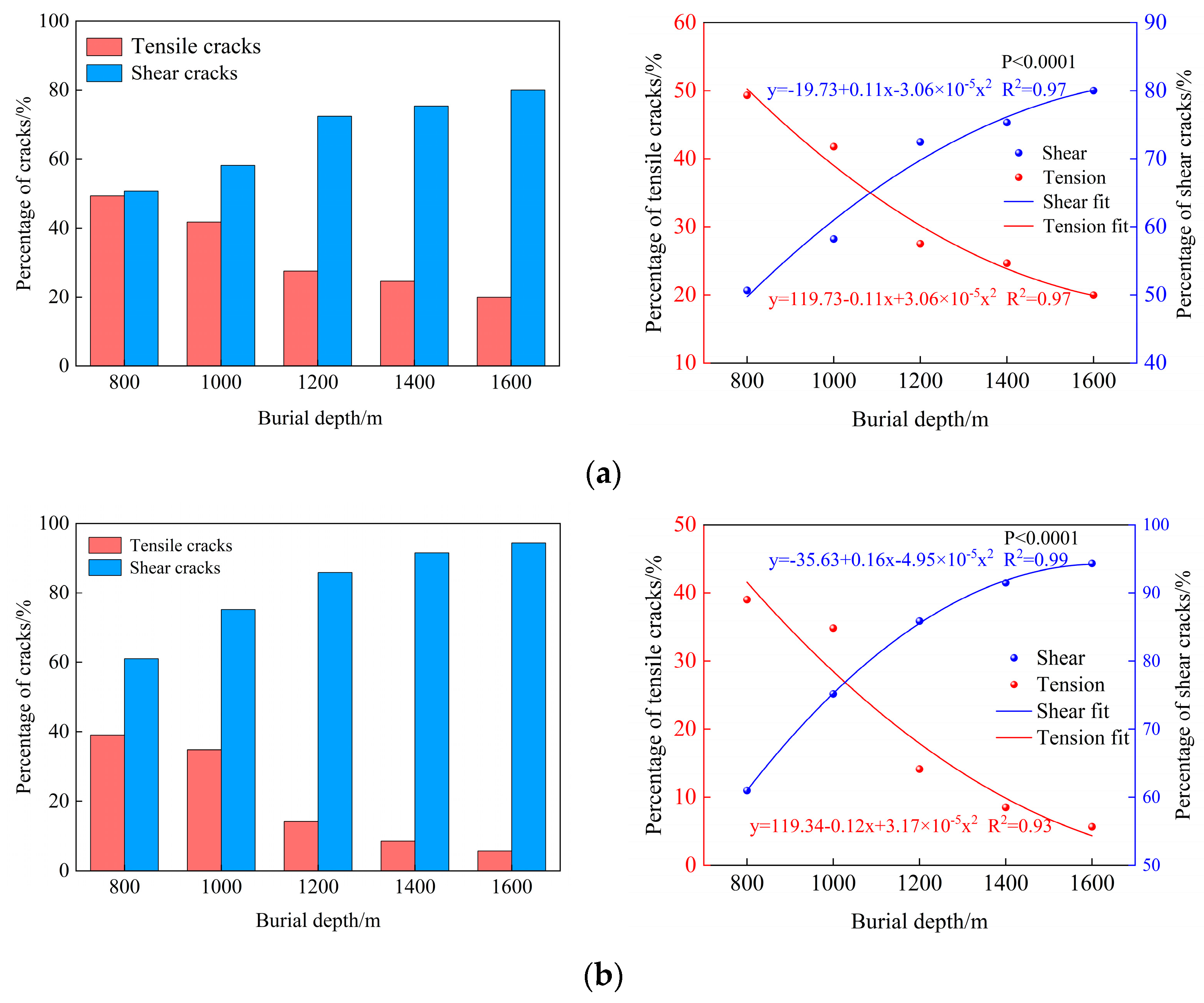
3.3. RA-AF and Sandstone Fracture Characteristics
3.4. Time-Frequency and Spatial Evolution Characteristics of Sound Emission
3.5. Evolutionary Characteristics of Acoustic Emission Parameters
4. Discussion
5. Conclusions
- (1)
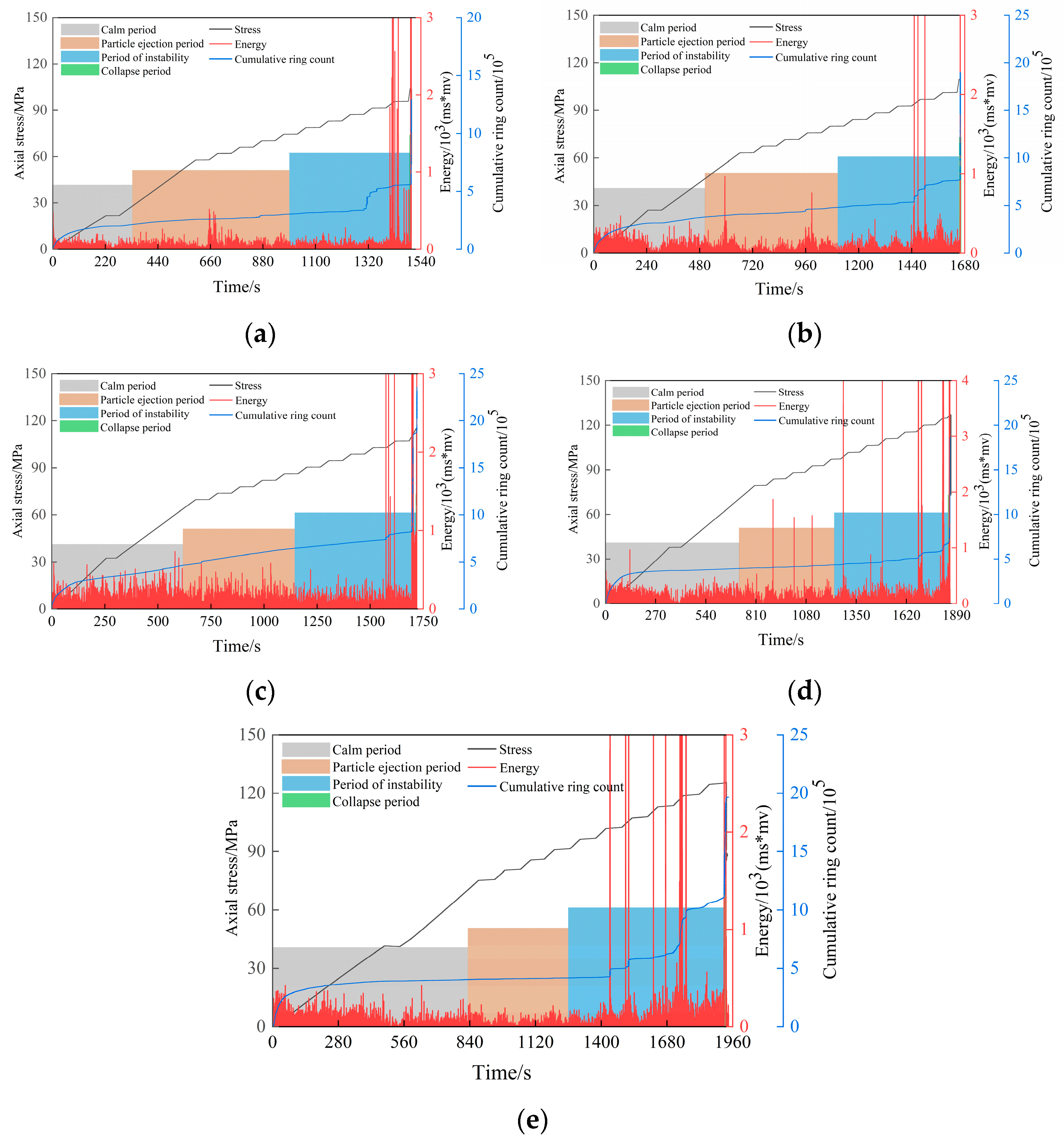
- The peak strength of porous sandstone specimens increases quadratically with increasing burial depth. From a macro perspective, the pore failure process of sandstone specimens can be divided into four stages: the calm period, the particle ejection period, the stable failure period, and the total collapse period.
- (2)
- Under high-stress conditions, the failure of porous sandstone specimens is primarily shear. As burial depth increases, the failure mode of sandstone specimens changes from a composite failure of tensile–shear cracks to shear crack-dominated failure. During the particle ejection period and stable failure period, shear cracks and tensile cracks exhibit quadratic growth and decreasing trends, respectively. But the possible influence of specimen anisotropy and hole machining tolerance should be included as a caveat.
- (3)
- The particle ejection phase is characterised by low-frequency, low-amplitude signals, corresponding to crack initiation phenomena, and this stage is classified as small- to medium-scale damage. The stable damage phase is characterised by low-frequency, high-amplitude signals, reflecting macro-scale crack propagation characteristics, and this period is classified as medium- to large-scale damage. Continuous, dense multi-frequency signals can serve as an indicator of rock mass instability. The number of locating points in the four phases shows a trend of increasing from a few to many. During the complete collapse phase, the locating points exhibit penetrating oblique shear failure centred around the holes.
- (4)
- The peak stress during the particle ejection phase exhibits a trend of first increasing and then decreasing, with specimens S-3, S-4, and S-5 concentrated in the 56–57% peak stress range. The peak stress during the stable failure phase first decreases and then stabilises, with specimens S-2, S-3, S-4, and S-5 entering the accelerated failure phase at 77–80% peak stress. The duration of the calm phase before unstable failure shows a significant negative correlation with burial depth, decreasing from 5.2 s for the S-1 specimen to 2.9 s for the S-5 specimen.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, H.; Xu, G.; Wang, B.; Wu, Y.; Jiang, P.; Pan, J.; Ren, H.; Zhang, Y.; Pang, Y. Forty years development and prospects of underground coal mining and strata controltechnologies in China. J. Min. Strat. Control Eng. 2019, 1, 013501. [Google Scholar]
- Xie, H. Research review of the state key research development program of China: Deep rock mechanics and mining theory. J. China Coal Soc. 2019, 44, 1283–1305. [Google Scholar]
- Gu, J.; Guo, J.; Zhu, Z.; Sun, F.; He, B.; Zhang, H. Sensitivity Analysis on Influential Factors of Strain Rockburst in Deep Tunnel. Buildings 2024, 14, 2886. [Google Scholar] [CrossRef]
- He, M.; Xie, H.; Peng, S.; Jiang, Y. Study on rock mechanics in deep mining Engineering. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Li, X.; Weng, L.; Xie, X.; Wu, H. Study on the degradation of hard rock with a pre-existing opening under static-dynamic loadings using nuclear magnetic resonance technique. J. Rock Mech. Eng. 2015, 34, 1985–1993. [Google Scholar]
- Ali, S.; Côme, C.; Abbas, K.; Alireza, S. Evaluation of the Effect of Geomechanical Parameters and In Situ Stress on Tunnel Response Using Equivalent Mohr-Coulomb and Generalized Hoek-Brown Criteria. Geosciences 2022, 12, 262. [Google Scholar]
- He, M. Research progress of deep shaft construction mechanics. J. China Coal Soc. 2021, 46, 726–746. [Google Scholar]
- Yuan, L.; Xue, J.; Liu, Q.; Liu, B. Surrounding rock stability control theory and support techniquein deep rock roadway for coal mine. J. Coal Sci. Eng. 2011, 36, 535–543. [Google Scholar]
- Zhao, J.; Li, C.; Huang, W. Long-Term Anisotropic Mechanical Characterization of Layered Shale—An Experimental Study for the BaoKang Tunnel of the Zhengwan Railway, China. Processes 2025, 13, 1900. [Google Scholar] [CrossRef]
- Kang, H. Analysis on types and interaction of stress fileds in underground coal mines. J. Coal Sci. Eng. 2008, 33, 1329–1335. [Google Scholar]
- Du, M.; Jing, H.; Su, H. Study on the influence of elliptical hole on strengthand deformation characteristics of sandstone sample. J. Min. Saf. Eng. 2017, 34, 141–147. [Google Scholar]
- Zhu, T.; Jing, H.; Su, H.; Yin, Q.; Du, M. Mechanical behavior of sandstone containing double circularcavities under uniaxial compression. J. Geotech. Eng. 2015, 37, 1047–1056. [Google Scholar]
- Dong, Z.; Cai, M.; Ma, C.; Wang, P.; Li, P. Rock damage and fracture characteristics considering the interaction between holes and joints. Theor. Appl. Fract. Mech. 2024, 133, 104628. [Google Scholar] [CrossRef]
- Li, D.; Liu, M.; Han, Z.; Zhou, Z. Dynamic compressive mechanical properties of bedding sandstone with pre-existing hole. J. China Coal Soc. 2019, 44, 1349–1358. [Google Scholar]
- Zhao, G.; Wang, E.; Wu, H.; Qiu, J.; Dai, Y. Micro-fracture evolution rule of sandstone specimens with a single hole under uniaxial compression. J. Cent. South Univ. Nat. Sci. Ed. 2019, 50, 1891–1900. [Google Scholar]
- Liu, H.; Feng, X.; Liu, L.; Li, T.; Tang, C. Mechanical properties and failure characteristics of anisotropic shale with circular hole under combined dynamic and static loading. Int. J. Rock Mech. Min. Sci. 2023, 170, 105524. [Google Scholar] [CrossRef]
- Du, K.; Niu, T.; Sun, Y.; Zhou, J.; Liu, J.; Wang, S.; Liu, K. Crack Evolution and Failure Mechanisms of Rock Specimens with Oblique Cylindrical Holes in Biaxial Compression Tests. Rock Mech. Rock Eng. 2024, 57, 3257–3280. [Google Scholar] [CrossRef]
- Shi, L.; Li, C.; Zhang, X. Laboratory Tests of Strain Burst in Boreholes of Four Types of Rocks Under Biaxial Loading. Rock Mech. Rock Eng. 2024, 58, 301–319. [Google Scholar] [CrossRef]
- Miao, S.; Shang, X.; Chang, N.; Ma, Y.; Yang, J. Mechanical properties and fracture mechanism of porous sandstoneunder biaxial compression. J. Min. Strat. Control Eng. 2025, 7, 023041. [Google Scholar]
- Bi, R.; Liu, M.; Li, G.; Zhou, J.; Du, K. Mechanical properties and risk characterization of surrounding rocks containing various blocks of arch-shaped holes under biaxial compression. Eng. Fail. Anal. 2024, 158, 107983. [Google Scholar] [CrossRef]
- Taherdangkoo, R. Study on the characteristics of crack initiation in deep dense shale containing circular hole under varying stress conditions. J. Cent. South Univ. 2025, 32, 244–261. [Google Scholar]
- Wei, J.; Liu, S.; Wu, L.; Huang, J.; Zhang, Y.; Tian, B. Comparative analysis on different AE parameters in biaxial loading of hole rock. J. Min. Saf. Eng. 2015, 32, 1017–1025. [Google Scholar]
- Yang, S. Experimental study on deformation, peak strength and crack damage behavior of hollow sandstone under conventional triaxial compression. Eng. Geol. 2016, 213, 11–24. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Xiong, X.; Chen, Z.; Yan, S.; Zhou, J. Zonal disintegration phenomenon based on triaxial dynamic load test of hollow cylindrical sandstone specimens. J. Cent. South Univ. 2023, 30, 1311–1324. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, Z.; Meng, X.; Zhang, R.; Gu, Q.; Qi, M. Energy evolution of sandstone under true triaxial cyclic principal stress. Rock Soil Mech. 2023, 44, 1875–1890. [Google Scholar]
- Liu, C.; Zhao, G.; Xu, W.; Meng, X.; Huang, S.; Zhou, J.; Wang, Y. Experimental investigation on failure process and spatio-temporal evolution of rockburst in granite with a prefabricated circular hole. J. Cent. South Univ. 2020, 27, 2930–2944. [Google Scholar] [CrossRef]
- Feng, X.; Haimson, B.; Li, X.; Chang, C.; Ma, X.; Zhang, X.; Ingraham, M.; Suzuki, K. ISRM Suggested Method: Determining Deformation and Failure Characteristics of Rocks Subjected to True Triaxial Compression. Rock Mech. Rock Eng. 2019, 52, 2011–2020. [Google Scholar] [CrossRef]
- Xie, H.; Lu, J.; Li, C.; Li, M.; Gao, M. Experimental study on the mechanical and failure behaviors of deep rock subjected to true triaxial stress: A review. Int. J. Min. Sci. Technol. 2022, 32, 915–950. [Google Scholar] [CrossRef]
- Huang, L.; Yang, S.; Cui, X.; Chen, Q.; Yao, R. Analysis of characteristics of measured stress and stability of faults in North China. Rock Soil Mech. 2013, 34 (Suppl. S1), 204–213. [Google Scholar]
- Huang, D.; Huang, R.; Zhang, Y. Experimental investigations on static loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression. J. Rock Mech. Eng. 2012, 31, 245–255. [Google Scholar]
- Liu, Y.; Feng, D. A review of experimental and theoretical research on the deformation and failure behavior of rocks subjected to cyclic loading. J. Rock Mech. Geotech. Eng. 2021, 13, 1203–1230. [Google Scholar] [CrossRef]
- Gong, F.; Luo, Y.; Li, X.; Si, X.; Tao, M. Experimental simulation investigation on rockburst induced by spalling failure in deep circular tunnels. Tunn. Undergr. Space Technol. 2018, 81, 413–427. [Google Scholar] [CrossRef]
- Shen, B.; Barton, N. Rock fracturing mechanisms around underground openings. Geomech. Eng. 2018, 16, 35–47. [Google Scholar]
- Du, K.; Luo, X.; Liu, M.; Liu, X.; Zhou, J. Understanding the evolution mechanism and classification criteria of tensile -shear cracks in rock failure process from acoustic emission (AE) characteristics. Eng. Fract. Mech. 2024, 296, 109864, Erratum in Eng. Fract. Mech. 2024, 302, 110063. [Google Scholar] [CrossRef]
- Bi, J.; Zhao, Y.; Wu, Z.; Li, J.; Wang, C. Research on crack classification method and failure precursor index based on RA-AF value of brittle rock. Theor. Appl. Fract. Mech. 2024, 129, 104179. [Google Scholar]
- Zhu, L.; Cui, S.; Pei, X.; Sun, P.; Liang, Y.; Sun, M. Characteristics of fatigue damage in secondary cemented rock mass based on acoustic emission spectrum. J. Cent. South Univ. Sci. Technol. 2024, 55, 2763–2779. [Google Scholar]
- Wang, J.; Yuan, G. Acoustic emission and fracture characteristics of deep sandstone under different loading rates. J. Min. Strat. Control Eng. 2023, 5, 65–76. [Google Scholar]
- Li, S.; Xu, F.; Li, L.; Wang, W.; Zhang, W.; Zhang, Q.; Shi, S. State of the art: Challenge and methods on large deformation in tunnelengineering and introduction of a new type supporting system. J. Rock Mech. Eng. 2016, 35, 1366–1376. [Google Scholar]






| Density (g·cm−3) | P-Wave Velocity (m·s−1) | S-Wave Velocity (m·s−1) | Porosity (%) | Poisson Ratio | Tensile Strength (MPa) | Modulus of Elasticity (GPa) |
|---|---|---|---|---|---|---|
| 2.41 | 2519 | 1503 | 0.47 | 0.28 | 2.92 | 27.1 |
| Specimen Number | Burial Depth | Initial Stress | ||
|---|---|---|---|---|
| σ1 | σ2 | σ3 | ||
| S-1 | 800 m | 21.6 MPa | 23.3 MPa | 15.1 MPa |
| S-2 | 1000 m | 27.0 MPa | 28.0 MPa | 18.3 MPa |
| S-3 | 1200 m | 32.4 MPa | 32.6 MPa | 21.5 MPa |
| S-4 | 1400 m | 37.8 MPa | 37.3 MPa | 24.8 MPa |
| S-5 | 1600 m | 43.2 MPa | 41.9 MPa | 28.0 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhao, G.; Xu, X.; Liu, C.; Xu, W.; Huang, S. Mechanical Response Mechanism and Acoustic Emission Evolution Characteristics of Deep Porous Sandstone. Infrastructures 2025, 10, 236. https://doi.org/10.3390/infrastructures10090236
Li Z, Zhao G, Xu X, Liu C, Xu W, Huang S. Mechanical Response Mechanism and Acoustic Emission Evolution Characteristics of Deep Porous Sandstone. Infrastructures. 2025; 10(9):236. https://doi.org/10.3390/infrastructures10090236
Chicago/Turabian StyleLi, Zihao, Guangming Zhao, Xin Xu, Chongyan Liu, Wensong Xu, and Shunjie Huang. 2025. "Mechanical Response Mechanism and Acoustic Emission Evolution Characteristics of Deep Porous Sandstone" Infrastructures 10, no. 9: 236. https://doi.org/10.3390/infrastructures10090236
APA StyleLi, Z., Zhao, G., Xu, X., Liu, C., Xu, W., & Huang, S. (2025). Mechanical Response Mechanism and Acoustic Emission Evolution Characteristics of Deep Porous Sandstone. Infrastructures, 10(9), 236. https://doi.org/10.3390/infrastructures10090236






