Towards Smarter Infrastructure Investment: A Comprehensive Data-Driven Decision Support Model for Asset Lifecycle Optimisation Using Stochastic Dynamic Programming

Abstract

Equipment renewal and replacement strategy as well as smart capital investment is a vital focus in engineering asset management, particularly for water utilities aiming to improve asset reliability, water quality, service continuity and affordability. This study presents a novel decision support model that integrates whole-life costing principles across all asset lifecycle phases—from capital delivery and daily operations to long-term maintenance. The proposed model uniquely combines asset degradation and failure patterns, operating and maintenance costs, and the impact of technological advancements to provide a holistic and comprehensive asset management decision-making tool. These dimensions are jointly analysed using a hybrid approach that combines optimisation with stochastic dynamic programming, allowing for the determination of optimal asset renewal and replacement timing. The model’s performance was validated using historical data from eight critical wastewater pump stations within a township’s sewerage network. This was performed by comparing the model’s cost-saving results to those achieved by the water utility’s current strategy. Results revealed that the proposed model achieved an average cost saving of 12%, demonstrating its effectiveness in supporting sustainable and cost-efficient asset renewal decisions.

1. Introduction

Developing effective approaches for equipment replacement and renewal is a central concern in engineering asset management research. Asset owners in various industries need to accurately predict the optimal time for equipment renewal and replacement. This proactive approach helps prevent declines in reliability and availability, ultimately reducing operational expenditure associated with poor asset performance. This topic has been a major focus of research for nearly a century, with numerous studies and case reports published annually in the fields of asset management to estimate the optimal timing for equipment renewal or replacement.

Traditional economic models primarily focus on renewal strategies designed to minimise the total cost of asset ownership [1]. These traditional models, such as the Parallel Machine Replacement Model (PMRM) and the Series Machine Replacement Model (SMRM), optimise asset replacement over a defined lifecycle by assessing Life Cycle Costs (LCCs) including purchase, operation, maintenance, and salvage costs. PMRM focuses on determining the optimal replacement schedule for a group of economically interdependent assets operating in parallel [2]. SMRM assumes that assets operate in series to provide products or services but are economically independent [3]. Taylor [4] first highlighted the link between equipment depreciation and replacement timing in 1923. Eilon et al. [5] studied optimal replacement of forklift trucks and developed a model based on discounted cash flow and maintenance cost data. Meyer and Robert [6] developed a stochastic model for vehicle replacement under uncertainty, incorporating maintenance costs. Hackemer and Dakin [7] continued Meyer’s work using the average total cost to propose the optimal replacement time of trucks. Lake and Muhlemann [8] developed a replacement model focused on production loss costs from breakdowns, validating it on food industry wrapping machines. Waddell [9] used dynamic programming to optimise discounted cash flows for replacing highway tractors and light trucks. Apeland and Scarf [10] developed a Bayesian model to optimise equipment replacement timing based on cost, discount rate, and productivity differences. Hartman et al. [11] proposed an integer programming model to minimise replacement costs for economically interdependent equipment operating in parallel. Al Chalabi et al. [12] developed a data-driven economic model to determine the optimal lifetime of a mining drilling machine by analysing costs and resale value using discounted cash flow. Raposo et al. [13] applied econometric LCC models to urban bus fleet maintenance and compared simulated replacement outcomes with real data. Sadeghpour et al. [14] employed genetic algorithm and dynamic programming to optimise transformer replacement, reducing costs and addressing uncertainty in state variables.

In summary, traditional models assume that equipment shares identical economic characteristics and relies on fixed or predetermined physical lifespans, neglecting the effects of technological advancements. Consequently, renewal or replacement decisions are typically based solely on economic life. Although widely used, these models incorporate simplifying assumptions that limit their real-world applicability. Key cost parameters such as maintenance, operational, and salvage costs are generally treated as fixed and deterministic. Additionally, traditional approaches often overlook essential factors like system reliability, asset degradation, and the influence of emerging technologies.

Later, researchers introduced equipment renewal and replacement models that account for nonstationary costs, including technological change [15]. In this study, we refer to these as models based on technological lifespan, termed here as technological life. In 1955, Bellman [16] applied dynamic programming to develop an equipment replacement model that accounts for age and technological change to determine optimal replacement timing. Kusaka [17] developed a parametric model for replacing milling and drilling machines under technological change, assuming a single replacement option at any given time. Bean et al. [15] proposed an equipment replacement model incorporating technological change, introducing an error-bounded approach to approximate infinite-horizon solutions using a finite horizon. The model was validated through a real-world vehicle replacement case study. Kusuka and Suzuki [18] applied dynamic programming to model equipment replacement decisions under the influence of technological innovation. Cheevaprawatdomrong and Smith [19] introduced a model highlighting the influence of emerging technologies on deferring equipment replacement, accounting for acquisition, operation, maintenance, and salvage costs. Yatsenko and Hritonenko [20] analysed equipment replacement under technological change using both discrete and continuous-time models with uncertain lifetimes. They found that while both approaches yielded similar total costs, the continuous model resulted in shorter optimal lifespans and delayed adoption of new technology despite improved maintenance cost benefits [21]. These studies view technological change as a continuous process that can prompt equipment replacement before the end of its economic life. However, technological change can also occur at discrete points in time, often triggered by major breakthroughs referred to as discontinuous technological change [22]. Barreca [23] presented a method to incorporate the effects of technological obsolescence into plant depreciation and economic life assessments. Nair and Hopp [24] proposed a Markov decision model to optimise equipment replacement timing, considering finite technological breakthroughs over an infinite horizon. In 1992, Hope and Nair [25] later enhanced the model by incorporating salvage values, improving computational efficiency. They studied equipment economic life under both continuous and discontinuous technological changes, finding that continuous change shortens the equipment’s economic lifespan. Tanaka et al. [26] developed a branch-and-bound algorithm to forecast optimal equipment replacement timing driven by technological breakthroughs, validated through circuit breaker replacements in primary substations. Wang and Nguyen [27] introduced an integer programming model for capacity planning in high-tech industries facing rapid obsolescence, aiming to maximise expected net present profit over a finite horizon. However, such models often neglect key factors like system reliability and equipment degradation, crucial for effective replacement decisions.

Other researchers have focused on condition-based renewal strategies, estimating optimal replacement timing based on equipment deterioration and physical life [28,29,30]. The literature classifies existing models into three categories: traditional lifetime models, model-based approaches, and data-driven methods [28,31]. The traditional lifetime approach analyses failure data of identical assets using lifetime distribution models, with Exponential and Weibull distributions being the most commonly applied in engineering [32]. Model-based approaches use mathematical models to detect faults and estimate Remaining Useful Life (RUL), relying on residual generation and parity relations for parameter estimation and fault diagnosis [33]. In contrast, data-driven approaches build models from operational and condition data without relying on physical system knowledge. They are typically classified into AI-based models, statistical covariate models, and stochastic process models [34,35]. Roll and Sachish [36] proposed a replacement model that accounts for equipment deterioration, integrating overhaul and replacement decisions while considering ageing effects on operational costs. Zhou et al. [37] proposed an optimal expansion planning method for distribution networks that incorporates equipment health indices and non-network solutions to address uncertainties in renewable generation replacement. Their risk-based approach prioritises safety, reliability, cost, and sustainability, optimised using an improved niche genetic algorithm and spanning tree technique. Zapf et al. [38] established network benchmark rules for optimal replacement of medium-voltage cables by using thermal imaging to assess ageing and estimate cable lifetimes. Na et al. [39] used a health index approach to estimate the RUL of feeder cables in salt-damaged areas, supporting informed replacement decision-making. Kang et al. [40] employed an Artificial Neural Network (ANN) to automate failure prediction in continuous production lines, enabling optimal equipment replacement strategies. Gritsyuk [41] explored deep learning techniques combining convolutional and long short-term memory networks to predict optimal equipment replacement timing, enabling proactive interventions that improve reliability and reduce maintenance costs. Bobos and Protonotarios [42] applied a Markov decision model to estimate optimal equipment replacement and renewal, incorporating a deterioration model with stage-wise maintenance actions and progressive ageing.

Several studies also integrate both physical and economic lifespans to more accurately estimate the optimal timing for equipment replacement or renewal. Chang [43] introduced a fuzzy methodology for equipment replacement through modelling degradation parameters and economic life. Takami et al. [44] proposed a mixed-integer dynamic programming model to optimise replacement timing by analysing the trade-off between equipment deterioration and capital costs. Kandic et al. [45] developed a model for managing ageing assets, combining system unavailability, economic analysis, and Monte Carlo simulations to support end-of-life decisions. However, its applicability is limited to ageing systems or assets. Wei et al. [46] introduced a continuous-time, discrete-state Markov chain model to represent the stochastic deterioration of a single component, later extending it to multi-state series systems. They optimised preventive maintenance and side-effect costs at the system level. Signore and Hadjerioua [47] developed a comprehensive hydropower equipment replacement model using physical life data, whole-life cost analysis, the Weibull distribution, and a joint cost ratio to determine optimal replacement timing. Filho et al. [48] proposed a model for optimal group asset replacement by balancing economic depreciation and failure rates, using an optimisation algorithm to determine the ideal replacement timing. El-Akruti et al. [49] introduced an LCC model that uses equipment condition data to estimate RUL and optimise replacement timing, validated with data from an electric arc furnace in the steel industry. Wijnia [50] proposed a replacement decision model combining ownership costs, failure rates, and both physical and economic lifespans to determine optimal timing, validated on gas distribution assets. Hernandez-Chover et al. [51] developed a multicriteria model that integrates economic costs and equipment condition to determine optimal replacement timing, validated using blower pump data from a wastewater treatment plant. Other researchers integrated economic and technological change models, recognising that new technologies introduce uncertainty in an asset’s economic life. The literature highlights dynamic programming as a suitable approach for modelling replacement decisions while minimising operating and maintenance costs [52,53]. These models account not only for economic factors but also for the impact of technological changes on equipment and systems. Lee et al. [54] investigated how geometric, non-proportional technological change affects the economic lifespan of equipment in various sizes, using a real-world case study that considers differing rates of change for capital and operating costs. Diniz and Sessions [55] developed a forward-looking algorithm that incorporates future equipment costs and technological change to optimise replacement timing, validated in the wood industry. Yatsenko et al. [56] proposed a multi-cycle method to minimise costs and determine optimal replacement timing for serial equipment amid technological advancements. Wang and Nguyen [27] developed a stochastic dynamic model that combines technological and economic lifespans to optimise replacement timing by maximising expected net present profit over a finite horizon. Büyüktahtakın and Hartman [57] introduced a mixed-integer programming model to optimise parallel equipment replacement, considering technological change and economies of scale to minimise costs.

In addition, limited research has explored integrating physical, technological, and economic lifespans comprehensively. Abdelwali et al. [58] developed a model that optimises equipment replacement by integrating physical degradation and technological advancements to improve management effectiveness and support business objectives. Yatsenko and Hritonenko [56,59] applied multi-cycle algorithms within an infinite-horizon framework to optimise equipment replacement timing by maximising profit, factoring in age-related deterioration and technological change. While their model addressed three lifespan aspects, it omitted equipment condition, which may vary independently from age due to operational environments. Hastings [60] proposed a replacement decision model for linear equipment such as pipelines, power lines, and rail lines, integrating economic replacement costs with age and condition factors under technological change.

However, many existing models, whether based on individual or combined equipment lifespans, may produce suboptimal replacement and renewal decisions due to the lack of a comprehensive framework that simultaneously incorporates equipment degradation, health management, technological change, and lifecycle costs. Consequently, there is a clear gap for a model that explicitly integrates these critical facets of asset life. To address these limitations, this study aims to develop a comprehensive model to determine the optimal replacement strategy for non-linear equipment through integrating all three equipment lifespans using dynamic programming.

The remainder of the paper is organised as follows. Section 2 outlines the calculation of equipment RUL using the novel Degradation Hidden Semi-Markov Model (DHSMM). Section 3 details the integration of technological change, operating, and maintenance costs into the equipment degradation model. Section 4 describes the determination of optimal replacement and renewal timing. Section 5 presents a real-life case study and the results of the integrated model considering the three equipment lifespans. Conclusions are given in Section 6.

2. Equipment Replacement Modelling Using Event and Condition Data

The equipment degradation process is inherently stochastic, making stochastic-based models the most suitable choice for accurately predicting RUL [61]. While numerous studies have focused on RUL prediction using equipment condition or event data, only a limited number have incorporated both types of data. As discussed in the previous section, this integrated approach can enhance prediction accuracy. In our previous research, we introduced a novel DHSMM for RUL prediction, leveraging both condition and event data to provide a comprehensive representation of the equipment’s physical lifespan [62].

The DHSMM for asset health prediction consists of four main steps. First, historical event data are analysed to calculate failure and renewal rates using the log-beta Weibull model. This model is particularly effective for handling both censored and uncensored event data, which are often encountered in real-world industrial settings. Its robustness against censored data makes it ideal for reliability analysis, enabling accurate predictions even in the absence of complete failure histories. Furthermore, it seamlessly integrates condition monitoring data with historical failure data, offering a comprehensive view of asset health and expected failure behaviour. The log-beta Weibull distribution model mathematical formulas are provided in Equations (1) and (2), where Equation (1) presents the distribution function and Equation (2) presents the failure rate [62]:

$$F\left(t\right)={\displaystyle \frac{1}{\beta (a,b)}}{\int }_0^{G\left(t\right)}{u}^{a-1} {(1-u)}^{b-1} du;0<a,b<\infty$$

(1)

$$\lambda ={\displaystyle \frac{\eta {\beta }^{\eta }{t}^{\eta -1}exp(-b{\left(\beta t\right)}^{\eta }){[1-\mathit{exp}\left(-{\left(\beta t\right)}^{\eta }\right)]}^{a-1}}{\beta (a,b)R\left(t\right)}}$$

(2)

where $F\left(t\right)$ indicates the cumulative distribution function of the log-beta Weibull model, and $G\left(t\right)$, represents the two-parameter Weibull distribution.$\beta \left(a,b\right)= \left[\Gamma \left(a\right)\Gamma \left(b\right)\right]/\Gamma (a+b)$ is the beta function, Γ(.) is the gamma function, a and b are two additional shape parameters to the Weibull distribution and $u\in [0, G\left(t\right)]$. $\lambda$ indicates the failure rate, also called hazard. $(\eta$) and $\left(\beta \right)$ denote the scale and shape parameters of the two-parameter Weibull model, respectively. $R\left(t\right)$ represents the reliability function.

Second, the Hidden Semi-Markov Model (HSMM) is applied to estimate health state rates and probabilities of state transitions. Third, the failure rates derived from the log-beta Weibull model are incorporated into the HSMM transition matrix. This integration facilitates the computation of degradation rates and the current health state of the asset. The key distinction between a typical HSMM and the proposed DHSMM is its ability to jointly model asset degradation and survival time using both event and condition data. 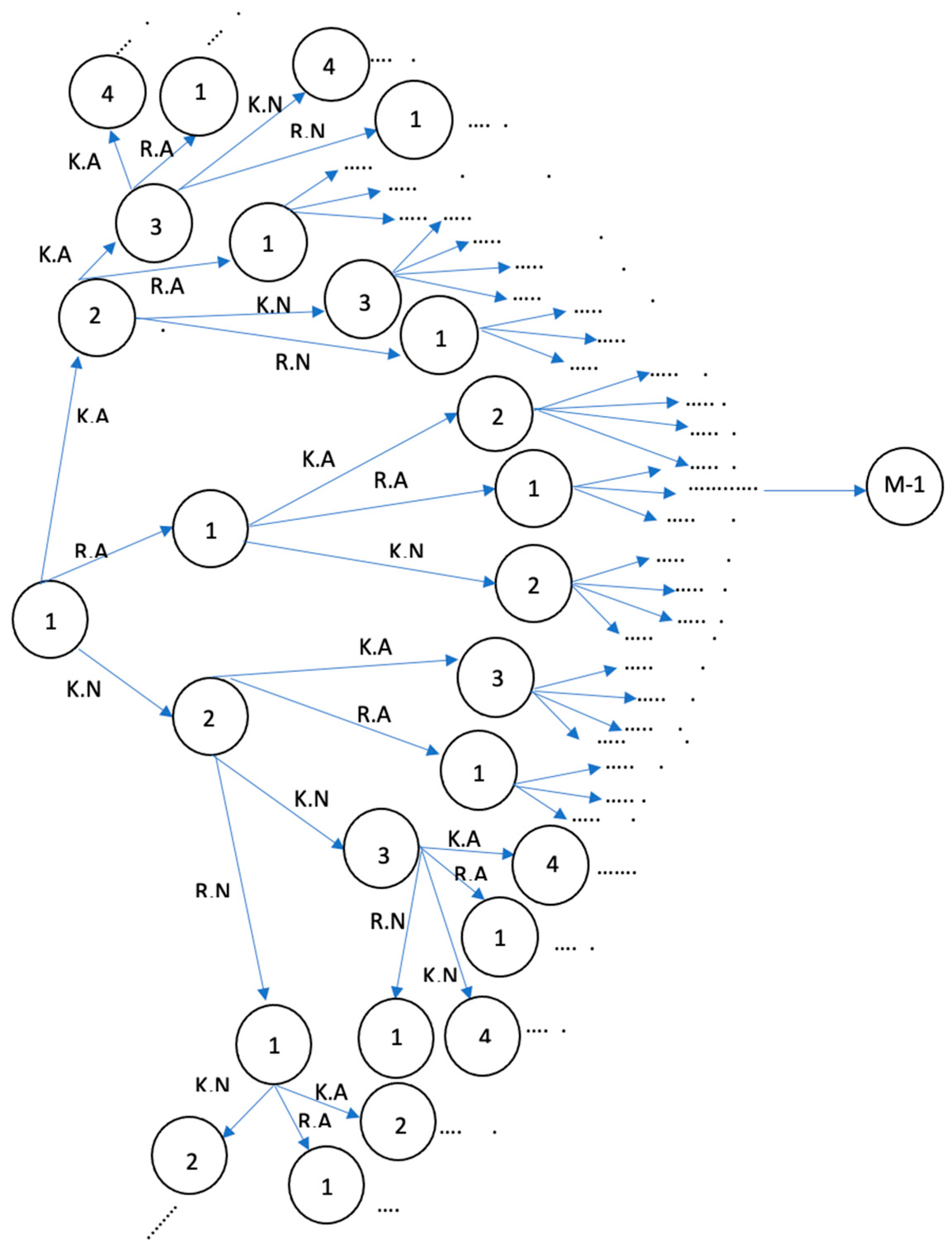Figure 1 illustrates the transitions of an asset’s condition from a healthy state to various deteriorating states before experiencing catastrophic failure [62].

State 1 indicates a healthy asset condition, while state M represents catastrophic failure. States $i$ and $j$ denote asset health levels, with $i$ representing a better condition than $j$. $P_{ij}$ denotes the transition probability from state $i$ to $j$, ${\lambda }_{i,j}$ is the failure rate, and ${\mu }_{m1}$ represents the renewal or replacement rate, restoring the asset to a healthy state. Equation (3) expresses the transition probability matrix in DHSMM [62].

$$Q=\left(q_{ij}\right)=\left[\begin{array}{c}{P}_{11}\\ {\mu }_{21}{P}_{21}\\ .\\ .\\ .\\ {\mu }_{m1}{P}_{m2}\end{array} \begin{array}{c}{ \lambda }_{12}{P}_{12}\\ P_{22}\\ \cdots \\ \cdots \\ \cdots \\ {\lambda }_{m2}{P}_{m2}\end{array}\begin{array}{c} \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \\ \cdots \end{array}\begin{array}{c}{ \lambda }_{1m}{P}_{1m}\\ { \lambda }_{2m}{P}_{2m}\\ .\\ .\\ .\\ P_{mm}\end{array}\right]$$

(3)

Finally, the forward–backward algorithm is employed to calculate the posterior health state based on the current health estimate based on Equations (4) and (5). This step enables accurate Remaining Useful Life (RUL) prediction [62].

$$B_j\left(t\right)=\left[\begin{array}{c}{\sum }_{u=1}^{\tau -2-t}{B}_j\left(t+u\right)\left\{{\prod }_{v=0}^{u-1}{\displaystyle \frac{b_j\left(x_{t+u-v}\right)}{N_{t+u-v}}}\right\}{d}_j\left(u\right)+\\ \left\{{\prod }_{v=0}^{\tau -2-t}{\displaystyle \frac{b_j\left(x_{\tau -1-v}\right)}{N_{\tau -1-v}}}\right\}{D}_j\left(\tau -1-t\right)\end{array}\right]{\sum }_{i\ne j }{p}_{ij}{F}_i\left(t\right)$$

(4)

$$F_j\left(t\right)={\displaystyle \frac{b_j\left(x_t\right)}{N_t}}\left[{\sum }_{u=1}^t\left\{{\prod }_{v=1}^{u-1}{\displaystyle \frac{b_j\left(x_{t-v}\right)}{N_{t-v}}}\right\}{d}_j\left(u\right){\sum }_{i\ne j}{p}_{ij}{F}_i\left(t-u\right)+\left\{{\prod }_{v=1}^t{\displaystyle \frac{b_j\left(x_{t-v}\right)}{N_{t-v}}}\right\}{d}_j\left(t+1\right){\pi }_j\right]$$

(5)

Once the health state and condition of an asset are predicted, the function $\mu \left(t\right)$ is calculated to represent the expected remaining time to failure, given that the asset has survived up to time $t$. Then the following equation gives $\mu \left(t\right)$:

$$\mu \left(t\right)=E\left[T-t\left|T>t\right.\right]=\left({\displaystyle \frac{1}{R\left(t\right)}}\right){\int }_t^{\infty }R\left(t\right)dt, for t, R\left(t\right)>0$$

(6)

$R\left(t\right)$ is the probability that the asset will stay in the healthy state at time $t$, if the asset goes through the health states $H_i\left(i=\mathrm{1,2},\dots ,n-1\right)$ before entering the failure state i =$n$. If ${D(H}_i)$ provides RUL of the asset staying in the health state $H_i$, then the total remaining time in the future health states before failure is given by Equation (7):

$${\sum }_{j=i+1}^{n-1}{D(H}_j)$$

(7)

where $\widehat{D(}{H}_i^{\left(I\right)})$ is the probable residual time of the asset at the $i$th observation time since it has entered the health state $H_i$ which is estimated as the following equation:

$${RUL}^{\left(I\right)}=\widehat{D(}{H}_i^{\left(I\right)})+{\sum }_{j=i+1}^{n-1}{D(H}_j)$$

(8)

3. Integrating Technological Change, Operating, and Maintenance Costs into Equipment Degradation Modelling

Building on the gaps identified in the literature and outlined in the Introduction, this study aims to develop a comprehensive model for determining the optimal equipment replacement or renewal strategy. To achieve this, the model integrates equipment degradation with operating and maintenance costs, while also accounting for the influence of technological change. This approach ensures that all key aspects of equipment lifespan are captured within the proposed integrated framework.

This section first presents the estimation of operating and maintenance costs based on the degradation process of equipment. Subsequently, the impact of technological advancement on the equipment Equivalent Annual Cost (EAC) is examined, ensuring that all cost components used as critical indicators in the modelling process are fully considered.

3.1. Operating and Maintenance Costs

In this study, all costs related to operating equipment, including power, labour, tools, and application expenses when the equipment is in operation, will be considered as the operating costs. The operation rate is represented by ${\phi }_i$, the operating cost incurred in state $i$ is denoted as $q_i$, and $P_i$ represents the steady-state probability of the equipment being in state $i$. Equipment degradation increases over time; therefore, ${\phi }_1\ge {\phi }_2 \ge \cdots \ge {\phi }_n \ge 0$. The total operating cost, $C_o,$ is given by [46]

$$C_o={\sum }_{i=1}^n(q_i{\phi }_i) P_i$$

(9)

The maintenance cost in each state $i$ consists of the sum of preventive maintenance, corrective maintenance, and breakdown (catastrophic failure) costs. Since preventive maintenance is performed from state $n+1$ to state $m$, the total maintenance cost $C_M$ depends on the preventive maintenance strategy applied during the transition from state $n+1$ to state $m$ [46]

$$C_M\left(n+1,m\right)=C_{{PM}_{(n+1,m)}}{P}_{n+1}+C_{{BD}_j}{P}_j+{\sum }_{i=1}^n{C}_{{CM}_i}{P}_{i }, j>i$$

(10)

where $C_M$ denotes the total maintenance cost, $C_{{PM}_{(n+1,m)}}$ indicates the cost of preventive maintenance strategy from state $n+1$ to state $m, C_{BD}$ is the cost of breakdown, $C_{CM}$ is the cost of corrective maintenance or repair, and $P_i$ represents the steady-state probability of the equipment being in state $i$. In the above equation, the steady-state probabilities are used to calculate the expected long-term cost of operating and maintaining the asset under a probabilistic degradation model. These probabilities reflect the proportion of the asset that is likely to be in each discrete health state in the long run. This approach is aligned with best practices in predictive maintenance modelling [63,64] and supports informed decision-making under uncertainty. In addition, all costs associated with Equations (9) and (10) are expressed in present value, and this assumption is explicitly reflected in Equation (11).

3.2. Technological Change

Section 1 explained that technological change can occur as a continuous improvement over time or as a breakthrough following an extended period, representing discontinuous technological change [65]. Hartman and Tan outlined [28] the EAC when there is no technological change as the following:

$$\mathrm{E}\mathrm{A}\mathrm{C} (T)=\left({\displaystyle \frac{r{\left(1+r\right)}^T}{{\left(1+r\right)}^T-1}}\right)\left(C_P+{\displaystyle \frac{S_T}{{\left(1+r\right)}^T}}+{\sum }_{i=1}^T{\displaystyle \frac{C_{{OM}_i}}{{\left(1+r\right)}^i}}\right)$$

(11)

where $\mathrm{E}\mathrm{A}\mathrm{C}\left(T\right)$ represents the equivalent annual cost of equipment with a lifespan of $T$ periods, $r$ denotes the discount rate per period, $C_P$ is the cost of purchasing new equipment, $S_T$ indicates the salvage value of equipment that is $T$ period old, and $C_{{OM}_i}$ represents the operating and maintenance cost over period $i$. They rewrote the EAC to consider continuous technological change using the study of Moor and Viscusi where α is the technological change rate:

$$\mathrm{E}\mathrm{A}\mathrm{C}=\left(T\right)= {\displaystyle \frac{1}{A(T,r)}}\left\{\begin{array}{c}{e}^{-\alpha T}\left[C_P-S_T+{\int }_0^T{C}_{OM}\left(t\right)e^{rt}dt\right]\\ +{\int }_o^T\alpha e^{-\alpha t}\left[C_{\theta }-S_T+{\int }_t^T{C}_{OM}\left(s\right)e^{rs}ds\right]dt\end{array}\right\}$$

(12)

where $C_P$ is the purchase cost of the current technology, $C_{\theta }$ presents the cost of the new technology after a breakthrough, $S_T$ indicates the salvage value of equipment at age $T$, and $C_{OM}\left(t\right)$ represents the operating and maintenance cost at time t. The parameter $r$ denotes the annual discount rate, α is the arrival rate of technology change, and A$\left(T,r\right)$ is the annuity factor, calculated using Equation (13):

$$A\left(T,r\right)= {\displaystyle \frac{1-e^{-rT}}{r}}$$

(13)

Hartman and Rogers [66] proposed a method for determining the EAC in the context of discontinuous technological change for engineering equipment, which we adopted in our analysis:

$$\mathrm{E}\mathrm{A}\mathrm{C} (T)=\left({\displaystyle \frac{(r+\alpha ){\left(1+r\right)}^T}{1-{(1+r)}^{-\frac{1}{\alpha }}}}\right)\left(C_P+{\displaystyle \frac{C_{\theta }-S_T}{{\left(1+r+\alpha \right)}^T}}+{\sum }_{i=1}^T{\displaystyle \frac{C_{{OM}_i}}{{\left(1+r+\alpha \right)}^i}}\right)$$

(14)

3.3. Joint Modelling

In each state of the equipment degradation model, there is a probability that new technology may or may not be introduced. Depending on this, along with the equipment’s degradation state, all parameters will be influenced by technological changes. For each degradation state, four decision scenarios arise: keep equipment if new technology arrives, renew equipment if new technology arrives, keep equipment if no new technology arrives, and renew equipment if no new technology arrives, which is presented in Figure 2.

Here, ‘KA’ represents ‘keep equipment’ when a breakthrough occurs, while ‘RA’ denotes ‘replace equipment’ when a breakthrough occurs. ‘KN’ refers to ‘keep equipment’ when a breakthrough does not occur, and ‘RN’ indicates ‘replace equipment’ when a breakthrough does not occur. Additionally, S = 1, 2, 3, …, M represent the different states of equipment health conditions based on degradation level. Condition 1 corresponds to a fully healthy state, and condition M represents the breakdown (catastrophic failure) state. To prevent failure, the model aims to predict the optimal renewal time at state M − 1 or earlier.

Therefore, EAC for equipment replacement due to technological change was explained in Section 3.2 which will be rewritten as Equation (15) by integrating three equipment lifespans:

$$EAC\left(T\right)=\left({\displaystyle \frac{\left(r+\alpha \right){\left(1+r\right)}^T}{1-{\left(1+r\right)}^{-\frac{1}{\alpha }}}}\right)\left(C_P+{\displaystyle \frac{C_{\theta }-S_T}{{\left(1+r+\alpha \right)}^T}}+{\sum }_{i,j=1}^S{\displaystyle \frac{\left(\left(q_{ij}{\phi }_i\right)P_{ij}\right)}{{\left(1+r+\alpha \right)}^T}}+{\sum }_{i,j=1}^S{\displaystyle \frac{C_{{PM}_{\left(i,j\right)}}{P}_{ij}}{{\left(1+r+\alpha \right)}^T}}+{\sum }_{i,j=1}^S{\displaystyle \frac{C_{{CM}_i}{P}_{i j }}{{\left(1+r+\alpha \right)}^T}}\right)+ {\displaystyle \frac{C_{BD}{P}_M}{{\left(1+r+\alpha \right)}^T}}$$

(15)

The next section details how optimisation algorithms support to solve the problem considering Equation (15) and identify optimal equipment replacement or renewal time from the integrated three lifespans of equipment.

4. Optimal Equipment Replacement and Renewal Model

Minimising EAC is essential for determining the optimal timing of equipment replacement or renewal, particularly when the objective is to maximise the equipment’s physical lifespan. This approach facilitates the best trade-off among operating costs, investment in new technologies, present value of the equipment, salvage value, maintenance costs—including preventive maintenance strategies—repair and breakdown costs, and the maximisation of the RUL.

In the presence of uncertainty and randomness, stochastic optimisation algorithms are commonly applied. These algorithms are generally categorised into two groups: heuristic and metaheuristic [67]. Although similar in nature, they differ in performance and scope. Heuristic algorithms aim to find high-quality solutions within a reasonable time frame, but they do not guarantee an optimal solution. They are suitable when finding a good, easily attainable solution is sufficient. Metaheuristic algorithms, which evolved from heuristic methods, typically offer better performance. They incorporate a defined balance between randomisation and local search, where randomisation helps the algorithm escape local optima and explore the global search space more effectively [65,68]. As a result, metaheuristic algorithms are well-suited for solving global optimisation problems.

Among metaheuristic algorithms, trajectory-based methods are well-suited for solving control problems using open-loop calculations. These algorithms explore the search space with a non-zero probability of reaching the global optimum. Dynamic programming is a well-known example of a trajectory-based algorithm [69]. It addresses complex problems by breaking them down into a sequence of simpler sub-problems, making it an effective optimisation approach [68]. A key feature of dynamic programming is its multistage decision-making process, which is central to its optimisation strategy. In addition to the techniques discussed earlier, dynamic programming offers a general framework for analysing a wide variety of problem types [68]. In this study, stochastic dynamic programming was applied to determine the optimal replacement or renewal time ($\tau$) for equipment in each health state, explicitly accounting for the uncertainty and probabilistic state transitions in equipment condition. Stochastic dynamic programming is a framework used to make sequential decisions under uncertainty, where the outcome of each decision is partly probabilistic [68]. Stochastic dynamic programming is a sequential decision-making framework under uncertainty, in which system states evolve over discrete stages according to a stochastic process rather than deterministically. In our study, each asset’s health state follows a stochastic degradation process. Stochastic dynamic programming enables us to compute an optimal replacement or renewal decision by minimising the expected total lifecycle cost across all possible decision paths whether to keep or replace the equipment at each state. This is achieved via Bellman’s principle of optimality, which ensures that the remaining decision from any given state forward is also optimal [69]. The decision-making process was guided by the following equation, which models the dynamic evolution of asset health and associated costs over time:

$$\tau ={\mathrm{m}\mathrm{i}\mathrm{n}}_t\left\{\left({\displaystyle \frac{EAC \left(t\right)}{t}}\right)\right\}$$

(16)

Subject to

$$\mathit{max}\left\{{RUL}^{\left(I\right)}=\widehat{D(}{H}_i^{\left(I\right)}){\sum }_{j=i+1}^{n-1}{D(H}_j)\right\}, \left(optimal equipment physical lifespan\right)$$

$$\min \left\{\left({\displaystyle \frac{(r+\alpha ){\left(1+r\right)}^T}{1-{(1+r)}^{-\frac{1}{\alpha }}}}\right)\left(C_P+{\displaystyle \frac{C_{\theta }-S_T}{{\left(1+r+\alpha \right)}^T}}+{\sum }_{i=1}^S{\displaystyle \frac{C_{{OM}_i}}{{\left(1+r+\alpha \right)}^T}}\right) \right\}, (\mathrm{o}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{l} \mathrm{n}\mathrm{e}\mathrm{w} \mathrm{t}\mathrm{e}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{y} \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t})$$

Equation (16) presents a single-objective optimisation problem that aims to minimise the total LCC associated with asset replacement decisions. The formulation incorporates key dynamic factors, including asset degradation (physical lifespan) and technological change.

The physical lifespan is estimated using RUL prediction derived from the DHSMM, as introduced in our previous publication [62]. The cost associated with technological change is quantified using Equation (15), and both factors are treated as constraints within the model.

These two constraints cannot be simultaneously optimised as maximising the physical lifespan supports asset retention, while minimising technology cost encourages early replacement which introduces a trade-off mechanism. Instead of classical hard constraint enforcement, the model adapts, where constraint satisfaction is implicitly balanced through their cost impacts within the objective function. 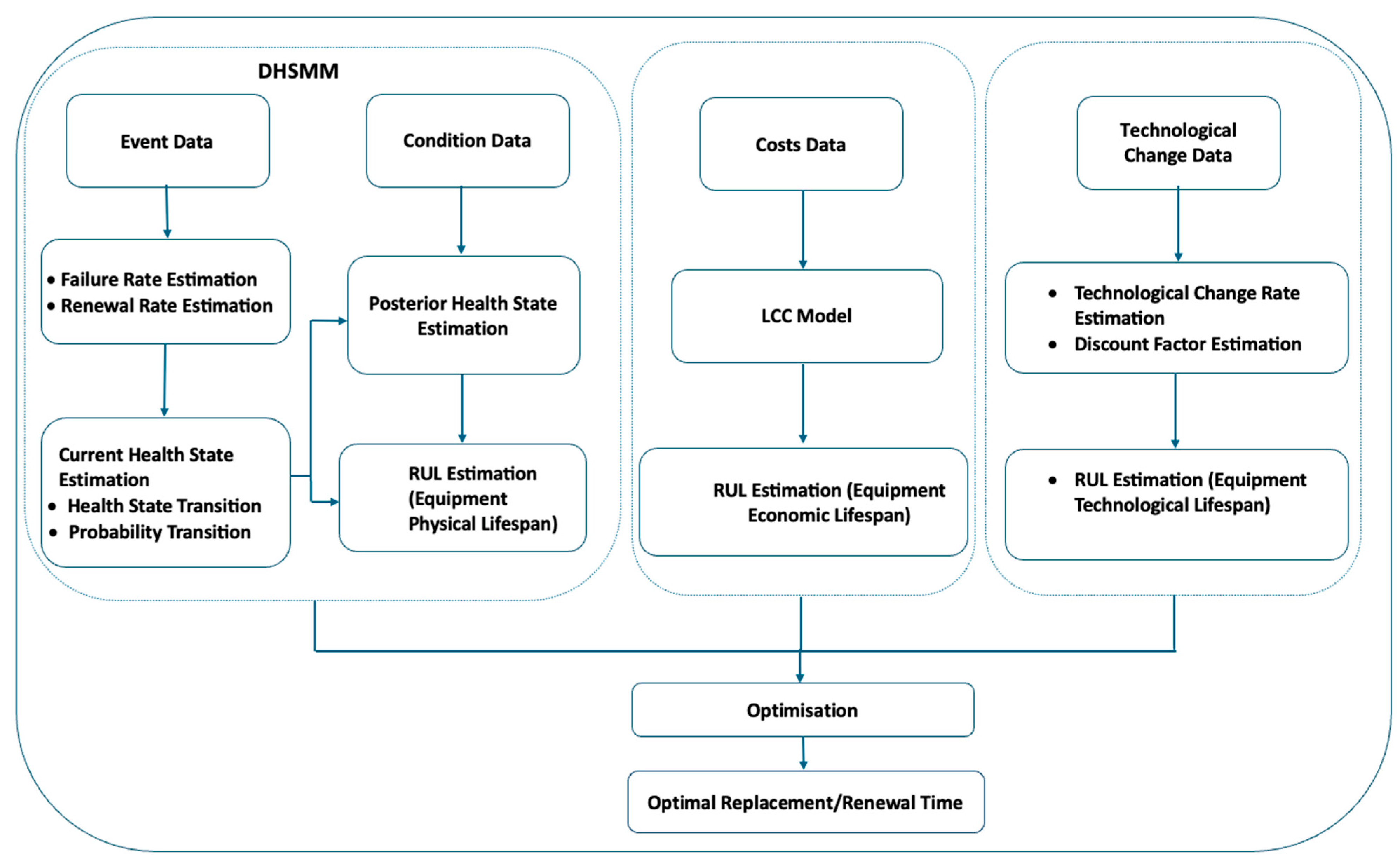Figure 3 presents the detailed steps of the novel equipment replacement and renewal time.

5. Case Study Results and Discussion

The wastewater pump station network in Murray Bridge, South Australia, was used as a case study to evaluate the proposed model. Located 75 km southeast of Adelaide, the township spans approximately 14 km² and features a mix of residential, commercial, and recreational land use. The network, which includes 31 pumping stations and integrates both gravity and pressure systems, conveys around 36 L/s—or roughly 3110 m³ per day—to the Murray Bridge Wastewater Treatment Plant (MB-WWTP). As a vital component of South Australia’s infrastructure, the system plays a key role in delivering reliable and cost-effective wastewater services while managing environmental impacts. Consequently, ensuring the reliability and availability of these assets has become a key priority for the water utility. Asset failures can lead to significant consequences, including service disruptions, environmental harm, risks to public health and wildlife, and potential regulatory penalties [62]. To address these challenges, asset managers need to adopt tactical asset management and replacement programmes that optimise renewal investment time while reducing downtime, minimising capital and operational costs and decreasing service interruptions.

Twenty years of historical maintenance records were obtained from multiple sources, including the Computerised Maintenance Management System (CMMS), Enterprise Data Warehouse (EDW), and Supervisory Control and Data Acquisition (SCADA). These data included equipment condition data (e.g., vibration, pump performance, flow and pressure data), event data, operating costs (e.g., electricity, fuel, chemical, labour), maintenance costs (e.g., preventive maintenance costs, repair or corrective maintenance costs, breakdown costs), cost of the new technology, arrival time of new technology, discount factor, purchase cost of new technology, equipment present value, and salvage value. These data covered 8 of the 31 pump stations within the Murray Bridge wastewater network. These eight pump stations were selected due to their classification as high-criticality assets for the business, based on factors such as customer impact, system redundancy, and the lead time for spare parts. Figure 4 illustrates the schematic diagram of the wastewater pump station network and highlights the target pump stations used in this study.

A data preprocessing phase was conducted using expert knowledge and fuzzy logic techniques to clean and transform the raw datasets into a format suitable for modelling and validating the performance of the proposed novel optimal equipment replacement and renewal approach. To evaluate the model’s effectiveness, its outcomes were assessed in terms of cost savings and improvements in equipment performance, both key industry performance indicators. These results were then compared with those from the water utility’s existing replacement and renewal approach.

The transition probability matrix was derived using DHSMM, while RUL associated with physical lifespans was quantified based on Equation (8). The authors evaluated asset health indicators and technical specifications within the operational context to identify the optimal number of states for modelling asset health using a DHSMM. This evaluation considered several critical factors, including the complexity of asset health state representation, the availability and resolution of relevant data, computational feasibility, and the application of statistical techniques such as the Bayesian Information Criterion. Furthermore, the analysis was informed by a review of the existing literature, industry best practices, and relevant international standards. Notably, international asset management standards commonly recommend a five-state classification scheme for asset condition assessment, a guideline derived from extensive cross-sectoral data analyses [70]. These five-state classifications of asset’s health include one (very good), two (fair, meaning good but minor defect), three (major maintenance required), four (poor condition), and five (very poor condition or catastrophic failure).

Table 1. Equipment health and condition ratings.

Equipment Condition Rating	Description of Equipment Condition
1	Very good condition. Equipment requires normal preventive maintenance.
2	Fair condition (good condition but minor defects only). Equipment requires minor repair and normal preventive maintenance.
3	Major maintenance and repair required to return equipment to accepted level of service.
4	Poor condition. Significant equipment renewal or upgrade required.
5	Very poor condition (catastrophic failure). Equipment unserviceable and requires full replacement.

presents the overview of these condition ratings along with their associated maintenance, renewal, and replacement strategies [62].

Accordingly, Equation (3) and the transition probability matrix can be expressed as:

$$Q=\left(q_{ij}\right)=\left[\begin{array}{c}{-\lambda }_1\\ 0\\ 0\\ 0\\ P_{51}{\mu }_{51}\end{array} \begin{array}{c}{P_{12}\lambda }_1\\ {-\lambda }_1\\ 0\\ 0\\ 0\end{array} \begin{array}{c}0\\ P_{23}{\lambda }_1\\ {-\lambda }_2\\ 0\\ 0\end{array} \begin{array}{c}0\\ 0\\ P_{34}\\ {-\lambda }_2\\ 0\end{array} \begin{array}{c}0\\ 0\\ 0\\ P_{45}{\lambda }_2\\ -{\mu }_{51}\end{array} \right]$$

(17)

Similarly, the probability function, i.e., $P_{11}\left(t\right),P_{12}\left(t\right),P_{13}\left(t\right),{\dots ,P}_{45}\left(t\right),P_{55}\left(t\right)$ will then generate the probability matrix for the new state process as shown below:

$$P=\left(P_{ij}\right)=\left| \begin{array}{c}{P}_{11}\\ P_{21}\\ P_{31}\\ P_{41}\\ P_{51}\end{array} \begin{array}{c}{P}_{12}\\ P_{22}\\ P_{32}\\ P_{42}\\ P_{52}\end{array} \begin{array}{c}{P}_{13}\\ P_{23}\\ P_{33}\\ P_{43}\\ P_{53}\end{array} \begin{array}{c}{P}_{14}\\ P_{24}\\ P_{34}\\ P_{44}\\ P_{54}\end{array} \begin{array}{c}{P}_{15}\\ P_{25}\\ P_{35}\\ P_{45}\\ P_{55}\end{array}\right|$$

(18)

Table 2. The critical Murray Bridge sewer pump stations.

Pump Station	Identification Number	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	$\mathit{\mu }$
Pump Station No.1	MBR001	0.37	0.068	0.068
Pump Station No.2	MBR002	0.41	0.13	0.034
Pump Station No.3	MBR003	0.51	0.10	0.17
Pump Station No.6	MBR006	0.95	0.068	0.068
Pump Station No.11	MBR011	0.41	0.10	0.068
Pump Station No.12	MBR012	0.38	0.58	0.10
Pump Station No.14	MBR014	0.51	0.14	0.10
Pump Station No.18	MBR018	0.82	0.068	0.10

provides the naming convention for these wastewater pump stations, and it also illustrates the estimated failure rates ${(\lambda }_1, {\lambda }_2)$ and renewal rate $\left(\mu \right)$ using the log-beta Weibull model, based on our previous work [71].

The novel DHSMM was applied to estimate the RUL of equipment based solely on degradation patterns, focusing on physical lifespan [71]. Historical data from eight critical wastewater pump stations in the Murray Bridge network were used to validate the model’s accuracy. A 70/30 split was employed for training and testing, respectively, to evaluate the model’s performance. The results demonstrated strong predictive capability, achieving an RUL estimation accuracy of around 88% from Equation (19) [62].

$$100\%\times \left({\displaystyle \frac{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{s}-\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{a}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{a}\mathrm{l} \mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e} \mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t} \mathrm{s}\mathrm{e}\mathrm{t} \mathrm{a}\mathrm{r}\mathrm{e} \mathrm{n}\mathrm{o}\mathrm{t} \mathrm{s}\mathrm{a}\mathrm{m}\mathrm{e} \mathrm{a}\mathrm{s} \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{o}\mathrm{n}\mathrm{e}}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{s}}}\right)$$

(19)

In this study, the estimated RUL is considered as the optimal interval for equipment replacement and renewal.

Table 3. Predicted replacement/renewal interval using DHSMM for Murray Bridge sewer pump stations.

Pump Station	Identification Number	Predicted Replacement and Renewal Interval (Years)
Pump Station No.1	MBR001	17.6
Pump Station No.2	MBR002	8.0
Pump Station No.3	MBR003	4.1
Pump Station No.6	MBR006	10.1
Pump Station No.11	MBR011	15.5
Pump Station No.12	MBR012	5.0
Pump Station No.14	MBR014	8.1
Pump Station No.18	MBR018	8.8

presents these results for eight critical wastewater pump stations in Murray Bridge.

Given the uncertainty associated with the arrival time of the new technology, historical data were utilised in conjunction with a Poisson process to estimate the technology change rate α. The estimated value of α was determined to be 0.45. Furthermore, a discount rate of 5% was adopted in this study based on national guidelines and industry practice across Australian water utilities. This value reflects the typical project rate used in public infrastructure investment evaluations. While asset behaviour can vary across locations, the pumps analysed in this study were selected from a representative and standardised wastewater network. Their operational and degradation characteristics are consistent with national benchmarks, justifying the generalisation used in the model.

These parameters were subsequently incorporated into Equation (15), enabling the application of stochastic dynamic programming to address the optimisation problem. The optimisation framework determined the optimal timing for the replacement or renewal of submersible pumps by simultaneously minimising EAC, subject to the constraints of maximising the RUL and minimising the introduction cost of the new technology.

Table 4. Predicted replacement and renewal interval of eight critical wastewater pumps at Murray Bridge sewer network using the novel model that integrates three aspects of their lifespans.

Pump Station	Identification Number	Predicted Replacement and Renewal Interval Using Integrated Model (Years)	Replacement and Renewal Interval Using Economic Lifespan and OEM Recommendation (Years)
Pump Station No.1	MBR001	16.0	10.0
Pump Station No.2	MBR002	7.0	10.0
Pump Station No.3	MBR003	3.0	10.0
Pump Station No.6	MBR006	8.5	10.0
Pump Station No.11	MBR011	13.3	10.0
Pump Station No.12	MBR012	5.0	10.0
Pump Station No.14	MBR014	7.0	10.0
Pump Station No.18	MBR018	7.0	10.0

illustrates the projected optimal replacement and renewal timing for the selected wastewater pump stations. These projections are derived from the proposed integrated decision-making model, which accounts for three critical dimensions of asset lifespan. The model’s outcomes are compared against the current asset management strategy employed by the water utility, which is primarily based on operating and maintenance costs in conjunction with Original Equipment Manufacturer (OEM) recommendations.

Although relying on OEM recommendations and economic lifespan is a common industry practice, this approach may not always lead to optimal asset replacement or renewal outcomes. In many cases, such strategies are based on fixed lifespan assumptions that do not reflect the actual condition, performance, or operating environment of the equipment. Therefore, assets may be replaced prematurely, before their useful life is fully utilised, or too late, risking failure and service disruption.

Furthermore, this conventional approach often fails to consider dynamic factors such as equipment degradation, condition-based maintenance requirements, and the timing of technological change. In contrast, the proposed integrated model addresses these limitations by combining real-time health data, operating costs, and technology change, enabling more precise and cost-effective decision-making.

These results demonstrate that the proposed integrated model can predict the RUL of each pump by simultaneously incorporating degradation and failure (physical lifespan), operating and maintenance costs (economic lifespan), and technological advancements offering a distinct advantage over the utility’s current normalised strategy.

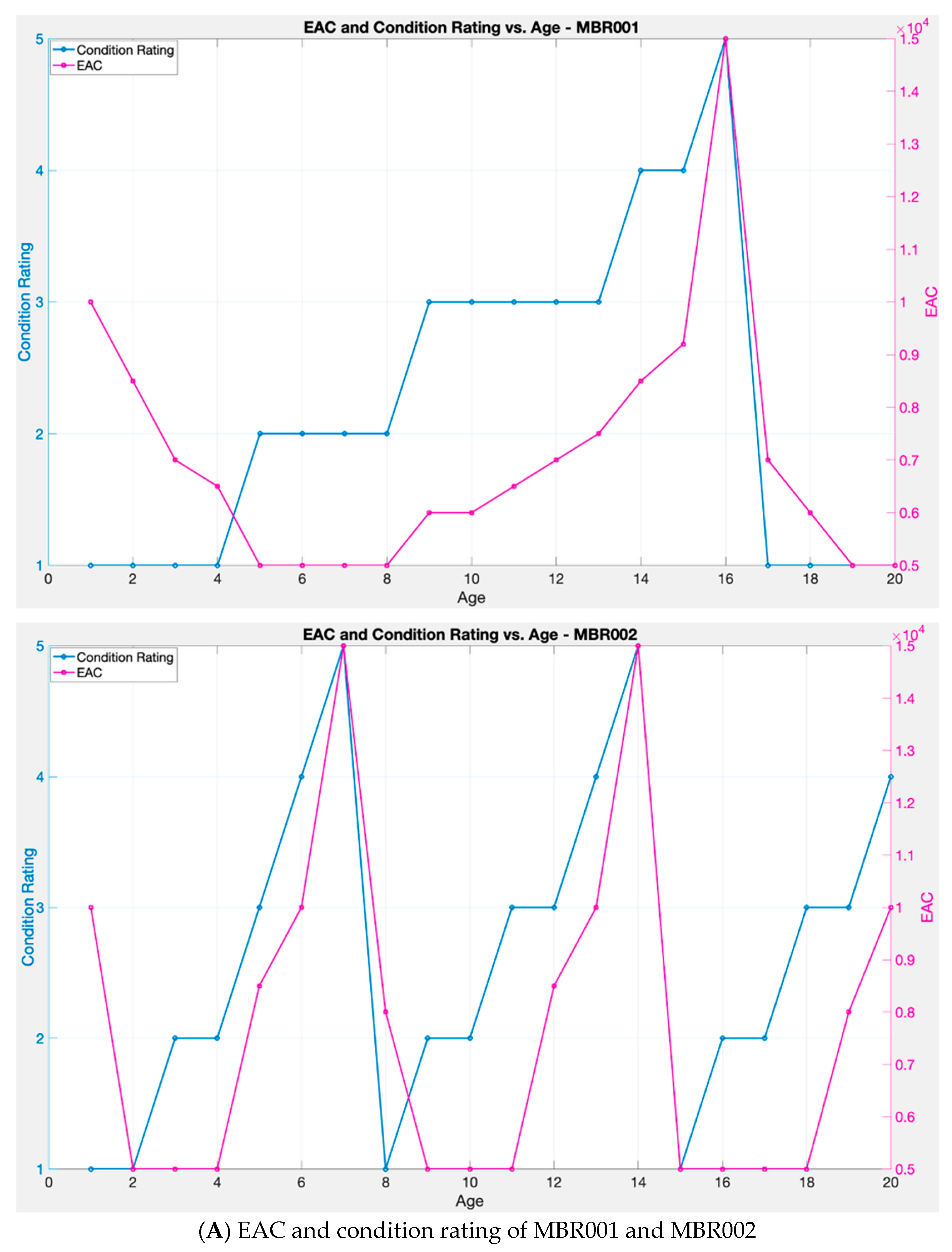
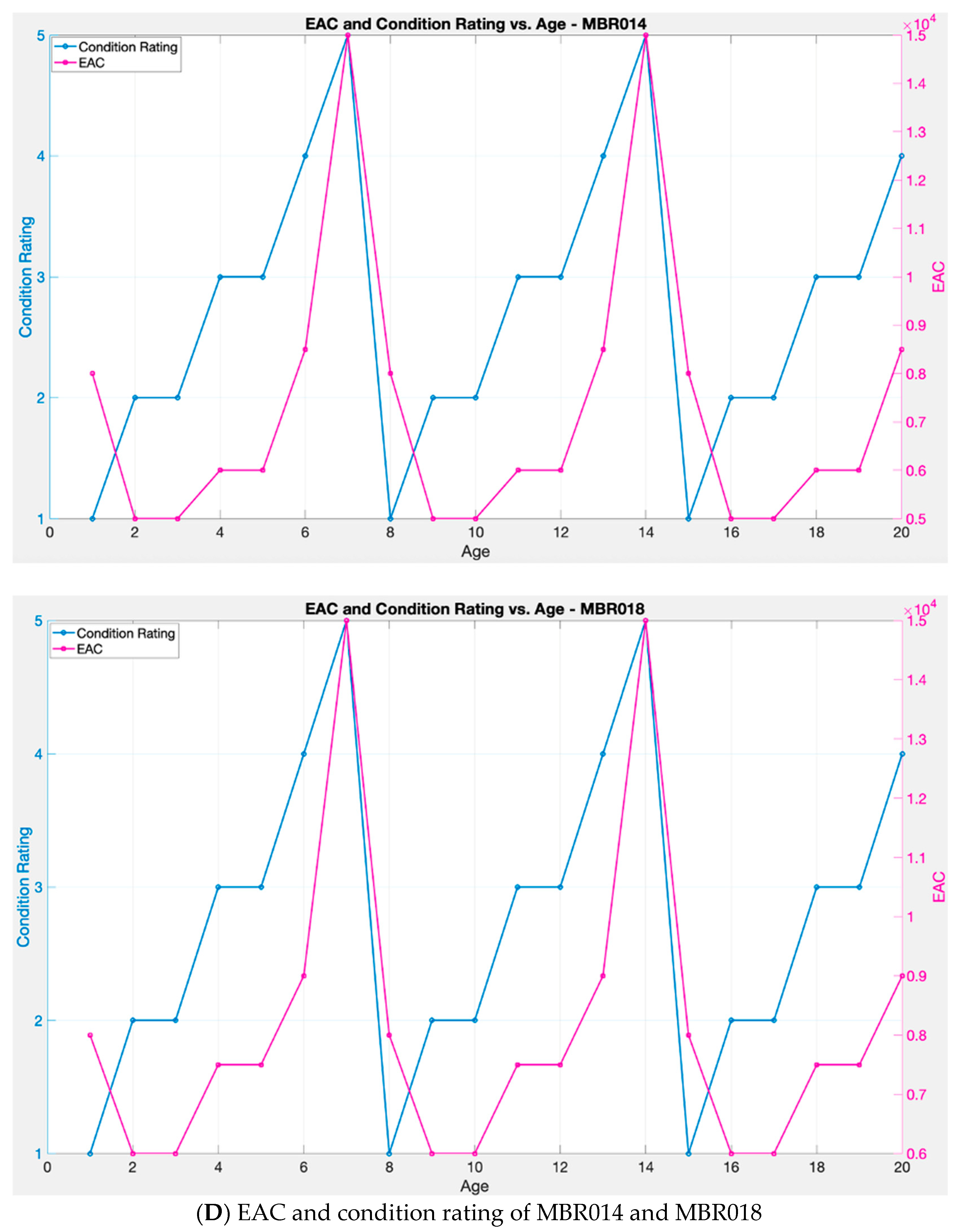
Figure 5 presents these data graphically, including EAC, equipment health, and condition rating for the selected eight pumps.

Figure 5 illustrates the relationship between component age, costs, and equipment health condition rating across multiple case scenarios. It is important to clarify that the EAC presented in Figure 5 represents the annualised cost of owning and operating the asset over its expected lifespan, including capital expenditure, salvage value, and operating and maintenance costs. As equipment age increases, EAC tends to rise, while the health and condition rating correspondingly declines. This trend is consistent with typical equipment degradation behaviour, wherein ageing infrastructure or equipment requires increased operation and maintenance expenditures to sustain functionality. When equipment is renewed, its health and condition rating is restored to state 1, and the degradation curve resets accordingly. However, the EAC reflects a smoothed cost profile over the full lifecycle and includes the operating and maintenance cost which, even after renewal, persists to ensure the asset is maintained appropriately and to prevent premature degradation.

The comparative analysis of eight wastewater pumps highlights variability in asset behaviour, emphasising the critical importance of tailored maintenance strategies. Assets maintained through proactive and periodic interventions exhibit more stable health profiles and restrained cost escalation. Conversely, systems subject to reactive or delayed maintenance demonstrate pronounced cost spikes and accelerated health deterioration. These findings underscore the value of predictive, data-driven asset management frameworks to identify optimal equipment replacement/renewal timing through optimising lifecycle costs while ensuring service reliability and operational performance improvement.

The results presented in Table 4 further demonstrate that the replacement or renewal interval for equipment is reduced when newer technologies assessed using the integrated model developed in this study are adopted. The adoption of advanced technologies enhances operational efficiency, resulting in significant reductions in operating expenses. Furthermore, newly installed equipment, being in optimal physical condition, demands less maintenance, thereby lowering associated costs and extending the RUL.

To evaluate the performance of the proposed model, key industry metrics such as cost savings and efficiency improvements were utilised. In this study, efficiency improvements were translated into cost savings using Equation (20), as cost reduction is widely recognised as a primary performance indicator in industry practice. This approach provides a comprehensive basis for assessing the model’s effectiveness in supporting asset renewal decisions for long-term strategy.

$$\mathrm{P}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e} \mathrm{I}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{r}={\displaystyle \frac{E.(\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{p}\mathrm{e}\mathrm{r} \mathrm{k}\mathrm{W})}{C_o+C_m}}={\displaystyle \frac{Q\cdot H\cdot \gamma }{\eta \cdot 1000}}$$

(20)

where E presents pump output power usage (kW), Q denotes flow rate (${\displaystyle \raisebox{1ex}{$m^3$}\!\left/ \!\raisebox{-1ex}{$s$}\right.}$), H is the total dynamic head (m), γ gives the specific weight of the fluid (≈9.91 kN/m³ for wastewater), η is pump efficiency (as a decimal, e.g., 0.90), $C_o$ indicates operating cost, and $C_m$ is total maintenance cost.

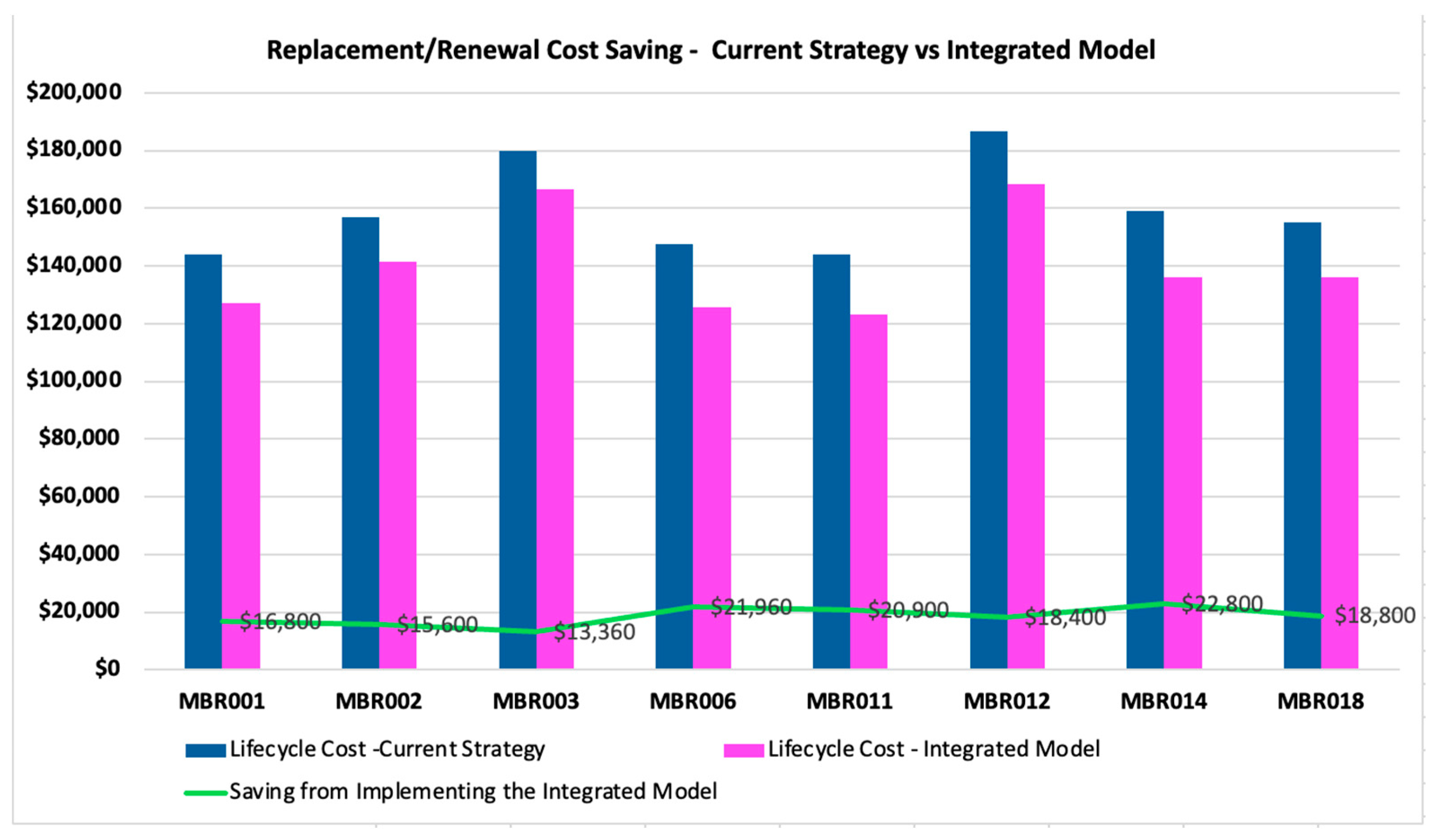
Figure 6 presents the estimated cost savings for each wastewater pump. On average, the implementation of the novel integrated model for equipment replacement and renewal strategy results in a cost reduction of approximately 12%.

Additional analysis revealed that cost savings varied across the sewer pump stations due to several influencing factors. These included differences in operating conditions shaped by customer type and volume, variation in pump cycling frequency influenced by wet well levels and fluctuations in energy pricing, and disparities in wet well capacities. Furthermore, site-specific chemical dosing tailored to the nature of the incoming wastewater (e.g., residential vs. commercial) and the diverse designs and network roles (primary or secondary) of the stations also contributed to the observed differences.

In addition, the performance of the proposed integrated model was evaluated by using a 70/30 split of the dataset for training and testing, respectively and comparing its results with the actual replacement and renewal intervals recorded in the test dataset for the wastewater pumps. Accuracy was calculated using Equation (19) and was determined to be 91%.

6. Conclusions

Optimised asset lifecycle decision-making represents a critical area of research and practice within engineering asset management. Water utilities are increasingly seeking advanced methods to enhance their asset management maturity to improve water quality, increase service reliability, implement smarter investment strategies, minimise customer disruptions, and strengthen decision-making capabilities, all while maintaining the lowest possible service delivery costs. In this context, the integration of whole-life costing principles across the full asset lifecycle, from capital delivery through daily operations to long-term maintenance, has become a strategic priority. It enables utilities to optimise both asset performance and operational processes while minimising associated risks and expenses.

This study introduces a novel optimal asset lifecycle decision-making model that explicitly incorporates the key dimensions of asset life and their influencing factors. The innovation of the model manifests in its integrated consideration of three critical aspects: (1) asset degradation and failure events, (2) operating and maintenance costs, and (3) technological advancements. These are jointly modelled and optimised using a combination of single-objective optimisation with two constraints and stochastic dynamic programming, enabling the estimation of the optimal timing for asset renewal and replacement.

To evaluate the model’s effectiveness, historical data from eight critical wastewater pump stations in the Murray Bridge wastewater network were analysed. The results demonstrate that the application of the proposed integrated model for equipment replacement and renewal can lead to substantial economic benefits. Specifically, an average cost saving of approximately 12% was achieved across the assessed wastewater pumps, highlighting the model’s potential to enhance decision-making efficiency and support more sustainable asset management.

While the current model does not include explicit technical or budgetary constraints, it captures two critical decision drivers: physical degradation and technological change. Future research could extend this framework by incorporating additional constraints such as capital expenditure limits, downtime tolerances, or operational availability requirements to enhance the model’s practical applicability.

Moreover, the model can be improved by incorporating considerations of technological obsolescence a growing concern for industries managing electrical and mechanical equipment. Furthermore, the model could be extended to account for government incentives, such as depreciation benefits or tax credits, for investing in environmentally sustainable technologies, thus integrating tax implications into the decision-making framework.