Machine Learning-Based Highway Pavement Performance Prediction in Xinjiang
Abstract
1. Introduction
1.1. Development of Pavement Performance Evaluation
1.2. Application of Machine Learning in Pavement Performance Evaluation
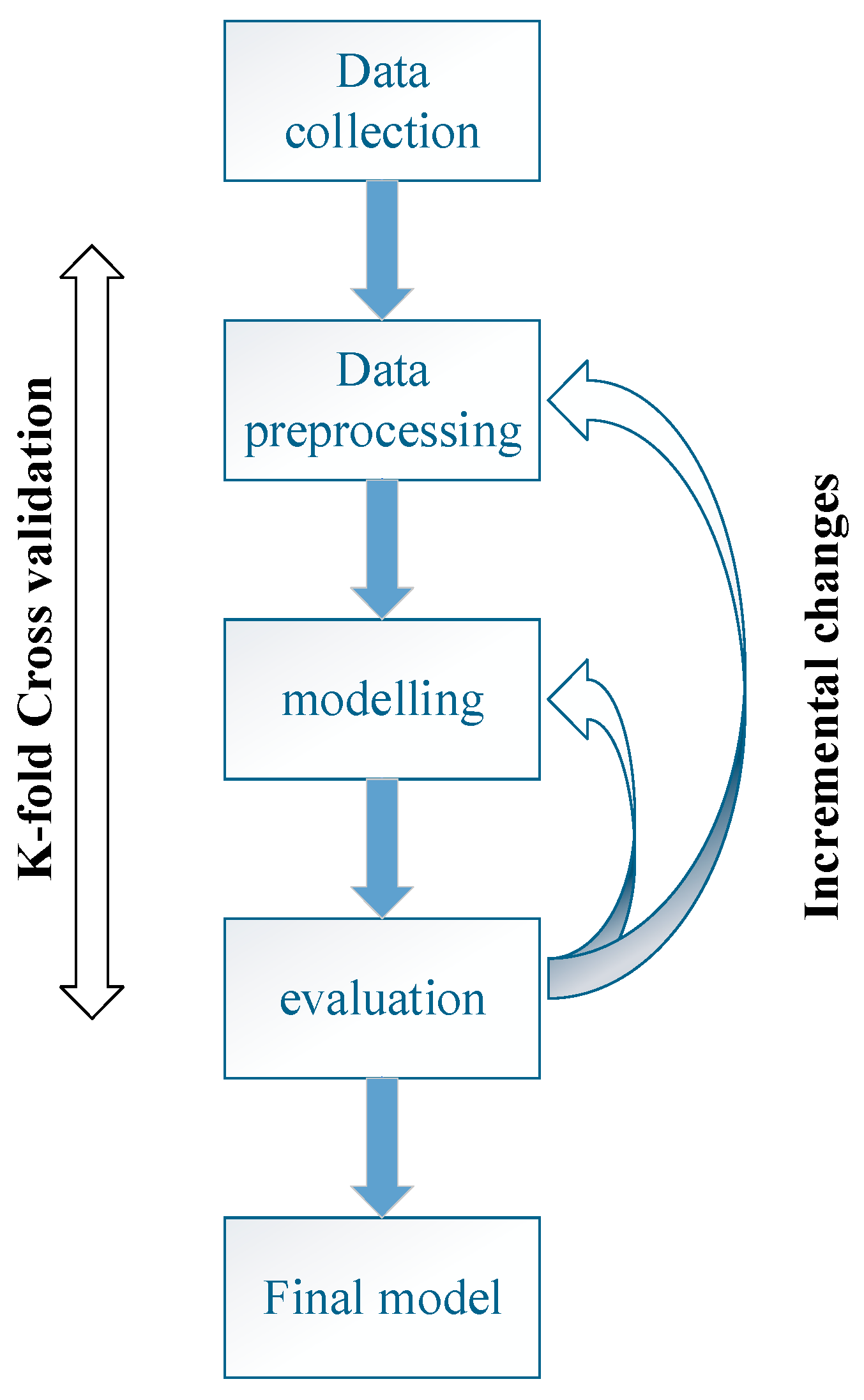
2. Methodology
2.1. Machine Learning Framework and Computational Process
2.1.1. BP Neural Network
2.1.2. PSO-BP Neural Network
2.1.3. Random Forest
2.1.4. Convolutional Neural Network
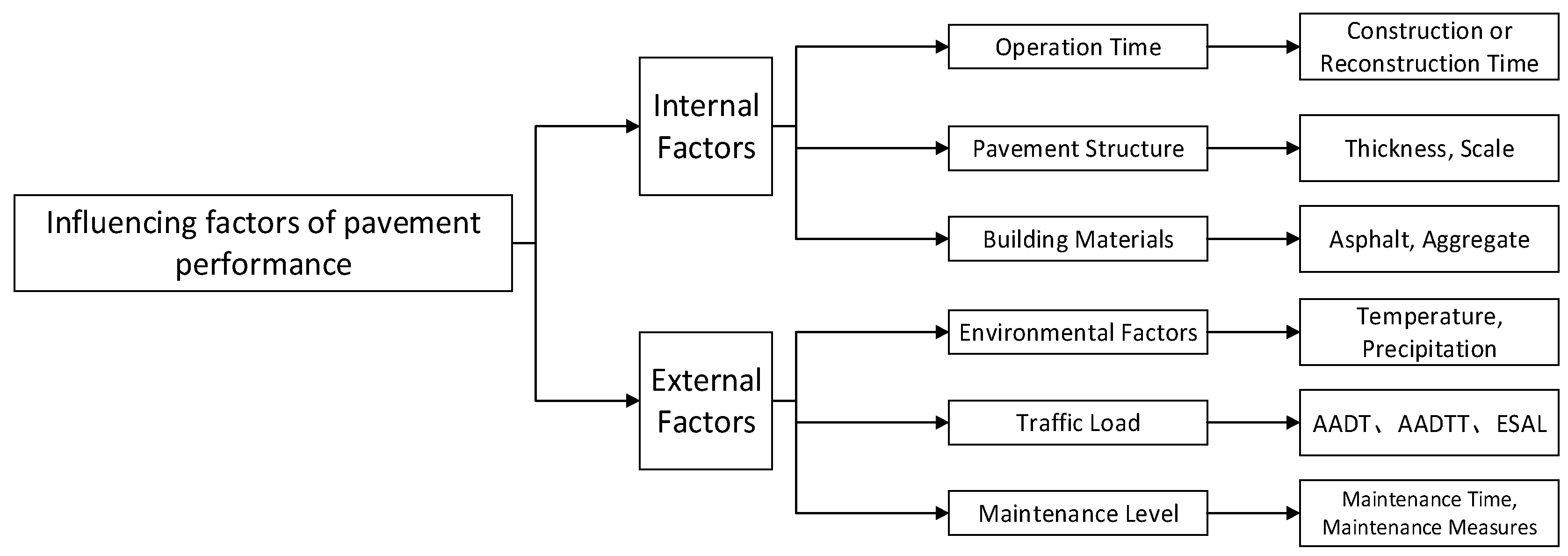
2.2. Data Collection and Indicator Determination
2.3. Performance Indicators
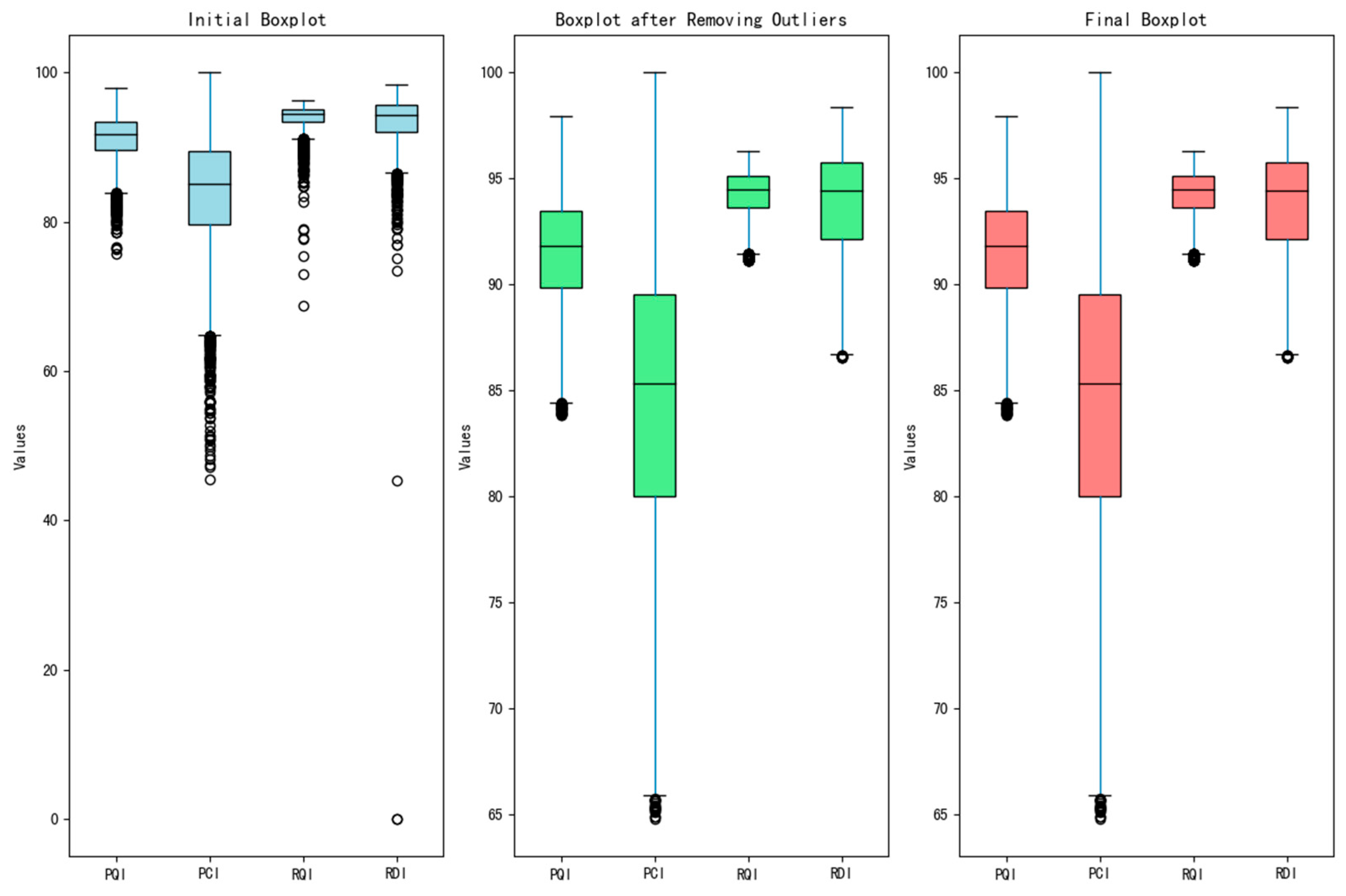
2.4. Data Preprocessing
3. Results
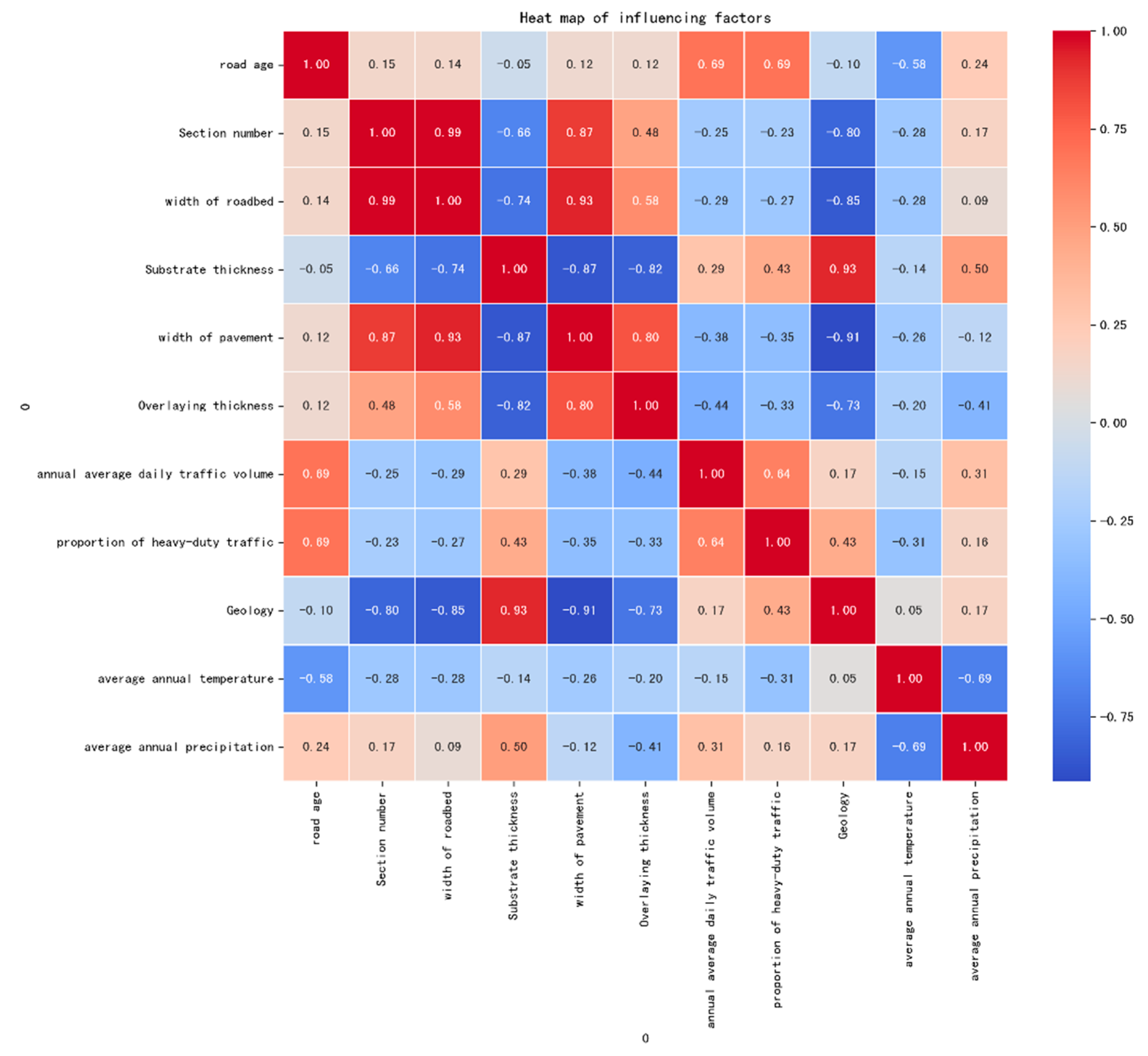
3.1. Analysis of Influencing Factors
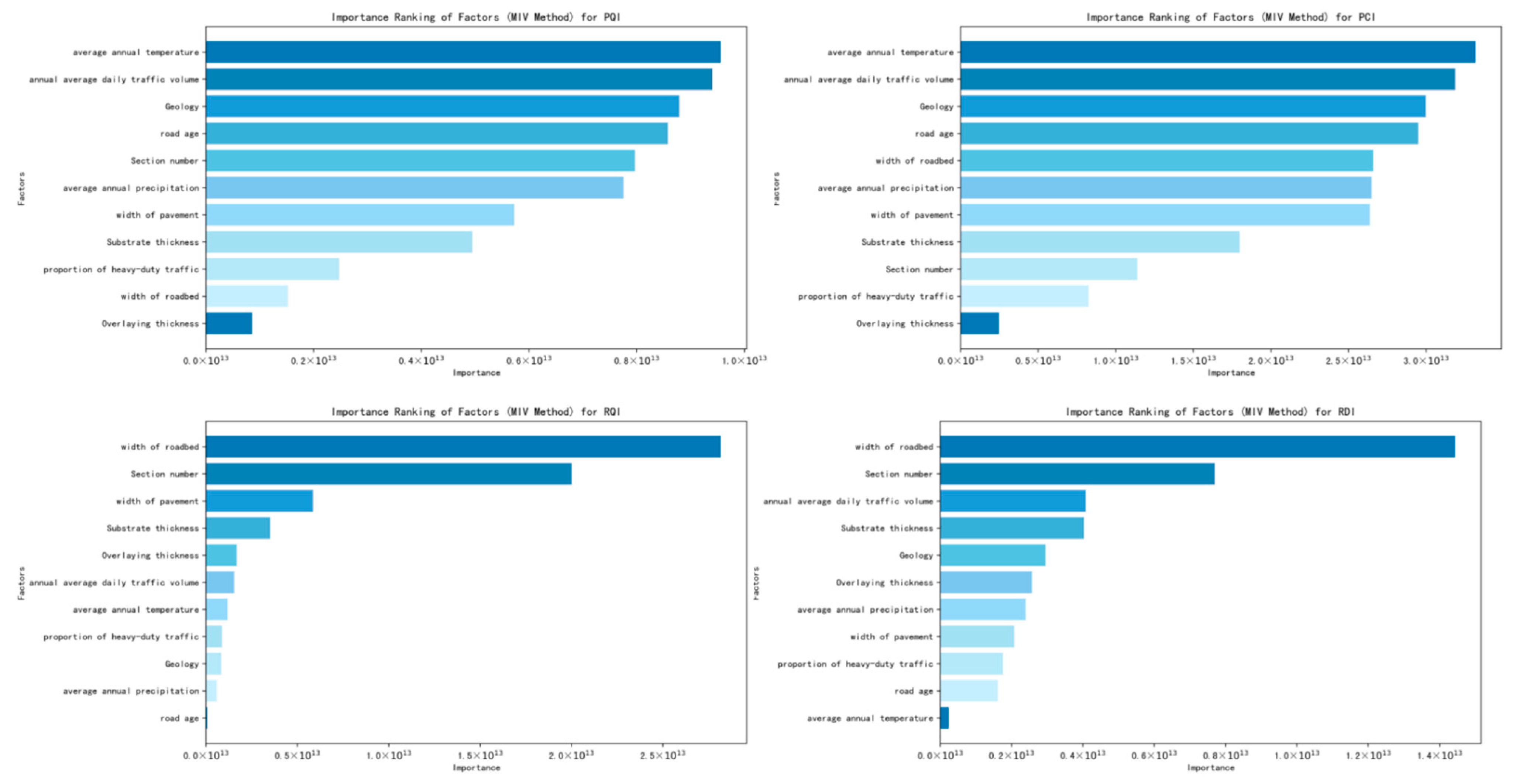
3.2. The Importance of Influencing Factors
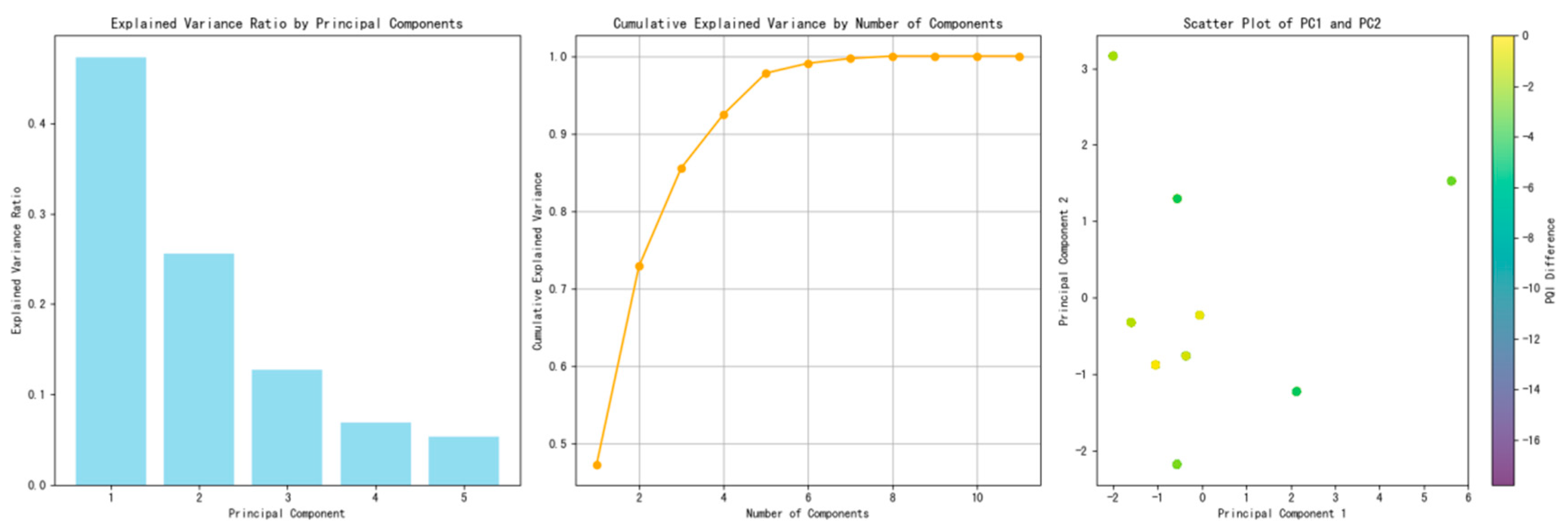
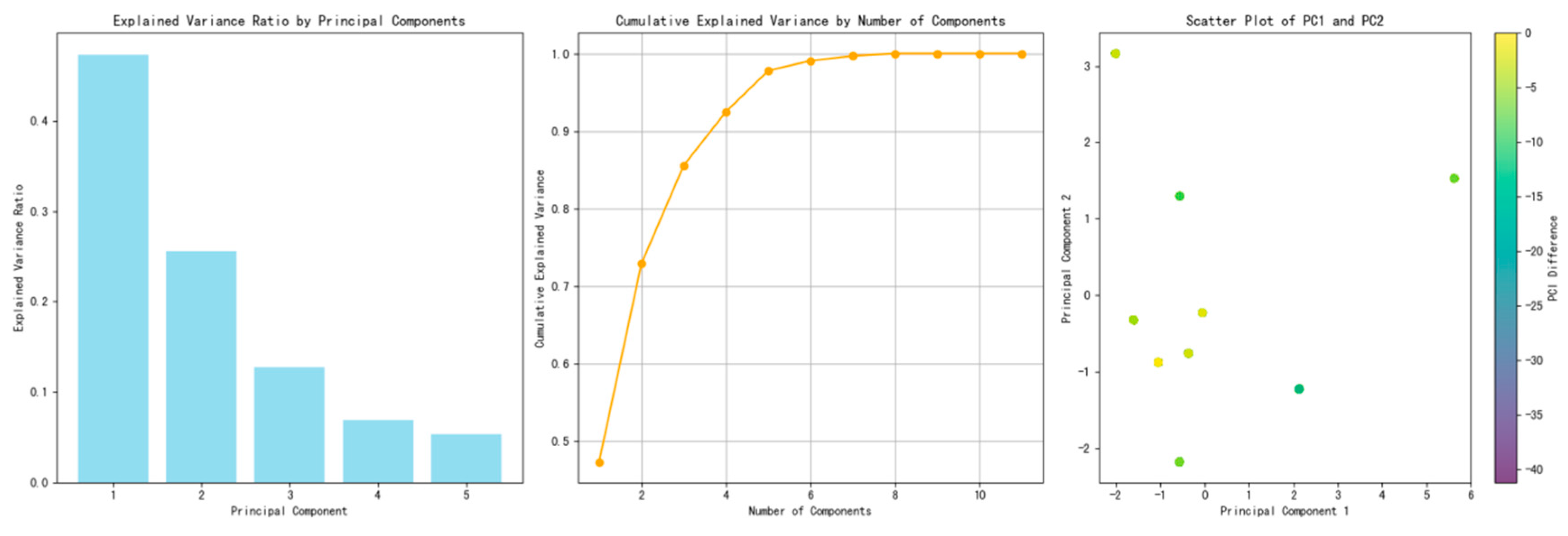
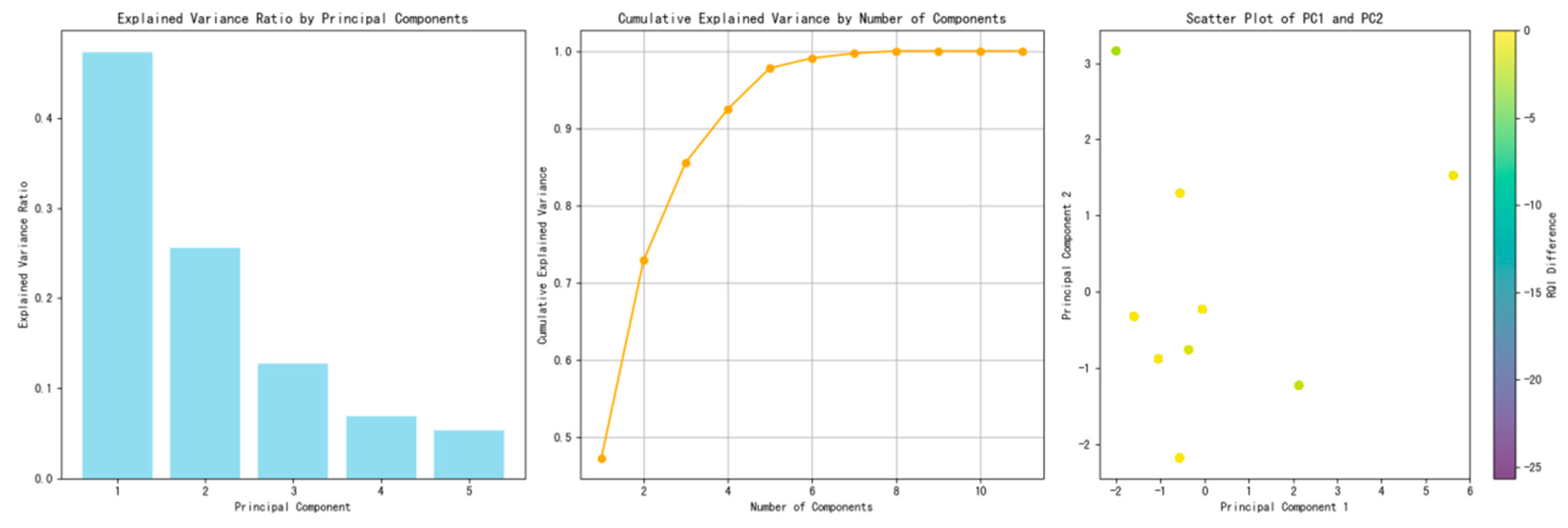
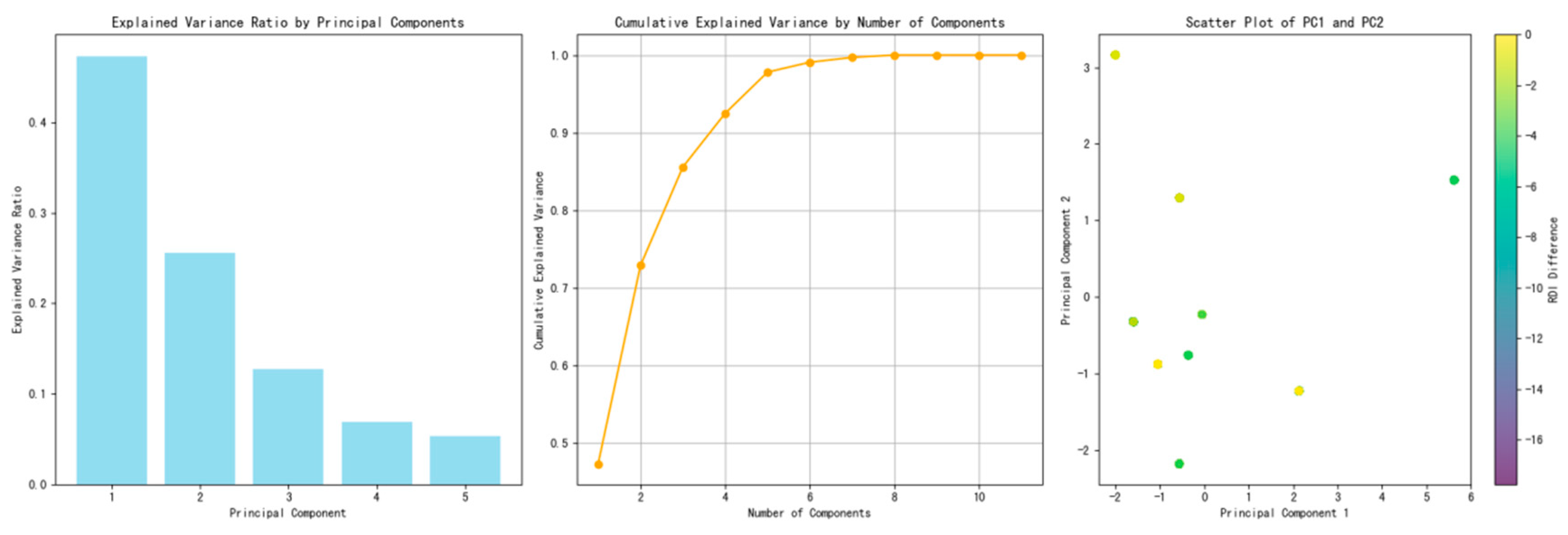
3.2.1. Principal Component Analysis
- Identification of Variance Contributors: Principal Component Analysis (PCA) facilitates the identification of variables that predominantly contribute to the variance within the dataset, thereby elucidating the most influential factors.
- Simplification of Data Structure: By reducing the complexity of the data structure, Principal Component Analysis (PCA) makes the analytical process more manageable and computationally efficient.
3.2.2. Feature Importance Analysis
- Model Training: A Random Forest regression model is trained for each evaluation metric (PCI difference, RQI difference, RDI difference), treating each as the dependent variable.
- Importance Scoring: Importance scores are assigned to each influencing factor, reflecting the average contribution of each variable across the ensemble of Decision Trees.
- Influence Assessment: A higher score indicates a greater influence of the factor on the model’s predictive capacity.
3.2.3. Synergistic Analysis
3.3. Neural Network Modeling
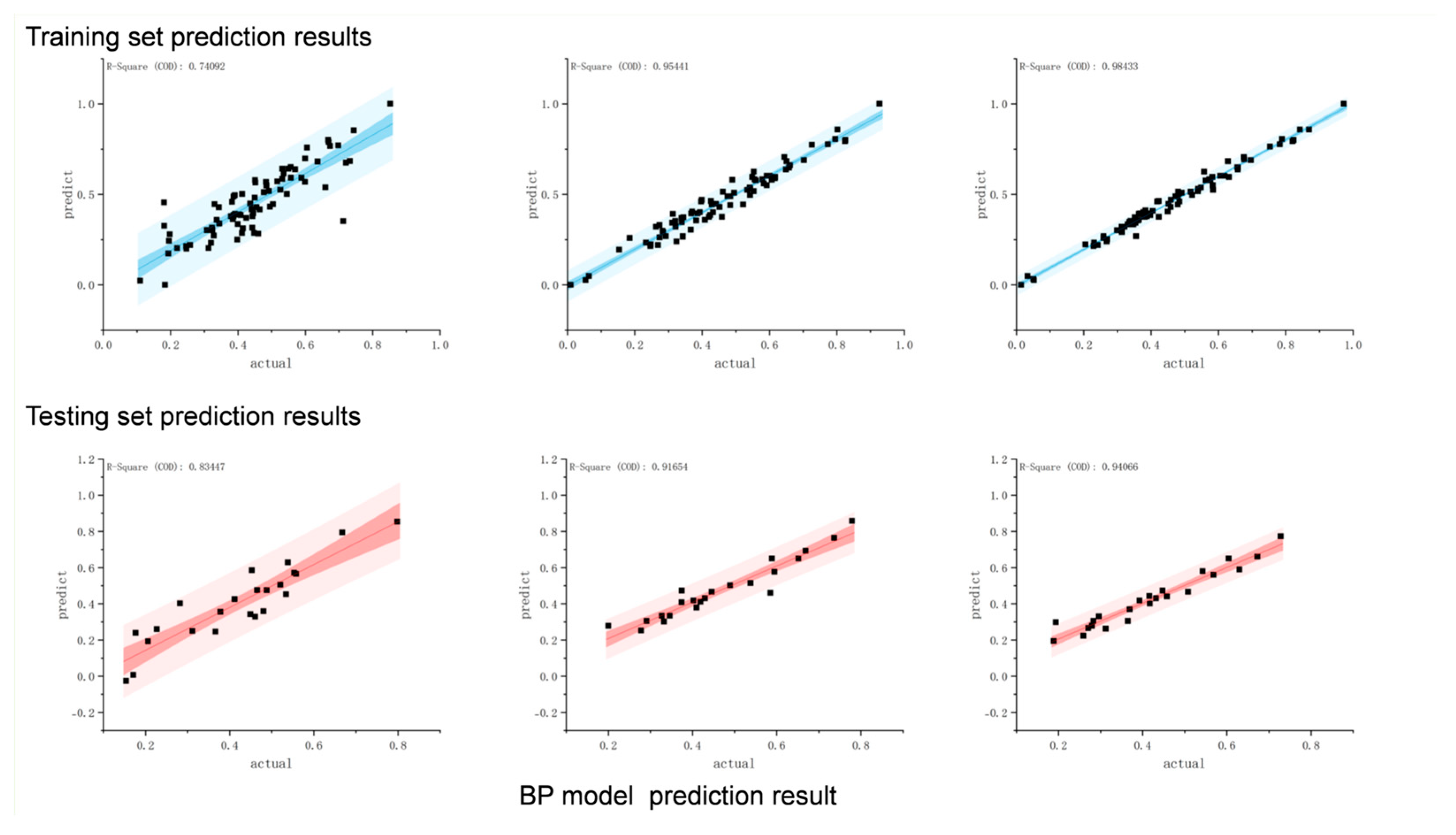
3.3.1. BP Neural Network
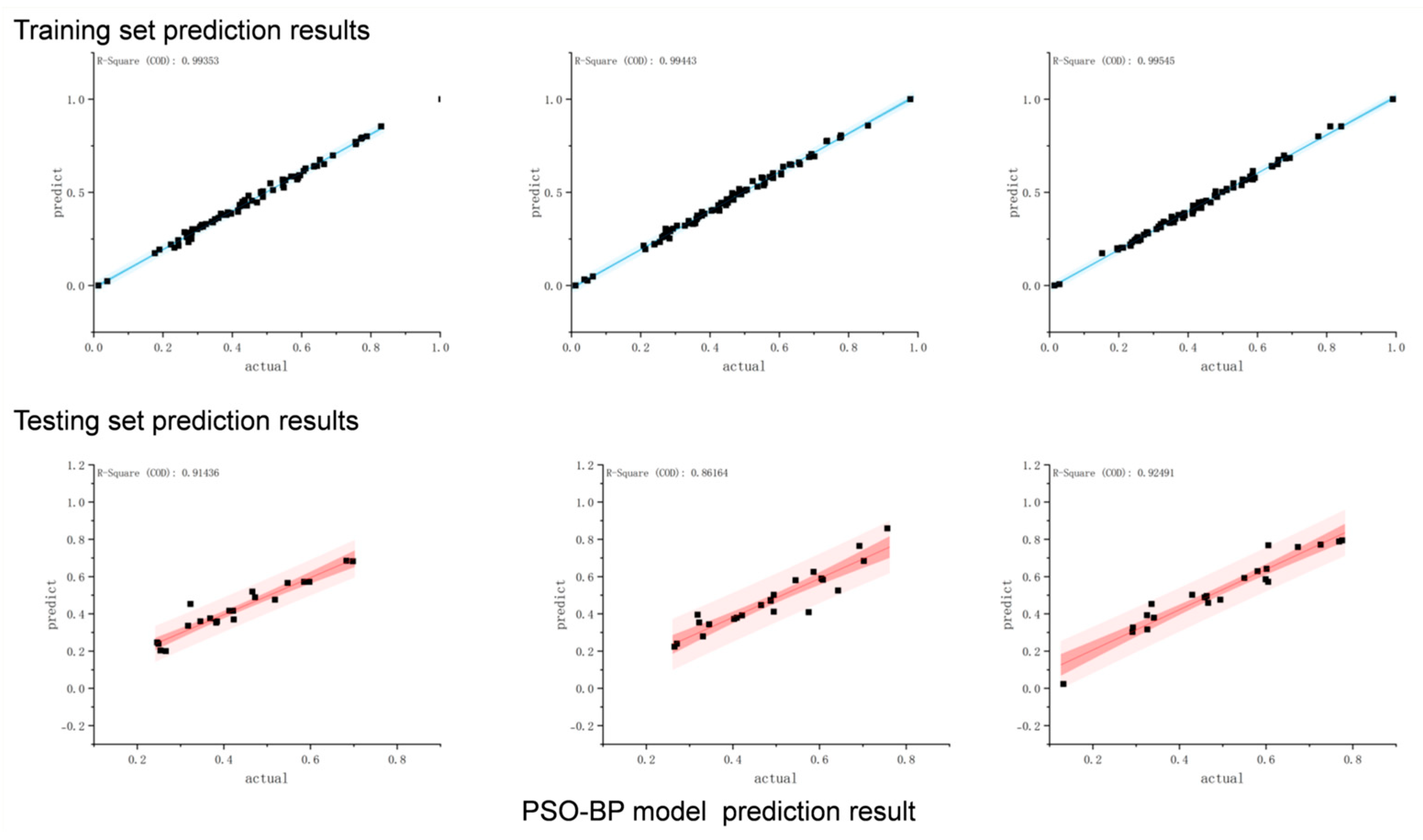
3.3.2. PSO-BP Neural Network
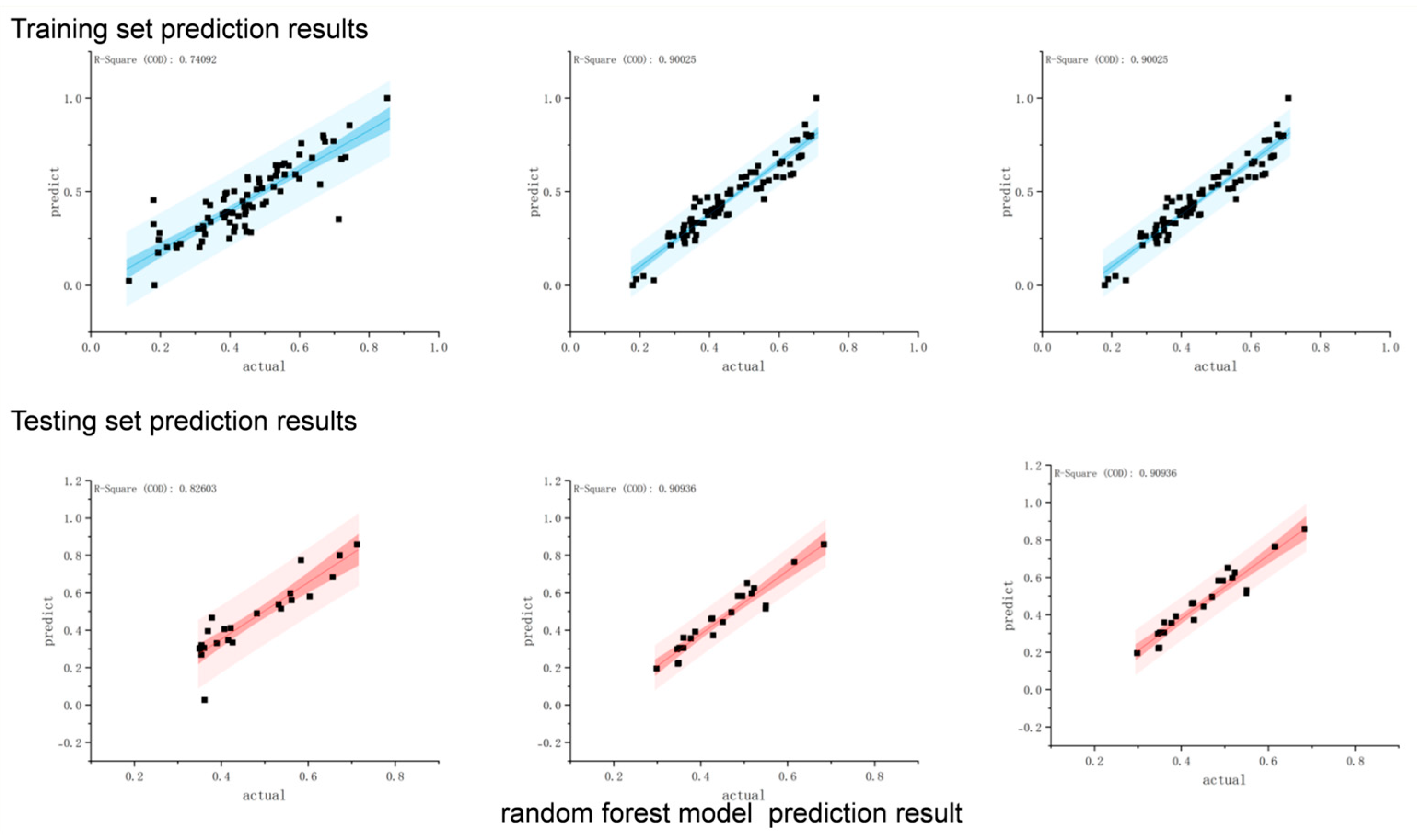
3.3.3. Random Forest
3.3.4. Convolutional Neural Network
3.3.5. Characterization of Model Performance
3.3.6. Model Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chan, C.Y.; Huang, B.; Yan, X.; Richards, S. Relationship Between Highway Pavement Condition, Crash Frequency, and Crash Type. J. Transp. Saf. Secur. 2009, 1, 268–281. [Google Scholar] [CrossRef]
- Aleadelat, W.; Saha, P.; Ksaibati, K. Development of Serviceability Prediction Model for County Paved Roads. Int. J. Pavement Eng. 2018, 19, 526–533. [Google Scholar] [CrossRef]
- Isradi, M.; Prasetijo, J.; Aden, T.S.; Rifai, A.I. Relationship of Present Serviceability Index for Flexible and Rigid Pavement in Urban Road Damage Assessment Using Pavement Condition Index and International Roughness Index. E3S Web Conf. 2023, 429, 03012. [Google Scholar] [CrossRef]
- Nur, W.; Subagio, B.S.; Hariyadi, E.S. Relationship between the Pavement Condition Index (PCI), Present Serviceability Index (PSI), and Surface Distress Index on Soekarno Hatta Road, Bandung. J. Tek. Sipil 2019, 26, 111–120. [Google Scholar] [CrossRef]
- Abed, A.; Rahman, M.; Thom, N.; Hargreaves, D.; Li, L.; Airey, G. Predicting Pavement Performance Using Distress Deterioration Curves. Road Mater. Pavement Des. 2024, 25, 1174–1190. [Google Scholar] [CrossRef]
- Morisugi, H. Evaluation Methodologies of Transportation Projects in Japan. Transp. Policy 2000, 7, 35–40. [Google Scholar] [CrossRef]
- Yao, L.; Dong, Q.; Jiang, J.; Ni, F. Deep Reinforcement Learning for Long-term Pavement Maintenance Planning. Comput. Aided Civ. Eng. 2020, 35, 1230–1245. [Google Scholar] [CrossRef]
- JTJ 075-94; Quality Inspection and Evaluation Standards for Highway Maintenance. China Communications Press: Beijing, China, 1994.
- JTJ 073-1996; Highway Maintenance Technical Specifications. China Communications Press: Beijing, China, 1996.
- JTJ 073.1-2001; Technical Specifications of Cement Concrete Pavement Maintenance for Highway. China Communications Press: Beijing, China, 2001.
- JTG H10-2009; Technical Specifications of Maintenance for Highway. China Communications Press: Beijing, China, 2009.
- JTG H20-2007; Highway Performance Assessment Standards. China Communications Press: Beijing, China, 2007.
- JTG 5210-2018; Highway Performance Assessment Standards. Issued 2018-12-25, Effective 2019-05-01. China Communications Press: Beijing, China, 2018.
- Qureshi, W.S.; Hassan, S.I.; McKeever, S.; Power, D.; Mulry, B.; Feighan, K.; O’Sullivan, D. An Exploration of Recent Intelligent Image Analysis Techniques for Visual Pavement Surface Condition Assessment. Sensors 2022, 22, 9019. [Google Scholar] [CrossRef] [PubMed]
- Marcelino, P.; De Lurdes Antunes, M.; Fortunato, E.; Gomes, M.C. Machine Learning Approach for Pavement Performance Prediction. Int. J. Pavement Eng. 2021, 22, 341–354. [Google Scholar] [CrossRef]
- Sandamal, K.; Shashiprabha, S.; Muttil, N.; Rathnayake, U. Pavement Roughness Prediction Using Explainable and Supervised Machine Learning Technique for Long-Term Performance. Sustainability 2023, 15, 9617. [Google Scholar] [CrossRef]
- Mers, M.; Yang, Z.; Hsieh, Y.-A.; Tsai, Y. Recurrent Neural Networks for Pavement Performance Forecasting: Review and Model Performance Comparison. Transp. Res. Rec. J. Transp. Res. Board 2023, 2677, 610–624. [Google Scholar] [CrossRef]
- Choi, S.; Do, M. Development of the Road Pavement Deterioration Model Based on the Deep Learning Method. Electronics 2019, 9, 3. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.D.; Hu, X.; Liu, J. An Efficient and Explainable Ensemble Learning Model for Asphalt Pavement Condition Prediction Based on LTPP Dataset. IEEE Trans. Intell. Transport. Syst. 2022, 23, 22084–22093. [Google Scholar] [CrossRef]
- Baykal, T.; Ergezer, F.; Eriskin, E.; Terzi, S. Using Ensemble Machine Learning to Estimate International Roughness Index of Asphalt Pavements. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 2773–2784. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Gong, H.; Fanijo, E.O.; Wang, L. Improving Asphalt Mix Design by Predicting Alligator Cracking and Longitudinal Cracking Based on Machine Learning and Dimensionality Reduction Techniques. Constr. Build. Mater. 2022, 354, 129162. [Google Scholar] [CrossRef]
- Xue, K.; Wang, J.; Chen, Y.; Wang, H. Improved BP Neural Network Algorithm for Predicting Structural Parameters of Mirrors. Electronics 2024, 13, 2789. [Google Scholar] [CrossRef]
- Mulumba, D.M.; Liu, J.; Hao, J.; Zheng, Y.; Liu, H. Application of an Optimized PSO-BP Neural Network to the Assessment and Prediction of Underground Coal Mine Safety Risk Factors. Appl. Sci. 2023, 13, 5317. [Google Scholar] [CrossRef]
- Wang, Y.; Ge, Q.; Lu, W.; Yan, X. Well-Logging Constrained Seismic Inversion Based on Closed-Loop Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5564–5574. [Google Scholar] [CrossRef]
- Hassanat, A.B.; Alqaralleh, M.K.; Tarawneh, A.S.; Almohammadi, K.; Alamri, M.; Alzahrani, A.; Altarawneh, G.A.; Alhalaseh, R. A Novel Outlier-Robust Accuracy Measure for Machine Learning Regression Using a Non-Convex Distance Metric. Mathematics 2024, 12, 3623. [Google Scholar] [CrossRef]
- Miettinen, O. Protostellar Classification Using Supervised Machine Learning Algorithms. Astrophys. Space Sci. 2018, 363, 197. [Google Scholar] [CrossRef]
| Model | Architecture/Parameters | Optimization Method |
|---|---|---|
| BP Neural Network |
| Adam optimizer (learning rate = 0.001) |
| Batch size: 32 | |
| PSO-BP |
| Particle Swarm Optimization: |
| global best-guided velocity update | |
| Random Forest |
| Gini impurity criterion |
| Bootstrap sampling | |
| Convolutional Neural Network |
| Iteration > 500 |
| Factor Category | Specific Factors | Unit |
|---|---|---|
| Intrinsic | Pavement structure type | - |
| Base course thickness | mm | |
| Asphalt binder type | - | |
| Aggregate gradation | % | |
| Extrinsic | Road age | years |
| Cumulative traffic volume (ESALs) | million | |
| Average annual temperature | °C | |
| Annual rainfall | mm | |
| Width of roadbed | m | |
| Width of pavement | m | |
| Overlying thickness | mm | |
| Last maintenance year | year | |
| Maintenance method | - |
| Index Name | Abbr. | Measurement Index | Mean | Std Dev | Min | Formula | Description |
|---|---|---|---|---|---|---|---|
| Pavement Quality Index | PQI | DR, IRI, RD | 90.82 | 3.83 | 44.57 | Comprehensive performance | |
| Pavement Condition Index | PCI | DR | 83.41 | 9.16 | 24.66 | Road damage degree | |
| Riding Quality Index | RQI | IRI | 93.91 | 3.26 | 11.30 | Surface roughness | |
| Rutting Depth Index | RDI | RD | 92.10 | 9.60 | 0.00 | Rutting depth |
| Factor 1 | Factor 2 | Correlation Coefficient |
|---|---|---|
| Road age | Section number | 0.99 |
| Width of roadbed | Section number | 0.99 |
| Width of pavement | Section number | 0.87 |
| Width of pavement | Width of roadbed | 0.93 |
| Overlying thickness | Width of pavement | 0.80 |
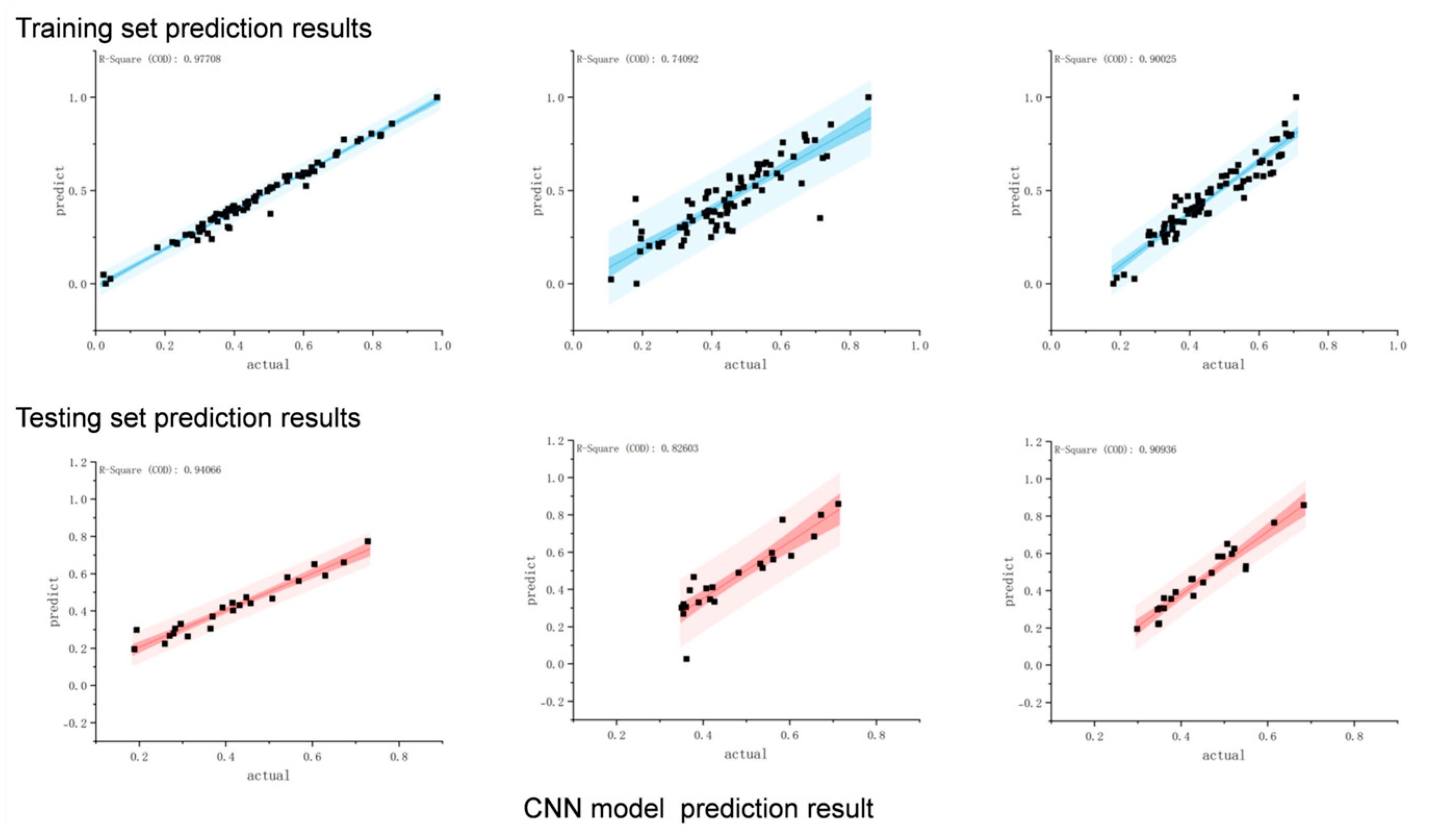
| MODEL | R2 | MAE | MBE | ||||
|---|---|---|---|---|---|---|---|
| Training Dataset | Testing Dataset | Training Dataset | Testing Dataset | Training Dataset | Testing Dataset | ||
| PCI | BP | 0.74092 | 0.83447 | 0.074 | 0.074 | −0.005 | 0.016 |
| PSO-BP | 0.95241 | 0.97708 | 1.457 | 1.739 | −1.7397 | 0.2597 | |
| Random Forest | 0.74092 | 0.82603 | 0.336 | 0.419 | 0.0068 | 0.317 | |
| Convolutional Neural Network | 0.99353 | 0.91436 | 1.2313 | 1.8422 | 0.0849 | 0.5711 | |
| RQI | BP | 0.95441 | 0.91654 | 0.558 | 0.546 | −0.478 | −0.467 |
| PSO-BP | 0.9787 | 0.95384 | 0.89876 | 1.3392 | −0.16571 | 0.56496 | |
| Random Forest | 0.90025 | 0.90936 | 2.4522 | 2.8408 | −0.03024 | 0.49321 | |
| Convolutional Neural Network | 0.99443 | 0.86164 | 0.431 | 1.89 | −0.0001 | 0.4298 | |
| RDI | BP | 0.98433 | 0.94066 | 0.019 | 0.002 | 0.029 | −0.003 |
| PSO-BP | 0.9747 | 0.94384 | 0.89876 | 1.3392 | −0.16571 | 0.56496 | |
| Random Forest | 0.89648 | 0.78099 | 2.0545 | 2.7684 | 0.039943 | 0.97489 | |
| Convolutional Neural Network | 0.99545 | 0.92491 | 1.2107 | 2.8265 | −0.45 | 1.59 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Tian, W.; Dai, X. Machine Learning-Based Highway Pavement Performance Prediction in Xinjiang. Infrastructures 2025, 10, 189. https://doi.org/10.3390/infrastructures10070189
Yang Q, Tian W, Dai X. Machine Learning-Based Highway Pavement Performance Prediction in Xinjiang. Infrastructures. 2025; 10(7):189. https://doi.org/10.3390/infrastructures10070189
Chicago/Turabian StyleYang, Qi, Wei Tian, and Xiaomin Dai. 2025. "Machine Learning-Based Highway Pavement Performance Prediction in Xinjiang" Infrastructures 10, no. 7: 189. https://doi.org/10.3390/infrastructures10070189
APA StyleYang, Q., Tian, W., & Dai, X. (2025). Machine Learning-Based Highway Pavement Performance Prediction in Xinjiang. Infrastructures, 10(7), 189. https://doi.org/10.3390/infrastructures10070189






