Statistical Reliability Analysis for Assessing Bridge Structural Integrity: A Review Paper
Abstract
1. Introduction
2. Data Collection and Parameter Determination
3. Reliability Analysis
3.1. Sampling-Based Methods
3.2. Metamodeling-Based Methods
3.3. Approximate Methods
4. Sensibility Analysis
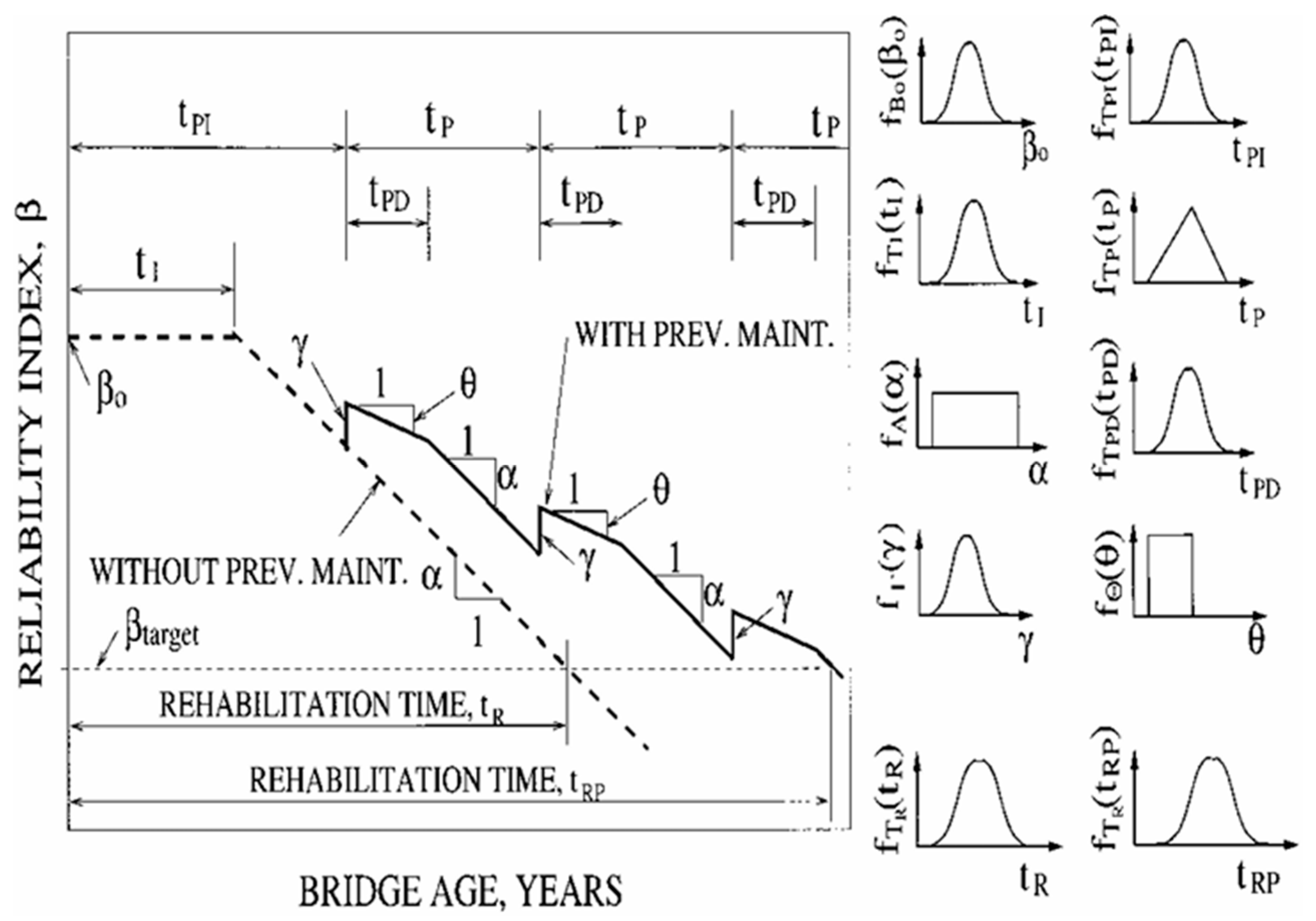
5. Remaining Service Life
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| CDF | Cumulative Distribution Function |
| FEM | Finite Element Method |
| FORM | First-Order Reliability Method |
| FOSM | First-Order Second Moment |
| GPR | Ground-Penetrating Radar |
| LHS | Latin Hypercube Sampling |
| MCS | Monte Carlo simulations |
| NDT | Non-destructive testing |
| PCE | Polynomial Chaos Expansion |
| Probability Distribution Function | |
| SVM | Support Vector Machines |
| TLS | Terrestrial Laser Scanner |
References
- Confederação Nacional Dos Transportes. Anuário CNT do Transporte—Estatísticas Consolidadas 2022. Brasil. 2022. Available online: https://anuariodotransporte.cnt.org.br/2022/Rodoviario/1-3-1-1-1-/Malha-rodovi%C3%A1ria-total (accessed on 24 June 2024).
- Relação Entre o Transporte Rodoviário de Carga e PIB Pode Chegar a 29%, Segundo Cálculos da FGV. Fundação Getúlio Vargas. 2020. Available online: https://portal.fgv.br/noticias/relacao-entre-transporte-rodoviario-carga-e-pib-pode-chegar-29-segundo-calculos-fgv (accessed on 13 November 2024).
- Srikanth, I.; Arockiasamy, M. Deterioration models for prediction of remaining useful life of timber and concrete bridges: A review. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 152–173. [Google Scholar] [CrossRef]
- Alguém sabe quantas pontes existem nas rodovias do Brasil? Guiadotrc. 2020. Available online: https://guiadotrc.com.br/publicacao/alguem-sabe-quantas-pontes-existem-nas-rodovias-do-brasil/36867 (accessed on 12 April 2024).
- Baron, E.; Galvão, N.; Docevska, M.; Matos, J.C.; Markovski, G. Application of quality control plan to existing bridges. Struct. Infrastruct. Eng. 2023, 19, 990–1006. [Google Scholar] [CrossRef]
- Koch, C.; German Paal, S.; Rashidi, A.; Zhu, Z.; König, M.; Brilakis, I. Achievements and Challenges in Machine Vision-Based Inspection of Large Concrete Structures. Adv. Struct. Eng. 2014, 17, 303–318. [Google Scholar] [CrossRef]
- Oliveira, C.B.L.; Greco, M.; Bittencourt, T.N. Analysis of the Brazilian federal bridge inventory. Rev. Ibracon De Estrut. E Mater. 2019, 12, 1–13. [Google Scholar] [CrossRef]
- Thompson, P.D.; Small, E.P.; Johnson, M.; Marshall, A. The Pontis Bridge management system. Struct. Eng. Int. 1998, 8, 303–308. [Google Scholar] [CrossRef]
- Turner, D.S.; Richerdson, J.A. Bridge Management System Data Needs and Data Collection—Characteristics of Bridge Management Systems; University of Alabama: Tuscaloosa, AL, USA, 1994. [Google Scholar]
- Das, P.C. Reliability based bridge management procedures. In Bridge Management 4; Ryall, M.J., Parke, G.A.R., Harding, J.E., Eds.; Thomas Telford: London, UK, 2000; pp. 1–11. [Google Scholar]
- Wisniewski, D.F.; Cruz, P.J.S.; Henriques, A.A.R.; Simoes, R.A.D. Probabilistic models for mechanical properties of concrete, reinforcing steel and pre-stressing steel. Struct. Infrastruct. Eng. Maint. Manag. Life-Cycle Des. Perform. 2012, 8, 111–123. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. An active-learning algorithm that combines sparse polynomial chaos expansions and bootstrap for structural reliability analysis. Struct. Saf. 2018, 75, 67–74. [Google Scholar] [CrossRef]
- Hajdin, R.; Kusar, M.; Masovic, S.; Linneberg, P.; Amado, J.L.; Matos, J.C.; Ademovic, N.; Costa, C.; Maric, M.K.; Almeida, J.O.; et al. Establishment of a Quality Control Plan—WG3. In TU1406 Cost Action; Univerzitet u Beogradu: Belgrade, Serbia, 2018; Available online: https://www.researchgate.net/publication/334122094_Establishment_of_a_Quality_Control_Plan_-_WG3 (accessed on 25 July 2024).
- Matos, J.C.; Moreira, V.N.; Valente, I.B.; Cruz, P.J.S.; Neves, L.C.; Galvão, N. Probabilistic-based assessment of existing steel-concrete composite bridges—Application to Sousa River Bridge. Eng. Struct. 2019, 181, 95–110. [Google Scholar] [CrossRef]
- Moreira, V.N.; Fernandes, J.; Matos, J.C.; Oliveira, D.V. Reliability-based assessment of existing masonry arch railway bridges. Constr. Build. Mater. 2016, 115, 544–554. [Google Scholar] [CrossRef]
- Arias, P.; Armesto, J.; Di-Capua, D.; Gonzalez-Drigo, R.; Lorenzo, H.; Perez-Gracia, V. Digital photogrammetry, GPR and computational analysis of structural damages in a mediaeval bridge. Eng. Fail. Anal. 2007, 14, 1444–1457. [Google Scholar] [CrossRef]
- Bouzas, O.; Conde, B.; Matos, J.C.; Solla, M.; Cabaleiro, M. Reliability-based structural assessment of historical masonry arch bridges: The case study of Cernadela bridge. Case Stud. Constr. Mater. 2023, 18, e02003. [Google Scholar] [CrossRef]
- Vital, W.; Silva, R.; Morais, M.V.G.; Sobrinho, B.E.; Pereira, R.; Evangelista, E., Jr. Application of bridge information modelling using laser scanning for static and dynamic analysis with concrete damage plasticity. Alex. Eng. J. 2023, 79, 608–628. [Google Scholar] [CrossRef]
- Armijo, A.; Zamora-Sanchez, D. Integration of Railway Bridge Structural Health Monitoring into the Internet of Things with a Digital Twin: A Case Study. Sensors 2024, 24, 2115. [Google Scholar] [CrossRef]
- Lai, X.; Kan, Z.; Sun, W.; Song, X.; Tian, B.; Yuan, T. Digital twin-based non-destructive testing for structural health monitoring of bridges. Nondestruct. Test. Eval. 2023, 39, 57–74. [Google Scholar] [CrossRef]
- Wittenberghe, J.V.; Adriano, V.; Yilmaz, O.; Abeele, F.V.D. Increasing the Reliability of Industrial Overhead Cranes by Structural Health Monitoring. Procedia Struct. Integr. 2024, 57, 95–103. [Google Scholar] [CrossRef]
- Liu, P.; Shi, Y.; Xiong, R.; Tang, P. Quantifying the reliability of defects located by bridge inspectors through human observation behavioral analysis. Dev. Built Environ. 2023, 14, 100167. [Google Scholar] [CrossRef]
- Mandirola, M.; Casarotti, C.; Peloso, S.; Lanese, I.; Brunesi, E.; Senaldi, I. Use of UAS for damage inspection and assessment of bridge infrastructures. Int. J. Disaster Risk Reduct. 2022, 72, 102824. [Google Scholar] [CrossRef]
- Seo, J.; Duque, L.; Wacker, J. Drone-enabled bridge inspection methodology and application. Autom. Constr. 2018, 94, 112–126. [Google Scholar] [CrossRef]
- Alam, J.; Neves, L.A.C.; Zhang, H.; Dias-da-Costa, D. Assessment of remaining service life of deteriorated concrete bridges under imprecise probabilistic Information. Mech. Syst. Signal Process. 2022, 167, 108565. [Google Scholar] [CrossRef]
- Baron, E.A. Structural Damage Identification for Robustness Assessment of Railway Infrastructure Under Flood Effects. Doctorate Thesis, Escola de Engenharia, Universidade de Minho, Minho, Portugal, 2023; 162p. [Google Scholar]
- Casas, J.R.; Wisniewski, D.F. Safety formats and required safety levels—SB4.4.1. In Sustainable Bridges; VI Framework Programme: Brussels, Belgium, 2007. [Google Scholar]
- Cruz, P.; Wisniewski, D.; Casas, J.R. Métodos de Avaliação da Segurança de Pontes Existentes. Rev. Port. De Eng. De Estrut. 2008, 2, 19–30. [Google Scholar]
- Galvão, N.P.; Matos, J.C.; Oliveira, D.C.; Hajdin, R. Human error impact in structural safety of a reinforced concrete bridge. Struct. Infrastruct. Eng. 2021, 18, 836–850. [Google Scholar] [CrossRef]
- Henriques, A.A.R. Aplicação de Novos Conceitos de Segurança no Dimensionamento do Betão Estrutural. Doctorate Thesis, Faculdade de Engenharia, Universidade do Porto, Porto, Portugal, 1998; 502p. [Google Scholar]
- Jacinto, L.; Neves, L.C.; Santos, L.O. Bayesian assessment of an existing bridge: A case study. Struct. Infrastruct. Eng. 2016, 12, 61–77. [Google Scholar] [CrossRef]
- Matos, J.C.; Cruz, P.J.S.; Valente, I.B.; Neves, L.C.; Moreira, V.N. An innovative framework for probabilistic-based structural assessment with an application to existing reinforced concrete structures. Eng. Struct. 2016, 111, 552–564. [Google Scholar] [CrossRef]
- Mirza, S.A.; Hatzinikolas, M.; Macgregor, J.G. Statistical description of strength of concrete. J. Struct. Div. 1979, 105, 1021–1037. [Google Scholar] [CrossRef]
- Parmiani, M.G.; Orta, L. Reliability assessment of a continuous bridge beam with exposed reinforcement. Eng. Struct. 2022, 262, 114281. [Google Scholar] [CrossRef]
- Santiago, W.C.; Kroetz, H.M.; Santos, S.H.C.; Stucchi, F.R.; Beck, A.T. Reliability-based calibration of main Brazilian structural design codes. Lat. Am. J. Solids Struct. 2020, 17. [Google Scholar] [CrossRef]
- Santos, A.F.; Bonatte, M.S.; Sousa, H.S.; Bittencourt, T.N.; Matos, J.C. Safety Assessment of Brazilian Concrete Bridges Through Reliability Analysis. Struct. Eng. Int. 2024, 34, 244–255. [Google Scholar] [CrossRef]
- Wisniewski, D.F. Safety Formats for the Assessment of Concrete Bridges. Doctorate Thesis, Department of Civil Engineering, School of Engineering, University of Minho, Braga, Portugal, 2007. [Google Scholar]
- Al-Mosawe, D.; Neves, L.; Owen, J. Reliability analysis of deteriorated post-tensioned concrete bridges: The case study of Ynys-y-Gwas bridge in UK. Structures 2022, 41, 242–259. [Google Scholar] [CrossRef]
- Barlett, F.M.; Macgregor, J.G. Statistical Analysis of compressive Strength of Concrete Structures. ACI Mater. J. 1996, 93, 158–168. [Google Scholar]
- Cavaco, E.S.; Neves, L.A.; Casas, J.R. On the robustness to corrosion in the life cycle assessment of an existing reinforced concrete bridge. Struct. Infrastruct. Eng. 2017, 8, 137–150. [Google Scholar] [CrossRef]
- Enright, M.P.; Frangopol, D.M. Probabilistic analysis of resistance degradation of reinforced concrete bridge beams under corrosion. Eng. Struct. 1998, 20, 960–971. [Google Scholar] [CrossRef]
- Hanley, C.; Frangopol, D.M.; Kelliher, D.; Palrashi, V. Reliability index and parameter importance for bridge traffic loading definition changes. Bridge Eng. 2017, 171, 13–24. [Google Scholar] [CrossRef]
- Matos, J.A.S.C.C. Avaliação de Incertezas no Comportamento de Estruturas de Betão Armado e Mistas. Doctorate Thesis, Escola de Engenharia, Universidade de Minho, Braga, Portugal, 2013. [Google Scholar]
- Spaethe, G. Die Sicherheit Tragender Baukonstruktionen, Zweite Neubearbeitete Auflage; Springer: New York, NY, USA, 1992. [Google Scholar]
- Zhang, Z.; Tao, M.; Li, B.; Wang, L.; Wei, G. DPIM-based global reliability analysis method for the cable-stayed bridges and the determination of global target reliability index. Eng. Struct. 2024, 302, 117330. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Eng. Mech. 2010, 25, 183–197. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, L.; Lai, Z.; Xiang, P.; Chen, Y. Sensitivity and dynamic analysis of train-bridge coupled system with multiple random factors. Eng. Struct. 2020, 221, 111083. [Google Scholar] [CrossRef]
- Rocha, J.M.; Henriques, A.A.; Calçada, R.; Ronnquist, D. Efficient methodology for the probabilistic safety assessment of high-speed railway bridges. Eng. Struct. 2015, 101, 138–149. [Google Scholar] [CrossRef]
- Cabanzo, C.M.; Santamaria, M.; Sousa, H.S.; Matos, J.C. In-Plane Fragility and Parametric Analyses of Masonry Arch Bridges Exposed to Flood Hazard Using Surrogate Modeling Techniques. Appl. Sci. 2022, 12, 1886. [Google Scholar] [CrossRef]
- Choudhury, T.; Kaushik, H.B. Treatment of uncertainties in seismic fragility assessment of RC frames with masonry infill walls. Soil Dyn. Earthq. Eng. 2019, 126, 105771. [Google Scholar] [CrossRef]
- Kong, J.S.; Ababneh, A.N.; Frangopol, D.M.; Xi, Y. Reliability analysis of chloride penetration in saturated concrete. Probabilistic Eng. Mech. 2002, 17, 305–315. [Google Scholar] [CrossRef]
- Stewart, M.G. Workmanship and Its Influence on Probabilistic Models of Concrete Compressive Strength. ACI Mater. J. 1995, 92, 361–372. [Google Scholar]
- Mirza, S.A.; Macgregor, J.G. Variability of mechanical properties of reinforcing bars. J. Struct. Div. 1979, 105, 921–937. [Google Scholar] [CrossRef]
- Nowak, A.S.; Szerszen, M.M. Calibration of Design Code for Buildings (ACI 318): Part 1—Statistical Models for Resistance. ACI Struct. J. 2003, 100, 377–382. [Google Scholar]
- Sobrino, J.A. Evaluación del Comportamiento Funcional y de la Seguridad Estructural de Puentes Existentes de Hormigón Armado y Pretensado. Doctorate Thesis, Department of Construction Engineering, Technical University of California, Pasadena, CA, USA, 1993. [Google Scholar]
- Jacinto, L.; Pipa, M.; Neves, L.A.C.; Santos, L.O. Probabilistic models for mechanical properties of prestressing strands. Constr. Build. Mater. 2012, 36, 84–89. [Google Scholar] [CrossRef]
- Chen, D.; Guo, W.; Wu, B.; Shi, J. Service life prediction and time-variant reliability of reinforced concrete structures in harsh marine environment considering multiple factors: A case study for Qingdao Bay Bridge. Eng. Fail. Anal. 2023, 154, 107671. [Google Scholar] [CrossRef]
- Mirza, S.A.; Macgregor, J.G. Variations in dimensions of reinforced concrete members. J. Struct. Div. 1979, 105, 751–766. [Google Scholar] [CrossRef]
- Chen, D.; Guo, W.; Quan, X.; Duan, B.; Guo, L. Mesoscopic statistics-based probability characteristics of chloride transport and reliability-based corrosion initiation life of bridge tower. Thin-Walled Struct. 2024, 198, 111680. [Google Scholar] [CrossRef]
- Moreira, V.N. Safety Assessment of Existing Bridges: Application to Durães Railway Viaduct. Master’s Dissertation, Universidade de Minho, Minho, Portugal, 2014. [Google Scholar]
- Feng, L.; Wu, Y.F.; Guo, B.C.; Huang, X.X. Reducing target reliability index of concrete bridge beams through compression yielding. Eng. Struct. 2024, 316, 118506. [Google Scholar] [CrossRef]
- Galambos, T.V.; Ellingwood, B.; MacGregor, J.G.; Cornell, C.A. Probability based load criteria: Assessment of current design practice. J. Struct. Div. 1982, 108, 959–977. [Google Scholar] [CrossRef]
- Holicky, M.; Sykora, M. Conventional probabilistic models for calibration of codes. In Proceedings of the ICASP11, Zurich, Switzerland, 1–4 August 2011; pp. 969–976. [Google Scholar]
- Jiang, H.; Li, S.; Jiang, R. Residual Service Life Prediction for Bridges Based on Critical Life Curves. J. Perform. Constr. Facil. 2017, 31. [Google Scholar] [CrossRef]
- Nowak, A.S. Live load model for highway bridges. Struct. Saf. 1993, 13, 53–66. [Google Scholar] [CrossRef]
- Nowak, A.S.; Szerszen, M.M. Bridge Load and Resistance Models. Eng. Struct. 1998, 20, 985–990. [Google Scholar] [CrossRef]
- Portela, E.L. Analysis and Development of a Live Load Model for Brazilian Concrete Bridges Based on Wim Data. Doctorate Thesis, Universidade de São Paulo, São Paulo, Brazil, 2018. [Google Scholar]
- Sykora, M.; Diamantidis, D.; Holicky, M.; Jung, K. Target reliability for existing structures considering economic and -societal aspects. Struct. Infrastruct. Eng. 2017, 13, 181–194. [Google Scholar] [CrossRef]
- Vejdirectoratet. Reliability-Based Classification of the Load Carrying Capacity of Existing Bridges—Report 291; Road Directorate, Ministry of Transport: Copenhagen, Denmark, 2004.
- Lyra, P.H.C.; Beck, A.T.; Stucchi, F.R. Reliability analysis of a prestressed bridge beam designed in serviceability limit state as recommended by NBR 6118 and 7188. Rev. Ibracon De Estrut. E Mater. 2020, 13. [Google Scholar] [CrossRef]
- Melbourne, C.; Holm, G.; Bien, J.; Casas, J.R.; Tommor, A.; Bengtsson, P.E.; Kaminski, T.; Rawa, P.; Roca, P.; Molins, C. Masonry Arch Bridges Background Document D4.7. In Sustainable Development Global Change & Ecosystems Integrated Project, Sustainable Bridges; European Commission DG Research; ZAG: Ljubljana, Slovenia, 2007. [Google Scholar]
- Conde, B.; Matos, J.C.; Oliveira, D.V.; Riveiro, B. Probabilistic-based structural assessment of a historic stone arch bridge. Struct. Infrastruct. Eng. 2021, 17, 379–391. [Google Scholar] [CrossRef]
- Getter, G.J.; Consolazio, G.R. Barge Bow Force-Deformation Relationships for Bridge Design with Probabilistic Consideration of Oblique Impact Scenarios. In Proceedings of the TRB 90th Annual Meeting (CD-ROM), Transportation Research Board, Washington, DC, USA, 23–27 January 2011. [Google Scholar]
- Gholipour, G.; Billah, A.M.; Mousavi, A.A. Finite element-based reliability analysis of RC bridge piers subjected to the combination of barge impact and blast loads. Ocean Eng. 2022, 264, 112543. [Google Scholar] [CrossRef]
- Ghosn, M.; Moses, F.; Wang, J. Design of Highway Bridges for Extreme Events, NCHRP Report 489; Transportation Research Board of The National Academies: Washington, DC, USA, 2003. [Google Scholar]
- Kunz, C.U. Ship Collision Analysis. In Ship Bridge Collision in River Traffic, Analysis and Design Practice; Gluver, H., Olsen, D., Eds.; Balkema: Rotterdam, The Netherlands, 1998; pp. 13–22. [Google Scholar]
- Wang, W.; Morgenthal, G. Reliability analyses of RC bridge piers subjected to barge impact using efficient models. Eng. Struct. 2018, 166, 485–495. [Google Scholar] [CrossRef]
- CONWEP (Conventional Weapons Effects Program). Waterways Experimental Station; CONWEP: Vicksburg, MI, USA, 1991. [Google Scholar]
- Stewart, M.G. Reliability-based load factor design model for explosive blast loading. Struct. Saf. 2018, 71, 13–23. [Google Scholar] [CrossRef]
- Su, L.; Li, X.-L.; Jiang, Y.-P. Comparison of methodologies for seismic fragility analysis of unreinforced masonry buildings considering epistemic uncertainty. Eng. Struct. 2019, 205, 110059. [Google Scholar] [CrossRef]
- Zampieri, P.; Zanini, M.A.; Faleschini, F. Derivation of analytical seismic fragility functions for common masonry bridge types: Methodology and application to real cases. Eng. Fail. Anal. 2016, 68, 275–291. [Google Scholar] [CrossRef]
- Cavicchi, A.; Gambarotta, L. Two-dimensional finite element upper bound limit analysis of masonry bridges. Comput. Struct. 2006, 84, 2316–2328. [Google Scholar] [CrossRef]
- Conde, B.; Ramos, L.F.; Oliveira, D.V.; Riveiro, B.; Solla, M. Structural assessment of masonry arch bridges by combination of non-destructive testing techniques and three-dimensional numerical modelling: Application to Vilanova bridge. Eng. Struct. 2017, 148, 621–638. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Lourenço, P.B.; Lemos, C. Geometric issues and ultimate load capacity of masonry arch bridges from the northwest Iberian Peninsula. Eng. Struct. 2010, 32, 3955–3965. [Google Scholar] [CrossRef]
- Kallias, A.N.; Imam, B. Probabilistic assessment of local scour in bridge piers under changing environmental conditions. Struct. Infrastruct. Eng. 2016, 12, 1228–1241. [Google Scholar] [CrossRef]
- Wang, K.; Fang, X.; Fan, Z.; Zeng, J.; Wang, P. Durability design for concrete structure in Shenzhen-Zhongshan Bridge. Corros. Prot. 2022, 12, 84–89. [Google Scholar]
- Zhu, Y.; Macdonald, D.; Yang, J.; Qiu, J.; Engelhardt, G.R. Corrosion of rebar in concrete. Part II: Literature survey and statistical analysis of existing data on chloride threshold. Corros. Sci. 2021, 185, 109439. [Google Scholar] [CrossRef]
- Kala, Z. Stochastic inverse analysis of fatigue cracks based on linear fracture mechanics. Int. J. Math. Comput. Methods 2017, 2, 60–65. [Google Scholar]
- Kala, Z. Probabilistic modelling of fatigue crack-Some observations about conditional probability. Int. J. Mech. 2018, 12, 121–130. [Google Scholar]
- Kala, Z. Global sensitivity analysis of reliability of structural bridge system. Eng. Struct. 2019, 194, 36–45. [Google Scholar] [CrossRef]
- Krejsa, M.; Kala, Z.; Seitl, S. Inspection based probabilistic modeling of fatigue crack progression. Procedia Eng. 2016, 142, 146–153. [Google Scholar] [CrossRef]
- Maljaars, J.; Vrouwenvelder, T. Fatigue failure analysis of stay cables with initial defects: Ewijk bridge case study. Struct. Saf. 2014, 51, 47–56. [Google Scholar] [CrossRef]
- Kala, Z.; Omishore, A.; Seitl, S.; Krejsa, M.; Kala, J. The effect of skewness and kurtosis on the probability evaluation of fatigue limit states. Int. J. Mech. 2017, 11, 166–175. [Google Scholar]
- Krejsa, M.; Koubova, L.; Flodr, J.; Protivinsky, J.; Nguyen, Q.T. Probabilistic prediction of fatigue damage based on linear fracture mechanics. Fract. Struct. Integr. 2017, 11, 143–159. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.X.; Li, A.Q. Combined use of SHMS and finite element strain data for assessing the fatigue reliability index of girder components in long-span cable-stayed bridge. Theor. Appl. Fract. Mech. 2010, 54, 127–136. [Google Scholar] [CrossRef]
- Gertsbakh, I.B. Statistical Reliability Theory; Marcel Dekker Inc.: New York, NY, USA, 1989. [Google Scholar]
- Ditlevsen, O.; Madsen, H.O. Structural Reliability Methods, 1st ed.; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Avila, V.H.; Real, M.V. Verification of structural reliability of a highway bridge in the state of Rio Grande do Sul. Ciência E Nat. 2023, 45, e73885. [Google Scholar] [CrossRef]
- Nowak, A.S.; Collins, K.R. Reliability of Structures; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Lemaire, M. Structural Reliability; ISTE Ltd.: London, UK, 2009. [Google Scholar]
- Wu, J.; Yan, Q.; Huang, S.; Zou, C.; Zhong, J.; Wang, W. Finite Element Model Updating in Bridge Structures Using Kriging Model and Latin Hypercube Sampling Method. Adv. Civ. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Mccuen, R.H. Simulation-Based Reliability Methods. In Probabilistic Structural Mechanics Handbook; Sundarajan, C., Ed.; Springer: Boston, MA, USA, 1995. [Google Scholar]
- Olsson, A.M.J.; Sandberg, G.E. Latin Hypercube Sampling for Stochastic Finite Element Analysis. J. Eng. Mech. 2002, 128, 121–125. [Google Scholar] [CrossRef]
- Xiang, H.; Tang, P.; Zhang, Y.; Li, Y. Random dynamic analysis of vertical train–bridge systems under small probability by surrogate model and subset simulation with splitting. Railw. Eng. Sci. 2020, 28, 305–315. [Google Scholar] [CrossRef]
- Au, S.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]
- Tabandeh, A.; Jia, G.; Gardoni, P. A review and assessment of importance sampling methods for reliability analysis. Struct. Saf. 2022, 97, 102216. [Google Scholar] [CrossRef]
- Melchers, R.E. Importance Sampling in Structural Systems. Stuctural Saf. 1989, 6, 3–10. [Google Scholar] [CrossRef]
- Bjerager, P.; Krenk, S. Parametric sensitivity in first order reliability theory. J. Eng. Mech. 1989, 115, 1577–1582. [Google Scholar] [CrossRef]
- Teixeira, R.; Nogal, M.; O’connor, A. Adaptive approaches in metamodel-based reliability analysis: A review. Struct. Saf. 2021, 89, 102019. [Google Scholar] [CrossRef]
- Li, P.; Wang, Z.; Zhao, B.; Becker, T.; Soga, K. Surrogate modeling for identifying critical bridges in traffic networks under earthquake conditions. Transp. Res. Part D 2025, 138, 104512. [Google Scholar] [CrossRef]
- Li, H.; Wang, T.; Wu, G. Probabilistic safety analysis of coupled train bridge system using deep learning based surrogate model. Struct. Infrastruct. Eng. 2021, 19, 1138–1157. [Google Scholar] [CrossRef]
- Krizek, M.; Novak, L. Uncertainty Quantification of Existing Bridge using Polynomial Chaos Expansion. Sect. Build. Struct. Struct. Mech. 2023, 23, 13–19. [Google Scholar]
- Baron, E.; Cabanzo, C.M.; Bento, A.M.; Matos, J.C.; Calçada, R.; Gavin, K. A study of stone arch bridge’s flood reliability through a surrogate model approach. Struct. Infrastruct. Eng. 2024. [Google Scholar] [CrossRef]
- Hoang, P.H.; Phan, H.N.; Nguyen, D.T.; Paolacci, F. Kriging Metamodel-Based Seismic Fragility Analysis of Single-Bent Reinforced Concrete Highway Bridges. Buildings 2021, 11, 238. [Google Scholar] [CrossRef]
- Ni, P.; Li, J.; Hao, H.; Zhou, H. Reliability based design optimization of bridges considering bridge-vehicle interaction by Kriging surrogate model. Eng. Struct. 2021, 246, 112989. [Google Scholar] [CrossRef]
- Kaymaz, I. Application of kriging method to structural reliability problems. Struct. Saf. 2005, 27, 133–151. [Google Scholar] [CrossRef]
- Yepes-Bellver, L.; Brun-Izquiedo, A.; Alcala, J.; Yepes, V. Artificial Neural Network and Kriging Surrogate Model for Embodied Energy Optimization of Prestressed Slab Bridges. Sustainability 2024, 16, 8450. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Alcala, J.; Kripka, M.; Yepes, V. Life Cycle Assessment of Bridges Using Bayesian Networks and Fuzzy Mathematics. Appl. Sci. 2021, 11, 4916. [Google Scholar] [CrossRef]
- Maroni, A.; Tubaldi, E.; Val, D.V.; McDonald, H.; Zonta, D. Using Bayesian networks for the assessment of underwater scour for road and railway bridges. Struct. Health Monit. 2021, 50, 2446–2460. [Google Scholar] [CrossRef]
- Gehl, P.; D’ayala, D. Development of Bayesian Networks for the multi-hazard fragility assessment of bridge systems. Struct. Saf. 2016, 60, 37–46. [Google Scholar] [CrossRef]
- Al-Hijazeen, A.Z.O.; Fawad, M.; Gerges, M.; Koris, K.; Salamak, M. Implementation of digital twin and support vector machine in structural health monitoring of bridges. Arch. Civ. Eng. 2023, 69, 31–47. [Google Scholar]
- Chen, P.H.; Shen, H.K.; Lei, C.Y.; Chang, L.M. Support-vector-machine-based method for automated steel bridge rust assessment. Autom. Constr. 2012, 23, 9–19. [Google Scholar] [CrossRef]
- Bourinet, J.M.; Deheeger, F.; Lemaire, M. Assessing small failure probabilities by combined subset simulation and Support Vector Machines. Struct. Saf. 2001, 33, 343–353. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and Invariant Second-Moment Code Format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Bocchini, P.; Frangopol, D.M. Generalized bridge network performance analysis with correlation and time-variant reliability. Struct. Saf. 2011, 33, 155–164. [Google Scholar] [CrossRef]
- Xiao, Q.; Liu, Y.; Zhou, L.; Liu, Z.; Jiang, Z.; Tang, L. Reliability analysis of bridge girders based on regular vine Gaussian copula model and monitored data. Structures 2022, 39, 1063–1073. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Ye, X. Time-dependent reliability assessment of a simply supported girder bridge based on the third-moment method. Structures 2023, 50, 1353–1367. [Google Scholar] [CrossRef]
- JCSS (Joint Committee on Structural Safety). Probabilistic Model Code, 12th Draft; JCSS: Zurich, Switzerland, 2001. [Google Scholar]
- EN 1990; Eurocode 0—Basis of Structural Design. CEN (European Committee for Standardization): Brussels, Belgium, 2004.
- ISO 13822; Bases for Design of Structures—Assessment of Existing Structures. ISO (International Organization for Standardization): Geneva, Switzerland, 2015; pp. 1–44.
- ISO 2394; General Principles on Reliability for Structures. ISO (International Organization for Standardization): Geneva, Switzerland, 2015.
- FIB (International Federation for Structural Concrete). Bulletin No. 22: Monitoring and Safety Evaluation of Existing Concrete Structures: State-of-Art; FIB: Lausanne, Switzerland, 2003. [Google Scholar]
- BS 153; Part 3: British Standard Specification for Girder Bridges–Loads and Stresses. BSI (British Standards Institution): London, UK, 1937.
- BS 5400; Part 2: Steel, Concrete and Composite Bridges Specification for Loads. BSI (British Standards Institution): London, UK, 1978.
- HA (Highways Agency); DMRB (Design Manual for Roads and Bridges). Part 3: BD 21—The Assessment of Highway Bridges and Structures; HA: London, UK, 1984; Volume 3, Section 4.
- HA (Highways Agency); DMRB (Design Manual for Roads and Bridges). Part 14: Bd 37—Loads for Highway Bridges; HA: London, UK, 1988; Volume 1, Section 3.
- EN 1991-2; Eurocode 1: Actions on Structures—Traffic Loads on Bridges. CEN (European Committee for Standardization): Brussels, Belgium, 1994.
- Hohenbichler, M.; Rackwitz, R. Sensitivity and importance measures in structural reliability. Civ. Eng. Syst. 1986, 3, 203–209. [Google Scholar] [CrossRef]
- Madsen, H.O.; Krenk, S.; Lind, N.C. Methods of Structural Safety; Prentice Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Frangopol, D.M.; Kong, J.S.; Gharaibeh, E.S. Reliability based life-cycle management of highway bridges. J. Comput. Civ. Eng. 2001, 15, 27–34. [Google Scholar] [CrossRef]
- Thoft-Christensen, P. Advanced bridge management systems. Struct. Eng. Rev. 1995, 7, 151–163. [Google Scholar]
- Frangopol, D.M.; Das, P.C. Management of bridge stocks based on future reliability and maintenance costs. In Current and Future Trends in Bridge Design, Construction, and Maintenance; Das, P.C., Frangopol, D.M., Nowak, A.S., Eds.; Thomas Telford: London, UK, 1999; pp. 45–58. [Google Scholar]
- Thoft-Christensen, P. Estimation of Bridge Reliability Distributions. In Current and Future Trends in Bridge Design Construction and Maintenance: Proceedings of the International Conference, Singapore, 4–5 October 1999; Thomas Telford Publishing Company: London, UK, 1999. [Google Scholar]
- Ghosn, M.; Frangopol, D.M. Chapter 4: Bridge reliability: Components and systems. In Bridge Safety and Reliability; Frangopol, D.M., Ed.; ASCE: Reston, VA, USA, 1999; pp. 83–112. [Google Scholar]
- Kong, J.S.; Frangopol, D.M. Prediction of Reliability and Cost Profiles of Deteriorating Bridges under Time- and Performance-Controlled Maintenance. J. Struct. Eng. 2004, 130. [Google Scholar] [CrossRef]
- Kong, J.S.; Frangopol, D.M. Sensitivity Analysis in Reliability-Based Lifetime Performance Prediction Using Simulation. J. Mater. Civ. Eng. 2005, 17. [Google Scholar] [CrossRef]
- Val, D.V.; Andrade, C.; Sykora, M.; Stewart, M.G.; Bastidas-Arteaga, E.; Mlcoch, J.; Truong, Q.C.; Soueidy, C.P.E. Probabilistic modelling of deterioration of reinforced concrete structures. Struct. Saf. 2025, 113, 102454. [Google Scholar] [CrossRef]
- Vorechovska, D. Concrete structures under combined mechanical and environmental actions: Modelling of durability. Comput. Concr. 2017, 20, 99–110. [Google Scholar]
| Variable | References | |
|---|---|---|
| Concrete | ||
| Concrete compressive strength | Normal | [5,11,14,25,26,27,28,29,30,31,32,33,34,35,36,37] |
| Lognormal | [11,33,37,38,39,40,41,42,43] | |
| Concrete tensile strength | Normal | [11,14,29,30,32,33,37,38,44] |
| Lognormal | [11,37,43,44,45] | |
| Concrete modulus of elasticity | Normal | [5,11,12,14,26,29,30,32,33,37,38,46,47,48] |
| Lognormal | [43,45] | |
| Concrete density | Normal | [5,14,26,29,34,37,40,43,47,48,49,50] |
| Pavement density | Normal | [14,34] |
| Poisson’s ratio | Normal | [5,26] |
| Concrete tensile strain | Normal | [30] |
| Concrete compressive strain | Normal | [30] |
| Lognormal | [43] | |
| Creep coefficient | Normal | [30] |
| Water-cement ratio | Triangular | [51] |
| Curing time | Normal | [51] |
| Compaction of concrete | Normal | [52] |
| Lognormal | [52] | |
| Reinforcing Steel | ||
| Cross-sectional area of reinforcement steel | Normal | [5,11,14,26,27,28,29,32,34,35,36,37,41,43,53] |
| Lognormal | [42] | |
| Steel yield strength | Normal | [5,11,14,25,26,27,28,29,30,31,32,35,36,37,38,40,43,53,54] |
| Lognormal | [11,34,37,41,42,55] | |
| Beta | [53] | |
| Prestressing steel yield strength | Normal | [11,29,30,35,36,38,56] |
| Lognormal | [11] | |
| Steel ultimate tensile strength | Normal | [5,11,14,26,30,37,38,43] |
| Lognormal | [11,37] | |
| Prestressing steel ultimate tensile strength | Normal | [11,29,30,36,38,56] |
| Lognormal | [11] | |
| Steel modulus of elasticity | Normal | [11,32,34,37,38,43,53,56] |
| Lognormal | [45] | |
| Steel ultimate strain | Normal | [11,38,43,56] |
| Lognormal | [11] | |
| Geometry | ||
| Concrete cover | Normal | [14,25,31,32,36,38,43,55,57,58] |
| Lognormal | [41,59] | |
| Pavement thickness | Triangular | [17,58] |
| Normal | [34] | |
| Width | Normal | [14,15,17,28,32,34,36,37,43,45,49,55,58,60] |
| Length | Normal | [43,49] |
| Height/Thickness | Normal | [14,15,17,27,28,29,30,32,34,36,37,43,55,58,60] |
| Moment of inertia | Normal | [12,45,46] |
| Cross-sectional area | Normal | [12,46] |
| Loading | ||
| Dead loads | Normal | [25,27,28,30,31,32,35,36,38,45,61,62,63,64,65,66,67,68,69] |
| Live loads | Gumbel | [13,14,15,27,30,32,34,36,37,38,43,45,64,65,70,71,72] |
| Normal | [5,26,27,28,29] | |
| Exponential | [40] | |
| Wind load | Normal | [45] |
| Snow load | Gumbel | [63,68] |
| Impact load | Lognormal | [73,74,75,76,77] |
| Explosion load | Lognormal | [74,78,79] |
| Temperature | Gumbel | [30] |
| Masonry | ||
| Masonry modulus of elasticity | Normal | [26] |
| Masonry cohesion | Normal | [26] |
| Lognormal | [17] | |
| Masonry angle of friction | Normal | [26] |
| Masonry angle of dilatancy | Normal | [17,26] |
| Masonry tensile strength | Normal | [26] |
| Masonry compressive strength | Lognormal | [15,26,60] |
| Normal | [72] | |
| Masonry density | Normal | [15,26,49,60,80] |
| Soil/Backfill | ||
| Soil modulus of elasticity | Normal | [26] |
| Soil density | Normal | [15,26,60] |
| Lognormal | [49,72,81] | |
| Soil cohesion | Normal | [15,26,60,72] |
| Lognormal | [17,49,81,82,83] | |
| Soil angle of friction | Normal | [15,17,60,72,82,84] |
| Lognormal | [49,72] | |
| Slope | Lognormal | [49,85] |
| Pathologies | ||
| Steel corrosion rate | Lognormal | [25] |
| Surface chloride concentration | Lognormal | [57,59,86] |
| Critical chloride concentration | Lognormal | [57,59,87] |
| Chloride transport coefficient | Lognormal | [57,59,86] |
| Crack initial length | Lognormal | [88,89,90,91,92] |
| Crack width | Normal | [88,89,90,93] |
| Crack stress range | Normal | [90,91,94] |
| Crack smallest detectable length | Normal | [90,91,94] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Primo, G.S.P.; Silva, R.; Evangelista, F., Jr.; Oliveira, M.H. Statistical Reliability Analysis for Assessing Bridge Structural Integrity: A Review Paper. Infrastructures 2025, 10, 156. https://doi.org/10.3390/infrastructures10070156
Primo GSP, Silva R, Evangelista F Jr., Oliveira MH. Statistical Reliability Analysis for Assessing Bridge Structural Integrity: A Review Paper. Infrastructures. 2025; 10(7):156. https://doi.org/10.3390/infrastructures10070156
Chicago/Turabian StylePrimo, Gustavo S. P., Ramon Silva, Francisco Evangelista, Jr., and Marcos H. Oliveira. 2025. "Statistical Reliability Analysis for Assessing Bridge Structural Integrity: A Review Paper" Infrastructures 10, no. 7: 156. https://doi.org/10.3390/infrastructures10070156
APA StylePrimo, G. S. P., Silva, R., Evangelista, F., Jr., & Oliveira, M. H. (2025). Statistical Reliability Analysis for Assessing Bridge Structural Integrity: A Review Paper. Infrastructures, 10(7), 156. https://doi.org/10.3390/infrastructures10070156






