Numerical Modelling and Parametric Study of Steel-Concrete Composite Slim-Floor Flexural Beam Using Dowel Shear Connectors
Abstract
1. Introduction
2. Brief Introduction to Experimental Study
3. Development of FE Model and Validation
3.1. Description of Finite Element Model
3.2. Material Properties
3.3. Element Type and Mesh
3.4. Interaction and Constraint
3.5. Loading and Boundary Conditions
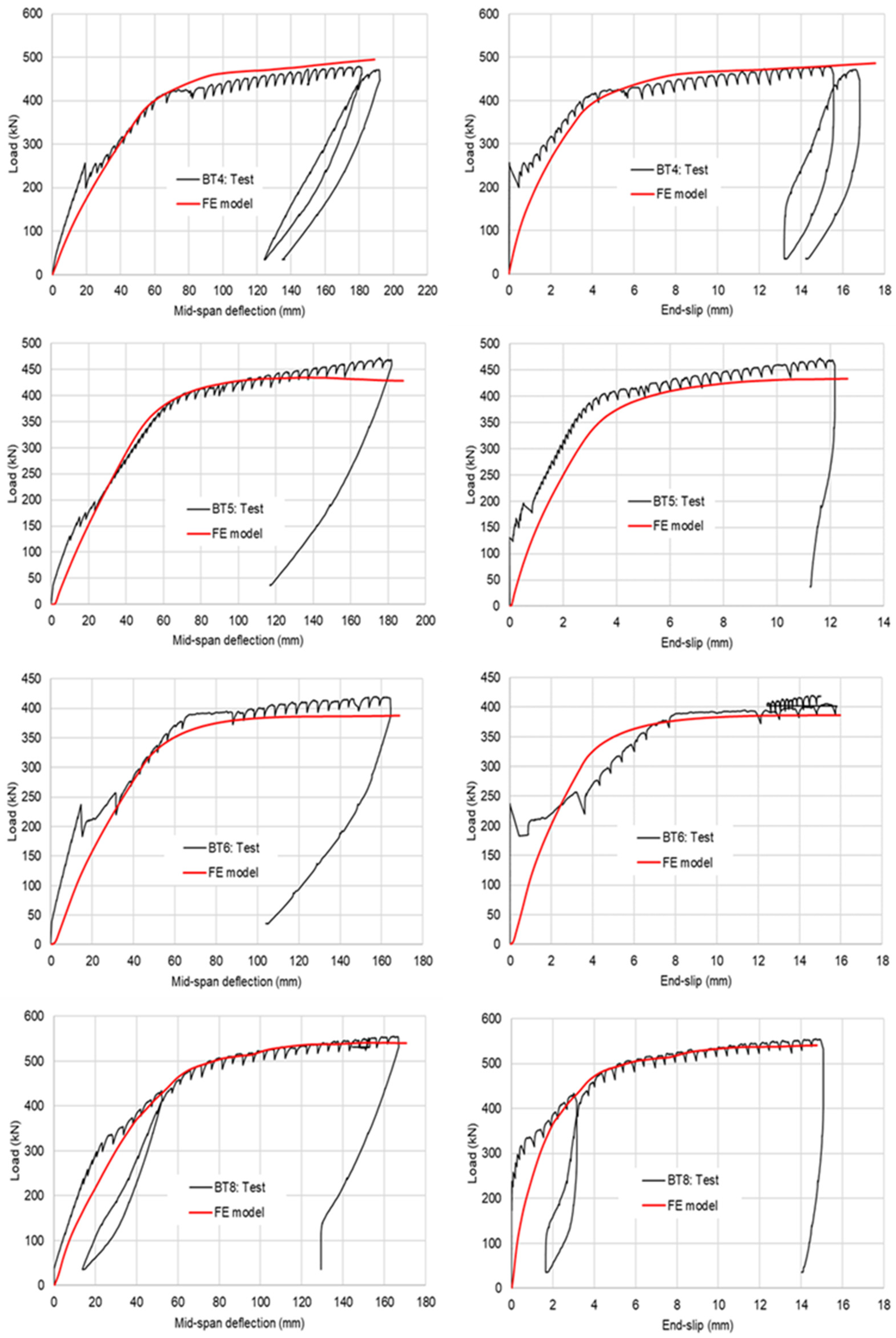
3.6. Validation of FE Model
4. Parametric Study
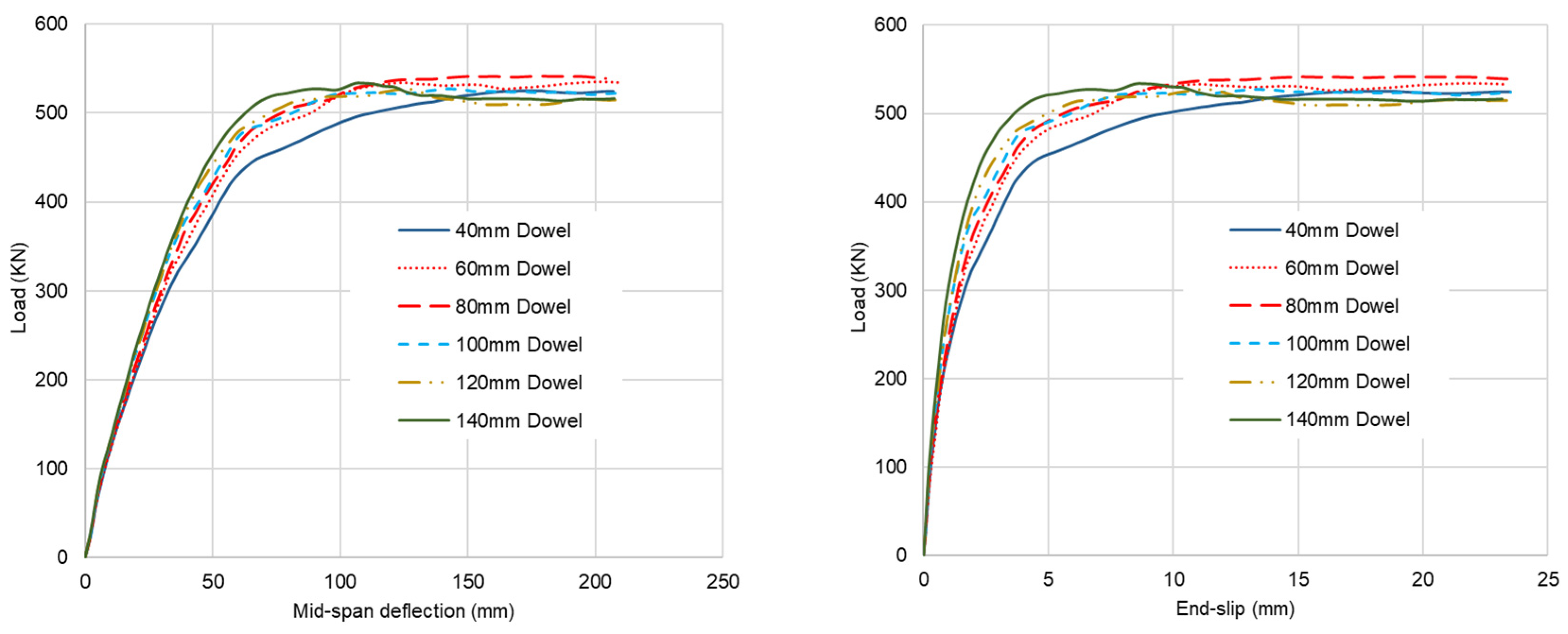
4.1. Effect of Concrete Dowel Diameter
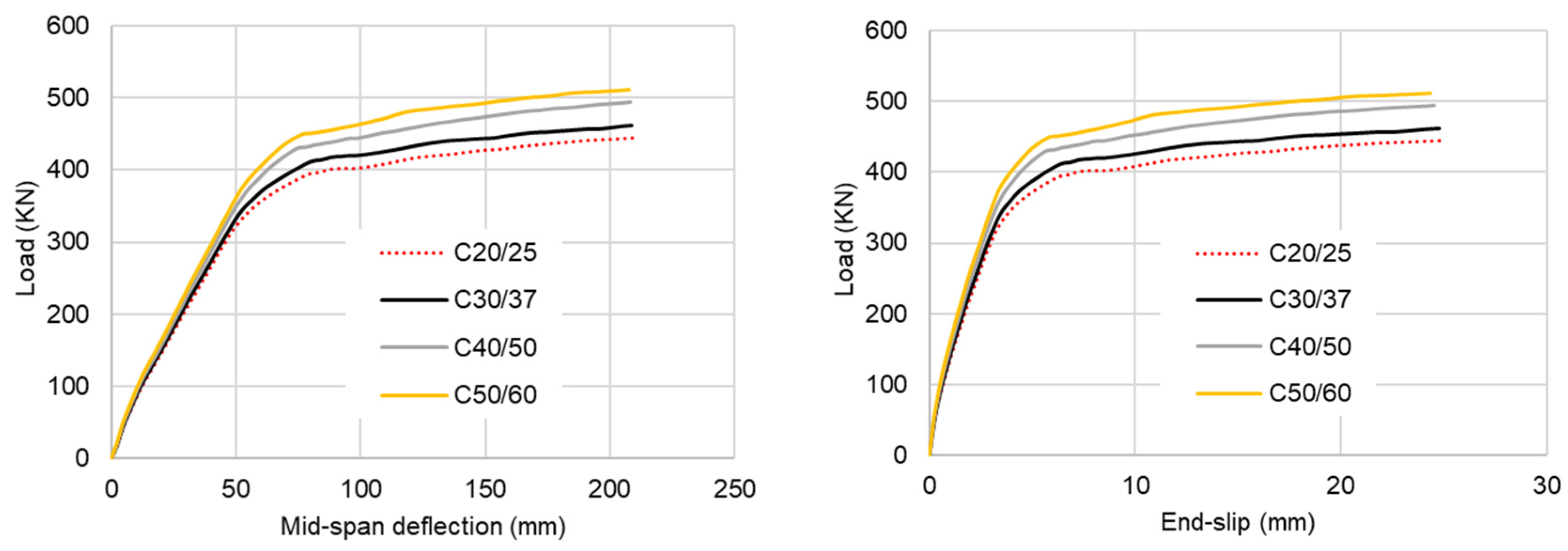
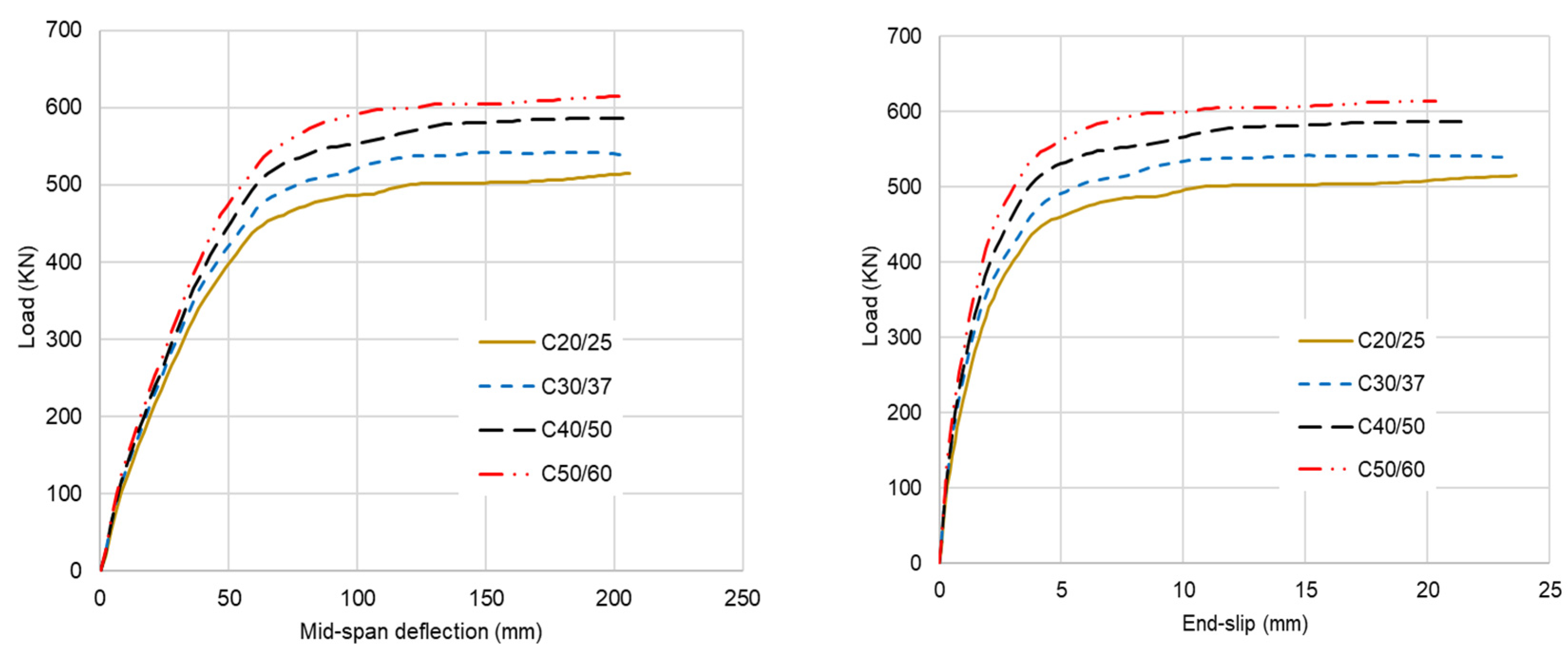
4.2. Effect of the Concrete Strengths
4.3. Effect of Diameter of Reinforcing Bar
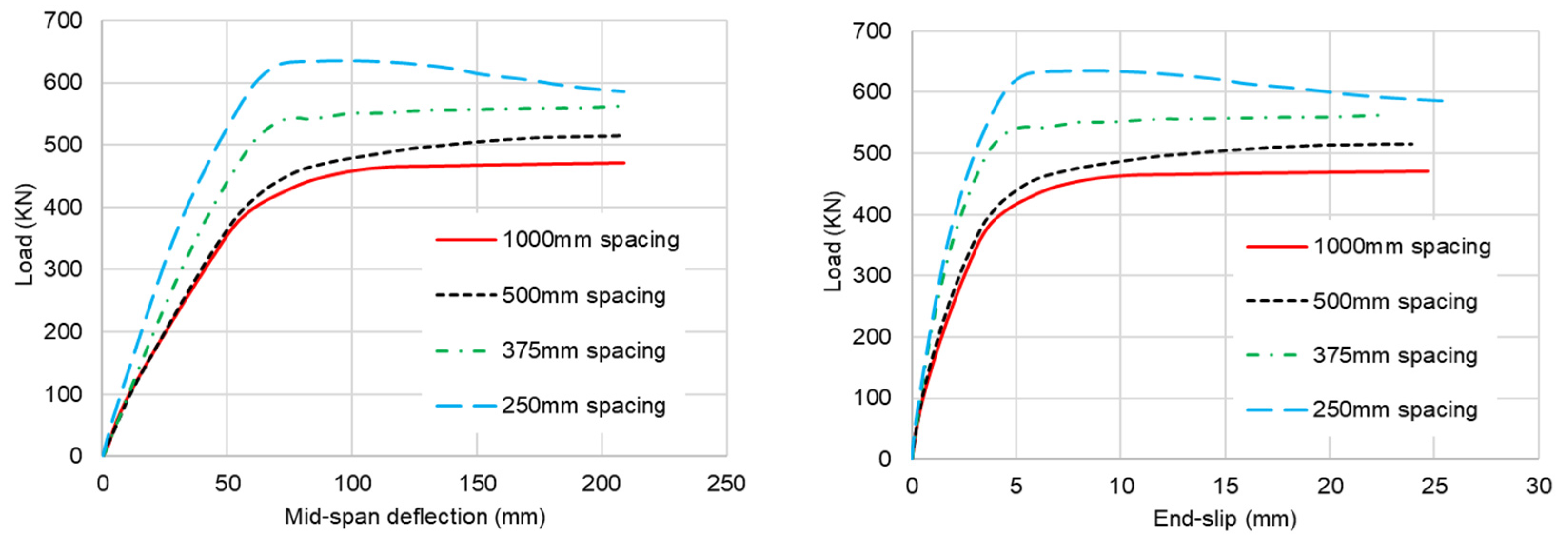
4.4. Effect of Concrete Dowel Spacing
4.5. Failure of Slim-Floor Composite Beam
5. Prediction of Maximum Bending Moment Capacity
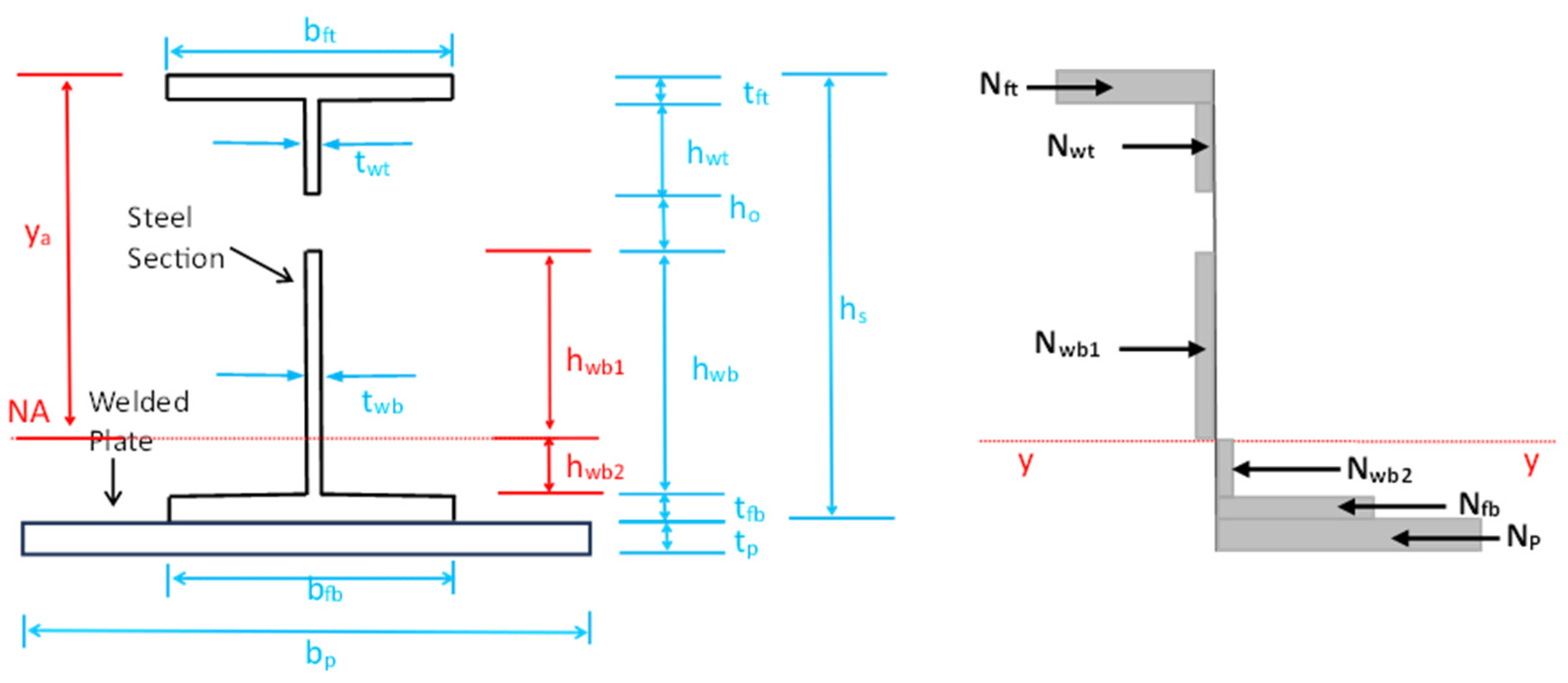
5.1. Bending Moment Resistance of Steel Profile
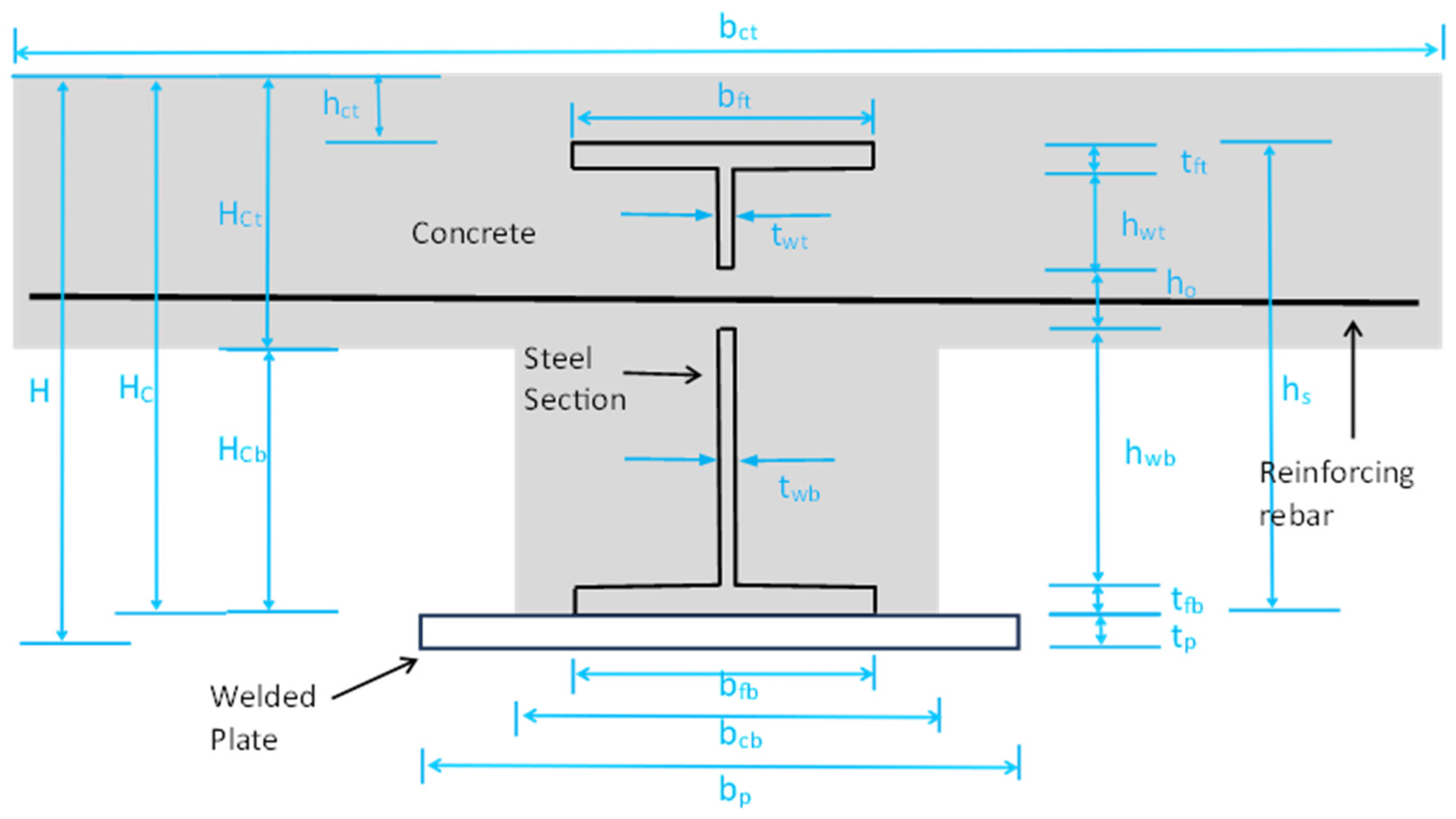
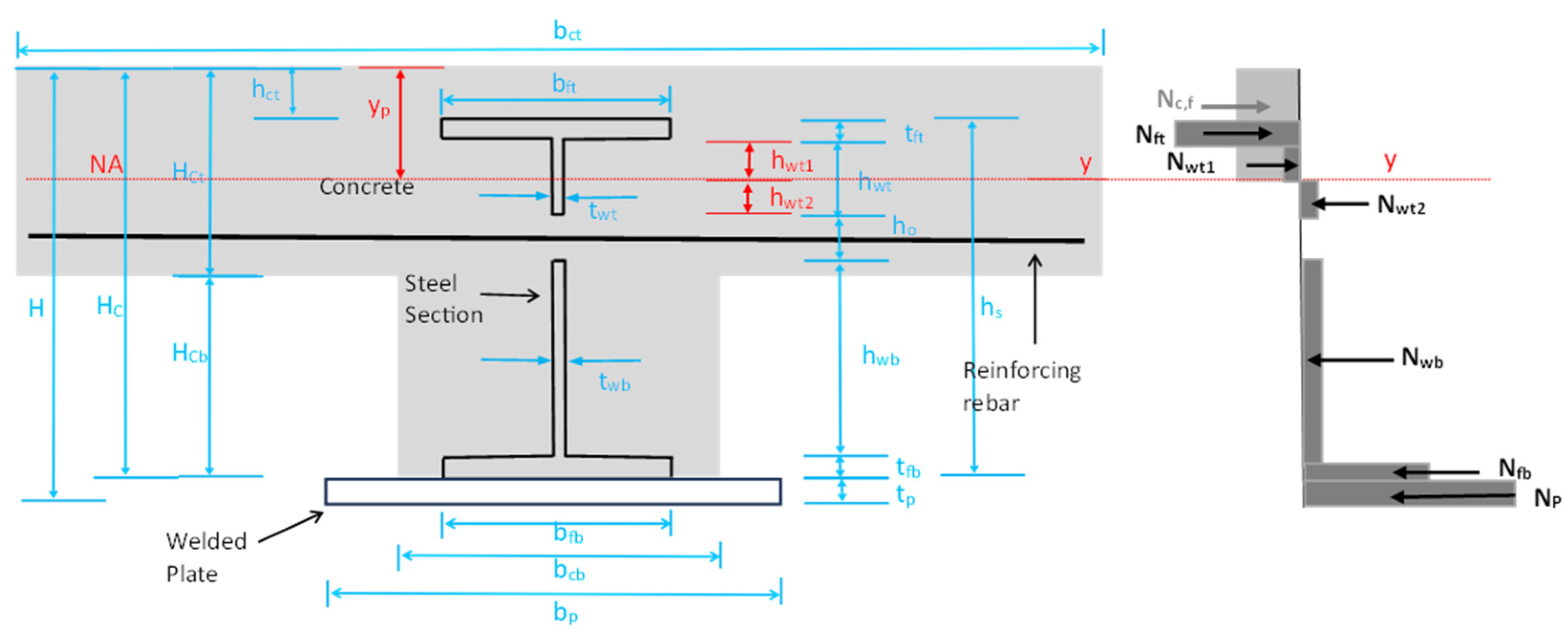
5.2. Bending Moment Resistance of Composite Beam with Full Shear Connection
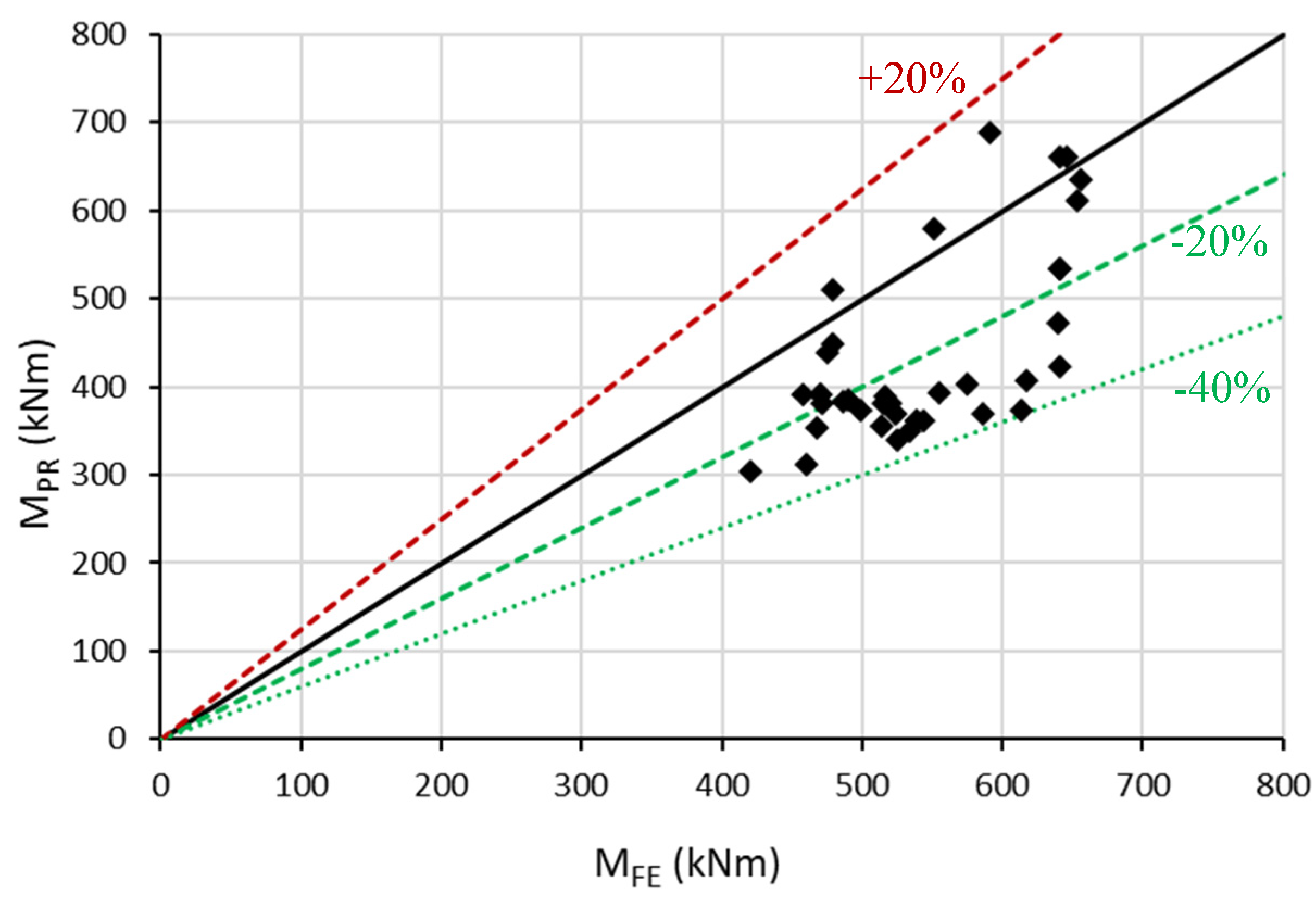
5.3. Validation of the Proposed Expressions
6. Conclusions
- The finite element (FE) model developed using ABAQUS [24] for the flexural composite slim-floor beam utilising dowel shear connectors can be used to predict the load-bearing capacity, deflection, end-slip, and failure patterns.
- The load-bearing capacity of the composite beam increases with a bigger dowel diameter if the shear connection degree is less than 100%, no matter whether there is a reinforcing bar or not. However, the load-bearing capacity diminishes when the concrete dowel diameter exceeds 80 mm in the absence of reinforcing rebar. For composite beams with dowels that incorporate reinforcing rebar, the load-bearing capacity decreases sharply after reaching the maximum load when the dowel diameter exceeds 50 mm. This finding suggests that while a larger concrete dowel enhances the shear resistance of composite beams, it adversely affects the load-bearing capacity of steel beams. Consequently, an optimal dowel size should be considered in the design process. Regardless of dowel size, the composite beam shows excellent ductility. The maximum load corresponds to a midspan deflection over L/60. When the midspan deflection exceeds L/30, the reduction of maximum load capacity is less than 15%.
- Concrete strength significantly influences the load-bearing capacity of the composite beams but not stiffness. The load-bearing capacity increases by approximately 5–10% for every 10 N/mm2 rise in concrete compressive strength. Importantly, when there is rebar in the dowel, the strength of the concrete has a smaller impact on the load-bearing capacity of composite beams because it is primarily the rebar that determines the strength of the shear connector. In terms of ductility, concrete strength appears to have minimal impact.
- The diameter of the reinforcing rebar in the concrete dowel influences the load-bearing capacity but not the stiffness. The load-bearing capacity increases by approximately 2% when the diameter of the rebar is increased by 4 mm for composite beams with a dowel diameter of 40 mm. However, for composite beams with a dowel diameter of 80 mm, there is no noticeable increase in load-bearing capacity because, in larger concrete dowels, the concrete primarily governs the dowel shear resistance, making the rebar diameter less significant. The composite beams exhibit excellent ductility, with the maximum load remaining stable from L/60 midspan deflection to L/30 midspan deflection.
- Both the load-bearing capacity and stiffness of composite beams increase with the dowel spacing reduction due to shear connection degree increases. The increase is more significant for composite beams with a smaller diameter of dowel because the shear connection degree is boosted quicker when dowel spacing is reduced. Furthermore, the distance between dowels influences the load-bearing capacity of the composite beam after it has reached the highest load, but the decrease in load capacity is less than 15% when the midspan deflection is from L/60 to L/30 and the end slip is more than 20 mm.
- The proposed prediction method showed higher accuracy for those composite beams with a shear connection degree exceeding 40%. The average prediction-to-simulation ratio is 0.94 with a standard deviation of 0.14, although the overall average prediction-to-simulation proportion is 0.79, accompanied by a standard deviation of 0.14. Therefore, the proposed prediction method can be used for estimating the bending moment resistance of composite slim-floor beams with a shear connection degree above 40%.
- The research has provided a deep comprehension of how various parameters influence the structural performance of slim-floor composite beams, and the suggested prediction method has proven to be accurate enough. However, the range of parameters considered is limited; in particular, the overall dimensions of composite beams, such as length, width, and thickness, are constant. Therefore, further research into the structural behaviour of slim-floor beams through experiments and numerical simulations employing a wider range of parameters is essential. Additionally, it would help with design if a prediction method could be developed that considers how the strength of shear connectors changes in different places along the composite beam.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, I.M.; Tsavdaridis, K.D. The evolution of composite flooring systems: Applications, testing, modelling and eurocode design approaches. J. Constr. Steel Res. 2019, 155, 286–300. [Google Scholar] [CrossRef]
- Simms, W.I.; Hughes, A.F. Composite Design of Steel Framed Buildings (SCI P359); The Steel Construction Institute: Ascot, UK, 2011; Available online: https://www.steelconstruction.info/images/c/c7/SCI_P359.pdf (accessed on 30 May 2025).
- Lawson, M.; Hicks, S.J. Design of Composite Beams with Large Web Openings (SCI P355); The Steel Construction Institute: Ascot, UK, 2022; Available online: https://www.steelconstruction.info/images/e/e7/SCI_P355.pdf (accessed on 30 May 2025).
- ArcelorMittal Europe—Long Products and Sections and Merchant Bars. Slim-Floor, an Innovative Concept for Floors. 2017. Available online: https://sections.arcelormittal.com/repository2/Sections/5_5_1_SlimFloor.pdf (accessed on 30 May 2025).
- Tsavdaridis, K.D.; D’Mello, C.; Huo, B.Y. Experimental and computational study of the vertical shear behaviour of partially encased perforated steel beams. Eng. Struct. 2013, 56, 805–822. [Google Scholar] [CrossRef]
- BS EN 1994-1-1; Eurocode 4—Design of Composite Steel and Concrete Structures. Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- Hosseinpour, E.; Baharom, S.; Badaruzzaman, W.H.W.; Al Zand, A.W. Push-out test on the web opening shear connector for a slim-floor steel beam: Experimental and analytical study. Eng. Struct. 2018, 163, 137–152. [Google Scholar] [CrossRef]
- Coldebella, G.; Ferreira, F.P.V.; De Nardin, S. Shear forces transfer in steel-concrete slim floor with circular web opening and PCHCS. Structures 2022, 38, 1295–1307. [Google Scholar] [CrossRef]
- Mesquita, L.C.; Marques, M.G.; Paes, J.L.R. Evaluation of the structural behavior of composite slim-floor beams with openings in the web. Eng. Proc. 2023, 53, 6. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; McKinley, B.; Kacaroglu, B.N.; Corfar, D.; Lawson, R.M. Bending test of long-span ultra-shallow floor beam (USFB) with two lightweight concretes. Structures 2024, 66, 106895. [Google Scholar] [CrossRef]
- Baldassino, N.; Roverso, G.; Ranzi, G.; Zandonini, R. Service and Ultimate Behaviour of Slim Floor Beams: An Experimental Study. Structures 2019, 17, 74–86. [Google Scholar] [CrossRef]
- Sheehan, T.; Dai, X.; Yang, J.; Zhou, K.; Lam, D. Flexural behaviour of composite slim floor beams. Structures 2019, 21, 22–32. [Google Scholar] [CrossRef]
- Dai, X.; Lam, D.; Sheehan, T.; Yang, J.; Zhou, K. Effect of dowel shear connector on performance of slim-floor composite shear beams. J. Constr. Steel Res. 2020, 173, 106243. [Google Scholar] [CrossRef]
- Junior, S.E.P.; Ferreira, F.P.V.; Tsavdaridis, K.D.; De Nardin, S. Flexural behavior of steel–concrete ultra-shallow floor beams (USFBs) with precast hollow-core slabs. Eng. Struct. 2023, 278, 115524. [Google Scholar] [CrossRef]
- Allali, A.A.; Tsavdaridis, K.D. Experimental investigation on flexural behaviour of prefabricated ultra-shallow steel concrete composite slabs. J. Constr. Steel Res. 2024, 217, 108632. [Google Scholar] [CrossRef]
- Lin, Z.; Monti, G.; Wu, Z. Composite action in Shallow Steel-beam-Concrete Composite decks. Eng. Struct. 2023, 286, 116114. [Google Scholar] [CrossRef]
- Xia, Y.; Han, C.; Zhou, D.; Wang, Y.; Wang, P. Ultimate flexural strength analysis of composite slim floor beam. Adv. Struct. Eng. 2021, 24, 2214–2226. [Google Scholar] [CrossRef]
- Chen, S.; Limazie, T.; Tan, J. Flexural behavior of shallow cellular composite floor beams with innovative shear connections. J. Constr. Steel Res. 2015, 106, 329–346. [Google Scholar] [CrossRef]
- Lam, D.; Dai, X.; Kuhlmann, U.; Raichle, J.; Braun, M. Slim-floor construction—Design for ultimate limit state. Steel Constr. 2015, 8, 79–84. [Google Scholar] [CrossRef]
- Limazie, T.; Chen, S. Numerical procedure for nonlinear behavior analysis of composite slim floor beams. J. Constr. Steel Res. 2015, 106, 209–219. [Google Scholar] [CrossRef]
- Huo, B.Y.; D’Mello, C.A. Shear Transferring Mechanisms in a Composite Shallow Cellular Floor Beam with Web Openings. Structures 2017, 9, 134–146. [Google Scholar] [CrossRef]
- Limazie, T.; Chen, S. FE modeling and numerical investigation of shallow cellular composite floor beams. J. Constr. Steel Res. 2016, 119, 190–201. [Google Scholar] [CrossRef]
- Limazie, T.; Chen, S. Effective shear connection for shallow cellular composite floor beams. J. Constr. Steel Res. 2017, 128, 772–788. [Google Scholar] [CrossRef]
- Dassault Systèmes. Abaqus/CAE 2022; Dassault Systèmes SIMULIA Corp.: Cleveland, OH, USA, 2022. [Google Scholar]
- BS EN 1992-1-1:2004; Eurocode 2—Design of Concrete Structures-Part 1-1. General Rules and Rules for Buildings. British Standards Institution (BSI): London, UK, 2010.
- Qureshi, J.; Lam, D.; Ye, J. Effect of shear connector spacing and layout on the shear connector capacity in composite beams. J. Constr. Steel Res. 2011, 67, 706–719. [Google Scholar] [CrossRef]
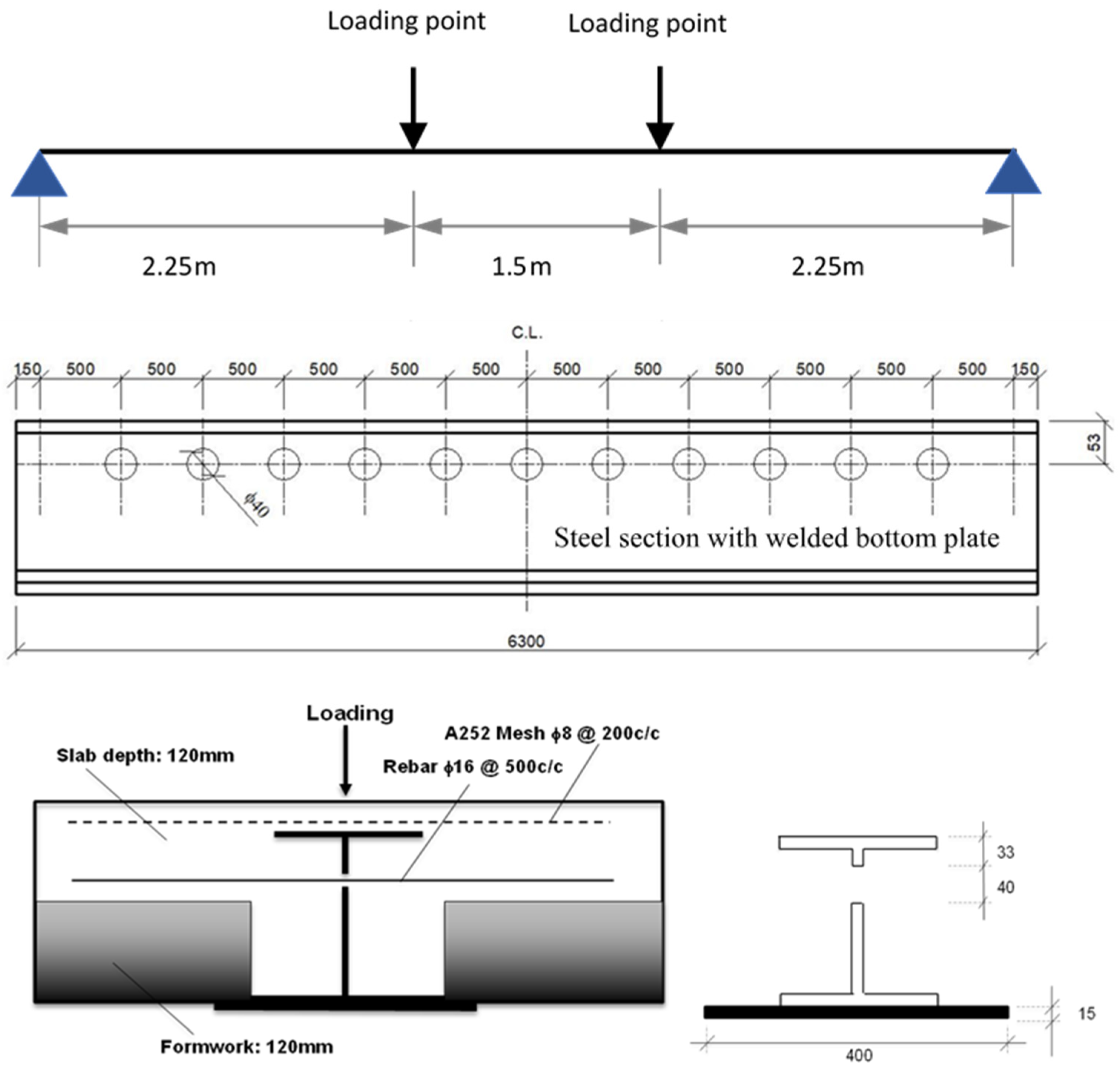
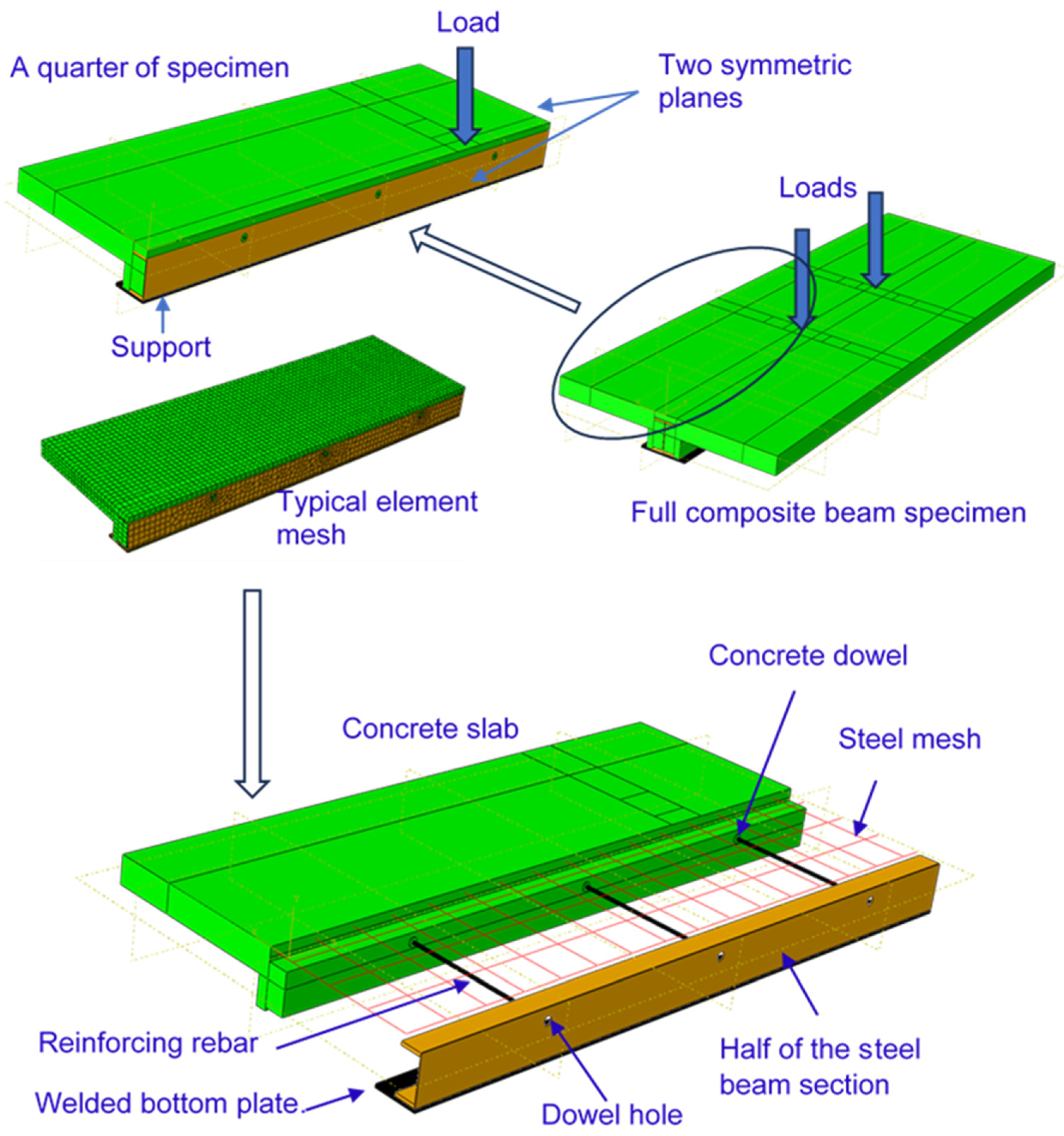
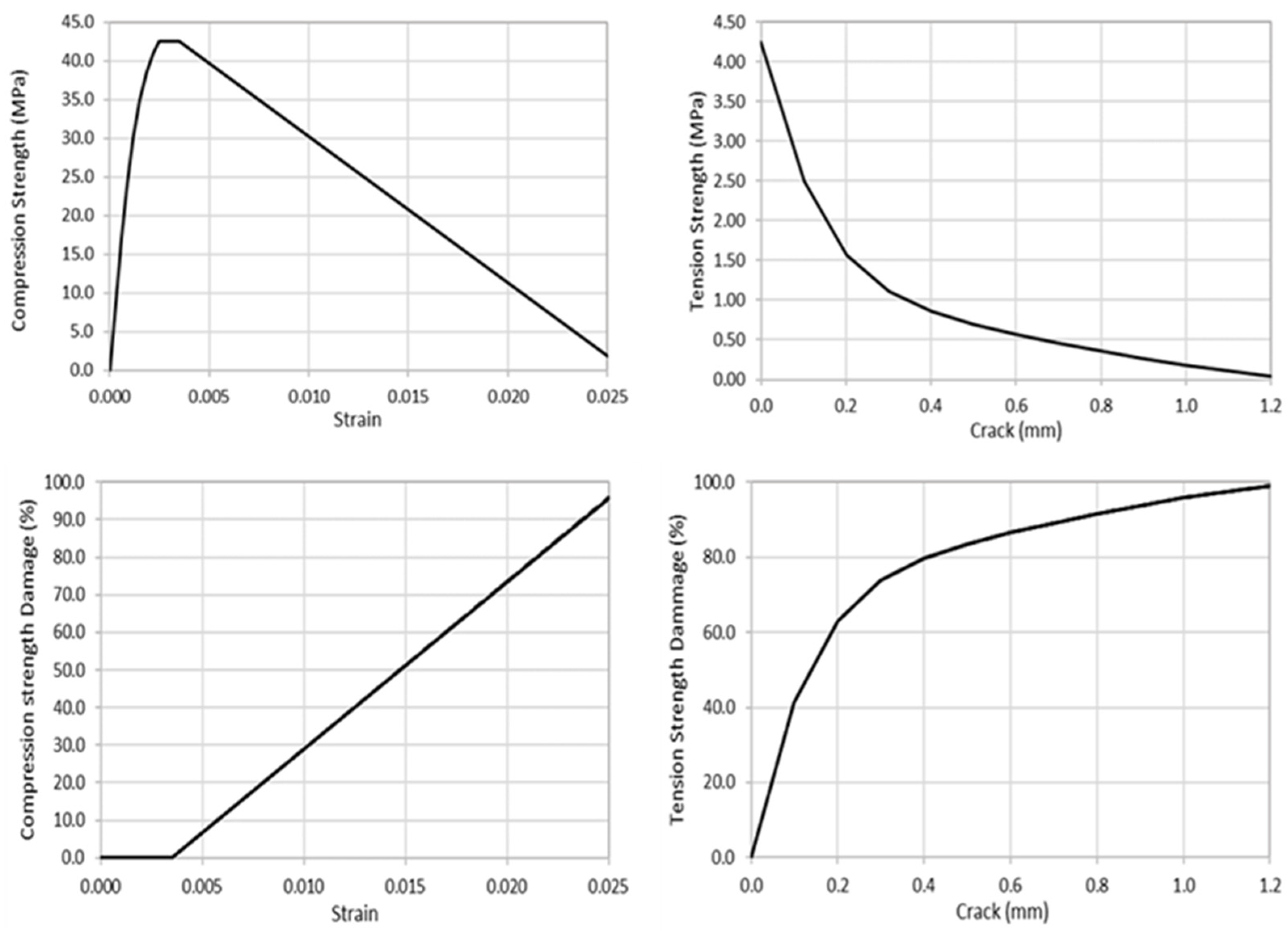
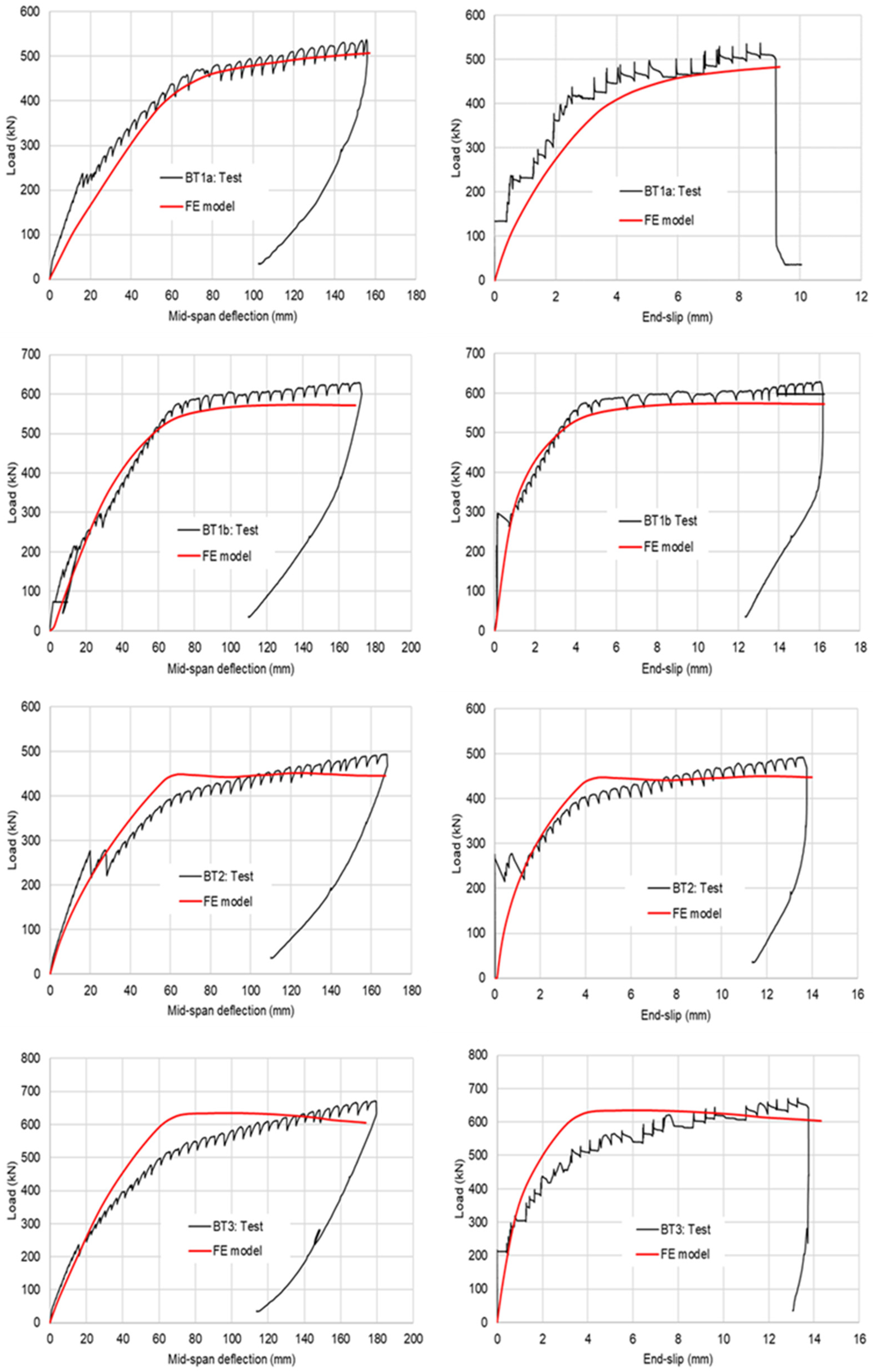







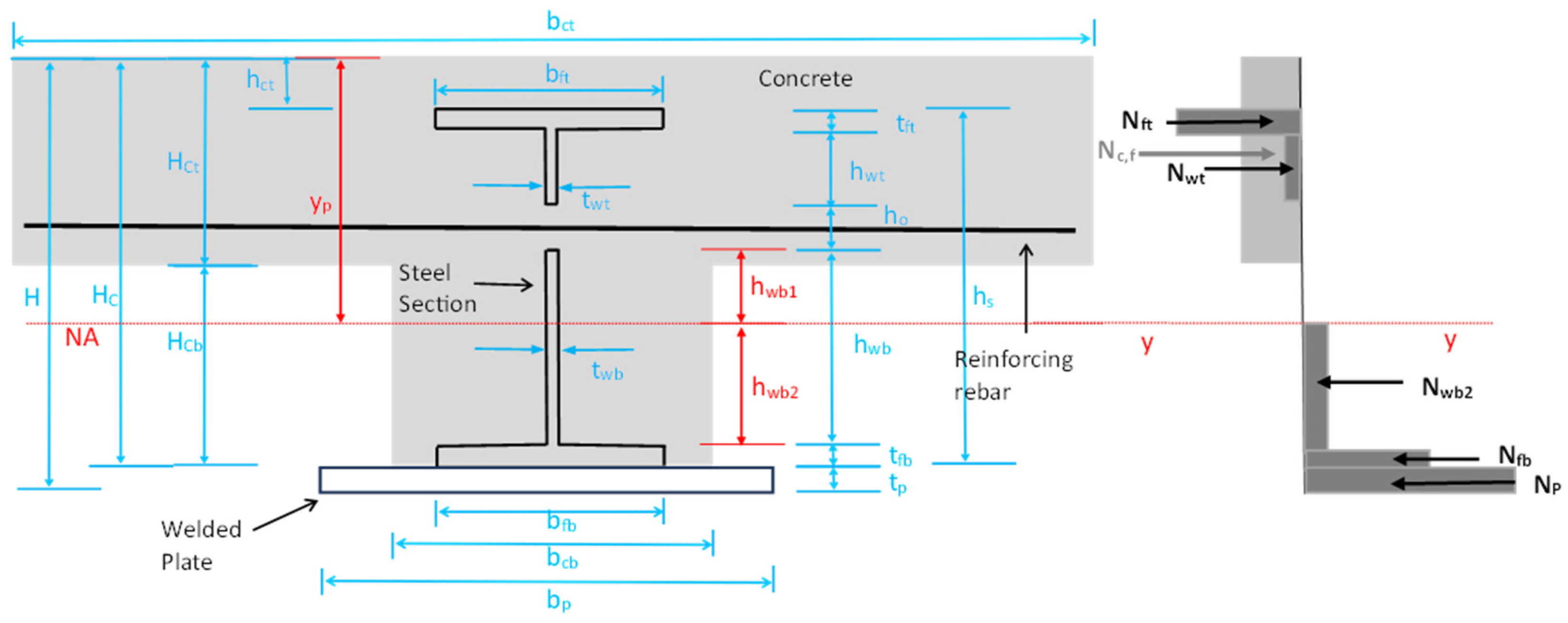
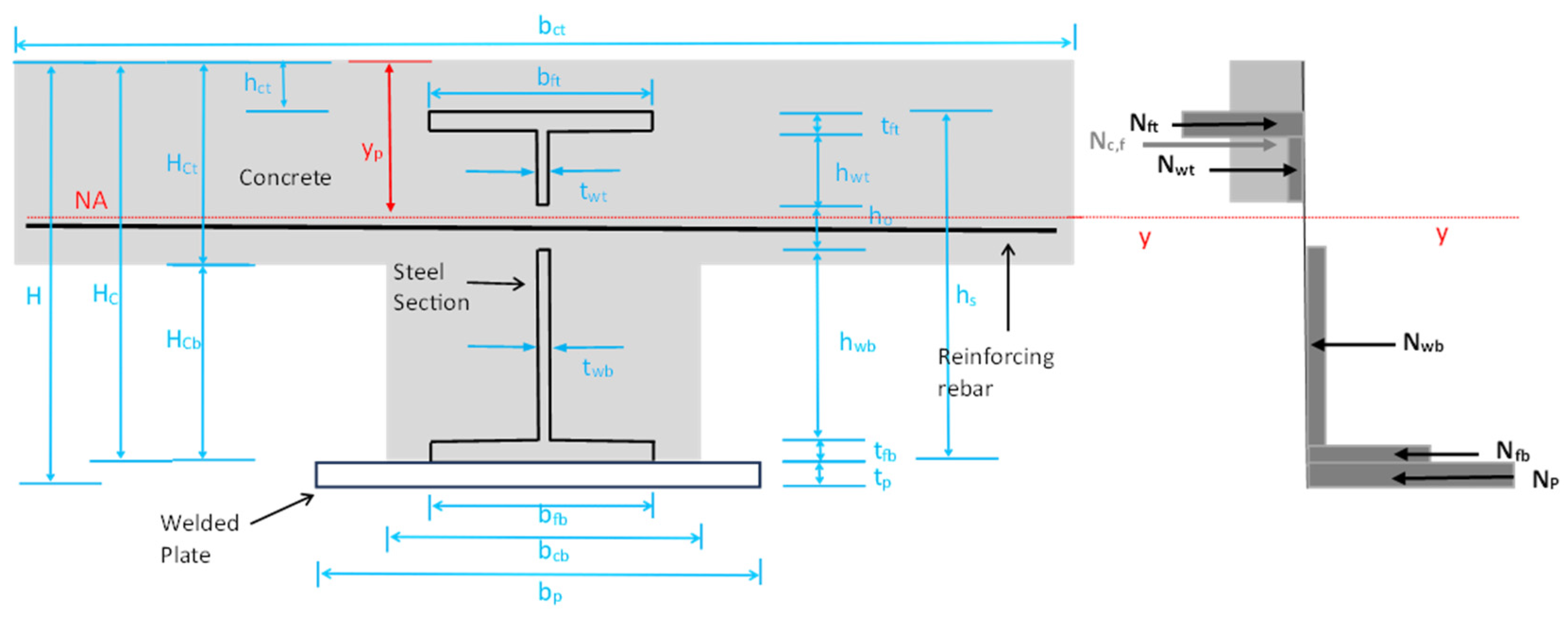

| Specimen ID | Loading Regime (mm) | Shear Connector Type | Dowel Diameter (mm) | Rebar Diameter (mm) | Beam Depth (mm) | SC Spacing (mm) | Design Shear Connection Degree |
|---|---|---|---|---|---|---|---|
| BT 1a | Concentric | Dowel | 40 | 16 | 240 | 500 | 40% |
| BT 1b | Concentric | - | - | - | 240 | - | 0 |
| BT 2 | Eccentric | Dowel | 40 | 16 | 240 | 500 | 40% |
| BT 3 | Concentric | Dowel | 40 | 16 | 240 | 250 | 100% |
| BT 4 | Concentric | Dowel | 40 | 16 | 240 | 1000 | 25% |
| BT 5 | Concentric | Dowel | 40 | 16 | 200 | 500 | 50% |
| BT 6 | Eccentric | - | - | - | 240 | - | 0 |
| BT 7 | Concentric | Stud | - | - | 240 | 375 | 40% |
| BT 8 | Concentric | Dowel | 80 | - | 240 | 500 | 64% |
| Specimen ID | Maximum Load | Load at 6 mm End Slip | Load at 30 mm Mid-Span Deflection | Load at 60 mm Mid-Span Deflection | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PEX-M (KN) | PFE-M (KN) | PEX-M/PFE-M | PEX-6 (kN) | PFE-6 (kN) | PEX-6/PFE-6 | PEX-30 (kN) | PFE-30 (kN) | PEX-30/PFE-30 | PEX-60 (kN) | PFE-60 (kN) | PEX-60/PFE-60 | |
| BT1a | 535 | 507 | 1.055 | 476 | 461 | 1.033 | 296 | 321 | 0.922 | 436 | 408 | 1.069 |
| BT1b | 630 | 574 | 1.098 | 588 | 558 | 1.054 | 278 | 336 | 0.825 | 506 | 513 | 0.986 |
| BT2 | 492 | 451 | 1.091 | 420 | 444 | 0.946 | 246 | 287 | 0.857 | 392 | 443 | 0.885 |
| BT3 | 668 | 634 | 1.054 | 541 | 635 | 0.852 | 337 | 370 | 0.911 | 497 | 696 | 0.714 |
| BT4 | 479 | 494 | 0.970 | 430 | 436 | 0.986 | 261 | 246 | 1.061 | 398 | 402 | 0.990 |
| BT5 | 469 | 434 | 1.081 | 412 | 409 | 1.007 | 225 | 227 | 0.991 | 376 | 380 | 0.989 |
| BT6 | 419 | 387 | 1.083 | 326 | 363 | 0.898 | 251 | 220 | 1.141 | 371 | 350 | 1.060 |
| BT7 | 698 | 654 | 1.067 | 678 | 653 | 1.038 | 340 | 379 | 0.897 | 530 | 616 | 0.860 |
| BT8 | 553 | 531 | 1.041 | 505 | 490 | 1.031 | 335 | 298 | 1.124 | 456 | 456 | 1.000 |
| Average | 1.060 | 0.983 | 0.970 | 0.950 | ||||||||
| SD | 0.036 | 0.066 | 0.108 | 0.0106 | ||||||||
| Specimen ID | Rebar Diameter (mm) | Dowel Hole Diameter (mm) | Concrete Strength (N/mm2) | SC Spacing (mm) | Design Shear Connection Degree | (kNm) | (kNm) | |
|---|---|---|---|---|---|---|---|---|
| BT1a | 16 | 40 | 41 | 500 | 40% | 604.1 | 499.8 | 0.827 |
| BT1b | - | - | 27.5 | - | 0 | 455.3 | 455.1 | 1.000 |
| BT2 | 16 | 40 | 35.6 | 500 | 40% | 554.6 | 497.7 | 0.897 |
| BT3 | 16 | 40 | 44.5 | 250 | 100% | 725.6 | 715.5 | 0.986 |
| BT4 | 16 | 40 | 43.1 | 1000 | 25% | 539.4 | 397.3 | 0.737 |
| BT5 | 16 | 40 | 38.4 | 500 | 50% | 531.9 | 496.7 | 0.934 |
| BT6 | - | - | 47.9 | - | 0 | 455.6 | 399.7 | 0.877 |
| BT8 | - | 80 | 47.9 | 500 | 64% | 624.2 | 536.8 | 0.860 |
| Average | 0.891 | |||||||
| SD | 0.086 |
| FE Model ID | Rebar Diameter (mm) | Dowel Hole Diameter (mm) | Concrete Strength | SC Spacing (mm) | SC Degree (%) | |||
|---|---|---|---|---|---|---|---|---|
| BT4-1 | 16 | 40 | C25/30 | 1000 | 28 | 499.5 | 372.78 | 0.75 |
| BT4-2 | 16 | 40 | C30/37 | 1000 | 29 | 519.75 | 380.45 | 0.73 |
| BT4-3 | 16 | 40 | C40/50 | 1000 | 30 | 555.3 | 393.15 | 0.71 |
| BT4-4 | 16 | 40 | C50/60 | 1000 | 31 | 574.875 | 403.05 | 0.70 |
| BT4-5 | 16 | 40 | C38 | 250 | 100 | 591.148 | 689.56 | 1.17 |
| BT4-6 | 16 | 40 | C38 | 375 | 74 | 550.828 | 578.96 | 1.05 |
| BT4-7 | 16 | 40 | C38 | 500 | 55 | 479.568 | 449.44 | 0.94 |
| BT4-8 | 16 | 40 | C38 | 1000 | 30 | 458.212 | 391.78 | 0.86 |
| BT4-9 | 16 | 0 | C38 | 1000 | 0 | 419.98 | 303.69 | 0.72 |
| BT4-10 | 16 | 40 | C38 | 1000 | 30 | 470.896 | 391.78 | 0.83 |
| BT4-11 | 16 | 50 | C38 | 1000 | 29 | 490.832 | 384.42 | 0.78 |
| BT4-12 | 16 | 60 | C38 | 1000 | 29 | 471.756 | 381.43 | 0.81 |
| BT4-13 | 16 | 70 | C38 | 1000 | 30 | 486.592 | 382.88 | 0.79 |
| BT4-14 | 0 | 40 | C38 | 1000 | 11 | 460.132 | 310.95 | 0.68 |
| BT4-15 | 12 | 40 | C38 | 1000 | 21 | 467.624 | 353.49 | 0.76 |
| BT4-16 | 16 | 40 | C38 | 1000 | 30 | 470.896 | 391.78 | 0.83 |
| BT4-17 | 20 | 40 | C38 | 1000 | 41 | 475.1 | 438.57 | 0.92 |
| BT4-18 | 24 | 40 | C38 | 1000 | 58 | 478.74 | 510.89 | 1.07 |
| BT5-1 | x | 40 | C30/37 | 500 | 19 | 524.72 | 340.35 | 0.65 |
| BT5-2 | x | 60 | C30/37 | 500 | 23 | 533.448 | 350.34 | 0.66 |
| BT5-3 | x | 80 | C30/37 | 500 | 27 | 538.928 | 361.29 | 0.67 |
| BT5-4 | x | 100 | C30/37 | 500 | 30 | 524.248 | 368.79 | 0.70 |
| BT5-5 | x | 120 | C30/37 | 500 | 34 | 515.26 | 380.72 | 0.74 |
| BT5-6 | x | 140 | C30/37 | 500 | 37 | 516.54 | 388.65 | 0.75 |
| BT5-7 | x | 80 | C25/30 | 1000 | 27 | 514.336 | 355.68 | 0.69 |
| BT5-8 | x | 80 | C30/37 | 1000 | 27 | 538.928 | 361.29 | 0.67 |
| BT5-9 | x | 80 | C40/50 | 1000 | 27 | 585.576 | 368.33 | 0.63 |
| BT5-10 | x | 80 | C50/60 | 1000 | 27 | 614.076 | 372.79 | 0.61 |
| BT5-11 | x | 80 | C30/37 | 1000 | 27 | 543.884 | 361.29 | 0.66 |
| BT5-12 | 12 | 80 | C30/37 | 1000 | 42 | 641.412 | 422.68 | 0.66 |
| BT5-13 | 16 | 80 | C30/37 | 1000 | 54 | 640.088 | 471.79 | 0.74 |
| BT5-14 | 20 | 80 | C30/37 | 1000 | 69 | 641.564 | 533.18 | 0.83 |
| BT5-15 | 24 | 80 | C30/37 | 1000 | 88 | 653.412 | 610.93 | 0.93 |
| BT5-16 | 20 | 80 | C30/37 | 125 | 100 | 641.196 | 660.04 | 1.03 |
| BT5-17 | 20 | 80 | C30/37 | 250 | 100 | 646.512 | 660.04 | 1.02 |
| BT5-18 | 20 | 80 | C30/37 | 375 | 94 | 655.424 | 635.49 | 0.97 |
| BT5-19 | 20 | 80 | C30/37 | 500 | 69 | 641.564 | 533.18 | 0.83 |
| BT5-20 | 20 | 80 | C30/37 | 1000 | 38 | 617.864 | 406.31 | 0.66 |
| Average | 0.79 | |||||||
| SD | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Dai, X.; Lam, D. Numerical Modelling and Parametric Study of Steel-Concrete Composite Slim-Floor Flexural Beam Using Dowel Shear Connectors. Infrastructures 2025, 10, 146. https://doi.org/10.3390/infrastructures10060146
Xu X, Dai X, Lam D. Numerical Modelling and Parametric Study of Steel-Concrete Composite Slim-Floor Flexural Beam Using Dowel Shear Connectors. Infrastructures. 2025; 10(6):146. https://doi.org/10.3390/infrastructures10060146
Chicago/Turabian StyleXu, Xinxin, Xianghe Dai, and Dennis Lam. 2025. "Numerical Modelling and Parametric Study of Steel-Concrete Composite Slim-Floor Flexural Beam Using Dowel Shear Connectors" Infrastructures 10, no. 6: 146. https://doi.org/10.3390/infrastructures10060146
APA StyleXu, X., Dai, X., & Lam, D. (2025). Numerical Modelling and Parametric Study of Steel-Concrete Composite Slim-Floor Flexural Beam Using Dowel Shear Connectors. Infrastructures, 10(6), 146. https://doi.org/10.3390/infrastructures10060146





