Numerical Simulation and Analysis of the Influencing Factors of Ice Formation on Electrified Railway Contact Lines
Abstract
1. Introduction
2. Calculation and Simulation of Basic Parameters of Iced Contact Line
2.1. Establishment of the Fluid Calculation Domain
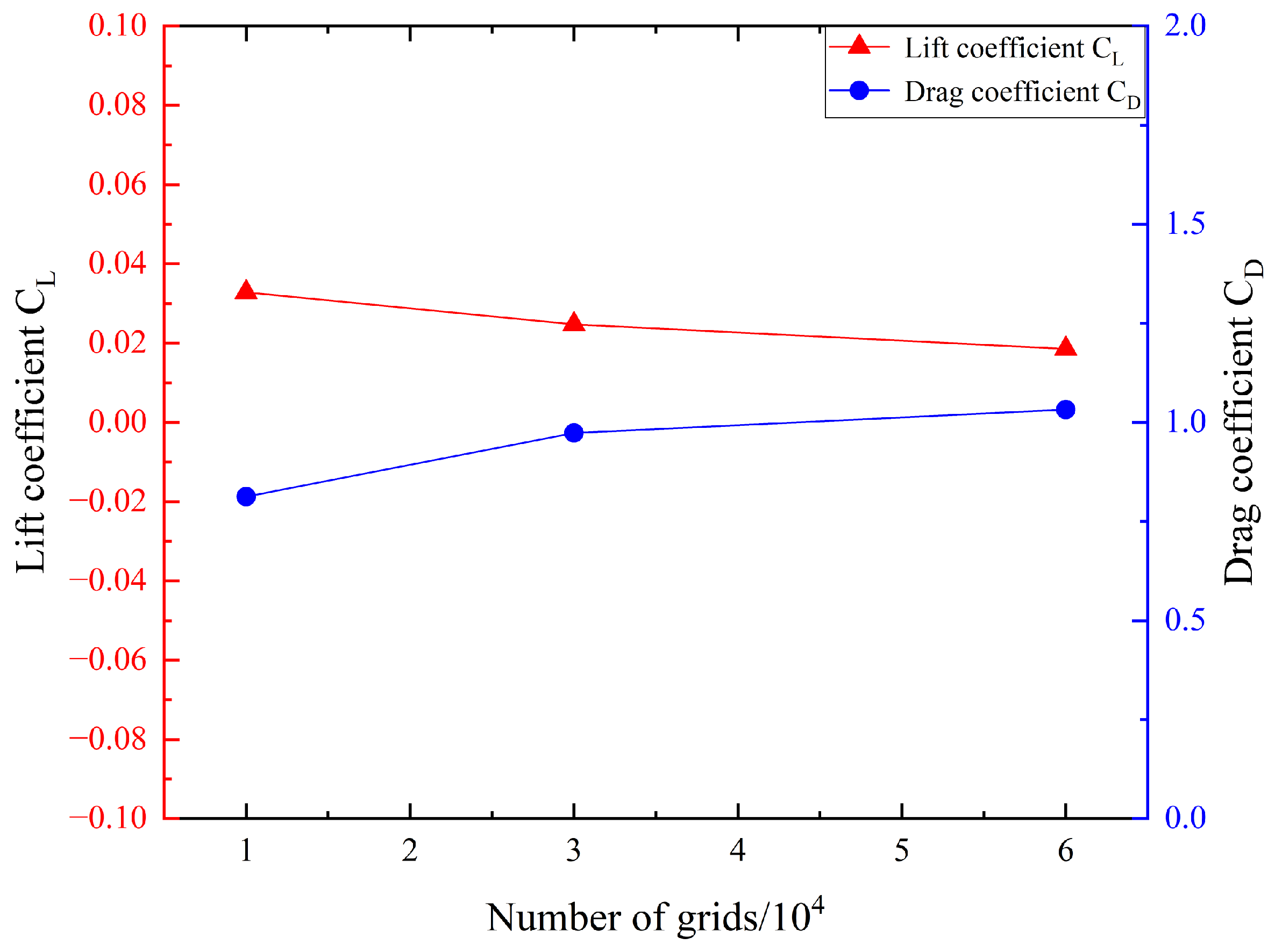
2.2. Mesh-Independent Verification
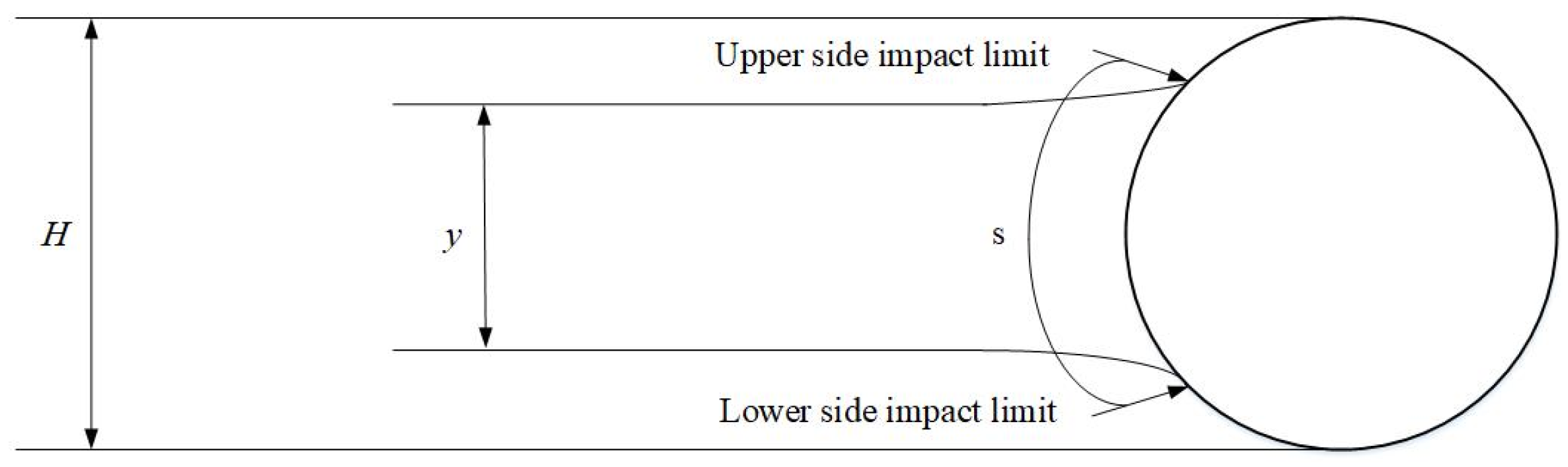
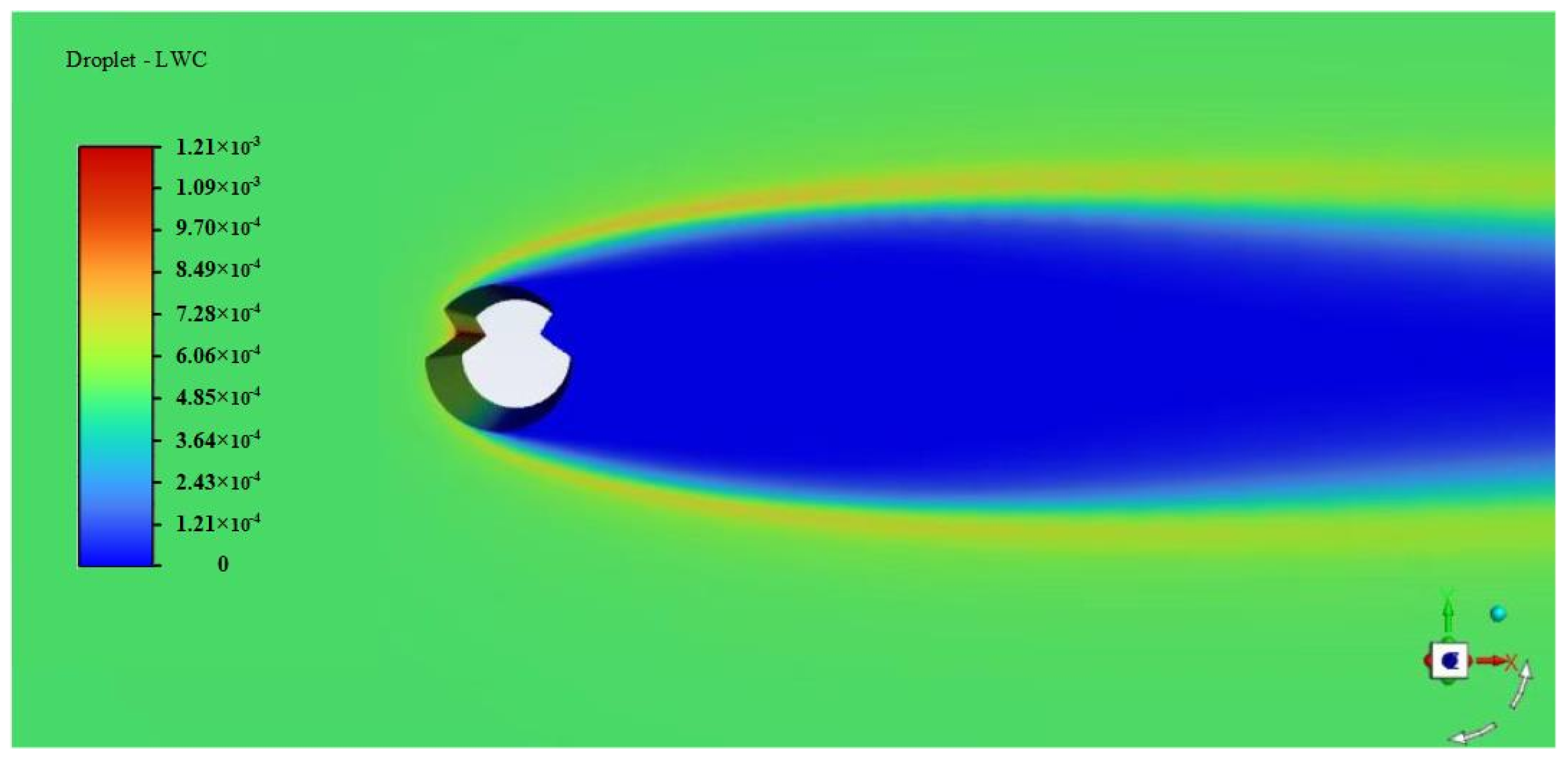
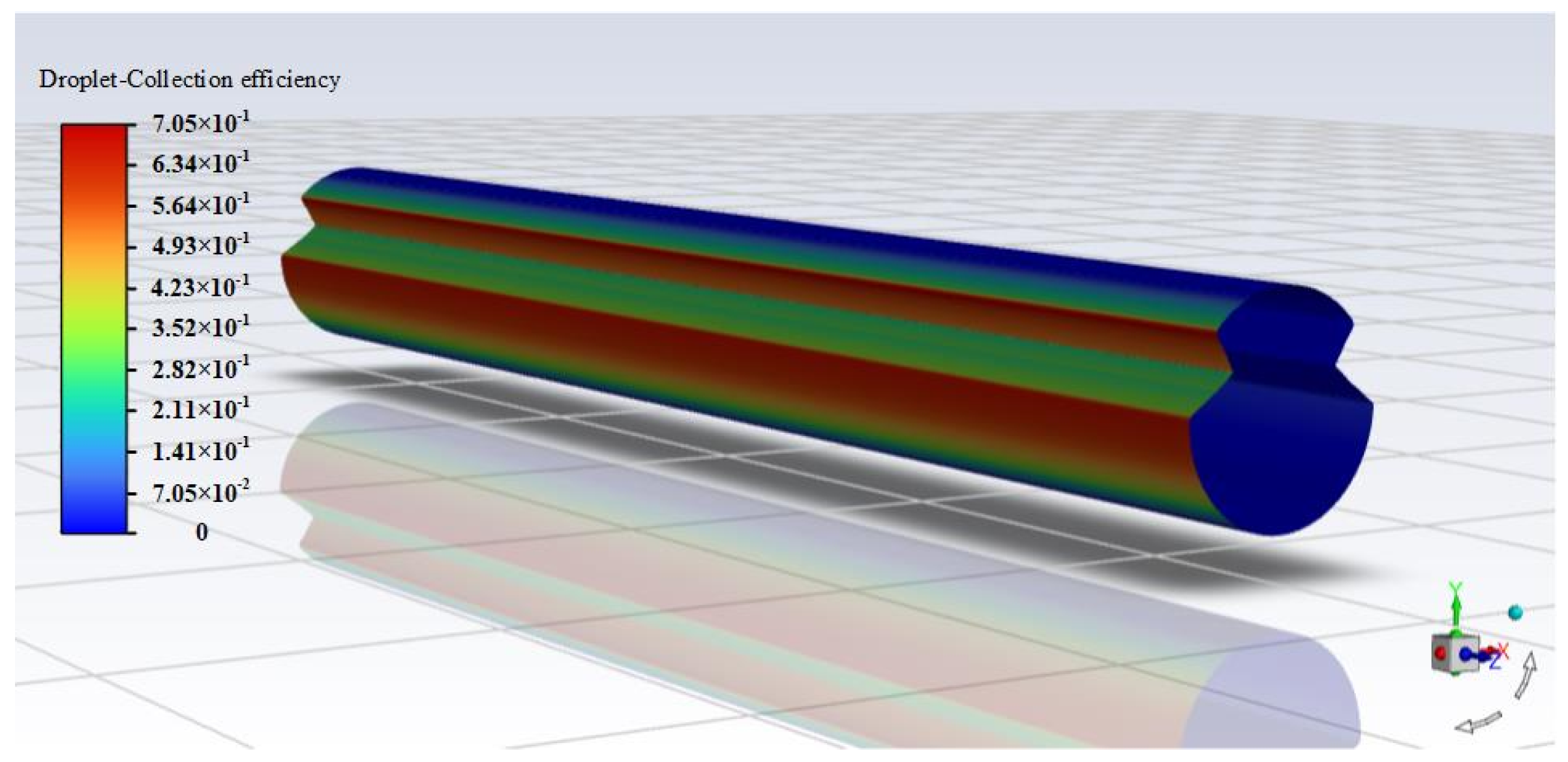
2.3. Study of Droplet Collision in the Overhead Contact Line System
2.4. Droplet Trajectory Equation and Its Solution
2.5. Study of Ice Formation on the Contact Line Surface
3. Analysis of Calculation Results
3.1. Icing Model Validation
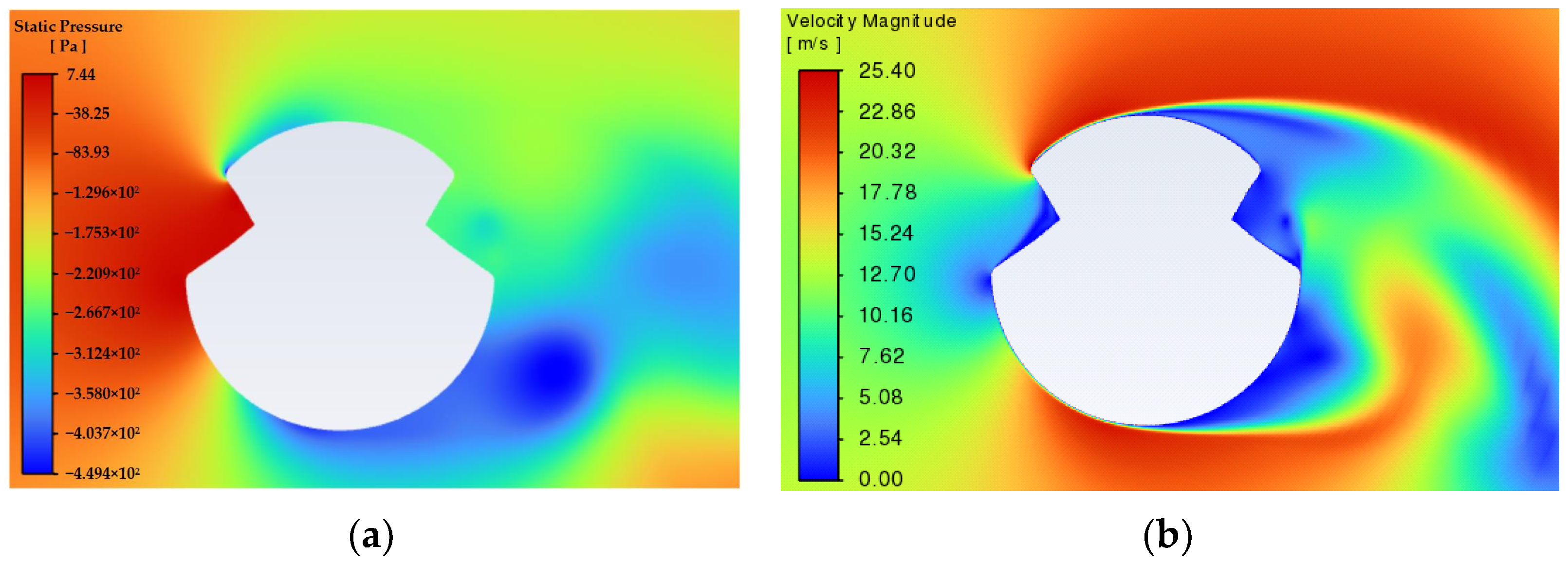
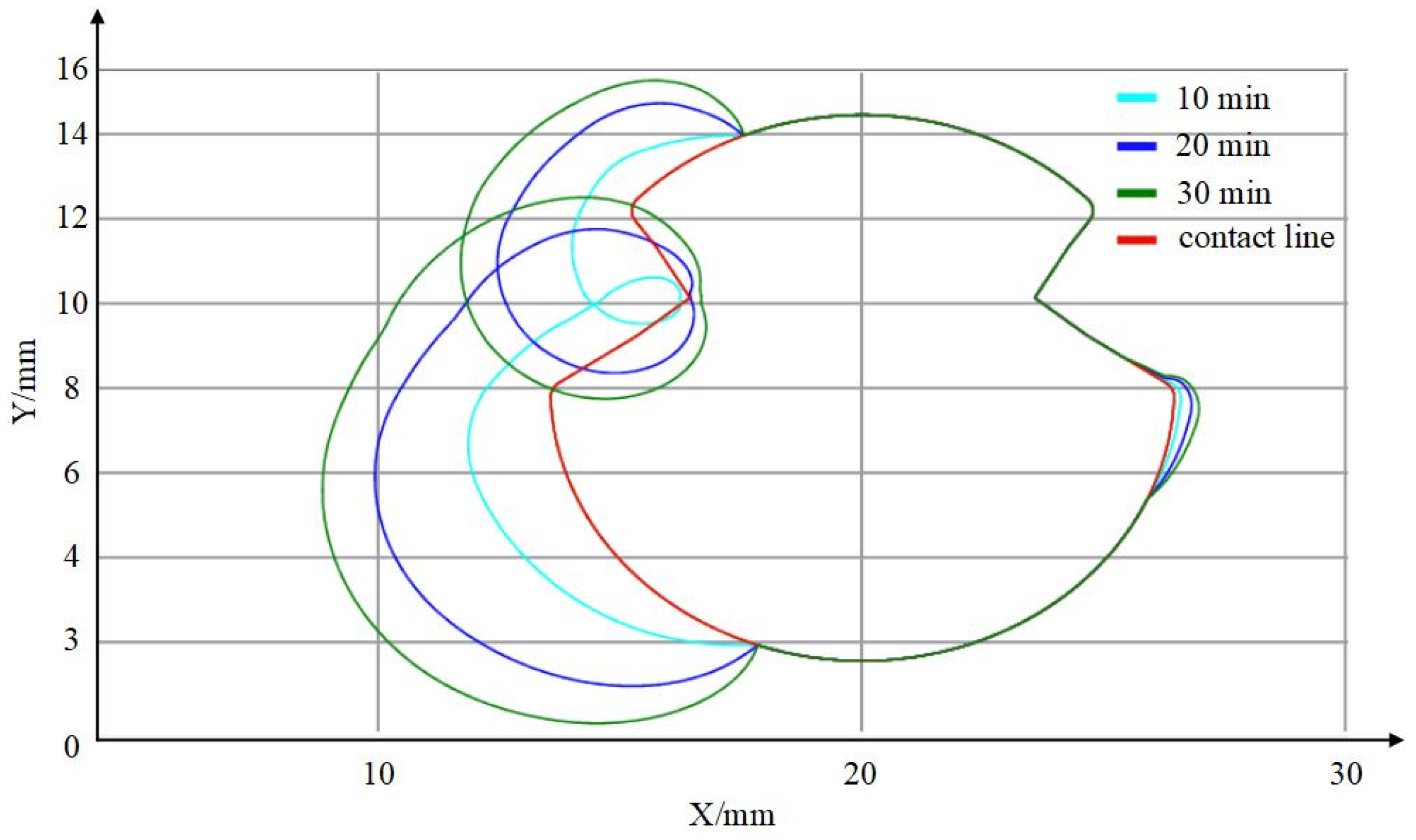
3.2. Contact Line Icing Model Simulation
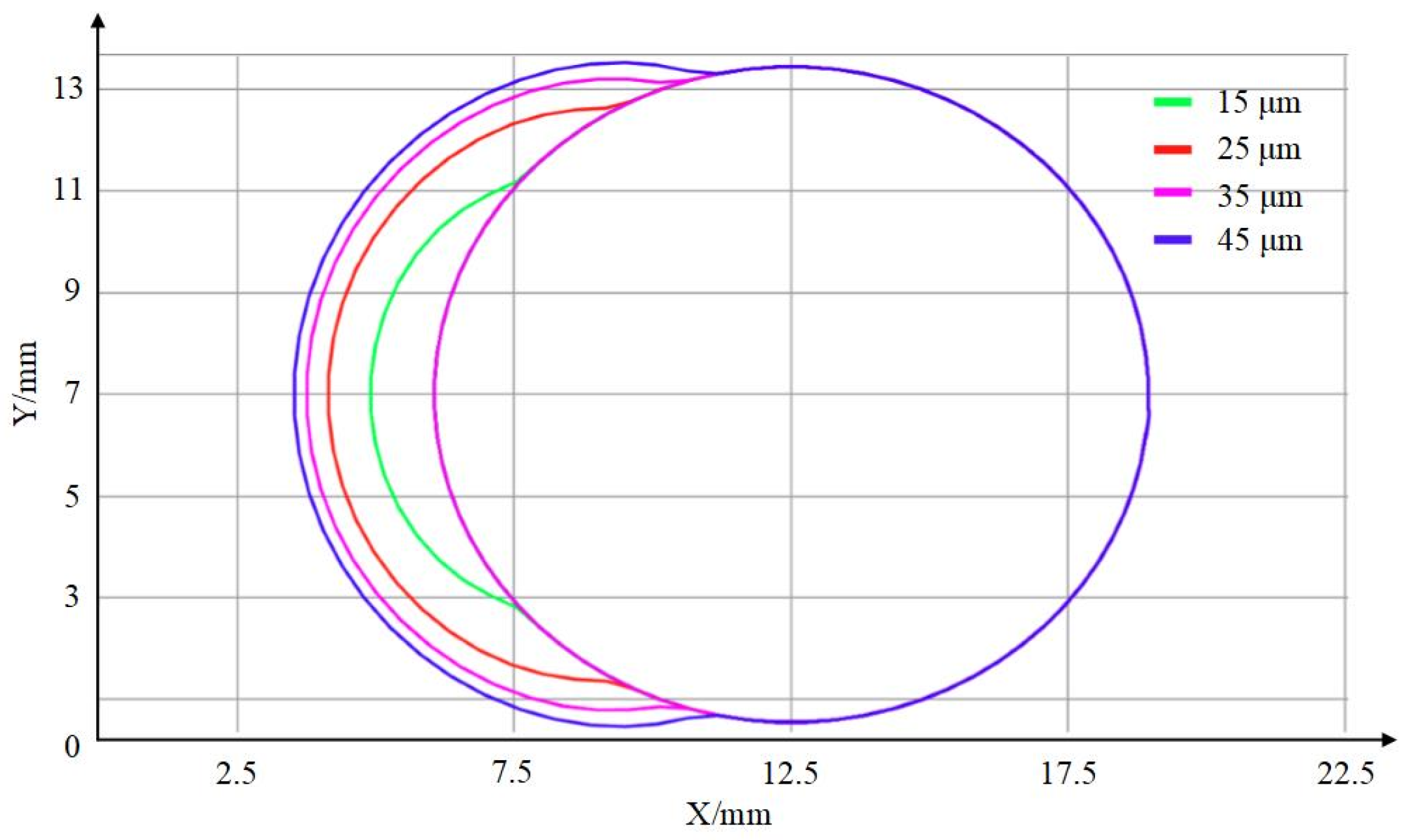
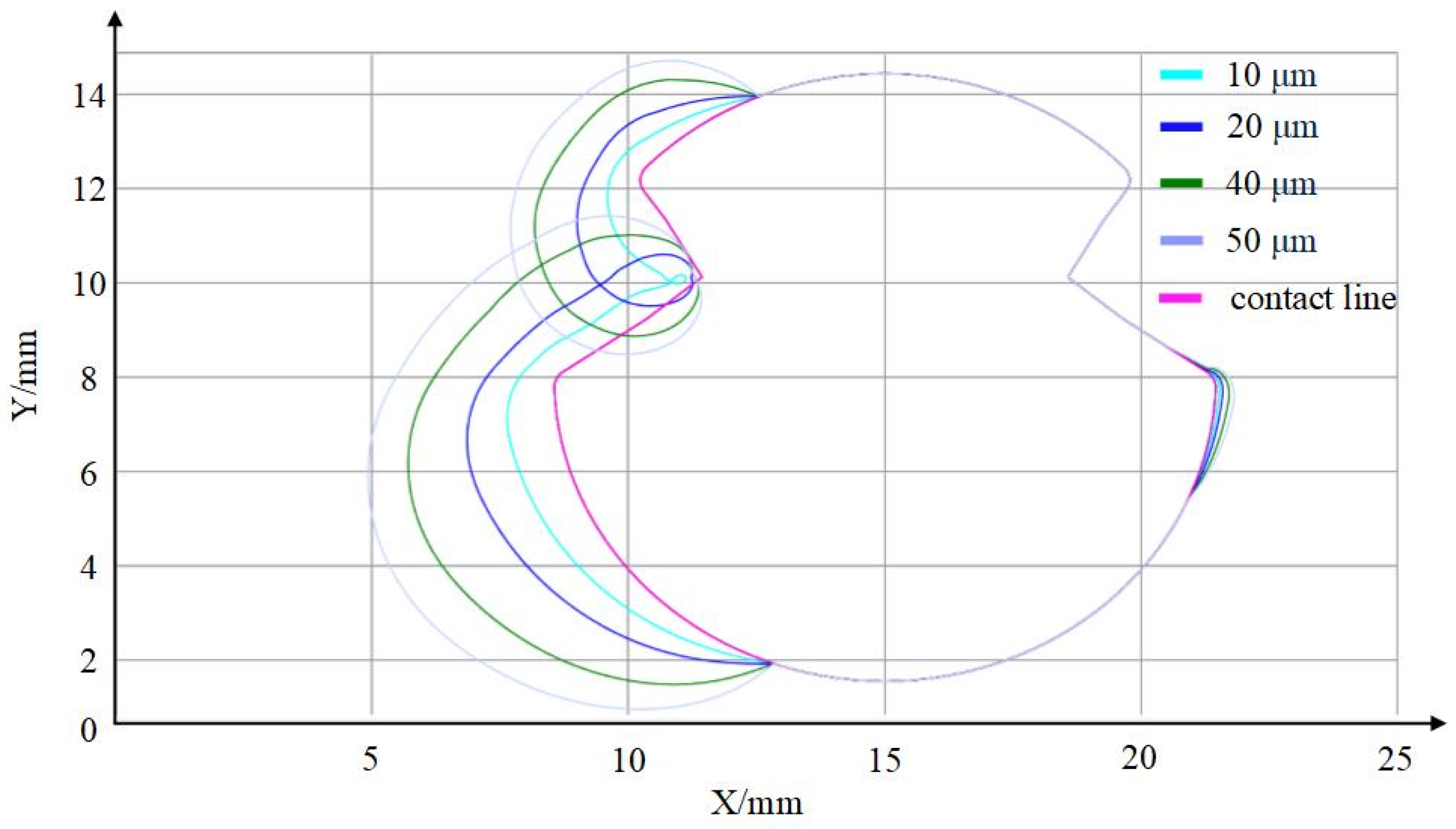
3.3. Analysis of Computational Results for Different Droplet Diameters
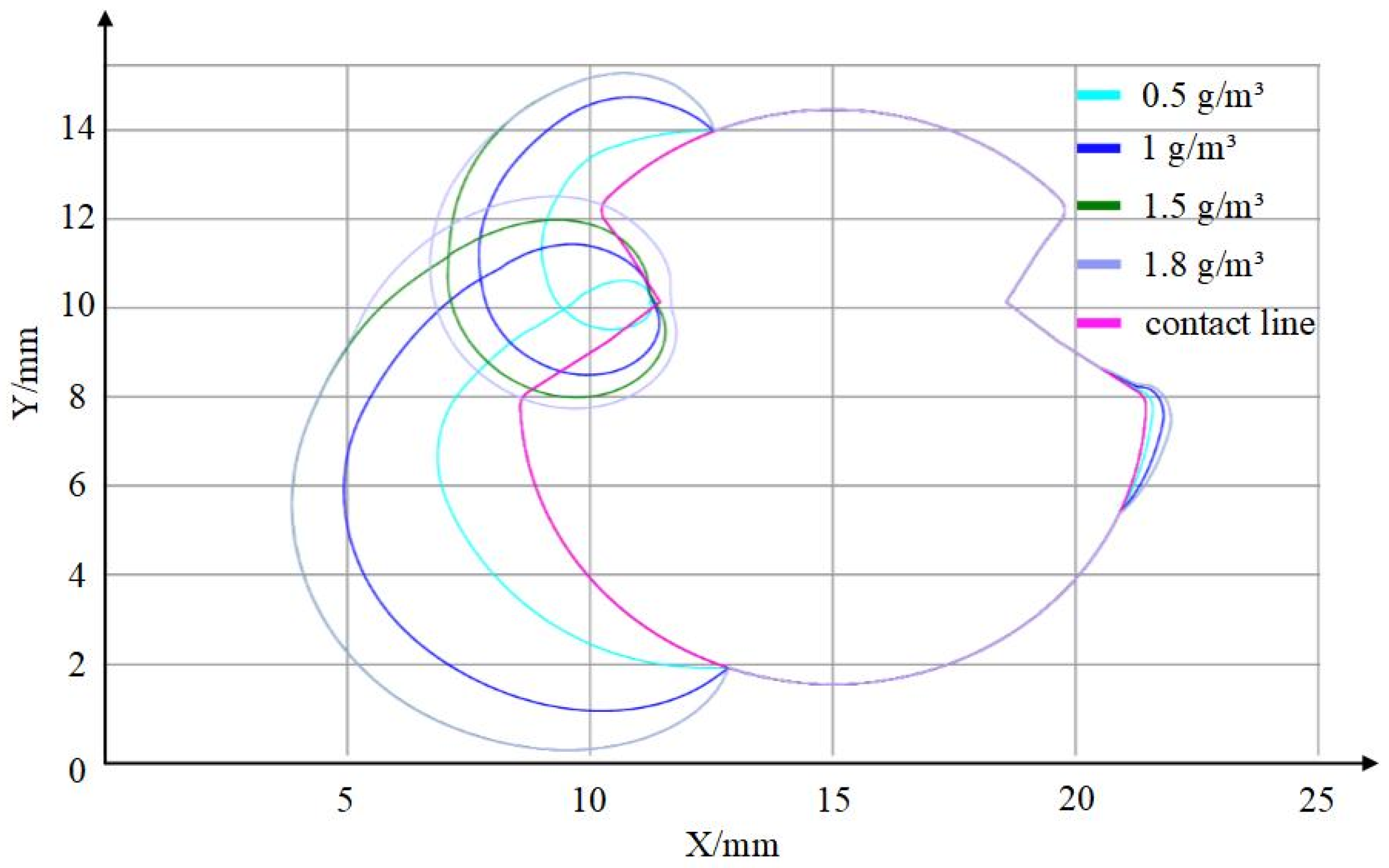
3.4. Analysis of Computational Results for Different Air–Liquid Water Content
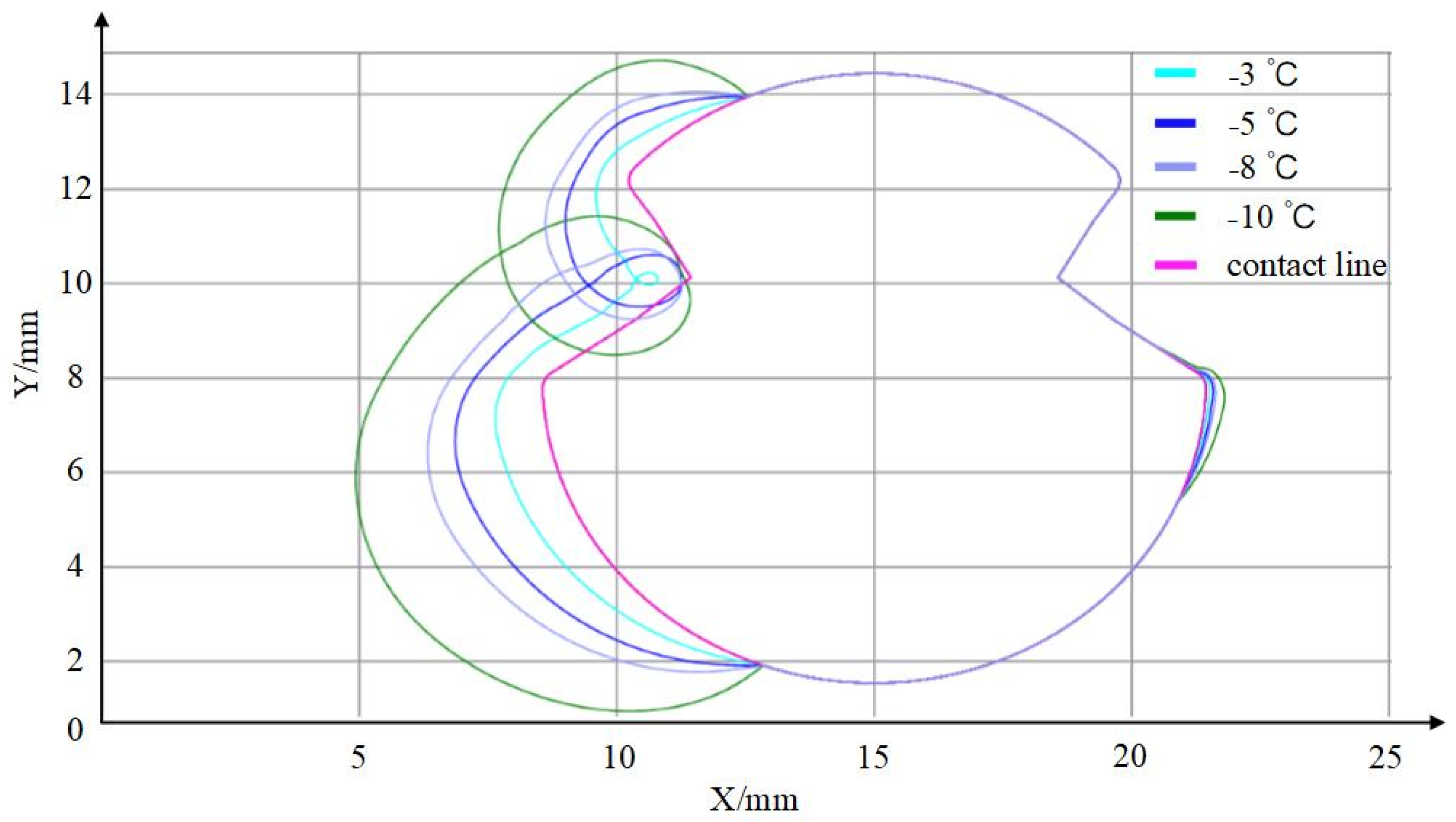
3.5. Analysis of Computational Results at Different Ambient Temperatures
4. Conclusions
- (1)
- Compared with traditional circular conductors, due to the obvious tail-groove structure and asymmetric cross-section of the contact line, the water droplet collection coefficient on the windward side shows a locally concentrated distribution, and the icing morphology is more likely to develop asymmetrically up and down. However, due to the symmetrical structure of the conductor, the icing morphology is more uniform and has fuller icing.
- (2)
- Under different water droplet diameters and air–liquid water contents, although the thickness of the ice layer on the contact line changes significantly, restricted by the groove and edge structures, the expansion of the icing area is limited, and the limited position of the icing area is more stable.
- (3)
- Under the condition that the wind speed reaches 15 m/s, some water droplets, after the first impact on the surface of the contact line, are carried to its downstream surface by the bypass airflow, slide along the surface curvature, and freeze, forming a small-scale “secondary icing area” on the leeward side of the contact line. This phenomenon is not obvious in the conductor simulation, indicating that the geometric characteristics of the contact line are more sensitive to the disturbed airflow, and the icing area is more complex.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Mei, G.; Lu, L. Analysis of the pantograph’s mass distribution affecting the contact quality in high-speed railway. Int. J. Rail Transp. 2022, 11, 529–551. [Google Scholar] [CrossRef]
- Agüero-Barrantes, P.; Hain, A. Structural performance of porcelain insulators in overhead railway power systems: Experimental evaluations and findings. Infrastructures 2024, 9, 138. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y.; Lu, B.; Wang, H.; Liu, Z. Assessment of current collection performance of rail pantograph-catenary considering long suspension bridges. IEEE Trans. Instrum. Meas. 2025, 74, 7500714. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Z.; Gao, S. Current Collection Quality of High-Speed Rail Pantograph-Catenary Considering Geometry Deviation at 400 km/h and Above. IEEE Trans. Veh. Technol. 2024, 73, 14415–14424. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Y.; Gao, S.; Wang, H. Review of Perspectives on Pantograph-Catenary Interaction Research for High-Speed Railways Operating at 400 km/h and Above. IEEE Trans. Transp. Electrif. 2024, 10, 7236–7257. [Google Scholar] [CrossRef]
- Makkonen, L.; Lozowski, E.P. Numerical Modeling of Icing on Power Network Equipment. In Atmospheric Icing of Power Networks; Springer: Dordrecht, The Netherlands, 2008; pp. 83–117. [Google Scholar]
- Xingbo, H.; Xingliang, J. Analysis of critical condition for dry and wet growth icing on insulators. Electr. Power Syst. Res. 2021, 192, 107006. [Google Scholar]
- Tabakova, S.; Feuillebois, F. On the solidification of a supercooled liquid droplet lying on a surface. J. Colloid Interface Sci. 2004, 272, 225–234. [Google Scholar] [CrossRef]
- Prodi, F.; Levi, L.; Levizzani, V. Ice accretions on fixed cylinders. Q. J. Roy. Meteorol. Soc. 1986, 112, 1091–1109. [Google Scholar] [CrossRef]
- Fumoto, K. Experimental Study on the Critical Heat Flux of Ice Accretion Along a Fine Wire Immersed in a Cold Air Flow with Water Spray. Adv. Cold Region Therm. Eng. Sci. 1999, 533, 45–54. [Google Scholar]
- Lu, L.M.; Popplewell, N.; Shah, H.A. Freezing rain simulations for fixed, unheated conductor samples. Am. Meteorol. Soc. 2000, 39 Pt 2, 2385–2396. [Google Scholar] [CrossRef]
- Personne, P.; Gayet, J.F. Ice Accretion on Wires and Anti-Icing Induced by Joule Effect. J. Appl. Meteorol. 2010, 27, 101–114. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, T.; Zhou, G.; Wang, Y.; Feng, Y.; Jiang, C.; Song, Z.; Li, H. Wind tunnel experimental investigation on the performance of the ice-melting system for high-speed train bogies. Transp. Saf. Environ. 2025, 7, tdae022. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Hu, G.; Wang, X.; Han, Z. Offline Meta-Reinforcement Learning for Active Pantograph Control in High-Speed Railways. IEEE Trans. Ind. Inform. 2024, 20, 10669–10679. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Han, Z. HO2RL: A Novel Hybrid Offline-and-Online Reinforcement Learning Method for Active Pantograph Control. IEEE Trans. Ind. Electron. 2025, 72, 6286–6296. [Google Scholar] [CrossRef]
- Savadjiev, K.; Farzaneh, M. Modeling of icing and ice shedding on overhead power lines based on statistical analysis of meteorological data. IEEE Trans. Power Deliv. 2004, 19, 715–721. [Google Scholar] [CrossRef]
- Jiang, X.; Fan, S.; Zhang, Z.; Sun, C.; Shu, L. Simulation and Experimental Investigation of DC Ice-Melting Process on an Iced Conductor. IEEE Trans. Power Deliv. 2010, 25, 919–929. [Google Scholar] [CrossRef]
- Yang, L.; Hu, Z.; Nian, L.; Hao, Y.; Li, L. Prediction on freezing fraction and collision coefficient in ice accretion model of transmission lines using icing mass growth rate. IET Gener. Transm. Distrib. 2021, 16, 364–375. [Google Scholar] [CrossRef]
- Xu, F.; Li, D.; Gao, P.; Zang, W.; Duan, Z.; Ou, J. Numerical simulation of two-dimensional transmission line icing and analysis of factors that influence icing. J. Fluids Struct. 2023, 118, 103858. [Google Scholar] [CrossRef]
- Morris, J.; Robinson, M.; Palacin, R. Use of dynamic analysis to investigate the behaviour of short neutral sections in the overhead line electrification. Infrastructures 2021, 6, 62. [Google Scholar] [CrossRef]
- Chen, G.; Yang, Y.; Yang, Y.; Li, P. Study on Galloping Oscillation of Iced Catenary System under Cross Winds. Shock Vib. 2017, 2017, 1634292. [Google Scholar] [CrossRef]
- Sadov, S.Y.; Shivakumar, P.N.; Firsov, D.; Lui, S.H.; Thulasiram, R. Mathematical Model of Ice Melting on Transmission Lines. J. Math. Model. Algorithms 2007, 6, 273–286. [Google Scholar] [CrossRef]
- Li, Z.; Wu, G.; Huang, G.; Guo, Y.; Zhu, H. Study on Icing Prediction for High-Speed Railway Catenary Oriented to Numerical Model and Deep Learning. IEEE Trans. Transp. Electrif. 2024, 11, 1189–1200. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, D.; Fan, L.; Jia, Y. Study on Icing Prediction of Power Transmission Lines Based on Ensemble Empirical Mode Decomposition and Feature Selection Optimized Extreme Learning Machine. Energies 2019, 12, 2163. [Google Scholar] [CrossRef]
- Peter, Z.; Farzaneh, M.; Kiss, L.I. Assessment of the Current Intensity for Preventing Ice Accretion on Overhead Conductors. IEEE Trans. Power Deliv. 2007, 22, 565–574. [Google Scholar] [CrossRef]
- Cinieri, E.; Fumi, A. Deicing of The Contact Lines of the High-Speed Electric Railways: Deicing Configurations. Experimental Test Results. IEEE Trans. Power Deliv. 2014, 29, 2580–2587. [Google Scholar] [CrossRef]
- Snaiki, R.; Jamali, A.; Rahem, A.; Shabani, M.; Barjenbruch, B.L. A Metaheuristic-Optimization-Based Neural Network for Icing Prediction on Transmission Lines. Cold Reg. Sci. Technol. 2024, 224, 104249. [Google Scholar] [CrossRef]
- Meng, X.; Tian, L.; Liu, J.; Jin, Q. Failure Prediction of Overhead Transmission Lines Incorporating Time Series Prediction Model for Wind-Ice Loads. Reliab. Eng. Syst. Saf. 2025, 259, 110927. [Google Scholar] [CrossRef]
- Wang, F.; Lin, H.; Ma, Z. Transmission Line Icing Prediction Based on Dynamic Time Warping and Conductor Operating Parameters. Energies 2024, 17, 945. [Google Scholar] [CrossRef]
- Wang, G.; Shen, J.; Jin, M.; Huang, S.; Li, Z.; Guo, X. Prediction Model for Transmission Line Icing Based on Data Assimilation and Model Integration. Front. Environ. Sci. 2024, 12, 1403426. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Song, Y.; Jiang, J. Aerodynamic parameters simulation and wind-induced vibration responses of contact wire of high-speed railway. J. Vib. Shock 2015, 34, 6–12. [Google Scholar]
- Makkonen, L. Models for the Growth of Rime, Glaze, Icicles and Wet Snow on Structures. Philos. Trans. Math. Phys. Eng. Sci. 2000, 358, 2913–2939. [Google Scholar] [CrossRef]
- Fu, P. Modelling and Simulation of the Ice Accretion Process on Fixed or Rotating Cylindrical Objects by the Boundary Element Method; Universite du Quebec a Chicoutimi: Chicoutimi, QC, Canada, 2004; pp. 62–66. [Google Scholar]
- Song, Y.; Liu, Z.; Wang, H.; Lu, X.; Zhang, J. Nonlinear analysis of wind-induced vibration of high-speed railway catenary and its influence on pantograph-catenary interaction. Veh. Syst. Dyn. 2016, 54, 723–747. [Google Scholar] [CrossRef]
- Gao, P.; Zang, W.; Li, D. Numerical simulation and analysis of influencing factors of icing on transmission lines. J. Vib. Shock. 2023, 42, 77–85. [Google Scholar]
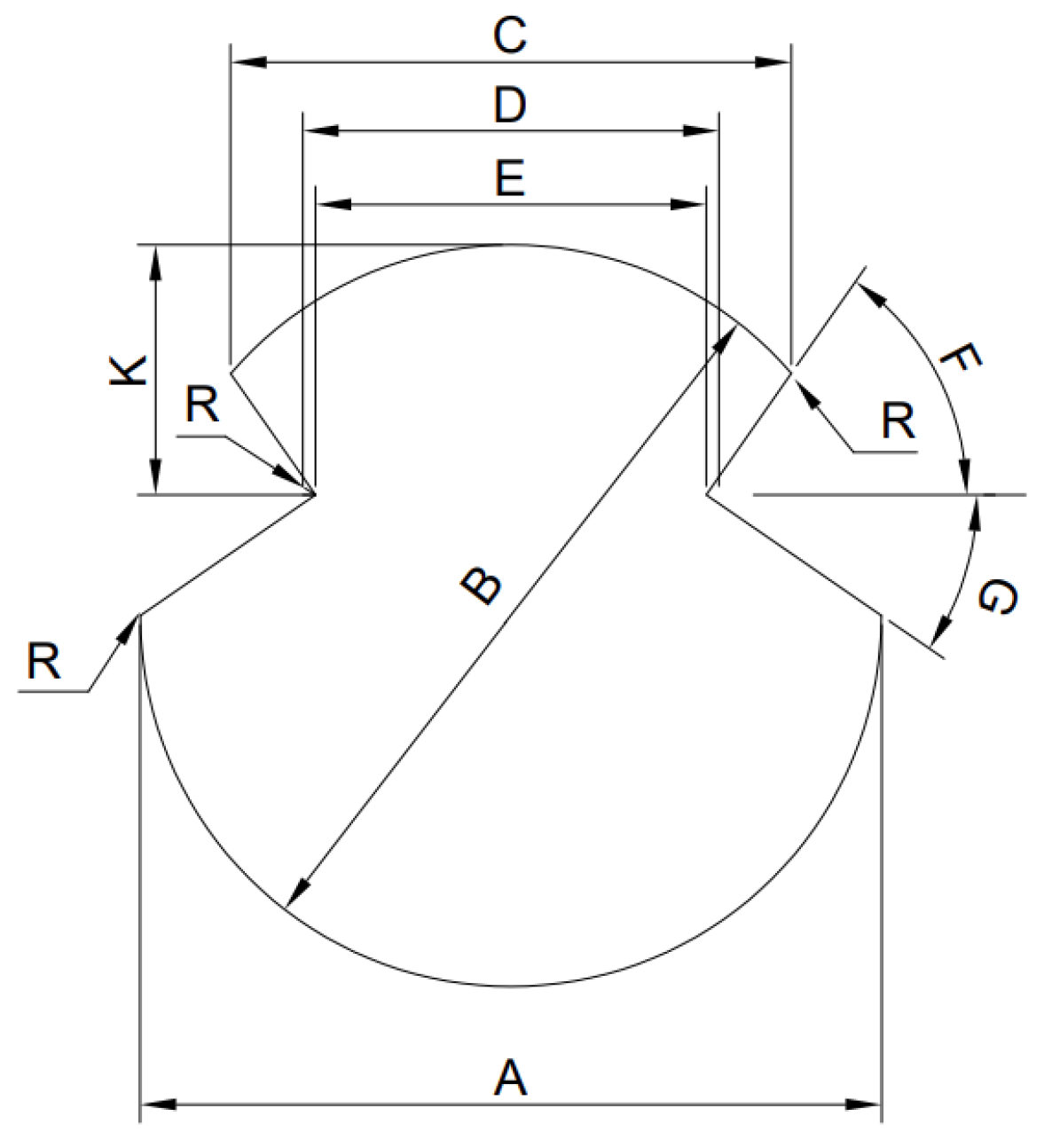

| Nominal | Calculation | Size (mm) | Angle (°) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Area (mm2) | Area (mm2) | A | B | C | D | E | K | R | F | G |
| 120 | 121 | 12.9 | 12.9 | 9.76 | 7.24 | 6.8 | 4.35 | 0.4 | 51 | 27 |
| Droplet Diameter/μm | 44.4 | 34.8 | 27.4 | 20 | 14.2 | 10.4 | 6.2 |
| Volume Fraction/% | 5 | 10 | 20 | 30 | 20 | 10 | 5 |
| Time (min) | 10 | 20 | 30 |
| Maximum ice thickness (mm) | 1.775 | 3.568 | 4.951 |
| MVD (μm) | 10 | 20 | 40 | 50 |
| Maximum ice thickness (mm) | 1.274 | 1.821 | 2.359 | 3.562 |
| LWC (g/m3) | 0.5 | 1 | 1.5 | 1.8 |
| Maximum ice thickness (mm) | 1.837 | 3.556 | 5.012 | 5.012 |
| Temperatures (°C) | −3 | −5 | −8 | −10 |
| Maximum ice thickness (mm) | 1.345 | 1.853 | 2.184 | 3.589 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Zhang, Y.; Ma, W.; Song, Y. Numerical Simulation and Analysis of the Influencing Factors of Ice Formation on Electrified Railway Contact Lines. Infrastructures 2025, 10, 121. https://doi.org/10.3390/infrastructures10050121
Liu C, Zhang Y, Ma W, Song Y. Numerical Simulation and Analysis of the Influencing Factors of Ice Formation on Electrified Railway Contact Lines. Infrastructures. 2025; 10(5):121. https://doi.org/10.3390/infrastructures10050121
Chicago/Turabian StyleLiu, Changyi, Yifan Zhang, Wei Ma, and Yang Song. 2025. "Numerical Simulation and Analysis of the Influencing Factors of Ice Formation on Electrified Railway Contact Lines" Infrastructures 10, no. 5: 121. https://doi.org/10.3390/infrastructures10050121
APA StyleLiu, C., Zhang, Y., Ma, W., & Song, Y. (2025). Numerical Simulation and Analysis of the Influencing Factors of Ice Formation on Electrified Railway Contact Lines. Infrastructures, 10(5), 121. https://doi.org/10.3390/infrastructures10050121







