Evaluation of an Approximate Seismic Assessment Procedure for Load-Bearing Masonry Buildings
Abstract
1. Introduction
2. The Building Inspection Priority Index Method for Masonry Buildings
2.1. Determination of the Seismic Hazard Index
2.2. Determination of the Seismic Resistance Index of the Building
2.2.1. Index for Shear Resistance at the Critical Floor Level (R1)
2.2.2. Index for Openings in Load-Bearing Walls (R2)
2.2.3. Index for Horizontal Ties (R3)
2.2.4. Index for Diaphragm Action (R4)
2.2.5. Index for Openings near Wall Corners (R5)
2.2.6. Index for Damage to Load-Bearing Walls (R6)
2.2.7. Index for Transverse Walls Connections (R7)
2.2.8. Index for Out-of-Plane Loading of Perimeter Walls (R8)
2.2.9. Index for Regularity in Floor Plan (R9)
- -
- λ < 4.0: regular (R9 = 1.00)
- -
- 4.0 ≤ λ < 8.0: partially regular (R9 = 0.75)
- -
- λ ≥ 8.0: irregular (R9 = 0.50)
- -
- ∑AE < 0.25Atot or AE,max < 0.15Atot: regular (R9 = 1.00)
- -
- 0.25Atot ≤ ∑AE < 0.40Atot or 0.15Atot ≤ AE,max < 0.25Atot: partially regular (R9 = 0.75)
- -
- ∑AE ≥ 0.40Atot or AE,max ≥ 0.25Atot: irregular (R9 = 0.50)
2.2.10. Index for Regularity in Height (R10)
- -
- If one floor’s area is ≥75% of the one above/below, or if upper recesses <40% of ground floor: regular
- -
- If one floor’s area ranges from 60% to 75% of the one above/below, or if recesses range from 40% to 60% of the ground floor area: partially regular
- -
- If one floor’s area is <60% of the one above/below, or if recesses >60% of the ground floor area: irregular
- -
- <30% between floors: regular
- -
- 30–50%: partially regular
- -
- >50%: irregular
- -
- <1 story: regular
- -
- 1–2 stories: partially regular
- -
- >2 stories: irregular
2.3. Calculation of the Control Priority Index
3. Application of the BIPI Method to Four Existing Masonry Buildings
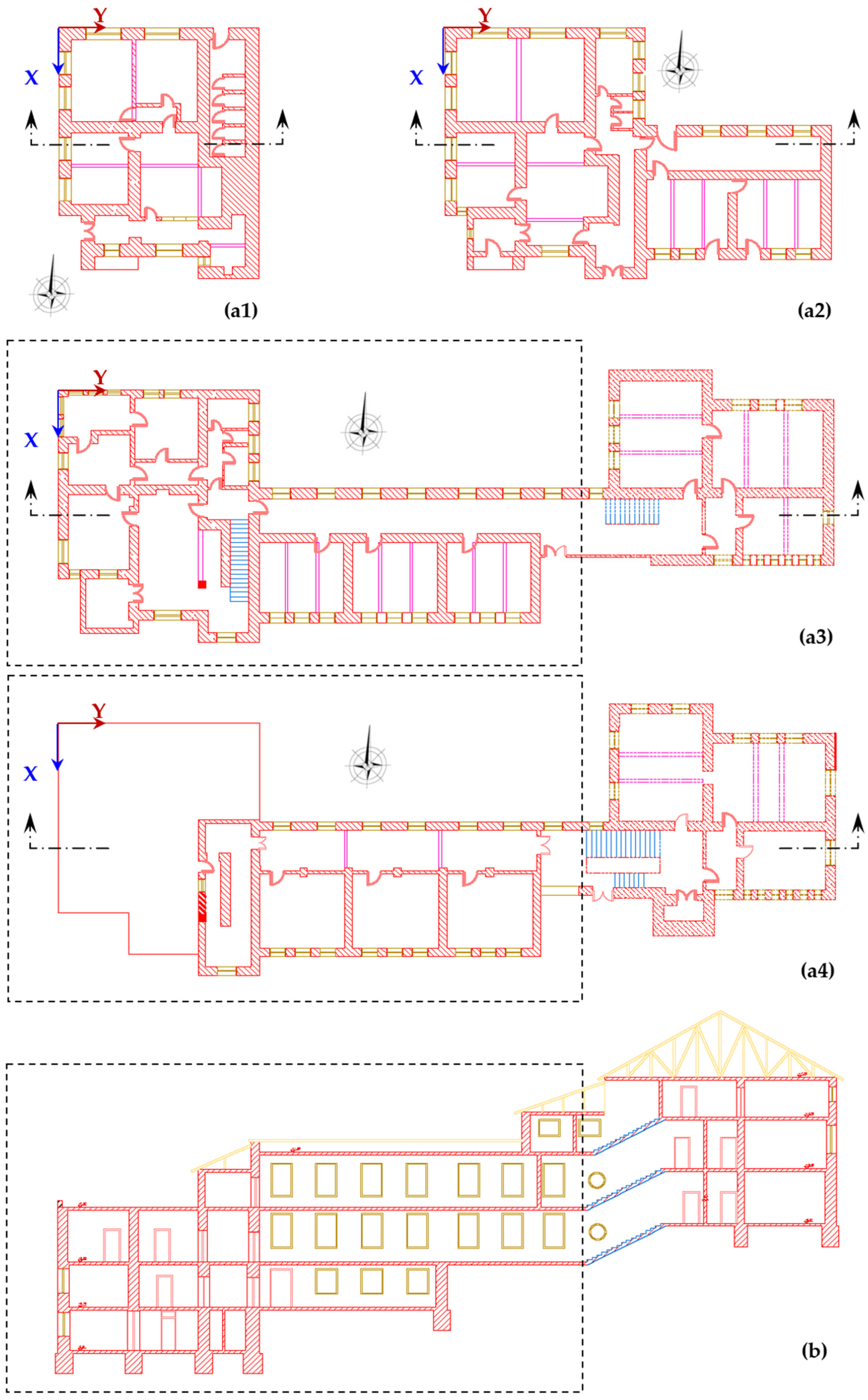
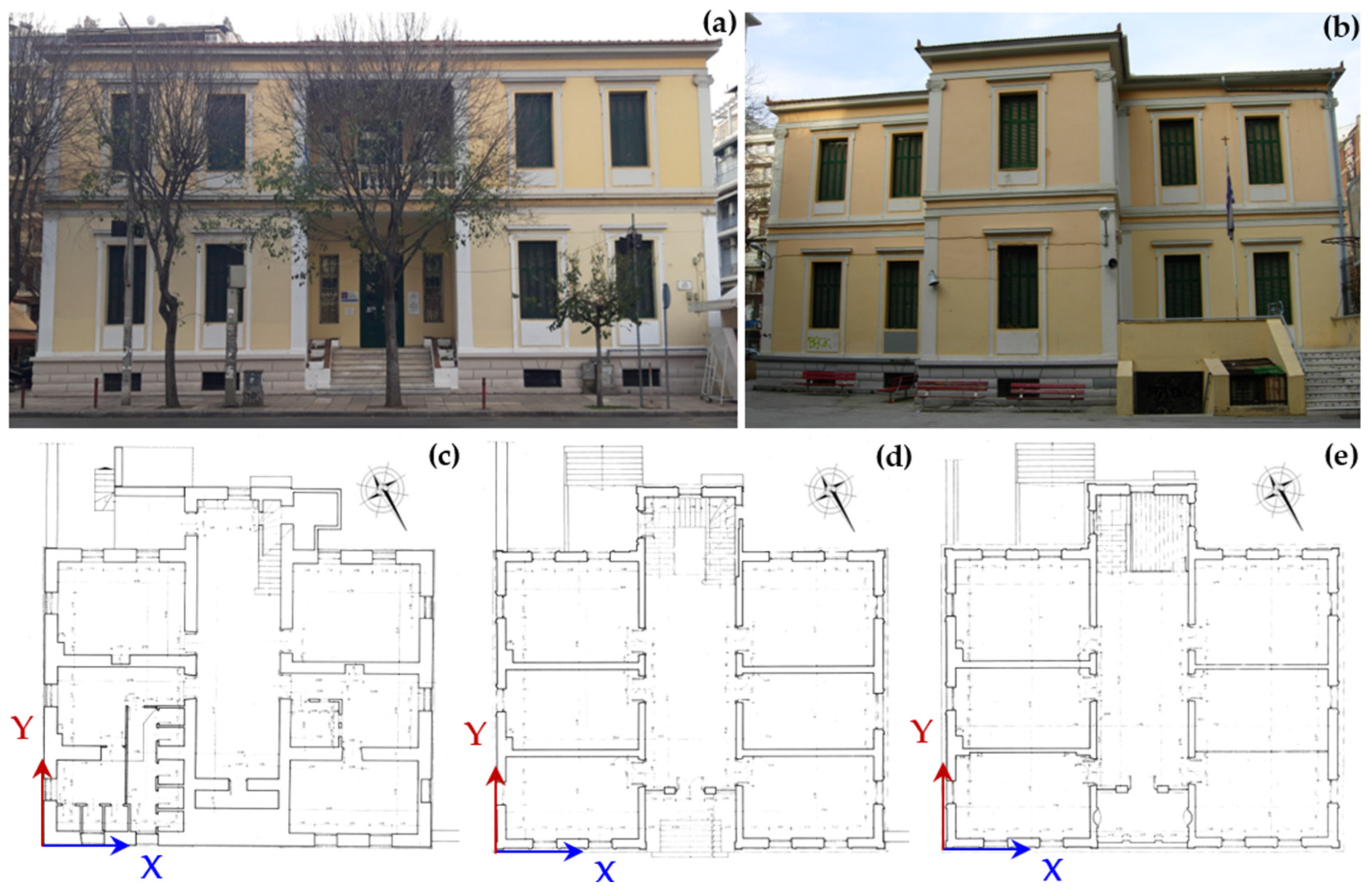
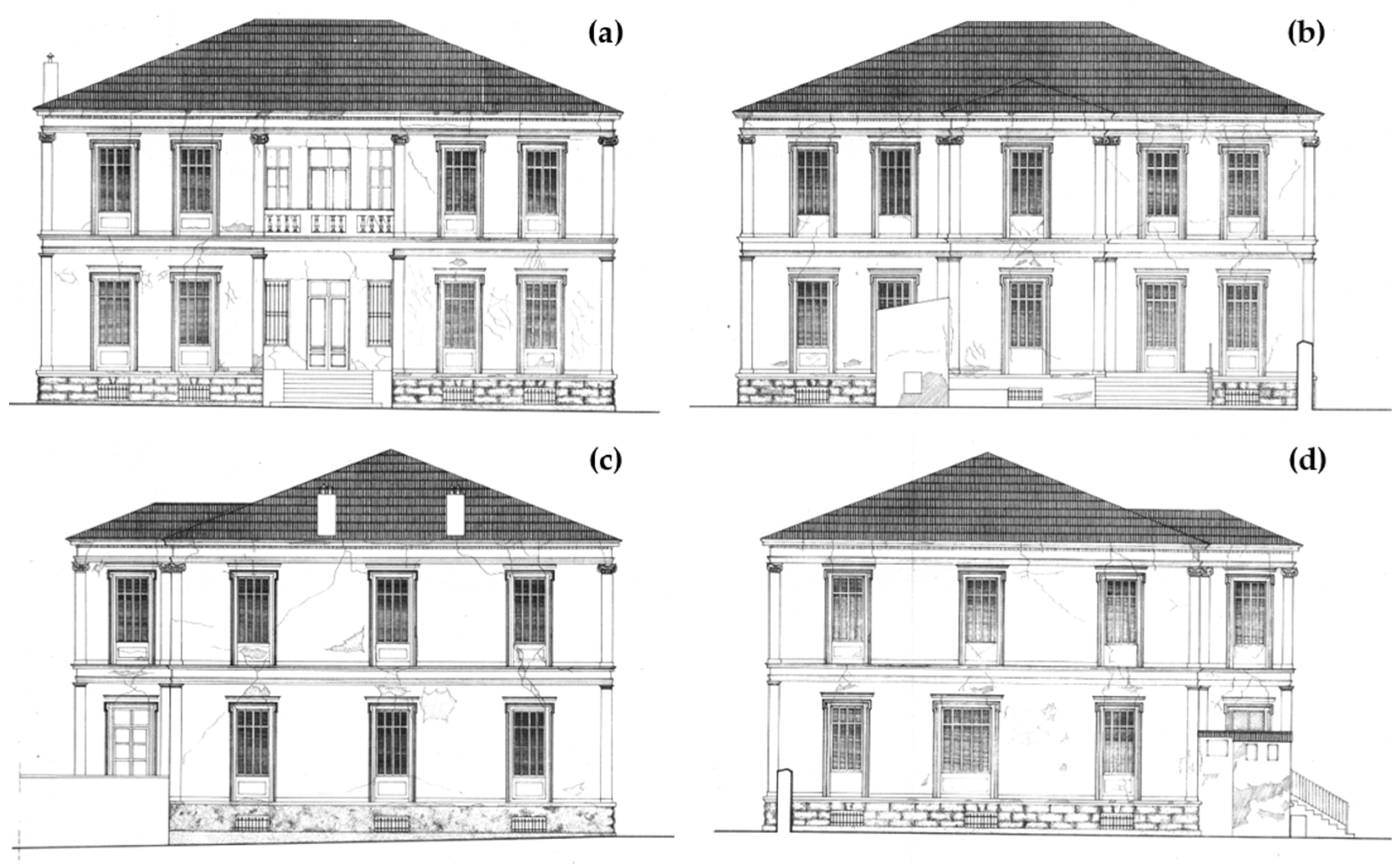
3.1. Description of the Examined Buildings
3.1.1. The Holy Monastery of the Nativity of Theotokos
3.1.2. The Hellenic Gymnasium
3.1.3. The Hellenic Consulate
3.1.4. The 12th Primary School
3.2. Determination of the Seismic Hazard Index for the Examined Buildings
3.2.1. Seismic Action Index
3.2.2. Influence Index of Neighboring Buildings
3.2.3. Estimation of the Seismic Hazard Index
3.3. Determination of the Seismic Resistance Index of the Examined Builgings
3.4. Determination of the Control Priority Index λ
4. Evaluation of the Accuracy of the Building Inspection Priority Index Method
4.1. Seismic Response of the North Wing of the Vellas Monastery During the 15 October 2016 Epirus Earthquake
4.2. Seismic Response of the Thessaloniki Buildings During the 20 June 1978 Volvi Earthquake
4.3. Evaluation of the BIPI Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Federal Emergency Management Agency (FEMA). Rapid Visual Screening of Buildings for Potential Seismic Hazards: A Handbook, 3rd ed.; Government Printing Office: Washington, DC, USA, 2015.
- American Society of Civil Engineers (ASCE). Seismic Evaluation and Retrofit of Existing Buildings; ASCE/SEI 41-23; ASCE: Reston, VA, USA, 2023; ISBN 978-0-7844-8476-0. [Google Scholar]
- New Zealand Society for Earthquake Engineering (NZSEE); Structural Engineering Society (SESOC); NZ Geotechnical Society (NZGS). The Seismic Assessment of Existing Buildings–Technical Guidelines for Engineering Assessments, 2017. Available online: http://EQ-Assess.org.nz (accessed on 10 December 2024).
- Sextos, A.G.; Kappos, A.J.; Stylianidis, K.C. Computer-aided pre- and post-earthquake assessment of buildings involving database compilation, GIS visualization, and mobile data transmission. Comput.-Aided Civ. Infrastruct. Eng. 2008, 23, 59–73. [Google Scholar] [CrossRef]
- Karbassi, A.; Nollet, M.J. Development of an index assignment procedure compatible with the regional seismicity in the province of Quebec for the rapid visual screening of existing buildings. Can. J. Civ. Eng. 2008, 35, 925–937. [Google Scholar] [CrossRef]
- Arya, A.S.; Agarwal, A. Rapid Visual Screening of Masonry Buildings; Technical Report; National Disaster Management Division, Ministry of Home Affairs, Government of India: New Delhi, India, 2006.
- Sucuoğlu, H.; Yazgan, U.; Yakut, A. A screening procedure for seismic risk assessment in urban building stocks. Earthq. Spectra 2007, 23, 441–458. [Google Scholar] [CrossRef]
- Earthquake Planning and Protection Organization (EPPO). First-Tier Seismic Assessment of Buildings, 6th ed.; EPPO: Athens, Greece, 2024.
- Lourenço, P.B.; Oliveira, D.V.; Leite, J.C.; Ingham, J.M.; Modena, C.; da Porto, F. Simplified indexes for the seismic assessment of masonry buildings: International database and validation. Eng. Fail. Anal. 2013, 34, 585–605. [Google Scholar] [CrossRef]
- Chieffo, N.; Clementi, F.; Formisano, A.; Lenci, S. Comparative fragility methods for seismic assessment of masonry buildings located in Muccia (Italy). J. Build. Eng. 2019, 25, 100813. [Google Scholar] [CrossRef]
- D’Amato, M.; Laguardia, R.; Di Trocchio, G.; Coltellacci, M.; Gigliotti, R. Seismic Risk Assessment for Masonry Buildings Typologies from L’Aquila 2009 Earthquake Damage Data. J. Earthq. Eng. 2020, 26, 4545–4579. [Google Scholar] [CrossRef]
- Tatangelo, M.; Audisio, L.; D’Amato, M.; Gigliotti, R. Seismic risk analysis on masonry buildings damaged by L’Aquila 2009 and Emilia 2012 earthquakes. Procedia Struct. Integr. 2023, 44, 990–997. [Google Scholar] [CrossRef]
- Rosti, A.; Rota, M.; Penna, A. Clustering of empirical damage data for the vulnerability classification of the Italian residential building stock. Procedia Struct. Integr. 2023, 44, 83–90. [Google Scholar] [CrossRef]
- Rosti, A.; Rota, M.; Penna, A. Empirical fragility curves for Italian URM buildings. Bull. Earthq. Eng. 2021, 19, 3057–3076. [Google Scholar] [CrossRef]
- Zuccaro, G.; Perelli, F.L.; De Gregorio, D.; Cacace, F. Empirical vulnerability curves for Italian mansory buildings: Evolution of vulnerability model from the DPM to curves as a function of accelertion. Bull. Earthq. Eng. 2021, 19, 3077–3097. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency (FEMA); American Society of Civil Engineers (ASCE). Handbook for the Seismic Evaluation of Buildings: A Prestandard; FEMA 310; Federal Emergency Management Agency (FEMA): Washington, DC, USA, 1998.
- Calvi, G.M. A displacement-based approach for vulnerability evaluation of classes of buildings. J. Earthq. Eng. 1999, 3, 411–438. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Roque, J. Simplified indexes for the seismic vulnerability of ancient masonry buildings. Struct. Mason. Earthq. 2006, 20, 200–208. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Pantazopoulou, S. Simplified Mechanical Model to Estimate the Seismic Vulnerability of Heritage Unreinforced Masonry Buildings. J. Earthq. Eng. 2016, 20, 298–325. [Google Scholar] [CrossRef]
- Di Gennaro, L.; de Cristofaro, M.; Loreto, G.; Minutolo, V.; Olivares, L.; Zona, R.; Frunzio, G. In-situ load testing of an ancient masonry structure using fibre optics. Structures 2024, 70, 107567. [Google Scholar] [CrossRef]
- Guadagnuolo, M.; Di Gennaro, L.; Basile, A.; De Matteis, G. Simplified methods for the evaluation of mechanical properties of tuff masonry walls in Campania (Italy). Procedia Struct. Integr. 2023, 44, 878–885. [Google Scholar] [CrossRef]
- Sreejith, P.P.; Sivan, P.P.; Praveen, A.; Gajendran, C.; Nisha, V. Simplified Method for Shear Strength Prediction of Confined Masonry Walls Subjected to in Plane Loads. Procedia Technol. 2016, 24, 155–160. [Google Scholar] [CrossRef]
- Earthquake Planning and Protection Organization (EPPO). KADET: Code for Assessment and Structural Interventions in Masonry Buildings; EPPO: Athens, Greece, 2023.
- EN 1998-3; Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings. CEN: Brussels, Belgium, 2005.
- Pardalopoulos, S.I.; Pantazopoulou, S.J. Methodology for practical seismic assessment of unreinforced masonry buildings with historical value. Earthq. Eng. Struct. Dyn. 2017, 46, 2793–2810. [Google Scholar] [CrossRef]
- Pardalopoulos, S.I.; Karantoni, F.V.; Pantazopoulou, S.J. Practical assessment of the seismic behavior of a confined masonry system. Soil Dyn. Earthq. Eng. 2019, 127, 105831. [Google Scholar] [CrossRef]
- Croce, P.; Landi, F.; Formichi, P.; Beconcini, M.L.; Puccini, B.; Zotti, V. Non-linear methods for the assessment of seismic vulnerability of masonry historical buildings. In Protection of Historical Constructions; Vayas, I., Mazzolani, F.M., Eds.; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2022; Volume 209, pp. 651–670. [Google Scholar] [CrossRef]
- Kappos, A.; Penelis, G.; Drakopoulos, C. Evaluation of simplified models for lateral load analysis of unreinforced masonry buildings. J. Struct. Eng. 2002, 128, 890–897. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Galasco, A.; Penna, A. Pushover and dynamic analysis of 3D masonry buildings by means of a non-linear macro-element model. In Proceedings of the International Conference on Earthquake Loss Estimation and Risk Reduction, Bucharest, Romania, 24–26 October 2002. [Google Scholar]
- Lagomarsino, S.; Cattari, S. PERPETUATE guidelines for seismic performance-based assessment of cultural heritage masonry structures. Bull. Earthq. Eng. 2015, 13, 13–47. [Google Scholar] [CrossRef]
- Salonikios, T.; Karakostas, C.; Lekidis, V.; Anthoine, A. Comparative inelastic pushover analysis of masonry frames. Eng. Struct. 2003, 25, 1515–1523. [Google Scholar] [CrossRef]
- Galasco, A.; Lagomarsino, S.; Penna, A.; Resemini, S. Non-linear seismic analysis of masonry structures. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Galasco, A.; Lagomarsino, S.; Penna, A. On the use of pushover analysis for existing masonry buildings. In Proceedings of the 1st European Conference on Earthquake Engineering and Seismology, Geneva, Switzerland, 3–8 September 2006. [Google Scholar]
- Rizzano, G.; Sabatino, R. An equivalent frame model for seismic analysis of masonry structures. In Proceedings of the 8th National Conference on Seismology and Earthquake Engineering, Aveiro, Portugal, 20–23 October 2010. [Google Scholar]
- Sabatino, R.; Rizzano, G. A simplified approach for the seismic analysis of masonry structures. Open Constr. Build. Technol. J. 2011, 5, 97–104. [Google Scholar]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull. Earthq. Eng. 2006, 4, 415–443. [Google Scholar] [CrossRef]
- Borzi, B.; Crowley, H.; Pinho, R. Simplified pushover-based earthquake loss assessment (SP-BELA) method for masonry buildings. Int. J. Archit. Herit. 2008, 2, 353–376. [Google Scholar] [CrossRef]
- Ferreira, T.M.; Costa, A.A.; Vicente, R.; Varum, H. A simplified four-branch model for the analytical study of the out-of-plane performance of regular stone URM walls. Eng. Struct. 2015, 83, 140–153. [Google Scholar] [CrossRef]
- Giordano, N.; De Luca, F.; Sextos, A. Out-of-plane closed-form solution for the seismic assessment of unreinforced masonry schools in Nepal. Eng. Struct. 2020, 203, 109548. [Google Scholar] [CrossRef]
- Di Gennaro, L.; Guadagnuolo, M.; Monaco, M. Rocking Analysis of Towers Subjected to Horizontal Forces. Buildings 2023, 13, 762. [Google Scholar] [CrossRef]
- Pingaro, N.; Buzzetti, M.; Milani, G. Advanced FE nonlinear numerical modeling to predict historical masonry vaults failure: Assessment of risk collapse for a long span cloister vault heavily loaded at the crown by means of a general-purpose numerical protocol. Eng. Fail. Anal. 2025, 167, 109070. [Google Scholar] [CrossRef]
- Parisi, F.; Augenti, N. Uncertainty in seismic capacity of masonry buildings. Buildings 2012, 2, 218–230. [Google Scholar] [CrossRef]
- Croce, P.; Landi, F.; Formichi, P. Probabilistic seismic assessment of existing masonry buildings. Buildings 2019, 9, 237. [Google Scholar] [CrossRef]
- Rota, M.; Penna, A.; Magenes, G. A framework for the seismic assessment of existing masonry buildings accounting for different sources of uncertainty. Earthq. Eng. Struct. Dyn. 2014, 43, 1045–1066. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Castori, G.; De Maria, A. A method for the analysis and classification of historic masonry. Bull Earthq. Eng. 2015, 13, 2647–2665. [Google Scholar] [CrossRef]
- Earthquake Planning and Protection Organization (EPPO). Second-Tier Pre-Seismic Assessment of Masonry Buildings; EPPO: Athens, Greece, 2018.
- Vintzilaiou, E.; Tasios, T. Assessment of the Relative Seismic Risk of Historical Masonry Buildings; Seminar proceedings; Technical Chamber of Greece: Athens, Greece. (In Greek)
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- EN 1996-1-1; Eurocode 6: Design of Masonry Structures—Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures. CEN: Brussels, Belgium, 2005.
- Pardalopoulos, S.I.; Pantazopoulou, S.J.; Kontari, M.T. Rapid seismic assessment procedure of masonry buildings with historic value. In Seismic Assessment, Behavior and Retrofit of Heritage Buildings and Monuments; Psycharis, I., Pantazopoulou, S., Papadrakakis, M., Eds.; Computational Methods in Applied Sciences; Springer: Cham, Switzerland, 2015; pp. 113–137. [Google Scholar] [CrossRef]
- Pardalopoulos, S.I.; Pantazopoulou, S.J.; Ignatakis, C.E. Practical seismic assessment of unreinforced masonry historical buildings. Earthq. Struct. 2016, 11, 195–215. [Google Scholar] [CrossRef]
- Pardalopoulos, S.I.; Pantazopoulou, S.J. Rapid seismic assessment of two four-storey R.C. test buildings. Bull Earthq. Eng 2019, 17, 1379–1406. [Google Scholar] [CrossRef]





| Seismic Hazard Zone | Coefficient a | Soil Category/Coefficient s | ||||
|---|---|---|---|---|---|---|
| A | B, C | D | E | S1, S2 * | ||
| 0.85 | 1.00 | 1.15 | 1.25 | - | ||
| Z1 | 1.6 | 1.36 | 1.60 | 1.84 | 2.00 | - |
| Z2 | 2.4 | 2.04 | 2.40 | 2.76 | 3.00 | - |
| Z2 | 3.6 | 3.06 | 3.60 | 4.14 | 4.50 | - |
| Characteristics of Neighboring Buildings | H2 |
|---|---|
| Freestanding building or adjacent with sufficient seismic gap or buildings in contact at the same level without significant difference in lateral stiffness | 0.00 |
| Building of the same height but with significant difference in lateral stiffness | 0.30 |
| One floor difference without the risk of pounding | 0.50 |
| Equal number of floors but uneven floor heights (risk of pounding) | 0.80 |
| Difference of two or more floors without risk of pounding | 1.00 |
| Difference of two or more floors with risk of pounding | 1.20 |
| Arrangement of Load-Bearing Walls in Plan View | Stability and Degree of Connection of the Diaphragms with the Underlying Walls | ||
|---|---|---|---|
| Weak | Moderate | Strong | |
| Symmetrical | 0.80 | 0.90 | 1.00 |
| Partially symmetrical | 0.60 | 0.75 | 0.90 |
| Asymmetrical | 0.40 | 0.55 | 0.70 |
| Resistance Indices of the Examined Building, Ri | Weighting Coefficient, ri |
|---|---|
| R1. Index for shear resistance at the critical floor level | r1 = 0.20 |
| R2. Index for openings in load-bearing walls | r2 = 0.05 |
| R3. Index for horizontal ties | r3 = 0.15 |
| R4. Index for diaphragm action | r4 = 0.10 |
| R5. Index for openings near wall corners | r5 = 0.15 |
| R6. Index for damage to load-bearing walls | r6 = 0.05 |
| R7. Index for transverse walls connections | r7 = 0.10 |
| R8. Index for out-of-plane loading of perimeter walls | r8 = 0.10 |
| R9. Index for regularity in floor plan | r9 = 0.05 |
| R10. Index for regularity in height | r10 = 0.05 |
| Building | Story | t (m) | ℓ (m) | R8 |
|---|---|---|---|---|
| The Monastery of the Nativity of Theotokos | 1st | 0.90 | 11.48 | 0.50 |
| 2nd | 0.80 | 12.03 | 0.45 | |
| 0.83 | 7.77 | 0.70 | ||
| 0.85 | 12.70 | 0.44 | ||
| 3rd | 0.60 | 4.61 | 1.01 | |
| 0.65 | 2.97 | 1.63 | ||
| 0.70 | 8.71 | 0.58 | ||
| 0.75 | 18.29 | 0.28 | ||
| 0.80 | 20.51 | 0.26 | ||
| 4th | 0.50 | 10.71 | 0.40 | |
| 0.60 | 10.71 | 0.43 | ||
| 0.65 | 19.94 | 0.24 | ||
| The Hellenic Gymnasium | 1st | 0.60 | 3.46 | 1.00 |
| 0.70 | 7.50 | 0.67 | ||
| 2nd | 0.35 | 3.46 | 1.00 | |
| 0.45 | 7.50 | 0.54 | ||
| 3rd | 0.35 | 3.46 | 1.00 | |
| 0.45 | 7.50 | 0.54 | ||
| The Hellenic Consulate | 1st | 0.60 | 18.35 | 0.25 |
| 2nd | 0.50 | 7.20 | 0.59 | |
| 3rd | 0.50 | 7.93 | 0.54 | |
| The 12th Primary School | 1st | 0.65 | 4.42 | 1.00 |
| 0.70 | 5.12 | 0.98 | ||
| 0.90 | 4.71 | 1.00 | ||
| 2nd | 0.45 | 9.64 | 0.42 | |
| 0.55 | 9.33 | 0.48 | ||
| 0.65 | 4.71 | 1.00 | ||
| 3rd | 0.35 | 9.64 | 0.37 | |
| 0.50 | 9.33 | 0.45 | ||
| 0.55 | 4.71 | 0.94 |
| Building | Story | ∑AE (m2) | AE,max (m2) | Atot (m2) | ∑AE/Atot | AE,max/Atot | R9 |
|---|---|---|---|---|---|---|---|
| The Monastery of the Nativity of Theotokos | 1st | 17.80 | 7.61 | 257.04 | 0.07 | 0.03 | 1.00 |
| 2nd | 136.23 | 99.54 | 393.64 | 0.35 | 0.25 | 0.75 | |
| 3rd | 195.45 | 148.97 | 460.25 | 0.42 | 0.32 | 0.50 | |
| 4th | 31.81 | 29.08 | 257.46 | 0.12 | 0.11 | 1.00 | |
| The Hellenic Gymnasium | 1st | 31.71 | 13.06 | 350.04 | 0.09 | 0.04 | 1.00 |
| 2nd | 40.26 | 13.06 | 345.62 | 0.12 | 0.04 | 1.00 | |
| 3rd | 40.26 | 13.06 | 345.62 | 0.12 | 0.04 | 1.00 | |
| The 12th Primary School | 1st | 29.42 | 29.42 | 267.77 | 0.11 | 0.11 | 1.00 |
| 2nd | 29.42 | 29.42 | 267.77 | 0.11 | 0.11 | 1.00 | |
| 3rd | 29.42 | 29.42 | 267.77 | 0.11 | 0.11 | 1.00 |
| Building | Story | ∑Aw in X Dir. (m2) | ∑Aw in Y Dir. (m2) |
|---|---|---|---|
| The Monastery of the Nativity of Theotokos | Story 1 | 52.36 | 36.78 |
| Story 2 | 51.97 | 49.34 | |
| Story 3 | 49.15 | 56.81 | |
| Story 4 | 26.86 | 23.28 | |
| The Hellenic Gymnasium | Story 1 | 46.56 | 39.45 |
| Story 2 | 26.35 | 23.15 | |
| Story 3 | 21.14 | 23.44 | |
| The Hellenic Consulate | Story 1 | 24.27 | 34.32 |
| Story 2 | 16.30 | 27.47 | |
| Story 3 | 16.04 | 26.10 | |
| The 12th Primary School | Story 1 | 37.54 | 38.09 |
| Story 2 | 17.70 | 21.97 | |
| Story 3 | 14.83 | 17.32 |
| Building | Neighboring Stories | Δ∑Aw in X Dir. (%) | Δ∑Aw in Y Dir. (%) |
|---|---|---|---|
| The Monastery of the Nativity of Theotokos | 1st–2nd | −1 | 34 |
| 2nd–3rd | −5 | 15 | |
| 3rd–4th | −45 | −59 | |
| The Hellenic Gymnasium | 1st–2nd | −43 | −41 |
| 2nd–3rd | −20 | 1 | |
| The Hellenic Consulate | 1st–2nd | −33 | −20 |
| 2nd–3rd | −2 | −5 | |
| The 12th Primary School | 1st–2nd | −53 | −42 |
| 2nd–3rd | −16 | −21 |
| Index i | ri | The Monastery of the Nativity of Theotokos | The Hellenic Gymnasium | The Hellenic Consulate | The 12th Primary School | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ri,X | Ri,Y | Ri,final | Ri·ri | Ri,X | Ri,Y | Ri,final | Ri·ri | Ri,X | Ri,Y | Ri,final | Ri·ri | Ri,X | Ri,Y | Ri,final | Ri·ri | ||
| 1 | 0.20 | 0.25 | 0.27 | 0.25 | 0.050 | 0.36 | 0.34 | 0.34 | 0.068 | 0.25 | 0.48 | 0.25 | 0.050 | 0.31 | 0.39 | 0.31 | 0.062 |
| 2 | 0.05 | 0.90 | 0.74 | 0.74 | 0.037 | 0.62 | 0.79 | 0.62 | 0.031 | 0.68 | 0.74 | 0.68 | 0.034 | 0.67 | 0.73 | 0.67 | 0.034 |
| 3 | 0.15 | - | - | 0.50 | 0.075 | - | - | 1.00 | 0.150 | - | - | 1.00 | 0.150 | - | - | 1.00 | 0.150 |
| 4 | 0.10 | - | - | 0.70 | 0.070 | - | - | 0.75 | 0.075 | - | - | 0.75 | 0.075 | - | - | 0.40 | 0.040 |
| 5 | 0.15 | - | - | −0.62 | −0.093 | - | - | 0.00 | 0.000 | - | - | 0.00 | 0.000 | - | - | 0.00 | 0.000 |
| 6 | 0.05 | - | - | 0.75 | 0.038 | - | - | 0.75 | 0.038 | - | - | 0.75 | 0.038 | - | - | 0.75 | 0.038 |
| 7 | 0.10 | - | - | 1.00 | 0.100 | - | - | 1.00 | 0.100 | - | - | 1.00 | 0.100 | - | - | 1.00 | 0.100 |
| 8 | 0.10 | - | - | 0.24 | 0.024 | - | - | 0.54 | 0.054 | - | - | 0.25 | 0.025 | - | - | 0.37 | 0.037 |
| 9 | 0.05 | - | - | 0.50 | 0.025 | - | - | 1.00 | 0.050 | - | - | 1.00 | 0.050 | - | - | 1.00 | 0.050 |
| 10 | 0.05 | - | - | 0.50 | 0.025 | - | - | 0.75 | 0.038 | - | - | 0.75 | 0.038 | - | - | 0.50 | 0.025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardalopoulos, S.I.; Gkektsi, A.E.; Lekidis, V.A. Evaluation of an Approximate Seismic Assessment Procedure for Load-Bearing Masonry Buildings. Infrastructures 2025, 10, 118. https://doi.org/10.3390/infrastructures10050118
Pardalopoulos SI, Gkektsi AE, Lekidis VA. Evaluation of an Approximate Seismic Assessment Procedure for Load-Bearing Masonry Buildings. Infrastructures. 2025; 10(5):118. https://doi.org/10.3390/infrastructures10050118
Chicago/Turabian StylePardalopoulos, Stylianos I., Anastasia E. Gkektsi, and Vassilios A. Lekidis. 2025. "Evaluation of an Approximate Seismic Assessment Procedure for Load-Bearing Masonry Buildings" Infrastructures 10, no. 5: 118. https://doi.org/10.3390/infrastructures10050118
APA StylePardalopoulos, S. I., Gkektsi, A. E., & Lekidis, V. A. (2025). Evaluation of an Approximate Seismic Assessment Procedure for Load-Bearing Masonry Buildings. Infrastructures, 10(5), 118. https://doi.org/10.3390/infrastructures10050118






