A Multi-Objective Approach for Optimizing Aisle Widths in Underground Parking

Abstract

This study presents a multi-objective optimization approach for determining optimal aisle widths in underground parking facilities, balancing vehicle maneuverability against parking capacity. The research methodology integrates geometric modeling, computational simulations, and empirical validation to establish evidence-based recommendations for aisle width design. Through systematic testing of aisle widths ranging from 4.5 to 6.0 m across various vehicle types, the study identifies 5.0–5.5 m as the optimal range that maximizes both objectives for modern vehicle fleets. Geometric modeling establishes theoretical minimum widths based on vehicle turning radii, while software simulations quantify maneuverability metrics including parking success rates, time requirements, and collision probabilities. Physical testing in operational underground parking facilities validates these findings through controlled experiments with drivers of varying experience levels. The research demonstrates that aisle widths below 5.0 m significantly compromise maneuverability, particularly for larger vehicles, while widths exceeding 5.5 m provide negligible additional benefits while reducing capacity. A case study application in Kazakhstan, examining regional vehicle distributions and regulatory frameworks, confirms the model’s practical utility. The findings suggest that current parking standards in some regions may require revision to accommodate changing vehicle dimensions. This optimization framework provides urban planners, architects and engineers with a data-driven methodology for designing underground parking facilities that enhance both user experience and space utilization efficiency.

1. Introduction

1.1. Background and Motivation

The rising density of urban development, coupled with the ever-increasing number and variety of private vehicles, has intensified the demand for efficient parking solutions [1]. Underground parking structures are becoming more prevalent as they conserve ground-level space for other commercial or public uses [2]. Despite their growing importance, the design of underground parking facilities remains a complex challenge. A critical element in this design process is determining the optimal distance between opposing parking rows. If the distance (or aisle width) is set too wide, the parking structure uses up valuable floor area, resulting in fewer total spaces—a less profitable or less serviceable outcome. Conversely, if the distance is too narrow, drivers, especially those with larger vehicles or limited maneuvering skills, face difficulty navigating tight turns and stalls.

Vehicle dimensions have been steadily growing. Sports utility vehicles and pickup trucks making up a larger portion of urban fleets, yet not all parking guidelines account for these trends. As a result, existing standard practices might not reflect current vehicle distributions or the diversity of driver abilities.

There is a pressing need for a systematic, data-driven study to determine how best to optimize the spacing between parking rows in underground facilities. By examining ease of maneuvering as an indicator of user satisfaction and safety alongside total capacity as key factor in both economic feasibility and public benefit, this research aims to provide clear, actionable guidance for future parking structure designs. Ultimately, such insights can enhance driver experience, minimize the incidence of parking-related collisions, and help developers maximize the utility of limited underground space.

1.2. Related Works

Many guidelines and standards address aisle widths for 90° parking because they directly impact vehicle maneuverability and user safety. The recommended dimensions help ensure smooth turning paths, reduce the risk of collisions, and provide enough space for fire or emergency services when needed.

Table 1. National and international standards on parking aisle width ranges.

Standard/Guideline	Typical Aisle Width (ft)	Typical Aisle Width (m)	Notes	Reference
IBC (International Building Code, US)	22–24 ft	~6.7–7.3 m	IBC itself does not specify a strict dimension. Local codes typically require 22–24 ft for 90° stalls.	[3]
NFPA 88A (Parking Structures, US)	No direct spec. (Focus on fire/emergency access)	No direct spec.	Emphasizes clearances for emergency vehicles & occupant egress; does not prescribe exact aisle width.	[4]
ITE/APA (US Planning & Traffic Eng.)	~20–24 ft	~6.1–7.3 m	Common references for municipal parking requirements; 22 ft often used as a standard minimum for 90°.	[5]
IStructE “Design Recommendations for Multi-storey and Underground Car Parks” (UK)	~19.7 ft	~6.0 m	Typical guidance for standard cars; can vary if columns or structural elements reduce effective turning space.	[6]
British Parking Association (BPA) (UK)	~19.7 ft	~6.0 m	Best-practice guidance rather than a strict standard; often aligns with local authority requirements.	[7]
European Parking Association (EPA) (EU)	~19.7–21.3 ft	~6.0–6.5 m	Offers Europe-wide “best practice” guidelines; local building codes may require slightly different widths.	[8]
National Building Code of Canada (NBC)	~19.7–24 ft (in local bylaws)	~6.0–7.3 m (in local bylaws)	NBC does not specify exact aisle widths; most provinces/municipalities set ranges in their zoning bylaws.	[9]
Accessibility Regulations (ADA in US, BS 8300 in UK, etc.)	Varies	Varies	Primarily address accessible stall widths & adjacent transfer aisles; can indirectly affect overall layout.	[10,11]

outlines typical aisle width ranges under various national and international standards. It also highlights that local building and planning authorities often adapt or refine these baseline recommendations to suit specific conditions in underground or multi-level parking garages.

Most codes and standards do not provide a single, universal number but rather defer to local zoning, traffic engineering guidelines, or best-practice documents. For 90° parking, a common range is around 6.0–7.3 m (20–24 ft).

Research on aisle widths in underground parking typically spans multiple disciplines—architecture, structural engineering, traffic engineering, and human factors. One common thread in the literature is the trade-off between space efficiency and user safety/convenience.

Study [12] introduces a novel concept of parking comfort and develops a quantitative calculation model to address the challenge of evaluating parking comfort across numerous spaces in underground garages. The model operates by analyzing potential collision points throughout the parking process, establishing coordinate relationships between vehicle collision points and environmental obstacles to generate specific comfort values.

Through examining Hangzhou as a case study, study [13] investigates how achieving equilibrium between road infrastructure and vehicle resources while optimizing parking allocation can support urban growth and improve transportation accessibility.

Study [14] presents a dual-phase research methodology to analyze parking patterns and enhance parking space distribution. The first phase develops a hierarchical framework of parking lots, zones, and berths to evaluate parking characteristics through metrics including saturation, turnover, and duration, the second phase introduces a nonlinear optimization model.

A method integrating automated planning with manual adjustments is proposed in [15] to address escalating parking challenges caused by increasing vehicle usage, focusing on optimizing existing parking facility utilization. The approach segments parking lots into optimal rectangular zones, applying automatic planning to each section to maximize space efficiency, followed by manual refinements to account for obstacles and maintain necessary access routes. This methodology is supported by a mathematical optimization model, with its practical effectiveness demonstrated through case study validation, offering a systematic solution to enhance parking space distribution and utilization in existing facilities.

The growing disparity between parking demand and availability in urban central business districts necessitates the development of underground parking systems to reduce surface traffic congestion. Study [16] examines key planning components for these systems, including hierarchical organization, capacity determination, access point placement, and internal traffic flow management.

Urban complexes above subway stations, encompassing diverse functions like residential, office, and commercial spaces, present unique opportunities for shared parking due to their varying peak usage times. Study [17] examines parking demand patterns and user behavior to develop a predictive model incorporating shared parking concepts for more efficient approach to parking space allocation in mixed-use transit-oriented developments.

Study [18] presents comprehensive models for autonomous vehicle navigation at low speeds, focusing on parking and docking maneuvers within confined spaces. Utilizing kinematic vehicle models due to low-speed operations, the study examines three vehicle types: passenger cars, long wheelbase trucks, and articulated vehicles with variable steering configurations.

Through analysis of existing parking management research and evaluation of simulation modeling applications, one study [19] proposes a decision support system incorporating intelligent parking management solutions with environmental considerations.

Paper [20] develops guidelines for optimizing parking space dimensions based on design vehicle specifications. The study introduces and defines the concept of a “design vehicle,” establishing optimal parameters and proposing a standardized template for parking space design, ultimately providing practical recommendations for transportation infrastructure planning that can be applied in various urban contexts.

Study [21] examines the inadequacy of current parking space standards, which have not kept pace with the significant increase in passenger vehicle dimensions over the past three decades. Using Croatia as a case study, where there has been substantial growth in mid-sized and large vehicle ownership, the research presents an analytical methodology that considers the nation’s vehicle registration data to determine reference vehicle dimensions. The study then combines these reference measurements with ergonomic requirements to propose updated parking space standards, offering both specific recommendations for Croatian parking design and a replicable analytical framework that can be applied to parking space standardization in other regions.

Study [22] addresses the growing challenges of parking organization in modern multi-story residential developments, where insufficient planning leads to disorganized vehicle parking that encroaches on green spaces, playgrounds, and access routes. The study aims to optimize parking space organization in densely populated residential areas, focusing specifically on maximizing the efficient use of available courtyard space.

Architectural layout configuration for underground parking is often constrained by complex factors such as site conditions and design requirements, leading to reduced design efficiency. Study [23] presents a design tool that leverages site information to produce practical reference solutions for underground parking layouts. By extracting spatial modules and translating design constraints into adjacency rules, the research develops a generation and optimization model.

Study [24] analyzes smart parking systems from a technical standpoint by providing a comprehensive overview of smart parking technologies, the study classifies these systems within the broader category of vehicular detection technologies and explores communication modules in detail.

While individual studies provide valuable insights into specific aspects of parking design, a broader synthesis reveals several recurring themes. First, much of the literature highlights the importance of balancing space efficiency with user safety and maneuverability—especially as urban vehicle sizes grow, and parking becomes increasingly constrained. Second, several contributions integrate simulation or optimization techniques, yet relatively few studies combine these with real-world validation. Third, there is a notable regional gap, as most studies are concentrated in urban areas in China, the EU, or North America, with limited empirical focus on Central Asian contexts like Kazakhstan. These patterns collectively suggest that a unified, multi-objective optimization framework—validated through simulation and empirical testing—remains underexplored. This paper seeks to address that gap by combining geometric modeling, simulation-based performance assessment, and physical testing in a Central Asian case study.

1.3. Research Gap, Contributions and Paper Structure

The design of underground parking facilities, particularly the optimization of aisle width, has been addressed in numerous guidelines and studies. However, existing research often lacks a comprehensive, multi-objective approach that systematically balances vehicle maneuverability with parking capacity. Many national and international standards define broad aisle width recommendations but do not provide a detailed, data-driven methodology for determining the optimal range based on real-world vehicle behavior. Additionally, prior studies have primarily focused on geometric modeling or empirical observations, with limited integration of computational simulations and controlled physical testing.

Most parking standards have not been updated to account for evolving vehicle dimensions, especially the increasing prevalence of SUVs and pickup trucks in urban environments. Existing regulations may still adhere to outdated vehicle size distributions, leading to aisle widths that compromise either parking capacity or maneuverability. Previous studies have also largely overlooked regional variations in vehicle distributions and regulatory frameworks, limiting their applicability to diverse urban environments.

This study addresses these gaps by integrating geometric modeling, software-based simulations, and empirical validation to develop a data-driven approach for aisle width optimization in underground parking facilities. Unlike prior research, which often focuses on a single aspect of parking design, this study considers both maneuverability constraints and parking capacity trade-offs in a unified framework. Additionally, the case study application in Kazakhstan ensures that the findings are not only theoretically sound but also practically relevant to urban planners, architects, and engineers working in diverse regulatory environments.

The primary contributions of this study are as follows:

• Development of a multi-objective optimization framework which presents a novel methodology that systematically balances vehicle maneuverability and parking capacity by integrating geometric modeling, computational simulations, and empirical testing. This approach allows for a more precise determination of optimal aisle widths than conventional regulatory guidelines.
• Unlike previous studies that rely solely on theoretical models or simulations, this research incorporates real-world parking trials using a diverse fleet of vehicles. The findings confirm the feasibility and practicality of the proposed aisle width recommendations.
• Identification of an optimal aisle width range through a systematic analysis of maneuverability metrics, including parking success rates, time requirements, and collision probabilities.
• Application to a real-world case study ensures that the findings are grounded in real-world conditions and can serve as a guideline for policymakers, urban planners, and transportation engineers.

The remainder of this paper is structured as follows. Section 2 describes the conceptual framework and research methodology, detailing the geometric modeling, software-based simulations, and empirical validation processes used to optimize aisle width. Section 3 presents the findings from each stage of the research, including geometric modeling outcomes, simulation-based maneuverability metrics, physical testing results, and case study applications. Section 4 interprets the results, compares them with existing parking regulations, discusses study limitations, and outlines potential future research directions. Section 5 summarizes the key findings and their implications for underground parking design, offering practical recommendations for engineers, urban planners, and policymakers.

2. Materials and Methods

2.1. Conceptual Model & Theoretical Framework

The conceptual model and theoretical framework of this study are built upon the fundamental principles of parking design optimization, integrating geometric modeling, computational simulations, and empirical validation to develop an optimal approach for aisle width determination in underground parking facilities. The model is structured around two key objectives: ensuring maneuverability for different vehicle types while maximizing parking capacity within spatial constraints.

At the core of this framework is the geometric modeling component, which establishes the fundamental relationships between aisle width, vehicle turning radii, and required clearance for successful parking maneuvers. The model incorporates Ackermann steering geometry [25], which governs vehicle turning behavior, along with swept path analysis to determine the minimum space required for different vehicle classes, including compact cars, sedans, SUVs, and pickup trucks. These theoretical calculations provide the first set of constraints for defining aisle width limits, ensuring that vehicles can enter and exit parking stalls with minimal corrective maneuvers.

Building upon this foundation, the study integrates software-based simulations to analyze vehicle dynamics in real-time parking scenarios. Using tools such as AutoTURN-2024 [26] and ParkCAD-2024 [27] the conceptual model simulates driver behavior, trajectory adjustments, and potential collision risks under varying aisle width configurations. This simulation-based approach refines the initial geometric constraints by incorporating real-world driving variability, such as driver hesitation, multi-step corrections, and reaction times, which cannot be captured purely through theoretical calculations. The results from these simulations provide quantitative maneuverability metrics, including parking success rate, time required for parking, number of reversing attempts, and collision probability, which are essential for validating the theoretical framework.

The final component of the framework involves empirical validation through physical testing in real underground parking facilities. This phase ensures that the conceptual model is not only mathematically robust but also practically feasible. By conducting controlled parking trials across different aisle widths and vehicle types, the study collects real-world maneuverability data, refining the maneuverability function within the optimization model. This empirical testing phase provides critical insights into driver adaptability, environmental influences (e.g., column placements, ramp gradients), and actual parking success rates, which help fine-tune the theoretical predictions and simulation results.

By combining geometric modeling, computational simulations, and empirical validation, the conceptual model ensures that the optimal aisle width recommendations are both data-driven and applicable to real-world parking infrastructure (

Table 2. Key components of the study.

Study Component	Use in Research
Geometric Modeling	$\mathrm{Establish} \mathrm{theoretical} \mathrm{aisle} \mathrm{width} \mathrm{requirements} \mathrm{based} \mathrm{on} \mathrm{turning} \mathrm{radii} \mathrm{and} \mathrm{vehicle} \mathrm{sizes}. \mathrm{Validate} \mathrm{mathematical} \mathrm{formulation} \mathrm{of} E\left(x\right)$$\mathrm{and} N\left(x\right)$.
Software Simulations	Test aisle widths in a controlled virtual environment. Compare failure rates, maneuvering time, and clearance distances. Generate parking trajectory visualizations for study.
Physical Testing	Provide real-world validation of theoretical and simulated results. Identify critical widths where user experience declines. Ensure recommendations are practical and usable.
Regulatory Analysis	Compare results with existing standards and propose updates if needed. Support practical policy recommendations for urban planning.

).

The theoretical framework integrates mathematical modeling, dynamic simulations, and empirical testing to create a multi-objective optimization model, balancing maneuverability and capacity while aligning with urban planning standards and engineering best practices. This approach provides a scientifically validated foundation for improving underground parking layouts, ensuring that aisle width recommendations enhance both usability and efficiency in parking facility design.

2.2. Data Collection

The data collection process for this study was designed to ensure a comprehensive, evidence-based approach to optimizing underground parking aisle widths.

2.2.1. Sources of Data

To achieve reliable and practical insights, the study gathered data from three primary sources.

• Geometric Modeling Data

Geometric modeling was conducted to determine the minimum required aisle width for different vehicle types based on their turning radii, wheelbase lengths, and approach angles. These data were derived from:

• Manufacturer vehicle specifications (length, width, turning radius).
• CAD-based modeling (AutoCAD and Revit 2024) to graphically simulate vehicle movement and clearance zones.
• Mathematical calculations of swept path and turning envelopes, identifying the minimum space required for successful parking maneuvers.

2.

Software-Based Simulation Data

Simulation data were collected using specialized software applications to test parking scenarios under controlled digital conditions. This included:

• AutoTURN Online for simulated turning paths and vehicle clearance in parking layouts.
• ParkCAD 4.0 for optimized stall arrangements and measured efficiency in space utilization.
• Revit + Dynamo Scripts for tested 3D parking layouts and clearance zones dynamically.

The simulation results provided empirical maneuverability metrics for various aisle widths, including:

• Success rate—part of vehicles parked without additional maneuvers.
• Time to park—the duration required to complete a parking maneuver.
• Number of reversing attempts as additional adjustments needed due to space constraints.
• Collision risk—probability of hitting adjacent vehicles or obstacles.

3.

Physical Testing Data

Real-world testing was conducted in operational underground parking facilities to validate geometric and simulation findings. Data were collected by performing controlled parking tests at aisle widths of 4.5 m, 5.0 m, 5.5 m, and 6.0 m, using a diverse fleet of vehicles. Key parameters recorded during physical testing included:

• Parking success rates for different vehicle classes.
• Observed driver corrections and overcorrections due to insufficient space.
• Time taken per parking attempt to assess efficiency.
• Maneuverability constraints near structural elements such as columns and ramps.
• The physical testing phase helped refine the maneuverability function E(x) by incorporating actual driver behavior, error rates, and real-world space limitations.

2.2.2. Summary of Vehicle Fleet and Parking Standards

The study considered a representative sample of vehicle types, ensuring that the results were applicable to diverse urban traffic compositions. The test fleet and key dimensions used for modeling and validation are summarized in

Table 3. Vehicle fleet characteristics.

Vehicle Type	Example Models	Turning Radius	Length	Width
Compact Cars	Toyota Corolla, VW Golf	5.2–5.5 m	4.2–4.6 m	1.75–1.80 m
Sedans	Toyota Camry, Honda Accord	5.5–5.8 m	4.7–5.0 m	1.80–1.85 m
SUVs	Haval Dargo, Toyota RAV4	5.8–6.3 m	4.7–5.2 m	1.85–1.95 m
Pickups	Toyota Hilux, Ford Ranger	6.2–6.7 m	5.2–5.5 m	1.90–2.00 m

.

The study reviewed global and national parking guidelines to establish reference aisle width standards (Table 3).

After collection, the data were systematically processed and analyzed to extract meaningful insights:

• Geometric calculations were used to establish minimum width constraints based on turning radii.
• Simulation results were processed to generate statistical distributions of parking success rates, maneuvering times, and failure rates for each aisle width scenario.
• Physical testing observations were compiled to identify critical width thresholds where driver errors significantly increased.

A comparative analysis was conducted to align results from the three data sources. If discrepancies arose between simulated and real-world parking success rates, the optimization model was adjusted to reflect empirical findings more accurately.

The collected data were incorporated into the multi-objective optimization model, ensuring that theoretical calculations, simulation-based findings, and physical test results were fully aligned.

The geometric modeling results defined the lower bound of feasible aisle widths.

The simulation data provided performance curves for different widths, guiding maneuverability penalties in the optimization function.

The physical testing results validated the final aisle width recommendations, confirming that the model reflects real-world driver behavior and constraints.

By combining geometric modeling, software-based simulations, and physical testing, the data collection process ensured that the study’s findings were comprehensive, evidence-backed, and practical. The integration of these datasets ensured that the recommended aisle widths maximize maneuverability, efficiency, and parking capacity while remaining grounded in real-world feasibility.

2.3. Model Formulation

In this study, the core design variable is the aisle distance x between two opposing rows of parking stalls in an underground lot. While respecting geometric and regulatory constraints, the model seeks to link this decision variable to two competing objectives: (1) ease of maneuvering and (2) parking capacity.

The decision variable $x$ is aisle distance between two opposing rows of parking stalls. This distance is measured from the edge of one parking stall to the edge of the stall immediately facing it across the aisle. Practically, $x$ is bounded by both physical (available floor space, location of columns or walls) and regulatory (minimum fire-lane widths, code requirements) limits. We denote these bounds as

$$x_{min}\le x\le x_{max}$$

(1)

In the study, there are two objective functions.

1.

Ease of maneuvering $E\left(x\right)$

E(x) is intended to quantify how easily drivers can enter, park, and exit stalls. It typically increases with x: larger aisle widths make maneuvering simpler, reducing multi-point turns and collision risks.

Depending on data availability, E(x) can be formulated using:

• Analytical geometry with turning-circle or swept-path calculations.
• Simulation with recording the success rate or average time to park in a virtual environment for a range of aisle widths.
• Empirical metrics with field observations (e.g., average stall-entry time, frequency of corrective maneuvers).

2.

Parking capacity $N\left(x\right)$

$N\left(x\right)$ denotes the total number of vehicles that can be parked within the fixed underground facility footprint. It generally decreases as $x$ increases, since wider aisles occupy more of the available floor space.

A typical geometric approach is to calculate how many stalls fit along each row, multiplied by the number of rows that can be arranged, considering the aisles needed for vehicular circulation

$$N\left(x\right)=\left[{\displaystyle \frac{W-kx}{w_s}}\right]\times L_r$$

(2)

where $W$ is the total width available for parking plus aisles, $w_s$ is the stall width (or effective width required per stall + buffer), $k$ is s the number of aisles in the layout, $L_r$ is the total length available for rows (or the number of stalls that can fit in the longitudinal dimension). Expression (2) for the capacity function $N\left(x\right)$ is derived from foundational models in transportation engineering that relate aisle geometry to vehicle movement dynamics. These principles are frequently applied in software tools such as AutoTURN and ParkCAD [25,26], which simulate vehicle paths using Ackermann steering geometry and clearance envelopes.

The details may vary based on the exact configuration of the garage.

3.

Constraints

• Physical and structural constraints. The physical layout of the underground lot (columns, ramps, load-bearing walls) may limit the placement of parking rows or reduce the effective width where cars can park. These constraints can be represented by adjustments to $x_{min}$ or specific additional inequalities. For instance, if columns encroach on the turning path, a larger $x$ might be required near specific columns.
• Regulatory constraints. Many local or national building codes specify minimum aisle width and minimum stall dimensions for different vehicle classes. Denote this lower bound as $x_{min}^{code}$. If the building code sets $x_{min}^{code}>x_{min}$ for structural reasons, then the actual feasible region starts at $x_{min}^{code}$. Fire safety regulations could impose additional constraints, such as emergency access lanes.
• Operational constraints. Requirements for pedestrian walkways, handicap-accessible stalls, and special-use stalls (e.g., electric charging stations) may indirectly constrain how many conventional stalls fit, effectively affecting $N\left(x\right)$ or imposing a separate feasible region for $x$.
• Speed constraints. In underground parking facilities, vehicle speeds are typically low, ranging from 5 to 10 km/h due to spatial constraints, signage, and safety regulations. At these speeds, maneuverability is primarily governed by geometric constraints such as turning radii and available clearance, rather than velocity-dependent dynamics like braking distance. Therefore, the optimization model in this study assumes low-speed conditions typical of real-world parking behavior. Although vehicle speed is not an explicit parameter in the objective functions, it is indirectly captured through simulation and empirical testing, where maneuvering times and collision risk reflect realistic driver behavior. This approach ensures that the recommended aisle widths remain valid and safe under practical speed conditions commonly observed in underground garages.

In most formulations, these constraints can be grouped into a set $\mathcal{C}$, such as $x\in \mathcal{C}$.

4.

Optimization approaches

Depending on the project’s objectives, the model can be expressed in one of the following ways:

• Single-objective optimization combines both criteria (ease of maneuvering and capacity) into a single objective function, typically by assigning weights $\alpha$ and $\beta$

  $$\underset{x\in \mathcal{C}}{\max }F\left(x\right)=\alpha E\left(x\right)+\beta N\left(x\right)$$

  (3)

  where $\alpha$ and $\beta$ are user-defined to reflect the relative importance of maneuverability vs. capacity. The optimal solution $x^{*}$ s found by maximizing $F\left(x\right)$ over the feasible region $\mathcal{C}$. In the multi-objective optimization formulation, the weights $\alpha$ and $\beta$ represent the relative importance assigned to maneuverability and parking capacity, respectively. The selection of these weights depends on the design priorities of the parking facility and the specific needs of stakeholders. In practice, these weights can be determined through one or more of the following approaches:

(1)

Stakeholder input—urban planners, facility managers, or transportation authorities can define priorities (e.g., prioritizing capacity in high-demand areas or maneuverability in premium residential zones);

(2)

Scenario analysis—multiple optimizations runs can be performed with varying α and β values to identify Pareto-optimal solutions and support trade-off decisions;

(3)

Empirical calibration—user satisfaction surveys or observational data (e.g., from physical tests) can inform the relative utility of improved maneuverability vs. lost capacity.

In this study, a balanced weighting scheme was adopted ($\alpha =0.5, \beta =0.5$) to reflect an equal prioritization of both objectives, but the framework allows for flexible adjustment based on contextual needs.

• Constrained optimization uses one criterion as the objective and set the other as a constraint

$$\underset{x\in \mathcal{C}}{\max }N\left(x\right)$$

(4)

$$subject to E\left(x\right)\ge E_{min}$$

(5)

The model seeks to maximize capacity while guaranteeing a minimum ease-of-maneuver standard $E_{min}$

• Multi-objective optimization treats $E\left(x\right)$ and $N\left(x\right)$ as distinct objectives to be optimized simultaneously

  $$\underset{x\in \mathcal{C}}{\max }\left\{E\left(x\right),N\left(x\right)\right\}$$

  (6)

This approach yields a Pareto frontier—a set of aisle distances for which no single objective can be improved without negatively impacting the other. Decision-makers then select the most suitable trade-off point based on additional criteria (e.g., cost, expected user mix).

In essence, the model formulation starts with the decision variable $x$ and quantifies how it affects ease of maneuvering $E\left(x\right)$ and capacity $N\left(x\right)$. It then incorporates relevant constraints (physical, regulatory, and operational) to define the feasible range for $x$. An optimization approach is selected depending on whether the study focuses on a single combined metric or seeks an informed balance among multiple design priorities.

This formulation ensures a transparent, data-driven framework for deciding the aisle distance that aligns with both engineering constraints and user needs, ultimately guiding the design of underground parking facilities toward better usability and efficient space utilization.

2.4. Model Implementation and Validation

The implementation and validation of the optimization model for underground parking aisle widths follow a structured approach that integrates computational modeling, simulation analysis, and empirical validation. The goal is to ensure that the proposed model accurately captures the trade-off between maneuverability and parking capacity while aligning with real-world parking constraints. The process involves developing the model within a computational environment, validating its assumptions through simulations, and confirming its practical applicability through physical testing.

The model implementation begins with the formulation of maneuverability constraints and capacity calculations, based on geometric relationships and real vehicle movement dynamics. The aisle width is the primary decision variable, affecting both ease of vehicle entry and exit and the total number of available parking spaces. The model incorporates two competing objective functions: the maneuverability function E(x), which quantifies the ease of parking in terms of turning clearance, number of corrective maneuvers, and time required for parking; and the capacity function N(x), which represents the total number of parking spaces available within a fixed parking lot footprint.

To implement the model, software-based simulations are conducted, which simulate real-world vehicle trajectories, turning paths, and driver behaviors across different aisle widths. These simulations allow for the fine-tuning of model parameters by incorporating realistic driving constraints, such as reaction delays, multi-step parking attempts, and minor errors in steering angles. The simulation results are used to refine the model’s mathematical formulations, ensuring that theoretical predictions align with observed vehicle behavior in virtual environments.

The validation phase of the study involves empirical testing in real underground parking facilities, where the simulated results are compared against actual parking performance metrics. A diverse fleet of compact cars, sedans, SUVs, and pickup trucks is used to assess maneuverability constraints across multiple aisle widths. Each vehicle undergoes repeated parking attempts at different aisle widths, and key performance indicators are measured to determine whether the simulated results hold true in real-world conditions.

The final step of validation involves iterative refinement of the model, where discrepancies between simulated and real-world results are analyzed to update the optimization parameters. If the empirical tests indicate that maneuverability constraints are underestimated or overestimated in the computational model, adjustments are made to penalty functions, constraint thresholds, and weighting factors to improve accuracy. The validated model is then used to generate optimized aisle width recommendations, ensuring that the final design strikes the optimal balance between maximizing parking capacity while maintaining a high level of usability for drivers.

By following this multi-stage validation process, the study ensures that the proposed aisle width optimization model is both theoretically rigorous and practically applicable. The integration of geometric modeling, software-based validation, and real-world empirical testing provides a scientifically grounded framework for improving underground parking facility design, making the findings relevant to urban planners, civil engineers, and parking facility designers seeking to optimize parking layouts for both efficiency and user experience.

2.5. Case Study: Application to the Republic of Kazakhstan

To illustrate the practical implementation of the proposed optimization model for underground parking aisle widths, the study uses the Republic of Kazakhstan as a case study. This selection is based on the country’s urban development trends, regulatory frameworks, and growing demand for efficient parking solutions in densely populated cities. By applying the model within this regional context, the study ensures that its findings are aligned with real-world urban infrastructure constraints and local parking standards.

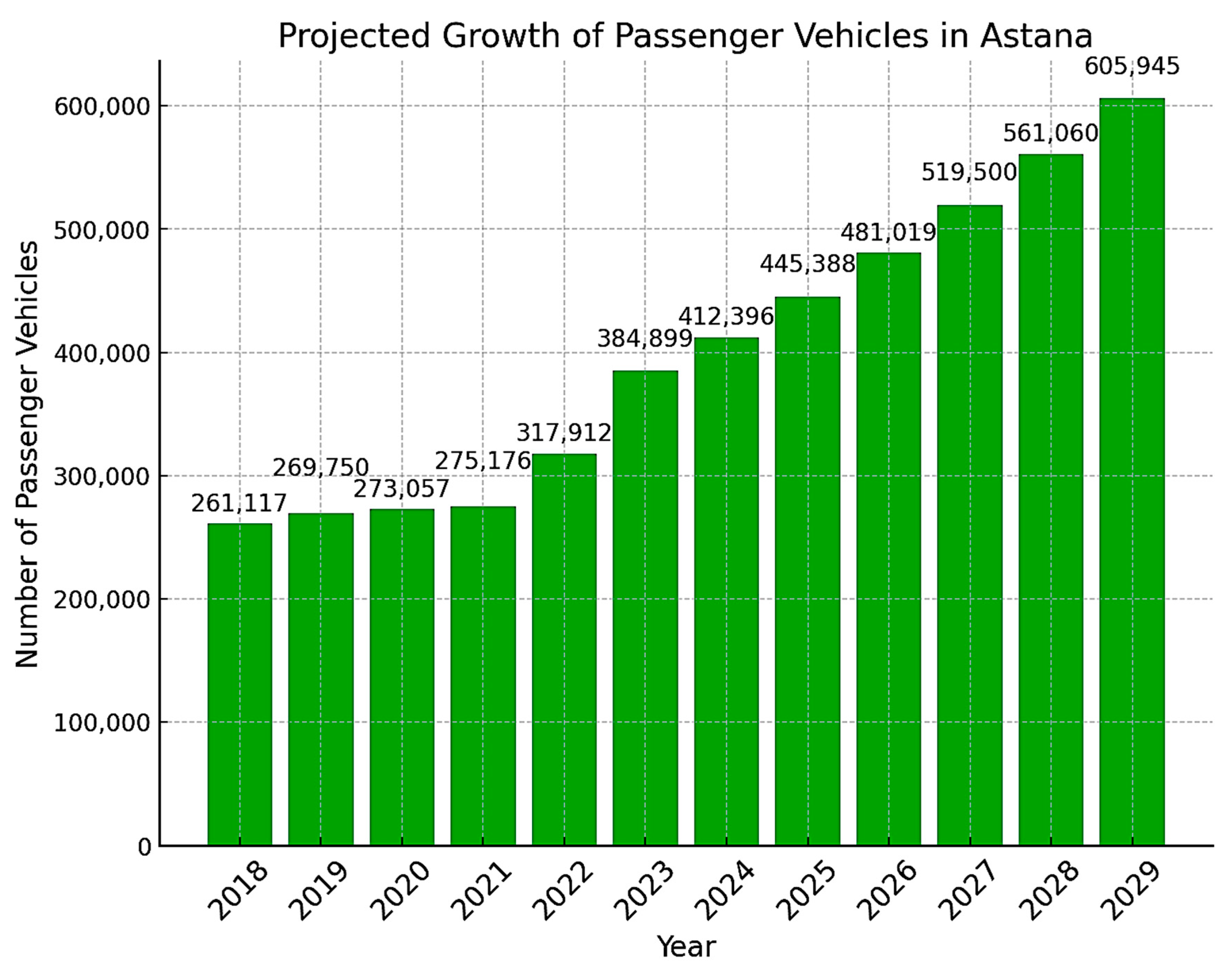
The Republic of Kazakhstan has experienced rapid urbanization, particularly in cities such as Astana, Almaty, Shymkent, and Karaganda, leading to increased vehicle ownership and parking congestion.

The average annual growth rate of motorization in Kazakhstan over the past five years was 8% [28]. Based on the current growth trend, the number of vehicles as of 1 January 2028 is projected to reach 561,060 units, reflecting a 32% increase [28]. As an example, Figure 1 presents data from the same source on the number of passenger vehicles in Astana.

The existing parking infrastructure in these cities often faces challenges related to space utilization and maneuverability, making it an ideal setting to test and refine the proposed model. Furthermore, Kazakhstan’s building codes and urban planning policies provide a structured regulatory framework against which the optimization model can be assessed.

To ensure relevance, the study incorporates local parking design standards, national construction regulations, and vehicle fleet composition data from Kazakhstan. Key parameters, such as standard stall dimensions, regulatory aisle width requirements, and the typical mix of vehicle types, were gathered from Kazakhstan’s building codes and urban planning documents [29]. For example,

Table 4. Recommended minimum aisle width between rows of parked cars.

Parking Angle, Degrees	Traffic Flow	Width of Passage, m	Parking Space Width, m
90	Double-sided	6.95	Full width—3.0
90	One-sided	6.0	Full width—3.0
60	One-sided	4.2	3.0
45	One-sided	3.6	3.0

presents the recommended minimum aisle width between rows of parked cars.

The model was tested across real underground parking facilities in Kazakhstan, where empirical validation is conducted through physical testing in operational parking lots. These facilities represent a range of modern and older parking structures, allowing for a comprehensive assessment of how different aisle widths affect maneuverability and parking efficiency in local conditions.

The vehicle fleet composition in Kazakhstan was also considered, ensuring that the study reflects the types of vehicles commonly used in urban environments. As an example, Figure 2 illustrates the distribution of the top 10 new passenger cars over three years in Kazakhstan, along with their key overall dimensions, which are presented in Figure 3.

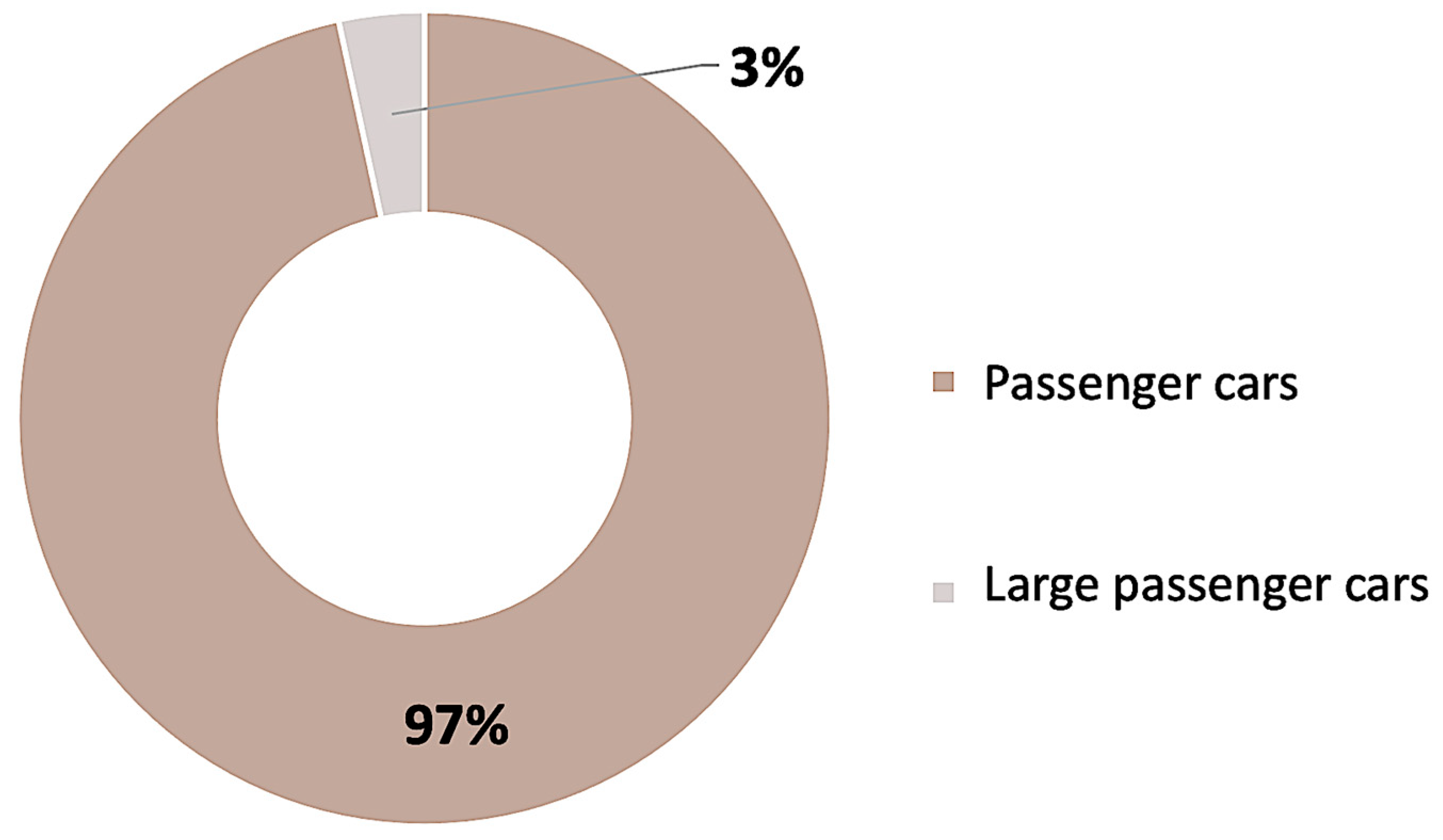
Similar data on large passengers’ cars in Kazakhstan are shown in Figure 4 and Figure 5.

The distribution between the two types of passenger cars is shown in Figure 6.

Given the prevalence of both compact cars and larger vehicles such as SUVs and pickup trucks, the optimization model was designed to accommodate a diverse range of vehicle sizes and turning capabilities. Empirical tests were conducted using vehicles frequently found on Kazakhstani roads, such as Toyota Camry, Hyundai Tucson, Kia Sportage, Toyota Land Cruiser, and Nissan Patrol, ensuring that the study’s findings are applicable to real-world driving conditions.

The case study approach allows for direct comparison between the model’s theoretical predictions, simulation results, and real-world performance in Kazakhstan’s parking facilities. The findings provide valuable insights into how local conditions, regulatory frameworks, and driver behavior influence optimal aisle width design. Furthermore, the study’s results can serve as a guideline for policymakers, urban planners, and engineers in Kazakhstan, helping to optimize future underground parking facilities to improve both efficiency and usability.

By using Kazakhstan as a reference, the study ensures that its recommendations are grounded in practical applications while still being adaptable for other urban environments with similar parking challenges. The methodology used in this case study can be extended to other cities and regions, providing a scalable framework for optimizing underground parking layouts based on data-driven analysis and empirical validation.

3. Results

3.1. Geometric Modeling Predictions

This section describes the geometric modeling methodology used to predict the required aisle width for underground parking, based on vehicle dimensions, turning radii, and spatial constraints. Geometric modeling provides a theoretical foundation for evaluating maneuverability and setting minimum width constraints before conducting simulations or real-world testing.

Geometric modeling aims to:

• Establish minimum aisle width requirements based on vehicle kinematics.
• Determine the turning paths and clearances needed for different vehicle categories.
• Provide an initial constraint framework for optimization before validating results with simulations and physical tests.

By graphically and mathematically analyzing vehicle movement within parking aisles, the model quantifies clearance distances, turning angles, and stall-accessibility limits.

The geometric model is built using key vehicle parameters:

• Turning radius $R_t$—the minimum circular path a vehicle can turn without reversing.
• Wheelbase $W_b$ —distance between the front and rear axles, influencing turning characteristics.
• Overall vehicle length $L_v$—affects the entry angle into parking stalls.
• Vehicle width $W_v$—determines lateral clearance in tight turns.

To ensure that the model accounts for diverse vehicle sizes, the different categories were considered (Table 3). These values were extracted from manufacturer specifications and validated against previous parking design studies.

The turning movement of a vehicle is defined by the Ackermann steering principle, which governs how the front wheels rotate during turns. The swept path is calculated using

$$R_{inner}=R_t-{\displaystyle \frac{W_v}{2}}$$

(7)

$$R_{outer}=R_t+{\displaystyle \frac{W_v}{2}}$$

(8)

where $R_{inner}$ is the inner turning radius of the front wheel, $R_{outer}$ is the outer turning radius required for clearance, and $W_v$ is the vehicle width.

For a vehicle to successfully turn into or out of a parking stall, the minimum required aisle width $x_{min}$ is derived from

$$x_{min}=2R_{outer}+K$$

(9)

where $K$ is an additional clearance buffer for driver errors and safety margins (typically 0.5–1.0 m).

For different vehicle classes, these yields are shown in

Table 5. Required aisle width.

Vehicle Type	$\mathbf{Required} \mathbf{Aisle} \mathbf{Width} {\mathit{x}}_{\mathit{m}\mathit{i}\mathit{n}}$
Compact Cars	4.8–5.2 m
Sedans	5.2–5.5 m
SUVs	5.5–6.0 m
Pickups	6.0–6.5 m

.

This serves as the first constraint in the optimization problem: aisle widths below these values significantly increase maneuvering difficulty.

To validate these calculations, CAD-based geometric modeling was performed using AutoCAD and Revit. Two-dimensional turn paths were plotted for each vehicle type (Figure 7).

The clearance area required for smooth turns was visualized. Variations in entry angles and multi-point turns were examined.

Key findings from CAD analysis:

• At $x$ = 4.5 m, compact cars could turn with some difficulty. Larger sedans and SUVs required extra maneuvers. Pickup trucks required reversing maneuvers before completing turns.
• At $x$ = 5.0 m, most sedans and SUVs could park smoothly. Pickup trucks still faced occasional multi-turn adjustments.
• At $x\ge$ 5.5 m, all vehicle types, including pickup trucks, could park without multi-turn adjustments.

The geometric modeling results directly inform the optimization constraints. They show that increasing x above 5.5 m offers diminishing returns in ease of parking. This leads to a capacity optimization trade-off. When the design objective emphasizes maximizing parking capacity, an aisle width of approximately 5.0 m is recommended. In contrast, if driver comfort and maneuverability are prioritized, a wider aisle in the range of 5.5 to 6.0 m is more appropriate.

Geometric modeling predicted that 5.0 m should be the practical minimum for general usability.

3.2. Software-Based Modeling: Methodology and Application

This section outlines the methodology for software-based modeling, which was used to simulate vehicle movement in underground parking aisles. The goal of this approach was to validate geometric predictions, test various aisle width configurations, and evaluate vehicle maneuverability under controlled conditions before conducting real-world experiments. By leveraging computational tools, the study ensured that the proposed aisle widths were not only mathematically feasible but also practically functional in real parking scenarios.

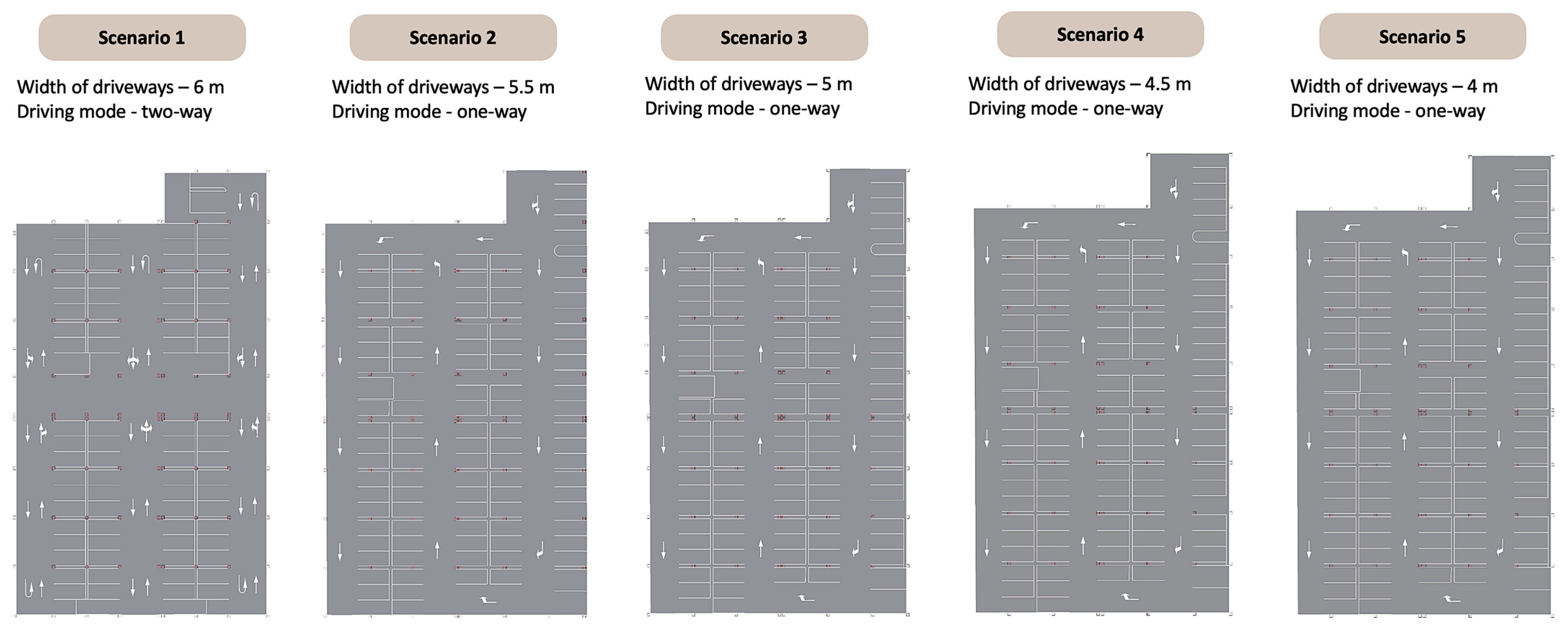
3.2.1. Modeling Scenarios

The software modeling stage was designed to simulate vehicle movement in different aisle width scenarios and measure maneuverability constraints (Figure 8), compare theoretical geometric predictions with real-world driving behavior through dynamic simulations, identify critical thresholds where parking success rates decline due to insufficient space, and provide quantitative insights for optimizing the aisle width function $E\left(x\right)$ in the optimization model.

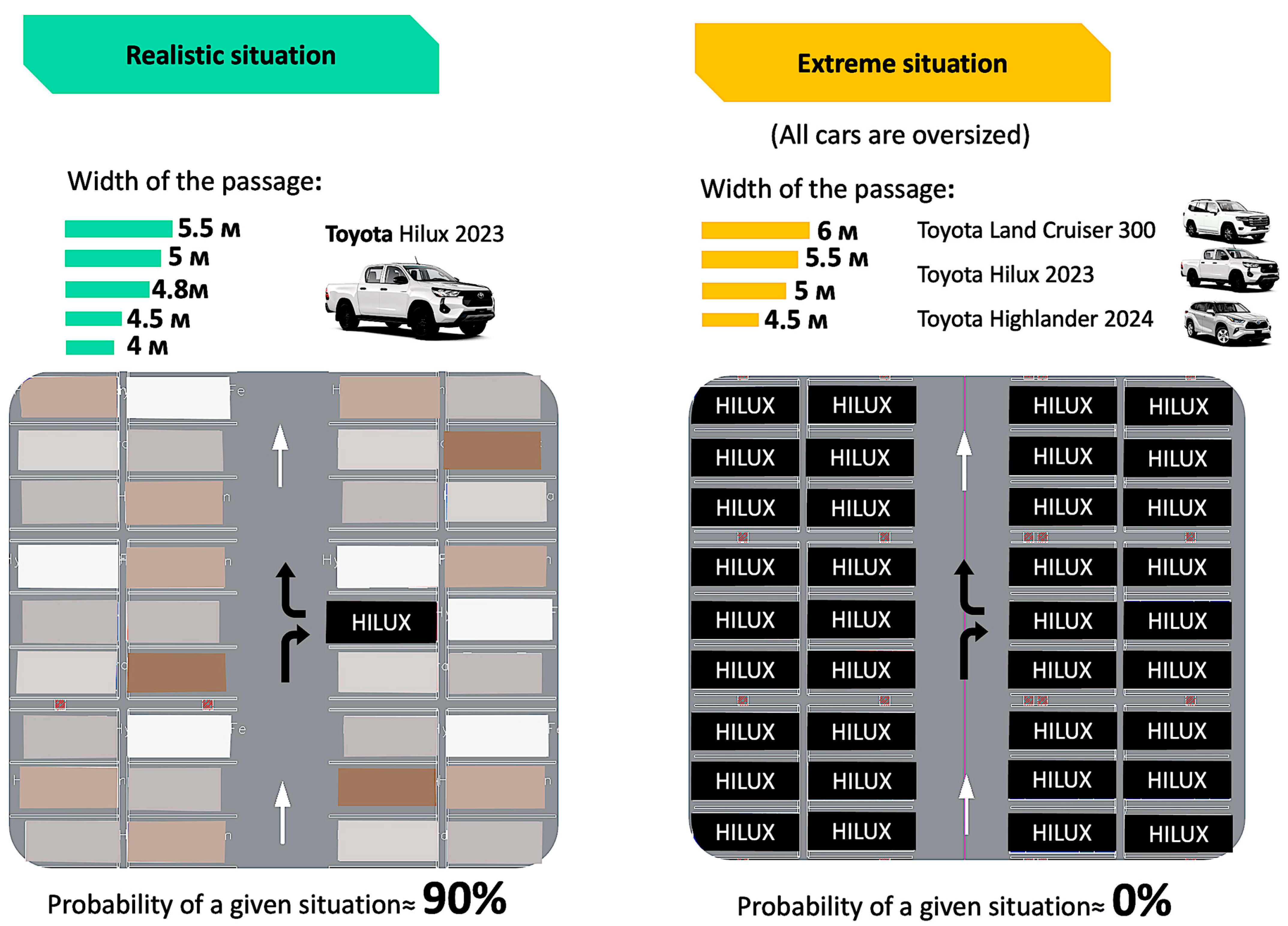
The Figure 9 illustrates two main extreme situations in underground parking modeling based on vehicle size and passage width.

1.

Realistic situation (common scenario)

This situation represents a typical underground parking environment where a variety of vehicles are present, including compact cars, sedans, SUVs, and some larger vehicles like pickup trucks.

The passage width varies from 4 m to 5.5 m, ensuring that most vehicles, including a Toyota Hilux 2023 (a mid-sized pickup truck), can maneuver and park without excessive difficulty.

The probability of occurrence is estimated at 90%, meaning that in most real-world parking lots, the mix of vehicles is diverse, and the aisle width is generally within a practical range.

Parking layout allows for smooth traffic flow and reasonable parking success rates, with only minor maneuverability challenges at narrower aisle widths (e.g., 4.5 m).

2.

Extreme situation (all vehicles are oversized)

This scenario models an unrealistic yet worst-case parking scenario, where all vehicles are large SUVs or pickup trucks (Toyota Hilux 2023, Toyota Land Cruiser 300, Toyota Highlander 2024).

The parking area is filled exclusively with oversized vehicles, dramatically reducing maneuverability and increasing congestion.

The passage width remains within the range 4.5 m to 6 m, but the need for larger turning radii results in blocked access, failed parking attempts, and increased risk of collision.

The probability of this scenario occurring is close to 0%, since real parking lots generally accommodate a mix of vehicle sizes, reducing the likelihood of complete congestion due to oversized vehicles.

The parking layout in this scenario results in significant maneuverability challenges, where turning and reversing require additional space that is not available, leading to gridlock and ineffective use of parking capacity.

These two extreme cases highlight how vehicle distribution and passage width impact maneuverability in underground parking lots. The realistic situation demonstrates a functional parking environment with high usability, while the extreme situation with oversized vehicles creates a highly inefficient, impractical parking scenario where vehicles struggle to navigate the space effectively.

Unlike static geometric modeling, which relies on predefined turning radii, software-based simulations allow for real-time dynamic analysis of vehicle motion, accounting for steering, acceleration, and braking patterns.

3.2.2. Defining Input Parameters

The simulation models were set up using real-world vehicle dimensions, driver behavior constraints, and site-specific conditions. Key input parameters included:

• Vehicle fleet composition with modeling different types of vehicles, including compact cars, sedans, SUVs, and pickup trucks.
• Aisle width variations with simulation parking scenarios for 4.5 m, 5.0 m, 5.5 m, and 6.0 m aisles to observe maneuverability differences.
• Driver behavior constraints with assumed realistic turning speeds, reaction times, and parking approach angles.
• Structural obstacles with consideration the impact of columns, ramps, and clearance heights on maneuverability.

Each simulation run tested entry and exit maneuvers, including:

• Forward parking entry and reverse exit.
• Reverse parking entry and forward exit.
• Adjustments required if the initial maneuver was unsuccessful.

3.2.3. Software Applications Used in Practice

To conduct the simulations, the study used specialized parking design and vehicle movement software tools, including AutoTURN for simulating vehicle turning paths and clearance zones, ParkCAD for optimizing parking layouts and evaluating space efficiency, and Revit with Dynamo Scripts for modeling 3D parking layouts and dynamically testing clearance zones. Each software tool was applied to specific modeling tasks, ensuring comprehensive validation of the optimal aisle width predictions.

This study employs computational simulations to evaluate parking maneuverability under different conditions, focusing on the impact of aisle width and vehicle type on parking efficiency. The analysis consists of two primary cases: an extreme parking scenario with only oversized vehicles and a realistic scenario with a diverse mix of vehicle types. Additionally, specific vehicle simulations provide detailed insights into maneuvering challenges within each case.

The extreme parking case, illustrated in Figure 10, represents a worst-case scenario where all parked vehicles are oversized models, including the Toyota Land Cruiser 300, Toyota Hilux, and Toyota Highlander 2024. This simulation assesses maneuverability across different aisle widths ranging from 4.5 m to 6.0 m. The results show that aisle widths below 5.5 m significantly reduce maneuverability, forcing vehicles to make multiple correctives turns and increasing congestion. At 4.5 m width, severe traffic bottlenecks form, preventing smooth circulation, while 5.5 m and 6.0 m allow for fluid movement and successful parking.

A more detailed analysis of the Toyota Land Cruiser 300, shown in Figure 11, highlights the specific maneuvering challenges associated with large SUVs. The simulation tracks its turning radius and clearance space, identifying critical points where the vehicle struggles due to aisle width constraints. The results confirm that at widths ≤5.0 m, multi-step adjustments become necessary, leading to prolonged parking times and potential traffic blockages. However, at 5.5 m or greater, maneuverability improves considerably, reducing reversing attempts and enhancing parking efficiency.

In contrast, the realistic parking case, depicted in Figure 12, presents a more common urban underground parking scenario with a mix of compact cars, sedans, SUVs, and pickups. The study evaluates how aisle width affects maneuverability in driveways ranging from 4.0 m to 6.0 m. The results indicate that compact and mid-sized vehicles can successfully park in widths as narrow as 4.5 m, but larger SUVs and pickups require additional corrective maneuvers. At 5.0 m, most vehicles can enter and exit parking stalls efficiently, with minimal reversing adjustments. Increasing the aisle width to 5.5 m or more facilitates seamless parking but slightly reduces the total parking capacity.

To further refine these findings, Figure 13 focuses on a Toyota Hilux 2023, analyzing its maneuverability within the realistic parking case. The simulation reveals that at 4.5 m, the Hilux requires extra steering corrections, increasing parking time. At 5.0 m, maneuverability improves significantly, with smooth entry and exit movements. At 5.5 m or more, parking becomes effortless, but the trade-off is a reduction in the number of available spaces.

The simulation models were set up using real-world vehicle dimensions, driver behavior constraints, and site-specific conditions. Key input parameters included vehicle fleet composition, which modeled different types of vehicles such as compact cars, sedans, SUVs, and pickup trucks; aisle width variations, which tested parking scenarios at 4.5 m, 5.0 m, 5.5 m, and 6.0 m to observe maneuverability differences; driver behavior constraints, which assumed realistic turning speeds, reaction times, and parking approach angles; and structural obstacles, which considered the impact of columns, ramps, and clearance heights on maneuverability. Each simulation run tested various parking maneuvers, including forward parking entry with reverse exit, reverse parking entry with forward exit, and adjustments required if the initial maneuver was unsuccessful.

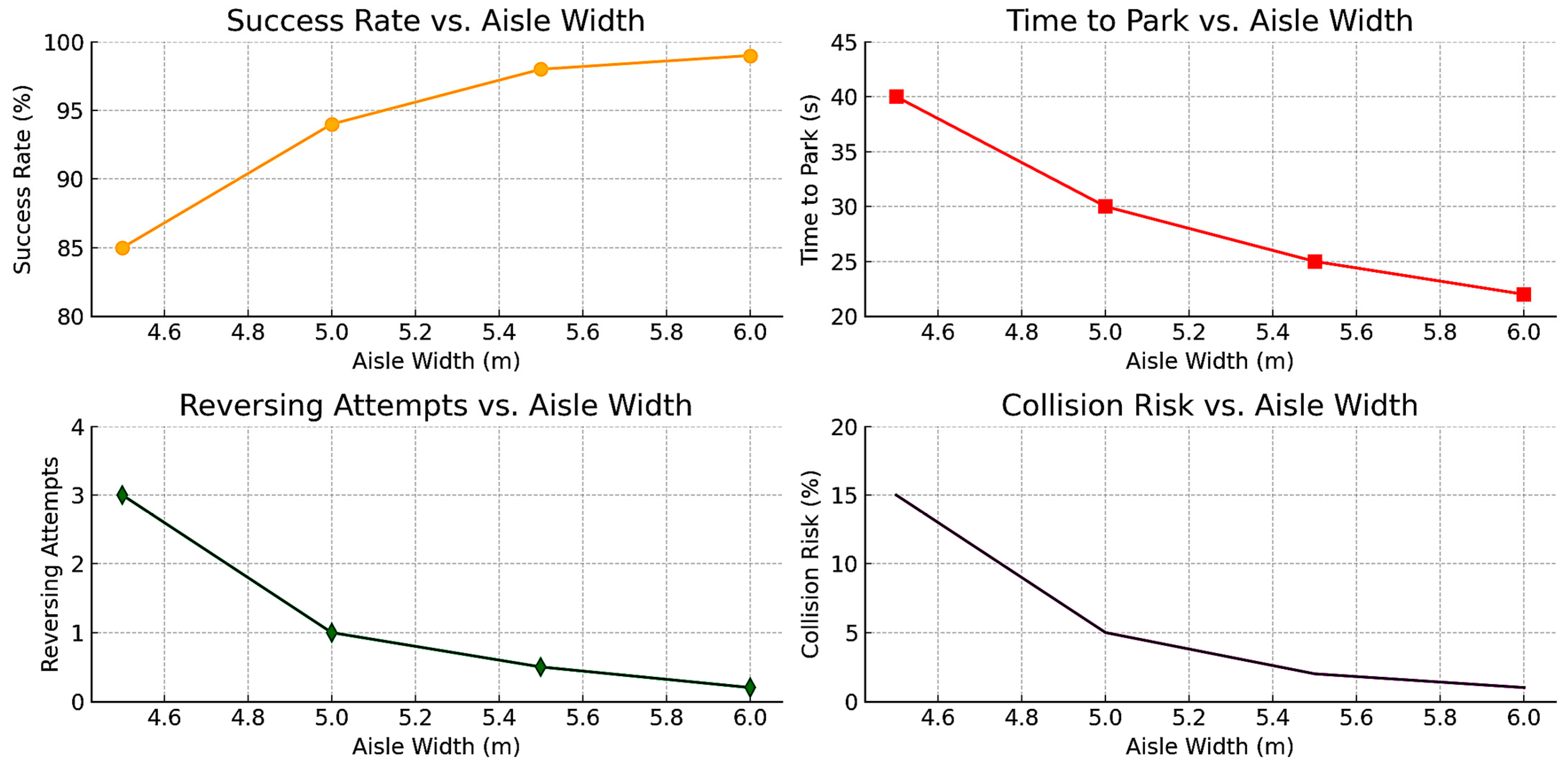
To measure maneuverability performance across different aisle widths, the study used key evaluation metrics, including success rate, which measured the percentage of vehicles that successfully parked without additional maneuvers; time to park (seconds), which captured the total time required for a vehicle to complete parking; number of reversing attempts, which tracked additional maneuvers needed to fit into a parking stall; and collision risk, which calculated the probability of hitting adjacent vehicles or obstacles. The simulation results showed that at 4.5 m aisle width, compact cars parked successfully 85% of the time, but SUVs and pickups required additional maneuvers, with an increased collision risk and time to park exceeding 40 s. At 5.0 m aisle width, the parking success rate improved to 94%, with fewer extra maneuvers needed. SUVs and sedans parked comfortably, though pickups required occasional adjustments. At 5.5 m aisle width, the success rate reached 98%, with near-optimal ease of parking, and the time to park remained consistent at ~25 s, with minimal extra adjustments. At 6.0 m aisle width, maneuverability was excellent, but total parking capacity was significantly reduced, and no meaningful improvement in parking success was observed compared to 5.5 m. The software-based modeling confirmed that 5.0–5.5 m provides the best trade-off between ease of maneuvering and space efficiency.

The findings from the software simulations were incorporated into the optimization model by refining the maneuverability function $E\left(x\right)$. Empirical data were used to adjust $E\left(x\right)$, penalizing aisle widths below 5.0 m due to increased failed parking attempts. The simulation results also informed the multi-objective optimization framework, ensuring that the chosen width balances maximum parking spaces with high success rates for vehicle entry and exit. The geometric model’s predictions were validated through the software models, reinforcing the validity of theoretical constraints.

3.2.4. Evaluation Metrics and Key Findings

To measure maneuverability performance across different aisle widths, the different evaluation metrics were used (

Table 6. Evaluation metrics for assessing parking maneuverability across different aisle widths.

Metric	Description	Ideal Value
Success rate (%)	Percentage of vehicles that successfully park without additional maneuvers.	>90%
Time to park (seconds)	Total time required for a vehicle to complete parking.	<30 s
Number of reversing attempts	Number of extra maneuvers needed to fit into the parking stall.	≤1
Collision risk (%)	Probability of hitting adjacent vehicles or obstacles.	<5%

).

3.2.5. Aisle Width Impact on Maneuverability

At 4.5 m aisle width:

• Compact cars parked successfully 85% of the time, but SUVs and pickups required additional maneuvers.
• Collision risk increased significantly due to limited clearance.
• Time to park exceeded 40 s in some cases.

At 5.0 m aisle width:

• Parking success rate improved to 94%, with fewer extra maneuvers needed.
• SUVs and sedans parked comfortably, though pickups required occasional adjustments.

At 5.5 m aisle width:

• Success rate reached 98%, with near-optimal ease of parking.
• Time to park was consistent at ~25 s, with minimal extra adjustments.

At an aisle width of 6.0 m, maneuverability was optimal; however, the overall parking capacity was notably reduced. The improvement in parking success compared to the 5.5-m width was marginal and did not justify the additional space consumption.

The software-based modeling confirmed that 5.0–5.5 m provides the best trade-off between ease of maneuvering and space efficiency.

3.2.6. The Role of Software-Based Modeling in the Study

By using advanced parking simulation tools, this study systematically tested realistic vehicle behavior in different aisle width scenarios. The software-based approach allowed:

• Validation of geometric predictions using dynamic simulations.
• Precise measurement of maneuverability constraints using real-time parking maneuvers.
• Optimization of aisle width based on empirical success rates.
• Identification of an optimal width range (5.0–5.5 m) that ensures both usability and efficiency.

The insights gained from software-based modeling were essential in refining the optimization framework, ensuring that the recommended aisle widths are not only mathematically sound but also proven to be functional in real parking environments.

3.3. Physical Testing

The primary goal of physical testing was to empirically confirm the minimum required aisle width for various vehicle types by observing real driver behavior, parking success rates, and the number of corrective maneuvers required. By conducting tests under controlled but practical conditions, the study ensured that the optimization model reflects actual driving challenges and constraints rather than relying solely on theoretical assumptions or simulated behavior.

The physical testing phase aimed to empirically validate theoretical predictions regarding aisle width requirements, assess real-world driver behavior, including variations in maneuvering skills and parking strategies, identify the impact of structural constraints such as columns, ramps, and lighting obstructions, and refine the maneuverability function $E\left(x\right)$ by integrating actual success rates and failure scenarios. Unlike software-based modeling, which assumes idealized vehicle movements, physical testing accounts for real-world uncertainties, such as driver hesitation, overcorrection, and inconsistent approach angles.

3.3.1. Testing Environment

The physical tests were conducted in operational underground parking facilities, selected to ensure representative site conditions for realistic evaluation. Testing locations included standard underground parking garages with 90-degree perpendicular parking stalls and constrained environments with fixed column placements and limited maneuvering space. A diverse set of vehicles with varying dimensions and turning radii was used to ensure broad applicability of results. The test fleet included compact cars (Toyota Corolla, VW Golf), sedans (Toyota Camry, Honda Accord), SUVs (Haval Dargo, Toyota RAV4), and pickup trucks (Toyota Hilux, Ford Ranger). The inclusion of various vehicle types allowed for a more comprehensive analysis of aisle width requirements across different categories.

To ensure consistency across all tests, environmental conditions were kept constant during physical trials:

• Controlled lighting to simulate real underground parking environments.
• All external vehicular movement was restricted during testing to ensure consistency and eliminate interference, with only authorized test drivers present in the facility.
• Standardized approach angles marked for each test vehicle to maintain consistent entry positions.

3.3.2. Measured Performance Metrics

Key performance indicators (KPIs) were recorded for each vehicle at each aisle width (

Table 7. Key performance indicators of physical testing.

Metric	Description	Measurement Method
Success rate (%)	Percentage of vehicles successfully parked without adjustments.	Direct observation, pass/fail recording.
Time to park (s)	Time taken to complete a parking maneuver.	Timer from start of entry to full stop.
Reversing attempts	Additional maneuvers required to align properly.	Number of times the driver had to reverse or adjust.
Collision risk (%)	Probability of hitting adjacent vehicles/obstacles.	Driver reports, observed near-miss incidents.

).

Each parking test was recorded using video tracking (Figure 14) and direct observation, with data analysts logging key metrics such as:

• Time to complete parking.
• Number of reversing attempts.
• Successful parking without errors.
• Observed driver stress levels (qualitative assessment).

Participant feedback was collected regarding perceived maneuvering difficulty under each scenario. Data were logged in structured sheets, capturing each KPI across all four aisle widths for each vehicle type. Each vehicle type was tested in multiple parking attempts, with different drivers to account for skill variability.

3.3.3. Driver Skill and Experience Levels

To ensure reliable and representative results, the simulation and physical testing incorporated variability in driver skill levels, vehicle types, and the number of experimental parking’s performed. These factors were carefully selected to mirror real-world parking conditions and provide robust data for maneuverability analysis.

Since underground parking is used by a diverse range of drivers, it was crucial to simulate and test varying levels of skill and experience. The experiment included participants from different driving backgrounds (

Table 8. Driving experience of test participants.

Driver Category	Experience Level	Characteristics	Percentage of Participants
Novice drivers	<2 years of experience	Less confident, slower parking speeds, more corrections	30%
Regular drivers	2–10 years of experience	Moderate confidence, average parking times, occasional corrections	50%
Experienced drivers	>10 years of experience	Confident, efficient parking, minimal adjustments	20%

).

Including novice drivers ensured that the study accounted for realistic parking delays, errors, and hesitation.

Regular drivers formed the majority, as they represent the largest proportion of parking users.

Experienced drivers helped establish the best-case performance benchmark under ideal maneuvering conditions.

To maintain consistency, each driver received clear instructions before testing but was left to park as they normally would, minimizing external influence on their approach.

3.3.4. Number of Experimental Parking’s Performed

To ensure statistical reliability, each vehicle type was tested across all four aisle widths (4.5 m, 5.0 m, 5.5 m, and 6.0 m), with multiple drivers performing repeated parkings (

Table 9. Summary of experimental parking tests.

Vehicle Type	Number of Parkings per Aisle Width	Total Experimental Parkings per Vehicle
Compact cars	30	120
Sedans	30	120
SUVs	30	120
Pickups	30	120

).

Total experimental parkings conducted—480 (4 vehicle types × 4 aisle widths × 30 parking’s per width).

A total of 30 repetitions per condition ensured statistical significance and helped eliminate outliers due to unexpected driver behavior.

All tests were randomized to prevent systematic biases from affecting results.

Different drivers performed the tests, providing variability in skill level, confidence, and reaction time.

3.3.5. Results and Interpretation

The key findings from physical testing revealed that at 4.5 m aisle width, compact cars parked successfully ~85% of the time, but sedans and SUVs required multiple corrections. Pickup trucks consistently required reversing maneuvers to complete parking, indicating spatial inadequacy at narrower aisle widths. The time to park exceeded 40 s due to additional steering adjustments. At 5.0 m aisle width, the parking success rate improved to ~94%, with SUVs and sedans maneuvering smoothly, though pickups still required occasional extra maneuvers. The collision risk dropped significantly compared to 4.5 m. At 5.5 m aisle width, the parking success rate reached ~98%, with minimal need for adjustments, while the time to park stabilized around 25 s for all vehicle types. At 6.0 m aisle width, maneuverability was optimal, but total parking capacity was significantly reduced, with no meaningful improvement in success rates compared to 5.5 m. The physical tests confirmed that 5.0–5.5 m provides the best trade-off between ease of maneuvering and space efficiency.

The empirical findings directly impacted the optimization framework by refining the maneuverability function $E\left(x\right)$. Empirical success rates and failure points were incorporated into the penalty structure for aisle widths below 5.0 m, ensuring that parking failure rate thresholds were used to reject suboptimal aisle widths. The model established a hard lower bound of 5.0 m for practical usability, while aisle widths between 5.0 m and 5.5 m were confirmed as the optimal range based on physical results. The software simulations were validated against real driver behavior, reinforcing the model’s reliability and ensuring that it accounted for human factors such as driver hesitation and overcorrection, making the recommendations practical rather than idealized.

By incorporating real-world parking trials, this study ensured that theoretical and simulated results aligned with actual driver experiences. The physical testing phase confirmed key insights, including 5.0–5.5 m as the optimal aisle width range, ensuring both capacity and usability; parking success rates declining sharply below 5.0 m, reinforcing geometric predictions; empirical validation of maneuverability constraints, ensuring realistic design recommendations; and the elimination of overly narrow aisle widths (4.5 m) from optimization models based on failure rates. The integration of physical testing results into the final optimization model ensures that recommended aisle widths are not only theoretically optimal but also practically proven in real-world conditions. This evidence-based approach enhances the study’s credibility, offering a data-driven methodology for designing underground parking layouts that optimize efficiency, safety, and user satisfaction.

3.4. Calculating Collision Risk vs. Aisle Width

The collision risk in underground parking facilities is directly influenced by aisle width, as it determines the space available for vehicle maneuvering, parking precision, and interaction with adjacent vehicles or obstacles. To quantify this relationship, a systematic methodology was employed, integrating geometric modeling, software-based simulations, and empirical validation. The calculation process consists of four key steps:

Step 1.

Defining collision risk factors

Collision risk is influenced by several maneuverability constraints, including:

• Turning radius and clearance space—Wider aisles provide more room for turning, reducing the likelihood of side or corner collisions.
• Reversing frequency—Narrower aisles require more multi-step adjustments, increasing the chance of driver error.
• Vehicle interaction zones—Locations where multiple vehicles maneuver simultaneously pose a higher collision probability.
• Obstacle proximity—Structural elements such as columns, walls, and support beams can further restrict movement in narrow aisles.

Step 2.

Simulation-based risk assessment

Using simulation tools, the study models vehicle trajectories under different aisle width conditions. Each scenario includes:

• Randomized vehicle entries into parking spaces to simulate real-world behavior.
• Calculation of failed parking attempts, where vehicles either contact obstacles or require excessive corrections.
• Dynamic driver behavior modeling, incorporating variations in reaction time, parking angle, and error frequency.

For each aisle width, the number of simulated parking events leading to near-miss or actual collisions is recorded and translated into a collision probability.

Step 3.

Empirical validation through physical testing

To ensure that the simulation results reflect real-world conditions, controlled parking tests were conducted in operational underground parking lots. Vehicles of different sizes attempted parking at varying aisle widths, and the following data were collected:

• Observed collision or near-miss incidents (e.g., bumper-to-bumper contact, curb strikes).
• Driver difficulty assessments, rating ease of parking and maneuvering space.
• Required corrective maneuvers, as an indirect indicator of collision risk.

The empirical data were compared against the simulation results, ensuring consistency between modeled predictions and real-world performance.

Step 4.

Statistical calculation and model adjustment

The final collision risk values were computed by applying a weighted probability model

$$CR\left(x\right)={\displaystyle \frac{C_f+C_n}{T}}\times 100$$

(10)

where $CR\left(x\right)$ is collision risk (%) for a given aisle width $x$, $C_f$ is number of actual collisions recorded in simulations and physical tests, $C_n$ is number of near-miss incidents requiring abrupt corrections, and $T$ is total number of parking attempts across all tests.

By comparing results across 4.5 m, 5.0 m, 5.5 m, and 6.0 m, a collision risk curve was generated, illustrating the inverse relationship between aisle width and collision probability.

The Figure 15 illustrates the relationship between aisle width in underground parking facilities and the probability of vehicle collisions during parking maneuvers. This analysis helps identify the optimal aisle width that minimizes collision risk while maintaining space efficiency.

At 4.5 m aisle width, the collision risk is at its highest (~15%), indicating that tight maneuvering space increases the likelihood of vehicles hitting adjacent parked cars, structural elements, or requiring multiple corrections.

As aisle width increases to 5.0 m, collision risk significantly drops (~7%), demonstrating that slightly wider passages provide better clearance for turning and reversing.

At 5.5 m aisle width, the collision risk further decreases to approximately 3%, suggesting that drivers can complete parking maneuvers more smoothly with fewer adjustments.

Beyond 5.5 m (toward 6.0 m), the collision risk approaches near-zero, implying that at wider aisles, vehicles have ample space to park with minimal risk of accidental contact.

Implications for parking design:

Narrower aisles (≤4.5 m) pose a significant safety concern, particularly for larger vehicles such as SUVs and pickup trucks.

An optimal range of 5.0–5.5 m provides a balance between maneuverability and space efficiency, reducing collision probability while preserving parking capacity.

Aisle widths above 5.5 m show diminishing returns, as the additional space only marginally improves safety while reducing the number of available parking spots.

This illustration underscores the importance of carefully selecting aisle widths in underground parking layouts to enhance driver safety, minimize vehicle damage, and optimize space utilization.

4. Discussion

4.1. Interpretation of Key Findings

The findings of this study provide a comprehensive analysis of how aisle width influences maneuverability, parking success rates, and overall parking facility efficiency in underground parking structures. By integrating geometric modeling, software-based simulations, and empirical physical testing, the study identifies an optimal aisle width range that balances maneuverability and parking capacity.

The geometric modeling results established the theoretical minimum aisle width required for different vehicle types based on their turning radii, swept path analysis, and clearance requirements. The analysis revealed that aisle widths below 5.0 m significantly constrained vehicle movement, particularly for larger vehicles such as SUVs and pickup trucks, leading to a high probability of multi-step parking maneuvers and increased collision risk. The modeling also indicated that increasing aisle width beyond 5.5 m provided diminishing returns in maneuverability improvement while reducing total parking capacity.

The software-based simulations reinforced these geometric predictions by dynamically modeling vehicle trajectories in controlled parking scenarios. The simulations quantified key performance indicators such as parking success rate, time required to park, number of reversing attempts, and collision risk under varying aisle width conditions.

The results demonstrated that:

• At 4.5 m, parking success rates were notably lower, especially for larger vehicles, with high collision probability due to limited maneuvering space.
• At 5.0 m, maneuverability improved significantly, with most sedans and SUVs parking efficiently, though pickup trucks occasionally required corrective maneuvers.
• At 5.5 m, nearly all vehicle types could park smoothly without excessive adjustments, optimizing both success rate and time to park.
• At 6.0 m, while maneuverability was at its peak, the reduction in total parking capacity made it less practical for high-density urban environments.

The physical testing phase in operational underground parking facilities further validated these findings by providing real-world evidence of how different aisle widths affect driver behavior and maneuvering success. The tests confirmed that an aisle width of 5.0–5.5 m represents the most effective compromise between ease of parking and maximizing available space. Parking attempts at aisle widths below 5.0 m were characterized by a higher frequency of reversing maneuvers, prolonged parking durations, and a notable increase in near-collision events. The empirical findings also highlighted the influence of driver experience levels, with novice drivers struggling more at narrower aisle widths compared to experienced drivers.

One of the most critical insights from this study is the strong correlation between aisle width and collision risk. The analysis showed that at widths below 5.0 m, the probability of accidental vehicle contacts or curb strikes increased sharply. At 5.0–5.5 m, collision risk dropped significantly, suggesting that this range provides a safe and practical balance for urban underground parking designs.

The study’s findings confirm that, while increasing aisle width enhances maneuverability, it must be carefully optimized to avoid unnecessary reductions in parking density. The optimal range of 5.0–5.5 m ensures that underground parking facilities maximize usability while maintaining efficient space allocation, making it a practical recommendation for urban planners, civil engineers, and facility designers.

4.2. Comparison with Existing Standards and Guidelines

Existing parking regulations provide minimum aisle width recommendations, but they often fail to specify optimal widths that balance maneuverability and space efficiency. This study’s findings highlight key differences and suggest potential updates to align with modern vehicle trends.

Aisle width regulations vary across countries (Table 1). Kazakhstan and the U.S. require 5.5–6.0 m, ensuring ample maneuverability but reducing capacity. European standards (5.0–5.5 m) align closely with this study’s findings. Some municipal codes allow widths as low as 4.5 m, which our results show is insufficient for larger vehicles. This study confirms that a 5.0–5.5-m range offers the best compromise between efficiency and usability, suggesting that some existing regulations are overly rigid or outdated.

Numerous existing regulations appear overly rigid or outdated, as they do not adequately account for the widespread increase in SUV and pickup truck usage in contemporary vehicle fleets. Many regulations were developed before SUVs and pickups became widespread. This study shows:

• SUVs and pickups require at least 5.0 m for smooth parking.
• Standards allowing less than 5.0 m may not accommodate modern vehicle sizes.
• Regulations should be updated to reflect changing vehicle compositions.

Current guidelines often lack adaptability for different parking scenarios. Recommended updates include:

• Allowing mixed-width parking zones (e.g., 4.5–5.0 m for compact cars, 5.5 m for large vehicles).
• Encouraging dynamic parking layouts using smart parking technology.
• Revising national codes to define both minimum and optimal aisle widths.

Adopting more flexible, data-driven regulations will improve efficiency, safety, and user experience in underground parking facilities.

The original capacity function formulation in Formula (2) assumes a uniform average stall width, which is appropriate for simplified layouts or for compliance with design codes. However, mixed-width parking layouts can enhance both space utilization and operational efficiency. To extend the model accordingly, the capacity function in Formula (2) can be modified to incorporate weighted stall widths based on the composition of the vehicle fleet. The adjusted formula becomes

$$N\left(x\right)=\sum _{i=1}^k⌊{\displaystyle \frac{W}{w_i+b_i}}⌋·R_i$$

(11)

where $w_i$ is the stall width for vehicle category $i$, ${ b}_i$ is the buffer space required for maneuverability or structural offsets, $R_i$ is the proportion of vehicle type $i$ in the fleet, and $k$ is the number of designated zones. This zoned formulation allows layout optimization tailored to observed or projected vehicle distributions, which may vary by geographic region or building function. Such a model can be integrated into the planning process by using local vehicle registration data, as was done in the Kazakhstan case study, to determine fleet proportions and dynamically assign stall sizes across the layout.

4.3. Limitations and Sources of Uncertainty

While this study provides valuable insights into optimizing aisle widths for underground parking, several limitations and sources of uncertainty must be acknowledged. One primary constraint is the limited scope of physical testing, which was conducted in selected underground parking facilities. This may not fully capture variations in structural layouts, environmental conditions, and regional parking designs.

Simulations were conducted under idealized vehicle movements, meaning factors such as driver hesitation, distractions, or unexpected obstacles were not fully modeled. While the software tools used provide realistic approximations, they cannot fully replicate human factors and environmental effects.

External influences further contribute to uncertainty in aisle width performance. Structural elements such as columns, ramps, and irregular layouts can limit maneuverability in ways that standardized tests do not always capture.

Despite these limitations, the study provides a robust empirical foundation for optimizing aisle width in underground parking. While certain contextual variations may exist, the core findings remain applicable to urban planners, facility designers, and transportation engineers. By refining these insights through further research and integrating emerging vehicle technologies, future studies can enhance underground parking designs to maximize both maneuverability and space efficiency.

4.4. Future Research Directions

Future studies should focus on incorporating emerging vehicle technologies, diverse urban environments, and advanced modeling techniques to improve underground parking design.

One key area for future research is the impact of automated vehicles on aisle width requirements. The increasing adoption of self-parking systems and autonomous vehicles may reduce the need for wider aisles, as these technologies enable precise maneuvering with minimal human error.

Real-world driver behavior analysis through AI-powered monitoring systems could further refine the study’s findings. By using computer vision and real-time data collection, researchers could track actual parking patterns, corrective maneuvers, and collision risks over extended periods. This would help validate simulation-based predictions and ensure that recommended aisle widths account for the full range of human driving behaviors, including hesitation, misalignment, and varying skill levels.

Another promising research direction is the development of adaptive parking layouts that adjust aisle width dynamically based on real-time occupancy and vehicle type distribution. Smart parking systems, incorporating sensor-based monitoring and automated guidance, could optimize aisle space depending on whether a facility is predominantly occupied by compact cars, SUVs, or a mix of both.

By addressing these research areas, future studies can build on this work to create smarter, safer, and more efficient underground parking facilities that accommodate technological advancements, evolving vehicle types, and the needs of modern urban mobility.

5. Conclusions

This study provides a comprehensive analysis of aisle width optimization in underground parking facilities, integrating geometric modeling, software-based simulations, and empirical physical testing to determine the optimal balance between maneuverability, safety, and parking capacity. The findings highlight that aisle widths below 5.0 m significantly hinder vehicle maneuverability, increasing parking time, reversing attempts, and collision risk, particularly for larger vehicles such as SUVs and pickup trucks. Conversely, aisle widths above 5.5 m provide only marginal maneuverability improvements while reducing overall parking density, making them less efficient for high-capacity facilities. The optimal aisle width range of 5.0–5.5 m was identified as the best compromise between usability and space efficiency.

Comparing the study’s results with existing parking standards, it was found that many regulations specify minimum aisle widths but do not always define an optimal range. Some municipal codes permit aisle widths as low as 4.5 m, which this research demonstrates is insufficient for modern vehicle sizes. European guidelines (5.0–5.5 m) align closely with the study’s recommendations, whereas American and Kazakhstani standards (5.5–6.0 m) tend to be more conservative. These findings suggest that regulatory updates are needed to better reflect current vehicle trends and real-world maneuverability constraints.

Several limitations of the study were acknowledged, including the geographic scope of physical testing, driver variability, and assumptions in simulation modeling. Future research should expand real-world testing across diverse parking environments, incorporate AI-driven monitoring of actual parking behaviors, and explore adaptive parking layouts that dynamically adjust aisle widths based on vehicle type and occupancy levels. Additionally, the rise of autonomous and electric vehicles may introduce new space requirements, necessitating further investigations into how underground parking design should evolve in response to emerging technologies.

The findings are relevant for urban planners, civil engineers, and facility designers, offering practical guidance to improve parking efficiency and user experience.