A Study on the Direct Application of the Gaussian Kernel Smoothing Filter for Bridge Health Monitoring
Abstract
1. Introduction
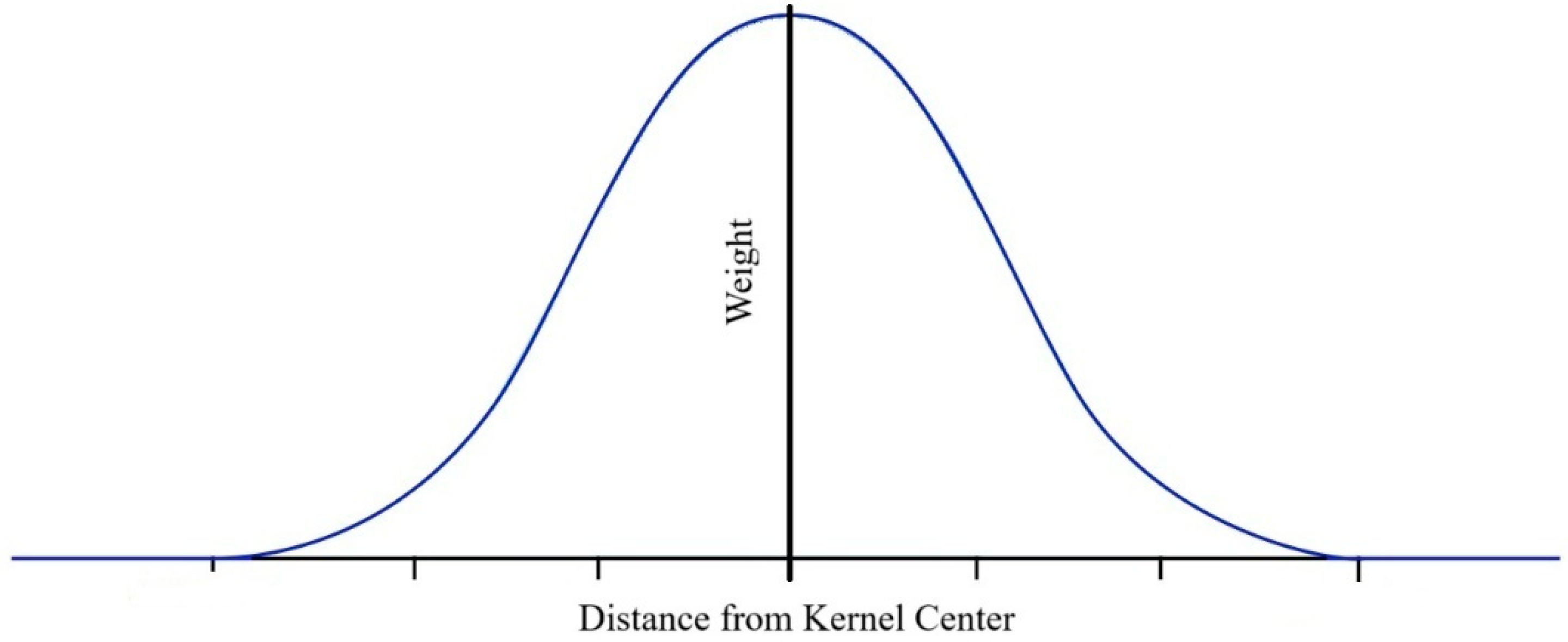
2. GKSF Background
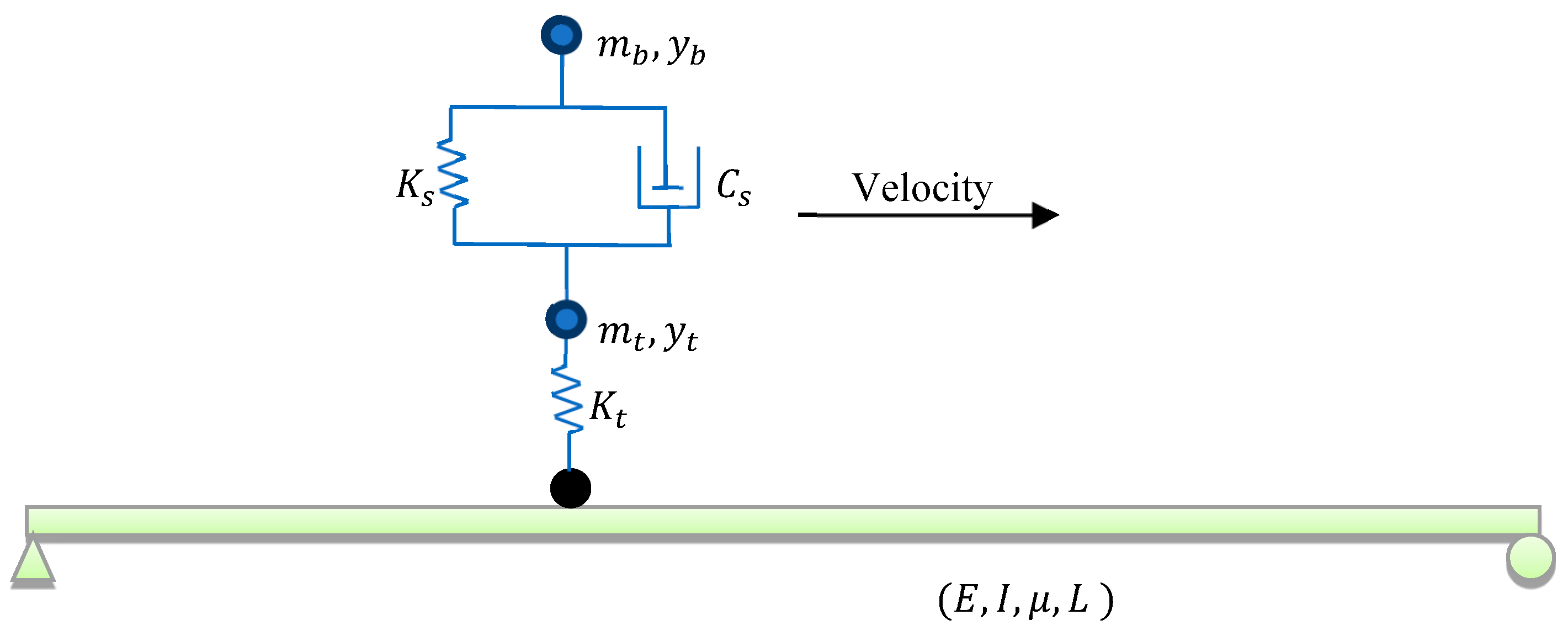
3. Numerical Model of Bridge with Simple Supports and Sprung Mass
4. Results and Discussion
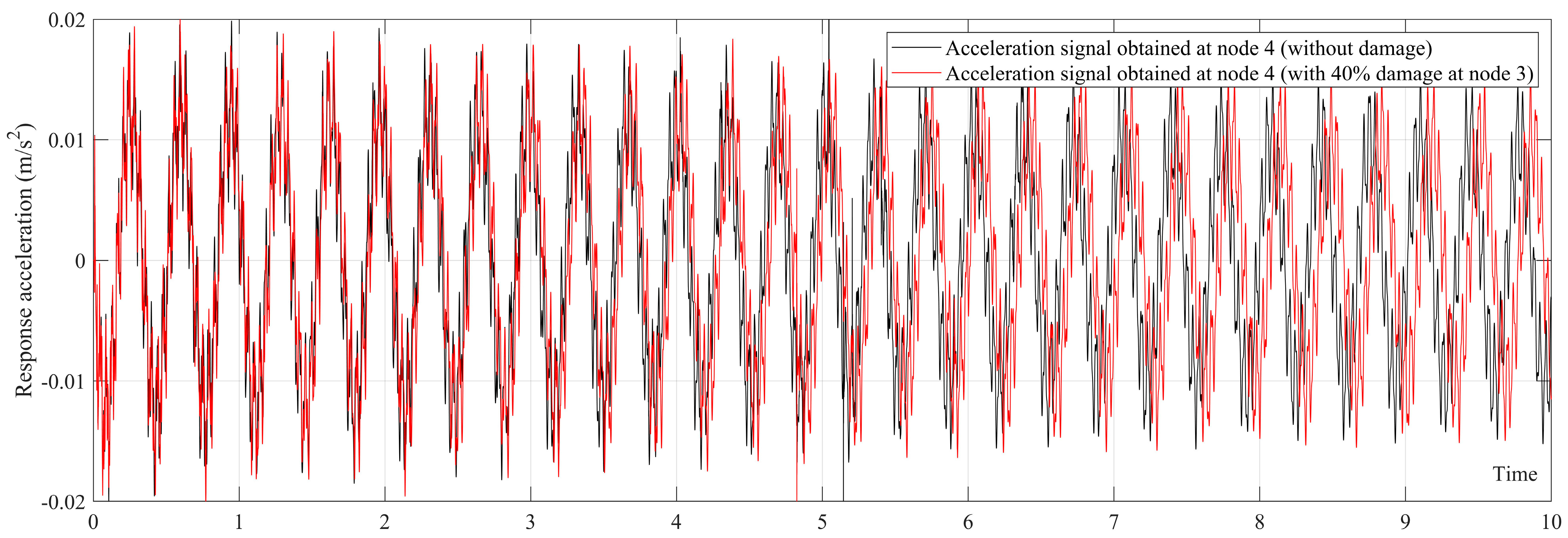
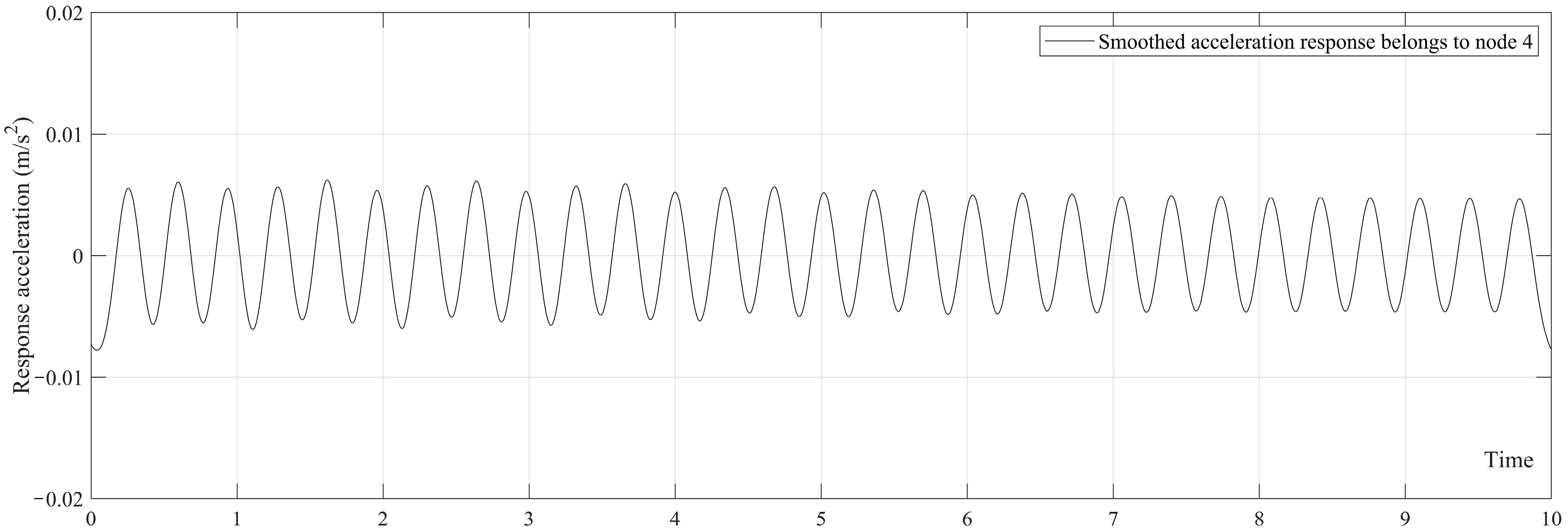
4.1. Applying GKSF to Acceleration Data
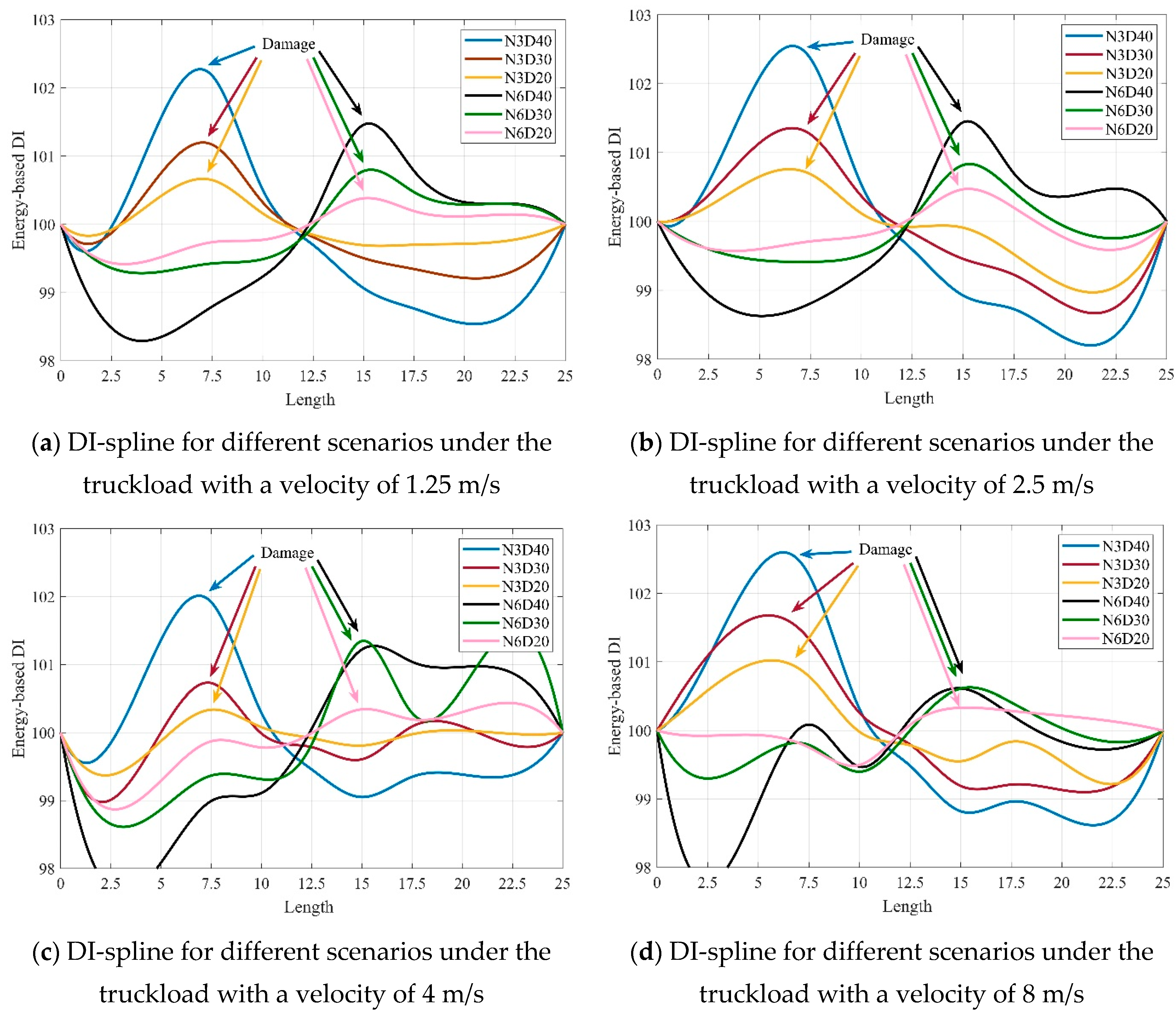
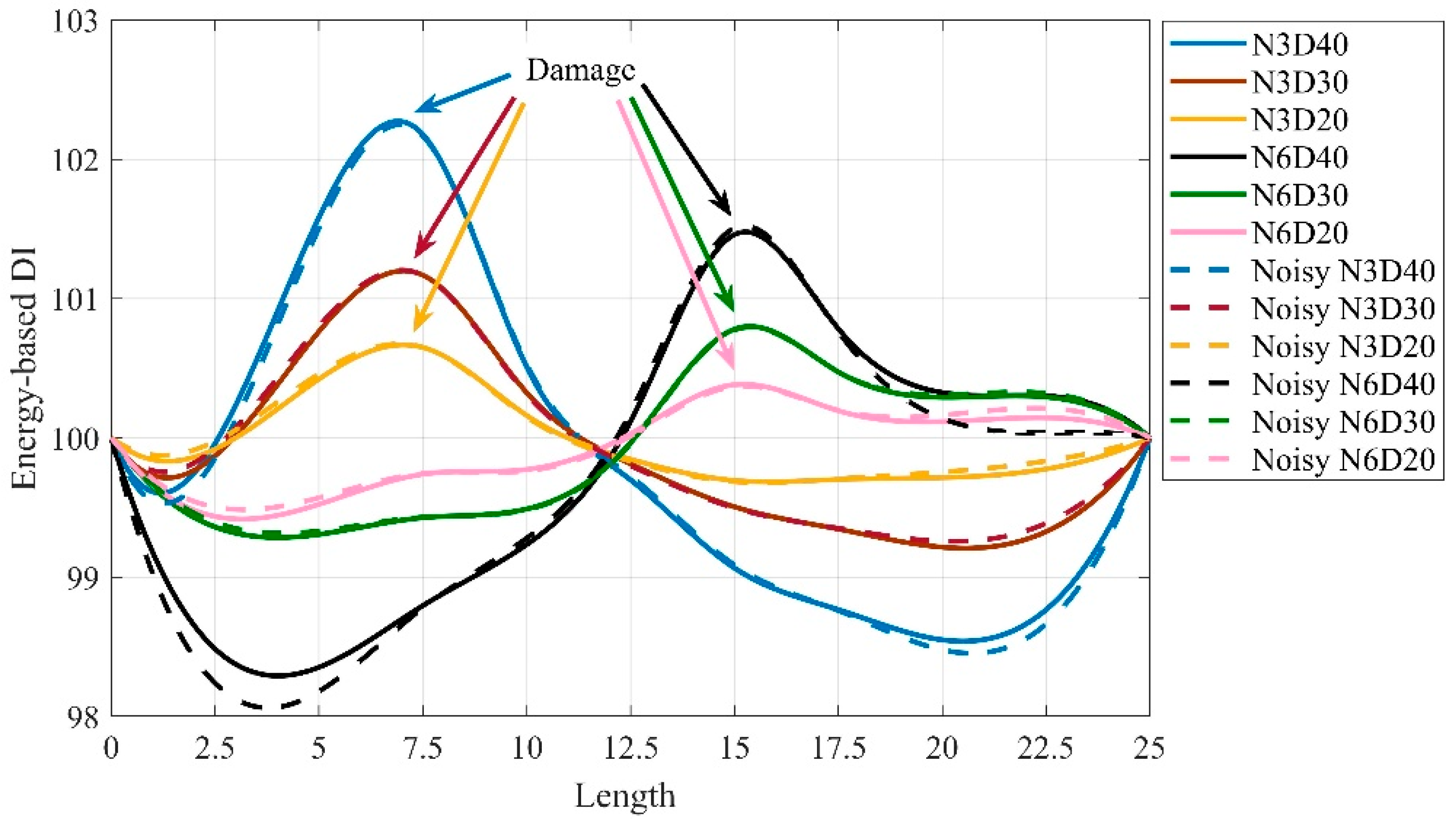
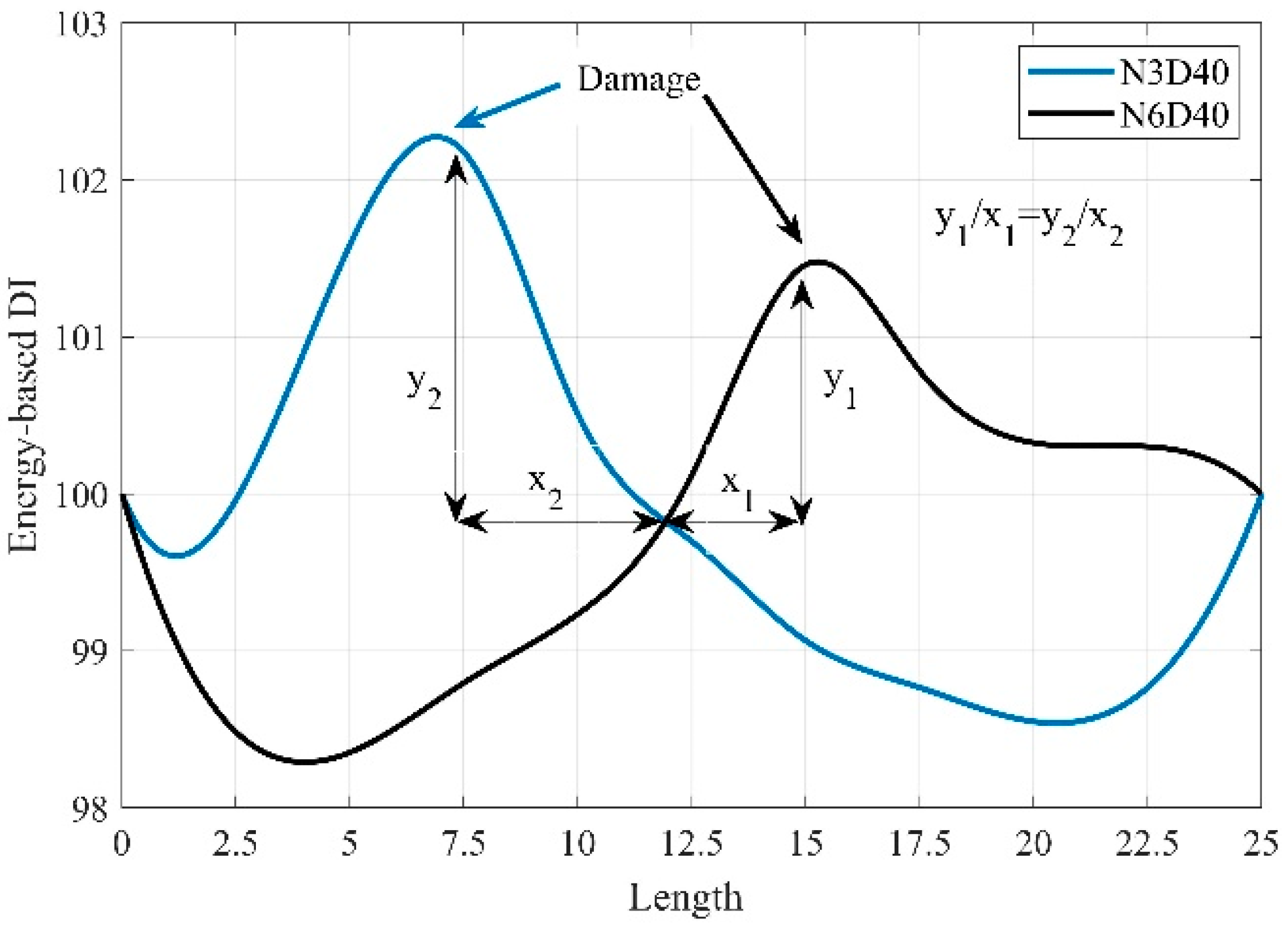
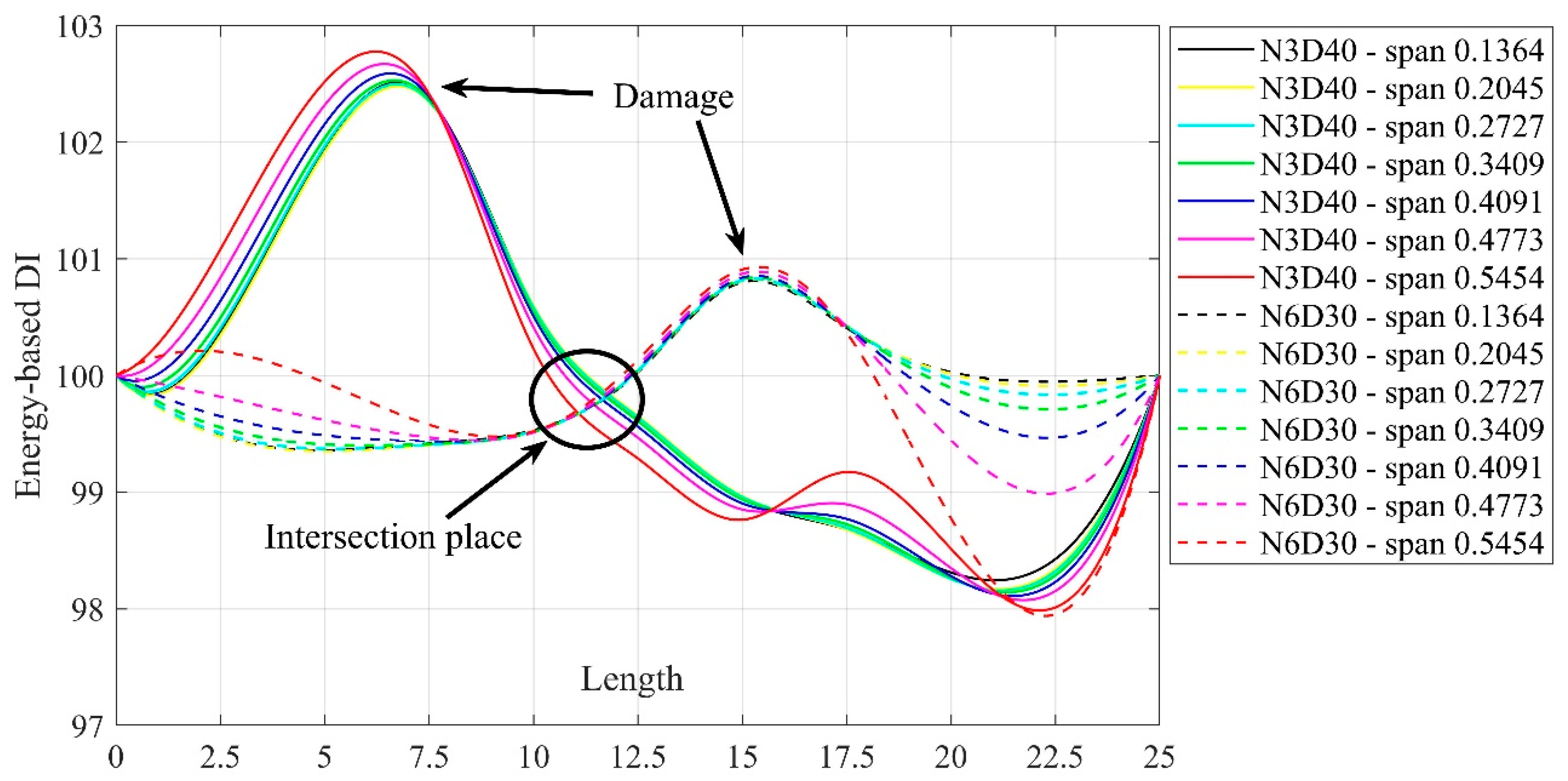
4.2. Locating Structural Damage
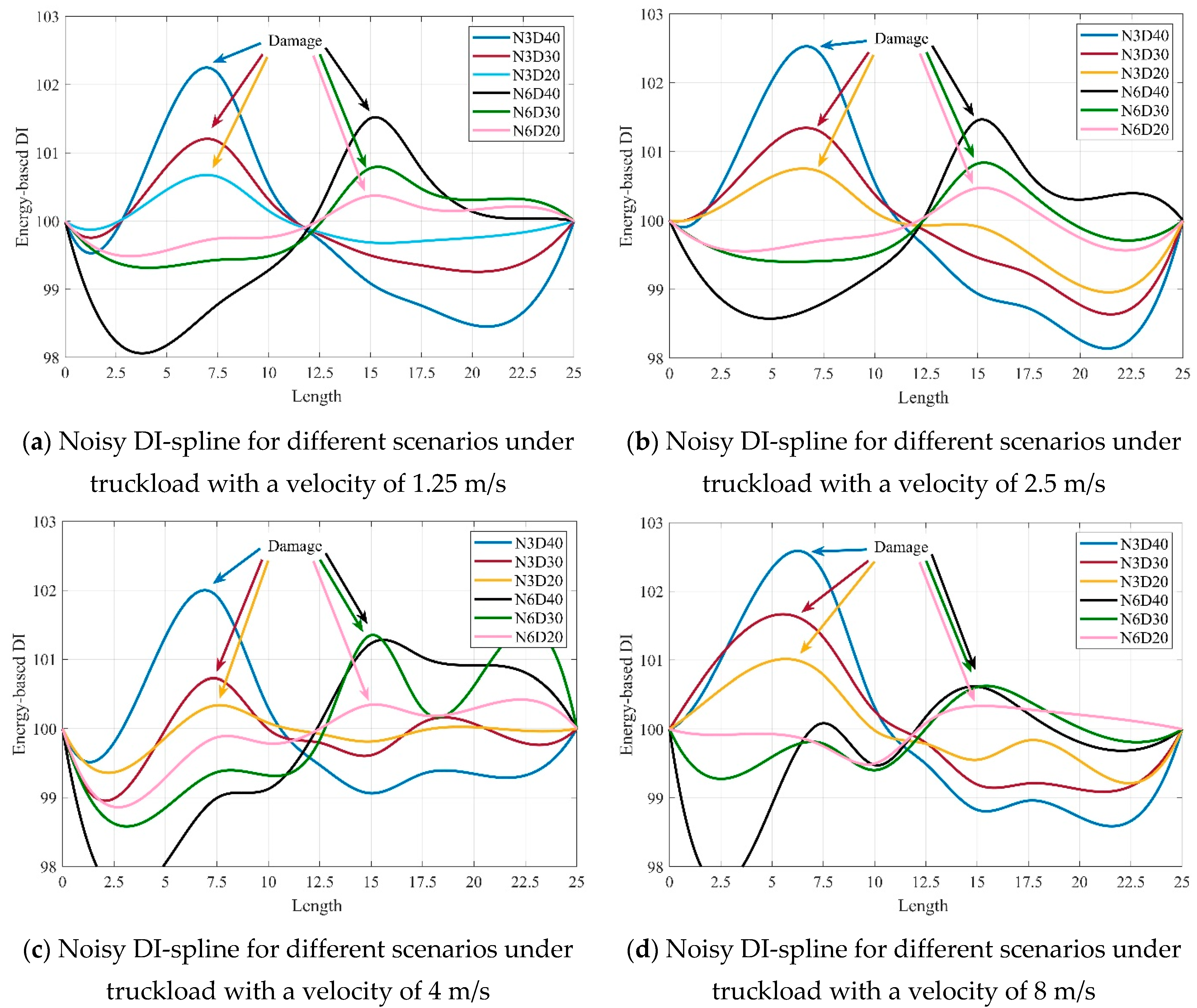
4.3. Effect of Noise
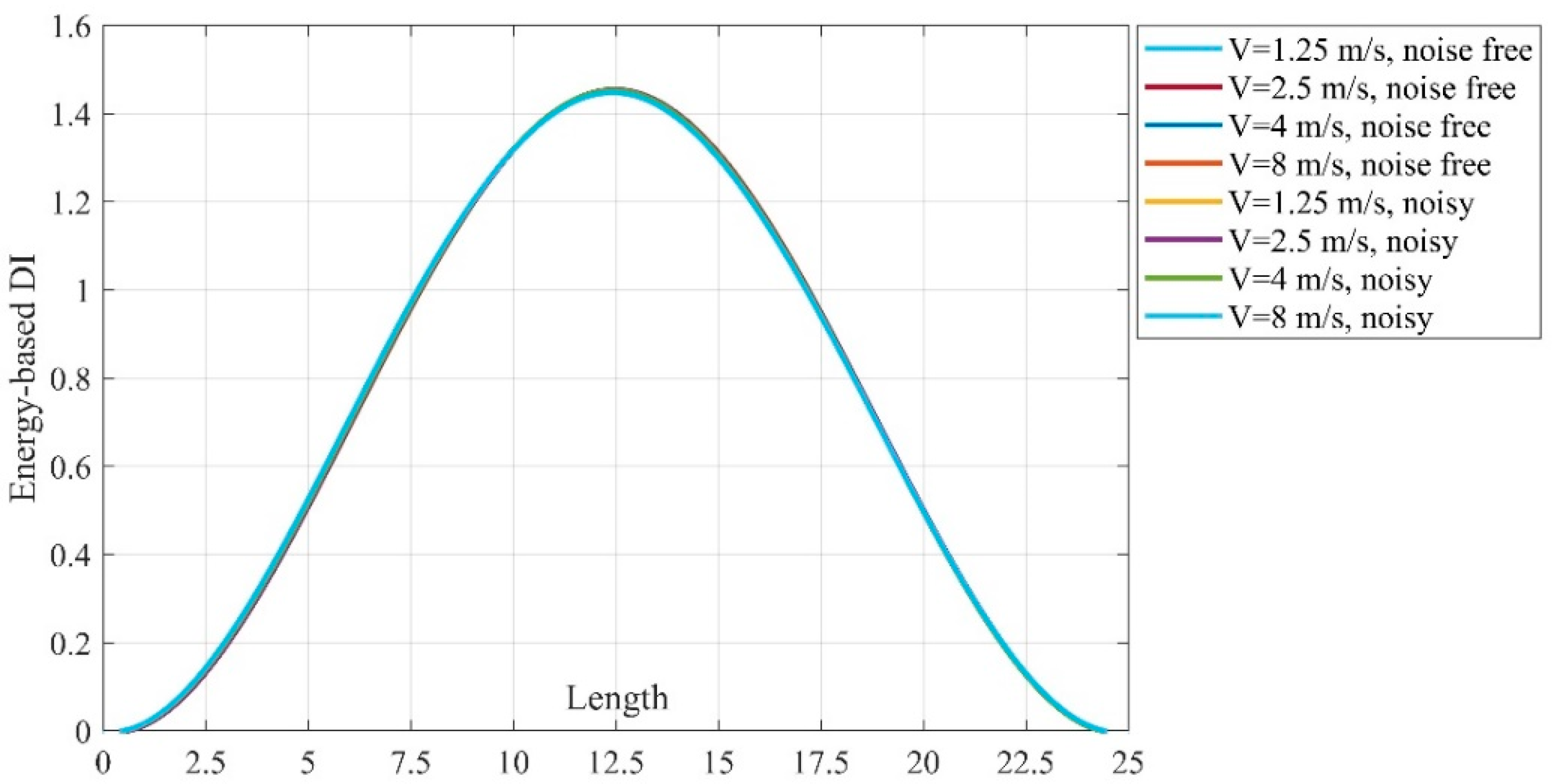
4.4. Baseline Estimation
4.5. Structural Damage Quantification
4.6. Natural Frequency Changes Due to Bridge Structural Damage
4.7. Further Study on the Span of GKSF
5. Conclusions
- The GKSF is widely recognized as a de-noising filter, and the resulting GKSF-based method exhibits strong noise insensitivity.
- The GKSF-based method is capable of determining both the location and severity of damage in both noisy and noise-free environments.
- Fitting a Gaussian curve to the normalization factor enables the GKSF-based method to operate as a reference-free approach.
- Effect of speed on accuracy: Increasing the vehicle speed reduces the accuracy of the proposed method.
- Limitation in detecting damage near the midspan: If damage occurs around the midspan of the bridge, accurately determining its severity is not possible.
- The provided formula is designed only for single-damage scenarios.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, W.Y.; Ren, W.X.; Zhu, S. Damage detection of beam structures using quasi-static moving load induced displacement response. Eng. Struct. 2017, 145, 70–82. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Zhu, X.; Kang, W.H.; Mao, X.; Uy, B. Design and experimental investigations of a vibration based wireless measurement system for bridge cable tension monitoring. Adv. Struct. Eng. 2014, 17, 1657–1668. [Google Scholar] [CrossRef]
- Pakrashi, V.; O’Connor, A.; Basu, B. A bridge-vehicle interaction based experimental investigation of damage evolution. Struct. Health Monit. 2010, 9, 285–296. [Google Scholar] [CrossRef]
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W. Output-only damage detection of steel beam using moving average filter. Shock Vib. 2018, 2018, 2067680. [Google Scholar] [CrossRef]
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W.; Jia, Y.K. Application of the random decrement technique in damage detection under moving load. Appl. Sci. 2018, 8, 753. [Google Scholar] [CrossRef]
- Hester, D.; Gonzalez, A. A wavelet-based damage detection algorithm based on bridge acceleration response to a vehicle. Mech. Syst. Signal Process. 2012, 28, 145–166. [Google Scholar] [CrossRef]
- Balafas, K.; Kiremidjian, A.S. Development and validation of a novel earthquake damage estimation scheme based on the continuous wavelet transform of input and output acceleration measurements. Earthq. Eng. Struct. Dyn. 2015, 44, 501–522. [Google Scholar] [CrossRef]
- Cantero, D.; Basu, B. Railway infrastructure damage detection using wavelet transformed acceleration response of traversing vehicle. Struct. Control Health Monit. 2015, 22, 62–70. [Google Scholar] [CrossRef]
- Hester, D.; González, A. Impact of road profile when detecting a localised damage from bridge acceleration response to a moving vehicle. In Damage Assessment of Structures X; Trans Tech Publications Ltd.: Zurich, Switzerland, 2013; Volume 569, pp. 199–206. [Google Scholar] [CrossRef]
- Zhu, X.; Law, S.S. Structural health monitoring based on vehicle-bridge interaction: Accomplishments and challenges. Adv. Struct. Eng. 2015, 18, 1999–2015. [Google Scholar] [CrossRef]
- Asayesh, M.; Khodabandeloo, B.; Siami, A. A random decrement technique for operational modal analysis in the presence of periodic excitations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1525–1534. [Google Scholar] [CrossRef]
- Rodrigues, J.; Brincker, R. Application of the random decrement technique in operational modal analysis. In Proceedings of the 1st International Operational Modal Analysis Conference, Copenhagen, Denmark, 26–27 April 2005; pp. 191–200. [Google Scholar]
- Lee, J.W.; Kim, J.D.; Yun, C.B.; Yi, J.H.; Shim, J.M. Health-monitoring method for bridges under ordinary traffic loadings. J. Sound Vib. 2002, 257, 247–264. [Google Scholar] [CrossRef][Green Version]
- He, X.H.; Hua, X.G.; Chen, Z.Q.; Huang, F.L. EMD-based random decrement technique for modal parameter identification of an existing railway bridge. Eng. Struct. 2011, 33, 1348–1356. [Google Scholar] [CrossRef]
- Wu, W.H.; Chen, C.C.; Liau, J.A. A multiple random decrement method for modal parameter identification of stay cables based on ambient vibration signals. Adv. Struct. Eng. 2012, 15, 969–982. [Google Scholar] [CrossRef]
- Buff, H.; Friedmann, A.; Koch, M.; Bartel, T.; Kauba, M. Design of a random decrement method based structural health monitoring system. Shock Vib. 2012, 19, 787–794. [Google Scholar] [CrossRef][Green Version]
- Poncelet, F.; Kerschen, G.; Golinval, J.C.; Verhelst, D. Output-only modal analysis using blind source separation techniques. Mech. Syst. Signal Process. 2007, 21, 2335–2358. [Google Scholar] [CrossRef]
- Kerschen, G.; Poncelet, F.; Golinval, J.C. Physical interpretation of independent component analysis in structural dynamics. Mech. Syst. Signal Process. 2007, 21, 1561–1575. [Google Scholar] [CrossRef]
- Zhou, W.; Chelidze, D. Blind source separation based vibration mode identification. Mech. Syst. Signal Process. 2007, 21, 3072–3087. [Google Scholar] [CrossRef]
- Loh, C.H.; Hung, T.; Chen, S.; Hsu, W. Damage detection in bridge structure using vibration data under random travelling vehicle loads. J. Phys. Conf. Ser. 2015, 628, 012044. [Google Scholar] [CrossRef]
- Huang, C.; Nagarajaiah, S. Experimental study on bridge structural health monitoring using blind source separation method: Arch bridge. Struct. Monit. Maint. 2014, 1, 69–87. [Google Scholar] [CrossRef]
- Manie, S.; Karami, K.; Fatehi, P. Online system identification by sparse component analysis based on wavelet transform. Amirkabir J. Civ. Eng. 2020, 52, 2301–2320. [Google Scholar] [CrossRef]
- Karami, K.; Fatehi, P.; Yazdani, A. On-line system identification of structures using wavelet-Hilbert transform and sparse component analysis. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 870–886. [Google Scholar] [CrossRef]
- Zhu, B.; Leung, A.Y.T.; Wong, C.K.; Lu, W.Z. On-line health monitoring and damage detection of structures based on the wavelet transform. Int. J. Struct. Stab. Dyn. 2008, 8, 367–387. [Google Scholar] [CrossRef]
- Talebi, M.; Tabrizian, Z.; Amiri, G.G. Identification of the modal parameters of a concrete bridge deck using traffic loads. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Mojtahedi, A.; Hokmabady, H.; Kouhi, M.; Mohammadyzadeh, S. A novel ANN-RDT approach for damage detection of a composite panel employing contact and non-contact measuring data. Compos. Struct. 2022, 279, 114794. [Google Scholar] [CrossRef]
- Azizi, S.; Karami, K.; Mariani, S. Full-Field Modal Analysis Using Video Measurements and a Blind Source Separation Methodology. Eng. Proc. 2023, 58, 105. [Google Scholar] [CrossRef]
- Yang, Y.; Xie, R.; Li, M.; Cheng, W. A review on the application of blind source separation in vibration analysis of mechanical systems. Measurement 2024, 227, 114241. [Google Scholar] [CrossRef]
- Gonzalez, A.; Hester, D. An investigation into the acceleration response of a damaged beam-type structure to a moving force. J. Sound Vib. 2013, 332, 3201–3217. [Google Scholar] [CrossRef]
- Kordestani, H.; Zhang, C.; Shadabfar, M. Beam damage detection under a moving load using random decrement technique and Savitzky–Golay Filter. Sensors 2020, 20, 243. [Google Scholar] [CrossRef]
- Kordestani, H.; Zhang, C. Direct use of the Savitzky–Golay filter to develop an output-only trend line-based damage detection method. Sensors 2020, 20, 1983. [Google Scholar] [CrossRef]
- Kordestani, H.; Zhang, C.; Masri, S.F.; Shadabfar, M. An empirical time-domain trend line-based bridge signal decomposing algorithm using Savitzky–Golay filter. Struct. Control Health Monit. 2021, 28, e2750. [Google Scholar] [CrossRef]
- O’Brien, E.J.; Malekjafarian, A.; González, A. Application of empirical mode decomposition to drive-by bridge damage detection. Eur. J. Mech. A Solids 2017, 61, 151–163. [Google Scholar] [CrossRef]
- Ouyang, H. Moving-load dynamic problems: A tutorial (with a brief overview). Mech. Syst. Signal Process. 2011, 25, 2039–2060. [Google Scholar] [CrossRef]
- Yang, Y.B.; Cheng, M.C.; Chang, K.C. Frequency variation in vehicle-bridge interaction systems. Int. J. Struct. Stab. Dyn. 2013, 13, 1350019. [Google Scholar] [CrossRef]
- Cantero, D.; O’Brien, E.J. The Non-Stationarity of Apparent Bridge Natural Frequencies During Vehicle Crossing Events. FME Trans. 2013, 41, 279–284. Available online: https://www.mas.bg.ac.rs/_media/istrazivanje/fme/vol41/4/03_dcantero_ver2.pdf (accessed on 1 January 2025).
- Cantero, D.; Ronnquist, A. Numerical evaluation of modal properties change of railway bridges during train passage. Procedia Eng. 2017, 199, 2931–2936. [Google Scholar] [CrossRef]
- Malekjafarian, A.; O’Brien, E.J. Identification of bridge mode shapes using short time frequency domain decomposition of the responses measured in a passing vehicle. Eng. Struct. 2014, 81, 386–397. [Google Scholar] [CrossRef]
- Available online: https://www.researchgate.net/publication/338358257_Bridge_acceleration_responsesxlsx (accessed on 30 January 2025).
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Qiao, P.; Cao, M. Waveform fractal dimension for mode shape-based damage identification of beam type structures. Int. J. Solids Struct. 2008, 45, 5946–5961. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Ding, Y.; Pang, Y.T. Selection of optimal intensity measures in seismic damage analysis of cable-stayed bridges subjected to far-fault ground motions. J. Earthq. Tsunami 2015, 9, 1550003. [Google Scholar] [CrossRef]
- Kordestani, H.; Xiang, Y.Q.; Ye, X.W.; Yun, C.B.; Shadabfar, M. Localization of damaged cable in a tied-arch bridge using Arias intensity of seismic acceleration response. Struct. Control Health Monit. 2019, 27, e2491. [Google Scholar] [CrossRef]
- Kordestani, H.; Zhang, C.; Arab, A. An Output-Only, Energy-Based, Damage Detection Method Using the Trend Lines of the Structural Acceleration Response. Buildings 2023, 13, 3007. [Google Scholar] [CrossRef]


| Properties | Unit | Symbol | Value |
|---|---|---|---|
| Length | 25 | ||
| Mass per unit | 18,360 | ||
| Stiffness | 4.865 × 1010 | ||
| First natural frequency | ---- | 2.933 |
| Properties | Unit | Symbol | Value |
|---|---|---|---|
| Body mass | 16,500 | ||
| Axle mass | 700 | ||
| Suspension stiffness | 8 × 105 | ||
| Suspension damping | 2 × 104 | ||
| Tire stiffness | 3.5 × 106 | ||
| Velocity | V | 1.25, 2.5, 4, 8 |
| Scenarios | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Crack depth to beam height ratio | 40% | 30% | 20% | 40% | 30% | 20% |
| Location | Node 3 | Node 3 | Node 3 | Node 6 | Node 6 | Node 6 |
| Name | N3D40 | N3D30 | N3D20 | N6D40 | N6D30 | N6D20 |
| Speed | Nodes | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Noise-free | 1.25 | 0.508 | 0.957 | 1.318 | 1.455 | 1.312 | 0.949 | 0.500 |
| 2.5 | 0.510 | 0.960 | 1.318 | 1.454 | 1.310 | 0.948 | 0.501 | |
| 4 | 0.518 | 0.966 | 1.320 | 1.453 | 1.305 | 0.942 | 0.496 | |
| 8 | 0.527 | 0.973 | 1.318 | 1.447 | 1.298 | 0.939 | 0.498 | |
| Noisy | 1.25 | 0.509 | 0.958 | 1.317 | 1.454 | 1.312 | 0.949 | 0.501 |
| 2.5 | 0.510 | 0.960 | 1.317 | 1.454 | 1.310 | 0.948 | 0.501 | |
| 4 | 0.518 | 0.966 | 1.319 | 1.452 | 1.305 | 0.943 | 0.497 | |
| 8 | 0.527 | 0.973 | 1.318 | 1.447 | 1.298 | 0.939 | 0.498 | |
| Scenario | Velocity (m/s) | Slope | Scenario | Velocity (m/s) | Slope | Average |
|---|---|---|---|---|---|---|
| N3D40 | 1.25 | 0.5283 | Noisy-N3D40 | 1.25 | 0.5259 | 0.5519 |
| 2.5 | 0.5709 | 2.5 | 0.5697 | |||
| N6D40 | 1.25 | 0.5532 | Noisy-N6D40 | 1.25 | 0.5688 | |
| 2.5 | 0.5468 | 2.5 | 0.5513 | |||
| N3D30 | 1.25 | 0.3040 | Noisy-N3D30 | 1.25 | 0.3039 | 0.3241 |
| 2.5 | 0.3259 | 2.5 | 0.3251 | |||
| N6D30 | 1.25 | 0.3271 | Noisy-N6D30 | 1.25 | 0.3250 | |
| 2.5 | 0.3397 | 2.5 | 0.3422 | |||
| N3D20 | 1.25 | 0.1887 | Noisy-N3D20 | 1.25 | 0.1891 | 0.2002 |
| 2.5 | 0.1973 | 2.5 | 0.1972 | |||
| N6D20 | 1.25 | 0.1941 | Noisy-N6D20 | 1.25 | 0.1897 | |
| 2.5 | 0.2224 | 2.5 | 0.2234 |
| First Natural Frequency | Change % | Second Natural Frequency | Change % | Third Natural Frequency | Change % | |
|---|---|---|---|---|---|---|
| No damage | 2.933 | ---- | 11.602 | ---- | 25.638 | ---- |
| N3D20 | 2.928 | 0.17 | 11.571 | 0.27 | 25.631 | 0.03 |
| N3D30 | 2.921 | 0.40 | 11.537 | 0.56 | 25.622 | 0.06 |
| N3D40 | 2.910 | 0.78 | 11.475 | 1.09 | 25.608 | 0.12 |
| N6D20 | 2.925 | 0.27 | 11.590 | 0.10 | 25.613 | 0.10 |
| N6D30 | 2.916 | 0.57 | 11.577 | 0.21 | 25.584 | 0.21 |
| N6D40 | 2.900 | 1.12 | 11.553 | 0.42 | 25.533 | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kordestani, H.; Pegah, E. A Study on the Direct Application of the Gaussian Kernel Smoothing Filter for Bridge Health Monitoring. Infrastructures 2025, 10, 58. https://doi.org/10.3390/infrastructures10030058
Kordestani H, Pegah E. A Study on the Direct Application of the Gaussian Kernel Smoothing Filter for Bridge Health Monitoring. Infrastructures. 2025; 10(3):58. https://doi.org/10.3390/infrastructures10030058
Chicago/Turabian StyleKordestani, Hadi, and Ehsan Pegah. 2025. "A Study on the Direct Application of the Gaussian Kernel Smoothing Filter for Bridge Health Monitoring" Infrastructures 10, no. 3: 58. https://doi.org/10.3390/infrastructures10030058
APA StyleKordestani, H., & Pegah, E. (2025). A Study on the Direct Application of the Gaussian Kernel Smoothing Filter for Bridge Health Monitoring. Infrastructures, 10(3), 58. https://doi.org/10.3390/infrastructures10030058











