Simplified Impact Load Model Analysis of Vehicle-to-Bridge Pier Collision
Abstract
1. Introduction/Literature Review
1.1. Codes
1.2. Numerical Studies
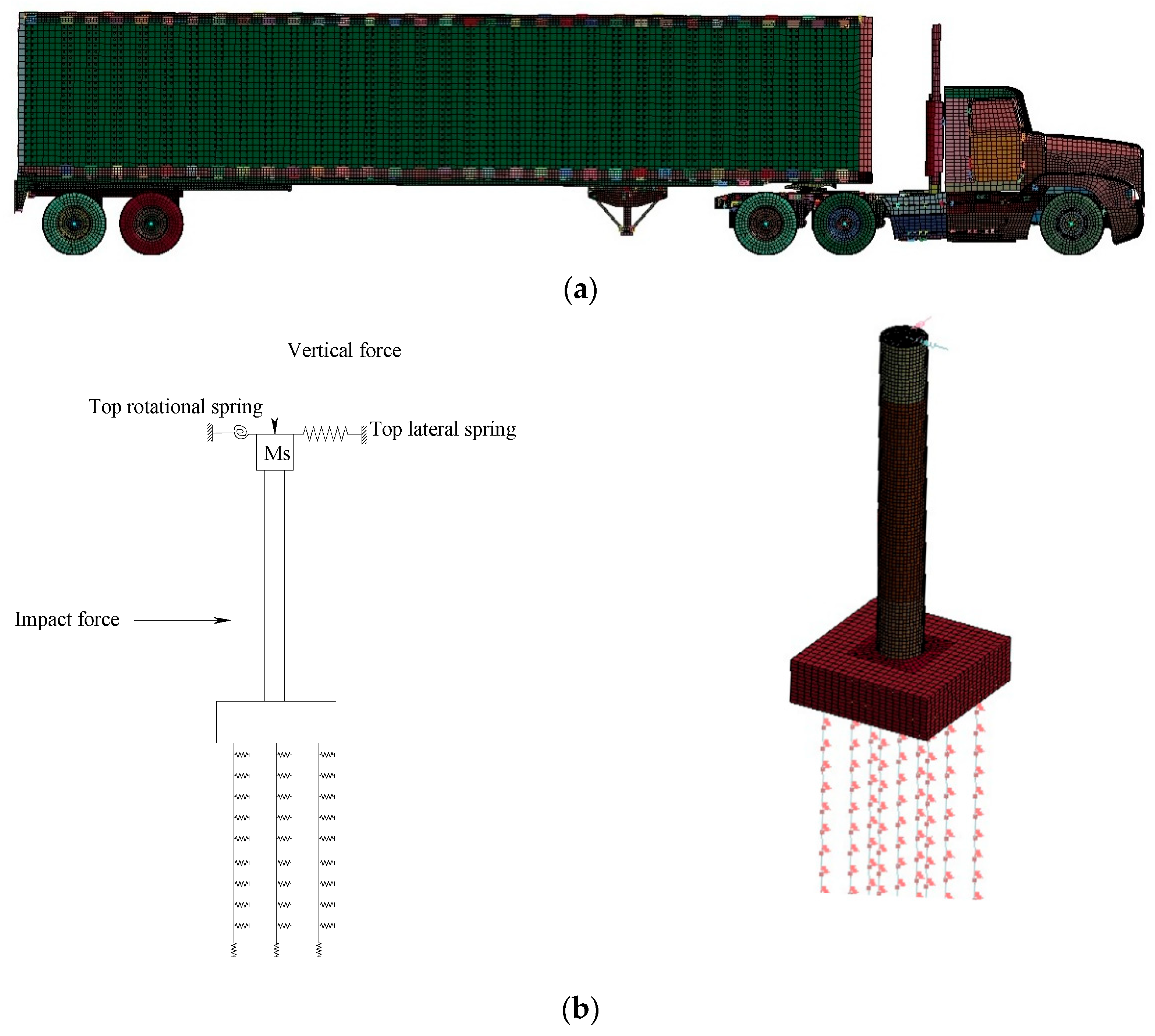
2. Finite Element Analysis
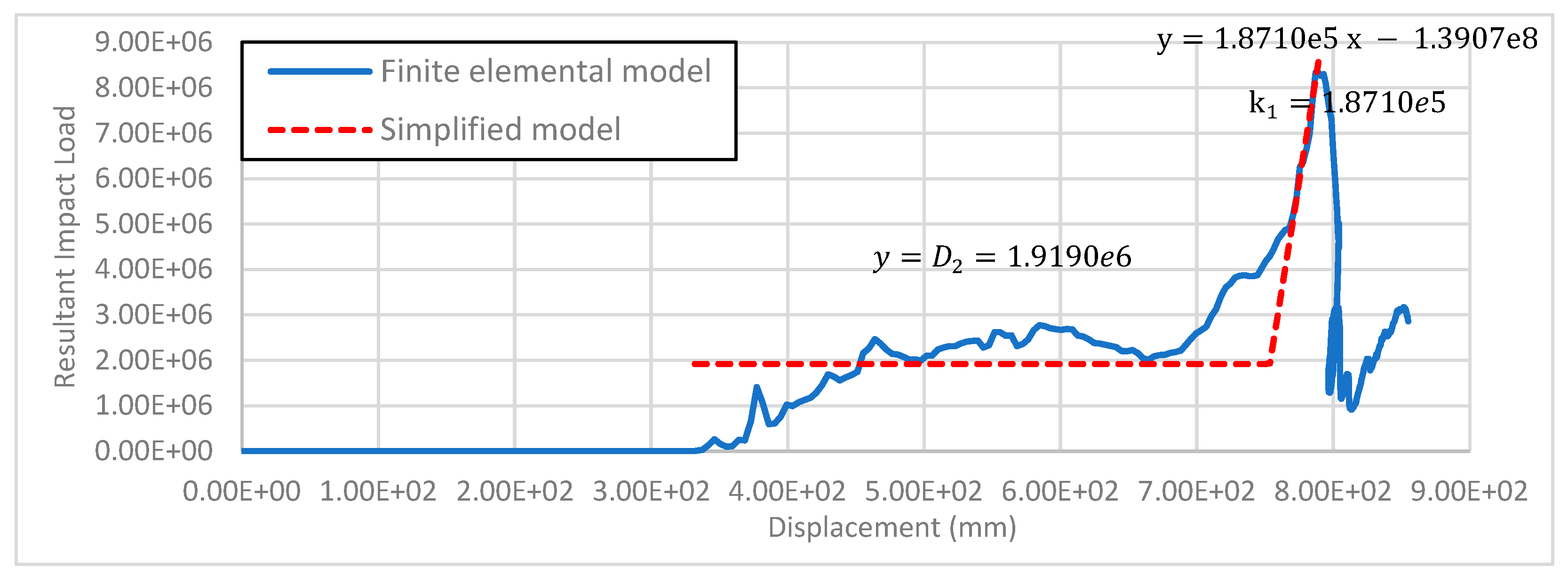
3. Simplified Load Model for Vehicle-Induced Impact
- (1)
- Impact Load Model Based on Reduced-Order Dynamic Model
3.1. Assumptions of Reduced-Order Dynamic Model
3.2. Vehicle Model
3.3. Tractor–Trailer
3.4. Pier Model
- (A)
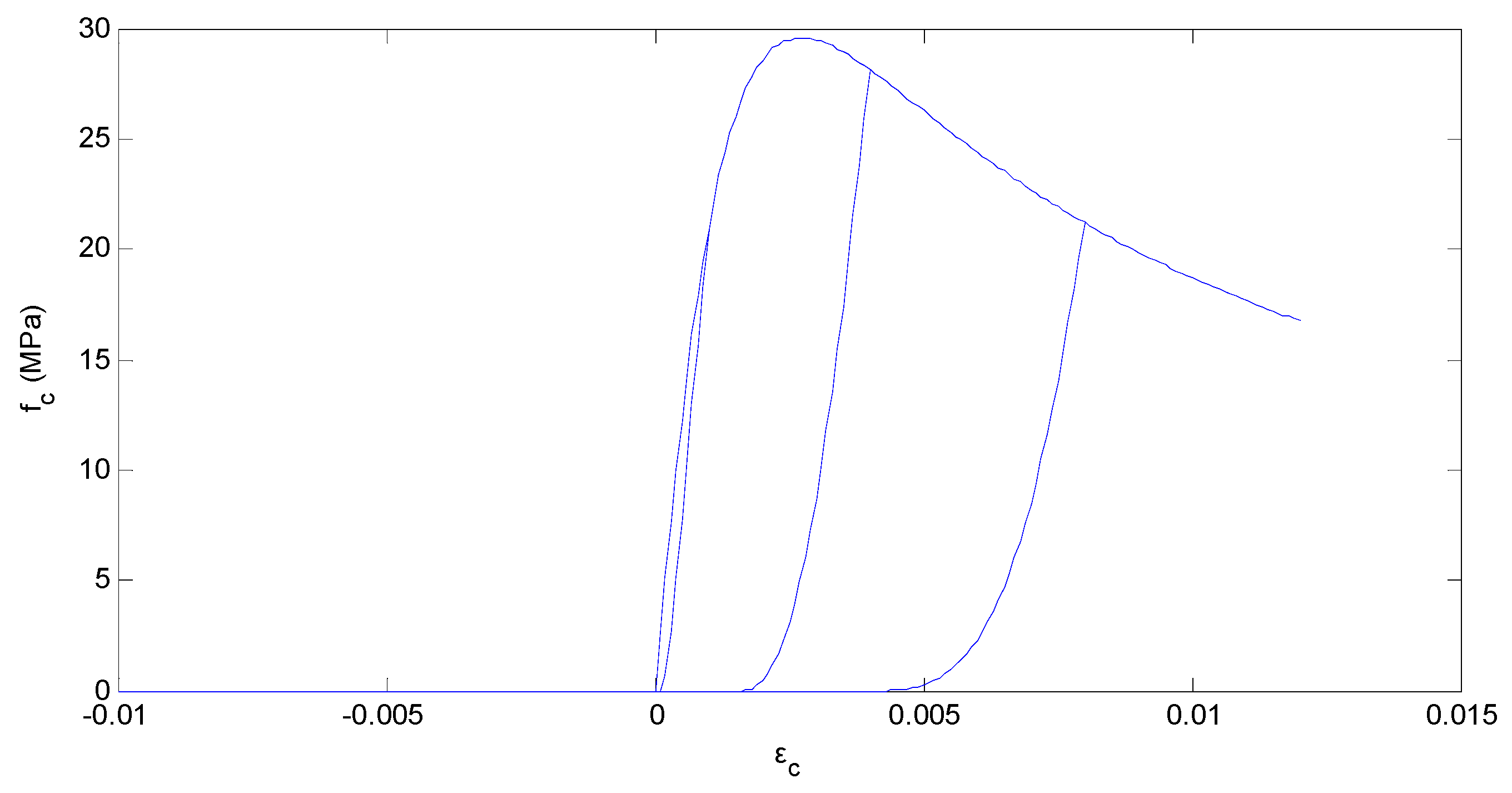
- Concrete model
- (B)
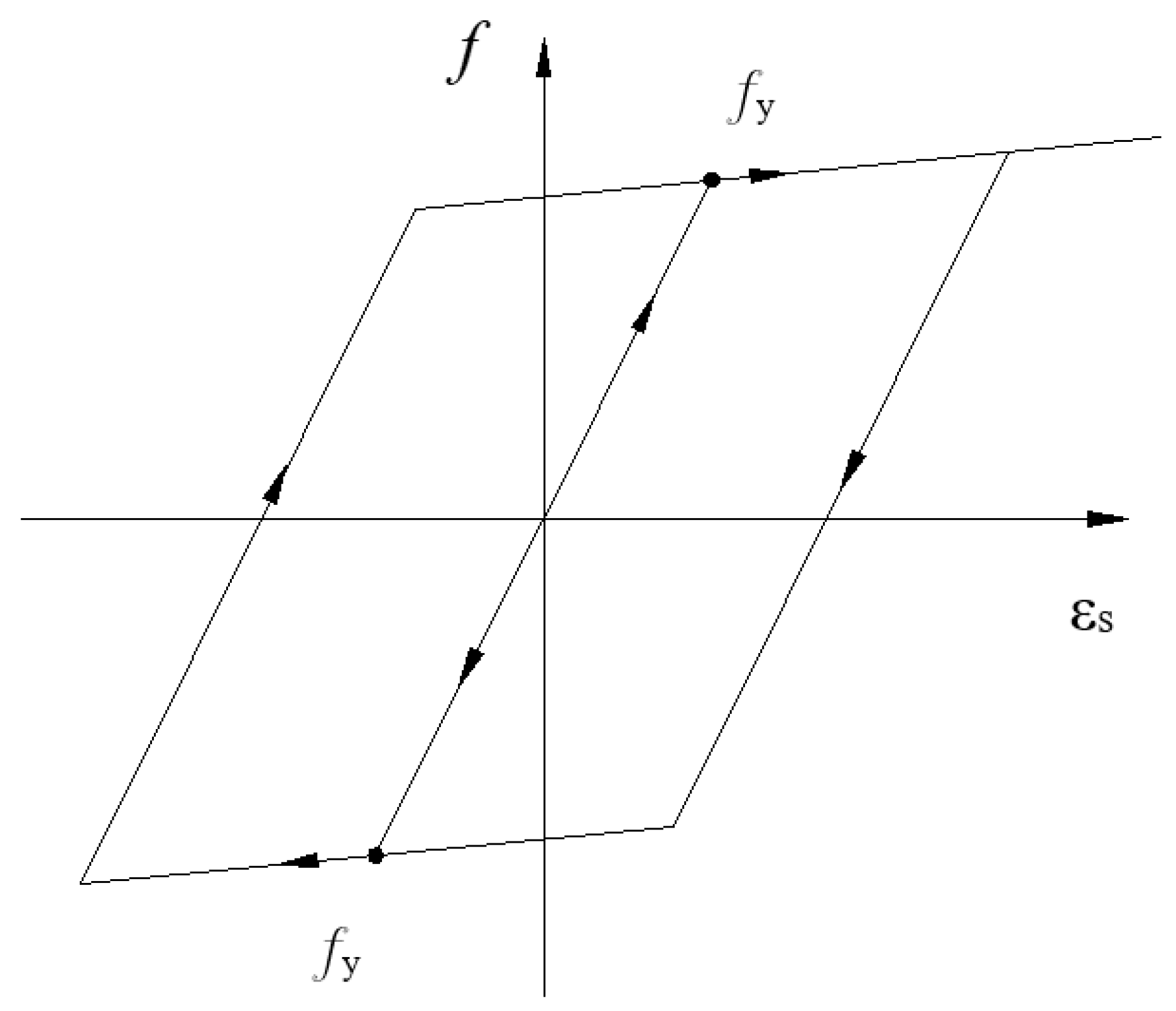
- Steel model
- (C)
- Fiber model of pier section for analytical moment–curvature relationship
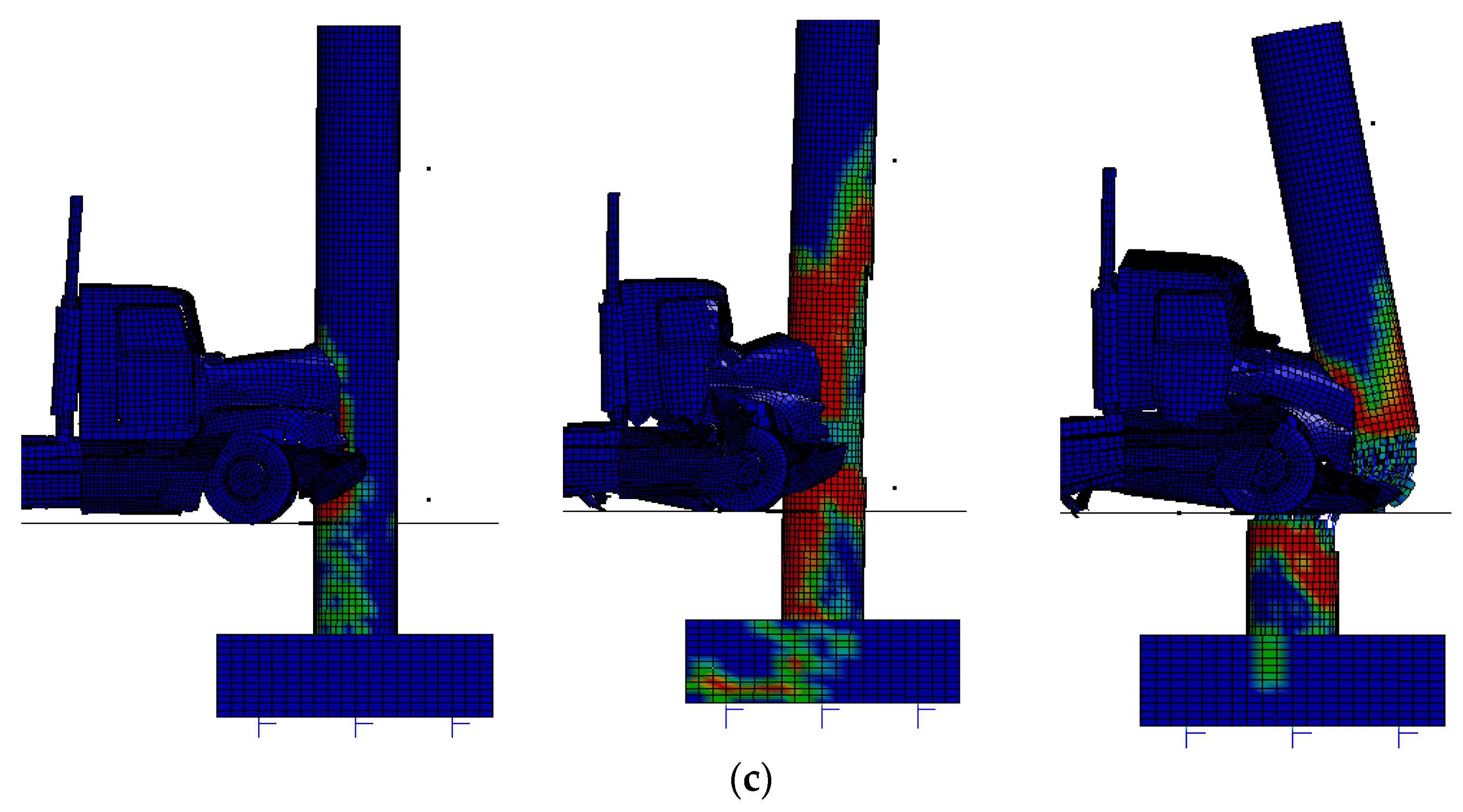
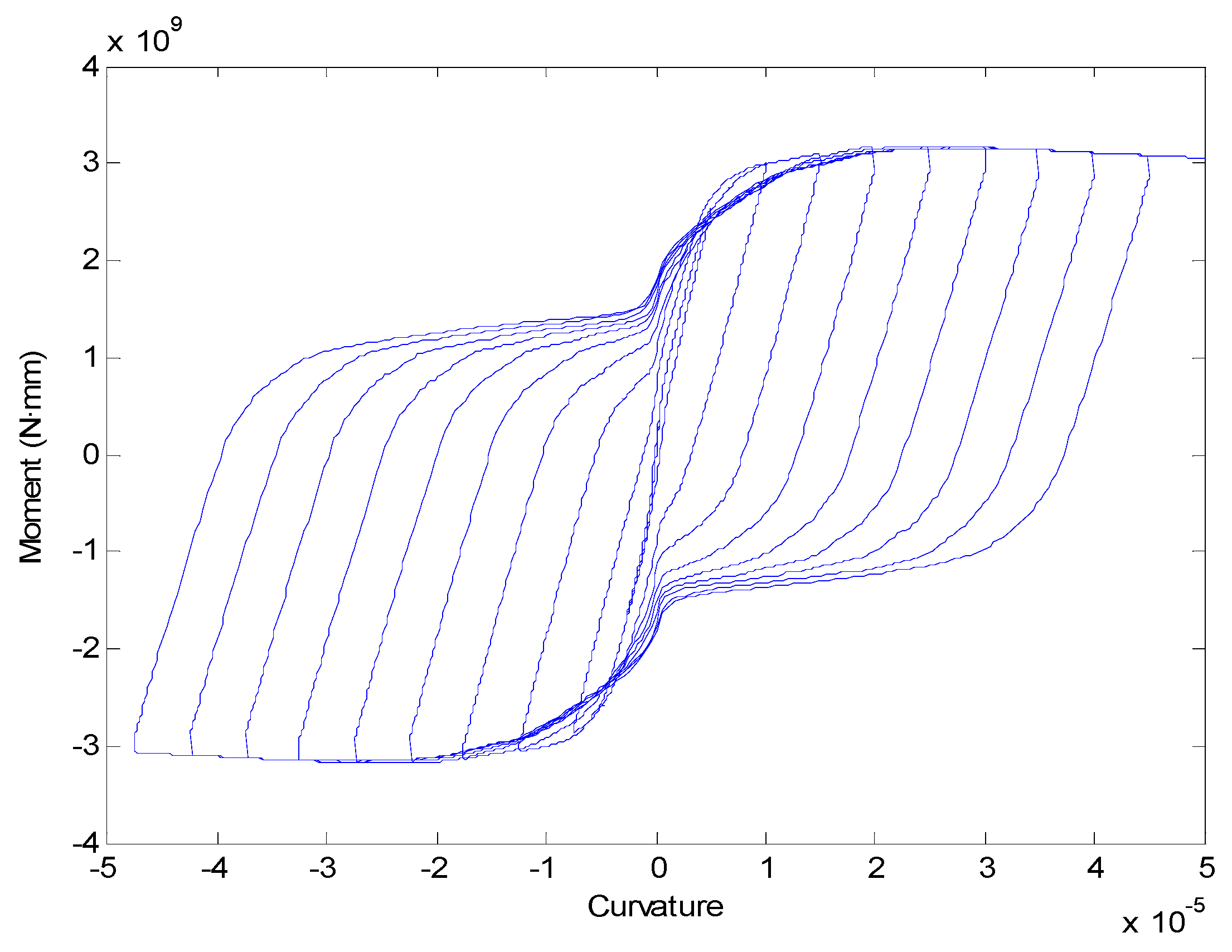
3.5. Explicit Dynamic Analysis for Coupling System
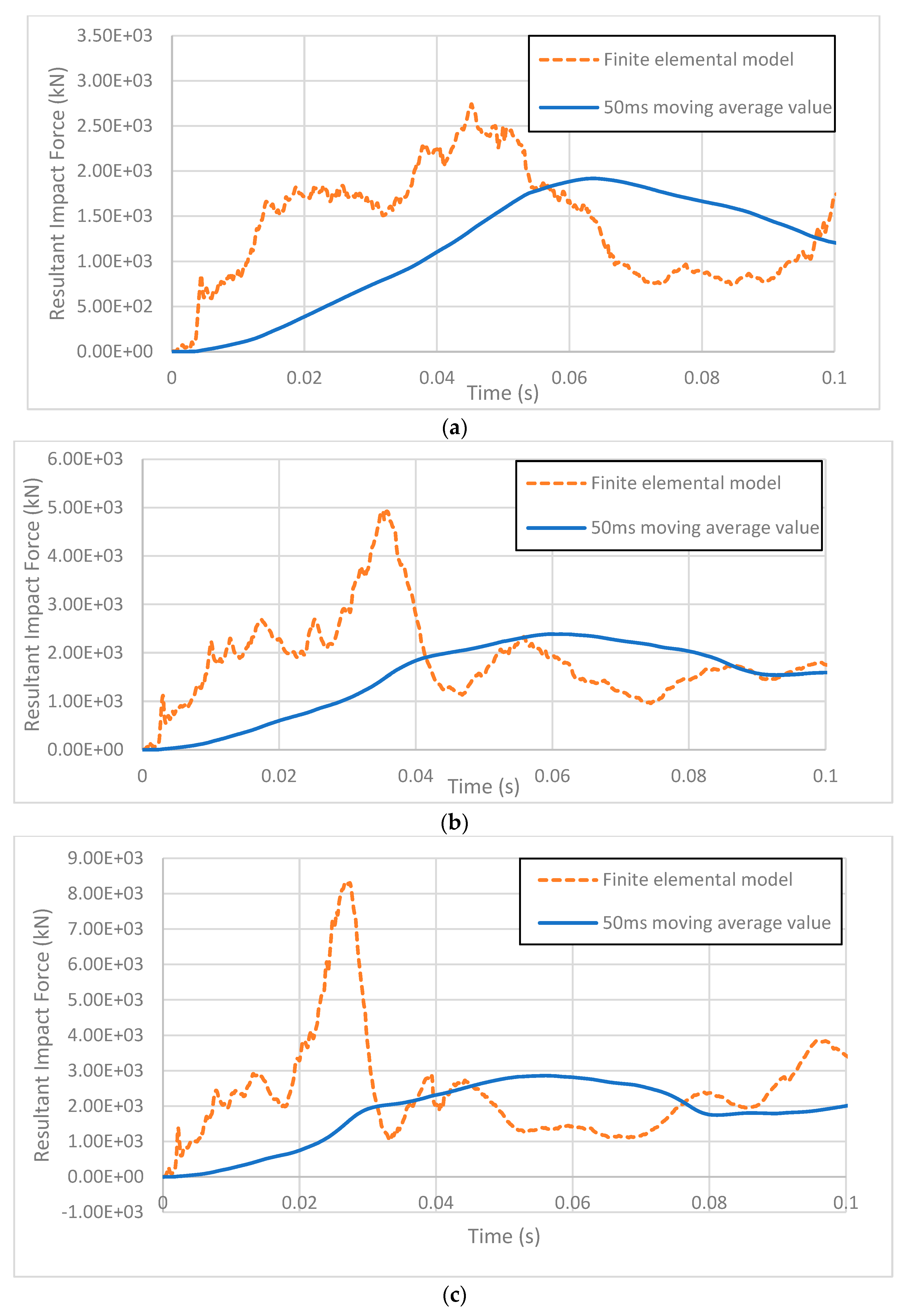
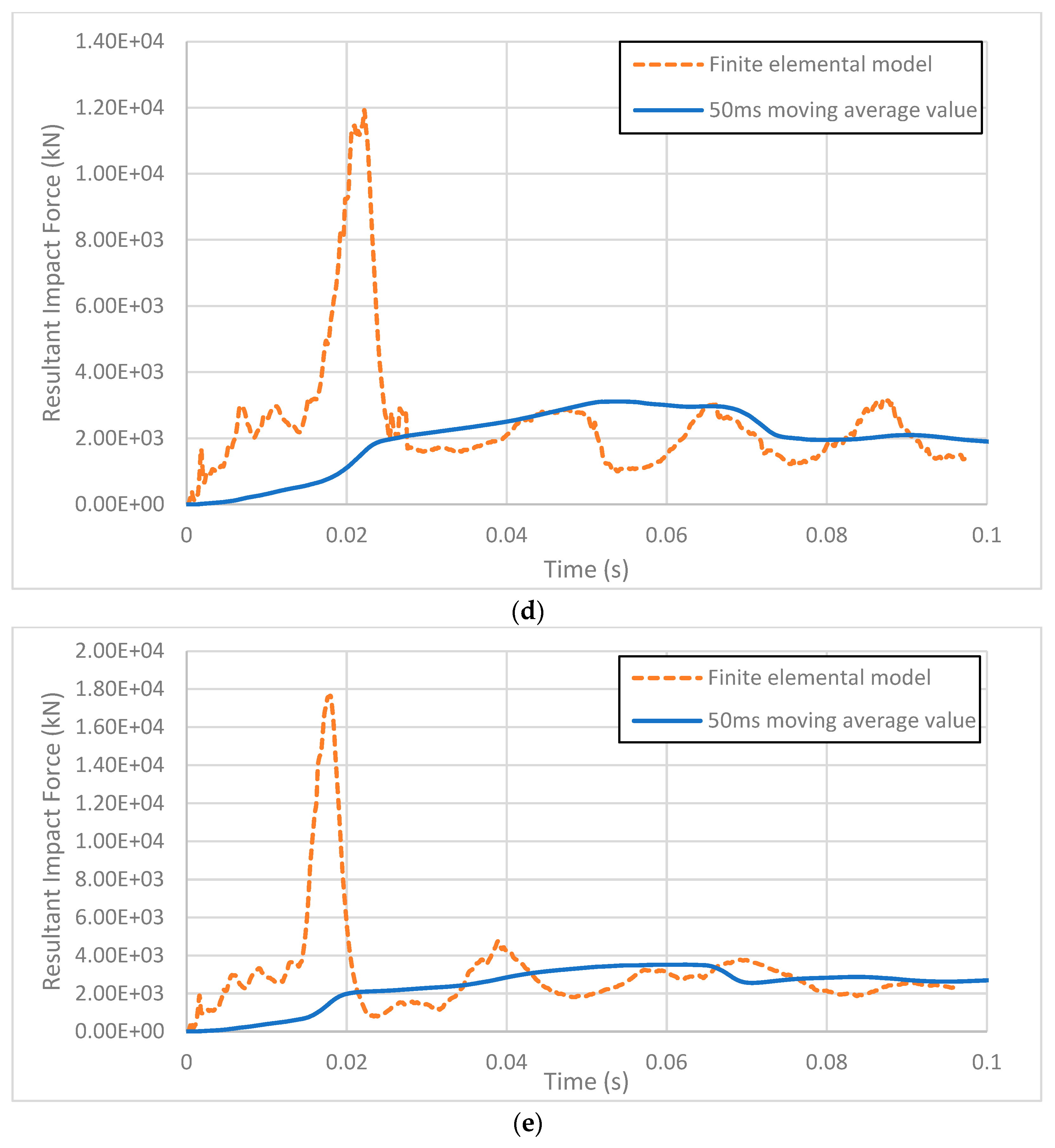
3.6. Analyzed Results
- (2)
- Impact Load Model Based on Response Surface Method
3.7. Overview
3.8. Response Surface Model
4. Summary
5. Conclusions
- (1)
- Reduced-order dynamic model: This approach provides the time history response of impact forces through an idealized mass–spring–damper system. Although it requires appropriate assumptions for stiffness and damping and case-by-case explicit analyses, it effectively captures the dynamic behavior of the pier, including plastic deformation modeled through fiber section analysis. The framework can be extended to simulate various truck-to-pier and ship-to-pier impact scenarios and is particularly suitable when time history responses are of interest.
- (2)
- Response surface model: This method offers a direct analytical function for estimating impact loads based on key parameters such as vehicle speed, cargo mass, and pier geometry. By employing second-order polynomial fitting, it can efficiently predict both peak dynamic and equivalent static impact loads. The model can be further refined using large datasets or advanced sensitivity analysis; however, it cannot reproduce detailed time history responses.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Parameters Used in Response Surface Model
| Case | Variables | Responses | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | Peak Dynamic Load (N) | Equivalent Static Load (N) | |
| 1 | 40 | 55.16 | 0.762 | 9.144 | 0.3048 | 10 | 0 | 3.4619E+06 | 1.2285E+06 |
| 2 | 80 | 41.37 | 0.762 | 5.4864 | 1.2192 | 10 | 11.0895 | 1.0121E+07 | 2.5005E+06 |
| 3 | 40 | 55.16 | 0.762 | 9.144 | 2.1336 | 0 | 22.179 | 1.7149E+06 | 2.2995E+06 |
| 4 | 40 | 27.58 | 1.0668 | 5.4864 | 0.3048 | 10 | 0 | 2.7548E+06 | 1.7274E+06 |
| 5 | 40 | 27.58 | 0.762 | 9.144 | 0.3048 | 0 | 22.179 | 1.9289E+06 | 1.3252E+06 |
| 6 | 80 | 27.58 | 0.9144 | 5.4864 | 2.1336 | 10 | 0 | 9.5244E+06 | 2.8214E+06 |
| 7 | 60 | 27.58 | 1.0668 | 9.144 | 1.2192 | 10 | 0 | 6.8068E+06 | 2.3703E+06 |
| 8 | 40 | 27.58 | 0.762 | 5.4864 | 0.3048 | 5 | 22.179 | 2.1252E+06 | 2.0344E+06 |
| 9 | 40 | 55.16 | 1.0668 | 9.144 | 2.1336 | 10 | 11.0895 | 2.8614E+06 | 1.6051E+06 |
| 10 | 40 | 55.16 | 0.762 | 5.4864 | 0.3048 | 0 | 11.0895 | 2.1145E+06 | 2.0041E+06 |
| 11 | 120 | 27.58 | 0.9144 | 7.3152 | 0.3048 | 5 | 11.0895 | 1.7659E+07 | 3.5847E+06 |
| 12 | 100 | 55.16 | 1.0668 | 5.4864 | 0.3048 | 10 | 0 | 1.0190E+07 | 3.0335E+06 |
| 13 | 80 | 41.37 | 0.762 | 9.144 | 1.2192 | 5 | 0 | 8.6926E+06 | 2.5215E+06 |
| 14 | 120 | 27.58 | 1.0668 | 9.144 | 0.3048 | 0 | 0 | 2.0769E+07 | 3.6278E+06 |
| 15 | 40 | 27.58 | 0.762 | 5.4864 | 2.1336 | 0 | 22.179 | 1.9126E+06 | 1.9536E+06 |
| 16 | 40 | 55.16 | 1.0668 | 5.4864 | 1.2192 | 5 | 22.179 | 2.4520E+06 | 1.7415E+06 |
| 17 | 40 | 27.58 | 1.0668 | 5.4864 | 2.1336 | 5 | 22.179 | 2.6966E+06 | 1.8981E+06 |
| 18 | 80 | 27.58 | 1.0668 | 5.4864 | 0.3048 | 0 | 22.179 | 1.0220E+07 | 2.8853E+06 |
| 19 | 100 | 41.37 | 1.0668 | 9.144 | 2.1336 | 5 | 22.179 | 1.1900E+07 | 3.4272E+06 |
| 20 | 80 | 27.58 | 1.0668 | 5.4864 | 0.3048 | 0 | 22.179 | 1.0220E+07 | 2.8853E+06 |
| 21 | 40 | 41.37 | 1.0668 | 9.144 | 0.3048 | 10 | 22.179 | 2.4932E+06 | 1.9003E+06 |
| 22 | 120 | 41.37 | 1.0668 | 7.3152 | 2.1336 | 10 | 0 | 1.7971E+07 | 3.5437E+06 |
| 23 | 40 | 27.58 | 1.0668 | 9.144 | 2.1336 | 0 | 22.179 | 2.3190E+06 | 1.5052E+06 |
| 24 | 120 | 27.58 | 0.762 | 9.144 | 0.3048 | 10 | 0 | 1.4901E+07 | 2.4729E+06 |
| 25 | 120 | 55.16 | 0.762 | 9.144 | 2.1336 | 10 | 22.179 | 1.6006E+07 | 2.5510E+06 |
| 26 | 40 | 27.58 | 0.762 | 9.144 | 2.1336 | 0 | 0 | 2.7663E+06 | 1.3999E+06 |
| 27 | 120 | 27.58 | 0.762 | 5.4864 | 2.1336 | 5 | 22.179 | 1.4304E+07 | 3.5092E+06 |
| 28 | 120 | 27.58 | 0.762 | 9.144 | 2.1336 | 0 | 22.179 | 1.4778E+07 | 2.7548E+06 |
| 29 | 80 | 27.58 | 0.762 | 7.3152 | 0.3048 | 0 | 0 | 8.3097E+06 | 2.6637E+06 |
| 30 | 100 | 41.37 | 0.762 | 9.144 | 0.3048 | 10 | 22.179 | 1.0769E+07 | 3.2134E+06 |
| 31 | 120 | 55.16 | 1.0668 | 9.144 | 1.2192 | 0 | 22.179 | 1.9481E+07 | 3.4803E+06 |
| 32 | 40 | 27.58 | 0.762 | 7.3152 | 2.1336 | 10 | 22.179 | 3.5317E+06 | 2.2011E+06 |
| 33 | 40 | 55.16 | 1.0668 | 5.4864 | 2.1336 | 0 | 0 | 2.1534E+06 | 1.8325E+06 |
| 34 | 80 | 27.58 | 0.762 | 7.3152 | 0.3048 | 0 | 0 | 8.3097E+06 | 2.6637E+06 |
| 35 | 120 | 55.16 | 0.762 | 9.144 | 0.3048 | 0 | 11.0895 | 1.6099E+07 | 3.2187E+06 |
| 36 | 120 | 27.58 | 1.0668 | 5.4864 | 2.1336 | 0 | 0 | 1.5672E+07 | 3.5898E+06 |
| 37 | 120 | 55.16 | 1.0668 | 5.4864 | 2.1336 | 0 | 22.179 | 1.7877E+07 | 3.2495E+06 |
| 38 | 40 | 55.16 | 1.0668 | 9.144 | 0.3048 | 0 | 0 | 2.9305E+06 | 1.9843E+06 |
| 39 | 120 | 55.16 | 0.762 | 5.4864 | 2.1336 | 5 | 0 | 1.6073E+07 | 3.2817E+06 |
| 40 | 120 | 27.58 | 0.9144 | 7.3152 | 0.3048 | 5 | 11.0895 | 1.7659E+07 | 3.5847E+06 |
| 41 | 120 | 41.37 | 1.0668 | 7.3152 | 2.1336 | 10 | 0 | 1.7971E+07 | 3.5437E+06 |
| 42 | 120 | 55.16 | 0.762 | 5.4864 | 0.3048 | 10 | 22.179 | 1.6815E+07 | 3.3439E+06 |
| 43 | 120 | 55.16 | 0.9144 | 9.144 | 2.1336 | 0 | 0 | 1.5576E+07 | 3.5722E+06 |
| 44 | 120 | 41.37 | 0.9144 | 5.4864 | 0.3048 | 0 | 0 | 1.6636E+07 | 3.5934E+06 |
| 45 | 120 | 27.58 | 1.0668 | 5.4864 | 1.2192 | 10 | 22.179 | 1.8760E+07 | 3.4939E+06 |
| 46 | 120 | 41.37 | 0.9144 | 5.4864 | 0.3048 | 0 | 0 | 1.6636E+07 | 3.5934E+06 |
| 47 | 40 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 5 | 22.179 | 2.1601E+06 | 1.3423E+06 |
| 48 | 60 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 5 | 22.179 | 4.9249E+06 | 2.3863E+06 |
| 49 | 80 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 5 | 22.179 | 8.3425E+06 | 2.8580E+06 |
| 50 | 100 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 5 | 22.179 | 1.1924E+07 | 3.1123E+06 |
| 51 | 120 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 5 | 22.179 | 1.7635E+07 | 3.5218E+06 |
| 52 | 80 | 41.37 | 0.9144 | 5.4864 | 1.2192 | 5 | 22.179 | 7.9537E+06 | 2.8298E+06 |
| 53 | 80 | 55.16 | 0.9144 | 5.4864 | 1.2192 | 5 | 22.179 | 7.0132E+06 | 2.8663E+06 |
| 54 | 80 | 27.58 | 0.762 | 5.4864 | 1.2192 | 5 | 22.179 | 7.4634E+06 | 2.7753E+06 |
| 55 | 80 | 27.58 | 1.0668 | 5.4864 | 1.2192 | 5 | 22.179 | 1.1108E+07 | 2.9915E+06 |
| 56 | 80 | 27.58 | 0.9144 | 7.3152 | 1.2192 | 5 | 22.179 | 8.1201E+06 | 2.8389E+06 |
| 57 | 80 | 27.58 | 0.9144 | 9.144 | 1.2192 | 5 | 22.179 | 8.2502E+06 | 2.8461E+06 |
| 58 | 80 | 27.58 | 0.9144 | 5.4864 | 0.3048 | 5 | 22.179 | 8.4439E+06 | 2.9086E+06 |
| 59 | 80 | 27.58 | 0.9144 | 5.4864 | 2.1336 | 5 | 22.179 | 6.9615E+06 | 2.5847E+06 |
| 60 | 80 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 0 | 22.179 | 7.6976E+06 | 2.8485E+06 |
| 61 | 80 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 10 | 22.179 | 8.4141E+06 | 2.8627E+06 |
| 62 | 80 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 5 | 0 | 6.8596E+06 | 2.8173E+06 |
| 63 | 80 | 27.58 | 0.9144 | 5.4864 | 1.2192 | 5 | 11.0895 | 8.3987E+06 | 2.8025E+06 |
| Peak Dynamic Load | Equivalent Static Load | |||
|---|---|---|---|---|
| Factors | Coded ) | Actual ) | Coded ) | Actual ) |
| 8.889389 | 4.174923 | 29.18179 | 6.002955 | |
| 6.865914 | −0.11118 | 7.883143 | 0.509356 | |
| −0.18992 | 0.422433 | 0.46696 | 0.660195 | |
| 0.417361 | −38.587 | 0.975437 | −103.369 | |
| −0.04677 | 2.084407 | −0.53181 | 5.842994 | |
| 0.00549 | 3.298193 | −0.27507 | 2.227506 | |
| 0.134067 | 0.533173 | −1.04737 | 0.820623 | |
| −0.06459 | −0.12258 | 0.569889 | 0.289221 | |
| 0.003224 | 5.85E−06 | −0.63602 | −0.00115 | |
| 0.632972 | 0.103834 | 1.073208 | 0.176051 | |
| 0.099999 | 0.001367 | −0.3731 | −0.0051 | |
| −0.43816 | −0.01198 | −1.01407 | −0.02772 | |
| −0.35636 | −0.00178 | −0.59336 | −0.00297 | |
| 0.574775 | 0.001296 | −0.28269 | −0.00064 | |
| −0.47741 | −0.22717 | −0.7044 | −0.33517 | |
| −0.11736 | −0.00465 | 0.552715 | 0.021916 | |
| 0.396327 | 0.031431 | −0.26954 | −0.02138 | |
| 0.073125 | 0.001061 | −1.54085 | −0.02235 | |
| −0.04174 | −0.00027 | 0.023875 | 0.000156 | |
| 0.251363 | 0.901884 | 1.048898 | 3.763416 | |
| −0.23306 | −1.6724 | −0.4007 | −2.87539 | |
| −0.3373 | −0.44266 | 0.470922 | 0.618008 | |
| 0.300136 | 0.177591 | −0.82898 | −0.49051 | |
| −0.22258 | −0.1331 | 0.194711 | 0.116436 | |
| −0.34645 | −0.03789 | 0.085623 | 0.009364 | |
| −0.21603 | −0.01065 | 0.161948 | 0.007985 | |
| 0.554441 | 0.121269 | −0.31117 | −0.06806 | |
| −0.23899 | −0.02357 | −0.68908 | −0.06796 | |
| −0.16175 | −0.00292 | 0.543671 | 0.009805 | |
| 1.867885 | 0.001167 | −3.32544 | −0.00208 | |
| −0.54128 | −0.00285 | −0.57887 | −0.00304 | |
| 0.483897 | 20.83451 | 1.116026 | 48.05121 | |
| −0.54445 | −0.16279 | −2.36625 | −0.7075 | |
| −0.50619 | −0.6054 | 1.181414 | 1.41296 | |
| 0.396827 | 0.015873 | −1.31902 | −0.05276 | |
| −0.09293 | −0.00076 | 1.278742 | 0.010398 | |
Appendix B. Three-Dimensional Response Surface Plots of Tractor–Trailer Truck
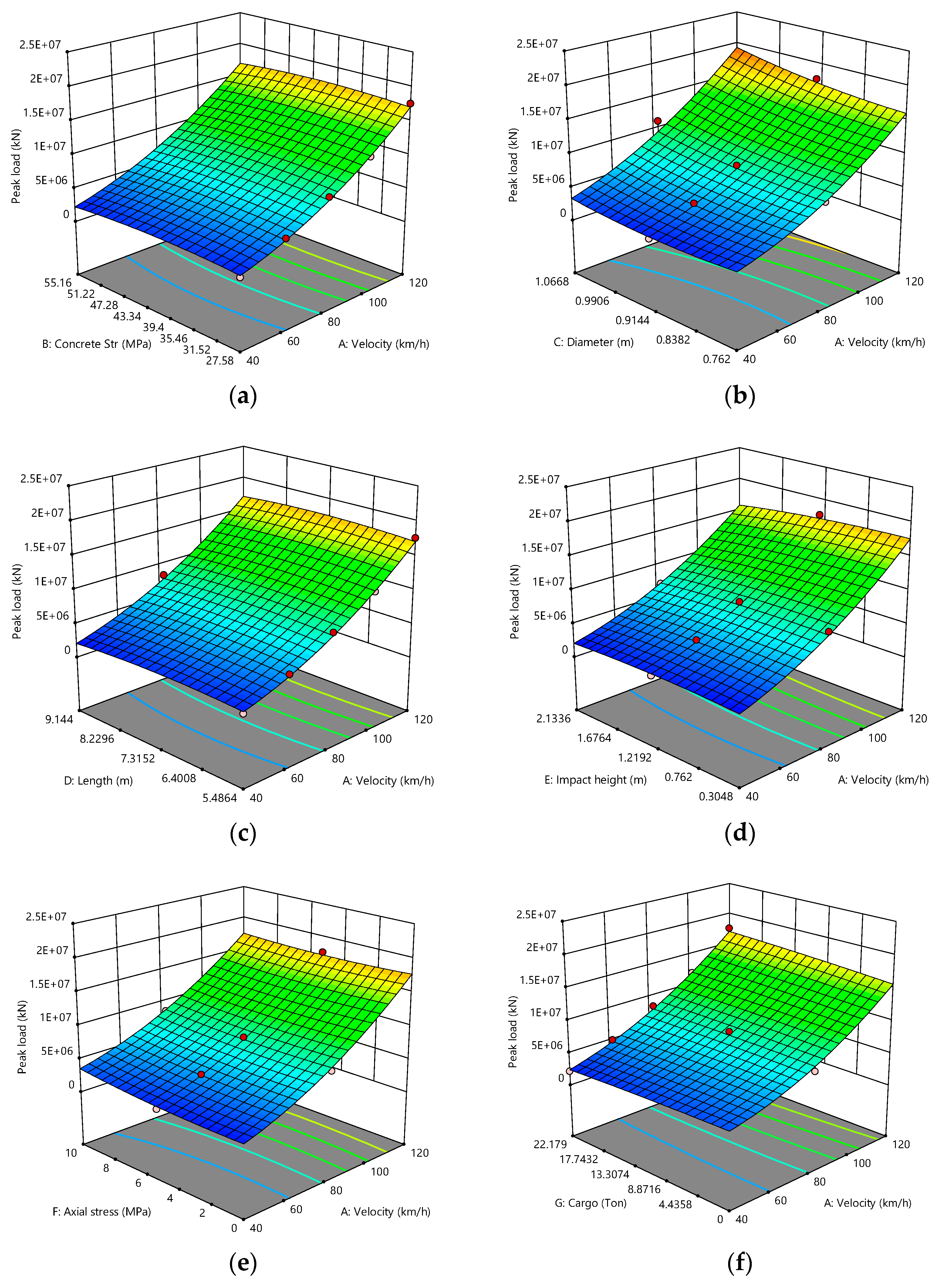
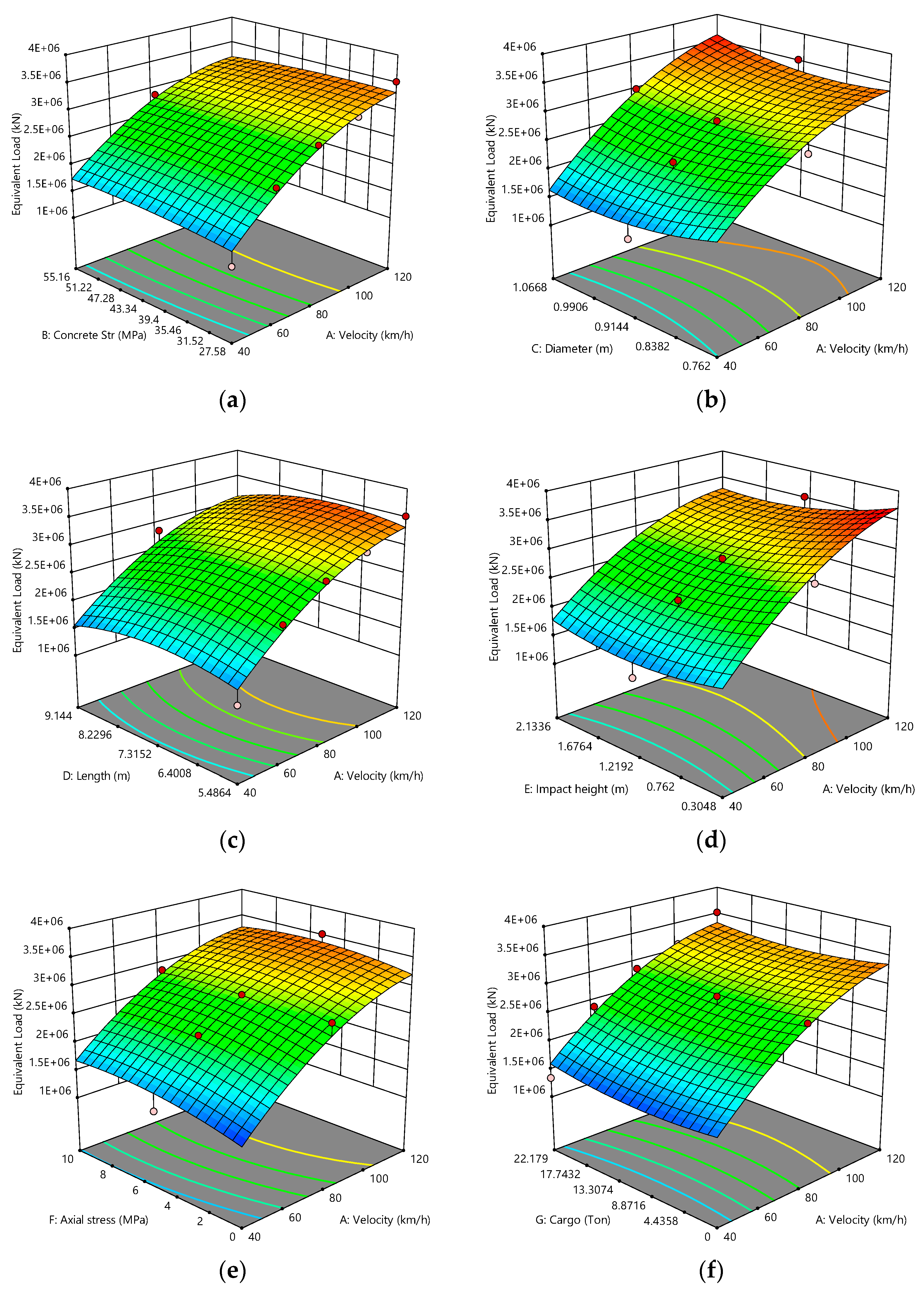
Appendix C. European Code
References
- Fu, C.C.; Burhouse, J.R.; Chang, G.L. Overheight vehicle collisions with highway bridges. Transport. Res. Rec. 2004, 1865, 80–88. [Google Scholar] [CrossRef]
- AASHTO. Load Resistance and Factor Design: Bridge Design Specifications, 9th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2020. [Google Scholar]
- Buth, C.E.; Michael, S.B.; William, F.W.; Gary, T.F. Collision Loads on Bridge Piers: Phase 2, Report of Guidelines for Designing Bridge Piers and Abutments for Vehicle Collisions; Report FHWA/TX-11/9-4973-2; Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
- ASCE7-10; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2010.
- Final Draft prEN 1991-1-1; Eurocode 1: Actions on Structures–Part 1-1: General Actions–Densities, Self-Weight, Imposed Loads for Buildings. Comité Europeo de Normalización: Brussels, Belgium, 2001. Available online: https://gaprojekt.com/wp-content/uploads/2021/11/Eurocode-1-Actions-on-Structures.pdf (accessed on 12 September 2017).
- Final Project Team Draft (Stage 34), Draft prEN 1991-1-7; Eurocode 1: Actions on Structures–Part 1-7: General Actions–Accidental Actions. Comité Europeo de Normalización: Brussels, Belgium, 2003. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1991.1.7.2006.pdf (accessed on 12 September 2017).
- Ferrer, B.; Ivorra, S.; Segovia, E.; Irles, R. Tridimensional Modelization of the Impact of a Vehicle against a Metallic Parking Column at a Low Speed. Eng. Struct. 2010, 32, 1986–1992. [Google Scholar] [CrossRef]
- Sherif, E.-T.; Edward, S.; Priscilla, F. Vehicle Collision with Bridge Pier; Report BC355_06; University of Michigan: Ann Arbor, MI, USA, 2004. [Google Scholar]
- NCAC. 1994 Chevy C2500 Pick-Up. Available online: https://www.ccsa.gmu.edu/capability/ (accessed on 24 February 2016).
- NCAC. F800 Single Unit Truck FEM Model for Crash Simulations with LS-DYNA. Available online: https://thyme.ornl.gov/FHWA/F800WebPage/downloads/downloads.html (accessed on 12 September 2017).
- Consolazio, G.R.; Cowan, D.R. Numerically Efficient Dynamic Analysis of Barge Collisions with Bridge Pier. J. Struct. Eng. 2005, 131, 1256–1266. [Google Scholar] [CrossRef]
- Buth, C.E.; William, F.W.; Michael, S.B.; Dominique Lord, S.R.G.; Akram, Y.A.-O. Analysis of Large Truck Collisions with Bridge Piers: Phase 1, Report of Guidelines for Designing Bridge Piers and Abutments for Vehicle Collisions; Report FHWA/TX-10/9-4973-1; Texas A&M University: College Station, TX, USA, 2010. [Google Scholar]
- Liu, G. Behavior of Bridge Piers During Vehicular Impacts. Ph.D. Dissertation, City University of New York, New York, NY, USA, 2012. [Google Scholar]
- Fujikake, K.; Bing, L.; Sam, S. Impact Response of Reinforced Concrete Beam and Its Analytical Evaluation. J. Struct. Eng. 2009, 135, 938–950. [Google Scholar] [CrossRef]
- Mohammed, T. Reinforced Concrete Structural Members Under Impact Loading. Ph.D. Dissertation, University of Toledo, Toledo, OH, USA, 2011. [Google Scholar]
- Gomez, N.L. Performance of Circular Reinforced Concrete Bridge Piers Subjected to Vehicular Collisions. Master’s Thesis, University of Massachusetts—Amherst, Amherst, MA, USA, 2014. [Google Scholar]
- Abdelkarim, O.I.; Mohamed, A.E. Performance of Hollow-core FRP–concrete–steel Bridge Columns Subjected to Vehicle Collision. Eng. Struct. 2016, 123, 517–531. [Google Scholar] [CrossRef]
- Chen, L.; Sherif, E.-T.; Yan, X. Reduced Models for Simulating Collisions between Trucks and Bridge Piers. J. Bridge Eng. 2016, 21, 04016020. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%29BE.1943-5592.0000810 (accessed on 12 September 2017). [CrossRef]
- Do, T.V.; Thong, M.P.; Hong, H. A Dynamic responses and failure modes of bridge columns under vehicle collision. Eng. Struct. 2018, 156, 243–259. [Google Scholar] [CrossRef]
- Alomari, Q.A.; Daniel, G.L. Advanced analysis of intact, fire-damaged, and CFRP retrofitted bridge pier columns under vehicle collisions: Empirical equivalent static force equation and framework. Eng. Struct. 2024, 314, 118250. [Google Scholar] [CrossRef]
- Xu, C. Impact Load Model Analysis on the Vehicle-to-Pier Collision. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2019. [Google Scholar]
- NCAC. FEM Models for Semitrailer Trucks. Available online: https://thyme.ornl.gov/fhwa/tractortrailer/download/download.cgi (accessed on 12 September 2017).
- Greimann, L.; Wolde-Tinsae, A.M. Design Model for Piles in Jointless Bridges. J. Struct. Eng. 1998, 114, 1354–1371. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Cosenza, E.; Carmine, G.; Giuseppe, M. A simplified method for flexural capacity assessment of circular RC cross-sections. Eng. Struct. 2011, 33, 942–946. [Google Scholar] [CrossRef]
- Sierakowski, R.L.; Chaturvedi, S.K. Dynamic Loading and Characterization of Fiber-Reinforced Composite; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Box, G.E.; Wilson, K.B. On the Experimental Attainment of Optimum Conditions. J. R. Stat. Soc. 1951, 13, 1–45. [Google Scholar] [CrossRef]
- Cook, R.D. Detection of Influential Observation in Linear Regression. Technometrics 1977, 19, 15–18. [Google Scholar] [CrossRef]
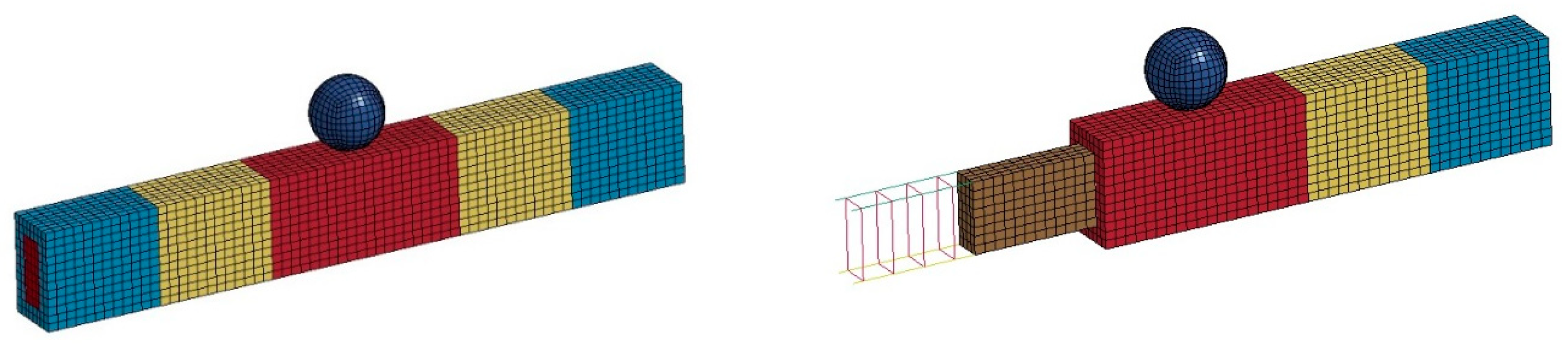
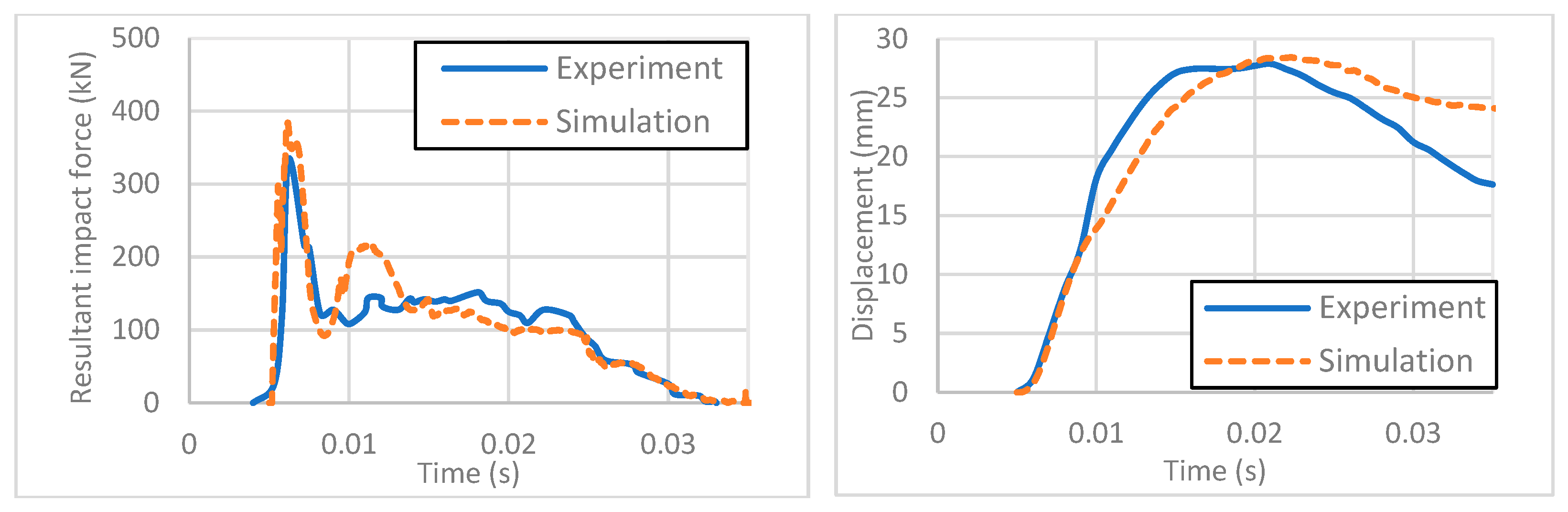
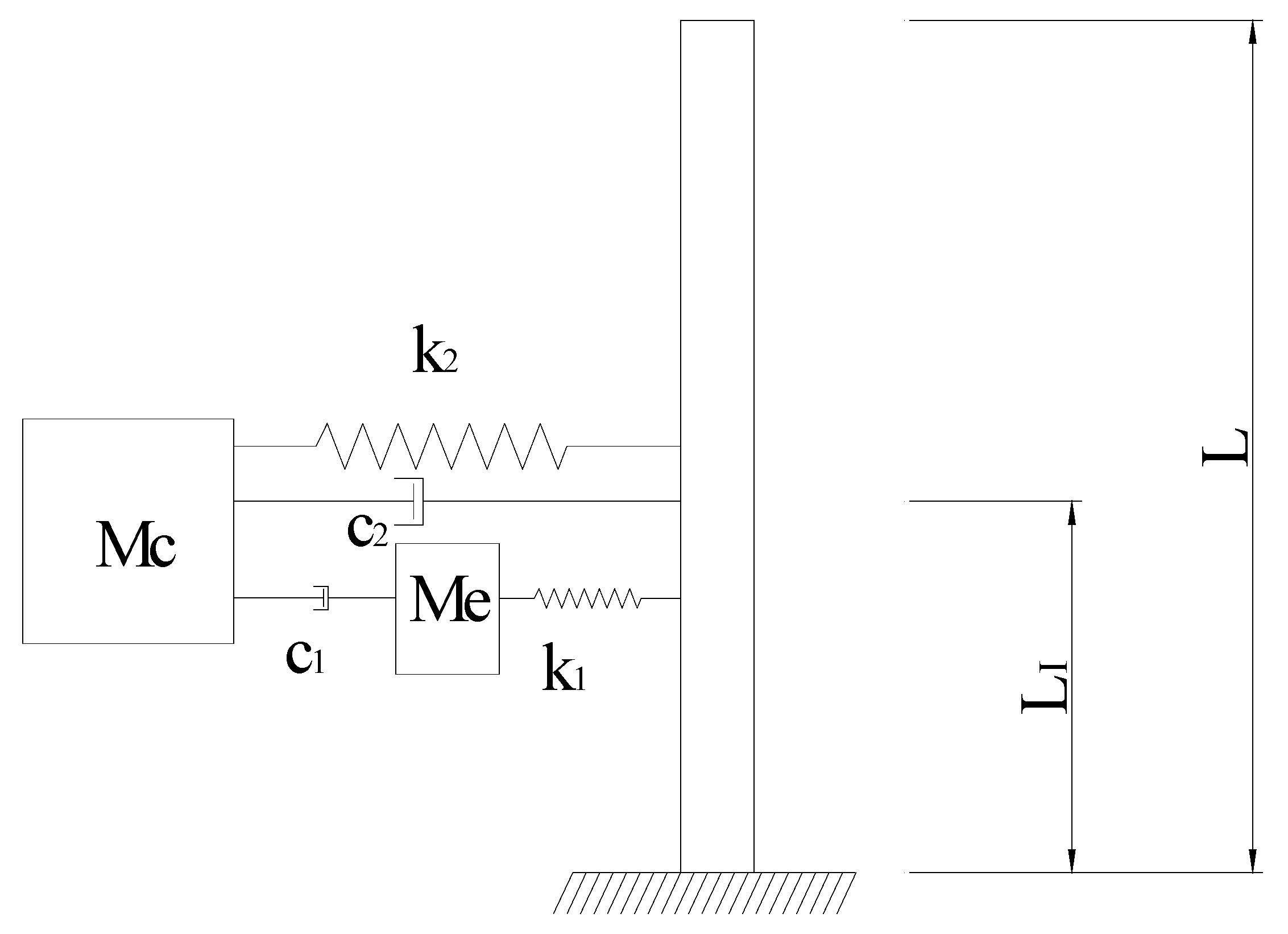
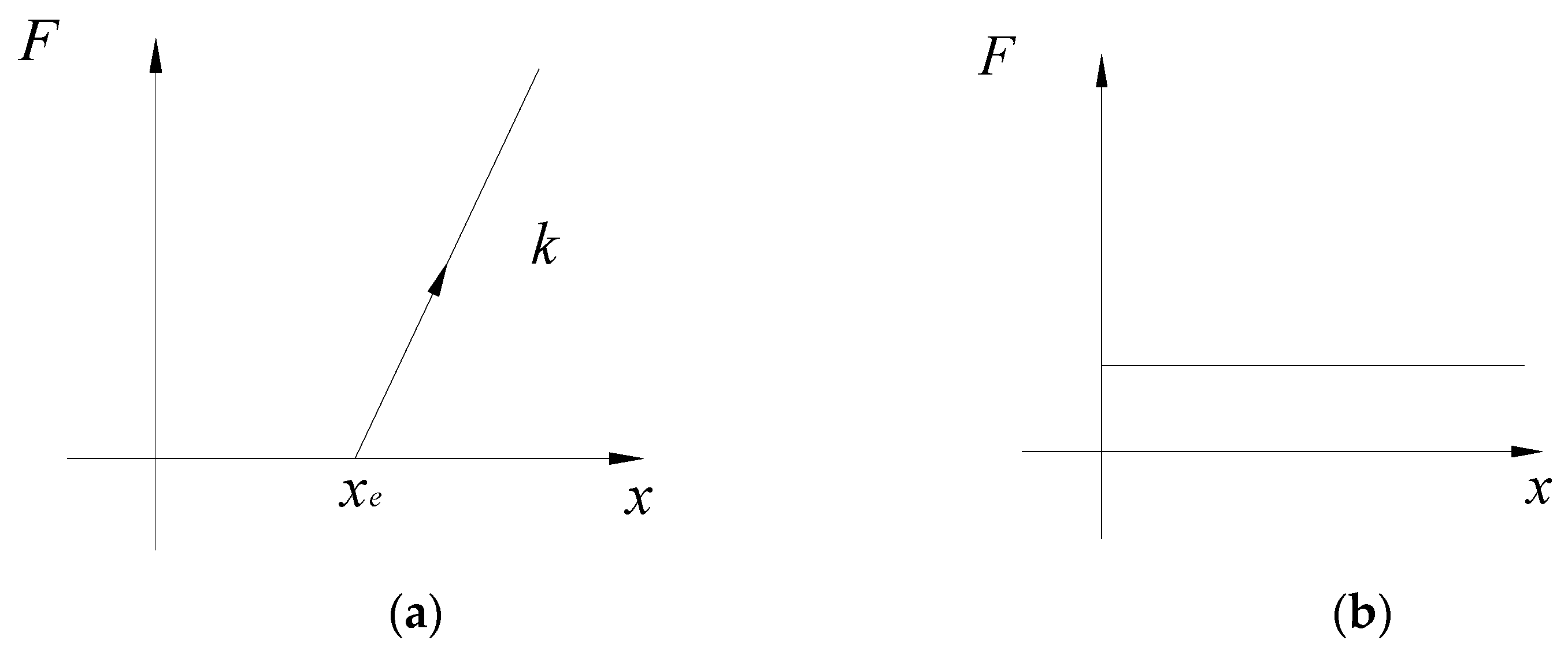
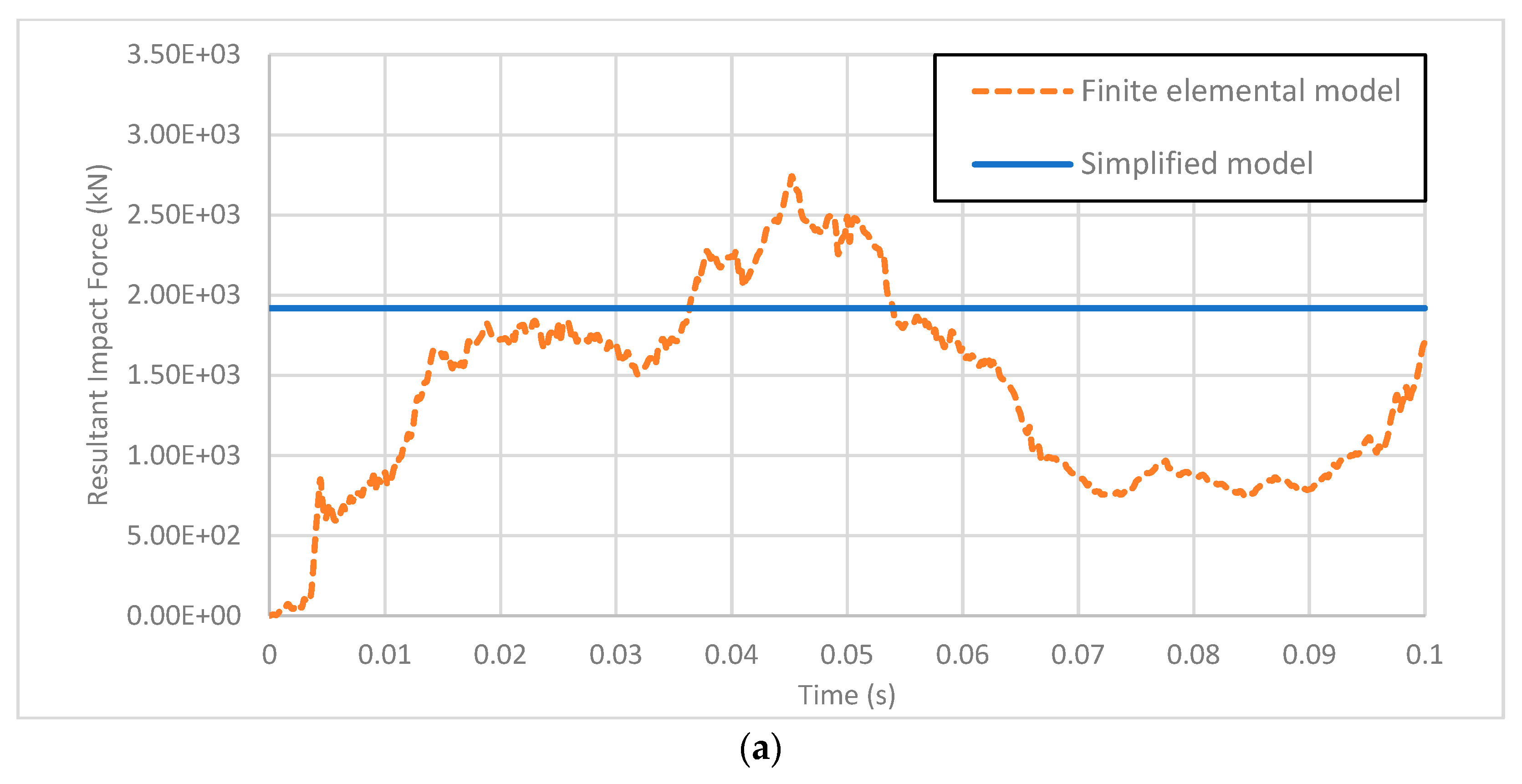
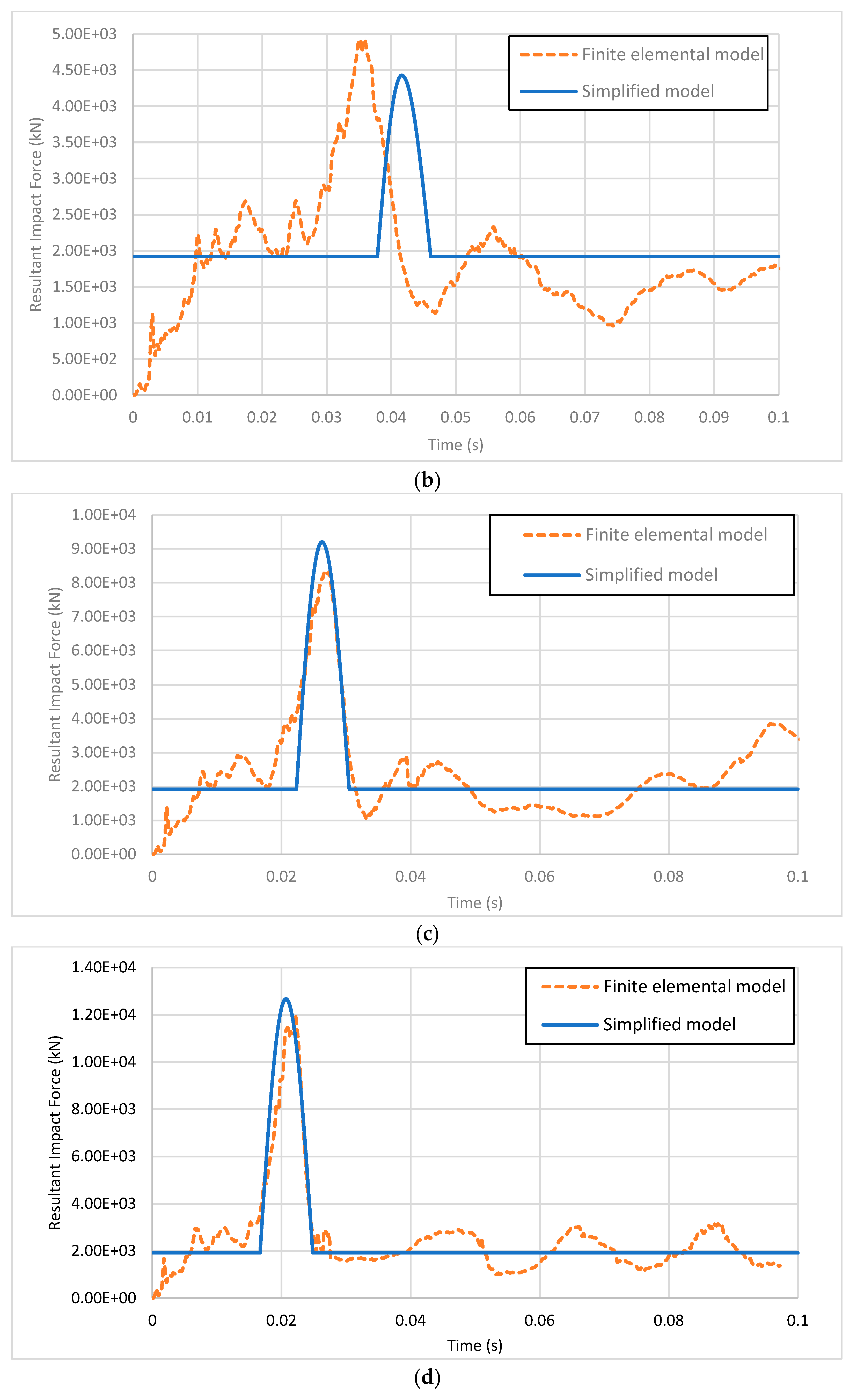
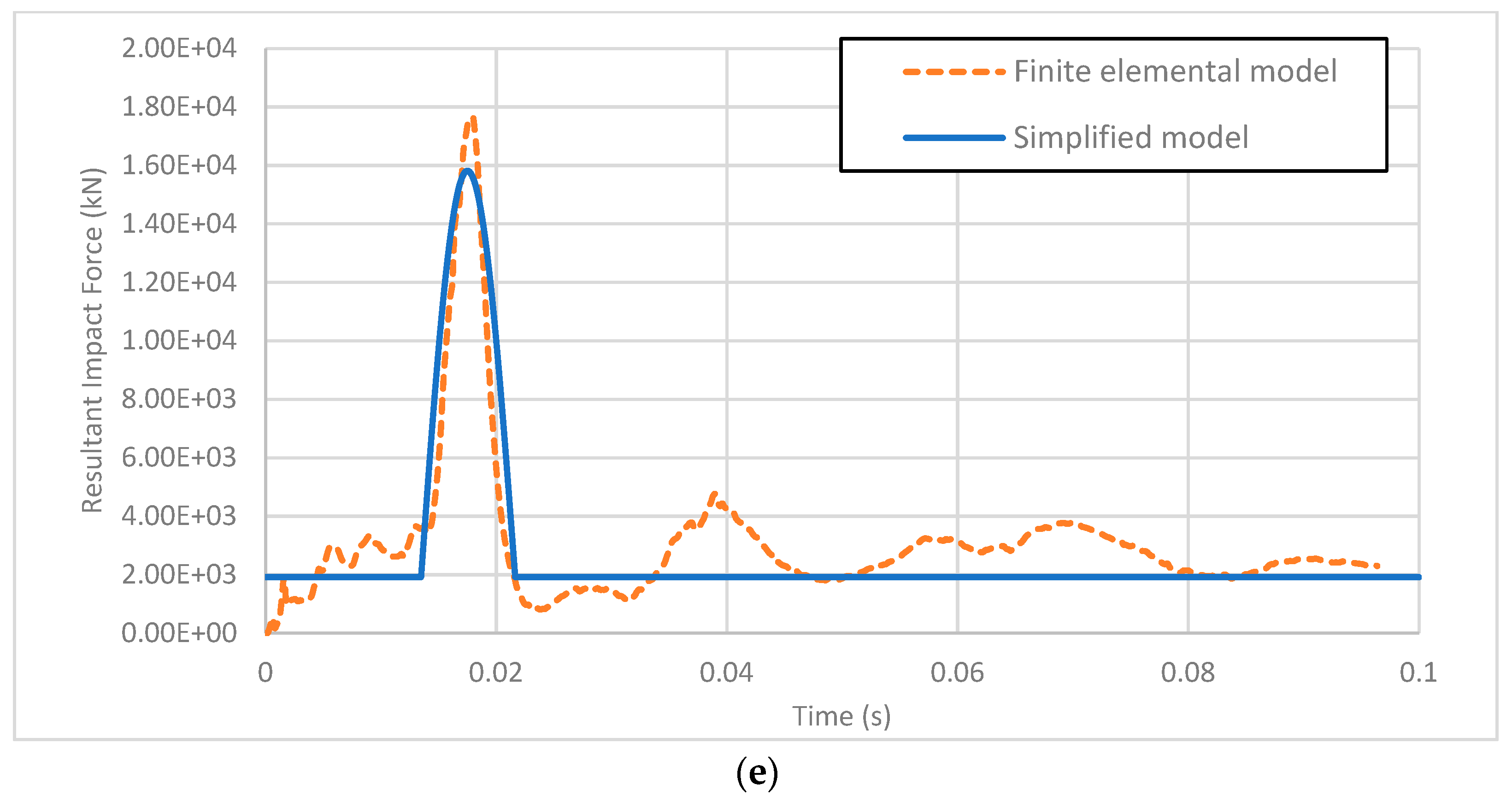
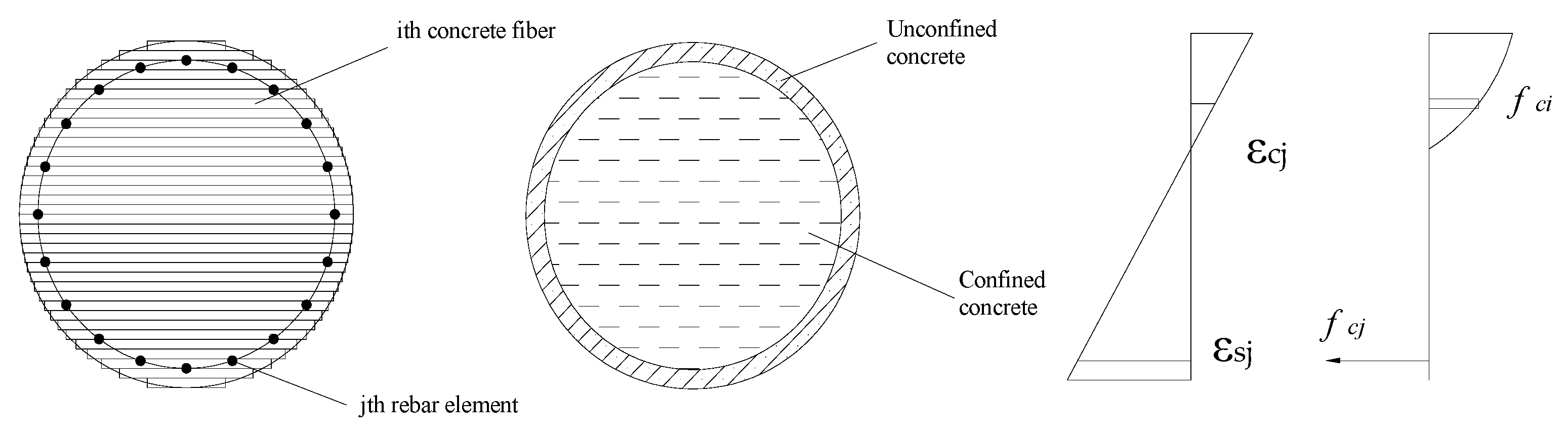
| Initial Velocity | Peak Dynamic Load (kN) | Equivalent Static Load (kN) | AASHTO LRFD (kN) | ||||
|---|---|---|---|---|---|---|---|
| Finite Element | Simplified Model | Error | Finite Element | Simplified Model | Error | ||
| 40 km/h | 2742.4 | 1919.0 | 30.02% | 1919.0 | 1919.0 | 0.00% | 2669 |
| 60 km/h | 4924.9 | 4427.3 | 10.10% | 2386.3 | 2182.0 | 8.56% | |
| 80 km/h | 8342.5 | 9198.9 | 10.27% | 2858.0 | 2675.9 | 6.38% | |
| 100 km/h | 11,923.7 | 12,670.4 | 6.26% | 3112.2 | 3036.1 | 2.45% | |
| 120 km/h | 17,634.7 | 15,814.4 | 10.32% | 3521.8 | 3362.4 | 4.53% | |
| Variables | Name | Units | Minimum | Maximum | Level | L[1] | L[2] | L[3] | L[4] | L[5] |
|---|---|---|---|---|---|---|---|---|---|---|
| A | Velocity | km/h | 40.00 | 120.00 | 5 | 40 | 60 | 80 | 100 | 120 |
| B | Concrete Strength | MPa | 27.58 | 55.16 | 3 | 27.58 | 41.37 | 55.16 | ||
| C | Diameter | m | 0.7620 | 1.07 | 3 | 0.762 | 0.9144 | 1.0668 | ||
| D | Length | m | 5.49 | 9.14 | 3 | 5.4864 | 7.3152 | 9.144 | ||
| E | Impact height | m | 0.3048 | 2.13 | 3 | 0.3048 | 1.2192 | 2.1336 | ||
| F | Axial stress | MPa | 0.0000 | 10.00 | 3 | 0 | 5 | 10 | ||
| G | Cargo | Ton | 0.0000 | 22.179 | 3 | 0 | 11.09 | 22.179 |
| Standard deviation | 6.264E+05 |
| Mean value (N) | 9.660E+06 |
| 0.9949 | |
| RMSE | 0.00535 |
| Standard deviation | 1.548E+05 |
| Mean value (N) | 2.705E+06 |
| 0.9779 | |
| RMSE | 0.00472 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Fu, C.C. Simplified Impact Load Model Analysis of Vehicle-to-Bridge Pier Collision. Infrastructures 2025, 10, 320. https://doi.org/10.3390/infrastructures10120320
Xu C, Fu CC. Simplified Impact Load Model Analysis of Vehicle-to-Bridge Pier Collision. Infrastructures. 2025; 10(12):320. https://doi.org/10.3390/infrastructures10120320
Chicago/Turabian StyleXu, Chaoran, and Chung C. Fu. 2025. "Simplified Impact Load Model Analysis of Vehicle-to-Bridge Pier Collision" Infrastructures 10, no. 12: 320. https://doi.org/10.3390/infrastructures10120320
APA StyleXu, C., & Fu, C. C. (2025). Simplified Impact Load Model Analysis of Vehicle-to-Bridge Pier Collision. Infrastructures, 10(12), 320. https://doi.org/10.3390/infrastructures10120320






