Seismic Vulnerability Assessment and Prioritization of Masonry Railway Tunnels: A Case Study
Abstract
1. Introduction
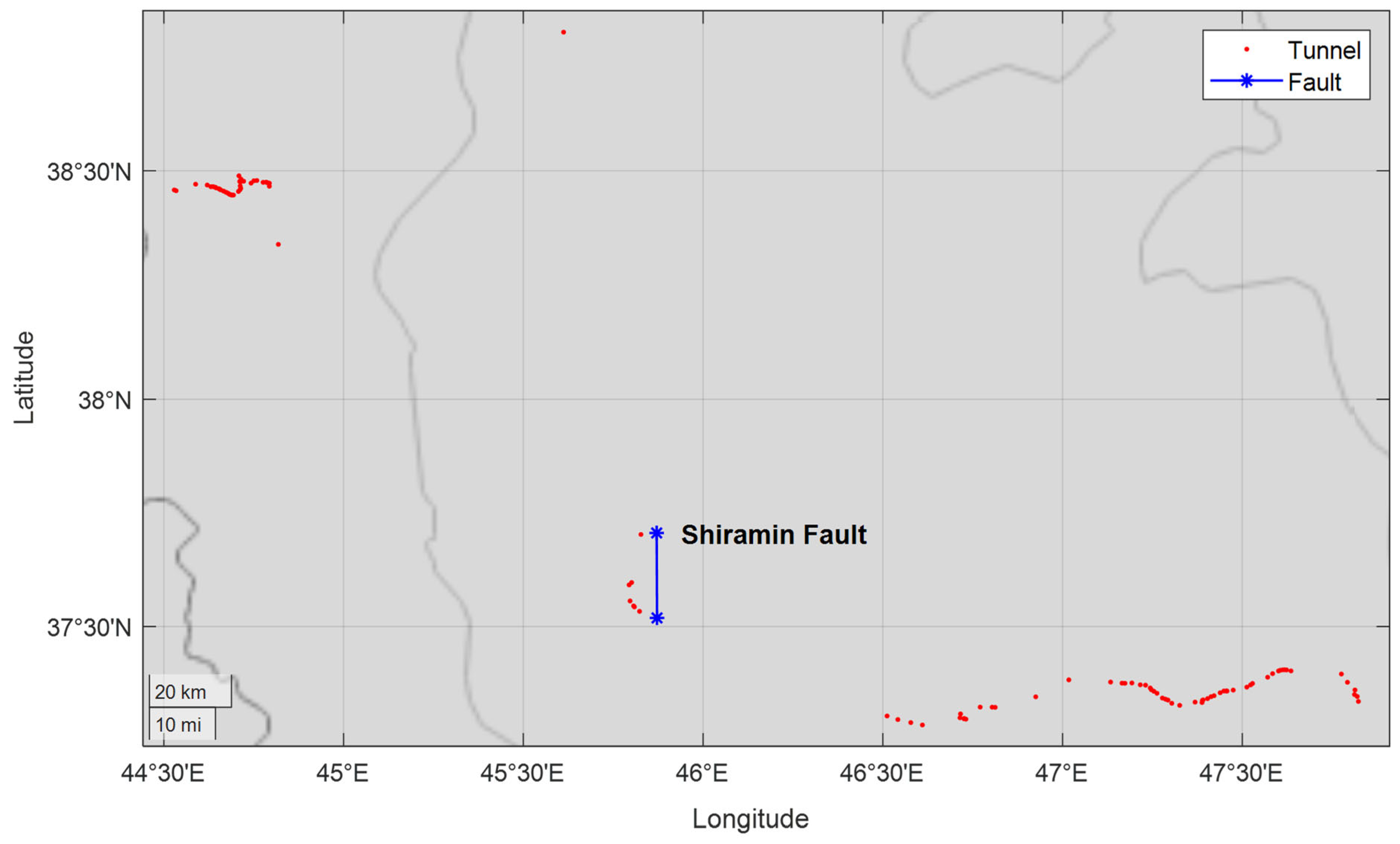
2. Network Topology and Tunnel Location Identification
3. Identification of Active Faults in the Region and Calculation of Intensity Measures
3.1. Determining Seismicity Parameters of Faults
3.1.1. Determination of Fault Length and Faulting Mechanism
3.1.2. Determination of the Maximum Magnitude of the Fault
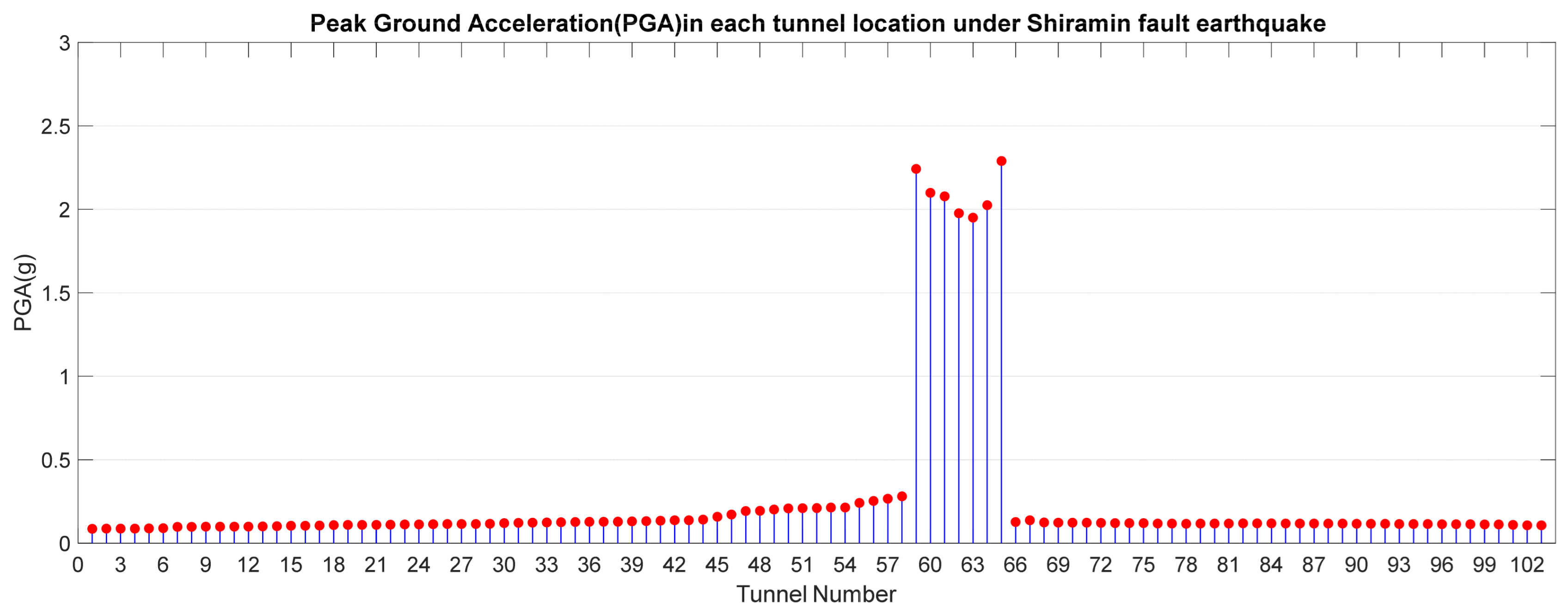
3.1.3. Calculation of the Peak Ground Acceleration and Peak Ground Displacement
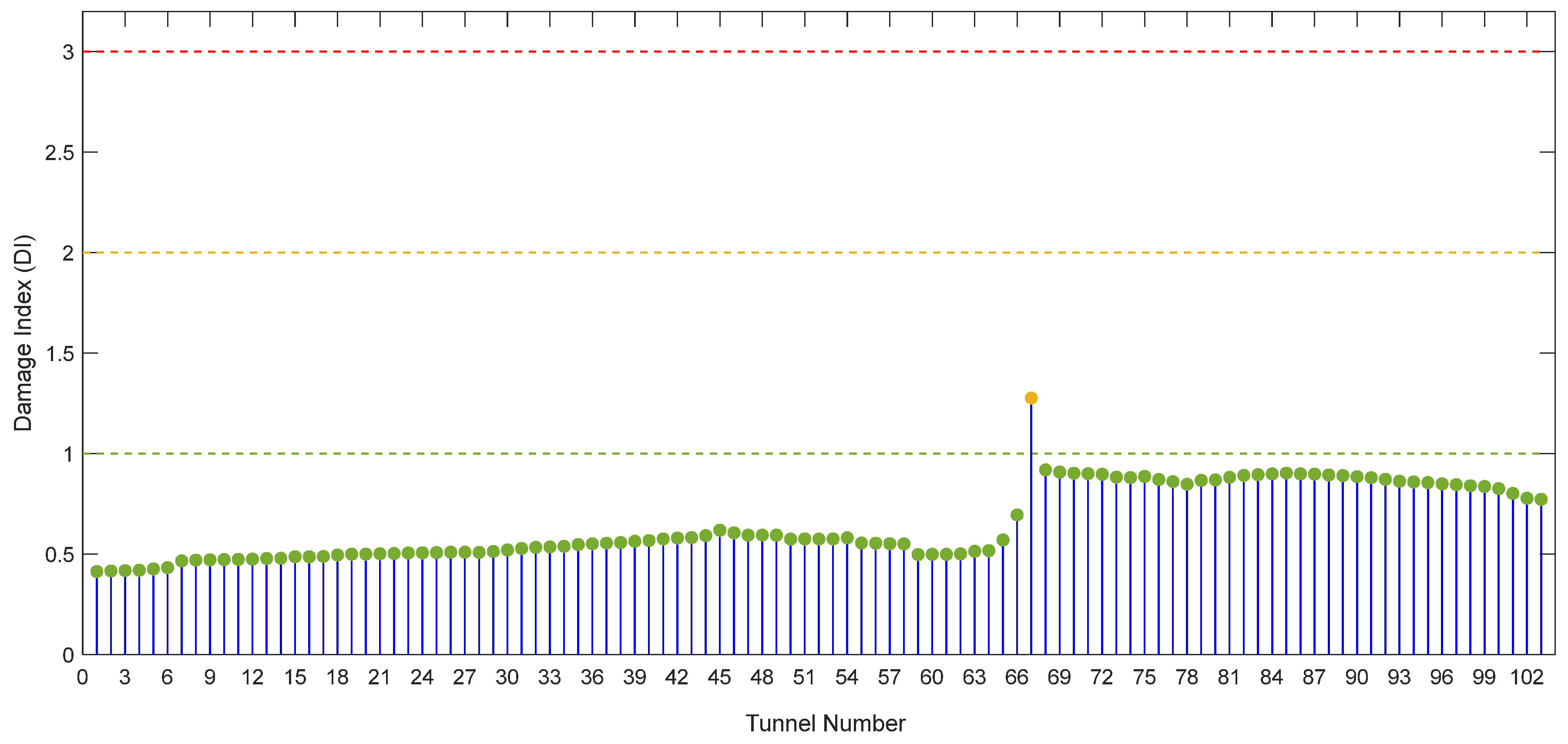
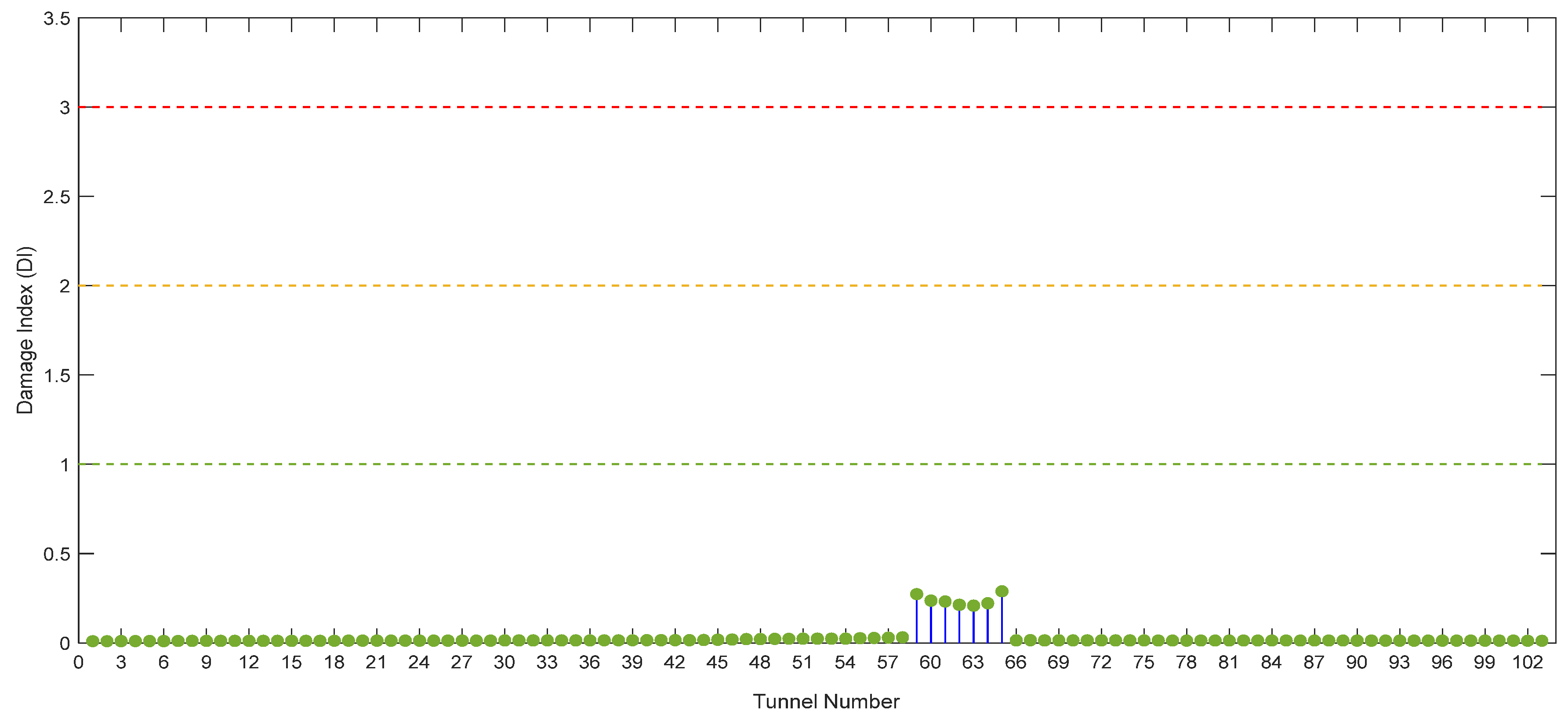
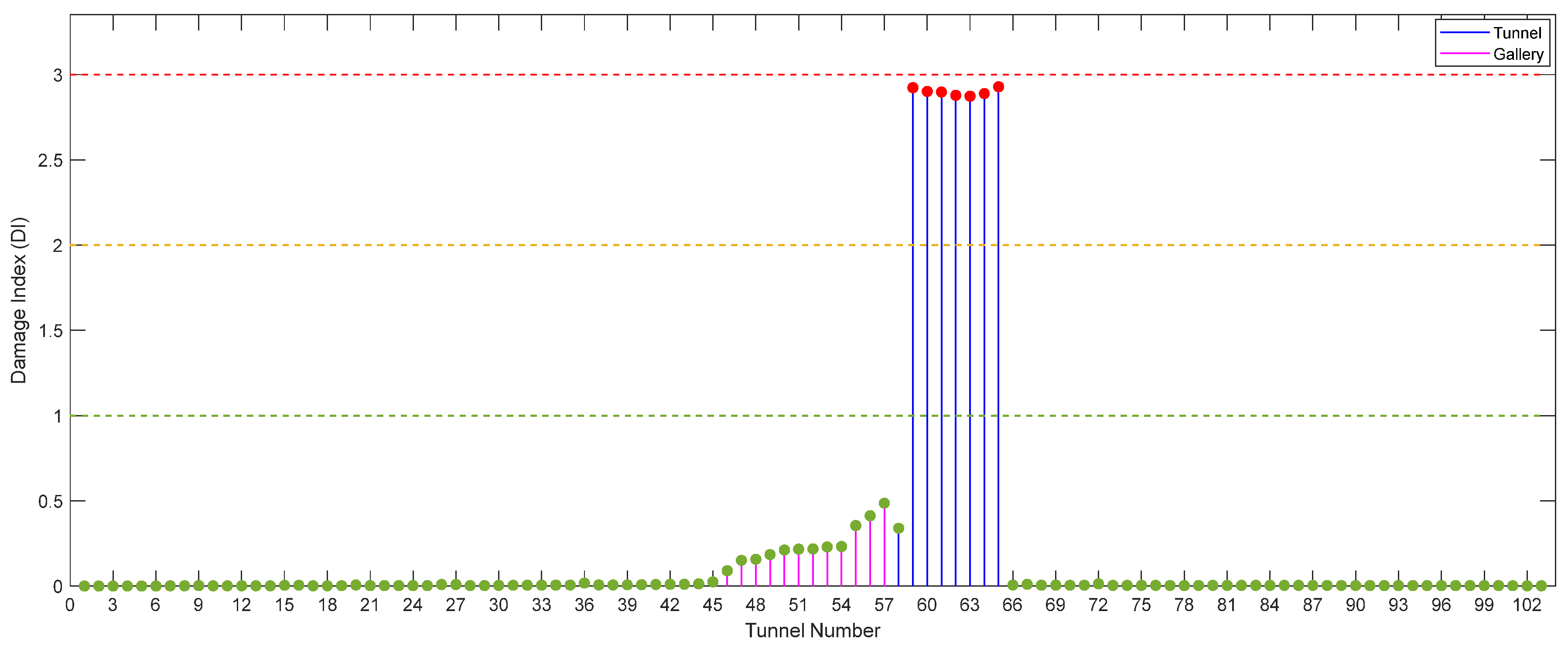
4. Tunnel Vulnerability Assessment
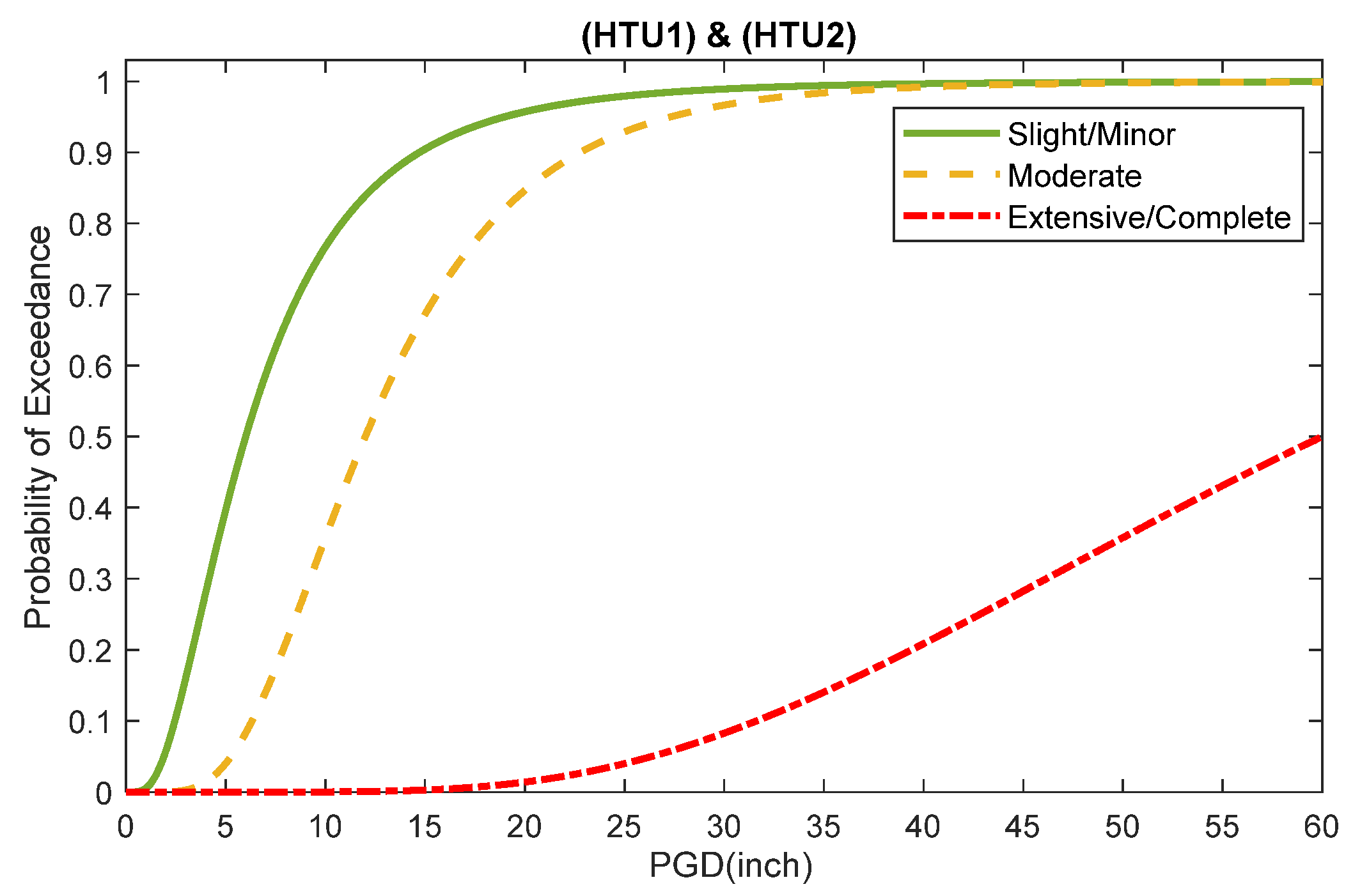
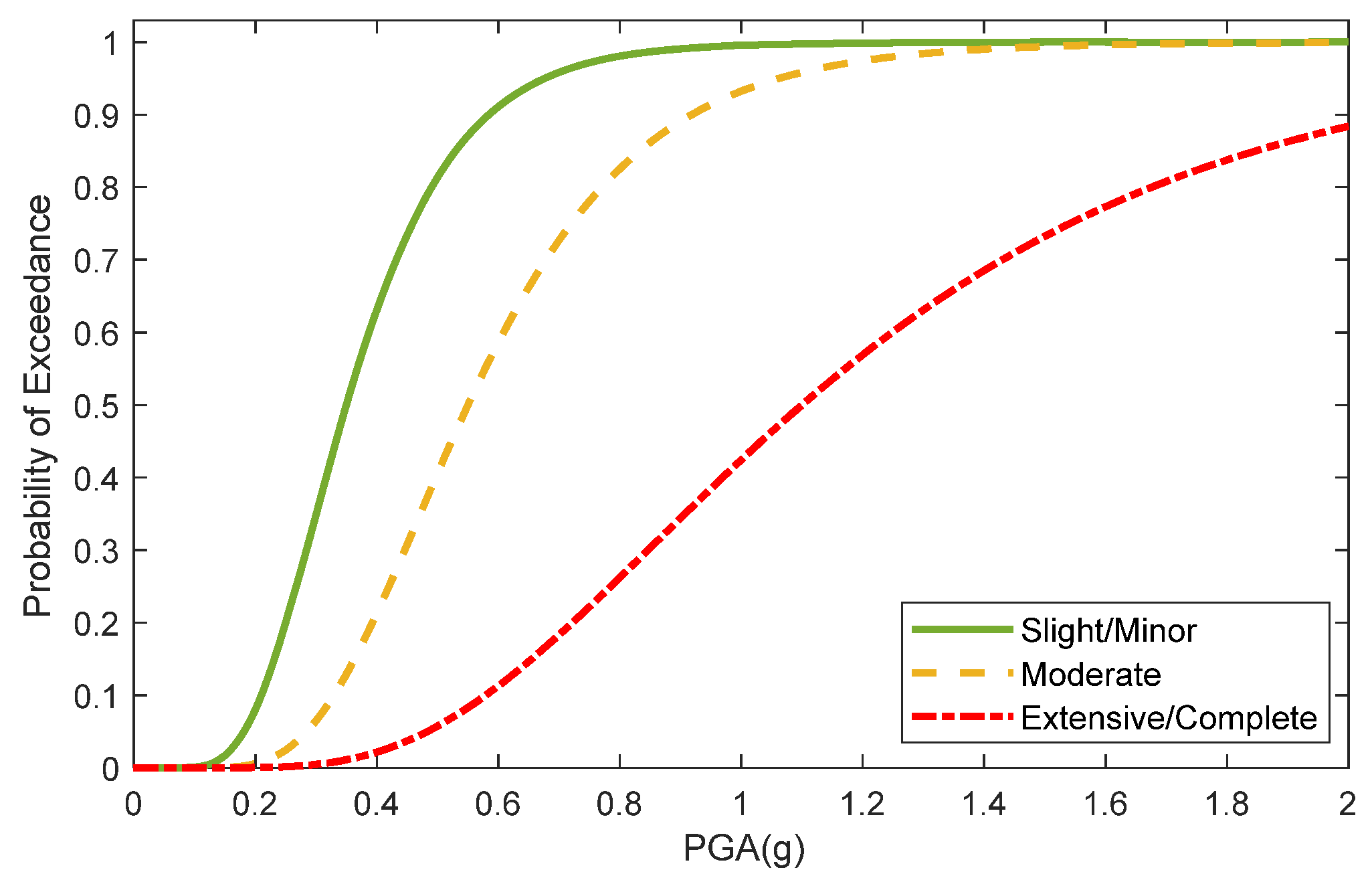
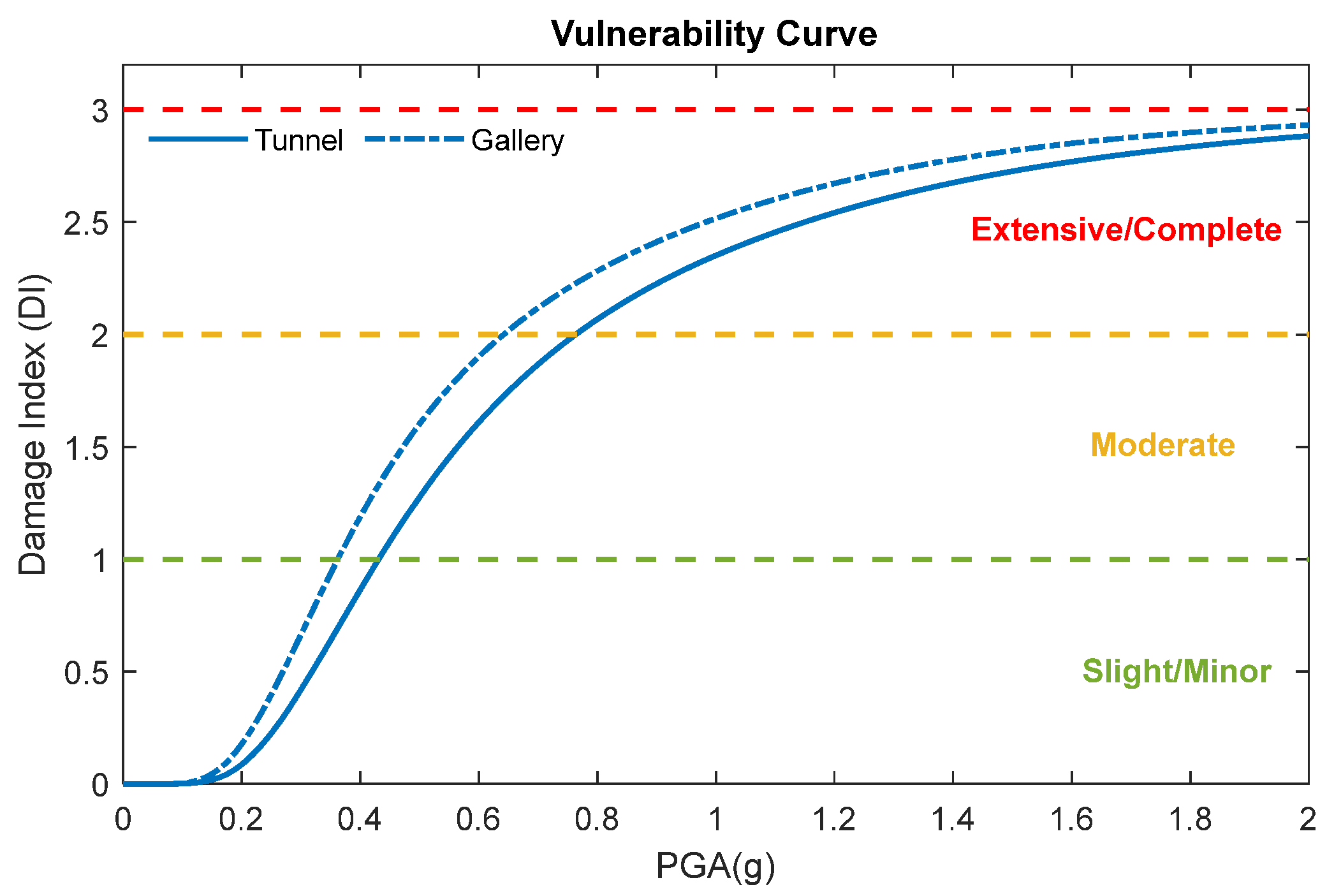
Damage Index and Vulnerability Curve
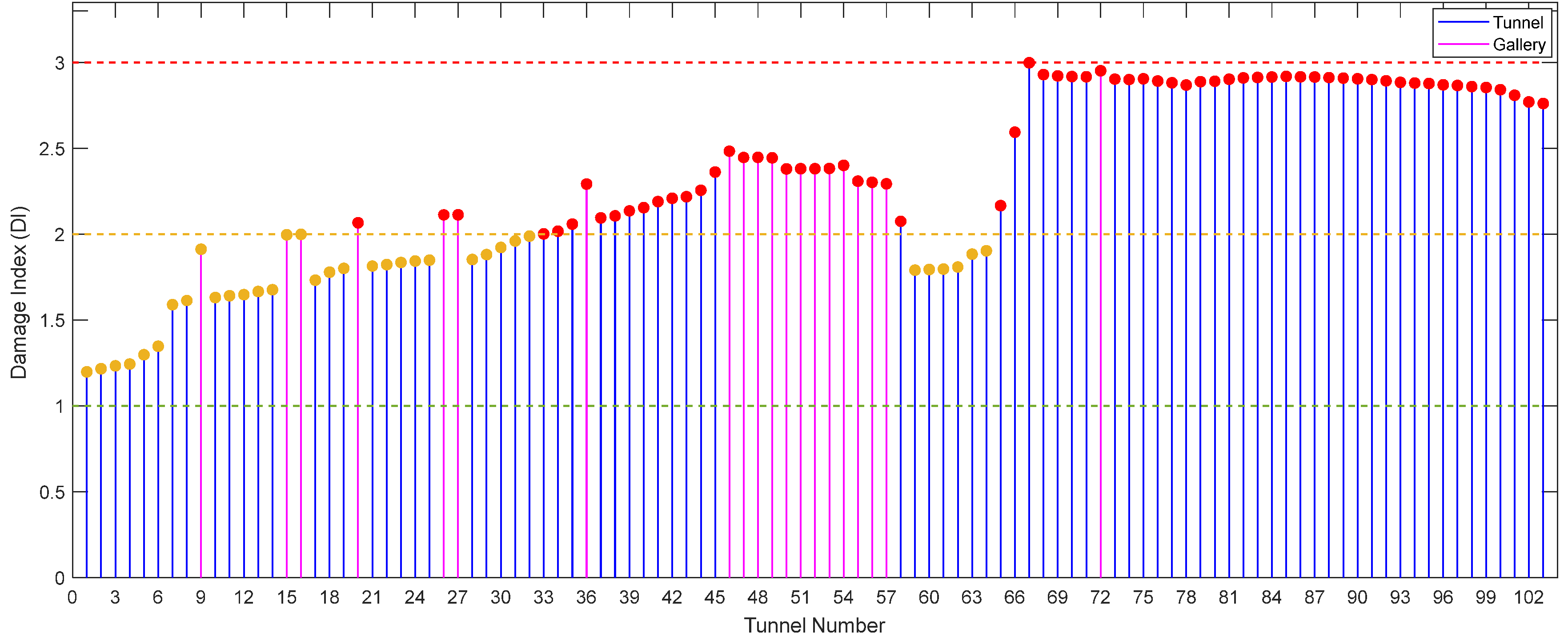
5. Tunnels Prioritization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IM | Intensity measure |
| PGA | Peak ground acceleration |
| PGD | Peak ground displacement |
| DI | Damage index |
| DS | Damage state |
| HTU | HAZUS tunnel |
| SVI | Seismic vulnerability index |
| VIW | Visual inspection weight |
| NPI | Normalized prioritization index |
References
- Huang, S.; Xin, C.; Song, D.; Feng, W.; Liu, X.; Wang, E.; Xu, T.; Xiong, X. Resilience assessment of the seismic damage mechanism of the Daliang high-speed railway tunnel in the 2022 Menyuan earthquake (Mw 6.7) in China. Transp. Geotech. 2024, 49, 101417. [Google Scholar] [CrossRef]
- Callisto, L.; Ricci, C. Interpretation and back-analysis of the damage observed in a deep tunnel after the 2016 Norcia earthquake in Italy. Tunn. Undergr. Space Technol. 2019, 89, 238–248. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Bobet, A.; Yuan, Y. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Space Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Asakura, T.; Sato, Y. Damage to mountain tunnels in hazard area. Soils Found. 1996, 36, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, T.; Su, J.; Lin, C.; Seng, C.; Huang, T. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, B.; Yang, X.; Tao, S. Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after Wenchuan earthquake. Eng. Geol. 2014, 180, 85–98. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Y.; Sugimoto, S. Seismic damage assessment of mountain tunnel: A case study on the Tawarayama tunnel due to the 2016 Kumamoto Earthquake. Tunn. Undergr. Space Technol. 2018, 71, 138–148. [Google Scholar] [CrossRef]
- Yao, C.; He, C.; Wang, T.; Chen, C.; Geng, P.; Dong, W.; Yuan, F.; Xu, G. Damages of highway tunnels during 2022 Luding earthquake (Mw = 6.6). Soil Dyn. Earthq. Eng. 2024, 177, 108357. [Google Scholar] [CrossRef]
- Chen, P.; Geng, P.; Chen, J.; Gu, W. The seismic damage mechanism of Daliang tunnel by fault dislocation during the 2022 Menyuan Ms6.9 earthquake based on unidirectional velocity pulse input. Eng. Fail. Anal. 2023, 145, 107047. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Y.; Maegawa, K. Mountain tunnel under earthquake force: A review of possible causes of damages and restoration methods. J. Rock Mech. Geotech. Eng. 2020, 12, 414–426. [Google Scholar] [CrossRef]
- Roy, N.; Sarkar, R. A review of seismic damage of mountain tunnels and probable failure mechanisms. Geotech. Geol. Eng. 2017, 35, 1–28. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, C.; Li, T.; Yuan, Y. Damage characteristics and influence factors of mountain tunnels under strong earthquakes. Nat. Hazards 2012, 61, 387–401. [Google Scholar] [CrossRef]
- Tsinidis, G.; de Silva, F.; Anastasopoulos, I.; Bilotta, E.; Bobet, A.; Hashash, Y.M.; He, C.; Kampas, G.; Knappett, J.; Madabhushi, G.; et al. Seismic behaviour of tunnels: From experiments to analysis. Tunn. Undergr. Space Technol. 2020, 99, 103334. [Google Scholar] [CrossRef]
- Wang, G.; Shi, L.; Wang, J. Experimental and numerical studies on the seismic response of adjacent horizontal parallel tunnels. Soil Dyn. Earthq. Eng. 2023, 172, 107992. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, Y.; Yao, X. Dynamic Response of Curved Tunnels under Vertical Incidence of Transversal SV Waves. Shock Vib. 2023, 8561647. [Google Scholar] [CrossRef]
- Lei, H.; Wu, H.; Lai, T. Shaking Table Tests for Seismic Response of Oblique Overlapped Tunnel. Shock Vib. 2021, 8816755. [Google Scholar] [CrossRef]
- Daraei, A.; Ali, H.F.; Qader, D.N.; Zare, S. Seismic retrofitting of rubble masonry tunnel: Evaluation of steel fiber shotcrete or inner concrete lining alternatives. Arab. J. Geosci. 2022, 15, 1074. [Google Scholar] [CrossRef]
- Chen, H.M.; Yu, H.S.; Smith, M.J. Physical model tests and numerical simulation for assessing the stability of brick-lined tunnels. Tunn. Undergr. Space Technol. 2016, 53, 109–119. [Google Scholar] [CrossRef]
- Idris, J.; Al-Heib, M.; Verdel, T. Numerical modelling of masonry joints degradation in built tunnels. Tunn. Undergr. Space Technol. 2009, 24, 617–626. [Google Scholar] [CrossRef]
- Idris, J.; Verdel, T.; Al-Heib, M. Numerical modelling and mechanical behaviour analysis of ancient tunnel masonry structures. Tunn. Undergr. Space Technol. 2008, 23, 251–263. [Google Scholar] [CrossRef]
- Far, A.M.; Nejati, H.R.; Goshtasbi, K.; Khosrotash, M.; Moosavi, S.A. Seismic fragility analysis for probabilistic risk assessment of underground structures. J. Earthq. Eng. 2024, 29, 265–287. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Q.; Zhou, X.; Wang, J.; Xu, B.; Liu, B. Research on structural defect characteristics and influencing factors for high-fill cut-and-cover tunnels in mountainous areas. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 4409–4422. [Google Scholar] [CrossRef]
- Antoniou, M.; Mantakas, A.; Nikitas, N.; Fuentes, R. A numerical case study on the long-term seismic assessment of reinforced concrete tunnels in corrosive environments. J. Rock Mech. Geotech. Eng. 2023, 15, 551–572. [Google Scholar] [CrossRef]
- Tsinidis, G.; Karatzetzou, A.; Stefanidou, S.; Markogiannaki, O. Developments in seismic vulnerability assessment of tunnels and underground structures. Geotechnics 2022, 2, 209–249. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, Y.; Liu, H.; Liu, H.; Miao, Y. Performance-based seismic assessment of shield tunnels by incorporating a nonlinear pseudostatic analysis approach for the soil-tunnel interaction. Tunn. Undergr. Space Technol. 2021, 114, 103981. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, Z.; Chen, H.; Ren, Y. Seismic fragility analysis of tunnels with different buried depths in a soft soil. Sustainability 2020, 12, 892. [Google Scholar] [CrossRef]
- Andreotti, G.; Lai, C.G. Use of fragility curves to assess the seismic vulnerability in the risk analysis of mountain tunnels. Tunn. Undergr. Space Technol. 2019, 91, 103008. [Google Scholar] [CrossRef]
- HAZUS. Multi-Hazard Loss Estimation Methodology: Earthquake Model Hazus-MH 2.1 Technical Manual; Federal Emergency Management Agency: Washington, DC, USA, 2013. [Google Scholar]
- Argyroudis, S.A.; Pitilakis, K.D. Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. Earthq. Eng. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Huang, G.; Qiu, W.; Zhang, J. Modelling seismic fragility of a rock mountain tunnel based on support vector machine. Soil Dyn. Earthq. Eng. 2017, 102, 160–171. [Google Scholar] [CrossRef]
- Avanaki, M.J.; Hoseini, A.; Vahdani, S.; de Santos, C.; de la Fuente, A. Seismic fragility curves for vulnerability assessment of steel fiber reinforced concrete segmental tunnel linings. Tunn. Undergr. Space Technol. 2018, 78, 259–274. [Google Scholar] [CrossRef]
- Zhao, G.; Gardoni, P.; Xu, L.; Xie, L. Seismic probabilistic capacity models and fragility estimates for the transversal lining section of circular tunnels. J. Earthq. Eng. 2023, 27, 1281–1301. [Google Scholar] [CrossRef]
- Ansari, A.; Rao, K.S.; Jain, A.K. Seismic vulnerability of tunnels in Jammu and Kashmir for post seismic functionality. Geotech. Geol. Eng. 2023, 41, 1371–1396. [Google Scholar] [CrossRef]
- Saleh, A.M.; Rahgozar, M.A. Finite element seismic analysis of soil–tunnel interactions in clay soils. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 835–849. [Google Scholar] [CrossRef]
- Luo, H.; Du, L.; Zheng, C.; Yang, X.; Wang, T.; Wang, Y. Study on the performance of mountain tunnel against mainshock–aftershock based on resilience evaluation framework. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 2215–2234. [Google Scholar] [CrossRef]
- Junwei, Z.; Wan, Y.; Chenling, Z.; Tuo, C. Seismic stability of a mountain tunnel portal section lining. Int. J. Geotech. Eng. 2020, 14, 376–394. [Google Scholar] [CrossRef]
- Ghadimi, C.A.; Tahghighi, H. Numerical finite element analysis of underground tunnel crossing an active reverse fault: A case study on the Sabzkouh segmental tunnel. Geomech. Geoengin. 2019, 14, 155–166. [Google Scholar] [CrossRef]
- Yu, H.; Yuan, Y.; Bobet, A. Seismic analysis of long tunnels: A review of simplified and unified methods. Undergr. Space 2017, 2, 73–87. [Google Scholar] [CrossRef]
- Reddy, A.D.; Singh, A. A simplistic method for assessing seismic damage in rock tunnels before earthquake: Part 1—Damage prediction and validation using seismic damage classification of tunnels. Rock Mech. Rock Eng. 2024, 57, 11001–11032. [Google Scholar] [CrossRef]
- Ansari, A.; Rao, K.S.; Jain, A.K.; Ansari, A. Deep learning model for predicting tunnel damages and track serviceability under seismic environment. Model. Earth Syst. Env. 2023, 9, 1349–1368. [Google Scholar] [CrossRef]
- Wang, L.; Geng, P.; Chen, J.; Wang, T. Machine learning-based fragility analysis of tunnel structure under different impulsive seismic actions. Tunn. Undergr. Space Technol. 2023, 133, 104953. [Google Scholar] [CrossRef]
- Huang, Z.; Argyroudis, S.A.; Pitilakis, K.; Zhang, D.; Tsinidis, G. Fragility assessment of tunnels in soft soils using artificial neural networks. Undergr. Space 2022, 7, 242–253. [Google Scholar] [CrossRef]
- Jafari, M. System identification of a soil tunnel based on a hybrid artificial neural network–numerical model approach. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 889–899. [Google Scholar] [CrossRef]
- Xu, M.; Cui, C.; Zhao, J.; Xu, C.; Zhang, P.; Su, J. Fuzzy seismic fragility analysis of underground structures considering multiple failure criteria. Tunn. Undergr. Space Technol. 2024, 145, 105614. [Google Scholar] [CrossRef]
- Jin, H.; Jin, X. Performance assessment framework and deterioration repairs design for highway tunnel using a combined weight-fuzzy theory: A case study. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 3259–3281. [Google Scholar] [CrossRef]
- Trifunac, M.D.; Todorovska, M.I. Note on the useable dynamic range of accelerographs recording translation. Soil Dyn. Earthq. Eng. 2001, 21, 275–286. [Google Scholar] [CrossRef]
- Talebian, M.; Jackson, J. A reappraisal of earthquake focal mechanisms and active shortening in the Zagros mountains of Iran. Geophys. J. Int. 2004, 156, 506–526. [Google Scholar] [CrossRef]
- Kowsari, M.; Ghazi, H.; Kijko, A.; Javadi, H.R.; Shabani, E. Estimating the maximum earthquake magnitude in the Iranian Plateau. J. Seismol. 2021, 25, 845–862. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar] [CrossRef]
- Nowroozi, A.A. Probability of peak ground horizontal and peak ground vertical accelerations at tehran and surrounding areas. Pure Appl. Geophys. 2010, 167, 1459–1474. [Google Scholar] [CrossRef]
- Ghassemi, M.R. Surface ruptures of the Iranian earthquakes 1900–2014: Insights for earthquake fault rupture hazards and empirical relationships. Earth-Sci. Rev. 2016, 156, 1–13. [Google Scholar] [CrossRef]
- Thingbaijam, K.S.; Martin, M.P.; Goda, K. New empirical earthquake source-scaling laws. Bull. Seismol. Soc. Am. 2017, 107, 2225–2246. [Google Scholar] [CrossRef]
- Darzi, A.; Zolfaghari, M.R.; Cauzzi, C.; Fäh, D. An empirical ground-motion model for horizontal PGV, PGA, and 5% damped elastic response spectra (0.01–10 s) in Iran. Bull. Seismol. Soc. Am. 2019, 109, 1041–1057. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H.; Modaresnezhad, M.; Mousavi, M. New ground-motion prediction equations using multi expression programing. J. Earthq. Eng. 2011, 15, 511–536. [Google Scholar] [CrossRef]
- SYNER-G. Guidelines for Deriving Seismic Fragility Functions of Elements at Risk: Buildings, Lifelines, Transportation Networks and Critical Facilities; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hosseini, Y.; Mohammadi, R.K.; Yang, T.Y. A comprehensive approach in post-earthquake blockage prediction of urban road network and emergency resilience optimization. Reliab. Eng. Syst. Saf. 2024, 244, 109887. [Google Scholar] [CrossRef]
- Hosseini, Y.; Mohammadi, R.K.; Yang, T.Y. Resource-based seismic resilience optimization of the blocked urban road network in emergency response phase considering uncertainties. Int. J. Disaster Risk Reduct. 2023, 85, 103496. [Google Scholar] [CrossRef]



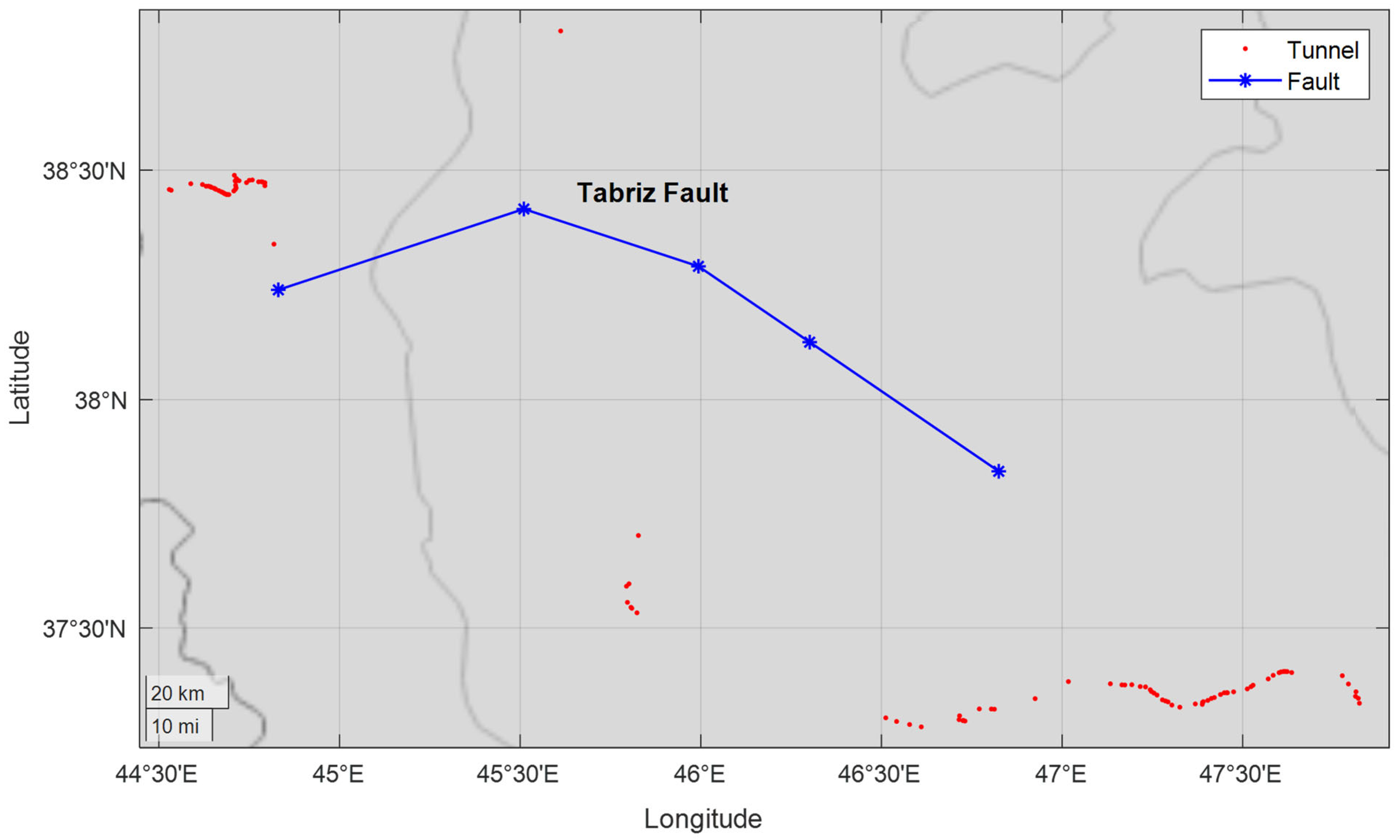

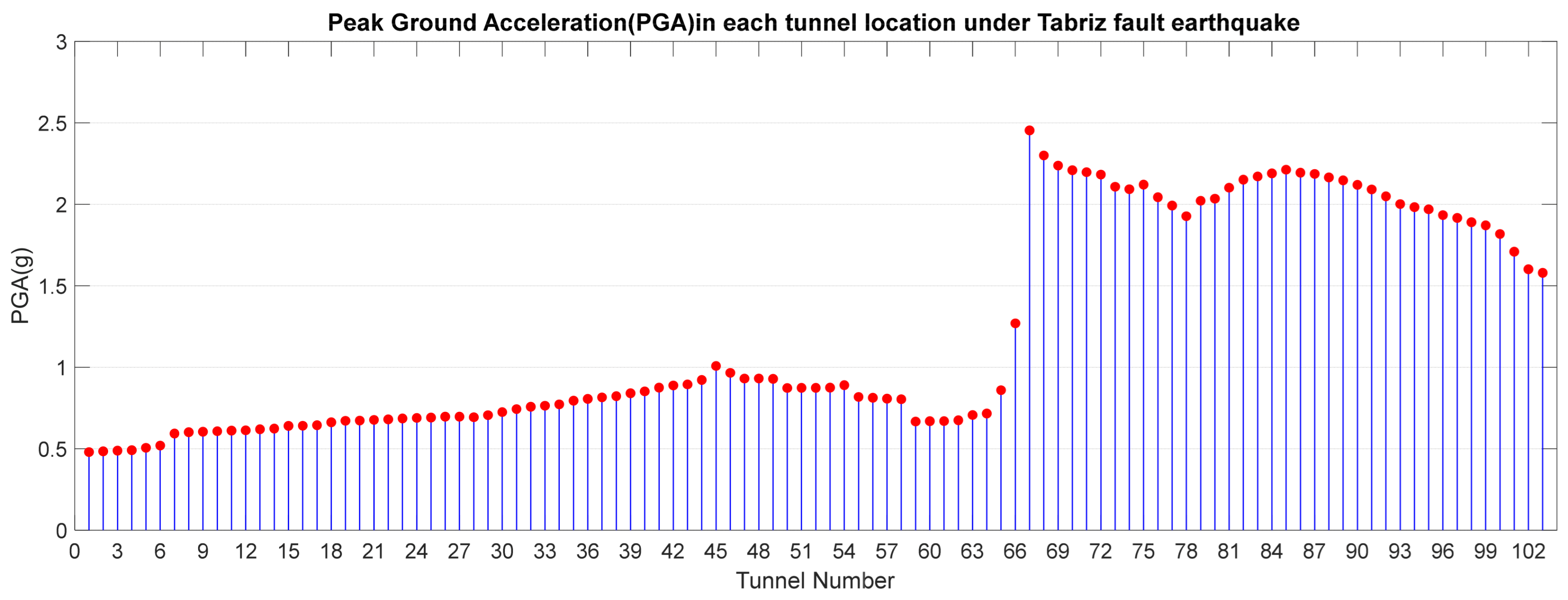





| Number | Fault Name | Length (km) | Faulting Mechanism |
|---|---|---|---|
| 1 | Tabriz | 240 | Strike-Slip (right-lateral) |
| 2 | Bozqush | 102 | Reverse |
| 3 | Maku | 100 | Strike-Slip (right-lateral) |
| 4 | Takhte Solaiman (Tekab) | 70 | Strike-Slip (right-lateral) and Thrust |
| 5 | Ahar | 65 | Strike-Slip (right-lateral) |
| 6 | Chahar Sotun | 32 | Reverse (thrust) |
| 7 | Buket | 25 | Reverse (thrust) |
| 8 | Hessar Talkhuk | 23 | Reverse (thrust) |
| 9 | Shiramin | 21 | Reverse (thrust) |
| 10 | Talesh Kandi | 21 | Reverse (thrust) |
| 11 | Khanyordi | 19 | Strike-Slip (left-lateral) |
| 12 | Mahkuh | 17 | Reverse |
| Number | Fault Name | |
|---|---|---|
| 1 | Tabriz | 7.7 |
| 2 | Bozqush | 7.2 |
| 3 | Maku | 7.2 |
| 4 | Takhte Solaiman (Tekab) | 7 |
| 5 | Ahar | 7 |
| 6 | Chahar Sotun | 6.7 |
| 7 | Buket | 6.6 |
| 8 | Hessar Talkhuk | 6.6 |
| 9 | Shiramin | 6.5 |
| 10 | Talesh Kandi | 6.5 |
| 11 | Khanyordi | 6.5 |
| 12 | Mahkuh | 6.4 |
| Damage State | Damage Description |
|---|---|
| None Damage (k = 0) | --- |
| Slight/Minor (k = 1) | Minor cracking of the tunnel liner (damage requires no more than cosmetic repair) and some rock falling, or slight settlement of the ground at a tunnel portal |
| Moderate (k = 2) | Moderate cracking of the tunnel liner and rock falling |
| Extensive/Complete (k = 3) | Major ground settlement at a tunnel portal and extensive cracking of the tunnel liner/Major cracking of the tunnel liner, which may include possible collapse |
| Classification | Damage State | Θ | β |
|---|---|---|---|
| Bored/Drilled (HTU1) & Cut/Cover (HTU2) | Slight/Minor | 6.0 | 0.7 |
| Moderate | 12.0 | 0.5 | |
| Extensive/Complete | 60.0 | 0.5 |
| PGD and PGA | |
|---|---|
| Damage State | Damage Index |
| Slight/Minor | |
| Moderate | |
| Extensive/Complete | |
| Typology | Damage State | Θ (g) | β |
|---|---|---|---|
| Rock tunnels with poor-to-average conditions | Slight/Minor | 0.35 | 0.4 |
| Moderate | 0.55 | 0.4 | |
| Extensive/Complete | 1.1 | 0.5 | |
| Rock tunnels with good conditions | Slight/Minor | 0.61 | 0.4 |
| Moderate | 0.82 | 0.4 | |
| Extensive/Complete | NA * | - | |
| Alluvial (Soil) and Cut and Cover Tunnels with poor to average conditions | Slight/Minor | 0.3 | 0.4 |
| Moderate | 0.45 | 0.4 | |
| Extensive/Complete | 0.95 | 0.5 | |
| Alluvial (Soil) and Cut and Cover Tunnels with good conditions | Slight/Minor | 0.5 | 0.4 |
| Moderate | 0.7 | 0.4 | |
| Extensive/Complete | NA * | - |
| Damage Level | Damage Description |
|---|---|
| High | Forming large gaps in the expansion joints, Significant ground settlement in the tunnel portal, High instability of the trench at the entrance-exit of the tunnel, Major horizontal cracks in the roof and sidewall of the tunnel, severe breakage and detachment of the lining, and water seepage from the crack, Falling rock cover of the tunnel |
| Medium | Minor vertical crack in the sidewall, Protrusion of the rock lining, defects of the drainage system, cracking of the tunnel portal and head-wall |
| Low | Slight cracks in the lining, Slight water leakage from the cover and floor, laxity of the rock lining |
| Damage level | Non | Low | Medium | High |
|---|---|---|---|---|
| Visual Inspection Weight (VIW) | 0 | 1 | 2 | 3 |
| NPI | <60 | 60–70 | 70–80 | 80–100 |
|---|---|---|---|---|
| Prioritization | Fourth Priority | Third Priority | Second Priority | First Priority |
| Prioritization | Tunnel ID | Location | SVI | VIW | NPI | ||
|---|---|---|---|---|---|---|---|
| Main Class | Sub Class | Longitude | Latitude | ||||
| First Priority | 1-1 | 27G * | ° | ° | 14.008 | 2 | 93.46 |
| 1-2 | 33 | ° | ° | 12.067 | 3 | 87.97 | |
| 1-3 | 79 | ° | ° | 11.448 | 3 | 86.36 | |
| 1-4 | 92 | ° | ° | 11.224 | 3 | 83.05 | |
| 1-5 | 16G | ° | ° | 14.127 ** | 0 | 82.48 | |
| 1-6 | 15G | ° | ° | 14.117 | 0 | 82.42 | |
| 1-7 | 20G | ° | ° | 14.110 | 0 | 82.38 | |
| 1-8 | 97 | ° | ° | 11.085 | 3 | 82.23 | |
| 1-9 | 26G | ° | ° | 14.012 | 0 | 81.81 | |
| 1-10 | 9G | ° | ° | 13.858 | 0 | 80.91 | |
| Second Priority | 2-1 | 46G | ° | ° | 10.522 | 3 | 78.95 |
| 2-2 | 36 | ° | ° | 13.519 | 0 | 78.92 | |
| 2-3 | 78 | ° | ° | 11.414 | 2 | 78.32 | |
| 2-4 | 103 | ° | ° | 10.326 | 3 | 77.80 | |
| 2-5 | 72G | ° | ° | 11.885 | 1 | 75.23 | |
| 2-6 | 3 | ° | ° | 10.731 | 2 | 74.33 | |
| 2-7 | 69 | ° | ° | 11.717 | 1 | 74.25 | |
| 2-8 | 70 | ° | ° | 11.702 | 1 | 74.16 | |
| 2-9 | 74 | ° | ° | 11.598 | 1 | 73.57 | |
| 2-10 | 17 | ° | ° | 12.55 | 0 | 73.30 | |
| 2-11 | 1 | ° | ° | 10.547 | 2 | 73.26 | |
| 2-12 | 18 | ° | ° | 12.534 | 0 | 73.18 | |
| 2-13 | 19 | ° | ° | 12.513 | 0 | 73.06 | |
| 2-14 | 21 | ° | ° | 12.495 | 0 | 72.95 | |
| 2-15 | 22 | ° | ° | 12.488 | 0 | 72.91 | |
| 2-16 | 14 | ° | ° | 12.473 | 0 | 72.83 | |
| 2-17 | 23 | ° | ° | 12.469 | 0 | 72.80 | |
| 2-18 | 81 | ° | ° | 11.466 | 1 | 72.78 | |
| 2-19 | 24 | ° | ° | 12.453 | 0 | 72.71 | |
| 2-20 | 25 | ° | ° | 12.436 | 0 | 72.61 | |
| 2-21 | 13 | ° | ° | 12.409 | 0 | 72.45 | |
| 2-22 | 28 | ° | ° | 12.406 | 0 | 72.43 | |
| 2-23 | 29 | ° | ° | 12.343 | 0 | 72.07 | |
| 2-24 | 12 | ° | ° | 12.336 | 0 | 72.02 | |
| 2-25 | 11 | ° | ° | 12.311 | 0 | 71.88 | |
| 2-26 | 10 | ° | ° | 12.284 | 0 | 71.72 | |
| 2-27 | 8 | ° | ° | 12.251 | 0 | 71.53 | |
| 2-28 | 67 | ° | ° | 11.228 | 1 | 71.39 | |
| 2-29 | 7 | ° | ° | 12.216 | 0 | 71.32 | |
| 2-30 | 30 | ° | ° | 12.201 | 0 | 71.24 | |
| 2-31 | 93 | ° | ° | 11.175 | 1 | 71.09 | |
| 2-32 | 31 | ° | ° | 12.125 | 0 | 70.79 | |
| 2-33 | 32 | ° | ° | 12.090 | 0 | 70.59 | |
| 2-34 | 34 | ° | ° | 12.037 | 0 | 70.28 | |
| Third Priority | 3-1 | 35 | ° | ° | 11.972 | 0 | 69.90 |
| 3-2 | 37 | ° | ° | 11.894 | 0 | 69.44 | |
| 3-3 | 38 | ° | ° | 11.872 | 0 | 69.32 | |
| 3-4 | 39 | ° | ° | 11.793 | 0 | 68.86 | |
| 3-5 | 68 | ° | ° | 11.732 | 0 | 68.50 | |
| 3-6 | 101 | ° | ° | 10.731 | 1 | 68.49 | |
| 3-7 | 40 | ° | ° | 11.710 | 0 | 68.37 | |
| 3-8 | 71 | ° | ° | 11.694 | 0 | 68.28 | |
| 3-9 | 73 | ° | ° | 11.622 | 0 | 68.86 | |
| 3-10 | 75 | ° | ° | 11.581 | 0 | 67.62 | |
| 3-11 | 41 | ° | ° | 11.555 | 0 | 67.46 | |
| 3-12 | 76 | ° | ° | 11.494 | 0 | 67.11 | |
| Third Priority | 3-13 | 82 | ° | ° | 11.477 | 0 | 67.01 |
| 3-14 | 83 | ° | ° | 11.467 | 0 | 66.95 | |
| 3-15 | 80 | ° | ° | 11.458 | 0 | 66.90 | |
| 3-16 | 77 | ° | ° | 11.456 | 0 | 66.88 | |
| 3-17 | 84 | ° | ° | 11.447 | 0 | 66.83 | |
| 3-18 | 42 | ° | ° | 11.422 | 0 | 66.69 | |
| 3-19 | 85 | ° | ° | 11.373 | 0 | 66.40 | |
| 3-20 | 43 | ° | ° | 11.362 | 0 | 66.34 | |
| 3-21 | 86 | ° | ° | 11.346 | 0 | 66.25 | |
| 3-22 | 87 | ° | ° | 11.337 | 0 | 66.19 | |
| 3-23 | 50G | ° | ° | 8.327 | 3 | 66.13 | |
| 3-24 | 88 | ° | ° | 11.318 | 0 | 66.08 | |
| 3-25 | 89 | ° | ° | 11.306 | 0 | 66.01 | |
| 3-26 | 90 | ° | ° | 11.287 | 0 | 65.90 | |
| 3-27 | 91 | ° | ° | 11.262 | 0 | 65.76 | |
| 3-28 | 6 | ° | ° | 11.166 | 0 | 65.20 | |
| 3-29 | 94 | ° | ° | 11.159 | 0 | 65.15 | |
| 3-30 | 95 | ° | ° | 11.146 | 0 | 65.08 | |
| 3-31 | 44 | ° | ° | 11.101 | 0 | 64.82 | |
| 3-32 | 96 | ° | ° | 11.085 | 0 | 64.72 | |
| 3-33 | 98 | ° | ° | 11.048 | 0 | 64.51 | |
| 3-34 | 99 | ° | ° | 11.006 | 0 | 64.26 | |
| 3-35 | 5 | ° | ° | 10.988 | 0 | 64.20 | |
| 3-36 | 100 | ° | ° | 10.937 | 0 | 63.86 | |
| 3-37 | 65 | ° | ° | 8.754 | 2 | 62.74 | |
| 3-38 | 4 | ° | ° | 10.736 | 0 | 62.68 | |
| 3-39 | 2 | ° | ° | 10.625 | 0 | 62.04 | |
| 3-40 | 55G | ° | ° | 7.368 | 3 | 60.54 | |
| 3-41 | 102 | ° | ° | 10.358 | 0 | 60.48 | |
| Fourth Priority | 4-1 | 54G | ° | ° | 8.237 | 2 | 59.77 |
| 4-2 | 64 | ° | ° | 8.168 | 2 | 59.37 | |
| 4-3 | 63 | ° | ° | 8.097 | 2 | 58.96 | |
| 4-4 | 57G | ° | ° | 7.083 | 3 | 58.87 | |
| 4-5 | 59 | ° | ° | 7.945 | 2 | 58.05 | |
| 4-6 | 60 | ° | ° | 7.914 | 2 | 57.89 | |
| 4-7 | 61 | ° | ° | 7.891 | 2 | 57.75 | |
| 4-8 | 62 | ° | ° | 7.862 | 2 | 57.58 | |
| 4-9 | 45 | ° | ° | 9.823 | 0 | 57.35 | |
| 4-10 | 49G | ° | ° | 8.781 | 1 | 57.11 | |
| 4-11 | 51G | ° | ° | 8.295 | 1 | 54.27 | |
| 4-12 | 52G | ° | ° | 8.281 | 1 | 54.19 | |
| 4-13 | 47G | ° | ° | 9.200 | 0 | 53.72 | |
| 4-14 | 48G | ° | 9.113 | 0 | 53.21 | ||
| 4-15 | 56G | ° | ° | 7.214 | 1 | 47.96 | |
| 4-16 | 53G | ° | ° | 8.195 | 0 | 47.85 | |
| 4-17 | 58 | ° | ° | 5.184 | 1 | 36.11 | |
| 4-18 | 66 | ° | ° | 4.781 | 0 | 27.91 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, Y.; Karami Mohammadi, R.; Yang, T.Y. Seismic Vulnerability Assessment and Prioritization of Masonry Railway Tunnels: A Case Study. Infrastructures 2025, 10, 254. https://doi.org/10.3390/infrastructures10100254
Hosseini Y, Karami Mohammadi R, Yang TY. Seismic Vulnerability Assessment and Prioritization of Masonry Railway Tunnels: A Case Study. Infrastructures. 2025; 10(10):254. https://doi.org/10.3390/infrastructures10100254
Chicago/Turabian StyleHosseini, Yaser, Reza Karami Mohammadi, and Tony Y. Yang. 2025. "Seismic Vulnerability Assessment and Prioritization of Masonry Railway Tunnels: A Case Study" Infrastructures 10, no. 10: 254. https://doi.org/10.3390/infrastructures10100254
APA StyleHosseini, Y., Karami Mohammadi, R., & Yang, T. Y. (2025). Seismic Vulnerability Assessment and Prioritization of Masonry Railway Tunnels: A Case Study. Infrastructures, 10(10), 254. https://doi.org/10.3390/infrastructures10100254








