Towards Sustainable Construction: Hybrid Prediction Modeling for Compressive Strength of Rice Husk Ash Concrete

Abstract

Rice husk ash (RHA) offers an eco-friendly way to improve concrete. Owing to the complex mix design of RHA concrete, accurately predicting its strength remains a challenge. This study addresses this need by compiling a dataset of 291 compressive strength records for RHA concrete. Using seven key input variables (e.g., cement, water, and RHA content), three novel hybrid models were developed by integrating the XGBoost algorithm with advanced metaheuristic optimizers: Northern Goshawk Optimization (NGO), Arctic Puffin Optimization (APO), and Catch Fish Optimization Algorithm (CFOA). These hybrid models were compared against classic Random Forest (RF), and Support Vector Regression (SVR), and unoptimized XGBoost models. The results demonstrated that all hybrid models significantly outperformed the unoptimized classic models. The APO–XGBoost model achieved the highest prediction accuracy on the testing set (RMSE = 3.5462, R² = 0.9579 on testing set), followed by CFOA–XGBoost and NGO–XGBoost. Cement content was revealed to be the most influential parameter on compressive strength, as determined by a sensitivity analysis, ahead of both water and coarse aggregate content. This research confirms the superiority of metaheuristic-optimized hybrid models for predicting the strength of RHA concrete, providing a reliable data-driven tool to support its mix design and promote its application in sustainable construction.

1. Introduction

Concrete, as an indispensable fundamental material in the field of construction engineering, relies heavily on the widespread use of Portland cement in its production process, which is accompanied by substantial carbon dioxide emissions, imposing a significant environmental challenge [1,2]. The incorporation of industrial and agricultural by-products—including fly ash, silica fume, and bagasse—into concrete mix designs has been pursued to lower the carbon footprint linked to its production [3,4]. This effectively decreases the consumption of traditional cement and yields positive environmental benefits. Among these alternatives stands rice husk ash (RHA). RHA is not merely an agricultural waste product; after appropriate processing it becomes rich in amorphous silica with significant pozzolanic activity. Enhancing the sustainability of concrete, and improving its microstructure and long-term performance, are both achievable all through the incorporation of RHA [5,6]. RHA concrete typically demonstrates higher final strength, superior impermeability, and stronger resistance to chemical corrosion, making it highly suitable for structural engineering applications with stringent durability requirements. Therefore, RHA concrete has been recognized as a promising green construction material. The application of RHA concrete in infrastructure helps extend the service life of structures while simultaneously reducing maintenance demands and environmental impacts [7].

Given its role as the principal indicator for assessing the safety of concrete structures, it follows that the compressive strength of concrete is regulated by mix design. For example, advances in 3D-printed concrete highlight how optimized mix design parameters can significantly influence concrete properties [8]. Similarly, sustainable pavement design studies incorporating recycled concrete aggregate have demonstrated that integrating life-cycle assessment and cost analysis can guide strength and economically viable infrastructure designs [9]. According to Ganesan et al. [10], the strength of RHA concrete with up to 30% RHA replacement surpassed the baseline group; it reached a maximum at 15% replacement, after which a decline was observed. It was demonstrated by Chopra et al. [11] that the incorporation of RHA as a 15% cement replacement in self-compacting concrete resulted in significantly enhanced tensile and compressive strengths; the compressive strength, in particular, showed a 36% rise following 56 days of curing. Employing highly reactive RHA of cement-comparable fineness at replacement levels of 7.5% and 15%, Ferraro et al. [12] conducted measurements on the compressive strength, tensile strength, and durability of concrete. It was demonstrated that RHA incorporation enhanced both the compressive strength at multiple curing ages and the 28-day tensile strength across different replacement ratios. Moreover, a notable reduction in concrete porosity was also achieved. It has been indicated by several studies that the compressive strength of RHA concrete is not solely determined by the replacement ratio but is also shaped by contributors such as curing age, water content, and the proportion of coarse to fine aggregates [13,14,15]. Nowadays, the compressive strength determination of RHA concrete still heavily relies on standardized laboratory experiments, which are time-consuming, labor-intensive, and costly, posing challenges in scaling up from small-scale testing to practical engineering applications. It becomes imperative, therefore, to develop prediction models capable of delivering both efficiency and accuracy. In this way, the complex behavior of RHA concrete under varying conditions can be understood. Moreover, a reliable basis for its mix design and engineering application could also be provided.

The rapid advancement of supervised learning techniques in recent years has catalyzed a multitude of successful intelligent regression and classification applications throughout various disciplines [16,17,18,19,20,21]. In the field of construction engineering, scholars have addressed the accuracy limitations of empirical models in predicting concrete strength by introducing multiple artificial intelligence models. Al-Hashem et al. [22] initially demonstrated the applicability of artificial neural network (ANN) and gene expression programming in predicting the compressive strength of RHA concrete. Subsequently, Amin [23] compared the performance of decision trees, bagging regression, and AdaBoost regression in predicting RHA concrete properties, finding that the bagging regression model delivered the best performance. Paul et al. [24] proposed the use of algorithms such as Categorical boosting (CatBoost), gradient boosting machine (GBM), convolutional neural network (CNN), and gated recurrent units (GRU) to predict the compressive strength of RHA concrete, identifying the GRU as yielding the smallest prediction error. Kovacevic et al. [25] systematically evaluated several machine learning models, such as Boosted Trees and neural network ensembles, for predicting the compressive strength of rice husk ash concrete, ultimately identifying Boosted Trees as the optimal model.

The recent introduction of hybrid machine-learning models has expanded the toolkit for estimating the compressive strength of RHA concrete, supplementing single models. In an investigation by Huang et al. [26] into the optimization capabilities of three evolutionary algorithms (FA, PSO, and GWO) for support vector regression (SVR) models, the FA-SVR combination was identified as the top performer. A study was conducted by Li et al. [27] to explore the capability of the seagull optimization algorithm (SOA)–SVR, SOA–RF, CMRSA–ANN, and ELM models for predicting compressive strength of RHA concrete, with the CMRSA–ANN model being identified as the top performer. In recent years, XGBoost, as an emerging ensemble learning tool, has demonstrated outstanding prediction performance in many fields [28,29]. It not only has an efficient gradient boosting framework, but also can generally achieve better prediction accuracy and robustness on small- and medium-sized structured data sets through parallel computing and regularization. Sathiparan [30] has found that the XGBoost shows excellent performance in RHA concrete strength prediction, with R² of 0.89 on the testing set. A summary of RHA concrete strength prediction studies was given, as shown in

Table 1. Summary of RHA concrete strength prediction studies.

Reference No.	Dataset Size	Sample Size	Method	Accuracy
[22]	310	cement; fine aggregate; coarse aggregate; water; superplasticizer; fly ash; rice husk ash; age	Gene expression programming, ANN (best model)	R2 = 0.89 (Training); R2 = 0.77 (Testing)
[23]	192	age, cement, RHA, water, superplasticizer, aggregate	Decision trees, bagging (best model), AdaBoost	R2 = 0.93 (Testing)
[24]	1212	cement, water, fine aggregate, coarse aggregate, RHA, age, superplasticizer	CatBoost, GBM, CNN, GRU (best model)	R2 = 0.99 (Training); R2 = 0.97 (Testing)
[25]	909	cement, water, fine aggregate, coarse aggregate, RHA, age, superplasticizer	Multiple linear regression, regression tree, tree bagger, random forest, boosted trees (best model), support vector regression (SVR), neural network, an ensemble of neural networks, Gaussian process regression	R2 = 0.943 (Testing)
[26]	291	water, fine aggregate, coarse aggregate, cement, RHA, superplasticizer, age	FA–SVR (best model), PSO–SVR, GWO–SVR	R2 = 0.9530 (Training); R2 = 0.9560 (Testing)
[27]	192	age, cement, RHA, superplasticizer, aggregate, water	CMRSA (circular mapping-reptile search algorithm)–ANN (best model), SOA–SVR, SOA–random forest, ANN, Extreme Learning Machine	R2 = 0.9679 (Training); R2 = 0.9709 (Testing)
[30]	795	fine aggregate-to-binder ratio, RHA-to-binder ratio, water-to-binder ratio, age	linear regression, ANN, k-nearest neighbors, SVR, eXtreme Gradient Boosting (XGBoost, best model)	R2 = 0.94 (Training); R2 = 0.89 (Testing)

. In fact, if we select hyperparameters reasonably, there may be still room for improvement in the performance of the XGBoost model in RHA concrete strength prediction. Metaheuristic algorithms, as an efficient hyperparameter tuning method, have demonstrated considerable optimization ability. However, in the context of accurately predicting the compressive strength of RHA concrete, newly developed metaheuristic algorithms in recent years have not yet been effectively integrated into the hyperparameter optimization of the XGBoost model. Combining the XGBoost model with advanced metaheuristic algorithms is expected to provide more accurate predictions of RHA concrete strength.

In light of this, to address the need for high-precision prediction of RHA concrete, this study compiled a dataset of 291 compressive strength records of RHA concrete. Three hybrid models leveraging XGBoost and advanced metaheuristics were developed using seven mix design variables as inputs. Moreover, three single regression models—XGBoost, RF, and SVR—were developed for comparative evaluation of prediction performance. The optimal model was identified through a comprehensive multi-metric evaluation. Furthermore, the importance of each input was also analyzed. This study is expected to furnish the methodological support required for engineering application of RHA concrete. Thereby, it promotes the resource utilization of agricultural waste, thus contributing to the sustainable evolution of concrete.

2. Database Description

The compiled rice husk ash (RHA) concrete database integrates experimental data from multiple published papers [31,32,33,34,35,36,37], comprising a total of 291 sets of RHA concrete strength data. Ranging from 16 to 92.21 MPa, the compressive strengths of the gathered specimens are characterized by key parameters that incorporate the contents of water, cement, fine aggregate (FA), coarse aggregate (CA), rice husk ash (RHA), superplasticizer (SP), and age. Statistical indexes of variables in the RHA concrete strength database could be found in

Table 2. Statistical indexes of variables in the RHA concrete strength database.

Variables	Water (kg/m3)	Cement (kg/m3)	FA (kg/m3)	CA (kg/m3)	RHA (kg/m3)	Age (Days)	SP (kg/m3)	CS (MPa)
Median	165.00	450.00	633.00	1006.70	43.60	14.00	2.60	54.62
Maximum	221.00	783.00	956.90	1324.00	153.00	91.00	72.60	92.21
Minimum	132.40	240.00	344.00	906.00	0.00	1.00	0.00	16.00
Mean	168.89	449.93	649.43	1061.99	44.10	21.92	6.05	53.56
Standard deviation	24.936	90.684	111.805	141.66	34.372	24.585	9.905	17.847

. Note that, like existing concrete strength prediction research, this study does not consider the impact of material manufacturer and specimen size on compressive strength of RHA concrete, but all data collected followed standard concrete testing procedures. Furthermore, relationships among variables were analyzed using a data matrix plot along with Spearman’s correlation coefficient (Figure 1). An examination of the database reveals that the absolute correlation coefficients between input variables are all beneath the 0.5 threshold, indicating weak linear correlations among the inputs. This suggests no significant redundancy among the input variables, supporting their suitability for use in nonlinear modeling of the strength of RHA concrete.

3. Data-Driven Approaches

3.1. XGBoost

Built upon the gradient boosting framework, XGBoost functions as an efficient machine learning tool. Its core concept lies in establishing a powerful prediction model by integrating multiple weak learners. To reduce the prediction error progressively, the algorithm operates by continuously adding modified tree models. In each cycle, it fits the negative gradient of the current model’s loss function to generate a new weak learner [38]. The workflow of XGBoost could be found in Figure 2. Building upon traditional gradient boosting, XGBoost introduces a regularization term into the objective function. To control model complexity and mitigate overfitting risks, the regularization term functions by penalizing the leaf node count and applying L1 or L2 regularization to their weights, which in turn enhances generalization. Moreover, the approximation of the loss function in XGBoost is achieved through a second-order Taylor expansion. This approach, which leverages both the first-order gradients and the second-order Hessian matrix, allows for more precise determination of tree structures and optimal leaf node weights, thereby accelerating model convergence. XGBoost also supports feature and instance subsampling, further improving model robustness. Additionally, by using a weighted quantile sketch algorithm to approximate candidate split points, it optimizes the efficiency of split point selection on large-scale datasets. Owing to its exceptional prediction performance, flexible parameter tuning mechanisms, and strong scalability, the extensive adoption of XGBoost spans a diverse range of regression and classification tasks. Its proven efficacy in practical engineering [39,40].

3.2. Northern Goshawk Optimization (NGO)

Drawing inspiration from the northern goshawk’s distinctive hunting techniques comes Northern Goshawk Optimization (NGO), a recently proposed metaheuristics [41]. This algorithm simulates two key phases of the goshawk’s predation process: prey identification (exploration phase), chasing and escaping (exploitation phase), thereby achieving an effective optimization (Figure 3). The algorithm initializes by randomly generating a set of candidate solutions, known as the goshawk population. Each of these goshawks corresponds to a potential answer for the problem. To enhance the global exploratory potential of the NGO, each iteration begins with a prey identification phase. During this phase, every goshawk randomly selects a prey and formulates its attack strategy guided by fitness value. Following this, the algorithm enters the chase and escape phase. This critical step emulates the close-range hunting behavior of goshawks. It also refines solution quality through localized fine search, thereby strengthening the local exploitation ability of goshawk population. The NGO algorithm could update goshawk positions using straightforward formulas, offering advantages such as few parameters, clear structure, and ease of implementation. Therefore, researchers have successfully employed it in several fields, including photovoltaic model parameter identification [42] and UAV path planning [43].

3.3. Arctic Puffin Optimization (APO)

The biological behaviors of the Arctic puffin serve as the inspiration for the Arctic Puffin Optimization (APO), a novel metaheuristic optimization technique [43]. In natural environment, puffins survive efficiently through collective flight and cooperative foraging—behaviors that APO skillfully maps into an optimization search process (Figure 4). Two primary phases form the foundation of this algorithm: aerial flight and underwater foraging. Represented by these phases are the crucial optimization processes of exploration and exploitation. During the exploration phase, APO employs a Lévy flight pattern to simulate the long-distance movement of puffins, enabling the algorithm to conduct a broad global search and avoid the local optima. The introduction of a velocity factor further enhances the search diversity. For the exploitation, the algorithm mimics the underwater hunting strategy, using a cooperation mechanism that allows search individuals to work together to encircle and approach the optimal solution. An adaptive factor is also incorporated, permitting the algorithm to adjust search intensity according to environmental feedback, thereby achieving precise localization. The framework of APO emphasizes balance and adaptability, enabling it to effectively handle complex optimization problems without requiring gradient information, demonstrating strong global optimization capability. With proven effectiveness, the APO algorithm serves important functions in network detection and power system engineering [44,45].

3.4. Catch Fish Optimization Algorithm (CFOA)

Simulating the cooperative fishing behaviors observed in human communities is the Catch Fish Optimization Algorithm (CFOA)—a metaheuristic inspired by traditional fishing methodologies [46]. Corresponding to three fishing strategies (independent search, group encircling, and collective capture) are the two primary phases of the algorithm: exploration and exploitation (Figure 5). In exploration, individuals first search independently based on personal experience and water surface disturbance, while adjusting their direction according to others’ capture results. They then form small teams to encircle promising areas, enhancing local search capability. During exploitation, all individuals converge around the global best solution. CFOA uses Gaussian distribution to simulate the gradually sparse surrounding strategy of fishermen from the center to the periphery to achieve fine development and rapid convergence. By dynamically balancing global exploration and local exploitation, CFOA effectively avoids local optima and achieves strong convergence. With its clear structure and emphasis on collaboration, CFOA is well-suited for complex optimization problems. It has been utilized in battery box design, CT Image Analysis [47,48], etc.

3.5. Cross-Validation

The evaluation of model performance employs cross-validation, a method specifically conceived to maximize the utility of limited datasets while enhancing the stability and reliability of obtained results. In the modeling of regression models, five-fold cross-validation is frequently adopted in various regression modeling tasks due to its computational efficiency [15].

The key procedure of five-fold cross-validation involves randomly partitioning the original dataset into five mutually exclusive subsets of approximately equal size, referred to as the folds (Figure 6). The training set in this study-utilizing five-fold cross-validation-consist of four groups with 37 samples and one group with 38 samples, ensuring complete data utilization. Serving as the validation fold in sequential order is each individual fold, with the other four being merged to create a total training fold. A total of five rounds of training and testing are conducted in this manner. The overall performance of the data-driven model is then evaluated based on the average of the results from these five rounds. This process effectively reduces evaluation bias caused by the randomness of the database split.

4. Hybrid Model Establishment and Evaluation

When developing hybrid XGBoost models based on metaheuristic algorithms, hyperparameter optimization serves as a core step. This study selects three key parameters in XGBoost that significantly influence model performance—subsampling rate, maximum tree depth, and learning rate—as the optimization targets. Each metaheuristic algorithm continuously approximates the best solution of the fitness function by simulating the movement of individuals within the search space, thereby enhancing the prediction performance of XGBoost. The development process of hybrid XGBoost models, as shown in Figure 7, could be found with the following steps:

(1)

Data Splitting: The dataset of 291 samples was initially and randomly split into a training set (80%, 232 samples) and a testing set (20%, 59 samples).

(2)

Data Normalization: Z-score normalization was used to carry out the data preprocessing [49]. The mean and standard deviation for each input variable were calculated based on the training set. These derived parameters were then used to normalize both the training and testing sets.

(3)

Initial parameter settings: The hyperparameters (subsampling rate, maximum tree depth, learning rate) of the XGBoost models were optimized by NGO, APO, and CFOA. In this study, the subsampling rate is set to [0.5, 1.0]. The search ranges of maximum tree depth and learning rate are [3, 10] and [0.01, 0.3]. Here the maximum tree depth is a discrete variable, while the remaining two parameters are continuous variables. For the XGBoost model of this study, the number of trees, column sampling rate and minimum child weight are 100, 0.8, and 2. L1 and L2 regularization term equal 0 and 1. Moreover, the loss function of XGBoost is the mean squared error.

(4)

Cross-Validation: This optimization process was conducted on the training set using five-fold cross-validation. As mentioned above, the training set was partitioned into five folds, and in each iteration, four folds were used for training the model, and the remaining one was chosen for validation. In the process, the fixed random seed was chosen to ensure that all models could be compared under the same data partitioning structure. In addition, early stopping was also applied to prevent overfitting. The coefficient of determination (R²) and root mean square error (RMSE) were used to choose the optimal model. During this process, each model is trained under different population sizes. After performance evaluation is completed, the optimal population size for each model can be determined.

(5)

Final Model Training and Evaluation: Once the optimal population size of metaheuristics was identified for a hybrid model, a final model was retrained on the entire training set using this population size. This final model was then evaluated once on the testing set.

Note that, in this study, model performance is comprehensively evaluated from both error and trend dimensions, employing four metrics: mean absolute error (MAE), variance account for (VAF), RMSE, R² [16], which could be calculated by following equations:

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|m_{\exp }-m_{\mathrm{pred}}\right|$$

(1)

$$\mathrm{VAF}=\left[1-{\displaystyle \frac{\mathrm{var}\left(m_{\exp }-m_{\mathrm{pred}}\right)}{\mathrm{var}\left(m_{\exp }\right)}}\right]\times 100$$

(2)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(m_{\exp }-m_{\mathrm{pred}}\right)}^2}$$

(3)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^N{(m_{\exp }-m_{\mathrm{pred}})}^2}}{{\displaystyle \sum _{i=1}^N{(m_{\exp }-m_{\mathrm{ea}})}^2}}}$$

(4)

where m_exp, m_pred, and m_ea denote the actual value, the predicted value, and the mean of the actual data. Additionally, the importance of each input parameter is also evaluated.

5. Predicted Results of Developed Models

Among the architectural elements of metaheuristics, it is population size that stands as a pivotal factor governing their performance. While a scarce population impedes solution space exploration and obscures the global optimum, an excessive one disproportionately increases computational burden while offering diminishing returns on performance. Since a clear theoretical relationship between population size and algorithm performance has not yet been established, the optimal population size is generally determined by a trial method. Therefore, this study investigates the performance of three hybrid models under five different population sizes: 20, 40, 60, 80, and 100.

All models, under the configuration of 500 maximum iterations, show well-defined convergence. Using the RMSE and R² on the testing set as the primary evaluation criteria, a multi-metric evaluation approach was adopted to determine the optimal population size. Based on these metrics, the models were ranked. Following the method of Zorlu et al. [50], models under different population sizes were assigned scores from 1 to 5, from lowest to highest performance, with the highest total score identified as the optimal model.

Figure 8 provides a systematic presentation of the comprehensive evaluation outcomes for all three hybrid models with varying population scales, indicating clear performance differentiations associated with population size modifications. The optimal population sizes for the NGO–XGBoost, APO–XGBoost, and CFOA–XGBoost models were ultimately determined to be 20, 80, and 60, indicating that these configurations yield the best optimization effect of each algorithm on the XGBoost model.

This study leverages the determined optimal population sizes along with the hybrid modeling methodology to conduct strength prediction for RHA concrete. Moreover, three unoptimized models (XGBoost, random forest, and SVR) was also developed as baseline models. Identical datasets were utilized for the training and testing procedures of these baseline models. Among these, random forest is one of the most widely employed ensemble learning methods and exhibits strong nonlinear mapping capabilities. As an extension of support vector machines, SVR is known for its high accuracy and low risk of overfitting. Due to their notable advantages, both methods are extensively applied in civil engineering. Their fundamental principles can be found in prior literature [16,51]. The hyperparameters for these three single models are shown in

Table 3. Hyperparameters for single XGBoost, RF, SVR model.

Model	Parameter	Value
XGBoost	n_estimators	100
	max_depth	8
	colsample_bytree	0.8
	learning_rate	0.1
	subsample	0.6
	min_child_weight	2
	reg_lambda	1
	reg_alpha	0
RF	max_depth	18
	min_samples_split	4
	min_samples_leaf	2
	n_estimators	250
SVR	Kernel Type	RBF
	C	20
	gamma	0.05
	epsilon	0.6

.

The relationship comparing predicted with actual strength values for RHA concrete is visualized in Figure 9, accompanied by comprehensive model evaluation metrics. When evaluating model performance, the diagonal line shows the ideal prediction trajectory, while the distance of scatter points from this line reflects modeling accuracy. The diagonal line shows tighter clustering of scatter points for the hybrid models in Figure 9. Training set R² values surpassing 0.96 and testing set values above 0.95 were consistently achieved by the hybrid frameworks. In contrast, the scatter points of the unoptimized models are more dispersed, with lower R² values on both training and testing sets, indicating that the hybrid models outperform the unoptimized ones.

There is a certain gap in the model performance between the training and testing set. This gap is common in machine learning modeling, reflecting information loss in the generalization process of the model from training data to unknown data. In this study, the performance differences between the training and testing sets are within a reasonable range. The R² of the testing set remains above 0.95, indicating that the model has good generalization ability. To further analyze whether there is overfitting in the model, a scatter plot between the error and the predicted compressive strength was drawn, as shown in Figure 10. It is obvious that the error points are randomly distributed on both sides of the zero baseline and do not show a distinct trend. This indicates that the prediction error of the model in different RHA concrete strength intervals (approximately 20–90 MPa) is random, and no systematic overestimation or underestimation phenomena have been found.

For a quantitative comparison of the prediction performance of the developed six machine-learning models, each model was scored according to its evaluation metrics and the scoring method of Zorlu et al. [52], and the models were ranked based on their total scores. Figure 11 displays the comprehensive scoring outcomes obtained from the three hybrid and three baseline models. The descending performance ranking of the six data-driven methods is determined to be: APO–XGBoost, CFOA–XGBoost, NGO–XGBoost, XGBoost, SVR, and RF. The quantitative scoring results further confirm that hybrid models provide better prediction results for compressive strength than unoptimized models.

Following comparative analysis, APO–XGBoost is regarded as the most reliable prediction model of compressive strength in RHA concrete. On the training set, the APO–XGBoost model achieved RMSE = 1.7146, MAE = 1.3350, R² = 0.9909, and VAF = 99.0873. On the testing set, it achieved RMSE = 3.5462, MAE = 2.4494, R² = 0.9579, and VAF = 95.7982.

In addition to the above evaluation methods, the Taylor diagram is also a commonly used approach in the performance evaluation of machine-learning models. Originally introduced by climatologist Karl Taylor in 2001 [53], the Taylor diagram is designed to efficiently assess and compare the agreement between multiple models and benchmark observational data. It integrates three crucial metrics—the standard deviation, R², and RMSE—into a single two-dimensional plot, thereby overcoming the potential one-sidedness that may arise from relying on any single metric.

The six prediction models developed in this study are visually compared through the Taylor diagram displayed in Figure 11. The straight-line distance between each model points and the basis point (i.e., obs in Figure 12) representing the observed data is proportional to the model’s centered root-mean-square error. A shorter distance indicates a smaller overall error and thus better model performance. As shown in Figure 11, the models ranked from closest to farthest from the basis point are: APO–XGBoost, CFOA–XGBoost, NGO–XGBoost, XGBoost, SVR, and RF. The superior performance of APO–XGBoost in predicting RHA concrete strength is further validated through systematic evaluation using the Taylor diagram.

6. Sensitivity Analysis

For determining the influence of each input variable on predicted compressive strength of this study, conducting global sensitivity analysis represents an indispensable step. The Cosine Amplitude Method is an effective data-driven approach often used to quantitatively assess the strength of association or similarity between factors within a system [54]. The idea of this method originates from the vector space model, where each data sample is treated as a vector in a multidimensional space. By calculating the cosine of the angle between any two vectors, their similarity can be well evaluated. A cosine value closer to 1 indicates smaller directional differences between the vectors, suggesting greater similarity in their trends and a stronger correlation. On the contrary, a cosine value closer to 0 implies almost no correlation between the two.

The key strength of this methodology involves computational simplicity and intuitive application, characterized by its disregard for absolute numerical scales and preferential focus on relative pattern evaluations. Therefore, it is widely applied fuzzy relation analysis, and modeling factor correlations in complex systems, providing a powerful mathematical tool for extracting intrinsic information from data. Given these significant advantages, this study conducted sensitivity analysis for each parameter using the Cosine Amplitude Method. Figure 13 presents the sensitivity indexes corresponding to the seven input variables considered in this study.

The sensitivity analysis results presented in Figure 12 reveal that the input variables of this study demonstrate varying degrees of influence on predicted strength of RHA concrete, ranked in decreasing order as follows: Cement > Water = CA > FA > RHA > Age > SP. Here, the sensitivity indexes corresponding to Cement, Water, CA, and FA are 0.953, 0.939, 0.939, 0.925. These four sensitivity indexes all exceed 0.9, indicating that these four parameters exhibit the highest sensitivity in the model and are the dominant variables determining the strength. Among them, cement content emerges as the predominant variable with the highest sensitivity in predicting RHA concrete strength.

Cement exhibits the highest sensitivity, consistent with its role as the primary binder. Its hydration generates calcium silicate hydrate (C-S-H) gel, the principal source of strength. Any variation in cement content directly governs the binding phase volume and dominates compressive strength. Water and coarse aggregate demonstrate similarly high sensitivity. The water-cement ratio critically determines concrete porosity and microstructure. For example, excess water increases capillary porosity, weakening the interfacial transition zone. Meanwhile, coarse aggregate forms the skeletal framework, governing load-bearing capacity and internal stress distribution through its packing density. Fine aggregate shows a comparatively lower impact, because it primarily serves to fill voids between coarse particles and enhance mix homogeneity, with a secondary contribution to strength development. The sensitivity of RHA aligns with its function as a supplementary cementitious material. While RHA refines the pore structure through pozzolanic reactions and micro-filler effects, its influence remains subordinate to cement and aggregate. Note that the importance of RHA in this study may not be as significant as we expected, which may be related to the narrow range and replacement ratio of RHA in the database. Curing age reflects the time-dependent progression of hydration. The influence of concrete age on strength growth over time has a typical marginal effect. This marginal effect depends heavily on the composition of cement and aggregate. Therefore, the curing age has low sensitivity. Superplasticizer has the lowest sensitivity, as its primary role is to improve workability without directly enhancing strength. Its effect is indirect and typically saturates beyond a specific dosage, explaining its minimal influence.

7. Discussion

While the proposed APO–XGBoost model demonstrates strong prediction performance, it is necessary to conduct the performance comparison with existing prediction models, such as the models in Table 1. As shown in Table 1, except for the GRU model, all single models performed worse than the APO–XGBoost model, demonstrating the performance advantages of the hybrid model. The GRU model is the best single model. It achieved high accuracy (R² = 0.97 on testing set) in predicting RHA concrete strength. However, GRU model requires substantial computational resources for training and tuning, and a lot of parameter-tuning works are required. In contrast, our hybrid framework could automate hyperparameter search, reducing manual intervention while maintaining competitive accuracy (R² = 0.9579 on testing set). Even if our model is slightly lower than the GRU model in accuracy, it significantly simplifies the model parameter adjustment process while ensuring the predictive accuracy. Moreover, compared to three SVR-based hybrid models, the APO–XGBoost model shows better performance. The performance of APO–XGBoost on the testing set is slightly worse than the CMRSA–ANN model, but its performance on the training set is better. Since CMRSA is developed by introducing circular mapping based on the reptile search algorithm, its modeling process is more complex than the hybrid model in this study. Note that the ensemble structure of XGBoost with regularization avoids kernel sensitivity in SVR and structural complexity selection in ANN. Moreover, benefit from the excellent algorithm design, APO–XGBoost has lower structural complexity and hardware demands, faster execution, and greater computational efficiency than SVR-based and CMRSA–ANN models. In a word, APO–XGBoost model provides a balanced solution for RHA concrete strength prediction, showing accuracy, efficiency, and automation in practical engineering applications.

In actual construction projects, a designer can use the APO–XGBoost model interactively to explore the performance of candidate mixes within the range of RHA replacement ratios covered by our database. By fixing other constituents and varying the one parameter, the model provides quick strength predictions for different replacement levels of different materials. This allows the designer to quickly identify mix designs that meet a specific strength target while maximizing RHA incorporation to reduce cement use and carbon emissions. It should be emphasized that the model reliable applicability is strictly confined to the RHA replacement ranges present in our dataset; extrapolating predictions beyond these bounds may be inaccurate. Within the validated ranges, the model thus serves as an efficient computational tool to navigate the trade-off between concrete performance and sustainability in mix design.

Although the developed hybrid models have significant advantages, several limitations of this study should be acknowledged. Firstly, the database was compiled from multiple sources, introducing inherent heterogeneity due to variations in raw material sources and compressive strength testing devices. Secondly, while the proposed hybrid framework with XGBoost proved effective, the exploration was limited to this specific ensemble learner, and other advanced models were not compared. Moreover, the model was developed on a constrained dataset of 291 samples, and its performance could potentially benefit from a larger, more granular dataset and greater computational resources for expanded hyperparameter optimization. Finally, interpretable machine learning is a good means to understand the effect of input parameters, and it can also be tried in the future to further enhance the interpretability of the model.

8. Conclusions

The mix proportions of constituent materials significantly influence the compressive strength of RHA concrete. This study adopted a data-driven modeling strategy, introducing XGBoost and three metaheuristics to develop hybrid strength prediction models of RHA concrete. These models utilized metaheuristics for XGBoost hyperparameter optimization. Comparative assessment with classic machine learning approaches was simultaneously performed. Evaluation incorporated four performance indicators, with variable importance determined via sensitivity analysis. The conclusions derived from this study include:

(1)

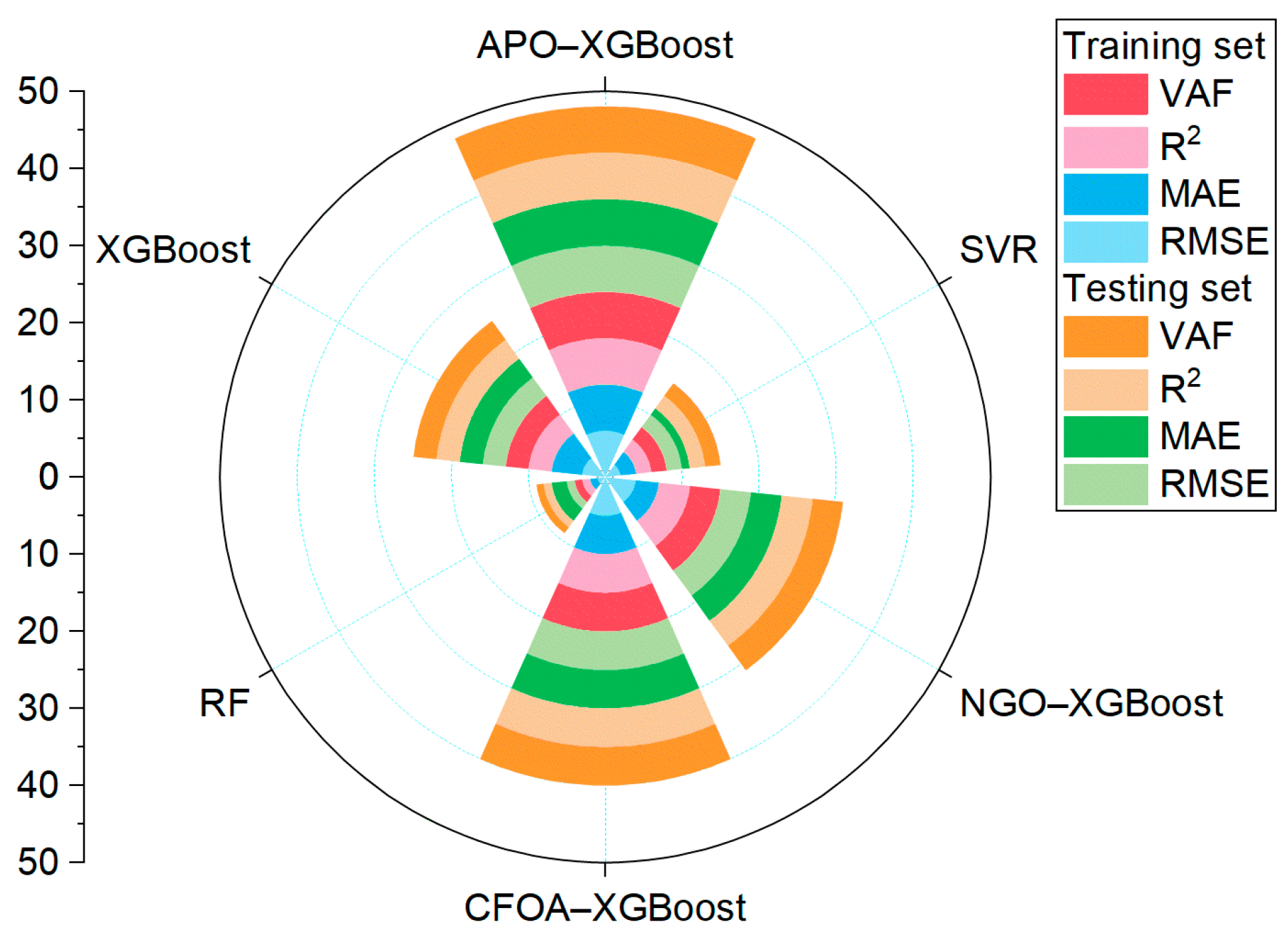
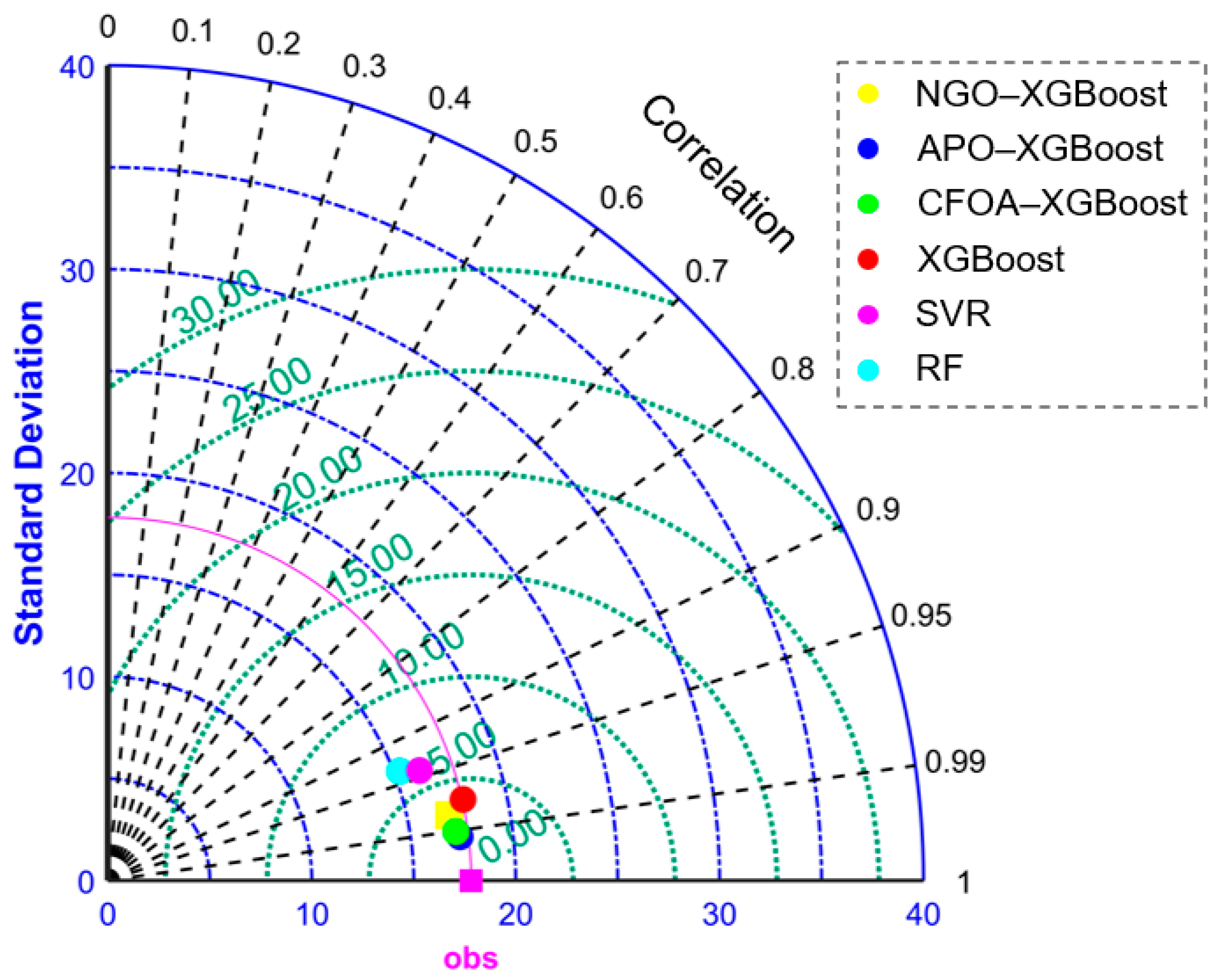
All three hybrid XGBoost models in this study effectively predicted the strength of RHA concrete. The optimization effects of the metaheuristics on XGBoost, in descending order, were: APO, CFOA, NGO. The APO–XGBoost model demonstrated the best prediction performance.

(2)

On the training set, the best APO–XGBoost model produced these performance metrics: RMSE = 1.7146, MAE = 1.3350, R² = 0.9909, and VAF = 99.0873. Meanwhile, the testing set yielded the following results through this optimized model: RMSE = 3.5462, MAE = 2.4494, R² = 0.9579, VAF = 95.7982. APO–XGBoost model exhibits high prediction accuracy and successfully achieves precise estimation of RHA concrete strength.

(3)

Compared to the enhanced XGBoost models, the three baseline models—XGBoost, RF, and SVR—demonstrated reduced prediction accuracy. Advanced hybrid algorithms hold a distinct advantage over classic models in strength estimation of RHA concrete.

(4)

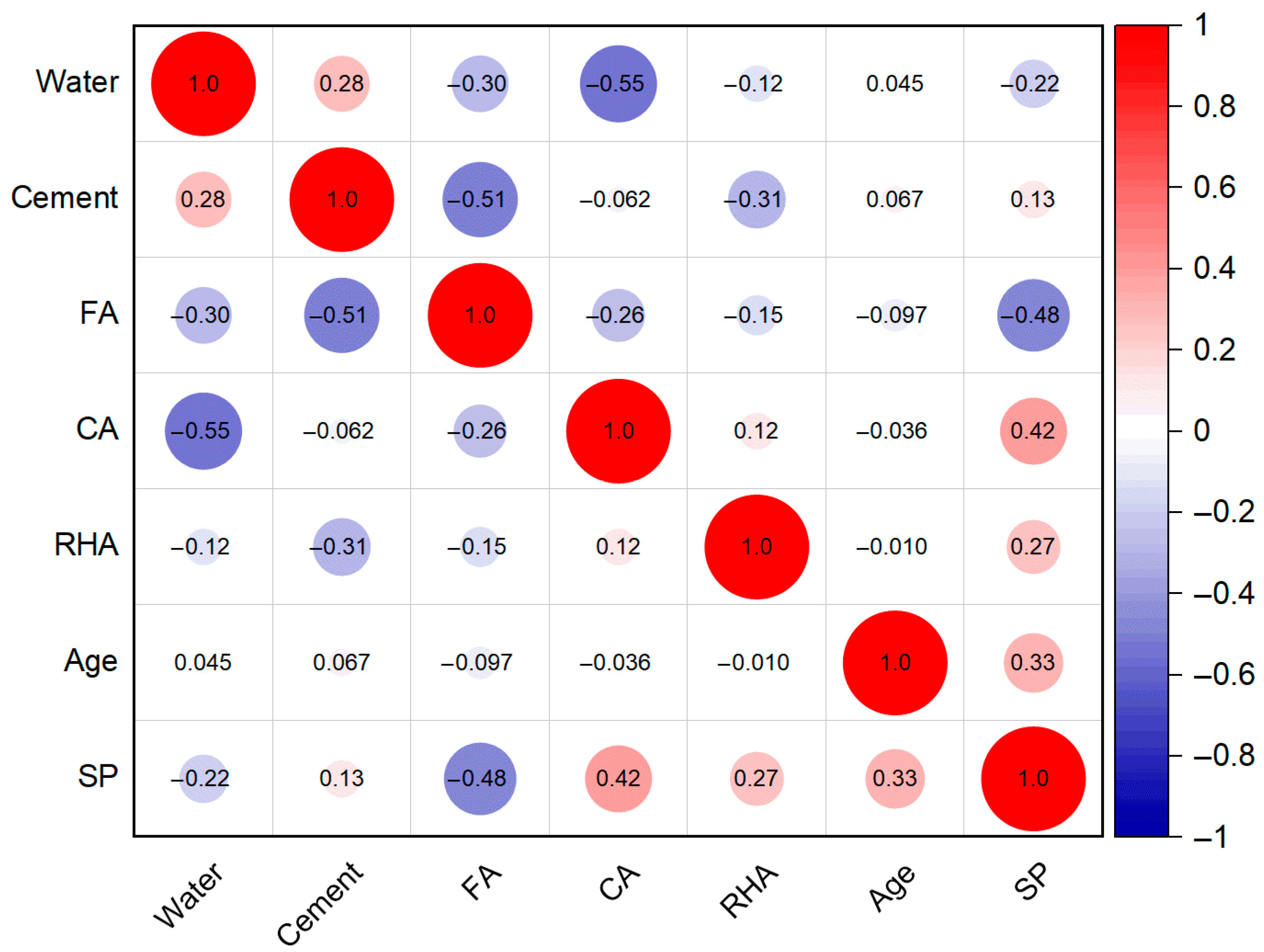
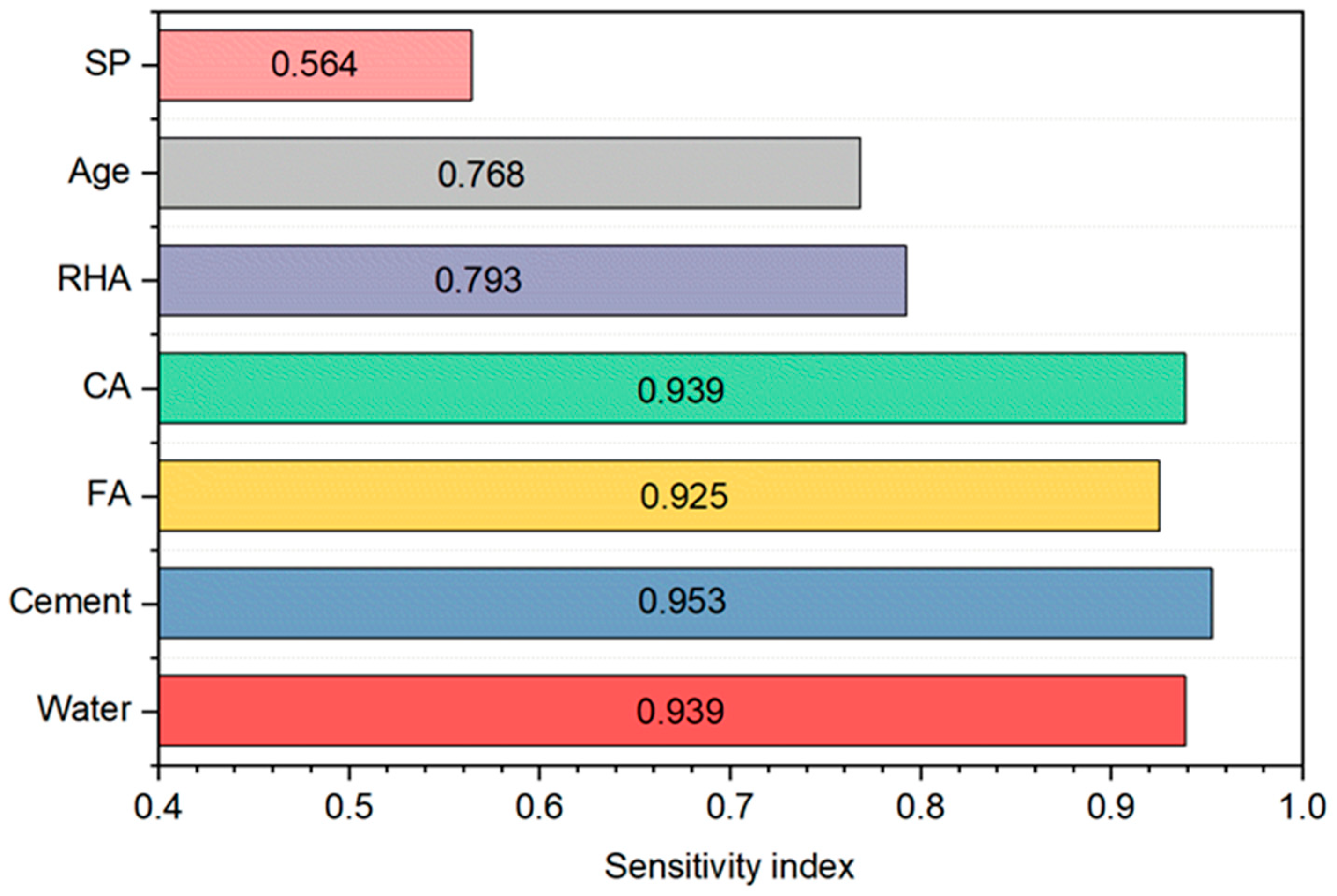
The influence of input variables on the RHA concrete strength ranks as follows: Cement > Water = CA > FA > RHA > Age > SP. Cement exhibited a significant correlation with the strength, suggesting that its effect should be prioritized in the mix design of RHA concrete.