Coupled LEM–CZM Numerical Framework for Landslide Simulation and Its Application to Geotechnical Design
Abstract
1. Introduction
2. Method
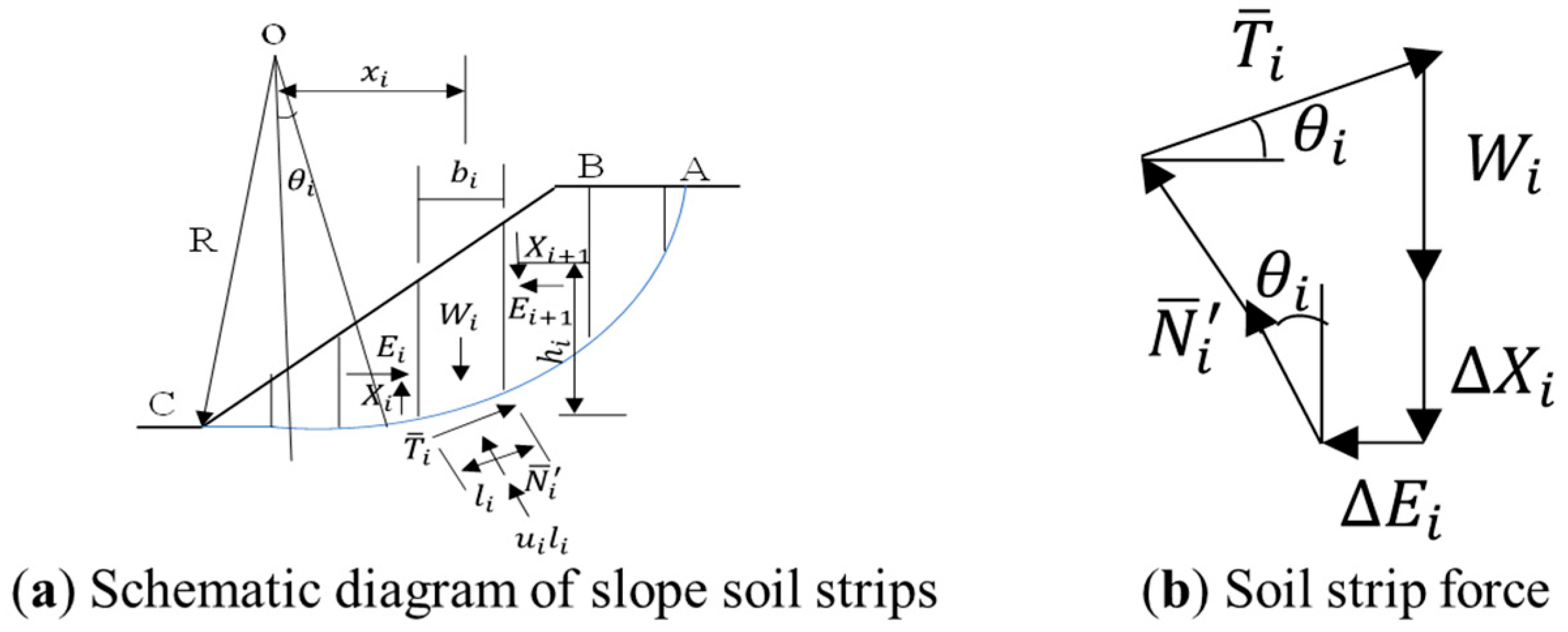
2.1. Limit Equilibrium Analysis
2.2. Cohesive Zone Model Modeling
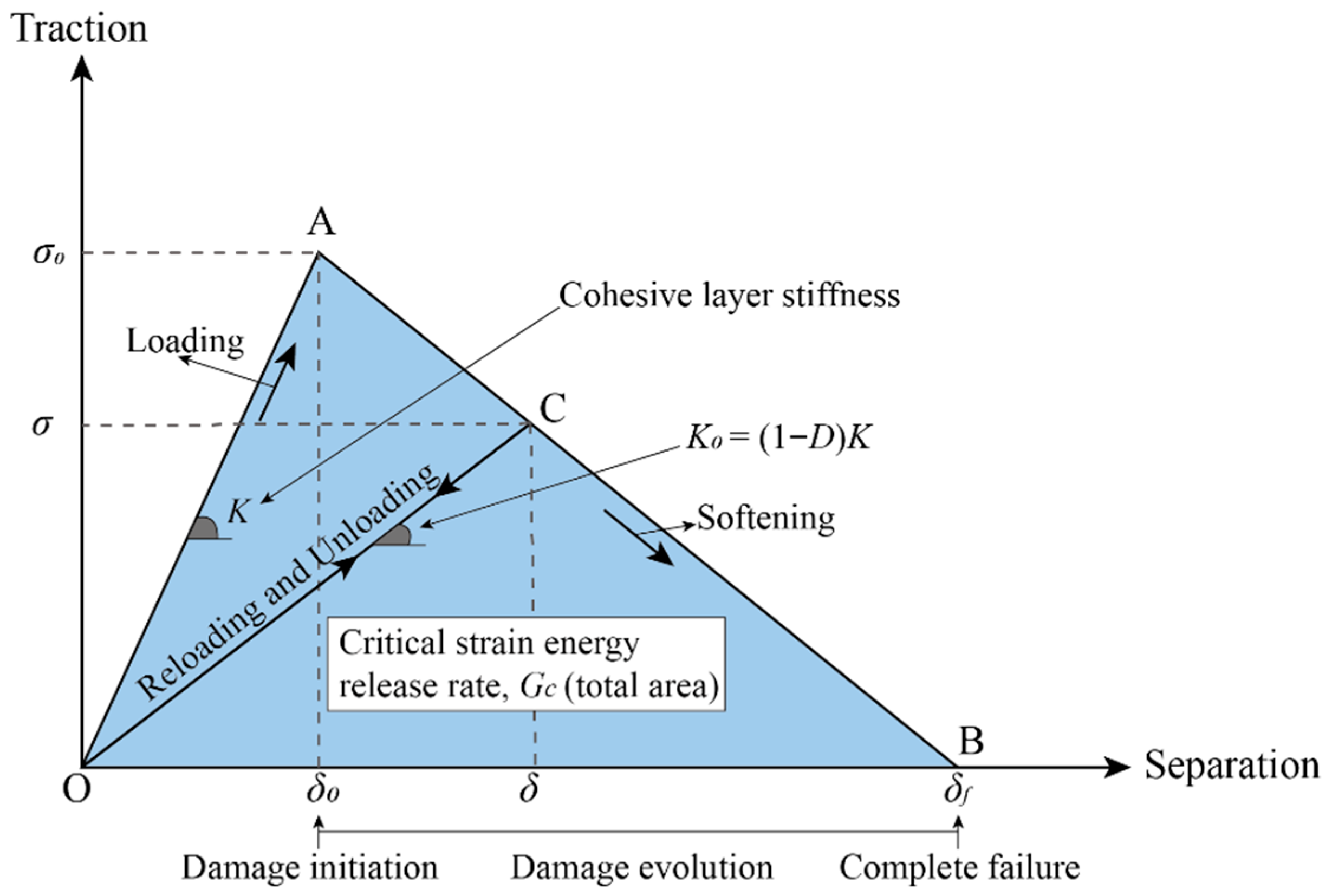
2.2.1. The Constitution of Cohesive Zone Model
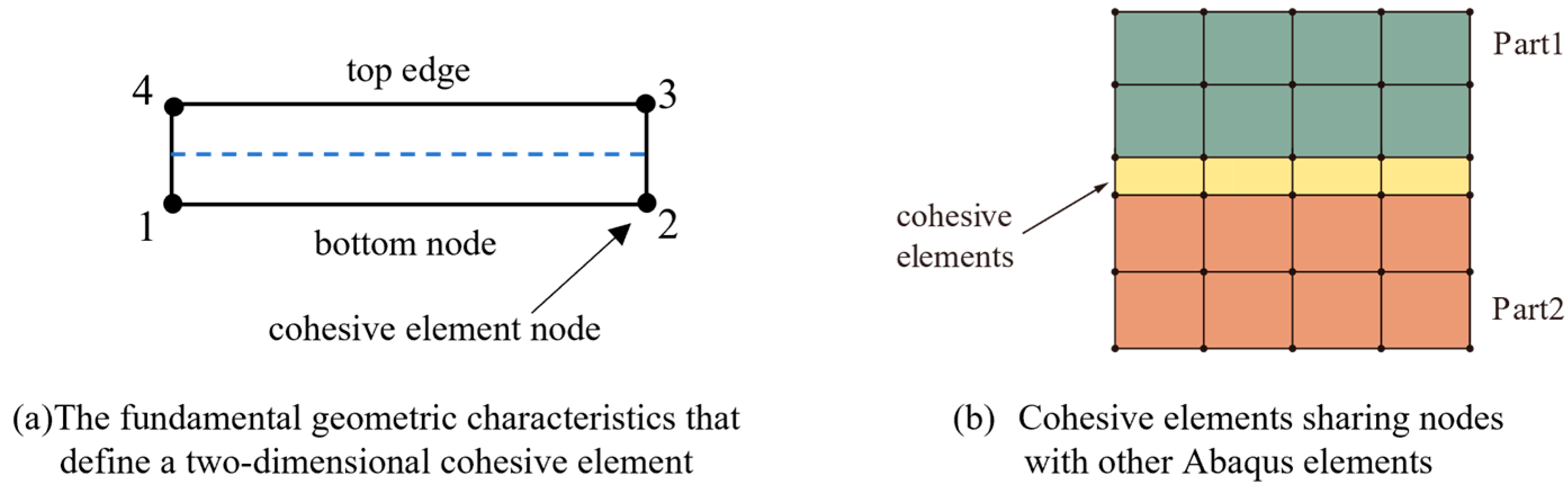
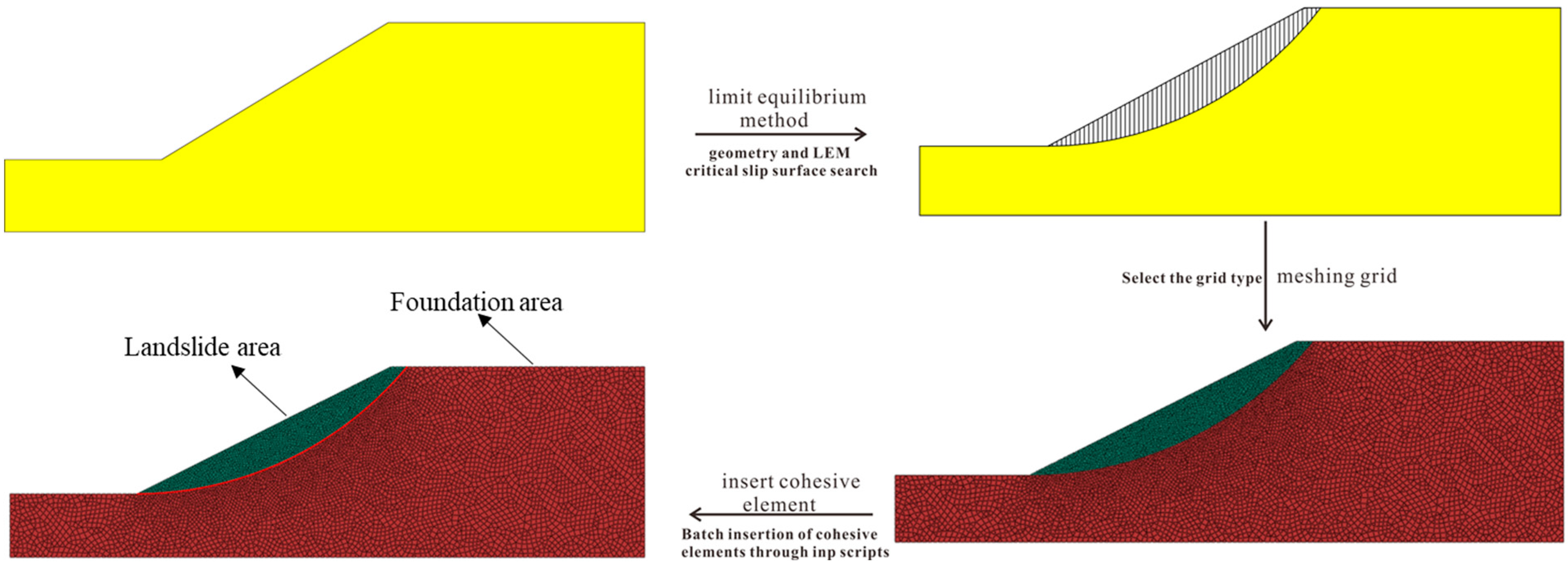
2.2.2. Generation of Cohesive Elements
2.3. LEM and CZM Coupled Simulation Process
2.3.1. LEM-to-CZM Data Transfer, Assumptions, and Boundary Conditions
- (1)
- Stress recovery from LEM
- (2)
- Key mapping assumptions
- (3)
- Mesh partitioning and node duplication
- (4)
- Boundary and loading conditions for the CZM stage
- (5)
- Verification and tolerance checks
2.3.2. Mesh Discretisation and Sensitivity Analysis
2.3.3. Cohesive Zone Parameters: Calibration and Justification
3. Results
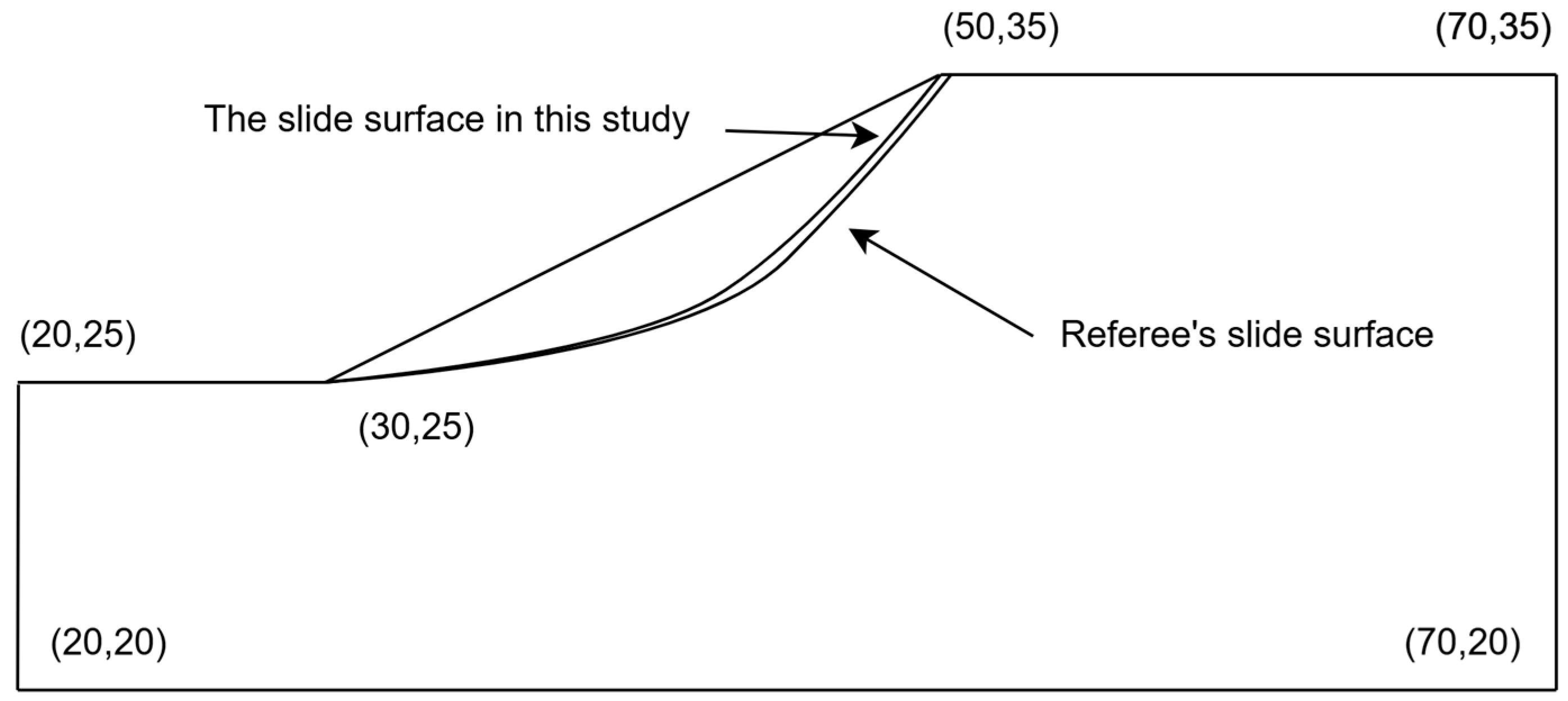
3.1. Analysis of the Results of EX11
3.2. Analysis of the Results of Real Slope
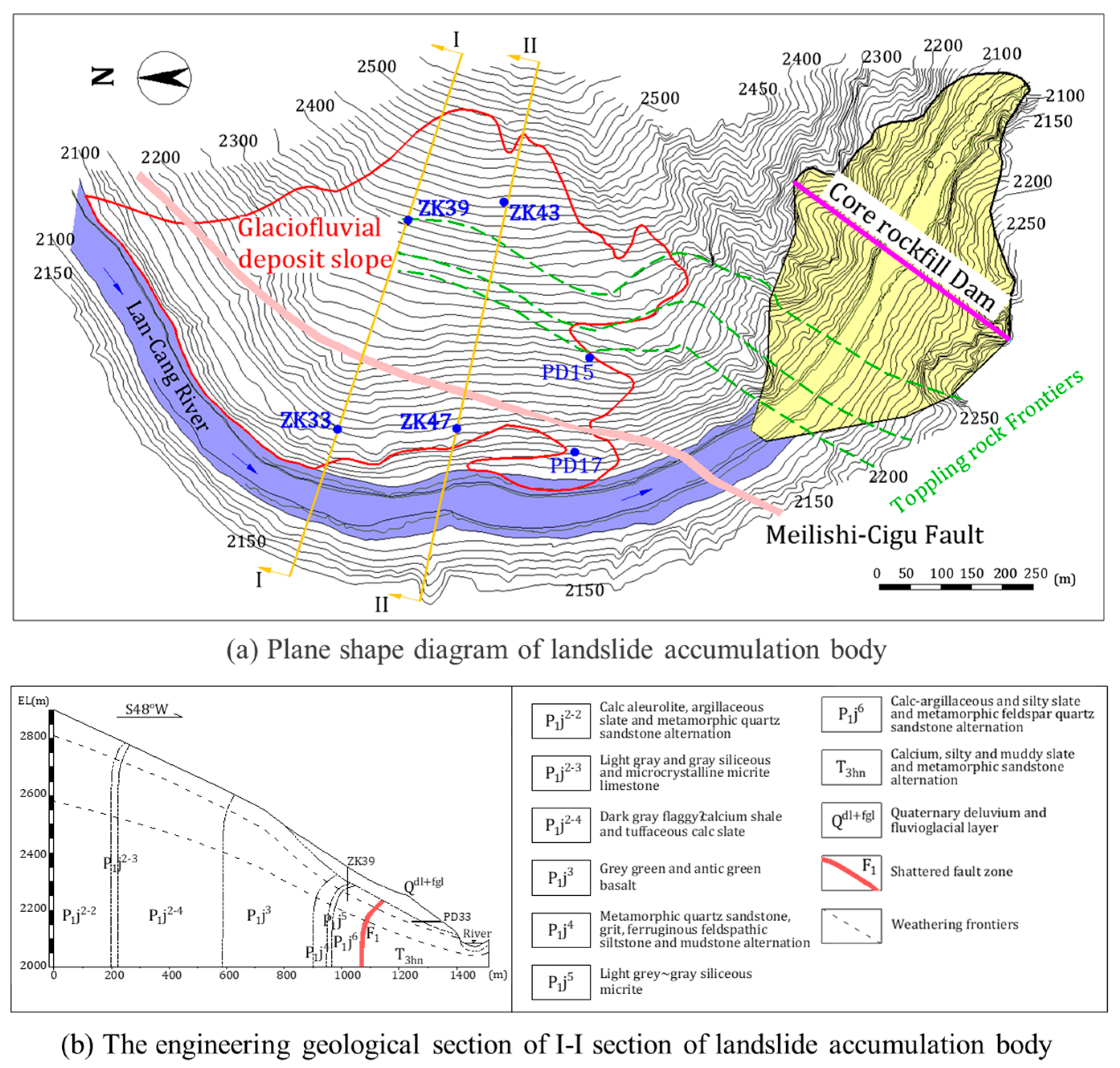
3.2.1. Geological Background
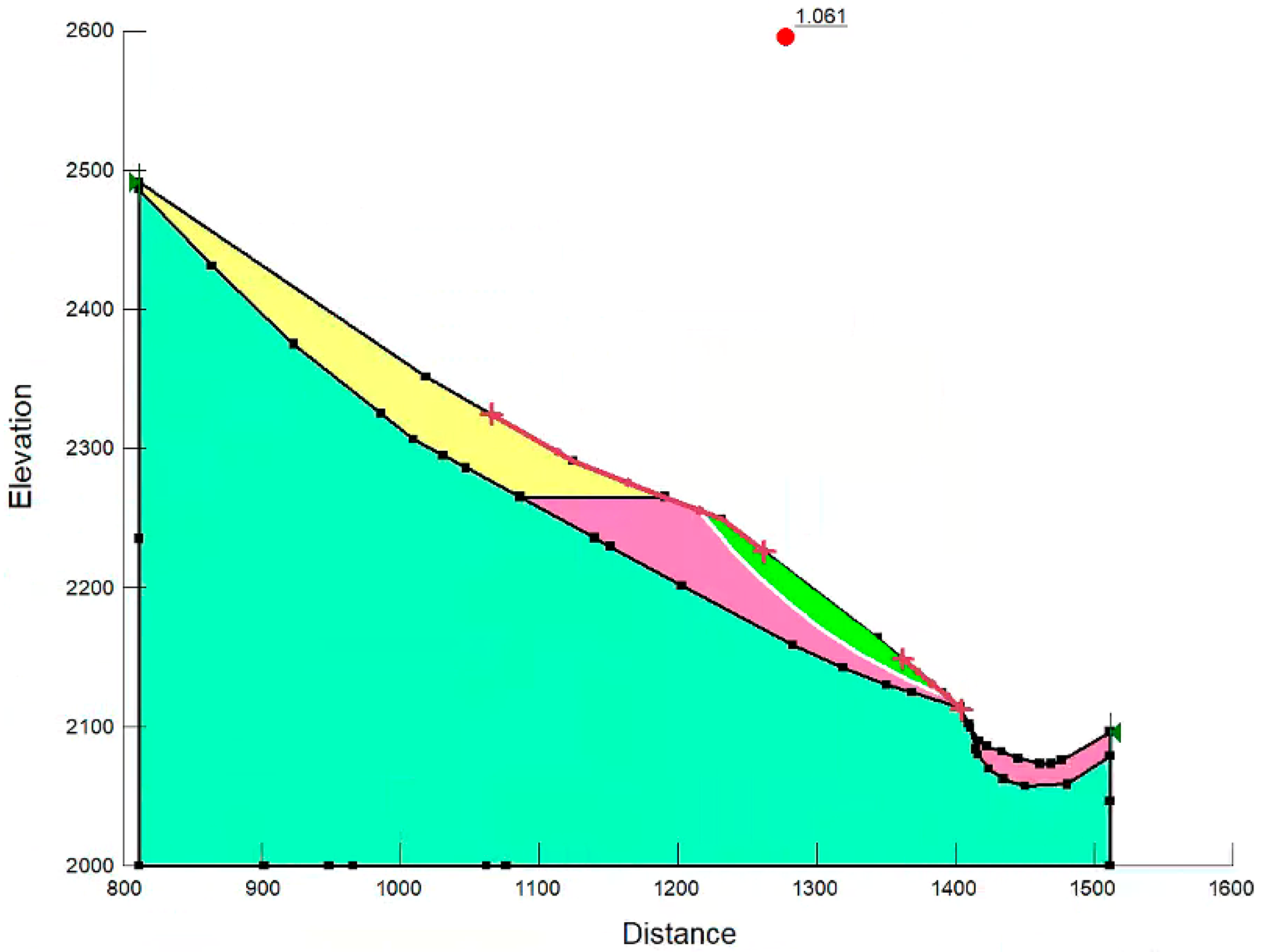
3.2.2. LEM Modeling for Safety Factor
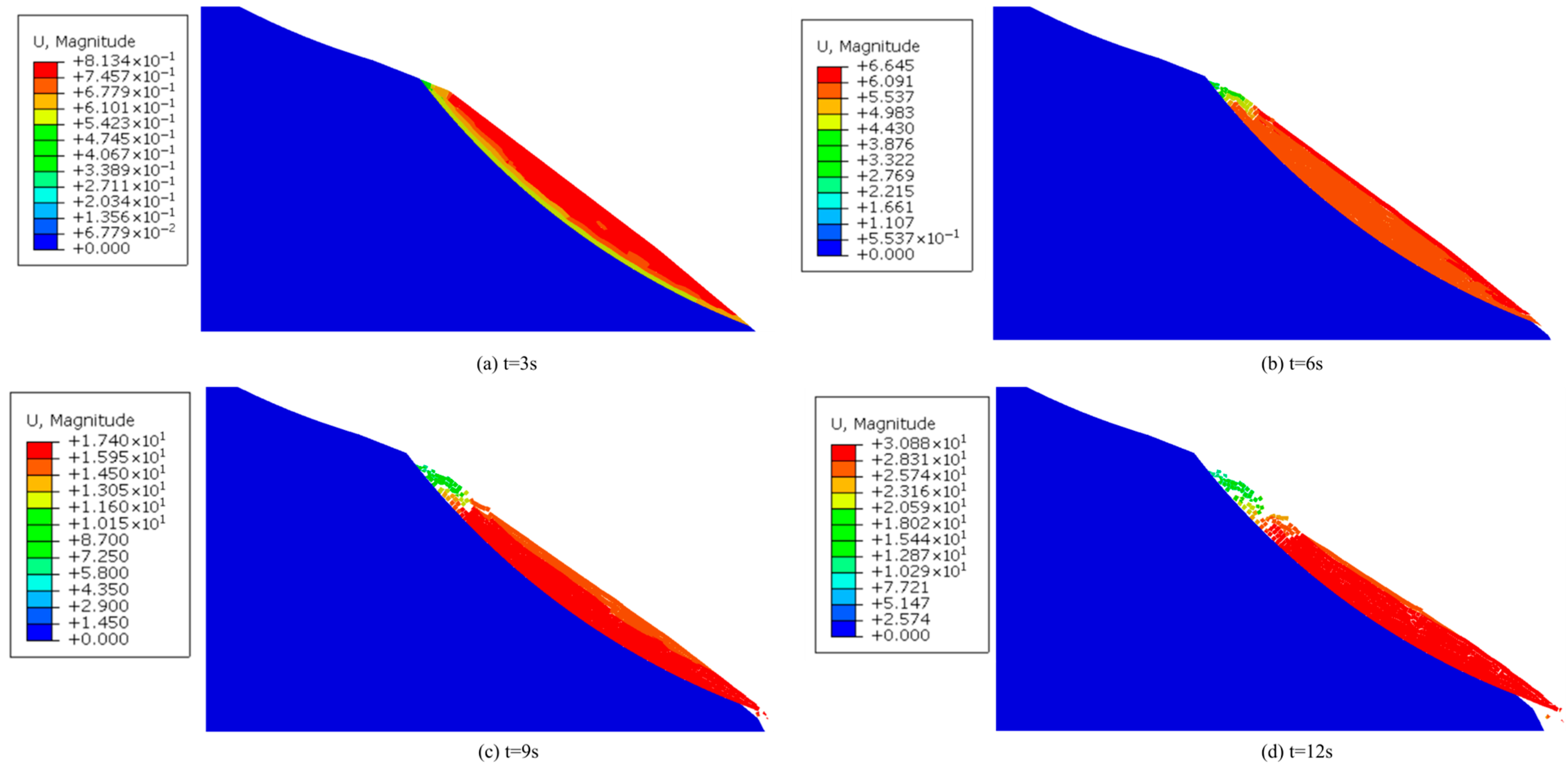
3.2.3. CZM Modeling for Landslide Hazard
4. Discussion
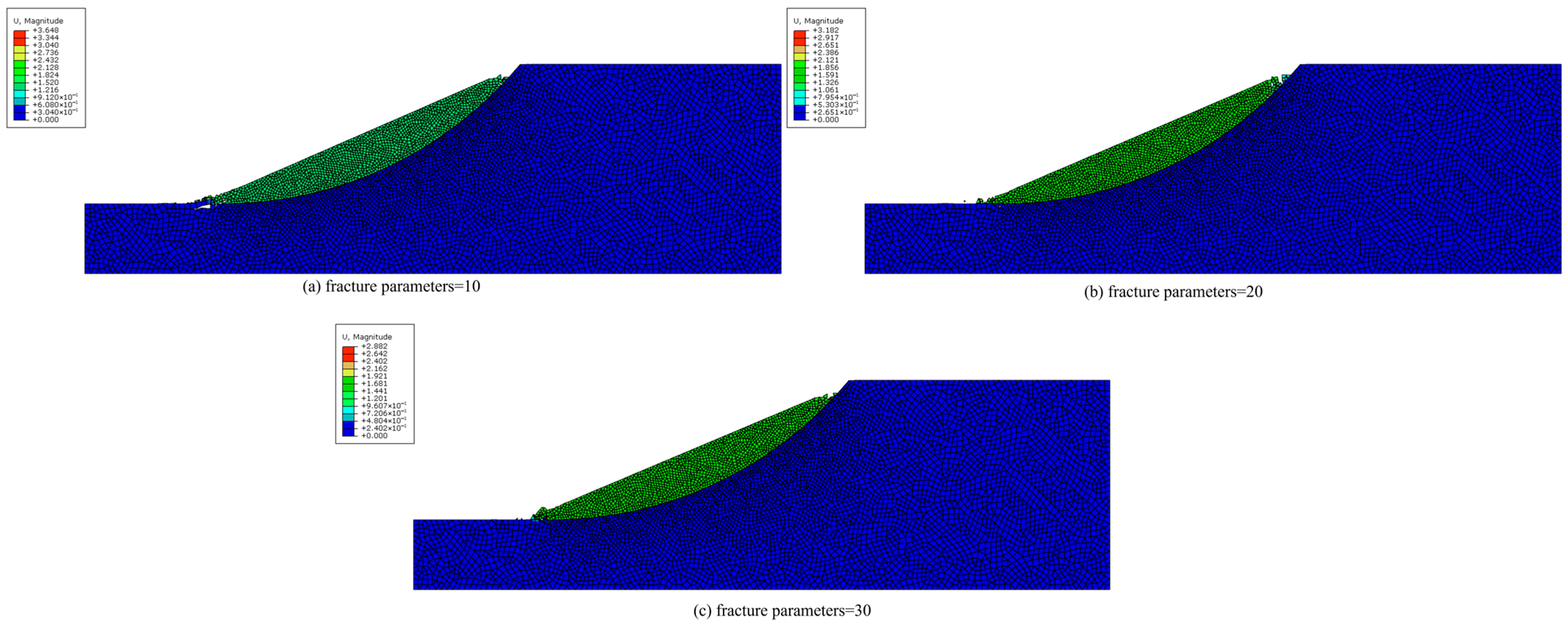
4.1. Effect of Fracture Parameters
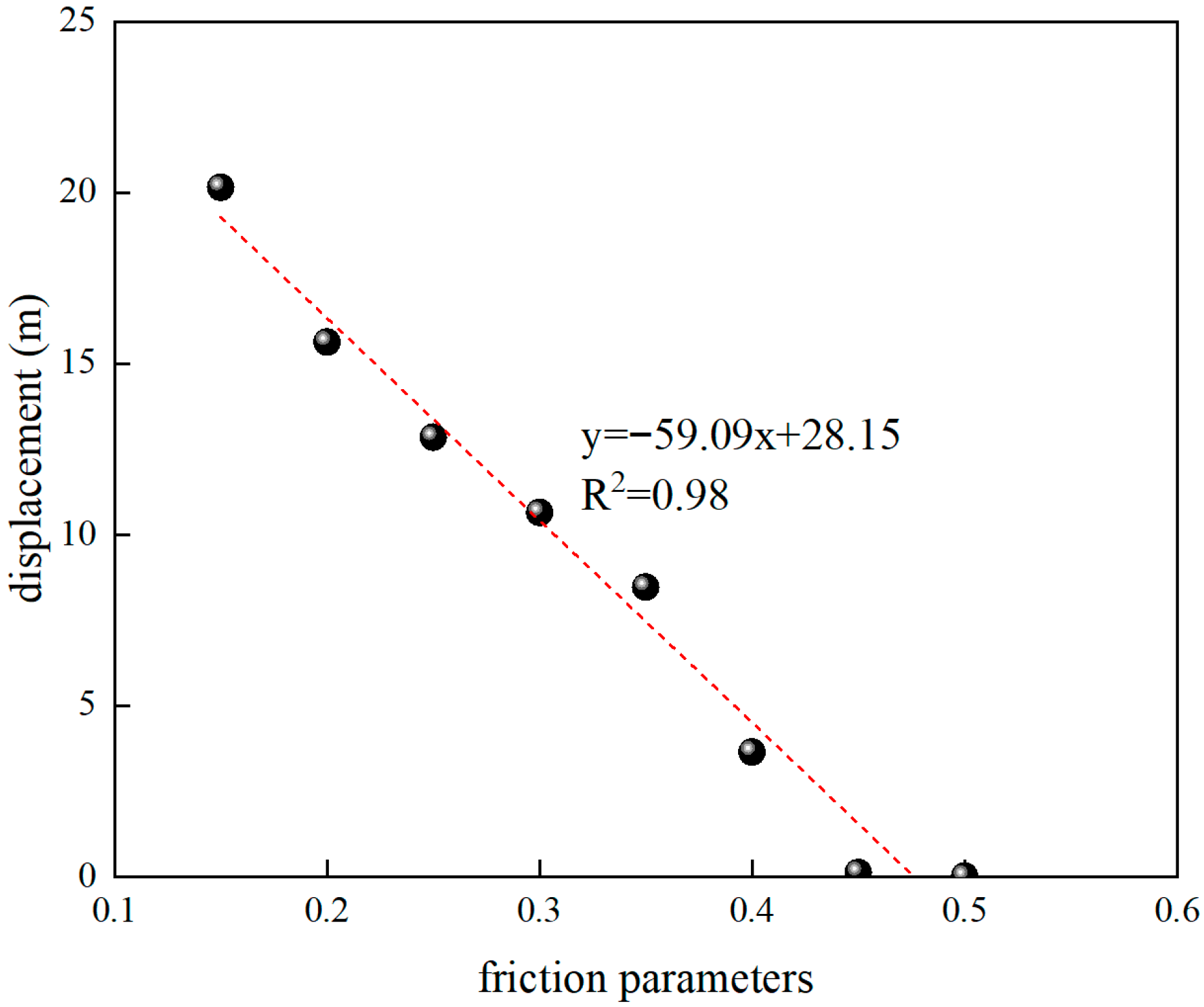
4.2. Effect of Friction Parameters
4.3. Comparison with Traditional LEM and FEM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Romana, M. SMR Classification. In Proceedings of the Seventh International Congress on Rock Mechanics, Aachen, Germany, 16–20 September 1991; pp. 955–960. [Google Scholar]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Tomás, R.; Delgado, J.; Serón, J.B. Modification of slope mass rating (SMR) by continuous functions. Int. J. Rock Mech. Min. Sci. 2007, 44, 1062–1069. [Google Scholar] [CrossRef]
- Sajjad, H.; Siddiqui, M.A.; Rahman, A.; Siddiqui, L.; Naqvi, H.R.; Shakeel, A. (Eds.) Landslide Risk Assessment and Mitigation in India: Proceedings of the National Conference, New Delhi, India, 1–2 November 2022; Springer Nature: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Huang, M.; Tang, Z.; Zhou, W.; Yuan, J. Upper bound solutions for face stability of circular tunnels in non-homogeneous and anisotropic clays. Comput. Geotech. 2018, 98, 189–196. [Google Scholar] [CrossRef]
- Michalowski, R.L. Stability charts for uniform slopes. J. Geotech. Geoenviron. Eng. 2002, 128, 351–355. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; Leong, E.C.; Santoso, V.A.; Ng, Y.S. Performance of an instrumented slope covered with shrubs and deep-rooted grass. Soils Found. 2014, 54, 417–425. [Google Scholar] [CrossRef]
- Zhou, W.; Yuan, W.; Ma, G.; Chang, X.L. Combined finite-discrete element method modeling of rockslides. Eng. Comput. 2016, 33, 1530–1559. [Google Scholar] [CrossRef]
- Wu, X.; Wang, G.; Li, G.; Han, W.; Sun, S.; Zhang, S.; Bi, W. Research on shear behavior and crack evolution of symmetrical discontinuous rock joints based on FEM-CZM. Symmetry 2020, 12, 1314. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Munjiza, A.A. The Combined Finite-Discrete Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bui, H.H.; Sako, K.; Fukagawa, R.; Wells, J. SPH-based numerical simulations for large deformation of geomaterial considering soil-structure interaction. In Proceedings of the The 12th International Conference of International Association for Computer Methods and Advances in Geomechanics (IACMAG), Goa, India, 1–6 October 2008; Volume 1, pp. 570–578. [Google Scholar]
- Dai, F.C.; Lee, C.F.; Ngai, Y.Y. Landslide Risk Assessment and Management: An Overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Lam, L.; Fredlund, D.G. A General Limit Equilibrium Model for Three-Dimensional Slope Stability Analysis. Can. Geotech. J. 1993, 30, 905–919. [Google Scholar] [CrossRef]
- Morgenstern, N.R.U.; Price, V.E. The Analysis of the Stability of General Slip Surfaces. Geotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Abramson, L.Y.; Alloy, L.B.; Hankin, B.L.; Haeffel, G.J.; MacCoon, D.G.; Gibb, B.E. Cognitive Vulnerability-Stress Models of Depression in a Self-Regulatory and Psychobiological Context; The Guilford Press: New York, NY, USA, 2002. [Google Scholar]
- Chen, Z.Y.; Morgenstern, N.R. Extensions to the Generalized Method of Slices for Stability Analysis. Can. Geotech. J. 1983, 20, 104–119. [Google Scholar] [CrossRef]
- Agbelele, K.J.; Adeoti, G.O.; Agossou, D.Y.; Aïsse, G.G. Study of Slope Stability Using the Bishop Slice Method: An Approach Combining Analytical and Numerical Analyses. Open J. Appl. Sci. 2023, 13, 1446–1456. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Rao, B.; Choudhary, S.S.; Burman, A. Analysis of 2D and 3D Slope Stability Using the Bishop Simplified Method. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2024; Volume 1326, p. 012117. [Google Scholar]
- Hu, G.; Li, B.; Yan, X.; Ren, R.; Zeng, J. Research on the Stability of Loess Landslides under Seismic Action Based on Simplified Bishop Method. Front. Earth Sci. 2024, 12, 1490558. [Google Scholar] [CrossRef]
- Ramadhani, S.; Chauf, K.A.; Dwijaka, A.; Bierhofa, M.Z.; Gagaramusu, Y. Slope Stability Using Simplified Bishop Method in Kebun Kopi Area Donggala Regency, Central Sulawesi Province. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2022; Volume 1075, p. 012027. [Google Scholar]
- Wei, H.B.; Zhang, Q.; Zhao, J.H. Simplified Bishop Method Homogeneous Soil Slope Stability Analysis Based on the C# Language. Appl. Mech. Mater. 2014, 580, 291–295. [Google Scholar] [CrossRef]
- Bishop, A.W. The Use of the Slip Circle in the Stability Analysis of Slopes. Geotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of Steel Sheets Containing Slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The mathematical theory of equilibrium cracks in brittle fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Scheider, I. Numerical Simulation of Material Separation Using Cohesive Zone Models. In Handbook of Mechanics of Materials; Springer: Singapore, 2019; pp. 1715–1756. [Google Scholar]
- Akhavan-Safar, A.; Marques, E.A.; Carbas, R.J.; da Silva, L.F. Cohesive Zone Modelling for Fatigue Life Analysis of Adhesive Joints; Springer: Cham, Switzerland, 2022; pp. 19–42. [Google Scholar]
- Park, K.; Paulino, G.H. Cohesive zone models: A critical review of traction-separation relationships across fracture surfaces. Appl. Mech. Rev. 2011, 64, 060802. [Google Scholar] [CrossRef]
- Benmebarek, M.A.; Benmebarek, S.; Rad, M.M.; Ray, R. Pile optimization in slope stabilization by 2D and 3D numerical analyses. Int. J. Geotech. Eng. 2022, 16, 211–224. [Google Scholar] [CrossRef]
- Peng, L.Q. Discussion on the ACADS Standard Problems for Slope Stability Analysis. In Proceedings of the 3rd National Symposium on Geotechnical and Engineering, Hangzhou, China, 8–10 September 2009. (In Chinese). [Google Scholar]
- Meng, Q.; Qian, K.; Zhong, L.; Gu, J.; Li, Y.; Fan, K.; Yan, L. Numerical Analysis of Slope Stability under Reservoir Water Level Fluctuations Using a FEM-LEM-Combined Method. Geofluids 2020, 2020, 6683311. [Google Scholar] [CrossRef]
- Wang, B.; Liu, L.; Li, Y.; Jiang, Q. Reliability analysis of slopes considering spatial variability of soil properties based on efficiently identified representative slip surfaces. J. Rock Mech. Geotech. Eng. 2020, 12, 642–655. [Google Scholar] [CrossRef]
- Meng, Y.; Jing, H.; Yuan, L.; Zhang, L. Numerical investigation on the effect of bedding plane properties on mode I fracture characteristics of mudstone with FEM-CZM method. Bull. Eng. Geol. Environ. 2022, 81, 3. [Google Scholar] [CrossRef]




| Grid Size | Fs | Umax (m) | Tcpu (h) |
|---|---|---|---|
| 1 m | 1.42 | 4.12 | 0.3 |
| 0.5 m | 1.39 | 3.65 | 1.1 |
| 0.25 m | 1.38 | 2.18 | 4.8 |
| Assessment Question | c(kN/m2) | γ(kN/m3) |
|---|---|---|
| EX11 | 3.0 | 20.0 |
| Assessment Question | c (kN/m2) | γ (kN/m3) | φ/° |
|---|---|---|---|
| EX11 | 3.0 | 20.0 | 19.6 |
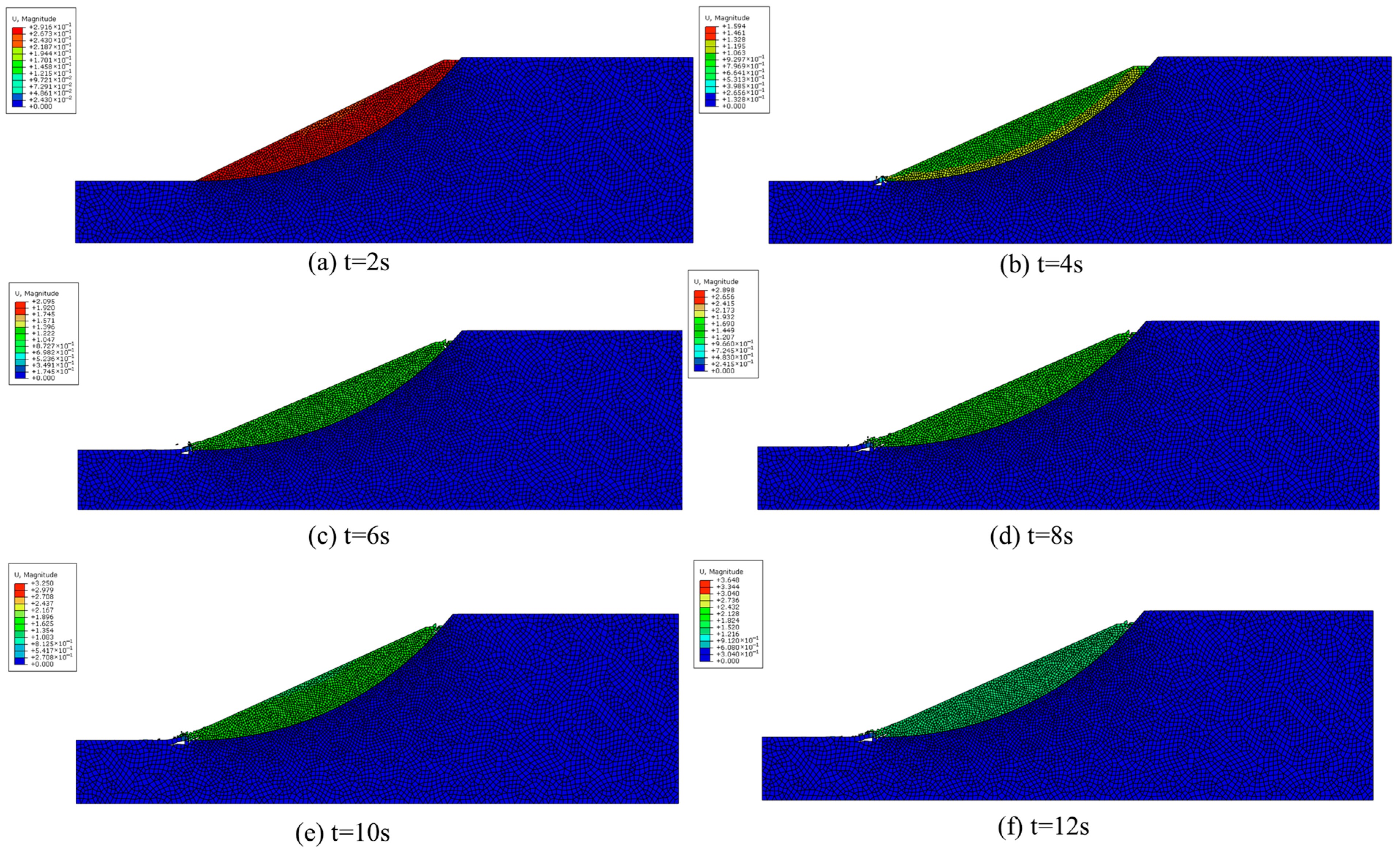
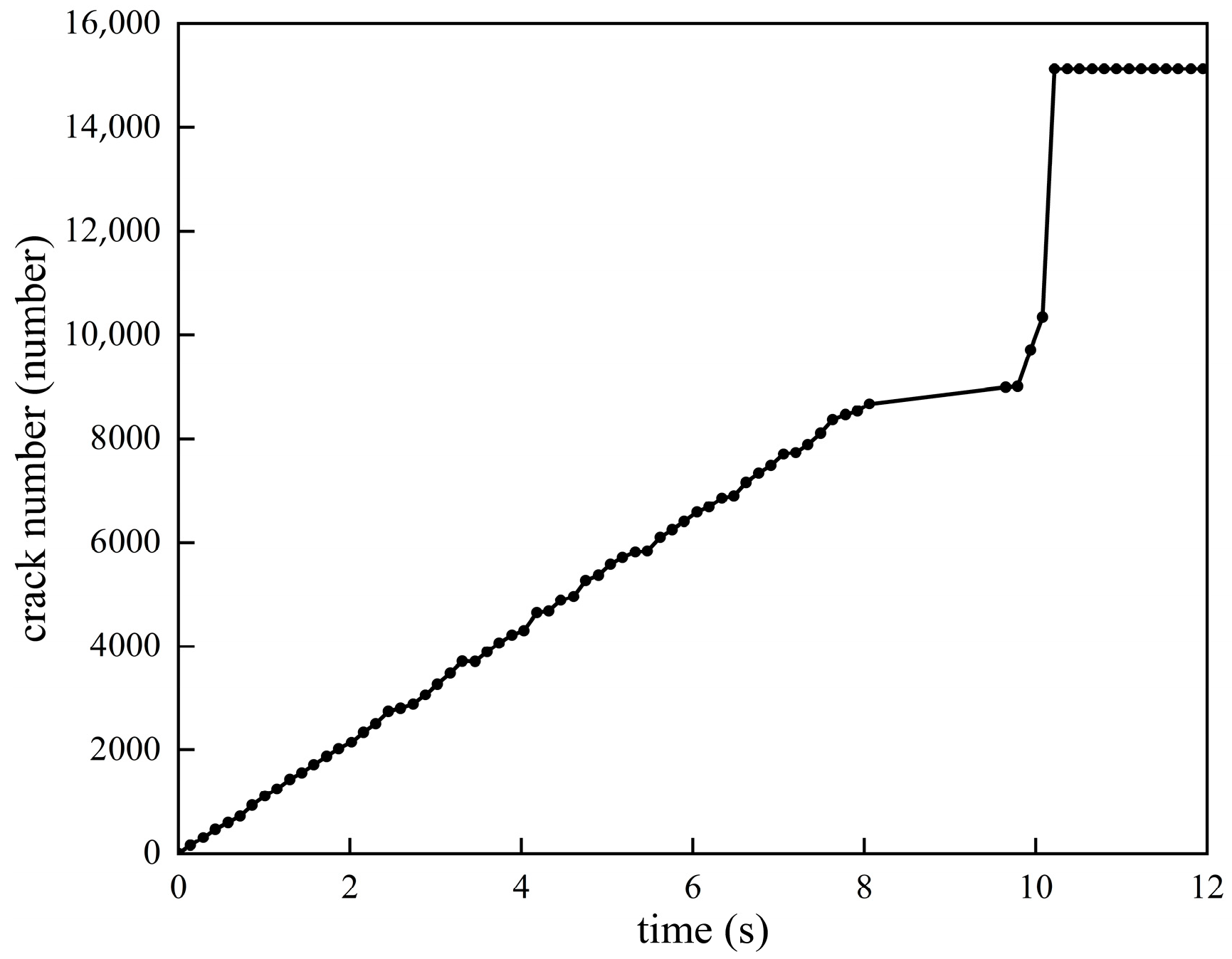
| Deformation Stage | Time (s) | Maximum Displacement U_max (m) | Crack Number (Number) | Crack Growth Rates (Number/s) |
|---|---|---|---|---|
| Crack initiation and sliding initiation stage | T = 2 | 2.92 × 10−1 | 2149 | 1074.5 |
| The stage of crack propagation and foundation separation | T = 4 | 1.59 | 4299 | 1075 |
| T = 6 | 2.10 | 6589 | 1145 | |
| The sliding stage of the ruptured landslide | T = 8 | 2.90 | 8671 | 1041 |
| T = 10 | 3.25 | 10,341 | 835 | |
| T = 12 | 3.65 | 15,131 | 2395 |
| Components | Unit Weight (kN/m3) | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|---|
| Foundation area | 25 | 4500 | 48.0 |
| Accumulation body | 21 | 25 | 28.5 |
| Method | Bishop LEM | SRM-FEM | LEM–CZM (This Work) |
|---|---|---|---|
| Factor of safety(Fs) | 0.983 | 0.981 | 0.983 |
| The maximum post-sliding displacement(m) | - | 3.61 | 3.65 |
| Fracture path visualization | no | no | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Chen, T.; Liu, H.; Guo, R.; He, R.; Meng, Q. Coupled LEM–CZM Numerical Framework for Landslide Simulation and Its Application to Geotechnical Design. Designs 2025, 9, 133. https://doi.org/10.3390/designs9060133
Li L, Chen T, Liu H, Guo R, He R, Meng Q. Coupled LEM–CZM Numerical Framework for Landslide Simulation and Its Application to Geotechnical Design. Designs. 2025; 9(6):133. https://doi.org/10.3390/designs9060133
Chicago/Turabian StyleLi, Li, Tiansheng Chen, Haibo Liu, Rui Guo, Ruiyu He, and Qingxiang Meng. 2025. "Coupled LEM–CZM Numerical Framework for Landslide Simulation and Its Application to Geotechnical Design" Designs 9, no. 6: 133. https://doi.org/10.3390/designs9060133
APA StyleLi, L., Chen, T., Liu, H., Guo, R., He, R., & Meng, Q. (2025). Coupled LEM–CZM Numerical Framework for Landslide Simulation and Its Application to Geotechnical Design. Designs, 9(6), 133. https://doi.org/10.3390/designs9060133






