Optimization of the Human–Robot Collaborative Disassembly Process Using a Genetic Algorithm: Application to the Reconditioning of Electric Vehicle Batteries
Abstract
1. Introduction
2. Related Works
3. Methodology
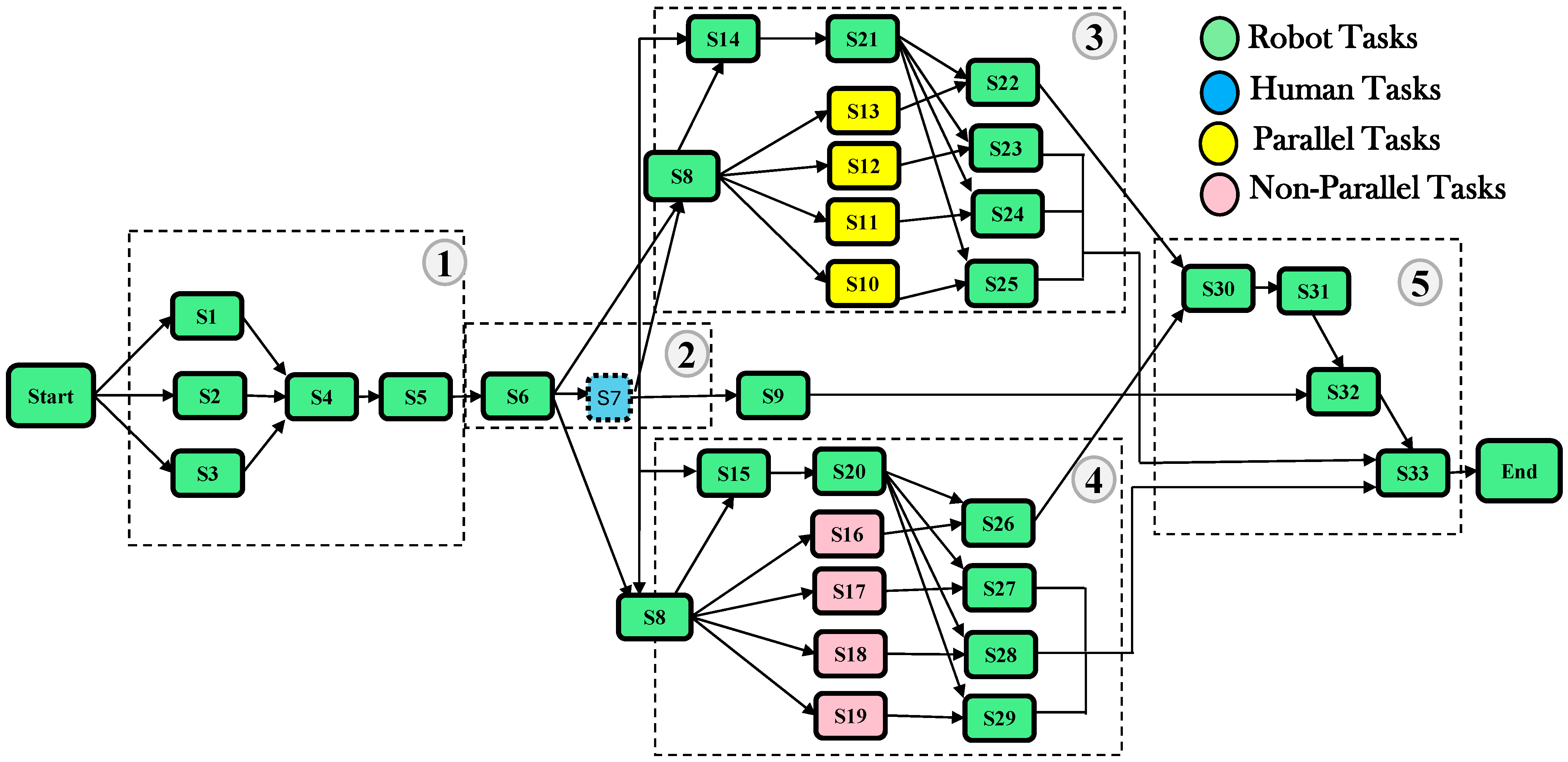
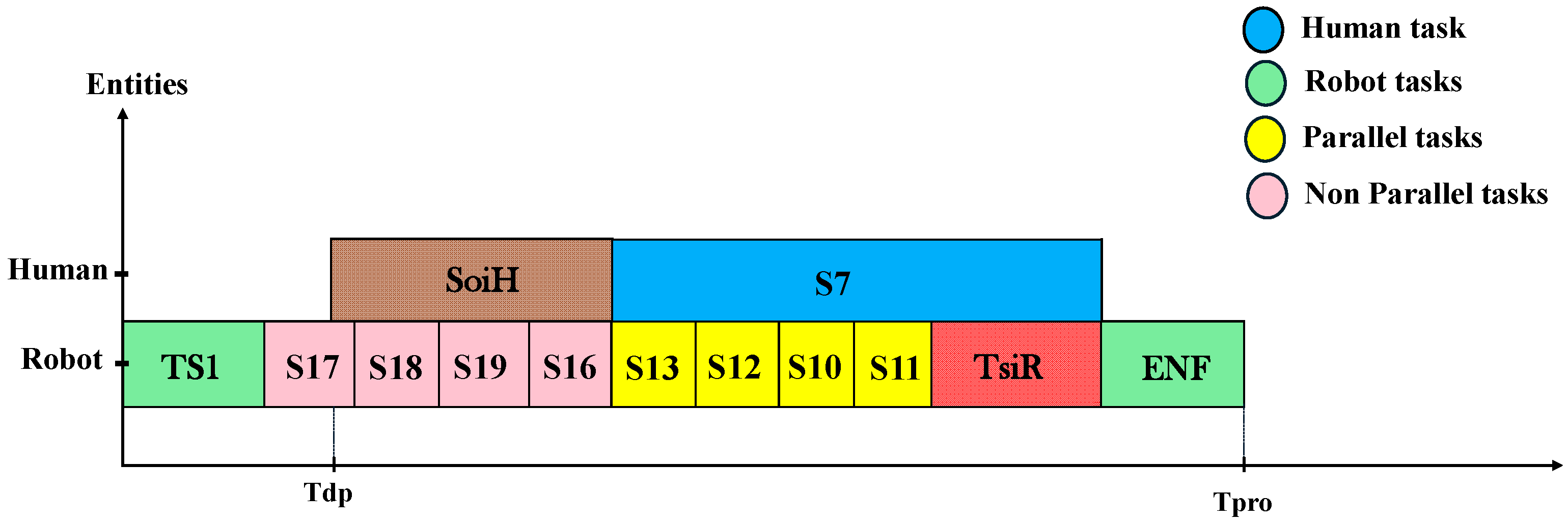
3.1. Disassembly Relationship Graph
3.2. Mathematical Model
- -
- xij: A binary variable that equals 1 if task i is executed immediately before task j and 0 otherwise.
- -
- yij: A binary variable that equals 1 if task i is completed before the start of task j and 0 otherwise.
- -
- tis: The start time of task i.
- -
- tif: The finish time of task i.
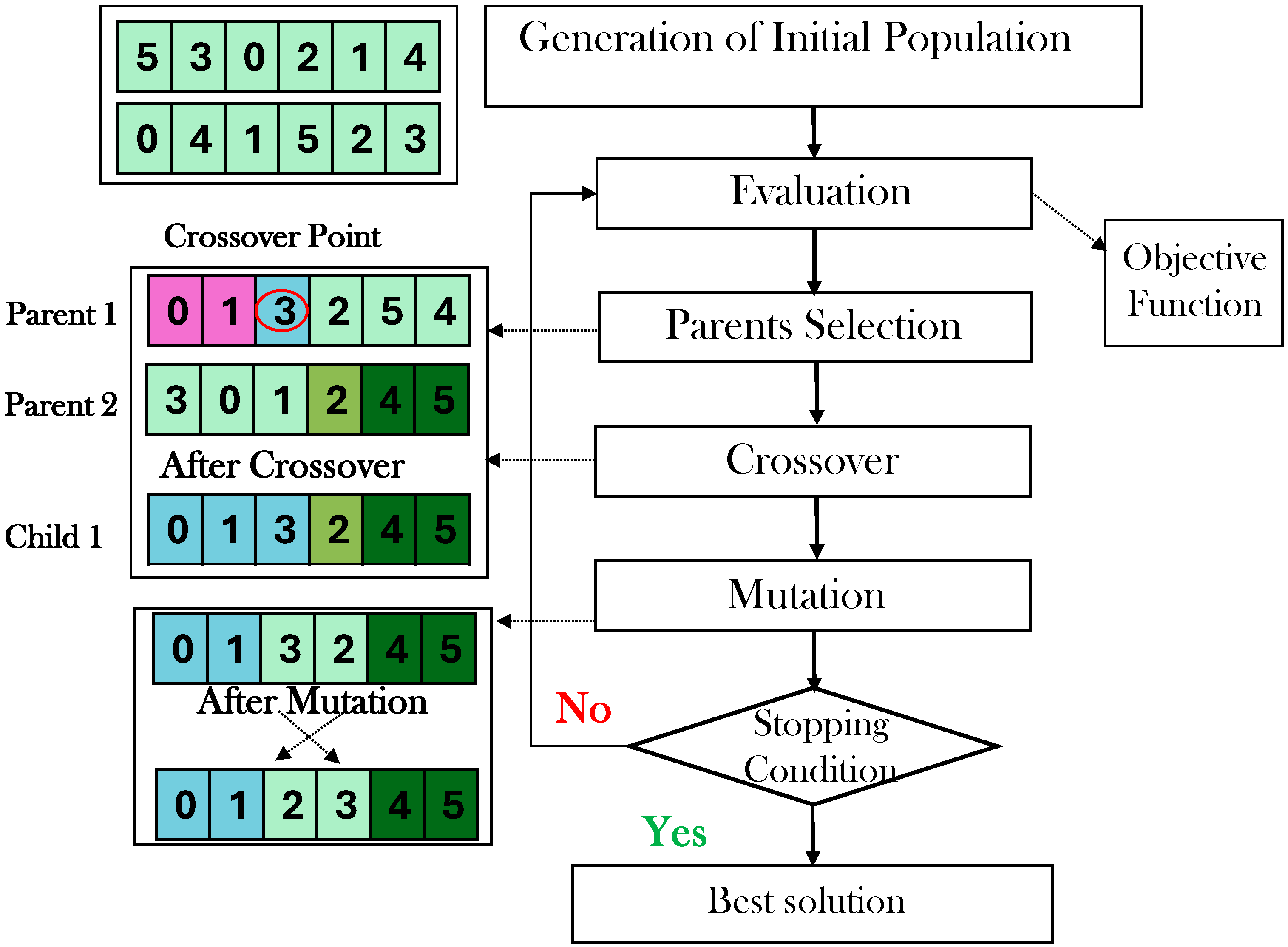
3.3. Implementation of Genetic Algorithm
3.4. Methodological Differences Between the Global Genetic Algorithm and the Non-Global TSP–KP Approach
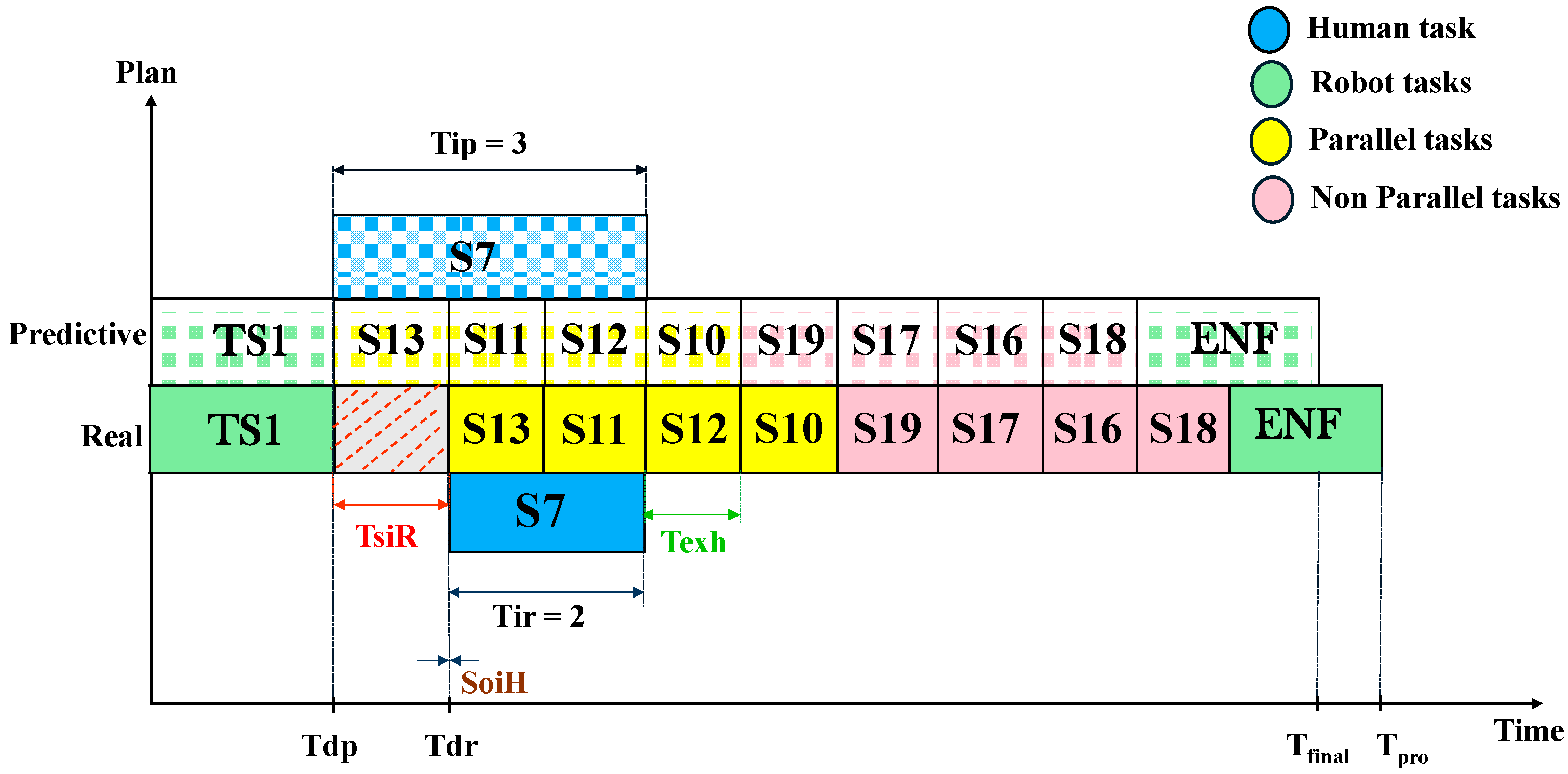
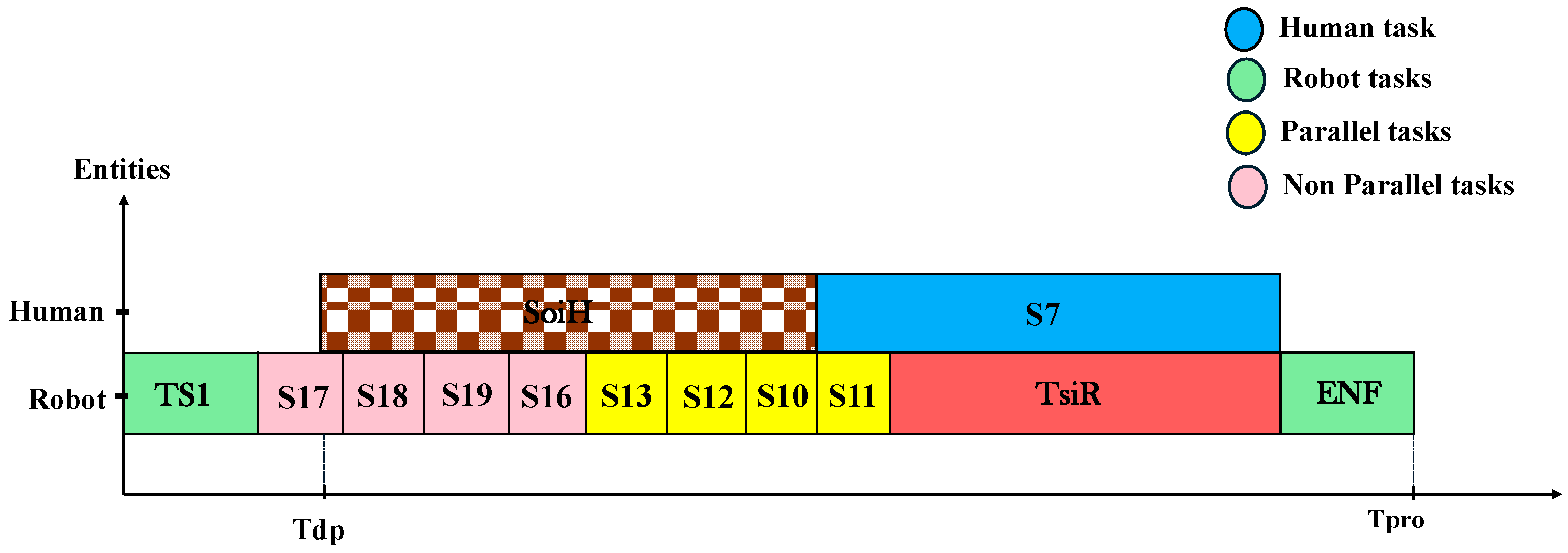
3.5. Implementation of the Reactive Optimization Approach
4. Results
4.1. Parameters and Comparison Metrics
4.2. Comparison Results of Two Optimization Approaches
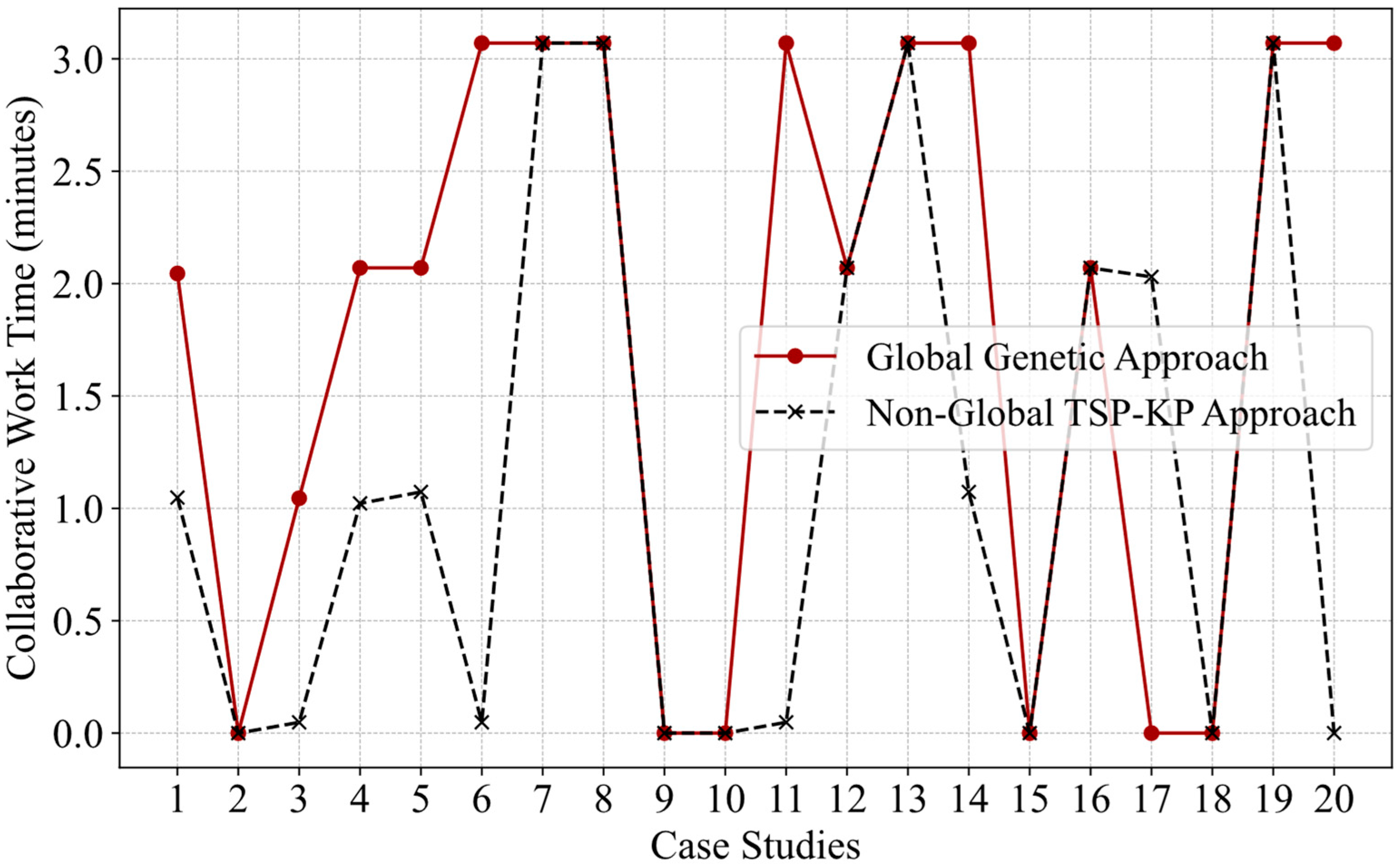
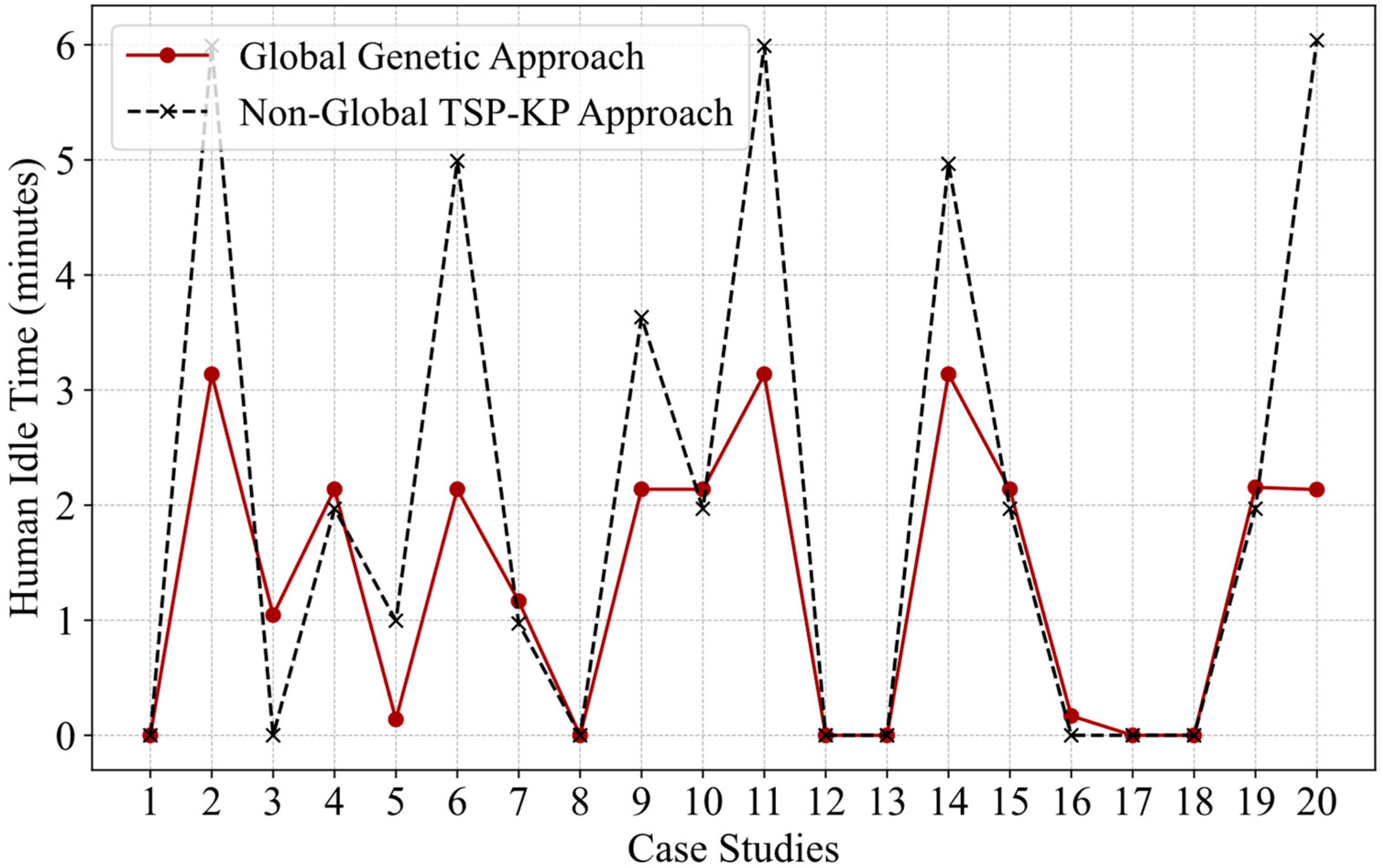
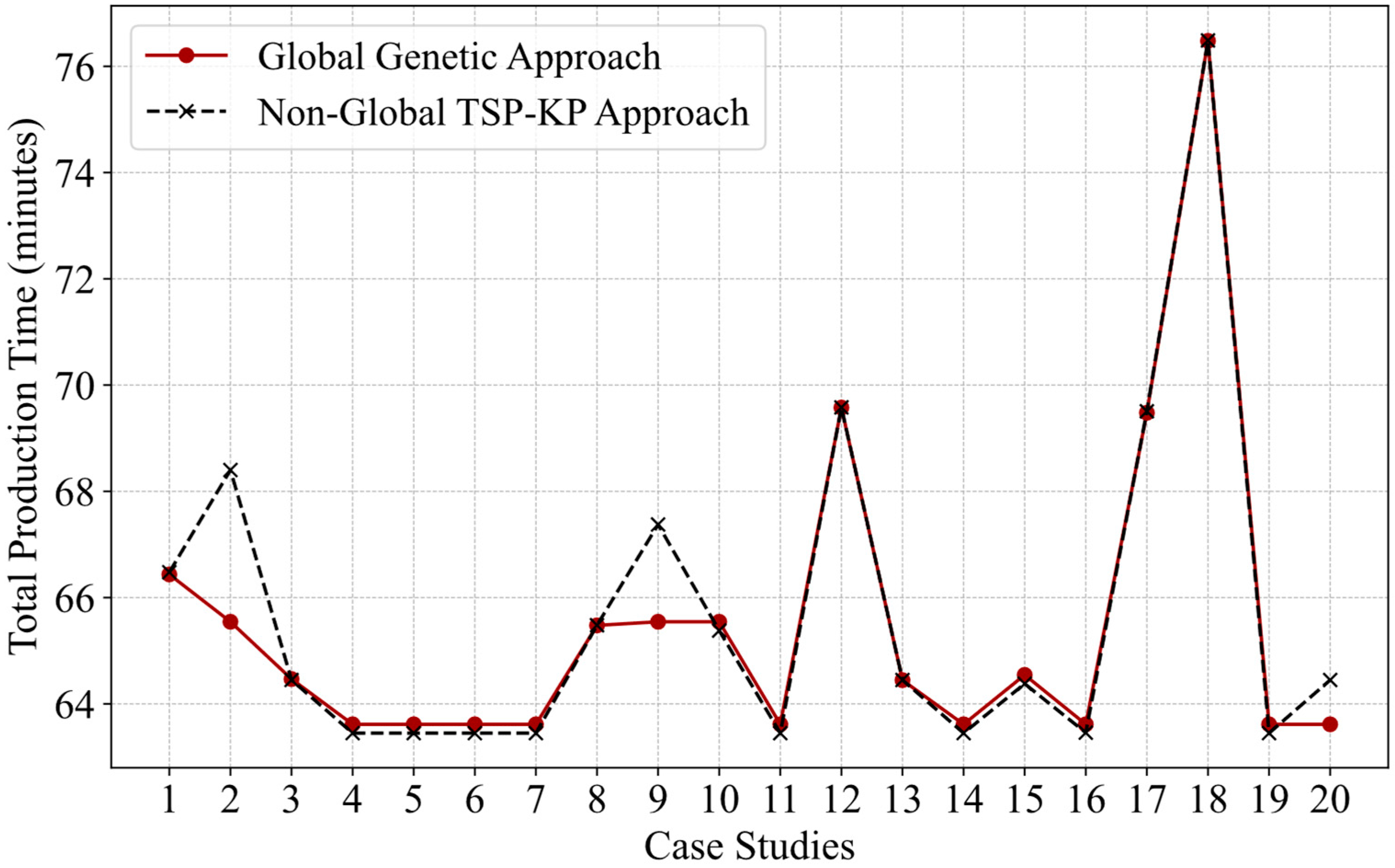
4.3. Analysis of Predictive Approach Results
- -
- Collaborative Work Time Texh:
- -
- Human idle time:
- -
- Robot idle time:
- -
- Production time:
4.4. Analysis of Reactive Approach Results
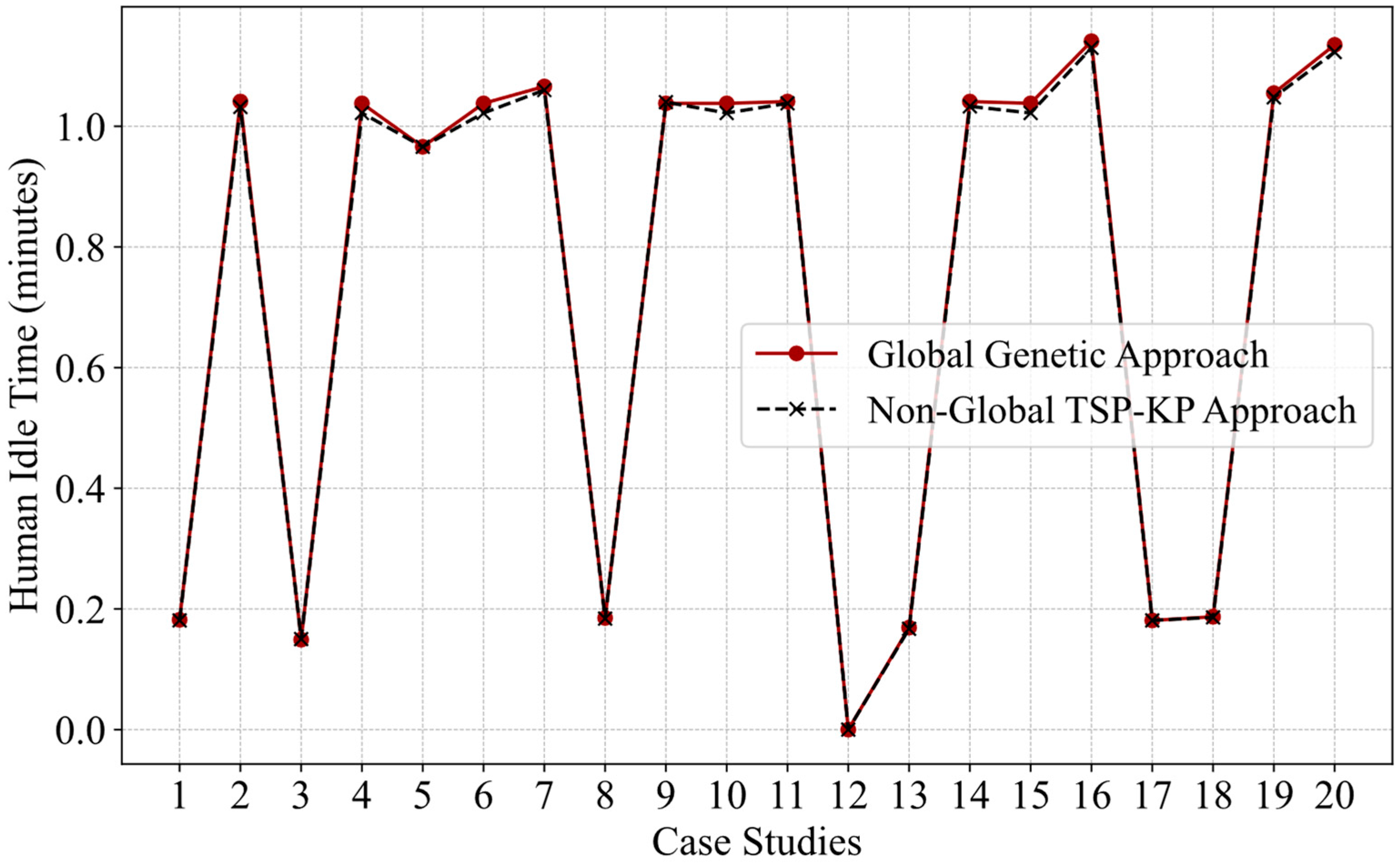
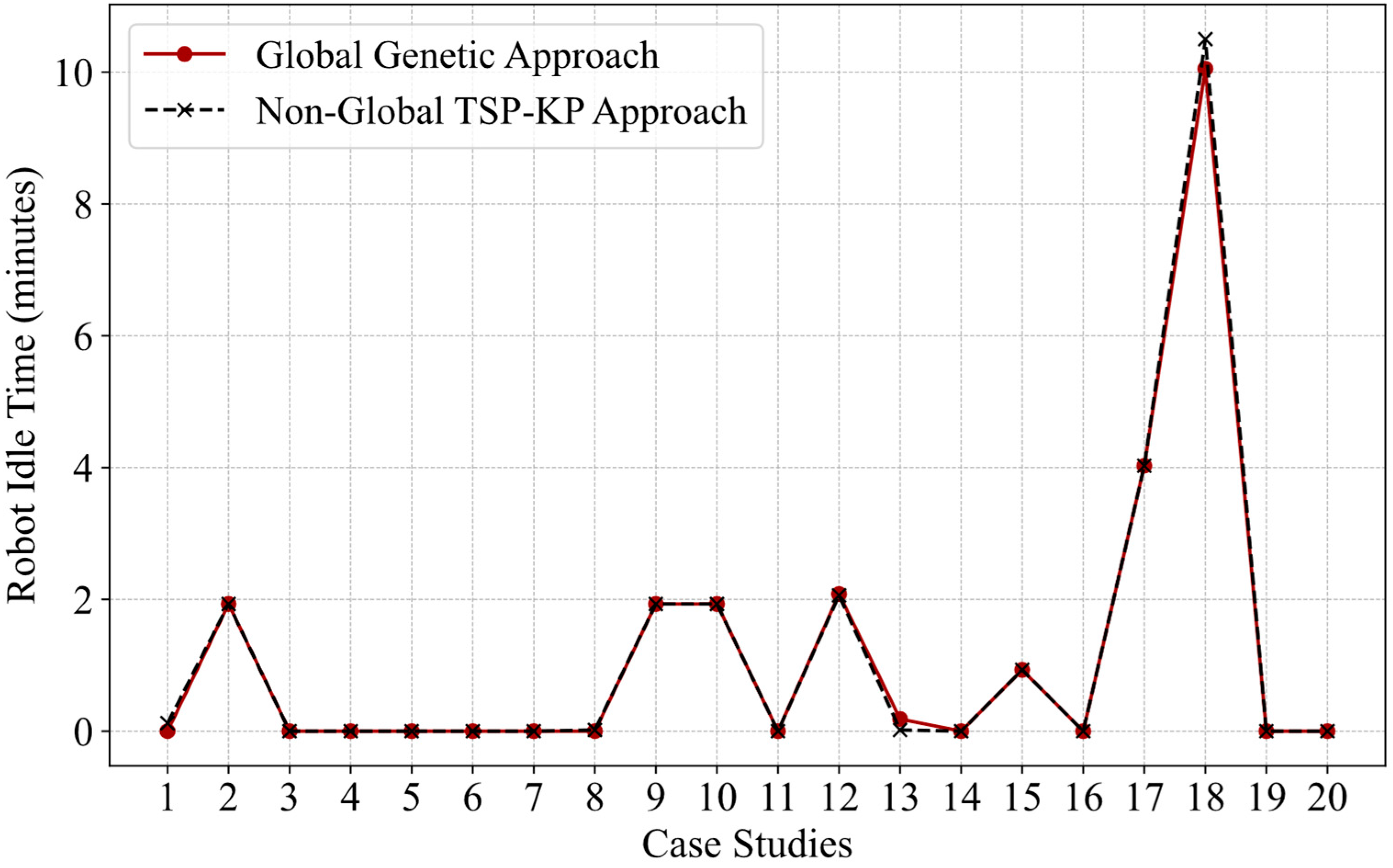
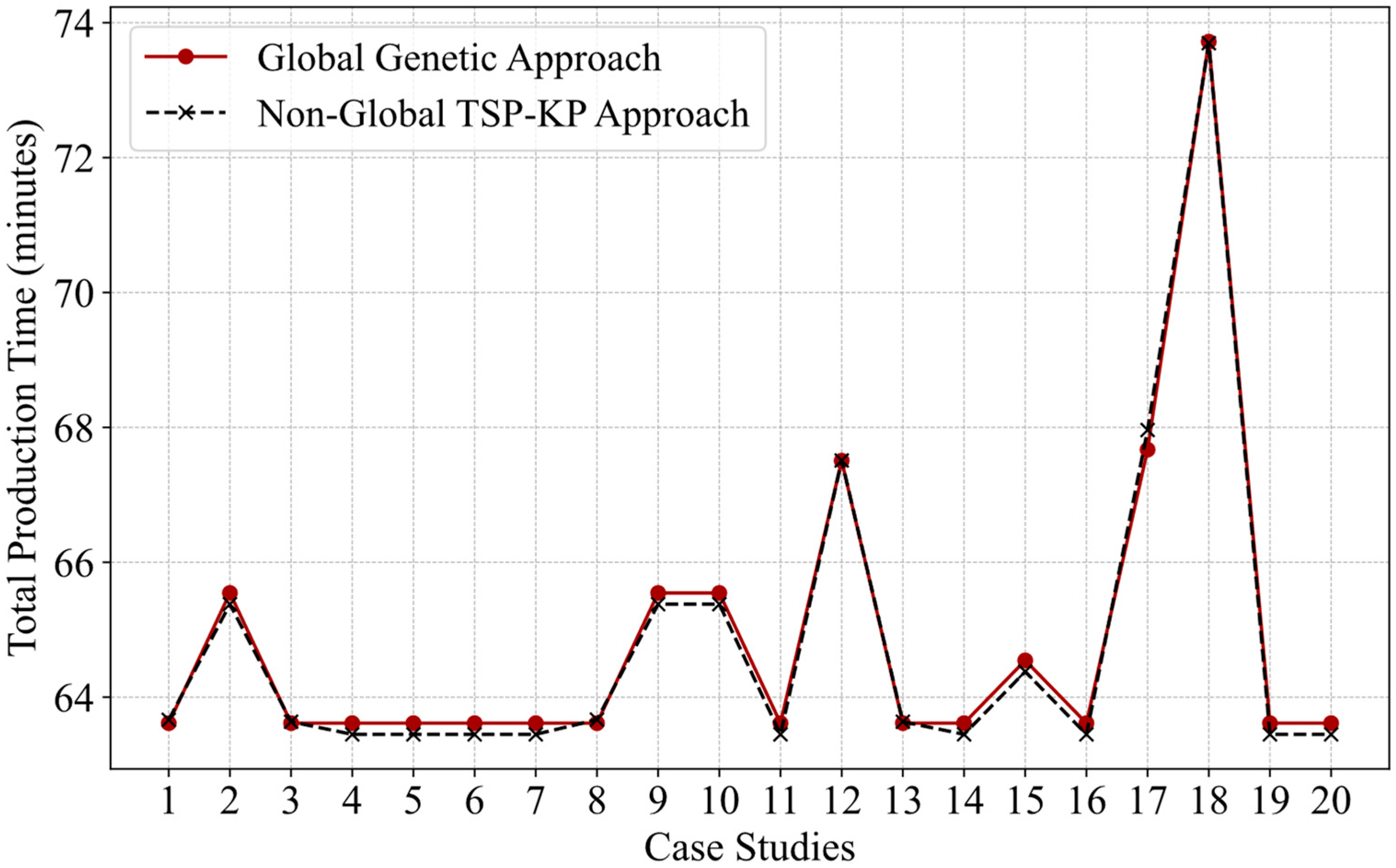
4.5. Comparative Study of Two Optimization Approaches
- -
- Collaborative Work Time (Texh):
- -
- Human idle time:
- -
- Robot idle time:
- -
- Production time:
5. Discussion
6. Conclusions and Future Work
7. Limit of the Study
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| HRC | Human–Robot Collaboration |
| KP | Knapsack Problem |
| GGA | Global approach utilizing a genetic algorithm |
| R-GA | Reactive approach employing a genetic algorithm |
| TSP | Traveling salesman problem |
References
- Ke, Q.; Zhang, P.; Zhang, L.; Song, S. Electric vehicle battery disassembly sequence planning based on frame-subgroup structure combined with genetic algorithm. Front. Mech. Eng. 2020, 6, 576642. [Google Scholar] [CrossRef]
- Alfaro-Algaba, M.; Ramirez, F.J. Techno-economic and environmental disassembly planning of lithium-ion electric vehicle battery packs for remanufacturing. Resour. Conserv. Recycl. 2020, 154, 104461. [Google Scholar] [CrossRef]
- Wood, E.; Alexander, M.; Bradley, T.H. Investigation of battery end-of-life conditions for plug-in hybrid electric vehicles. J. Power Sources 2011, 196, 5147–5154. [Google Scholar] [CrossRef]
- Qu, W.; Li, J.; Zhang, R.; Liu, S.; Bao, J. Adaptive planning of human–robot collaborative disassembly for end-of-life lithium-ion batteries based on digital twin. J. Intell. Manuf. 2023, 35, 2021–2043. [Google Scholar] [CrossRef]
- Yu, D.; Huang, Z.; Makuza, B.; Guo, X.; Tian, Q. Pretreatment options for the recycling of spent lithium-ion batteries: A comprehensive review. Miner. Eng. 2021, 173, 107218. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Z.; Zeng, Y.; Zhang, Y. Mixed-integer programming model and hybrid local search genetic algorithm for human–robot collaborative disassembly line balancing problem. Int. J. Prod. Res. 2024, 62, 1758–1782. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Chu, M.; Chen, W. Human-robot collaboration disassembly planning for end-of-life power batteries. J. Manuf. Syst. 2023, 69, 271–291. [Google Scholar] [CrossRef]
- Ogenyi, U.E.; Liu, J.; Yang, C.; Ju, Z.; Liu, H. Physical Human–Robot Collaboration: Robotic Systems, Learning Methods, Collaborative Strategies, Sensors, and Actuators. IEEE Trans. Cybern. 2021, 51, 1888–1901. [Google Scholar] [CrossRef]
- Tchane Djogdom, G.V.; Meziane, R.; Otis, M.J.D. Robust dynamic robot scheduling for collaborating with humans in manufacturing operations. Robot. Comput.-Integr. Manuf. 2024, 88, 102734. [Google Scholar] [CrossRef]
- Ren, Y.; Tian, G.; Zhao, F.; Yu, D.; Zhang, C. Selective cooperative disassembly planning based on multi-objective discrete artificial bee colony algorithm. Eng. Appl. Artif. Intell. 2017, 64, 415–431. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Z.; Zeng, Y.; Zhang, Y.; Guo, L.; Liu, J. Techno-economic and environmental benefits-oriented human–robot collaborative disassembly line balancing optimization in remanufacturing. Robot. Comput.-Integr. Manuf. 2024, 86, 102650. [Google Scholar] [CrossRef]
- Tian, G.; Ren, Y.; Feng, Y.; Zhou, M.; Zhang, H.; Tan, J. Modeling and planning for dual-objective selective disassembly using AND/OR graph and discrete artificial bee colony. IEEE Trans. Ind. Inform. 2018, 15, 2456–2468. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, X.; Liu, Z.; Jiang, X.; Xue, J. Product cooperative disassembly sequence and task planning based on genetic algorithm. Int. J. Adv. Manuf. Technol. 2019, 105, 2103–2120. [Google Scholar] [CrossRef]
- Lou, P.; Liu, Q.; Zhou, Z.; Wang, H.; Sun, S.X. Multi-agent-based proactive–reactive scheduling for a job shop. Int. J. Adv. Manuf. Technol. 2012, 59, 311–324. [Google Scholar] [CrossRef]
- Cardin, O.; Trentesaux, D.; Thomas, A.; Castagna, P.; Berger, T.; El-Haouzi, H.B. Coupling predictive scheduling and reactive control in manufacturing hybrid control architectures: State of the art and future challenges. J. Intell. Manuf. 2017, 28, 1503–1517. [Google Scholar] [CrossRef]
- Xu, W.; Tang, Q.; Liu, J.; Liu, Z.; Zhou, Z.; Pham, D.T. Disassembly sequence planning using discrete Bees algorithm for human-robot collaboration in remanufacturing. Robot. Comput.-Integr. Manuf. 2020, 62, 101860. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Pham, D.T.; Xu, W.; Ramirez, F.J.; Ji, C.; Liu, Q. Disassembly sequence planning: Recent developments and future trends. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 233, 1450–1471. [Google Scholar] [CrossRef]
- Vongbunyong, S.; Kara, S.; Pagnucco, M. Basic behaviour control of the vision-based cognitive robotic disassembly automation. Assem. Autom. 2013, 33, 38–56. [Google Scholar] [CrossRef]
- Wang, G.; Wu, H.; Xiao, J. A Genetic Algorithm-Based Optimization Approach for Disassembly Tool Selections toward Electric Vehicle Battery Disassembly. In Proceedings of the International Conference on Mechatronics and Robotics Engineering (ICMRE), Shenzhen, China, 10–12 February 2023. [Google Scholar]
- Liau, Y.Y.; Ryu, K. Genetic algorithm-based task allocation in multiple modes of human–robot collaboration systems with two cobots. Int. J. Adv. Manuf. Technol. 2022, 119, 7291–7309. [Google Scholar] [CrossRef]
- Lee, M.-L.; Behdad, S.; Liang, X.; Zheng, M. Disassembly Sequence Planning Considering Human-Robot Collaboration. In Proceedings of the American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020. [Google Scholar]
- Lee, M.-L.; Behdad, S.; Liang, X.; Zheng, M. Task Allocation and Planning for Product Disassembly with Human-Robot Collaboration. Robot. Comput.-Integr. Manuf. 2022, 76, 102306. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Gupta, S.M. Artificial bee colony algorithm for solving sequence-dependent disassembly line balancing problem. Expert Syst. Appl. 2013, 40, 7231–7241. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Z.; Pham, D.T.; Xu, W.; Ji, C.; Liu, Q. Collaborative optimization of robotic disassembly sequence planning and robotic disassembly line balancing problem using improved discrete Bees algorithm in remanufacturing. Robot. Comput.-Integr. Manuf. 2020, 61, 101829. [Google Scholar] [CrossRef]
- Failli, F.; Dini, G. Optimization of Disassembly Sequences for Recycling of End-of-Life Products by Using a Colony of Ant-Like Agents. In Engineering of Intelligent Systems, Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Budapest, Hungary, 4–7 June 2001; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Xing, Y.; Wu, D.; Qu, L. Parallel disassembly sequence planning using improved ant colony algorithm. Ant Colony algorithm. Int. J. Adv. Manuf. Technol. 2021, 113, 2327–2342. [Google Scholar] [CrossRef]
- McGovern, S.M.; Gupta, S.M. Ant colony optimization for disassembly sequencing with multiple objectives. Int. J. Adv. Manuf. Technol. 2006, 30, 481–496. [Google Scholar] [CrossRef]
- Guo, X.; Fan, C.; Zhou, M.; Liu, S.; Wang, J.; Qin, S.; Tang, Y. Human–robot collaborative disassembly line balancing problem with stochastic operation time and a solution via multi-objective shuffled frog leaping algorithm. IEEE Trans. Autom. Sci. Eng. 2023, 21, 4448–4459. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Z.; Zhang, Y.; Zeng, Y. Modelling and optimisation of two-sided disassembly line balancing problem with human–robot interaction constraints. Expert Syst. Appl. 2023, 230, 120589. [Google Scholar] [CrossRef]
- Luo, Z.; Xu, C.; Dong, X.; Hong, P. Optimization of Disassembly Sequence Based on Improved Bald Eagle Search Optimization Algorithm. In Proceedings of the International Conference on Advanced Algorithms and Control Engineering (ICAACE), Shanghai, China, 1–3 March 2024. [Google Scholar]
- Fu, W.; Liu, X.; Chu, F.; Li, B.; Gu, J. A disassembly sequence planning method with improved discrete grey wolf optimizer for equipment maintenance in hydropower station. J. Supercomput. 2023, 79, 4351–4382. [Google Scholar] [CrossRef]
- Liao, H.-Y.; Chen, Y.; Hu, B.; Behdad, S. Optimization-Based Disassembly Sequence Planning Under Uncertainty for Human–Robot Collaboration. J. Mech. Des. 2022, 145, 1–100. [Google Scholar]
- Askarpour, M.; Mandrioli, D.; Rossi, M.; Vicentini, F. Formal model of human erroneous behavior for safety analysis in collaborative robotics. Robot. Comput.-Integr. Manuf. 2019, 57, 465–476. [Google Scholar] [CrossRef]
- Alirezazadeh, S.; Alexandre, L.A. Dynamic Task Scheduling for Human-Robot Collaboration. IEEE Robot. Autom. Lett. 2022, 7, 8699–8704. [Google Scholar] [CrossRef]
- Fusaro, F.; Lamon, E.; De Momi, E.; Ajoudani, A. A human-aware method to plan complex cooperative and autonomous tasks using behavior trees. In Proceedings of the International Conference on Humanoid Robots (Humanoids), Munich, Germany, 19–21 July 2021. [Google Scholar]
- Angleraud, A.; Sefat, A.M.; Netzev, M.; Pieters, R. Coordinating shared tasks in human-robot collaboration by commands. Front. Robot. AI 2021, 8, 734548. [Google Scholar] [CrossRef]
- Zanchettin, A.M. Robust scheduling and dispatching rules for high-mix collaborative manufacturing systems. Flex. Serv. Manuf. J. 2022, 34, 293–316. [Google Scholar] [CrossRef]
- Pupa, A.; Secchi, C. A safety-aware architecture for task scheduling and execution for human-robot collaboration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021. [Google Scholar]
- Guner Goren, H.; Tunali, S.; Jans, R. A review of applications of genetic algorithms in lot sizing. J. Intell. Manuf. 2010, 21, 575–590. [Google Scholar] [CrossRef]
- Salma, N.; Vanel, T.D.G.; Martin, J.O. Source Code for Battery Disassembly Optimisation Using One Humain, One Station. 2025. Available online: https://osf.io/mrta4/overview (accessed on 4 October 2025).



| Article | Fixed Human Tasks | Human as Non-Controllable Agent | Non-Fixed Time Distribution | Constraints | Scheduling Approach | Global Problem Formulation | ||
|---|---|---|---|---|---|---|---|---|
| Cooperation | Exclusion | Predictive | Reactive | |||||
| Our Approach | X | X | X | X | X | X | X | |
| [1] | X | X | X | X | ||||
| [38] | X | X | X | X | X | |||
| [30] | X | X | X | X | X | |||
| [23] | X | X | X | X | X | |||
| [29] | X | X | X | X | X | X | ||
| [39] | X | X | X | X | X | |||
| [10] | X | X | X | X | X | X | X | |
| Tasks Group | Tasks | Definitions |
|---|---|---|
| 1—Removing the battery cover (Ts1) | S1 to S3 | Remove screws of the cover |
| S5-S6 | Extract cover | |
| S7 | Human intervention to remove cables of the BMS (robot far from human) | |
| S8 | Robot tool change | |
| 2—Removing the BMS (Battery Management System) | S9 | Remove rear support block |
| 3—Removing the cells located on the side of the robot at right (robot’s tasks that may be performed in parallel with operator) | S10 to S13 | Move four right bloc supports (for each compartment) |
| S14 | Move right block electrical junction screws | |
| S21 | Move right electrical junction block | |
| S22 to S25 | Four right blocs removed (for each compartment) | |
| 4—Removing the cells that are situated at the closest possible distance to the operator at left (operator outside workspace for safety) | S15 | Move left block electrical junction screws |
| S16 to S19 | Move four left bloc supports (for each compartment) | |
| S20 | Move left electrical junction block | |
| S26 to S29 | Four right blocs removed (for each compartment) | |
| 5—Extracting the cells in the battery compartment at the rear | S30–S33 | Rear block electrical junction to remove (S30 screw, S31 block, S32 end moved, S33 back cover) |
| Indices | |
|---|---|
| i,j | Index of the disassembly task, i/j = 1, 2, ..., n |
| w | Index of the worker type, w ∈ W |
| W | Set of worker groups, W = [10] |
| Iw | Set of tasks to be performed by worker w |
| I | Set of all disassembly tasks performed by the set of workers W |
| Sets | |
| P(i) | Set of predecessor tasks for task i, ∀ i ∈ Iw |
| E(i) | Set of tasks exclusive to human presence, ∀ i ∈ I_H |
| C(i) | Set of tasks that can be performed in the presence of a human, ∀ i ∈ I_H |
| Parameters | |
| N | Total number of disassembly tasks |
| dij [min] | Execution time of task j started after task i |
| Tdp [min] | Expected human availability time required to be ready to work |
| Tdr [min] | Real human availability time |
| Tip [min] | Expected time for human intervention |
| Tir [min] | Real human work time intervention |
| Tih [min] | Human idle time |
| M | A very large coefficient used as a substitute for infinity |
| Cmax [min] | Total disassembly time |
| Use Case | Approach | Before Collaboration | During Collaboration | After Collaboration | Texh [min] | SoiH [min] | TsiR [min] | Tpro [min] |
|---|---|---|---|---|---|---|---|---|
| Case 1 (Tdp = 12, Tip = 3, Tdr = 14.813, Tir = 1) | NG-TSPKP | Ts1-S17-S18 | S10-S13 | S11-S12-S19-S16-Enf | 1.048 | 0 | 3.028 | 66.477 |
| G-GA | Ts1-S18-S12 | S13-S10-S11 | S17-S19-S16-Enf | 2.045 | 0 | 2.817 | 66.436 | |
| R-TSPKP | Ts1-S17-S18-S19-S16-S11 | S10 | S12-S13-Enf | 0 | 0.181 | 0.215 | 63.664 | |
| R-GA | Ts1-S18-S17-S19-S16-S12- | S13 | S10-S11-Enf | 0 | 0.132 | 0 | 63.615 | |
| Case 2 (Tdp = 18, Tip = 7, Tdr = 10.81, Tir = 6) | NG-TSPKP | Ts1-S17-S18-S16-S19-S11-S10-S12 | S13 | Enf | 0 | 5.991 | 4.742 | 68.401 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 0 | 3.138 | 1.930 | 65.545 | |
| R-TSPKP | Ts1-S17-S18 | S13-S11-S10-S12 | S16-S19-Enf | 0 | 0.972 | 1.93 | 65.379 | |
| R-GA | Ts1-S17-S18 | S13-S12-S10-S11 | S19-S16-Enf | 0 | 1.041 | 1.93 | 65.545 | |
| Case 3 (Tdp = 10, Tip = 3, Tdr = 10.81, Tir = 2) | NG-TSPKP | Ts1 | S10-S13 | S11-S12-S17-S18-S19-S16-Enf | 0.048 | 0 | 1 | 64.449 |
| G-GA | Ts1 | S13-S12-S10 | S17-S18-S19-S11-S16-Enf | 1.045 | 0 | 0.831 | 64.467 | |
| R-TSPKP | Ts1-S17 | S10-S13 | S11-S12-S18-S19-S16-Enf | 0.048 | 0.167 | 0 | 63.636 | |
| R-GA | Ts1-S17 | S13-S12 | S18-S19-S11-S16-S10-Enf | 0 | 0.149 | 0 | 63.615 | |
| Case 4 (Tdp = 14, Tip = 4, Tdr = 11.81, Tir = 2) | NG-TSPKP | Ts1-S17-S18-S19-S16 | S11-S10-S12 | S13-Enf | 1.022 | 1.969 | 0 | 63.449 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 2.07 | 2.138 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18-S19 | S11-S10-S12 | S13-S16-Enf | 1.022 | 0.969 | 0 | 63.449 | |
| R-GA | Ts1-S17-S18-S19 | S13-S12-S10 | S11-S16-Enf | 1.022 | 1.038 | 0 | 63.615 | |
| Case 5 (Tdp = 15, Tip = 6, Tdr = 13.81, Tir = 2) | NG-TSPKP | Ts1-S17-S18-S19-S16-S11 | S10-S12-S13 | Enf | 1.073 | 0.966 | 0 | 63.449 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 2.07 | 0.138 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18-S19-S16-S11 | S10-S12 | S13-Enf | 0.025 | 0.966 | 0 | 63.449 | |
| R-GA | Ts1-S17-S18-S19-S16-S11 | S10-S12 | S13-Enf | 0.025 | 0.966 | 0 | 63.615 | |
| Case 6 (Tdp = 18, Tip = 8, Tdr = 11.81, Tir = 1) | NG-TSPKP | Ts1-S17-S18-S19-S16-S11-S10-S12 | S13 | Enf | 0.048 | 4.991 | 0 | 63.449 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 3.07 | 2.138 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18-S19 | S13 | S10-S11-S12-S16-Enf | 0.048 | 0.969 | 0 | 63.449 | |
| R-GA | Ts1-S17-S18-S19 | S13 | S12-S10-S11-S16-Enf | 0.048 | 1.038 | 0 | 63.615 | |
| Case 7 (Tdp = 12, Tip = 5, Tdr = 10.81, Tir = 1) | NG-TSPKP | Ts1-S17-S18 | S11-S10-S12-S13 | S19-S16-Enf | 3.07 | 0.972 | 0 | 63.449 |
| G-GA | Ts1-S19-S16 | S13-S12-S10-S11 | S17-S18-Enf | 3.07 | 1.166 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18 | S11-S10 | S12-S13-S19-S16-Enf | 0.997 | 0.972 | 0 | 63.449 | |
| R-GA | Ts1-S19-S16 | S11-S10 | S17-S18-S12-S13-Enf | 0.997 | 1.066 | 0 | 63.615 | |
| Case 8 (Tdp = 14, Tip = 9, Tdr = 15.81, Tir = 1) | NG-TSPKP | Ts1-S17-S18-S19-S16 | S11-S10-S12-S13 | Enf | 3.07 | 0 | 2.031 | 65.480 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 3.07 | 0 | 1.862 | 65.477 | |
| R-TSPKP | Ts1-S17-S18-S19-S16-S11-S10 | S12 | S13-Enf | 0.025 | 0.184 | 0.218 | 63.667 | |
| R-GA | Ts1-S17-S18-S19-S16-S13-S12 | S10 | S11-Enf | 0 | 0.135 | 0 | 63.615 | |
| Case 9 (Tdp = 16, Tip = 8, Tdr = 11.81, Tir = 6) | NG-TSPKP | Ts1-S18-S17-S19-S16-S11-S10 | S12-S13 | Enf | 0 | 3.633 | 3.927 | 67.376 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 0 | 2.138 | 1.93 | 65.545 | |
| R-TSPKP | Ts1-S18-S17-S19 | S11-S10-S12-S13 | S16-Enf | 0 | 0.969 | 1.93 | 65.379 | |
| R-GA | Ts1-S17-S18-S19 | S13-S12-S10-S11 | S16-Enf | 0 | 1.038 | 1.93 | 65.545 | |
| Case 10 (Tdp = 14, Tip = 8, Tdr = 11.81, Tir = 6) | NG-TSPKP | Ts1-S17-S18-S19-S16 | S11-S10-S12-S13 | Enf | 0 | 1.969 | 1.93 | 65.379 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 0 | 2.138 | 1.93 | 65.545 | |
| R-TSPKP | Ts1-S17-S18-S19 | S11-S10-S12-S13 | S16-Enf | 0 | 0.969 | 1.93 | 65.379 | |
| R-GA | Ts1-S17-S18-S19 | S13-S12-S10-S11 | S16-Enf | 0 | 1.038 | 1.93 | 65.545 | |
| Case 11 (Tdp = 17, Tip = 5, Tdr = 10.81, Tir = 1) | NG-TSPKP | Ts1-S17-S18-S19-S16-S11-S10-S12 | S13 | Enf | 0.048 | 5.991 | 0 | 63.449 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 3.07 | 3.138 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18 | S13 | S11-S10-S19-S16-Enf | 0.048 | 0.972 | 0 | 63.449 | |
| R-GA | Ts1-S17-S18 | S13 | S12-S10-S11-S19-S16-Enf | 0.048 | 1.041 | 0 | 63.615 | |
| Case 12 (Tdp = 14, Tip = 7, Tdr = 19.91, Tir = 2) | NG-TSPKP | Ts1-S17-S18-S19-S16 | S11-S10-S12-S13 | Enf | 2.07 | 0 | 6.131 | 69.580 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 2.07 | 0 | 5.962 | 69.577 | |
| R-TSPKP | Ts1-S18-S17-S19-S16-S11-S10-S12-S13 | N/A | Enf | 0 | 0 | 2.061 | 67.510 | |
| R-GA | Ts1-S17-S18-S19-S16-S13-S12-S10-S11 | N/A | Enf | 0 | 0 | 3.891 | 67.507 | |
| Case 13 (Tdp = 10, Tip = 5, Tdr = 10.81, Tir = 1) | NG-TSPKP | Ts1 | S11-S10-S12-S13 | S18-S17-S19-S16-Enf | 3.07 | 0 | 1 | 64.449 |
| G-GA | Ts1 | S11-S10-S12-S13 | S17-S18-S19-S16-Enf | 3.07 | 0 | 0.831 | 64.446 | |
| R-TSPKP | Ts1-S17 | S11-S10 | S12-S13-S18-S19-S16-Enf | 0.997 | 0.167 | 0.187 | 63.636 | |
| R-GA | Ts1-S17 | S11-S10 | S18-S19-S16-S12-S13-Enf | 0.997 | 0.149 | 0 | 63.615 | |
| Case 14 (Tdp = 16, Tip = 8, Tdr = 10.81, Tir = 1) | NG-TSPKP | Ts1-S17-S18-S19-S16-S11-S10 | S12-S13 | Enf | 1.073 | 4.966 | 0 | 63.449 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 3.07 | 3.138 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18 | S12 | S11-S10-S13-S19-S16-Enf | 0.025 | 0.972 | 0 | 63.449 | |
| R-GA | Ts1-S17-S18 | S13 | S12-S10-S11-S18-S19-S16-Enf | 0.048 | 1.041 | 0 | 63.615 | |
| Case 15 (Tdp = 14, Tip = 7, Tdr = 11.81, Tir = 5) | NG-TSPKP | Ts1-S17-S18-S19-S16 | S11-S10-S12-S13 | Enf | 0 | 1.969 | 0.93 | 64.379 |
| G-GA | Ts1-S17-S18-S19-S16 | S13-S12-S10-S11 | Enf | 0 | 2.138 | 0.93 | 64.545 | |
| R-TSPKP | Ts1-S17-S18-S19 | S11-S10-S12-S13 | S16-Enf | 0 | 0.969 | 0.93 | 64.379 | |
| R-GA | Ts1-S17-S18-S19 | S13-S12-S10-S11 | S16-Enf | 0 | 1.038 | 0.93 | 64.545 | |
| Case 16 (Tdp = 11, Tip = 5, Tdr = 10.81, Tir = 2) | NG-TSPKP | Ts1-S18 | S11-S10-S12-S13 | Enf | 2.07 | 0 | 0.008 | 63.457 |
| G-GA | Ts1-S16 | S11-S10-S12-S13 | S17-S18-S19-Enf | 2.07 | 0.169 | 0 | 63.615 | |
| R-TSPKP | Ts1-S18-S17 | S11-S10-S12 | S13-S16-S19-Enf | 1.02 | 0.972 | 0 | 63.449 | |
| R-GA | Ts1-S16-S17 | S11-S10-S12 | S18-S19-S13-Enf | 1.022 | 1.141 | 0 | 63.615 | |
| Case 17 (Tdp = 12, Tip = 8, Tdr = 15.81, Tir = 6.1) | NG-TSPKP | Ts1-S17-S18 | S11-S10-S12-S13 | S19-S16-Enf | 2.03 | 0 | 4.028 | 69.507 |
| G-GA | Ts1-S19-S16 | S13-S12-S10-S11 | S17-S18-Enf | 0 | 0 | 5.864 | 69.479 | |
| R-TSPKP | Ts1-S17-S18-S19-S16-S11-S10 | S13-S12 | Enf | 0 | 0.181 | 4.027 | 67.691 | |
| R-GA | Ts1-S19-S16-S17-S18-S13-S12 | S10-S11 | Enf | 0 | 0.135 | 4.027 | 67.670 | |
| Case 18 (Tdp = 11, Tip = 10, Tdr = 16.813, Tir = 11.1) | NG-TSPKP | Ts1-S18 | S11-S10-S12-S13 | S17-S19-S16-Enf | 0 | 0 | 13.04 | 76.487 |
| G-GA | Ts1-S16 | S13-S12-S10-S11 | S17-S18-S19-Enf | 0 | 0 | 12.864 | 76.479 | |
| R-TSPKP | Ts1-S18-S17-S19-S16-S11-S10-S12 | S13 | Enf | 0 | 0.186 | 10.050 | 73.696 | |
| R-GA | Ts1-S16-S17-S18-S19-S11-S10-S12 | S13 | Enf | 0 | 0.157 | 10.051 | 73.719 | |
| Case 19 (Tdp = 13, Tip = 8, Tdr = 10.813, Tir = 1) | NG-TSPKP | Ts1-S18-S17-S19 | S11-S10-S12-S13 | S16-Enf | 3.07 | 1.969 | 0 | 63.449 |
| G-GA | Ts1-S18-S19-S16 | S13-S12-S10-S11 | S17-Enf | 3.07 | 2.155 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18 | S11-S10 | S12-S13-S19-S16-Enf | 0.997 | 0.972 | 0 | 63.449 | |
| R-GA | Ts1-S18-S19 | S11-S10 | S17-S12-S13-S16-Enf | 0.997 | 1.055 | 0 | 63.615 | |
| Case 20 (Tdp = 20, Tip = 9, Tdr = 11.813, Tir = 1) | NG-TSPKP | Ts1-S17-S18-S19-S16-S11-S10-S12-S13 | N/A | Enf | 0 | 6.039 | 1 | 64.449 |
| G-GA | Ts1-S17-S18-S19-S16 | S11-S10-S12-S13 | Enf | 3.07 | 2.135 | 0 | 63.615 | |
| R-TSPKP | Ts1-S17-S18-S19 | S11-S10 | S12-S13-S16-Enf | 0.997 | 0.969 | 0 | 63.449 | |
| R-GA | Ts1-S17-S18-S19 | S11-S10 | S12-S13-S16-Enf | 0.997 | 1.135 | 0 | 63.615 |
| Metric | Percentage Difference |
|---|---|
| Collaboration Time Texh | 98.63% |
| Human Idle Time | 93.15% |
| Robot Idle Time | 69.58% |
| Production Time | 2.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nabli, S.; Djogdom, G.V.T.; Otis, M.J.-D. Optimization of the Human–Robot Collaborative Disassembly Process Using a Genetic Algorithm: Application to the Reconditioning of Electric Vehicle Batteries. Designs 2025, 9, 122. https://doi.org/10.3390/designs9050122
Nabli S, Djogdom GVT, Otis MJ-D. Optimization of the Human–Robot Collaborative Disassembly Process Using a Genetic Algorithm: Application to the Reconditioning of Electric Vehicle Batteries. Designs. 2025; 9(5):122. https://doi.org/10.3390/designs9050122
Chicago/Turabian StyleNabli, Salma, Gilde Vanel Tchane Djogdom, and Martin J.-D. Otis. 2025. "Optimization of the Human–Robot Collaborative Disassembly Process Using a Genetic Algorithm: Application to the Reconditioning of Electric Vehicle Batteries" Designs 9, no. 5: 122. https://doi.org/10.3390/designs9050122
APA StyleNabli, S., Djogdom, G. V. T., & Otis, M. J.-D. (2025). Optimization of the Human–Robot Collaborative Disassembly Process Using a Genetic Algorithm: Application to the Reconditioning of Electric Vehicle Batteries. Designs, 9(5), 122. https://doi.org/10.3390/designs9050122








