Effect of Cross-Section Designs on Energy Absorption of Mechanical Metamaterials
Abstract
1. Introduction
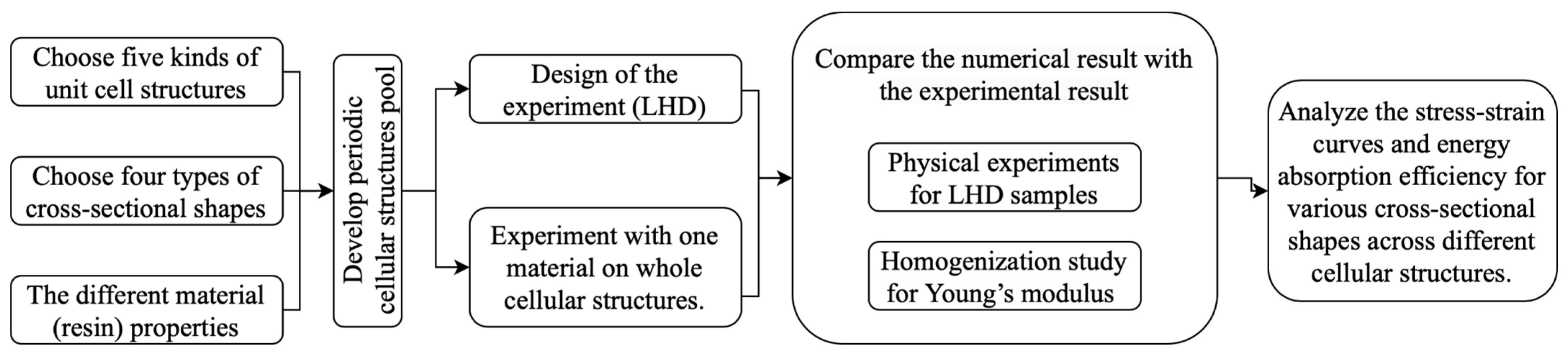
2. Research Methodology
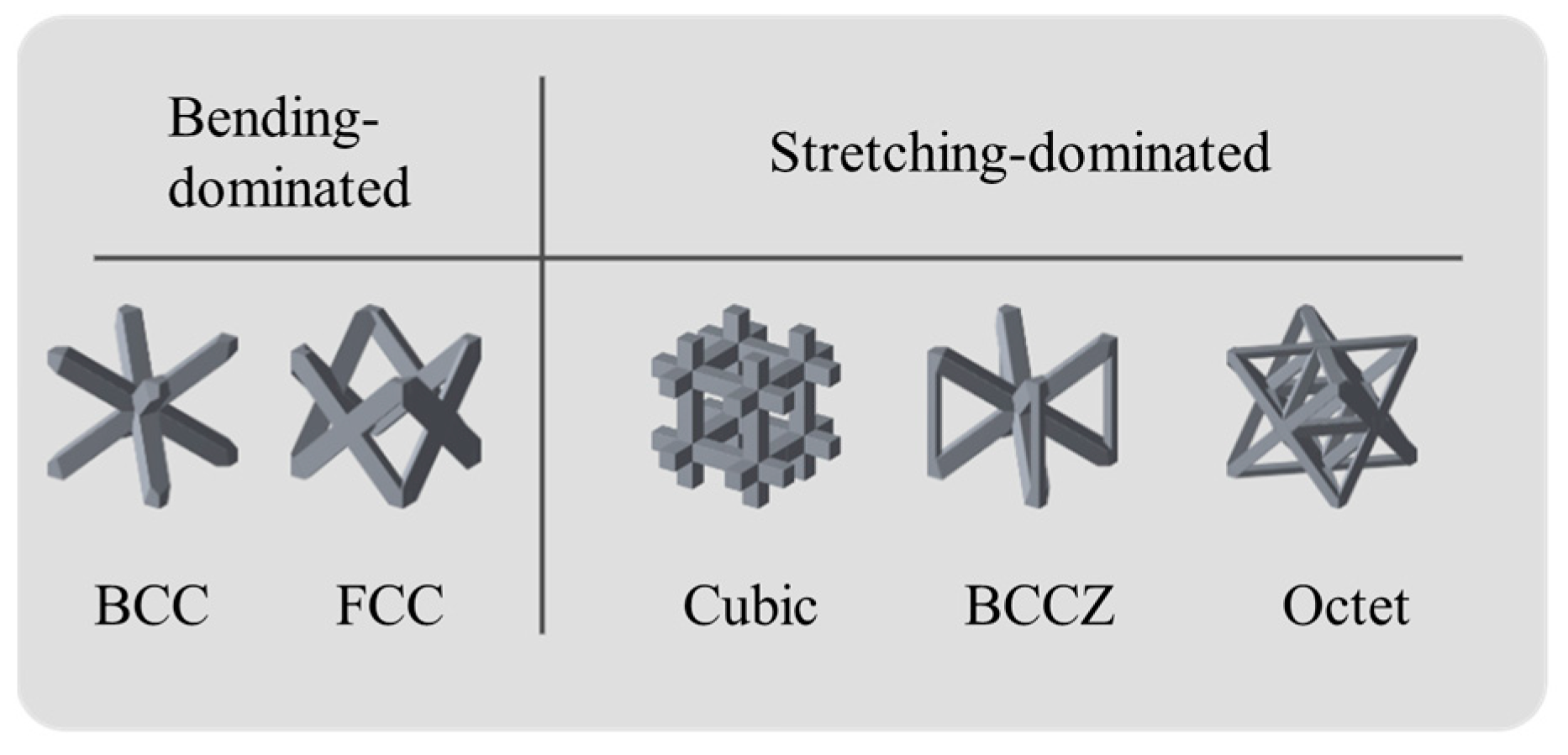
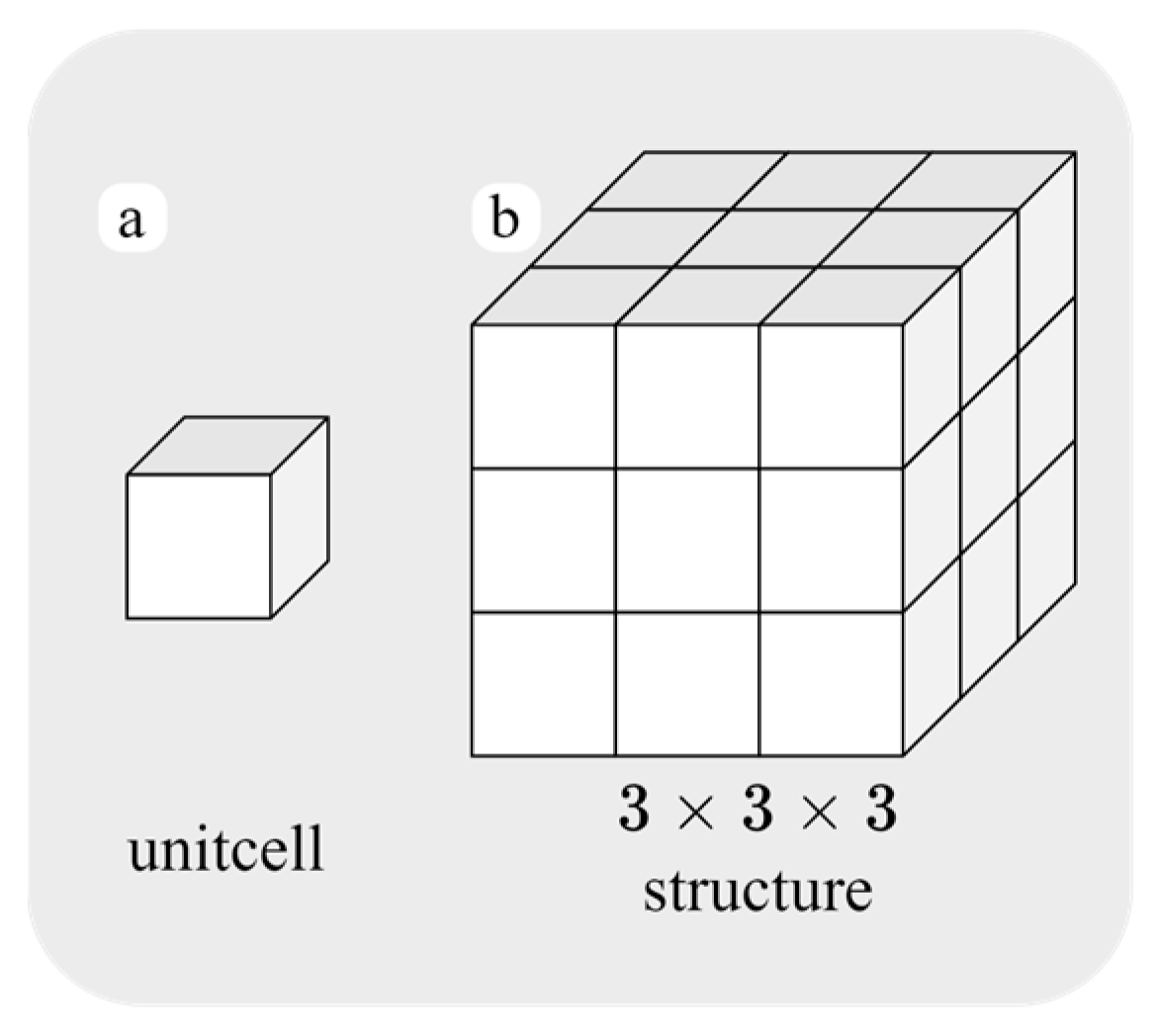
2.1. Structure Specimens
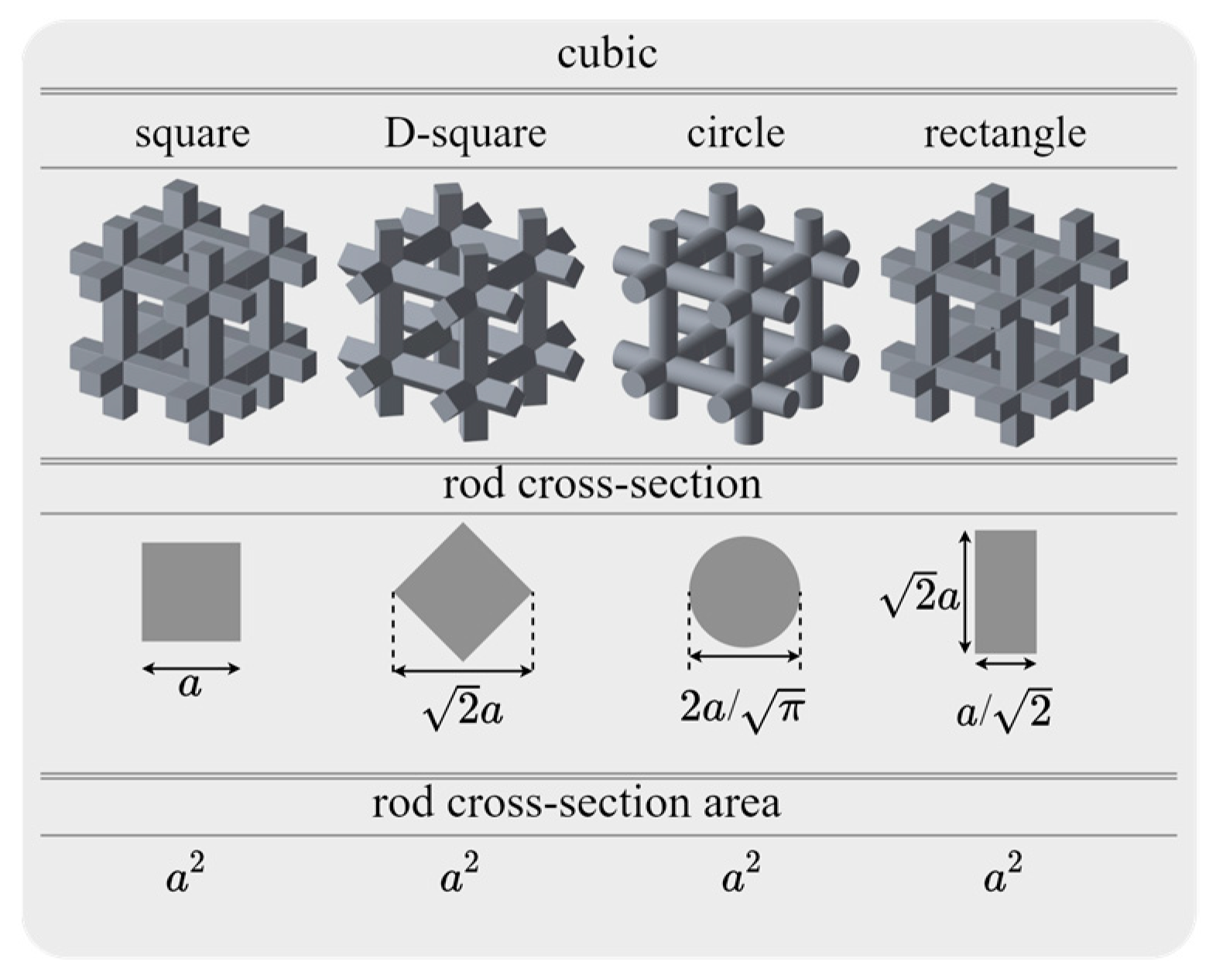
2.2. Strut Cross-Section Design
2.3. Elastic Response
2.4. Energy Absorption Efficiency
2.5. Manufacturing Process
2.6. Mechanical Testing Experiments
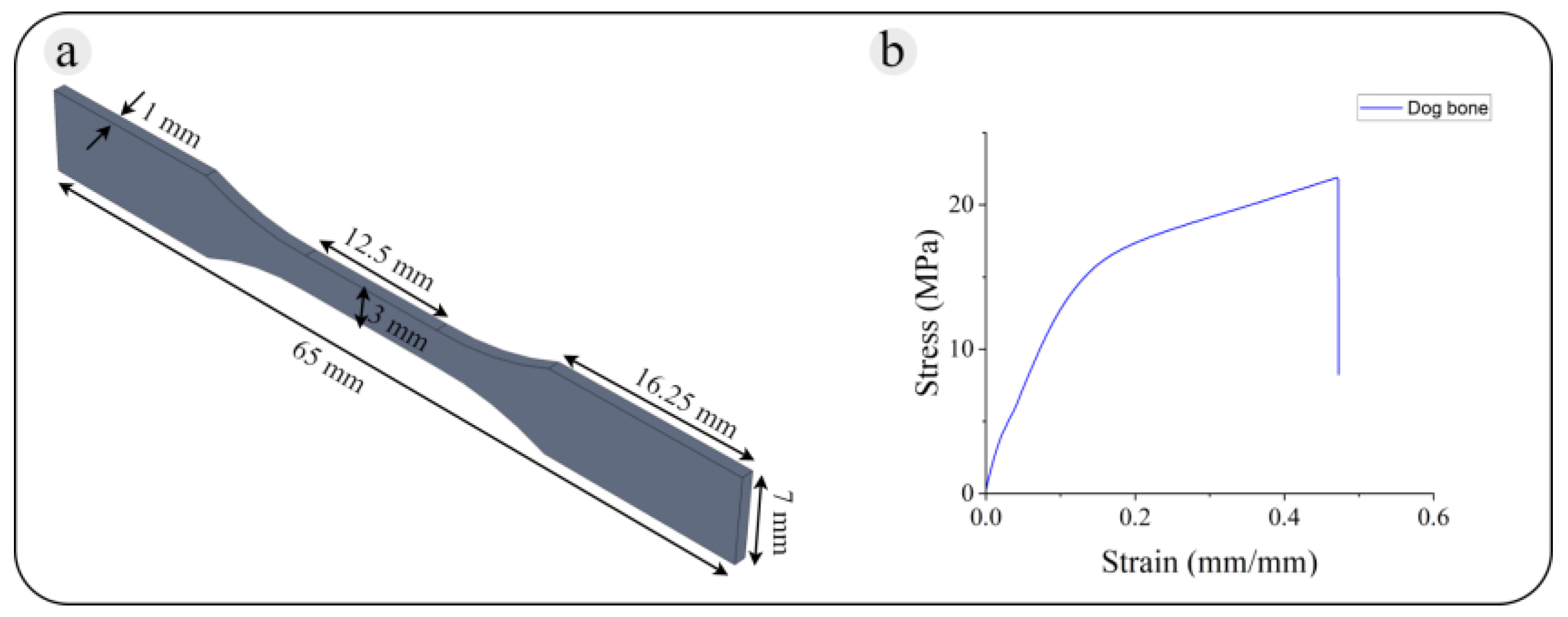
2.6.1. Based Material
2.6.2. Specimens
2.6.3. Compression Experiment
- Compressive modulus of elasticity.
- Yield stress.
- Deformation beyond the yield point.
- Compressive strength.
3. Results
3.1. Homogenized Stiffness
3.2. Bending-Dominated Lattice Structures
3.2.1. BCC Lattice Structures
3.2.2. FCC Lattice Structures
3.3. Stretching-Dominated Lattice Structures
3.3.1. cubic Lattice Structures
3.3.2. BCCZ Lattice Structures
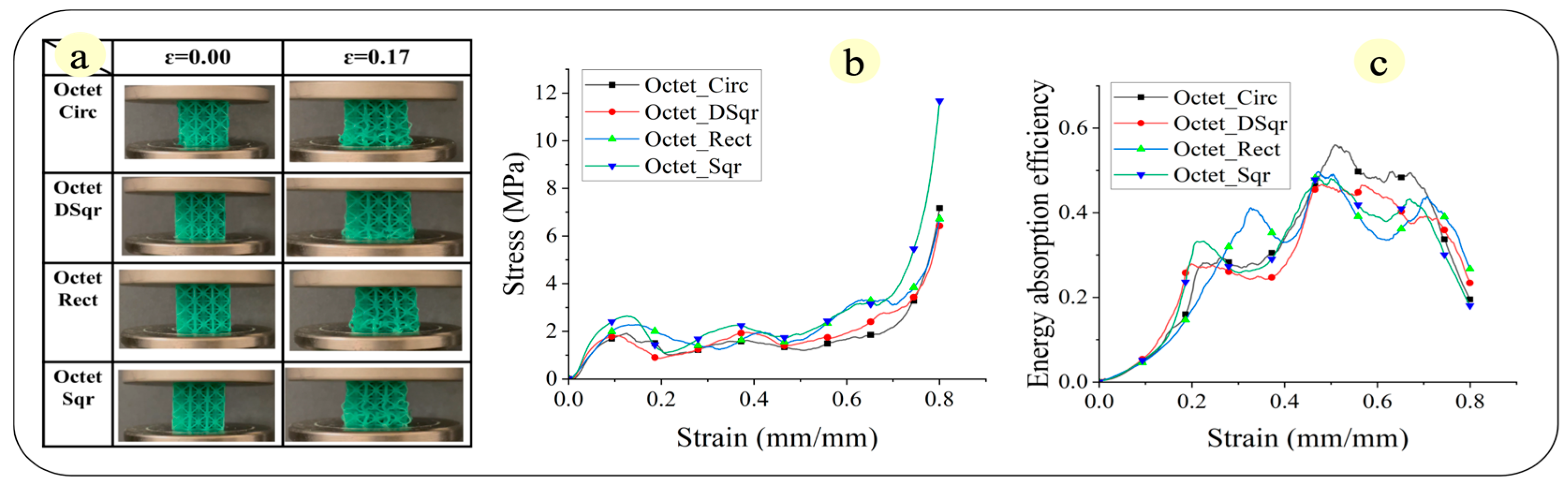
3.3.3. octet Lattice Structures
3.4. Optimal LHD Samples
4. Conclusions
- Bending-dominated structures. For the BCC and FCC structures, we recommend a square cross-section.
- Stretching-dominated structure. For the cubic structures, we suggest a circular cross-section; For the BCCZ structures, we suggest a diagonal-square cross-section; For the octet structure, we suggest a square cross-section.
- Energy absorption. The bending domain structure is more energy absorptive if the resin has a larger Young’s modulus. Different cross-sections also result in different energy absorption efficiency and densification strains.
- Energy absorption efficiency. The results show no relation between cross-section type and the energy absorption efficiency of the cellular structures for small strains (7.5%). So, for the applications with small strains and the energy absorption efficiency as the primary target, we suggest considering either the material cost or the yield stress as the secondary target.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vardi, I. Quantifying accidents: Cars, statistics, and unintended consequences in the construction of social problems over time. Qual. Sociol. 2014, 37, 345–367. [Google Scholar] [CrossRef]
- Steele, G. Industrial accidents: An economic interpretation. Appl. Econ. 1974, 6, 143–155. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, X.; Guo, C.; Dai, N. Toughness-improving design of lattice sandwich structures. Mater. Des. 2023, 226, 111600. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Charalampous, P.; Tsongas, K.; Kostavelis, I.; Tzetzis, D.; Tzovaras, D. Experimental and computational investigation of lattice sandwich structures constructed by additive manufacturing technologies. J. Manuf. Mater. Process. 2021, 5, 95. [Google Scholar] [CrossRef]
- Tarlochan, F. Sandwich structures for energy absorption applications: A review. Materials 2021, 14, 4731. [Google Scholar] [CrossRef]
- Lu, Q.; Qi, D.; Li, Y.; Xiao, D.; Wu, W. Impact energy absorption performances of ordinary and hierarchical chiral structures. Thin-Walled Struct. 2019, 140, 495–505. [Google Scholar] [CrossRef]
- Sun, Z.; Guo, Y.; Shim, V. Characterisation and modeling of additively manufactured polymeric hybrid lattice structures for energy absorption. Int. J. Mech. Sci. 2021, 191, 106101. [Google Scholar] [CrossRef]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 325–332. [Google Scholar]
- Dong, G.; Tang, Y.; Zhao, Y.F. A survey of modeling of lattice structures fabricated by additive manufacturing. J. Mech. Des. 2017, 139, 100906. [Google Scholar] [CrossRef]
- Han, Y.; Lu, W.F. A novel design method for nonuniform lattice structures based on topology optimization. J. Mech. Des. 2018, 140, 091403. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Xu, Y.; Zhang, W.; Zhu, J. Compressive behavior and energy absorption of polymeric lattice structures made by additive manufacturing. Front. Mech. Eng. 2020, 15, 319–327. [Google Scholar] [CrossRef]
- Nagesha, B.; Dhinakaran, V.; Shree, M.V.; Kumar, K.M.; Chalawadi, D.; Sathish, T. Review on characterization and impacts of the lattice structure in additive manufacturing. Mater. Today Proc. 2020, 21, 916–919. [Google Scholar] [CrossRef]
- Tang, Y.; Dong, G.; Zhou, Q.; Zhao, Y.F. Lattice structure design and optimization with additive manufacturing constraints. IEEE Trans. Autom. Sci. Eng. 2017, 15, 1546–1562. [Google Scholar] [CrossRef]
- Lichade, K.M.; Joyee, E.B.; Pan, Y. Gradient light video projection-based stereolithography for continuous production of solid objects. J. Manuf. Process. 2021, 65, 20–29. [Google Scholar] [CrossRef]
- Guerra Silva, R.; Torres, M.J.; Zahr Viñuela, J. A comparison of miniature lattice structures produced by material extrusion and vat photopolymerization additive manufacturing. Polymers 2021, 13, 2163. [Google Scholar] [CrossRef]
- Zhang, P.; Biligetu; Qi, D.; Xue, R.; Liu, K.; Huang, Z.; Wu, W.; Li, Y. Mechanical design and energy absorption of 3D novel hybrid lattice metamaterials. Sci. China Technol. Sci. 2021, 64, 2220–2228. [Google Scholar] [CrossRef]
- Meza, L.R.; Zelhofer, A.J.; Clarke, N.; Mateos, A.J.; Kochmann, D.M.; Greer, J.R. Resilient 3D hierarchical architected metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 11502–11507. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Elastically-isotropic truss lattice materials of reduced plastic anisotropy. Int. J. Solids Struct. 2018, 138, 24–39. [Google Scholar] [CrossRef]
- Dara, A.; Bahubalendruni, M.A.R.; Mertens, A.J.; Balamurali, G. Numerical and experimental investigations of novel nature inspired open lattice cellular structures for enhanced stiffness and specific energy absorption. Mater. Today Commun. 2022, 31, 103286. [Google Scholar] [CrossRef]
- Sharma, D.; Hiremath, S.S. Bio-inspired repeatable lattice structures for energy absorption: Experimental and finite element study. Compos. Struct. 2022, 283, 115102. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, J.; Wang, W.; Gao, L. Compression behaviors of the bio-inspired hierarchical lattice structure with improved mechanical properties and energy absorption capacity. J. Mater. Res. Technol. 2022, 17, 2755–2771. [Google Scholar] [CrossRef]
- He, G.; Yang, H.; Chen, T.; Ning, Y.; Zou, H.; Zhu, F. Lattice structure design method aimed at energy absorption performance based on bionic design. Machines 2022, 10, 965. [Google Scholar] [CrossRef]
- Niknam, H.; Akbarzadeh, A. Graded lattice structures: Simultaneous enhancement in stiffness and energy absorption. Mater. Des. 2020, 196, 109129. [Google Scholar] [CrossRef]
- Bai, L.; Yi, C.; Chen, X.; Sun, Y.; Zhang, J. Effective design of the graded strut of BCC lattice structure for improving mechanical properties. Materials 2019, 12, 2192. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Hamzehei, R.; Zolfagharian, A.; Dariushi, S.; Bodaghi, M. 3D-printed bioinspired zero Poisson’s ratio graded metamaterials with high energy absorption performance. Smart Mater. Struct. 2022, 31, 035001. [Google Scholar] [CrossRef]
- Alkhatib, S.E.; Karrech, A.; Sercombe, T.B. Isotropic energy absorption of topology optimized lattice structure. Thin-Walled Struct. 2023, 182, 110220. [Google Scholar] [CrossRef]
- Gharehbaghi, H.; Farrokhabadi, A. Experimental, analytical, and numerical studies of the energy absorption capacity of bi-material lattice structures based on quadrilateral bipyramid unit cell. Compos. Struct. 2024, 337, 118042. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, F.; Li, P.; Li, L.; Zhao, M.; Shi, J.; Zhang, L.; Cai, Y. A partially hollow BCC lattice structure with capsule-shaped cavities for enhancing load-bearing and energy absorption properties. Eng. Struct. 2024, 305, 117777. [Google Scholar] [CrossRef]
- Wagner, M.A.; Lumpe, T.S.; Chen, T.; Shea, K. Programmable, active lattice structures: Unifying stretch-dominated and bending-dominated topologies. Extreme Mech. Lett. 2019, 29, 100461. [Google Scholar] [CrossRef]
- Deshpande, V.; Ashby, M.; Fleck, N. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, mechanical properties, and optimization of BCC lattice structures with taper struts. Compos. Struct. 2022, 295, 115830. [Google Scholar] [CrossRef]
- Yun, G.; Park, H.S. Surface stress effects on the bending properties of fcc metal nanowires. Phys. Rev. B—Condens. Matter Mater. Phys. 2009, 79, 195421. [Google Scholar] [CrossRef][Green Version]
- Xie, Z.; Fu, X.; Zhang, Q.; Liu, L.; Zhu, X.; Ren, Y.; Chen, W. Ballistic performance of additive manufacturing metal lattice structures. Thin-Walled Struct. 2025, 208, 112763. [Google Scholar] [CrossRef]
- Abusabir, A.; Khan, M.A.; Asif, M.; Khan, K.A. Effect of architected structural members on the viscoelastic response of 3D printed simple cubic lattice structures. Polymers 2022, 14, 618. [Google Scholar] [CrossRef]
- Li, Y.; Gu, H.; Pavier, M.; Coules, H. Compressive behaviours of octet-truss lattices. Proceedings of the Institution of Mechanical Engineers. Part C J. Mech. Eng. Sci. 2020, 234, 3257–3269. [Google Scholar] [CrossRef]
- Yang, X.; Yang, Q.; Shi, Y.; Yang, L.; Wu, S.; Yan, C.; Shi, Y. Effect of volume fraction and unit cell size on manufacturability and compressive behaviors of Ni-Ti triply periodic minimal surface lattices. Addit. Manuf. 2022, 54, 102737. [Google Scholar] [CrossRef]
- Majari, P.; Olvera-Trejo, D.; Estrada-Díaz, J.A.; Elías-Zúñiga, A.; Martinez-Romero, O.; Ramírez-Herrera, C.A.; Perales-Martínez, I.A. Enhanced Lightweight Structures Through Brachistochrone-Inspired Lattice Design. Polymers 2025, 17, 654. [Google Scholar] [CrossRef] [PubMed]
- Safar, A.; Mihai, L.A. The nonlinear elasticity of hyperelastic models for stretch-dominated cellular structures. Int. J. Non-Linear Mech. 2018, 106, 144–154. [Google Scholar] [CrossRef]
- Huang, B.; Duan, Y.-H.; Hu, W.-C.; Sun, Y.; Chen, S. Structural, anisotropic elastic and thermal properties of MB (M= Ti, Zr and Hf) monoborides. Ceram. Int. 2015, 41, 6831–6843. [Google Scholar] [CrossRef]
- Li, Q.; Magkiriadis, I.; Harrigan, J.J. Compressive strain at the onset of densification of cellular solids. J. Cell. Plast. 2006, 42, 371–392. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; American Mathematical Society: Providence, RI, USA, 2011; Volume 374. [Google Scholar]
- Glaesener, R.N.; Lestringant, C.; Telgen, B.; Kochmann, D.M. Continuum models for stretching-and bending-dominated periodic trusses undergoing finite deformations. Int. J. Solids Struct. 2019, 171, 117–134. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Zhao, Y.F. A 149 line homogenization code for three-dimensional cellular materials written in MATLAB. J. Eng. Mater. Technol. 2019, 141, 011005. [Google Scholar] [CrossRef]
- Calladine, C.; English, R. Strain-rate and inertia effects in the collapse of two types of energy-absorbing structure. Int. J. Mech. Sci. 1984, 26, 689–701. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Al-Rub, R.K.A. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Alberdi, R.; Dingreville, R.; Robbins, J.; Walsh, T.; White, B.C.; Jared, B.; Boyce, B.L. Multi-morphology lattices lead to improved plastic energy absorption. Mater. Des. 2020, 194, 108883. [Google Scholar] [CrossRef]
- Gibson, L.J. Cellular solids. MRS Bull. 2003, 28, 270–274. [Google Scholar] [CrossRef]






| cubic | BCC | BCCZ | FCC | Octet |
|---|---|---|---|---|
| a 1.11 | 2.5674 | 1.11 | 2.5674 | 1.11 |
| Material | ρ (Kg/L) | E (MPa) | Exposure Time (s) |
|---|---|---|---|
| Spot-E (Spot_e) | 1.11 | 2.5674 | 0.3 |
| EnvisionTEC LS600 (Yellow) | 1.17 | 87.9313 | 0.4 |
| Makerjuice standard (Makerjuice) | 1.05 | 338.3071 | 0.3 |
| Surgical Guide (Bio) | 1.10 | 441.8149 | 0.2 |
| 1st Variable | 2nd Variable | 3rd Variable | |||
|---|---|---|---|---|---|
| Structure Type | Cross-Section | Resin | |||
| Ref. # | Referent | Ref. # | Referent | Ref. # | Referent |
| 1 | cubic | 1 | square | 1 | Spot-E (Spot_e) |
| 2 | BCC | 2 | d-square | 2 | EnvisionTEC LS600 (Yellow) |
| 3 | BCCZ | 3 | circle | 3 | Makerjuice standard (Makerjuice) |
| 4 | FCC | 4 | rectangle | 4 | Surgical Guide (Bio) |
| 5 | octet | - | - | - | - |
| # | Structure Type | Cross-Section | Resin | # | Structure Type | Cross-Section | Resin |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 3 | 11 | 3 | 3 | 3 |
| 2 | 1 | 2 | 3 | 12 | 3 | 4 | 3 |
| 3 | 1 | 3 | 3 | 13 | 4 | 1 | 3 |
| 4 | 1 | 4 | 3 | 14 | 4 | 2 | 3 |
| 5 | 2 | 1 | 3 | 15 | 4 | 3 | 3 |
| 6 | 2 | 2 | 3 | 16 | 4 | 4 | 3 |
| 7 | 2 | 3 | 3 | 17 | 5 | 1 | 3 |
| 8 | 2 | 4 | 3 | 18 | 5 | 2 | 3 |
| 9 | 3 | 1 | 3 | 19 | 5 | 3 | 3 |
| 10 | 3 | 2 | 3 | 20 | 5 | 4 | 3 |
| # | Structure Type | Cross-Section | Resin | # | Structure Type | Cross-Section | Resin |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 11 | 3 | 4 | 2 |
| 2 | 1 | 4 | 2 | 12 | 4 | 3 | 1 |
| 3 | 1 | 3 | 3 | 13 | 4 | 3 | 2 |
| 4 | 1 | 4 | 3 | 14 | 4 | 1 | 3 |
| 5 | 1 | 4 | 4 | 15 | 4 | 4 | 3 |
| 6 | 2 | 2 | 1 | 16 | 5 | 2 | 1 |
| 7 | 2 | 3 | 2 | 17 | 5 | 1 | 3 |
| 8 | 2 | 2 | 3 | 18 | 5 | 1 | 4 |
| 9 | 3 | 1 | 1 | 19 | 5 | 2 | 4 |
| 10 | 3 | 1 | 2 | 20 | 5 | 4 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Rastegarzadeh, S.; Pan, Y.; Huang, J. Effect of Cross-Section Designs on Energy Absorption of Mechanical Metamaterials. Designs 2025, 9, 106. https://doi.org/10.3390/designs9050106
Wang X, Rastegarzadeh S, Pan Y, Huang J. Effect of Cross-Section Designs on Energy Absorption of Mechanical Metamaterials. Designs. 2025; 9(5):106. https://doi.org/10.3390/designs9050106
Chicago/Turabian StyleWang, Xinnian, Sina Rastegarzadeh, Yayue Pan, and Jida Huang. 2025. "Effect of Cross-Section Designs on Energy Absorption of Mechanical Metamaterials" Designs 9, no. 5: 106. https://doi.org/10.3390/designs9050106
APA StyleWang, X., Rastegarzadeh, S., Pan, Y., & Huang, J. (2025). Effect of Cross-Section Designs on Energy Absorption of Mechanical Metamaterials. Designs, 9(5), 106. https://doi.org/10.3390/designs9050106







