Assessment of Accuracy in Geometry Reconstruction, CAD Modeling, and MEX Additive Manufacturing for Models Characterized by Axisymmetry and Primitive Geometries
Abstract
1. Introduction
2. Materials and Methods
2.1. The Process of Measuring and Reconstructing Geometries Using the GOM Scan 1 System
- Probing error—test performed on a single ball;
- Sphere—spacing error—test performed on a ‘ball bar’ standard;
- Flatness measurement error—test performed on a flat rectangular plate.
2.2. The Process of CAD Modeling
- Select the binary format to save the STL file, as the ASCII format (American Standard Code for Information Interchange) results in larger file sizes;
- Set the chordal deviation to less than 0.01 mm;
2.3. The Process of Additive Manufacturing and Measuring 3D Printed Models
3. Results
- Remove All Contaminants: The model’s surface must be free from any dust, dirt, oil, fingerprints, or residue from manufacturing. Even microscopic particles can affect the accuracy of high-precision scanners. Use compressed air, a soft brush, or a lint-free cloth with a suitable solvent (like isopropyl alcohol) that will not damage the part’s material. Handle the model with gloves to prevent transferring oils from your hands to the surface.
- Applying Surface Coatings: If the object has highly reflective, transparent, or glossy surfaces, use a matte anti-reflective spray to make them detectable by optical scanners. The coating should be applied as thinly and uniformly as possible to avoid altering the object’s true geometry.
- Applying Reference Points: Use high-quality, adhesive reference points that are compatible with your measurement system. Distribute the targets evenly across the model’s surface. Place them in non-critical areas to avoid interfering with key geometric features. Ensure there are enough targets to guarantee at least three are visible from any scanning angle.
- Data Acquisition and Reconstruction.
- Securing the Object: The object must be securely fixture to prevent any movement during the measurement process. Vibrations or accidental shifts can cause significant measurement errors. Let the object acclimate to the temperature of the measurement environment to prevent thermal expansion or contraction, which is especially important for polymer parts.
- Scanning Technique: Use a high-precision 3D scanner to capture data. Optimize the scanning process by selecting the appropriate type of measuring head, which determines the size of the measuring area and thus the resolution of the point cloud. In addition, it is necessary to determine the optimal number of measuring steps for the table.
- Alignment Point Clouds: To create a complete and accurate 3D model from multiple scans, it is essential to properly align or “fit” the individual point clouds together. The most reliable method for fitting point clouds together is to use reference points. When reference points are not available, or as a complementary method, a best-fit algorithm can be used. This method works by finding the optimal position and orientation for two overlapping point clouds to minimize the average distance between all corresponding points.
- CAD Modeling
- Clean the 3D Mesh: Before meshing, process the raw data to remove any noise, programming errors of the 3D Mesh, outliers, or duplicate points.
- Parameterization CAD Model: Choose a reconstruction method that is appropriate for the object’s geometry.
- Primitive Detection: For models with regular, geometric shapes (planes, cylinders, cones), this method converts the point cloud into a precise, parametric CAD model. Set the appropriate fitting tolerance. Tolerance defines the maximum deviation that points can have from the ideal surface of the primitive in order to be included in it. Too high a tolerance can lead to noisy data being combined into a single primitive, while too low a tolerance will prevent the primitive from being detected at all.
- Profile Extraction: Always select cross-sections at key, representative locations of the object (e.g., at the beginning and end of segments, at locations where the geometry changes). Use a minimal but sufficient number of profiles to reproduce the shape accurately. Too many profiles can complicate the model, while too few will lead to errors in the final shape. Before extracting profiles, remove noise from the point cloud so that the cross-section lines are as smooth as possible. Ensure that the cross-section planes are perfectly perpendicular to the object’s axis so that the profiles are accurate.
- Auto-Surfacing: For organic or complex, free-form shapes, this method automatically generates a surface mesh (NURBS) that is smooth and easy to manipulate in CAD software. Set the appropriate parameters for the algorithm, such as matching tolerance, surface density, and number of patches. Too low a tolerance may cause the model to be noisy, while too high a tolerance will smooth out essential details.
- MEX Additive Manufacturing Process
- Model Orientation: Orient the model to minimize the need for support structures, especially on critical surfaces. Selecting an appropriate orientation also equalizes the stresses along the print layers, which minimizes distortion (e.g., material shrinkage) and increases the strength of the finished part.
- 3D Printing Parameters: Use the thinnest layers possible to increase dimensional accuracy and surface smoothness. You can also optimize the infill pattern to achieve adequate strength while saving material and reducing print time.
- Flatness: Deviations should ensure adhesion to the wall and fittings. The obtained deviation values should be within the range ±0.2 mm.
- Mounting hole spacing: Must be within the range ±0.2 mm to fit the standard socket and switch spacing.
- Depth: Must be uniform and within tolerance, typically ±0.3 mm, to ensure that the hardware fits in the box and does not protrude.
- Flatness of the sealing surface: The flatness requirements for maintaining tightness should be within the range ±0.2 mm.
- Geometric accuracy at the edges: This is important for the cover to fit the body. The recommended manufacturing tolerance should be within the range of ±0.2 mm.
- Flatness of contact surfaces: To ensure that the cover does not fall out and protects the interior from dirt, the flatness of the contact surfaces is crucial. The required deviation values should be within the range of ±0.2 mm.
- Dimensional accuracy of the fixing holes: These elements are critical for proper fastening. Tolerances must ensure that the latch will function reliably and that the threads will not loosen. These values should be within the range of ±0.2 mm.
4. Discussion
4.1. Evaluation of Geometrical Reconstruction Errors
- The manufacturing process of the models is subject to specific tolerances, which the manufacturer states should remain within ±0.8 mm. This indicates that any discrepancies in the physical dimensions of the models due to production imperfections should not exceed this threshold.
- The measurement system used has its limitations concerning accuracy. For calibration measurements taken on flat surfaces, the maximum allowable error is ±0.02 mm.
- The scanning parameters used during data collection can lead to specific errors. In this case, data is collected at a point cloud resolution of 0.037 mm. This resolution affects the quality and fidelity of the scanned data, which can ultimately influence the overall accuracy of the measurements obtained.
- Scanning reflective surfaces, a matte layer is often applied to mitigate issues caused by glare and reflections. However, the application of this matte finish is not without its limitations; the errors introduced by this process should not exceed 0.015 mm. Proper application is essential to ensure that the scanned data remains as accurate as possible.
- Fitting scans—the process of aligning and merging multiple scan datasets—introduces its own set of potential inaccuracies. The errors associated with this fitting process can vary widely, typically falling within a range of 0.01 mm to 0.05 mm per individual scan. This variance emphasizes the importance of careful alignment and processing to minimize cumulative error in the final output.
4.2. Evaluation of CAD Modeling Errors
- According to the research findings, using the primitive detection technique allows for the creation of CAD models with an average accuracy tolerance of ±0.2 mm. The error values result from the incorrect matching of the parameterized surface to the obtained point cloud and from connections at the edges and between surfaces.
- According to the research findings, using the profile extraction technique allows for the creation of CAD models with an average accuracy tolerance of ±0.4 mm. The error values obtained result from the incorrect selection of the cross-section against which the profile is extracted, as well as errors in interpolation, curve fitting, and connecting them.
- According to the research findings, using the auto-surfacing technique allows for the creation of CAD models with an average accuracy tolerance of ±0.9 mm. The error values obtained stem from the automatic generation of NURBS surfaces over the entire triangular surface. As a result, to satisfy the fitting conditions, the parameterized surface is often smoothed. This smoothing can complicate the accurate mapping of object edges and the transitions between connected surfaces.
4.3. Evaluation of MEX Additive Manufacturing Errors
4.4. Evaluation of RE + CAD + AM—Total Errors
5. Conclusions
- First, it highlights the utilization of an advanced optical scanner, which employs structured light to illuminate the object being measured. This technique not only enhances the clarity of the captured data but also allows for the fine-tuning of scanner settings to improve measurement resolution. Additionally, the research emphasizes the importance of optimizing the number of rotations of the measurement table during the scanning process, as this can lead to more accurate and reliable data capture.
- Furthermore, the paper discusses the selection of an efficient CAD modeling approach. By adopting methods that streamline the modeling process, designers can mitigate the complexities often associated with parametric modeling. This, in turn, reduces potential sources of error that can arise during the conversion from a concept to a digital model.
- The investigation also addresses the challenge of AM errors. It underscores the necessity of carefully selecting the 3D printing layer thickness and determining the optimal model orientation within the 3D printer. These choices play a crucial role in the final output’s dimensional accuracy and surface quality, ultimately influencing the integrity of the manufactured part.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raja, V. Introduction to reverse engineering. In Reverse Engineering: An Industrial Perspective; Springer: London, UK, 2008; pp. 1–9. [Google Scholar] [CrossRef]
- She, S.; Lotufo, R.; Berger, T.; Wąsowski, A.; Czarnecki, K. Reverse engineering feature models. In Proceedings of the 33rd International Conference on Software Engineering, Honolulu, HI, USA, 21–28 May 2011; pp. 461–470. [Google Scholar] [CrossRef]
- Roithmeier, R. Measuring Strategies in Tactile Coordinate Metrology; Carl Zeiss AG: Oberkochen, Germany, 2014. [Google Scholar]
- Li, F.; Hiley, J.; Syed, T.M.; Hitchens, C.; Garcia Lopez-Astilleros, M. A region segmentation method to measure multiple features using a tactile scanning probe. Int. J. Comput. Integr. Manuf. 2019, 32, 569–579. [Google Scholar] [CrossRef]
- Wang, X.; Xian, J.; Yang, Y.; Zhang, Y.; Fu, X.; Kang, M. Use of coordinate measuring machine to measure circular aperture complex optical surface. Measurement 2017, 100, 1–6. [Google Scholar] [CrossRef]
- Gapinski, B.; Wieczorowski, M.; Marciniak-Podsadna, L.; Dybala, B.; Ziolkowski, G. Comparison of different method of measurement geometry using CMM, optical scanner and computed tomography 3D. Procedia Eng. 2014, 69, 255–262. [Google Scholar] [CrossRef]
- Li, F.; Longstaff, A.P.; Fletcher, S.; Myers, A. Integrated tactile and optical measuring systems in three dimensional metrology. In Proceedings of the Queen’s Diamond Jubilee Computing and Engineering Annual Researchers’ Conference 2012: CEARC’12, Huddersfield, UK, 29 February 2012; University of Huddersfield: Huddersfield, UK, 2012. [Google Scholar]
- Chen, S.; Chen, H. Research on Triangulation Method of Object Surface with Holes in Reverse Engineering. In Proceedings of the 2009 International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009; IEEE: New York, NY, USA, 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, J. An adaptive process of reverse engineering from point clouds to CAD models. Int. J. Comput. Integr. Manuf. 2020, 33, 840–858. [Google Scholar] [CrossRef]
- Ali, S.; Durupt, A.; Adragna, P.A.; Bosch-Mauchand, M. A reverse engineering for manufacturing approach. Comput.-Aided Des. Appl. 2014, 11, 694–703. [Google Scholar] [CrossRef]
- Wojnarowska, W.; Kwolek, M.; Miechowicz, S. Selection of a workpiece clamping system for computer-aided subtractive manufacturing of geometrically complex medical models. Open Eng. 2021, 11, 239–248. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, P.; Singh, H.; Haleem, A.; Mittal, R.K. Integration of reverse engineering with additive manufacturing. In Advances in Additive Manufacturing; Elsevier: Amsterdam, The Netherlands, 2023; pp. 43–65. [Google Scholar] [CrossRef]
- Vukašinović, N.; Duhovnik, J. Introduction to reverse engineering. In Advanced CAD Modeling: Explicit, Parametric, Free-Form CAD and Re-Engineering; Springer International Publishing: Cham, Switzerland, 2018; pp. 165–177. [Google Scholar] [CrossRef]
- Mahmood, D.M.; Mahmood, A.Z. Improving Reverse Engineering Processes by using Articulated Arm Coordinate Measuring Machine. Al-Khwarizmi Eng. J. 2020, 16, 42–54. [Google Scholar] [CrossRef]
- Turek, P.; Bezłada, W.; Cierpisz, K.; Dubiel, K.; Frydrych, A.; Misiura, J. Analysis of the accuracy of CAD modeling in engineering and medical industries based on measurement data using reverse engineering methods. Designs 2024, 8, 50. [Google Scholar] [CrossRef]
- Jang, A.; Jeong, S.; Park, M.J.; Ju, Y.K. Structural evaluation by reverse engineering with 3D laser scanner. ce/papers 2023, 6, 308–314. [Google Scholar] [CrossRef]
- Vazzana, A.; Higgins, O.A.; Oxilia, G.; Lugli, F.; Silvestrini, S.; Nava, A.; Benazzi, S. High-accuracy methodology for the integrative restoration of archaeological teeth by using reverse engineering techniques and rapid prototyping. J. Archaeol. Sci. Rep. 2022, 44, 103511. [Google Scholar] [CrossRef]
- Saiga, K.; Ullah, A.S.; Kubo, A. A sustainable reverse engineering process. Procedia CIRP 2021, 98, 517–522. [Google Scholar] [CrossRef]
- Gerbino, S.; Martorelli, M. Reverse Engineering. In Springer Handbook of Additive Manufacturing; Springer: Cham, Switzerland, 2023; pp. 253–268. [Google Scholar] [CrossRef]
- ISO/ASTM 52910:2018; Additive Manufacturing—Design—Requirements, Guidelines and Recommendations. ISO: Geneva, Switzerland, 2018.
- ISO/ASTM 52902:2023; Additive Manufacturing—Test Artefacts—Geometric Capability Assessment of Additive Manufacturing Systems. ISO: Geneva, Switzerland, 2023.
- ISO/ASTM 52915:2020; Specification for Additive Manufacturing File Format (AMF) Version 1.2. ISO: Geneva, Switzerland, 2020.
- ISO/ASTM 52950:2021; Additive Manufacturing—General Principles—Overview of Data Processing. ISO: Geneva, Switzerland, 2021.
- Zhang, Z.; Zhao, M.; Shen, Z.; Wang, Y.; Jia, X.; Yan, D.M. Interactive reverse engineering of CAD models. Comput. Aided Geom. Des. 2024, 111, 102339. [Google Scholar] [CrossRef]
- Varitis, E. A Reverse Engineering method for 3d parametric modeling of geometries based on processing of laser scanning data and a sweep technique. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 012047. [Google Scholar] [CrossRef]
- Turek, P. Evaluation of the auto surfacing methods to create a surface body of the mandible model. Rep. Mech. Eng. 2022, 3, 46–54. [Google Scholar] [CrossRef]
- Kreuz, S.; Zubiri, B.A.; Englisch, S.; Buwen, M.; Kang, S.G.; Ramachandramoorthy, R.; Rolfes, J. Improving reconstructions in nanotomography for homogeneous materials via mathematical optimization. Nanoscale Adv. 2024, 6, 3934–3947. [Google Scholar] [CrossRef]
- Ding, Z.; Lu, Y.; Shao, S.; Qin, Y.; Lu, M.; Song, Z.; Sun, D. Research on 3D Reconstruction Methods for Incomplete Building Point Clouds Using Deep Learning and Geometric Primitives. Remote Sens. 2025, 17, 399. [Google Scholar] [CrossRef]
- Liu, Y.; Obukhov, A.; Wegner, J.D.; Schindler, K. Point2cad: Reverse engineering cad models from 3d point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 3763–3772. [Google Scholar] [CrossRef]
- Thengane, V.; Zhu, X.; Bouzerdoum, S.; Phung, S.L.; Li, Y. Foundational Models for 3D Point Clouds: A Survey and Outlook. arXiv 2025, arXiv:2501.18594. [Google Scholar]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Budzik, G.; Dziubek, T.; Kawalec, A.; Turek, P.; Bazan, A.; Dębski, M.; Kuric, I. Geometrical Accuracy of Threaded Elements Manufacture by 3D Printing Process. Adv. Sci. Technol. Res. J. 2023, 17, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Turek, P.; Filip, D.; Przeszłowski, Ł.; Łazorko, A.; Budzik, G.; Snela, S.; Paszkiewicz, A. Manufacturing polymer model of anatomical structures with increased accuracy using cax and am systems for planning orthopedic procedures. Polymers 2022, 14, 2236. [Google Scholar] [CrossRef]
- García Plaza, E.; López, P.J.N.; Torija, M.Á.C.; Muñoz, J.M.C. Analysis of PLA geometric properties processed by FFF additive manufacturing: Effects of process parameters and plate-extruder precision motion. Polymers 2019, 11, 1581. [Google Scholar] [CrossRef] [PubMed]
- Pelzer, L.; Hopmann, C. Additive manufacturing of non-planar layers with variable layer height. Addit. Manuf. 2021, 37, 101697. [Google Scholar] [CrossRef]
- Shen, H.; Guo, S.; Fu, J.; Lin, Z. Building orientation determination based on multi-objective optimization for additive manufacturing. 3D Print. Addit. Manuf. 2020, 7, 186–197. [Google Scholar] [CrossRef]
- Matos, M.A.; Rocha, A.M.A.; Pereira, A.I. Improving additive manufacturing performance by build orientation optimization. Int. J. Adv. Manuf. Technol. 2020, 107, 1993–2005. [Google Scholar] [CrossRef]
- Allaire, G.; Bogosel, B. Optimizing supports for additive manufacturing. Struct. Multidiscip. Optim. 2018, 58, 2493–2515. [Google Scholar] [CrossRef]
- Alzyod, H.; Ficzere, P.; Borbas, L. Cost-efficient additive manufacturing: Unraveling the economic dynamics of material Extrusion (MEX) technology. Int. Rev. 2024, 3–4, 185. [Google Scholar] [CrossRef]
- Asami, K.; Kuehne, M.; Röver, T.; Emmelmann, C. Application of Machine Learning in Predicting Quality Parameters in Metal Material Extrusion (MEX/M). Metals 2025, 15, 505. [Google Scholar] [CrossRef]
- ISO 8015:2011; Geometrical Product Specifications (GPS)—Fundamentals—Concepts, Principles and Rules. ISO: Geneva, Switzerland, 2011.
- ISO 1101:2017; Geometrical Product Specifications (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out. ISO: Geneva, Switzerland, 2017.
- ISO 286-2:2010; Geometrical Product Specifications (GPS)—ISO Code System for Tolerances on Linear Sizes—Part 2: Tables of Standard Tolerance Classes and Limit Deviations for Holes and Shafts. ISO: Geneva, Switzerland, 2010.
- ISO 22081:2021; Geometrical Product Specifications (GPS)—Geometrical Tolerancing—General Geometrical Specifications and General Size Specifications. ISO: Geneva, Switzerland, 2021.
- ASME Y14.5; Dimensioning and Tolerancing. ASME: New York, NY, USA, 2018.
- VDI/VDE 2634; Blatt 3 Optical 3D-Measuring Systems—Multiple View Systems Based on Area Scanning. VDI/VDE: Berlin, Germany, 2008.
- PN-EN IEC 60670; Boxes and Enclosures for Accessories for Household and Similar Fixed Electrical Installations. IEC: Geneva, Switzerland, 2021.
- Buonamici, F.; Carfagni, M.; Furferi, R.; Governi, L.; Lapini, A.; Volpe, Y. Reverse engineering of mechanical parts: A template-based approach. J. Comput. Des. Eng. 2018, 5, 145–159. [Google Scholar] [CrossRef]
- Armstrong, D. Automating Scan-Based Inspection for Repeatable Process Control. Quality 2022, 61, 17. [Google Scholar]
- Milde, J.; Dubnicka, M.; Buransky, I. Impact of powder coating types on dimensional accuracy in optical 3d scanning process. MM Sci. J. 2023, 6800–6806. [Google Scholar] [CrossRef]
- Guo, H.; Wang, Y.; Wang, M.; Yang, H.; Gu, B.; Xu, G.; Gao, X. Microstructure, wear, and corrosion resistance of HVOF WC24-Cr3C257-NiCr19 coating. Tribol. Int. 2025, 211, 110806. [Google Scholar] [CrossRef]
- Bagci, E. Reverse engineering applications for recovery of broken or worn parts and re-manufacturing: Three case studies. Adv. Eng. Softw. 2009, 40, 407–418. [Google Scholar] [CrossRef]
- Chang, K.H. A review on shape engineering and design parameterization in reverse engineering. In Reverse Engineering: Recent Advances and Applications; BoD–Books on Demand: Norderstedt, Germany, 2012; pp. 161–186. [Google Scholar] [CrossRef]
- Turek, P. The Influence of the Layer Thickness Change on the Accuracy of the Zygomatic Bone Geometry Manufactured Using the FDM Technology. Eng. Proc. 2022, 24, 26. [Google Scholar] [CrossRef]
- Turek, P.; Bazan, A.; Bulicz, M. Effect of 3D Printing Orientation on the Accuracy and Surface Roughness of Polycarbonate Samples. Machines 2024, 13, 9. [Google Scholar] [CrossRef]
- Pellizzon, N.; Šeta, B.; Kruse, C.S.; Salajeghe, R.; Spangenberg, J. Investigating thermal strains and chemical shrinkage in tomographic volumetric additive manufacturing. Addit. Manuf. 2025, 105, 104781. [Google Scholar] [CrossRef]
- Bonnie, M. The Accuracy Myth. Don’t Make the Mistake of Confusing High Resolution with Accuracy. Available online: https://www.stratasys.com/contentassets/08614c7bcd824cfb99fe37f6af0e0189/wp_fdm_accuracymyth_a4_0116a_web.pdf?v=48fd13 (accessed on 1 August 2025).
- Turek, P.; Budzik, G. Estimating the Accuracy of Mandible Anatomical Models Manufactured Using Material Extrusion Methods. Polymers 2021, 13, 2271. [Google Scholar] [CrossRef]




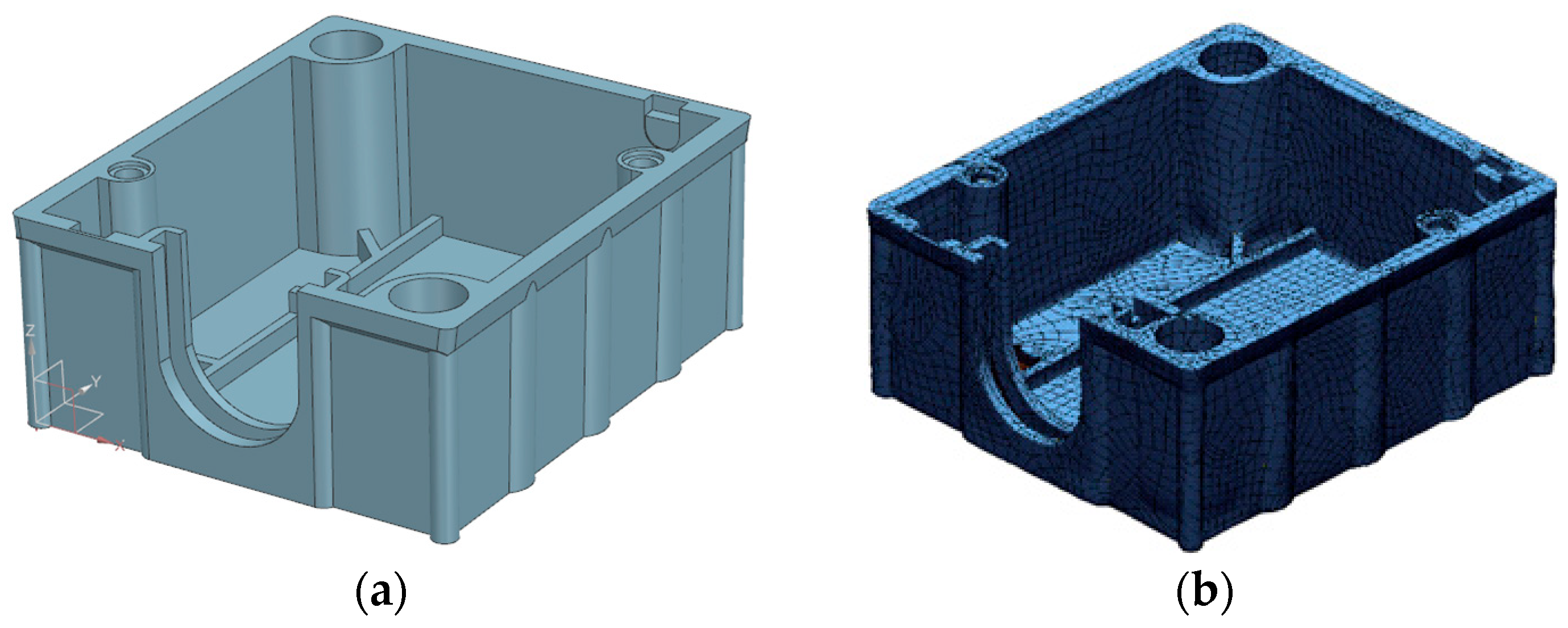
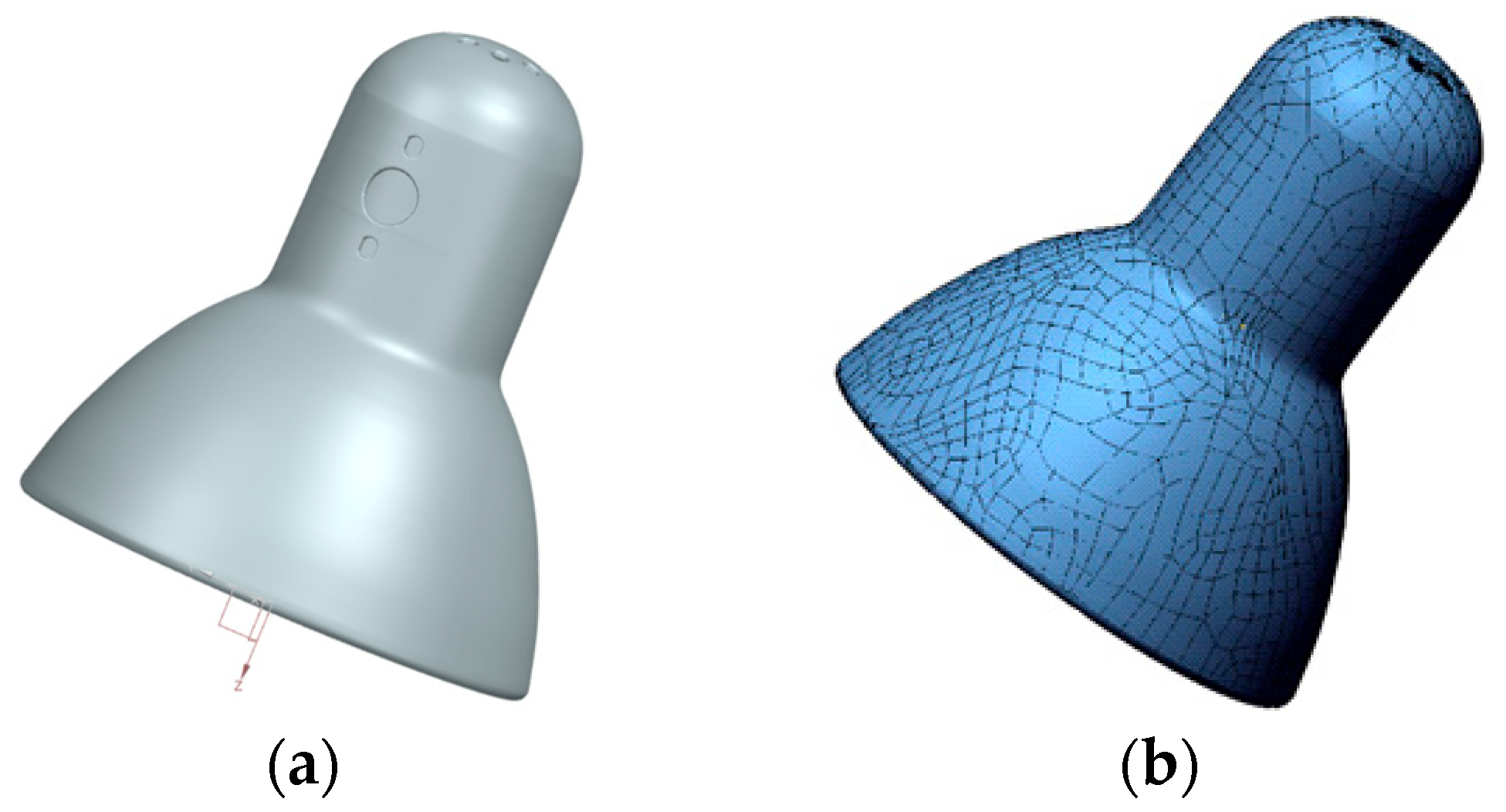
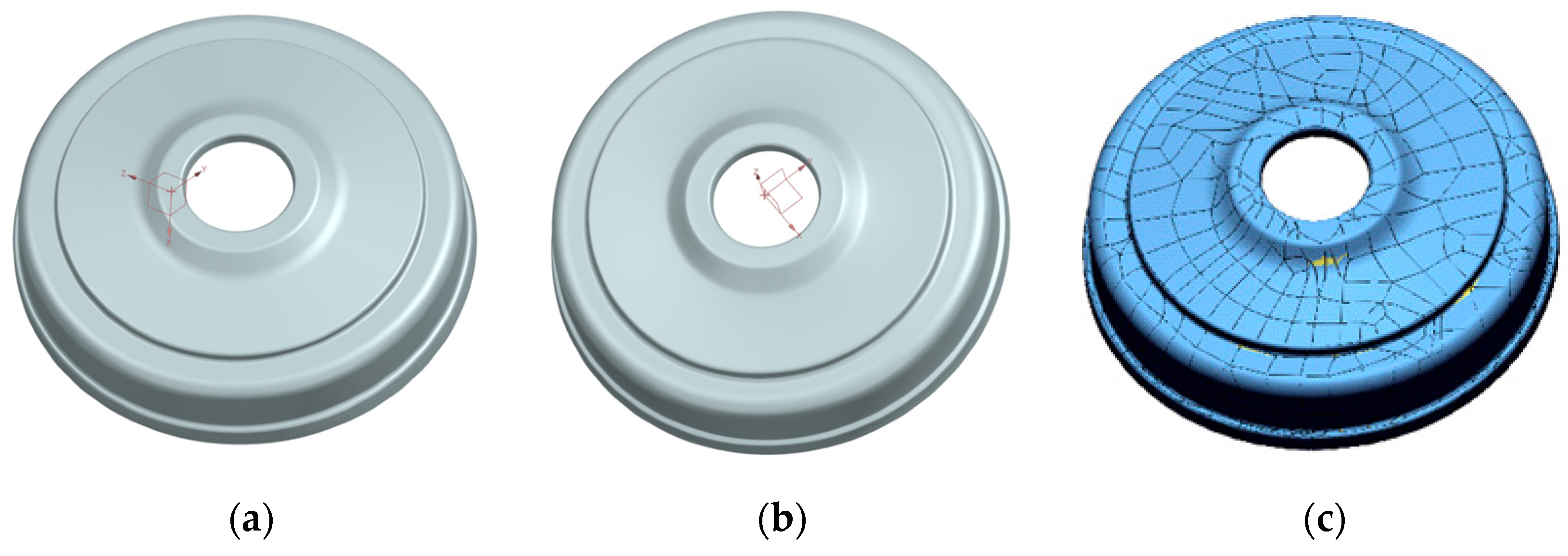





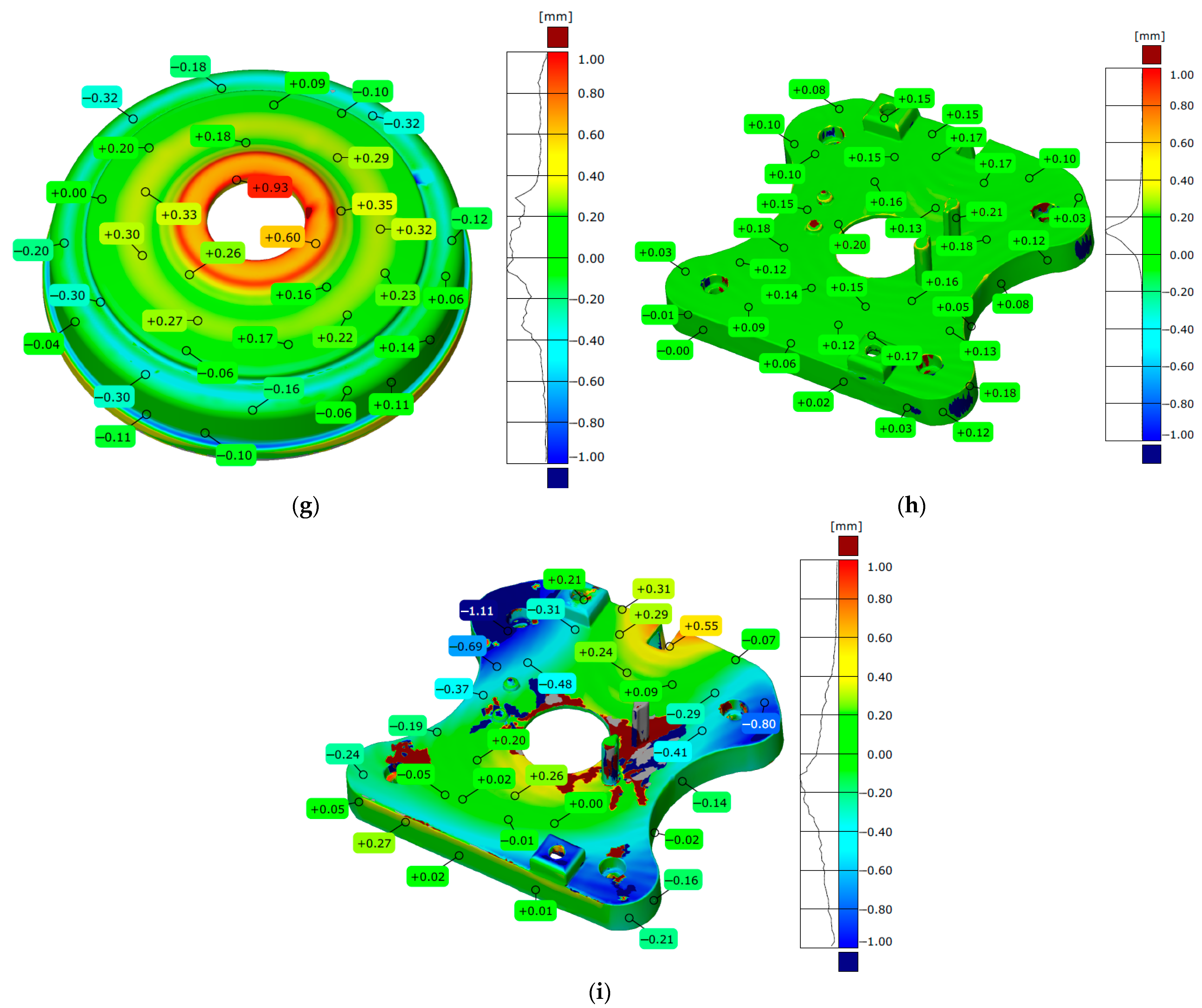




| Acceptance Test | Measured Value/Maximum Permission Error (2σ) |
|---|---|
| Probing error | ±0.003 mm/±0.006 mm |
| Sphere—spacing error | ±0.007 mm/±0.020 mm |
| Flatness measurement error | ±0.020 mm |
| Parameters | Value |
|---|---|
| Pixel resolution cameras | 5,000,000 |
| Measuring area | 100 mm × 65 mm × 400 mm |
| Min. point resolution | 0.037 mm |
| Number of points per scan | 5,000,000 |
| Number of rotations of the measuring table | 15 |
| Parameters | Electrical Box | Lampshade | Cover for a Vacuum Unit | Battery Cover |
|---|---|---|---|---|
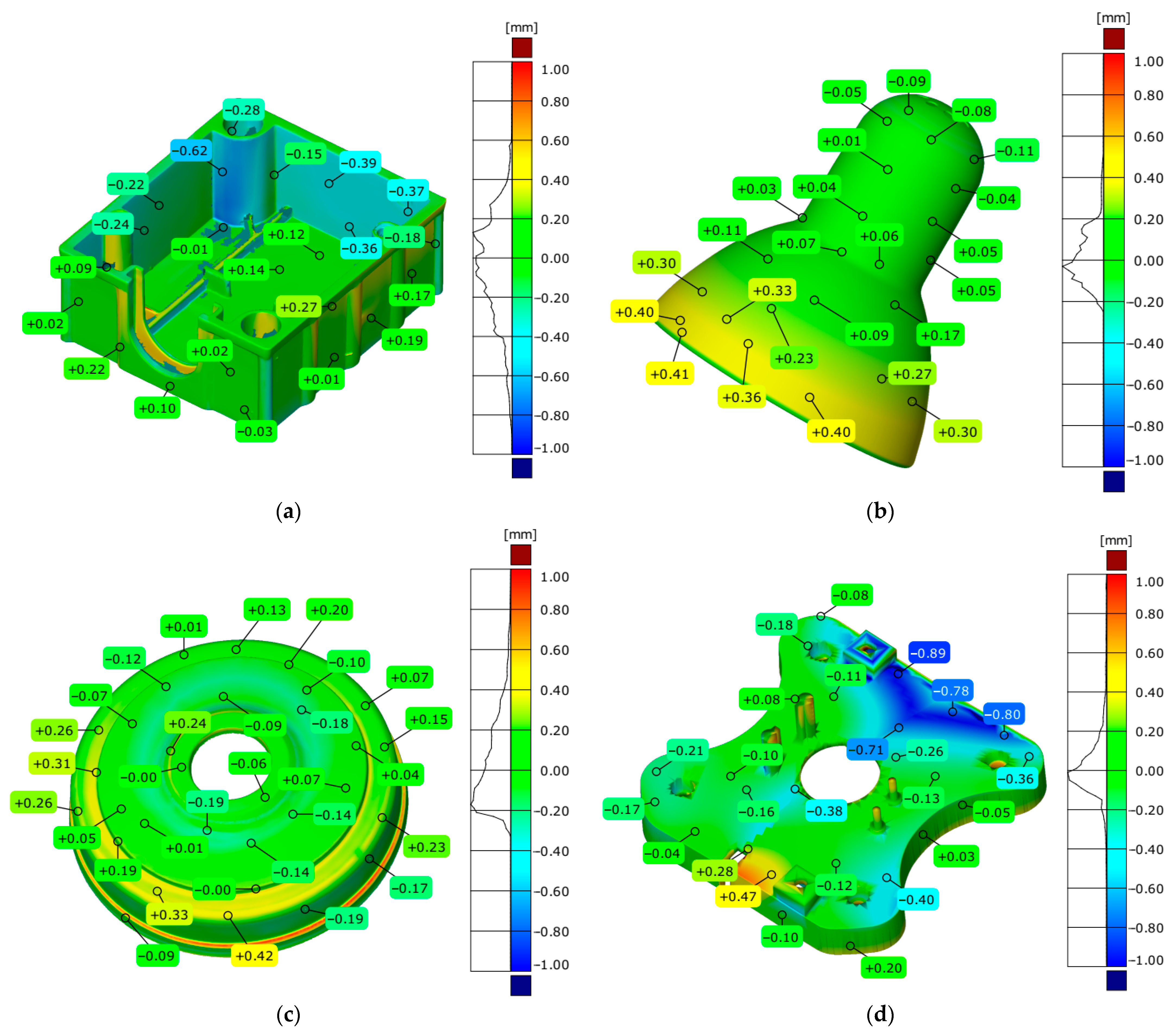
| Maximum deviation [mm] | 1.414 | 0.618 | 2.210 | 1.325 |
| Minimum deviation [mm] | −1.025 | −0.713 | −1.069 | −1.403 |
| Range [mm] | 2.440 | 1.332 | 3.279 | 2.728 |
| Mean deviation [mm] | −0.020 | 0.105 | 0.119 | −0.231 |
| Standard deviation [mm] | 0.364 | 0.467 | 0.559 | 0.387 |
| Parameters | Electrical Box | Lampshade | Cover for a Vacuum Unit | Battery Cover | |||||
|---|---|---|---|---|---|---|---|---|---|
| Detect Primitive | Auto Surfacing | Profile Extraction | Auto Surfacing | Detect Primitive | Profile Extraction | Auto Surfacing | Detect Primitive | Auto Surfacing | |
| Maximum deviation [mm] | 1.074 | 1.381 | 2.176 | 2.147 | 0.874 | 0.749 | 1.459 | 1.669 | 2.788 |
| Minimum deviation [mm] | −1.762 | −1.463 | −1.421 | −1.602 | −0.774 | −0.721 | −0.828 | −1.698 | −2.274 |
| Range [mm] | 2.835 | 3.844 | 3.597 | 3.749 | 1.649 | 1.470 | 2.287 | 3.367 | 5.062 |
| Mean deviation [mm] | −0.108 | −0.122 | −0.056 | −0.196 | 0.010 | −0.012 | 0.122 | 0.194 | 0.306 |
| Standard deviation [mm] | 0.291 | 0.427 | 0.273 | 0.428 | 0.123 | 0.250 | 0.461 | 0.259 | 0.512 |
| Parameters | Electrical Box | Lampshade | Cover for a Vacuum Unit | Battery Cover |
|---|---|---|---|---|
| Maximum deviation [mm] | 0.929 | 0.892 | 1.373 | 0.653 |
| Minimum deviation [mm] | −0.385 | −0.422 | −0.431 | −0.848 |
| Range [mm] | 1.314 | 1.314 | 1.804 | 1.501 |
| Mean deviation [mm] | −0.050 | −0.087 | −0.026 | −0.137 |
| Standard deviation [mm] | 0.091 | 0.102 | 0.163 | 0.109 |
| Parameters | Electrical Box | Lampshade | Cover for a Vacuum Unit | Battery Cover |
|---|---|---|---|---|
| Maximum deviation [mm] | 0.834 | 0.715 | 1.286 | 0.754 |
| Minimum deviation [mm] | −0.973 | −0.713 | −0.937 | −0.947 |
| Range [mm] | 1.806 | 1.428 | 2.223 | 1.701 |
| Mean deviation [mm] | −0.057 | 0.125 | 0.014 | −0.102 |
| Standard deviation [mm] | 0.382 | 0.452 | 0.410 | 0.409 |
| Stage | Electrical Box | Lampshade | Cover for a Vacuum Unit | Battery Cover |
|---|---|---|---|---|
| Reconstruction processs * | ±0.6 mm | ±0.8 mm | ±1 mm | ±0.6 mm |
| CAD modeling | ±0.6 mm | ±0.6 mm | ±0.2 mm | ±0.4 mm |
| Additive manufacturing | ±0.2 mm | ±0.2 mm | ±0.2 mm | ±0.2 mm |
| RE + CAD + AM | ±0.5 mm | ±0.4 mm | ±0.6 mm | ±0.4 mm |
| Type of the Model | Parameters | Stage | Average Deviation Value | Recommended Deviation Values |
|---|---|---|---|---|
| Electrical box | Flatness | Reconstruction process | ±0.1 mm | ±0.2 mm |
| CAD modeling | ±0.08 mm | |||
| Additive manufacturing | ±0.05 mm | |||
| RE + CAD + AM | ±0.1 mm | |||
| Mounting hole spacing | Reconstruction process | ±0.1 mm | ±0.2 mm | |
| CAD modeling | ±0.1 mm | |||
| Additive manufacturing | ±0.03 mm | |||
| RE + CAD + AM | ±0.12 mm | |||
| Depth | Reconstruction process | ±0.13 mm | ±0.3 mm | |
| CAD modeling | ±0.09 mm | |||
| Additive manufacturing | ±0.04 mm | |||
| RE + CAD + AM | ±0.15 mm | |||
| Vacuum cover | Flatness of the sealing surface | Reconstruction process | ±0.2 mm | ±0.2 mm |
| CAD modeling | ±0.09 mm | |||
| Additive manufacturing | ±0.1 mm | |||
| RE + CAD + AM | ±0.15 mm | |||
| Geometric accuracy at the edges | Reconstruction process | ±0.24 mm | ±0.2 mm | |
| CAD modeling | ±0.1 mm | |||
| Additive manufacturing | ±0.2 mm | |||
| RE + CAD + AM | ±0.18 mm | |||
| Battery cover | Flatness of contact surfaces | Reconstruction process | ±0.2 mm | ±0.2 mm |
| CAD modeling | ±0.15 mm | |||
| Additive manufacturing | ±0.15 mm | |||
| RE + CAD + AM | ±0.11 mm | |||
| Dimensional accuracy of the fixing holes | Reconstruction process | ±0.13 mm | ±0.2 mm | |
| CAD modeling | ±0.12 mm | |||
| Additive manufacturing | ±0.1 mm | |||
| RE + CAD + AM | ±0.1 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turek, P.; Bielarski, P.; Czapla, A.; Futoma, H.; Hajder, T.; Misiura, J. Assessment of Accuracy in Geometry Reconstruction, CAD Modeling, and MEX Additive Manufacturing for Models Characterized by Axisymmetry and Primitive Geometries. Designs 2025, 9, 101. https://doi.org/10.3390/designs9050101
Turek P, Bielarski P, Czapla A, Futoma H, Hajder T, Misiura J. Assessment of Accuracy in Geometry Reconstruction, CAD Modeling, and MEX Additive Manufacturing for Models Characterized by Axisymmetry and Primitive Geometries. Designs. 2025; 9(5):101. https://doi.org/10.3390/designs9050101
Chicago/Turabian StyleTurek, Paweł, Piotr Bielarski, Alicja Czapla, Hubert Futoma, Tomasz Hajder, and Jacek Misiura. 2025. "Assessment of Accuracy in Geometry Reconstruction, CAD Modeling, and MEX Additive Manufacturing for Models Characterized by Axisymmetry and Primitive Geometries" Designs 9, no. 5: 101. https://doi.org/10.3390/designs9050101
APA StyleTurek, P., Bielarski, P., Czapla, A., Futoma, H., Hajder, T., & Misiura, J. (2025). Assessment of Accuracy in Geometry Reconstruction, CAD Modeling, and MEX Additive Manufacturing for Models Characterized by Axisymmetry and Primitive Geometries. Designs, 9(5), 101. https://doi.org/10.3390/designs9050101







