Design Evaluation of a Single Wheelset Roller Rig for Railroad Curving Dynamics and Creepage Studies
Abstract
1. Introduction
Roller Rig Needs
- Key challenges associated with emulating curving dynamics, using a constrained, independently powered wheelset;
- The effect on the roller speed control accuracy (governed by the hardware capabilities) for emulating curves with various radii;
- The impact of rollers’ diameters on contact patch distortion at WRI, relative to a wheel on a tangent track;
- Designing a force measurement platform for determining creep forces at each wheel with high accuracy, without affecting the WRI dynamics;
- Overcoming the design challenges associated with adding a new wheel and roller in a roller rig with a single wheel and roller (i.e., the VT-FRA roller rig), within the existing geometric and spatial constraints.
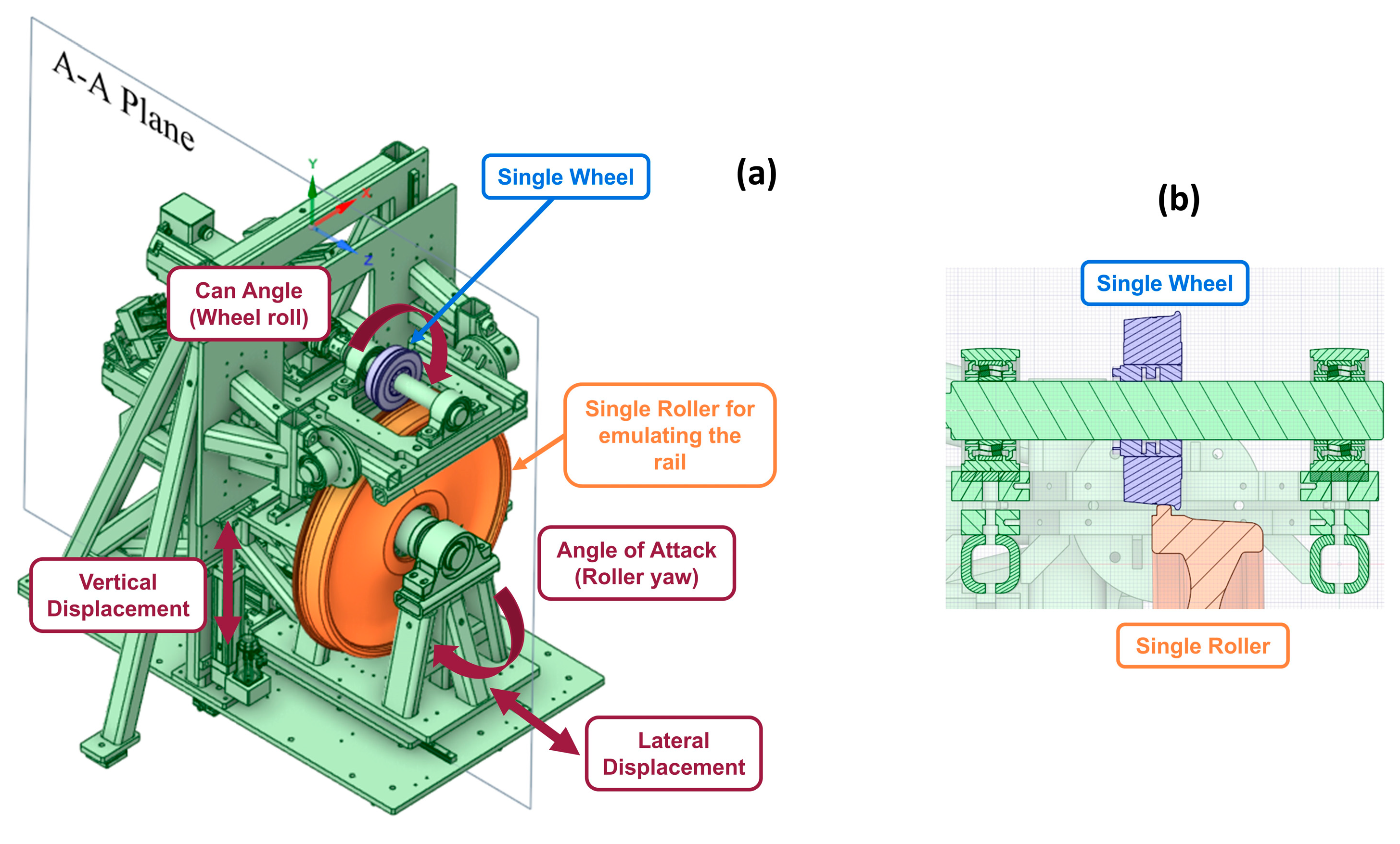
2. VT-FRA Roller Rig
2.1. Single Wheel Configuration
- Cross-sectional lengths by a linear factor equal to the rig’s scaling factor (i.e., four for the VT-FRA roller rig).
- Force measurements by a quadratic factor of the rig’s scaling factor (i.e., 16 for the VT-FRA roller rig). This implies that the maximum roller rig wheel load of 10 kN corresponds to 160 kN (36 kips) for a full-scale wheel.
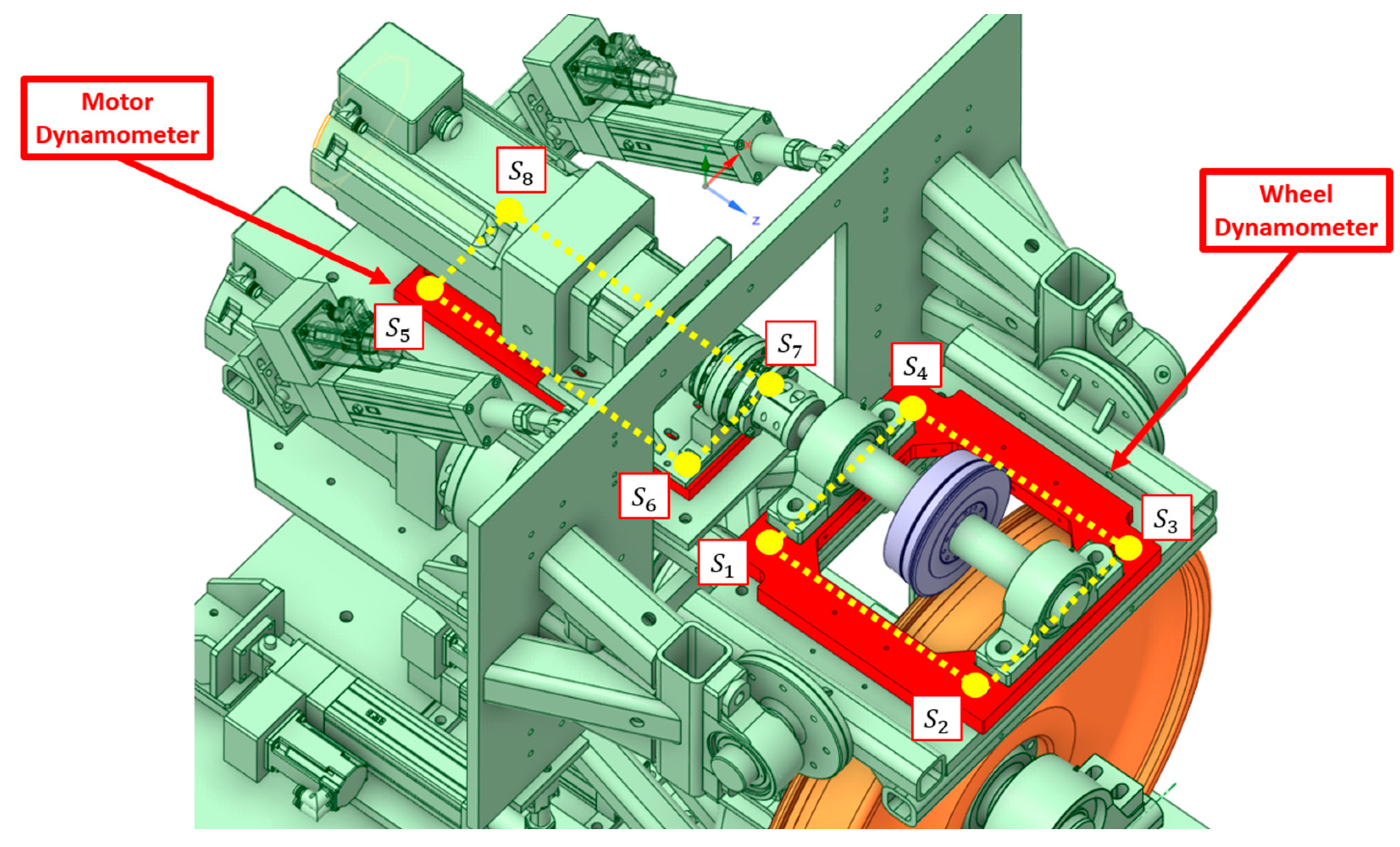
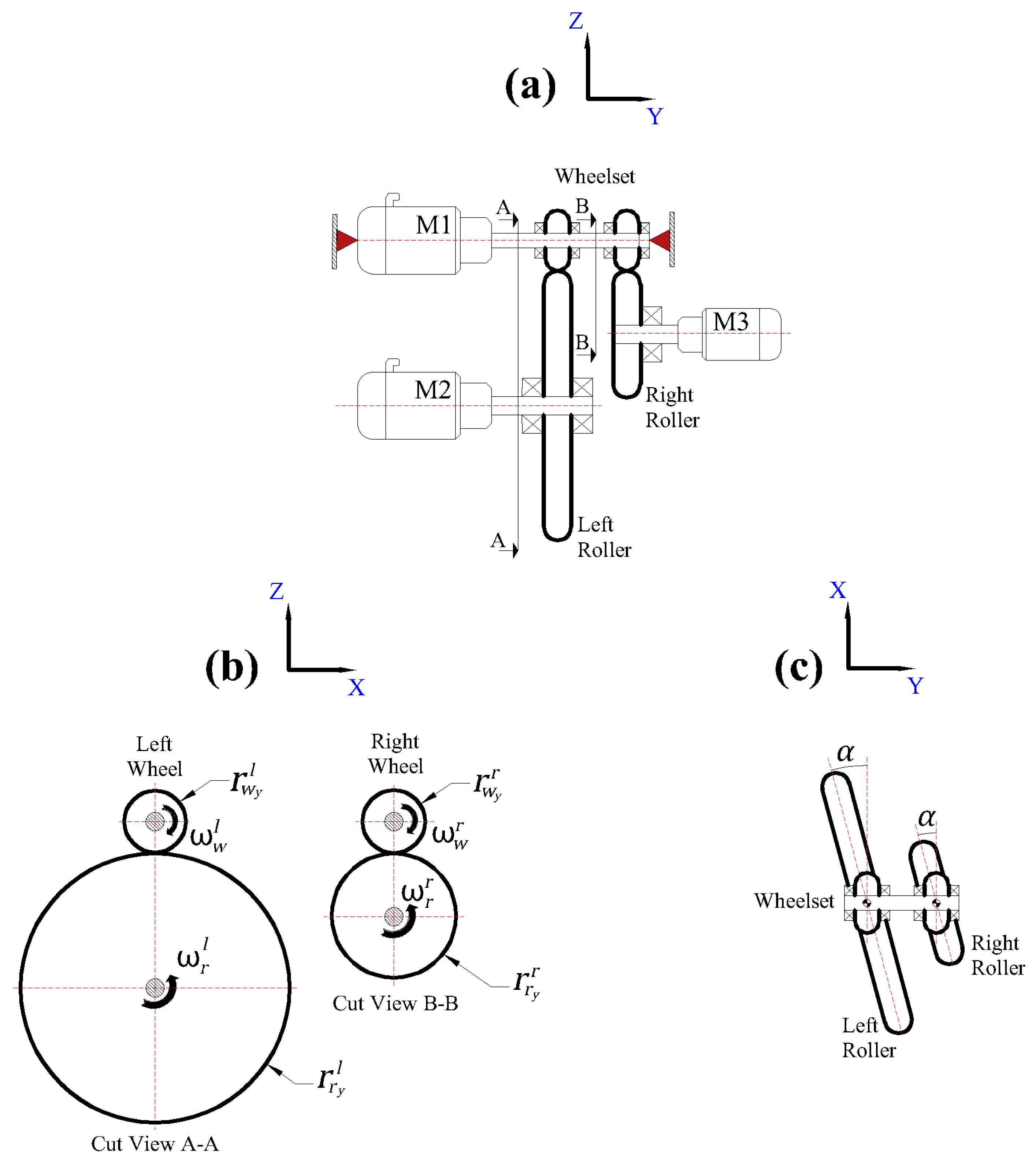
2.2. New Roller Rig Setup
3. Discussions
3.1. Independent Creepage Control
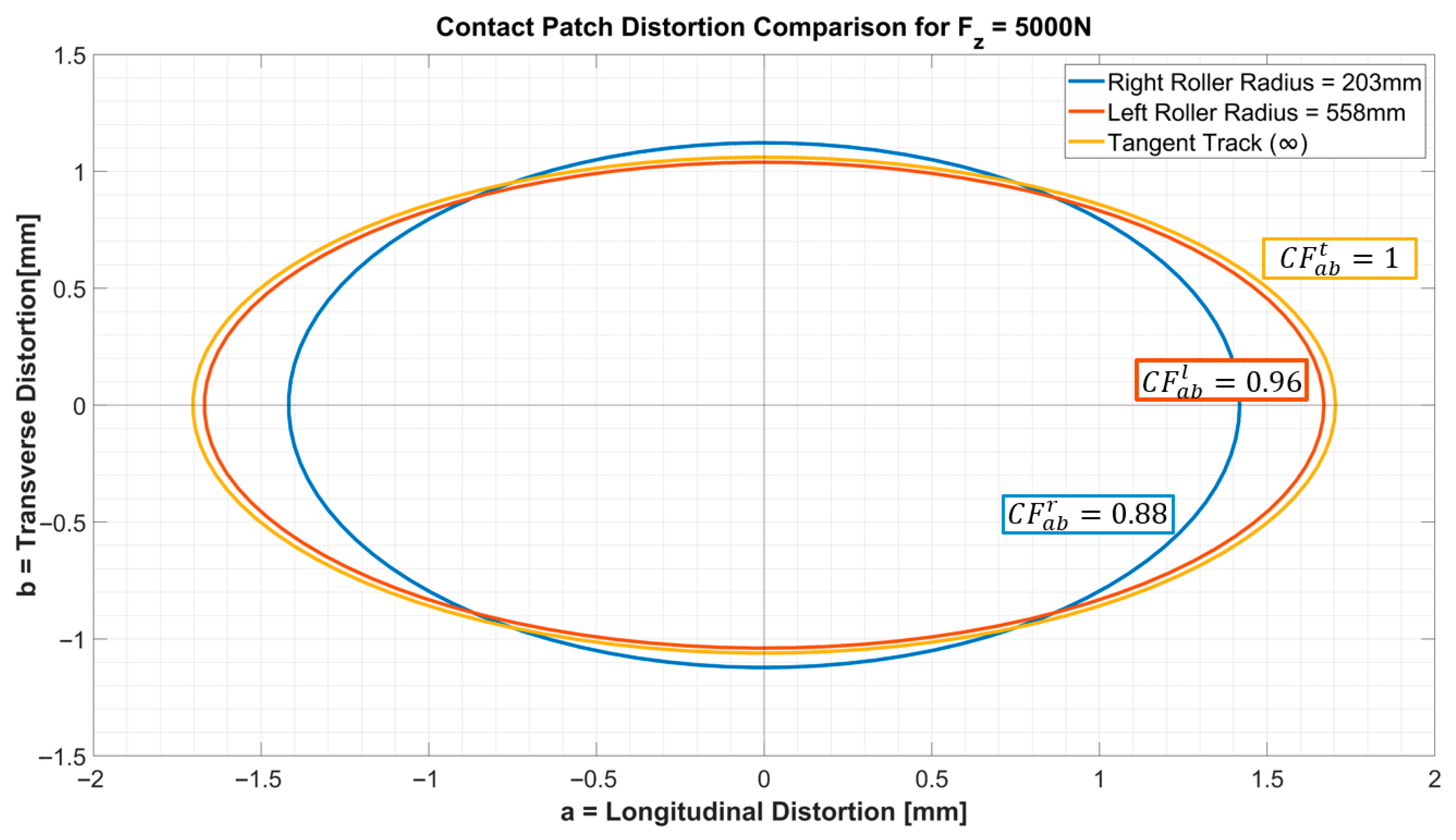
3.2. Contact Patch Distortion Comparison
3.3. Correction Factor
- Outer Ellipse: A 5 kN loaded steel wheel in contact with a flat rail for which the correction factor is set to 1.
- Intermediate Ellipse: The contact patch for the left roller, with a correction factor of 0.96 as calculated by Equation (9).
- Inner Ellipse: The right wheel’s contact patch, with a correction factor of 0.88 as calculated by Equation (10).
3.4. Equalization Factor
3.5. Curve Emulation Sensitivity
3.6. Force Measurement Decoupling
4. Conclusions
- A novel roller rig design is proposed to emulate wheelset dynamics using rollers with different diameters. Although contact patches on each wheel will inevitably differ due to contact mechanics, the proposed correction factors (CF) quantify these differences in contact patch distortion relative to a flat rail.
- Similarly, for dynamic loading, a longitudinal creepage equalization factor, , is derived to equalize the creep forces, accounting for the dissimilar contact patches between the wheel and roller at the two wheel–roller interfaces. The factor quantifies the additional longitudinal creepage required on the smaller roller to match the larger roller.
- Controlling the percentage creepage at each wheel is used to emulate the radius differential that exists in a high- and low-rail wheel in a curve. The analysis proved that the accuracy of emulating a curve with a given radius (or degree) is significantly influenced by minor deviations in changes in the percentage creepages. This implies that the drive motors must be controlled with extremely high precision to yield the required roller rotational velocity. The analysis further indicates that variations as small as 0.0525 RPM can cause errors as large as 2.78% in the emulated curve radius. The precise control of roller velocities, however, is deemed achievable in the proposed design due to the selection of state-of-the-art hardware and controllers that can meet the challenge.
- The equivalent curve radius replicated by the roller rig is highly sensitive to the ratio between the rollers’ tangential velocity and the wheelset’s theoretical forward velocity.
- Unlike unconstrained wheelsets in some earlier roller rig designs, the proposed constrained configuration improves the accuracy of the calculated contact forces by enabling precise determination of contact patch locations, which are critical inputs in solving for the contact forces.
- Sensor measurement errors were found to have a minor effect on the calculated contact forces in a constrained wheelset, as confirmed by the condition number analysis of the linear system used to solve the force and moment equations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CF | Correction Factor |
| DoA | Degrees of Freedom |
| VT-FRA | Virginia Tech—Federal Railroad Administration |
| WRI | Wheel–Rail Interface |
Appendix A
| Variable | Description | Units |
|---|---|---|
| Effective lateral curvature parameter, combining the curvatures of the wheel and roller in the X–Z plane for contact analysis | [1/mm] | |
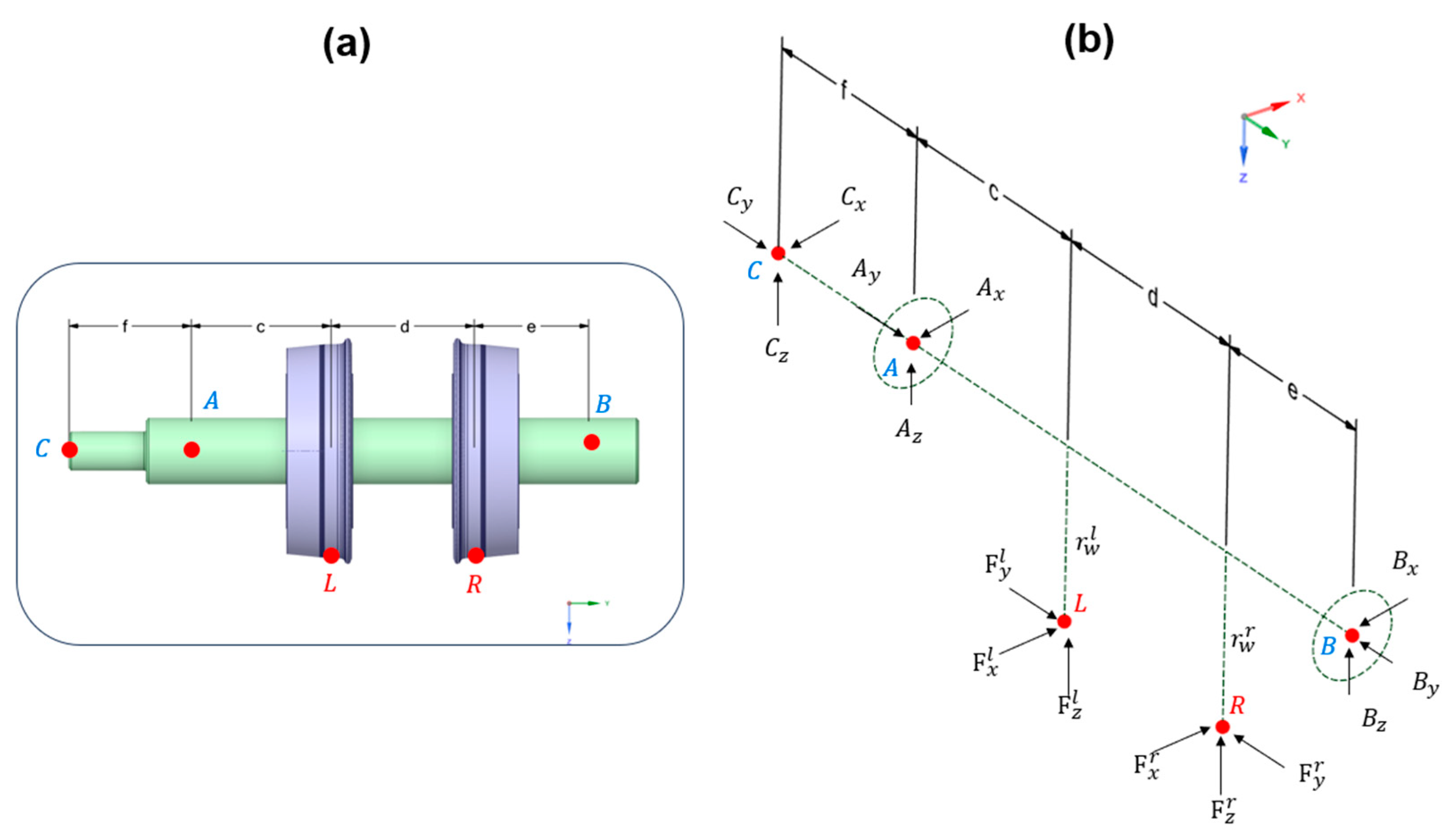
| Reaction forces at the bearing ‘A’ (see Figure 6) | [N] | |
| ’) | [mm2] | |
| Longitudinal ellipse dimension | [mm] | |
| Effective lateral curvature parameter, combining the curvatures of the wheel and roller in the Y–Z plane for contact analysis | [1/mm] | |
| Reaction forces at the bearing ‘B’ (see Figure 6) | [N] | |
| Transversal ellipse dimension | [mm] | |
| Reaction forces at the shaft coupling ‘C’ (see Figure 6) | [N] | |
| ’) | [dimensionless] | |
| Geometric variables defined as illustrated in Figure 6 | [mm] | |
| Creepage coefficient given in [34] for longitudinal creep force | [dimensionless] | |
| Equalization factor defined by Equation (14) | [dimensionless] | |
| Young modulus | [Pa] | |
| ’) contact patches | [N] | |
| ’) contact patches | [N] | |
| ’) contact patches | [N] | |
| Shear Modulus | [Pa] | |
| Half the distance between the contact patches on each wheel | [mm] | |
| Tabulated correction factor used in Hertzian contact mechanics. See [36] | [dimensionless] | |
| Tabulated correction factor used in Hertzian contact mechanics. See [36] | [dimensionless] | |
| Vertical load for calculating contact patch distortion | [N] | |
| Curve radius | [m] | |
| ’) wheels | [mm] | |
| ’) rollers | [mm] | |
| Wheelset forward velocity | [m/s] | |
| ’) wheels | [m/s] | |
| ’) rollers | [m/s] | |
| Angle of attack | ||
| Longitudinal creepage at the left (‘l’) and right (‘r’) contact patches | [dimensionless] | |
| Lateral creepage at the left (‘l’) and right (‘r’) contact patches | [dimensionless] | |
| ratio | [%] | |
| Poisson’s ratio | [dimensionless] |
References
- Meymand, S.Z.; Craft, M.J.; Ahmadian, M. On the Application of Roller Rigs for Studying Rail Vehicle Systems. In Proceedings of the American Society of Mechanical Engineers, Rail Transportation Division (Publication) RTD, Altoona, PA, USA, 15–17 October 2013; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2013. [Google Scholar]
- Myamlin, S.; Kalivoda, J.; Neduzha, L. Testing of Railway Vehicles Using Roller Rigs. Procedia Eng. 2017, 187, 688–695. [Google Scholar] [CrossRef]
- Wickens, A.H. Fundamentals of Rail Vehicle Dynamics: Guidance and Stability; Swets & Zeitlinger Publishers: Lisse, The Netherlands, 2005; ISBN 90-265-1946-X. [Google Scholar]
- Antali, M.; Stepan, G.; Hogan, S.J. Kinematic Oscillations of Railway Wheelsets. Multibody Syst. Dyn. 2015, 34, 259–274. [Google Scholar] [CrossRef]
- Powell, A.F.; Gräbe, P.J. Exploring the Relationship between Vertical and Lateral Forces, Speed and Superelevation in Railway Curves. J. S. Afr. Inst. Civ. Eng. 2017, 59, 25–35. [Google Scholar] [CrossRef][Green Version]
- Meijaard, J.P. The Motion of a Railway Wheelset on a Track or on a Roller Rig. Procedia IUTAM 2016, 19, 274–281. [Google Scholar] [CrossRef][Green Version]
- Hsu, S.S.; Huang, Z.; Iwnicki, S.D.; Thompson, D.J.; Jones, C.J.C.; Xie, G.; Allen, P.D. Experimental and Theoretical Investigation of Railway Wheel Squeal. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2007, 221, 59–73. [Google Scholar] [CrossRef]
- Ichiyanagi, Y.; Michitsuji, Y.; Matsumoto, A.; Sato, Y.; Ohno, H.; Ogata, S.; Tanimoto, M.; Fukushima, T.; Matsuda, T.; Shinagawa, D. Simulation-Based Estimation of Wheel/Rail Friction Coefficient and Wear Number Considering Results of Full-Scale Roller-Rig Test. Mech. Eng. J. 2023, 10, 22–00299. [Google Scholar] [CrossRef]
- Matsumoto, A.; Sato, Y.; Ono, H.; Wang, Y.; Yamamoto, M.; Tanimoto, M.; Oka, Y. Creep Force Characteristics between Rail and Wheel on Scaled Model. Wear 2002, 253, 199–203. [Google Scholar] [CrossRef]
- Kalousek, J. Development of a 1/8 Scale Dual Disc-an-Disc Railjwheel Wear Testing Facility. Can. Metall. Q. 1982, 21, 67–72. [Google Scholar] [CrossRef]
- Meymand, S.Z. State of the Art Roller Rig for Precise Evaluation of Wheel-Rail Contact Mechanics and Dynamics; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2015. [Google Scholar]
- Liu, W.; Jiang, R.; Liu, F.; Zhang, L.; Li, Y. Method of Curve Simulation of Railway Vehicle on Roller Rig. Jixie Gongcheng Xuebao/J. Mech. Eng. 2018, 54, 127–133. [Google Scholar] [CrossRef]
- Bruni, S.; Cheli, F.; Resta, F. A Model of an Actively Controlled Roller Rig for Tests on Full-Size Railway Wheelsets. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2001, 215, 277–288. [Google Scholar] [CrossRef]
- Gómez, E.; Alonso, A.; Giménez, J.G.; Vinolas, J. Railway Dynamometric Wheelsets: A Comparison of Existing Solutions and a Proposal for the Reduction of Measurement Errors. In Proceedings of the 1st International Workshop on High-Speed Railways (IWHIR), Berlin, Germany, 8–10 May 2012; Springer: Berlin/Heidelberg, Germany; Volume 2, pp. 261–284. [Google Scholar]
- Bracciali, A.; Cavaliere, F.; Macherelly, M. Review of Instrumented Wheelset Technology and Applications. In Proceedings of the Second International Conference on Railway Technology: Research, Development and Maintenance, Ajaccio, Corsica, France, 8–11 April 2014; Pombo, J., Ed.; Civil-Comp Press: Stirlingshire, UK, 2014. [Google Scholar] [CrossRef]
- AAR. Manual of Standards and Recommended Practices, Section C, Part II: Safety and Operations, Chapter 11; Association of American Railroads: Washington, DC, USA, 2007; Available online: https://aar.com/standards/ (accessed on 19 August 2025).
- EN 14363; Railway Applications–Testing for the Acceptance of Running Characteristics of Railway Vehicles–Testing of Running Behaviour and Stationary Tests. European Committee for Standardization: Brussels, Belgium, 2006. Available online: https://standards.iteh.ai/catalog/standards/cen/b3c41e35-9f1b-4f5c-9e0d-c1e91ad1915b/en-14363-2005 (accessed on 19 August 2025).
- Jin, X. A Measurement and Evaluation Method for Wheel-Rail Contact Forces and Axle Stresses of High-Speed Train. Measurement 2020, 149, 106983. [Google Scholar] [CrossRef]
- Eadie, D.T.; Elvidge, D.; Oldknow, K.; Stock, R.; Pointner, P.; Kalousek, J.; Klauser, P. The Effects of Top of Rail Friction Modifier on Wear and Rolling Contact Fatigue: Full-Scale Rail-Wheel Test Rig Evaluation, Analysis and Modelling. Wear 2008, 265, 1222–1230. [Google Scholar] [CrossRef]
- Tournay, H.; Shu, X.; Keylin, A.; Cakdi, S. Investigation of Wheel and Rail Rolling Contact Fatigue Using a Full-Scale Simulator; Technical Report DOT/FRA/ORD-22/13; Transportation Technology Center, Inc.: Pueblo, CO, USA, March 2022. Available online: https://railroads.dot.gov/elibrary/investigation-wheel-and-rail-rolling-contact-fatigue-using-full-scale-simulator (accessed on 19 August 2025).
- Ahmadian, M.; Craft, M. Evaluation of Wheel/Rail Contact Mechanics: Concepts Report; Technical Report DOT/FRA/ORD-14/28; Center for Vehicle Systems and Safety, Virginia Tech: Blacksburg, VA, USA, July 2014. Available online: https://railroads.dot.gov/elibrary/evaluation-wheelrail-contact-mechanics-concepts-report (accessed on 19 August 2025).
- Kumar, N.; Radmehr, A.; Ahmadian, M. Experimental Evaluation of Effect of Leaves on Railroad Tracks in Loss of Braking. Machines 2024, 12, 301. [Google Scholar] [CrossRef]
- Kumar, N.; Radmehr, A.; Ahmadian, M. Traction Enhancement Evaluation of Magnetite and Alumina. Int. J. Rail Transp. 2025, 13, 1–19. [Google Scholar] [CrossRef]
- Radmehr, A.; Pan, Y.; Tajaddini, A.; Vollebregt, E.; Ahmadian, M. Wheel-Rail Contact Force and Traction Analysis Under Wet and Oil-Contaminated Conditions. In Proceedings of the 2022 ASME Joint Rail Conference (JRC2022), Baltimore, MD, USA, 19–21 April 2022; ASME: New York, NY, USA, 2022. Paper No. JRC2022-78233. Available online: https://doi.org/10.1115/JRC2022-78233 (accessed on 19 August 2025).
- Radmehr, A.; Kothari, K.; Ahmadian, M. Evaluating the Effect of Natural Third Body Layers on Friction Using the Virginia Tech Roller Rig. In Proceedings of the 2019 ASME Joint Rail Conference (JRC2019), Snowbird, UT, USA, 10–12 April 2019; ASME: New York, NY, USA, 2019. Paper No. JRC2019-1292. Available online: https://doi.org/10.1115/JRC2019-1292 (accessed on 19 August 2025).
- Hosseini, S.M.; Radmehr, A.; Hosseinian Ahangarnejad, A.; Gramacy, R.B.; Ahmadian, M. A Statistical Evaluation of Multiple Regression Models for Contact Dynamics in Rail Vehicles Using Roller Rig Data. Int. J. Rail Transp. 2022, 10, 717–729. [Google Scholar] [CrossRef]
- Kumar, N.; Tech, V.; Mantovani, G.; Radmehr, A.; Ahmadian, M. Estimation of Wheel-Rail Contact Patch Geometry Under Curving Conditions. In Proceedings of the AREMA 2024 Annual Conference & Expo, Louisville, KY, USA, 30 September 2024. [Google Scholar] [CrossRef]
- Radmehr, A.; Ahmadian, M. Real-Time Wheel Wear Estimation Using Non-Contact Measurements. In Proceedings of the 20th International Wheelset Congress (IWC), Chicago, IL, USA, 8–11 May 2023; Available online: https://doi.org/10.1115/JRC2022-78233 (accessed on 19 August 2025).
- Thomson Industries. PC Series, Precision Linear Actuators; Thomson Industries: Radford, VA, USA, 2021; Available online: https://www.thomsonlinear.com/en/products/precision-linear-actuators/pc-series (accessed on 19 August 2025).
- Meymand, S.Z.; Hosseinipour, M.; Ahmadian, M. The Development of a Roller Rig for Experimental Evaluation of Contact Mechanics for Railway Vehicles. In Proceedings of the 2015 Joint Rail Conference, San Jose, CA, USA, 23 March 2015. [Google Scholar]
- Keylin, A.; Ahmadian, M.; Taheri, M.; Tajaddini, A. Wheel-Rail Contact Characteristics on a Tangent Track vs. a Roller Rig. In Proceedings of the ASME 2012 Rail Transportation Division Fall Technical Conference, Omaha, NA, USA, 16–18 October 2012. [Google Scholar]
- Kollmorgen Corporation. AKM2G Series Servo Motors; Kollmorgen Corporation: Radford, VA, USA, 2022; Available online: https://www.kollmorgen.com/en-us/products/motors/servo/akm-series/akm2g/akm2g-servo-motor (accessed on 19 August 2025).
- Hosseinipour, M.; Vick, B.; Taheri, S.; Mirzaeifar, R. Electromechanical Design and Development of the Virginia Tech Roller Rig Testing Facility for Performing Various Studies on Wheel-Rail Contact Mechanics and Dynamics. Ph.D. Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2016. Available online: http://hdl.handle.net/10919/82542 (accessed on 19 August 2025).
- Kalker, J.J. Wheel-Rail Rolling Contact Theory. Wear 1991, 144, 243–261. [Google Scholar] [CrossRef]
- Keylin, A. Analytical Evaluation of the Accuracy of Roller Rig Data for Studying Creepage in Rail Vehicles; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2012. [Google Scholar]
- Iwnicki, S. Handbook of Railway Vehicle Dynamics, 1st ed.; CRC Press: Boca Raton, FL, USA, 2006; ISBN 9780429129803. [Google Scholar]
- Hibbeler, R.C. Mechanics of Materials; Trimer, R., Ed.; Pearson: London, UK, 2010; pp. 85–116. ISBN 978-85-7605-373-6. [Google Scholar]
- Kistler Group. Technical Data Sheet: 3-Component Quartz Force Sensor Type 9027C, 9028C, Type 9027C, 9028C, 9026C4; Kistler Group: Winterthur, Switzerland, 2020. [Google Scholar]
- Deif, A. Sensitivity Analysis in Linear Systems; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
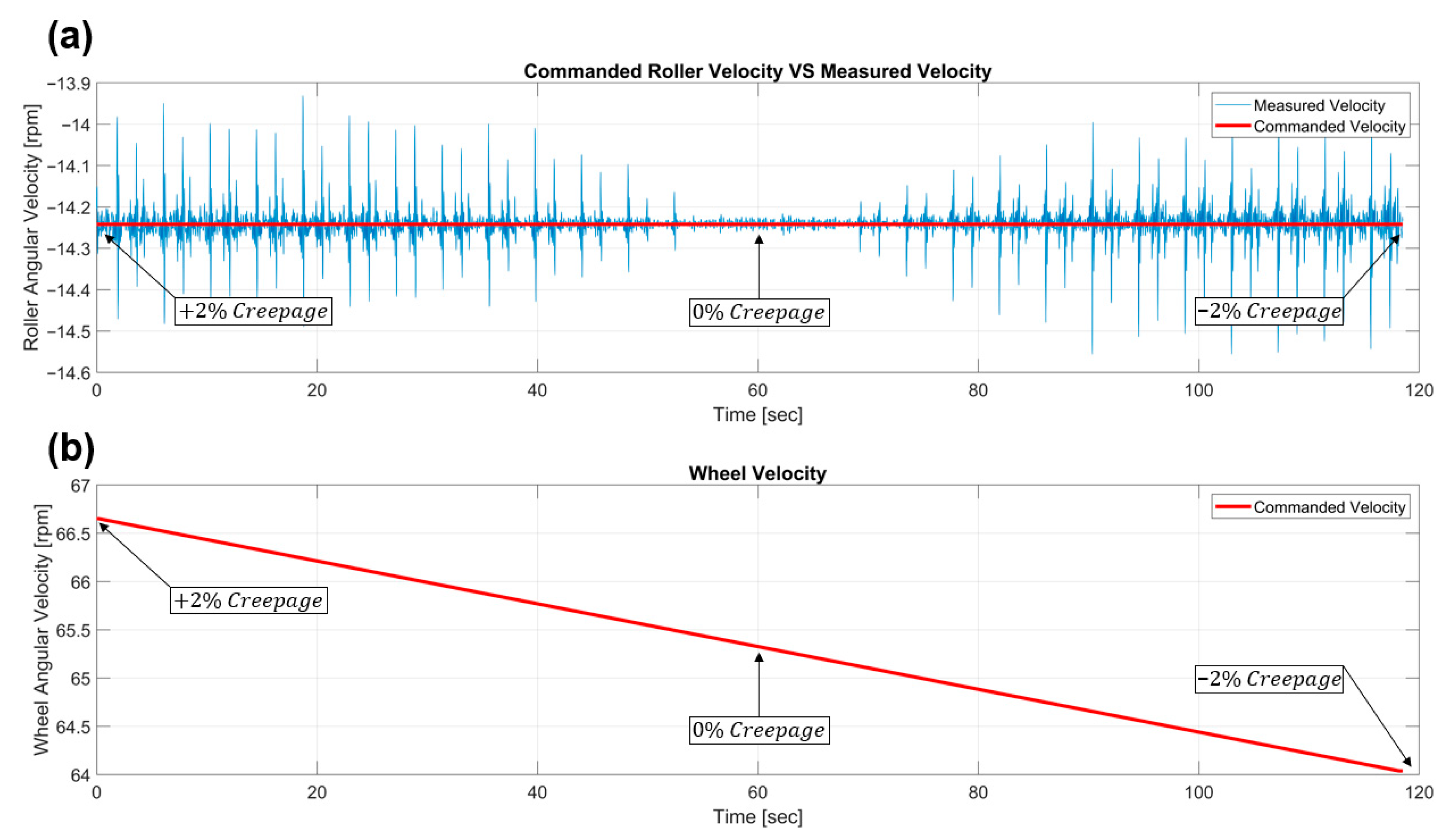
| Section Number | Time Range [sec] | Creepage Range [%] | ||
|---|---|---|---|---|
| [rpm] | [%] of Actual Value | |||
| 1 | 0 to 30 s | +2% to +1% | 0.0486 | 0.34% |
| 2 | 30 s to 60 s | +1% to 0% | 0.0290 | 0.20% |
| 3 | 60 s to 90 s | 0% to −1% | 0.0262 | 0.18% |
| 4 | 90 s to 120 s | −1% to −2% | 0.0525 | 0.37% |
| 5 | 0 to 120 s | +2% to −2% | 0.0407 | 0.29% |
| 6 | 45 s to 75 s | +0.5% to −0.5% | 0.0150 | 0.11% |
| 7 | 50 s to 70 s | +0.33% to −0.33% | 0.0096 | 0.07% |
| Variables | Nominal Value [mm] | Maximum Variation [mm] |
|---|---|---|
| 166 | ||
| 158 | ||
| e | 133 | |
| 140 | 0 | |
| 122 | ||
| 122 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mantovani, G.; Kumar, N.; Ahmadian, M. Design Evaluation of a Single Wheelset Roller Rig for Railroad Curving Dynamics and Creepage Studies. Designs 2025, 9, 99. https://doi.org/10.3390/designs9040099
Mantovani G, Kumar N, Ahmadian M. Design Evaluation of a Single Wheelset Roller Rig for Railroad Curving Dynamics and Creepage Studies. Designs. 2025; 9(4):99. https://doi.org/10.3390/designs9040099
Chicago/Turabian StyleMantovani, Giovanni, Nikhil Kumar, and Mehdi Ahmadian. 2025. "Design Evaluation of a Single Wheelset Roller Rig for Railroad Curving Dynamics and Creepage Studies" Designs 9, no. 4: 99. https://doi.org/10.3390/designs9040099
APA StyleMantovani, G., Kumar, N., & Ahmadian, M. (2025). Design Evaluation of a Single Wheelset Roller Rig for Railroad Curving Dynamics and Creepage Studies. Designs, 9(4), 99. https://doi.org/10.3390/designs9040099








