EMM Project—LD GRIDS: Design of a Charged Dust Analyser for Moon Exploration
Abstract
1. Introduction
2. Materials and Methods
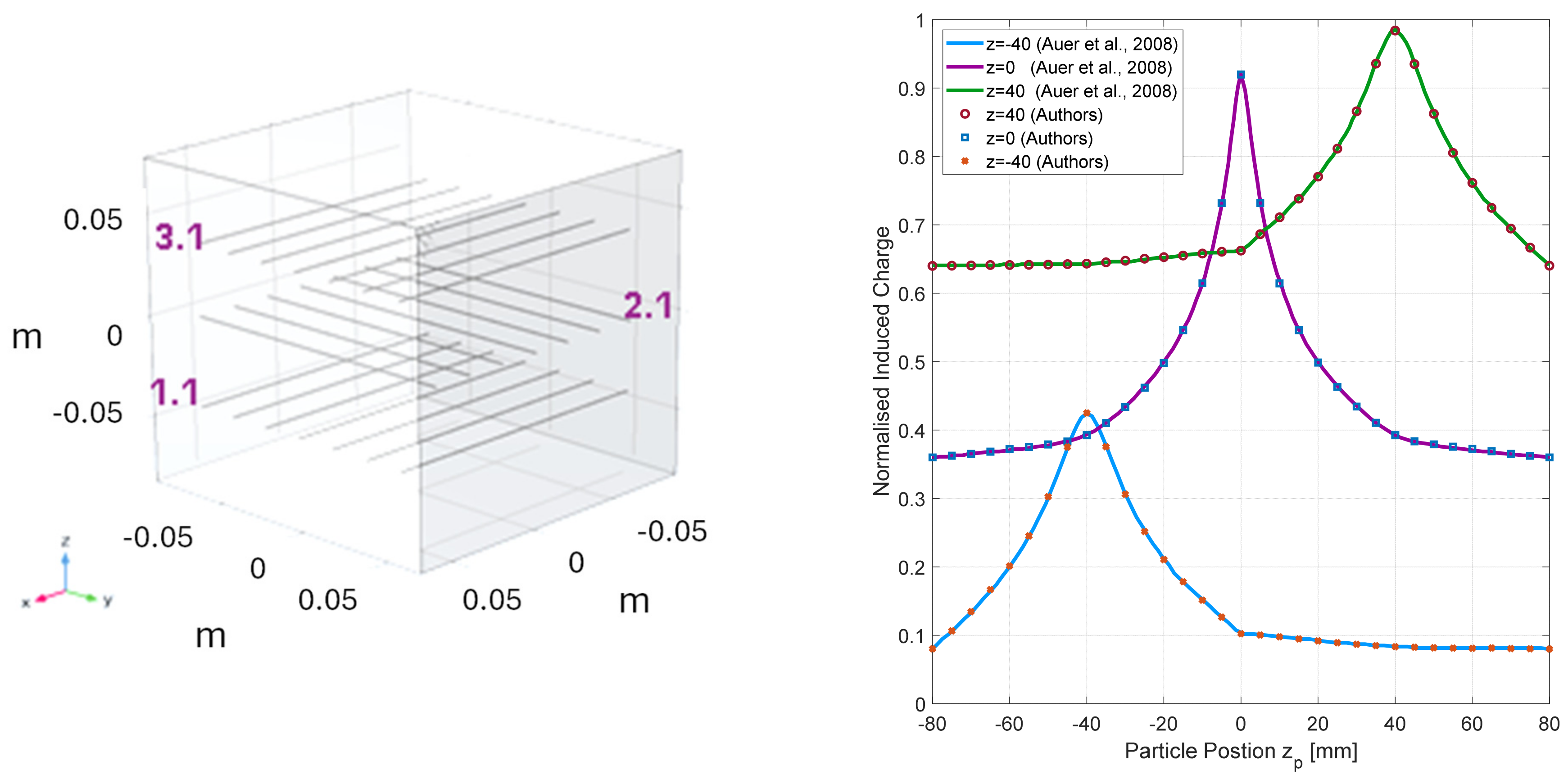
2.1. Electrostatic Modelling Validation
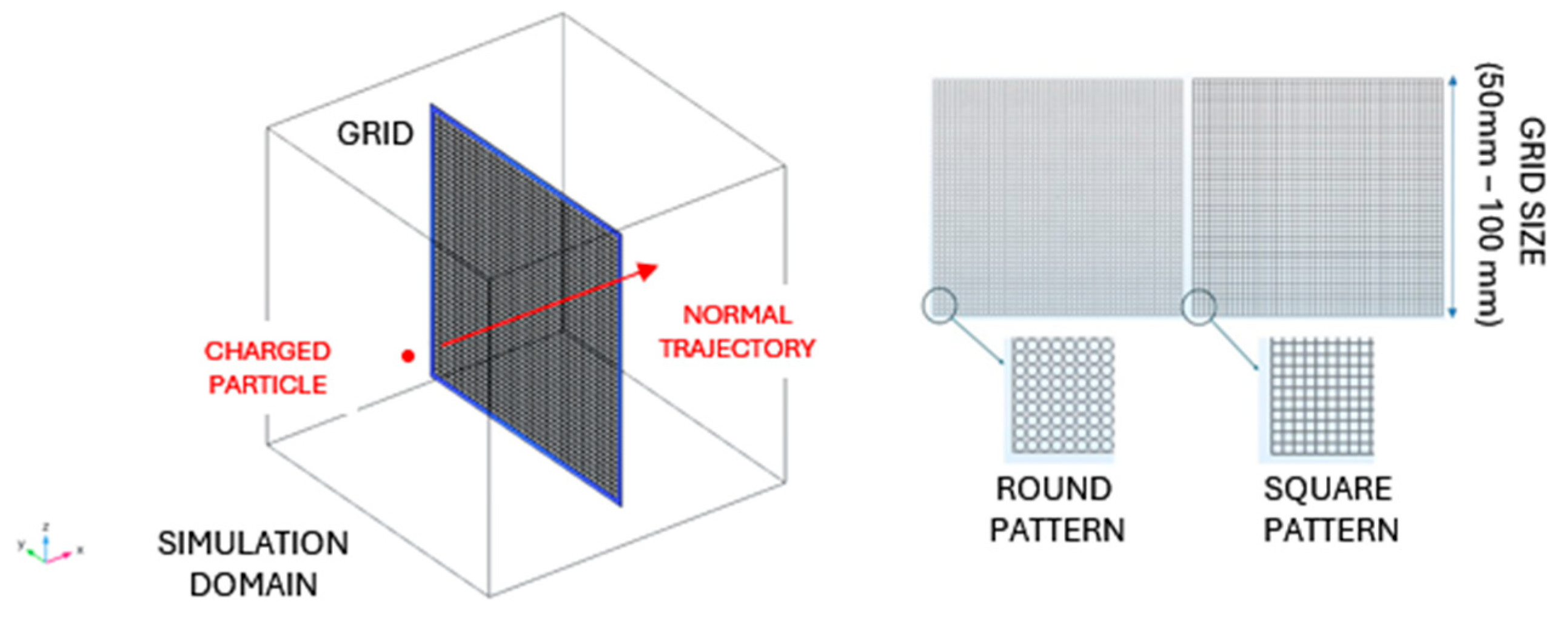
2.2. FE Models Description and Numerical Analyses
2.2.1. Electrostatic Performance
2.2.2. Modal Analysis
2.2.3. Quasi-Static Analysis
3. Results and Discussion
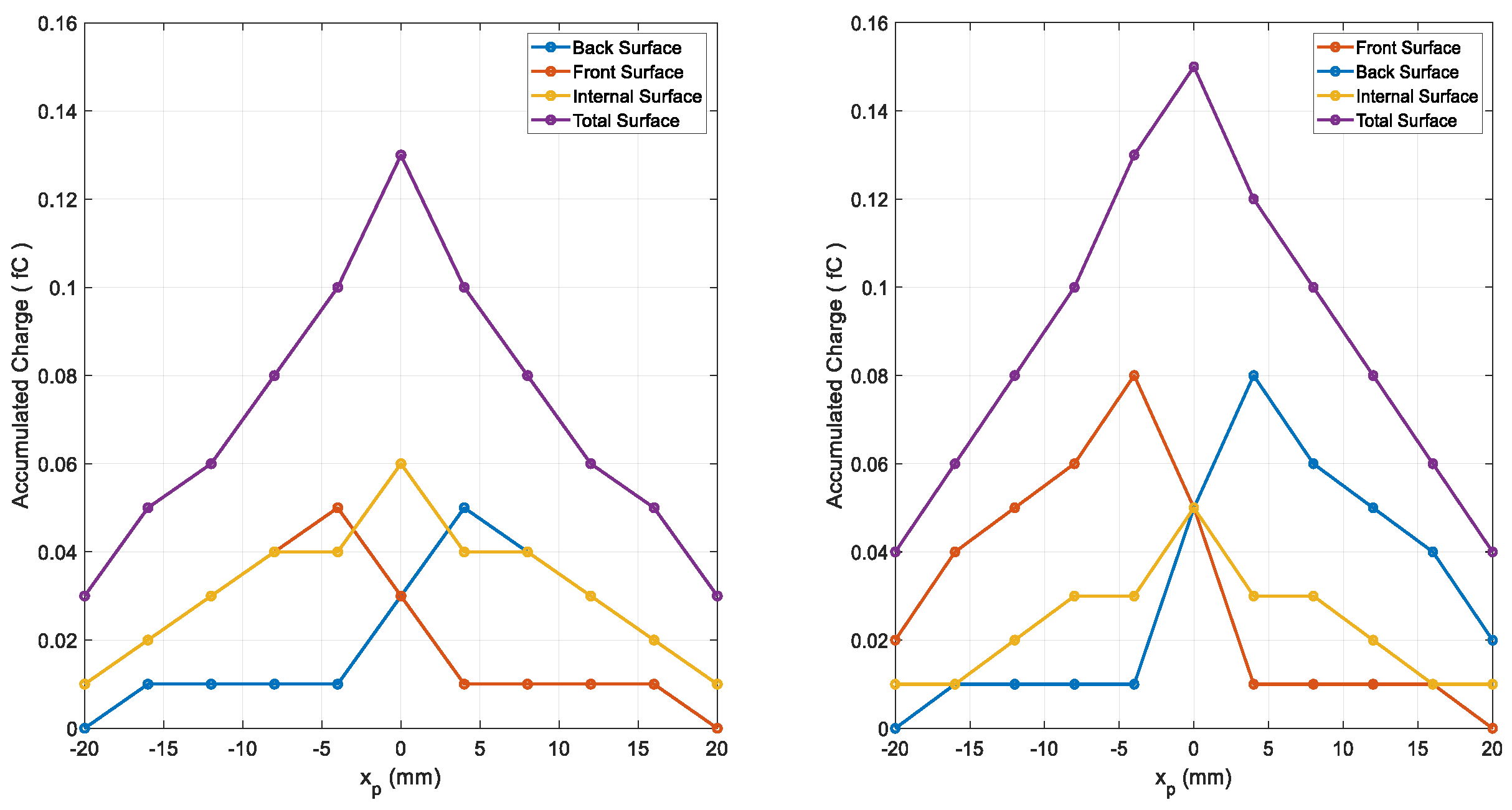
3.1. Pattern Influence
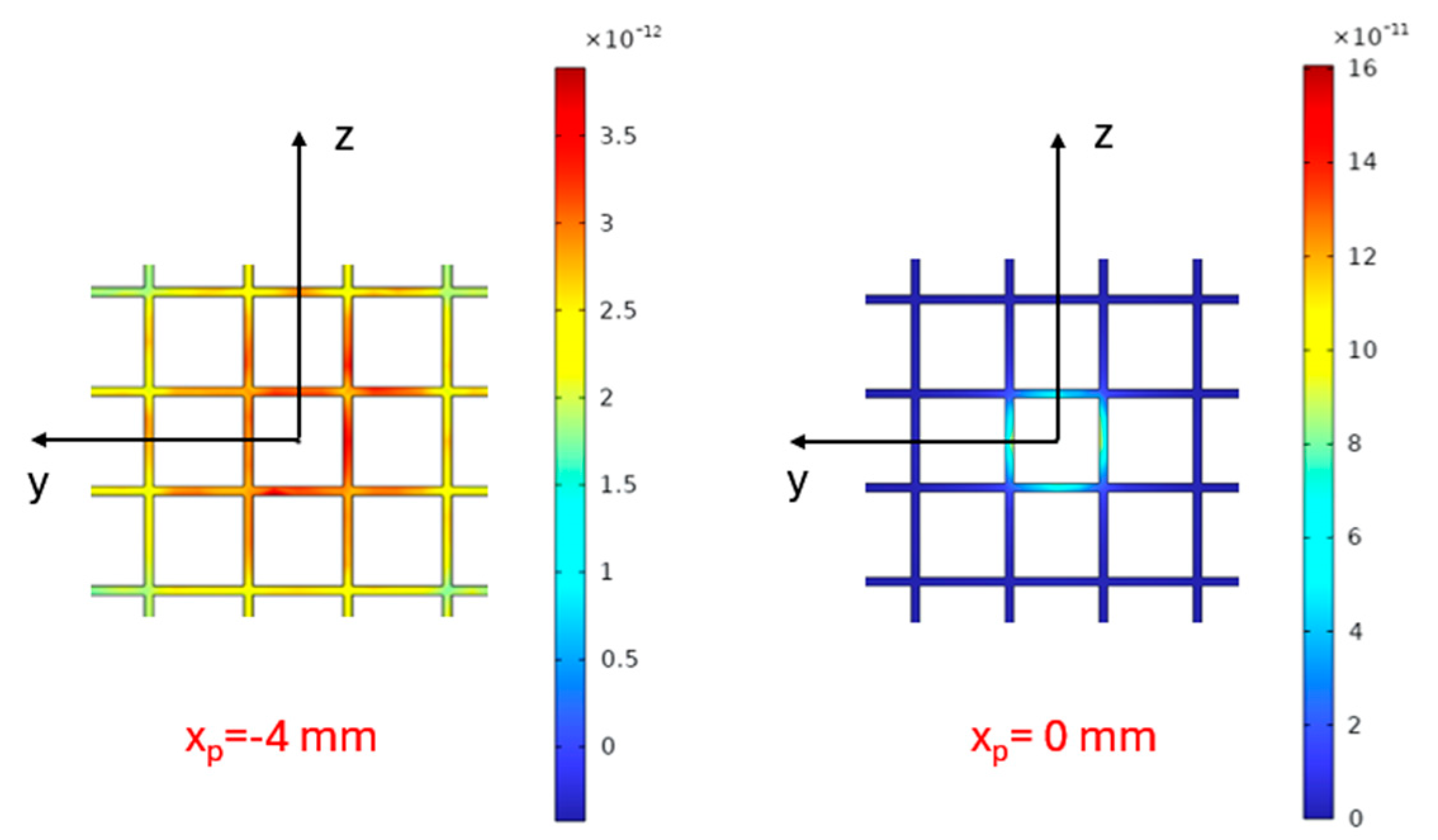
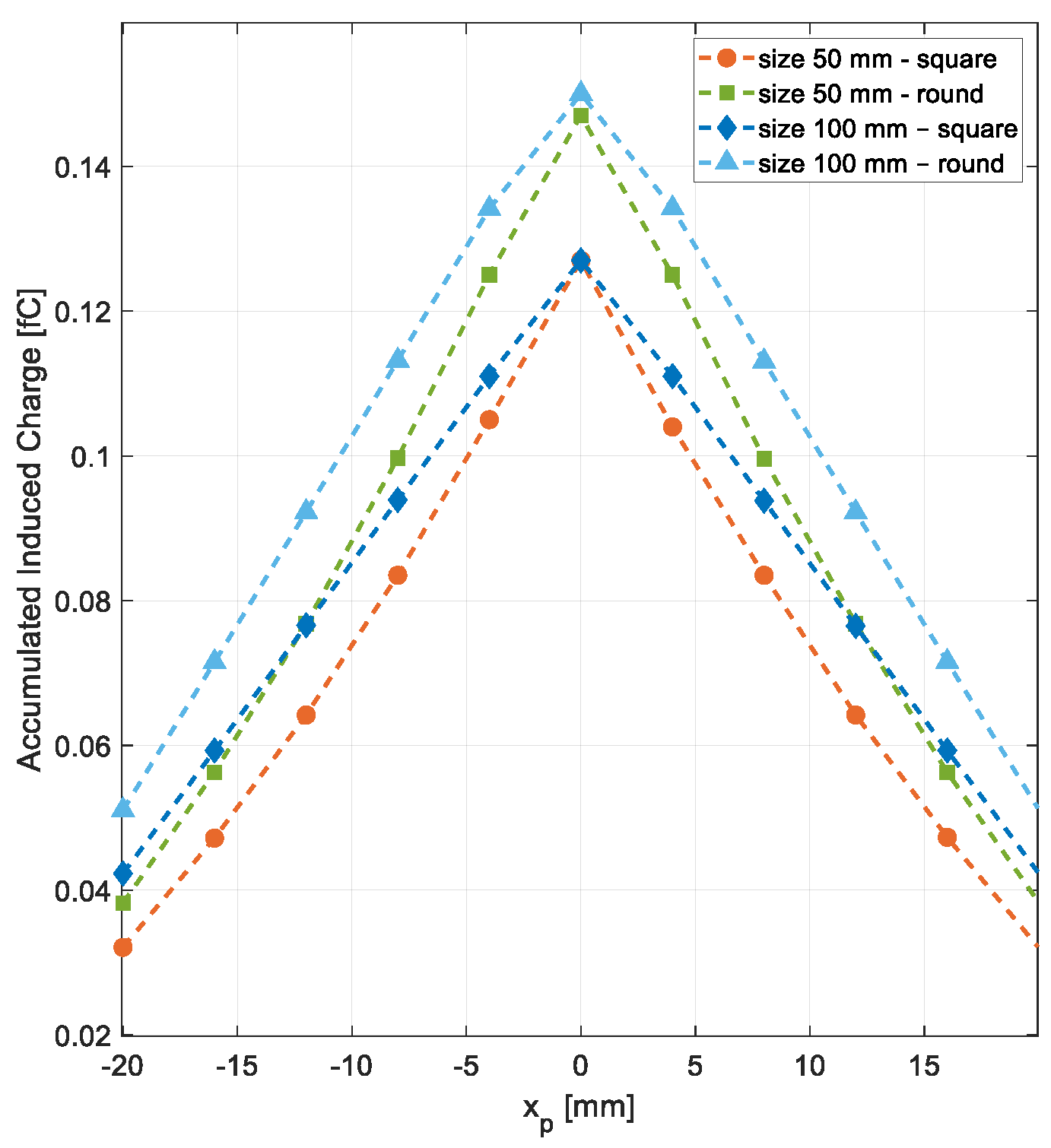
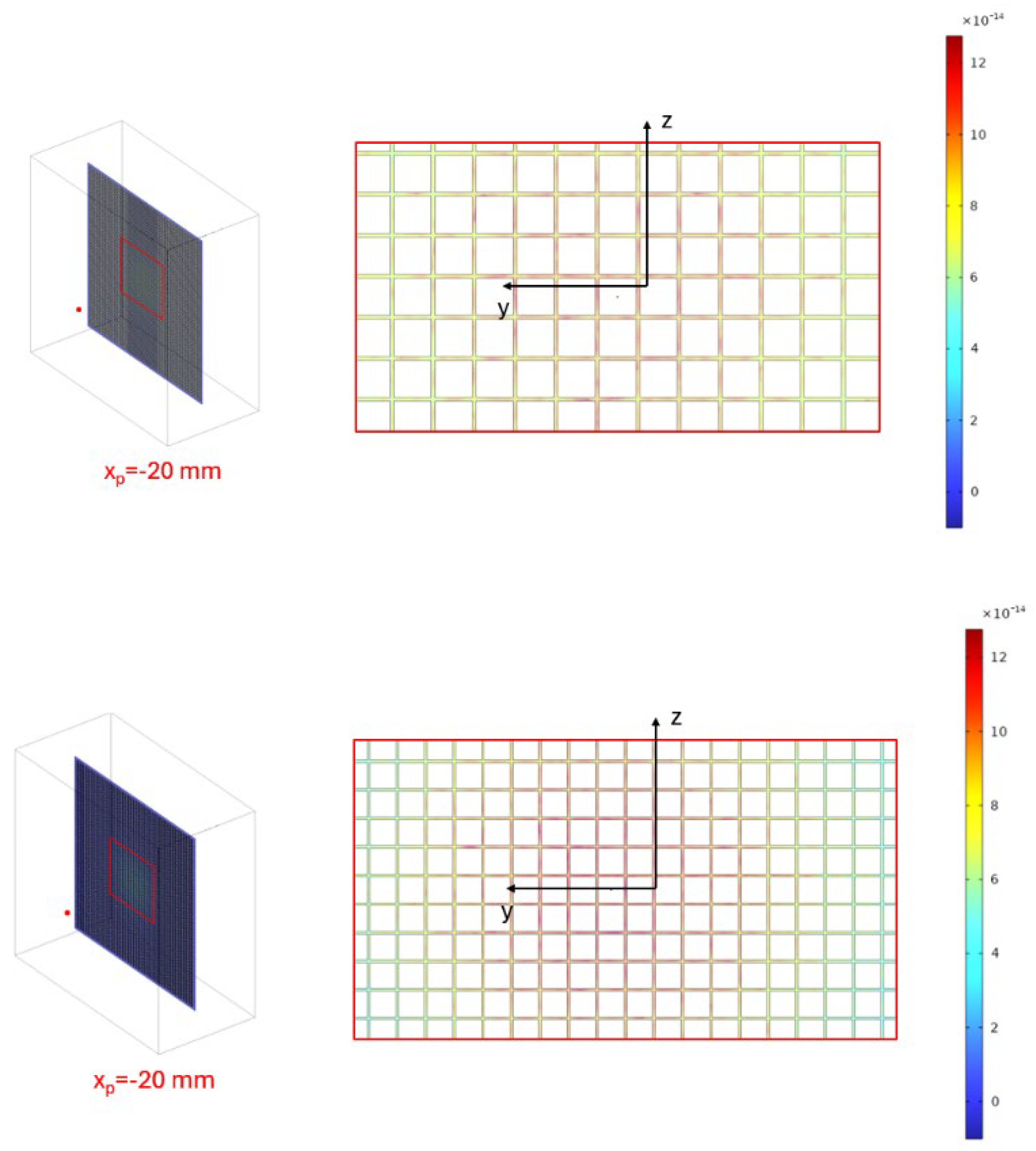
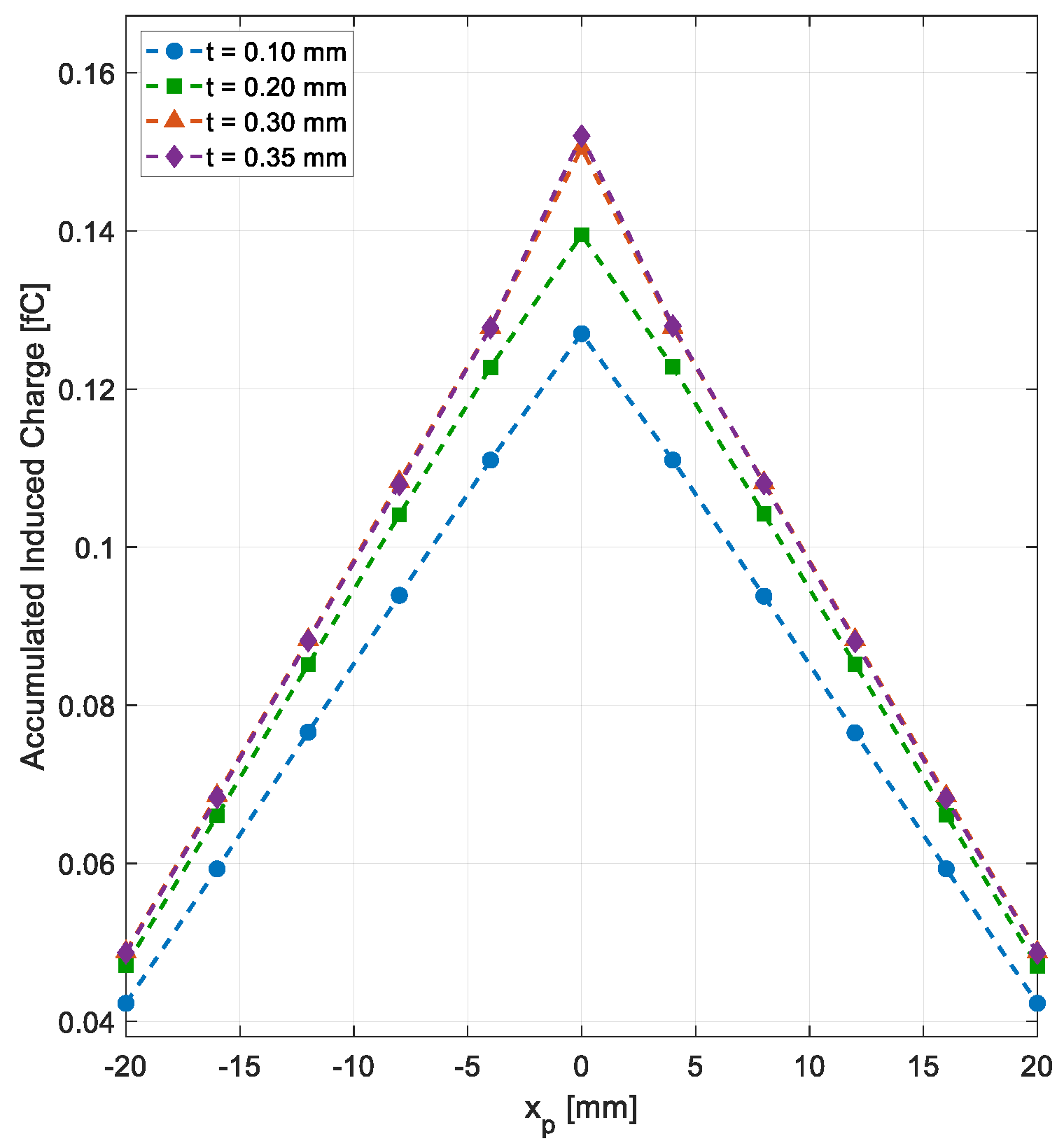
3.1.1. Electrostatic Performance
3.1.2. Modal Analysis
3.1.3. Quasi-Static Analysis
3.2. Thickness Influence with Fixed Pattern and Geometry
3.2.1. Electrostatic Performance
3.2.2. Modal Analysis
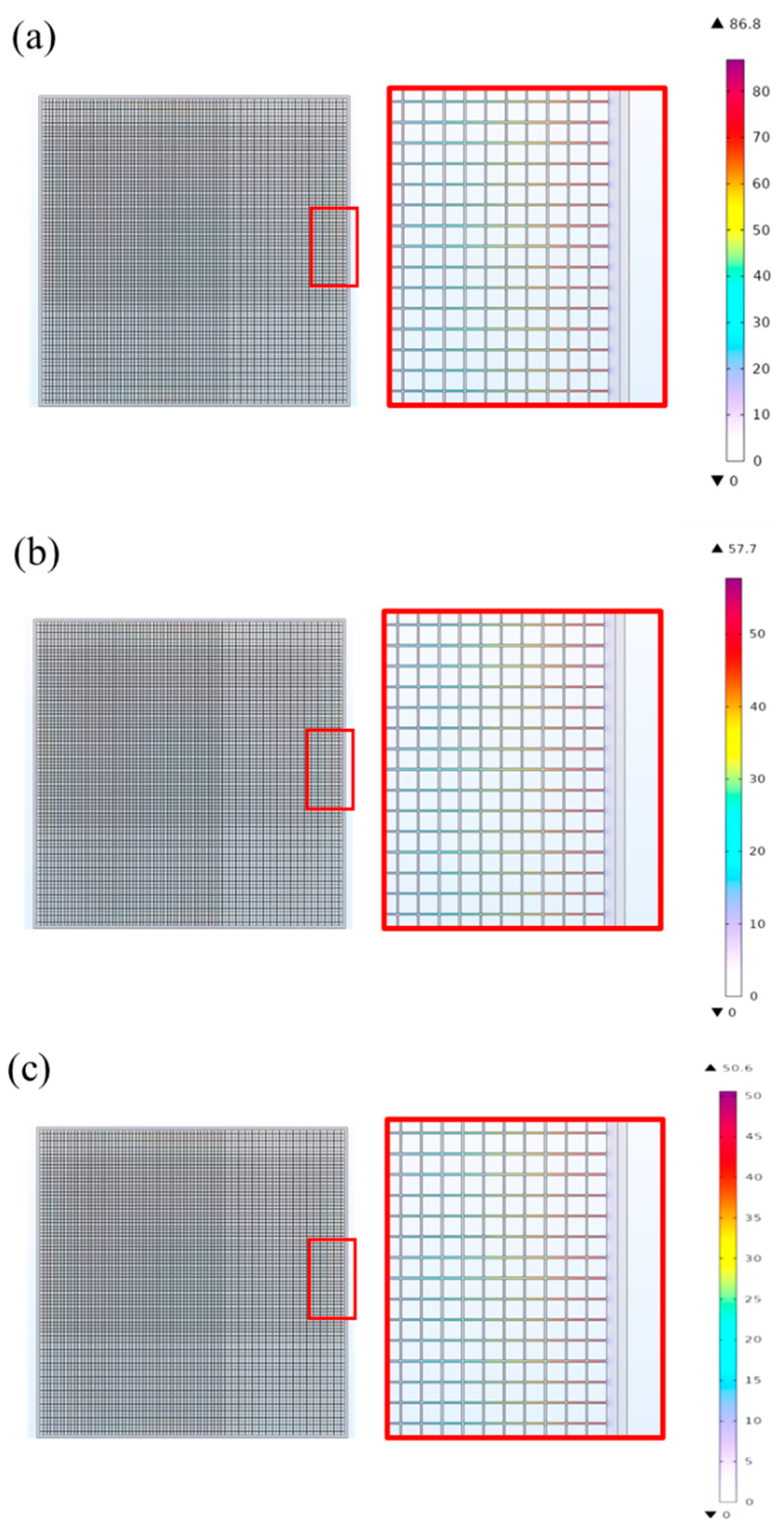
3.2.3. Quasi-Static Analysis
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Creech, S.; Guidi, J.; Elburn, D. Artemis: An Overview of NASA’s Activities to Return Humans to the Moon. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Smith, M.; Craig, D.; Herrmann, N.; Mahoney, E.; Krezel, J.; McIntyr, N.; Goodliff, K. The Artemis Program: An Overview of NASA’s Activities to Return Humans to the Moon. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–10. [Google Scholar] [CrossRef]
- Auer, S.; Grün, E.; Kempf, S.; Srama, R.; Srowig, A.; Sternovsky, Z.; Tschernjawski, V. Characteristics of a dust trajectory sensor. Rev. Sci. Instrum. 2008, 79, 084501. [Google Scholar] [CrossRef] [PubMed]
- Grün, E.; Srama, R.; Altobelli, N.; Altwegg, K.; Carpenter, J.; Colangeli, L.; Glassmeier, K.-H.; Helfert, S.; Henkel, H.; Horanyi, M. DuneXpress. Exp. Astron. 2009, 23, 981–999. [Google Scholar] [CrossRef]
- Xie, J.; Sternovsky, Z.; Grün, E.; Auer, S.; Duncan, N.; Drake, K.; Le, H.; Horanyi, M.; Srama, R. Dust trajectory sensor: Accuracy and data analysis. Rev. Sci. Instrum. 2011, 82, 105104. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Sternovsky, Z.; Auer, S.; Drake, K.; Grün, E.; Horanyi, M.; Le, H.; Srama, R. Laboratory testing and data analysis of the Electrostatic Lunar Dust Analyzer (ELDA) instrument. Planet. Space Sci. 2013, 89, 63–70. [Google Scholar] [CrossRef]
- Srama, R.; Ahrens, T.J.; Altobelli, N.; Auer, S.; Bradley, J.G.; Burton, M.; Dikarev, V.V.; Economou, T.; Fechtig, H.; Görlich, M.; et al. The Cassini Cosmic Dust Analyzer. Space Sci. Rev. 2014, 114, 465–518. [Google Scholar] [CrossRef]
- Auer, S.; Grün, E.; Srama, R.; Kempf, S.; Auer, R. The charge and velocity detector of the cosmic dust analyzer on Cassini. Planet. Space Sci. 2002, 50, 773–779. [Google Scholar] [CrossRef]
- Horanyi, M.; Sternovsky, Z.; Lankton, M.; Dumont, C.; Gagnard, S.; Gathright, D.; Wright, G. The lunar dust experiment (LDEX) onboard the lunar atmosphere and dust environment explorer (LADEE) mission. In The Lunar Atmosphere and Dust Environment Explorer Mission (LADEE); Springer: Cham, Switzerland, 2015; pp. 93–113. [Google Scholar]
- Sommer, M.; Li, Y.; Srama, R.; Simolka, J.; Strack, H.; Gläser, J.; Arai, T. Measuring micro-debris In-Situ with the DESTINY+ dust analyzer. In Proceedings of the 2nd NEO and Debris Detection Conference, Darmstadt, Germany, 24–26 January 2023; p. 37. [Google Scholar]
- Scaccabarozzi, D.; Ahmed, A.M.R.; Saggin, B.; Esposito, F.; Porto, C.; Mongelluzzo, G. Feasibility Design of LD GRIDS, a Dust Analyzer for the Moon. In Proceedings of the 2024 11th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Lublin, Poland, 3–5 June 2024; pp. 427–431. [Google Scholar] [CrossRef]
- Rezinkina, M.; Braxmaier, C. Designs of Miniature Optomechanical Sensors for Measurements of Acceleration with Frequencies of Hundreds of Hertz. Designs 2024, 8, 67. [Google Scholar] [CrossRef]
- Mejía Rodríguez, M.; González-Estrada, O.A.; Villegas-Bermúdez, D.F. Finite Element Analysis of Patient-Specific Cranial Implants under Different Design Parameters for Material Selection. Designs 2024, 8, 31. [Google Scholar] [CrossRef]
- Al-Haddad, L.A.; Jaber, A.A.; Giernacki, W.; Khan, Z.H.; Ali, K.M.; Tawafik, M.A.; Humaidi, A.J. Quadcopter unmanned aerial vehicle structural design using an integrated approach of topology optimization and additive manufacturing. Designs 2024, 8, 58. [Google Scholar] [CrossRef]
- Cecere, G.; Irimescu, A.; Merola, S.S. System Design and Stress–Strain Analysis for Cranking and Motoring Small-Size Engines. Designs 2024, 8, 14. [Google Scholar] [CrossRef]
- Scaccabarozzi, D.; Martina, C.; Saggin, B.; Vieira Vaz, E.; Palomba, E.; Longobardo, A.; Gisellu, C.; Dirri, F.; Zampetti, E.; Pedone, M. Feasibility Design of DIANA, a Dust Analyzer developed for the Tianwen-2 Mission. In Proceedings of the 2024 11th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Lublin, Poland, 3–5 June 2024; pp. 422–426. [Google Scholar] [CrossRef]
- Scaccabarozzi, D.; Saggin, B.; Magni, M.; Valnegri, P.; Corti, M.G.; Palomba, E.; Longobardo, A.; Dirri, F.; Zampetti, E. Design of 3D printed holder for quartz crystal microbalances. In Proceedings of the 2021 IEEE 8th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Naples, Italy, 23–25 June 2021; pp. 715–719. [Google Scholar] [CrossRef]


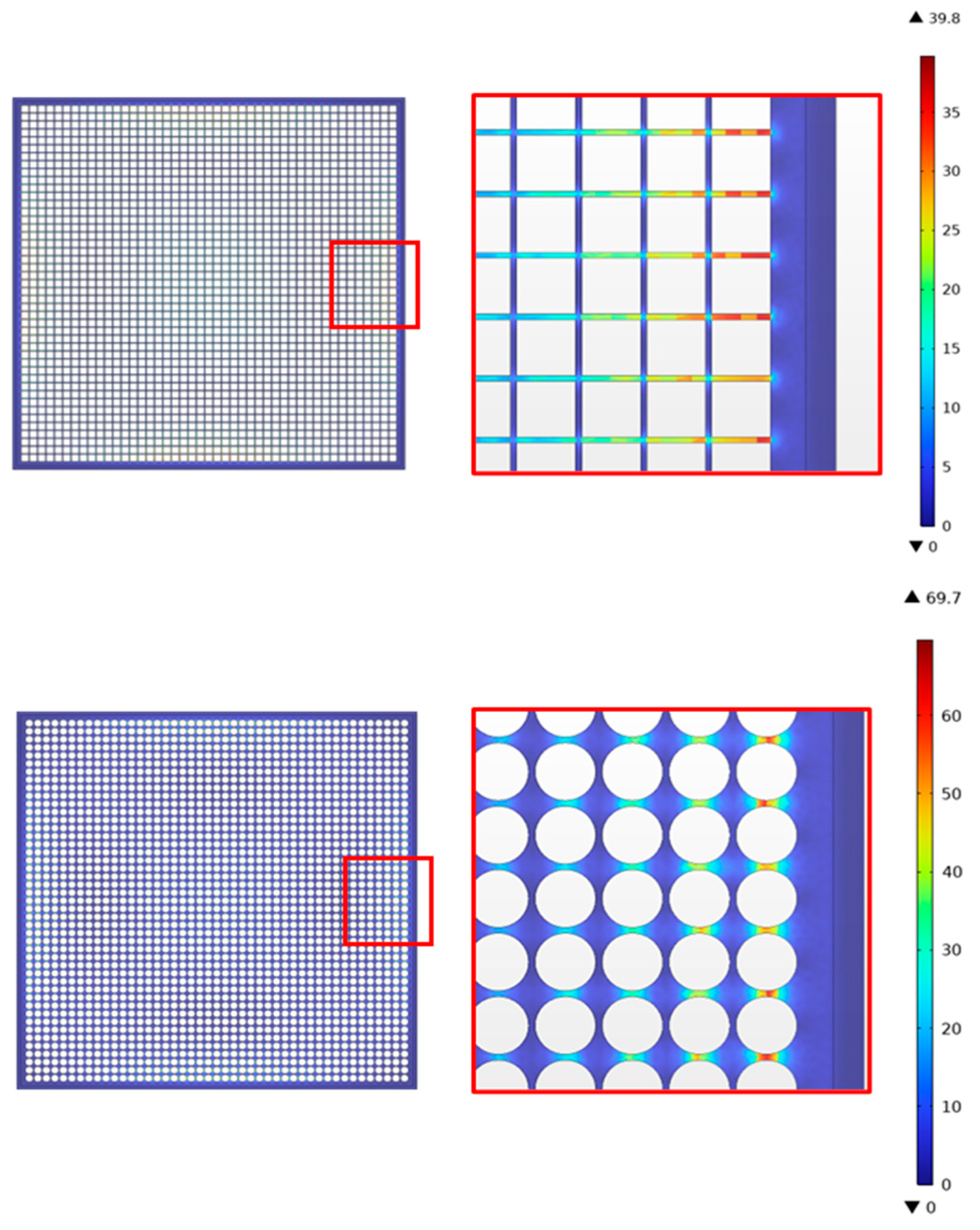
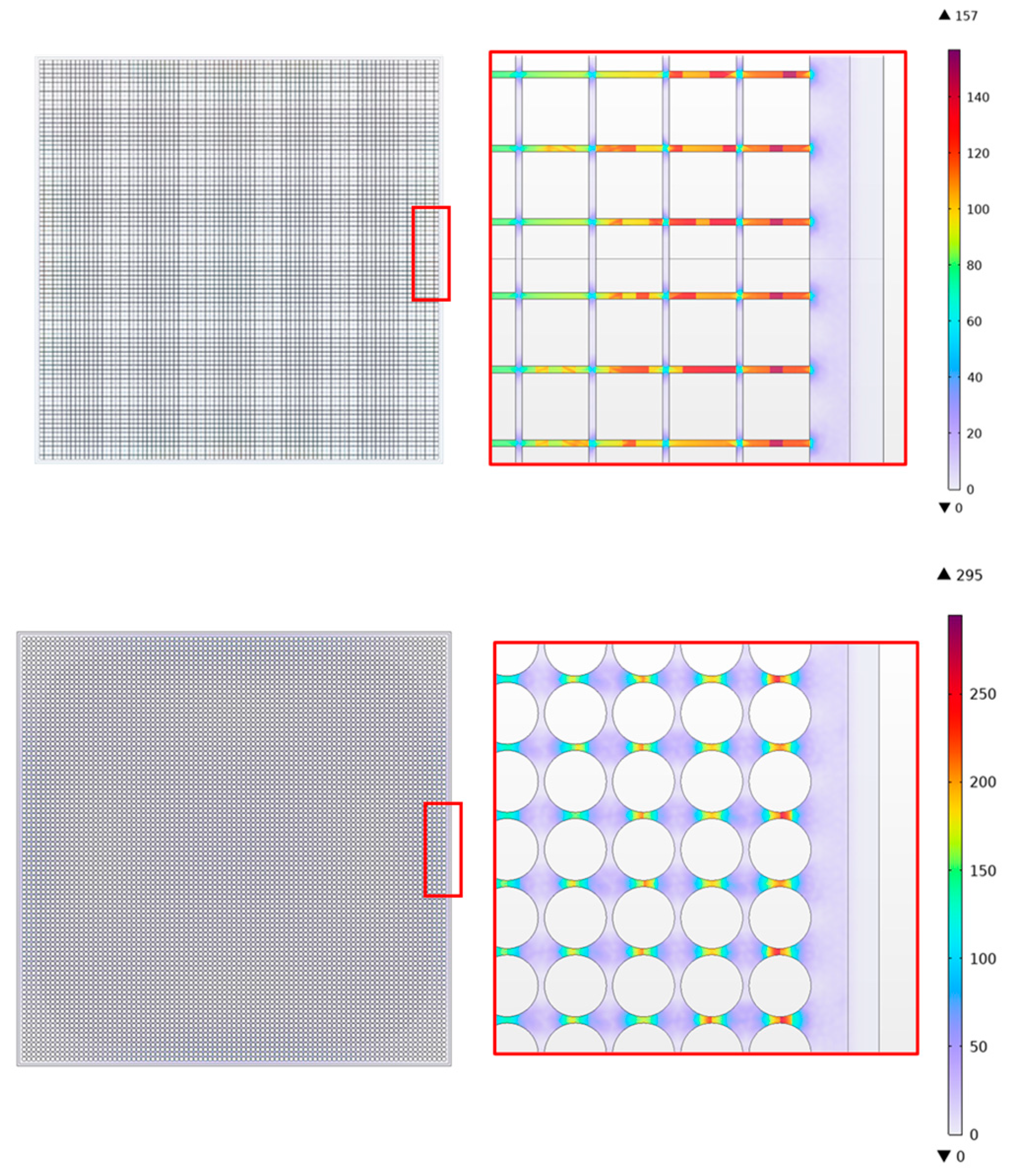

| Mode | 50 mm Size (Square Pattern) | 50 mm Size (Round Pattern) | 100 mm Size (Square Pattern) | 100 mm Size (Round Pattern) |
|---|---|---|---|---|
| 1 | 245.3 | 250.7 | 63.1 | 63.8 |
| 2 | 501.7 | 511.4 | 129.1 | 130.2 |
| 3 | 501.7 | 511.8 | 186.9 | 130.2 |
| 4 | 726.5 | 751.7 | 233.3 | 191.0 |
| 5 | 906.5 | 918.7 | 234.3 | 233.9 |
| 50 mm Size (Square Pattern) | 50 mm Size (Round Pattern) | 100 mm Size (Square Pattern) | 100 mm Size (Round Pattern) | |
|---|---|---|---|---|
| Maximum Stress (MPa) | 40 | 70 | 157 | 295 |
| MOS | 4.52 | 2.15 | 0.4 | −0.25 |
| Mode | t = 0.1 mm | t = 0.2 mm | t = 0.3 mm | t = 0.35 mm |
|---|---|---|---|---|
| 1 | 63.1 | 119.1 | 174.6 | 202.3 |
| 2 | 129.1 | 245.3 | 360.5 | 418.1 |
| 3 | 186.9 | 245.3 | 360.6 | 418.1 |
| 4 | 233.3 | 341.1 | 492.9 | 568.9 |
| 5 | 234.3 | 451.4 | 668.1 | 776.2 |
| t = 0.1 mm | t = 0.2 mm | t = 0.3 mm | t = 0.35 mm | |
|---|---|---|---|---|
| Maximum Stress (MPa) | 157 | 86.8 | 57.7 | 50.6 |
| MOS | 0.4 | 1.54 | 2.83 | 3.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scaccabarozzi, D.; Ahmed, A.M.R.M.; Appiani, A.; Saggin, B.; Porto, C.; Esposito, F. EMM Project—LD GRIDS: Design of a Charged Dust Analyser for Moon Exploration. Designs 2025, 9, 70. https://doi.org/10.3390/designs9030070
Scaccabarozzi D, Ahmed AMRM, Appiani A, Saggin B, Porto C, Esposito F. EMM Project—LD GRIDS: Design of a Charged Dust Analyser for Moon Exploration. Designs. 2025; 9(3):70. https://doi.org/10.3390/designs9030070
Chicago/Turabian StyleScaccabarozzi, Diego, Abdelrahman Mohamed Ragab M. Ahmed, Andrea Appiani, Bortolino Saggin, Carmen Porto, and Francesca Esposito. 2025. "EMM Project—LD GRIDS: Design of a Charged Dust Analyser for Moon Exploration" Designs 9, no. 3: 70. https://doi.org/10.3390/designs9030070
APA StyleScaccabarozzi, D., Ahmed, A. M. R. M., Appiani, A., Saggin, B., Porto, C., & Esposito, F. (2025). EMM Project—LD GRIDS: Design of a Charged Dust Analyser for Moon Exploration. Designs, 9(3), 70. https://doi.org/10.3390/designs9030070







