Experimental Study of Wear Resistance Improvement of Modular Disk Milling Cutter by Preliminary Pre-Processing Method

Abstract

The problem of increasing the tool durability (service life) when machining hard-to-machine materials is one of the major practical problems of modern mechanical engineering. This paper aims to improve the wear resistance of modular disk mills using the pre-processing method. Second-order rotatable planning was applied for the experimental study of the pre-processing of modular disk mills. Experimental research on the pre-processing of modular disk mills was carried out on a vertical milling machine XH950A when milling a workpiece made of steel 45. It was revealed that the increase in pre-processing modes up to specific values (f = 60 mm/min; $v_c$ = 17 m/min; t = 6 min) on the tool durability period has a positive effect. At the same time, the tool durability period was increased up to T = 155 min. Tests of the machined modular disk mills were carried out in the conditions of the laboratory base to determine the durability period. After pre-processing at different modes, each modular disk mill was used to machine the workpiece until wear signs appeared on the cutting edge. At the same time, the time was recorded to determine the durability period. It was found that the optimum mode of tool preliminary pre-processing provides the best deformation and thermal conditions for hardening the tool cutting part. As a result of modeling with the ANSYS 2024 R1 program, it was found that a hardened layer is indeed formed on the cutting part of the modular disk mill after pre-processing. The results obtained show the possibility of using the preliminary pre-processing method to improve the wear resistance of other metal-cutting tools.

1. Introduction

The efficiency of mechanical engineering production is determined by many factors, among which metal-cutting tools occupy an essential place. Most tool failures (up to 75%) are due to cutting-edge wear [1,2]. Global integration of domestic and foreign manufacturers has led to an increase in the application of foreign technology in the domestic industry. Following this, new materials differing in chemical composition and mechanical properties are increasingly used in production facilities. Mechanical processing of such materials also negatively affects the consumption of metal-cutting tools. Due to the absence of appropriate recommendations in the available technical reference sources, errors made when setting cutting modes and selecting the cutting part material of the tool resulted in premature cutting-edge wear or breakage [3].

The situation is further aggravated by the fact that for countries (which include Kazakhstan) that do not have their tool production facilities, metal-cutting tools have to be purchased at a high (inflated) cost from foreign manufacturers. All this leads to an increase in the price of mechanical operations and ultimately to a rise in the cost of manufactured products. In this regard, the problem of increasing the durability (service life) of cutting tools [4,5] when machining difficult-to-machine materials is one of the essential practical problems of modern mechanical engineering. Many domestic and foreign scientists solve this problem by conducting scientific research aimed at improving the cutting tool’s durability.

Investigations [6] have shown that carbide cutting tool failure adversely affects tool durability, machined surface quality and surface dimensional accuracy and consequently the economics of cutting operations. It has been observed that milling parameters affect the durability of carbide tools such as cutting velocity, feed rate, cutting depth and coolant application. In [7], deep cryogenic treatment of a carbide cutting insert (KC5010) followed by double tempering was used to increase the cutting tool’s durability. It is revealed that cutting velocity is the most critical parameter that directly influences machining characteristics. The increase in cutting velocity and feed rate creates more tangential pressure, which reduces the chip contact length, and the decrease in contact length leads to a reduction in surface roughness and lateral surface wear rate, respectively. In the study [8], experimental testing and finite element modeling were conducted to investigate chip formation and its effect on cutting force, tool temperature, tool stress, and cutting edge wear during high-speed and ultra-high-speed ($v_c$ = 200∼2000 m/min) milling. In this study, it was found that tool temperature had a greater influence on tool stress than cutting force at relatively high cutting velocity. In [9], methods of increasing the cutting tools reliability for heavy machine tools are investigated. It is revealed that a significant share of heavy machine tool downtime is related to the maintenance of the technological system associated with the wear and failure of prefabricated cutting tools. Mathematical models for determining the readiness function of assembly cutting tools are obtained.

Laboratory and operational tests have established that treating the tool with a pulsed magnetic field can increase the stability of its cutting properties. In [10], a model for predicting cutting tool wear during the turning of Nimonic© C-263 superalloy at high cutting modes was proposed. A comparative analysis of different inserts with different positioning angles is performed, and the influence of various cooling methods on the quality of the machined surface is analyzed. It is found that the characteristic wear during turning of Nimonic© C-263 with high feed is adhesion wear together with the rising edge effect. In [11], cutting inserts fabricated using additive technology by material extrusion were investigated. The inserts were subjected to various experimental tests using Taguchi’s orthogonal L9 scheme. The experiments were organized into four preliminary sets of L9 to determine the sensitivity of cutting-edge wear to the process variables (input factors) under study. ANOVA analysis of variance was performed on the effect of machining parameters on tool wear and cycle time. It was found that the insert can be operated at cutting velocity ($v_c$) from 40 to 260 m/min, feeds (f) from 0.05 to 0.25 mm/rev, and depth of pass (a_p) from 0.1 to 2.4 mm. It is also found that tool wear is not very sensitive to changes in cutting velocity ($v_c$) up to values of $v_c$ = 210 m/min.

Known methods of increasing the cutting tool durability are not acceptable for the conditions of domestic mechanical engineering industries of the Republic of Kazakhstan, due to inexpediency from an economic point of view. It is necessary to develop such a method of increasing the wear resistance of cutting tools, which has universality and easy accessibility and, at the same time, provides high resistance and wear resistance. Such a method is the pre-processing method of cutting tools. It is known that preliminary pre-processing as a method of increasing tool durability and reliability is economically justified for expensive tools, the work of which is associated with significant material–technical costs [12,13,14].

In the works [15,16,17,18] on the preliminary pre-processing to substantiate the physical essence of optimal modes, studies on the independent influence of temperature and speed factors on the formation process of wear-resistant contact structures were given. It was noted that the temperature and speed factors are inseparable in the actual cutting process and determined by the machining modes. Thus, it is established that the experimental character of the cutting velocity effect on hardening and wear resistance of the tool’s secondary contact structure is determined by the temperature factor, and the speed factor determines the degree of hardening and the numerical value of wear resistance. In addition, it is shown that the autonomous velocity effect is one of many, and not consistently dominant, factors responsible for the degree of hardening. Indeed, the degree of hardening is determined by the degree of plastic deformation, the numerical value of which depends on specific contact loads, adhesive interaction forces in contact, process duration, and sliding speed. Therefore, it can be assumed that at many cutting modes, the contact layers of the tool reach the state of ultimate hardening, and the degree of completion of this process will mainly depend on time.

In the works [19,20], research was carried out on increasing the wear resistance of cutting tools by using preliminary pre-processing. In [19], an experimental study of increasing the durability of a cup cutter by the preliminary pre-processing method was carried out. It was found experimentally that the durability period can be increased by 25–30 min using optimal modes of preliminary pre-processing. By the method of experiment planning, the dependence for determining the period of durability of cup cutters is deduced. The influence of the hardness of the machined material on the durability period of a cup cutter is confirmed, and it is established that with increasing hardness, the durability period decreases. It is revealed that with the increase in machined material hardness, the durability period of the worked cup cutter decreases. The results of computer modeling with the ANSYS program of the preliminary pre-processing confirmed the formation of a secondary contact structure due to intensive plastic deformation of the contact surfaces of the cup cutter.

In [20], a study on the relationship between the machined material hardness and the preliminary pre-processing rate was carried out. The preliminary pre-processing of turning tools equipped with T5C10 (titanium-tungsten group, carbides: WC = 79%; TiC = 15%) inserts were carried out on two heat-hardened materials of steel 20Cr with hardnesses HRC 21…23 and HRC 19…20.

The research results have shown that the efficiency of turning tool preliminary pre-processing can be increased if steels with higher hardness are used as a pre-processing material. Higher contact loads in the cutting process provide more significant strain hardening and shorten the pre-processing time. It has been found that the preliminary pre-processing increases the wear resistance of tool working surfaces, the operational reliability, and the heat resistance of contact structures. It is established that varying the hardness of the machined material during tool pre-processing can increase the hardening effect and significantly reduce material consumption. At present, scientific research is being carried out on the use of the pre-processing method as a way to improve the wear resistance of various metal-cutting tools. This paper aims to improve the wear resistance of modular disk mills using the pre-processing method.

2. Materials and Methods

The methodology of modular disk mill pre-treatment is based on experimental research. Experimental research on the pre-processing of the modular disk mill was carried out on the vertical milling machine KH950A (Foshan Nanhai Jingcheng Machinery Co., Ltd., Foshan, China) in the conditions of the laboratory base of the Department of “Technological Machines and Equipment” of S. Seifullin Kazakh Agrotechnical Research University. Figure 1 shows the equipment, materials, and tools used.

A metallographic study was carried out according to the method to compare the microstructure of modular disc mill cutting part (from P6M5 steel) before and after pre-processing. Figure 2 shows the equipment used in the metallographic study.

Four pre-processed (at different cutting modes) modular disc mills were selected for sample preparation. Figure 3 shows the cut samples of the modular disc mills for grind preparation.

The material structure is analyzed through metallographic slides (micro slides). The production process includes cutting samples and facing, grinding, polishing, and subsequent etching. Micro slides were subjected to etching with chemical reagents for microanalysis. The reagents used were solutions of acids, alkalis, and salts, which cause selective dissolution of phases and their boundaries.

Rotatable planning of the second order was applied to study the pre-processing of a disk modular mill. It is required to establish the dependence of modular disk mill durability T on cutting modes when turning steel 45. The following cutting modes were considered influencing factors: cutting velocity $v_c$, feed rate f and pre-processing time t_pp. It was decided to approximate the dependence T = f ($v_c$, f, t_pp) by a second-degree polynomial. The experiment was carried out using the central composite rotatable planning program for the second order.

Modeling of the Pre-Processing

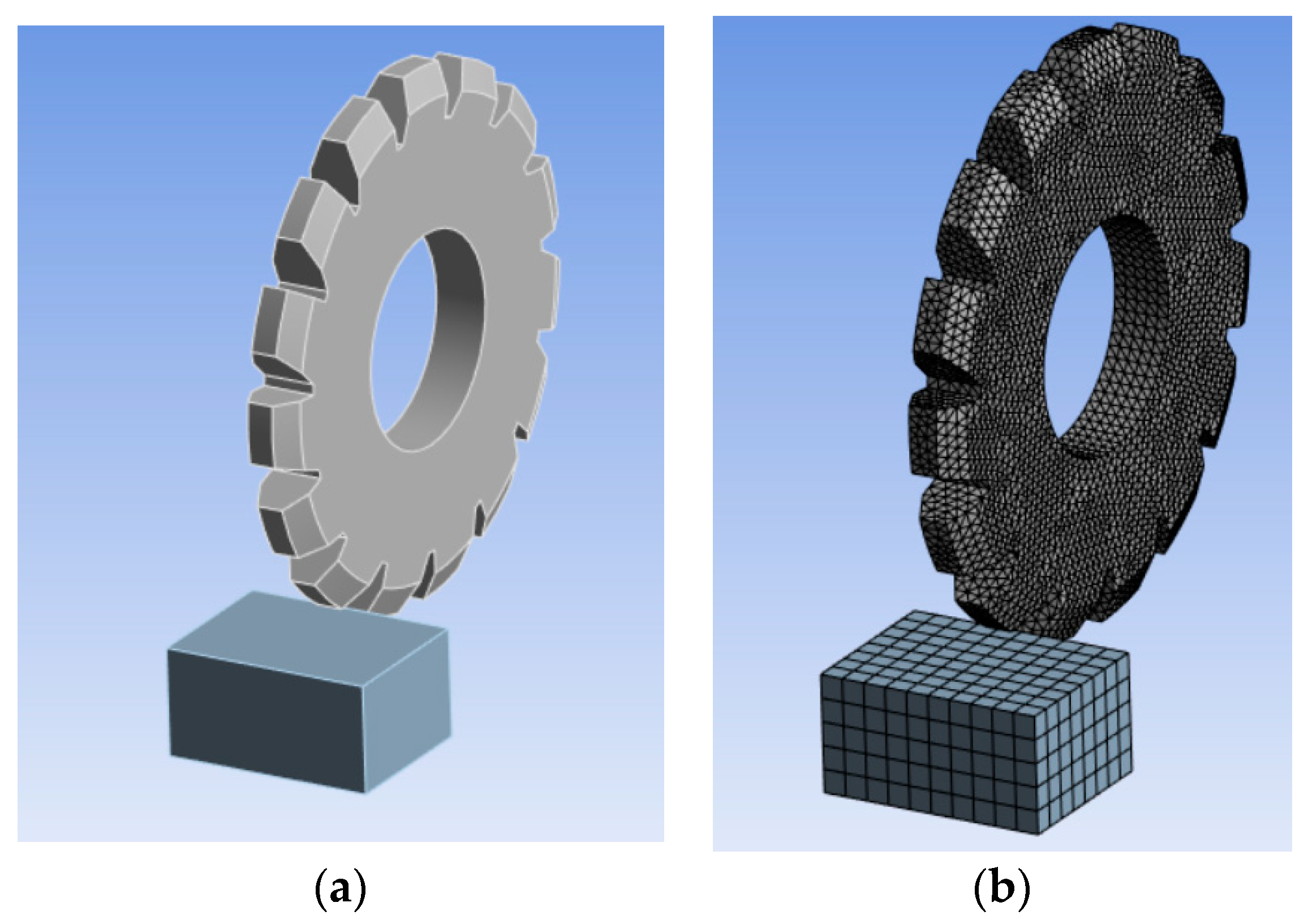
The modeling of the pre-processing method was carried out through the ANSYS computer program to verify the formation of strain hardening in the tool cutting-edge. The spatial gear milling dynamics model includes 3D models of the tool and the workpiece. A disk modular mill made of high-speed steel P6M5(HS6-5-2) with 15 teeth was selected as a tool. The diameter of the tool is 50 mm. In this case, the workpiece is a plate made of steel 45.

Figure 4 shows the three-dimensional model of workpiece machining and mesh creation.

The ANSYS program represents tool and workpiece materials as linear-elastic materials. When modeling the chip removal process, Johnson–Cook models [21] specify the mechanical properties of the workpiece material.

Table 1. Physical and mechanical properties of machined and tool material.

Material	Density, kg/m3	Young’s Modulus, Pa	Poisson’s Ratio	Melting Temperature (°C)	Room Temperature (°C)
Steel 45	7850	2 × 1011	0.29	1460	25
Steel P6M5	8850	2.5 × 1011	0.27	-	25

and

Table 2. Material parameters of workpiece steel 45 [22].

A, Pa	B, Pa	n	C	m	${\dot{\mathit{\epsilon }}}_0$	Tm, °C	T0, °C
553 × 106	600 × 106	0.234	0.0134	1.078	1	1460	25

present the linear–elastic properties of tool and workpiece material.

The properties of the Johnson–Cook constitutive model are most often represented by an expression for the equivalent voltage [22]:

$$\overline{\sigma }=\left[A+B{\left({\overline{\epsilon }}^{pl}\right)}^n\right]\left[1+Cln\left({\displaystyle \frac{{\dot{\overline{\epsilon }}}^{pl}}{{\dot{\epsilon }}_0}}\right)\right]\left[1-{\left({\displaystyle \frac{T-T_r}{T_m-T_r}}\right)}^m\right]$$

(1)

where $\overline{\sigma }$—dynamic yield strength; A—static yield strength; B—strain hardening modulus; C—strain rate coefficient; n—degree exponent in the law of strain hardening; m—degree exponent in the law of thermal unstrengthening; T—absolute instantaneous temperature of the model; T_m—melting point of the material; T_r—room temperature; ${\overline{\epsilon }}^{pl}$—plastic strain rate; ${\dot{\overline{\epsilon }}}^{pl}$—instantaneous plastic strain rate; ${\dot{\mathit{\epsilon }}}_0$—threshold value of plastic strain rate (1 s⁻¹).

The modeling of chip formation in the milling process is based on the finite element mesh fracture theory. The Johnson–Cook dynamic fracture model used in this work assumes that material removal (finite element mesh removal) occurs when the value of the parameter D_ω exceeds 1. The fracture parameter D_ω is defined as follows [21]:

$$D_{\omega }=\sum \left({\displaystyle \frac{∆{\overline{\epsilon }}^{pl}}{{\overline{\epsilon }}_f}}\right)$$

(2)

where $∆{\overline{\epsilon }}^{pl}$—increment of effective plastic strain, ${\overline{\epsilon }}_f$—strain at fracture. The summation is performed for all increments.

The Johnson–Cook dynamic fracture model assumes that the equivalent strain at mesh failure is of the form [21]:

$${\overline{\epsilon }}_f=\left[D_1+D_2\exp \left(D_3{\displaystyle \frac{p}{q}}\right)\right]\left[1+D_4\mathrm{l}\mathrm{n}\left({\displaystyle \frac{{\dot{\overline{\epsilon }}}^{pl}}{{\dot{\epsilon }}_0}}\right)\right]\left[1+D_5\left({\displaystyle \frac{T-T_r}{T_m-T_r}}\right)\right]$$

(3)

where D₁…D₅—Johnson–Cook fracture parameters; p—pressure in the considered finite element; q—effective stress. The values of Johnson–Cook fracture parameters for steel 45 are presented in

Table 3. Johnson-Cook fracture parameters of steel 45 [22].

D1	D2	D3	D4	D5
0.06	3.31	−1.96	0.002	0.58

.

3. Results and Discussion

Planning of the experiment was conducted as follows. Rotatable planning of the second order was applied to study the pre-processing of a disk modular mill. It is required to establish the dependence of modular disk mill durability T on cutting modes when turning steel 45. The following cutting modes were considered influencing factors: cutting velocity $v_c$, feed rate f and pre-processing time t_pp. It was decided to approximate the dependence T = f ($v_c$, f, t_pp) by a second-degree polynomial. The experiment was carried out using the central composite rotatable planning program for the second order [23,24,25]. The levels and intervals of factor variation accepted in the study are shown in

Table 4. Levels and intervals of factor variation.

Factors	Code Designation	Intervals of Variation	Natural Factor Levels, Corresponding to the Coded
			+1.682	+1	0	−1	−1.682
$v_c$—cutting velocity, m/min	x1	4	25	21	17	13	9
f—tool feed, mm/min	x2	12.5	85	72.5	60	47.5	35
tpp—pre-processing time, min	x3	2	10	8	6	4	2

.

Table 5. Planning matrix and experiment results.

Experiment Number	${\mathit{x}}_0$	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_1{\mathit{x}}_2$	${\mathit{x}}_1{\mathit{x}}_3$	${\mathit{x}}_2{\mathit{x}}_3$	${\mathit{x}}_1{\mathit{x}}_2{\mathit{x}}_3$	${\mathit{x}}_1^2$	${\mathit{x}}_2^2$	${\mathit{x}}_3^2$	y
1	1	1	1	1	1	1	1	−1	1	1	1	133
2	1	−1	1	1	−1	−1	1	1	1	1	1	118
3	1	1	−1	1	−1	1	−1	1	1	1	1	138
4	1	−1	−1	1	1	−1	−1	−1	1	1	1	118
5	1	1	1	−1	1	−1	−1	1	1	1	1	123
6	1	−1	1	−1	−1	1	−1	−1	1	1	1	132
7	1	1	−1	−1	−1	−1	1	−1	1	1	1	118
8	1	−1	−1	−1	1	1	1	1	1	1	1	128
9	1	0	0	1.682	0	0	0	0	2.829	0	0	129
10	1	0	0	−1.682	0	0	0	0	2.829	0	0	121
11	1	0	1.682	0	0	0	0	0	0	2.829	0	121
12	1	0	−1.682	0	0	0	0	0	0	2.829	0	128
13	1	1.682	0	0	0	0	0	0	0	0	2.829	122
14	1	−1.682	0	0	0	0	0	0	0	0	2.829	123
15	1	0	0	0	0	0	0	0	0	0	0	152
16	1	0	0	0	0	0	0	0	0	0	0	151
17	1	0	0	0	0	0	0	0	0	0	0	153
18	1	0	0	0	0	0	0	0	0	0	0	152
19	1	0	0	0	0	0	0	0	0	0	0	150
20	1	0	0	0	0	0	0	0	0	0	0	151
sum	20	0	0	0	0	0	0	0	13.658	13.658	13.658	2661

shows the planning matrix and the experiment results. The second-order central composite rotatable plan for the three factors consists of a full-factor experiment plan of type 2³ (Table 2, experiments 1–8), six experiments at the “star points” (experiments 9–14), and six experiments in the center of the plan (experiments 15–20).

According to the experiment results performed by the adopted experimental plan, it is possible to estimate the coefficients of the regression equation of the following form

$$y=b_o+b_1{x}_1+b_2{x}_2+b_3{x}_3+b_{12}{x}_1{x}_2+b_{13}{x}_1{x}_3+b_{23}{x}_2{x}_3+b_{11}{x}_1^2+b_{22}{x}_2^2+b_{33}{x}_3^2.$$

(4)

The coefficients of the regression equation are determined using the formulas given in the paper:

$$b_0={\displaystyle \frac{A}{N}}\left[{2\lambda }^2\left(k+2\right){\sum }_{j=1}^N{y}_j-2\lambda c{\sum }_{i=1}^k{\sum }_{j=1}^N{x}_{ij}^2{y}_j\right];$$

(5)

$$b_i={\displaystyle \frac{c}{N}}{\sum }_{j=1}^N{x}_{ij}{y}_j;$$

(6)

$$b_{ii}={\displaystyle \frac{c^2}{N\lambda }}{\sum }_{j=1}^N{x}_{ij}{x}_{ij}{y}_j;$$

(7)

$$b_{ii}={\displaystyle \frac{A}{N}}\left\{c^2\left[\left(k+2\right)\lambda -k\right]{\sum }_{j=1}^N{x}_{ij}^2{y}_j+c^2(1-\lambda ){\sum }_{i=1}^k{\sum }_{j=1}^N{x}_{ij}^2{y}_j-2\lambda c{\sum }_{j=1}^N{y}_j\right\}.$$

(8)

where A—a square matrix, N—number of experiments, λ—a constant not exceeding unity, k—amount of factors, j—number of experiments, i—number of factor, x—input parameter, y—output parameter, c—matrix element.

The coefficients of Equation (5) were determined by Formulas (5)–(8). At k = 3, Formulas (5)–(8) for calculating the coefficients of the equation take the form

$$\begin{gathered} b_o=0.16666{\sum }_{j=1}^{20}{y}_j-0.05694{\sum }_{i=1}^3{\sum }_{j=1}^{20}{x}_{ij}^2{y}_j; \\ {b}_i=0.07322{\sum }_{j=1}^{20}{x}_{ij}{y}_j; b_{il}=0.125{\sum }_{j=1}^{20}{x}_{ij}{x}_{lj}{y}_j; \\ {b}_{ii}=0.06254{\sum }_{j=1}^{20}{x}_{ij}^2{y}_j+0.00695{\sum }_{i=1}^3{\sum }_{j=1}^{20}{x}_{ij}^2{y}_j-0.05694{\sum }_{j=1}^{20}{y}_j. \end{gathered}$$

According to Table 5, the sums included in the formulas for calculating the coefficients of the equation:

$$\begin{gathered} {\sum }_{j=1}^{20}{y}_j=2661; {\sum }_{j=1}^{20}{x}_{1j}{y}_j=14.3; {\sum }_{j=1}^{20}{x}_{2j}{y}_j=-7.8; \\ {\sum }_{j=1}^{20}{x}_{3j}{y}_j=19.5; \\ {\sum }_{j=1}^{20}{x}_{1j}{x}_{2j}{y}_j=-4; {\sum }_{j=1}^{20}{x_{1j}{x}_{3j}y}_j=54; \\ {\sum }_{j=1}^{20}{x}_{2j}{x}_{3j}{y}_j=-14; {\sum }_{j=1}^{20}{x}_{1j}^2{y}_j=1747.25; \\ {\sum }_{j=1}^{20}{x}_{2j}^2{y}_j=1712.42; {\sum }_{j=1}^{20}{x}_{3j}^2{y}_j=1701.11; {\sum }_{i=1}^3{\sum }_{j=1}^{20}{x}_{ij}^2{y}_j=5128.8; \end{gathered}$$

Using the above formulas, we find the coefficients of the regression Equations (5)–(8):

$$\begin{gathered} b_o=150.5; b_1=1.05; b_2=-0.56; b_3=1.43; b_{12}=0.5; \\ {b}_{13}=6.75; b_{23}=-1.75; \\ {b}_{11}=-8.6; b_{22}=-8.78; b_{33}=-9.49. \end{gathered}$$

The variance $s_y^2$ of reproducibility is determined by the experiment results in the center of the plan. An auxiliary table (

Table 6. Auxiliary table for calculation of $s_y^2.$

Experiment Number	${\mathit{y}}_{\mathit{u}}$	$\overline{\mathit{y}}$	${\mathit{y}}_{\mathit{u}}-\overline{\mathit{y}}$	${\left({\mathit{y}}_{\mathit{u}}-\overline{\mathit{y}}\right)}^2$	${\mathit{s}}_{\mathit{y}}^2$
15	152	$$\begin{gathered} {\displaystyle \frac{\sum _{u=1}^{n_0}{y}_u}{n_0}}={\displaystyle \frac{909}{6}} \\ =151.5 \end{gathered}$$	0.5	0.25	$$\begin{gathered} {\displaystyle \frac{\sum _{u=1}^{n_0}{\left(y_u-\overline{y}\right)}^2}{n_0-1}} \\ ={\displaystyle \frac{5.5}{6-1}}=1.1 \end{gathered}$$
16	151		−0.5	0.25
17	153		1.5	2.25
18	152		0.5	0.25
19	150		−1.5	2.25
20	151		−0.5	0.25
	${\displaystyle \sum _{u=1}^{n_0}}{y}_u=909$			${\displaystyle \sum _{u=1}^{n_0}}{\left(y_u-\overline{y}\right)}^2=5.5$

) was made to calculate $s_y^2$.

The dispersions characterizing errors in determining the coefficients of the regression equation were calculated using Formulas (9)–(12).

$$s^2\left\{b_0\right\}={\displaystyle \frac{2A{\lambda }^2\left(k+2\right)}{N}}{s}_y^2$$

(9)

$$s^2\left\{b_i\right\}={\displaystyle \frac{c}{N}}{s}_y^2;$$

(10)

$$s^2\left\{b_{il}\right\}={\displaystyle \frac{c^2}{\lambda N}}{s}_y^2;$$

(11)

$$s^2\left\{b_{ii}\right\}={\displaystyle \frac{A{c}^2\left[\left(k+2\right)\lambda -\left(k-1\right)\right]}{N}}{s}_y^2.$$

(12)

At k = 3, these formulas will take the form

$$s^2\left\{b_0\right\}=0.16666s_y^2; s^2\left\{b_i\right\}=0.07322s_y^2; s^2\left\{b_{il}\right\}=0.125s_y^2; s^2\left\{b_{ii}\right\}=0.0695s_y^2.$$

Dispersions of the coefficients of the regression equation

$$s^2\left\{b_0\right\}=0.183; s^2\left\{b_i\right\}=0.08; s^2\left\{b_{il}\right\}=0.137; s^2\left\{b_{ii}\right\}=0.07.$$

Confidence intervals for the coefficients were determined:

$$\begin{gathered} \Delta b_0=\pm ts\left\{b_0\right\}=\pm 1.1; \Delta b_i=\pm ts\left\{b_i\right\}=\pm 0.729 \\ \Delta b_{il}=\pm ts\left\{b_{il}\right\}=\pm 0.952; \Delta b_{ii}=\pm ts\left\{b_{ii}\right\}=\pm 0.71 \end{gathered}$$

where t = 2.57 is the tabulated value of Student’s criterion at a 5% significance level and number of freedom degrees f = 5.

An auxiliary table (

Table 7. Auxiliary table for calculation of $s_{\mathrm{a}d}^2.$

Experiment Number	${\mathit{y}}_{\mathit{j}}$	$\overline{{\mathit{y}}_{\mathit{j}}}$	${\mathit{y}}_{\mathit{j}}-\overline{\mathit{y}}$	${\left({\mathit{y}}_{\mathit{j}}-\overline{{\mathit{y}}_{\mathit{j}}}\right)}^2$	${\mathit{s}}_{\mathbf{a}\mathit{d}}^2$
1	133	131.11	1.89	3.57	$$\begin{gathered} {\displaystyle \frac{\sum _{j=1}^N{\left(y_u-\overline{y_j}\right)}^2}{N-\left(k+1\right)}} \\ =4.01 \end{gathered}$$
2	118	115.51	2.49	6.2
3	138	134.61	3.39	11.49
4	118	119.01	−1.01	1.02
5	123	118.25	4.75	22.56
6	132	129.65	2.32	5.38
7	118	114.75	3.25	10.56
8	128	126.15	1.85	3.42
	${\displaystyle \sum _{u=1}^{n_0}}{y}_u=1040$	${\displaystyle \frac{\sum _{u=1}^{n_0}{y}_u}{n_0}}=123.63$		${\displaystyle \sum _{u=1}^{n_0}}{\left(y_u-\overline{y}\right)}^2=64.2$

) was made to calculate $s_{\mathrm{a}d}^2$.

Calculations show that the value of dispersion $s_{\mathrm{a}d}^2=0.016$. Verification of the obtained model showed that the model is adequate at a 5% significance level, as evidenced by the comparison of calculated and tabulated values of the F-criterion:

$$F_c<F_t$$

(13)

$$F_c={\displaystyle \frac{s_{ad}^2}{s_y^2}}$$

(14)

$$F_c={\displaystyle \frac{4.01}{1.1}}=3.65<F_t=5.41.$$

The coefficients b₂ and b₁₂ are smaller than the confidence intervals so that they can be recognized as statistically insignificant and excluded from the regression equation. After excluding insignificant coefficients, Equation (4) takes the following form

$$y=b_o+b_1{x}_1+b_3{x}_3+b_{13}{x}_1{x}_3+b_{23}{x}_2{x}_3+b_{11}{x}_1^2+b_{22}{x}_2^2+b_{33}{x}_3^2$$

(15)

Since among the insignificant were the coefficients at quadratic terms, the coefficients of Equation (13) were recalculated using the least squares method. A system of normal equations was made to recalculate the coefficients of Equation (15):

$$\left\{\begin{array}{c}20b_0{+b}_1{\displaystyle \sum _{j=1}^{20}}{x}_{1j}+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{3j}+b_{13}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}{x}_{3j}+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2+b_{22}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2+b_{33}{\displaystyle \sum _{j=1}^{20}}{x}_{3j}^2={\displaystyle \sum _{j=1}^{20}}{y}_j;\\ b_0{\displaystyle \sum _{j=1}^{20}}{x}_{1j}+b_1{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}+b_{13}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{2j}{x}_{3j}+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^3+b_{22}{\displaystyle \sum _{j=1}^{20}}{x_{1j}x}_{2j}^2+b_{33}{\displaystyle \sum _{j=1}^{20}}{x_{1j}x}_{3j}^2={\displaystyle \sum _{j=1}^{20}}{y}_j{x}_{1j};\\ b_0{\displaystyle \sum _{j=1}^{20}}{x}_{3j}+b_1{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{3j}^2+b_{13}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}^2+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}{x}_{3j}^2+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}+b_{22}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2{x}_{3j}+b_{33}{\displaystyle \sum _{j=1}^{20}}{x}_{3j}^3={\displaystyle \sum _{j=1}^{20}}{y}_j{x}_{3j};\\ b_0{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}+b_1{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}^2+b_{13}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}^2+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{2j}{x}_{3j}^2+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^3{x}_{3j}+b_{22}{\displaystyle \sum _{j=1}^{20}}{x_{1j}x}_{2j}^2{x}_{3j}+b_{33}{\displaystyle \sum _{j=1}^{20}}{x_{1j}x}_{3j}^3={\displaystyle \sum _{j=1}^{20}}{y}_j{x}_{1j}{x}_{3j};\\ b_0{\displaystyle \sum _{j=1}^{20}}{x}_{2j}{x}_{3j}+b_1{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{2j}{x}_{3j}+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{2j}{x}_{3j}^2+b_{13}{\displaystyle \sum _{j=1}^{20}}{x_{1j}{x}_{2j}x}_{3j}^2+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2{x}_{3j}^2+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{2j}{x}_{3j}+b_{22}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^3{x}_{3j}+b_{33}{\displaystyle \sum _{j=1}^{20}}{x_{2j}x}_{3j}^3={\displaystyle \sum _{j=1}^{20}}{y}_j{x}_{2j}{x}_{3j};\\ b_0{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2+b_1{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^3+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}+b_{13}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^3{x}_{3j}+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{2j}{x}_{3j}+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^4+b_{22}{\displaystyle \sum _{j=1}^{20}}{x_{1j}^{2}x}_{2j}^2+b_{33}{\displaystyle \sum _{j=1}^{20}}{x_{1j}^{2}x}_{3j}^2={\displaystyle \sum _{j=1}^{20}}{y}_j{x}_{1j}^2;\\ b_0{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2+b_1{\displaystyle \sum _{j=1}^{20}}{x_{1j}x}_{2j}^2+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2{x}_{3j}+b_{13}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x_{2j}^{2}x}_{3j}+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^3{x}_{3j}+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{2j}^2+b_{22}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^4+b_{33}{\displaystyle \sum _{j=1}^{20}}{x_{2j}^{2}x}_{3j}^2={\displaystyle \sum _{j=1}^{20}}{y}_j{x}_{2j}^2;\\ b_0{\displaystyle \sum _{j=1}^{20}}{x}_{3j}^2+b_1{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}^2+b_3{\displaystyle \sum _{j=1}^{20}}{x}_{3j}^3+b_{13}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}^3+b_{23}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}{x}_{3j}^3+b_{11}{\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}^2+b_{22}{\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2{x}_{3j}^2+b_{33}{\displaystyle \sum _{j=1}^{20}}{x}_{3j}^4={\displaystyle \sum _{j=1}^{20}}{y}_j{x}_{3j}^2;\end{array}\right.$$

The sums included in the system of normal equations were determined

$$\begin{gathered} {\displaystyle \sum _{j=1}^{20}}{x}_{1j}={\displaystyle \sum _{j=1}^{20}}{x}_{3j}={\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}={\displaystyle \sum _{j=1}^{20}}{x}_{2j}{x}_{3j}={\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}={\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{2j}{x}_{3j}={\displaystyle \sum _{j=1}^{20}}{x}_{1j}^3=\sum _{j=1}^{20}{x}_{1j}{x}_{2j}^2=0 \\ {\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}^2={\displaystyle \sum _{j=1}^{20}}{x}_{2j}{x}_{3j}^2=\sum _{j=1}^{20}{x}_{2j}^2{x}_{3j}=\sum _{j=1}^{20}{x}_{3j}^3=\sum _{j=1}^{20}{x}_{1j}{x}_{2j}{x}_{3j}^2=\sum _{j=1}^{20}{x}_{1j}^3{x}_{3j}=\sum _{j=1}^{20}{x}_{1j}{x}_{2j}^2{x}_{3j}=0; \\ {\displaystyle \sum _{j=1}^{20}}{x}_{1j}{x}_{3j}^3={\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{2j}{x}_{3j}=\sum _{j=1}^{20}{x}_{2j}^3{x}_{3j}=\sum _{j=1}^{20}{x}_{2j}{x}_{3j}^3=0; \\ {\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2={\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2=\sum _{j=1}^{20}{x}_{3j}^2=13.658; \sum _{j=1}^{20}{x}_{1j}^4=\sum _{j=1}^{20}{x}_{2j}^4=\sum _{j=1}^{20}{x}_{3j}^4=24.007; \\ {\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{3j}^2={\displaystyle \sum _{j=1}^{20}}{x}_{1j}^2{x}_{2j}^2={\displaystyle \sum _{j=1}^{20}}{x}_{2j}^2{x}_{3j}^2=8. \end{gathered}$$

The sums on the right-hand sides of the equations have been calculated earlier. After substituting the values of the sums, the system of normal equations takes the form

$$\left\{\begin{array}{c}20b_0{+0\times b}_1+0\times b_3+0\times b_{13}+0\times b_{23}+13.658\times b_{11}+13.658\times b_{22}+13.658\times b_{33}=2661;\\ 0\times b_0+13.658\times b_1+0\times b_3+0\times b_{13}+0\times b_{23}+0\times b_{11}+0\times b_{22}+0\times b_{33}=14.318;\\ 0\times b_0+0\times b_1+13.658\times b_3+0\times b_{13}+0\times b_{23}+0\times b_{11}+0\times b_{22}+0\times b_{33}=19.456;\\ 0\times b_0+0\times b_1+0\times b_3+8\times b_{13}+0\times b_{23}+0\times b_{11}+0\times b_{22}+0\times b_{33}=54;\\ 0\times b_0+0\times b_1+0\times b_3+0\times b_{13}+8\times b_{23}+0\times b_{11}+0\times b_{22}+0\times b_{33}=-14;\\ 13.658\times b_0+0\times b_1+0\times b_3+0\times b_{13}+0\times b_{23}+24.007\times b_{11}+8\times b_{22}+8\times b_{33}=1715.25;\\ 13.658\times b_0+0\times b_1+0\times b_3+0\times b_{13}+0\times b_{23}+8\times b_{11}+24.007\times b_{22}+8\times b_{33}=1712.42;\\ 13.658\times b_0+0\times b_1+0\times b_3+0\times b_{13}+0\times b_{23}+8\times b_{11}+8\times b_{22}+24.007\times b_{33}=1701.11.\end{array}\right.$$

Solving the system of normal equations, the coefficient’s values were determined as b₀ = 153.07, b₁ = 1.05, b₃ = 1.42, b₁₃ = 6.75, b₂₃ = −1.75, b₁₁ = −9.27, b₂₂ = −9.44, and b₃₃ = −10.15.

The following regression equation was obtained by using second-order rotatable planning:

$$\mathit{y}=\mathbf{153.07}+\mathbf{1.05}{\mathit{x}}_{\mathbf{1}}+\mathbf{1.42}{\mathit{x}}_{\mathbf{3}}+\mathbf{6.75}{\mathit{x}}_{\mathbf{1}}{\mathit{x}}_{\mathbf{3}}-\mathbf{1.75}{\mathit{x}}_{\mathbf{2}}{\mathit{x}}_{\mathbf{3}}-\mathbf{9.27}{\mathit{x}}_{\mathbf{1}}^{\mathbf{2}}-\mathbf{9.44}{\mathit{x}}_{\mathbf{2}}^{\mathbf{2}}-\mathbf{10.15}{\mathit{x}}_{\mathbf{3}}^{\mathbf{2}}$$

(16)

The values of y calculated by Equation (16) differ from the experimental ones by values not exceeding the experiment error.

The coded factor values are related to the natural ones by the following relationships:

$$x_1={\displaystyle \frac{v_c-V_{c0}}{{\epsilon }_1}}={\displaystyle \frac{V-17}{4}}; x_2={\displaystyle \frac{f-f_0}{{\epsilon }_2}}={\displaystyle \frac{f-60}{12.5}}; x_3={\displaystyle \frac{t_{pp}-t_{pp0}}{{\epsilon }_3}}={\displaystyle \frac{t_{pp}-6}{2}};$$

where $v_c$, $f_0$, $t_{pp0 }$—basic levels of factors in natural terms; ${\epsilon }_1$, ${\epsilon }_2$, ${\epsilon }_3$—intervals of variation of factors.

Passing from coded x₁, x₂, x₃ values of factors to natural values $v_c$, $f_0$, $t_{pp }$, the dependence of mill resistance on cutting modes was obtained:

$$\begin{array}{ll}T& =153.07+1.05 \left({\displaystyle \frac{v_c-17}{4}}\right)+1.42 \left({\displaystyle \frac{t_{pp}-6}{2}}\right)+6.75 \left({\displaystyle \frac{v_c-17}{4}}\right)\left({\displaystyle \frac{t_{pp}-6}{2}}\right)\\ & -1.75 \left({\displaystyle \frac{f-60}{12.5}}\right)\left({\displaystyle \frac{t_{pp}-6}{2}}\right)-9.27 {\left({\displaystyle \frac{v_c-17}{4}}\right)}^2-9.44{\left({\displaystyle \frac{f-60}{12.5}}\right)}^2-10.15 {\left({\displaystyle \frac{t_{pp}-6}{2}}\right)}^2.\end{array}$$

(17)

After the conversion

$$T=0.84v_c{t}_{pr}-0.58{v_c}^2+14.89v_c-0.07f{t}_{pp}-2.54{t_{pp}}^2+21.05t_{pp}-0.06f^2+7.59f-271.08.$$

(18)

Equation (18) is adequate, so it can be used as an interpolation formula to calculate the value of T.

3.1. Experimental Research

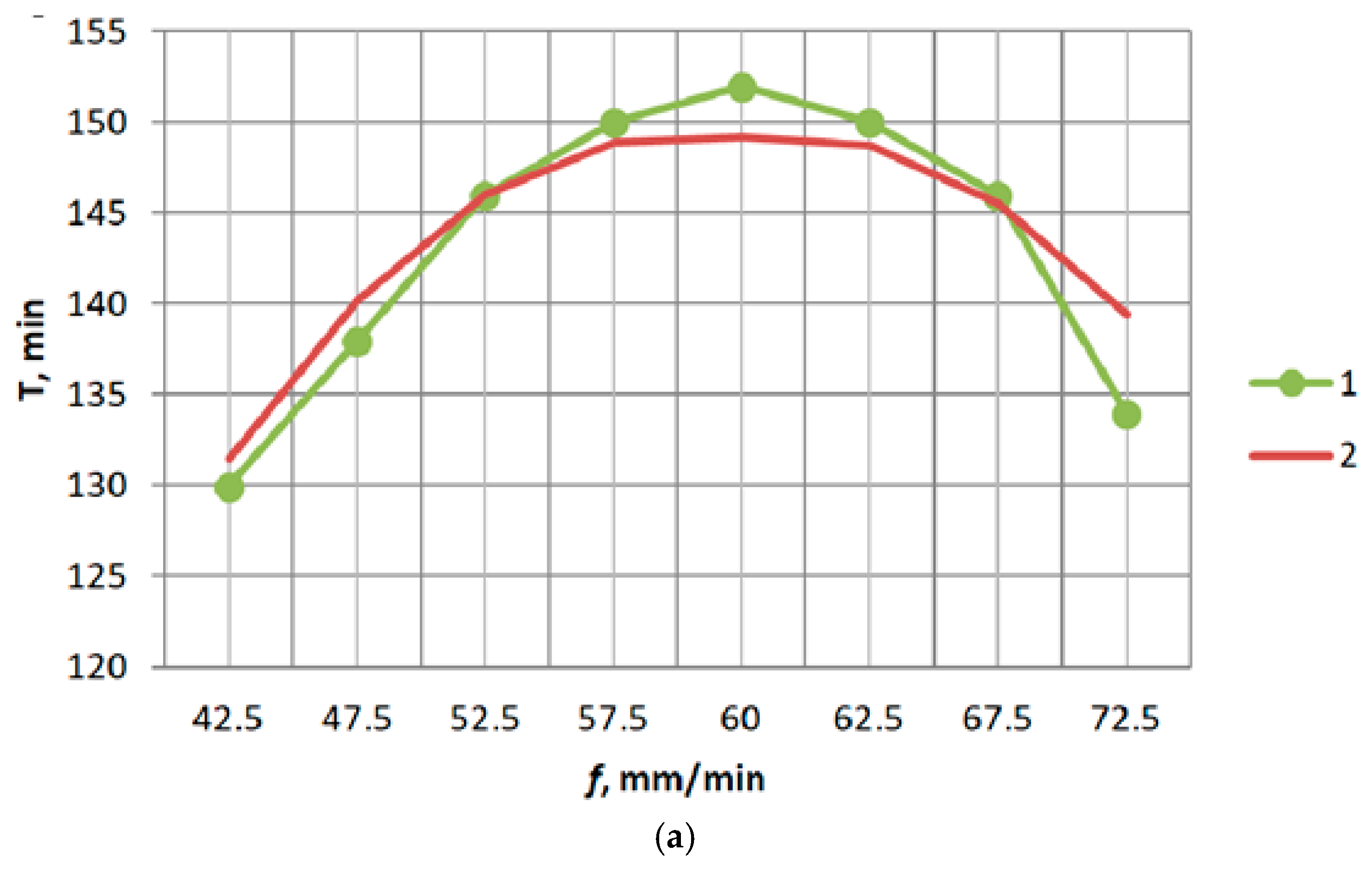
Figure 3 shows the pre-processing of modular disk mills. The modular disk mills were pre-processed on the following modes: f = 42.5–72.5 mm/min; $v_c$ = 13–21 m/min; t = 2–8 min. Tests of the pre-processed modular disk mills were carried out in the conditions of the laboratory base to determine the durability period. After pre-processing at different modes, each of the modular disk mills was used to process the workpiece until the wear signs of the cutting-edge appeared. At the same time, the time was recorded to determine the durability period. The test results to determine the durability period of the modular disk mills are shown in the graphs (Figure 5).

Figure 6 shows photographs of some worn modular disc mills.

The time was recorded to determine the durability period. The results of the test to determine the durability period of the modular disc mills are shown in the graphs (see Figure 7). The data analysis according to Figure 7 indicates that the dependence of tool durability period on the cutting mode of pre-processing, obtained from the regression model is in sufficient agreement with the experimental data. The graphs indicate the influence of the pre-processing modes on the durability period of modular disk mills, and increasing the pre-processing modes to specific values positively influences the tool durability period. Increasing the feed from f = 42.5 mm/min to f = 60 mm/min increases the tool durability period, and further feed increases negatively (Figure 7a). Increasing the cutting velocity from $v_c$ = 13 m/min to the value $v_c$ = 17 m/min positively affects the tool durability period, and at $v_c$ = 17 m/min reaches its maximum value T = 155 min (Figure 7b).

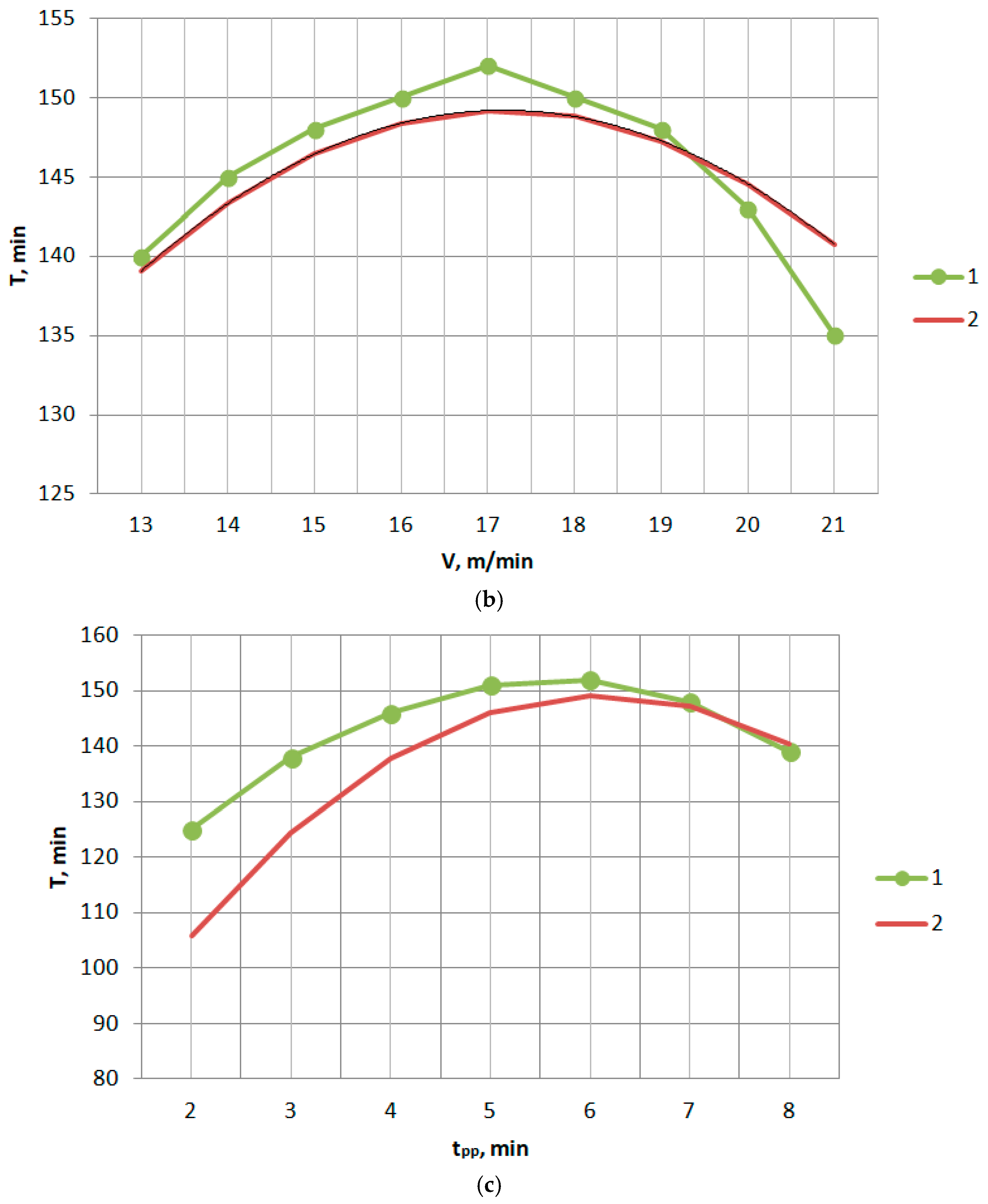
Increasing the pre-processing time also positively affects the increase in the tool durability period up to specific values (Figure 7c). When the pre-processing time increases from t = 2 to t = 6 min, the tool durability period increases from T = 125 min to T = 155 min (Figure 7c).

Based on the obtained results (see Figure 7), it is possible to assign the optimum modes of pre-processing of disc model mills (when machining steel 45)—f = 60 mm/min; $v_c$ = 17 m/min; t = 6 min.

It is scientifically interesting to increase the optimal values of pre-processing modes for modular disk milling cutters, in particular, the time (duration) t of the pre-processing operation in comparison with the results obtained in [26,27,28]. The optimum pre-processing time for cup cutters was found to be t = 3 min [26], and for worm cutters t = 5 min [27,28]. In the analysis, it can be observed that as the pre-processing time t increases, the values of other modes of pre-processing increase accordingly. This shows the wide technological possibility of pre-processing methods and a new direction for scientific research.

It should be noted that the optimal modes of tool preliminary pre-processing provide the best strain and heat hardening conditions, which can be further increased if preliminary machining is carried out on a hard material [26].

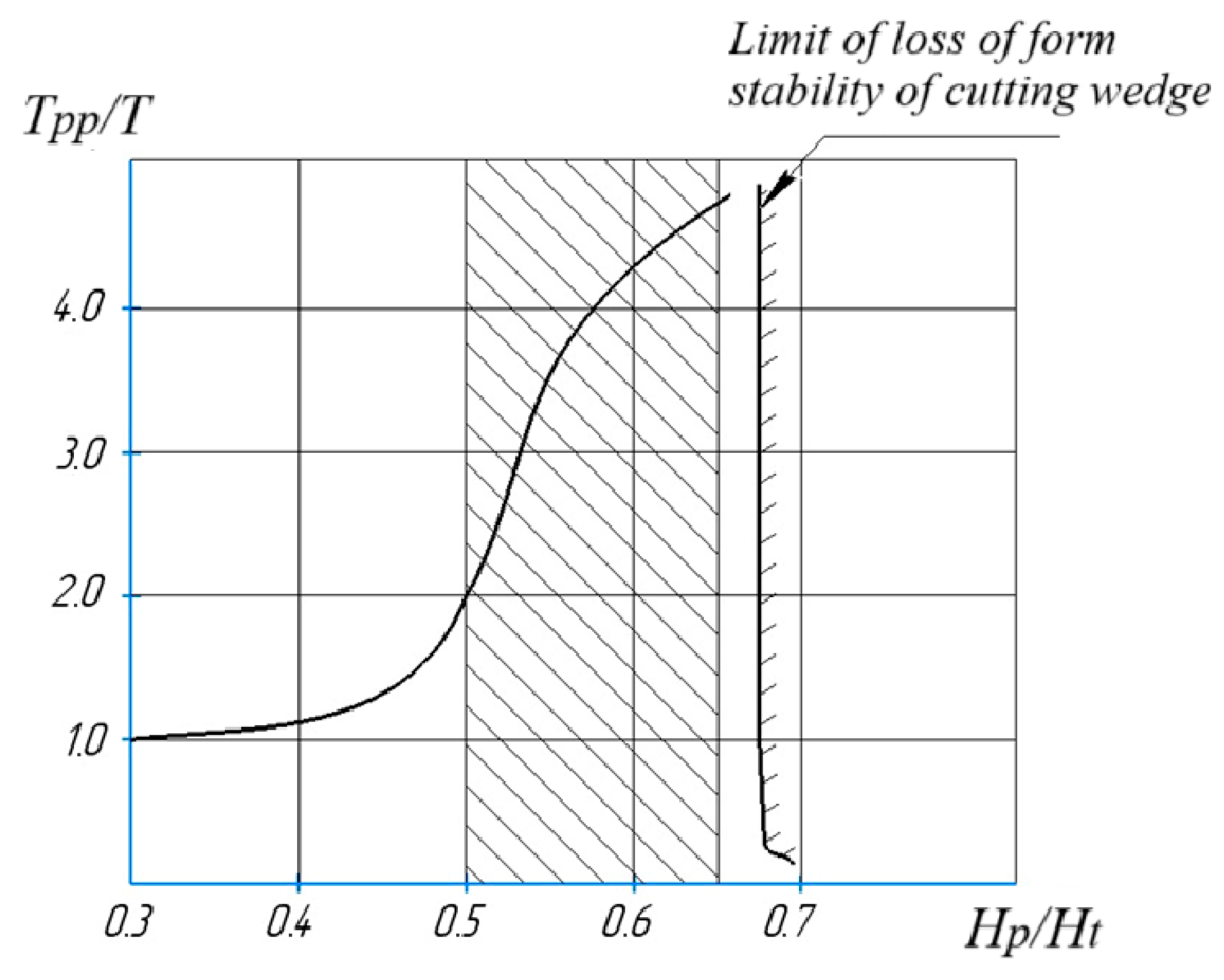
Figure 8 shows the influence of the hardness ratio of the machined and tool materials on the magnitude of the increase in the durability of preliminary pre-processing [29].

Dependence has a monotonically increasing character, showing that with increasing hardness of the machined material, the effect of hardening of the tool working surfaces increases, and the degree of increase in durability can reach a value of 4.5…4.6 times. The nature of this dependence once again confirms that deformation processes play an important role in the mechanism of formation of wear-resistant secondary contact structures [30,31].

A serious limiting factor restraining the application of harder metals and alloys as workpiece materials is the loss of form stability of the cutting edge, when, due to high contact loads, its plastic deformation occurs with deterioration of cutting properties caused by changes in the geometry of the cutting edge. According to the existing ideas [32,33,34], the loss of form stability takes place if the hardness ratio of the tool material to the machined material is 1.4…1.6. Then, the boundary of form stability loss in Figure 1 can be represented by a vertical line drawn through the abscissa axis at the level ${\displaystyle \frac{H_q}{H_{ч}}}\approx 0.66$. The twofold increase in resistance starts from the hardness ratio at the level of 0.5. Therefore, the hardness range of machined materials, providing a twofold increase in durability, will be 0.5…0.65 [30,31,32].

It is also found that an important parameter of the preliminary pre-processing is its duration, which determines the completion degree of the secondary hardened structure formation. In earlier works on preliminary pre-processing to substantiate the physical essence of optimal modes, studies on the independent influence of temperature and speed factors on the formation of wear-resistant contact structures were given in [15,16]. It was noted that during the cutting process, the temperature and velocity factors are inseparable and determined by the machining modes. It was found that the experimental nature of the cutting velocity effect on hardening and wear resistance of the secondary contact tool structure is determined by the temperature factor. In contrast, the hardening degree itself and the numerical value of wear resistance are determined through the speed factor. In addition, it has been shown that the autonomous velocity effect is one of the non-dominant factors responsible for the hardening degree. Indeed, the hardening degree will be determined by the plastic deformation degree, the numerical value of which depends on specific contact loads, adhesive interaction forces in contact, process duration, and sliding speed. Therefore, it can be assumed that at many cutting modes, the contact layers of the tool reach the state of ultimate hardening, and the completion degree of this process will mainly depend on the pre-processing time.

3.2. Modeling of the Pre-Processing

The extreme character of the dependence of the influence of pre-processing speed on the wear resistance of the tool contact surfaces, as well as the presence of a limiting cutting velocity (in our case $v_c$ = 17 m/min), above which there is no effect of pre-treatment (see Figure 5b) confirms the dominant role of strain hardening in the process of secondary structure adaptability. In this connection, to verify this issue, we simulated the pre-processing using the ANSYS computer program.

Figure 9 shows the hardening models of the cutting part of the modular disk mill when machining steel 45.

When machining steel 45, the hardened layer thickness of the disc modular mill cutting part at cutting velocity $v_c$ = 17 m/min is 0.43 mm (see Figure 9a), and at cutting velocity $v_c$ = 13 m/min and $v_c$ = 21 m/min is 0.33 mm and 0.29, respectively (see Figure 9b,c). The research results have shown that, indeed, after pre-processing at optimum modes of preliminary pre-processing ($v_c$ = 17 m/min, f = 60 mm/min, t = 6 min), a hardened layer is formed in the cutting part of the modular disc mill.

It was noted before that the tool pre-processing can be considered a process of adaptation of the initial surface structure to the conditions of contact interaction [19,20,35]. In the modes of rational tool operation, this process is accompanied by hardening, it can be represented as an increase in the chemical potential of the contact structures up to a certain value from the energy point of view. Each mode of contact interaction corresponds to its maximum value of chemical potential, which is reached by the surface structure at the end of the pre-processing period. During further operation of the formed secondary structure the value of its chemical potential practically does not change during the whole period of steady wear, determining the working capacity and the tool reliability. Strengthening is provided only by increasing the dislocation density. This case refers to hardening technologies based on purely deformation phenomena when in the hardened zone there are no sources of active chemical elements (e.g., coatings or films) that could enter into metallographic interactions with the increasing density of crystal structure defects, blocking the mobility of the latter [36]. The kinetics of this process, referred to as the topmost layer, is represented by hypothetical dependencies and graphical images in [19].

3.3. Metallographic Study of the Pre-Processing Influence on the Structure of P6M5 Steel

A metallographic study was carried out according to the method in [37,38] to compare the microstructure of modular disc mill cutting part (from P6M5 steel) before and after pre-processing. Figure 10 shows the microstructure of P6M5 steel samples after pre-processing. The microstructure was obtained using an Altami microscope (Altami Ltd, Imatra, Finland).

As can be seen in Figure 10, the initial sample after the quenching process consists of martensite and residual austenite up to 30% and primary carbides. It is known that residual austenite can reduce the cutting properties of the tool.

Cutting operations on metals and other non-metallic surfaces involve various thermal transformations. There is a certain specificity in the conversion of the mechanical work of the tool into heat during the pre-processing. This has a strong influence on the tool, in particular on the microstructure of the tool cutting part.

At certain pre-processing speeds, the temperature of the tool cutting part can reach 560–600 °C. At this temperature, steel tempering can occur. This causes the amount of residual austenite to decrease. The decrease in the amount of residual austenite leads to an increase in the hardness of the alloy in question (see Figure 10a,b). The steel cooling process after pre-processing takes place at room temperature. It is known that control of the steel cooling process allows for controlling the microstructure formation, increasing their reliability and operational durability.

When realizing the process of pre-processing at higher speeds (see Figure 10c,d), the tool cutting part can be heated to higher temperatures of the order of up to 950 °C. In addition to the martensitic base, the steel structure contains a significant number of large carbides. As the temperature increases to 1150 and 1250 °C (see Figure 10d) a condition is created which leads to a greater degree of molybdenum carbides dissolution. It is observed that the number and size of carbides decreases. This process confirms the increase in hardness of the cutting part of the tool after pre-processing.

It is also necessary to note that with the cutting velocity increase, the sliding speed in the friction contact zone rises, leading to an increase in the speed and plastic deformation degree of the tool contact layers. This, in turn, leads to an increase in the defect density of the crystal structure, which determines the hardening value. As the cutting velocity increases, the process temperature increases, which, up to a certain level, facilitates deformation, stimulating more hardening. However, when the temperature reaches a certain value equal to the recrystallization temperature, the defects in the crystal structure come to an active state. Recrystallization temperature moving to the surface and decreasing the amount of hardening reduces the total defect density. In addition, with rising temperature, the defect stability decreases and its ‘dissolution’ in the main crystal increases [39]. Thus, the wear resistance extremum as a function of cutting velocity is the two competing process results of strain hardening and thermal relaxation.

4. Conclusions

Experimental studies found that increasing pre-processing modes to certain values (f = 60 mm/min; $v_c$ = 17 m/min; t = 6 min) has a positive effect on the tool durability period. At the same time, the tool durability period was increased up to T = 155 min.

It is also established that the optimum modes of tool pre-processing provide the best deformation and thermal conditions for hardening the tool-cutting part. Computer modeling results have shown that, indeed, after pre-processing, a hardened layer with a thickness of 0.41 mm is formed on the cutting part of the modular disk mill.

The following general conclusions can be drawn based on the obtained results:

-

In the mechanism of wear resistance enhancement of tool working surfaces by pre-processing, the dominant role is played by the strain hardening processes, the manifestation of which is the microhardness enhancement and crystal structure defect density;

-

Pre-processing increases not only the wear resistance of tool working surfaces but also the operational reliability and heat resistance of contact structures;

-

By varying the optimum cutting modes and hardness of the machined material in the process of tool pre-processing, it is possible to enhance the hardening effect;

-

The experimental, computer simulation and metallographic results confirmed the hardened layer formation on the modular disc mill cutting part.

The results obtained show the possibility of using the preliminary pre-processing method to improve the wear resistance of other metal-cutting tools. Also, it is scientifically and practically interesting to study in more detail the formation of hardened layers and the influence of treatment modes on their thickness depending on the machined material and tool material.