Optimized Green Unrelated Parallel Machine Scheduling Problem Subject to Preventive Maintenance

Abstract

Manufacturing areas typically conduct machine maintenance to prevent early failures and to ensure a safe working environment and efficient production. In this study, the green unrelated parallel machine scheduling problem (GUPMSP) is studied. Besides preventive maintenance, machine availability and non-preemption are considered. A globally optimal solution (mathematical model) and local optimal solution (a modified Moore heuristic algorithm) are used to optimize the number of products returned early in the GUPMSP. Three datasets, namely, a most favorable case, an average case, and a least favorable case, are created to test the performance of the two solutions’ approaches. The results demonstrate the ability of the mathematical model to dominate the results of the modified Moore’s algorithm in the tested datasets. However, optimizing the number of products returned early in the UPMSP with preventive maintenance reduces costs as a step to support the concept of sustainability and enhance efficiency.

1. Introduction

GUPMSP refers to a system where more than one machine with similar capabilities exists. The returned products can be used on any machine using different reprocessing times. Typically, unrelated parallel machines are characterized by having an irregular pattern among reprocessing times and machines. The scheduling process aims to assign returned products to machines over time periods and to achieve one or more objectives, such as optimizing the number of early jobs, total tardiness, completion time, average flow time, etc. [1,2]. In this manner, the strategies of effective scheduling play an important role in enhancing resource utilization, productivity, and profitability [3,4,5].

Different studies have been conducted in the literature to tackle the GUPMSP problem while considering several constraints, such as machine availability [6,7]. Wang et al. [8] aimed to reduce the total tardiness and makespan in the GUPMSP. They developed a new solution approach known as the knowledge and Pareto-based memetic algorithm. The findings explained the ability of their approach to dominate other state-of-the-art findings. Fanjul-Peyro et al. [9] introduced metaheuristic strategies and mixed integer programming to minimize the makespan in the unrelated parallel machine scheduling problem. The results showed the ability of the metaheuristic strategies to outperform the performance of a mathematical model as the size of the problem increased. Vallada and Ruiz [10] developed a metaheuristic genetic algorithm and mixed integer programming to optimize the makespan in the unrelated parallel machine scheduling subject to set-up times with independent products. The small, medium, and large instances were utilized to assess the performance of the proposed genetic algorithm and mixed integer programming. The obtained results illustrated the ability of their proposed solution approaches to dominate the performance of other existing solution approaches in the literature.

Cota et al. [11] studied the product allocations to a sustainable unrelated parallel machine to speed up the processing of the jobs to minimize the makespan and energy consumption. Mixed-integer linear programming and the math-heuristic algorithm were used to optimize the two targeted objectives subject to sequence-dependent setup times. The results illustrated the efficiency of the proposed solution approaches in solving small- to medium-sized problems. Frid et al. [12] introduced the concept of the GUPMSP, where they aimed to reduce the total energy consumption during the scheduling process under dynamic conditions by utilizing genetic programming. The results explained the effectiveness of genetic programming to optimize the problem in green manufacturing systems. Parichehreh et al. [13] aimed to study the impact of workers’ learning and job degradation in the energy-efficient unrelated parallel machine scheduling problem. The augmented epsilon-constraint method and metaheuristic were utilized to tackle the proposed problem subject to optimize multiple objectives, tardiness, the overall weighted flowtime, energy consumption, and the makespan. The metaheuristic algorithm was utilized to tackle large-sized problems, while the augmented epsilon-constraint method was used to deal with small- to medium-sized problems. The findings highlighted the significance of workers’ learning and job degradation in optimizing energy efficiency in real scenarios.

Yaghtin and Javid [14] focused on the minimization of the total tardiness in the UPMSP subjected to periodic maintenance, machine availability, and fuzzy processing time and due dates. They developed a mathematical model and fuzzy-based genetic algorithm to deal with this problem. The performance of the mathematical model and genetic algorithm was assessed using several numerical examples. The results illustrated the superiority of the mathematical model and fuzzy-based genetic algorithm in dealing with small problems and large problems, respectively. Shen and Zhu [15] considered the parallel machine scheduling problem with preventive maintenance. They developed a mathematical model and a modified version of the longest processing time to minimize the makespan. The numerical examples showed the ability of the modified version to outperform the longest processing time rule. Khalili [16] studied the UPMSP subjected to emergent maintenance, product preemption, and the availability of machines. They aimed to minimize the total weighted completion time. The genetic algorithm and simulated annealing were utilized to solve the problem. The findings illustrated the ability of simulated annealing to dominate the findings of the genetic algorithm. Lei and He [17] applied the adaptive artificial bee colony algorithm to minimize the makespan in the UPMSP, along with the periodic maintenance and resource availability. The results explained that the findings of the adaptive artificial bee colony algorithm could outperform the findings of other algorithms proposed in the literature. Hsu et al. [18] considered the periodic maintenance in the unrelated parallel machine scheduling problem, where they relied on the three main types of aging effect models to minimize the total completion time. The results illustrated the ability of the three types of models to obtain optimal results in polynomial time. Ghaleb et al. [19] aimed to minimize the total completion time and total maintenance cost, utilizing a simulated annealing algorithm. The results illustrated the superiority of their proposed algorithm compared with others. Fu et al. [20] summarized the main machine learning algorithms and metaheuristics utilized in the literature to solve manufacturing scheduling problems, such as single and parallel machine scheduling problems.

The inclusion of preventive maintenance in the GUPMSP was found to enhance the reliability of machines and reduce unexpected machine downtime [21]. It also improved overall system performance and efficiency and enhanced the customer satisfaction level by increasing the number of products returned early.

Table 1. Summary of some related works.

Reference	Objective	Machine Type	Consideration of Green Scheduling	Preventive Maintenance	Solution Approach
Avalos-Rosales et al. [22]	Minimize completion time	Unrelated parallel machine	No	Yes	Mixed integer programming and metaheuristic
Su et al. [23]	Minimize makespan	Identical parallel machine	No	Yes	Analytical algorithm
Poongothai et al. [24]	Minimize completion time	Unrelated parallel machine	No	Yes	Mixed integer programming
Tavana et al. [25]	Minimize total maintenance cost and completion time and maximum earliness and tardiness times	Unrelated parallel machine	No	Yes	Fuzzy analytic hierarchy process and goal programming
Zarook et al. [26]	Minimize the total early and tardy coat and minimize the cost of maintenance	Unrelated parallel machine	No	Yes	Genetic Algorithm
Muniasamy et al. [27]	Minimize makespan	Identical parallel machine	No	Yes	Genetic Algorithm and mixed-integer programming
Geurtsen et al. [28]	Minimize completion time and total tardiness	Unrelated parallel machine	No	Yes	Hybrid genetic algorithm and mixed-integer programming
Liu et al. [29]	Minimize completion time	Unrelated parallel machine	No	Yes	Assignment problem
Wang et al. [30]	Total weighted completion times	Unrelated parallel machine	No	No	Tabu Search
Santoro et al. [31]	Minimize makespan	Unrelated parallel machine	No	Yes	Mixed integer linear programming
This Research	Maximize the number of products returned early	Unrelated parallel machine	Yes	Yes	Mathematical model and heuristic algorithm

summarizes some related works. In this study, the returned products refer to those that are damaged during production or transportation. As the number of returned products that are reprocessed or handled according to their agreed-upon deadlines or schedules increases, customer satisfaction increases. In this manner, their requirements are met within certain deadlines. The contributions of this paper are summarized as follows:

• Minimizing the number of tardily returned products as an objective function of the proposed mathematical model while considering the machines’ availability.
• Considering preventive maintenance and the average reprocessing times of the returned products.
• Developing a heuristic algorithm to tackle the large size of the problem and evaluate the performance of the proposed mathematical model.
• Determining the returned product allocation to each machine

The structure of this paper is as follows: Section 2 outlines the notations and problem statement. The developed methodology is detailed in Section 3, followed by a numerical example in Section 4. Section 5 presents the experimental results and discusses them in detail. Lastly, Section 6 concludes the study and draws on future works.

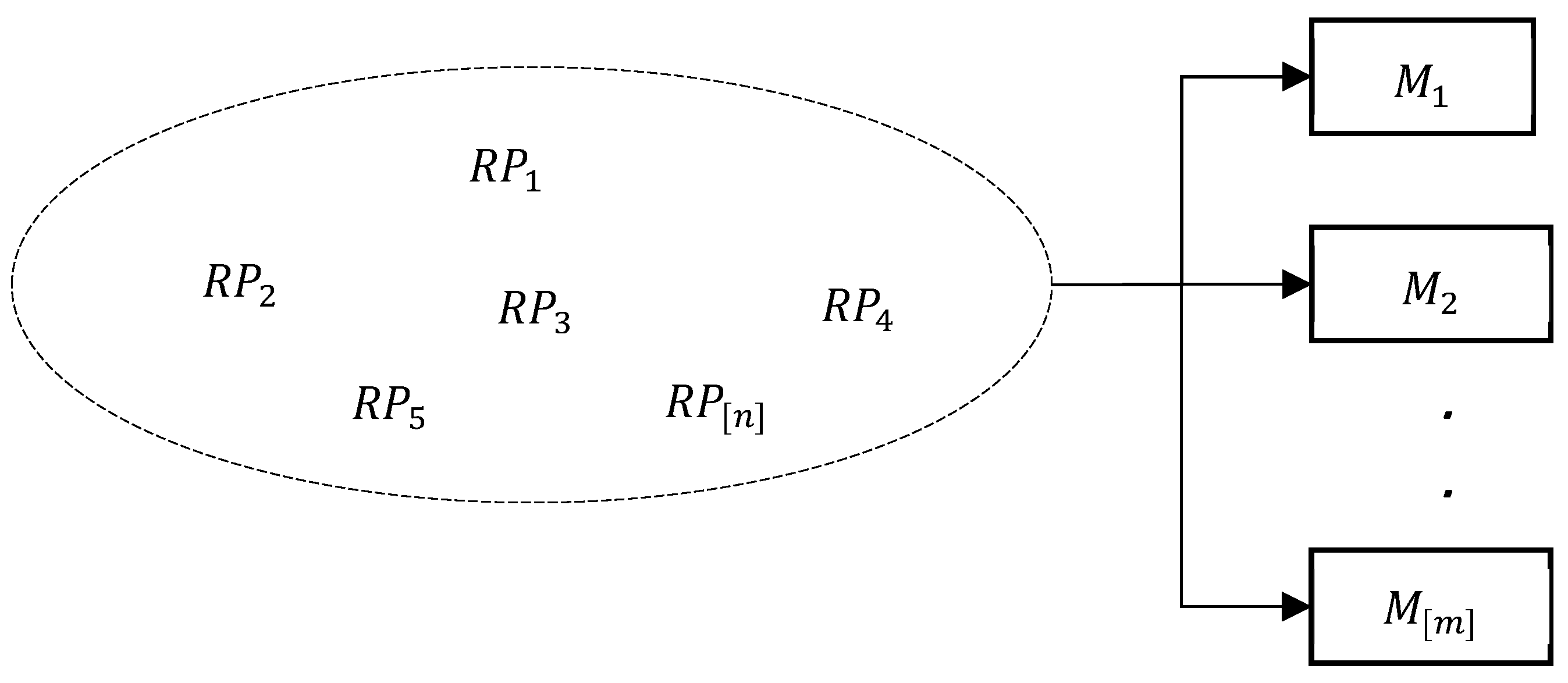
2. Problem Statement and Notation

In GUPMSP, a set of returned products (${RP}_i$), $i=1\dots ,n$ is assigned to be processed through unrelated parallel machines $j=1\dots ,m,$ subject to preventive maintenance.

Table 2. The Main Abbreviations Used in the Paper.

Indices:
$i$	Index for the returned product.
$j$	Index for unrelated machine.
$k$	Index for set.
Parameters:
${MT}_{jp}$	Maintenance period $p$ of unrelated machine $j$.
$B_{jk}$	Set $k$ of unrelated machine $j$.
$n$	Total number of returned products to be reprocessed at time zero.
$m$	Total number of unrelated machines available.
$\pi$	Group of tardily returned products.
${RP}_t$	Tardily returned product.
${RP}_{mj}$	Returned product with maximum average reprocessing time.
${RP}_i$	Returned product $i$.
${RPT}_{ij}$	Re-processing time of returned product $i$ at unrelated machine $j$.
${DD}_i$	Deadline of returned product $i$.
${WT}_{jk}$	Set available time of set $k$ at unrelated machine $j$ between two maintenance periods.
$t$	Maintenance time.
Decision variables:
$y_{ijk}$	1 if returned product $i$ is assigned to set $k$ of unrelated machine $j$. 0 otherwise.
$C_{ij}$	Completion time of returned product $i$ at unrelated machine $j$.
$T_{ij}$	Tardiness of returned product $i$ at unrelated machine $j$.
$C{T}_{jk}$	Completion time of set time interval of set $k$ at unrelated machine $j$.
$N_T$	Total number of tardily returned products.

presents the main abbreviations used in this study. The length of maintenance is known [32]. The implementation period for the periodic maintenance is different from one machine to another, where there is only a single resource available to implement the maintenance process. Figure 1 represents an overview of the proposed problem. The main notations utilized in this study are summarized as follows.

This study aims to optimize the number of tardily returned products in unrelated parallel machines subject to preventive maintenance. In this regard, the mathematical model is utilized to achieve the targeted objective. The heuristic algorithm, the modified Moore heuristic algorithm, is also utilized to handle the unrelated parallel machine green scheduling problem. The main assumptions in this study are as follows:

• Returned products are independent.
• No preemption is allowed; once reprocessing begins on a returned product, it is processed to completion without interruption.
• All returned products are available at time zero.
• All returned products are equally important.
• No cancellation is allowed. Each returned product must be processed to completion.

This study involves $n$ returned products being assigned to be reprocessed at $m$ unrelated parallel machines. Additionally, the schedule for maintenance is adjusted from one machine to another to reduce the number of maintenance staff required.

3. Methodology

In this section, the mathematical model and a modified Moore heuristic algorithm [33] used in this study to tackle the GUPMSP while considering the preventive maintenance are described as follows:

3.1. Mathematical Model

The number of products returned early in GUPMSP subject to preventive maintenance is optimized using a mathematical model. The required sets must not exceed the number of returned products. Additionally, the number of sets for each machine should also be limited to the number of returned products. Initially, the returned products are sorted using the EDD rule (Earliest Due Date), and then the mathematical model is implemented.

Objective function:

$$\mathrm{Maximize}\sum _{k=1}^n\sum _{j=1}^m\sum _{i=1}^n{y}_{ijk}$$

(1)

Subject to

$${\sum }_{k=1}^n{\sum }_{j=1}^m{y}_{ijk}\le 1 i=1\dots n$$

(2)

$${\sum }_{i=1}^n{RPT}_{ij}\times y_{ijk}\le {WT}_{jk} k=1\dots l j=1\dots m$$

(3)

$$\begin{gathered} \sum _{i=1}^r{RPT}_{ij}\times y_{ijk}+\left(\left({CT}_{jk-1}+t\right)\times \mathit{max}\left(y_{ijk},y_{\left(i+1\right)jk},\dots ,y_{rjk}\right)\right)\le {DD}_r \\ r=1\dots n, j=1\dots m {CT}_{j0}=0 k=1\dots r \end{gathered}$$

(4)

$$y_{ijk}\in \left\{0,1\right\}, j=1\dots m, k=1\dots l i=1\dots n$$

(5)

A mathematical model is utilized to optimize the number of products returned early (Equation (1)). As the number of products returned early ($N_E$) increases, the number of tardy returned products ($N_T)$ decreases (${maximumN}_E\equiv minimum{N}_T$). Equation (2) guarantees that each returned product is assigned to be reprocessed at most to one set of the available unrelated machines. Equation (3) is used in the model to ensure that the total average reprocessing time for the returned products at each set does not exceed the available time per set, defined as (set’s available time). Equation (4) determines if the returned products are delayed or not based on the completion times, maintenance times, and deadlines, where ${CT}_{j0}=0$. Additionally, $\mathit{max}\left(y_{ijk},y_{\left(i+1\right)jk},\dots ,y_{rjk}\right)$ is formulated as a binary number, where it is equal to 1 in case the set $k$ on unrelated machine $j$ opens. Finally, Equation (5) explains that the values of the decision variables ($y_{ijk}$) are binary numbers.

3.2. Modified Moore’s Heuristic Algorithm

A modified Moore’s heuristic algorithm is considered to find solutions that are not guaranteed to be optimal but are sufficient for specific purposes. Two stages should be followed to optimize the tardily returned products in GUPMSP subject to preventive maintenance based on the modified Moore heuristic algorithm. In the first stage, the returned products are allocated to unrelated parallel machines using the rule of EDD. This rule involves several steps to reduce the number of tardily returned products as follows. Firstly, the returned products are sorted according to their deadlines. Next, the returned products are assigned to machines based on which has the least workload. In case a returned product is tardy, the next returned products from the EDD list are assigned to be reprocessed through the available machine with minimum load. If a returned product is not early, the returned products with the longest average reprocessing time among the assigned returned products are removed from the unrelated machines, and again the process of scheduling begins. Finally, the removed returned products are reintroduced based on the least loaded machines. Preventive maintenance is considered in the second stage by inserting it into the unrelated parallel machines timelines, and tardily returned products might be rescheduled within any available slack time.

Moore’s heuristic algorithm is utilized in the first stage as an optimizing procedure for minimizing the number of tardily returned products [34]. A returned product is classified as tardy when the completion time for the returned product is greater than its deadline. The procedure is summarized as follows:

• Order returned products using EDD.

  $${DD}_1\le {DD}_2\le \dots \le {DD}_{\left[n\right]}$$
• Assign returned products for the EDD list and minimum completion time until there is a tardily returned product (${RP}_t$) and then go to step 3. If none, go to step 4.
• Find the returned product with the maximum average reprocessing time returned product (${RP}_m$) among the returned products already assigned in sequences of unrelated parallel machines $s=\{{RP}_1,{RP}_2,\dots ,{RP}_t\}$ and then remove ${RP}_m$ from the timetable of the unrelated machines. Shift the returned products following ${RP}_m$ to the left and then go to step 2.
• Find the optimal sequence by taking the current schedule and adding the removed returned products to it.

In the second stage, the maintenance periods are inserted into the timetable for unrelated machines; thus, the Moore heuristic algorithm schedule is divided into several sets ($B_{jk}$) based on the set’s available time and periodic preventive maintenance time. Then, the following steps are implemented:

• All returned products should be assigned to unrelated parallel machines.
• If the ${WT}_{jk}\ge C_{\left[i-1\right]\left[j\right]}+P_{ij}$, the ${RP}_{ij}$ should be placed in the set $B_{jk}$, and then the next step is implemented.
• The ${RP}_{ij}$ is classified as a tardily returned product in case $T_{ij}>0$; thus, is removed from the unrelated machines schedule, where it should be added to $\pi$, where $\pi$ represents the group of tardily returned products.
• Repeat this step by applying step 2 in this stage.
• The slacking time for each set at every unrelated machine should be calculated to determine the unscheduled time (idle time) at the sets in the unrelated machines.
• The returned products in $\pi$ are sorted based on EDD.
• To minimize $N_T$, the returned products in $\pi$ could be rescheduled during the slack time if possible.

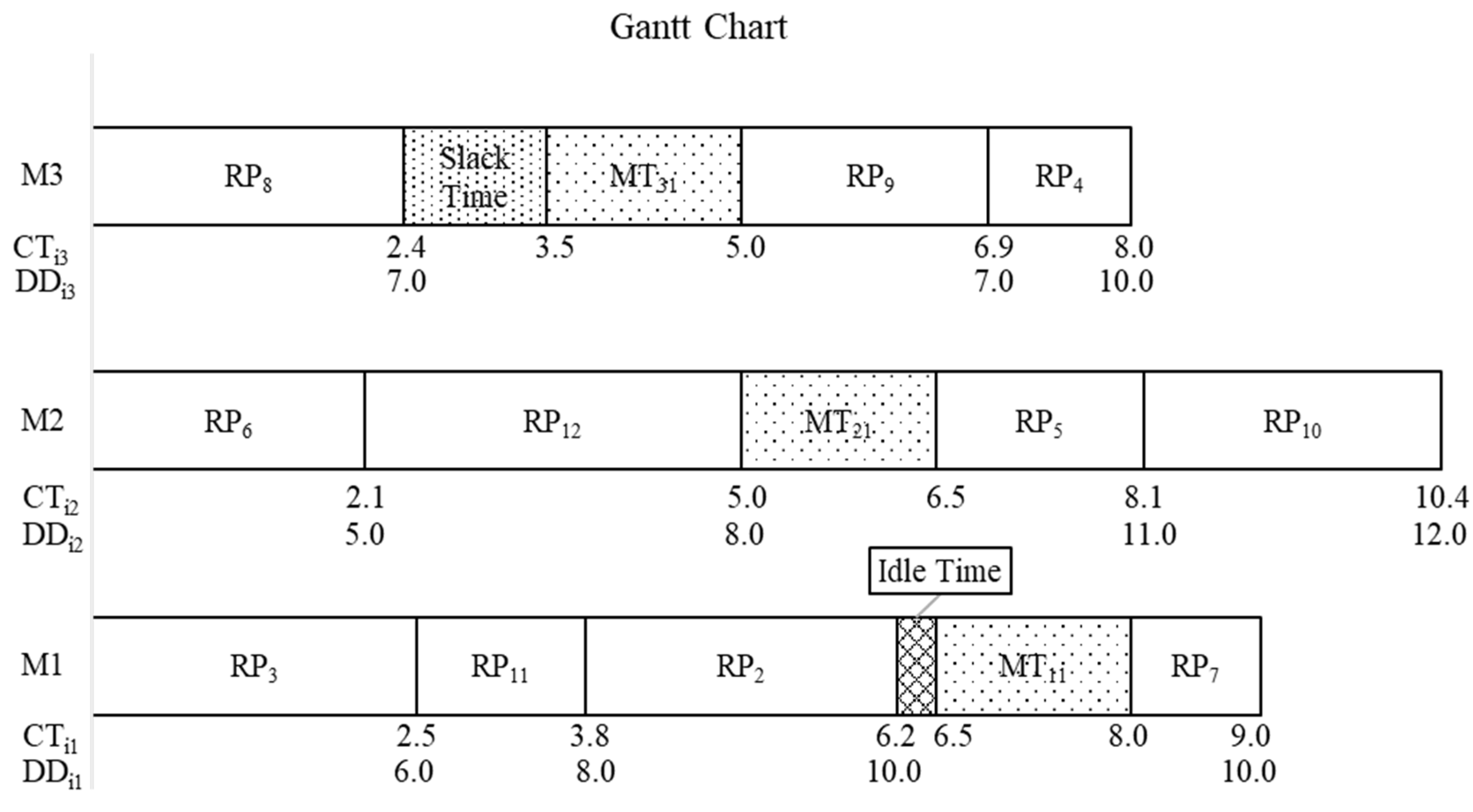
4. Numerical Example

In this section, ten returned products are assigned to be reprocessed in three unrelated parallel machines. At each machine, the maintenance process should be implemented every 8 h, whereas the length of the maintenance period is 1.5 h. The length of the maintenance time in the three machines is identical. The starting times for the maintenance process in the first, second, and third machines are 6.5, 5.0, and 3.5 h, because the single resource should move among the machines to implement the maintenance. In this manner, the set’s available times of set $1$ at unrelated machines 1, 2, and 3 are 6.5, 5.0, and 3.5 h, while the set’s available times of other sets and the unrelated parallel machines are 6.5 h.

Table 3. The average reprocessing times and deadlines for 12 returned products.

		Returned Product
	1	2	3	4	5	6	7	8	9	10	11	12
${RPT}_{i1}$ hours	4.1	2.4	2.5	3.3	1.3	4.4	1	4.8	4.7	1.7	1.3	3.4
${RPT}_{i2}$ hours	2.5	1.7	2.4	3.1	1.6	2.1	5	4.3	4.3	2.3	4.8	2.9
${RPT}_{i3}$ hours	2.6	3.8	2.9	1.1	1.3	4.2	1.3	2.4	1.9	4.2	1.8	4.2
Deadline hours	9.0	10.0	6.0	11.0	11.0	5.0	10.0	7.0	7.0	12.0	8.0	8.0

represents the average reprocessing times and deadlines for the 12 returned products at three unrelated parallel machines, where ${RPT}_{i1}$ represents the average reprocessing time for product $i$ at machine 1. The average reprocessing times and deadlines for the 12 returned products followed the uniform distribution [1,5].

The results in Figure 2 depict the Gantt chart based on the results of the mathematical model. The results illustrate that the number of products returned early is 12, where there is no tardily returned product. Returned products 8 and 4 are assigned to be processed in set 1 at machine 3 and returned products 9 and 5 are processed in set 2 at machine 3. In set 1 at machine 1, returned products 3, 11, and 2 are processed, where the total average reprocessing time is 6.2 and the idle time is 0.3. The maintenance periods in the three machines are non-synchrony, where the end of the first period maintenance (${MT}_{31}$) at M3 is the beginning of the first period maintenance at M2 (${MT}_{21}$), and so on.

Figure 3 represents the returned product scheduling in the three unrelated parallel machines based on the results of the first stages of the modified Moore heuristic algorithm. In this stage, the returned products are assigned to be scheduled in the unrelated parallel machines without considering the periodic maintenance. The initial results show that the number of tardily returned products is zero, where all returned products are scheduled before deadlines. In the second stage, the periods of preventive maintenance are added to the timelines for machines in non-synchrony order. Once returned product splitting is not allowed, it is not allowed to divide the returned products into more than one set. Figure 4 represents the returned product scheduling in the unrelated parallel machines based on the results of the second phase of the modified Moore’s heuristic algorithm, where the preventive maintenance is inserted into the timelines for machines. The results illustrate that the number of products returned early is 11, where there is a tardily returned product, which is ${RP}_1$. The mathematical model was found to maximize the number of products returned early compared to the modified Moore’s heuristic algorithm. The number of products returned early based on the results of the mathematical model and modified Moore’s heuristic algorithm is 12 and 11, respectively.

5. Experimentation and Results

5.1. Datasets

The mathematical model and heuristic algorithm are examined using several categories of datasets generated as follows:

• The total number of unrelated parallel machines: 2, 2, 4, and 5.
• The total number of returned products: 10, 20, 20, and 20.
• The uniform distribution is utilized to generate the average reprocessing time for the returned products following the intervals [1.0, 3.5] and [1.5, 5.0].
• The length of each period of preventive maintenance is identical and equal to 1.5 and non-synchrony.
• Available time of set 1 at $M_1$, $M_2$, $M_3$, $M_4$, and $M_5$ is 6.5, 5.0, 3.5, 2.0, and 0.5. Meanwhile, the available time of other sets at other machines is 6.5.
• The parameter of tardiness factor ($tf$) and the parameter of range factor ($rf$) are considered when the deadlines are created, where $0\le tf\le 1$, and $0<rf<1$. Three values for each parameter are considered to estimate the values of deadlines to guarantee a variety of tightness.

  Table 4. The categorization of deadlines [35].

  Category of Dataset	$\mathbf{t}\mathbf{f}$	$\mathbf{r}\mathbf{f}$	Tardiness of Deadline	The Range of Deadline	Remarks
  1	0.20	0.20	L	N	Most Favorable Case
  2	0.20	0.50	L	M
  3	0.20	0.80	L	W
  4	0.50	0.20	M	N	Average Case
  5	0.50	0.50	M	M
  6	0.50	0.80	M	W
  7	0.80	0.20	T	N	Least Favorable Case
  8	0.80	0.50	T	M
  9	0.80	0.80	T	W

  Loose ⟶ L, medium ⟶ M, tight ⟶ T, narrow ⟶ N, and wide ⟶ W.

  represents the classification of data sets considering the values of ($tf) and (rf)$. However, the returned product’s deadlines were generated from the uniform distribution $\left[(d-w/2,d+w/2\right].$ The value of $d$ is computed using Equation (6); $\overline{RPT}$ is the average of the average reprocessing time. Equation (7) is utilized to calculate the value of $w$ [35]. The first three categories of data are categorized as the most favorable case, where the gap between the average reprocessing times and deadlines is high.

$$d={\displaystyle \frac{\overline{RPT}\times (1-tf)\times n}{m}}$$

(6)

$$w={\displaystyle \frac{rf}{m}}\times \sum _{i=1}^n(\min \left\{{RPT}_{ij}\right\}1\le j\le m)$$

(7)

5.2. Analysis of Results

Three datasets were created to test each category of datasets using the mathematical model and a modified Moore’s heuristic algorithm, and the results are summarized in

Table 5. A summary of mathematical model and modified Moore’s heuristic algorithm—most favorable.

$\mathbf{Number}\mathbf{of}\mathbf{Returned}\mathbf{Products}(\mathbf{n}$)	$\mathbf{Number}\mathbf{of}\mathbf{Machines}(\mathbf{m}$)	Average Reprocessing Time	Average Number of Products Returned Early
			Mathematical Model	Modified Moore’s Heuristic Algorithm
10	2	[1.5, 5.0]	8.00	8.00
20	2	[1.5, 5.0]	15.00	15.00
20	4	[1.5, 5.0]	17.67	17.00
20	5	[1.5, 5.0]	18.00	17.33
10	2	[1.0, 3.5]	8.00	8.00
20	2	[1.0, 3.5]	16.00	15.00
20	4	[1.0, 3.5]	19.33	18.00
20	5	[1.0, 3.5]	17.33	16.00

,

Table 6. A summary of mathematical model and modified Moore’s heuristic algorithm—average case.

$\mathbf{Number}\mathbf{of}\mathbf{Returned}\mathbf{Products}(\mathbf{n}$)	$\mathbf{Number}\mathbf{of}\mathbf{Machines}(\mathbf{m}$	Average Reprocessing Time	Number of Products Returned Early
			Mathematical Model	Modified Moore’s Heuristic Algorithm
10	2	[1.5, 5.0]	5.00	4.00
20	2	[1.5, 5.0]	11.00	10.00
20	4	[1.5, 5.0]	12.33	11.67
20	5	[1.5, 5.0]	9.00	9.00
10	2	[1.0, 3.5]	6.00	5.00
20	2	[1.0, 3.5]	11.33	10.67
20	4	[1.0, 3.5]	12.00	11.33
20	5	[1.0, 3.5]	9.33	8.00

and

Table 7. A summary of mathematical model and modified Moore’s heuristic algorithm—least favorable.

Number of Returned Products	Number of Machines	Average Reprocessing Time	Number of Products Returned Early
			Mathematical Model	Modified Moore’s Heuristic Algorithm
10	2	[1.5, 5.0]	1.67	1.00
20	2	[1.5, 5.0]	4.67	4.00
20	4	[1.5, 5.0]	4.30	3.00
20	5	[1.5, 5.0]	4.00	3.00
10	2	[1.0, 3.5]	2.67	2.00
20	2	[1.0, 3.5]	5.67	5.00
20	4	[1.0, 3.5]	5.00	4.67
20	5	[1.0, 3.5]	4.00	3.00

. Table 5 represents the average number of products returned early in the most favorable case. The performance of the average case and least favorable case are summarized in Table 6 and Table 7, respectively. The results illustrate the variability in the average number of early products in GUPMSP based on the number of machines, returned products, and the range of the average reprocessing times.

The results lead to the following findings. Firstly, in the most favorable case, the average case, and the least favorable case, the mathematical model can either dominate or duplicate the findings of the modified Moor’s heuristic algorithm. Secondly, the number of products returned early increases in the most favorable case, as the number of machines increases. Thirdly, it is noticed that as the number of machines increases to schedule a given set of returned products, the value of the average number of products returned early decreases. Finally, in the case where the average reprocessing time varies widely, the number of early products decreases. On the other hand, the running times for the mathematical model and modified Moore’s heuristic algorithm were a fraction of a second.

6. Conclusions

In this study, the GUPMSP under preventive maintenance has been tackled. A mathematical model and modified Moore’s heuristic algorithm were developed to optimize the number of products returned early. Different categories of datasets were generated to examine the performance of the solution approaches based on the values of the tardiness factor, the parameter of the range factor, and the number of available unrelated parallel machines. Based on the gap between the reprocessing times and deadlines, these categories are grouped into three cases: the most favorable, the average, and the least favorable case. The results illustrate the ability of the proposed mathematical model to dominate the performance of the modified Moore’s heuristic algorithm. The number of products returned early increased as the number of machines increased, and the range among the reprocessing times decreased. Although adding preventive maintenance as a part of the unrelated parallel machine scheduling problem led to an increase in the complexity of the problem, it played a significant role in enhancing the overall performance of the problem, reliability, and accuracy of scheduling. It is expected to help decision makers to be more robust, ensure sustainable reproduction schedules, and be realistic.

This study was developed based on the average processing time. However, in real-world problems, the processing times are uncertain; thus, this issue could be considered for future work. Additionally, metaheuristics and simulation could be utilized to deal with the GUPMSP under uncertainty subject to preventive maintenance.