Abstract
The objective of this research is to incorporate system failure into a robust design formation and solution process. The system failure referred to here will be built using fault tree analysis (FTA), which will take all lower-level failure events into consideration. Two examples are investigated here. One will directly treat the probabilities of the basis events as design variables, The other will be formulated in five different models: deterministic design optimization, the reliability index-based, the “and” gate-based, the “or” gate-based and the “inhibit” gate-based robust design. Their corresponding optimization solutions will be compared with each other. The post-optimality analysis of each of the design optimization models is also investigated to evaluate the effect of the change in the problem parameters to the optimal solution. These problem parameters are deterministic and not treated as design variables in the optimization formulation. This research paves the way for much more broad applications of robust design optimization in the future by incorporating more advanced FTA models into the optimization solution process, such as fuzzy sets and dynamic FTA.
1. Introduction
The background information presented here is divided into a description of robust design optimization, which deals with uncertainty, and a brief description of fault tree analysis. It is followed by a section detailing the direction of the rest of this paper, which is to demonstrate the usefulness of a probability-based, robust design optimization methodology that incorporates fault tree analysis to define the system-level reliability in a multi-level optimization problem. The paper presents two examples, the first of which shows the system reliability constraint formed by the probabilities of basic events, and the second example demonstrates the use of Fault Tree Analysis (FTA) in constructing the system-level reliability. In other words, the reliabilities of the basic events are used to build the top-level event as the system reliability, which is considered the design constraint.
1.1. Design Optimization Background
The usefulness of design optimization is not just limited to producing an optimal solution but also includes enabling a designer to understand and formulate the design problem of concern mathematically in a comprehensive format. The solution of an optimal design is one that pushes all resources to their limits within a bound defined by the required constraints. The solution could be critical and unstable because it falls into the borderline between success and failure. The design optimization problem is indeed one of the models mentioned in a workshop on Robustness in Statistics in 1978 by a great statistician, George Box, who stated that “All models are wrong, but some are useful”. To make design optimization useful for engineering applications, different features of uncertainty have recently been implemented to model the design variables, the state variables, the objective, the constraints and the state equations. Such a design optimization formulation is called robust design, which specifically aims to create an engineering product that can avoid failure due to uncertainty caused by dimension tolerance, manufacturing or environmental variations, etc.
The mathematical formulation of a robust design problem follows the standard design optimization format. However, the major task of a robust design problem is to quantify the uncertainty of constraint in terms of the statistical terms of the input random variables, such as their means and the standard deviations. To this end, many approaches have been proposed in the literature, which may be grouped into two categories: the direct approach and the indirect approach. The direct approach can be further divided into non-intrusive or intrusive. The non-intrusive ones include the Monte Carlo simulation and smart sampling such as the Latin hypercube [1]. The intrusive ones include the polynomial chaos expansion [2,3,4,5], the perturbation method [6,7,8] and the Kriging surrogate model [9]. These methods are popular as they can conveniently compute the reliability index of a response function in statistical terms of the input random variables. In the cases when the number of random variables becomes large, dimensional reduction methods [10,11,12] are available to improve their computational efficiency. The indirect approach includes the first- and the second-order reliability methods [1]. The former led to the development of the reliability index analysis method and the performance measurement method [13,14,15,16].
The reliability index referred to above is in fact the standard normal variable, which is the only variable used to express the probability density function of a normal distribution [1]. Using a reliability index to quantify the failure probability of constraints has been the focus in the early research on robust design, which was specifically called reliability-based design optimization (RBDO) [17,18,19,20,21,22,23]. In most of the RBDO studies, the constraint is assumed to be a continuous function of random variables. Its probability distribution is assumed to be normal and time-independent. Indeed, the RBDO has begun to be widely used in practical engineering such as the design of offshore wind turbine structures [24,25]
Recent developments have extended robust design to include time-dependent reliability indexes, discontinuous random variables, fuzzy parameters, multi-disciplinary state equations and multi-objective functions design. For example, the Kriging model [26,27] is used to build the time-varying fatigue reliability state equation based on the collected field data. The stochastic perturbation theory up to the fourth order is used to approximate the time-dependent reliability index and the reliability of time-dependent fatigue failure. The design sensitivity analysis is also applied to find the gradients of reliability with respect to its means and the standard deviation of the time-varying fatigue reliability. The magnitude of these gradients is the objective of the reliability-based design along with constraints on event reliabilities. Another example is presented in [28] which conducted the Accelerated Degradation Testing (ADT) experiments to estimate the probability of failure of a time-dependent event. The first step of the process is collecting a small number of samples to build the ADT model. The model parameters including termination time and test parameters are determined by minimizing the regression error. The reliability of each component can then be predicted based on the ADT model with optimized parameters.
Reference [29] establishes the probability distribution of water usage with Bernoulli random variables as the amount of water usage depends randomly upon the times to turn on and off the water faucet. The robust design problem of a complicated aerospace engineering application is formulated based on a multi-level, multi-disciplinary design optimization framework [30]. It uses the fuzzy set theory to model the uncertainty of an event with limited data or poor information. Furthermore, References [31,32] built and solved a robust design problem with multi-objective cost functions.
The failure constraints presented in most of the robust design formulations presented above are associated with a single event modeled by a single failure probability, which can be easily converted in terms of the reliability index. Reference [33], however, recommended the use of the fault tree analysis to raise the constraint failure in the robust design formulation from a basic event level to a system level to broaden the applications of the robust design. The study in this reference only considered statistically independent basic events leading to the system-level event, and it recommended the use of other analysis techniques to examine statistical dependence.
1.2. Fault Tree Analysis (FTA) Background
Fault tree analysis aims to model a system failure graphically by connecting the causes and consequences of all failure modes of a system together into a hierarchical structure [34]. The fault tree analysis groups basic events into statistically independent cut sets. The set theory can then be applied through different logic “gates” to count intersections between the considered events to predict system failure. In the traditional FTA structure, the event probabilities are usually assumed to be constant and unable to handle repairable and time-dependent events [35]. Ruijters et al. [36] presents the results of reviewing 150 FTA papers. It mentioned two areas, qualitative and quantitative, for the future extension of the risk analysis capability of FTA; the qualitative one considers building a comprehensive FTA structure efficiently and the quantitative one considers computing an event probability accurately. Moreover, it briefly outlines the basic FTA structure with “and”, “or”, “voting” and “inhibit” gates. The rule for the “and” gate dictates that, for an event to occur, all the immediate lower-level events must occur. The “or” gate rule dictates that, for an event to occur, only one of the immediate lower-level events must occur. Moreover, the “inhibit” gate rule represents a conditional probability relation between two events. Table 1 summarizes the probability of intersection, “and”, union, “or”, and inhibit, “inhibit” gates, which will be used in this study.

Table 1.
Major gates used in this study.
Recent research works have successively developed much more sophisticated examples of FTA with broader applications in the two areas mentioned above. For example, Andrew [37] incorporates a binary decision diagram, a stochastic Petri Net and Markov methods to enhance the FTA structure to handle statistically dependent events and time-dependent failures. The Markov chains are used to represent changing states of events over time. Martinez et al. [38] investigated the use of artificial intelligence components in FTA. Shao et al. [39] applied the programming language Little-JIL to construct an FTA structure graphically. The efforts of References [37,38,39] are examples of recent research building more accurate FTA structures to model failure modes of real-world applications.
When there are complex interdependent relationships between events, the modified FTA such as [37] can be used, but using a Bayesian Network is another possibility. Bayesian networks model events as nodes. The nodes are connected by unidirectional arrows representing cause–effect relationships, and arcs between nodes represent conditional probabilities [40]. While Bayesian Networks are an effective modeling technique when there are many statistical interdependencies, in this paper, FTA is used as a simple, hierarchical model to represent the system-level reliability constraint.
Sezer [41] introduces Z-numbers to evaluate probability of events, which combines both fuzzy and reliability variables. The fuzzy variable represents the experts’ judgment about the failure of the event. Sun [42] established an FTA structure to manage smartphone disassembly failure. The failure probabilities of the basic events are quantified by the fuzzy sets of the linguistic judgements. References [41,42] advanced the second research area of FTA which brought time-dependency and discontinuity into the reliability calculation [43,44,45].
In summary, FTA can offer an effective approach to conducting failure analysis of events at different levels in a system. In particular, it has been recently extended to cover discontinuous, time-dependent failures and statistically dependent events. The focus of this paper is to incorporate FTA with the robust design applications and thus to incorporate failure criteria not only related to the basic events but system failure as well. Since this research represents an initial attempt, the system probability of event constraints in the study will be built as time-independent by using the traditional FTA. Future research will incorporate the advanced FTA structure with a robust design to handle discontinuous and time-dependent events.
1.3. Purpose and Outline
The main thrust of this paper presents a probability-based, system-level, robust design optimization analysis, where a system-level reliability (the inverse of the failure probability) is presented as a fault tree. The top event is considered as the system-level reliability dependent on random variables and response functions. The probabilities of the basic events, which combine to form the reliability constraint, are equivalent to the basic-level events in the system fault tree. These basic-level events will be combined according to the logic of the “and”, “or” and “inhibit” gates in the intermediate-level events. A cost function will then be optimized subject to the reliability constraint. Additionally, post-optimization analysis of the top event reliability with respect to any of the random design variables will be accomplished just as in any ordinary optimization problem.
The main benefit of using FTA in RBDO problems is that it allows for the expansion of the RBDO problem space by visualizing the basic- and intermediate-level events and their interrelationships and raising the cost function from an element to a system-level event. This would allow us to quickly explore changes to the reliability constraint or the event interdependencies or add new events altogether. In this paper, “and”, “or” and “inhibit” gates are used in the example problem. However, other logical structures might exist that would be difficult to capture in the constraints of the RBDO problem without at least performing the qualitative analysis portion of the FTA.
Two examples are provided to demonstrate both the use of the system-level reliability constraint and the use of the traditional FTA to build various failure models. The first example is an electrical circuit, and the second is a bolted plate. The electrical circuit problem uses the probabilities of the basic events based on two simple scenarios to minimize the cost while satisfying the reliability constraint. In the bolted plate problem, four different robust design formulations are constructed for the bolted plate design with different FTA gates. Their optimal solutions are presented for comparison. Furthermore, post-optimality analysis is conducted to investigate the impact of the variations in problem parameters on the optimal objectives of different robust design formulations. These problem parameters are deterministic and used to build constraint events.
The rest of the paper is organized as follows. Section 2.1 uses an electrical circuit example with one series and one parallel configuration gate to show how a target system-level reliability can be achieved after minimizing the cost. The probabilities of the basic events are all statistically independent. Section 2.2 will provide the statement of the bolted plate example along with the associated design optimization problem formulation in which the objective, design variables and constraints are all deterministic. Section 2.3 will reconstruct the bolted plate design problem according to the reliability index-based design optimization formulation. The design variables include both means and standard deviations. Section 2.4 will reformulate the bolted plate design problem with its system failure as a constraint. The system failure is constructed based upon three different FTA structures to model the failure of a group of two identical bolts, with the “and” gate, “or” gate or “inhibit” gate. Section 2.5 also presents the sensitivity equations of the upper-level system failures described by the FTA chart with respect to a design variable. These derived equations lead the way for gradient-based stochastic design optimization and for post-optimization analysis. The latter is presented in Section 2.5. The numerical results of optimization and post-optimality analysis are presented in Section 3. These numerical results are also summarized in a table form for comparison. The concluding remarks and discussion of this research are presented in the final section, Section 4.
2. Materials and Methods
Two examples are presented in this section to demonstrate the use of FTA to formulate reliability constraints to achieve different design objectives in a robust design problem. The first example is to minimize the cost of a parallel circuit configuration which is an assembly of three different circuit boards. The performance of a single circuit board is considered a basic event, while the performance of an entire parallel circuit configuration is considered a system event. In this problem, the reliability of each circuit board is treated as a design variable and the system reliability of the entire parallel circuit configuration is the concern of a constraint. The second example is a bolted plate problem. The bolts are used to connect the plate to a column. The problem is more comprehensive than the first example. The design variables are random and related to the bolt diameter and the width of the plate. The related robust design problem will be formulated differently, and the post-optimality analysis will be conducted with each design formulation to investigate the quality of the optimal solutions.
2.1. Parallel Circuit Configuration: A Demonstrative Example
This example is taken from reference [34]. The parallel circuit configuration is an assembly of three different circuit boards, , and three of as shown in Figure 1. The reliabilities of these circuit boards are assigned by three different events, , and , which are statistically independent of each other. The design concern here is to produce the assembled circuit configuration with minimal cost and 95% of system reliability. Neither reliability indices nor random variables are involved in the problem formation.
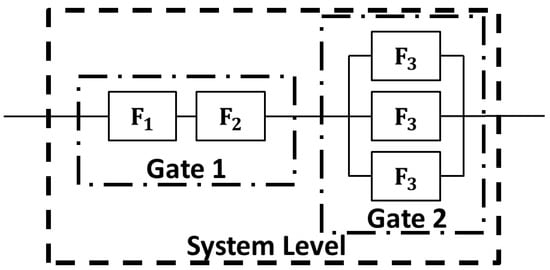
Figure 1.
Parallel circuit configuration.
The system reliability of the parallel circuit configuration can be generated by FTA. The parallel circuit configuration is made of two cut sets, Gate 1 and Gate 2. Gate 1 is an “and” Gate, a union of two events, and . Its reliability can be mathematically represented by,
Two failure scenarios are considered hereafter for Gate 2. Scenario 1 assumes the system has failed if only one event fails, while Scenario 2 assumes the system has failed if two out of three events fail. In Scenario 1, the reliability of Gate 2 can be calculated as,
Consequently, the system reliability can be computed as,
The robust design problem of Scenario 1 is mathematically expressed as follows,
subject to a single constraint related to the system reliability as,
The cost, , is cast as a linear combination of the circuit board. The reliability of each circuit board is set as 95% with the initial value of the objective function as 85.3248. The initial value of system reliability, , is 78.03%, which violates the system reliability constraint. The optimal solutions for both are listed below. The initial design violates the constraints. To satisfy the system reliability constraint, the cost objective is raised from the initial value of 85.3248 up to 88.739 with the optimal reliability of each circuit board as 0.99, 0.9887 and 0.99. Note that the upper bound of the reliability of each circuit board is set to 0.99.
Scenario 2 considers the system failure if two out of three events fail. In this scenario, the system reliability constraint is reformulated as,
The optimal reliability of each circuit board in Scenario 2 is obtained, respectively, as 0.99, 0.9887 and 0.9727 with the new optimal objective being 87.1697.
2.2. A Bolted Plate Design Problem and Deterministic Design Optimization
A bolted plate design problem taken from [46] will be investigated in this section. The bolted plate is shown in Figure 2. The basic events are the reliabilities of the strength of the bolts and the plate, and the design variables are random parameters related to the dimensions of the bolts and the plate. The bolted plate problem will be optimized first based on the deterministic model. Then, the deterministic optimal solution will be used as a basis for comparison with those results in Section 2.3, obtained from different robust design formulations.
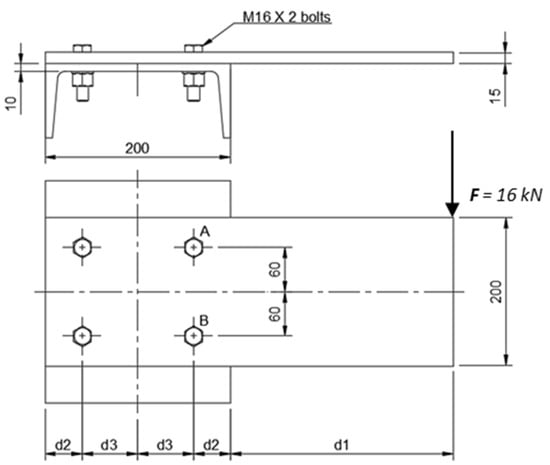
Figure 2.
The bolted plate.
The dimension variables of the bolted plate, , and , are considered as design variables. The design objective is to minimize the total length of the plate. Furthermore, two groups of constraints are considered to ensure the bolted plate remains operational: the strength of the bolted plate and the limits of the distance between the bolts. The strength of the bolted plate includes the contact stress between the bolts and the plate, , the bending stress, , of the plate along the vertical line connecting bolts A and B, and the tip deflection of the plate, . Their equations are expressed below in terms of design variables:
with the values of parameters, . Note that these equations are simplified from their physical models as the focus of this study is not on the individual equation but on the whole robust design formulation. The mathematical expression of the optimal design problem of the bolted plate can then be summarized as follows,
subject to two stress constraints and one tip deflection constraint,
and the dimension constraint,
The values of 14 and 3 in Equation (3) are the problem parameters, assigned as the maximum allowable stress and the displacement. Furthermore, the symbols, , denote the related constraint events.
This deterministic model will serve as a baseline for comparison with the results of different robust design models. The latter will represent all design variables, constraints, and the objective expressed in terms of random variables. In particular, the design variables in this study will be treated as normal and represented by their means and standard deviations, for . Consequently, those design variable-dependent responses, such as and , will be random as well. Many methods are available in the literature to compute the means and the standard deviations of random responses, including the Monte Carlo method, the perturbation method, the spectral expansion method, the reliability index analysis method, etc. As the focus of this study is placed on robust design optimization, the first-order Taylor’s series expansion [1,46] will be employed in this study for its simplicity in computing the means and standard deviation of any response function.
Consequently, the design variable-dependent quantities, such as, and , can be treated now as normal with the related mean and standard deviation approximated in terms of those of the assigned design variables, . In particular, the means and the standard deviations of the contact stress are approximated by,
where in Equation (5) are the mean and the standard deviation of the term, These statistical terms can be employed to measure not only the reliability or probability of failures of the constraint events, , and, but different levels of system reliabilities presented in the FTA formulation as well.
2.3. Robust Design and Reliability Index-Based Design Optimization
Robust design aims to control the uncertainty of the optimization solution by setting the minimal requirement of reliability for each constraint event. Specifically, the optimization formulation can be stated in terms of statistical terms of random variables such as
subject to the confidence level of success of each constraint event, which is measured in terms of event probability as,
where are the vectors of means and standard deviations of the design variables.
The value is a pre-determined probability, serving as the lower bound of the confidence level for each constraint event. The latter is measured by the corresponding standard normal variable, . Equation (7) can be further simplified if the means and the standard deviations of the constraint events are available. For the demonstration, the deterministic example problem presented by Equations (2) to (4) can be reformatted hereafter in the form of Equations (6) and (7).
The deterministic objective function of Equation (2) and the dimensional constraint of Equation (4) are related to the length measurements, and . These measurements can be bounded with natural tolerance to achieve 99.865% of confidence. For example, the objective, is set to be,
where is assumed to be normal with mean and standard deviation, . The optimal length of Equation (8) can be expressed explicitly in terms of the random design variables such as
It ensures that the total length of any plate has only a 0.135% chance of being longer than the one built based upon the optimized design variables. The same process can be applied to reformat the dimension constraint of Equation (4) to achieve a 99.865% of confidence.
As for the strength constraints described in Equation (3), their failure probabilities or reliabilities can also be fully quantified in terms of the means and the standard deviations of the associated constraint events. For example, once the terms and become available, as presented in Equation (5), the constraint event, in Equation (7) can now be explicitly expressed as
Since the probability function is one-to-one, the above constraint statement can be further simplified in terms of standard normal variables as,
The standard normal variable is in fact the reliability index of the constraint. Setting the term, , to be 1.65 leads to a value of reliability, . Consequently, the goal of the constraint of Equation (7) or Equation (10) is to enforce the optimal solution to achieve a 95.053% reliability for the constraint event, .
By setting the vectors of the means and the standard deviations of the design variables as and , the formulation of a robust design for the bolted plate problem can be summarized as follows,
subject to three reliability constraints related to strength, which are derived based on Equation (5)
and one related to two-dimension constraints derived from Equation (4) as,
Equation (13) can be combined into a single equation as,
Note that in Equation (5) are, respectively, the mean and the standard deviation of the term, The design derivatives of the above constraints with respect to a problem parameter, can be obtained analytically. For example, the design derivative of event defined in Equation (12), can be derived as
where the mean and the standard deviation of the event, , are treated as functions of the design variable, b. The availability of the above design derivatives can support a gradient-based robust design with improved computational efficiency.
2.4. Robust Design with System Failures Built by FTA
It is a common practice for a robust design to treat each constraint as independent, as presented in the example problem, in Equations (11)–(14). As a result, each of the three strength constraints presented in the optimal design problem, Equation (12), will achieve greater than 95.053% reliability. The system reliability of 3 simultaneously satisfied strength constraints can be expressed by . In the worst case, the probability of system failure of the optimal robust design is found to be 14.26% as follows,
Note that event , which is defined in Equation (9), uses the failure equation of a single bolt to model the strength reliability of a group of A and B bolts displayed in Figure 2 of the bolted plate.
To better control the robustness, three different FTA structures are developed to investigate the impact of different system reliability models of bolt joints on the results of robust design. The first robust design case uses the “and” gate to combine three individual failure events in Equation (12) together into one. The second case introduces the “or” gate in the design formulation to take advantage of the fact that two bolts are available, bolt A and bolt B, to resist the external load. The third case is an “inhibit” gate, which will take into consideration that the failure of one bolt will force the remaining one to carry more load. The robust design formulation for each of these three cases will be presented as follows, along with the design sensitivity analysis of its stress constraint event, .
2.4.1. Case 1: System Reliability with “and” Gate
The FTA structure of the first robust design formulation is displayed in Figure 3, which has two “and” gates, Gate 1 and Gate 2. Two basic events, and , representing the dimension constraints in Equation (13) are under Gate 1, while three events, and representing the strength constraints in Equation (12) are under Gate 2.
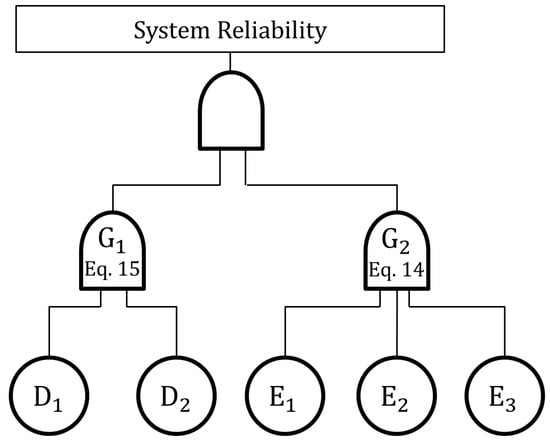
Figure 3.
FTA for robust design with “and” Gate. Change equation from Equations (13)–(15) and Equations (12)–(14).
The new robust design formulation is reformulated as,
subject to the reformatted strength reliability constraint
and the related dimension constraint as,
It has the same objective function and dimensional constraints as those of the traditional robust design. However, three strength constraints defined in Equation (12) are now combined into one single equation, Equation (16), to ensure that the system reliability of Gate 2 will be greater than 95.053% at the optimal design.
The design derivative of the failure probability with respect to a design variable, b, can be derived analytically as well, under the assumption that the probability follows normal distribution. Assume that the design variable, b, is related to the mean and the standard deviation of the event, . It leads to the computation of the design derivative of with respect to b as,
where the derivative of probability of the event, can be further derived as follows,
2.4.2. Case 2: System Reliability with “or” Gate
The bolted plate as shown in Figure 2 is bolted to the C-channel with four bolts. Two of them at joints A and B are subjected to the maximum contact stress constraint with equal value. This example will address the system reliability of the bolted plate which allows one of the bolts to fail due to high contact stress. The FTA structure of the reliability of event of the bolts in Figure 3 is now replaced by an “or” gate, , as shown in Figure 4, where and are the failure events of bolt A and bolt B, respectively. This replacement will ensure that the bolted plate is working as long as one bolt is still working. Consequently, the reliability defined in Equation (16) is revised as,
where the failure of the bolt joints, is defined by an “or” gate as,
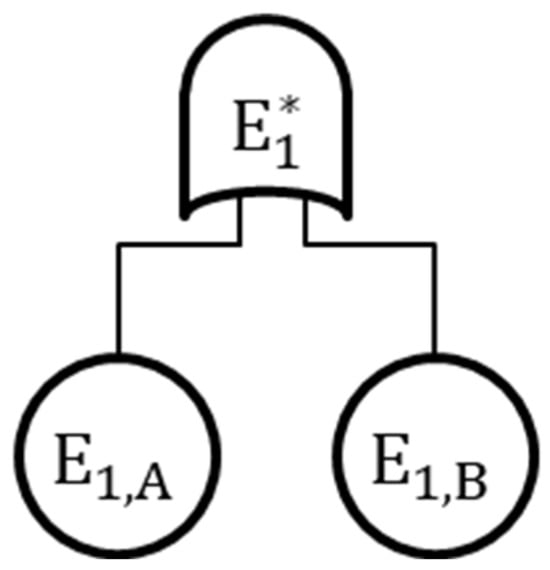
Figure 4.
Failure of bolt A or bolt B.
The terms, and , are the reliabilities of bolt A and bolt B, each of which is the same as defined in Equation (12) as being the failure event of a typical bolt. Therefore, the related robust design formulation is presented as,
subject to the newly defined reliability constraint,
and the other related to the dimension constraint as,
In this case, the design sensitivity of with respect to b is the same as the case of Equation (19). However, the design derivative of the constraint, , needs to be revised as,
2.4.3. Case 3: System Reliability with “Inhibit” Gate
One may consider a practical case that if either bolt A or bolt B fails, the remaining one will be available to carry more load. To take this into consideration, the conditional probability of the remaining bolt, denoted by will replace the independent in Equation (12) to account for 40% of the load increase as represented below in Equation (26),
The failure of the group of two bolt joints, is now defined by an “inhibit” gate as demonstrated in the FTA structure of Figure 5 as,
where represents the reliability of bolt A if bolt B fails. Since bolt A and bolt B have the same failure mode as described by Equation (12), , both of which can be simply denoted as . Moreover, the event considers the case when both bolts are working properly.
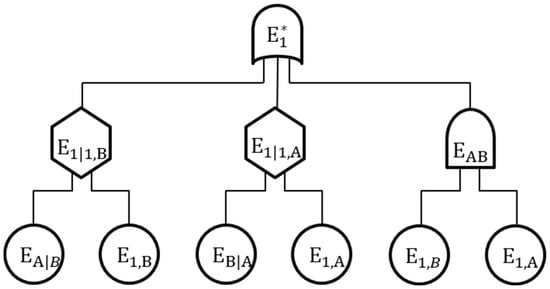
Figure 5.
Conditional failure of the second bolt after one of two bolts fails.
As a result, the revised robust design formulation is presented as,
subject to the further revised constraint,
and the other one related to the dimension constraint as,
The design derivative of the new constraint, , is now found to be,
where the design derivative of the conditional probability, , is given by, based upon Equation (26),
2.5. Post-Optimality Design Sensitivity Analysis
The robust design optimization formulations have incorporated randomness into most of its variables and constraints as presented in Section 2.3. However, some variables in those formulations are still treated as deterministic such as the lower bound of the allowable reliability and the maximum allowable stress. Therefore, it would be beneficial to confirm and investigate whether the variations in such deterministic parameters could improve or hurt the optimal solution. The efficient way to resolve this issue can be achieved by conducting sensitivity analysis of the optimal solutions with respect to those deterministic parameters if the value of Lagrange multiplier becomes available as part of the optimal solutions. Specifically, the design derivative of the optimized objective, , with respect to a problem parameter, , in the optimal solution can be computed as follows [47],
where is the vector of active constraints evaluated at the optimal solution and is the associated vector of the Lagrange multipliers. The proof of the above equation can be found in Appendix A.
By taking the bolted plate design problem as an example, it would be of interest to find out what the impact will be on the optimal objective by altering two parameters, and , which are not treated as design variables presented in the robust design formulations. Specifically, is assigned to be the lower bound of the reliability of the bolt stress constraint and , the magnitude of the maximum allowable bolt stress. As a result, the bolt strength constraint in Equation (12) of the robust design problem can now be recast as,
The optimal solutions of the robust designs presented in Section 2.3 are obtained based upon the assigned values of the problem parameters of concern: and . The equations to compute the changes in the optimal objective with respect to the perturbation of each of the designated problem parameters, , can be expressed below, based upon Equation (33),
where of Equation (34) is the only active constraint at the optimal solutions of all robust design examples, and is the associated Lagrange multiplier.
Next, the sensitivity analysis of the optimal objective of the “and” gate-based design formulation with respect to the change in problem parameters can be conducted by following the same process presented above. However, in this time, the active constraint equation of the event is Equation (16) which is rewritten with two problem parameters as,
where the first problem parameter , is assigned with a value of 0.95053, and the second problem parameter, , 14. The perturbation of the optimal objective caused by the perturbation of the first problem parameter, is found to be,
which is in the same form of Equation (35), derived based upon the traditional robust design. However, the values of can be different as the corresponding values of the Lagrange multipliers are different. As for the value of due to the perturbation of alone, it can be computed by,
where the derivative of the reliability, with respect to is found to be,
Similarly, the post-optimality sensitivity analysis of the “or” gate-based design solution with respect to the changes in problem parameters can be computed in the same process as presented above. In this case, however, the active constraint of the “or” gate problem is defined by Equation (21) as,
which leads to a way to compute the perturbations of the optimal objective function at the optimal design variables with respect to as,
and
Again, the above Equation (42) is in the same form as the early Equation (35).
As for the post-optimality sensitivity analysis of the “inhibit” gate-based design solution, the perturbation equation of the optimal objective, , generated by the perturbation is in the same form of Equation (42). However, the perturbation equation of the optimal objective, , with respect to in the case with “inhibit” gate can be computed as,
where the constraint, , is specified as, based upon Equation (27),
and the design derivative of with respect to can be found by Equation (40), while the design derivative of at is found to be,
which is like that of presented earlier by Equation (40).
3. Numerical Results
The numerical study presented in this section is to demonstrate and validate that the robust design can incorporate FTA to enhance its capability to handle a design problem with uncertainty. This presentation is organized into three subsections. Section 3.1 investigates the impact of different robust design formulations on the optimal design solutions. The last two sub-sections look at the effects of the variation in problem parameters on the optimal solutions, which are not part of the design variables. Section 3.2 conducts a post-optimality sensitivity analysis of the optimal solutions with respect to two parameters, the system reliability and the upper bound of the bolt contact stress. The system failure in this case is set to be 95.05%. Finally, Section 3.3 extends the above study to cover a range of variations in system reliability from 95.05% to 99.99%. The optimal results affected by such variations will be investigated in detail, which include the optimal design variable, , the active Langange multiplier corresponding to the contact stress constraint of the bolt joints and the design derivative of reliability of the bolt-joint contact stress with respect to the upper bound of the allowable stress.
3.1. Robust Design Optimization
Five different robust design problem formulations presented in Section 2.2 and Section 2.3 will be solved numerically in this section. They are summarized hereby for further reference:
- Deterministic Design Optimization: Equations (2)–(4).
- Robust Design with Reliability-Indices: Equations (11)–(13).
- Robust Design with “and” Gate: Equations (15)–(17).
- Robust Design with “or” Gate: Equations (22)–(24).
- Robust Design with “Inhibit” Gate: Equations (28)–(30).
Two sets of results are reported in this section: one focuses on the optimal solution of these five robust designs, and the other on their related post-optimality analyses. The latter mainly aims to investigate the sensitivity of the optimal solutions with respect to the problem parameters which are not treated as design variables in the robust design. This effort ensures that the robust design formulation and solution investigated here is comprehensive and useful for design consideration.
The deterministic design optimization considers only the mean values as the design values, starting with the initial values, . It produces an initial objective function of 580 while violating the third constraint, . The optimal design of this deterministic problem generated by the Matlab built-in function, fmincon, is . The design variables, , hit their lower bounds. The optimal objective is 319.6463 and the first constraint, is tight and is associated with the Lagrange multiplier, 11.2439, in the optimal design. By setting the perturbation of the optimal solution in this case can be simply calculated based upon Equation (35) as . This deterministic model presented above will serve as a baseline for comparison with the results of robust design models.
All robust design problems start with initial mean values of the design variables, , and the associated standard deviations, . Their lower bounds are set to be (150, 20, 50, 3, 0.5, 0.75). The initial design produces an objective function of 685 which violates two constraints associated with and . The optimal solutions by solving these robust design formulations produce very similar results. The optimal values of all six design variables hit their lower bounds, except the mean of the third design variable, . Besides the optimal design variables and the optimal objective, the active constraint and its associated Lagrange multipliers are also demanded as output. The details of the optimal results are listed in Table 2 and Table 3.

Table 2.
Optimal results of proposed optimization formulations. RD and MC are for robust design and Monte Carlo respectively.

Table 3.
Perturbations of optimal objective.
The bolt stress event is the major concern in the robust design process. In this study, its reliability is approximated by the first-order Taylor’s series expansion as stated by Equation (5). To validate the results, the optimized reliabilities of bolt stress event, are validated by the results of Monte Carlo simulation with samples. The results are listed in Table 2 in the last two columns, RD and MC, which are the results from robust design and Monte Carlo simulation, respectively.
3.2. Post-Optimality Sensitivity Analysis
The results of the post-optimality sensitivity analysis are summarized in Table 3. These sensitivity results are evaluated at different optimal solutions reported in Table 2. In particular, the results of the changes in the optimal objective, , under the column of the post-optimality sensitivity analysis in Table 3, are produced by using the analytical equations presented in Section 2.4, in which the Lagrange multipliers are obtained in a single optimization run based upon the initial values of and In the initial optimal design run, is set to be 95.053%, while , 14. These results are validated by comparing with the results of obtained by finite differencing between the original and the perturbed optimal objectives. The finite differencing results are obtained with a total of three optimization runs. One is based upon the initial values of problem parameters, and , and two others are run by perturbing one of these two parameters at a time.
In this specific example, the traditional robust design produces an optimal result like that of the design with a single “and” gate. As for the case of an “or” gate with a redundant bolt joint, it produces a lighter design with lower target reliability requirement as shown in Figure 6. Furthermore, the sensitivity analyses of the optimal objectives are performed for each design formulation with respect to two problem parameters: , where is the lower bound of the reliability and is the other maximum allowable stress. The results of the sensitivity analyses are then applied to estimate the changes in the optimal objective, . These analytical results are compared well with those obtained by the finite differencing. The results of Table 3 show that the change in the upper bound of the allowable stress will affect the optimal objective with the same amount. On the other hand, a change in the reliability will impact the “and” gate more than the “or” gate.
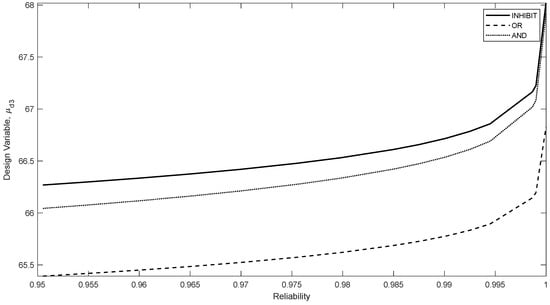
Figure 6.
Optimal vs. required system reliability.
3.3. Design Evolution by Increasing System Reliability
The optimal results affected by variations in the wide range of system reliability from 95.05% to 99.99% will be investigated in detail in this section. These results are obtained by solving three different robust design formulations with “and”, “or” and “inhibit” gates. In particular, the optimal results will be investigated, which include the optimal design variable, , the active Lagrange multiplier corresponding to the stress constraint of the bolt joints and the design derivative of reliability of the bolt-joint contact stress with respect to the upper bound of the allowable stress.
Figure 6 displays the relations between the optimal values of and the reliability of stress constraint of the bolt joints. The constraint of the “and” gate requires the optimal of a single bolt satisfying the required contact-stress reliability. On the other hand, the “or” gate has two identical bolts, one of which can be used as back-up to reduce the risk. Therefore, the required size of of “or” gate can be smaller than that of the “and” gate. The design problem of the “inhibit” gate also has two bolts, if any one of which fails, the remaining one needs to carry a 40% increase in the applied load. As such, the optimal of the “inhibit” gate has the larger value among all three robust design cases.
Figure 7 displays the relations between the Lagrange multiplier, , associated with the reliability of the stress constraint of the bolt joints. Based upon Equation (35), the value of is equal to the derivative of the optimal objective function, , with respect to parameter , which in this case is the targeted system reliability. Note that only one design variable among six, which is , is different among all results produced by different robust design formulations subject to different values of targeted system reliability. Consequently, the design derivative of , with respect to parameter , is equal to that of with respect to . This conclusion can be revealed by comparing the slopes of the curves presented in Figure 6 with the corresponding ones in Figure 7. Specifically, the slope of the “and” gate curve in Figure 6 is slightly larger than that of the “inhibit” gate for reliability less than 99%. As a result, the curve of the value of the “and” gate is notably higher than that of the “inhibit” gate in Figure 7.
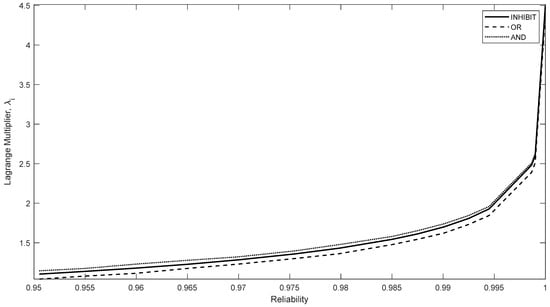
Figure 7.
Lagrange multiplier, vs. required system reliability.
Figure 8 shows the trend of the design derivative of the system reliability of Gate 2, with respect to the second problem parameter, , which is the maximum allowable stress in constraint . The Gate 2 event models the state of the bolt-joint stress, while the value of is set to be 14 for all robust design problems. Since at all optimal solutions, the design derivatives of concern can be expressed as follows, based upon Equations (18), (23) and (29) for “and”, “or” and “inhibit” gates, respectively:
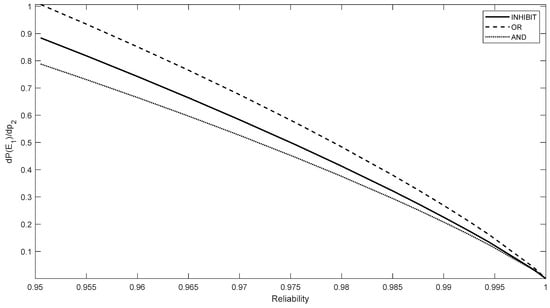
Figure 8.
vs. required system reliability.
Note that the curve of the derivative value of the “or” gate is higher than that of the “and” gate, while that of the “inhibit” gate falls in between. This is understandable as the increase in the constraint bound on a bolt joint will benefit the “or” gate more than the “and” gate, as the former one has two bolts while the latter has only one. Note that all three curves approach zero while the reliability reaches the right end tail of the normal distribution where the function curve is flat with its value close to 1.
4. Discussion
The goal of this research is to enhance the capability of robust design optimization to handle real-world applications. To this end, the fault tree analysis is incorporated in the constraint formulation, which enables the optimization problem to model different levels of system reliabilities. Furthermore, post-optimality analysis is conducted in this study to investigate the stability of the optimal robust design solution with respect to deterministic problem parameters such as the lower bound of reliability and the maximum allowable stress, which are not considered as design variables.
The FTA has wide applications to deal with more sophisticated stochastic modeling. This work represents an initial intent to reach this goal. It applies only “and”, “or” and “inhibit” gates in the FTA structure in the current optimization formulations. Nevertheless, it has paved the way to incorporate more complicated models of FTA such as the fuzzy set theory and dynamic FTA in the robust design optimization formulation.
Also, in regard to the more complex dynamic dependencies briefly mentioned earlier, FTA was chosen based its usefulness in representing the top-down relationship of a system-level event to various intermediate and basic (lowest level) events. For statistical dependencies between events and time-dependent failures, a Markov chain could be used to simulate the failure probabilities of the subset of the FTA structure representing the dependent failure events. In other words, the Markov chain would be used to handle the quantitative portion of the subset of dependent failure events in the FTA structure as in [37]. Although not pursued by the authors in this study, a Bayesian network could be used to model complex statistical dependencies, which the authors find compelling for investigation in the future after the potential usefulness of FTA for robust design has been fully explored [40].
In the case of future research involving more complex dynamic or dependent events in the FTA structure, Markov chains could be used by incorporating this dynamic state modeling to make full use of the FTA structure and its main benefit stated earlier, which is to represent the full system-level reliability in a top-down hierarchical system model.
After the qualitative work of the FTA was carried out, the reliability index method was used in this study to estimate the probabilities of the basic events. At this moment, its applications are limited to statistically independent events. To broaden the applications of stochastic design optimization, Monte Carlo simulation could also be applied in future research to directly estimate the probabilities of different events whether they are statistically independent or not.
Author Contributions
Conceptualization, G.J.-W.H. and J.D.; methodology, G.J.-W.H.; software, J.D.; validation, J.D. and G.J.-W.H.; formal analysis, J.D.; investigation, G.J.-W.H.; resources, J.D.; data curation, G.J.-W.H.; writing—original draft preparation, G.J.-W.H.; writing—review and editing, J.D.; visualization, J.D.; supervision, G.J.-W.H.; project administration, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Set to represent the vector of collected parameters. One can rewrite the objective function at the optimal design point in a general form as,
where the constraint vector, is a collection of all tight constraints at the optimal solution, and are the Lagrange multipliers associated with the tight constraints. Note that at the optimal design, , , and The design derivative of Equation (A1) with respect to any problem parameter, , is obtained as,
The final equality resulted by the substitution of the conditions, and the Kuhn–Tucker necessary condition at the optimal solution. Finally, the sensitivity of the optimal objective function with respect to a problem parameter is specified as,
The above equation is valid only if functions of concern are continuous and the active constraint set will not be changed under the change in the problem parameters.
References
- Haldar, A.; Mahadevan, A. Probability, Reliability and Statistical Methods in Engineering Design; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Ghanem, R.; Spanos, P. Stochastic Finite Elements—A Spectral Approach, 1st ed.; Springer: New York, NY, USA, 1991. [Google Scholar]
- Isukapalli, S.S.; Roy, A.; Georgopoulos, P.G. Efficient Sensitivity/Uncertainty Analysis Using the Combined Stochastic Response Surface Method and Automated Differentiation: Application to Environmental and Biological Systems. Risk Anal. 2000, 20, 591–602. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener--Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Kim, N.H.; Wang, H.; Queipo, V. Efficient Shape Optimization under Uncertainty using Polynomial Chaos Expansions and Local Sensitivities. AIAA J. 2006, 44, 1112–1116. [Google Scholar] [CrossRef][Green Version]
- Huang, B.; Du, X. A Robust Design Method using Variable Transformation and Gauss-Hermite Integration. Int. J. Numer. Meth. Eng. 2006, 66, 1841–1858. [Google Scholar] [CrossRef]
- Kamiński, M. Potential Problems with Random Parameters by the Generalized Perturbation-Based Stochastic Finite Element Method. Comput. Struct. 2010, 88, 437–445. [Google Scholar] [CrossRef]
- Navarro-Quiles, A.; Laudani, R.; Giovanni, G. A New Stochastic Method Based on the Taylor Expansion to Compute Response Probability Densities of Uncertain Systems. Int. J. Numer. Meth. Eng. 2023, 124, 1111–1127. [Google Scholar] [CrossRef]
- Moustapha, M.; Sudret, B.; Bourinet, J.-M.; Guillaume, B. Quantile-Based Optimization under Uncertainties Using Adaptive Kriging Surrogate Models. Struct. Multidiscip. Optim. 2016, 54, 1403–1421. [Google Scholar] [CrossRef]
- Ren, X.; Rahman, S. Stochastic Design Optimization Accounting for Structural and Distributional Design Variables. Eng. Comput. 2018, 35, 2654–2695. [Google Scholar] [CrossRef]
- Xu, H.; Rahman, S. A Generalized Dimension-Reduction Method for Multidimensional Integration in Stochastic Mechanics. Int. J. Numer. Meth. Eng. 2004, 61, 1992–2019. [Google Scholar] [CrossRef]
- Rahman, S. A Polynomial Dimensional Decomposition for Stochastic Computing. Int. J. Numer. Meth. Eng. 2008, 76, 2091–2116. [Google Scholar] [CrossRef]
- Barthelemy, J.-F.M.; Sobieszczanski-Sobieski, J. Extrapolation of Optimum Design Based on Sensitivity Derivatives. AIAA J. 1983, 21, 797–799. [Google Scholar] [CrossRef]
- Barthelemy, J.-F.M.; Sobieszczanski-Sobieski, J. Optimum Sensitivity Derivatives of Objective Functions in Nonlinear Programming. AIAA J. 1983, 21, 913–915. [Google Scholar] [CrossRef]
- Tu, J.; Choi, K.K. A New Study on Reliability-Based Design Optimization. J. Mech. Des. 1999, 121, 557–564. [Google Scholar] [CrossRef]
- Hou, G.J.-W. A Most Probable Point-Based Method for Reliability Analysis, Sensitivity Analysis, and Design Optimization; NASA/CR-2004-213002; National Aeronautics and Space Administration, NASA Langley Research Center: Hampton, VA, USA, 2004. Available online: https://ntrs.nasa.gov/citations/20040045166 (accessed on 8 November 2024).
- Youn, B.D.; Choi, K.K. Hybrid Analysis Method for Reliability-Based Design Optimization. J. Mech. Des. 2003, 125, 221–232. [Google Scholar] [CrossRef]
- Du, X.; Chen, W. Sequential Optimization and Reliability Assessment Method for Efficient Probabilistic Design. J. Mech. Des. 2004, 126, 225–233. [Google Scholar] [CrossRef]
- Yang, R.J.; Gu, L. Experience with Approximate Reliability Based Optimization Method. Struct. Multidisc. Optim. 2004, 26, 152–159. [Google Scholar] [CrossRef]
- Gumbert, C.R.; Newman, P.A.; Hou, G.J.-W. High-Fidelity Computational Optimization for 3-D Flexible Wings: Part II—Effect of Random Geometric Uncertainty on Design. Optim. Eng. 2005, 6, 139–156. [Google Scholar] [CrossRef]
- Cho, T.M.; Lee, B.C. Reliability-Based Design Optimization Using Convex Linearization and Sequential Optimization and Reliability Assessment Method. Struct. Saf. 2011, 33, 42–50. [Google Scholar] [CrossRef]
- Doltsinis, I.; Kang, Z. Robust Design of Structures Using Optimization Methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 2221–2237. [Google Scholar] [CrossRef]
- Zhang, W.; Kang, Z. Robust Shape and Topology Optimization Considering Geometric Uncertainties with Stochastic Level Set Perturbation. Int. J. Numer. Meth. Eng. 2017, 110, 31–56. [Google Scholar] [CrossRef]
- Meng, D.; Yang, H.; Yang, S.; Zhang, Y.; De Jesus, A.M.P.; Correia, J.; Fazeres-Ferradosa, T.; Macek, W.; Branco, R.; Zhu, S.P. Kriging-Assisted Hybrid Reliability Design and Optimization Of Offshore Wind Turbine Support Structure Based On A Portfolio Allocation Strategy. Ocean Eng. 2024, 295, 116842. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; De Jesus, A.M.P.; Fazeres-Ferradosa, T.; Zhu, S.P. A Novel Hybrid Adaptive Kriging And Water Cycle Algorithm For Reliability-Based Design And Optimization Strategy: Application In Offshore Wind Turbine Monopile. Comput. Methods Appl. Mech. Eng. 2023, 412, 116083. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, B.; Lu, F. A Reliability-Based Robust Design Optimization Method for Rolling Bearing Fatigue under Cyclic Load Spectrum. Mathematics 2023, 11, 2843. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, B.; Lu, F. An Adaptive Kriging-Based Fourth-Moment Reliability Analysis Method for Engineering Structures. Appl. Sci. 2024, 14, 3247. [Google Scholar] [CrossRef]
- Liao, H.; Elsayed, E.A. Optimization of System Reliability Robustness Using Accelerated Degradation Testing. In Proceedings of the 51st Annual Reliability and Maintainability Symposium, Alexandria, VA, USA, 24–27 January 2005. [Google Scholar] [CrossRef]
- Babonneau, F.; Gilbert, D.; Piller, O.; Vial, J.P. Robust Optimal Design of a Tree-based Water Distribution Network with Intermittent Demand. Eur. J. Oper. Res. 2024, 319, 834–844. [Google Scholar] [CrossRef]
- Wang, C.; Fan, H.; Qiang, X. A Review of Uncertainty-Based Multidisciplinary Design Optimization Methods Based on Intelligent Strategies. Symmetry 2023, 15, 1875. [Google Scholar] [CrossRef]
- Veyna, U.; Blasco, X.; Pajares, A. Strategy for Obtaining Robust Solutions in Multi-objective Design with Uncertainties. Appl. Math. Model. 2025, 138, 115767. [Google Scholar] [CrossRef]
- Shahraki, A.F.; Noorossana, R. Reliability-Based Robust Design Optimization: A General Methodology Using Genetic Algorithm. Comput. Ind. Eng. 2014, 74, 199–207. [Google Scholar] [CrossRef]
- Ortmeier, F.; Reif, W. Safety Optimization: A Combination of Fault Tree Analysis and Optimization Techniques. In Proceedings of the International Conference on Dependable Systems and Networks, Florence, Italy, 28 June–1 July 2004. [Google Scholar] [CrossRef]
- Krasich, M. Fault Tree Analysis for Product Reliability Improvement. In Proceedings of the Annual Reliability and Maintainability Symposium, Alexandria, VA, USA, 24–27 January 2005. [Google Scholar]
- Baig, A.A.; Ruzli, R.; Buang, A.B. Reliability Analysis Using Fault Tree Analysis: A Review. Int. J. Chem. Eng. Appl. 2013, 4, 169–173. [Google Scholar] [CrossRef]
- Ruijters, E.; Stoelinga, M. Fault Tree Analysis: A Survey of the State-of-the-Art in Modeling, Analysis and Tools. Comput. Sci. Rev. 2015, 15–16, 29–62. [Google Scholar] [CrossRef]
- Andrews, J.; Tolo, S. Dynamic and Dependent Tree Theory (D2T2): A Framework for The Analysis of Fault Trees with Dependent Basic Events. Reliab. Eng. Syst. Saf. 2023, 230, 108959. [Google Scholar] [CrossRef]
- Martinez, J.; Eguia, A.; Urretavizcaya, I.; Negro, P.L. Fault Tree Analysis and Failure Modes and Effects Analysis for Systems with Artificial Intelligence: A Mapping Study. In Proceedings of the IEEE 7th International Conference on System Reliability and Safety, Bologna, Italy, 22–24 November 2023; pp. 464–473. [Google Scholar] [CrossRef]
- Shao, T.; Lin, Z.; Krishnamurty, S.; Grosse, I.R.; Osterwell, L.J. Automated Fault Tree Analysis for Engineering Design Optimization. In Proceedings of the ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Volume 5: 6th International Conference on Multibody Systems, Nonlinear Dynamics, and Control, Parts A, B, and C, Las Vegas, NV, USA, 4–7 September 2007; pp. 589–598. [Google Scholar] [CrossRef]
- Sun, J.; Bathgate, K.; Zhang, Z. Bayesian Network-Based Resilience Assessment of Interdependent Infrastructure Systems under Optimal Resource Allocation Strategies. Resilient Cities Struct. 2024, 2, 46–56. [Google Scholar] [CrossRef]
- Sezer, S.I.; Ceylan, B.O.; Akyuz, E.; Gardoni, P. Improved Z-Number and Fault Tree Analysis to Predict the Risk of Air Pollution due to Ship Boiler Operation. Mar. Pollut. Bull. 2024, 206, 116801. [Google Scholar] [CrossRef]
- Sun, H.; Li, H.; Fan, F.; Wang, P.; Yin, F.; Liang, Z. Waste Smartphone Disassembly Fault Detection Based upon Fuzzy Set Fault Tree Analysis. Procedia CIRP 2022, 105, 553–558. [Google Scholar] [CrossRef]
- Li, F.; Meng, G.; Sha, L.; Zhou, L. Robust Optimization Design for Fatigue Life. Finite Elem. Anal. Des. 2011, 47, 1186–1190. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Yan, Q.; Hu, Y.; Wang, C.; Luo, W.; Cai, B. A Dynamic Failure Analysis Methodology for Fault Diagnosis of Fatigue Cracks of Subsea Wellhead Connectors with Material Aging. Process Saf. Environ. Prot. 2022, 159, 36–52. [Google Scholar] [CrossRef]
- Arsic, D.; Kirin, S.; Nikolic, R.; Nikolic, R.; Arsic, A.; Radovic, L. Probabilistic Approach and Fault-Tree Analysis for Increased Bucket Wheel Excavator Welded Joints Reliability. Procedia Struct. Integr. 2022, 42, 189–195. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design, 11th ed.; McGraw Hill: New York, NY, USA, 2020. [Google Scholar]
- Belegundu, A.D.; Chandrupatlia, T.R. Optimization Concepts and Applications in Engineering, 3rd ed.; Cambridge University Press: New York, NY, USA, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).