Author Contributions
Methodology, Investigation, Writing—Review and Editing—Funding Acquisition, N.A.J., I.Y.H.; Validation, Funding Acquisition, Writing—Review and Editing, O.I.A.; Formal Analysis, Writing—Review and Editing, Funding Acquisition, Resources, M.N.M. All authors have read and agreed to the published version of the manuscript.
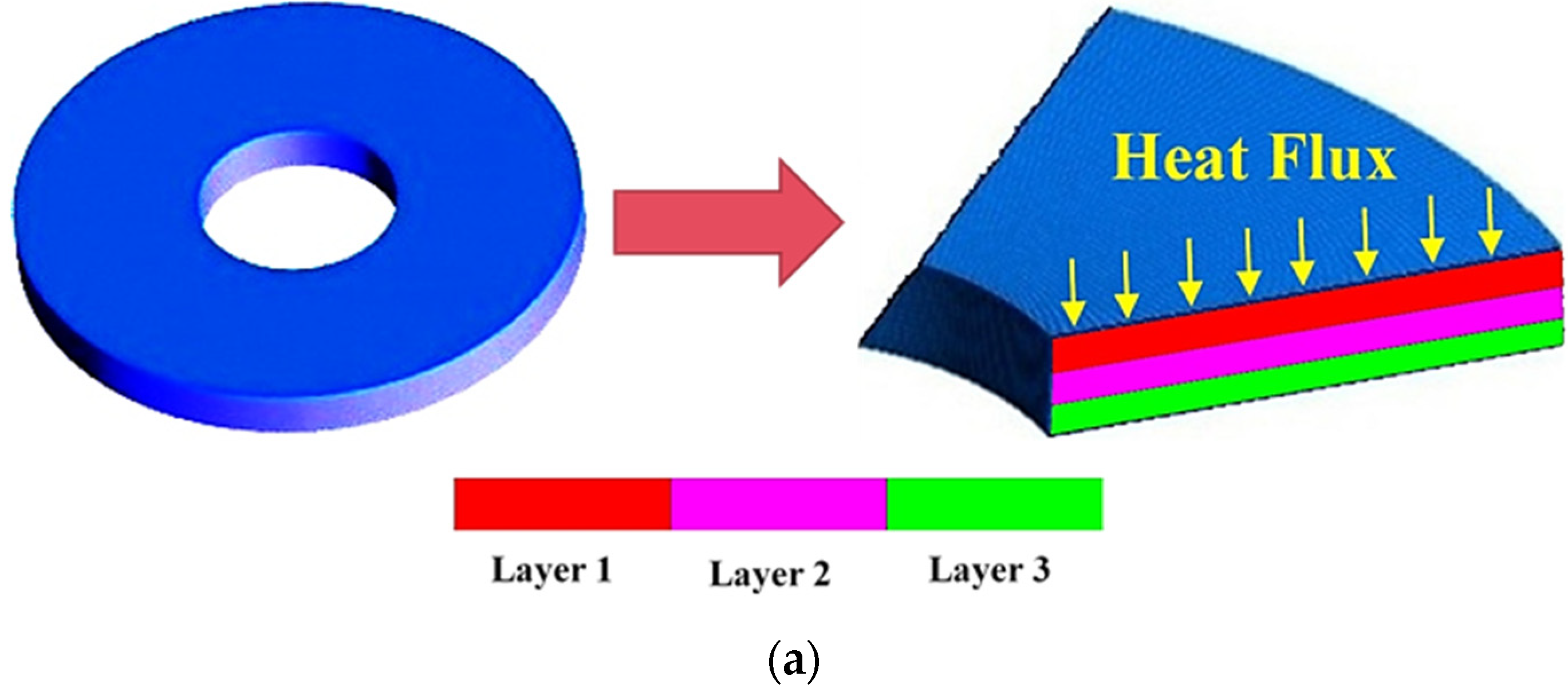
Figure 1.
Details of the frictional facing: (a) the layer arrangement and (b) the dimensions.
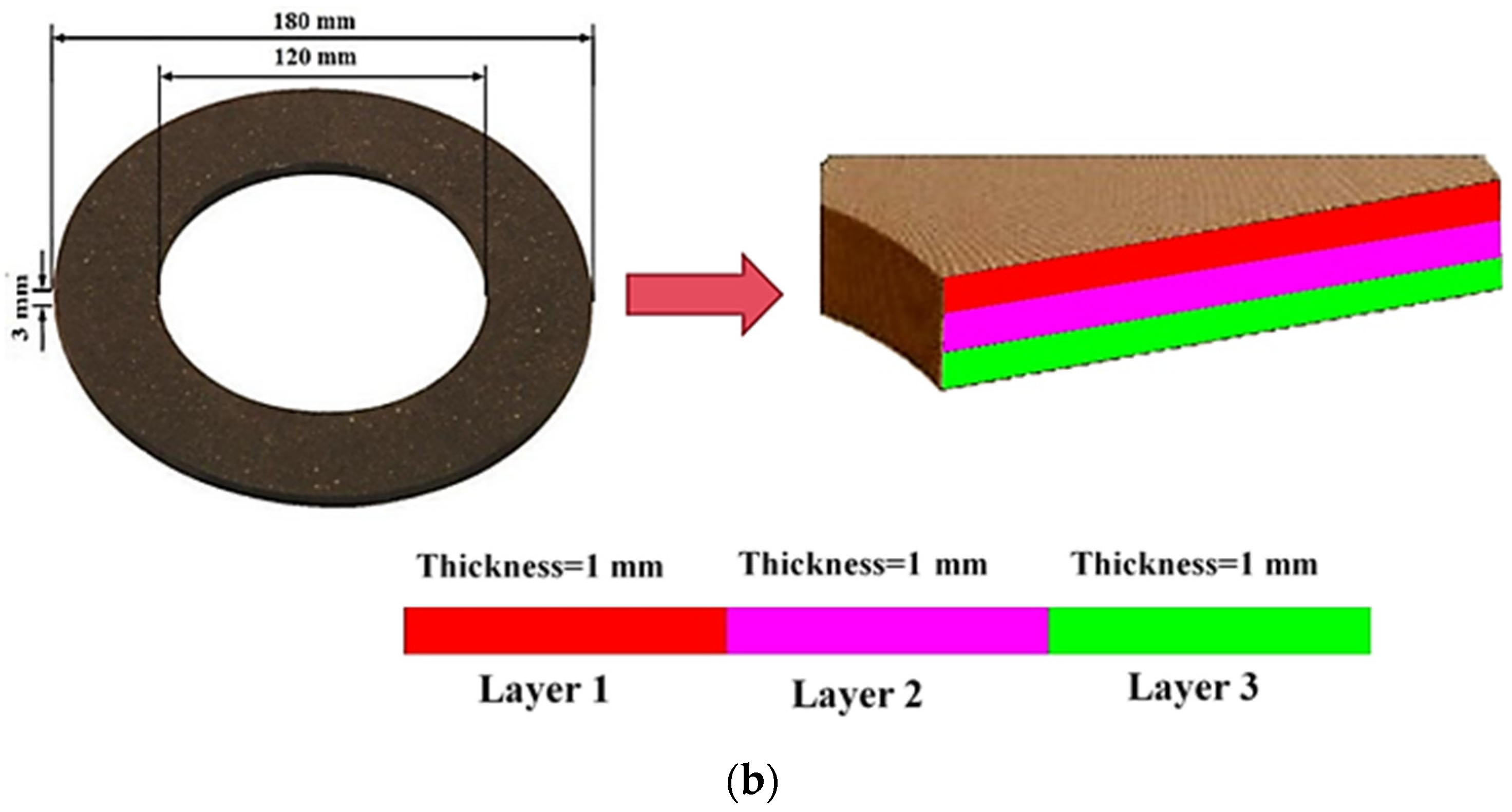
Figure 1.
Details of the frictional facing: (a) the layer arrangement and (b) the dimensions.
Figure 2.
The manufacturing devices: (a) the pressing machine and (b) the die.
Figure 2.
The manufacturing devices: (a) the pressing machine and (b) the die.
Figure 3.
The final product of the clutch disc using FGM.
Figure 3.
The final product of the clutch disc using FGM.
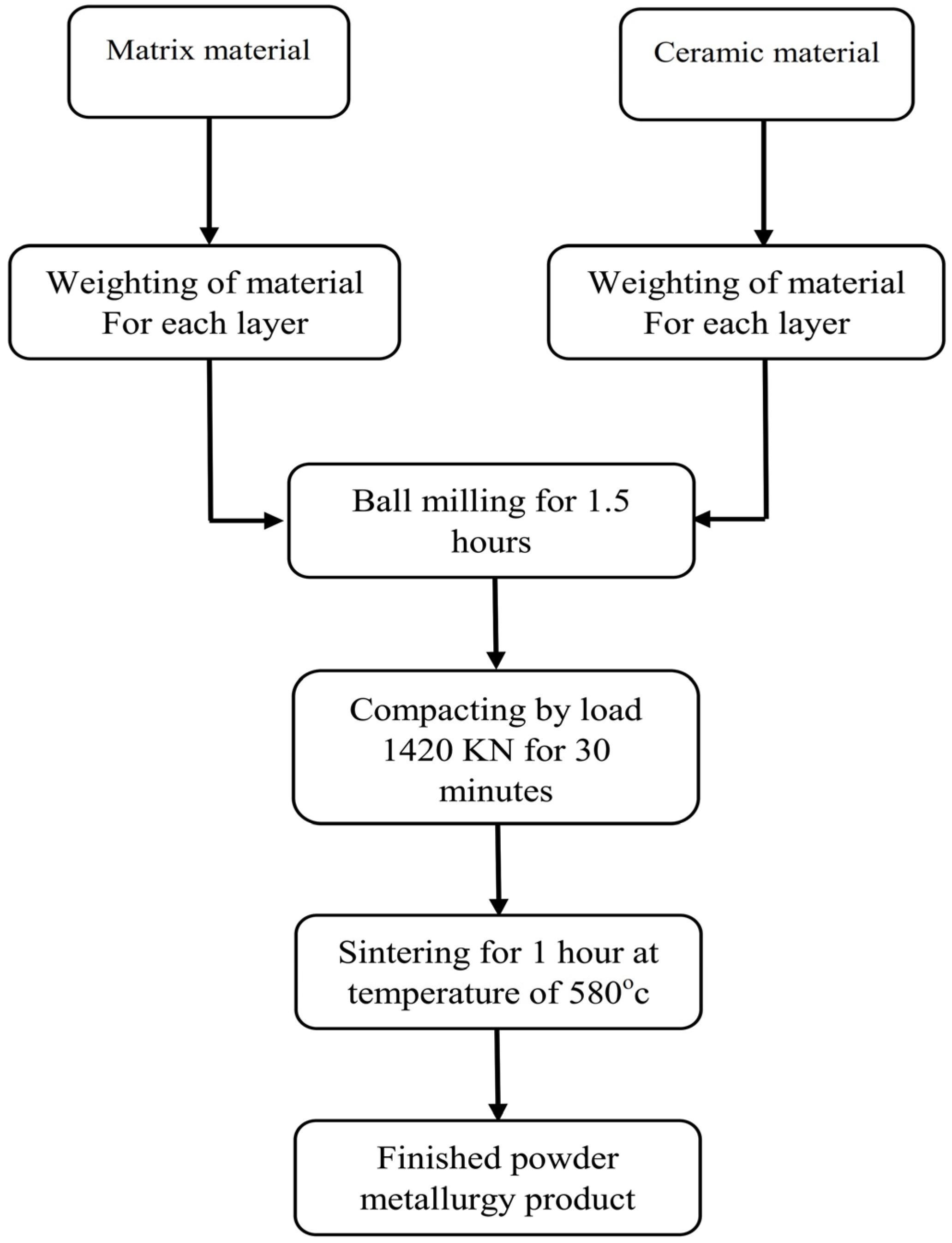
Figure 4.
The manufacturing steps of the FGM clutch disc.
Figure 4.
The manufacturing steps of the FGM clutch disc.
Figure 5.
The developed test rig of the dry clutch system.
Figure 5.
The developed test rig of the dry clutch system.
Figure 6.
The distribution of thermocouples on the flywheel and the pressure plate parts.
Figure 6.
The distribution of thermocouples on the flywheel and the pressure plate parts.
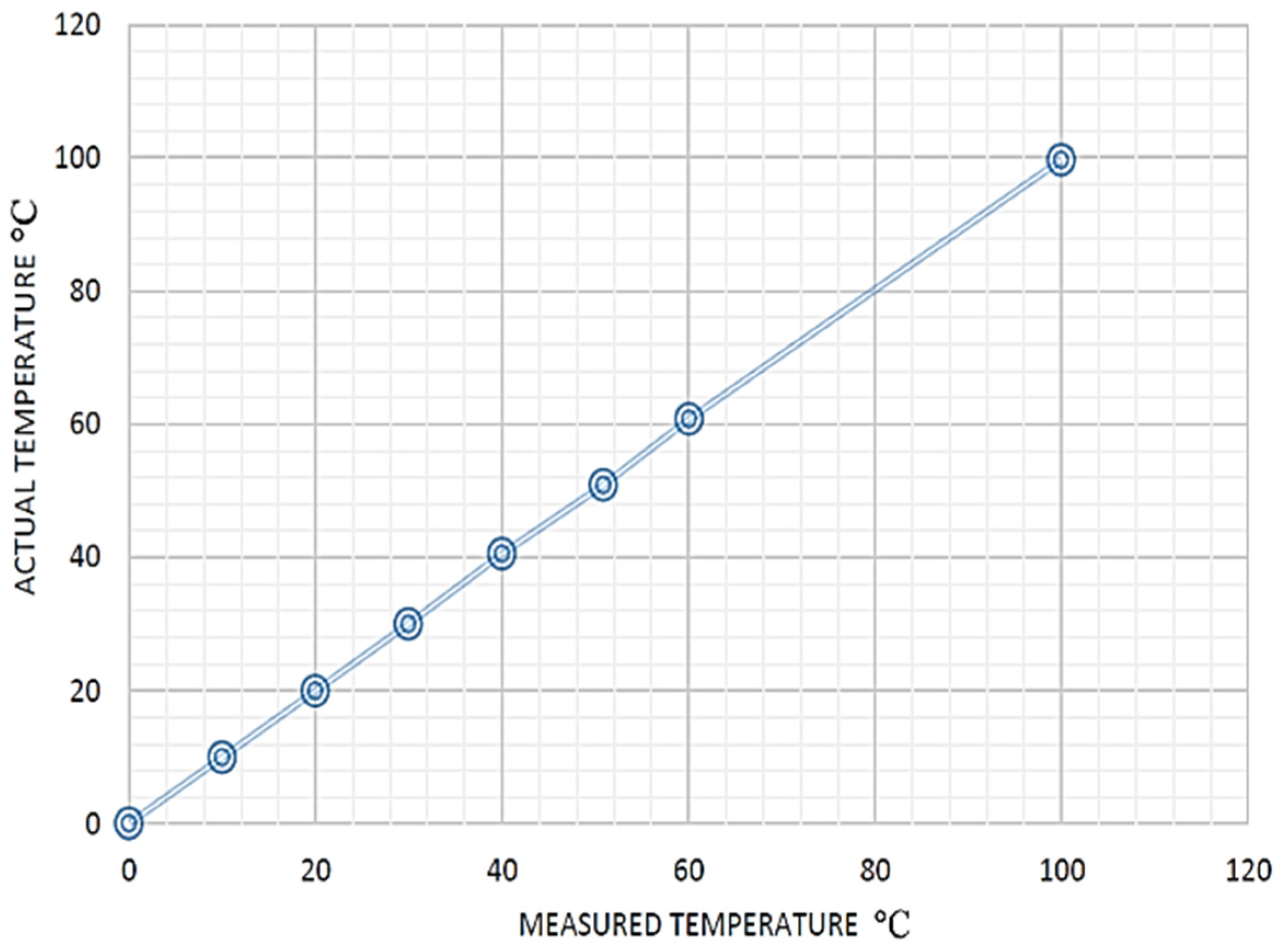
Figure 7.
Thermocouple calibration.
Figure 7.
Thermocouple calibration.
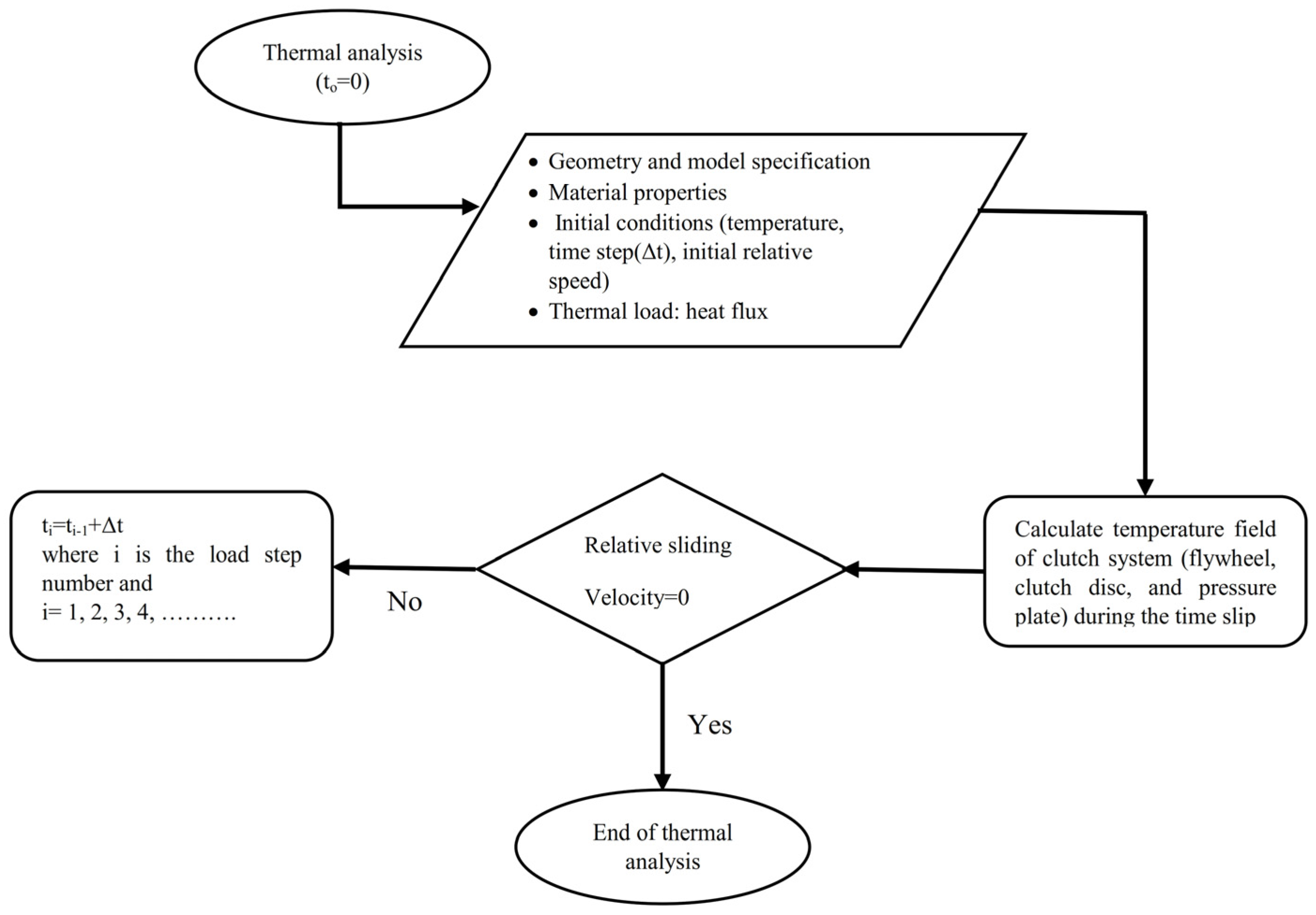
Figure 8.
The flowchart depicts the finite element solution of a thermoelastic problem.
Figure 8.
The flowchart depicts the finite element solution of a thermoelastic problem.
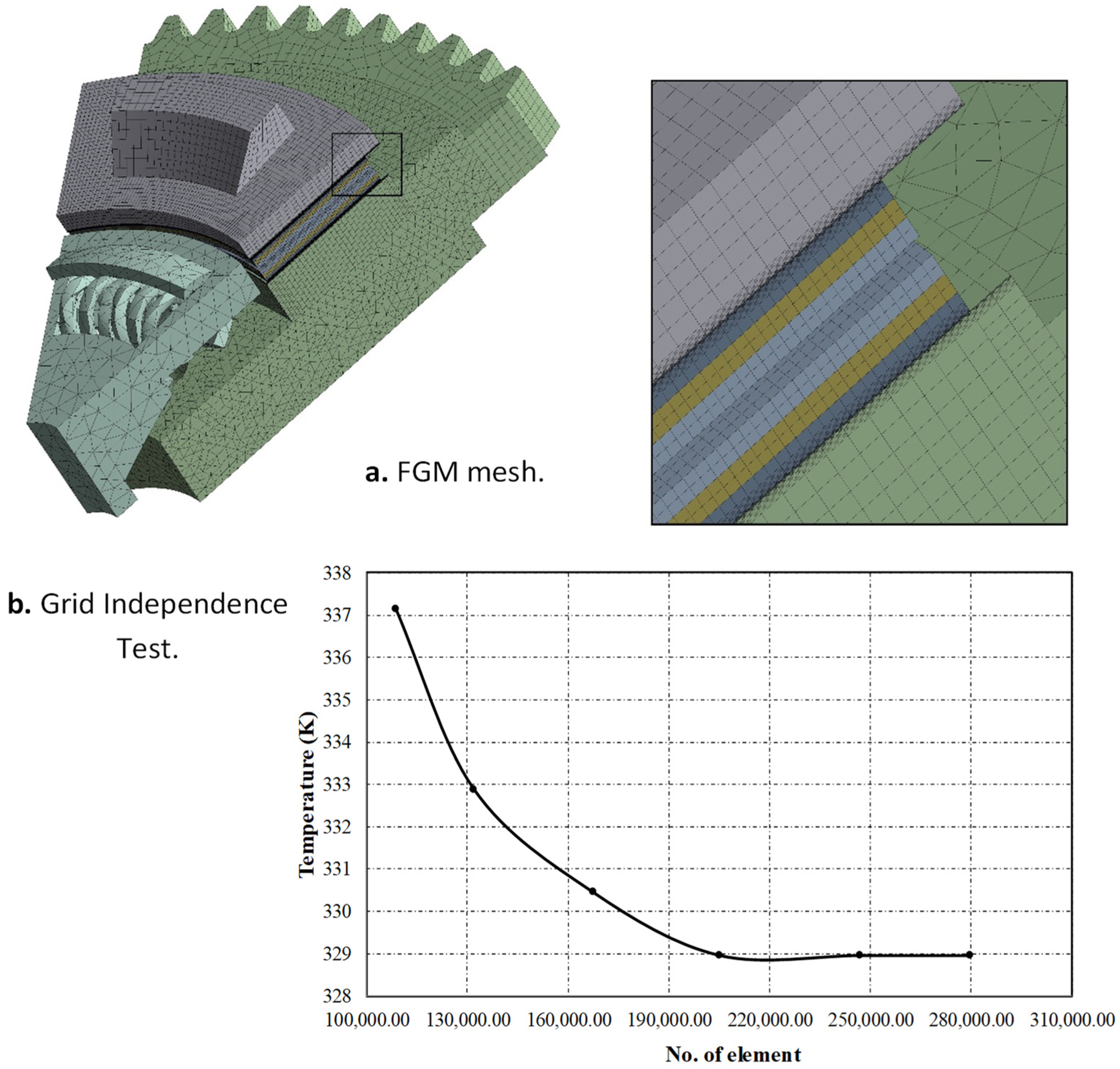
Figure 9.
(a) The optimal mesh of the clutch system using FGM and (b) the Grid Independence Test for mesh.
Figure 9.
(a) The optimal mesh of the clutch system using FGM and (b) the Grid Independence Test for mesh.
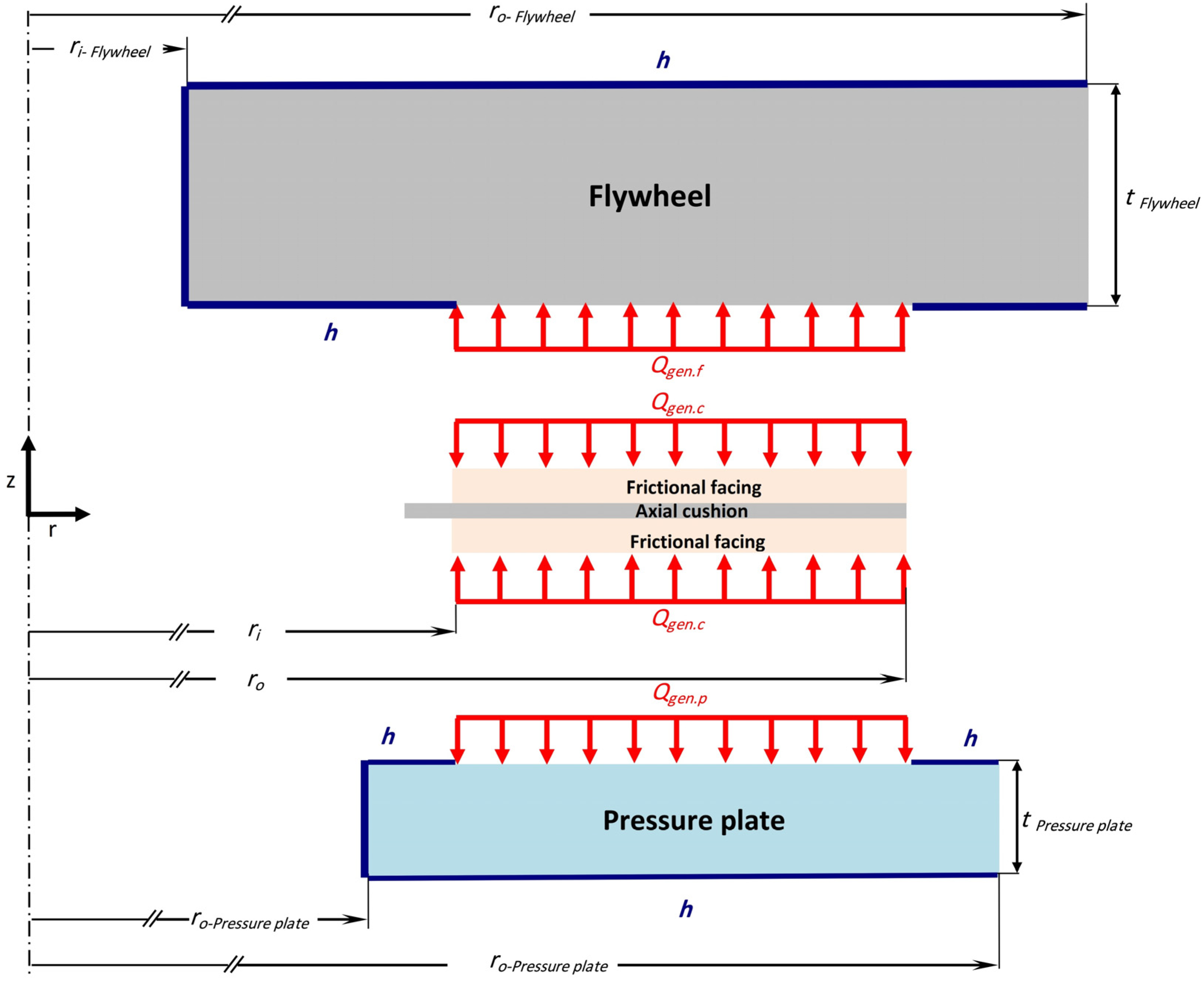
Figure 10.
The boundary conditions of the clutch system model.
Figure 10.
The boundary conditions of the clutch system model.
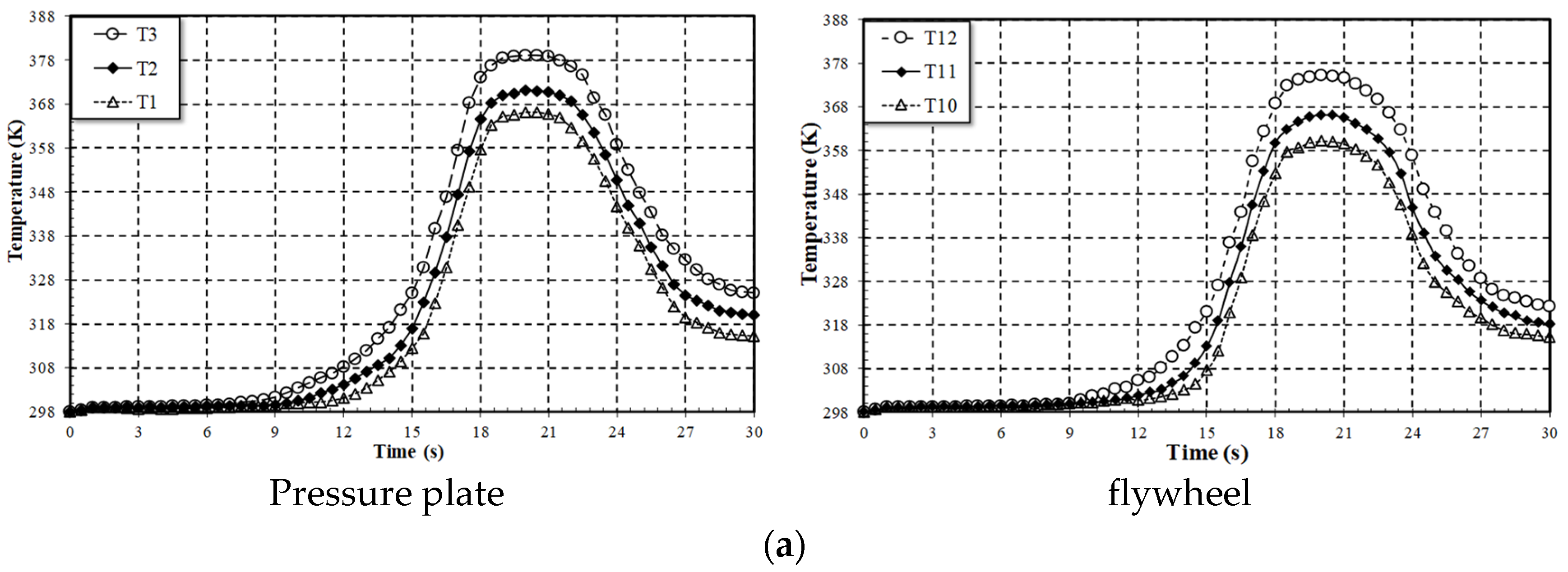
Figure 11.
Temperature distributions applied to different speeds (Torque = 4.5 kg·m). (a). Rotational speed = 680 (rpm) using VH-03. (b). Rotational speed = 860 (rpm) using HDS57. (c). Rotational speed = 1200 (rpm) using FGM.
Figure 11.
Temperature distributions applied to different speeds (Torque = 4.5 kg·m). (a). Rotational speed = 680 (rpm) using VH-03. (b). Rotational speed = 860 (rpm) using HDS57. (c). Rotational speed = 1200 (rpm) using FGM.
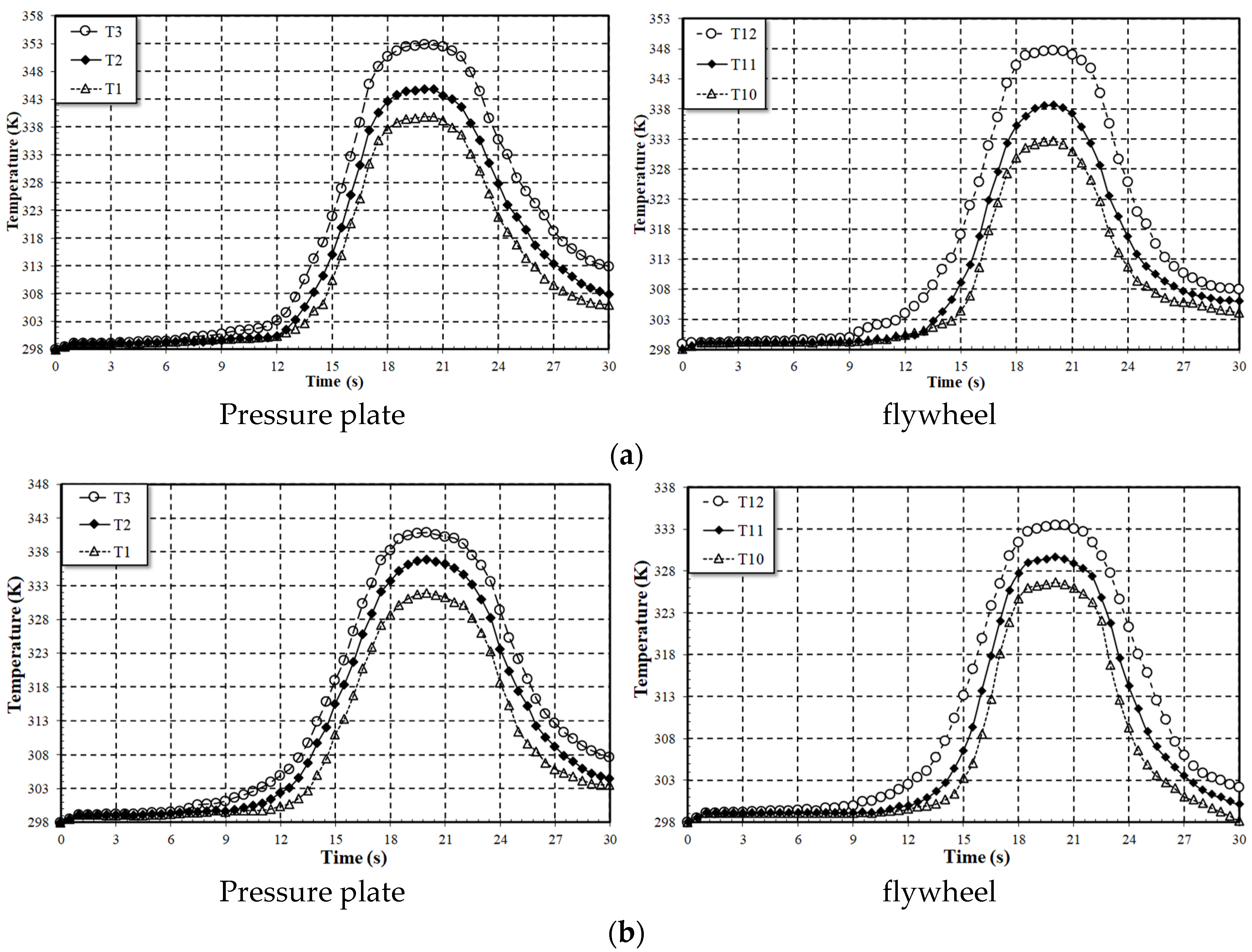
Figure 12.
Temperature distribution at a constant torque (3.5 kg·m) for different speed values. (a). Rotational speed = 680 (rpm) using HDS57. (b). Rotational speed = 860 (rpm) using FGM. (c). Rotational speed = 1200 (rpm) using VH-03.
Figure 12.
Temperature distribution at a constant torque (3.5 kg·m) for different speed values. (a). Rotational speed = 680 (rpm) using HDS57. (b). Rotational speed = 860 (rpm) using FGM. (c). Rotational speed = 1200 (rpm) using VH-03.
Figure 13.
Temperature distribution at a constant torque (2.5 kg·m) for different speed values. (a). Rotational speed = 680 (rpm) using FGM. (b). Rotational speed = 860 (rpm) using VH-03. (c). Rotational speed = 1200 (rpm) using HDS57.
Figure 13.
Temperature distribution at a constant torque (2.5 kg·m) for different speed values. (a). Rotational speed = 680 (rpm) using FGM. (b). Rotational speed = 860 (rpm) using VH-03. (c). Rotational speed = 1200 (rpm) using HDS57.
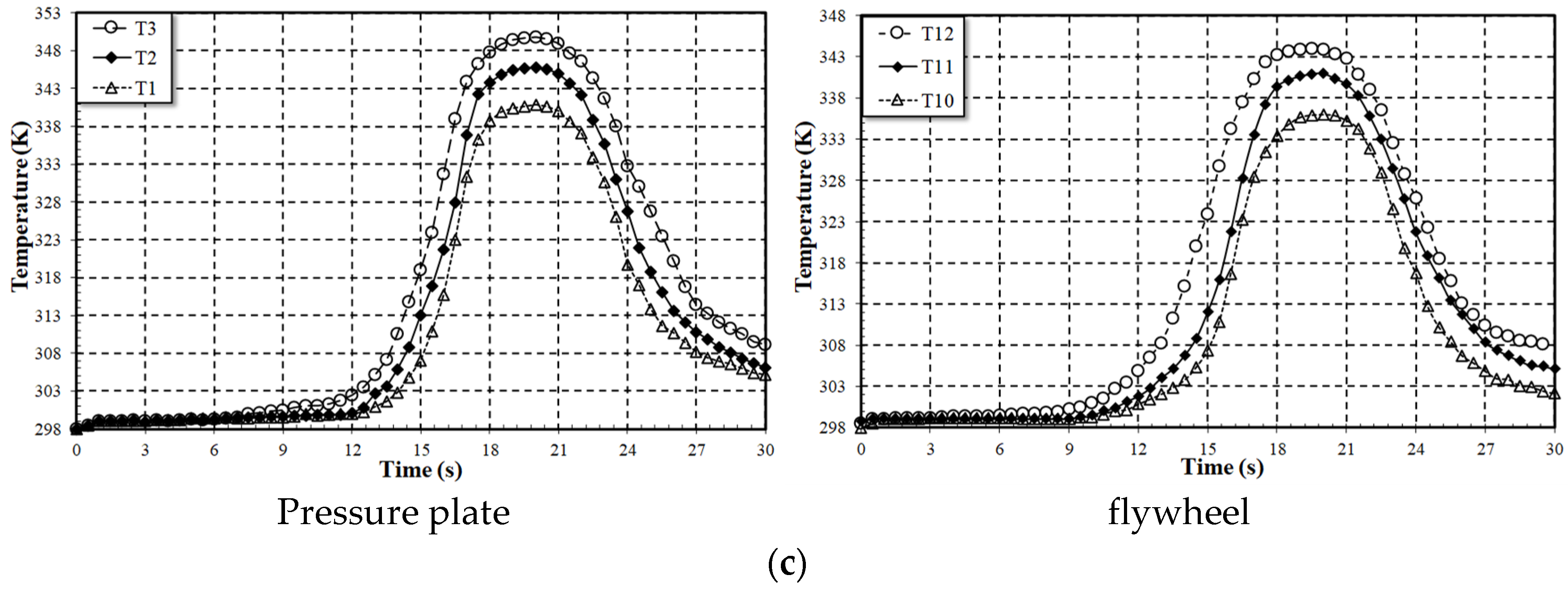
Figure 14.
Temperature distribution at a constant speed (680 rpm) when applying different torques. (a). Torque = 4.5 (kg·m) using VH-03. (b). Torque = 3.5 (kg·m) using HDS57. (c). Torque = 2.5 (kg·m) using FGM.
Figure 14.
Temperature distribution at a constant speed (680 rpm) when applying different torques. (a). Torque = 4.5 (kg·m) using VH-03. (b). Torque = 3.5 (kg·m) using HDS57. (c). Torque = 2.5 (kg·m) using FGM.
Figure 15.
Temperature distribution at a constant speed (860 rpm) when applying different torques. (a). Torque = 4.5 (kg·m) using HDS57. (b). Torque = 3.5 (kg·m) using FGM. (c). Torque = 2.5 (kg·m) using VH-03.
Figure 15.
Temperature distribution at a constant speed (860 rpm) when applying different torques. (a). Torque = 4.5 (kg·m) using HDS57. (b). Torque = 3.5 (kg·m) using FGM. (c). Torque = 2.5 (kg·m) using VH-03.
Figure 16.
Temperature distribution at a constant speed (1200 rpm) when applying different torques. (a). Torque = 4.5 (kg·m) using FGM. (b). Torque = 3.5 (kg·m) using VH-03. (c). Torque = 2.5 (kg·m) using HDS57.
Figure 16.
Temperature distribution at a constant speed (1200 rpm) when applying different torques. (a). Torque = 4.5 (kg·m) using FGM. (b). Torque = 3.5 (kg·m) using VH-03. (c). Torque = 2.5 (kg·m) using HDS57.
Figure 17.
A comparison of the maximum temperature distribution of speed (1200 rpm) and torque (4.5 Kg·m) for different materials.
Figure 17.
A comparison of the maximum temperature distribution of speed (1200 rpm) and torque (4.5 Kg·m) for different materials.
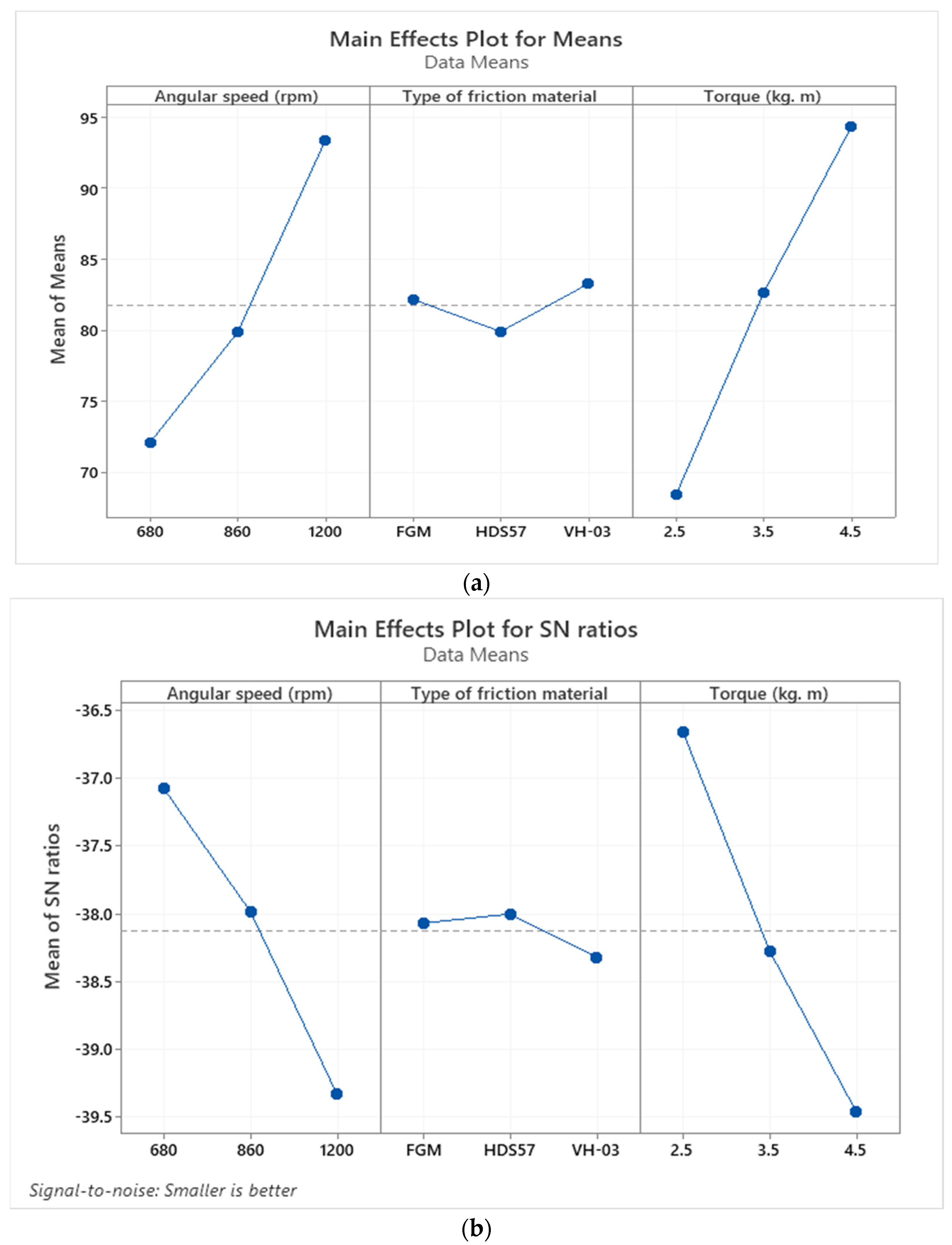
Figure 18.
The diagnostic plots of parameter effects: (a) Main effect plot of means and (b) the main effect of SN ratios.
Figure 18.
The diagnostic plots of parameter effects: (a) Main effect plot of means and (b) the main effect of SN ratios.
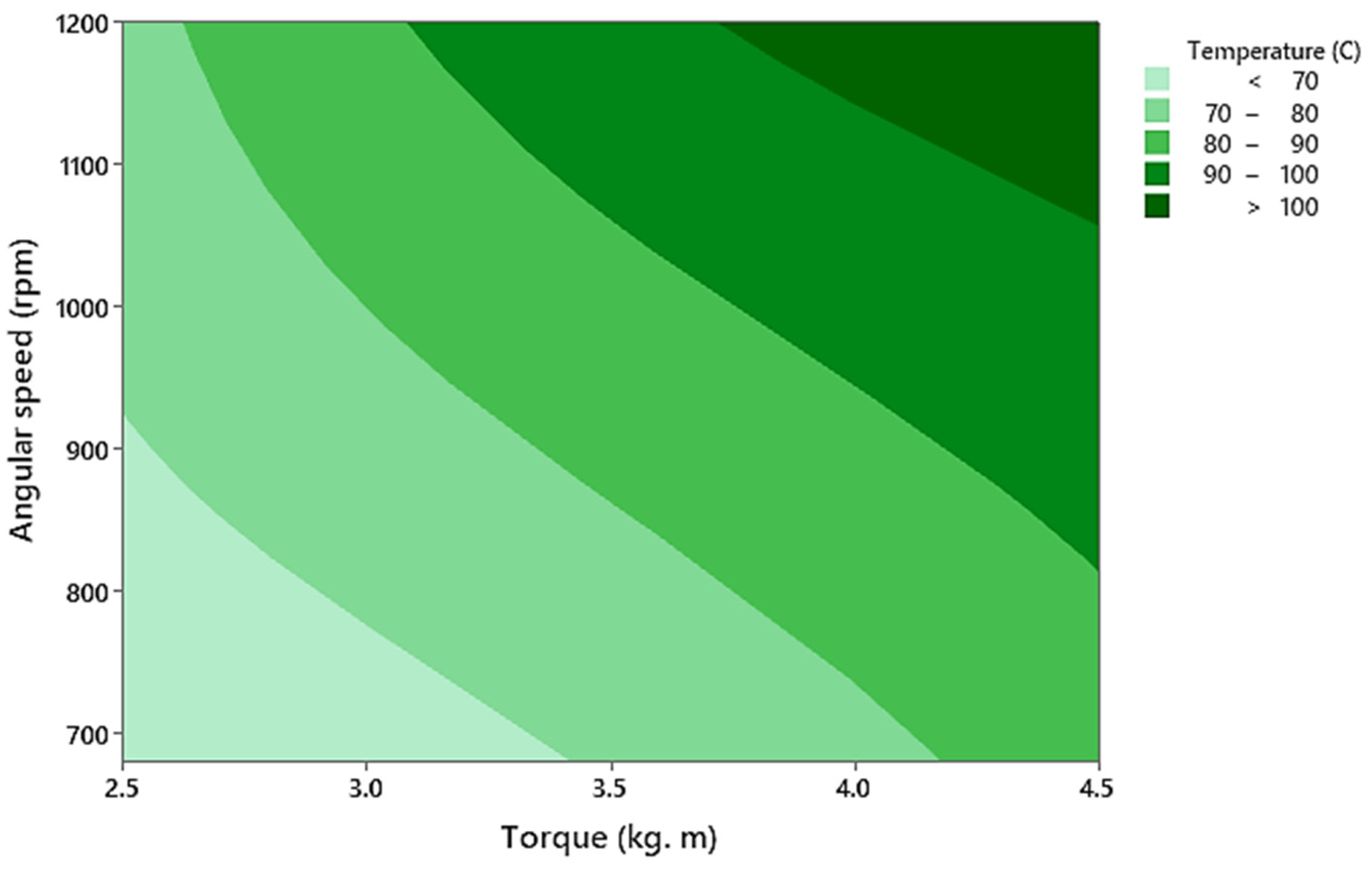
Figure 19.
The contour plot of temperature (°C) vs. angular speed (rpm) and torque (kg·m).
Figure 19.
The contour plot of temperature (°C) vs. angular speed (rpm) and torque (kg·m).
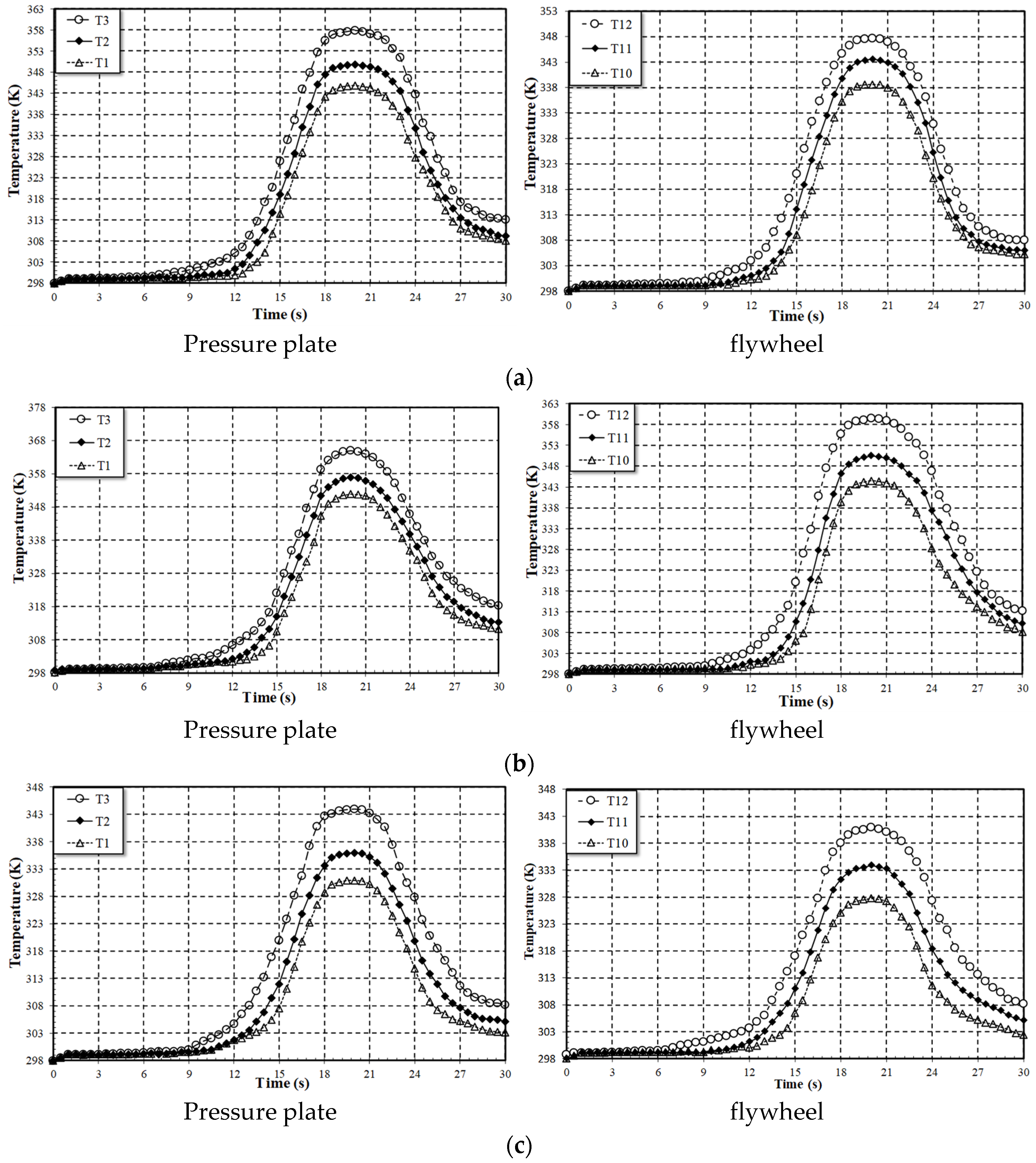
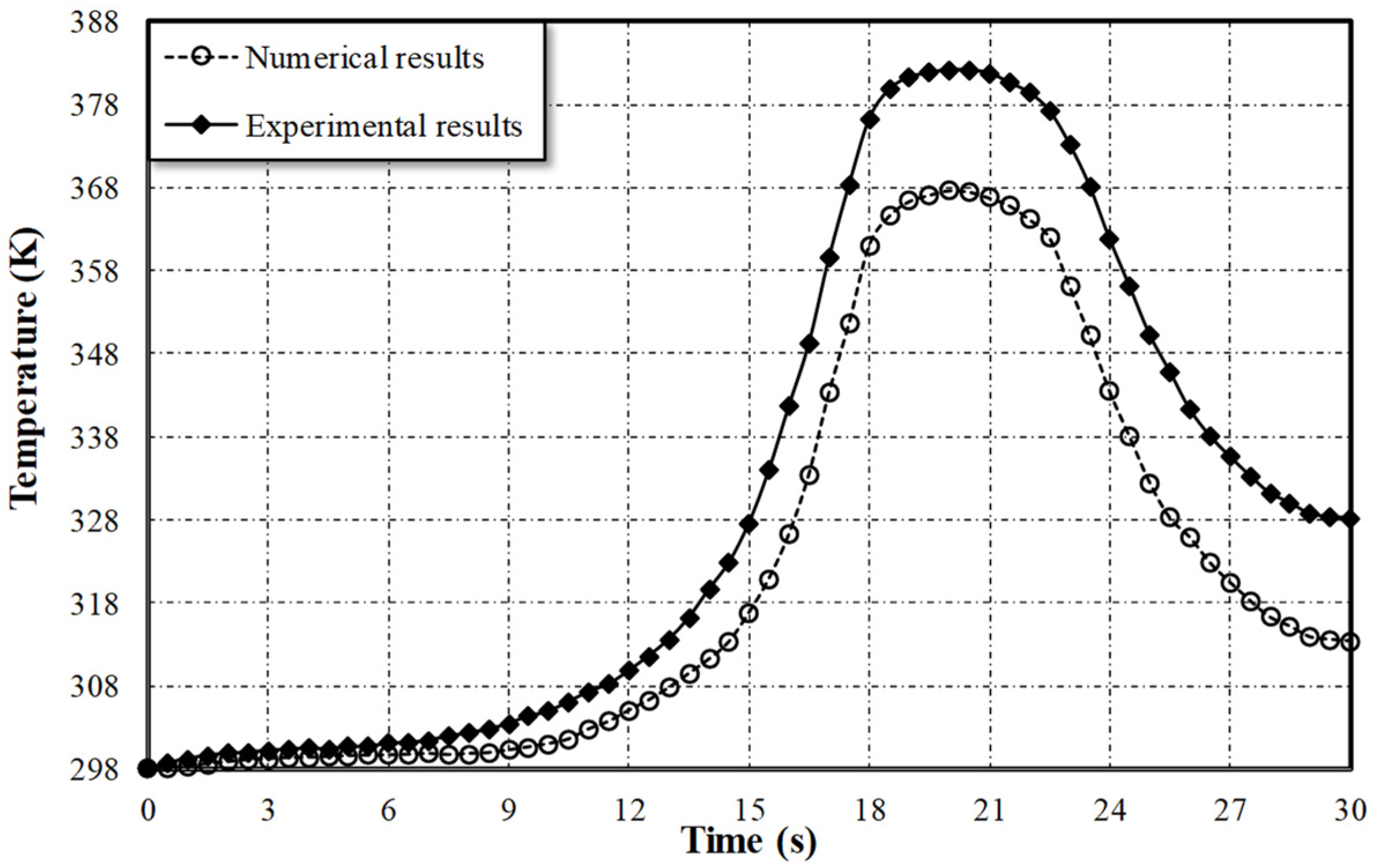
Figure 20.
A comparison between numerical and experimental results.
Figure 20.
A comparison between numerical and experimental results.
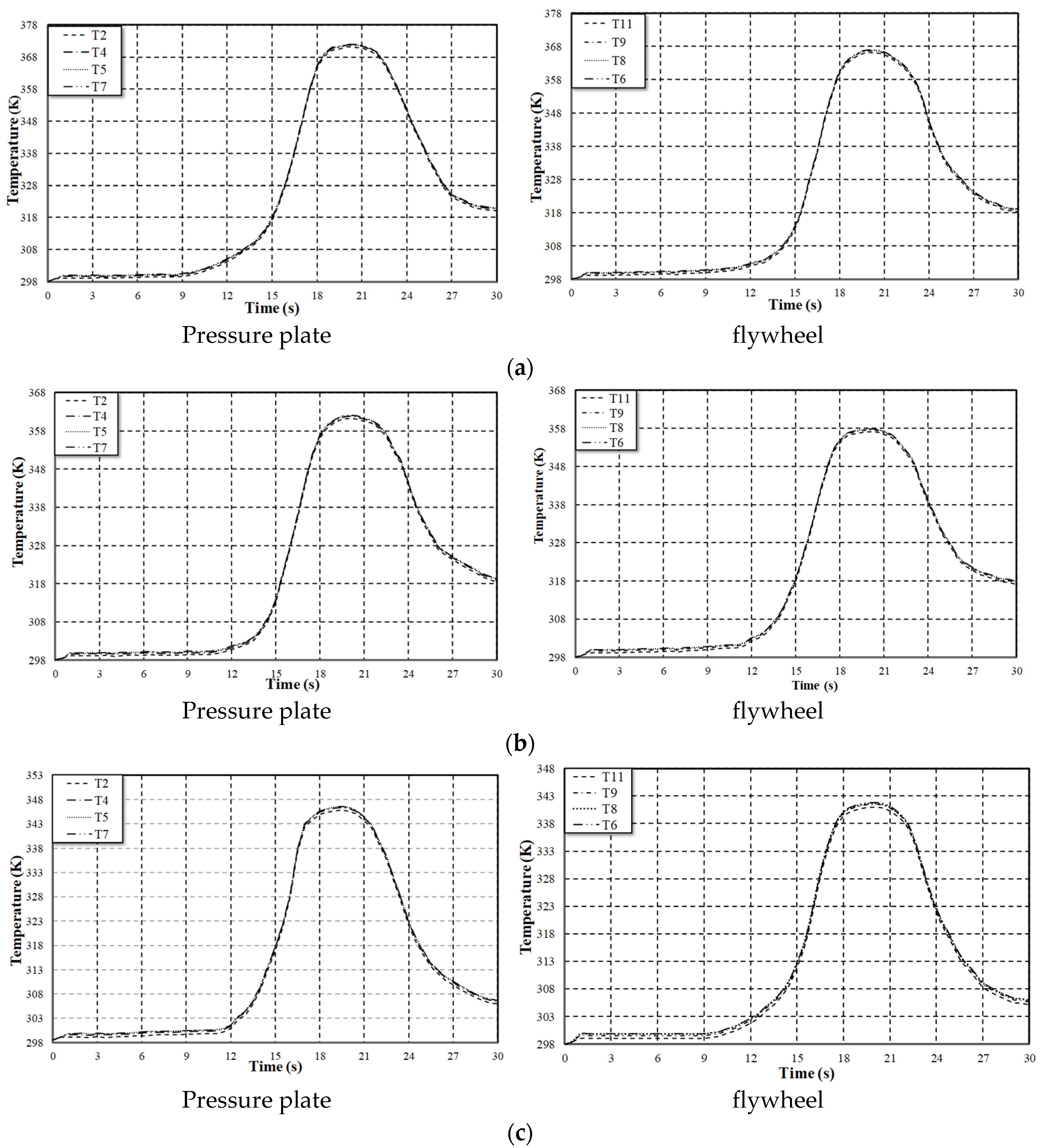
Figure 21.
Temperature distributions using an FE model of the friction clutch system.
Figure 21.
Temperature distributions using an FE model of the friction clutch system.
Table 1.
The properties of the materials in each layer of the FGM clutch disc.
Table 1.
The properties of the materials in each layer of the FGM clutch disc.
| Layer | Al | Sic |
|---|
| 1 | 93% | 7% |
| 2 | 96.5% | 3.5% |
| 3 | 100% | 0% |
Table 2.
The average values of the hardness for the selected frictional materials.
Table 2.
The average values of the hardness for the selected frictional materials.
| Composition | FGM (Al–Sic) | FGM (Al-Ni) [19] |
|---|
| Max. value | 110 HV | 95 HV |
Table 3.
The material properties of the selected frictional materials.
Table 3.
The material properties of the selected frictional materials.
| Material | FGM | HDS57 | VH-03 |
|---|
| AL | Sic |
|---|
| Density (kg/m3) | 2770 | 3100 | 1700 | 2100 |
| Thermal conductivity (W/m·K) | 160 | 120 | 0.23 | 0.30 |
| Specific Heat (J/kg·K) | 923.5 | 750 | 1350 | 1368 |
Table 4.
The properties of the layers of FGM.
Table 4.
The properties of the layers of FGM.
| Property | First Layer | Second Layer | Third Layer |
|---|
| Density (kg/m3) | 2793.1 | 2781.55 | 2770 |
| Thermal conductivity (W/m·K) | 157.2 | 158.6 | 160 |
| Specific Heat (J/kg·K) | 911.355 | 917.4275 | 923.5 |
| Coefficient of Friction | 0.52494 | 0.49385 | 0.47 |
Table 5.
The selected factors and their levels of experimental work.
Table 5.
The selected factors and their levels of experimental work.
| Variable | Values |
|---|
| Angular speed (rpm) | 1200, 860, 680 |
| Torque (kg·m) | 4.5, 3.5, 2.5 |
| Frictional material types | FGM, HDS57, VH-03 |
Table 6.
The working conditions of the nine cases based on the Taguchi method (L9 matrix).
Table 6.
The working conditions of the nine cases based on the Taguchi method (L9 matrix).
| Test No. | Rotational Speed (rpm) | Torque (kg·m) | Material Type |
|---|
| 1 | 680 | 2.5 | FGM |
| 2 | 680 | 3.5 | HDS57 |
| 3 | 680 | 4.5 | VH-03 |
| 4 | 860 | 3.5 | FGM |
| 5 | 860 | 4.5 | HDS57 |
| 6 | 860 | 2.5 | VH-03 |
| 7 | 1200 | 4.5 | FGM |
| 8 | 1200 | 2.5 | HDS57 |
| 9 | 1200 | 2.5 | VH-03 |
Table 7.
The results for the Analysis of Variance (ANOVA).
Table 7.
The results for the Analysis of Variance (ANOVA).
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | Contributions % |
|---|
| Angular speed (rpm) | 2 | 694.85 | 347.423 | 68.15 | 0.014 | 40.11 |
| Type of friction material | 2 | 17.68 | 8.842 | 1.73 | 0.366 | 1.02 |
| Torque (kg·m) | 2 | 1009.52 | 504.762 | 99.02 | 0.010 | 58.27 |
| Error | 2 | 10.20 | 5.098 | | | |
| Total | 8 | 1732.25 | | | | |
| R-sq | R-sq(adj) | | | | |
| 99.41% | 97.65% | | | | |