Airfoil Shape Morphing through a Novel Parameterization and Fitting Optimization Method Based on Uniform Non-Rational B-Spline Functions
Abstract
1. Introduction
1.1. PARSEC Method
1.2. Bezier Parameterization
1.3. Bezier-Parsec Parameterization
1.4. BP 3333 Parameterization
- easily allows airfoil shape morphing for leading edge/trailing edge rotation (global morphing) and skin deformation (local morphing).
- easily enables the identification of functional areas and their contribution evaluation to the forces involved in the physical phenomena under analysis.
- easily allows the application of geometric constraints.
- involves a limited/reduced number of parameters for airfoil representation.
- is eligible/suitable for developing aerodynamic, structural, or FSI optimization design processes on existing wing aircraft airfoils to evaluate the opportunity for morphing technology implementation [4].
- variables separation during the geometric fitting process.
- smooth modification of the geometry of curved segments’ edges.
2. Descriptions of the Methodology
- MATLAB is the main software for implementing optimization algorithms and for calling the CFD Xfoil 6.99 code inside the optimization loops.
- Xfoil 6.99 is the aerodynamics solver for evaluating the 2D airfoil aerodynamic properties.
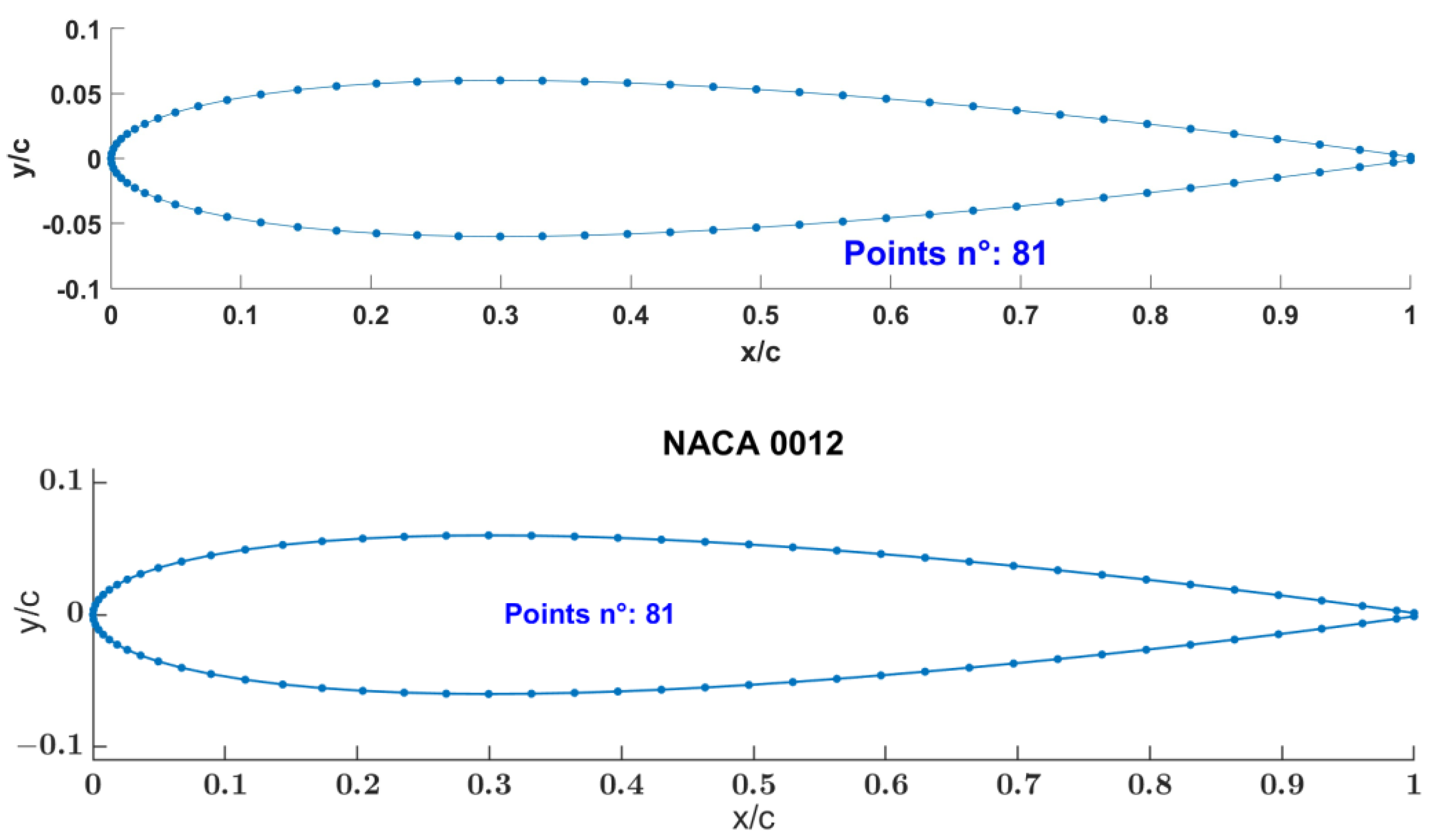
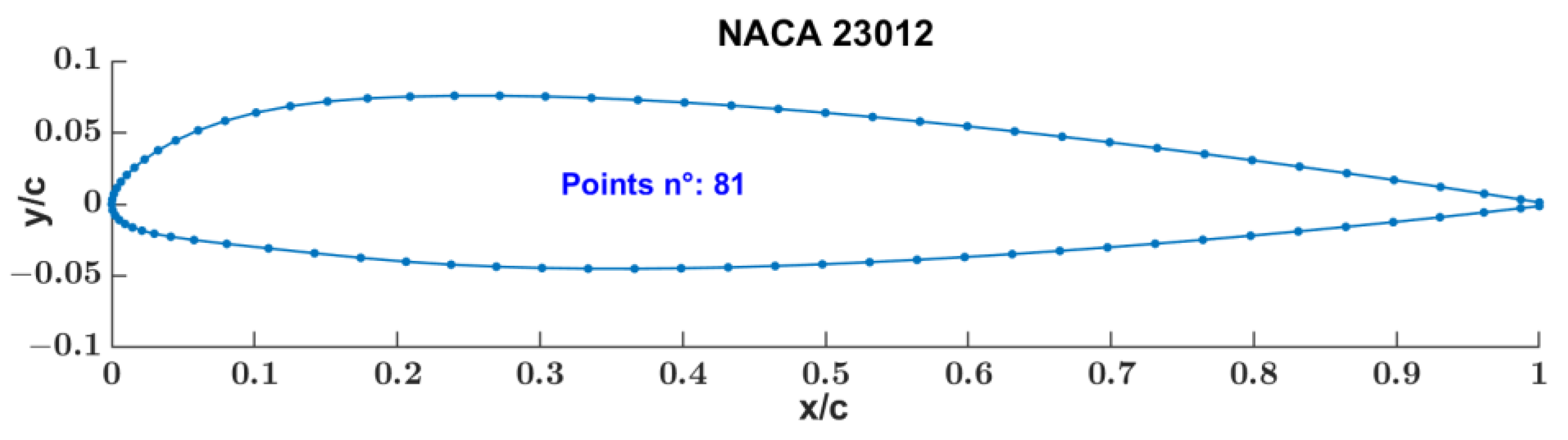
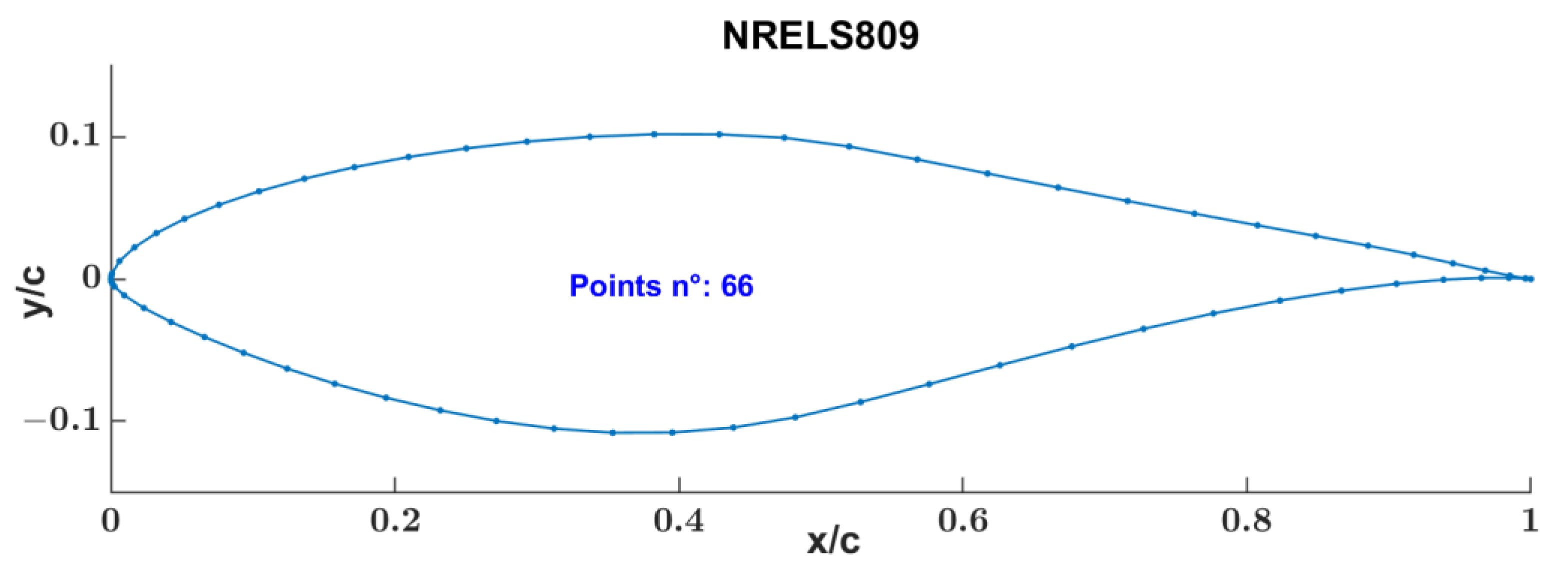
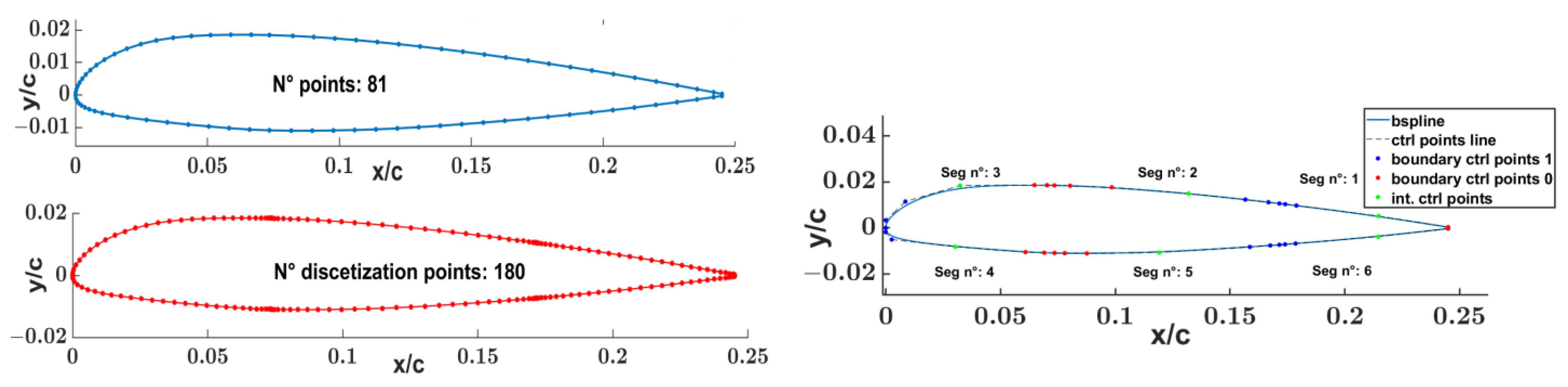
2.1. Input 2D Airfoil
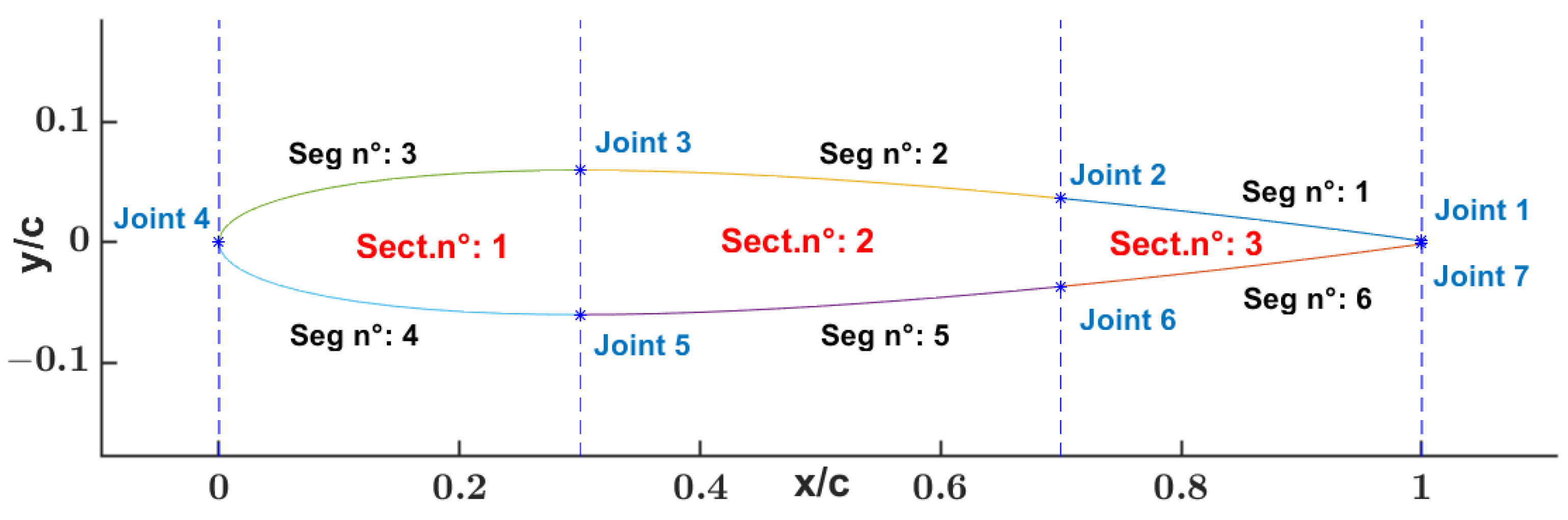
2.2. Airfoil Partitioning
- LE section starting from the airfoil point P(x, y) of minimum x coordinate up to the 30% of the airfoil chord: 0 ≤ x/c ≤ 0.3.
- CB section starting from 30% up to 70% of the airfoil chord: 0.3 ≤ x/c ≤ 0.70.
- TE section starting from 70% up to 100% of the airfoil chord: 0.70 ≤ x/c ≤ 1.
2.3. Mathematical Airfoil Segments Representation
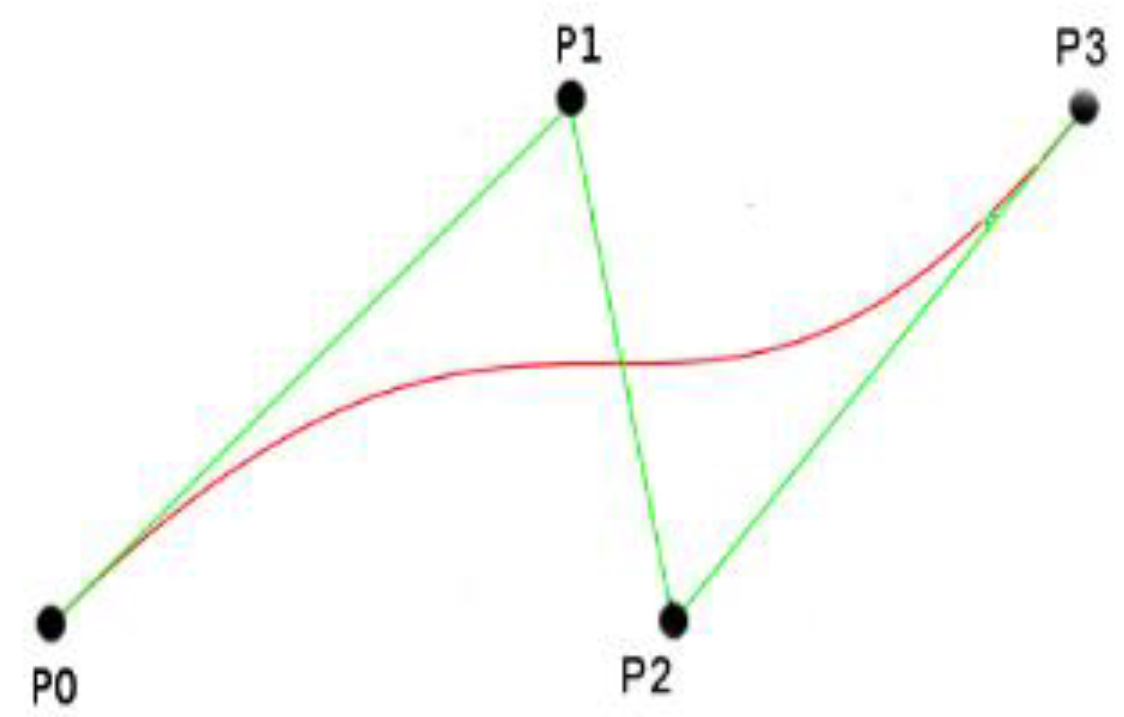
2.3.1. UNRBS
2.3.2. Curve Derivatives in Parametric and Cartesian Formulation & SF Parameter
2.3.3. UNRBS Boundaries Control Points in Terms of C′ C″ and SF
- extremities of the curve segment coordinates P0 = P(x0, y0) and Pn = P(xn,yn)
- tangent vectors at the extremities of the curve segment C′(0) and C′(1)
- curvature vectors at the extremities of the curve segment C″(0) and C″(1)
2.3.4. Segment Parameters
- boundary control points (BCps).
- interior control points (InCps).
- boundary conditions assigned at the extremities of each segment: C0 up to C2 continuity.
- required number of BCPs to satisfy the boundary conditions.
- desired number of InCPs.
2.3.5. Segments Reduced Parameters
2.4. Segment Geometric Boundary Conditions
2.5. Segment Fitting Procedure for Reduced Parameters
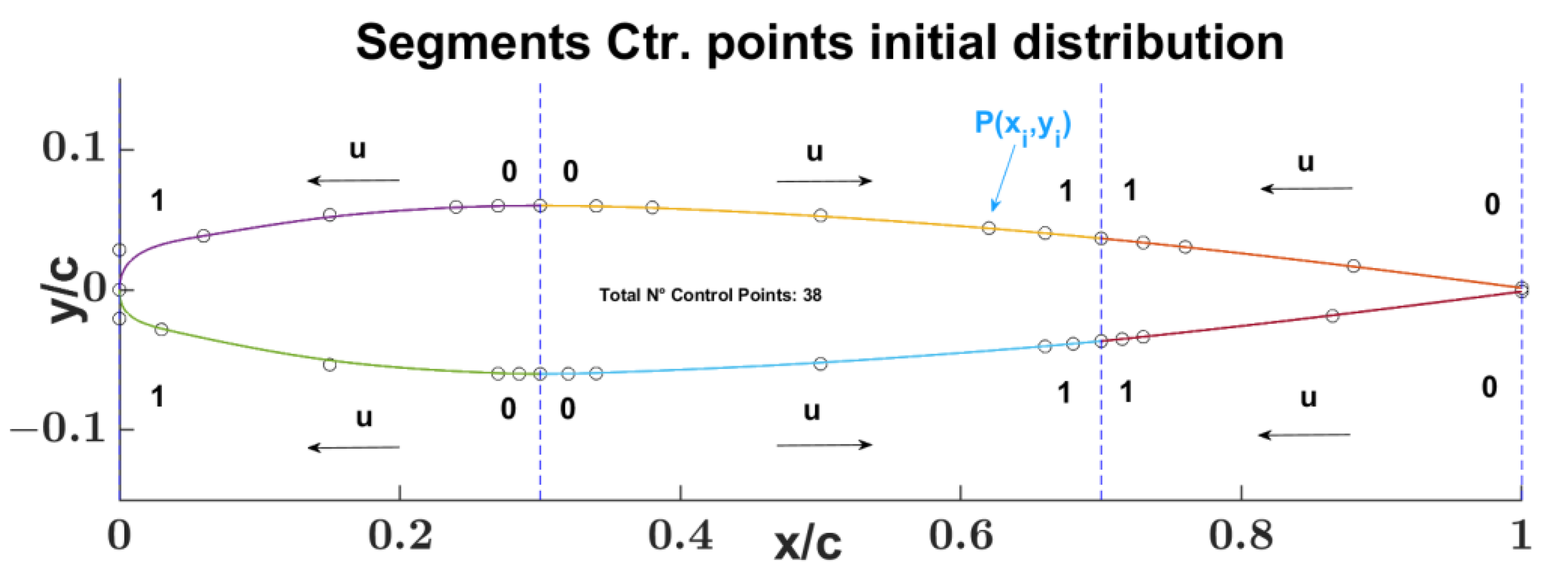
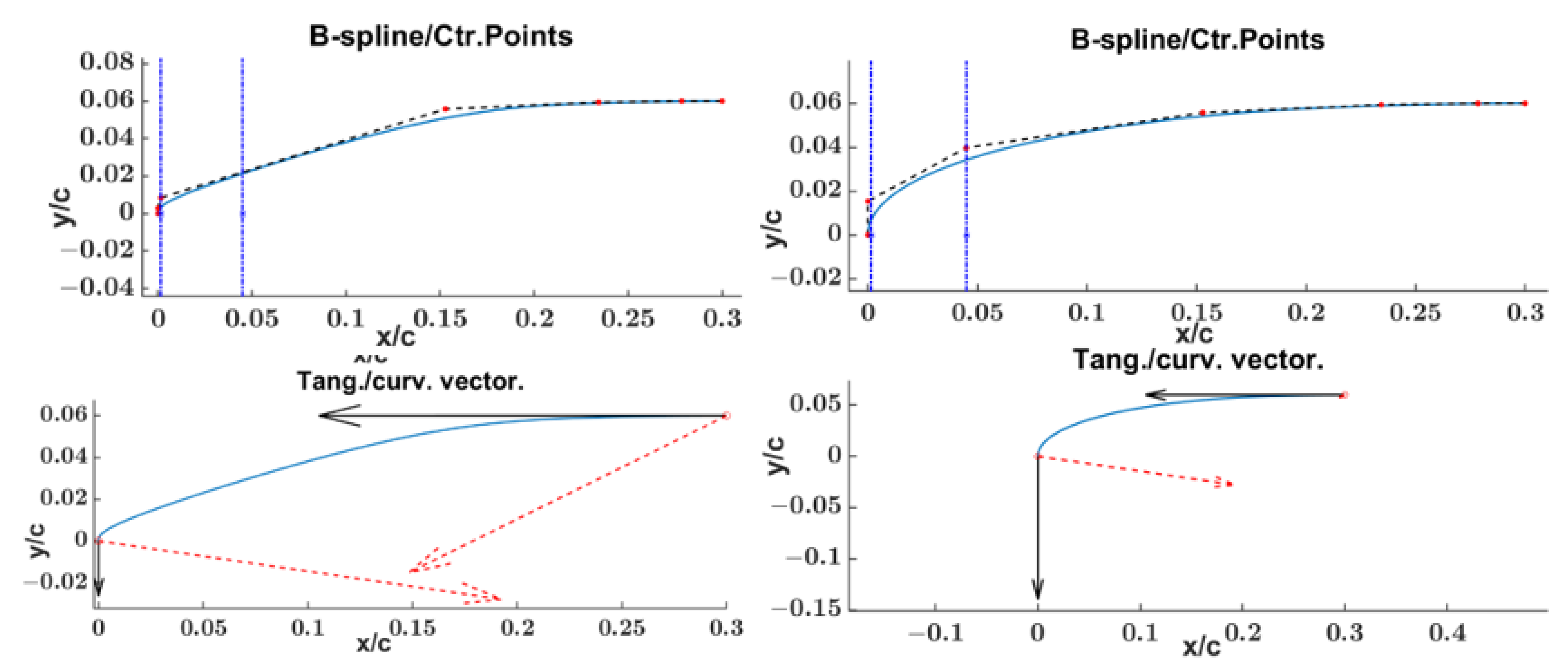
- 1st phase of pre-processing the airfoil data (Figure 11): this phase is characterized by three steps:
- C′ and C″ vectors evaluation at each segment joint.
- segments BCPs positioning in accordance with the C′ and C″ vectors.
- SFps upper and lower bounds evaluation.
| Algorithm 1 [InitialAirfoil C′,C″,SF_lb, SF_ub]=Airfoil_preprocessing ( ) | |
| 1 | Variable_Declaration ( ) /* Airfoil global variable…definition*/ |
| 2 | File_Inizialization ( ) /* fine name definition */ |
| 3 | Folder_Inizialization ( ) /* making working folders */ |
| 4 | Airfoil_Topology ( ) /* x partitions, seg.s discretization typology, fixed/free CPs, x% seg. boundaries …definition */ |
| 5 | Airfoil_Load() /* load target airfoil points, */ |
| 6 | Initial_Airfoil_PartitioningSeg( ) /* target airfoil partitioning */ |
| 7 | Create_Initial_B-pline_curves ( ) /* create segment b-spline curves */ |
| 8 | [C’,C″]=Segments_Joints_dC_ddC ( ) /*evaluating C’ & C″ vectors at each joint from the target airfoil points coordinates and apply the same to the current airfoil b-spline segments */ |
| 9 | [SF_lb,SF_ub]=Segment_bounds ( ) /* given the x% seg. boundaries the SFs upper and lowerboundaries are evaluated*/ |
| 10 | end Airfoil_preprocessing |
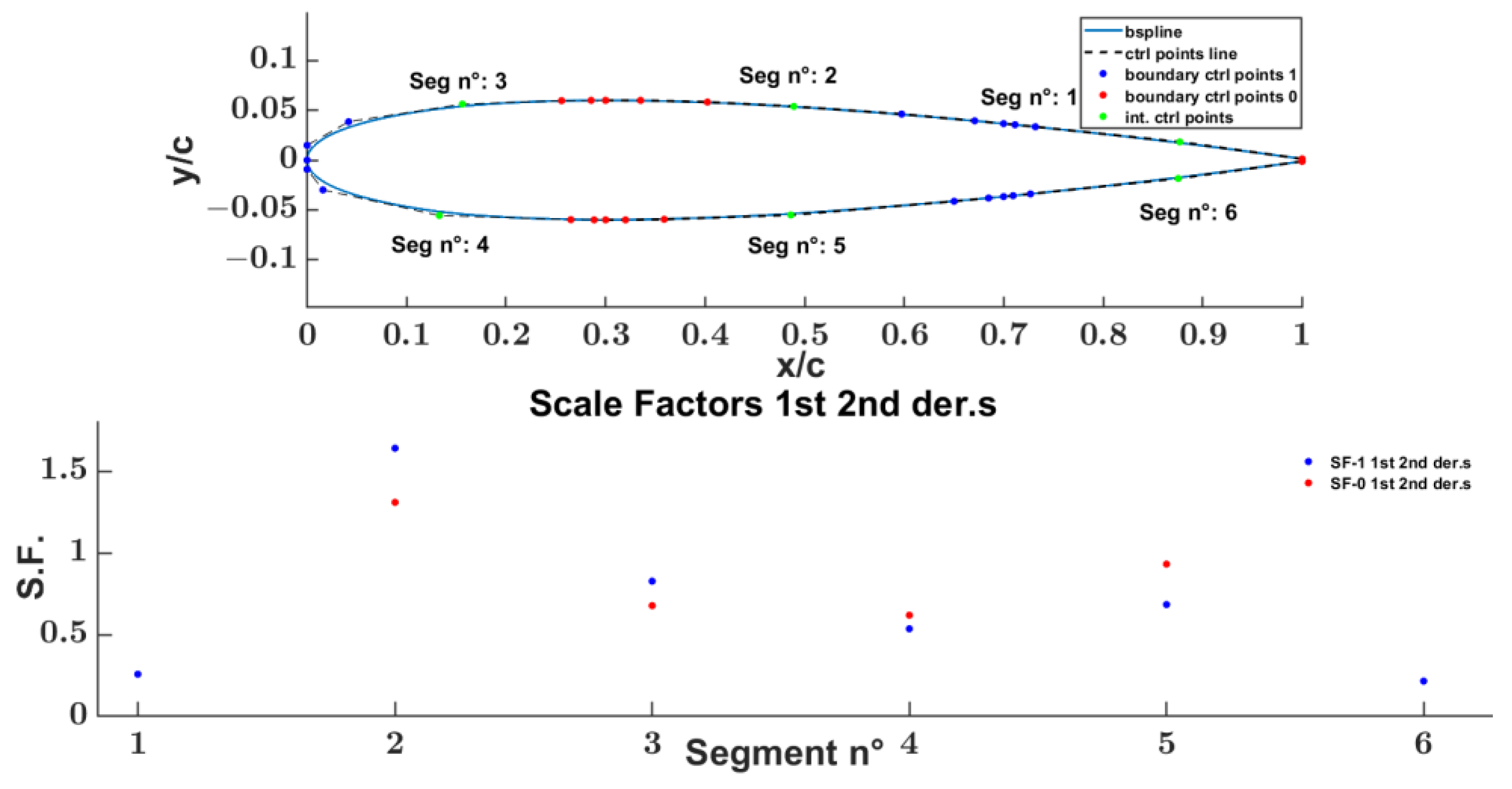
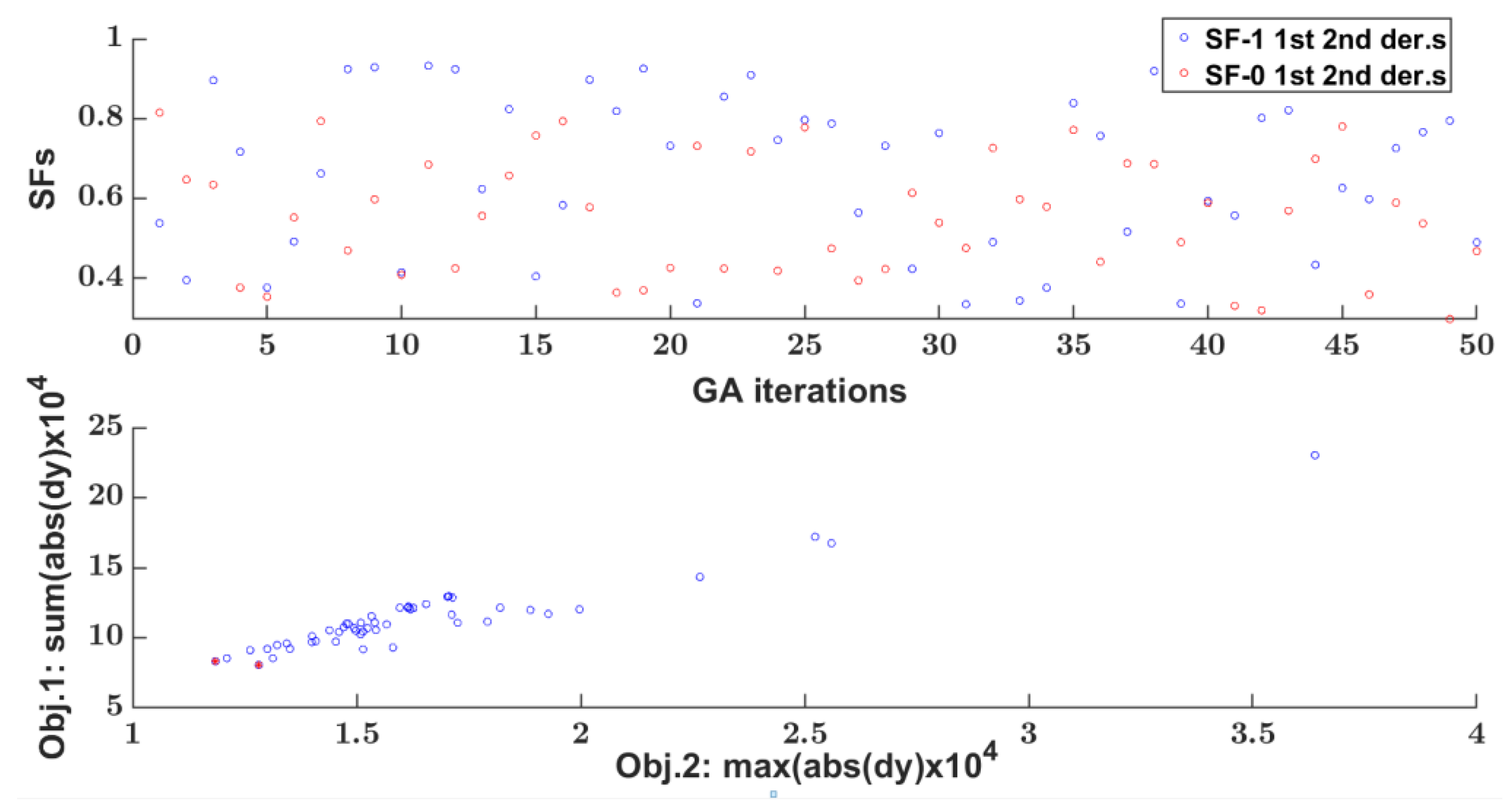
- 2nd phase segment reduced parameters evaluation (Figure 12): This step applies to all the segments whose C’ and C” extremity vectors are already known and assigned. The aim is to find the optimum segment UNRBS curve parameters that best fit the input segment airfoil points with the desired continuity boundary extremity conditions. Two nested optimization routines perform the parameter evaluations, an external and an internal one, considering the reduced segment parameters as variables, namely the SFs for the external routine, varying between the upper and lower bounds assessed in step 1, and the InCPs for the internal one. More specifically,
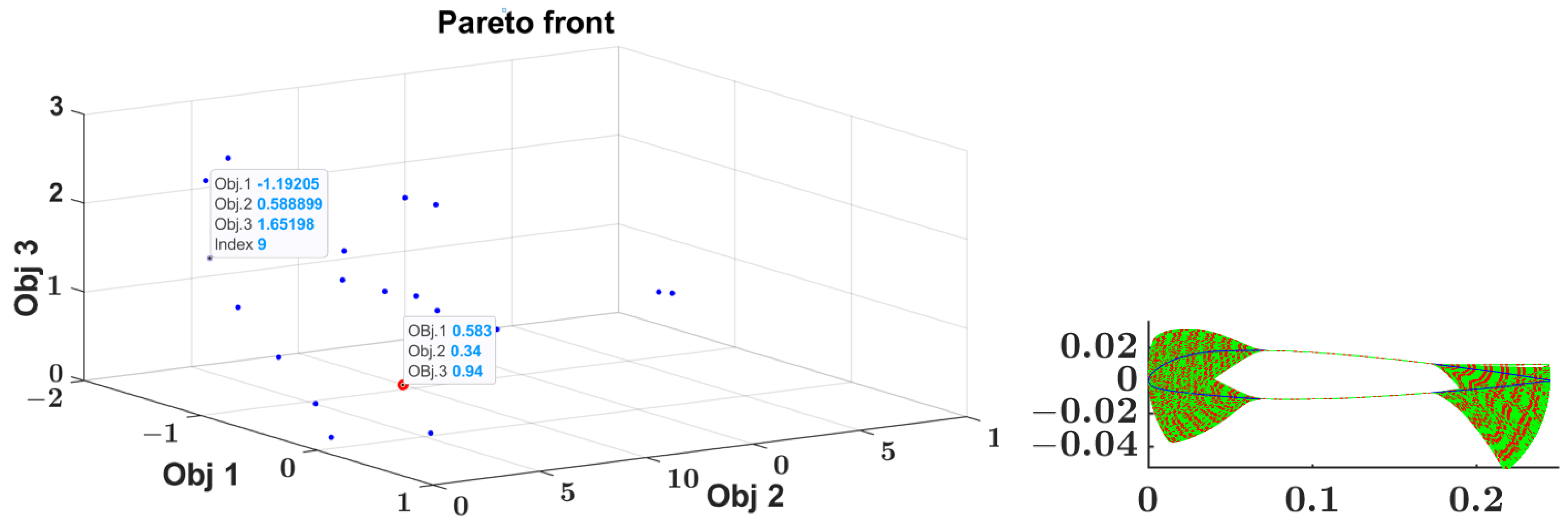
- the external optimization cycle is based on a MATLAB genetic optimization function gamultiobj [18,19,20,21,22] dedicated to the two SFps only with two objective functions:obj1: sum((Euclidean distance between points).obj2: max(Euclidean distance between points).The two SFs parameters affect the position of the BCPs that define the lower and upper bounds of the interior CPs coordinates used for the inside optimization cycle.
- the internal optimization cycle is based on MATLAB non-linear optimization fmincon [23,24,25,26,27] function involving the interior CPs parameters with:-objective function obj: minimizing the max (Euclidean distance between points);-upper and lower bounds: defined by the BCPs coordinates as a function of the SFps, output of the GA external cycle optimization.

| Alghoritm 2 [InitialAirfoil]=Airfoil_Fitting_process (InitialAirfoil, C’,C″,SF_lb, SF_ub) | |
| 1 | For each curve segment |
| 2 | [InitialAirfoil]=SegOptim_InCPs_SFs_nested_GA_Fmin(InitialAirfoil) /* evaluation of segment SFps and InCPs coordinates by: - external gamultiobj - nested fmincon MATLAB algorithms */ |
| 3 | SaveAirfoil (InitialAirfoil); /* save working InitialAirfoil variables*/ |
| 4 | Endfor |
| 5 | end Airfoil_Fitting_process |
| Alghoritm 3 Matlab gamultiobj genetic algorithm settings | |
| 1 | [f1,f2]= fit_fcn (Airfoil current segment) /*fitness function for evaluation of two objective functions: f1: max abs(Euclidean points distances); f2: sum abs(Euclidean points distances); fit_fnc calls the MATLAB fmincon algorithm*/ / |
| 2 | n_vars:= n_SFs /* number of segment curve SFs */ |
| 3 | A = []; b = []; Aeq = [];beq = []; /* linear constrains */ |
| n_seg=current segment number /* segment under fitting procedure*/ | |
| 4 | lbGa= SF_lb (n_seg); /*assign segment lower bound ubGa= SF_ub(n_seg) and upper bound*/ |
| 5 | [c,ceq]=nonlcon(Airfoil current segment) /*check for avoiding b-spline segment curve x coordinates inversion*/ |
| 6 | n_generationsGA=1; population_n=50; |
| opt = optimoptions(@gamultiobj,’PlotFcn’,’gaplotpareto’, ‘MaxGenerations’,n_generationsGA, ‘PopulationSize’,population_n, ‘PopulationType’,’doubleVector’ | |
| 7 | [SFs_GA,fval_GA]=gamultiobj(fit_fcn,n_vars,A,b,Aeq,beq,lbGa,ubGa,nonlcon,opt) |
| 8 | AirfoilPoints(InitialAirfoil); /*update the segment curve geometry properties and discretization*/ |
| Alghoritm 4 MATLAB fmincon gradient based algorithm settings | |
| 1 | [BCPs0,InCPS0]=B-spline_SegmentCurve_updating(InitialAirfoil, C′,C″,SF_GA) |
| 2 | [y]=fit (InitialAirfoil) /* updating InCPsand B-spline cuve, Evaluating objective function: y=max(abs(Eucledian curve points distance)) */ |
| 3 | IntCps0 /* initial internal control points*/ |
| 4 | A = []; b = []; Aeq = [];beq = []; |
| 5 | lb = flb(BCPs0); ub= flb(BCPs0) /* InCPs upper and lower bounds evaluated as function of the defined boundary control points BCPs0 */ |
| 6 | [c,ceq]=nonlcon(Airfoil current segment) /*check for avoiding b-spline segment curve x coordinates inversion*/ |
| 7 | opts = optimset(‘fmincon’, ‘TolFun ‘,1.e−12, FinDiffRelStep, 1.e−12); |
| 8 | [InCP_fmin,fval_fmin]=fmincon(fit, InCP 0,A,b,Aeq,beq,lb,ub,[],opts); |
| 9 | AirfoilPoints(InitialAirfoil); /*update the segment curve geometry properties and discretization*/ |
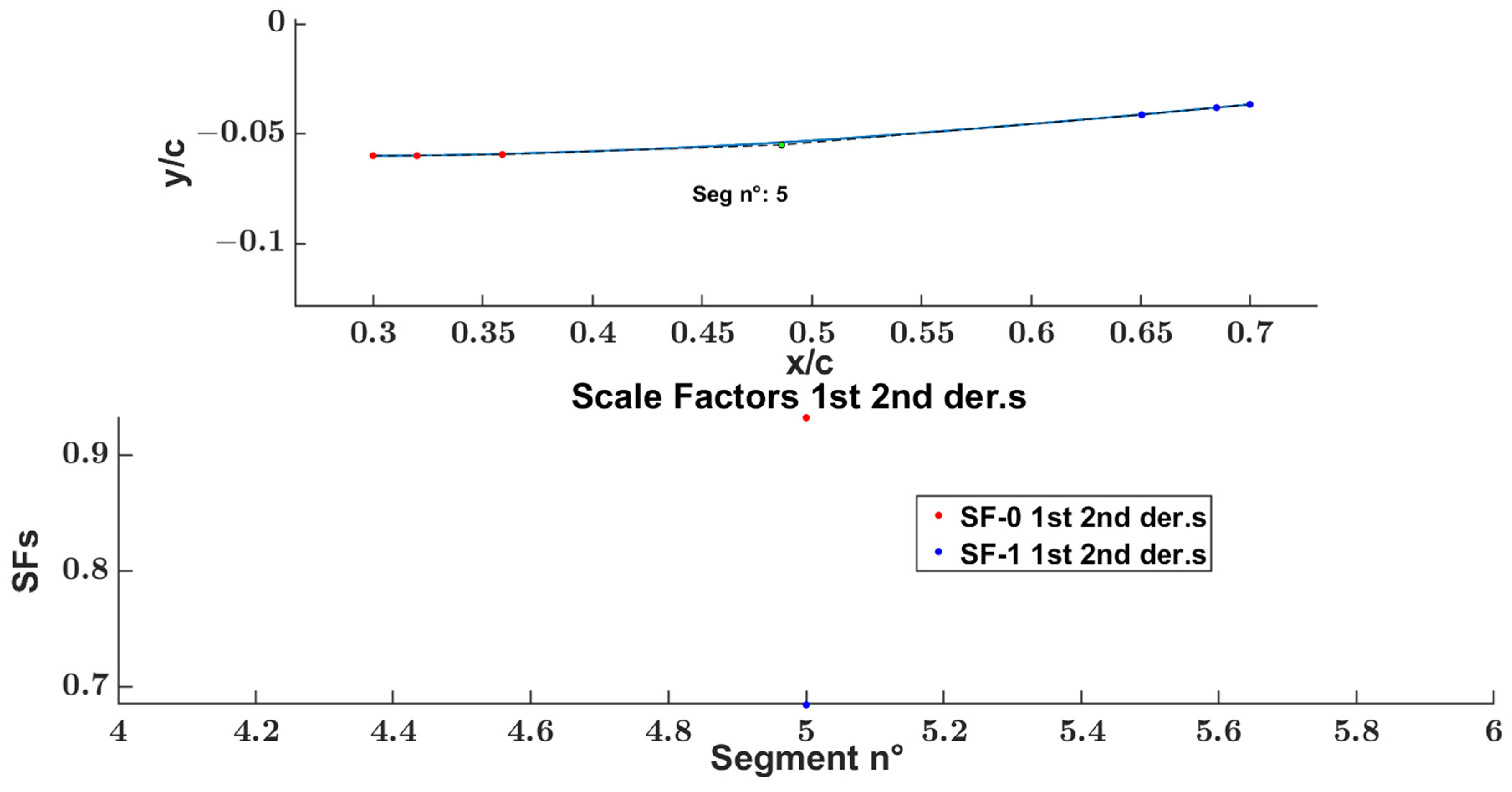
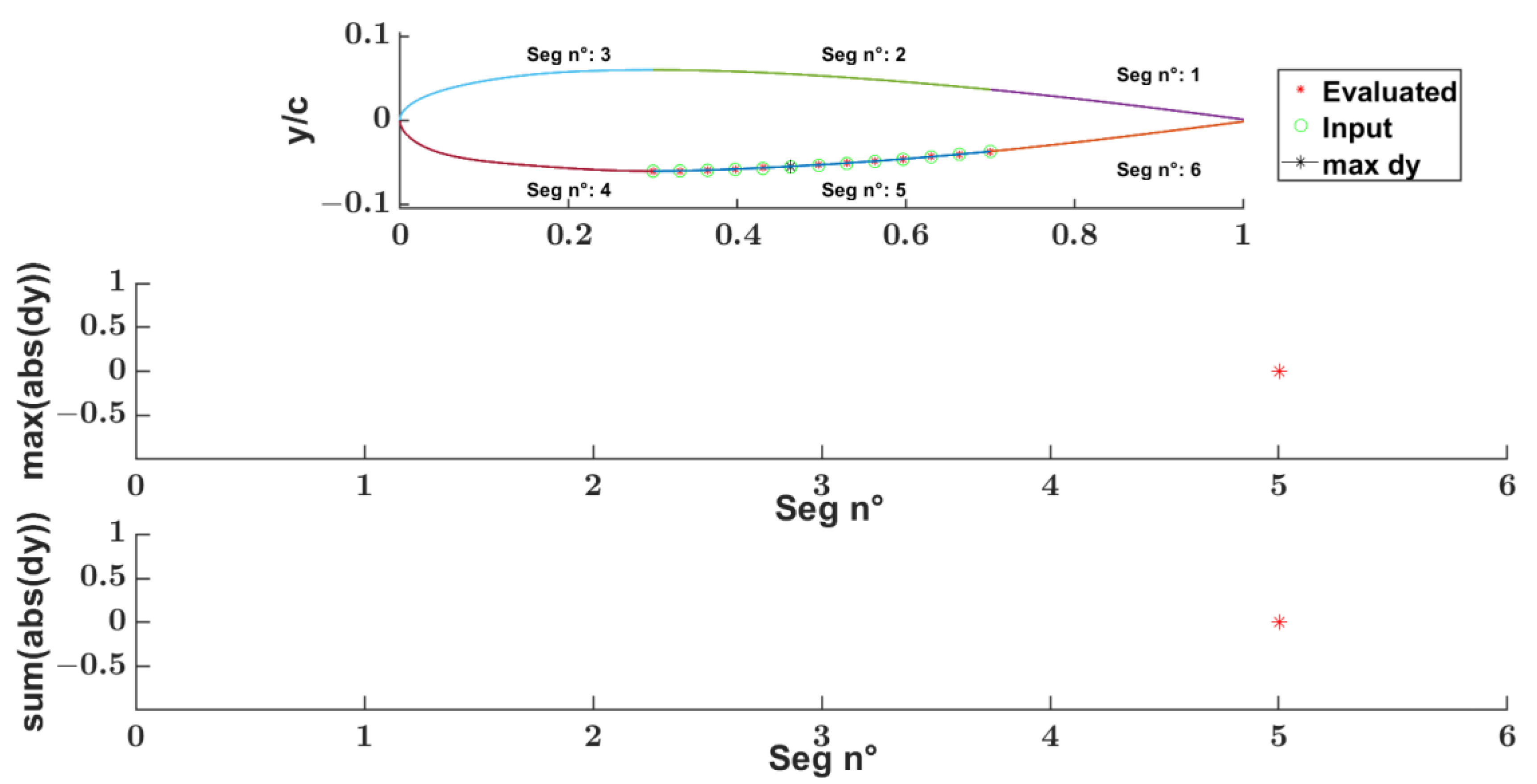
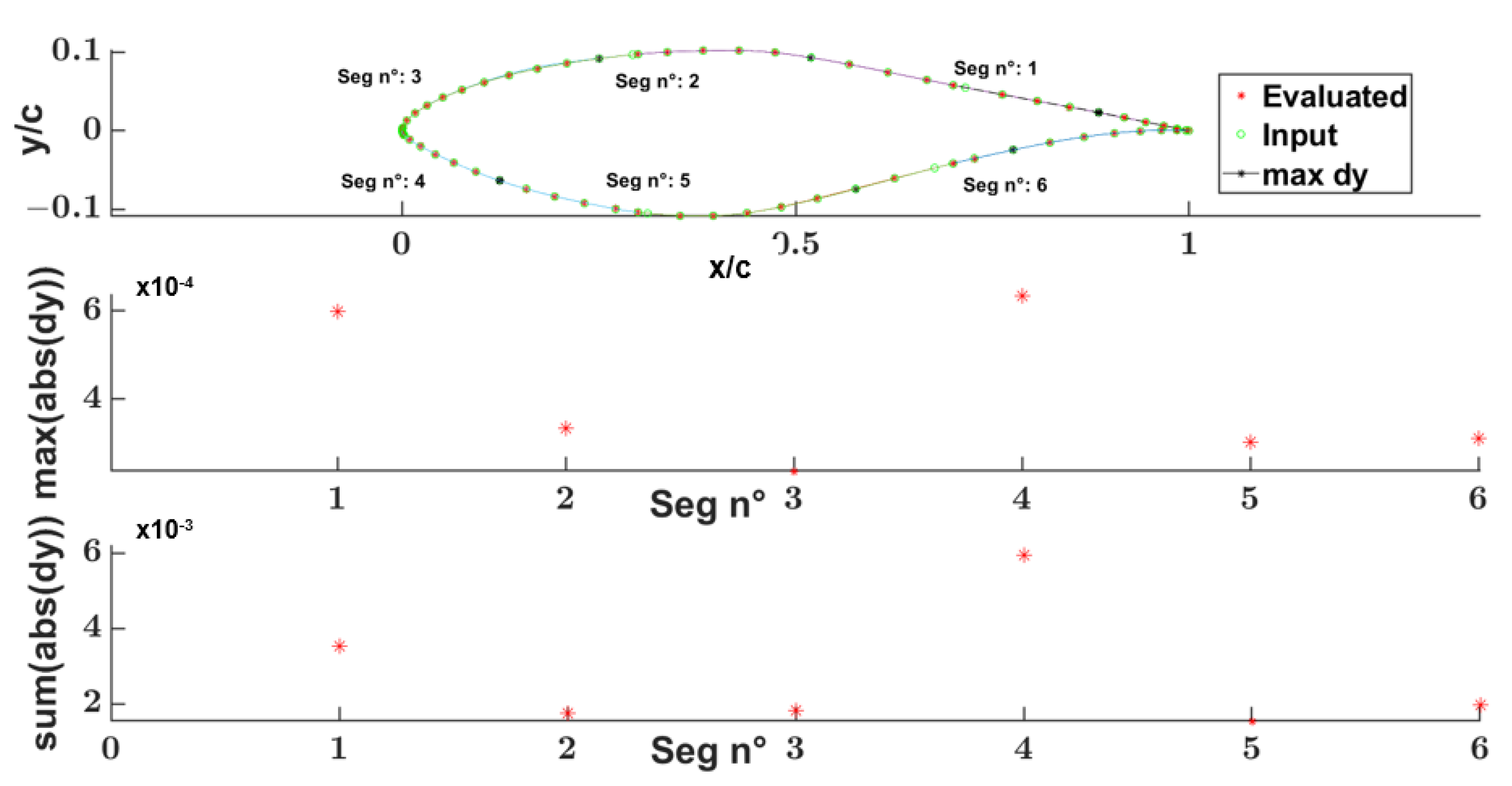
Segments 5 (CB section) Fitting Process Results
- The first step for evaluating the extremities boundary conditions, C’ C” vectors, and the SFps upper and lower bounds.
- The second step for evaluating 4 reduced parameters: two (2) InCPs coordinates and two (2) SFps.
3. Results
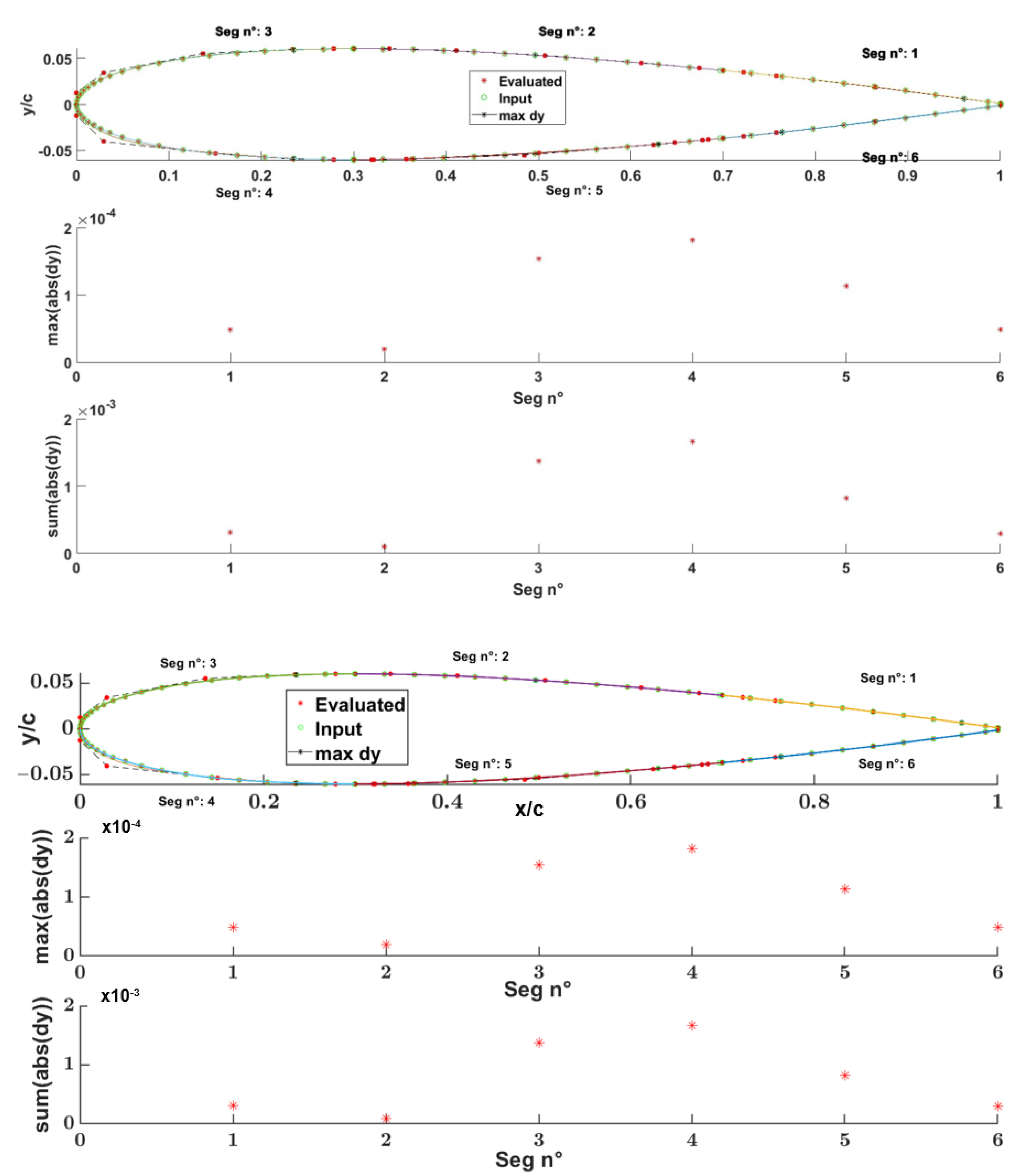
- geometrical input airfoil.
- maximum Euclidean distance for each segment between the input airfoil and evaluated airfoil points.
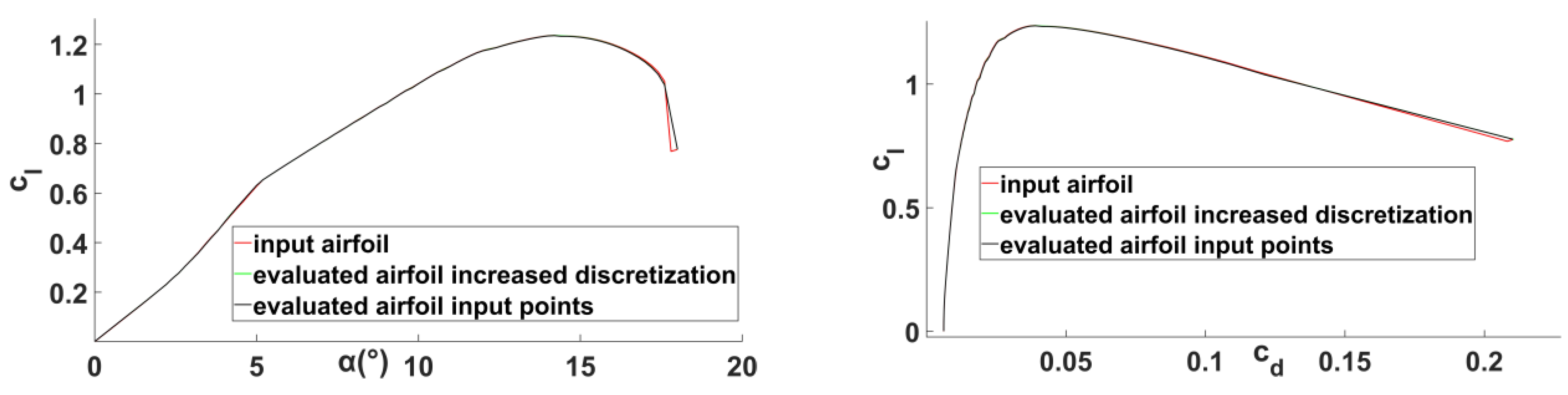
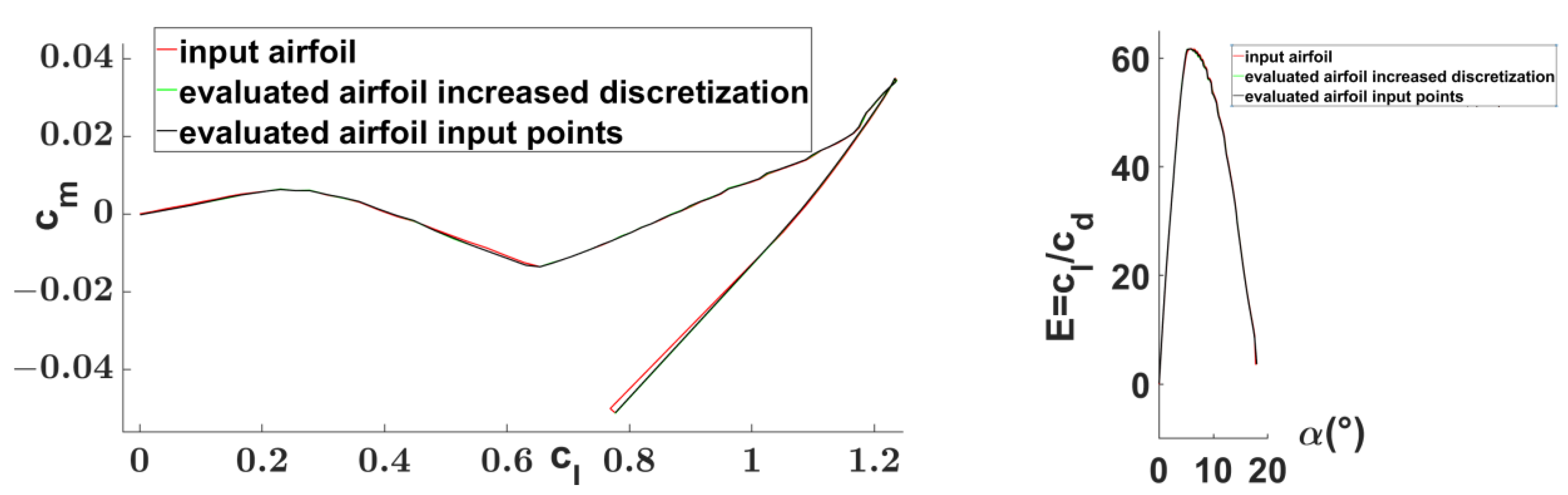
- the input airfoil aerodynamic properties compared with the evaluated airfoil properties considering two different discretizations: the input airfoil and an augmented one.
3.1. NACA 0012
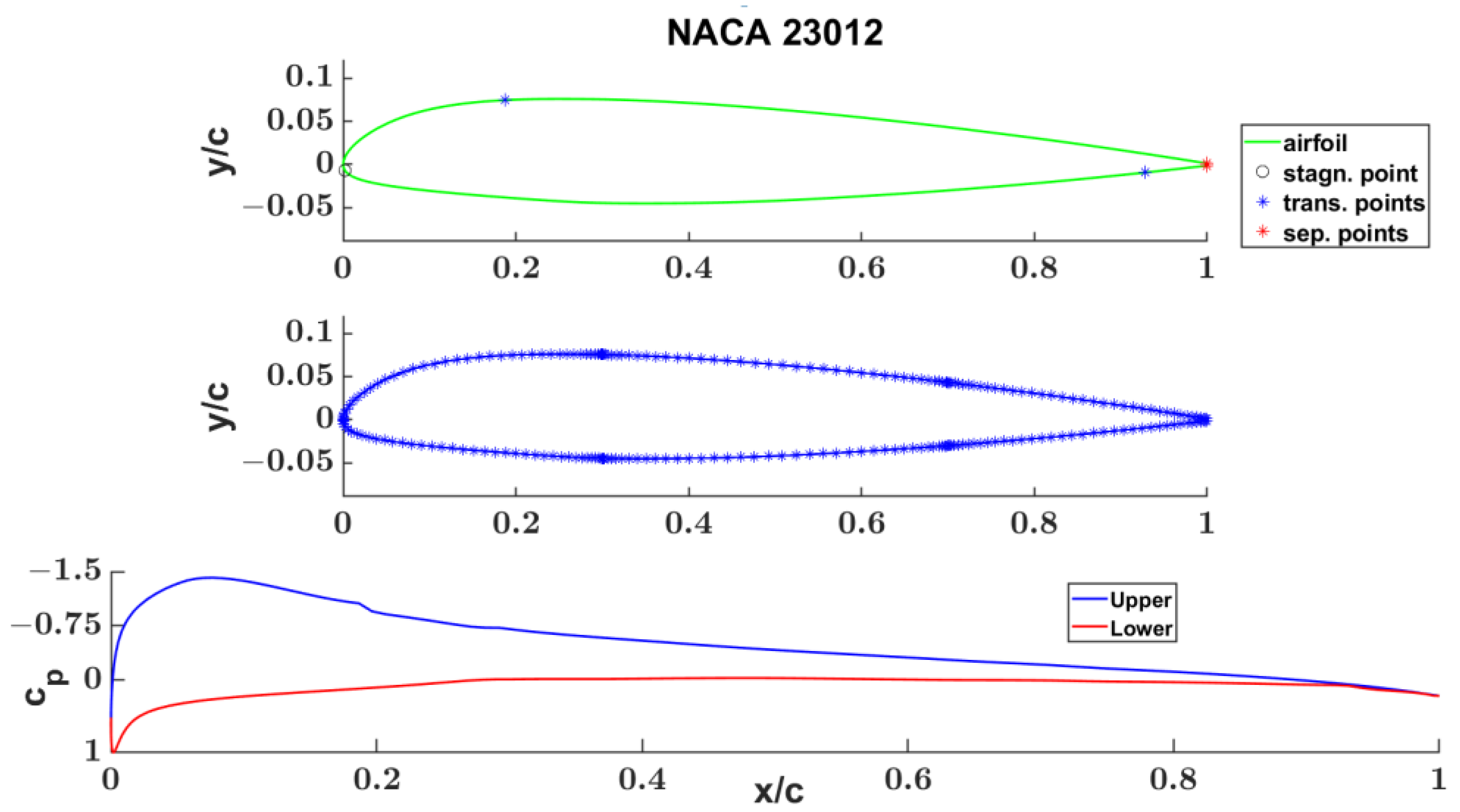
3.2. NACA 23012
3.3. NREL’s S809
3.4. Comparison between Existing Methods and the Proposed One
- B-spline interpolation method for the considered number of parameters.
- Numerical basis functions and B-spline interpolation methods for the geometrical approximation, which is more accurate by a magnitude.
4. Discussion
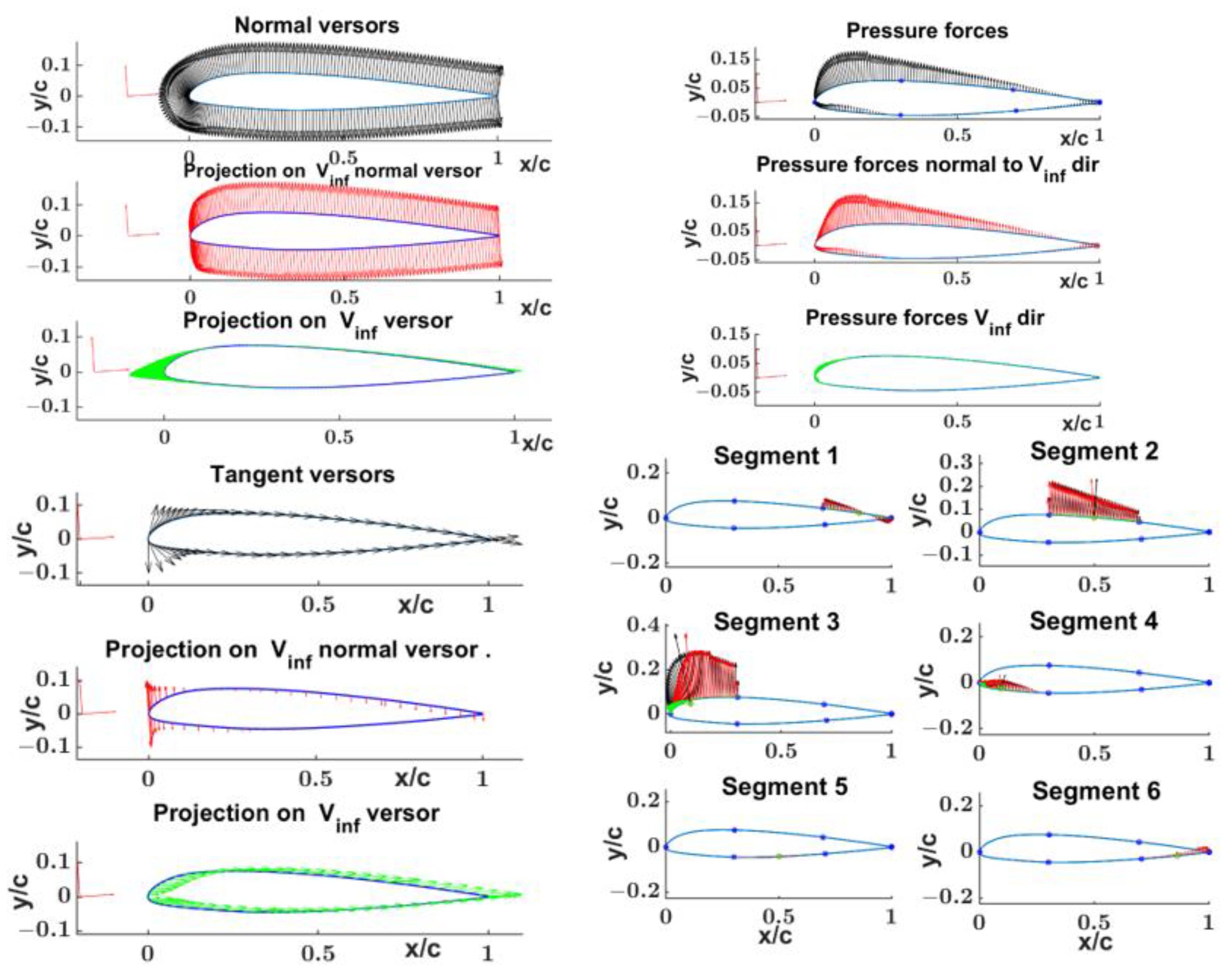
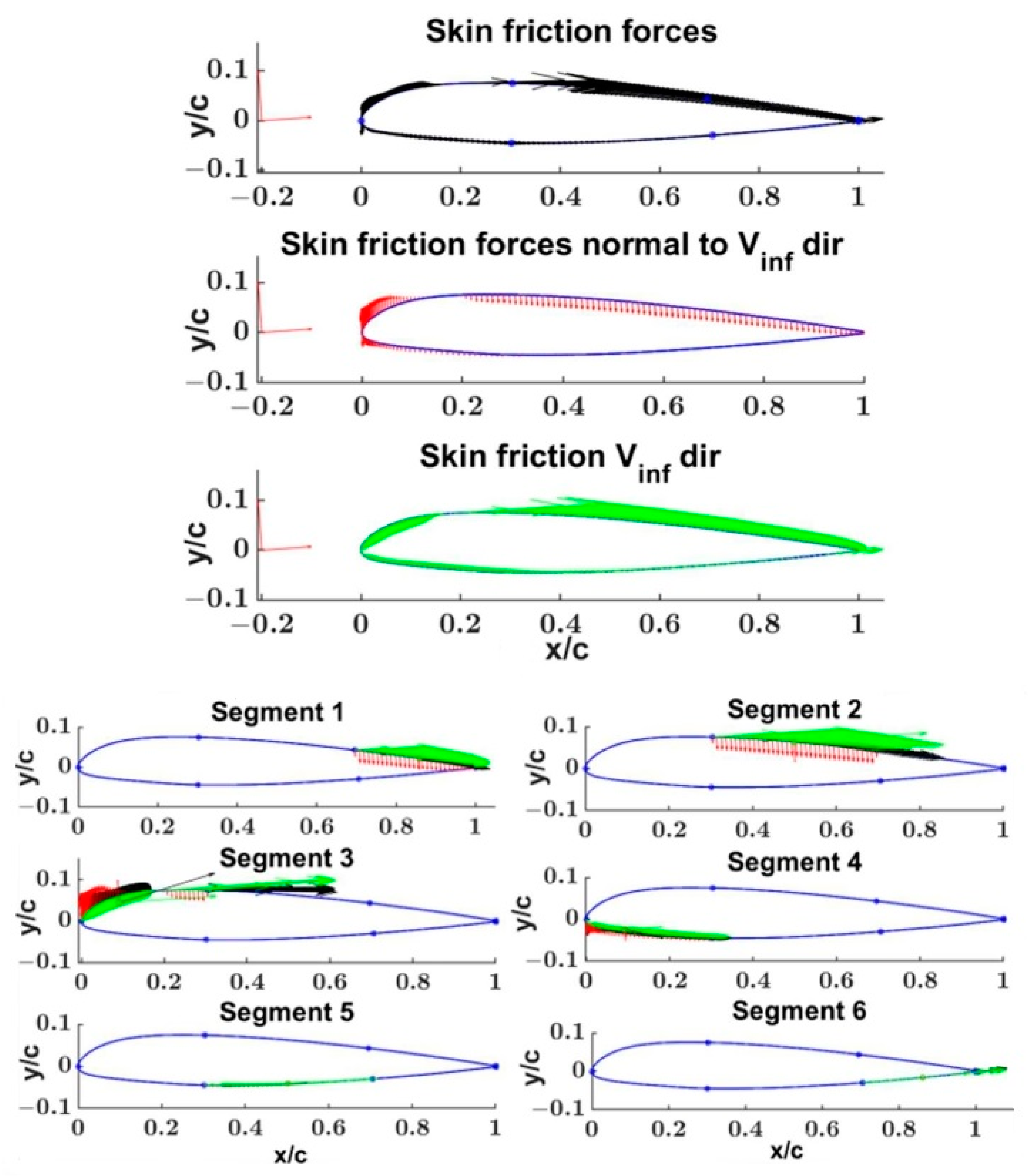
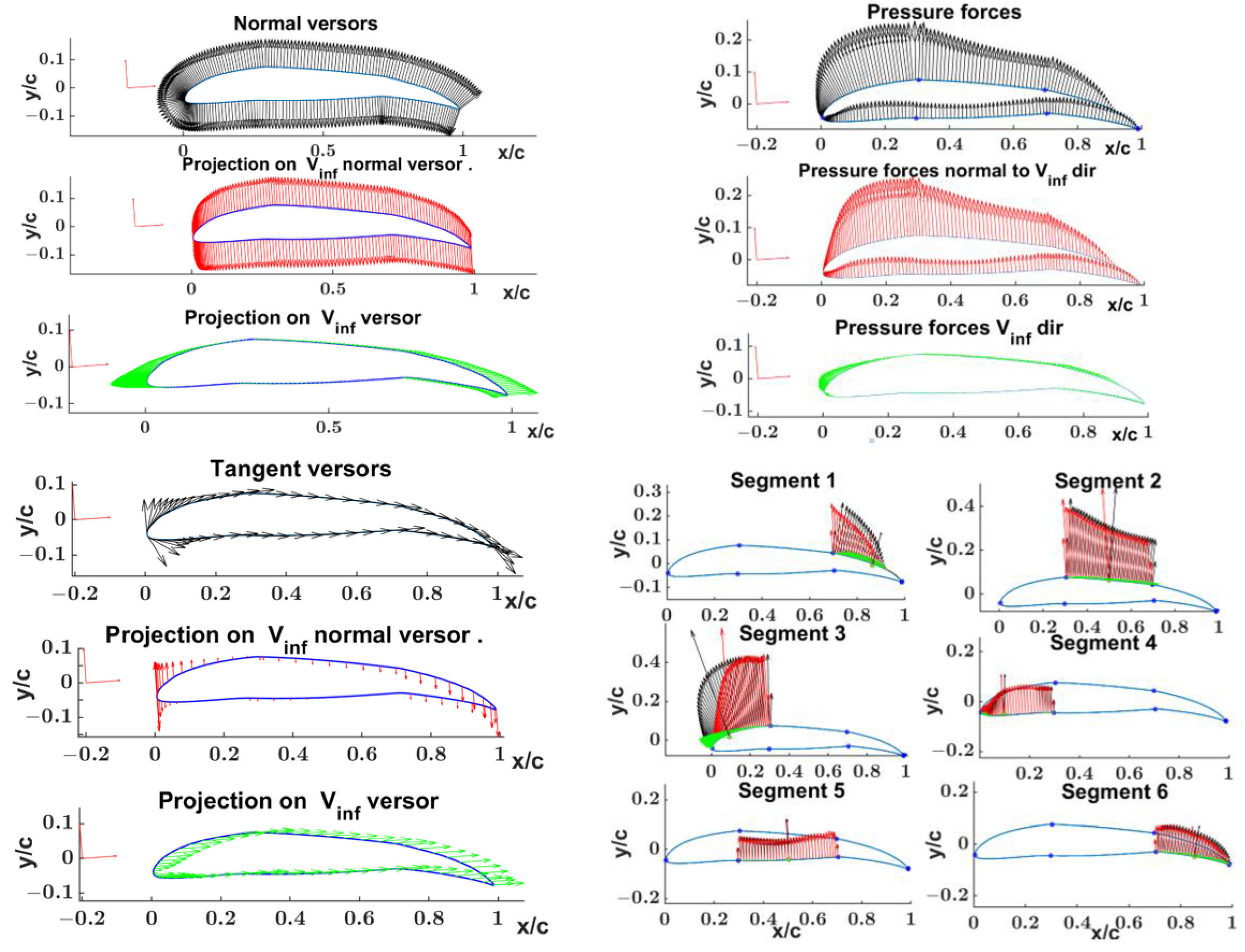
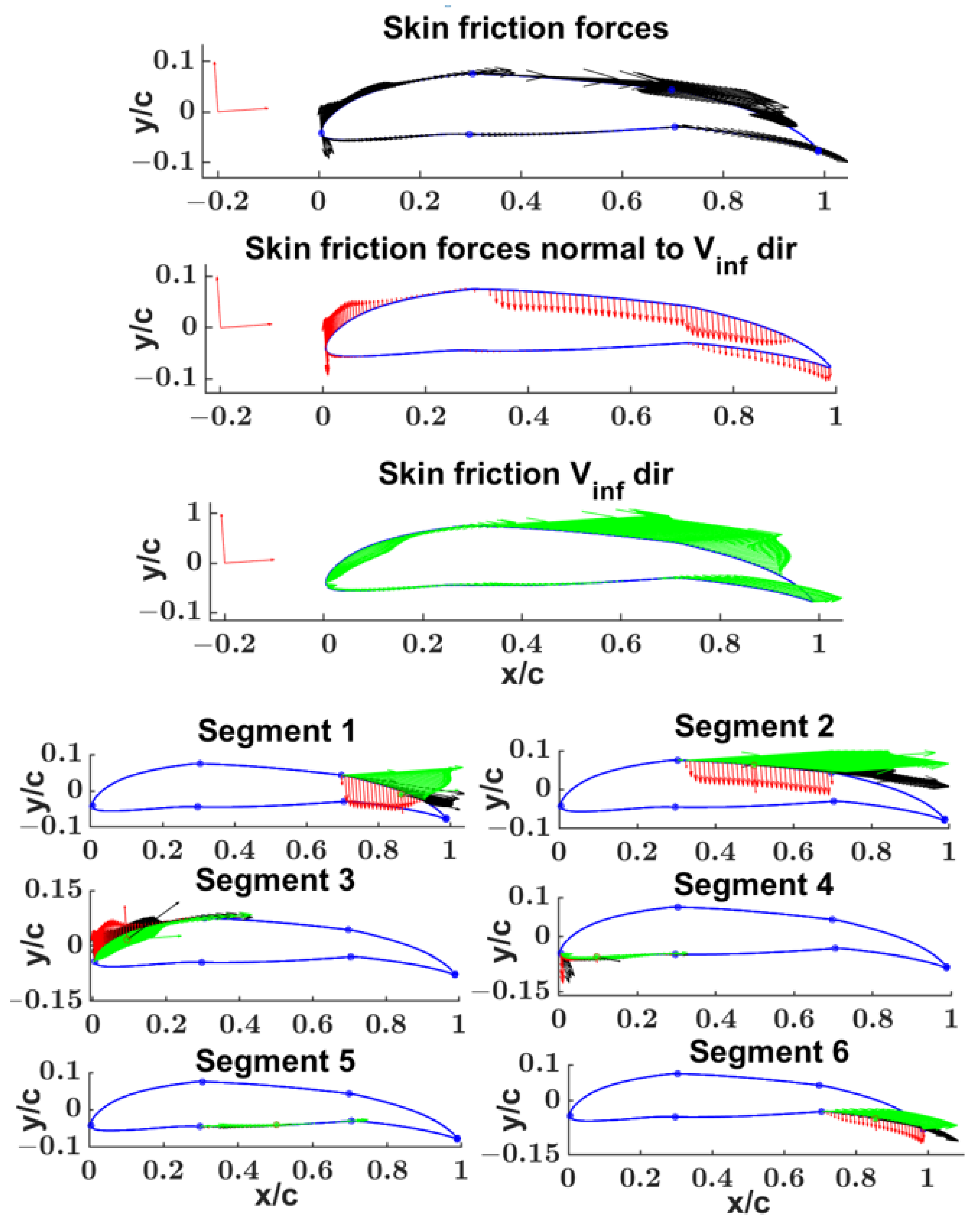
- two examples of segment-wise evaluation of pressure and skin friction forces and their contribution to the airfoil lift and drag.
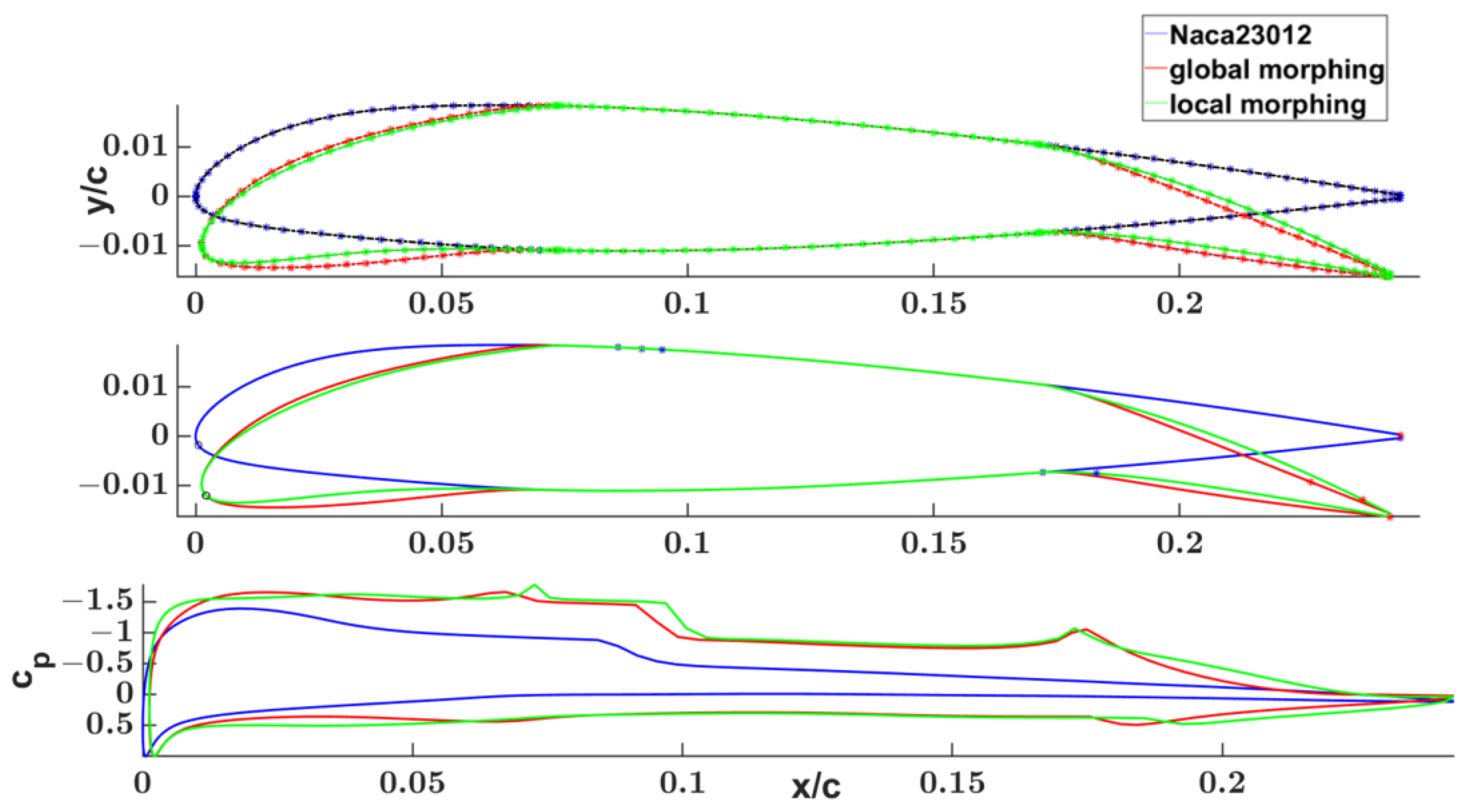
- “global morphing CFD optimization” and the next “local morphing CFD optimization” for exploring a further improvement of the aerodynamic properties.
4.1. NACA 23012 Segments Wise Aerodynamics Properties Evaluation
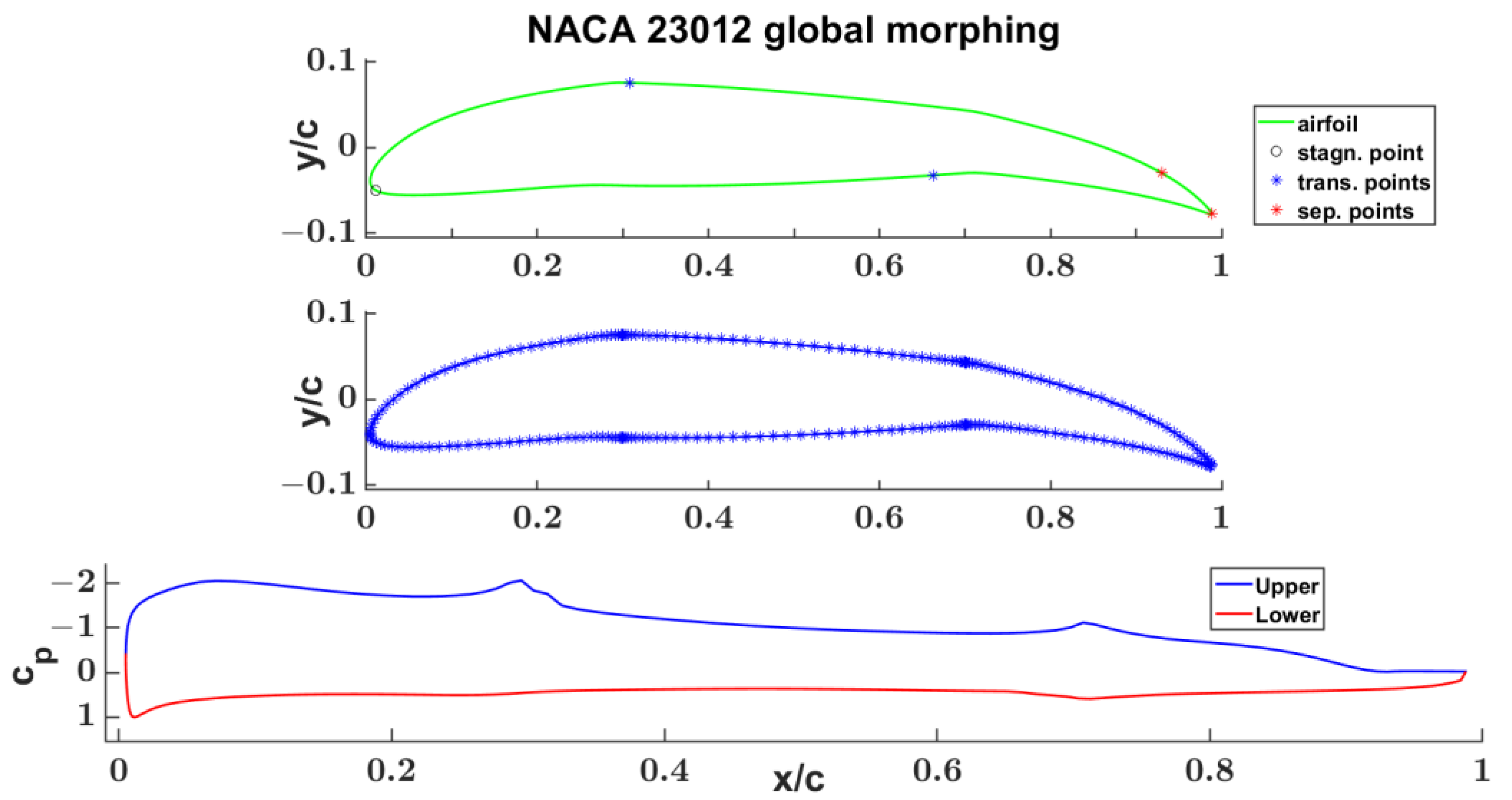
4.2. Morphed NACA 23012 Segment-Wise Aerodynamic Properties Evaluation
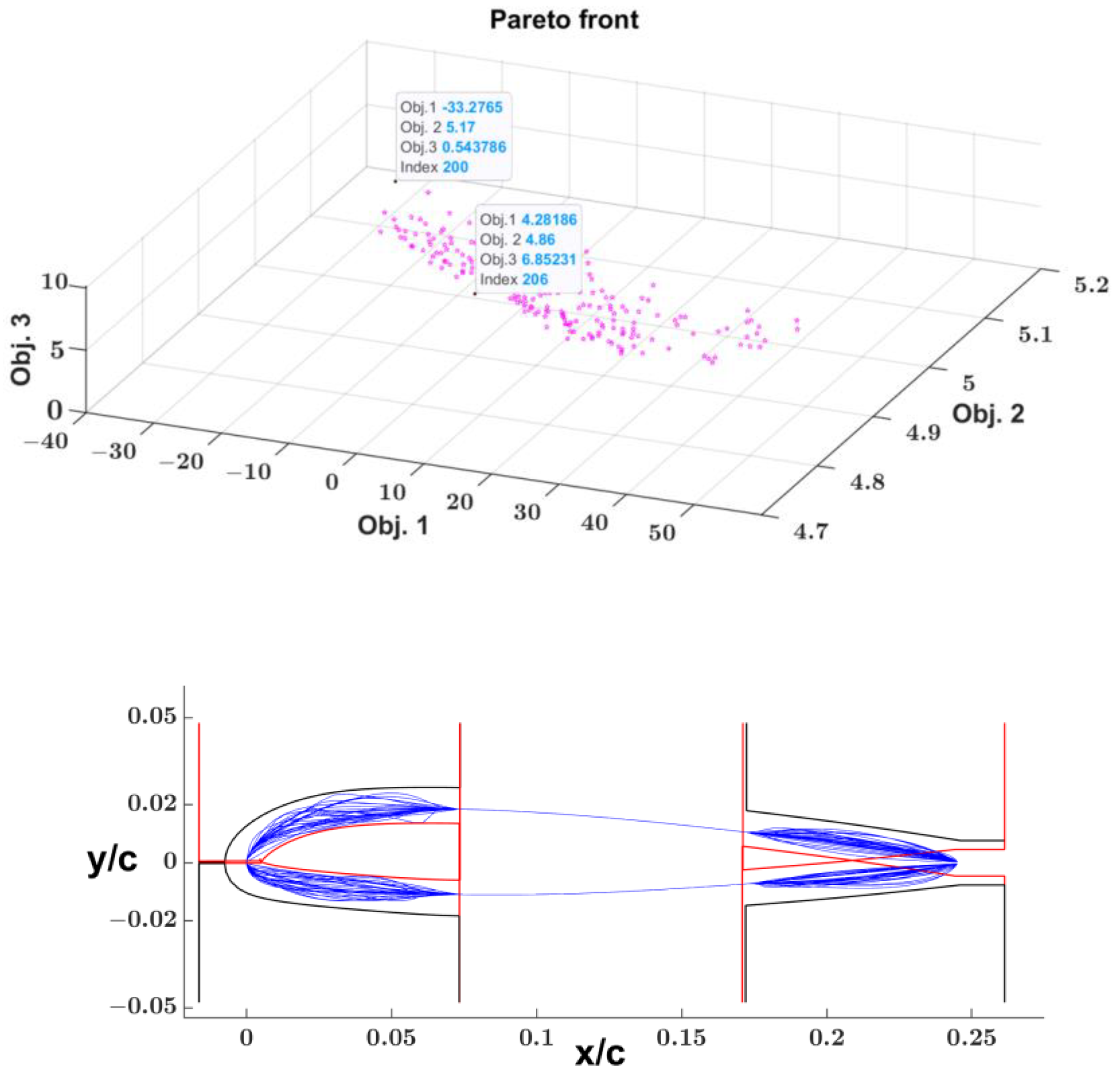
4.3. NACA 0012 CFD “Global & Local” Morphing CFD Design Optimization
- = aerodynamic efficiency resulting from global morphing optimization = 74.39
- = aerodynamic efficiency of the current airfoil
- = airfoil circulation resulting from global morphing optimization = 1.192
- = airfoil circulation of the current airfoil
- from NACA 23012 to global morphed airfoil: 18.19%
- from global morphed airfoil to skin morphed: 4.47%
5. Conclusions
- to represent geometrically a wide range of 2D profile families, with the Euclidean points error distance in the order of O (10−4).
- to generate airfoils aerodynamically equivalent to the related input 2D profile (both qualitatively and quantitatively).
- to implement LE and TE morphing at both local and global levels (the properties of the airfoil mathematical model ensure that, for both the local and global morphing, the desired continuity boundary conditions between the neighbor segments are always satisfied);
- to apply geometrical constraints, i.e., considering CB as a rigid/fixed section;
- to change the relative size of each section (LE, CB, and TE) just acting on the x/c location of the partition points;
- to evaluate the contribution of each segment/section to the aerodynamic lift and drag forces;
- to implement CFD, structural, and FSI design optimization processes, with the opportunity to adjust the parameter topology and airfoil model complexity according to the analyst’s needs.
- Different strategies/framework can be implemented considering the opportunity to manage the variable Sfps and InCps separately.
- The airfoil design optimization process could be implemented for defining a desired elliptical span-wise load on a LE, TE morphing rectangular wing.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| BCPs | Boundary Control Points |
| C | the segment vector-valued function of the u-independent variable |
| C′ | the tangent vector-valued function of the u-independent variable |
| C″ | the curvature vector-valued function of the u-independent variable |
| CB | Central Box |
| CFD | Computational Fluid Dynamics |
| CPs | Control Points |
| E = | Aerodynamic efficiency |
| InCPs | Interior Control Points |
| LE | Leading-Edge |
| NURBS | Non-Uniform Rational B-Spline |
| SF | Scale Factor |
| SFps | Scale Factor Parameters |
| TE | Trailing-Edge |
| UNRBS | Uniform Non-Rational B-spline |
References
- Salunke, N.P.; Juned Ahamad, R.A.; Channiwala, S.A. Airfoil Parameterization Techniques: A Review. Am. J. Mech. Eng. 2014, 2, 99–102. [Google Scholar] [CrossRef]
- Song, W.; Keane, A.J. A Study of Shape Parameterisation Methods for Airfoil Optimisation. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004. [Google Scholar] [CrossRef]
- Lépine, J.; Guibault, F.; Trépanier, J.-Y. Optimized Nonuniform Rational B-Spline Geometrica Representation for Aerodynamic Design of Wings. AIAA J. 2001, 39, 2033–2041. [Google Scholar] [CrossRef]
- Hilbig, R.; Szodruch, J. The Intelligent Wing—Aerodynamic Developments for Future Transport Aircraft. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989. [Google Scholar] [CrossRef]
- Venkataraman, P. A new procedure for airfoil definition. In Proceedings of the 13th Applied Aerodynamics Conference, San Diego, CA, USA, 19–22 June 1995; Volume 10. [Google Scholar] [CrossRef]
- Documentation—MATLAB & Simulink—MathWorks Italia. Available online: https://it.mathworks.com/help/ (accessed on 3 March 2022).
- Xfoil Subsonic Airfoil Development System. Available online: https://web.mit.edu/drela/Public/web/xfoil/ (accessed on 8 June 2022).
- Spink, M.; Claxton, D.; de Falco, C.; Vazquez, R. Nurbs 1.4.3. Collection of Routines for the Creation, and Manipulation of Non-Uniform Rational B-Splines (NURBS), Based on the NURBS Toolbox. 2021. Available online: https://gnu-octave.github.io/packages/nurbs/ (accessed on 11 April 2022).
- UIUC Applied Aerodynamics Group. Available online: https://m-selig.ae.illinois.edu/ (accessed on 18 May 2022).
- UIUC Airfoil Coordinates Database. Available online: https://m-selig.ae.illinois.edu/ads/coord_database.html (accessed on 18 May 2022).
- Abbot, I.H.; Doenhoff, A.E.V. Theory of Wing Sections; Dover: New York, NY, USA, 1985. [Google Scholar]
- Drela, M.; Youngren, H. xfoil_doc. 2001. Available online: http://web.mit.edu/aeroutil_v1.0/xfoil_doc.txt (accessed on 8 June 2022).
- Piegel, L.; Tiller, W. The NURBS Books, 2nd ed.; Springer: Berlin, Germany, 1997. [Google Scholar]
- Buosi, D. Development of a Parametric Tool for Shape Manipulation and Fluid Dynamics Optimization of a UHBR Engine Nacelle. Bachelor’s Thesis, University of Padova, Padua, Italy, 2019. [Google Scholar]
- Safari, A.; Lemu, H.G. Optimum NURBS curve fitting for geometry parameterization of gas turbine blades’ sections: Part I—evolutionary optimization techniques, in ASME 2012. In Proceedings of the International Mechanical Engineering Congress, ASME, Houston, TX, USA, 9–15 November 2012; p. 7. [Google Scholar] [CrossRef]
- Safari, A.; Lemu, H.G. Optimum NURBS curve fitting for geometry parameterization of gas turbine blades’ sections: Part II: Swarm intelligence techniques, in ASME 2012. In Proceedings of the International Mechanical Engineering Congress & Exposition, Houston, TX, USA, 9–15 November 2012; p. 6. [Google Scholar] [CrossRef]
- Safari, A.; Lemu, H.G.; Assadi, M.A.; Lemu, H.G.; Assadi, M. A novel combination of adaptive tools for turbomachinery airfoil shape optimization using a real-coded genetic algorithm. In ASME Turbo Expo 2013, Proceedings of the Turbine Technical Conference and Exposition, ASME, San Antonio, TX, USA, 3–7 June 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Branke, J.; Deb, K.; Miettinen, K.; Słowìnskì, R. Multiobjective Optimization Interactive and Evolutionary Approaches; Springer: Berlin, Germany, 2008. [Google Scholar]
- Oyama, A.; Obayashi, S.; Nakahashi, K. Fractional factorial design of genetic coding for aerodynamic optimization. In Proceedings of the 14th Computational Fluid Dynamics Conference, Norfolk, VA, USA, 1–5 November 1999; Volume 11. [Google Scholar] [CrossRef]
- Performing a Multiobjective Optimization Using the Genetic Algorithm. Available online: https://it.mathworks.com/help/gads/gamultiobj-plot-vectorize.html (accessed on 22 March 2022).
- Gamultiobj Find Pareto Front of Multiple Fitness Functions Using Genetic Algorithm. Available online: https://it.mathworks.com/help/gads/gamultiobj.html (accessed on 24 March 2022).
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Program. 2000, 37, 149–185. [Google Scholar] [CrossRef]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM j. Optim. 1999, 24, 877–900. [Google Scholar] [CrossRef]
- Coleman, T.F.; Li, Y. An Interior Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM J. Optim. 1996, 24, 418–445. [Google Scholar] [CrossRef]
- Fmincon Find Minimum of Constrained Nonlinear Multivariable Function. Available online: https://it.mathworks.com/help/optim/ug/fmincon.html (accessed on 22 March 2022).
- Constrained Nonlinear Optimization Algorithms. Available online: https://it.mathworks.com/help/optim/ug/constrained-nonlinear-optimization-algorithms.html (accessed on 22 March 2022).











| Segment n° | Preceding Segment | Following Segment | Joints |
|---|---|---|---|
| 1 | 6 | 2 | 1,2 |
| 2 | 1 | 3 | 2,3 |
| 3 | 2 | 4 | 3,4 |
| 4 | 3 | 5 | 4,5 |
| 5 | 4 | 6 | 5,6 |
| 6 | 5 | 1 | 6,7 |
| Segment n° | BC 0 | int. | BC 1 | |||||
|---|---|---|---|---|---|---|---|---|
| Joint | Continuity | CPs | CPs | Joint | Continuity | CPs | Tot. Seg. Parameters | |
| 1 | 1 | C0 | 0 | 1 | 2 | C0 | 2 | 6 |
| 2 | 3 | C0 | 2 | 1 | 2 | C0 | 2 | 10 |
| 3 | 3 | C0 | 2 | 1 | 4 | C0 | 2 | 10 |
| 4 | 5 | C0 | 2 | 1 | 4 | C0 | 2 | 10 |
| 5 | 5 | C0 | 2 | 1 | 6 | C0 | 2 | 10 |
| 6 | 1 | C0 | 0 | 1 | 6 | C0 | 2 | 6 |
| Partial sum | 8 | 6 | 12 | |||||
| Tot CPs | 26 | |||||||
| Tot parameters | 52 | |||||||
| Segment n° | BC 0 | int. | BC 1 | |||||
|---|---|---|---|---|---|---|---|---|
| Joint | Continuity | CPs | CPs | Joint | Continuity | CPs | Tot. Parameters | |
| 1 | 1 | C0 | 0 | 1 | 2 | C2 | 0 | 2 |
| 2 | 3 | C2 | 0 | 1 | 2 | C2 | 0 | 2 |
| 3 | 3 | C2 | 0 | 1 | 4 | C2 | 0 | 2 |
| 4 | 5 | C2 | 0 | 1 | 4 | C2 | 0 | 2 |
| 5 | 5 | C2 | 0 | 1 | 6 | C2 | 0 | 2 |
| 6 | 1 | C0 | 0 | 1 | 6 | C2 | 0 | 2 |
| Partial sum | 0 | 6 | 0 | |||||
| Tot CPs | 6 | |||||||
| Tot parameters | 12 | |||||||
| Segment n° | BC 0 | int. | BC 1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Joint | Continuity | CPs | SF | CPs | Joint | Continuity | CPs | SF | Tot. Parameters | |
| 1 | 1 | C0 | 0 | 0 | 1 | 2 | C2 | 0 | 1 | 3 |
| 2 | 3 | C2 | 0 | 1 | 1 | 2 | C2 | 0 | 1 | 4 |
| 3 | 3 | C2 | 0 | 1 | 1 | 4 | C2 | 0 | 1 | 4 |
| 4 | 5 | C2 | 0 | 1 | 1 | 4 | C2 | 0 | 1 | 4 |
| 5 | 5 | C2 | 0 | 1 | 1 | 6 | C2 | 0 | 1 | 4 |
| 6 | 1 | C0 | 0 | 0 | 1 | 6 | C2 | 0 | 1 | 3 |
| Partial sum | 0 | 4 | 6 | 0 | 6 | |||||
| Tot parameters | 22 | |||||||||
| Seg. n° | BC 0 | BC 1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Joint | CP | CP | SF | SF | Joint | CP | CP | SF | SF | |
| Xmin% | Xmax% | Lb | Ub | Xmin% | Xmax% | Lb | Ub | |||
| 1 | 1 | - | - | - | - | 2 | 85 | 96 | 0.1549 | 0.4243 |
| 2 | 3 | 5 | 15 | 0.5819 | 1.6249 | 2 | 85 | 96 | 0.6282 | 1.8958 |
| 3 | 3 | 5 | 15 | 0.2335 | 0.6911 | 4 | 85 | 99 | 0.1958 | 1.0372 |
| 4 | 5 | 5 | 15 | 0.2747 | 0.8131 | 4 | 85 | 99 | 0.2303 | 0.9511 |
| 5 | 5 | 5 | 15 | 0.3141 | 0.9511 | 6 | 85 | 96 | 0.2909 | 0.8149 |
| 6 | 7 | - | - | - | - | 6 | 85 | 96 | 0.1549 | 0.4243 |
| BC 0—SFs | BC 1—SF | |||||||
|---|---|---|---|---|---|---|---|---|
| Seg. n° | Joint | Lb | Value | Ub | Joint | Lb | Value | Ub |
| 1 | 1 | - | - | 2 | 0.1549 | 0.2574 | 0.4243 | |
| 2 | 3 | 0.5819 | 1.3110 | 1.6249 | 2 | 0.6282 | 1.6527 | 1.8958 |
| 3 | 3 | 0.2335 | 0.6777 | 0.6911 | 4 | 0.1958 | 0.8279 | 1.0372 |
| 4 | 5 | 0.2747 | 0.6193 | 0.8131 | 4 | 0.2303 | 0.5360 | 0.9511 |
| 5 | 5 | 0.3141 | 0.9332 | 0.9511 | 6 | 0.2909 | 0.6846 | 0.8149 |
| 6 | 7 | - | - | 6 | 0.1549 | 0.2152 | 0.4243 | |
| Seg. | Priority | Joints | Continuity | Boundary Data | Tangent Curvature |
|---|---|---|---|---|---|
| Numerical Evaluation | |||||
| 1 | 2 | 1 | C0 | Input Airfoil point | - |
| 2 | C2 | Segment 2 | Segments 1 & 2 | ||
| Tangent curvature vector | B-spline interpolation | ||||
| 2 | 1 | 2 | C2 | Input Airfoil points | Segments 1 & 2 |
| B-spline interpolation | |||||
| 3 | C2 | Input Airfoil points | Segments 2 & 3 | ||
| B-spline interpolation | |||||
| 3 | 3 | 3 | C2 | Segment 2 | Segments 2 & 3 |
| Tangent curvature vector | B-spline interpolation | ||||
| 4 | C2 | Input Airfoil points | Segments 3 & 4 | ||
| B-spline interpolation | |||||
| 4 | 4 | 4 | C2 | Segment 3 | Segments 3 & 4 |
| Tangent curvature vector | B-spline interpolation | ||||
| 5 | C2 | Segment 5 | Segments 4 & 5 | ||
| Tangent curvature vector | B-spline interpolation | ||||
| 5 | 1 | 5 | C2 | Input Airfoil points | Segments 4 & 5 |
| B-spline interpolation | |||||
| 6 | C2 | Input Airfoil points | Segments 5 & 6 | ||
| B-spline interpolation | |||||
| 6 | 2 | 6 | C2 | Segment 5 | Segments 5 & 6 |
| Tangent curvature vector | B-spline interpolation | ||||
| 7 | C0 | Input Airfoil points | - |
| Seg. N° | NACA 0012 (hh:mm:ss) | NACA 23012 (hh:mm:ss) | NREL’s S089 (hh:mm:ss) |
|---|---|---|---|
| 1 | 00:09:26 | 00:08:54 | 00:07:56 |
| 2 | 00:16:01 | 00:14:05 | 00:07:53 |
| 3 | 00:14:22 | 00:13:38 | 00:14:07 |
| 4 | 00:14:25 | 00:06:30 | 00:15:13 |
| 5 | 00:15:14 | 00:16:00 | 00:13:51 |
| 6 | 00:08:24 | 00:09:35 | 00:10:40 |
| Tot | 01:17:52 | 01:08:42 | 01:09:40 |
| Seg. N° | NACA0012 | NACA 23012 | NREL’s S809 | |||
|---|---|---|---|---|---|---|
| max(abs(dy)) | sum(abs(dy)) | max(abs(dy)) | sum(abs(dy)) | max(abs(dy)) | sum(abs(dy)) | |
| 1 | 4.81 × 10−5 | 0.00029 | 4.79 × 10−5 | 0.00030 | 0.00060 | 0.00349 |
| 2 | 1.22 × 10−5 | 0.00007 | 1.94 × 10−5 | 0.00014 | 0.00033 | 0.00174 |
| 3 | 8.16 × 10−5 | 0.00074 | 9.06 × 10−5 | 0.00095 | 0.00022 | 0.00184 |
| 4 | 0.00019 | 0.00182 | 0.00062 | 0.00642 | 0.00060 | 0.00559 |
| 5 | 0.00012 | 0.00083 | 0.00011 | 0.00080 | 0.00035 | 0.00155 |
| 6 | 4.68 × 10−5 | 0.00030 | 4.79 × 10−5 | 0.00031 | 0.00060 | 0.00299 |
| Tot | 0.00405 | 0.00892 | 0.0172 | |||
| Segment N° | RAE2822 (hh:mm:ss) | NACA 0406 (hh:mm:ss) | NACA 0610 (hh:mm:ss) |
|---|---|---|---|
| 1 | 00:04:09 | 00:12:57 | 00:16:40 |
| 2 | 00:13:46 | 00:04:12 | 00:04:02 |
| 3 | 00:06:58 | 00:12:34 | 00:13:57 |
| 4 | 00:20:14 | 00:03:39 | 00:09:03 |
| 5 | 00:21:53 | 00:19:47 | 00:18:38 |
| 6 | 00:04:40 | 00:13:12 | 00:13:04 |
| Timing tot | 01:11:40 | 01:06:21 | 01:15:24 |
| Segment N° | RAE2822 sum(abs(dy)) | NACA 0406 sum(abs(dy)) | NACA 0610 sum(abs(dy)) |
|---|---|---|---|
| 1 | 0.00210 | 0.00237 | 0.00267 |
| 2 | 0.00051 | 0.00435 | 0.00426 |
| 3 | 0.00234 | 0.00418 | 0.00102 |
| 4 | 0.00260 | 0.00322 | 0.00294 |
| 5 | 0.00136 | 0.00236 | 0.00137 |
| 6 | 0.00210 | 0.00096 | 0.00226 |
| Tot | 0.01101 | 0.01744 | 0.01452 |
| Method | Parameters Number | Parameters Description |
|---|---|---|
| Numerical Basis Functions | 5 | Weights for the basis airfoil functions |
| B-spline interpolation | 34 | Point coordinates |
| Proposed method | 22 | SFs and point coordinates |
| Method | RAE2822 | NACA 0406 | NACA 0610 |
|---|---|---|---|
| Numerical Basis Functions | 0.2217 | 0.0582 | 0.1595 |
| B-spline interpolation | 0.1552 | 0.0758 | 0.1993 |
| Proposed method | 0.0110 | 0.0174 | 0.0145 |
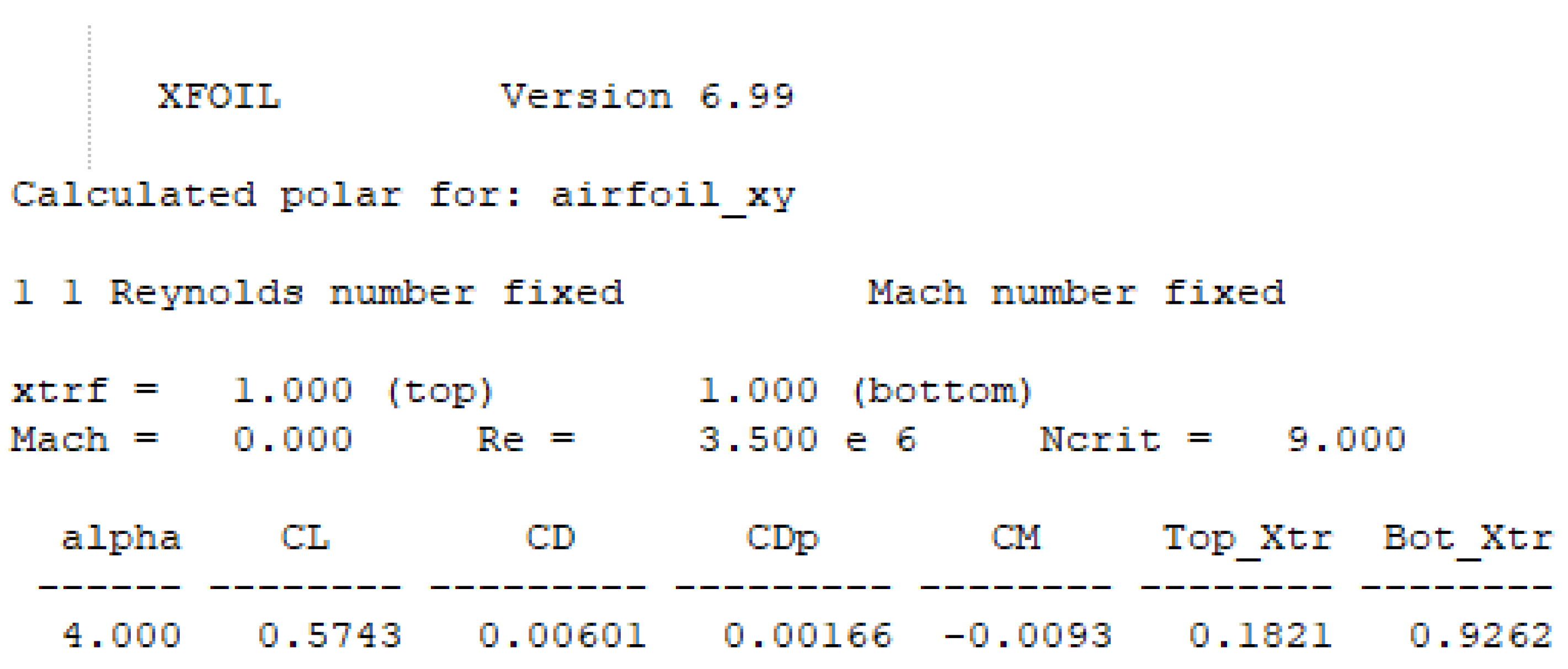
| cl | cd | cdp | ||
|---|---|---|---|---|
| Xfoil output | 0.5743 | 0.00601 | 0.00166 | |
| i | cli | cfi⊥ Vinf | cfi || Vinf | |
| Segment | 1 | 0.0126 | −0.00014 | 0.00068 |
| Segment | 2 | 0.1697 | −0.00024 | 0.00161 |
| Segment | 3 | 0.3218 | 0.00027 | 0.00120 |
| Segment | 4 | 0.0592 | −0.00013 | 0.00045 |
| Segment | 5 | −0.0073 | −0.00001 | 0.00023 |
| Segment | 6 | 0.0182 | 0.00001 | 0.00018 |
| Tot | 0.5742 | −0.00024 | 0.00435 | |
| cl = Σ cli + Σ (cfi ⊥ Vinf) | 0.5740 | |||
| cdp = cd − Σ(cfi || Vinf) | 0.00166 |
| . | cl | cd | cdp | |
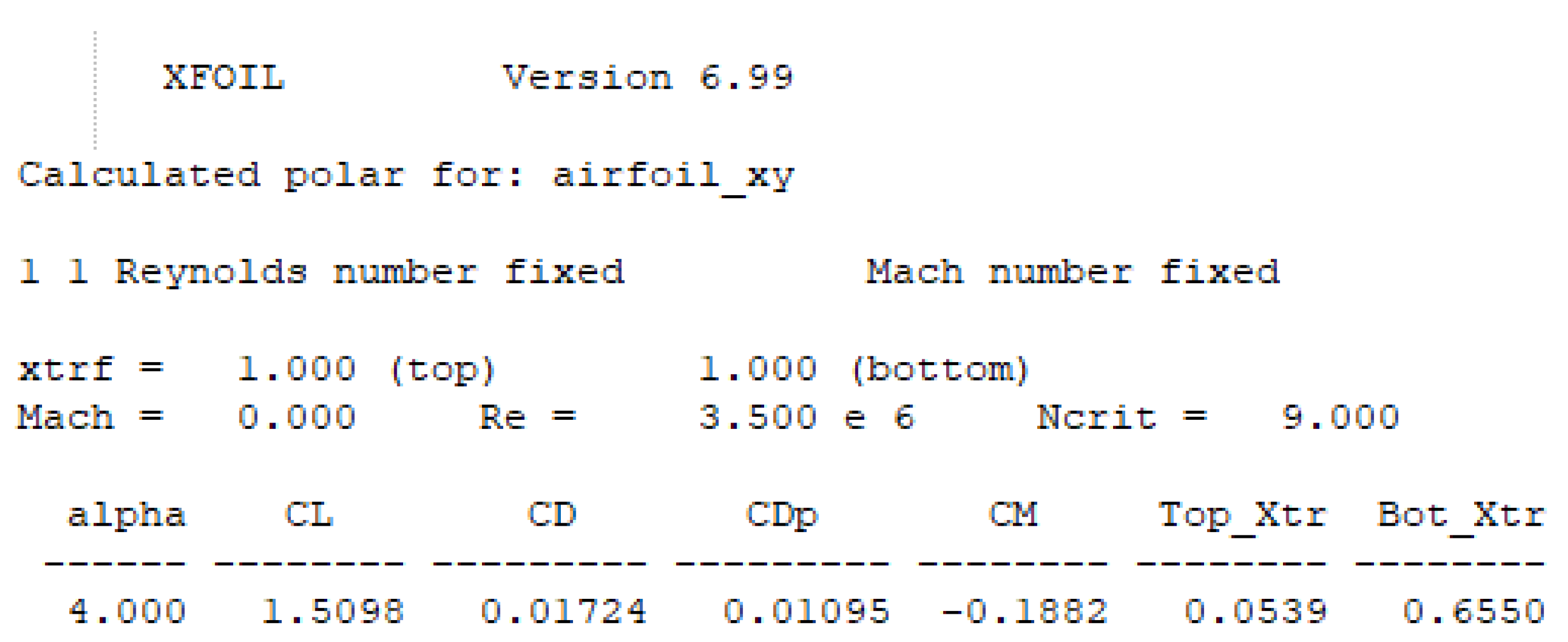
|---|---|---|---|---|
| Xfoil output | 1.5098 | 0.01724 | 0.01095 | |
| i | cli | cfi⊥ Vinf | cfi || Vinf | |
| Segment | 1 | 0.1106 | −0.00023 | 0.00062 |
| Segment | 2 | 0.4239 | −0.00031 | 0.00209 |
| Segment | 3 | 0.5472 | 0.00060 | 0.00246 |
| Segment | 4 | 0.1638 | −0.00016 | 0.00036 |
| Segment | 5 | 0.1535 | −0.00001 | 0.00019 |
| Segment | 6 | 0.1109 | −0.00017 | 0.00069 |
| Tot | 1.5099 | −0.00027 | 0.00640 | |
| cl = Σ cli + Σ (cfi ⊥ Vinf) | 1.5096 | |||
| cdp = cd – Σ(cfi || Vinf) | 0.01084 |
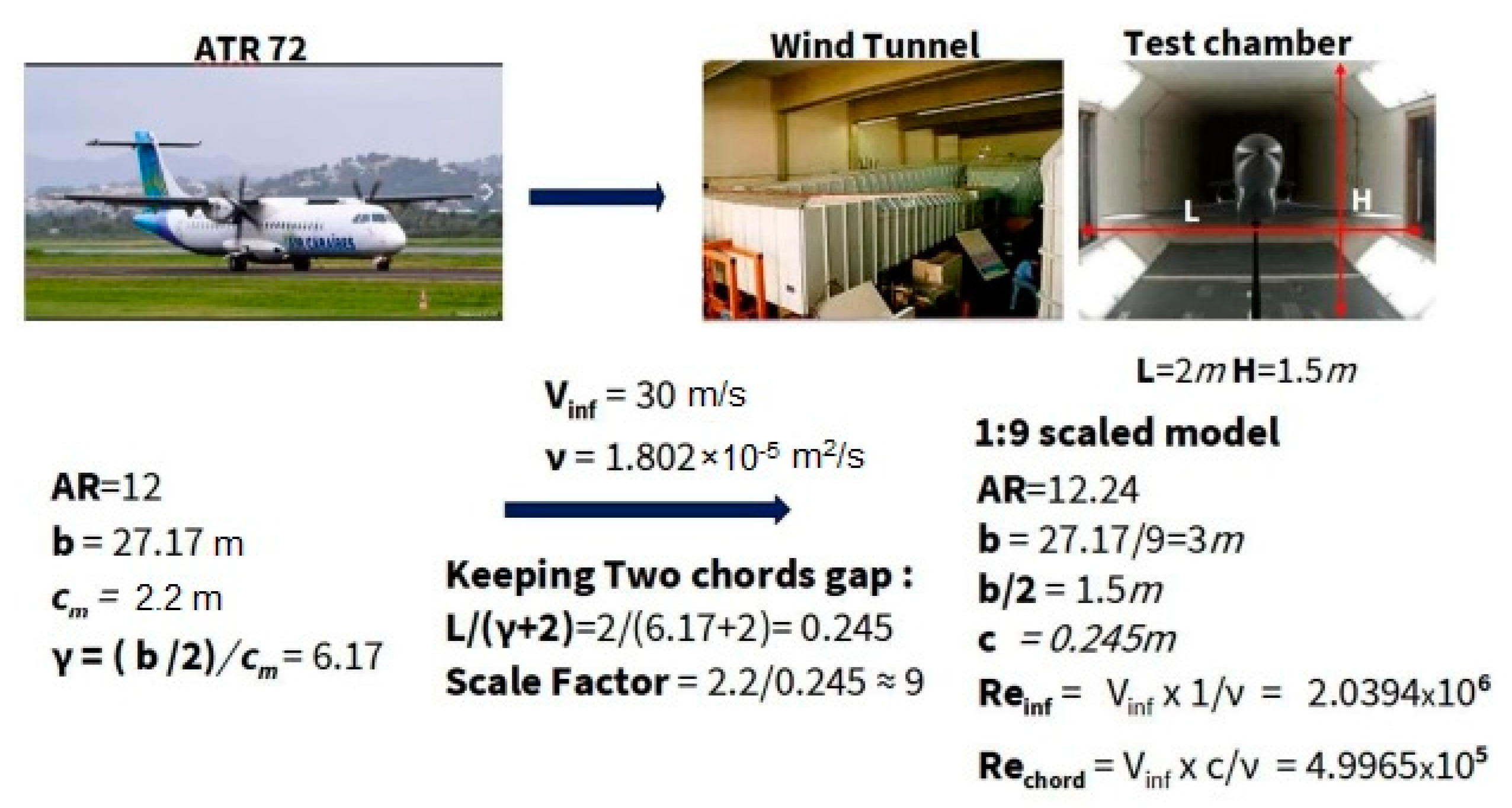
| = 4°, Re∞ = 2.0394 × 106 | NACA 23012 Initial | NACA 23013 Global Morphing |
|---|---|---|
| Obj.1 | 0.583 | 1.192 |
| Obj.2 | 0.340 | 0.589 |
| Obj.3 | 0.940 | 1.652 |
| c | 0.245 m | 0.242 m |
| 3.89 × 10−2 | 7.95 × 10−2 | |
| 6.17 × 10−4 | 1.07 × 10−3 | |
| 1.7 × 10−3 | 3.00 × 10−3 | |
| 0.1586 | 0.329 | |
| 2.52 × 10−3 | 4.42 × 10−3 | |
| 2.84 × 10−2 | 5.13 × 10−2 | |
| 62.94 | 74.39 | |
| LE (°) | 0 | 8.08 |
| TE (°) | 0 | 12.6 |
| = 4°, Re∞ = 2.0394 × 106 | NACA 23012 Initial | NACA 23013 Global Morphing | NACA 23013 Skin Morphing |
|---|---|---|---|
| c | 0.245 m | 0.242 m | 0.242 m |
| 3.89 × 10−2 | 7.95 × 10−2 | 7.98 × 10−2 | |
| 6.17 × 10−4 | 1.07 × 10−3 | 1.07 × 10−3 | |
| 1.7 × 10−3 | 3.00 × 10−3 | 3.03 × 10−3 | |
| 0.1586 | 0.329 | 0.330 | |
| 2.52 × 10−3 | 4.42 × 10−3 | 4.42 × 10−3 | |
| 2.84 × 10−2 | 5.13 × 10−2 | 5.17 × 10−2 | |
| 62.94 | 74.39 | 78.26 | |
| LE (°) | 0 | 8.08 | 8.08 |
| TE (°) | 0 | 12.6 | 12.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tortora, G.; Concilio, A.; Pecora, R. Airfoil Shape Morphing through a Novel Parameterization and Fitting Optimization Method Based on Uniform Non-Rational B-Spline Functions. Designs 2023, 7, 28. https://doi.org/10.3390/designs7010028
Tortora G, Concilio A, Pecora R. Airfoil Shape Morphing through a Novel Parameterization and Fitting Optimization Method Based on Uniform Non-Rational B-Spline Functions. Designs. 2023; 7(1):28. https://doi.org/10.3390/designs7010028
Chicago/Turabian StyleTortora, Giancarlo, Antonio Concilio, and Rosario Pecora. 2023. "Airfoil Shape Morphing through a Novel Parameterization and Fitting Optimization Method Based on Uniform Non-Rational B-Spline Functions" Designs 7, no. 1: 28. https://doi.org/10.3390/designs7010028
APA StyleTortora, G., Concilio, A., & Pecora, R. (2023). Airfoil Shape Morphing through a Novel Parameterization and Fitting Optimization Method Based on Uniform Non-Rational B-Spline Functions. Designs, 7(1), 28. https://doi.org/10.3390/designs7010028








