Abstract
The soil water retention curve (SWRC) or soil–water characteristic curve (SWCC) is a fundamental feature of unsaturated soil that simply shows the relationship between soil suction and water content (in terms of the degree of saturation and volumetric or gravimetric water content). In this study, the applications of the SWRC or SWCC have been extensively reviewed, taking about 403 previously published research studies into consideration. This was achieved on the basis of classification-based problems and application-based problems, which solve the widest array of geotechnical engineering problems relevant to and correlating with SWRC geo-structural behavior. At the end of the exercises, the SWRC geo-structural problem-solving scope, as covered in the theoretical framework, showed that soil type, soil parameter, measuring test, predictive technique, slope stability, bearing capacity, settlement, and seepage-based problems have been efficiently solved by proffering constitutive and artificial intelligence solutions to earthwork infrastructure; and identified matric suction as the most influential parameter. Finally, a summary of these research findings and key challenges and opportunities for future tentative research topics is proposed.
1. Introduction
The correlation of matric suction () with moisture content () is referred to as SWRC. It is also a graphical framework that evaluates the hydro-mechanical characteristics of unsaturated soils. Hence, it is utilized to predict the water retention capacity of soil. According to a previous research study [1], the SWRC is the soil’s capacity to retain water over a wide range of suction powers. Graphically, the SWRC is represented as a function of and volumetric water content (). Similarly, SWRC describes the correlation between the quantity of retained water in the soil pores, which is generally designated in terms of volumetric water content or degree of saturation (), and soil suction. SWRC is one of the critical factors, in conjunction with the hydraulic conductivity, that can be used for a reliable subsurface multi-phase flow analysis for scenarios such as transient drying or wetting. Consequently, this hydro-mechanical element’s rigorous characterization and modeling are inevitable for investigating slope stability, multi-immiscible phase flow, and volumetric or shear strength behavior [2,3,4,5].
Over the last decade, tremendous advancements have been made towards extending the principles of unsaturated soil mechanics in various geotechnical design projects. Since the drier soil is located on the Vadose zone, the soil above the groundwater table is considered unsaturated, with variations in degree of saturation. The geotechnical response of the expansive soil residual could be effectively characterized by using the principle of unsaturated soil mechanics (USM) for any given period, while considering the influence of suction as an independent stress state variable [6,7,8]. The SWRC provides a graphical way of evaluating unsaturated soil parameters with their corresponding hydraulic characteristics. The evaluation of soil’s water storage capacity can be estimated through the use of SWRC [9]. Similarly, in geotechnical engineering, the SWRC is also used to evaluate and estimate the bearing capacity of foundations and slope stability according to the volumetric moisture influx into the soil [10].
It is established that USM are suitable for the vadose zone of the soil profile. This vadose zone serves as the foundation for most geotechnical structures, ranging from pavement, earth dams, rail tracks, landfills, and to buildings [11,12,13]. The hydro-mechanical soil characteristics are illustrated using the principle of USM through the application of SWRC. The implementation of SWRC constitutes the moisture-holding mechanism of soil and is used for various geotechnical applications. Moreover, the SWRC depends on suction range. The application of the axis translation technique to evaluate the SWRC of soil has been successfully studied by Ng and Pang [14,15]. In addition, a filter paper test has also been applied to establish the SWRC using Whatman no.42 filter paper. Upon the completion of the test, the matric suction and the corresponding volumetric moisture content were obtained, followed by curve fitting using the models proposed by Fredlund and Xing [1], Van Genuchten [16], or Seki [17], for example. Aneke et al. [18] used these three mentioned models to establish the SWRC for a CH soil (based on the USCS classification system) from the Free State province in South Africa, as demonstrated in Figure 1.
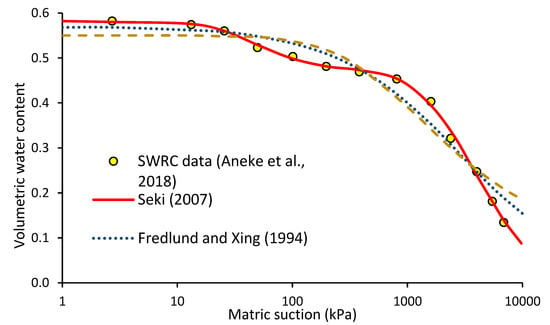
Figure 1.
Soil–water retention curve of a CH soil from the Free State province in South Africa with PI = 36.72, GS = 2.69 and a natural water content of 25.64% [1,17,18].
It has been established that the correlation of matric suction and soil moisture is equivalent to SWRC. As such, the soil moisture can represent gravimetric water content, (GMC), volumetric water content () or degree of saturation (). The SWRC classifies soil behavior into three distinct categories, as illustrated in Figure 2. These categories are as follows: the category of desaturation is known as the “boundary effect class”, which occurs at low soil suction; and the “transition class” is equivalent to intermediate soil suction. Lastly, there is a “residual class”, which manifests at a great soil suction and could be stretched up to 1,000,000 kPa of suction [19].
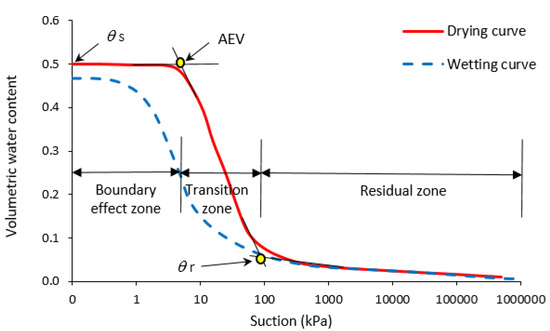
Figure 2.
Soil-water retention curve [1,8].
The non-uniformity of pore-size distribution within the soil voids is mobilized by the SWRC hysteresis due to the trapped water content within the soil void space [20]. Figure 2 describes that the retention of the water residual zone of unsaturation differs from the boundary effect zone due to air hedged within the soil [1]. The point of air-entry value (AEV) over a range of suction constitutes the soil storage potential [21]. The adsorption potential of the soil represents the steep difference between the slope of matric suction and the moisture content. It is expected that soil gets fully saturated during wetting; the soil may fail to reach its complete saturation as a result of a few entrapped air bubbles [22]. Based on the entrapped air, the hysteresis effect influences the SWRC response of the soil due to capillary sphere and changes in the morphological structure of the soil’s pore-size distribution [23].
The use of mechanics and hydraulic principles on various particulate materials has witnessed great strides over the past 50 years. The theoretical framework and formulations of unsaturated soil mechanics (USM) are consistent with saturated soil mechanics (SSM) previously established by a research study [24]. In this instance, the development of USM by a previous research study [25] emerged 40 years after the principles of SSM were established. The distinctive difference between the theoretical framework of SSM and USM is on the basis of the shearing response of saturated soil. It is already an established fact that shear stress of SSM is correlated to one stress-state variable (i.e., the effective stress () expressed as ()). The parameter is the total stress, while is equivalent to pore-water pressure (PWP). However, under the SSM pore-water pressures are typically positive or zero, whereas for USM, the PWP is negative. As such, the change in pore-air pressure () with equivalent change ing pore-water pressure () is simply described as the matric suction ( − ). Additionally, the hydro-mechanical response of unsaturated soils depends net normal stress () and matric suction ( − ), which are referred to as the variable stress tensors [20].
The concept of effective stress was firstly proposed by Terzaghi [24] as a single state variable that shows the portion of the total stress, which produces measurable impacts such as increasing compaction or shearing strength. The importance of this concept makes it the axiom of SSM and causes considerable achievement in solid mechanics, constitutive relationships, and numerical modeling [26,27,28,29,30,31]. Terzaghi’s classic, effective stress paves the way for scholars to extend this concept to USM. Bishop [32] proposed one of the well-known relationships that imposed a new term, ψ ( − ). ψ is the effective stress parameters modified progressively in literature as a degree of saturation and effective degree of saturation [33,34,35]. It is worth noting that the term ψ( − ), known as the suction stress and can be depicted in suction stress characteristics curves (SSCC) that has shown the increase in soil strength due to increasing the matric suction [35,36,37,38,39,40]. Despite the robust formulation of effective stress in SSM, scholars have debated whether to accept the single or two independent stress state variables [20,41,42,43] for USM. Both the concepts have their pros and cons. However, undoubtedly, they are based on soil suction or knowing the SWRCs.
In the 1950s, the need to further the understanding of USM with its application in geotechnical engineering increased despite many prevailing misconceptions. As such, one of the misconception theories was that water-flow occurs within the capillary zone and in the range of positive pore-water pressure. Lambe [44] attempted to find a single soil property flow within the negative pore-water pressure zone through the “capillary head” to explain wetting and drying conditions. In this context, the present interpretation of the SWRC has been performed possible by other researchers due to their illustration of water distribution and flow in soil voids through elementary capillary theory [45]. Subsequently, Fredlund and Morgenstern [42] articulated the stress state theoretical framework in an attempt to solve geotechnical engineering problems under unsaturated soils mechanics. Based on this concept, the principles of macroscopic multiphase continuum mechanics were achieved for interpreting stress state variables.
In the 1980s and 1990s, all major geotechnical engineering problems relied on the SWRC as an interpretative tool to predict non-linear unsaturated soil parameter functions as various prediction models for the calculations of the permeability function in unsaturated soils were proposed. Thus, three groups of models, namely macroscopic, empirical, and statistical were recommended. However, the statistical model was confirmed to be the most reliable due to its precision on the prediction of SWRC, irrespective of its rigorous procedure [21]. Nonetheless, Romero [46] argued that the statistical model had a drawback due to its limited capacity to predict only the permeability function of soils whose inter-particle porosity is controlled by suction. Assouline and Or [4] categorized the previous SWRC analytical models into four classes: (1) empirical or fitting-based models [16,47,48,49]; (2) soil’s particle size distribution-based models [50,51,52]; (3) fractal and pore size distribution based models [53,54,55]; and (4) pedo-transfer functions [56,57,58,59,60,61]. Alternatively, in recent times, methods incorporating advanced technologies with their corresponding software capacities to predict permeability function have been developed [7,62,63,64]. Besides permeability prediction, SWRC has virtually been applied to solve all complex geotechnical engineering problems that involve coupled and uncoupled estimation of shear strength, swelling pressure, hydro-mechanical soil-seepage analysis in earth dams, and in the estimation of resilient modulus for empirical-mechanistic pavement design.
This study aims to present a comprehensive review of the background and previous literature in the field of SWRC. To this end, we first try to classify the most important previous research about SWRC into four parts: soil type, soil parameters, measuring tests, and predicting techniques. In the following, we try to investigate some of the most critical applications of SWRC in slope stability, bearing capacity, settlement, and seepage. The theoretical frameworks of this research have been shown in Figure 3. In the last part of this study, a summary of this research findings will be proposed, and we close with a look at key challenges and opportunities for future tentative research topics.
Figure 3.
The theoretical framework of the SWRC/SWCC study in modeling geotechnical engineering problems.
2. Classification of SWRC Previous Research
There are several parameters that can affect the soil-water retention curve, such as soil structure, soil type, initial water content, void ratio, mineralogy, the distribution of pore sizes and densities, the density of organic material, the clay content, and the contact angle (e.g., [65,66,67]). For a uniform soil with a narrow range of pore sizes, the SWRC curve consists of three different sections: a straight segment up to the air entry pressure, a near-horizontal behavior within the middle part, and a relatively vertical end section. The curve, on the other hand, is shown to be smoother for a well-graded soil. In this case, with a decrease in water saturation, the capillary pressure rises gradually, and the middle section is not horizontal. In the following subsections, an overview of the SWRC of different soil types and the effect of different parameters on the SWRC are outlined. In addition, the methods developed to identify the SWRC of soils are briefly discussed.
2.1. According to Soil Type
Soil compressibility and pore size distribution in response to suction influence the shape of SWRC. The mineralogy, soil structure, initial water content, and stress history have an impact on these two porous material features (e.g., [65,66,67]). Soil pore size distribution has an effect on the shape of SWRCs, which tend to form in a S shape. For rigid porous materials with one pore size, the SWRC must be identical to the curve (a) in Figure 4. However, even if the suction rises above the air entry value, a little water remains in the soil, and total removal of the leftover water demands a lot of energy. Therefore, for a material with a single pore size, curve (b) in Figure 4 could better describe the SWRC. Figure 4 curve (c) illustrates the capillary phenomenon in action by depicting a material with two pore diameters, each of which corresponds to a suction value [20]. SWRC/SWCC reflects a more progressive drop in water content as suction increases in a soil with a wide range of pore sizes (such as fine-grained soils) (Figure 4 curve (d)).
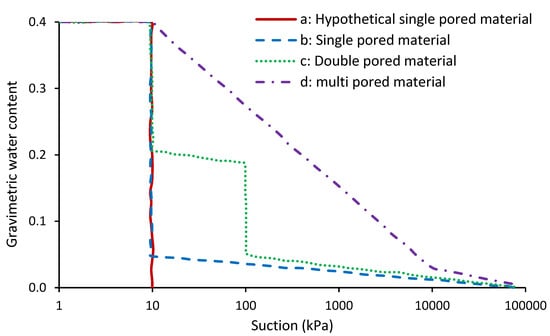
Figure 4.
General shape of soil-water characteristics curve (SWCC) according to pore size distribution [68].
2.1.1. Silty/Clayey Sand
The water-holding capacity of soils with a high sand component is often lower. However, changes in sand soil structure (due to addition of fine materials, compaction etc.) affect soil pore size distributions, which in turn can alter water retention capacity. As the fines content increased, the soil’s water-holding capacity dropped, except when it was between 10% and 60% (according to Jiang et al. [69], who used a pressure membrane apparatus to examine the soil-water properties of ten distinct groups of unsaturated soil samples). Similarly, Shen et al. [70], discovered that the proportion of large pores in calcareous silty sand falls considerably with increasing fines content. Hence, the soil–water retention curves of the samples differ greatly. From 7.5 to about 8 kPa, air entry was recorded for samples with particle level less than 50 percent. Smaller holes became more numerous as calcareous silty sand’s fines content climbed, increasing the volumetric water content of samples in the early residual stage. Samples at the late residual stage show little variation in SWRC, which may be due to calcareous sand’s meso-structure. A study of the changes in suction and volumetric behavior for compacted bentonite-sand mixtures by Montanez [71] confirmed the increase in water holding capacity with the rise in clay content. Pei-yong and Qing [72], and Agus and Schanz [73] achieved similar findings when they studied the SWRC drying and wetting suction retention curves for different combinations of sand and bentonite, respectively.
Soil inter-pore properties (connectivity and volume distribution) can be affected by adding biochar particles [74]. Sand particles can be filled with fine mesquite biochar particles (<0.251 mm) that reduce inter-pore spacing and alter inter-pore morphology [74]. Soil microstructure and water retention in a biochar-adjusted silty sand were experimentally studied by Chen et al. [75], which revealed that adding smaller biochar particles improved the silty sand’s water retention capacity. In addition, increased porosity and water capillary retention of biochar–sand mixes are known to be the reason for the observed improvement in the specimen’s water retention [76]. Likewise, the addition of small biochar particles according to Liao and Thomas [77] was found to increase water retention capacity in soil.
It has been found that compaction and dry density affect the water retention qualities of sand specimens. Sand with various dry densities and particle sizes was used by Gallage and Uchimura [78] to measure this property. They found that hysteresis was absent in samples with a more uniform range of grain sizes. Song [39] also discovered that the air entry value (AEV) of silica sand with varied relative densities decreased as the relative density rose. A silty-sand subgrade’s SWRCs were examined by Barus et al. [79], who looked at the effects of the moisture content and density of the compacted material on the SWRCs over the entire range of suction (0 to 1,000,000 kilopascal). For compacted samples at the same water content, the relationship between weighted water content (GWC) and suction seems to be independent of density levels between 10 and 20,000 kPa for the suction range between 10 and 20,000 kPa. Samples compacted at varying water contents had a similar association.
2.1.2. Fine Grained Soil
Typically, the grain and pore size distributions in clay soils are not consistent [80]. Therefore, for clays the water content normally changes in a very nonlinear fashion as the suction increases. Air-entry values in clayey soils are higher than in silty or sandy soils, and residual points are more difficult to detect. Nearly the whole range of soil suction is affected by adsorption forces, and vapor flow plays a significant role in moisture transfer past the residual limit [81,82]. Increasing the fineness of soil particles increases the soil’s air-entry value. Fine soil particles flatten the curve slope in the desaturation [83].
Furthermore, clay fabric and clay particle retentions can vary greatly between soils, which can significantly affect the fine-grained retention capacity [84,85,86,87]. Soil water retention qualities were studied by Majou and colleagues [84], who found that the amount of water retained by clayey soils was highly linked to its specific pore volume. A soil’s clay mineralogy and hydraulic history play a major role in how much water can be held in the soil’s pores; the latter determines how much water can be held in specific pores. Clayey soils’ water retention abilities were shown to be strongly related to their bulk density at field capacity.
Due to shrinkage, mechanical processes, or any other alteration in the pore size distribution of fine-grained soil, the water retention capacity of fine-grained soils has been demonstrated to be affected. Shrinkage is common in fine-grained soils that have a liquid limit larger compared to 25% when dried. During shrinking, pores become smaller, allowing water to remain in the gaps and increasing the amount of air that can enter. Mechanical over-consolidation can also lead to decline in clay pore size. In other word, a higher air entrance value and flat SWRC shape are typical for this sort of material as compared to the regularly consolidated soil.
Due to capillary forces, the aggregate size and soil pore structure is influenced by water used in compaction and the amount of effort used in compaction. Studies regarding the effect of compaction on fine-grained soils’ water retention curves may be found in the literature. These studies illustrate how compaction factors affect the retention curve of soil–water considering free swelling or shrinkage regardless of quantifying volume change, as described by Croney and Coleman [88], Tinjum et al. [89], Miller et al. [90], and Thakur et al. [91]. Compaction conditions significantly affected the retention curve of soil–water, which was studied by numerous researchers and showed a significant effect by compaction conditions in studies by Romero and Vaunat [92] and Romero et al. [93]. The volcanic soil–water properties were studied in previous research works [94,95]. Compaction conditions (dry densities and water contents) had a significant impact on the SWRC under varying vertical loads. There is a substantial correlation between SWRC and initial water content and drying and wetting histories in compacted fine-grained soils according to these findings. A substantial relationship between soil–water retention and the applied vertical tension and the precise determination of volume change was also demonstrated. A study by [96] presented data from an experimental investigation into how initial water content and dry density affect SWRC of a compacted Lias-clay. According to their findings, the SWRC derived using gravimetric water content is unaffected by the initial dry density of the sample. Compaction water content has a significant impact on water content over 11–12.5 percent. The SWRC is unaffected by compaction water content at lower water concentrations.
Chinese red clay soils formed in humid subtropical locations are highly sensitive to drought according to D’Angelo and colleagues [97]. They found a link between the low porosity and the ability of the clay to store water for plants due to a dense fabric formed by a high degree of consolidation. The inter- and intra-microgranular porosity of other clayey soils in tropical and subtropical regions is directly related to their water retention capabilities and exhibits a significant micro-granular structure [98,99,100]. The hydraulic conductivity of soil can be dramatically increased and the water infiltration facilitated by the presence and development of fissures [101,102,103,104]. The soil’s ability to retain water might be affected by this.
In cracked soils, the water content of a broken soil can change rapidly at very low suctions, making it difficult to reliably measure SWRC. According to Wang and colleagues [105], a crack had a definite and low AEV of 0.23 kPa Approximately 74 percent of the water in the crack was removed when the suction pressure was increased from 0.23 to 0.35 kilopascal. The normalized water content of broken clay dropped from 1 to 0.6 as suction increased. In addition, SWRC of a cracked clay showed that the normalized water content reduced from 1 to 0.06 [106]. SWRC measurements for expansive (or broken) soils often begin around 1 kPa due to the limits of previous testing methods [107,108].
According to Li et al. [109], the SWRC of fractured soil was determined during the wetting and drying processes. The SWRCs of silty clay having desiccation cracks may be measured from very low to high suctions by the device. The cracked silty clay’s drying and wetting curves were both measured. Soil saturated in water began to dry out with modest suction values of 0.08 kg/cm2 during the drying process. The water content stayed constant at 43.7% with a gradual rise in matric suction pressure. Once the matric suction reached 2.5 kPa, the water content declined even further. After reaching 300 kPa of suction, the water content in the matric fell to 24.6 percent. The suction rise to 300 kPa showed a significant drained water volume from the soil matrix and crack network.
When the matric suction decreased from 300 kPa to 4 kPa during the wetting process, the water content increased from 24.6 to 36.7 percent. The amount of water in the matrices rises when the suction pressure was reduced by 4 kPa. The silty clay’s microscopic pores, however, kept the surface fractures open and unsaturated, allowing water to seep into the soil matrix. When the pore water pressure value is more than zero, water can only enter the soil through the pores [110].
SWRC tests were carried out on Guilin lateritic clay (compacted and undisturbed specimens) by Sun et al. [111] showed a significant suction range difference, according to their findings. An undisturbed specimen’s transition zone has two distinct lines, each with a slightly varying gradient. Three sloping lines can be found in the compacted specimen’s transition zone. A compacted specimen’s SWRC is heavily reliant on the PSD’s bimodality. Compacted samples’ SWRC is to the right of an undisturbed sample’s when the suction is less than 10 MPa. There are horizontal and vertical cracks in the undisturbed specimen. An undisturbed specimen’s SWRC will be nearly identical to that of its compacted counterpart if the suction pressure is greater than 10 MPa. Due to the microstructure of the soil (or PSD), cracks in undisturbed specimens stabilized. The retention curve of soil-water regarding Yunnan red clay was obtained in a study by Ma et al. [112]. An air entry pressure as low as 7 kPa was found due to big pores in the non-uniform distribution of pore sizes, whereas the residual pressure exceeded 10 mp.
The hysteresis of fine-grained soils is poorly understood due to a lack of research in this regard. Saturating fine-grained soils, which is tedious and time consuming, may be the main reason for this difficulty in getting SWRC for fine-grained soils. According to Iyer and colleagues, a study in [113] sought to fill in this gap by looking at the drying and wetting trajectories of soil–water retention curves for eight different fine-grained soil samples. Researchers were able to quantify suction hysteresis by comparing the suction differences between wetting and drying path SWRCs at specific water contents. Increasing the water content of the soil improves the soil’s mineralogy and particle size distribution properties such as its cation exchange capacity, clay content, and surface area. (3) Soil mineralogy and particle-size distribution have a large impact on drying- and wetting-path SWRC hysteresis. During wetting and drying cycles, soils with active mineralogy experience varied shrinkage and swelling, which dramatically affects suction hysteresis and is also influenced by the structure of the soil.
Silty soils are also used in several experiments. Soil-water retention studies have traditionally focused on the drying path in pre-saturated and desaturated soil measurement or the drying-wetting path to study hysteresis [114]. Engineers in the loess area, which has an arid and semi-arid environment, are more interested in the wetting SWRC than the drying one since water penetration is the primary cause of most disasters [115,116,117,118,119]. An undamaged loess sample collected from northern France was evaluated for SWRC wetting and drying using the filter paper method by Munoz-Castelblanco et al. [120], who discovered no natural water content hysteresis. No comparison is performed between the wetness SWRC of compacted specimens and the whole specimen.
The volumetric behavior of compacted and intact loess SWRC were studied by Ng et al. [121]. Clay concentration in Xi’an loess was 28%, which was used in the study. The natural water content of the remolded sample was used to compress the sample. Neither the soil structure nor the SWRC were examined for the impact of molding water content.
The study by Hou et al. [122] evaluated the SWRCs compacted silt-loess silt specimens created at various water contents and dry densities. The results demonstrate that the intact loess has a stronger air occlusion value and a more comparable slope of soil–water retention curve in the transition zone when compared to specimens that had been remolded to compact at their original water content. This was determined by comparing the two types of loess to each other. The entire specimen’s SWRC (saturation versus suction/air occlusion value ratio) is similar to that of remolded specimens squeezed at natural water content. Different states of the clay particles cause the microstructure to alter between undamaged and compacted specimens, which in turn affect the soil–water retention curve.
Several researches have looked into the relationship between temperature variations and the SWRC of silty soils. Uchaipichat and Khalili [123] used a triaxial cell to conduct non-isothermal testing on a silt sample. Saturation decreases with increasing temperature, according to the soil-water curves obtained at various temperatures since as the temperature rises, the surface tension of water decreases, lowering the air entrance value. When the soil is unsaturated, the effective stress decreases with increasing temperature due to the effective stress parameter’s dependence on air entry value. The retention curve of soil-water was not dependent on stress level. Thus, the soil-water retention curves were not significantly affected by changes in the net stress of the samples in these tests, since their specific volumes were very similar at different stress levels (the elastic unloading path). The drying-wetting tests performed by Ghembaza et al. [124] on laboratory-prepared sandy clay, however, show how drying-wetting paths outputs are affected by thermal factor in its descending changes. They discovered that increasing the temperature decreased the voids ratio, which, in turn, reduced the water content. At 20 °C and 50 °C, Belal et al. [125] studied the effects of cement on a compacted silty soil from the Sidi Bel Abbes, Algeria. Air entry value (AEV) that rises with dosage of cement, falls with increasing suction, according to their findings. This was found to be the case for both 20 and 50 °C. The researchers also discovered that water content decreased with increasing suction and temperature rose. Finally, they discovered that as temperature rose, inlet air suction decreased.
2.1.3. Bentonite
For a deep underground deposit of high-level radioactive waste, bentonite pellet/powder mixes are being explored due to their low conductivity, swelling self-sealing capabilities, and longevity. Many researchers have studied the compacted bentonite in addition to water retention properties when it comes into contact with water. Bentonite’s water retention can be greatly affected by its initial physical qualities [126,127]. In addition to the wide applications of bentonite in geotechnical structures or works, it contains a high capacity of water retention and considerable volume change behavior under hydraulic loading. Therefore, using bentonite could effectively help to investigate the hydro mechanical behavior of the unsaturated zone and develop knowledge of unsaturated soil mechanics. Based on these reasons, much previous literature focuses on this remarkable material and conducts a laboratory test or develops a constitutive model in the context of USM.
Several scholars have drawn attention to the fact that compacted bentonite-based materials have two distinct water retention zones [128,129,130]. When suction values are very high, the water stored in the soil does not change regardless of the soil’s dry density. The clay minerals’ physicochemical properties, in particular the specific surface area, determine how much water is retained when it is adsorbed on their surfaces [131]. The microstructural water retention domain refers to this area of intra-aggregate controlling suction. Water content sensitivity to changes in dry density at lower suction values is significant. Capillarity is thought to store water in macropores, the volume of which is altered by variations in dry density. Dry density has effect on water content in macrostructural water retention domains such as the suction range. Bentonites are unique in that the material density changes along mechanical channels and, and perhaps most importantly, in response to wetting and drying, due to strong multi-physical and multiscale coupled processes.
Water retention tests were conducted on a single 32-mm-sized MX80 bentonite pellet in the study by Zhang et al. [132], in order to better understand its behavior. Given that adsorption of water is predominating and is predominantly contained inside the micropores of pellets, it appears that the water retention behavior of pellets throughout the tested suction range is independent of their size. While water content increases are negligible at high suction (59 MPa), they are large at low suction (59 MPa).
A water retention test was carried out in the laboratory by Liu et al. [133] on pellet mixtures of GaoMiaoZi (GMZ) bentonite pellets. Since clay minerals or inside the pellets adsorb water, the water retention curve of a pellet mixture under constant-volume conditions was comparable to that of a single pellet under free swelling conditions in the high suction range. Bentonite specimens from Zhu et al. [134] were subjected to a series of drying and wetting cycles to examine their water retention properties. Water retention is independent of the specimens’ dry density under the free-swelling condition. However, the degree of saturation drops dramatically with increased suction regardless of the suction channel. However, specimens with higher dry densities retain more water due to their greater swelling capacity even at lower suctions (14.2 MPa), while the saturation level changes very little during the wetting and drying procedures.
According to Liu’s research in [133], Pellet mixtures, single pellets, and compacted blocks of GMZ bentonite were tested for water retention. In the end, we came to the following conclusions. Under the free-swelling situation, water retention is irrespective of the specimens’ dry density; nevertheless, the degree of saturation drops drastically with increased suction, regardless of the suction channel.
The hysteretic soil–water retention curve data of bentonites with varying degrees of plasticity were determined using specimens of bentonite that were subjected to a broad range of suction (Gapak and Tadikonda, [135]). It was found that surface cations and clay concentration had very little of an impact on the drying of SWRCs at higher suction ranges. This was due to the fact that hydration had very little of an effect on the various surface cations. Plasticity has no effect on the bentonite specimens such as wetting SWRCs with restricted volume state since the water-retention behavior is controlled by the adsorptive storage mechanism. Under volume restraint, drying SWRCs determine the degree of hysteresis, which is a qualitative representation of the difference between the drying and wetting soil–water retention curves. There is a direct correlation between hysteresis and the plasticity of bentonites.
The water retention of compacted bentonite is also influenced by temperature and chemical content of the saturated fluid [136,137,138]. Expanding clays in deep repositories can be affected by temperature fluctuations caused by radioactive decay. The water retention capacity of Czech B75 bentonite was studied by Sun et al. [139]. A considerable decrease in water retention capacity was seen in their tests on the Czech bentonite B75, especially at high relative humidity. Using salt solutions to study the compacted bentonite, especially water retention properties, is critical geologically storing radioactive waste. There have been numerous investigations on the compacted bentonite WRCs that have shown a larger measured total suction in saturated specimens than those saturated with distilled water, while specimens saturated with salt water have a smaller measured matric suction [140,141,142,143].
According to He et al. [144], the SWRCs of bentonite confined compacted using various salt solutions were obtained through some suction-controlled tests. For the purpose of this study, the water retention features of GMZ bentonite were evaluated. The water retention capabilities of compacted GMZ bentonite are affected by the suction of the pore fluid chemistry. Specimen water content rises linearly with increasing pore fluid concentration at a given suction. Additionally, suction affects the influencing rate.
In the research carried out by He an et al. [145], suction-controlled experiments were carried out in order to investigate the water retention features of compacted GMZ01 bentonite specimens that had been soaked with a variety of solutions. Bentonite GMZ01 has been investigated to determine how the presence of salt solution influences the mineral’s volume change and its capacity to retain water. The following inferences could be drawn given the available evidence. The swelling strain of a compacted GMZ01 bentonite specimen reduces as the concentration of the NaCl solution that was infiltrated increases. A specimen of GMZ01 bentonite shrank in three distinct phases when it was subjected to regulated suctions. These stages were normal shrinkage, residual shrinkage, and no shrinkage at all. In general, with the same amount of suction pressure, a specimen that has been saturated with a salt solution contracts more than a specimen that has been saturated with dissolved water. In addition, the measured void ratio is somewhat higher when a specimen is saturated with salt solutions instead of pure water. This is in contrast to the situation in which the specimen is saturated with pure water. In addition to this, the slope of a typical shrink-age component goes up whenever there is an increase in the salt solution concentration.
The He et al. [145] investigation found a strong correlation between pore water chemistry and WRCs. As suction increased, the water content of all specimens decreased. Increasing the solution concentration resulted in a raise in water content. With a reduced suction, the effects of pore water chemistry on WRC are more pronounced.
2.1.4. Clay with Geo-Synthetics
The usage of geosynthetic clay liners (GCLs) is common as part of composite landfill base liners. The hydrated GCL may dry out as a result of the waste’s heat. Many applications necessitate an evaluation of water retention retentions under drying conditions to better realize GCL function in these circumstances [146,147,148].
The hysteretic behavior under high suction is not taken into account in most studies on the SWRC of GCLs. When subjected to a 20 kPa vertical stress and a vapor pressure ranging from about 3 to 198 MPa, granular bentonite GCL (GCL2), and powdered bentonite GCL (GCL1) were studied by Bouazza and Rouf [149]. Bentonite shape and mineralogy were shown to impact GCL absorption/desorption SWRCs at high suction. Granular bentonite-based GCL was able to absorb more water than powdered bentonite-based GCL due to the greater concentration of montmorillonite and larger pores in the former. During the desorption process, the granular bentonite GCL was able to keep more water due to its shape and its increased montmorillonite concentration. In addition, the water retention capacity of the granular bentonite-based GCL had a greater value than that of the powder bentonite GCL due to the granular bentonite GCL’s capacity to absorb more water while simultaneously releasing less of it. At high suction, the WRC of both GCLs, on the other hand, showed very little hysteretic behavior. The WRCs of both GCLs were only slightly pushed downward by repeated wetting-drying cycles, with no discernible effect on the degree of hysteresis.
There have been few studies that take into account the confining stress effect on the GCL’s water-retention capabilities, such as those conducted by and Hanson et al. [150] and Beddoe et al. [151]. To investigate the water retention properties of GCL, a drying route was equipped with a variety of confining pressures, ranging from 3 to 100 kPa. Their findings demonstrated that the water content of GCL was lower than that of bentonite at low capillary pressures. This was due to the influence that needle-punched fibers have on providing reinforcement. At capillary pressures greater than about 100 kPa, the capillary barrier effect of the carrier geotextile caused the GCL water content to be greater than the observed bentonite water content. This occurred when the capillary pressure was more than approximately 100 kPa.
Both Abuel-Naga and Bouazza [152] and Beddoe et al. [151] conducted research on the confining stress along a wetting path using a single stress of fifty kilopascals. Quantitative research was conducted by Siemens et al. to investigate the effect that two different confining strains, 2 and 100 kilopascals have on the amount of water retained in GCLs [153]. In these investigations, there was no investigation of the water retention along a wetting path for the broader range of confining pressures associated with deeper trash deposits. In order to gain a deeper comprehension of the hydromechanical reaction, Bannour et al. [154] investigated the effect that confining stress had when it was used with the wetting path of the WRC of GCLs. As a result of this research, it is possible to underline the need of covering GCLs as soon as possible once they are placed in a waste disposal facility, based on these findings. In Bannour et al. [154], there was no alteration in air-expulsion suction or the SWRC slope as a result of load.
Temperature and overburden stress were used to test the influence of SWRC of geosynthetic clay liners (GCLs) on temperature and overburden stress. The researchers found that the correlation among suction and moisture content changes depending on the void ratio and the ambient temperature. Air-entry values increase when the net vertical tension increases in studies at the same temperature, according to the findings. The GCL’s retention capacity decreases as the temperature rises. Risken [155] has undertaken a comprehensive examination of the impact of temperature on the SWRCs of GCLs. In the wetting path, it was found that the GCL’s air-expulsion suction decreased with rising temperature, while water retention decreased. The drying path, on the other hand, was unaffected. Due to a drop in water surface tension with increasing temperature, Risken [155] found that GCL’s retention capacity decreased.
In most investigations on GCL hydration and dehydration, non-uniform temperature-stress routes throughout hydration and dehydration processes are not taken into account. The suction measurement device developed by Tincopa and Bouazza [156] measures suctions across the whole suction range of GCLs. GCL water content and suction are examined under representative field settings, and the effect of non-uniform temperature and stress routes is examined in this study. The wetting and drying paths of a GCL were defined for the analysis of moisture dynamics (operation). Capillarity forms more quickly under high vertical stresses than under low, restricted strains, allowing for a faster intake of water. Due to the low water viscosity generated by high temperatures, drying curves often increase water desorption over the suction range studied. GCL volumetric water contents decreased after being wetted at 20 °C and dried at 70 °C under either low (2 kPa) or high (130 kPa) confining stress. Another factor that could lead to desiccation during drying is the combined effect of high temperature and high confining stress.
There have been reports from several researchers that high salt concentrations in the subsoil’s pore water may damage GCLs’ ability to retain water [157,158,159]. Intriguingly, a number of investigations on the impact of salinity in pore water on GCL hydraulic conductivity have been carried out to date [160,161]. However, according to the research in the literature, the salinity of the pore water appears to have a very minor impact on the ability of GCLs to retain water. It was discovered that the water retention capacities of a GCL were affected by the presence of salty pore water, and that this had an effect on the curvature of the water retention curve. This was one of the reasons why the water retention curve was curved (WRC). They discovered that the proportion of total suction that is attributed to matric suction might shift depending on the salinity of the water used for soaking the samples. At the same level of moisture content, GCL samples that have been hydrated with saline water have a greater matric suction than GCL samples that have been hydrated with distilled water. It’s possible that the effect that the salinity of the wetting water had on the microstructure of the GCL bentonite clay layer is to blame for its microstructure.
Other parameters that can affect the SWRCs of GCLs have also been investigated in the literature [150,151], for example, looked at the effect of geotextile configuration on SWRCs in addition to wet and dry paths for various GCL types. The SWRC of GCLs and the amount of hysteresis between the dry and wet curves were found to be strongly affected by the production method and configuration of geotextiles [151]. One other research looked at the unsaturated behavior of needle-punched GCLs based on bentonite powder and granular powder on the wetting and drying paths of the water retention curve [162]. GCL structure and bentonite forms influenced measurement duration and time, and time-dependent suction fluctuations in the bentonite component, at a constant gravimetric water concentration. Their findings show that the bentonite component is substantially responsible for the unsaturated behavior of GCLs.
2.1.5. Organic Soil
Increases in soil organic carbon (SOC) can influence the soil particle surface properties, the structure of pores, and thus the hydraulic properties of soil, and water retention [163]. The effects of SOC on water retention and hydraulic conductivity have been studied, however, the results have been contradictory. SOC concentration increases capillary water retention, according to the majority of researches carried out [164,165,166].
However, the effect of manure on the top layer of soil water content was significantly improved only at very low tensions, as compared to untreated soils [167,168,169,170]. On a Dark Brown Chernozemic soil, Sommerfeldt and Chang [171] discovered significantly higher water retentions for treatments that included manure at both 20 and 1500 kPa. It was demonstrated by Obi and Ebo [172] in a severely degraded Ultisol in southern Nigeria that manuring increased water retention at pressures ranging from 0 to 33 kilopascal but decreased water retention at tensions ranging from 33 to 1500 kilopascal. This was found to be the case.
According to a number of studies, field capacity (FC; soil water content 33 kilopascal) and water potential are unaffected by soil organic carbon [173]. Rawls and colleagues [173] discovered that the water retention capacity of the soil can be affected by both the soil’s texture and its soil organic carbon concentration. According to Hudson’s findings, the WP of a silt loam soil was not connected with the soil organic carbon concentration of the soil, but the FC was [166]. As FC and WP may react differently to shifts in soil organic carbon content, establishing a relationship between soil organic carbon content and plant available water content (PAWC, the difference between FC and WP) can be challenging. It was demonstrated by Hudson [166] and Ankenbauer and Loheide [164] that SOC led to a bigger increase in FC than WP, which resulted in an increase in PAWC. This was the cause of the increase. Based on soil texture, an increase in 1 percent in soil organic carbon can result in a 2 percent to more than 5 percent rise in PAWC. PAWC was unaffected by changes in soil organic carbon content, since other researchers discovered that FC and WP altered at a similar pace [174]. They determined that the effects of SOM on PAWC were insignificant, raising doubts about the technique of carbon sequestration as a means of increasing water storage [175].
Soil water molecule adsorption capacity in the SWRC’s dry range (matric potential 1500 kPa) has been understudied. The SWRC’s dry range must be understood in order to model the water behavior in soil [176,177]. Arid regions Many important soil features, such as clay content, cation exchange capacity, and specific surface area (cation exchange area), can be predicted with the use of SWRC [178,179,180]. As a consequence of this, the SWRC’s dry range may be impacted by actions related to soil management that have an effect on the SOC. According to Arthur et al., adding biochar (at levels ranging from 0 to 100 Mg ha−1) and manure (at levels ranging from 21 to 42 Mg ha−1) to sandy loam soil enhanced the dry range of soil water retention [178].
Zhou et al. [181] wanted to test the hypothesis that increasing the SOC content of a Vertisol, which is an important agricultural soil type but is prone to drought since it has a low available water capacity [182,183], would increase soil water retention over the long term. This was performed in order to see if increasing the SOC content of a Vertisol would increase soil water retention. The findings demonstrated that organic amendments primarily influenced the retention of capillary water but did not have any effect on the retention of hygroscopic water. These findings offered novel insights into the dynamics of soil water in the Vertisol.
SOC and soil hydraulic retentions, such as SWRC, and unsaturated and saturated hydraulic conductivity, were studied by Shi et al. [184] using 28-year in situ studies. SOC in the 0–10 cm depth increased (p = 0.05) with long-term manure treatment, but there was no significant chemical fertilizer effect alone on SOC. SOC concentration was somewhat higher in soils that were treated with MNP than in soils that were treated only with manure (M). Porosity and bulk density in the surface layer were considerably (p = 0.05) increased by M and MNP manuring treatments (M and MNP). However, the subsurface layer (10–20 cm) showed no significant effects. Only in the 0–5 cm depth did organic manure applications boost soil water retention, while the positive effect of chemical fertilizers on water retention was only detected in the 0–5 cm. Saturated hydraulic conductivity was unaffected by either organic or inorganic treatments. Unsaturated hydraulic conductivity, on the other hand, appeared to differ across treatments at the surface layer (0–5 cm). As a result, organic manure application reduced the flow of unsaturated water in the soil.
As organic content increases, the AEV of the finer soil (clayey sand) falls, but the AEV of the coarser soil (silt) does not change significantly, according to a study by Nong and colleagues [185] (clean sand). However, the suction of clean sand increases with organic stuff, which results in a decrease in the AEV of the sand. A higher range of suction values can be observed in clean sands (coarse sands) with a wider residual zone as a function of the residual water content of the sand. On the other hand, clayey sand has an AEV that decreases with the amount of organic matter while the transition zone, which is the SWRC zone between the AEV and suction and corresponds to the residual water content, is unaltered. A larger organic content was shown to be connected with a greater shrinkage rate and a stronger suction that was proportional to the samples’ total amount of remaining water. A larger organic content is typically found in finer soils, which also tend to have lower air-entry values.
Adding biochar to soil can alter the pore size distribution and overall porosity in soil-biochar composites [74,186]. The pyrolysis of biomass in an enclosed chamber with very little or no oxygen results in the production of biochar, which is rich in carbon [187]. The soil’s capillary action is affected by changes in pore size or porosity, which alters the SWRC [20]. To understand SWRC’s influence on the wettability of biochar, we must look at the biochar’s surface functional groups (carboxyl, hydroxyl, and phenolic) [188]. Some researchers found that soil amended with biochar had a different SWRC than soil that had not been amended, while others found no difference in the SWRC as a result of adding biochar [189,190,191,192,193]. Geotechnical and geo-environmental engineering constructions rarely study the effect of biochar on the soil’s SWRC [194,195].
A recent study by Hussain et al. [196] investigated the impact of biochar on soil water retention curve and factors affecting the SWRC. With the addition of biochar, they found that the water content at a dry condition water retention capacity and AEV improved dramatically. Changes in SWRC owing to the addition of biochar can be related to changes in soil type or texture, soil compaction condition, biochar type and pyrolysis condition, biochar particle size, amendment rate, and changes in the pore system and wettability features of the biochar.
Hydraulic retentions of polluted soil may be affected by the organic matter degradation trapped in the soil pores [197,198,199]. Consequently, understanding how organic matter degradation affects soil water retention is essential. Soil suction in non-engineered landfills can be affected by the breakdown of simple organic waste, such as in the case of Dubey and Borthakur’s research [200]. According to the study, organic matter admixed with 10 percent of soil resulted in a minor modification in water retention behavior over 28 days. Organic content declined from 10% to 3.23% throughout the course of 14 days of degradation before returning to pre-degradation levels. There was no change in organic content between the 14-day and 28-day degradation periods. Hence, the degradation process was halted.
2.1.6. Lime and Gypseous Soil
As gypseous soils have a poor water holding capacity, their ability to maintain crops and other plants is considerably more dependent on proper management than soils with higher clay concentration. There is a paucity of data on the impact of gypsum content on soil water retention. Gypseous soil, however, has been proven to be altered by its mineral composition, texture, structure and field circumstances in terms of its ability to hold water (compaction, relative humidity, etc.).
Compaction attempts, both standard and modified, have been studied by Aldaood et al. [201]. According to their results, compaction effort and gypsum content boosted soil samples’ water-holding capacity. Gypsum and compaction were found to increase the number of capillary holes in laboratory testing. At air-entry values, the volumetric water content of the examined soil samples was altered by these variations in the pore size distribution. Soil powder SWRC (S-shape) resulted in a similar form to that produced by compacted effort, according to their findings. The water retention of soil samples rises with gypsum concentration for the same amount of compaction effort. Water retention increases with soil compaction for a given gypsum concentration. Compaction has no effect on any of the high suctions, but it has a notable influence on the SWRC in other areas (relative humidity higher than 98%). Compaction and gypsum content alter the pore size distribution of soil samples, which accounts for the altered water retention. In samples containing 15% and 25% gypsum, the combined impact of compaction and the addition of gypsum eliminate all pore spaces larger than 10 nm. Compression and addition of gypsum work together to removes pore spaces more than or equal to 10 microns in modified compaction samples. Compaction and gypsum addition increase the number of capillary pores as shown by mercury porosimetry and scanning electron microscopy (SEM). One of the most essential and variable components in the soil water retention curve is the volumetric water content at the air entrance value. This is due to the fact that the volumetric water content is directly impacted by the soil texture, and more specifically by the capillary pores. As water retention will be lower for a fixed suction, the compaction effort in the field for gypseous soil should be reduced if the gypsum content increases. This is due to the fact that the risk of gypsum dissolution could be minimized if the standard compaction effort is used rather than a modified effort.
Water retention curves were analyzed for the impacts of soil gypsum content by Moret-Fernández and Herrero [202]. The WRC of soil was shown to be significantly influenced by the amount of gypsum present in the sample. Water retention capacity (WRC) was higher near saturation in soils with high gypsum content, as were the WRC slopes. Gypsum’s influence on WRC peaked at about 40% equivalent gypsum (EG).
The swelling potential diminishes with increasing soil gypsum content, according to laboratory studies by Alzaidy et al. [203], and the SWRC curve initially displays a noticeable reduction in variation before gradually decreasing with a moderate slope. As the gypsum content grew, so did the water storage capacity. SWRC variables denoting air entrance and residual moisture content are increased to achieve this effect. The amount of gypsum in the soil has a substantial impact on SWRC, and soils with a high gypsum content produced SWRCs with greater air entry values and residual states.
There are several physical–chemical reactions that occur during lime treatment, including lime hydration, cation exchange, and other reactions, all of which help to improve soil engineering behavior in response to environmental conditions. These reactions include those described by [204,205,206,207,208,209]. SWRC behavior of cement, lime, and fly ash, which are routinely employed for improving the ground in various engineering projects, has been studied only sporadically.
Chemically treated soils may behave in a different way from their untreated counterparts, for a variety of reasons. When conducting SWRC tests for a long period of time, it is expected that the structure (fabric and bonding) and mineralogy of chemically treated soils will undergo constant changes due to chemical reactions. Both of these factors impacted the soil SWRC [210].
When moisture content varies, lime-treated soils are less ductile than their untreated counterparts due to cementation bonding (either weak or robust) and/or probable mineralogy alterations [211]. Cycles of drying and wetting can also cause bond ageing or disintegration, which can gradually alter the soil structure [212]. Due to this, it is thought that alterations in the soil’s pore structure will further increase water retention properties; the remaining lime will also be depleted, making it less available for future reactions. It is anticipated that these interactions will have the effect of exacerbating soil hysteresis. It is also anticipated that these interactions will lead to changes in water flow among pores, which will finally modify soil water retention. It is essential, in the context of engineering applications of chemical ground improvement, to investigate whether the water retention and volume change behavior of chemically treated soil during wetting and drying displays any variations from the behavior of untreated soils. This is due to the behavior of chemically treated soil during drying and wetting can have a significant impact on engineering applications.
There has been a dearth of investigation into how lime-treated materials retain water in the soil. Studies such as those carried out by Tedesco and Russo [213] and Russo [207] examined the SWRC of an Italian alluvial silty soil that had been dynamically compacted and treated with quicklime. Curing time had a significant impact on the SWRC, which was linked to mercury intrusion porosity (MIP) measurements in the subsequent study. The soil water retention curve of three lime-stabilized expansive soil samples from Mosul City, Iraq, were studied using the osmotic method of Khattab and Al-Taie [214] under single drying paths in the suction range of zero to 1000 kPa.
Each of these investigations found that soil compacted dry had a lower water retention capacity than soil compacted wet, and their findings were in line with one another. It has been found that with increasing, the water retention of lime-treated soils has increased. According to previous research, the formation of massive macropores after lime treatment resulted in increased permeability [215,216].
In spite of the presence of large pores, Tedesco and Russo discovered in their investigation of soil that had been compacted to the ideal moisture level that the frequency of micropores (ranging from 0.01 to 0.2 nm) continuously increased with the addition of lime (modification stage). This long-term effect was linked to the development of cementation bonds, and it was observed for suction values that were greater than 100 kilopascals. The observed increase in water retention in the treated soil was attributed to the establishment of cementation bonds between aggregates, and it was observed that these cementation bonds increased water retention.
Water retention qualities and microstructure were examined in a compacted lime-treated silty soil by Wang and colleagues [217]. Due to cementitious compounds in the pozzolanic process, lime treatment steadily decreased the size of both macro and micropores. Increased water retention was achieved by filling the pores with cementitious materials. By producing more cementitious compounds, the soil with a smaller Dmax has greater AEV and water retention capacity, resulting in narrower pores with less pore interconnectivity.
Mavroulidou et al. [211] were the ones who concentrated on the water retention behavior of hydrated lime-treated London clay, which was only marginally greater than the lime consumption it had at the beginning (ICL). For the purpose of determining the drying soil water retention curve of the statically compacted treated and untreated soils, the compaction void ratio and water content were utilized as evaluation criteria. The soil water retention curve of the treated soil was examined in relation to free-swelling vs. constrained saturation conditions. Untreated soils’ SWRC was found to be affected under these conditions, which are relevant for shallow and deep in situ lime mixing [218,219]. The lime-treated soil had a distinct double-porosity structure at the previous saturation conditions, which, according to SWRC data, indicates that it could be partially saturated in situ, depending on the surrounding environment.
Aldaood et al. [220] studied the soil water retention curve of lime-treated gypseous soil with varied gypsum content at a variety of temperatures and curing times. They came to the conclusion that the effect of gypsum content on soil water retention curve was stronger than that of curing conditions. The higher gypsum content was accompanied by an increase in the water-holding capacity of the lime-treated gypsum soil. This behavior may be observed in the SWRC, and it states that the volumetric water content will grow during air entrance, whereas the residual water content will decrease as the gypsum content increases. The curing time had no effect on the volumetric water content or the suction at AEV of the SWRC of the lime-treated soil. However, as the pozzolanic reactions develop, the micro pore structure changes, resulting in an increase in residual retentions (suction and water content). There were significant increases in water holding capacity in all soil samples regardless of whether or not they contained gypsum, regardless of whether or not they contained pozzolanic redox reactions (i.e., pozzolanic redox processes).
Sedimentary limestones, such as tuffeau and Sébastopol stone, were studied for their water retention qualities by Beck et al. [221]. The pore size distribution of these two stones is vastly different despite their similar total porosities. Compared to water, this results in different behaviors. Sébastopol stone’s grains tend to be huge, but tuffeau’s grains are smaller and more variable in terms of size and shape. In Sébastopol stone, the grains are mainly arranged in macropores, but in tuffeau, the pore diameters range from small to large. The water retention curve and imbibition properties show this variation. Sébastopol stone is non-hygroscopic, in contrast to tuffeau, which readily absorbs moisture from the air. Sébastopol stone, on the other hand, has imbibition kinetics that are nearly two times higher.
Water retention properties of lime-treated specimens were researched by Ying et al. [222], who took curing time and salinity into account when conducting their research. Lime-treated specimens were tested for changes in PSD along the SWRC. The following conclusions can be taken from the data. The introduction of cementitious compounds that have a greater specific surface area has led to a remarkable increase in the matric suction of soils during the curing process. This has led to an increase in the water-absorption capacity of the soil. Indicating that salts had a significant role in the production of cementitious compounds, larger matric suctions were seen in the lime-treated specimens that had a higher salinity. There was not much of an influence that curing time had on total suction due to the delicate balance that existed between the enhanced matric and decreased osmotic suctions that were brought about by salt precipitation, cation exchanges, and pozzolanic reaction. The drying-induced microstructure changes were found to be unaffected by curing time, but the lime treatment had a substantial impact. When lime was applied, cation exchanges occurred quickly, leading to bigger aggregates of soil particles that prevented clay shrinkage and reduced pore size. Cementitious compounds formed by low-reactivity silty soil wilt lime had a little influence the drying-induced microstructure due to their poor ability to block clay shrinkage. Due to the silt’s low clay content, the salinity influence on drying-induced microstructure was evident.
However, all of these research works focus only on the drying SWRC and do not study the possibility of SWRC hysteresis, which would have been of great importance to in situ settings. In contrast, Cuisinier et al. [223] evaluated the soil water retention curve of a quicklime-treated statically contrasted expansive clayey soil from the east of France throughout the course of a soaking and drying cycle in a work that was presented at a recent conference.
A London clay, which is high plasticity compacted clay, treated with lime was wetted and dried in order to explore the effect of various parameters that could influence SWRC behavior [224]. According to them, lime-treated soil SWRC behavior was consistent with studies addressing the influence of initial dry density and water content on compacted untreated soils. However, in soil suctions where adsorptive pressures predominate in terms of compaction water content, the SWRC was shown to be unique. Wetting and drying SWRC caused a clear hysteresis just as in untreated soils. Even with chemically treated soil that is more rigid, increased confinement pressures have had an impact on the overall shape of the SWRC. When comparing water absorption and desorption rates, the differences between the treated and untreated clay specimens were startling, largely due to the decreased AEV, which suggests lesser water retention at low suctions. Due to the flocculation and chemical bonding effects, the lime treatment lowered the water retention ability of the soil. The influence of curing time and procedure appears to be minimal. There was some degree of hysteresis in all cases.
2.1.7. Frozen
Soil structure and SWRC are both affected by freeze-thaw (FT) cycles in seasonally frozen locations [225,226]. There have been only a few experimental studies on how the SWRC changes during freeze-thaw cycles for various soils. In the study by Ding et al. [227], the hydro-mechanical behavior of compacted subgrade soils, namely, a lean clay with a higher plasticity and low plastic lean clay, was investigated. According to their results, FT cycles significantly reduced the water retention of both soils in their laboratory testing, presumably as a result of the creation of fractures or big pores in both soils during the FT cycles. In addition, the hydro-mechanical properties of clayey subgrade soils subjected to FT cycles were more susceptible to the FT for soils with greater plasticity.
Ma et al. [228] carried out experiments on soil under various degradation conditions to examine the effects of FT cycles on soil physical properties and consequently the water retention capacity of seasonally frozen soils. In the original and deposited profiles, the water-holding capacity increased; on the compacted surface, it dropped; and in the deteriorated and parent profiles, there was no discernible variation in this capacity. All circumstances saw a boost in the amount of accessible moisture thanks to FT cycles.
Soil structures and water retention in seasonally frozen soil locations were studied by Fu et al. [229] using biochar applied at various times. It was found that biochar’s ability to retain moisture was highly dependent on the timing and amount of biochar applied. Water retention investigation showed that biochar prevented soil shrinkage during dehydration, showing that biochar can increase soil’s resilience to compacting. Biochar’s internal pores improve soil water retention by increasing water storage capacity in soil pores, while the improved soil structure also enhances water storage capacity in the soil pores.
The combined effects of the freezing-thawing cycle and the starting physical conditions were studied by Yao et al. [230] to determine the alteration regulation of water-holding function of low liquid silt soil (compaction and moisture content). They found that soil compacting degree and freezing-thawing cycle effect soil SWRC in a seasonal frozen location. Matric suction diminishes with the increase in freeze-thaw cycles with identical volume water content and compactness. The greater the compactness, the larger the matric suction for the identical freeze-thaw cycles.
2.1.8. Claystone
Long-lived and high-level radioactive waste could be buried in France using the Callovo-Oxfordian (COx) claystone as a host rock. At this point of time in operational mode, ventilation is causing desaturation of the galleries’ walls, which will be replaced with resaturation as soon as the galleries are closed. Understanding the COx claystone’s water retention retentions is critical to understanding this phenomenon. Various claystones, such as Callovo-Oxfordian (COx) and Opalinus clay samples, have been studied to date for their water retention properties [231,232,233,234,235,236,237,238,239].
Water retention qualities of the claystone/bentonite combination were explored by Middelhoff1 et al. [234] and it was found that the WRC of the mixture changed significantly as a result of changes in their initial dry density. It was shown by Gimmi and his colleagues [232] that pore network heterogeneity and topology affect the water retention function. The drying and wetting pathways of COx claystone samples were studied by Menaceur et al. [233] which demonstrated that a hysteresis effect is frequently observed in WRC behavior. Other experimental studies on Cox claystone samples have shown a similar hysteresis effect [240]. However, the water retention curve reported by Zhang et al. [241] revealed no hysteresis. The COx claystone water retention properties were investigated in depth by Wan et al. [239] in order to research hysteresis effects further by precisely determining the key drying and wetting curves. Claystone has hysteresis in its water retention capabilities, as seen by the considerable difference between the major wetting path and the main drying path in their study. In addition, M’jahad et al. [242] investigated the water retention properties of broken Callovo-Oxfordian claystone and discovered that the initial water saturation of the sample determines the water retention capacity of the sample, and the lower the initial water saturation, the lower the water retention capacity. In addition, the results of their testing showed that the water retention capacity had significantly decreased as a direct consequence of the damage.
Opalinus Clay shale’s water retention behavior has also been investigated. Muñoz [243] reported statistics on the change in water content and the saturation level with respect to total suction. For the wetting phase, it was discovered by Zhang et al. [241] that allowing the Opalinus Clay shale to swell led to a considerable raise in water that could be kept in the material. With respect to Opalinus Clay shale’s matric and total suction retention curves, Villar and Romero [244] measured air entrance pressures between 9 MPa and 21 MPa for free volume conditions and between 15 MPa and 35 MPa when the volume was constrained. Opalinus Clay shale has air entry values of between 13 and 18 MPa, according to Romero et al. [245].
Various shale samples were cored at different depths, and Ferrari et al. [231] conducted experimental investigations to characterize all aspects of retention behavior. Gravimetric water content changes are essential for the deeper shales for full wetting and drying cycles, according to their findings. For Beringen shale to dry materials to 90% saturation, a suction two orders of magnitude larger than that required for Lixhe chalk was reported by Da Silva et al. [246], who examined the water retention curve along drying paths.
2.2. According to Relationship with Soil Parameters
It can be inferred from the term “retention” that SWRC for soils is unique [247]. Studies have shown, however, that various factors can influence the retentions of the SWRC, and hence, impact its uniqueness. Therefore, these parametric influences need to be fully considered in the models where the SWRCs are involved [81,248]. In the following subsections, influence of the critical parameters on the SWRC is reviewed.
2.2.1. Particle Size
The grain size distribution (GSD) defines the texture of the soil. Indrawan et al. [249] investigated the soil water retentions of residual specimens with various proportions of medium and gravelly sand and discovered the fact that as the coarse-grained soil fraction increased, the water holding capacity dropped. Gallage et al. [78] investigated the retentions of the SWRCs for sandy soils with varied grain size distributions and found that a homogeneous coarse-grained soil displayed a lesser hysteresis behavior compared to a less uniform graded fine-grained soil. Rahardjo et al. [250] observed that the fitting parameters of SWRCs (e.g., the air-entry value (AEV)) were impacted by the coefficient of uniformity of the GSD and dry density in a mixture of 50% residual soil and 50% gravel with varied grain sizes. Soil water retentions experimental results on compacted soils showed that as the clay size fraction rose, the water holding capacity of soil sample increased [251]. In a study by Chen et al. [252], impacts of the GSD on the water retention capacity of wide-grading gravelly sample were examined. According to their results the water retention curve moves upwards from a higher grading coefficient (which describes the curve’s shape) to a lower coefficient. With increasing fine content, the residual water content and AEV increase linearly. The maximum slope of SWRC, on the other hand, grows linearly as effective grain size increases.
2.2.2. Consistency Limits
Soil suction rises in proportion to the soil’s plasticity [253]. There is an increasing correlation between suction capacity for normally and compacted consolidated soils, which represents the inclination of the retention curve, and liquid limit [254]. In addition, for suction values ranging from 100 to 1000 kPa, a straight-line SWRC can be used to represent soils with a LL greater than 25%, on a semi-log plot. This suggests that for a specific range of suction values a linearized SWRC could be used, thereby simplifying modeling of the unsaturated soils [255].
2.2.3. Temperature
Past studies have revealed that SWRC depends on the temperature [256,257,258,259] in addition to inherent properties of the soil, such as structure and texture [260]. Variations in soil temperature and water content can cause various geotechnical problems (e.g., frost heave, bank collapse, etc. [261,262,263,264,265]), and therefore, numerous studies have been performed thus far to identify the influence of temperature on the soils’ water holding capacity. In addition, Experimental observations performed by Uchaipichat and Khalili [123] on the retentions of the SWRC of a compacted silt specimen showed a reduction in the degree of saturation with increasing soil temperature. This was owing to the fact that as the temperature raises, the surface tension of water decreases, lowering the air entrance value.
Results of the drying-wetting experiments carried out by Ghembaza et al. [124] on an undisturbed natural argillite and a sandy clay specimen at high temperatures, proved the effect of temperature on the SWRC, showing a downward shift of water retention curve as a result of temperature rise. They discovered that as the temperature rises, the voids ratio reduces and, as a result, the water content decreases. Furthermore, Belal et al. [125] evaluated the impact of temperature on the SWRC of a cement-treated compacted silty sample at two temperatures of 20 °C and 50 °C. Their findings revealed that as the temperature rises, the water content reduces, and the inlet air suction diminishes. The effects of temperature on the water holding capacity are also investigated in the literature. For example, experiments conducted by Sun et al. [139] on the bentonite samples revealed a considerable reduction in water retention capacity at high temperatures, particularly when relative humidity was high.
Experimental investigation concerning the water holding capacity of geosynthetic clay liners (GCLs) confirmed that their SWRC is controlled by temperature [155,156,266]. In this regard, a systematic investigation conducted by Risken [155] on the retentions of water retention curve of GCLs showed that along the wetting path, temperature had a minor impact on the GCL’s air-expulsion suction, and water retention capacity of the GCL was decreased with temperature elevation. However, on the drying path no effect was noticed. It was concluded that the reduction in GCL’s water retention capacity was attributable to a decrease in water surface tension with rising temperature. Tincopa and Bouazza [156] investigated the GCL water content-suction relationship at non-uniform stress-temperature paths and their results indicated that due to the low viscosity of water in high temperatures, the drying curves elevate water desorption for the measured range of suction. The drying of the geosynthetic clay liners at 70 °C and wetting at 20 °C subjected to either high confining stress of 130 kPa or low stress of 2 kPa revealed a decline in the moisture contents.
2.2.4. Influence of Additives on the SWRC
Based on the available literature, little is known about the SWRC of improved soils (e.g., with fly ash, cement, and lime), which are routinely employed in a variety of engineering projects for ground improvement applications. Treated soils undergo continual changes due tp chemical reactions over the course of the SWRC experiments, which can influence the structure and mineralogy of treated soil, thereby affecting the soil’s SWRC [92].
Past studies have shown that water holding capacity can significantly increase upon addition of fly ash for coarse-grained sandy soils [267,268,269,270]. Fly ash addition into soil specimen resulted in an increased water retention capacity [271]. Sharma et al. [272] found a correlation between increased coal concentration and increased gravimetric water content at specific matric suctions. The enhancing effect of compost addition on water retention capacity was shown to be higher in loamy soils compared to clays [273], indicating that the magnitude of increased retention capacity can depend on the soil type. In addition, for soils with greater organic material content water retention capacity is observed to be higher [255]. The use of Aquasorb soil conditioner resulted in a decrease in the slope of the SWRC and an increased water retention [274].
An experimental study of Belal et al. [125] on a cement-treated compacted silty soil under two temperature conditions of 20 °C and 50 °C, showed that for both temperatures the air entry value rises upon an increase in the percentage of cement to a ~ 4% threshold. In addition, the water content, which rises in proportion to the cement percentage, reduces as the suction rises. A similar increase in the air entry value was observed by Hoyos et al. [275] for an expansive soil treated with cement.
Lime treatment is extensively used in geotechnical engineering practice for soil improvement projects [204,205,206,207,208,209]. Examples of studies on the soil water retention curve of lime-treated soils consist of Tedesco and Russo [213] and Russo [207] which examined the water holding capacity of a compacted lime-treated silty soil. Furthermore, Khattab and Al-Taie [214] studied the soil water retention curve of lime-treated expansive specimens, over the suction values ranging from 0 to1000 kPa under single drying paths. The greater voids generated in lime-treated soil compacted at dry of optimum resulted in a lower water retention in all three studies. However, it was shown that as the lime content increased, the water holding capacity increased for lime-stabilized soil as well. This is in contrast with the results that suggest that lime treatment increases permeability by increasing the number of large macropores formed (e.g., [215,216]). WANG et al. [276] investigated the water retention retentions of compacted lime-stabilized silty soils with varied aggregate size distributions. They observed that due to the cementitious compounds generated during the pozzolanic process, lime treatment steadily reduced both macro- and micropore sizes. These cementitious compounds significantly increased the soil’s water holding capacity by filling the pores. In addition, AEV and water holding capacity were higher for the improved soil with smaller Dmax, due to the reduction in both the pore interconnectivity and pore size induced by greater creation of cementitious compounds. The SWRC of lime-stabilized gypseous soil with varying quantities of gypsum was examined by Aldaood et al. [220] under different conditions of temperature and curing periods. Results indicated that the water holding capacity of the improved soil elevated as the gypsum content increased, which was characterized by growths in the volumetric water content at AEV and the residual water content. The investigations of Ying et al. [222] on the water holding retention of lime-stabilized specimens revealed that due to the increased formation of cementitious compounds with higher specific surface area, the soil matric suction elevated considerably, resulting in an increase in the water adsorption capacity of soil. Additionally, the soil treatment showed a declined AEV for lime-treated high plasticity clay upon wetting and drying [224]. Enhancement in the water retention retentions of treated soils was also noticed upon addition of vermiculite mineral [277] and waste application [278,279,280,281,282,283,284,285,286,287].
2.2.5. Aging Effects on SWRC
Agus et al. [288] investigated how ageing affected SWRCs of bentonite-sand mixtures and pure bentonite samples. Suction measured with filter paper (aged sample) was found to be greater than that recorded with a chilled-mirror hygrometer (nonaged). According to their results, different suction values were due to the impact of hydration that was caused by the aging. In fact, the pore-water redistribution within the soil medium is time dependent, and it ensues as a result of difference in the amount of total suction between the inter-aggregate, intra-laminar and intra-aggregate pores. Their results also showed that for samples of identical ages (i.e., five weeks) the SWRC determined by both methods is similar. It is worth mentioning that due to differences in time-dependent water redistribution, the impact of ageing would clearly vary depending on the soil type.
2.2.6. Compaction Level
Soil compaction leads to structural changes in the porous medium which in turn can affect the physical and hydraulic behavior of the soil [289,290]. Compaction has observed to influence water holding, thereby altering the water distribution in a soil medium [291,292,293]. Decline in the distribution of smaller pores, the fraction of large pores, and the overall decline in pore connectivity and pore space are the key causes of compaction’s effect on the soil’s water holding retention [294]. The impact of compaction on the SWRC has been extensively researched in the literature. For example, experimental observations indicated that compaction flattens the S-shaped water retention curve [295], which accords with results found in [296] research for soil specimens under 50-year conventional tillage. Past research has shown that as comp active effort rises, soil suction rises as well [248,297,298,299].
It has been widely established that increasing soil compaction will decrease water content while increasing unit weight. However, it is still unclear whether the observed increase in suction is linked to a water content loss, a soil unit weight rise, or a combination of the two. In this regard, few studies have shown that soil suction is unaffected by soil unit weight [96,300,301,302,303]. These investigations measured the change in suction values with respect to unit weight for specific gravimetric water content. The findings suggest that suction is highly dependent on the soil’s water content. The impact of initial compaction water content on SWRC can be linked to the variations in the soil’s macro and micro fabric [89,96]. In this regard, Blatz et al. [304] noticed that an increase in initial molding water content leads to a minor upward shift in the water retention curve.
The influence of compaction density for fine-grained soils on the SWRC is found to be greater than that of coarse-grained soils [305,306]. According to Gallage and Uchimura [78], less dense soils have lower AEV and residual suction than high density soils. Experimental results by Malaya and Sreedeep [307] on the sandy soil indicated that the initial dry density has no significant effect on the water retention retentions, while the initial water content influences the SWRC at small suction values. According to Liang-tong et al. [308] the AEV of a natural expansive soil compared to that of lab-compacted samples was relatively low and the hysteresis effect for the former was relatively less noticeable. For suction less than 200 kPa, the SWRCs differed significantly.
It is observed that a water retention curve with a varied initial water content at high suction values tends to converge [307,309]. According to these studies, the impact of the initial compaction condition is considerable for the near saturation part of the retention curve where there exist capillary pressures. The adsorptive forces become more important when desaturation develops, and thus the SWRC is largely determined by water content. As a result, in the high suction range, soil structure has slight effect on the SWRC. Baker and Frydman [310] confirmed this finding, stating that the water content influences the SWRC only when the macropores are unoccupied (i.e., adsorptive forces are prevalent).
2.2.7. Matric Suction
Suction value for specific volumetric water content is shown to increase for fine-grained soil. According to Aubertin et al. [311], this is mainly due to the fine soil particle’s high adsorptive and capillary forces, which are caused by its limited intra-particle pore space and large surface area. Gallage and Uchimura [78] discovered that when the effective size (D10) of the soil grows, the AEV, residual suction, and hysteresis decrease. According to Jotisankasa [248], the soil water retention curve is predominantly impacted by soil structure at low ranges of suction, and soil composition and soil specific surface area at higher suction ranges. According to this discovery, the water retention would be less dependent on soil structure and more distinct at greater suction ranges [312].
2.2.8. Swelling Pressure
To date, only limited research has been performed in the literature on the swelling behavior of expansive soils. Of the limited swelling experimental results, Liang et al. [313], measured the swelling pressure of compacted expansive soil over a broad range of suction with two various densities. For this, pore structure evolution and the retentions of water distribution in the soil wetting subjected to confined conditions were investigated. Their results indicated that under confined conditions, water content was unaffected by density of soil at high suction pressure and dry density had a substantial impact on water content at low suction. To identify the water states, characterized by adsorption and capillarity, a suction threshold of 22 MPa was determined. As the suction was reduced, the swelling pressure raised non-monotonously. The fluctuation in swelling pressure revealed two peaks with respect to suction: first within the low-suction range, linked to bi-modal pore structure collapse, and second in the high-suction range, linked to interlayer hydration absorption.
2.2.9. Stress History
Discrepancy in the SWRC of soil specimen, particularly at low suction conditions, is attributable to stress history [1,309]. The AEV was inferred to remain unchanged regardless of the pre-consolidation stress. It was also noticed that the rise in the over-consolidation ratio (OCR) leads to a decrease in the suction capacity. Experimental studies by Delage and Lefebvre [80] have shown that air entry value rises with respect to the pre-consolidation stress. Lee et al. [314] has noticed that with an increase in consolidation pressure of the soil specimen, AEV and the slope of the SWRC declines. Thu et al. [315] have observed that with rising net confining pressure, AEV and yield suction (i.e., the matric suction corresponding to the point on the retention curve where the saturation degree undergoes a rapid reduction [316] of the soil sample increases. In addition, it has been concluded that beyond yield stress, the inclination of the drying SWRC and that of the wetting curve is independent of the net confining pressure. According to Gens and Alonso [317], the impact of variations in confining pressure on the soil water retention curve is shown to be considerable in the lower matric suction values where the capillary and macropore forces are predominant in the soil.
Furthermore, some studies have been performed to investigate the retentions of soil water retention curve of stabilized soils under applied stresses. Elkady et al. [318] examined the influence of stress history on the water retention capacity of lime-stabilized soils (with lime dosages of 0, 2, 4, and 6%) under various net vertical stresses (7, 100, and 600 kilopascal). Their results showed that the net vertical stresses remarkably influenced the water holding capacity of the soils with 4% lime dosage, under the stresses of 100 and 600 kPa. In addition, upon increasing the suction, samples desaturated relatively more readily under lower stress (i.e., 7 kpa) condition than at the higher stress levels. In another study, Zhang et al. [319] analyzed the effect of stress state on the water retention retentions of two lime-stabilized samples under mean net stresses of 100 and 200 kPa. It was concluded that during the whole suction ranges, the SWRC almost remained level with the initial gravimetric content. Additionally, on the desorption curves under both stress conditions, no points of maximum curvature or air entry value were noticed. However, in another test, they observed a more noticeable point of air entry and a much greater imposed suction value (up to 200 kPa).
2.2.10. Void Ratio
The void ratio is one of the soil parameters that shows the ratio of the volume of the void to the volume of solids. Deformable soils show a different volume change behavior under hydromechanical loading. Specifically, expansive soils such as bentonite show an increase in the void ratio, but collapsible soils show a decrease in the void ratio under the wetting process [320,321,322,323,324,325]. It is worth mentioning that variation of void ratio changes the soil structure and both macro and micro pores that subsequently cause a considering change in SWRCs [121,210]. For instance, Ng et al. [121] showed that the void ratio obtained from the volume-mass relationship could be categorized into four classes for Chinese loess. To this end, they used the MIP test to detect micro and macro-structural void ratio changes under hydromechanical loading. The difference between the summation of these two void ratios (intrusion void ratio) shows the non-detected void ratio that is due to the MIP test weakness [326]. In the previous literature, there are two kinds of analytical modeling for the SWRC of deformable soils. The first type of modeling only considers the variation of total void ratio (that is obtained from volume mass relationship) in the SWRC model formulation [327,328,329,330,331,332]. However, the second types consider the macro and micro void ratio variation in their SWRC modeling approaches [219,333,334,335].
2.2.11. Micro-Structure
A combination of fabric, inter-particle forces, and composition which define the microstructure of the soil [336,337] are shown to have significant impacts on the hysteresis and the shape of the SWRC [20,23,113,121,338]. In fact, behavior and properties of soil can vary readily as a result of structural changes, which generally are associated with disturbances or the wetting–drying cycle. For example, studies have shown that variations in the structure of loess alter the SWRCs of compacted, remolded, and natural loess [120,121,339,340]. These experiments have also shown that minor structural changes can result in visible micropore alterations, resulting in differing SWRCs in loess samples.
Experimental results have shown that the compaction water contents have considerable impact on the microstructure and thus the water retention retentions. In this regard, in the study by Xie et al. [341], microstructure of loess compacted at three various water contents, and its impact on their SWRC was investigated. Results indicated that pores in loess compacted at optimum and dry of optimum, were remained relatively connected. At low suctions ( − < 1000 kPa), the wetting and drying SWRC curves of the three samples differ significantly, but they tend to converge in the higher suction values. In the matric suctions ranging between 0~100 kPa, hysteresis in the SWRCs is more noticeable for loess compacted at optimum and dry of optimum. However, for loess compacted at wet, there is a marked hysteresis in the whole matric suction range. In addition, the loess microstructure can well determine the retention of the SWRCs. As such, for the specimen with higher pore size distribution density, the water retention capacity is greater and the SWRC is shown to be gentler. For loess compacted at wet of optimum hysteresis is rather visible over the entire measurement range, which is believed to be due to more non-intruded pores in this sample.
Microstructure of soils can also undergo considerable changes during treatment process. Various studies have indicated that addition of lime lead to cation exchanges and hydration, causing the particles of soil to flocculate and form coarser aggregates; due to the development of cementitious compounds on the aggregates’ surface, the modal pore sizes were further reduced by the pozzolanic process [209,213,342,343,344,345,346,347]. According to the findings by Cuisinier et al. [348] and Wang et al. [349], the main effect of lime addition on soil structure is the creation of nanopores.
In an investigation into the influence of grain size on microstructure and water holding capacity of lime-stabilized soils, Ying et al. [350], studied the behavior of two specimens with maximum aggregate sizes (D max) of 4 mm and 5 mm. Their experimental results showed that due to the flocculation of soil grains, the lime treatment induced a quick increase in macro-pores and a drop in micro-pores. During curing, the percentage of nano-pores increased slightly whereas that of micro-pores declined. The matric suction was shown to increase considerably at 90-day curing, due to the change in microstructure. However, the effect of curing time on overall suction was negligible. In addition, the rise in matric suction was offset by a reduction in osmotic suction, resulting in a modest rise in overall suction. The enhanced soil with smaller (D max) has greater water holding capacity and higher air entry value resulting from a higher development of cementitious compounds which in turn reduce both the interconnectivity and pore size. These treatment-induced changes in soil microstructure are expected to improve soil’s water retention capacity by allowing the inner pores to hold higher amount of water [213,214,276,351,352].
2.2.12. Electrical Resistivity
A soil’s electrical flow, comparable to flow of water, is related to the presence of free water and depends on the soil properties, such as porosity and tortuosity. As a result, electrical conductivity and soil hydraulic properties can be correlated [353,354,355,356]. To date, some attempts have been performed to investigate the change in electrical resistivity with the saturation degree. For example, studies have shown a decrease in the degree of saturation to cause a rise in electrical resistivity due to the reduction in the mobility of charges (ions and electrons) resulting from the drop in the volume of liquid phase [356,357,358]. In addition, Bai et al. [359] reported a sudden growth in resistivity once the liquid phase becomes discontinuous, since resistivity for air is substantially greater relative to the liquid phase and the current flow is interrupted. In a recent study which attempted to relate the water potential to electrical resistivity, Cardoso and Dias [360] measured the electrical resistivity of kaolin specimens with various void ratios. Their experimental results showed that below the AEV, the electrical resistivity is greatly influenced by porosity when the same interstitial fluid is present. Electrical resistivity is determined by the saturation degree in the transition part prior to the residual state of saturation, where water is thought to be merely in the adsorbed state. The resistivity seems to be dependent on soil structure beyond the residual state of saturation, which is thought to be the result of the tortuosity caused by clay mineral arrangement.
2.3. According to Measuring Tests
Retention curves provide key information for deriving partially saturated soil properties such as permeability function, strength function (shear), water storage function, and thermal property functions [361]. Despite its importance in solving unsaturated soils processes, the determination of retention curves is a complex process. Retention curves can be obtained by laboratory measurements or by using field tests.
2.3.1. Laboratory Tests
Amongst many available methods, conventional methods such as the capillary column method, syringe method, and evaporation method are the most common techniques used in the laboratory to determine the retention curves. Conventional methods deal with three main steps to obtain a single point on WRC of one soil: (i) imposing a known value of suction to soil by different techniques (e.g., pressure plate extractors, osmotic control, relative humidity control, etc.); (ii) permitting the equilibrium of moisture with the applied suction; (iii) measuring the water content [362]. This sequence gives reliable measurements but has limitations. Firstly, there is no suction control method to capture the entire suction range. Distribution of WRC on suction axis will always be wider than the range of suction which the adopted technique is applicable. To resolve this, the use of the hanging column technique in relatively low suction values; axis translation techniques in the intermediate range of suction; and relative humidity control techniques in relatively high ranges of suction is required. This leads to the use of multiple methods. Another problem with conventional methods is that waiting for moisture equilibrium leads to large test durations. It takes about one day per point on the curve. Capillary column method handles the latter problem by providing lots of points on the curve with one specimen. The capillary column method provides advantage for obtaining continuous curves, but it is most reliable for sandy soils under low suctions [363]. The syringe method employs axis translation system where High Air Entry (HAE) ceramic is connected into a syringe. Then, whatever water is moving in or out, can be measured by the syringe [362]. Hence, the syringe method provides continuous curve rather than data points on WRC by continuously measuring how much water flows in or out as suction changes. This enables the whole behavior of WRC to be revealed (scanning curve, wetting, drying, wetting again etc.), and eliminates the need for oven drying. Additionally, the time at which equilibrium is reached can be seen at that instant; there is no need to wait to be sure as in conventional methods. However, the problem with the syringe method is that the dissolved air can diffuse to the water side of HAE ceramic, and become gas again, occupying extra volume. This in turn misleads the measurements. The evaporation method measures suction usually with a tensiometer [364]. When the suction exceeds the range of the tensiometer, it determines the water content. This method can be used to obtain drying curve only and can go up as much as the range of tensiometer allows. The evaporation system never reaches static equilibrium since evaporation occurs from the surface, where the suction is larger. Each of the techniques requires experienced labor. In addition, the apparatuses involved are not easy to assemble. Measuring matric suction is challenging due to cavitation. Total suction is difficult to deal with since it requires accurate temperature control. Pore-water pressures are highly negative, which is another challenge in measurements. Additionally, suction measurement is a key aspect, which should be considered when developing the SWRCs. Though different approaches for suction measurement can greatly vary based on their complexity, recent developments have been directed primarily to extend measurement range or reduce measurement time. An overview of some common laboratory measurement methods is briefly presented in the following sections.
Pressure Plate Test
In this experiment, a soil sample was located on a saturated ceramic disc surrounded by a steel pressure vessel. The tool controls the soil air pressure by changing it within the cell. The area under the ceramic disc can control pore water pressure [365]. To control suction, we can apply known air pressure to sample by using the axis translation method. Therefore, the water flow starts from the sample via the ceramic disc to a water reservoir. Normally, it is emitted to the atmosphere. Such a procedure is sustained until reaching equilibrium in the sample [23]. The ceramic disc’s AEV (air entry value) directs the measuring capacity of this device, which is limited normally to 1.5 MPa. It is a reliable technique, although it can be time-consuming extremely.
Filter Paper Technique
This method is an effective technique for soil suction measurement for a considerable period of time. Gardner [366] proposed that it is a relatively simple method to measure both matric and total suction over an extensive range of more than 30 MPa [367,368]. The method is oriented by the hydraulic equilibrium (soil-water and dry-paper). By establishing the equilibrium, the value of soil suction determines the content of water in the paper using a predetermined calibration plot. There are instances of calibration curves for Whatman No. 42 in different publications [369,370]. In this method, we can reach the amount of total or matric suction based on the hydraulic equilibrium between paper and soil-water. Matric suction will be calculated by establishing the equilibrium by direct contact between two environments (paper and soil sample). However, total suction will be calculated by placing filter papers in a sealed container contains soil sample and achieving equilibrium via the vapor phase (non-contact measurement) [23,371].
Dewpoint Hygrometer
A dewpoint hygrometer is used for total suction measurements in the higher suction range medium (>300 MPa). The suction measurement technique is oriented by the thermodynamic association between total suction and relative humidity (RH). In this procedure, a small specimen (~10 cm3) is placed into a sealed chamber comprising an exposed mirror. By reducing the mirror temperature gradually, condensation occurs on its surface. Here, the soil temperature and dewpoint are utilized for determining the relative humidity above the soil specimen. It directly measures the soil suction at temperature equilibrium [372]. This measurement technique has a very high measurement capacity. Moreover, it can lead to a single measurement within about 15 min.
Tensiometer Technique
Tensiometers are the most common and simplest instruments to directly measure soil suction. Generally, a tensiometer includes a porous HAE ceramic attached to a pressure sensor via a small water reservoir. The ceramic is located in contact with the soil. In this area, after measuring pore-water pressures, we should use it for creating a connection between a water-filled reservoir, the pressure sensor, and the soil pore water. Pore-water pressures are measured directly by the exchange of water between the soil pores and the pressure sensor [23]. Equal tensile stress will be created by pore water in tension in the reservoir water, which can be measured by the pressure sensor. The pressure sensor can be any tool able to reflect the changes in negative pressure. Accompanied by other types of tensiometers such as the small-tip laboratory tensiometer, these possess a restricted practical measurement range of 70–85 kPa of suction. The low range is caused by the relatively lower pressure when the cavitation happens in water. The existence of impurities in the pore water and concentrated in the minute crevices on the sensor body walls may act as air bubble nucleation sites, thus reducing the cavitation pressure [23]. To directly measure the considerably higher soil suction (over 100 kPa), it is essential to deal with the cavitation phenomenon practically. Cavitation leads to the expansion of air bubbles nucleated inside the measurement tool, interpreting it unable to accurately measure further suctions. Cavitation happens when reaching vapor pressure in absolute tension for water.
Axis-Translation Technique (ATT)
This method is utilized to estimate the matric suction in the lab directly. The suction estimation is within the range of 0 to 1500 kPa, and the equilibrium time ranges from 1 to 16 h. This technique involves translating the pore water pressure reference origin from the current value to a value greater equivalent to the air pressure. Therefore, the matric suction of sample stays constant regardless of the translation of pore water pressure and pore air. An ATT was developed to resolve the issue of cavitation at low negative pore pressure [373]. For measuring the matric suction, axis-translation needs the monitoring of the pore air pressure, and pore water pressure maintained at atmospheric pressure. This method is performed by isolating water and air phases in the sample via a saturated HAE (high air entry) permeable material. The saturated HAE ceramic disk permits water flow. However, it stops free air flow when applied, and the matric suction does not surpass the disk air-entry value. We need a good contact between two environments (soil sample and ceramic disk) to be set up all through the test to guarantee the coherence between the water state in the soil sample examined and that in the utilized ceramic disk pores [374]. Since the water pressure in the water container is as close to zero as possible, the method is designated the null-type axis-translation method [375].
2.3.2. Field Tests
Assessing the negative pore water pressures is very important in describing a partially saturated soil’s stress state. This kind of pressure is directly related to the suction, mainly the matric suction component affecting water content. Typically, the soil suction is presented as a soil water content function via SWRC. It is possible to measure SWRC either in the field or the laboratory. However, there may be differences in laboratory measurements of SWRC from those in situ owing to various stress and boundary circumstances [376], allowing for accounting for the spatiotemporal analysis of soil suction and water content through in-situ measurements. Therefore, identification of the initial stress state is highly based on measuring these unsaturated soil variables in the field providing related monitoring data, which complement the laboratory data in developing and validating the unsaturated soil models [19]. The electromagnetic indirect approaches such as frequency, amplitude, or time domain reflectometry and capacitive sensors are the basis for most common tools for assessment of soil water content in situ [377]. Moreover, water-filled tensiometers are extensively utilized tools for measuring the suction in the lowest range in situ (<−100 kPa). Ridley and Burland performed the pioneering work in this regard [367] to better understand high-capacity tensiometers (HTCs). Since then, several considerable advancements have occurred in measuring over 1 MPa [378]. However, designs specifically for field applications have been only recently developed [365]. However, HTCs are used only in situ in research applications. Moreover, these installations should present the possibility of eliminating the tool since conditioning is essential prior to installation and upon air entry. Heat dissipation sensors and thermocouple psychrometers are also frequently used to determine the water content and prolong the measurement range compared to the tensiometers. Generally, these tools need less maintenance and economic efforts in comparison with the more advanced HTCs. Thus, they provide a prolonged monitoring system with relatively lower operation costs. Positive values of pore pressure can be measured by HTCs, which is not possible with indirect approaches. Agriculture-based disciplines such as soil physics, soil science, and agronomy provide considerable contributions to developing these instruments since the amount of plant-available water is deeply governed by the SWRC, which has an essential effect on irrigation management measures. In these applications, the atmospheric coupling, evapo-transpiration process, and interaction with vegetation are specially considered. These tools have also been used in some geotechnical problems since their developments, mainly in the field of monitoring landslides [379,380] or volume changes in soil due to climate and weather fluctuations in water content for design [381] and Levees [382]. In these cases, the tools were installed in a maximum depth of 2 to 3 m. As far as we know, only in a few studies, deeper soil layers have been considered so far. In these explorations, HTCs were used and soil suction was measured in multiple installations in one borehole or in single installations [367,383]. Recently, Tarantino et al. [384] attempted to install high-capacity tensiometers for depth measurement. An experimental challenge is still presented by measurements of water content and soil suction in deep soil layers for various applications such as levees or river embankments, for which unsaturated circumstances may simply extend beyond 5 m from the ground surface [385]. Additionally, Fazel Mojtahedi et al. [386] conducted a novel in-situ monitoring procedure for evaluating changes in matric suction profiles in soil layers over a long period of time. The monitoring procedure used in this paper includes the placement of dielectric sensors in a 105-m borehole at a site in Iran. The site monitoring outputs were used to validate the numerical modelling forecasts. During these geotechnical works, water content and soil suction are exposed to changes as a function of alterations in the meteorological and hydraulic circumstances. Thus, continuous monitoring of variables during various seasonal periods (dry and wet) plays a key role in developing and assessing the stability and seepage analyses.
2.4. According to Prediction Technique
During the last three decades, considerable interest has existed in predicting the changes in hydro-mechanical features of unsaturated soils through the SWRC (soil water retention curve) as an instrument in the geo-environmental and geotechnical engineering fields [387,388]. There are considerable advances in the literature on designing infrastructure such as retaining walls, slopes, pavements, deep and shallow foundations for unsaturated soils [389,390], utilizing the SWRC as an instrument. However, no inexpensive and simple method exists for reliable and rapid prediction or estimation of the SWRC [391]. Therefore, by the extreme costs related to the direct measurement of SWRC, the pursuit of great quantities of indirect approaches has been encouraged to acquire SWRC. In this regard, some statistical regularity and empirical relationship of limited experimental data or known soil parameters are considered such as pedotransfer functions [392], physical-empirical equation [50,393], fractal equation [394,395], and empirical formula method [16]. To obtain more accurate features of SWRC, normally, these approaches are integrated [396,397]. Moreover, intelligent algorithms or machine learning are also applied with these approaches [398,399].
2.4.1. Empirical Formula Methods
Several empirical models have been established for SWRCs that are extensively used in different numerical simulations [16,47]. The wet end of the SWRC is primarily described by early empirical models [400]. For instance, the models of Brooks and Corey (BC) [47] and van Genuchten (VG) [16] are very common models for predicting SWRCs in wet conditions. However, SWRC is not predicted by two models oven dryness [401,402] since when soil water content reaches the amount of residual water, they assume the infinite matric suction [403,404]. Matric suction and soil water content in dry conditions can be accurately and quickly measured by developing measuring instruments for SWRCs [405,406]. Generally, the full range of water content for SWRCs was often obtained through the conventional models via correction factors or adsorption equations [407]. For instance, a term was added in the basic form of Campbell [408] model to extend water retention curves to dryness [409]. By utilizing an adsorption equation, the BC model was extrapolated by Morel et al. [410] to oven dryness. The lower bound of the VG and BC models was extended by Zhang [411] by adding a correction factor for residual water content to handle oven dryness. An SWRC is generalized by such extended empirical equations and models with a single segment (equation) that is invalid for all soil textures. Then, segmental soil water retention curve models were developed to explain the finalized soil water retention curve for a whole water content range. Two sub-equations are included in most segmental models describing the soil water retention curve as two segments [412,413]. A model was developed with three segments by integration of the logarithmic model and the power law [414]. A retention curve model was described by Silva and Grifoll [402] as four segments. Moreover, attempts were made to originate a general equation for whole water content range assuming that the retention curve’s shape is based on the distribution of soil pore size [1]. A novel retention model was developed by Kosugi [415] through a lognormal distribution equation to the distribution of the soil pore radius. These models were mainly constructed in terms of measurements performed on six soils by Campbell and Shiozawa [416]. Moreover, they have not been validated with other types of soils covering all soil textures. However, the SWRCs of all soil types were not perfectly described by any particular model.
2.4.2. Pedotransfer Functions
It is expensive to determine the hydraulic features of soil experimentally based on temporal and spatial factors, modifying the utilization of indirect approaches for estimating these key soil hydraulic variables. Frequently, pedotransfer functions (PTFs) are used in this regard to estimating soil hydraulic features in terms of easy-to-obtain features such as bulk density and particle-size distribution [52]. Predicting the hydraulic properties based on PTF was assessed as satisfactory to comprehend the soil hydraulic performance [392,417]. Most PTFs are statistical models purely, thus indicating restrictions on the extrapolation and applicability. These PTFs are effective for the specific conditions for which they were gained (climate, soil class, or geographic location). They should be utilized cautiously in other conditions or regions [417,418]. Most PTFs were established for temperate soils of Europe or North America and do not apply readily to the soil from tropical areas. A PTF was developed for estimating parameters of the Van Genuchten–Mualem [61] model (VGM) in terms of the soil from the tropical regions database [419]. Likewise, the fitting parameters of a model were estimated by Tomasella and Hodnett [420] for SWRCs considering the soil organic carbon and texture with a large database on the Amazon region. A key PTF was developed by Tomasella et al. [421] from the measured features of various tropical soils from Brazil. However, point-based and parametric PTFs were evaluated by Medeiros et al. [422] for soil from the Amazon area.
In general, PTFs can be characterized based on the output into two key kinds: (1) point PTFs for prediction of soil water contents at definite pressure heads and (2) parametric PTFs to estimate parameters of functions for explaining soil water content data across various pressure heads. There have been most efforts on developing the second type PTFs since they are able to present the essential inputs for explaining the SWRC mathematically [61,423]. Soil textural data, organic matter content (OMC), bulk density (BD) is the input data of these PTFs along with soil water content values at particular pressure heads. Among the most widely used PTFs are (1) the ROSETTA, established by Schaap et al. [424] from a soil datasets mostly comprising data from North America and Europe; (2) PTFs-HYPRES from European soil datasets [425]; (3) PTFs-USDA from the US Department of Agriculture (USDA) soil datasets [60]. Every PTF is established in terms of the specific composition of the calibration dataset reflecting its soil conditions and geographic origin. Extrapolation of PTFs to soil circumstances rather than their development conditions results in large uncertainties [426,427,428]. Soil sample dimension is another source of uncertainty effects on the development of PTFs [429]. For instance, it was reported that the inclusion of the sample internal diameter and height enhance the accuracy of the saturated hydraulic conductivity PTFs and SWRC substantially [430]. Therefore, it is very important to investigate the reliability of PTFs before prolonging their use in other areas.
Moreover, there are still problems in various textural classification systems utilized to represent the particle-size distribution all over the world for both developing and immediate utilization of PTFs [431]. The fundamental compatibility is limited by harmonization of the particle size amongst soil databases before even developing and utilizing PTFs. Commonly, approaches in this field can be categorized into regression, interpolation, curve fitting, and similarity approaches [432,433]. Curve fitting is more extensively used, with various mathematical equations available for explaining the soil’s cumulative PSD (particle size distribution) [433,434]. It is critical to select the model best fitting the soil for reducing errors and the uncertainties during hydraulic modeling of the soil.
2.4.3. Fractal Equations
Information on SWRC is required by modern hydrological models. There is a close relation between hydraulic properties, hydraulic conductivity, and soil-water retentions with a porous media’s geometry [47,435]. Recently, further attention has been attracted by the formulation of fractal geometry as a powerful instrument to describe different complex natural phenomena, particularly in physics and mechanics of soils and rocks [436,437]. With the current use of fractal geometry, an effective tool has been proposed to fill the gap between the physical interpretation of the parameters of experimental models and their use [438,439]. It was shown that there is a similarity between both solid and porous phases that can be considered by different fractals [440]. Hierarchical systems are described by fractals that are appropriate for modeling the heterogeneous soil structure with tortuous pore space [438,441]. The SWRC was modeled by Toledo et al. [442] utilizing thin-film theory and fractal geometry. The unsaturated hydraulic conductivity functions were derived by Tyler and Wheatcraft [443] in terms of the fractal model for SWRC and the relative conductive models established by Burdine [435] and Mualem [444]. Generally, fine-textured soils possess higher fractal dimensions which include smaller fractal dimensions [445,446,447]. The solid matrix’s fractal dimensions (that is, soil texture and soil particle size distribution), and the void phase, can be characterized by the soils’ fractal nature. However, further studies are required to calculate the association among the soil solid’s fractal dimensions, void phases, and the fractal dimension utilized in the SWRC [448]. Perfect [449] used fractal geometry to simulate porous media structure and was revised by Cihan et al. [450]. A sensitivity analysis performed on Tyler and Wheatcraft’s [443] model represented that the SWRC fractal dimension (DSWRC) is the most sensitive feature in the model, while this model has less sensitivity to the AEV and saturated water content [451]. Some other researchers applied the fractal theory to investigate the SWRC and used the fractal dimensions of the SWRC to describe the corresponding SWRC [452,453]. The exponent of the SWRC, DSWRC is meaningful physically. However, it is difficult to measure it directly experimentally. Moreover, also in-situ soil water retention experiments are laborious and time-consuming. So, the estimation of DSWRC based on the available data can be a very useful alternative. As mentioned, porous media are heterogeneous systems comprising different, numerous, and interacting components, their complex nature makes it difficult to predict their hydraulic features [454]. Soil particle size distribution has fractal properties. Hence, the fractal model can be utilized for the estimation of the SWRC.
2.4.4. AI Techniques
Different AI models are developed successfully for geotechnical engineering uses during the last ten years [455,456,457]. It is interesting to predict the SWRC from AI methods [458,459] as a result of its extensive utilization in interpreting of the unsaturated soils’ hydro-mechanical behavior [460,461,462]. However, there are fewer studies on the prediction of the SWRC via AI models [463,464]. Simple yet reliable methods are urgently required to predict the SWRC promotion to run our present comprehension of the unsaturated soils mechanics into conventional geo-environmental and geotechnical engineering practice uses.
Recently, machine learning (ML) and artificial intelligence (AI) methods developments have been developed as great tools in different scientific fields such as some applications in soil mechanics. By the incrementing quality and quantity of the available data, new possibilities are presented to solve complicated problems such as classification, clustering, and regression issues. Presently, attempts have been made to utilize AI approaches not requiring knowing the predictor-target association and utilizing data for training the model. Nguyen et al. [465] compared the performance of machine learning approaches including multiple linear (ML), k-Nearest neighbors regression, and support vector machine techniques to estimate the tropical delta soils’ SWRC. It was concluded that the higher efficiency is demonstrated by the latter. The predictors utilized are sand, clay, and silt contents, organic carbon percentage, and bulk density. Using the point approach, their regression models were examined with a pseudo-continuous model. They found a better behavior when using point data. The SVM machine learning algorithm was used by Lamorski et al. [466] for predicting the SWRC main wetting branch in terms of its drying branch fitted by the model of VG. Parametric and direct regression models were examined, and no substantial differences were found by the authors in the results gained utilizing soil water retention curve data points or the van Genuchten parameters as targets. It was reported that the performance of their PTF was not improved by the inclusion of further soil physical features to SWRC data (pedo-transfer function). The laboratory measurements were performed on different soils samples from Poland in the dataset used to train the regression model. Using the ANN method, the SWRC of Italian soils was predicted by D’Emilio et al. [464] utilizing a dataset of 359 soils. The inputs (particle size distribution, organic carbon content, bulk density, soil texture, and porosity) were utilized for predicting the van Genuchten SWRC parameters. Comparing various ANN configurations indicated the higher forecasting performance of clay, sand, and silt contents along with the organic carbon content. Furthermore, by a larger database of soil features, AI methods are used frequently for supporting hydrological modeling [467]. For instance, the ANN with a “black box” nature can simulate the human brain, which learns, memorizes, associates, and includes the complex interactions (networks) between data (neurons of the hidden layers, input, and output) [468]. No pre-existing information is implied on the associations between output and input. It means that no prior model concept is required by ANNs (commonly known as black boxes) and they can extract the highest quantity of information from the data. There have been several attempts to adopt ANNs for predicting soil hydraulic features. For instance, Haghverdi et al. [467] developed an ANN to predict the soil water content at any matric potential with no definite parameterizations or equations. Wösten et al. [425] provided two different models trained with fitted water content data. ANNs were used by Zhanga et al. [469] for predicting the soil water retention and the sandy soils’ available water. In some studies, it was proved the effectiveness of training an ANN with various soil matric potentials to consider most of the variations possibly encountered in the soil, rather than with the water retention data gathered in a limited range of water potential [470]. The artificial neural networks (ANNs) can mimic the complicated systems’ behavior by changing the strength of the effect of network architectures, and the interconnections structures among components. An ANN is merely a sophisticated regression with a network of several simple elements (or neurons). No prior model concept is required by ANNs, which extract the highest information from the data [464].
3. Applications of SWRC/SWCC
The soil water retention curve/soil water characteristic curve (SWRC/SWCC) reflects the relation between water content and matric suction. It measures the quantity of water held in a soil at a particular matric potential under equilibrium [131]. It is also indicative of the pore size and connectedness and is a function of gradation of soil, soil texture, structure, and the presence of organic matter. Figure 5 shows the effect of gradation on matric potential and illustrates its non-linear nature. It can be observed in Figure 5 that the greater the fines contents, say clay, the higher the water content at a specific matric suction and more gradual the SWRC/SWCC. However, in granular soils (due to the larger pore size) less water is retained and hence the SWRC/SWCC is steeper. SWRC/SWCC finds immense application in interpreting the properties of the unsaturated soil specially its strength and hydraulic conductivity [19,131].
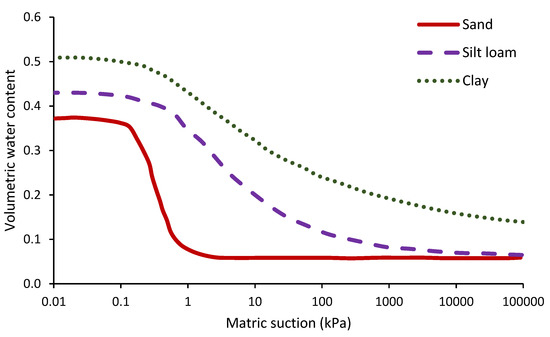
Figure 5.
Soil-water characteristics curve for soils of different gradations (After Tuller and Or [131]).
It is an important tool to assess the mechanical and hydraulic behavior of unsaturated soil which includes volume change behavior, strength, hydraulic conductivity, diffusivity and fluid flow, etc. It is also used to determine the water storage capacity of the soil and aggregate stability [471]. The SWRC/SWCC finds several applications in civil engineering, particularly in geotechnical engineering in the fields of slope stability, bearing capacity, settlement, and seepage related issues [19].
3.1. Slope Stability and Landslides
Soil in the slopes is in unsaturated condition generally and SWRC/SWCC presents a better option for assessing their stability. Shear strength of soil changes with suction in unsaturated soils indicating the necessity for predicting the relation between water content and matric suction [472] and hence SWRC/SWCC has immense application in slope stability analysis. In unsaturated soils, hydraulic conductivity is a function of matric suction and the capacity of soil to retain water also depends of matric suction making SWRC/SWCC important for understanding infiltration in unsaturated slopes and to assess its FS [15]. Fredlund et al. [25] extended the Mohr-Coulomb failure criteria to account for soil suction and subsequent change in shear strength. Ng and Pan [14] observed from their study that the state of stress and wetting-drying history has a significant influence on soil-water characteristics in an unsaturated soil. Ng and Pan [94] also concluded in their study that wetting stress dependent SWRC/SWCC yields safer and more accurate FS for the case of unsaturated slopes. Antinoro et al. [472] studied the effect of the degree of saturation on unsaturated slopes using SWRC/SWCC for 40 samples varying in texture and structure on the factor of safety of slopes with unsaturated soil. They used three different SWRC/SWCC models (van Genuchten [16], Ross and Smettem [473] and Dexter et al. [474]) for fitting the experimental SWRC/SWCC curves but on using the data for calculation of factor of safety (FS), the Dexter et al. [474] showed anomalous behavior such as decreasing FS with decreasing water content. The study underlines the need for selection of proper SWRC/SWCC models pertaining to the specific application. Comegna et al. [475] studied the hysteretic response of unsaturated soils and found that at the same degree of saturation suction can differ depending on its drying or wetting history. Conventional approaches adopting a single SWRC/SWCC can therefore, underestimate the reduction in FS during infiltration. Chen et al. [334] conducted field study on SWRC/SWCC of red clay slopes at shallow depths to understand the effect of long-term wetting and drying cycles and distribution of water content in red clay slopes. The red clay is characterized by low hydraulic conductivity, high liquid limit and tendency to dilate making it water sensitive and susceptible to instability. Field observations in the study conducted by Chen et al. [334] showed that SWRC/SWCC vary with depth due to the influence of the overburden pressure and show an exponential relation. Their results showed that FS using laboratory SWRC/SWCC is similar to the water content on the wetting side of the curve but using SWRC/SWCC on the drying side yields a more conservative FS. Cai et al. [476] conducted an experimental study to investigate the behavior of soil post landslides induced by earthquake and found that matric suction contributes to stability of rill banks of shallow depths in unsaturated condition. They used two popular models (i.e., van Genuchten [16] and Brook-Corey [47]) to establish the SWRC/SWCC and found that the van Genuchten model yielded a better fit reflecting the dominance of preferential flow in gravelly soil. Pam et al. (2018) developed a SWRC/SWCC model for slopes performed of unsaturated soil under transient seepage conditions. SWRC/SWCC was fit from a number of experimental investigations and was compared with field data obtained from Pohang, Korea. Their study pointed that more parameters improved the fit of SWRC/SWCC but at the same time resulted in a more complex and non-linear equation. Soil texture was observed to be the most important parameter that dictated the performance of the selected SWRC/SWCC model. The study also pointed out the need for a more elaborate and thorough transient analysis for selecting a suitable SWRC/SWCC model to analyze slope stability during rainfall. Ahmed and Bryson [477] studied the critical hydraulic behavior corresponding to slope failure using SWCC and found that SWRC/SWCC have a profound influence on the hydrological behavior of the slope during rainfall than the parameters in the drying SWRC/SWCC based on two case studies one from China and other from Singapore. The study considered both steady and transient infiltration on an unsaturated slope. This study however, did not include air entrapment behavior. Ip et al. [478] studied the rainfall induced landslides in on unsaturated soils for a small part of Singapore incorporating the SWCC using three different models and generated a 3D slope model using the Scoops3D analysis. Scoops3D analysis used a 3D limit equilibrium method by computing the FS for a slip direction by averaging the ground surface direction for the DEM cells in the potential failure zone [479]. Scoops3D used the equation developed by Fredlund and Xing [1] to develop the SWCC. Feng et al. [480] used a Bayesian framework capable of updating from experimental data to investigate the uncertainty of parameters in SWRC/SWCC. The study by Feng et al. [480] showed that Bayesian updating framework had yielded good results for monitoring landslides, particularly in case of large landslides and resulted in a narrower range of SWRC/SWCC parameters and the parameter ‘a’ of SWRC/SWCC tends to increase with time along with the changes in the posterior distribution. Uncertainty is inevitable due to a lack of data including in model selection and fitting [481]. Uncertainty in SWCC model parameters lead to error in prediction of pore pressure and subsequent error in estimating the FS affecting both seepage and slope stability analysis.
3.2. Bearing Capacity (BC)
Often shallow foundations rest on unsaturated soil [482] but conventional analysis uses the saturated strength which is generally two to four times lesser than that of unsaturated strength [483,484]. Several studies have also reported that the bearing capacity of unsaturated soil is considerably higher than saturated soil owing to the suction in the soil matrix [482,484,485,486] and using conventional saturated condition in the bearing capacity calculations largely underestimates the bearing capacity of the soil. Shear strength of unsaturated soil is a key factor that dictates the bearing capacity of soil [7]. SWCC is an important parameter for estimating the shear strength of the unsaturated soil [20] and the changes in the net normal stress affect the strength of unsaturated soil than the changes in the matric suction [487]. Vanapalli and Mohamed [482] proposed the modified effective stress approach (MESA) for improved prediction of bearing capacity for unsaturated coarse-grained soils using the SWCC. Fredlund et al. [361] reported in their study that considering unsaturated soil as a four-phase system is a definite advantage for analyzing the stress in the soil matrix. Terzaghi’s classical approach used effective shear strength parameters of saturated soil [488]. Numerous attempts were made by various authors to incorporate matric suction to account for the improvement in strength parameters of unsaturated soil [482,484,485,488]. It was reported the Terzaghi’s BC equation was modified into a linear BC equation for surface footings taking matric suction into account. However, the experimental data did not show a linear relation between BC and matric suction [482,485]. Vanapalli and Mohamed [482] bearing capacity model (VM model) results showed that shear strength increased with matric suction up to the residual suction value with bearing capacity following the similar trend of increase with matric suction till a critical limit and further decreased as it approached the residual desaturation zone. In the VM model, bearing capacity increased with matric suction and the matric suction value remained less than or equal to the air-entry value. The study also showed that the contribution of suction reduced to a negligible quantum when matric suction was greater than the air-entry value. This limitation was overcome by the authors by introducing an additional term for suction in residual zone. Vahedifard and Robinson [489] used the effective degree of saturation and average suction that took into account the various suction profiles to address the limitation of the previously reported BC equation [482,485]. Tang et al. [486,490] used both uniform and linear suction profiles to determine the BC of footings on unsaturated soil. Ghasemzadeh and Akbari [491] provided an improved BC equation over existing ones suggested by Vanapalli and Mohamed [482] by considering the non-linear variation of matric suction and the model performed appreciably in the residual and transition saturation zones. Safarzadeh and Aminfar [492] further investigated the VM model and found that bearing capacity of the Goomptah sand decreased by a large magnitude when the saturation of the soil approached zero. The revised model showed good agreement between the measured and predicted bearing capacity values for the entire range of the SWCC. Research also shows that the ultimate bearing capacity (UBC) was calculated for strip footings in unsaturated soil under linearly varying and uniform suction and found that UBC of strip footing is sensitive to the intermediate principal stress. Matric suction influences UBC to a considerable extent. It was found that UBC increases with matric suction linearly. Non-linear variation of matric suction with depth is a function of soil characteristics and environment conditions, which is typically ignored. However, Du et al. [488] accounted for the non-linear variation of matric suction. Du et al. [488] used the discretization approach of limit analysis to investigate the BC of shallow foundation as it offers an alternative to consider the variation of matric suction and shear strength with depth and concluded that their approach gave more realistic results. In this study, Du et al. [488] adopted the suction stress characteristic curves proposed by Lu et al. [493] to represent the variation of effective stress with saturation and matric suction spatially. Du et al. [488] also reported that BC increased with air-entry pressure for a specific ‘n’ value, flow conditions have negligible effect on granular soil but affect fine-grained soils, surcharge contributes BC and unit weight does not appreciably affect the BC of soils.
3.3. Settlement
Settlement is an important geotechnical design parameter and is prone to be affected by matric suction in unsaturated soil as shallow foundations are placed near the ground in the unsaturated zone. Neglecting matric suction leads to over estimation of settlement in unsaturated soils [494]. Oh et al. [495] derived a theoretical equation for modulus of elasticity (MoE) considering the matric suction using the SWCC. Rahardjo et al. [496] calculated the modulus of elasticity of an unsaturated soil considering matric suction and found that stiffness increased with matric suction. Oh et al. [495] studied the load-settlement behavior of three different granular soil under three matric suction and proposed a relation for MoE. Oh and Vanapalli [485] compared the surface settlement of unsaturated and saturated sand assuming elastic—perfectly plastic behavior. The authors established the stress-applied vertical stress relation using two segments of a straight line and calculated them using unsaturated cohesion, friction angle, hydraulic conductivity and SWCC. Oh and Vanapalli [497] proposed a simple finite element method by extending the modified total stress approach and observed from their study that Poisson’s ratio affected the settlement response of shallow foundation in unsaturated clay but settlement was not influenced the coefficient of earth pressure at rest as the friction angle in clay was zero. The load settlement response of unsaturated clay was reasonably predicted using average matric suction.
The wetting—drying cycles due to change in climate impacts the SWCC [20]. This hysteresis in turn affects the mechanical behavior of the unsaturated soil along with its transient behavior [247,498]. Kim et al. [499] studied the settlement behavior of shallow foundations resting on unsaturated soil under rainfall infiltration and found that taking matric suction into account resulted in good agreement between the experimental and field load-settlement curves. Kim et al. [500] also observed that stiffness of the soil increased with matric suction due to high MoE. Rainfall infiltration caused additional settlement and was attributed to the loss of matric suction. Jeong et al. [494] investigated the effects of rainfall infiltration, position of ground water table, and matric suction, and accounted for the non-linear variation of matric suction along the depth by considering the rainfall infiltration and deformation analysis sequentially. The authors observed in their study that rainfall infiltration and position of ground water table influenced settlement of shallow foundation. Analysis using wetting SWCC yielded settlement 5% higher than the drying side. Mohamoudabai and Ravichandran [501] used a coupled geotechnical hydrological model for determining the bearing capacity and elastic settlement of shallow foundation on partially saturated soil. The authors compared the bearing capacity and settlement of footing in two different sites and observed an increase in BC and decrease in settlement with decrease in degree of saturation. However, the magnitude of increase in BC and reduction in settlement was considerable in both the sites owing to the difference in geotechnical properties of the soil and hydrologic parameters. Thongpong et al. [502] studied the settlement behavior of an isolated footing on unsaturated loess which was collapsible in nature. The seasonal variation of water content was in the soil was also taken into account. The degree of saturation was inferred from the SWCC and the authors observed from their experimental investigation that size, depth of foundation and degree of saturation affected settlement significantly.
3.4. Seepage
Seepage analysis is crucial for the safety and optimal performance of slopes and hydraulic structures. Unsaturated soil is subject to cycles of wetting and drying causing a change in their water content, and therefore one needs a thorough understanding to predict their long-term behaviour [20]. Phoon et al. [503] observed that as the variability of SWCC parameters increase, impact on seepage and slope stability also increases. Bishop and Blight [504] identified two stress components, normal stress and matric suction that are independent to predict its behavior making unsaturated hydraulic conductivity and SWCC the most important parameters for estimating seepage [480,505] particularly in transient flow conditions. Li et al. (2011) presented a method to predict the SWCC and permeability of a cracked soil for seepage analysis. The model is based on calculating the crack volume changes in the wetting and drying process. The composite permeability functions derived in this study accounts for considerable increase in hydraulic conductivity when nearing complete saturation but they do not cause preferential flow. Simulation in the study results in a uniform wetting front which accelerates in ponding conditions. Additionally, the authors observed that the permeability function is akin to that of the soil matrix when pores tend to close under saturation and open when suction is high. Yang et al. (2012) investigated the hysteresis behavior of unsaturated soil in relation to its hydraulic properties. The hysteretic model proposed by the authors successfully predicted hydraulic state in a soil column. The hysteretic model on comparison with the non-hysteretic model demonstrated a large variation in suction and exhibited a high average percolation velocity in the soil column. This model was particularly useful for design of soil covers. Saadeldin and Henni [505] observed that a bimodal SWCC was a critical parameter in controlling the soil-water interaction. Bimodal SWCC offers a practical approach for simulating soil-water interaction in cracked soil and results in increased infiltration due to the discrepancy in distribution of pore space that is caused by cracks. Volumetric water content changes rapidly in the case of bimodal SWCC with time. Soil suction also changes with time as the volumetric water content. Tan et al. [506] investigated the seepage in hydraulic structures such as earth dams considering the spatial variation of hydraulic parameters using a combination of random field theory and Monte Carlo simulation. The results of their study showed that SWCC parameters and the saturated hydraulic conductivity were random fields that were lognormally cross-correlated. Walshire et al. [507] assessed the performance of SWCC prediction methods and found that of the five examined methods not one addressed all soil types and concluded SWCC is particular for a said soil type particularly in transient flow conditions. The methods assessed were Rawls et al. [56], Tomasella and Hodnett [420], Zapata et al. [254], Perera et al. [508] and Sleep [508]. Results of the study showed that Zapata et al. [254] and Sleep [509] predictive methods yielded better prediction of SWRC/SWCC over a wide range of soil types compared to other methods.
Generally, for the utilization of SWRC/SWCC behavior of soil (fundamentally for hydraulically-bound geo-structures), the vadose zone has been identified as the foundation and the hydro-mechanical soil properties are illustrated using the principle of unsaturated soil mechanics (USM). A total of 403 previous literatures were studied and reviewed in this research work and all has stated that SWRC/SWCC is an unsaturated soil condition the implementation of which constitutes the moisture holding mechanism of soil for different geotechnical applications. This emphasizes the geo-structural expediency to conduct SWRC analysis for all hydraulically-bound geo-structures for effective solution of affected earthwork problems. The analysis of the matric suction of soil under hydraulic influence has been emphasized by all of the reviews especially the most pronounce, which were by Fredlund (whose research focused on USM).
4. Conclusions
It can be concluded that 403 relevant literature references were studied and reviewed in this research work studying the utilization of soil water retention curve (SWRC) or the soil water characteristics curve (SWCC) as a tool in solving most geotechnical engineering problems (especially the hydraulically-bound geo-structural problems, which lie within the vadose zone of a substructure). This was successfully carried out on the bases of problem classification, which included soil types, soil parameters, measuring tests and prediction techniques, and problem application, which included slope stability problems, bearing capacity problems, settlement and consolidation problems and seepage problems. Several factors were identified on both overview bases. Matric suction was identified as the most influential soil parameter which affects the behavior of the SWRC of soils. It was also observed that various hydro-mechanical properties of hydraulically-bound soils, which are affected by water level changes, have been obviously correlated with the SWRC except hydraulic gradient which deserves serious research attention. This will enable SWRC form a basis for solving geo-structural problems related to soil consolidation under loading conditions. Due to the unsaturated soil mechanics base of Fredlund works, they have been identified as the most prominent in dealing with the SWRC problems in geotechnics and geo-structural engineering. Despite a large amount of previous research that focuses on SWRC numerical or laboratory modeling, there are still some important challenges that should be considered.
- Problematic soils, specifically expansive soil and loess, show a totally different retention behavior under hydraulic loading. There is much research in previous literature that considers the laboratory or numerical investigation on these soils. However, there are still no comprehensive frameworks that could investigate their retention mechanism based on macro and microstructural behavior.
- It is clear that the retention behavior and mechanism in a low and high suction range are different from each other. Due to the weaknesses of laboratory and field instruments, many previous scholars mainly consider the low to medium suction range behavior. Therefore, it is worth paying more attention to the high suction range of soils and their retention behavior.
- Hydraulic hysteresis is a fundamental issue in unsaturated soil that makes the difference between drying and wetting paths in SWRC. The causes of this phenomenon are still a question despite some previous investigation on this topic. It is necessary to better investigate it in both low and high suction range from laboratory, numerical, and analytical modeling frameworks.
- Most of the existing studies focused on investigating the effect of pure water on SWRCs. However, it is worth noting that osmotic suction is an important part of suction that could change the soil structures and, subsequently, liquid retention behavior. Therefore, it is significantly important to investigate the effects of pore fluid chemistry on the retention behavior of different soils.
Author Contributions
Conceptualization, K.C.O.; methodology, K.C.O. and A.M.E.; software, K.C.O. and A.M.E.; validation, K.C.O., A.M.E. and F.F.M.; formal analysis, K.C.O.; investigation, K.C.O.; resources, K.C.O. and F.F.M.; data curation, K.C.O. and F.F.M.; writing—original draft preparation, K.C.O., F.F.M., S.A., H.A.M., E.R.S., A.G.D. and F.I.A.; writing—review and editing, K.C.O., F.F.M., S.A., H.A.M., E.R.S., A.G.D. and F.I.A.; visualization, K.C.O., A.G.D. and A.M.E.; supervision, K.C.O.; project administration, K.C.O.; funding acquisition, K.C.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting the results of this research work has been reported in this manuscript.
Conflicts of Interest
The authors declare no form of conflict of interests that may appear to affect the publication of this research work.
References
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Sadeghi, H.; Golaghaei Darzi, A. A review of different approaches to analytical modeling of soil-water retention curves. Sharif J. Civ. Eng. 2021, 37, 111–123. [Google Scholar] [CrossRef]
- Sadeghi, H.; Darzi, A.G. Modelling of soil-water retention curve considering the effects of existing salt solution in the pore fluid. MATEC Web Conf. 2021, 337, 02001. [Google Scholar] [CrossRef]
- Assouline, S.; Or, D. Conceptual and parametric representation of soil hydraulic properties: A review. Vadose Zone J. 2013, 12, 4. [Google Scholar] [CrossRef]
- Ma, K.C.; Lin, Y.J.; Tan, Y.C. The influence of salinity on hysteresis of soil water-retention curves. Hydrol. Process. 2013, 27, 2524–2530. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Tu, H.; Oh, W.T. Soil-water characteristic curve-based methods for predicting the swelling pressure and ground heave in expansive soils. In Proceedings of the Indian Geotechnical Conference, kakinada, India, 18–28 December 2014. [Google Scholar]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A. Estimation of air permeability function from soil-water characteristic curve. Can. Geotech. J. 2019, 56, 505–513. [Google Scholar] [CrossRef]
- Wen, H.; Wang, J.; Wen, V.-F.W.; Muhunthan, B. Soil–Water Characteristic Curves for Soils Stabilized with Class C Fly Ash. Transp. Res. Rec. 2015, 2473, 147–154. [Google Scholar] [CrossRef]
- Fredlund, D.; Fredlund, M. Application of ‘Estimation Procedures’ in Unsaturated Soil Mechanics. Geoscience 2020, 10, 364. [Google Scholar] [CrossRef]
- Zhou, A.N.; Sheng, D.; Carter, J.P. Modelling the effect of initial density on soil-water characteristic curves. Geotechnique 2012, 10, 669–680. [Google Scholar] [CrossRef]
- Abbey, S.J.; Eyo, E.U.; Ng’ambi, S. Swell and microstructural characteristics of high-plasticity clay blended with cement. Bull. Eng. Geol. Environ. 2019, 79, 2119–2130. [Google Scholar] [CrossRef]
- Abbey, S.J.; Eyo, E.U.; Oti, J.; Amakye, S.Y.; Ngambi, S. Mechanical Properties and Microstructure of Fibre-Reinforced Clay Blended with By-Product Cementitious Materials. Geosciences 2020, 10, 241. [Google Scholar] [CrossRef]
- Al-Taie, A.; Disfani, M.; Evans, R.; Arulrajah, A.; Horpibulsuk, S. Volumetric behavior and soil-water characteristic curve of untreated and lime-stabilized reactive clay. Int. J. Geomech. 2019, 19, 1943–5622. [Google Scholar] [CrossRef]
- Ng, C.W.; Pang, Y.W. Experimental investigations of the soil-water characteristics of a volcanic soil. Can. Geotech. J. 2000, 37, 1252–1264. [Google Scholar] [CrossRef]
- Ng, C.W.; Pang, Y. Influence of stress state on soil-water characteristics and slope stability. J. Geotech. Geoenviron. Eng. 2000, 126, 157–166. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Seki, K. SWRC fit—A nonlinear fitting program with a water retention curve for soils 10 having unimodal and bimodal pore structure. Hydrol. Earth Syst. Sci. 2007, 4, 407–411. [Google Scholar]
- Aneke, F.I. Behaviour Of Unsaturated Soils Fof Road Pavement Structure Under Cyclic Loading. Ph.D. Dissertation, Central University of Technology, Bloemfontein, South Africa, 2018. [Google Scholar]
- Fredlund, D.G. Unsaturated soil mechanics in engineering practice. J. Geotech. Geoenviron. Eng. 2006, 132, 286–321. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993; ISBN 0-471-85008-X. [Google Scholar]
- Leong, E.C.; Rahardjo, H. Permeability functions for unsaturated soils. J. Geotech. Geoenviron. Eng. 1997, 123, 1118–1126. [Google Scholar] [CrossRef]
- Pham, H.Q.; Fredlund, D.G.; Lee Barbour, S. A study of hysteresis models for soil-water characteristic curves. Can. Geotech. J. 2005, 42, 2005. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W. Unsaturated Soil Mechanics; John Wiley&Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Terzaghi, K. The shearing resistance of saturated soils and the angle between the planes of shear. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Cambridge, MA, USA, 22–26 June 1936. [Google Scholar]
- Fredlund, D.G.; Morgenstern, N.R.; Widger, A. Shear strength of unsaturated soils. Can. Geotech. J. 1978, 15, 313–321. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Rice, J.R.; Cleary, M.P. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev. Geophys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- De Boer, R.; Ehlers, W. The development of the concept of effective stresses. Acta Mech. 1990, 83, 77–92. [Google Scholar] [CrossRef]
- Coussy, O.; Dormieux, L.; Detournay, E. From mixture theory to Biot’s approach for porous media. Int. J. Solids Struct. 1998, 35, 4619–4635. [Google Scholar] [CrossRef]
- Atkinson, J. The Mechanics of Soils and Foundations; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Khalili, N.; Romero, E.; Marinho, F.A. State of the Art Report. Constitutive Modelling, Experimental Investigation, and Field Instrumentation: Advances in Unsaturated Soil Mechanics. 2022. Available online: https://docs.google.com/viewer?url=https%3A%2F%2Fwww.unsw.edu.au%2Fcontent%2Fdam%2Fzz-drop%2Fsingle-import%2Fengineering%2Fwarassamon-kate-brown%2F2022-05-20ICSMGE-Full-Paper-SOA-Final.pdf&pdf=true (accessed on 1 August 2022).
- Bishop, A.W. The principle of effective stress. Tek. Ukebl. 1959, 39, 859–863. [Google Scholar]
- Schrefler, B.A. The Finite Element Method in Soil Consolidation. Ph.D. Thesis, University College of Swansea, Skewen, Wales, 1984. [Google Scholar]
- Khalili, N.; Khabbaz, M.H. A unique relationship for χ for the determination of the shear strength of unsaturated soils. Geotechnique 1998, 48, 681–687. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef]
- Lu, N.; Griffiths, D.V. Profiles of steady-state suction stress in unsaturated soils. J. Geotech. Geoenviron. Eng. 2004, 130, 1063–1076. [Google Scholar] [CrossRef]
- Kim, B.S.; Shibuya, S.; Park, S.W.; Kato, S. Application of suction stress for estimating unsaturated shear strength of soils using direct shear testing under low confining pressure. Can. Geotech. J. 2010, 47, 955–970. [Google Scholar] [CrossRef]
- Song, Y.S.; Hwang, W.K.; Jung, S.J.; Kim, T.H. A comparative study of suction stress between sand and silt under unsaturated conditions. Eng. Geol. 2012, 124, 90–97. [Google Scholar] [CrossRef]
- Song, Y.-S. Suction stress in unsaturated sand at different relative densities. Eng. Geol. 2014, 176, 1–10. [Google Scholar] [CrossRef]
- Dong, Y.; Lu, N. Measurement of suction-stress characteristic curve under drying and wetting conditions. Geotech. Test. J. 2017, 40, 107–121. [Google Scholar] [CrossRef]
- Fredlund, D.G. Volume Change Behavior of Unsaturated Soils. 1973. Available online: https://era.library.ualberta.ca/items/108fd903-873c-403b-bff6-5eb2a5db1c7e (accessed on 1 August 2022).
- Fredlund, D.G.; Morgenstern, N.R. Stress state variables for unsaturated soils. J. Geotech. Eng. 1977, 103, 447–466. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Pham, H.Q. A volume-mass constitutive model for unsaturated soils in terms of two independent stress state variables. In Unsaturated Soils, Proceedings of the Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2–6 April 2006; ASCE: Reston, VA, USA, 2006; Volume 2006, pp. 105–134. [Google Scholar]
- Lambe, T. The structure of compacted clay. J. Soil Mech. Found. 1958, 84, 1654-1–1654-34. [Google Scholar] [CrossRef]
- Gardner, W.R. Soil suction and water movement. In Pore Pressure and Suction in Soils/Conference Organized by the British National Society of the International Society of Soil Mechanics and Foundation Engineering; Butterworths: London, UK, 1961; pp. 137–140. [Google Scholar]
- Romero, E. A microstructural insight into compacted clayey soils and their hydraulic properties. Eng. Geol. 2013, 165, 3–19. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Hydrology Paper No. 3; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Kosugi, K.I. Three-parameter lognormal distribution model for soil water retention. Water Resour. Res. 1994, 30, 891–901. [Google Scholar] [CrossRef]
- Kosugi, K.I. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Arya, L.M.; Paris, J.F. A physicoempirical model to predict the soil moisture characteristic from particle size distribution and bulk density data. Soil Sci. Soc. Am. J. 1981, 45, 1023–1030. [Google Scholar] [CrossRef]
- Arya, L.M.; Leij, F.J.; Shouse, P.J.; van Genuchten, M.T. Relationship between the hydraulic conductivity function and the particle-size distribution. Soil Sci. Soc. Am. J. 1999, 63, 1063–1070. [Google Scholar] [CrossRef]
- Nimmo, J.R.; Herkelrath, W.N.; Laguna Luna, A.M. Physically based estimation of soil water retention from textural data: General framework, new models, and streamlined existing models. Vadose Zone J. 2007, 6, 766–773. [Google Scholar] [CrossRef]
- Crawford, J.W.; Matsui, N.; Young, I.M. The relation between the moisture-release curve and the structure of soil. Eur. J. Soil Sci. 1995, 46, 369–375. [Google Scholar] [CrossRef]
- Olk, D.C.; Cassman, K.G.; Randall, E.W.; Kinchesh, P.; Sanger, L.J.; Anderson, J.M. Changes in chemical properties of organic matter with intensified rice cropping in tropical lowland soil. Eur. J. Soil Sci. 1996, 47, 293–303. [Google Scholar] [CrossRef]
- Assouline, S.; Rouault, Y. Modeling the relationships between particle and pore size distributions in multicomponent sphere packs: Application to the water retention curve. Colloids Surf. Physicochem. Eng. Asp. 1997, 127, 201–210. [Google Scholar] [CrossRef]
- Rawls, W.J.; Gish, T.J.; Brakensiek, D.L. Estimating soil water retention from soil physical properties and characteristics. Adv. Soil Sci. 1991, 16, 213–234. [Google Scholar]
- Timlin, D.J.; Pachepsky, Y.A.; Acock, B.; Whisler, F. Indirect estimation of soil hydraulic properties to predict soybean yield using GLYCIM. Agric. Syst. 1996, 52, 331–353. [Google Scholar] [CrossRef][Green Version]
- Pachepsky, Y.; Rawls, W.J. (Eds.) Development of Pedotransfer Functions in Soil Hydrology; Elsevier: Amsterdam, The Netherlands, 2004; Volume 30. [Google Scholar]
- Romano, N. Spatial structure of PTF estimates. Dev. Soil Sci. 2004, 30, 295–319. [Google Scholar]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef]
- Vereecken, H.; Weynants, M.; Javaux, M.; Pachepsky, Y.; Schaap, M.G.; van Genuchten, M.T. Using pedotransfer functions to estimate the van Genuchten-Mualem soil hydraulic properties: A review. Vadose Zone J. 2010, 9, 795–820. [Google Scholar] [CrossRef]
- Beckett, C.T.S.; Augarde, C.E. Prediction of soil water retention properties using pore-size distribution and porosity. Can. Geotech. J. 2013, 50, 435–450. [Google Scholar] [CrossRef]
- Zhou, W.H.; Yuen, K.V.; Tan, F. Estimation of soil-water characteristic curve and relative permeability for granular soils with different initial dry densities. Eng. Geol. 2014, 179, 1–9. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H. Estimation of permeability function from the soil-water characteristic curve. Eng. Geol. 2015, 2015, 148–156. [Google Scholar] [CrossRef]
- Lapierre, C.; Leroueil, S.; Locat, J. Mercury intrusion and permeability of Louiseville clay. Can. Geotech. J. 1990, 27, 761–773. [Google Scholar] [CrossRef]
- Simms, P.H.; Yanful, E.K. Estimation of soil–water characteristic curve of clayey till using measured pore-size distributions. J. Environ. Eng. 2004, 130, 847–854. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E. The influence of soil structure and stress history on the soil–water characteristics of a compacted till. Geotechnique 1999, 49, 143–159. [Google Scholar] [CrossRef]
- Marinho, F.A.M. Nature of Soil–Water Characteristic Curve for Plastic Soils. J. Geotech. Geoenviron. Eng. 2005, 131, 654–661. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, L.; Wei, Y. Influence of fine content on the soil–water characteristic curve of unsaturated soils. Geotech. Geol. Eng. 2020, 38, 1371–1378. [Google Scholar] [CrossRef]
- Shen, J.-H.; Hu, M.-J.; Wang, X.; Zhang, C.-Y.; Xu, D.-S. SWCC of Calcareous Silty Sand Under Different Fines Contents and dry Densities. Front. Environ. Sci. 2021, 9, 682907. [Google Scholar] [CrossRef]
- Colmenares Montanez, J.E. Suction and Volume Changes of Compacted Sand-Bentonite Mixtures. Ph.D. Thesis, Imperial College London, London, UK, 2002. [Google Scholar]
- Pei-yong, L.; Qing, Y. Test study on soil-water characteristic curve of bentonite-sand mixtures. EJGE 2009, 14, 1–8. [Google Scholar]
- Agus, S.; Schanz, T. Drying, wetting, and suction characteristic curves of a bentonite-sand mixture. In Unsaturated Soils, Proceedings of the Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2–6 April 2006; ASCE: Reston, VA, USA, 2006; pp. 1405–1414. [Google Scholar]
- Liu, Z.; Dugan, B.; Masiello, C.A.; Gonnermann, H.M. Biochar particle size, shape, and porosity act together to influence soil water properties. PLoS ONE 2017, 12, e0179079. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, C.; Kamchoom, V.; Chen, R. Gas permeability and water retention of a repacked silty sand amended with different particle sizes of peanut shell biochar. Soil Sci. Soc. Am. J. 2020, 84, 1630–1641. [Google Scholar] [CrossRef]
- Trifunovic, B.; Gonzales, H.B.; Ravi, S.; Sharratt, B.S.; Mohanty, S.K. Dynamic effects of biochar concentration and particle size on hydraulic properties of sand. Land Degrad. Dev. 2018, 29, 884–893. [Google Scholar] [CrossRef]
- Liao, W.; Thomas, S.C. Biochar particle size and post-pyrolysis mechanical processing affect soil pH, water retention capacity, and plant performance. Soil Syst. 2019, 3, 14. [Google Scholar] [CrossRef]
- Gallage, C.P.K.; Uchimura, T. Effects of Dry Density and Grain Size Distribution on Soil-Water Characteristic Curves of Sandy Soils. Soils Found. 2010, 50, 161–172. [Google Scholar] [CrossRef]
- Barus, R.M.N.; Jotisankasa, A.; Chaiprakaikeow, S.; Sawangsuriya, A. Laboratory and field evaluation of modulus-suction-moisture relationship for a silty sand subgrade. Transp. Geotech. 2019, 19, 126–134. [Google Scholar] [CrossRef]
- Delage, P.; Lefebvre, G. Study of the structure of a sensitive Champlain clay and of its evolution during consolidation. Can. Geotech. J. 1984, 21, 21–35. [Google Scholar] [CrossRef]
- Barbour, S.L. Nineteenth Canadian Geotechnical Colloquium: The soil-water characteristic curve: A historical perspective. Can. Geotech. J. 1998, 35, 873–894. [Google Scholar] [CrossRef]
- Mitchell, J. Fabric, structure, and proterty relationships. In Fundamentals of Soil Behavior; John Wiley & Sons: New York, NY, USA, 1976; pp. 222–252. [Google Scholar]
- Sillers, W.S.; Fredlund, D.G.; Zakerzadeh, N. Mathematical attributes of some soil—water characteristic curve models. In Unsaturated Soil Concepts and Their Application in Geotechnical Practice; Springer: Berlin/Heidelberg, Germany, 2001; pp. 243–283. [Google Scholar]
- Al Majou, H.; Muller, F.; Penhoud, P.; Bruand, A. Prediction of water retention properties of Syrian clayey soils. Arid Land Res. Manag. 2022, 36, 125–144. [Google Scholar] [CrossRef]
- Boivin, P.; Garnier, P.; Tessier, D. Relationship between clay content, clay type, and shrinkage properties of soil samples. Soil Sci. Soc. Am. J. 2004, 68, 1145–1153. [Google Scholar] [CrossRef]
- Bruand, A.; Tessier, D. Water retention properties of the clay in soils developed on clayey sediments: Significance of parent material and soil history. Eur. J. Soil Sci. 2000, 51, 679–688. [Google Scholar] [CrossRef]
- Tessier, D.; Lajudie, A.; Petit, J.-C. Relation between the macroscopic behavior of clays and their microstructural properties. Appl. Geochem. 1992, 7, 151–161. [Google Scholar] [CrossRef]
- Croney, D.; Coleman, J. Soil structure in relation to soil suction (pF). J. Soil Sci. 1954, 5, 75–84. [Google Scholar] [CrossRef]
- Tinjum, J.M.; Benson, C.H.; Blotz, L.R. Soil-water characteristic curves for compacted clays. J. Geotech. Geoenviron. Eng. 1997, 123, 1060–1069. [Google Scholar] [CrossRef]
- Miller, C.J.; Yesiller, N.; Yaldo, K.; Merayyan, S. Impact of soil type and compaction conditions on soil water characteristic. J. Geotech. Geoenviron. Eng. 2002, 128, 733–742. [Google Scholar] [CrossRef]
- Thakur, V.K.; Sreedeep, S.; Singh, D.N. Parameters affecting soil–water characteristic curves of fine-grained soils. J. Geotech. Geoenviron. Eng. 2005, 131, 521–524. [Google Scholar] [CrossRef]
- Romero, E.; Vaunat, J. Retention curves of deformable clays. In Experimental Evidence and Theoretical Approaches in Unsaturated Soils; CRC Press: Boca Raton, FL, USA, 2000; pp. 99–114. [Google Scholar]
- Romero, E.; Gens, A.; Lloret, A. Water permeability, water retention and microstructure of unsaturated compacted Boom clay. Eng. Geol. 1999, 54, 117–127. [Google Scholar] [CrossRef]
- Mariamma, J. A Study on the Water Retention Characteristics of Soils and their Improvements. Ph.D. Thesis, Cochin University of Science and Technology, Kochi, India, 2010. [Google Scholar]
- Dorel, M.; Roger-Estrade, J.; Manichon, H.; Delvaux, B. Porosity and soil water properties of Caribbean volcanic ash soils. Soil Use Manag. 2006, 16, 133–140. [Google Scholar] [CrossRef]
- Birle, E.; Heyer, D.; Vogt, N. Influence of the initial water content and dry density on the soil–water retention curve and the shrinkage behavior of a compacted clay. Acta Geotech. 2008, 3, 191–200. [Google Scholar] [CrossRef]
- D’Angelo, B.; Bruand, A.; Qin, J.; Peng, X.; Hartmann, C.; Sun, B.; Hao, H.; Rozenbaum, O.; Muller, F. Origin of the high sensitivity of Chinese red clay soils to drought: Significance of the clay characteristics. Geoderma 2014, 223, 46–53. [Google Scholar] [CrossRef]
- Balbino, L.C.; Bruand, A.; Cousin, I.; Brossard, M.; Quétin, P.; Grimaldi, M. Change in the hydraulic properties of a Brazilian clay Ferralsol on clearing for pasture. Geoderma 2004, 120, 297–307. [Google Scholar] [CrossRef]
- Reatto, A.; Bruand, A.; da Silva, E.; Martins, E.; Brossard, M. Hydraulic properties of the diagnostic horizon of Latosols of a regional toposequence across the Brazilian Central Plateau. Geoderma 2007, 139, 51–59. [Google Scholar] [CrossRef]
- Tawornpruek, S.; Kheoruenromne, I.; Suddhiprakarn, A.; Gilkes, R. Microstructure and water retention of Oxisols in Thailand. Soil Res. 2005, 43, 973–986. [Google Scholar] [CrossRef]
- Krisnanto, S.; Rahardjo, H.; Fredlund, D.; Leong, E. Mapping of cracked soils and lateral water flow characteristics through a network of cracks. Eng. Geol. 2014, 172, 12–25. [Google Scholar] [CrossRef]
- Krisnanto, S.; Rahardjo, H.; Fredlund, D.; Leong, E. Water content of soil matrix during lateral water flow through cracked soil. Eng. Geol. 2016, 210, 168–179. [Google Scholar] [CrossRef]
- Rayhani, M.; Yanful, E.; Fakher, A. Physical modeling of desiccation cracking in plastic soils. Eng. Geol. 2008, 97, 25–31. [Google Scholar] [CrossRef]
- Yesiller, N.; Miller, C.; Inci, G.; Yaldo, K. Desiccation and cracking behavior of three compacted landfill liner soils. Eng. Geol. 2000, 57, 105–121. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.H.; Zhang, L.M.; Li, X.; Cai, C.Z. Measuring water retention curves for rough joints with random apertures. Geotech. Test. J. 2013, 36, 929–938. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Houston, S.L.; Nguyen, Q.; Fredlund, M.D. Moisture movement through cracked clay soil profiles. Geotech. Geol. Eng. 2010, 28, 865–888. [Google Scholar] [CrossRef]
- Miao, L.; Liu, S.; Lai, Y. Research of soil—Water characteristics and shear strength features of Nanyang expansive soil. Eng. Geol. 2002, 65, 261–267. [Google Scholar] [CrossRef]
- Puppala, A.J.; Punthutaecha, K.; Vanapalli, S.K. Soil-water characteristic curves of stabilized expansive soils. J. Geotech. Geoenviron. Eng. 2006, 132, 736–751. [Google Scholar] [CrossRef]
- Li, J.H.; Lu, Z.; Guo, L.B.; Zhang, L.M. Experimental study on soil-water characteristic curve for silty clay with desiccation cracks. Eng. Geol. 2017, 218, 70–76. [Google Scholar] [CrossRef]
- Wang, Z.; Feyen, J.; Ritsema, C.J. Susceptibility and predictability of conditions for preferential flow. Water Resour. Res. 1998, 34, 2169–2182. [Google Scholar] [CrossRef]
- Sun, D.; You, G.; Annan, Z.; Daichao, S. Soil–water retention curves and microstructures of undisturbed and compacted Guilin lateritic clay. Bull. Eng. Geol. Environ. 2016, 75, 781–791. [Google Scholar] [CrossRef]
- Ma, S.; Huang, M.; Hu, P.; Yang, C. Soil-water characteristics and shear strength in constant water content triaxial tests on Yunnan red clay. J. Cent. South Univ. 2013, 20, 1412–1419. [Google Scholar] [CrossRef]
- Iyer, K.K.; Joseph, J.; Lopes, B.C.; Singh, D.; Tarantino, A. Water retention characteristics of swelling clays in different compaction states. Geomech. Geoengin. 2018, 13, 88–103. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, D. Soil-water retention behavior of compacted soil with different densities over a wide suction range and its prediction. Comput. Geotech. 2017, 91, 17–26. [Google Scholar] [CrossRef]
- Gu, T.; Zhang, M.; Wang, J.; Wang, C.; Xu, Y.; Wang, X. The effect of irrigation on slope stability in the Heifangtai Platform, Gansu Province, China. Eng. Geol. 2019, 248, 346–356. [Google Scholar] [CrossRef]
- Hou, X.; Vanapalli, S.K.; Li, T. Water infiltration characteristics in loess associated with irrigation activities and its influence on the slope stability in Heifangtai loess highland, China. Eng. Geol. 2018, 234, 27–37. [Google Scholar] [CrossRef]
- Hou, X.; Vanapalli, S.K.; Li, T. Wetting-induced collapse behavior associated with infiltration: A case study. Eng. Geol. 2019, 258, 105146. [Google Scholar] [CrossRef]
- Peng, J.; Ma, P.; Wang, Q.; Zhu, X.; Zhang, F.; Tong, X.; Huang, W. Interaction between landsliding materials and the underlying erodible bed in a loess flowslide. Eng. Geol. 2018, 234, 38–49. [Google Scholar] [CrossRef]
- Wen, B.-P.; Yan, Y.-J. Influence of structure on shear characteristics of the unsaturated loess in Lanzhou, China. Eng. Geol. 2014, 168, 46–58. [Google Scholar] [CrossRef]
- Muñoz-Castelblanco, J.; Pereira, J.-M.; Delage, P.; Cui, Y.-J. The water retention properties of a natural unsaturated loess from northern France. Géotechnique 2012, 62, 95–106. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Sadeghi, H.; Hossen, S.B.; Chiu, C.; Alonso, E.E.; Baghbanrezvan, S. Water retention and volumetric characteristics of intact and re-compacted loess. Can. Geotech. J. 2016, 53, 1258–1269. [Google Scholar] [CrossRef]
- Hou, X.; Qi, S.; Li, T.; Guo, S.; Wang, Y.; Li, Y.; Zhang, L. Microstructure and soil-water retention behavior of compacted and intact silt loess. Eng. Geol. 2020, 277, 105814. [Google Scholar] [CrossRef]
- Uchaipichat, A.; Khalili, N. Experimental investigation of thermo-hydro-mechanical behaviour of an unsaturated silt. Géotechnique 2009, 59, 339–353. [Google Scholar] [CrossRef]
- Ghembaza, M.-S.; Taïbi, S.; Fleureau, J.-M. Effet de la température sur le comportement des sols non saturés sur les chemins de drainage et d’humidification. Can. Geotech. J. 2007, 44, 1064–1081. [Google Scholar] [CrossRef]
- Belal, T.; Ghembaza, M.S.; Bellia, Z. An investigation of the effects of cementation and temperature on the water retention curve of compacted silt. Int. J. Geotech. Eng. 2022, 16, 33–43. [Google Scholar] [CrossRef]
- Villar, M.V. Water retention of two natural compacted bentonites. Clays Clay Miner. 2007, 55, 311–322. [Google Scholar] [CrossRef]
- Li, J.H.; Guo, L.B.; Cai, C.Z. Influence of water content and soil type on soil cracking. In Proceedings of the 2012 World Congress on Advances in Civil, Environmental, and Materials Research (ACEM’ 12), Seoul, Korea, 26–30 August 2012. [Google Scholar]
- Wan, M.; Ye, W.-M.; Chen, Y.; Cui, Y.-J.; Wang, J. Influence of temperature on the water retention properties of compacted GMZ01 bentonite. Environ. Earth Sci. 2015, 73, 4053–4061. [Google Scholar] [CrossRef]
- Agus, S.S.; Arifin, Y.F.; Tripathy, S.; Schanz, T. Swelling pressure–suction relationship of heavily compacted bentonite–sand mixtures. Acta Geotech. 2013, 8, 155–165. [Google Scholar] [CrossRef]
- Gatabin, C.; Talandier, J.; Collin, F.; Charlier, R.; Dieudonné, A.-C. Competing effects of volume change and water uptake on the water retention behaviour of a compacted MX-80 bentonite/sand mixture. Appl. Clay Sci. 2016, 121, 57–62. [Google Scholar] [CrossRef]
- Tuller, M.; Or, D. Water films and scaling of soil characteristic curves at low water contents. Water Resour. Res. 2005, 41, 9. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, Y.-J.; Yang, J.; Mokni, N.; Ye, W.-M.; He, Y. Water retention and compression behavior of MX80 bentonite pellet. Acta Geotech. 2021, 17, 2435–2447. [Google Scholar] [CrossRef]
- Liu, Z.-R.; Cui, Y.-J.; Ye, W.-M.; Chen, B.; Wang, Q.; Chen, Y.-G. Investigation of the hydro-mechanical behaviour of GMZ bentonite pellet mixtures. Acta Geotech. 2020, 15, 2865–2875. [Google Scholar] [CrossRef]
- Zhu, Y.; Ye, W.; Wang, Q.; Lu, Y.; Chen, Y. Anisotropic volume change behaviour of uniaxial compacted GMZ bentonite under free swelling condition. Eng. Geol. 2020, 278, 105821. [Google Scholar] [CrossRef]
- Gapak, Y.; Tadikonda, V.B. Hysteretic Water-Retention Behavior of Bentonites. J. Hazard. Toxic Radioact. Waste 2018, 22, 04018008. [Google Scholar] [CrossRef]
- Ye, W.-M.; Wan, M.; Chen, B.; Chen, Y.; Cui, Y.; Wang, J. Temperature effects on the swelling pressure and saturated hydraulic conductivity of the compacted GMZ01 bentonite. Environ. Earth Sci. 2013, 68, 281–288. [Google Scholar] [CrossRef]
- Ye, W.M.; Zhang, F.; Chen, B.; Chen, Y.-G.; Wang, Q.; Cui, Y.-J. Effects of salt solutions on the hydro-mechanical behavior of compacted GMZ01 Bentonite. Environ. Earth Sci. 2014, 72, 2621–2630. [Google Scholar] [CrossRef]
- Shirazi, S.; Kazama, H.; Salman, F.A.; Othman, F.; Akib, S. Permeability and swelling characteristics of bentonite. Int. J. Phys. Sci. 2010, 5, 1647–1659. [Google Scholar]
- Sun, H.; Mašín, D.; Najser, J.; Scaringi, G. Water retention of a bentonite for deep geological radioactive waste repositories: High-temperature experiments and thermodynamic modeling. Eng. Geol. 2020, 269, 105549. [Google Scholar] [CrossRef]
- Ravi, K.; Rao, S.M. Influence of infiltration of sodium chloride solutions on SWCC of compacted bentonite–sand specimens. Geotech. Geol. Eng. 2013, 31, 1291–1303. [Google Scholar] [CrossRef]
- Mata Mena, C. Hydraulic Behaviour of Bentonite Based Mixtures in Engineered Barriers: The Backfill and Plug Test at the Äspö Hrl (Sweden); Universitat Politècnica de Catalunya: Barcelona, Spain, 2003; ISBN 84-689-1966-7. [Google Scholar]
- Mokni, N.; Olivella, S.; Valcke, E.; Mariën, A.; Smets, S.; Li, X. Deformation and flow driven by osmotic processes in porous materials: Application to bituminised waste materials. Transp. Porous Media 2011, 86, 635–662. [Google Scholar] [CrossRef]
- Thyagaraj, T.; Rao, S.M. Influence of osmotic suction on the soil-water characteristic curves of compacted expansive clay. J. Geotech. Geoenviron. Eng. 2010, 136, 1695–1702. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.-G.; Ye, W.-M.; Chen, B.; Cui, Y.-J. Influence of salt concentration on volume shrinkage and water retention characteristics of compacted GMZ bentonite. Environ. Earth Sci. 2016, 75, 535. [Google Scholar] [CrossRef]
- He, Y.; Ye, W.M.; Chen, Y.G.; Chen, B.; Ye, B.; Cui, Y.-J. Influence of pore fluid concentration on water retention properties of compacted GMZ01 bentonite. Appl. Clay Sci. 2016, 129, 131–141. [Google Scholar] [CrossRef]
- Touze-Foltz, N.; Duquennoi, C.; Gaget, E. Hydraulic and mechanical behavior of GCLs in contact with leachate as part of a composite liner. Geotext. Geomembr. 2006, 24, 188–197. [Google Scholar] [CrossRef]
- Bouazza, A.; Vangpaisal, T. Laboratory investigation of gas leakage rate through a GM/GCL composite liner due to a circular defect in the geomembrane. Geotext. Geomembr. 2006, 24, 110–115. [Google Scholar] [CrossRef]
- Barroso, M.; Touze-Foltz, N.; von Maubeuge, K.; Pierson, P. Laboratory investigation of flow rate through composite liners consisting of a geomembrane, a GCL and a soil liner. Geotext. Geomembr. 2006, 24, 139–155. [Google Scholar] [CrossRef]
- Bouazza, A.; Rouf, M.A. Hysteresis of the water retention curves of geosynthetic clay liners in the high suction range. Geotext. Geomembr. 2021, 49, 1079–1084. [Google Scholar] [CrossRef]
- Hanson, J.; Risken, J.; Yesiller, N. Moisture-suction relationships for geosynthetic clay liners. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; pp. 3025–3028. [Google Scholar]
- Beddoe, R.A.; Take, W.A.; Rowe, R.K. Water-retention behavior of geosynthetic clay liners. J. Geotech. Geoenviron. Eng. 2011, 137, 1028–1038. [Google Scholar] [CrossRef]
- Abuel-Naga, H.; Bouazza, A. A novel laboratory technique to determine the water retention curve of geosynthetic clay liners. Geosynth. Int. 2010, 17, 313–322. [Google Scholar] [CrossRef]
- Siemens, G.; Take, W.; Rowe, R.; Brachman, R. Effect of confining stress on the transient hydration of unsaturated GCLs. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; pp. 1187–1190. [Google Scholar]
- Bannour, H.; Stoltz, G.; Delage, P.; Touze-Foltz, N. Effect of stress on water retention of needlepunched geosynthetic clay liners. Geotext. Geomembr. 2014, 42, 629–640. [Google Scholar] [CrossRef]
- Risken, J.L. Development and Use of Moisture-Suction Relationships for Geosynthetic Clay Liners. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2014. [Google Scholar]
- Tincopa, M.; Bouazza, A. Water retention curves of a geosynthetic clay liner under non-uniform temperature-stress paths. Geotext. Geomembr. 2021, 49, 1270–1279. [Google Scholar] [CrossRef]
- Bouazza, A.; Ali, M.A.; Rowe, R.K.; Gates, W.P.; El-Zein, A. Heat mitigation in geosynthetic composite liners exposed to elevated temperatures. Geotext. Geomembr. 2017, 45, 406–417. [Google Scholar] [CrossRef]
- Indrawan, I.; Williams, D.; Scheuermann, A. Effects of saline coal seam gas water on consistency limits, compaction characteristics and hydraulic conductivities of clays used for liners. Geol. Soc. Lond. Eng. Geol. Spec. Publ. 2016, 27, 227–237. [Google Scholar] [CrossRef]
- Bradshaw, S.L.; Benson, C.; Scalia, J. Cation exchange during subgrade hydration and effect on hydraulic conductivity of geosynthetic clay liners. J. Geotech. Geoenviron. Eng. 2013, 139, 526–538. [Google Scholar] [CrossRef]
- Shackelford, C.D.; Benson, C.H.; Katsumi, T.; Edil, T.B.; Lin, L. Evaluating the hydraulic conductivity of GCLs permeated with non-standard liquids. Geotext. Geomembr. 2000, 18, 133–161. [Google Scholar] [CrossRef]
- Petrov, R.J.; Rowe, R.K. Geosynthetic clay liner (GCL)-chemical compatibility by hydraulic conductivity testing and factors impacting its performance. Can. Geotech. J. 1997, 34, 863–885. [Google Scholar] [CrossRef]
- Acikel, A.S.; Gates, W.P.; Singh, R.M.; Bouazza, A.; Fredlund, D.G.; Rowe, R.K. Time-dependent unsaturated behaviour of geosynthetic clay liners. Can. Geotech. J. 2018, 55, 1824–1836. [Google Scholar] [CrossRef]
- Zhou, H.; Fang, H.; Zhang, Q.; Wang, Q.; Chen, C.; Mooney, S.; Peng, X.; Du, Z. Biochar enhances soil hydraulic function but not soil aggregation in a sandy loam. Eur. J. Soil Sci. 2019, 70, 291–300. [Google Scholar] [CrossRef]
- Ankenbauer, K.J.; Loheide, S.P. The effects of soil organic matter on soil water retention and plant water use in a meadow of the Sierra Nevada, CA. Hydrol. Process. 2017, 31, 891–901. [Google Scholar] [CrossRef]
- Blanco-Canqui, H.; Hergert, G.W.; Nielsen, R.A. Cattle manure application reduces soil compactibility and increases water retention after 71 years. Soil Sci. Soc. Am. J. 2015, 79, 212–223. [Google Scholar] [CrossRef]
- Hudson, B.D. Soil organic matter and available water capacity. J. Soil Water Conserv. 1994, 49, 189–194. [Google Scholar]
- Arriaga, F.J.; Lowery, B. Soil physical properties and crop productivity of an eroded soil amended with cattle manure. Soil Sci. 2003, 168, 888–899. [Google Scholar] [CrossRef]
- Asada, K.; Yabushita, Y.; Saito, H.; Nishimura, T. Effect of long-term swine-manure application on soil hydraulic properties and heavy metal behaviour. Eur. J. Soil Sci. 2012, 63, 368–376. [Google Scholar] [CrossRef]
- Yang, X.; Li, P.; Zhang, S.; Sun, B.; Xinping, C. Long-term-fertilization effects on soil organic carbon, physical properties, and wheat yield of a loess soil. J. Plant Nutr. Soil Sci. 2011, 174, 775–784. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, X.; Wiss, M.; Grip, H.; Lövdahl, L. Changes in physical properties of a loess soil in China following two long-term fertilization regimes. Geoderma 2006, 136, 579–587. [Google Scholar] [CrossRef]
- Sommerfeldt, T.; Chang, C. Soil-water properties as affected by twelve annual applications of cattle feedlot manure. Soil Sci. Soc. Am. J. 1987, 51, 7–9. [Google Scholar] [CrossRef]
- Obi, M.; Ebo, P. The effects of organic and inorganic amendments on soil physical properties and maize production in a severely degraded sandy soil in southern Nigeria. Bioresour. Technol. 1995, 51, 117–123. [Google Scholar] [CrossRef]
- Rawls, W.; Pachepsky, Y.A.; Ritchie, J.; Sobecki, T.; Bloodworth, H. Effect of soil organic carbon on soil water retention. Geoderma 2003, 116, 61–76. [Google Scholar] [CrossRef]
- Bauer, A.; Black, A. Organic carbon effects on available water capacity of three soil textural groups. Soil Sci. Soc. Am. J. 1992, 56, 248–254. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A. Limited effect of organic matter on soil available water capacity. Eur. J. Soil Sci. 2018, 69, 39–47. [Google Scholar] [CrossRef]
- Chen, D.; Rolston, D.E. Coupling diazinon volatilization and water evaporation in unsaturated soils: II. Diazinon transport. Soil Sci. 2000, 165, 690–698. [Google Scholar] [CrossRef]
- Jackson, R.D. Water vapor diffusion in relatively dry soil: I. Theoretical considerations and sorption experiments. Soil Sci. Soc. Am. J. 1964, 28, 172–176. [Google Scholar] [CrossRef]
- Arthur, E.; Tuller, M.; Moldrup, P.; De Jonge, L. Effects of biochar and manure amendments on water vapor sorption in a sandy loam soil. Geoderma 2015, 243, 175–182. [Google Scholar] [CrossRef]
- Arthur, E.; Tuller, M.; Moldrup, P.; Greve, M.; Knadel, M.; de Jonge, L. Applicability of the Guggenheim–Anderson–Boer water vapour sorption model for estimation of soil specific surface area. Eur. J. Soil Sci. 2018, 69, 245–255. [Google Scholar] [CrossRef]
- Chen, C.; Hu, K.; Arthur, E.; Ren, T. Modeling soil water retention curves in the dry range using the hygroscopic water content. Vadose Zone J. 2014, 13, 1–7. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, C.; Wang, D.; Arthur, E.; Zhang, Z.; Guo, Z.; Peng, X.; Mooney, S.J. Effect of long-term organic amendments on the full-range soil water retention characteristics of a Vertisol. Soil Tillage Res. 2020, 202, 104663. [Google Scholar] [CrossRef]
- Sun, F.; Lu, S. Biochars improve aggregate stability, water retention, and pore-space properties of clayey soil. J. Plant Nutr. Soil Sci. 2014, 177, 26–33. [Google Scholar] [CrossRef]
- Hati, K.; Biswas, A.; Bandyopadhyay, K.; Misra, A. Soil properties and crop yields on a vertisol in India with application of distillery effluent. Soil Tillage Res. 2007, 92, 60–68. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, X.; Gao, X.; Zhang, S.; Wu, P. The Effects of Long-term Fertiliser Applications on Soil Organic Carbon and Hydraulic Properties of a Loess Soil in China. Land Degrad. Dev. 2016, 27, 60–67. [Google Scholar] [CrossRef]
- Nong, X.F.; Rahardjo, H.; Lee, D.T.T.; Leong, E.C.; Fong, Y.K. Effects of organic content on soil-water characteristic curve and soil shrinkage. Environ. Geotech. 2019, 8, 442–451. [Google Scholar] [CrossRef]
- Verheijen, F.; Jeffery, S.; Bastos, A.; Van der Velde, M.; Diafas, I. Biochar Application to Soils—A Critical Scientific Review of Effects on Soil Properties, Processes and Functions; European Commission: Brussels, Belgium, 2010; Volume 24099, p. 162. [Google Scholar]
- Joseph, S.; Peacocke, C.; Lehmann, J.; Munroe, P. Developing a biochar classification and test methods. Biochar Environ. Manag. Sci. Technol. 2009, 1, 107–126. [Google Scholar]
- Uzoma, K.; Inoue, M.; Andry, H.; Zahoor, A.; Nishihara, E. Influence of biochar application on sandy soil hydraulic properties and nutrient retention. J. Food Agric. Environ. 2011, 9, 1137–1143. [Google Scholar]
- Suliman, W.; Harsh, J.B.; Abu-Lail, N.I.; Fortuna, A.-M.; Dallmeyer, I.; Garcia-Pérez, M. The role of biochar porosity and surface functionality in augmenting hydrologic properties of a sandy soil. Sci. Total Environ. 2017, 574, 139–147. [Google Scholar] [CrossRef] [PubMed]
- Moragues-Saitua, L.; Arias-González, A.; Gartzia-Bengoetxea, N. Effects of biochar and wood ash on soil hydraulic properties: A field experiment involving contrasting temperate soils. Geoderma 2017, 305, 144–152. [Google Scholar] [CrossRef]
- Du, Z.; Chen, X.; Qi, X.; Li, Z.; Nan, J.; Deng, J. The effects of biochar and hoggery biogas slurry on fluvo-aquic soil physical and hydraulic properties: A field study of four consecutive wheat–maize rotations. J. Soils Sediments 2016, 16, 2050–2058. [Google Scholar] [CrossRef]
- Ojeda, G.; Mattana, S.; Àvila, A.; Alcañiz, J.M.; Volkmann, M.; Bachmann, J. Are soil–water functions affected by biochar application? Geoderma 2015, 249, 1–11. [Google Scholar] [CrossRef]
- Jeffery, S.; Meinders, M.B.; Stoof, C.R.; Bezemer, T.M.; van de Voorde, T.F.; Mommer, L.; van Groenigen, J.W. Biochar application does not improve the soil hydrological function of a sandy soil. Geoderma 2015, 251, 47–54. [Google Scholar] [CrossRef]
- Bordoloi, S.; Garg, A.; Sreedeep, S.; Lin, P.; Mei, G. Investigation of cracking and water availability of soil-biochar composite synthesized from invasive weed water hyacinth. Bioresour. Technol. 2018, 263, 665–677. [Google Scholar] [CrossRef]
- Wong, J.T.F.; Chen, Z.; Chen, X.; Ng, C.W.W.; Wong, M.H. Soil-water retention behavior of compacted biochar-amended clay: A novel landfill final cover material. J. Soils Sediments 2017, 17, 590–598. [Google Scholar] [CrossRef]
- Hussain, R.; Ravi, K.; Garg, A. Influence of biochar on the soil water retention characteristics (SWRC): Potential application in geotechnical engineering structures. Soil Tillage Res. 2020, 204, 104713. [Google Scholar] [CrossRef]
- Ahamad, A.; Raju, N.J.; Madhav, S.; Gossel, W.; Wycisk, P. Impact of non-engineered Bhalswa landfill on groundwater from Quaternary alluvium in Yamuna flood plain and potential human health risk, New Delhi, India. Quat. Int. 2019, 507, 352–369. [Google Scholar] [CrossRef]
- Reddy, K.R.; Hettiarachchi, H.; Giri, R.K.; Gangathulasi, J. Effects of degradation on geotechnical properties of municipal solid waste from Orchard Hills Landfill, USA. Int. J. Geosynth. Ground Eng. 2015, 1, 24. [Google Scholar] [CrossRef]
- Swati, M.; Joseph, K. Settlement analysis of fresh and partially stabilised municipal solid waste in simulated controlled dumps and bioreactor landfills. Waste Manag. 2008, 28, 1355–1363. [Google Scholar] [CrossRef] [PubMed]
- Dubey, A.A.; Borthakur, A.; Ravi, K. Investigation of Soil Suction Characteristics Induced by the Degradation of Organic Matter. Geotech. Geol. Eng. 2021, 40, 2371–2378. [Google Scholar] [CrossRef]
- Aldaood, A.; Bouasker, M.; Al-Mukhtar, M. Soil–Water Characteristic Curve of Gypseous Soil. Geotech. Geol. Eng. 2015, 33, 123–135. [Google Scholar] [CrossRef]
- Moret-Fernández, D.; Herrero, J. Effect of gypsum content on soil water retention. J. Hydrol. 2015, 528, 122–126. [Google Scholar] [CrossRef]
- Alzaidy, M. Effect of gypsum content on unsaturated engineering properties of clayey soil. Int. J. Eng. 2020, 9, 84–91. [Google Scholar] [CrossRef]
- Al-Mukhtar, M.; Lasledj, A.; Alcover, J.-F. Behaviour and mineralogy changes in lime-treated expansive soil at 20 °C. Appl. Clay Sci. 2010, 50, 191–198. [Google Scholar] [CrossRef]
- Boardman, D.; Glendinning, S.; Rogers, C. Development of stabilisation and solidification in lime–clay mixes. Geotechnique 2001, 51, 533–543. [Google Scholar] [CrossRef]
- Consoli, N.C.; da Silva Lopes Jr, L.; Heineck, K.S. Key parameters for the strength control of lime stabilized soils. J. Mater. Civ. Eng. 2009, 21, 210–216. [Google Scholar] [CrossRef]
- Russo, G. Water retention curves of lime stabilised soils. In Advanced Experimental Unsaturated Soil Mechanics: Proceedings of the International Symposium on Advanced Experimental Unsaturated Soil Mechanics, Trento, Italy, 27–29 June 2005; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Tang, A.M.; Vu, M.; Cui, Y.-J. Effects of the maximum soil aggregates size and cyclic wetting–drying on the stiffness of a lime-treated clayey soil. Géotechnique 2011, 61, 421–429. [Google Scholar] [CrossRef]
- Tran, T.D.; Cui, Y.-J.; Tang, A.M.; Audiguier, M.; Cojean, R. Effects of lime treatment on the microstructure and hydraulic conductivity of Héricourt clay. J. Rock Mech. Geotech. Eng. 2014, 6, 399–404. [Google Scholar] [CrossRef]
- Romero, E.; Della Vecchia, G.; Jommi, C. An insight into the water retention properties of compacted clayey soils. Géotechnique 2011, 61, 313–328. [Google Scholar] [CrossRef]
- Mavroulidou, M.; Zhang, X.; Gunn, M.J.; Cabarkapa, Z. Water Retention and Compressibility of a Lime-Treated, High Plasticity Clay. Geotech. Geol. Eng. 2013, 31, 1171–1185. [Google Scholar] [CrossRef]
- Khattab, S.; Al-Mukhtar, M.; Fleureau, J.-M. Long-term stability characteristics of a lime-treated plastic soil. J. Mater. Civ. Eng. 2007, 19, 358–366. [Google Scholar] [CrossRef]
- Tedesco, D.; Russo, G. Time dependency of the water retention properties of a lime stabilised compacted soil. In Unsaturated Soils. Advances in Geo-Engineering, Proceedings of the 1st European Conference on Unsaturated Soils, Durham, UK, 2–4 July 2008; CRC Press: London, UK, 2008; pp. 277–282. [Google Scholar]
- Khattab, S.; Al-Taie, L.K.I. Soil-water characteristic curves (SWCC) for lime treated expansive soil from Mosul City. In Unsaturated Soils, Proceedings of the Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2–6 April 2006; ASCE: Reston, VA, USA, 2006; pp. 1671–1682. [Google Scholar]
- El-Rawi, N.M.; Awad, A.A. Permeability of lime stabilized soils. Transp. Eng. J. ASCE 1981, 107, 25–35. [Google Scholar] [CrossRef]
- Nalbantoglu, Z.; Tuncer, E.R. Compressibility and hydraulic conductivity of a chemically treated expansive clay. Can. Geotech. J. 2001, 38, 154–160. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, Y.J.; Tang, A.M.; Benahmed, N. Aggregate size effect on the water retention properties of a lime-treated compacted silt during curing. E3S Web Conf. 2016, 9, 11013. [Google Scholar] [CrossRef]
- Cui, Y.-J.; Tang, A.M.; Loiseau, C.; Delage, P. Determining the unsaturated hydraulic conductivity of a compacted sand–bentonite mixture under constant-volume and free-swell conditions. Phys. Chem. Earth Parts ABC 2008, 33, S462–S471. [Google Scholar] [CrossRef]
- Della Vecchia, G.; Dieudonné, A.-C.; Jommi, C.; Charlier, R. Accounting for evolving pore size distribution in water retention models for compacted clays: Evolving pore size distribution in water retention modelling. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 702–723. [Google Scholar] [CrossRef]
- Aldaood, A.; Bouasker, M.; Al-Mukhtar, M. Soil–water characteristic curve of lime treated gypseous soil. Appl. Clay Sci. 2014, 102, 128–138. [Google Scholar] [CrossRef]
- Beck, K.; Rozenbaum, O.; Al-Mukhtar, M.; Plançon, A. Multi-scale characterization of monument limestones. arXiv 2006, arXiv:physics/0609111. [Google Scholar]
- Ying, Z.; Cui, Y.-J.; Benahmed, N.; Duc, M. Investigating the salinity effect on water retention property and microstructure changes along water retention curves for lime-treated soil. Constr. Build. Mater. 2021, 303, 124564. [Google Scholar] [CrossRef]
- Cuisinier, O.; Masrouri, F.; Stoltz, G.; Russo, G. Multi-scale analysis of the swelling and shrinkage of a lime-treated expansive clayey soil. In Unsaturated Soils: Research & Applications; CRC Press: Boca Raton, FL, USA, 2014; pp. 441–447. [Google Scholar]
- Al-Mahbashi, A.M.; Elkady, T.Y.; Alrefeai, T.O. Soil water characteristic curve and improvement in lime treated expansive soil. Geomech. Eng. 2015, 8, 687–706. [Google Scholar] [CrossRef]
- Sun, B.; Ren, F.; Ding, W.; Zhang, G.; Huang, J.; Li, J.; Zhang, L. Effects of freeze-thaw on soil properties and water erosion. Soil Water Res. 2021, 16, 205–216. [Google Scholar] [CrossRef]
- Kværnø, S.H.; Øygarden, L. The influence of freeze–thaw cycles and soil moisture on aggregate stability of three soils in Norway. Catena 2006, 67, 175–182. [Google Scholar] [CrossRef]
- Six, J.; Bossuyt, H.; Degryze, S.; Denef, K. A history of research on the link between (micro) aggregates, soil biota, and soil organic matter dynamics. Soil Tillage Res. 2004, 79, 7–31. [Google Scholar] [CrossRef]
- Ding, L.Q.; Han, Z.; Zou, W.L.; Wang, X.Q. Characterizing hydro-mechanical behaviours of compacted subgrade soils considering effects of freeze-thaw cycles. Transp. Geotech. 2020, 24, 100392. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, K.; Jabro, J.; Ren, L.; Liu, H. Freeze–thaw cycles effects on soil physical properties under different degraded conditions in Northeast China. Environ. Earth Sci. 2019, 78, 321. [Google Scholar] [CrossRef]
- Fu, Q.; Zhao, H.; Li, H.; Li, T.; Hou, R.; Liu, D.; Ji, Y.; Gao, Y.; Yu, P. Effects of biochar application during different periods on soil structures and water retention in seasonally frozen soil areas. Sci. Total Environ. 2019, 694, 133732. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Luo, S.; Qian, J.; Li, J.; Xiao, H. Soil-Water Characteristics of the Low Liquid Limit Silt considering Compaction and Freeze-Thaw Action. Adv. Civ. Eng. 2020, 2020, 8823666. [Google Scholar] [CrossRef]
- Ferrari, A.; Favero, V.; Marschall, P.; Laloui, L. Experimental analysis of the water retention behaviour of shales. Int. J. Rock Mech. Min. Sci. 2014, 72, 61–70. [Google Scholar] [CrossRef]
- Gimmi, T.; Churakov, S.V. Water retention and diffusion in unsaturated clays: Connecting atomistic and pore scale simulations. Appl. Clay Sci. 2019, 175, 169–183. [Google Scholar] [CrossRef]
- Menaceur, H.; Delage, P.; Tang, A.M.; Talandier, J. The Status of Water in Swelling Shales: An Insight from the Water Retention Properties of the Callovo-Oxfordian Claystone. Rock Mech. Rock Eng. 2016, 49, 4571–4586. [Google Scholar] [CrossRef]
- Middelhoff, M.; Cuisinier, O.; Masrouri, F.; Talandier, J. Hydro-mechanical path dependency of claystone/bentonite mixture samples characterized by different initial dry densities. Acta Geotech. 2021, 16, 3161–3176. [Google Scholar] [CrossRef]
- Savoye, S.; Page, J.; Puente, C.; Imbert, C.; Coelho, D. New experimental approach for studying diffusion through an intact and unsaturated medium: A case study with Callovo-Oxfordian argillite. Environ. Sci. Technol. 2010, 44, 3698–3704. [Google Scholar] [CrossRef]
- Savoye, S.; Beaucaire, C.; Fayette, A.; Herbette, M.; Coelho, D. Mobility of cesium through the callovo-oxfordian claystones under partially saturated conditions. Environ. Sci. Technol. 2012, 46, 2633–2641. [Google Scholar] [CrossRef]
- Savoye, S.; Imbert, C.; Fayette, A.; Coelho, D. Experimental study on diffusion of tritiated water and anions under variable water-saturation and clay mineral content: Comparison with the Callovo-Oxfordian claystones. Geol. Soc. Lond. Spec. Publ. 2014, 400, 579–588. [Google Scholar] [CrossRef]
- Savoye, S.; Lefevre, S.; Fayette, A.; Robinet, J.-C. Effect of water saturation on the diffusion/adsorption of 22Na and cesium onto the Callovo-Oxfordian claystones. Geofluids 2017, 2017, 1683979. [Google Scholar] [CrossRef]
- Wan, M.; Delage, P.; Tang, A.M.; Talandier, J. Water retention properties of the Callovo-Oxfordian claystone. Int. J. Rock Mech. Min. Sci. 2013, 64, 96–104. [Google Scholar] [CrossRef]
- Boulin, P.F.; Angulo-Jaramillo, R.; Daian, J.-F.; Talandier, J.; Berne, P. Pore gas connectivity analysis in Callovo-Oxfordian argillite. Appl. Clay Sci. 2008, 42, 276–283. [Google Scholar] [CrossRef]
- Zhang, C.-L.; Rothfuchs, T.; Su, K.; Hoteit, N. Experimental study of the thermo-hydro-mechanical behaviour of indurated clays. Clay Nat. Eng. Barriers Radioact. Waste Confin.-Part 2 2007, 32, 957–965. [Google Scholar] [CrossRef]
- M’Jahad, S.; Davy, C.A.; Skoczylas, F.; Talandier, J. Characterization of transport and water retention properties of damaged Callovo-Oxfordian claystone. Geol. Soc. Lond. Spec. Publ. 2017, 443, 159–177. [Google Scholar] [CrossRef]
- Muñoz, J.J. Thermo-Hydro-Mechanical Analysis of Soft Rock. Application to a Large Scale Heating Test and Large Scale Ventilation Test; Universitat Politècnica de Catalunya: Barcelona, Spain, 2007; ISBN 84-690-7124-6. [Google Scholar]
- Villar, M.; Romero, F. Opalinus clay 2-phase flow parameters. FORGE Rep. D 2013, 5, 14. [Google Scholar]
- Romero, E.; Senger, R.; Marschall, P. Air Injection Laboratory Experiments on Opalinus Clay. Experimental Techniques, Results and Analyses; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2012; p. cp-275. [Google Scholar]
- da Silva, M.R.; Schroeder, C.; Verbrugge, J.-C. Unsaturated rock mechanics applied to a low-porosity shale. Eng. Geol. 2008, 97, 42–52. [Google Scholar] [CrossRef]
- Nuth, M.; Laloui, L. Advances in modelling hysteretic water retention curve in deformable soils. Comput. Geotech. 2008, 35, 835–844. [Google Scholar] [CrossRef]
- Jotisankasa, A. Collapse Behaviour of a Compacted Silty Clay. Ph.D. Dissertation, University of London, London, UK, 2005. [Google Scholar]
- Indrawan, I.; Rahardjo, H.; Leong, E.C. Effects of coarse-grained materials on properties of residual soil. Eng. Geol. 2006, 82, 154–164. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; D’Amore, G.A.R.; Leong, E.-C. Soil–water characteristic curves of gap-graded soils. Eng. Geol. 2012, 125, 102–107. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, Y.; Zhou, H.; Feng, X.; Huang, Z. Effects of void ratio and grain size distribution on water retention properties of compacted infilled joint soils. Soils Found. 2017, 57, 50–59. [Google Scholar] [CrossRef]
- Chen, X.; Hu, K.; Chen, J.; Zhao, W. Laboratory Investigation of the Effect of Initial Dry Density and Grain Size Distribution on Soil–Water Characteristic Curves of Wide-Grading Gravelly Soil. Geotech. Geol. Eng. 2017, 36, 885–896. [Google Scholar] [CrossRef]
- Marinho, F.; Chandler, R. Aspects of the Behavior of Clays on Drying; ASCE: Reston, VA, USA, 1993; pp. 77–90. [Google Scholar]
- Zapata, C.E.; Houston, W.N.; Houston, S.L.; Walsh, K.D. Soil–water characteristic curve variability. In Advances in Unsaturated Geotechnics; ASCE: Reston, VA, USA, 2000; pp. 84–124. [Google Scholar]
- Malaya, C.; Sreedeep, S. Critical Review on the Parameters Influencing Soil-Water Characteristic Curve. J. Irrig. Drain. Eng. 2012, 138, 55–62. [Google Scholar] [CrossRef]
- Chahal, R. Effect of temperature and trapped air on the energy status of water in porous media. Soil Sci. 1964, 98, 107–112. [Google Scholar] [CrossRef]
- Chahal, R. Effect to temperature and trapped air on matric suction. Soil Sci. 1965, 100, 262–266. [Google Scholar] [CrossRef]
- Haridasan, M.; Jensen, R. Effect of temperature on pressure head-water content relationship and conductivity of two soils. Soil Sci. Soc. Am. J. 1972, 36, 703–708. [Google Scholar] [CrossRef]
- Hopmans, J.; Dane, J. Effect of temperature-dependent hydraulic properties on soil water movement. Soil Sci. Soc. Am. J. 1985, 49, 51–58. [Google Scholar] [CrossRef]
- Shao, M.; Horton, R. Integral method for estimating soil hydraulic properties. Soil Sci. Soc. Am. J. 1998, 62, 585–592. [Google Scholar] [CrossRef]
- Li, P.; Li, T.; Wang, H.; Liang, Y. Soil-water characteristic curve and permeability perdiction on Childs & Collis-Geroge model of unsaturated loess. Rock Soil Mech. 2013, 34, 184–189. [Google Scholar]
- Luo, P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.; Fukushi, K. Historical assessment of Chinese and Japanese flood management policies and implications for managing future floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar] [CrossRef]
- Luo, P.; He, B.; Duan, W.; Takara, K.; Nover, D. Impact assessment of rainfall scenarios and land-use change on hydrologic response using synthetic Area IDF curves. J. Flood Risk Manag. 2018, 11, S84–S97. [Google Scholar] [CrossRef]
- Luo, P.; Mu, D.; Xue, H.; Ngo-Duc, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 2018, 8, 12623. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; Zhou, M.; Deng, H.; Lyu, J.; Cao, W.; Takara, K.; Nover, D.; Schladow, S.G. Impact of forest maintenance on water shortages: Hydrologic modeling and effects of climate change. Sci. Total Environ. 2018, 615, 1355–1363. [Google Scholar] [CrossRef] [PubMed]
- Ghavam-Nasiri, A.; El-Zein, A.; Airey, D.; Rowe, R.K. Water retention of geosynthetics clay liners: Dependence on void ratio and temperature. Geotext. Geomembr. 2019, 47, 255–268. [Google Scholar] [CrossRef]
- Adriano, D.; Page, A.; Elseewi, A.; Chang, A.; Straughan, I. Utilization and disposal of fly ash and other coal residues in terrestrial ecosystems: A review. J. Environ. Qual. 1980, 9, 333–344. [Google Scholar] [CrossRef]
- Aitken, R.; Campbell, D.; Bell, L. Properties of Australian fly ashes relevant to their agronomic utilization. Soil Res. 1984, 22, 443–453. [Google Scholar] [CrossRef]
- Gangloff, W.; Ghodrati, M.; Sims, J.; Vasilas, B. Impact of fly ash amendment and incorporation method on hydraulic properties of a sandy soil. Water. Air. Soil Pollut. 2000, 119, 231–245. [Google Scholar] [CrossRef]
- Pathan, S.; Aylmore, L.; Colmer, T. Properties of several fly ash materials in relation to use as soil amendments. J. Environ. Qual. 2003, 32, 687–693. [Google Scholar] [CrossRef]
- Kalra, N.; Jain, M.; Joshi, H.; Choudhary, R.; Harit, R.; Vatsa, B.; Sharma, S.; Kumar, V. Flyash as a soil conditioner and fertilizer. Bioresour. Technol. 1998, 64, 163–167. [Google Scholar] [CrossRef]
- Sharma, P.; Carter, F.; Halvorson, G. Water retention by soils containing coal. Soil Sci. Soc. Am. J. 1993, 57, 311–316. [Google Scholar] [CrossRef]
- Aggelides, S.; Londra, P. Effects of compost produced from town wastes and sewage sludge on the physical properties of a loamy and a clay soil. Bioresour. Technol. 2000, 71, 253–259. [Google Scholar] [CrossRef]
- Al-Darby, A.; El-Shafei, Y.; Shalaby, A.; Mursi, M. Influence of a gel-forming conditioner on water retention, infiltration capacity, and water distribution in uniform and stratified sandy soils. Arid Land Res. Manag. 1992, 6, 145–161. [Google Scholar] [CrossRef]
- Hoyos, L.; Thudi, H.; Puppala, A. Soil-water retention properties of cement treated clay. In Problematic Soils and Rocks and In Situ Characterization; ASCE: Reston, VA, USA, 2007; pp. 1–8. [Google Scholar]
- Wang, Y.; Cui, Y.J.; Tang, A.M.; Tang, C.S.; Benahmed, N. Effects of aggregate size on water retention capacity and microstructure of lime-treated silty soil. Géotech. Lett. 2015, 5, 269–274. [Google Scholar] [CrossRef]
- Suganya, S. Moisture retention and cation exchange capacity of sandy soil as influenced by soil additives. J. Appl. Sci. Res. 2006, 2, 949–951. [Google Scholar]
- Epstein, E.; Taylor, J.; Chaney, R. Effects of Sewage Sludge and Sludge Compost Applied to Soil on Some Soil Physical and Chemical Properties. J. Environ. Qual. 1976, 5, 422–426. [Google Scholar] [CrossRef]
- Głąb, T.; Gondek, K. Effect of organic amendments on water retention characteristic of Stagnic Gleysol soil. Pol. J. Soil Sci. 2009, 42, 111–120. [Google Scholar]
- Gupta, S.C.; Dowdy, R.; Larson, W. Hydraulic and thermal properties of a sandy soil as influenced by incorporation of sewage sludge. Soil Sci. Soc. Am. J. 1977, 41, 601–605. [Google Scholar] [CrossRef]
- Illera, V.; Cala, V.; Walter, I.; Cuevas, G. Biosolid and municipal solid waste effects on physical and chemical properties of a degraded soil [Spain]. Agrochim 1999, 43, 178–186. [Google Scholar]
- Joshua, W.; Michalk, D.; Curtis, I.; Salt, M.; Osborne, G. The potential for contamination of soil and surface waters from sewage sludge (biosolids) in a sheep grazing study, Australia. Geoderma 1998, 84, 135–156. [Google Scholar] [CrossRef]
- Kladivko, E.; Nelson, D. Changes in soil properties from application of anaerobic sludge. J. Water Pollut. Control Fed. 1979, 51, 325–332. [Google Scholar]
- Kumar, S.; Malik, R.; Dahiya, I. Influence of different organic wastes upon water retention, transmission and contact characteristics of a sandy soil. Soil Res. 1985, 23, 131–136. [Google Scholar] [CrossRef]
- Morel, J.; Guckert, A.; Sedogo, M. Effects de l’epandage des boues residuaires urbaines sur l’etat physic du sol. In Proceedings of the 11th Congress of Int. Society of Soil Sciences, Edmonton, AB, Canada, 19–27 June 1978. [Google Scholar]
- Ojeda, G.; Mattana, S.; Alcañiz, J.; Marando, G.; Bonmatí, M.; Woche, S.; Bachmann, J. Wetting process and soil water retention of a minesoil amended with composted and thermally dried sludges. Geoderma 2010, 156, 399–409. [Google Scholar] [CrossRef]
- Tsadilas, C.; Mitsios, I.; Golia, E. Influence of biosolids application on some soil physical properties. Commun. Soil Sci. Plant Anal. 2005, 36, 709–716. [Google Scholar] [CrossRef]
- Agus, S.S.; Schanz, T.; Fredlund, D.G. Measurements of suction versus water content for bentonite–sand mixtures. Can. Geotech. J. 2010, 47, 583–594. [Google Scholar] [CrossRef]
- O’Sullivan, M.; Simota, C. Modelling the environmental impacts of soil compaction: A review. Soil Tillage Res. 1995, 35, 69–84. [Google Scholar] [CrossRef]
- Soane, B.; Van Ouwerkerk, C. Implications of soil compaction in crop production for the quality of the environment. Soil Tillage Res. 1995, 35, 5–22. [Google Scholar] [CrossRef]
- Horton, R.; Ankeny, M.; Allmaras, R. Effects of compaction on soil hydraulic properties. Dev. Agric. Eng. 1994, 11, 141–165. [Google Scholar]
- Ngo-Cong, D.; Antille, D.L.; van Genuchten, M.T.; Tekeste, M.Z.; Baillie, C.P. Predicting the hydraulic properties of compacted soils: Model validation. In Proceedings of the 2021 ASABE Annual International Virtual Meeting, Virtual, 12–16 July 2021; p. 1. [Google Scholar]
- Tian, Z.; Gao, W.; Kool, D.; Ren, T.; Horton, R.; Heitman, J.L. Approaches for estimating soil water retention curves at various bulk densities with the extended van Genuchten model. Water Resour. Res. 2018, 54, 5584–5601. [Google Scholar] [CrossRef]
- Hill, J.; Sumner, M. Effect of bulk density on moisture characteristics of soils. Soil Sci. 1967, 103, 234–238. [Google Scholar] [CrossRef]
- Smith, C.W.; Johnston, M.A.; Lorentz, S.A. The effect of soil compaction on the water retention characteristics of soils in forest plantations. South Afr. J. Plant Soil 2001, 18, 87–97. [Google Scholar] [CrossRef]
- Connolly, R.; Freebairn, D.; Bridge, B. Change in infiltration characteristics associated with cultivation history of soils in south-eastern Queensland. Soil Res. 1997, 35, 1341–1358. [Google Scholar] [CrossRef]
- Benson, C.; Daniel, D. Influence of clods on the hydraulic conductivity of compacted clay. J. Geotech. Eng. 1990, 116, 1231–1248. [Google Scholar] [CrossRef]
- Gao, L.; Luan, M.; Yang, Q. Experimental Study on Permeability of Unsaturated Remolded Clay”, EJGE, 13, Bund. 2008. Available online: https://r.search.yahoo.com/_ylt=AwrC3HxdDv5ilzQASgAnnIlQ;_ylu=Y29sbwNiZjEEcG9zAzEEdnRpZAMEc2VjA3Ny/RV=2/RE=1660845789/RO=10/RU=https%3a%2f%2fwww.researchgate.net%2fpublication%2f297129698_Experimental_study_on_permeability_of_unsaturated_remolded_clay/RK=2/RS=E13TlLiad4kO.xTzLuqZS_AL3Pg- (accessed on 1 August 2022).
- Yang, H.; Rahardjo, H.; Leong, E.-C.; Fredlund, D.G. Factors affecting drying and wetting soil-water characteristic curves of sandy soils. Can. Geotech. J. 2004, 41, 908–920. [Google Scholar] [CrossRef]
- Agus, S.S.; Schanz, T. Comparison of four methods for measuring total suction. Vadose Zone J. 2005, 4, 1087–1095. [Google Scholar] [CrossRef]
- Box, J.E.; Taylor, S. Influence of soil bulk density on matric potential. Soil Sci. Soc. Am. J. 1962, 26, 119–122. [Google Scholar] [CrossRef]
- Marinho, F.A.; Stuermer, M.M. The influence of the compaction energy on the SWCC of a residual soil. In Advances in Unsaturated Geotechnics; ASCE: Reston, VA, USA, 2000; pp. 125–141. [Google Scholar]
- Sreedeep, S.; Singh, D. A study to investigate the influence of soil properties on suction. J. Test. Eval. 2005, 33, 61–66. [Google Scholar] [CrossRef]
- Blatz, J.; Graham, J.; Chandler, N. Influence of suction on the strength and stiffness of compacted sand bentonite. Can. Geotech. J. 2002, 39, 1005–1015. [Google Scholar] [CrossRef]
- Swanson, D.; Barbour, S. The effects of loading on the moisture characteristic curve and permeability-suction relationship for unsaturated soils. In Proceedings of the Canadian Society for Civil Engineering Annual Conference; Canadian Society for Civil Engineering: Pointe Claire, QC, Canada, 1991; pp. 194–203. [Google Scholar]
- Veyera, G.; Martin, J. Composition, Density and Fabric Effects on Bulky Waste Capillary Retention Characteristics. In Role of the Unsaturated Zone in Radioactive and Hazardous Waste Disposal; Ann Arbor Science Publishers: Ann Arbor, MI, USA, 1983. [Google Scholar]
- Malaya, C.; Sreedeep, S. A study on the influence of measurement procedures on suction-water content relationship of a sandy soil. J. Test. Eval. 2010, 38, 691–699. [Google Scholar]
- Zhan, L.; Chen, P.; Ng, C.W.W. Effect of suction change on water content and total volume of an expansive clay. J. Zhejiang Univ.-Sci. A 2007, 8, 699–706. [Google Scholar] [CrossRef]
- Tuller, M.; Or, D. Water Retention And Characteristic Curve. In Encyclopedia of Soils in the Environment; Hillel, D., Ed.; Elsevier: Oxford, UK, 2005; pp. 278–289. [Google Scholar] [CrossRef]
- Baker, R.; Frydman, S. Unsaturated soil mechanics: Critical review of physical foundations. Eng. Geol. 2009, 106, 26–39. [Google Scholar] [CrossRef]
- Aubertin, M.; Mbonimpa, M.; Bussière, B.; Chapuis, R. A model to predict the water retention curve from basic geotechnical properties. Can. Geotech. J. 2003, 40, 1104–1122. [Google Scholar] [CrossRef]
- Jotisankasa, A.; Vathananukij, H.; Coop, M. Soil-water retention curves of some silty soils and their relations to fabrics. In Proceedings of the 4th Asia Pacific Conference on Unsaturated Soils, Newcastle, Australia, 23–25 November 2009; pp. 263–268. [Google Scholar]
- Liang, W.; Yan, R.; Xu, Y.; Zhang, Q.; Tian, H.; Wei, C. Swelling pressure of compacted expansive soil over a wide suction range. Appl. Clay Sci. 2021, 203, 106018. [Google Scholar] [CrossRef]
- Lee, I.-M.; Sung, S.-G.; Cho, G.-C. Effect of stress state on the unsaturated shear strength of a weathered granite. Can. Geotech. J. 2005, 42, 624–631. [Google Scholar] [CrossRef]
- Thu, T.M.; Rahardjo, H.; Leong, E.-C. Soil-water characteristic curve and consolidation behavior for a compacted silt. Can. Geotech. J. 2007, 44, 266–275. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Josa, A. A constitutive model for partially saturated soils. Géotechnique 1990, 40, 405–430. [Google Scholar] [CrossRef]
- Gens, A.; Alonso, E. A framework for the behaviour of unsaturated expansive clays. Can. Geotech. J. 1992, 29, 1013–1032. [Google Scholar] [CrossRef]
- Elkady, T.Y.; Al-Mahbashi, A.M.; Al-Refeai, T.O. Stress-dependent soil-water characteristic curves of lime-treated expansive clay. J. Mater. Civ. Eng. 2015, 27, 04014127. [Google Scholar] [CrossRef]
- Zhang, X.; Mavroulidou, M.; Gunn, M.J. A study of the water retention curve of lime-treated London Clay. Acta Geotech. 2017, 12, 23–45. [Google Scholar] [CrossRef]
- Pedarla, A.; Puppala, A.J.; Hoyos, L.R.; Vanapalli, S.K.; Zapata, C. SWRC modelling framework for evaluating volume change behavior of expansive soils. In Unsaturated Soils: Research and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 221–228. [Google Scholar]
- Tu, H.; Vanapalli, S.K. Prediction of the variation of swelling pressure and one-dimensional heave of expansive soils with respect to suction using the soil-water retention curve as a tool. Can. Geotech. J. 2016, 53, 1213–1234. [Google Scholar] [CrossRef]
- Khorshidi, M.; Lu, N. Determination of cation exchange capacity from soil water retention curve. J. Eng. 2017, 143, 6. [Google Scholar] [CrossRef]
- Haeri, S.M.; Garakani, A.A.; Roohparvar, H.R.; Desai, C.S.; Ghafouri, S.M.H.S.; Kouchesfahani, K.S. Testing and constitutive modeling of lime-stabilized collapsible loess. Exp. Investig. 2019, 19, 4. [Google Scholar]
- Zhang, F.; Zhao, C.; Lourenço, S.D.N.; Dong, S.; Jiang, Y. Factors affecting the soil–water retention curve of Chinese loess. Bull. Eng. Geol. Environ. 2021, 80, 717–729. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, M.A.; Han, X.; Liu, Z. Spatial variability of soil parameters of the van Genuchten model at a regional scale. CLEAN–Soil Air Water 2015, 43, 271–278. [Google Scholar] [CrossRef]
- Romero, E.; Simms, P.H. Microstructure investigation in unsaturated soils: A review with special attention to contribution of mercury intrusion porosimetry and environmental scanning electron microscopy. Geotech. Geol. Eng. 2008, 26, 705–727. [Google Scholar] [CrossRef]
- Tarantino, A. A water retention model for deformable soils. Géotechnique 2009, 59, 751–762. [Google Scholar] [CrossRef]
- Gallipoli, D.; Wheeler, S.J.; Karstunen, M. Modelling the variation of degree of saturation in a deformable unsaturated soil. Géotechnique 2003, 53, 105–112. [Google Scholar] [CrossRef]
- Gallipoli, D.; Bruno, A.W.; D’onza, F.; Mancuso, C. A bounding surface hysteretic water retention model for deformable soils. Géotechnique 2015, 65, 793–804. [Google Scholar] [CrossRef]
- Gallipoli, D. A hysteretic soil-water retention model accounting for cyclic variations of suction and void ratio. Geotechnique 2012, 62, 605–616. [Google Scholar] [CrossRef]
- Kawai, K.; Kato, S.; Karube, D. The model of water retention curve considering effects of void ratio. In Unsaturated Soils for Asia; CRC Press: Boca Raton, FL, USA, 2020; pp. 329–334. [Google Scholar]
- Qian, J.; Lin, Z.; Shi, Z. Soil-water retention curve model for fine-grained soils accounting for void ratio–dependent capillarity. Can. Geotech. J. 2022, 59, 498–509. [Google Scholar] [CrossRef]
- Dieudonne, A.-C.; Della Vecchia, G.; Charlier, R. Water retention model for compacted bentonites. Can. Geotech. J. 2017, 54, 915–925. [Google Scholar] [CrossRef]
- Chen, Y. Soil–water retention curves derived as a function of soil dry density. GeoHazards 2018, 1, 3–19. [Google Scholar] [CrossRef]
- Qiao, Y.; Tuttolomondo, A.; Lu, X.; Laloui, L.; Ding, W. A generalized water retention model with soil fabric evolution. Geomech. Energy Environ. 2021, 25, 5. [Google Scholar] [CrossRef]
- D’elia, B.; Picarelli, L.; Leroueil, S.; Vaunat, J. Geotechnical characterisation of slope movements in structurally complex clay soils and stiff jointed clays. Riv. Ital. Geotec. 1998, 32, 5–47. [Google Scholar]
- Feda, J. Physical models of soil behaviour. Eng. Geol. 2004, 72, 121–129. [Google Scholar] [CrossRef]
- Feng, W.; Li, S.-Q.; Gao, L.-X.; Zhang, Y. Study on relationship between microstructure and soil-water characteristics of remolded clay. Guangxi Daxue Xuebao Ziran Kexue Ban 2013, 38, 170–175. [Google Scholar]
- Li, P.; Li, T.; Vanapalli, S. Prediction of soil–water characteristic curve for Malan loess in Loess Plateau of China. J. Cent. South Univ. 2018, 25, 432–447. [Google Scholar] [CrossRef]
- Mu, Q.; Dong, H.; Liao, H.; Dang, Y.; Zhou, C. Water-retention curves of loess under wetting−drying cycles. Géotech. Lett. 2020, 10, 135–140. [Google Scholar] [CrossRef]
- Xie, X.; Li, P.; Hou, X.; Li, T.; Zhang, G. Microstructure of Compacted Loess and Its Influence on the Soil-Water Characteristic Curve. Adv. Mater. Sci. Eng. 2020, 2020, 3402607. [Google Scholar] [CrossRef]
- Guney, Y.; Sari, D.; Cetin, M.; Tuncan, M. Impact of cyclic wetting–drying on swelling behavior of lime-stabilized soil. Build. Environ. 2007, 42, 681–688. [Google Scholar] [CrossRef]
- Lemaire, K.; Deneele, D.; Bonnet, S.; Legret, M. Effects of lime and cement treatment on the physicochemical, microstructural and mechanical characteristics of a plastic silt. Eng. Geol. 2013, 166, 255–261. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Liu, S.; ShangGuan, Y.; Fu, H.; Ma, B.; Chen, H.; Yuan, X. Experimental investigation of the geotechnical properties and microstructure of lime-stabilized saline soils under freeze-thaw cycling. Cold Reg. Sci. Technol. 2019, 161, 32–42. [Google Scholar] [CrossRef]
- Locat, J.; Bérubé, M.-A.; Choquette, M. Laboratory investigations on the lime stabilization of sensitive clays: Shear strength development. Can. Geotech. J. 1990, 27, 294–304. [Google Scholar] [CrossRef]
- Russo, G.; Vecchio, S.D.; Mascolo, G. Microstructure of a lime stabilised compacted silt. In Experimental Unsaturated Soil Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 49–56. [Google Scholar]
- Russo, G.; Modoni, G. Fabric changes induced by lime addition on a compacted alluvial soil. Géotech. Lett. 2013, 3, 93–97. [Google Scholar] [CrossRef]
- Cuisinier, O.; Auriol, J.-C.; Le Borgne, T.; Deneele, D. Microstructure and hydraulic conductivity of a compacted lime-treated soil. Eng. Geol. 2011, 123, 187–193. [Google Scholar] [CrossRef]
- Wang, Y.; Duc, M.; Cui, Y.-J.; Tang, A.M.; Benahmed, N.; Sun, W.J.; Ye, W.M. Aggregate size effect on the development of cementitious compounds in a lime-treated soil during curing. Appl. Clay Sci. 2017, 136, 58–66. [Google Scholar] [CrossRef]
- Ying, Z.; Cui, Y.-J.; Benahmed, N.; Duc, M. Changes in microstructure and water retention property of a lime-treated saline soil during curing. Acta Geotech. 2022, 17, 319–326. [Google Scholar] [CrossRef]
- Cecconi, M.; Russo, G. Prediction of soil-water retention properties of a lime stabilised compacted silt. In Proceedings of the 1st European Conference, Durham, UK, 2–4 July 2008; CRC Press: London, UK, 2008; pp. 287–292. [Google Scholar]
- Wang, Y.; Cui, Y.-J.; Tang, A.M.; Tang, C.-S.; Benahmed, N. Changes in thermal conductivity, suction and microstructure of a compacted lime-treated silty soil during curing. Eng. Geol. 2016, 202, 114–121. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- De Lima, O.; Niwas, S. Estimation of hydraulic parameters of shaly sandstone aquifers from geoelectrical measurements. J. Hydrol. 2000, 235, 12–26. [Google Scholar] [CrossRef]
- Huntley, D. Relations between permeability and electrical resistivity in granular aquifers. Groundwater 1986, 24, 466–474. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Klein, K.A.; Fam, M.A. Soils and Waves; John Wiley & Sons: New York, NY, USA, 2001; ISBN 0-471-49058-X. [Google Scholar]
- Abu-Hassanein, Z.S.; Benson, C.H.; Blotz, L.R. Electrical resistivity of compacted clays. J. Geotech. Eng. 1996, 122, 397–406. [Google Scholar] [CrossRef]
- Kibria, G.; Hossain, M. Investigation of geotechnical parameters affecting electrical resistivity of compacted clays. J. Geotech. Geoenviron. Eng. 2012, 138, 1520–1529. [Google Scholar] [CrossRef]
- Bai, W.; Kong, L.; Guo, A. Effects of physical properties on electrical conductivity of compacted lateritic soil. J. Rock Mech. Geotech. Eng. 2013, 5, 406–411. [Google Scholar] [CrossRef]
- Cardoso, R.; Dias, A.S. Study of the electrical resistivity of compacted kaolin based on water potential. Eng. Geol. 2017, 226, 1–11. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice. In Unsaturated Soil Mechanics in Engineering Practice; John Wiley & Sons: New York, NY, USA, 2012; pp. 286–321. [Google Scholar]
- ASTM D1883-16; Standard Test Method for California Bearing Ratio (CBR) of Laboratory-Compacted Soils. ASTM International: West Conshohocken, PA, USA, 2016.
- Türkmen, M. Prediction of Water Retention Curves Using Neural Network. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2020. [Google Scholar]
- Toker, N.K.; Germaine, J.T.; Sjoblom, K.J.; Culligan, P.J. A new technique for rapid measurement of continuous soil moisture characteristic curves. Géotechnique 2004, 54, 179–186. [Google Scholar] [CrossRef]
- Toll, D.G. The behaviour of unsaturated soil. In Handbook of Tropical Residual Soils Engineering; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Gardner, R. A method of measuring the capillary tension of soil moisture over a wide moisture range. Soil Sci. 1937, 43, 277–284. [Google Scholar] [CrossRef]
- Ridley, A.M.; Burland, J.B. A new instrument for the measurement of soil moisture suction. Géotechnique 1993, 43, 321–324. [Google Scholar] [CrossRef]
- Al Haj, K.M.A.; Standing, J.R. Soil water retention curves representing two tropical clay soils from Sudan. Géotechnique 2016, 66, 71–84. [Google Scholar] [CrossRef]
- Hamblin, A.P. Filter-paper method for routine measurement of field water potential. J. Hydrol. 1981, 53, 355–360. [Google Scholar] [CrossRef]
- Chandler, R.J.; Gutierrez, C.I. The filter-paper method of suction measurement. Geotechnique 1986, 36, 265–268. [Google Scholar] [CrossRef]
- Kim, H.; Prezzi, M.; Salgado, R. Calibration of Whatman Grade 42 filter paper for soil suction measurement. Can. J. Soil Sci. 2016, 97, 93–98. [Google Scholar] [CrossRef][Green Version]
- Decagon Devices, Inc. WP4C Water Potential Meter; Meter Group, Inc.: Pullman, WA, USA, 2015. [Google Scholar]
- Hilf, J.W. An Investigation of Pore-Water Pressure in Compacted Cohesive Soils; University of Colorado at Boulder: Boulder, CO, USA, 1956; ISBN 1-08-354472-1. [Google Scholar]
- Murray, E.J.; Sivakumar, V. Unsaturated Soils: A Fundamental Interpretation of Soil Behaviour; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 1-4443-2504-3. [Google Scholar]
- Fredlund, D. Negative pore-water pressures in slope stability. In Proceedings of the Simposio Suramericano de Deslizamiento, Paipa, Colombia, 7–10 August 1989; Volume 1989, pp. 1–31. [Google Scholar]
- Bordoni, M.; Bittelli, M.; Valentino, R.; Chersich, S.; Meisina, C. Improving the estimation of complete field soil water characteristic curves through field monitoring data. J. Hydrol. 2017, 552, 283–305. [Google Scholar] [CrossRef]
- Bittelli, M. Measuring soil water content: A review. HortTechnology 2011, 21, 293–300. [Google Scholar] [CrossRef]
- Lourenço, S.D.N. Suction Measurements and Water Retention in Unsaturated Soils. Ph.D. Dissertation, Durham University, Durham, UK, 2008. [Google Scholar]
- Springman, S.M.; Thielen, A.; Kienzler, P.; Friedel, S. A long-term field study for the investigation of rainfall-induced landslides. Geotechnique 2013, 63, 1177–1193. [Google Scholar] [CrossRef]
- Bordoni, M.; Meisina, C.; Valentino, R.; Lu, N.; Bittelli, M.; Chersich, S. Hydrological factors affecting rainfall-induced shallow landslides: From the field monitoring to a simplified slope stability analysis. Eng. Geol. 2015, 193, 19–37. [Google Scholar] [CrossRef]
- Harris, J.; Davenport, F.; Lehane, B. Seasonal variations of soil suction profiles in the Perth metropolitan area. Aust. Geomech. J. 2013, 48, 65–73. [Google Scholar]
- Casagli, N.; Rinaldi, M.; Gargini, A.; Curini, A. Pore water pressure and stream bank stability: Results from a monitoring site on the Sieve River, Italy. Earth Surf. Process. Landf. 1999, 24, 1095–1114. [Google Scholar] [CrossRef]
- Mendes, J.; Toll, D.G.; Augarde, C.E.; Gallipoli, D. A system for field measurement of suction using high capacity tensiometers. In Proceedings of the 1st European Conference on Unsaturated Soils, Durham, UK, 2–4 July 2008; Augarde, C.E., Toll, D.G., Gallipoli, D., Wheeler, S.J., Eds.; CRC Press: London, UK, 2008; pp. 219–225. [Google Scholar]
- Tarantino, A.; Gallipoli, D.; Jommi, C.; Mendes, J.; Capotosto, A.; Amabile, A.; Pedrotti, M.; Pozzato, A.; Beneš, V.; Bottaro, F.; et al. Advances in the monitoring of geo-structure subjected to climate loading. In E-UNSAT 2016, Proceedings of the 3rd European Conference on Unsaturated Soils, Paris, France, 12–14 September 2016; Delage, P., Cui, Y.J., Ghabezloo, S., Pereira, J.M., Tang, A.M., Eds.; EDP Sciences: Les Ulis, France, 2016; Volume 9, p. 04001. [Google Scholar]
- Gottardi, G.; Gragnano, C.G.; Rocchi, I.; Bittelli, M. Assessing river embankment stability under transient seepage conditions. Procedia Eng. 2016, 158, 350–355. [Google Scholar] [CrossRef]
- Mojtahedi, F.F.; Ali, K.; Nazari, A.; Rezvani, S.; Khatami, A.; Ahmadi, N. Measurement of Moisture and Temperature Profiles in Different Layers of Soil. IFCEE 2018, 2018, 266–278. [Google Scholar]
- Yin, P.; Vanapalli, S.K. Model for predicting tensile strength of unsaturated cohesionless soils. Can. Geotech. J. 2018, 55, 1313–1333. [Google Scholar] [CrossRef]
- Alsherif, N.A.; McCartney, J.S. Thermal behaviour of unsaturated silt at high suction magnitudes. Géotechnique 2015, 65, 703–716. [Google Scholar] [CrossRef]
- Mahmoudabadi, V.; Ravichandran, N. Coupled geotechnical-climatic design procedure for drilled shaft subjected to axial load. Eng. Geol. 2020, 264, 7. [Google Scholar] [CrossRef]
- Shahrokhabadi, S.; Vahedifard, F.; Ghazanfari, E.; Foroutan, M. Earth pressure profiles in unsaturated soils under transient flow. Eng. Geol. 2019, 260, 8. [Google Scholar] [CrossRef]
- Alowaisy, A.; Yasufuku, N.; Ishikura, R.; Hatakeyama, M.; Kyono, S. Continuous pressurization method for a rapid determination of the soil water characteristics curve for remolded and undisturbed cohesionless soils. Soils Found. 2020, 60, 634–647. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Pachepsky, Y.A.; Rawls, W.J. Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics. J. Hydrol. 2001, 251, 123–150. [Google Scholar] [CrossRef]
- Rafraf, S.; Guellouz, L.; Guiras, H.; Bouhlila, R. A new model using dynamic contact angle to predict hysteretic soil water retention curve. Soil Sci. Soc. Am. J. 2016, 80, 1433–1442. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Application of fractal mathematics to soil water retention estimation. Soil Sci. Soc. Am. J. 1989, 53, 987–996. [Google Scholar] [CrossRef]
- Ghanbarian-Alavijeh, B.; Liaghat, A.; Huang, G.H.; Van Genuchten, M.T. Estimation of the van Genuchten soil water retention properties from soil textural data. Pedosphere 2010, 20, 456–465. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Z.; Weng, X.; Xie, Y. A new soil-water characteristic curve model for unsaturated loess based on wetting-induced pore deformation. Geofluids 2019, 2019, 1672418. [Google Scholar] [CrossRef]
- Tao, G.; Chen, Y.; Xiao, H.; Chen, Y.; Peng, W. Comparative analysis of soil-water characteristic curve in fractal and empirical models. Adv. Mater. Sci. Eng. 2020, 2020, 1970314. [Google Scholar] [CrossRef]
- Pham, K.; Kim, D.; Yoon, Y.; Choi, H. Analysis of neural network based pedotransfer function for predicting soil water characteristic curve. Geoderma 2019, 351, 92–102. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, W.; Chen, F. Bayesian approach for predicting soil-water characteristic curve from particle-size distribution data. Energies 2019, 12, 2992. [Google Scholar] [CrossRef]
- Madi, R.; de Rooij, G.H.; Mielenz, H.; Mai, J. Parametric soil water retention models: A critical evaluation of expressions for the full moisture range. Hydrol. Earth Syst. Sci. 2018, 22, 1193–1219. [Google Scholar] [CrossRef]
- Webb, S.W. A simple extension of two-phase characteristic curves to include the dry region. Water Resour. Res. 2000, 36, 1425–1430. [Google Scholar] [CrossRef]
- Silva, O.; Grifoll, J. A soil-water retention function that includes the hyper-dry region through the bet adsorption isotherm. Water Resour. Res. 2007, 43, W11420. [Google Scholar] [CrossRef]
- Nimmo, J.R. Comment on the treatment of residual water content in “A consistent set of parametric models for the twophase flow of immiscible fluids in the subsurface” by L. Luckner et al. Water Resour. Res. 1991, 27, 661–662. [Google Scholar] [CrossRef]
- Groenevelt, P.; Grant, C. A new model for the soil-water retention curve that solves the problem of residual water contents. Eur. J. Soil Sci. 2004, 55, 479–485. [Google Scholar] [CrossRef]
- Gee, G.W.; Campbell, M.D.; Campbell, G.S.; Campbell, J.H. Rapid measurement of low soil water potentials using a water activity meter. Soil Sci. Soc. Am. J. 1992, 56, 1068–1070. [Google Scholar] [CrossRef]
- Schneider, M.; Goss, K.U. Prediction of the water sorption isotherm in air dry soils. Geoderma 2012, 170, 64–69. [Google Scholar] [CrossRef]
- Iden, S.C.; Durner, W. Comment on “simple consistent models for water retention and hydraulic conductivity in the complete moisture range” by A. Peters Water Resour. Res. 2014, 50, 7530–7534. [Google Scholar] [CrossRef]
- Campbell, G.S. A simple method for determining unsaturated conductivity from moisture retention data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Ross, P.J.; Williams, J.; Bristow, K.L. Equation for extending water-retention curves to dryness. Soil Sci. Soc. Am. J. 1991, 55, 923–927. [Google Scholar] [CrossRef]
- Morel-Seytoux, H.J.; Nimmo, J.R. Soil water retention and maximum capillary drive from saturation to oven dryness. Water Resour. Res. 1999, 35, 2031–2041. [Google Scholar] [CrossRef]
- Zhang, Z.F. Soil water retention and relative permeability for conditions from oven-dry to full saturation. Vadose Zone J. 2011, 10, 1299–1308. [Google Scholar] [CrossRef]
- Peters, A. Simple consistent models for water retention and hydraulic conductivity in the complete moisture range. Water Resour. Res. 2013, 49, 6765–6780. [Google Scholar] [CrossRef]
- Dan, K.J.; Tuller, M.; de Jonge, L.W.; Arthur, E.; Moldrup, P. A new two-stage approach to predicting the soil water characteristic from saturation to oven-dryness. J. Hydrol. 2015, 521, 498–507. [Google Scholar]
- Rossi, C.; Nimmo, J.R. Modeling of soil water retention from saturation to oven dryness. Water Resour. Res. 1994, 30, 701–708. [Google Scholar] [CrossRef]
- Kosugi, K. General model for unsaturated hydraulic conductivity for soils with lognormal pore-size distribution. Soil Sci. Soc. Am. J. 1999, 63, 270–277. [Google Scholar] [CrossRef]
- Campbell, G.S.; Shiozawa, S. Prediction of hydraulic properties of soils using particle-size distribution and bulk density data. In Proceedings of the International Workshop on Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils, Riverside, CA, USA, 11–13 October 1992; pp. 317–328. [Google Scholar]
- Botula, Y.D.; Cornelis, W.M.; Baert, G.; Van Ranst, E. Evaluation of pedotransfer functions for predicting water retention of soils in Lower Congo (DR Congo). Agric. Water Manag. 2012, 111, 1–10. [Google Scholar] [CrossRef]
- Silva, A.C.; Armindo, R.A.; Brito, A.; Schaap, M.G. An assessment of pedotransfer function performance for the estimation of spatial variability of key soil hydraulic properties. Vadose Zone J. 2017, 16, 1–10. [Google Scholar] [CrossRef]
- Van den Berg, M.; Klamt, E.; Van Reeuwijk, L.; Sombroek, W. Pedotransfer functions for the estimation of moisture retention characteristics of Ferralsols and related soils. Geoderma 1997, 78, 161–180. [Google Scholar] [CrossRef]
- Tomasella, J.; Hodnett, M.G. Estimating soil water retention characteristics from limited data in Brazilian Amazonia. Soil Sci. 1998, 163, 190–202. [Google Scholar] [CrossRef]
- Tomasella, J.; Hodnett, M.G.; Rossato, L. Pedotransfer functions for the estimation of soil water retention in Brazilian soils. Soil Sci. Soc. Am. J. 2000, 64, 327–338. [Google Scholar] [CrossRef]
- Medeiros, J.C.; Cooper, M.; Rosa, J.D.; Grimaldi, M.; Coquet, Y. Assessment of pedotransfer functions for estimating soil water retention curves for the amazon region. Rev. Bras. Ciênc. Solo 2014, 38, 730–743. [Google Scholar] [CrossRef]
- Van Looy, K.; Bouma, J.; Herbst, M.; Koestel, J.; Minasny, B.; Mishra, U.; Montzka, C.; Nemes, A.; Pachepsky, Y.A.; Padarian, J.; et al. Pedotransfer functions in earth system science: Challenges and perspectives. Rev. Geophys. 2017, 55, 1199–1256. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Lilly, A.; Nemes, A.; Le Bas, C. Development and use of a database of hydraulic properties of European soils. Geoderma 1999, 90, 169–185. [Google Scholar] [CrossRef]
- Ungaro, F.; Calzolari, C.; Busoni, E. Development of pedotransfer functions using a group method of data handling for the soil of the Pianura Padano-Veneta region of North Italy: Water retention properties. Geoderma 2005, 124, 293–317. [Google Scholar] [CrossRef]
- Haghverdi, A.; Cornelis, W.M.; Ghahraman, B. A pseudo-continuous neural network approach for developing water retention pedotransfer functions with limited data. J. Hydrol. 2012, 442, 46–54. [Google Scholar] [CrossRef]
- Cornelis, W.M.; Ronsyn, J.; van Meirvenne, M.; Hartmann, R. Evaluation of pedotransfer functions for predicting the soil moisture retention curve. Soil Sci. Soc. Am. J. 2001, 65, 638–648. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Taslimitehrani, V.; Dong, G.; Pachepsky, Y. Sample dimensions effect on prediction of soil water retention curve and saturated hydraulic conductivity. J. Hydrol. 2015, 528, 127–137. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Taslimitehrani, V.; Pachepsky, Y. Accuracy of sample dimension-dependent pedotransfer functions in estimation of soil saturated hydraulic conductivity. Catena 2017, 149, 374–380. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. The Australian soil texture boomerang: A comparison of the Australian and USDA/FAO soil particle-size classification systems. Soil Res. 2001, 39, 1443–1451. [Google Scholar] [CrossRef]
- Ramos, T.B.; Horta, A.; Gonçalves, M.C.; Martins, J.C.; Pereira, L.S. Development of ternary diagrams for estimating water retention properties using geostatistical approaches. Geoderma 2014, 230, 229–242. [Google Scholar] [CrossRef]
- Nemes, A.; Wösten, J.H.M.; Lilly, A.; Oude Voshaar, J.H. Evaluation of different procedures to interpolate particle-size distributions to achieve compatibility within soil databases. Geoderma 1999, 90, 187–202. [Google Scholar] [CrossRef]
- Hwang, S.I.; Lee, K.P.; Lee, D.S.; Powers, S.E. Models for estimating soil particle-size distributions. Soil Sci. Soc. Am. J. 2002, 66, 1143–1150. [Google Scholar] [CrossRef]
- Burdine, N.T. Relative Permeability Calculations from Pore-Size Distribution Data. Trans Am 1953, 198, 71–79. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Borodich, F.M. Some Fractal Models of Fracture. J. Mech. Phys. Solids 1997, 45, 239–259. [Google Scholar] [CrossRef]
- Rieu, M.; Sposito, G. Fractal Fragmentation, Soil Porosity and Soil Water Properties: I. Theory Soil Sci 1991, 55, 1231–1238. [Google Scholar]
- Perfect, E.; McLaughlin, N.B.; Kay, B.D.; Topp, G.C. Reply to the Comment on “An Improved Fractal Equation for the Soil Water Retention Curve”. Water Resour Res 1998, 34, 933–935. [Google Scholar] [CrossRef]
- Gime’nez, D.; Perfect, E.; Rawls, W.J.; Pachepsky, Y. Fractal Models for Predicting Soil Hydraulic Properties: A Review. Eng. Geol. 1997, 48, 161–183. [Google Scholar] [CrossRef]
- Xu, Y.F.; Sun, D.A. A Fractal Model for Soil Pores and Its Application to Determination of Water Permeability. Phys. A 2002, 316, 56–64. [Google Scholar] [CrossRef]
- Toledo, P.G.; Novy, R.A.; Davis, H.T.; Scriven, L.E. Hydraulic Conductivity of Porous Media at Low Water Content. Soil Sci 1990, 54, 673–679. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal Process in Soil Water Retention. Water Resour. Res 1990, 26, 1047–1054. [Google Scholar] [CrossRef]
- Mualem, Y. A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media. Water Resour. Res 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Comegna, V.; Damiani, P.; Sommella, A. Scaling the Saturated Hydraulic Conductivity of a Vertic Ustorthens Soil under Conventional and Minimum Tillage. Soil Tillage Res. 2000, 54, 1–9. [Google Scholar] [CrossRef]
- Tyler, S.W.; Wheatcraft, S.W. Fractal Scaling of Soil Particle-Size Distributions: Analysis and Limitations. Soil Sci. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Huang, G.H.; Zhan, W.H. Fractal Property of Soil Particle Size Distribution and Its Application. Acta Pedol. Sin. 2002, 39, 490–497. [Google Scholar]
- Huang, G.; Zhang, R. Evaluation of Soil Water Retention Curve with the Pore-Solid Fractal Model. Geoderma 2005, 127, 52–61. [Google Scholar] [CrossRef]
- Perfect, E. Modeling the Primary Drainage Curve of Prefractal Porous Media. Vadose Zone J. 2005, 4, 959–966. [Google Scholar] [CrossRef]
- Cihan, A.; Perfect, E.; Tyner, J.S. Water Retention Models For Scale-Variant and ScaleInvariant Drainage of Mass Prefractal Porous Media. Vadose Zone J. 2007, 6, 786–792. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Liaghat, A.M.; Huang, G.H. Prediction of Soil Water Retention Curve: A Sensitivity Analysis and Calibration of SWRC Fractal Model; EGU General Assembly: Ienna, Austria, 2008. [Google Scholar]
- Ghanbarian-Alavijeh, B.; Hunt, A.G. Estimation of Soil-Water Retention from Particle-Size Distribution: Fractal Approaches. Soil Sci. 2012, 177, 321–326. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, Y.C.; Yu, N. Feasibility Research on Estimating the Soil Water Retention Curve of Brown Earth with Fractal Method. J. Shenyang Agric. Univ. 2005, 36, 570–574. [Google Scholar]
- Van Damme, H. Scale Invariance and Hydric Behaviour of Soils and Clays. CR Acad. Sci. 1995, 320, 665–681. [Google Scholar]
- Ren, J.; Vanapalli, S.K.; Han, Z.; Omenogor, K.O.; Bai, Y. The resilient moduli of five Canadian soils under wetting and freeze-thaw conditions and their estimation by using an artificial neural network model. Cold Reg. Sci. Technol. 2019, 168, 4. [Google Scholar] [CrossRef]
- Jin, Y.F.; Yin, Z.Y. An intelligent multi-objective EPR technique with multi-step model selection for correlations of soil properties. Acta Geotech. 2020, 15, 2053–2073. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhong, H.; Li, Y.; Wang, L. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]
- de Melo, M.T.; Pedrollo, O.C. Artificial Neural Networks for Estimating Soil Water Retention Curve Using Fitted and Measured Data. Appl. Environ. Soil Sci. 2015, 2015, 535216. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, V.P.; Van Genuchten, M.T. Analysis of soil water retention data using artificial neural networks. J. Hydrol. Eng. 2004, 9, 415–420. [Google Scholar] [CrossRef]
- Tripathy, S.; Tadza, M.Y.M.; Thomas, H.R. Soil-water characteristic curves of clays. Can. Geotech. J. 2014, 51, 869–883. [Google Scholar] [CrossRef]
- Chiu, C.F.; Ng, C.W. Coupled water retention and shrinkage properties of a compacted silt under isotropic and deviatoric stress paths. Can. Geotech. J. 2012, 49, 928–938. [Google Scholar] [CrossRef]
- Burton, G.J.; Sheng, D.; Airey, D.W. Critical state behaviour of an unsaturated high-plasticity clay. Géotechnique 2020, 70, 161–172. [Google Scholar] [CrossRef]
- Amanabadi, S.; Vazirinia, M.; Vereecken, H.; Vakilian, K.A.; Mohammadi, M. Comparative study of statistical, numerical and machine learning-based pedotransfer functions of water retention curve with particle size distribution data. Eurasian Soil Sci. 2019, 52, 1555–1571. [Google Scholar] [CrossRef]
- D’Emilio, A.; Aiello, R.; Consoli, S.; Vanella, D.; Iovino, M. Artificial neural networks for predicting the water retention curve of sicilian agricultural soils. Water 2018, 10, 1431. [Google Scholar] [CrossRef]
- Nguyen, P.M.; Haghverdi, A.; De Pue, J.; Botula, Y.D.; Le, K.V.; Waegeman, W.; Cornelis, W.M. Comparison of statistical regression and data-mining techniques in estimating soil water retention of tropical delta soils. Biosyst. Eng. 2017, 153, 12–27. [Google Scholar] [CrossRef]
- Lamorski, K.; Šimůnek, J.; Sławiński, C.; Lamorska, J. An estimation of the main wetting branch of the soil water retention curve based on its main drying branch using the machine learning method. Water Resour. Res. 2017, 53, 1539–1552. [Google Scholar] [CrossRef]
- Haghverdi, A.; Öztürk, H.S.; Cornelis, W.M. Revisiting Pseudo Continuous Pedotransfer Funct. Concept Impact Data Qual. Data Min. Method. Geoderma 2014, 226, 31–38. [Google Scholar] [CrossRef]
- Mukhlisin, M.; El-Shafie, A.; Taha, M.R. Regularized versus non-regularized neural network model for prediction of saturated soil-water content on weathered granite soil formation. Neural Comput. Appl. 2012, 21, 543–553. [Google Scholar] [CrossRef]
- Zhanga, Y.; Yu, N. Prediction of soil water retention and available water of sandy soils using pedotransfer functions. Procedia Eng. 2012, 37, 49–53. [Google Scholar]
- Patil, N.G.; Pal, D.K.; Mandal, C.; Mandal, D.K. Soil water retention characteristics of vertisols and pedotransfer functions based on nearest neighbor and neural networks approaches to estimate AWC. J. Irrig. Drain. Eng. 2012, 138, 177–184. [Google Scholar] [CrossRef]
- Eyo, E.U.; Ng’ambi, S.; Abbey, S.J. An overview of soil–water characteristic curves of stabilised soils and their influential factors. J. King Saud Univ.-Eng. Sci. 2022, 34, 31–45. [Google Scholar] [CrossRef]
- Antinoro, C.; Arnone, E.; Noto, L.V. The role of Soil Water Retention Curve in slope stability analysis in unsaturated and heterogeneous soils. In Proceedings of the EGU General Assembly 2015, Vienna, Austria, 12–17 April 2015; Volume 17, p. 12436. [Google Scholar]
- Ross, P.J.; Krj, S. Describing Soil Hydraulic Properties with Sums of Simple Functions. Soil Sci. Soc. Am. J. 1993, 57, 26–29. [Google Scholar] [CrossRef]
- Dexter, A.R.; Czyz, E.A.; Richard, G.; Reszkowska, A. A user-friendly water retention function that takes account of the textural and structural pore spaces in soil. Geoderma 2008, 143, 243–253. [Google Scholar] [CrossRef]
- Comegna, L.; Rianna, G.; Lee, S.G.; Picarelli, L. Influence of the wetting path on the mechanical response of shallow unsaturated sloping covers. Comput. Geotech. 2016, 73, 164–169. [Google Scholar] [CrossRef]
- Cai, H.; Yang, Z.J.; Wang, L.Y.; Lei, X.Q.; Fu, X.L.; Liu, S.H.; Qiao, J.P. An Experimental Study on the Hydromechanical Behaviours of the Evolution of post-earthquake Landslide Deposits. Geofluids 2019, 2019, 3032494. [Google Scholar] [CrossRef]
- Ahmed, F.S.; Bryson, L.S. Influence of Hydrologic Behavior in Assessing Rainfall-Induced Landslides. Geo-Congress 2019, 2019, 194–204. [Google Scholar]
- Ip, S.C.Y.; Rahardjo, H.; Alfrendo, S. Three-dimensional slope stability analysis incorporating unsaturated soil properties in Singapore. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2020, 15, 2. [Google Scholar] [CrossRef]
- Reid, M.E.; Christian, S.B.; Brien, D.L.; Henderson, S. Scoops 3D–Software to Analyze Three-Dimensional Slope Stability Throughout a Digital Landscape; U.S. Geological Survey: Reston, VA, USA, 2015. [Google Scholar]
- Feng, C.; Tian, B.; Lu, X.; Beer, M.; Broggi, M.; Bi, S.; Xiong, B.; He, T. Bayesian Updating of Soil–Water Character Curve Parameters Based on the Monitor Data of a Large-Scale Landslide Model Experiment. Appl. Sci. 2020, 10, 5526. [Google Scholar] [CrossRef]
- Li, D.Q.; Wang, L.; Cao, Z.J.; Qi, X.H. Reliability analysis of unsaturated slope stability considering SWCC model selection and parameter uncertainties. Eng. Geol. 2019, 260, 105207. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fmo, M. Bearing Capacity of Model Footings in Unsaturated Soils. In Experimental Unsaturated Soil Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 483–493. [Google Scholar]
- Trista, J.; Cristia, W.; Sotolongo, G. Bearing capacity of footings in unsaturated soils employing analytic methods. Ing. Desarro. 2017, 35, 417–430. [Google Scholar]
- Vanapalli, S.K.; Oh, W.T. Analytical and numerical methods for prediction of the bearing capacity of shallow foundations in unsaturated soils. Soils Rocks 2021, 44, 1–18. [Google Scholar] [CrossRef]
- Oh, W.T.; Vanapalli, S.K. Modelling the applied vertical stress and settlement relationship of shallow foundations in saturated and unsaturated sands. Can. Geotech. J. 2011, 48, 425–438. [Google Scholar] [CrossRef]
- Tang, Y.; Taiebat, H.A.; Senetakis, K. Effective stress based bearing capacity equations for shallow foundations on unsaturated soils. J. GeoEngin. 2017, 12, 59–64. [Google Scholar]
- Jeb, J.; Burland, J.B. Limitations to the Use of Effective Stresses in Partly Saturated Soils. Géotechnique 1962, 12, 125–144. [Google Scholar]
- Du, D.; Zhuang, Y.; Sun, Q.; Yang, X.; Dias, D. Bearing capacity evaluation for shallow foundations on unsaturated soils using discretization technique. Comput. Geotech. 2021, 137, 9. [Google Scholar] [CrossRef]
- Vahedifard, F.; Robinson, J.D. Unified Method for Estimating the Ultimate Bearing Capacity of Shallow Foundations in Variably Saturated Soils under Steady Flow. J. Geotech. Geoenviron. Eng. 2016, 142, 04015095. [Google Scholar] [CrossRef]
- Tang, Y.; Taiebat, H.A.; Russell, A.R. Bearing Capacity of Shallow Foundations in Unsaturated Soil Considering Hydraulic Hysteresis and Three Drainage Conditions. Int. J. Geomech. 2017, 17, 04016142. [Google Scholar] [CrossRef]
- Ghasemzadeh, H.; Akbari, F. Determining the bearing capacity factor due to nonlinear matric suction distribution in the soil. Can. J. Soil Sci. 2019, 99, 434–446. [Google Scholar] [CrossRef]
- Safarzadeh, Z.; Aminfar, M.H. Experimental study on bearing capacity of shallow footings based on sand in saturated and unsaturated conditions. J. Civ. Environ. Eng. 2020, 50, 23–32. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46, W05515. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, Y.; Park, H.; Kim, J. Effects of rainfall infiltration and hysteresis on the settlement of shallow foundations in unsaturated soil. Environ. Earth Sci. 2018, 77, 494. [Google Scholar] [CrossRef]
- Oh, W.T.; Vanapalli, S.K.; Puppala, A.J. Semi-empirical model for the prediction of modulus of elasticity for unsaturated soils. Can. Geotech. J. 2009, 48, 903–914. [Google Scholar] [CrossRef]
- Rahardjo, H.; Melinda, F.; Leong, E.C.; Rezaur, R.B. Stiffness of a compacted residual soil. Eng. Geol. 2011, 120, 60–67. [Google Scholar] [CrossRef]
- Oh, W.T.; Vanapalli, S.K. Modeling the stress versus settlement behavior of shallow foundations in unsaturated cohesive soils extending the modified total stress approach. Soils Found. 2018, 58, 382–397. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, S.; Kim, J. Coupled infiltration model of unsaturated porous media for steady rainfall. Soils Found. 2016, 56, 1073–1083. [Google Scholar] [CrossRef]
- Kim, Y.; Park, H.; Jeong, S. Settlement behavior of shallow foundations in unsaturated soils under rainfall. Sustainability 2017, 9, 1417. [Google Scholar] [CrossRef]
- Mahmoudabadi, V.; Ravichandran, N. Coupled geotechnical-hydrological design of shallow foundation considering site specific data—Theoretical framework and application. J. GeoEngin 2018, 13, 93–103. [Google Scholar]
- Thongpong, R.; Nuntasarn, R.; Hormdee, D.; Punrattanasin, P. the Settlement Behavior of Isolated Foundation on Khon Kaen Loess. Int. J. GEOMATE 2021, 20, 162–170. [Google Scholar] [CrossRef]
- Phoon, K.K.; Santoso, A.; Quek, S.T. Probabilistic analysis of soil-water characteristic curves. J. Geotech. Geoenviron. Eng. 2010, 136, 445–455. [Google Scholar] [CrossRef]
- Bishop, A.W.; Blight, G.E. Some aspects of effective stress in saturated and unsaturated soils. Geotechnique 1963, 13, 177–197. [Google Scholar] [CrossRef]
- Saadeldin, R.; Henni, A. A novel modeling approach for the simulation of soil–water interaction in a highly plastic clay. Geomech. Geophys. Geo-Energy Geo-Resour. 2016, 2, 77–95. [Google Scholar] [CrossRef][Green Version]
- Tan, X.; Wang, X.; Khoshnevisan, S.; Hou, X.; Zha, F. Seepage analysis of earth dams considering spatial variability of hydraulic parameters. Eng. Geol. 2017, 228, 260–269. [Google Scholar] [CrossRef]
- Walshire, L.A.; Robbins, B.; Taylor, O.D.S. Assessing the Influence of Errors in SWCC Prediction Methods on Transient Seepage Analyses. In Proceedings of the Second Pan-American Conference on Unsaturated Soils, Dallas, TX, USA, 12–15 November 2017; pp. 155–164. [Google Scholar]
- Perera, Y.Y.; Zapata, C.E.; Houston, W.N.; Houston, S.L. Prediction of the soil-water characteristic curve based on grain-size-distribution and index properties. Adv. Pavement Eng. 2005, 130, 49–60. [Google Scholar]
- Sleep, M.D. Analysis of Transient Seepage through Levees. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).