Estimating the Optimum Weight for Latticed Power-Transmission Towers Using Different (AI) Techniques
Abstract
:1. Introduction
2. Objective
3. Methodology
3.1. Phase I: The Parametric Study
- The plan of the tower is square;
- All legs have the same cross section;
- All diagonals have the same cross section;
- All cross-frame members have the same cross section;
- All subdivide members have the same cross section;
- Cross sections of all members are single angles;
- Only equal angles with size to thickness (a/t) equal to 10 are used;
- Minimum allowed cross sections are L40 × 40 × 4 for subdividers, and L50 × 50 × 5 for other members;
- All members have a minimum yield stress of 3.6 t/cm2 (36,000 t/m2);
- Since the leg slope ranged between 5° and 15°, all member lengths are calculated as in the vertical plane;
- The subdividers divide both legs and diagonals into equal lengths;
- The lateral load is considered in one direction;
- In the case of X-diagonals and K-diagonals, both diagonal members are active, and no post-buckling behavior is allowed;
- The maximum allowable values for the buckling factor (λ = KL/r) are 150, 200 and 250 for legs, diagonals and subdividers, respectively.
3.2. Phase II: Artificial Intelligence (AI) Models
4. Research Results
4.1. Model 1 Using GP
4.2. Model 2 Using ANN
4.3. Model 3 Using EPR
5. Dissection
- Segment volume (Vt = B2H);
- Overturning moment at segment base (M = Q.L);
- Segment aspect ratio (A = H/B);
- Yield stress of steel (Fy = 3.6 t/cm2 = 36,000 t/m2):
- The term in Equation (5) is minimized when A < 1.0 and sh = 2, and when A > 1.0 and sh = 1. This indicates that K-bracing is favorable when the aspect ratio (A) is less than 1.0, while X-bracing is favorable for an A greater than 1.0;
- In order to keep the diagonal angle in the optimum zone (from 30° to 60°), the segment aspect ratio (A) should be between 0.5 and 2.0;
- The term in Equation (5) indicates that using a two-member bracing system is always more economical than using a one-member bracing system;
- The buckling factor (K) appeared in two positive terms: and . This means that decreasing the K factor decreases the segment weight. However, decreasing the K value to below 10 a/H, which corresponds to (λ = 50), will not significantly affect the segment weight. Conversely, using a K value higher than 20 a/H, which corresponds to (λ = 100), eliminates the advantage of using high-strength steel due to the Euler buckling;
- The term tends to zero for large segments, which indicates that it presents the effect of not using subdividers in small segments (using large K values) when increasing their weights;
- Finally, the term in Equation (5) indicates that increasing the base width of the segments reduces their weights, but this is limited within the optimum range of the aspect ratio (A) (which lays between 0.5 and 2.0). The practical leg slope in most prefabricated latticed power-transmission towers ranges between 5° and 15°.
6. Verification
7. Conclusions
- The developed ANN model is the most accurate model, with an average error of 6.8%; however, it is too complicated to be applied manually and it cannot be used to extract design guidelines;
- The EPR model has the lowest level of accuracy, with an average error of 25.8%, and accordingly it is not recommended;
- The reasonable accuracy of the GP formula (error: 16.6%), in addition to its ability to be applied manually, makes it the best choice for further analysis to extract design guidelines to minimize the segment weight, as follows:
- o
- K-bracing is favorable when the aspect ratio (A) is less than 1.0, while X-bracing is favorable for an A more than 1.0;
- o
- The segment aspect ratio (A) should be between 0.5 and 2.0;
- o
- A double-member bracing system is always more economical than a single-member bracing system;
- o
- The distance between the subdividers should be between 10 and 20 times the leg-angle size;
- o
- The practical leg slope is between 5° and 15°, which corresponds to an x/H value between 0.10 and 0.25. However, the selected value should comply with the optimum range of the aspect ratio (A), which is between 0.5 and 2.0;
- The accuracies of both the GP and ANN models were verified using two types of preoptimized tower segments;
- As with any other regression technique, the developed models are valid within the considered range of the parameter values; beyond this range, the prediction accuracy should be verified;
- Further studies may be carried out to optimize the design of guided and communication towers using the same technique.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kiessling, F.; Nefzger, P.; Nolasco, J.E.; Kaintzyk, U. Overhead Power Lines Planning, Design, Construction; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003; ISBN 3-540-00297-9. [Google Scholar]
- Shea, K.; Smith, I.F.C. Improving Full-Scale Transmission Tower Design through Topology and Shape Optimization. J. Struct. Eng. 2006, 132, 781–790. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.Y.; Li, Z.L. Structural topology optimization of high-voltage transmission tower with discrete variables. Struct. Multidisc. Optim. 2011, 43, 851–861. [Google Scholar] [CrossRef]
- Couceiro, I.; París, J.; Martínez, S.; Colominas, I.; Navarrina, F.; Casteleiro, M. Structural optimization of lattice steel transmission towers. Eng. Struct. 2016, 117, 274–286. [Google Scholar] [CrossRef]
- Guo, H.; Li, Z. Adaptive Genetic Algorithm and Its Application to the Structural Optimization of Steel Tower. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjian, China, 14–16 August 2009. [Google Scholar] [CrossRef]
- Mohammed, A.F.; Özakça, M.; Tayşi, N. Optimal design of transmission towers using genetic algorithm. SDU Int. J. Technol. Sci. 2012, 4, 115–123. [Google Scholar]
- Sanah, R.S.; Airin, M.G. Optimization of Transmission Tower using Genetic Algorithm. Int. J. Sci. Res. 2016, 5, 2319–7064. [Google Scholar]
- Premalatha, J.; Vengadeshwari, R.S.; Veerendra, A. Optimization of Transmission Tower Using Genetic Algorithm. Int. J. Civ. Eng. Technol. 2017, 8, 654–662. [Google Scholar]
- Koner, B.; Surpur, P.; Venuraju, M.T. Design optimization of free standing communication tower using genetic algorithm. Int. Res. J. Eng. Technol. 2018, 5, 981–985. [Google Scholar]
- Talatahari, S.; Gandomi, A.H.; Yun, G.J. Optimum design of tower structures using Firefly Algorithm. Struct. Des. Tall Spec. Build. 2012, 23, 350–361. [Google Scholar] [CrossRef]
- Nagavinothini, R.; Subramanian, C. Weight Optimization of double circuit steel transmission line tower using PSO algorithm. Int. J. Sci. Eng. Technol. Res. 2015, 4, 316–319. [Google Scholar]
- Li, S.; Zhang, Z.; Li, H.; Ren, Z. Optimal Design of Truss Structures based on the New Improved Ant Colony Optimization Algorithm. In 5th International Conference on Civil Engineering and Transportation (ICCET 2015); Atlantis Press: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Ebid, A.M. Optimum Cross Section and Longitudinal Profile for Unstiffened Fully Composite Steel Beams. Future Eng. J. 2021, 2, 2. Available online: https://digitalcommons.aaru.edu.jo/fej/vol2/iss1/2 (accessed on 17 January 2021).
- Mohamed, A.E.-A.; Ahmed, M.E.; Kennedy, C.O. Optimum Design of Fully Composite, Unstiffened, Built-Up, Hybrid Steel Girder Using GRG, NLR, and ANN Techniques. J. Eng. 2022, 2022, 7439828. [Google Scholar] [CrossRef]
- Gencturk, B.; Attar, A.; Tort, C. Optimal design of lattice wind turbine towers. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; pp. 24–28. [Google Scholar]
- Hosseini, N.; Ghasemi, M.R.; Dizangian, B. ANFIS-based Optimum Design of Real Power Transmission Towers with Size, Shape and Panel Design Variables using BBO Algorithm. IEEE Trans. Power Deliv. 2021, 37, 29–39. [Google Scholar] [CrossRef]
- Nguyen, T.-H.; Vu, A.-T. Weight optimization of steel lattice transmission towers based on Differential Evolution and machine learning classification technique. Frat. Ed Integrità Strutt. 2022, 58, 172–187. [Google Scholar] [CrossRef]
- Ebid, A.M. Estimating the weights of latticed power transmission towers using Genetic programming. Future Eng. J. 2021, 3, 3. Available online: https://digitalcommons.aaru.edu.jo/fej/vol3/iss1/3 (accessed on 29 June 2022).
- Cramer, N.L. A Representation for the Adaptive Generation of Simple Sequential Programs. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications; Erlbaum: Mahwah, NJ, USA, 1985; pp. 183–187. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Ebid, A.M. 35 Years of (AI) in Geotechnical Engineering: State of the Art. Geotech. Geol. Eng. 2020, 39, 637–690. [Google Scholar] [CrossRef]
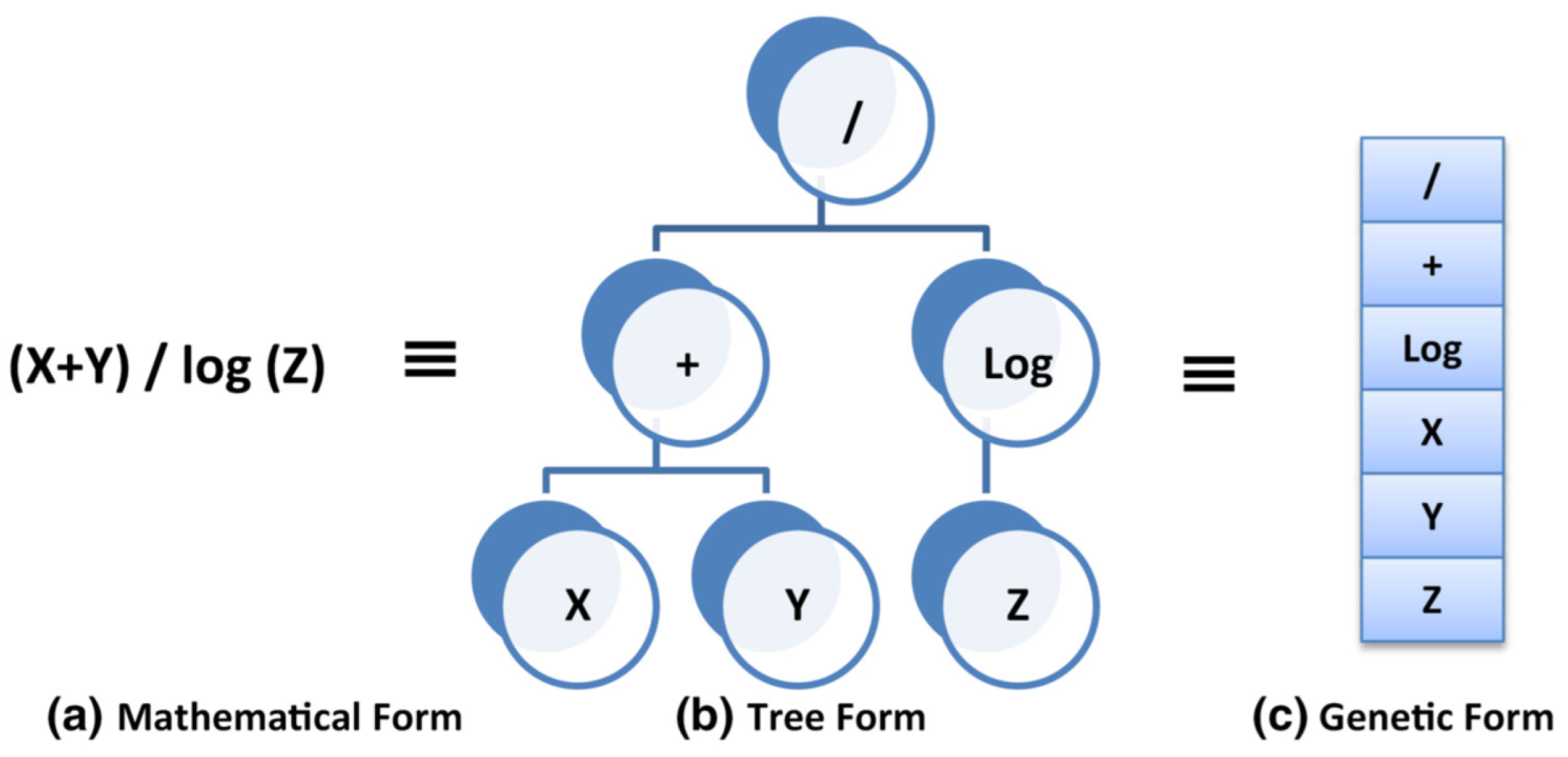
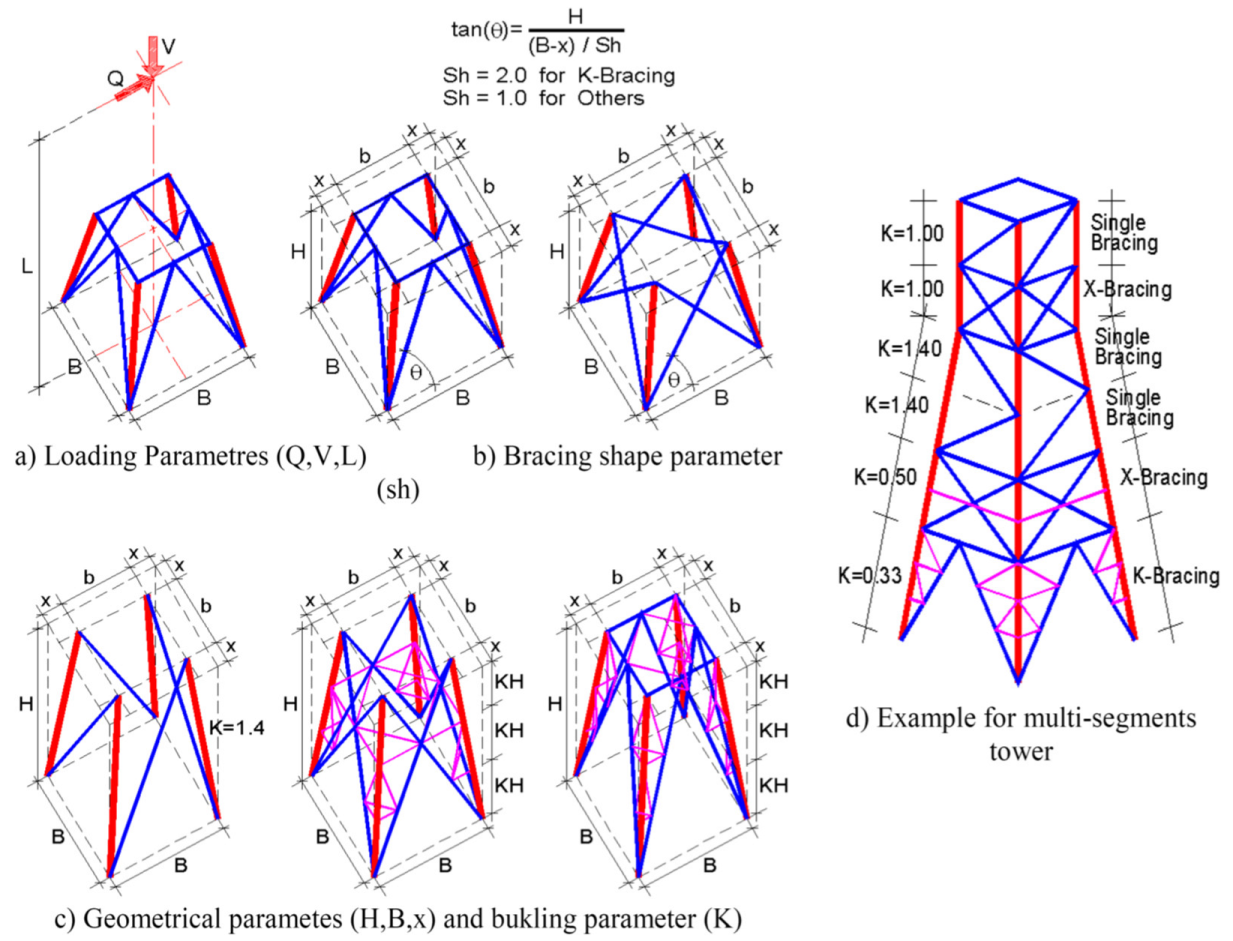
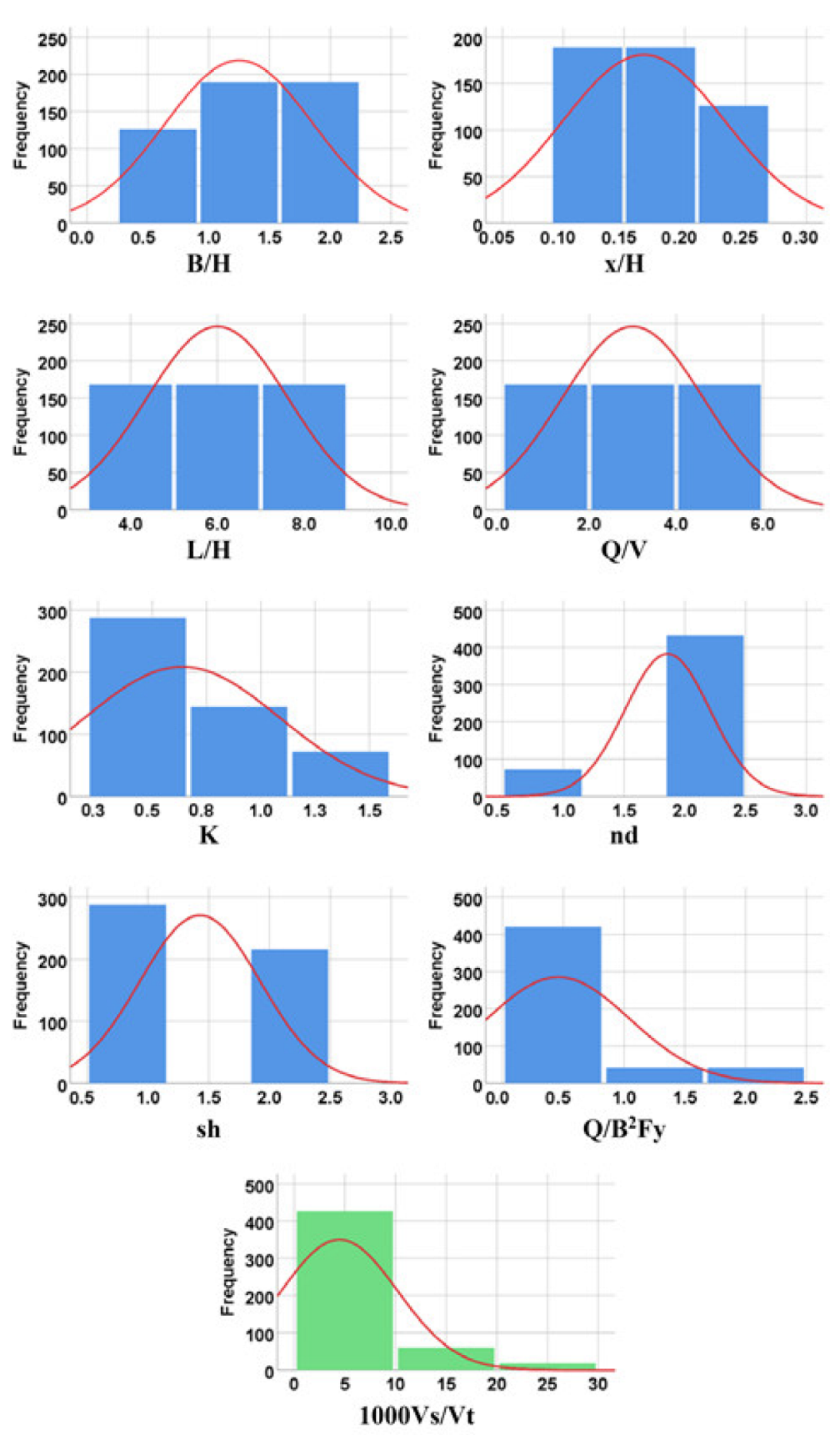
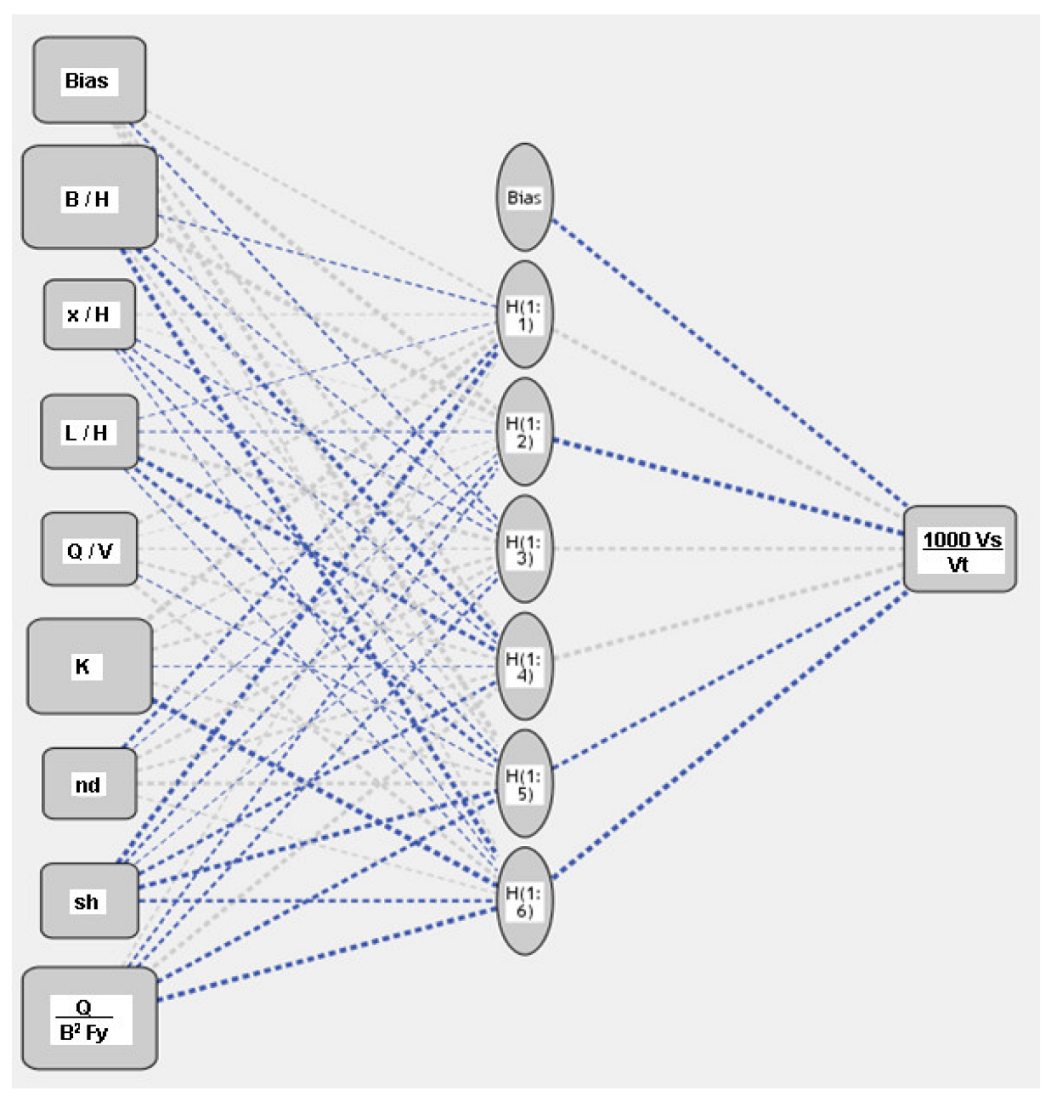

| Parameter | Symbol | Unit | Values |
|---|---|---|---|
| Segment height | (H) | (m) | 4.0 |
| Bottom width | (B) | (m) | 2.0, 4.0, 8.0 |
| (x) distance | (x) | (m) | 0.35, 0.70, 1.05 |
| (L) distance | (L) | (m) | 16.0, 24.0, 32.0 |
| Vertical load | (V) | (ton) | 6.0 |
| Lateral load | (Q) | (ton) | 6.0, 18.0, 30.0 |
| Buckling coefficient | (K) | - | 1.4, 1.0, 0.33, 0.2 |
| Shape factor | (sh) | - | 1.0, 2.0 |
| B/H | x/H | L/H | Q/V | K | nd | sh | Q/B2fy | 1000 Vs/Vt | |
|---|---|---|---|---|---|---|---|---|---|
| B/H | 1.00 | ||||||||
| x/H | 0.19 | 1.00 | |||||||
| L/H | 0.00 | 0.00 | 1.00 | ||||||
| Q/V | 0.00 | 0.00 | 0.00 | 1.00 | |||||
| K | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | ||||
| nd | 0.00 | 0.00 | 0.00 | 0.00 | −0.69 | 1.00 | |||
| sh | 0.00 | 0.00 | 0.00 | 0.00 | −0.24 | 0.35 | 1.00 | ||
| Q/B2fy | −0.67 | −0.21 | 0.00 | 0.42 | 0.00 | 0.00 | 0.00 | 1.00 | |
| 1000 Vs/Vt | −0.66 | −0.23 | 0.08 | 0.23 | 0.27 | −0.20 | −0.01 | 0.89 | 1.00 |
| B/H | x/H | L/H | Q/V | K | nd | sh | Q/B2fy | 1000 Vs/Vt | |
|---|---|---|---|---|---|---|---|---|---|
| Training set | |||||||||
| Min. | 0.50 | 0.09 | 4.00 | 1.00 | 0.20 | 1.00 | 1.00 | 0.03 | 0.32 |
| Max. | 2.00 | 0.26 | 8.00 | 5.00 | 1.40 | 2.00 | 2.00 | 2.08 | 28.15 |
| Avg. | 1.25 | 0.17 | 5.97 | 2.97 | 0.78 | 1.80 | 1.19 | 0.46 | 4.82 |
| SD | 0.61 | 0.07 | 1.63 | 1.63 | 0.45 | 0.40 | 0.39 | 0.59 | 6.00 |
| VAR | 0.49 | 0.40 | 0.27 | 0.55 | 0.58 | 0.22 | 0.33 | 1.28 | 1.24 |
| Validation set | |||||||||
| Min. | 0.50 | 0.09 | 4.00 | 1.00 | 0.20 | 2.00 | 2.00 | 0.03 | 0.35 |
| Max. | 2.00 | 0.26 | 8.00 | 5.00 | 1.00 | 2.00 | 2.00 | 2.08 | 28.70 |
| Avg. | 1.26 | 0.17 | 6.08 | 3.08 | 0.30 | 2.00 | 2.00 | 0.46 | 3.62 |
| SD | 0.61 | 0.07 | 1.65 | 1.65 | 0.16 | 0.00 | 0.00 | 0.59 | 4.96 |
| VAR | 0.49 | 0.40 | 0.27 | 0.53 | 0.53 | 0.00 | 0.00 | 1.28 | 1.37 |
| Hidden Layer 1 | Output Layer | |||||||
|---|---|---|---|---|---|---|---|---|
| H(1:1) | H(1:2) | H(1:3) | H(1:4) | H(1:5) | H(1:6) | 1000 VsVt | ||
| Input Layer | (Bias) | 0.215 | 0.660 | −0.177 | 0.353 | 0.779 | 0.206 | |
| B/H | −0.090 | 1.165 | −0.082 | −0.435 | 0.238 | −0.495 | ||
| x/H | 0.075 | 0.013 | −0.090 | −0.092 | −0.171 | −0.044 | ||
| L/H | −0.016 | −0.033 | 0.415 | −0.432 | −0.340 | −0.082 | ||
| Q/V | 0.274 | 0.008 | 0.158 | 0.256 | −0.068 | 0.345 | ||
| K | 0.662 | 0.186 | 0.271 | −0.015 | 0.222 | −1.012 | ||
| nd | −0.295 | −0.018 | 0.289 | 0.266 | 0.369 | 0.098 | ||
| sh | −0.509 | −0.220 | −0.023 | −0.320 | −0.471 | −0.281 | ||
| Q/B2fy | 0.116 | −0.205 | −0.230 | 0.401 | −0.373 | −0.615 | ||
| Hidden Layer 1 | (Bias) | −0.374 | ||||||
| H(1:1) | 0.381 | |||||||
| H(1:2) | −1.016 | |||||||
| H(1:3) | 0.327 | |||||||
| H(1:4) | 0.524 | |||||||
| H(1:5) | −0.362 | |||||||
| H(1:6) | −0.732 | |||||||
| Technique | Developed Equation | (MSE) | (MSE) | Error % | R2 |
|---|---|---|---|---|---|
| GP | Equation (2) | 0.917 | 424 | 16.6 | 0.976 |
| ANN | Figure 4 | 0.303 | 46 | 6.8 | 0.997 |
| EPR | Equation (3) | 1.154 | 671 | 25.8 | 0.959 |
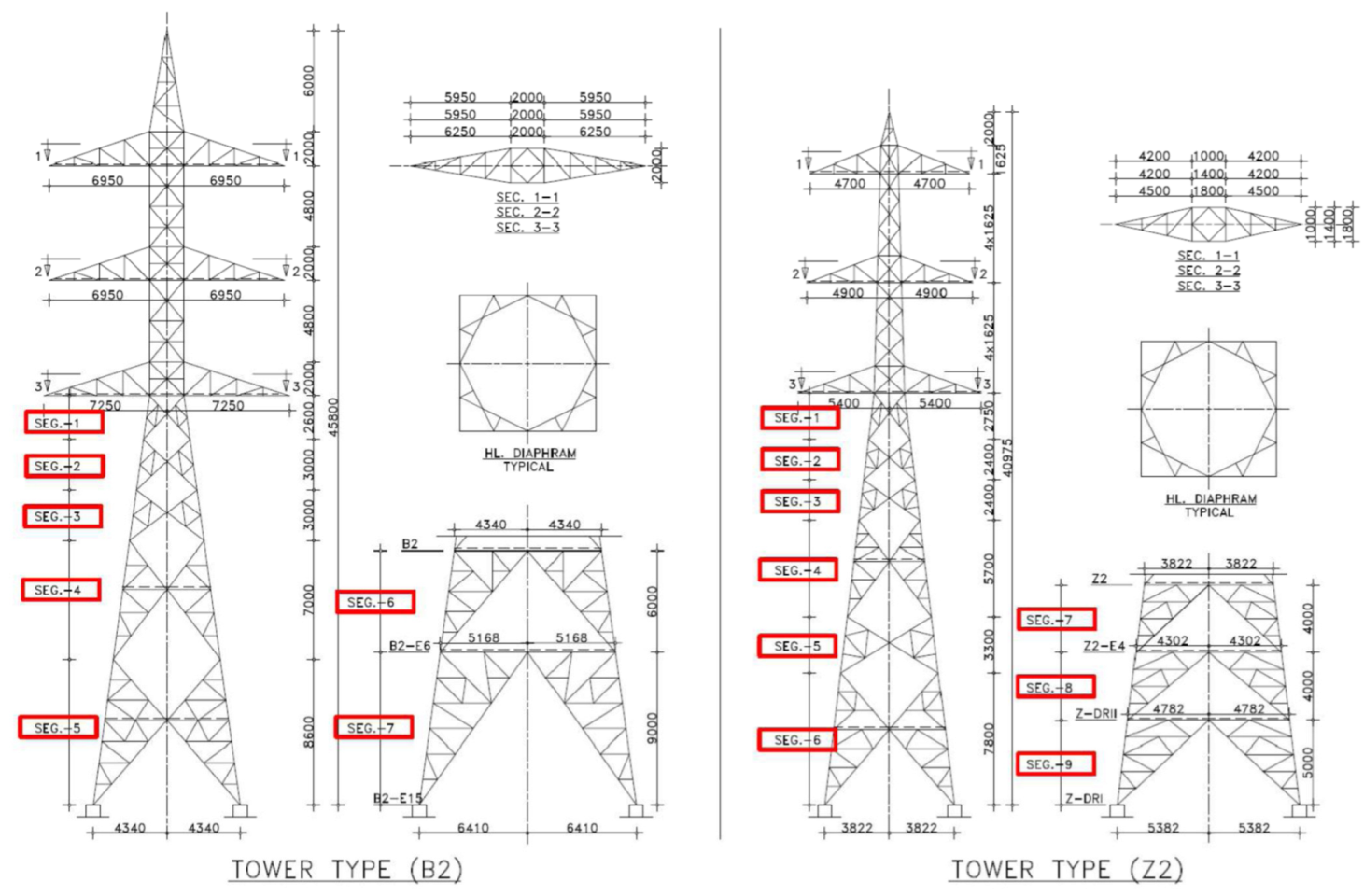
| Seg. | H | B | x | Q | L | K | nd | sh | Ws act | Ws Equation (5) | Ws ANN |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | (m) | (m) | (m) | (t) | (m) | (-) | (-) | (-) | (kg) | (kg) | (kg) |
| Tower Type (Z2) | |||||||||||
| 1 | 2.75 | 2.46 | 0.33 | 18.2 | 9.55 | 0.25 | 2.00 | 1.00 | 380 | 384 | 391 |
| 2 | 2.40 | 3.04 | 0.29 | 18.4 | 11.83 | 0.25 | 2.00 | 1.00 | 400 | 380 | 388 |
| 3 | 2.40 | 3.61 | 0.29 | 18.6 | 14.06 | 0.25 | 2.00 | 1.00 | 500 | 475 | 535 |
| 4 | 5.70 | 4.98 | 0.68 | 19.3 | 19.04 | 0.16 | 2.00 | 1.00 | 930 | 902 | 930 |
| 5 | 3.30 | 5.77 | 0.40 | 19.8 | 21.80 | 0.33 | 2.00 | 1.00 | 950 | 1017 | 931 |
| 6 | 7.80 | 7.64 | 0.94 | 21.3 | 27.52 | 0.14 | 2.00 | 1.00 | 1750 | 1785 | 1855 |
| 7 | 4.00 | 8.60 | 0.48 | 22.1 | 30.30 | 0.25 | 2.00 | 2.00 | 1344 | 1304 | 1277 |
| 8 | 4.00 | 9.56 | 0.48 | 23.1 | 32.88 | 0.25 | 2.00 | 2.00 | 1461 | 1373 | 1359 |
| 9 | 5.00 | 10.76 | 0.60 | 24.4 | 35.79 | 0.20 | 2.00 | 2.00 | 2022 | 2062 | 2123 |
| Total | 9737 | 8533 | 9789 | ||||||||
| Tower Type (B2) | |||||||||||
| 1 | 2.60 | 2.72 | 0.36 | 26.2 | 9.94 | 0.25 | 2.00 | 1.00 | 532 | 559 | 548 |
| 2 | 3.00 | 3.55 | 0.42 | 26.4 | 12.81 | 0.25 | 2.00 | 1.00 | 639 | 698 | 620 |
| 3 | 3.00 | 4.38 | 0.42 | 26.8 | 15.62 | 0.25 | 2.00 | 1.00 | 683 | 802 | 703 |
| 4 | 7.00 | 6.32 | 0.97 | 27.9 | 21.72 | 0.20 | 2.00 | 1.00 | 1758 | 1797 | 1758 |
| 5 | 8.60 | 8.70 | 1.19 | 29.7 | 28.42 | 0.14 | 2.00 | 1.00 | 2355 | 2262 | 2308 |
| 6 | 6.00 | 10.37 | 0.84 | 31.3 | 32.71 | 0.20 | 2.00 | 2.00 | 2091 | 1673 | 2091 |
| 7 | 9.00 | 12.86 | 1.25 | 34.2 | 38.19 | 0.16 | 2.00 | 2.00 | 2985 | 3084 | 3134 |
| Total | 11,043 | 10,875 | 11,162 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebid, A.M.; El-Aghoury, M.A.; Onyelowe, K.C. Estimating the Optimum Weight for Latticed Power-Transmission Towers Using Different (AI) Techniques. Designs 2022, 6, 62. https://doi.org/10.3390/designs6040062
Ebid AM, El-Aghoury MA, Onyelowe KC. Estimating the Optimum Weight for Latticed Power-Transmission Towers Using Different (AI) Techniques. Designs. 2022; 6(4):62. https://doi.org/10.3390/designs6040062
Chicago/Turabian StyleEbid, Ahmed M., Mohamed A. El-Aghoury, and Kennedy C. Onyelowe. 2022. "Estimating the Optimum Weight for Latticed Power-Transmission Towers Using Different (AI) Techniques" Designs 6, no. 4: 62. https://doi.org/10.3390/designs6040062
APA StyleEbid, A. M., El-Aghoury, M. A., & Onyelowe, K. C. (2022). Estimating the Optimum Weight for Latticed Power-Transmission Towers Using Different (AI) Techniques. Designs, 6(4), 62. https://doi.org/10.3390/designs6040062






