Deep Neural Network Models for the Prediction of the Aggregate Base Course Compaction Parameters
Abstract
:1. Introduction and Background
2. Methodology
2.1. Aggregate Base Types Selection
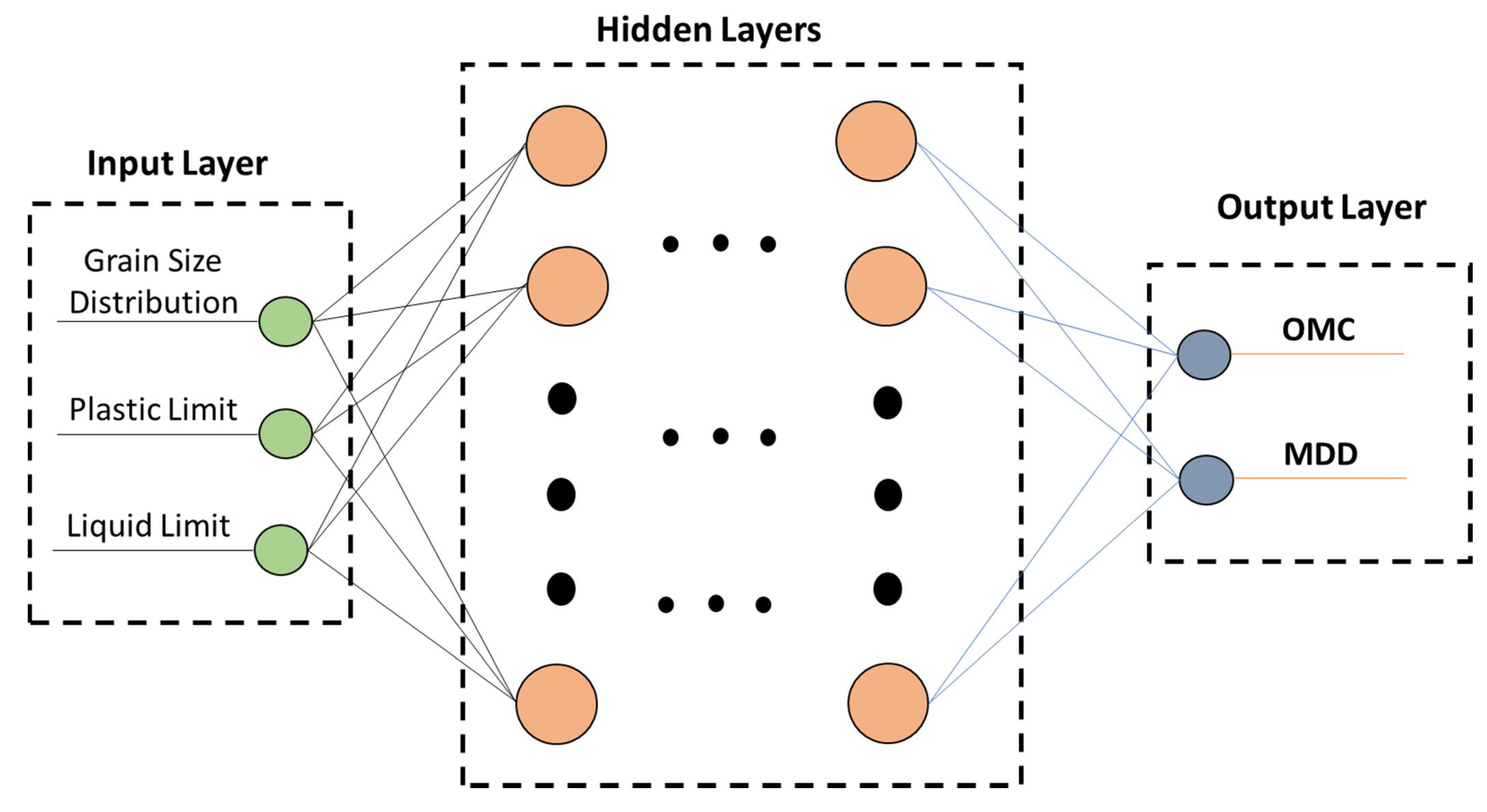
2.2. Artificial Neural Networks
- -
- The Linear activation function, also called the Rectified Linear Unit (ReLU) function
- -
- The logistic activation function, also called the sigmoid function
- -
- The hyperbolic activation function, also called the tanh activation function
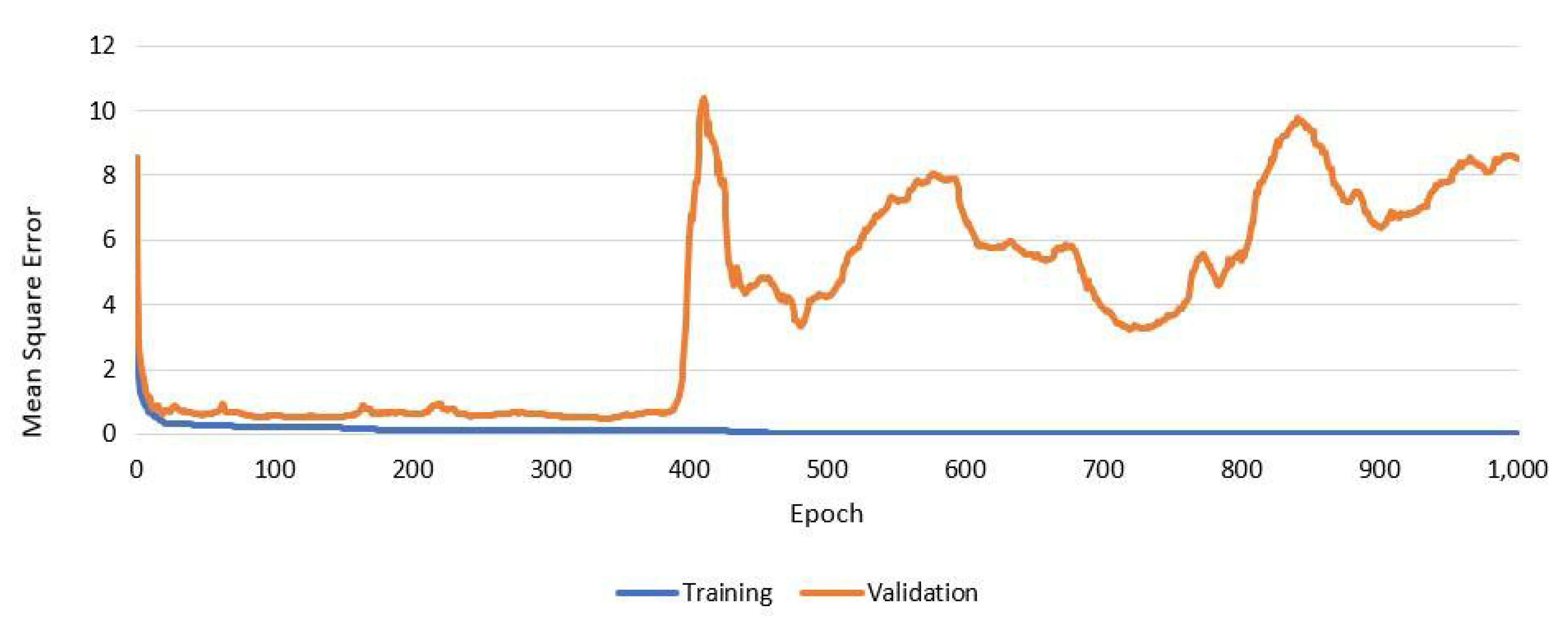
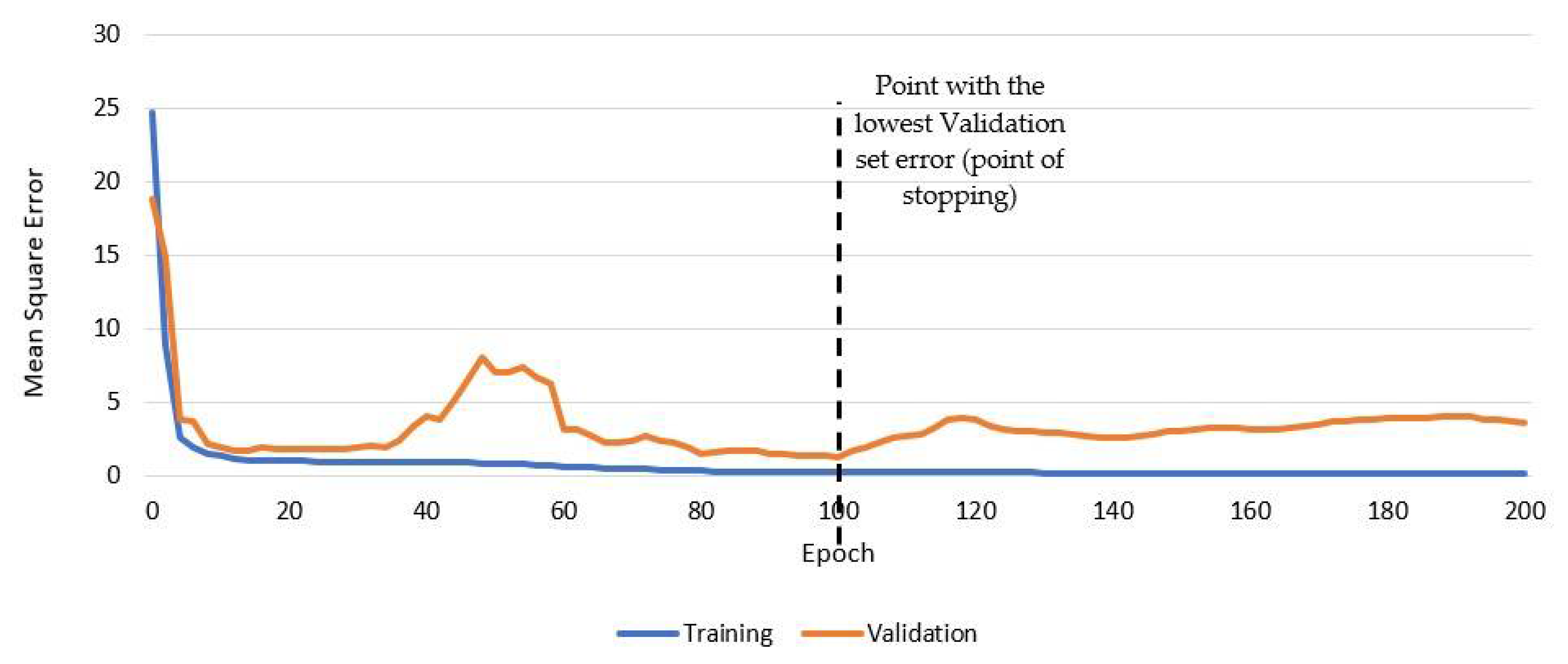
2.3. Early Stopping to Avoid Overfitting
2.4. ANN Performance Evaluation
3. Results and Analysis
3.1. MDD
3.2. OMC
3.3. Optimum ANN Architecture for the Predictions of Both the OMC and MDD
3.4. Comparing Previous Studies with the Proposed ANN
4. Multiple Linear Regression (MLR)
5. Conclusions
- -
- The optimum structure and hyperparameters of the ANN changes depending on the desired output, as shown in Table 12.
- -
- In general, the tanh activation function is the most efficient, as it outperforms the other two activation functions. Additionally, the simpler the ANN architecture, the better the predictions, as the performance of the ANNs deteriorates with the increase in the number of hidden layers or the number of neurons per hidden layers.
- -
- The optimum ANN proposed can be used for estimating the OMC and MDD of the aggregate base course in Egypt with high accuracy (R2 = 0.903 for OMC, and R2 = 0.928 for MDD). Thus, this ANN can be used as an alternative to the standard Proctor test and, in this case, it can save significant time, material, and effort.
- -
- The results show that the proposed ANN outperforms the MLR models and offers highly accurate predictions.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Networks |
| OMC | Optimum Moisture Content |
| MDD | Maximum Dry Density |
| LL | Liquid Limit |
| PL | Plastic Limit |
| PI | Plasticity Index |
| MLR | Multiple Linear Regression |
| %P(i) | Percentage of the Passing from Sieve (i) |
References
- Rakaraddi, P.G.; Gomarsi, V. Establishing Relationship between CBR with Different Soil Properties. Int. J. Res. Eng. Technol. 2015, 4, 182–188. [Google Scholar]
- Mousa, K.M.; Abdelwahab, H.T.; Hozayen, H.A. Models for estimating optimum asphalt content from aggregate gradation. Proc. Inst. Civ. Eng.-Constr. Mater. 2018, 174, 69–74. [Google Scholar] [CrossRef]
- Othman, K.M.M.; Abdelwahab, H. Prediction of the optimum asphalt content using artificial neural networks. Met. Mater. Eng. 2021, 27. [Google Scholar] [CrossRef]
- HMA Pavement Mix Type Selection Guide; Information Serise, 128; National Asphalt Pavement Association: Lanham, MD, USA; Federal Highway Administration: Washington, DC, USA, 2001.
- Sridharan, A.; Nagaraj, H.B. Plastic limit and compaction characteristics of finegrained soils. Proc. Inst. Civ. Eng.-Ground Improv. 2005, 9, 17–22. [Google Scholar] [CrossRef]
- Proctor, R. Fundamental Principles of Soil Compaction. Eng. News-Rec. 1933, 111, 245–248. [Google Scholar]
- Viji, V.K.; Lissy, K.F.; Sobha, C.; Benny, M.A. Predictions on compaction characteristics of fly ashes using regression analysis and artificial neural network analysis. Int. J. Geotech. Eng. 2013, 7, 282–291. [Google Scholar] [CrossRef]
- ASTM International. D 698: Standard Test Methods for Laboratory Compaction Characteristics Of Soil Using Standard Effort (12 400 Ftlbf/ft3 (600 Kn-m/m3); ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Zainal, A.K.E. Quick Estimation of Maximum Dry Unit Weight and Optimum Moisture Content from Compaction Curve Using Peak Functions. Appl. Res. J. 2016, 2, 472–480. [Google Scholar]
- Jumikis, A.R. Geology of Soils of the Newark (NJ) Metropolitan Area. J. Soil Mech. Found. ASCE 1946, 93, 71–95. [Google Scholar]
- Jumikis, A.R. Geology of Soils of the Newark (NJ) Metropolitan Area. J. Soil Mech. Found. Div. 1958, 84, 1–41. [Google Scholar] [CrossRef]
- Ring, G.W.; Sallberg, J.R.; Collins, W.H. Correlation Of Compaction and Classification Test Data. Highw. Res. Board Bull. 1962, 325, 55–75. [Google Scholar]
- Ramiah, B.K.; Viswanath, V.; Krishnamurthy, H.V. Interrelationship of compaction and index properties. In Proceedings of the 2nd South East Asian Conference on Soil Engineering, Singapore, 11–15 June 1970; Volume 587. [Google Scholar]
- Hammond, A.A. Evolution of One Point Method for Determining The Laboratory Maximum Dry Density. Proc. ICC 1980, 1, 47–50. [Google Scholar]
- Wang, M.C.; Huang, C.C. Soil Compaction and Permeability Prediction Models. J. Environ. Eng. 1984, 110, 1063–1083. [Google Scholar] [CrossRef]
- Sinha, S.K.; Wang, M.C. Artificial Neural Network Prediction Models for Soil Compaction and Permeability. Geotech. Geol. Eng. 2007, 26, 47–64. [Google Scholar] [CrossRef]
- Al-Khafaji, A.N. Estimation of soil compaction parameters by means of Atterberg limits. Q. J. Eng. Geol. Hydrogeol. 1993, 26, 359–368. [Google Scholar] [CrossRef]
- Blotz, L.R.; Benson, C.H.; Boutwell, G.P. Estimating Optimum Water Content and Maximum Dry Unit Weight for Compacted Clays. J. Geotech. Geoenviron. Eng. 1998, 124, 907–912. [Google Scholar] [CrossRef]
- Gurtug, Y.; Sridharan, A. Compaction Behaviour and Prediction of its Characteristics of Fine Grained Soils with Particular Reference to Compaction Energy. Soils Found. 2004, 44, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Suits, L.D.; Sheahan, T.; Sridharan, A.; Sivapullaiah, P. Mini Compaction Test Apparatus for Fine Grained Soils. Geotech. Test. J. 2005, 28, 240–246. [Google Scholar] [CrossRef]
- Di Matteo, L.; Bigotti, F.; Ricco, R. Best-Fit Models to Estimate Modified Proctor Properties of Compacted Soil. J. Geotech. Geoenviron. Eng. 2009, 135, 992–996. [Google Scholar] [CrossRef]
- Günaydın, O. Estimation of soil compaction parameters by using statistical analyses and artificial neural networks. Environ. Earth Sci. 2008, 57, 203–215. [Google Scholar] [CrossRef]
- Bera, A.; Ghosh, A. Regression model for prediction of optimum moisture content and maximum dry unit weight of fine grained soil. Int. J. Geotech. Eng. 2011, 5, 297–305. [Google Scholar] [CrossRef]
- Farooq, K.; Khalid, U.; Mujtaba, H. Prediction of Compaction Characteristics of Fine-Grained Soils Using Consistency Limits. Arab. J. Sci. Eng. 2015, 41, 1319–1328. [Google Scholar] [CrossRef]
- Ardakani, A.; Kordnaeij, A. Soil compaction parameters prediction using GMDH-type neural network and genetic algorithm. Eur. J. Environ. Civ. Eng. 2017, 23, 449–462. [Google Scholar] [CrossRef]
- Gurtug, Y.; Sridharan, A.; Ikizler, S.B. Simplified Method to Predict Compaction Curves and Characteristics of Soils. Iran. J. Sci. Technol. Trans. Civ. Eng. 2018, 42, 207–216. [Google Scholar] [CrossRef]
- Hussain, A.; Atalar, C. Estimation of compaction characteristics of soils using Atterberg limits. IOP Conf. Series Mater. Sci. Eng. 2020, 800, 012024. [Google Scholar] [CrossRef]
- Özbeyaz, A.; Söylemez, M. Modeling compaction parameters using support vector and decision tree regression algorithms. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 3079–3093. [Google Scholar] [CrossRef]
- ECP (Egyptian Code Provisions). ECP(104/4): Egyptian Code for Urban and Rural Roads; Part (4): Road Material and Its Tests; Housing and Building National Research Center: Cairo, Egypt, 2008. [Google Scholar]
- British Standard Institution. BS1377 Methods of Test for Soils for Civil Engineering Purposes; British Standards Institution: London, UK, 1990. [Google Scholar]
- Othman, K.; Abdelwahab, H. Using Deep Neural Networks for the Prediction of the Optimum Asphalt Content and the Asphalt mix Properties. 2021; in preparation. [Google Scholar]
- Othman, K.; Abdelwahab, H. Prediction of the Soil Compaction Parameters Using Deep Neural Networks. Transp. Infrastruct. Geotechnol. 2021. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks, a Comprehensive Foundation; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Liu, Y.; Starzyk, J.; Zhu, Z. Optimized Approximation Algorithm in Neural Networks without Overfitting. IEEE Trans. Neural Netw. 2008, 19, 983–995. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. A comparison of methods to avoid overfitting in neural networks training in the case of catchment runoff modelling. J. Hydrol. 2013, 476, 97–111. [Google Scholar] [CrossRef]
- Goodfellow, L.; Bengio, Y.; Courville, A. Deep Learning (Adaptive Computation and Machine Learning Series); MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Christopher, B. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Prechelt, L. Neural Networks: Tricks of the Trade; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1524, pp. 53–67. [Google Scholar]
- Alavi, A.H.; Gandomi, A.H.; Mollahassani, A.; Heshmati, A.A.; Rashed, A. Modeling of maximum dry density and optimum moisture content of stabilized soil using artificial neural networks. J. Plant Nutr. Soil Sci. 2010, 173, 368–379. [Google Scholar] [CrossRef]
- Kurnaz, T.F.; Kaya, Y. The performance comparison of the soft computing methods on the prediction of soil compaction parameters. Arab. J. Geosci. 2020, 13, 159. [Google Scholar] [CrossRef]
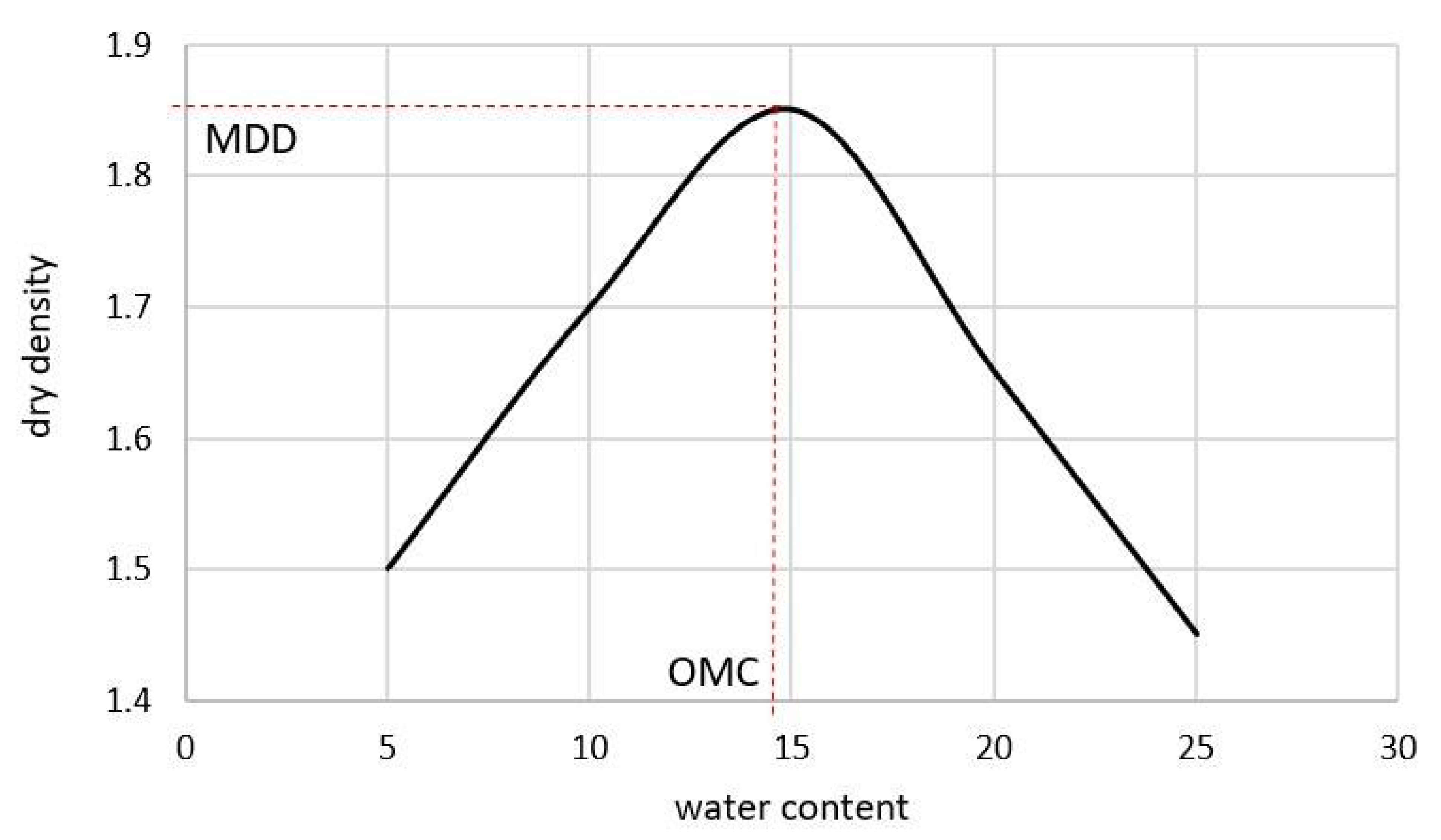
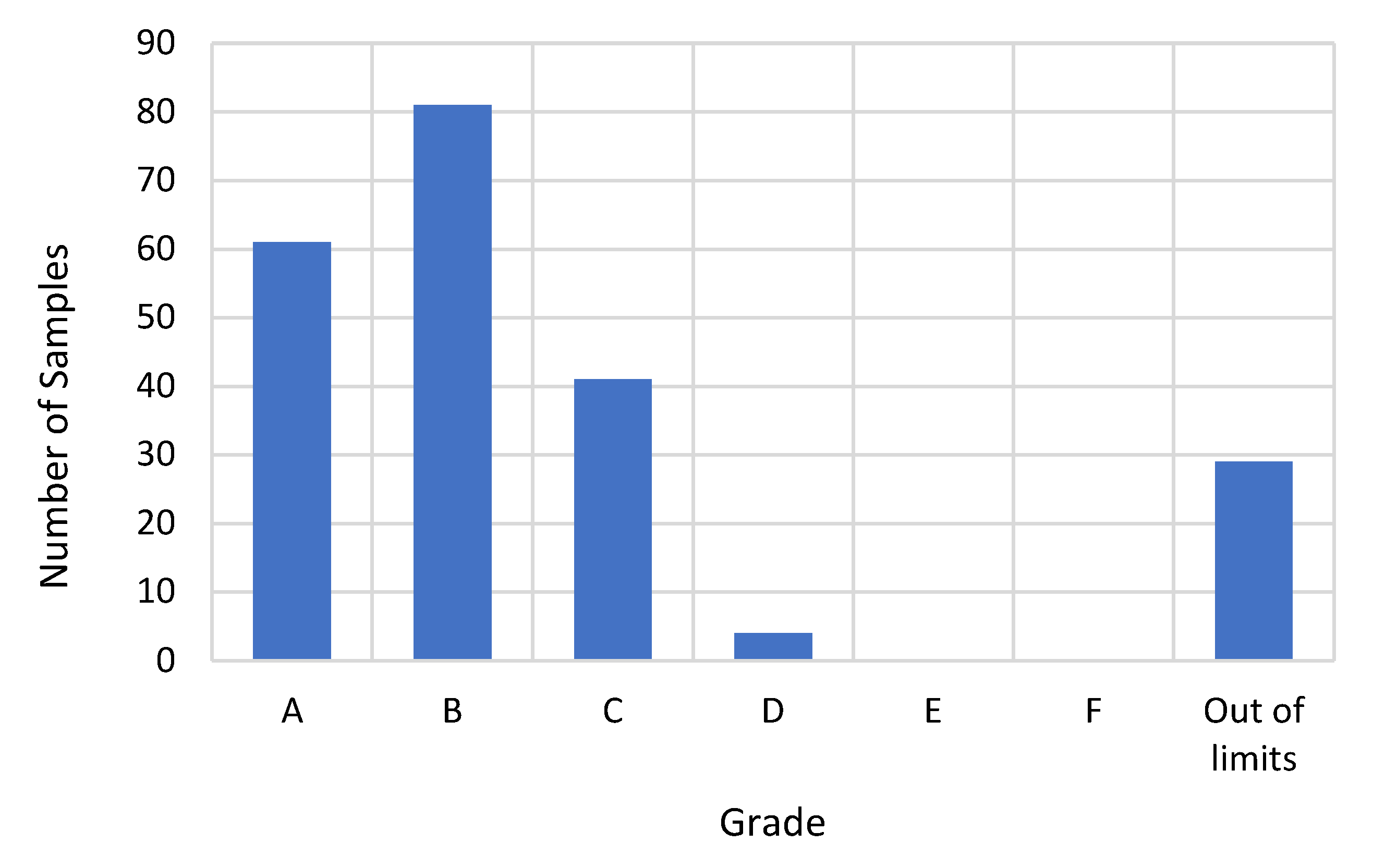
| Sieve Size | Limits | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | |||||||
| Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | Min | Max | |
| % Passing from sieve 2 in | 100 | 100 | 100 | 100 | 100 | 100 | ||||||
| % Passing from sieve 1.5 in | 70 | 100 | 100 | 100 | ||||||||
| % Passing from sieve 1 in | 55 | 85 | 75 | 95 | 70 | 100 | 100 | 100 | 100 | 100 | ||
| % Passing from sieve 3/4 in | 50 | 80 | 60 | 90 | 70 | 100 | ||||||
| % Passing from sieve 3/8 in | 30 | 65 | 40 | 70 | 40 | 75 | 45 | 75 | 50 | 85 | 50 | 80 |
| % Passing from sieve number 4 | 25 | 55 | 30 | 60 | 30 | 60 | 30 | 60 | 35 | 65 | 35 | 65 |
| % Passing from sieve number 10 | 15 | 40 | 20 | 50 | 20 | 45 | 20 | 50 | 25 | 50 | 25 | 50 |
| % Passing from sieve number 40 | 8 | 20 | 10 | 30 | 15 | 30 | 10 | 30 | 15 | 30 | 15 | 30 |
| % Passing from sieve number 200 | 2 | 8 | 5 | 15 | 5 | 20 | 5 | 15 | 5 | 15 | 5 | 15 |
| MDD | Number of Hidden Layers | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ReLu Activation Function | Sigmoid Activation Function | Tanh Activation Function | |||||||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| Number of Nuerons per Hidden Layer | 1 | 0.807 | 0.768 | 0.789 | 0.773 | 0.89 | 0.894 | 0.727 | 0.777 | 0.903 | 0.659 | 0.614 | 0.892 |
| 2 | 0.698 | 0.798 | 0.771 | 0.806 | 0.832 | 0.867 | 0.796 | 0.779 | 0.877 | 0.675 | 0.715 | 0.648 | |
| 3 | 0.75 | 0.759 | 0.752 | 0.729 | 0.843 | 0.809 | 0.687 | 0.744 | 0.708 | 0.792 | 0.559 | 0.844 | |
| 4 | 0.814 | 0.718 | 0.737 | 0.711 | 0.863 | 0.876 | 0.714 | 0.793 | 0.665 | 0.668 | 0.748 | 0.48 | |
| 5 | 0.677 | 0.777 | 0.816 | 0.793 | 0.79 | 0.649 | 0.829 | 0.747 | 0.652 | 0.882 | 0.471 | 0.754 | |
| 6 | 0.696 | 0.817 | 0.772 | 0.758 | 0.75 | 0.608 | 0.752 | 0.548 | 0.585 | 0.784 | 0.756 | 0.683 | |
| 7 | 0.66 | 0.656 | 0.777 | 0.8 | 0.768 | 0.741 | 0.756 | 0.761 | 0.778 | 0.709 | 0.781 | 0.42 | |
| 8 | 0.766 | 0.791 | 0.775 | 0.757 | 0.785 | 0.835 | 0.711 | 0.743 | 0.636 | 0.772 | 0.868 | 0.478 | |
| 9 | 0.831 | 0.761 | 0.697 | 0.683 | 0.863 | 0.86 | 0.805 | 0.675 | 0.473 | 0.544 | 0.294 | 0.773 | |
| 10 | 0.644 | 0.71 | 0.73 | 0.652 | 0.739 | 0.852 | 0.877 | 0.648 | 0.841 | 0.779 | 0.489 | 0.498 | |
| 11 | 0.651 | 0.715 | 0.742 | 0.675 | 0.811 | 0.684 | 0.843 | 0.725 | 0.621 | 0.599 | 0.455 | 0.936 | |
| 12 | 0.728 | 0.648 | 0.657 | 0.63 | 0.724 | 0.631 | 0.721 | 0.76 | 0.451 | 0.762 | 0.664 | 0.796 | |
| 13 | 0.692 | 0.653 | 0.657 | 0.657 | 0.707 | 0.765 | 0.549 | 0.604 | 0.538 | 0.756 | 0.797 | 0.392 | |
| 14 | 0.773 | 0.718 | 0.64 | 0.653 | 0.632 | 0.498 | 0.739 | 0.644 | 0.667 | 0.624 | 0.885 | 0.493 | |
| 15 | 0.73 | 0.663 | 0.649 | 0.644 | 0.748 | 0.529 | 0.81 | 0.69 | 0.51 | 0.656 | 0.711 | 0.349 | |
| 16 | 0.754 | 0.658 | 0.653 | 0.657 | 0.765 | 0.827 | 0.532 | 0.651 | 0.447 | 0.904 | 0.52 | 0.228 | |
| 17 | 0.656 | 0.653 | 0.727 | 0.75 | 0.799 | 0.768 | 0.742 | 0.651 | 0.587 | 0.574 | 0.749 | 0.292 | |
| 18 | 0.642 | 0.655 | 0.553 | 0.685 | 0.621 | 0.411 | 0.572 | 0.669 | 0.497 | 0.766 | 0.315 | 0.596 | |
| 19 | 0.656 | 0.614 | 0.675 | 0.657 | 0.654 | 0.746 | 0.752 | 0.563 | 0.694 | 0.491 | 0.782 | 0.231 | |
| 20 | 0.644 | 0.635 | 0.638 | 0.649 | 0.894 | 0.629 | 0.579 | 0.668 | 0.532 | 0.712 | 0.687 | 0.318 | |
| OMC | Number of Hidden Layers | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ReLu Activation Function | Sigmoid Activation Function | Tanh Activation Function | |||||||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| Number of Neurons per Hidden Layer | 1 | 0.79 | 0.766 | 0.781 | 0.783 | 0.848 | 0.92 | 0.814 | 0.832 | 0.928 | 0.821 | 0.772 | 0.93 |
| 2 | 0.724 | 0.812 | 0.75 | 0.8 | 0.878 | 0.929 | 0.817 | 0.836 | 0.794 | 0.69 | 0.575 | 0.458 | |
| 3 | 0.767 | 0.803 | 0.784 | 0.707 | 0.826 | 0.846 | 0.771 | 0.802 | 0.814 | 0.777 | 0.655 | 0.887 | |
| 4 | 0.756 | 0.668 | 0.671 | 0.725 | 0.798 | 0.846 | 0.717 | 0.785 | 0.625 | 0.52 | 0.818 | 0.538 | |
| 5 | 0.785 | 0.867 | 0.754 | 0.729 | 0.874 | 0.63 | 0.896 | 0.687 | 0.547 | 0.558 | 0.486 | 0.683 | |
| 6 | 0.793 | 0.754 | 0.675 | 0.755 | 0.75 | 0.61 | 0.82 | 0.527 | 0.662 | 0.568 | 0.83 | 0.635 | |
| 7 | 0.773 | 0.717 | 0.711 | 0.65 | 0.638 | 0.642 | 0.771 | 0.774 | 0.77 | 0.617 | 0.452 | 0.772 | |
| 8 | 0.796 | 0.794 | 0.769 | 0.734 | 0.731 | 0.714 | 0.684 | 0.752 | 0.636 | 0.775 | 0.273 | 0.335 | |
| 9 | 0.704 | 0.644 | 0.779 | 0.679 | 0.862 | 0.792 | 0.699 | 0.627 | 0.685 | 0.573 | 0.744 | 0.591 | |
| 10 | 0.87 | 0.579 | 0.604 | 0.613 | 0.683 | 0.535 | 0.732 | 0.724 | 0.739 | 0.693 | 0.364 | 0.215 | |
| 11 | 0.629 | 0.672 | 0.669 | 0.603 | 0.558 | 0.753 | 0.676 | 0.571 | 0.595 | 0.478 | 0.37 | 0.72 | |
| 12 | 0.662 | 0.596 | 0.604 | 0.68 | 0.726 | 0.498 | 0.719 | 0.728 | 0.426 | 0.931 | 0.291 | 0.478 | |
| 13 | 0.615 | 0.6 | 0.611 | 0.733 | 0.705 | 0.742 | 0.801 | 0.66 | 0.312 | 0.795 | 0.469 | 0.563 | |
| 14 | 0.852 | 0.679 | 0.654 | 0.598 | 0.683 | 0.523 | 0.732 | 0.801 | 0.527 | 0.845 | 0.636 | 0.28 | |
| 15 | 0.644 | 0.698 | 0.608 | 0.591 | 0.566 | 0.726 | 0.684 | 0.703 | 0.533 | 0.573 | 0.783 | 0.223 | |
| 16 | 0.825 | 0.634 | 0.585 | 0.663 | 0.79 | 0.714 | 0.681 | 0.625 | 0.629 | 0.357 | 0.263 | 0.28 | |
| 17 | 0.629 | 0.622 | 0.556 | 0.577 | 0.843 | 0.546 | 0.812 | 0.428 | 0.464 | 0.462 | 0.59 | 0.308 | |
| 18 | 0.612 | 0.617 | 0.76 | 0.665 | 0.696 | 0.734 | 0.533 | 0.621 | 0.305 | 0.613 | 0.23 | 0.435 | |
| 19 | 0.615 | 0.599 | 0.591 | 0.595 | 0.606 | 0.595 | 0.79 | 0.403 | 0.507 | 0.469 | 0.424 | 0.15 | |
| 20 | 0.644 | 0.633 | 0.622 | 0.617 | 0.76 | 0.467 | 0.555 | 0.719 | 0.545 | 0.525 | 0.608 | 0.744 | |
| Balanced | Number of Hidden Layers | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ReLu Activation Function | Sigmoid Activation Function | Tanh Activation Function | |||||||||||
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | ||
| Number of Neurons per Hidden Layer | 1 | 0.7985 | 0.767 | 0.785 | 0.778 | 0.869 | 0.907 | 0.7705 | 0.8045 | 0.9155 | 0.74 | 0.693 | 0.911 |
| 2 | 0.711 | 0.805 | 0.7605 | 0.803 | 0.855 | 0.898 | 0.8065 | 0.8075 | 0.8355 | 0.6825 | 0.645 | 0.553 | |
| 3 | 0.7585 | 0.781 | 0.768 | 0.718 | 0.83s45 | 0.8275 | 0.729 | 0.773 | 0.761 | 0.7845 | 0.607 | 0.8655 | |
| 4 | 0.785 | 0.693 | 0.704 | 0.718 | 0.8305 | 0.861 | 0.7155 | 0.789 | 0.645 | 0.594 | 0.783 | 0.509 | |
| 5 | 0.731 | 0.822 | 0.785 | 0.761 | 0.832 | 0.6395 | 0.8625 | 0.717 | 0.5995 | 0.72 | 0.4785 | 0.7185 | |
| 6 | 0.7445 | 0.7855 | 0.7235 | 0.7565 | 0.75 | 0.609 | 0.786 | 0.5375 | 0.6235 | 0.676 | 0.793 | 0.659 | |
| 7 | 0.7165 | 0.6865 | 0.744 | 0.725 | 0.703 | 0.6915 | 0.7635 | 0.7675 | 0.774 | 0.663 | 0.6165 | 0.596 | |
| 8 | 0.781 | 0.7925 | 0.772 | 0.7455 | 0.758 | 0.7745 | 0.6975 | 0.7475 | 0.636 | 0.7735 | 0.5705 | 0.4065 | |
| 9 | 0.7675 | 0.7025 | 0.738 | 0.681 | 0.8625 | 0.826 | 0.752 | 0.651 | 0.579 | 0.5585 | 0.519 | 0.682 | |
| 10 | 0.757 | 0.6445 | 0.667 | 0.6325 | 0.711 | 0.6935 | 0.8045 | 0.686 | 0.79 | 0.736 | 0.4265 | 0.3565 | |
| 11 | 0.64 | 0.6935 | 0.7055 | 0.639 | 0.6845 | 0.7185 | 0.7595 | 0.648 | 0.608 | 0.5385 | 0.4125 | 0.828 | |
| 12 | 0.695 | 0.622 | 0.6305 | 0.655 | 0.725 | 0.5645 | 0.72 | 0.744 | 0.4385 | 0.8465 | 0.4775 | 0.637 | |
| 13 | 0.6535 | 0.6265 | 0.634 | 0.695 | 0.706 | 0.7535 | 0.675 | 0.632 | 0.425 | 0.7755 | 0.633 | 0.4775 | |
| 14 | 0.8125 | 0.6985 | 0.647 | 0.6255 | 0.6575 | 0.5105 | 0.7355 | 0.7225 | 0.597 | 0.7345 | 0.7605 | 0.3865 | |
| 15 | 0.687 | 0.6805 | 0.6285 | 0.6175 | 0.657 | 0.6275 | 0.747 | 0.6965 | 0.5215 | 0.6145 | 0.747 | 0.286 | |
| 16 | 0.7895 | 0.646 | 0.619 | 0.66 | 0.7775 | 0.7705 | 0.6065 | 0.638 | 0.538 | 0.6305 | 0.3915 | 0.254 | |
| 17 | 0.6425 | 0.6375 | 0.6415 | 0.6635 | 0.821 | 0.657 | 0.777 | 0.5395 | 0.5255 | 0.518 | 0.6695 | 0.3 | |
| 18 | 0.627 | 0.636 | 0.6565 | 0.675 | 0.6585 | 0.5725 | 0.5525 | 0.645 | 0.401 | 0.6895 | 0.2725 | 0.5155 | |
| 19 | 0.6355 | 0.6065 | 0.633 | 0.626 | 0.63 | 0.6705 | 0.771 | 0.483 | 0.6005 | 0.48 | 0.603 | 0.1905 | |
| 20 | 0.644 | 0.634 | 0.63 | 0.633 | 0.827 | 0.548 | 0.567 | 0.6935 | 0.5385 | 0.6185 | 0.6475 | 0.531 | |
| Optimum ANN for Every Output | Optimum ANN for Both Predictions | R2 Difference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hidden Layers | Neurons/Layer | Activation Function | R2 (MDD) | R2 (OMC) | Hidden Layers | Neurons/Layer | Activation Function | R2 | ||
| MDD | 4 | 11 | Tanh | 0.936 | 0.72 | 1 | 1 | Tanh | 0.903 | 0.033 |
| OMC | 2 | 12 | Tanh | 0.762 | 0.931 | 0.928 | 0.003 | |||
| Study | R2 for the OMC | R2 for the MDD |
|---|---|---|
| Günaydın (2009) [22] | 0.837 | 0.793 |
| Alavi et al. (2010) [40] | 0.89 | 0.91 |
| Kurnaz and Kaya (2020) [41] | 0.85 | 0.86 |
| Özbeyaz and Solyemez (2020) [28] | 0.83 | 0.71 |
| Proposed ANN | 0.903 | 0.928 |
| Model | Excluded Variables | R | R Square | Adjusted R Square | Std. Error of the Estimate |
|---|---|---|---|---|---|
| 1 | - | 0.646 | 0.418 | 0.281 | 0.070509 |
| 2 | %P (1.5 in) | 0.646 | 0.418 | 0.295 | 0.069828 |
| 3 | %P (1.5 in), %P (3/8 in) | 0.646 | 0.417 | 0.307 | 0.069194 |
| 4 | %P (1.5 in), %P (3/8 in), %P(2 in) | 0.646 | 0.417 | 0.32 | 0.068589 |
| 5 | %P (1.5 in), %P (3/8 in), %P(2 in), LL | 0.643 | 0.414 | 0.329 | 0.068118 |
| 6 | %P (1.5 in), %P (3/8 in), %P(2 in), LL, %P(0.5 in) | 0.635 | 0.403 | 0.329 | 0.068119 |
| 7 | %P (1.5 in), %P (3/8 in), %P(2 in), LL, %P(0.5 in), %P (3/4 in) | 0.630 | 0.396 | 0.333 | 0.067909 |
| 8 | %P (1.5 in), %P (3/8 in), %P(2 in), LL, %P(0.5 in), %P (1 in) | 0.628 | 0.395 | 0.343 | 0.067409 |
| Model | Excluded Variables | R | R Square | Adjusted R Square | Std. Error of the Estimate |
|---|---|---|---|---|---|
| 1 | - | 0.673 | 0.453 | 0.325 | 1.4857 |
| 2 | %P (#4) | 0.673 | 0.453 | 0.338 | 1.4714 |
| 3 | %P (#4), %P(0.5 in) | 0.673 | 0.452 | 0.349 | 1.4586 |
| 4 | %P (#4), %P(0.5 in), %P(2 in) | 0.672 | 0.451 | 0.36 | 1.4467 |
| 5 | %P (#4), %P(0.5 in), %P(2 in), %P (1.5 in) | 0.671 | 0.45 | 0.37 | 1.4349 |
| 6 | %P (#4), %P(0.5 in), %P(2 in), %P (1.5 in), LL | 0.670 | 0.448 | 0.379 | 1.4244 |
| 7 | %P (#4), %P(0.5 in), %P(2 in), %P (1.5 in), LL, %P (3/8 in) | 0.658 | 0.433 | 0.373 | 1.4313 |
| 8 | %P (#4), %P(0.5 in), %P(2 in), %P (1.5 in), LL, %P (3/8 in), %P (#10) | 0.650 | 0.423 | 0.373 | 1.4312 |
| 9 | %P (#4), %P(0.5 in), %P(2 in), %P (1.5 in), LL, %P (3/8 in), %P (#10), %P(#40) | 0.644 | 0.415 | 0.375 | 1.4288 |
| 10 | %P (#4), %P(0.5 in), %P(2 in), %P (1.5 in), LL, %P (3/8 in), %P (#10), %P(#40), %P (3/4 in) | 0.638 | 0.407 | 0.377 | 1.4271 |
| 11 | %P (#4), %P(0.5 in), %P(2 in), %P (1.5 in), LL, %P (3/8 in), %P (#10), %P(#40), %P (3/4 in), %P (1in) | 0.627 | 0.393 | 0.374 | 1.4311 |
| Model-8 | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |
|---|---|---|---|---|---|
| B | Std. Error | Beta | |||
| (Constant) | 2.289 | 0.069 | 32.942 | 0 | |
| Passing Sieve Number 4 | 0.009 | 0.004 | 0.649 | 2.176 | 0.034 |
| Passing Sieve Number 10 | −0.015 | 0.007 | −0.984 | −2.114 | 0.039 |
| Passing Sieve Number 40 | 0.01 | 0.006 | 0.664 | 1.852 | 0.045 |
| PassingSieveNO200 | −0.015 | 0.003 | −0.771 | −4.252 | 0 |
| Plastic Limit | −0.005 | 0.003 | −0.191 | −1.815 | 0.048 |
| Model-11 | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | |
|---|---|---|---|---|---|
| B | Std. Error | Beta | |||
| (Constant) | 2.957 | 1.092 | 2.708 | 0.009 | |
| Passing Sieve number 200 | 0.239 | 0.041 | 0.577 | 5.763 | 0 |
| PlasticLimit | 0.105 | 0.053 | 0.198 | 1.974 | 0.05 |
| R-Square Value | |||||||
|---|---|---|---|---|---|---|---|
| MLR | Optimum ANN for the MDD | Optimum ANN for the OMC | Optimum ANN for Both OMC and MDD | ||||
| MDD | OMC | MDD | OMC | MDD | OMC | MDD | OMC |
| 0.395 | 0.393 | 0.936 | 0.72 | 0.931 | 0.762 | 0.903 | 0.928 |
| Optimum ANN for Every Output | |||
|---|---|---|---|
| Hidden Layers | Neurons/Layer | Activation Function | |
| MDD | 4 | 11 | Tanh |
| OMC | 2 | 12 | Tanh |
| Both (OMC and MDD) | 1 | 1 | Tanh |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Othman, K. Deep Neural Network Models for the Prediction of the Aggregate Base Course Compaction Parameters. Designs 2021, 5, 78. https://doi.org/10.3390/designs5040078
Othman K. Deep Neural Network Models for the Prediction of the Aggregate Base Course Compaction Parameters. Designs. 2021; 5(4):78. https://doi.org/10.3390/designs5040078
Chicago/Turabian StyleOthman, Kareem. 2021. "Deep Neural Network Models for the Prediction of the Aggregate Base Course Compaction Parameters" Designs 5, no. 4: 78. https://doi.org/10.3390/designs5040078
APA StyleOthman, K. (2021). Deep Neural Network Models for the Prediction of the Aggregate Base Course Compaction Parameters. Designs, 5(4), 78. https://doi.org/10.3390/designs5040078






