End Effects and Geometric Compensation in Linear Permanent Magnet Synchronous Generators with Different Topologies ^†

Abstract

Electricity production from ocean waves with different solutions is a topic of major research interest. Many of such designs are based on linear generators that inherently introduce end forces. In this paper, detent force using Maxwell Stress Tensor and induced voltage is initially investigated for two different winding patterns for a generator topology with buried magnets in a finite element software. Two ways of overcoming the end forces are further examined: the first method reduces the magnetic flux variations of the translator between stator and air. The second method aims at countering the end forces at both ends for full active stator area. A comparison is then made between buried and surface-mounted topologies for the second end effect compensation method. Both no-load and load conditions are investigated in the comparison. The end effect compensation shows promising results for both topologies. Some clear similarities of the extended stator used to counter the end forces are also apparent, where the stator extensions completely cover the outer poles of both topologies. The results also indicate a longer full active stator area for the buried topology for the same pole-pitch and stroke length, resulting in a higher average voltage for partial stator overlap.

1. Introduction

Linear electrical machines, though much less common than rotating electrical machines, can be utilized in several applications such as wave-powered electricity generation. The basic working principles for linear electrical machines and their rotating counterpart are in several aspects the same. However, in a linear electrical machine, there are open ends that cause an uneven flux distribution both in regards to the transition between air and stator iron and, as for a buried topology, the reduced flux for the outer poles [1]. The open ends also mean that the overlap between the translator, the moving part of the linear electrical machine, and the stator can vary. Further, the open ends lead to some special traits of the linear electrical machines, for example, that the stator experiences a varied number of poles for a partial stator overlap. As shown in [2], the flux distribution varies depending on if an even or odd number of poles are used, which means that the flux distribution will change when there is partial stator overlap.

Similar to the rotating permanent magnet (PM) machine topologies, there is a broad range in PM placement and utilization in linear electrical machines as well. The linear electrical PM machines can be constructed with surface-mounted PMs [3,4,5], buried PMs (also called sandwich-mounted PMs) [6], or a Halbach array [7]. The PMs are often placed on the moving translator but can also be placed on the stator to utilize the magnetic gearing effect in a linear Vernier hybrid machine for both surface-mounted [8] and buried (in this case V-shaped) [9] PMs.

When using buried PMs in a linear generator, the open ends for the outer poles of the translator result in different end forces compared to surface-mounted PMs. The flux concentration topology for buried PMs also results in different end forces in regards to the stator ends. The end forces combined with the cogging forces result in detent forces. The detent force can be approximated as a sum of sine-functions with periodicities depending on the different force components [4,10]. In the generator presented in [11], the three phases were separated into different stator packages. An advantage of this is that the detent forces can be reduced as the force peaks occur at different times. To further protect the brittle surfaces of the ferrite magnets, rubber films were placed between the magnets and pole shoes, which also could dampen forces in the longitudinal direction [12,13].

End forces of linear machines and ways of reducing these forces have been investigated in earlier studies. One study approximates the flux distribution to a reluctance model through a magnetic field similarity method and investigates end-teeth variations to counter the end forces under no-load, derived through virtual work [3]. One study separates the stator block into sections with two phases in each block to counter the end forces [14]. Another study adds assistant teeth and notes the different magnitudes in phase voltages for windings closer to the stator ends [15]. For a linear Vernier hybrid machine, the force ripple and cogging have been minimized by optimizing the consequent poles, translator poles, and PM width [16]. The study most similar to this paper studied surface-mounted PMs where the length of the end teeth are changed to reduce the end forces, where the end forces are calculated using inductance formulations derived from a frozen permeability technique [17]. The study by Yao et al. [17], however, has a greater focus on the skewing effects of the linear machine. Most end force optimization studies on linear electrical machines are done for surface-mounted PMs [3,14,16,17].

The translator can, during operation, fully or partially overlap the stator. The partial overlap of the stator can be significant, unless the relative length of the stator is short compared to the translator. The stator can also be made much longer than the translator to have a constant partial overlap during operation [18]. Partial overlap has previously been studied both experimentally [4,6,19] and through simulations [4,5], though there is still more to learn. As for the studies on end-force minimization, most of the studies for partial overlap are also done for surface-mounted PMs [4,5,18,19]. According to [6], the induced voltage should decrease linearly with decreasing stator overlap and thereby the power generation should decrease quadratically. In [4], it was observed that the cogging force is larger when the stator is fully overlapped.

The longitudinal ends of a linear electrical machine influence the flux distribution significantly [2], can cause non-negligible end forces [14], and can have a dominating effect on the thrust ripple [17], making it a topic worth investigating further.

In this paper, the detent forces and induced voltages are initially investigated in a linear synchronous generator with buried PMs through finite element simulations. Alterations of the stator ends to reduce the detent forces are also proposed and investigated through simulations. A preliminary force comparison between Maxwell Stress Tensor (MST) and Virtual Work (VW) is done to show that the results of the two methods match. The linear synchronous generator with PMs (LPMSG) has a stator that is shorter than the translator and can during operation have partial stator overlap. The influence of partial overlap can thus be studied for detent forces, attraction force, and induced voltage. The buried topology is further compared to a topology with surface-mounted PMs. Currents in the stator windings are also introduced to see if similar behavior in end force reduction can be achieved under load. The magnitude of the power associated with the electric current and the detent forces can ultimately be compared to further verify the validity of the results.

2. Method

2.1. Force Calculations

The electromagnetic forces in an electrical machine can be derived in several ways, whereof one common way is to use the principle of Virtual Work (VW), which is used by, e.g., [3,5,7]. When utilizing the principle of VW, the force in the y-direction is calculated as the gradient of the magnetic co-energy: $F=\frac{\partial W_{\varphi }}{\partial \mathbf{y}}$. The magnetic co-energy is expressed as

$$W_{\varphi }={\int }_V\left({\int }_0^{H}BdH\right)dV.$$

(1)

For a linear case, such as air, the inner integration can be simplified to ${\int }_0^{H}BdH=\frac{\mu }{2}{\left|H\right|}^2$ [20]. The force calculation using virtual work is more often used in rotating machines when the relevant air is enclosed between the rotor and stator. For linear generators, the translator does not enclose the stator, or vice versa, leading to non-negligible flux passing between the stator and the translator on the upper and lower sides of the stator. The flux passing through the translator ends is greater for a linear generator with buried PMs than it is for surfance-mounted PMs.

Another way to calculate the force is the line integration of Maxwell’s stress tensor (MST) [21] (ch.1). This is used by, e.g., [22,23]. The tangential magnetic component of the stress tensor, or in this case the y-direction, is given by

$${\sigma }_y=\frac{1}{{\mu }_0}{B}_y{B}_x.$$

(2)

The total tangential force for a rotating electrical machine is expressed as the line integral enclosing the rotor and further averaged over the air gap, resulting in Arkkio’s method [21,24] (p. 56). For a linear electrical machine, the line integral is instead a line enclosing the translator. Ergo, the line integral runs through the air gap and splits the translator from the stator. The line on the opposite side of the translator is arbitrary. Having it at the border of the translator gives, as one might expect, negligible force. The line integration of the tangential stress tensor is, however, sensitive to the mesh [1]. Therefore, the same principle as Arkkio’s method is used, where the line integration is averaged over the air gap by integrating the tangential stress tensor over the air gap surface and dividing by the length of the air gap. Rather than torque, the force F is expressed as

$$F=\frac{l}{{\mu }_0{l}_{ag}}{\int }_S{B}_x{B}_{y}dS.$$

(3)

where l is the stack length of the machine, ${\mu }_0$ is the permeability of the vacuum, $l_{ag}$ is the length of the air gap, S is the area of the air gap, and B is the magnetic flux density. The force F is calculated instead of torque, since there ideally should be no torque in a linear electrical machine.

When using Maxwell stress tensor, one does not have to look at all domains with a significant flux density: only a boundary that encloses the translator (or stator). This is illustrated in Figure 1 for the slot per pole and phase, $q=1$, which shows that the detent force from Maxwell stress tensor (MST) is equal to the total detent force from virtual work for all domains (VW All) for an incremental displacement of one pole-pitch ${\tau }_p$. The end position of the displacement is when the generator reaches full stator overlap at $t=0.6$ s. It also shows two components of the virtual work outside of the air-gap domain that are not negligible: the domains above and below the stator (ABS) and the domains within the stator slots (VW $S_{slots}$).

These two force contributions give a clear representation of the detent forces in the linear generator for $q=1$: cogging force of three times the frequency of the pole pitch and the end force with a period the same as the pole pitch. In the figure, the same two contributions are plotted for the starting position of 50% stator overlap for half a pole pitch. From this, one can see that the cogging force increases with stator overlap, while the magnitude of the end force remains the same with less than 100% stator overlap. As the Maxwell Stress Tensor is based on the values given at the closed surface around the translator, it is more difficult to determine the separate contributions of end effects and cogging effects in comparison to the use of virtual work.

Similar to the tangential forces, one can calculate the attraction forces (normal forces) from the stress tensor elements given in (4). The force is acquired from the surface integral of the same boundaries as in (3).

$${\sigma }_n=\frac{1}{2}{\mu }_0(H_x^2-H_y^2),$$

(4)

where $H_x$ and $H_y$ are the normal and tangential components of the magnetic field strength, respectively.

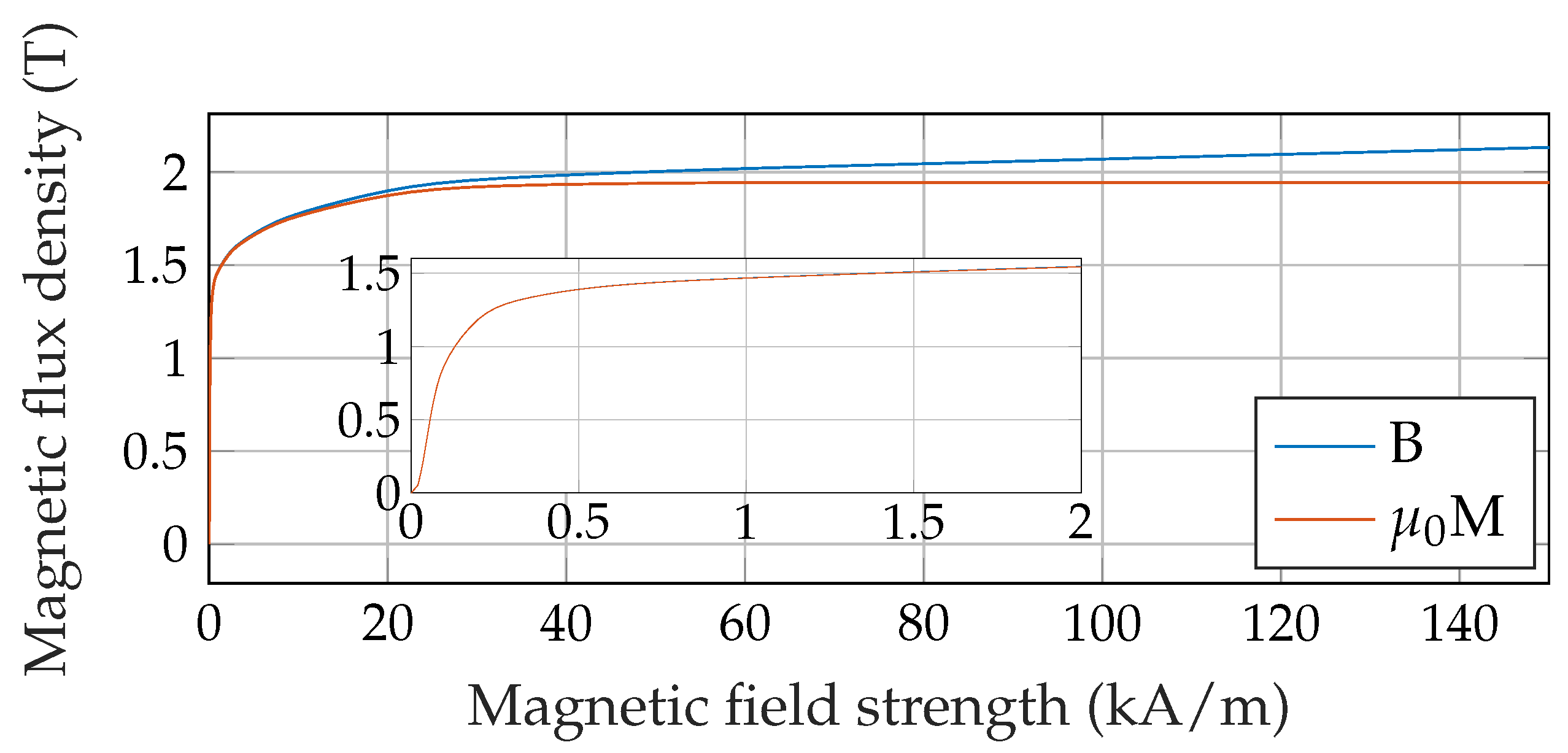
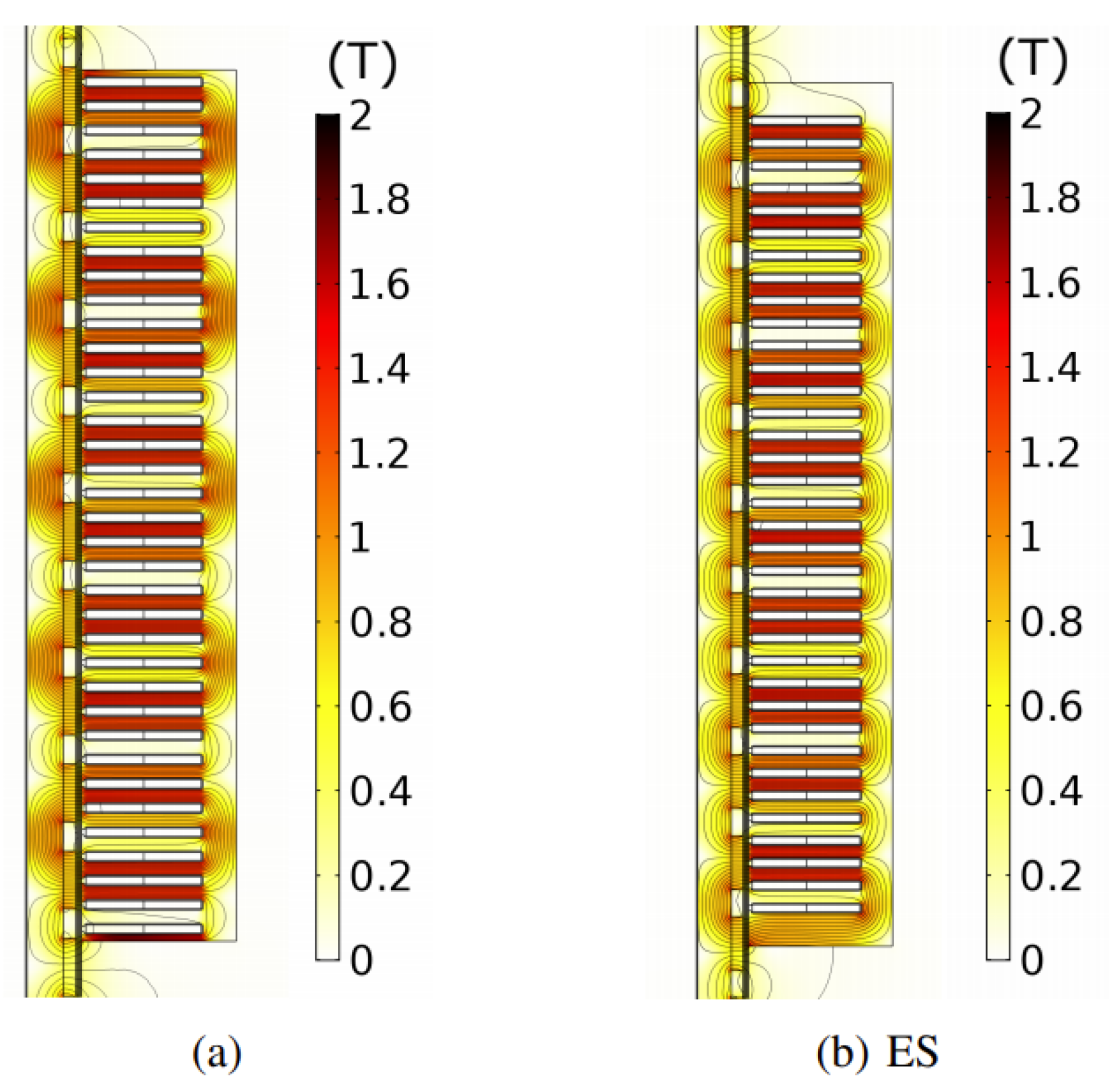
2.2. Finite Element Simulations

The software used in the simulations is the finite element software COMSOL Multiphysics^TM (COMSOL Multiphysics^® is a Trademark of COMSOL AB). In the simulations for the buried topology, a translator with pole shoes and buried permanent magnets of alternating polarity are used. The PMs are rectangular, while the pole shoes are slightly extruded towards the air gap and have a rounded surface towards the air gap. The PM sizes of the flux concentrating topology are dimensioned to reach an adequate flux density level in the stator. The top and bottom pole shoes were split into halves. An example of buried PMs can be seen in Figure 2, together with the different winding patterns and the coordinate system used in this paper.

The numbers of slots per pole and per phase q used in this paper are 1 and 6/5, respectively. The translator is kept the same, while the number of slots are set to match the two winding topologies and the slot-pitch is determined by q and ${\tau }_p$. The windings closest to the stator yoke is shifted by one for $q=1$, reducing the thirdrd harmonic, with a trade-off of an increased fifth harmonic [1]. The cables are rectangular and take up 33% of the slot-pitch with 1 mm space on either side of the cables, representing the non-magnetic insulation. In the simulation model, this space is filled with air. The length of the stator tooth is then expressed as the remainder of the slot-pitch.

The full active stator area covers 10 pole-pitches, but to allow for partial translator overlap with a maintained full stator overlap, 6 more PMs are added. From Figure 2, one can see that each pole-pitch overlaps exactly three stator slots for $q=1$ and slightly more than three slots for $q=\frac{6}{5}$. As all PMs for $q=1$ enter a new slot at the same time, the cogging force is much higher for integer q numbers. Translator and stator parameters used in the simulation for the buried topology can be seen in

Table 1. Translator parameters.

	Buried	Surface
$B_{\mathrm{r}}$	0.45	1.2
${\mu }_{\mathrm{r}}$	1.016	1.05
${\left(BH\right)}_{\max }$	$39.67\mathrm{kJ}/{\mathrm{m}}^3$	-
pole-pitch ${\tau }_p$	60 mm	60 mm
${\mathrm{PM}}_{\mathrm{x}}$	90 mm	8.6 mm
${\mathrm{PM}}_{\mathrm{y}}$	30 mm	40 mm
Yoke	-	25 mm
Translator iron	Silicon Steel NGO 50PN270

and

Table 2. Stator parameters.

	Parameter Values
Slot depth	81.875 mm
Slot face	1.875 mm × 3.75 mm
Copper	33%
Cable insulation (air)	1 mm
Yoke	24.8 mm
Stator iron	Silicon Steel NGO 50PN270

, respectively.

The formulation for the PMs are based on the relative permeability ${\mu }_{\mathrm{r}}$ and the remanent magnetic flux density $B_{\mathrm{r}}$ and given as

$$B={\mu }_0{\mu }_{\mathrm{r}}H+B_{\mathrm{r}}.$$

(5)

Assuming a linear BH-curve in the second quadrant until the point of maximum energy product, the relative permeability ${\mu }_r$ is given by

$${\mu }_{\mathrm{r}}=\frac{B_{\mathrm{r}}^2}{4{\mu }_0{\left(BH\right)}_{\max }}$$

(6)

where ${\left(BH\right)}_{\max }$ is the maximum energy product. In the simulations for the buried topology, ferrites of grade Y40 are used. Values for $B_{\mathrm{r}}$ and ${\left(BH\right)}_{\max }$ are taken from online (https://e-magnetsuk.com/ferrite_magnets/ferrite_grades.aspx, accessed on 3 December 2020).

The stator iron and translator pole shoes are of Silicon Steel NGO 50PN270, taken from COMSOL material library. The non-linear BH-curve can be seen in Figure 3. Induced eddy currents and hysteresis losses are not considered in the study. The translator and its adjacent moving boundary has a constant velocity set to 0.5 m/s. The detent force and induced voltage are calculated for a stack length of 1 m. It can thus directly correspond to the force and voltage per unit of stack length.

The simulations are conducted in a two-dimensional finite element environment with the formulation for the Magnetic vector potential. The translator motion is acquired by using a moving mesh. A continuous boundary between the two bodies enforces a continuous magnetic vector potential at the boundary. The air gap is separated into layers, which, together with a quadratic discretization, increases the accuracy of the model. The coil groups are assumed homogeneous, with a uniform current density for each phase. The mesh is finer in the translator and the stator. The mesh is extra-fine in the air gap, since the boundary between the moving domain and the stationary domain is located in the air gap, and many of the data presented in the results are retrieved from the air gap. The complete mesh consists of a total of 171,056 elements in the simulation files with buried topology and of totally 151,931 elements in the simulations files with surface-mounted topology. The configuration of the finite element environment is also detailed in [1].

A preliminary comparison between experimental results and the simulated linear generator of a buried topology can be seen in [1]. Experimental measurements show similar behaviour for partial stator overlap and the ripple associated with the detent forces.

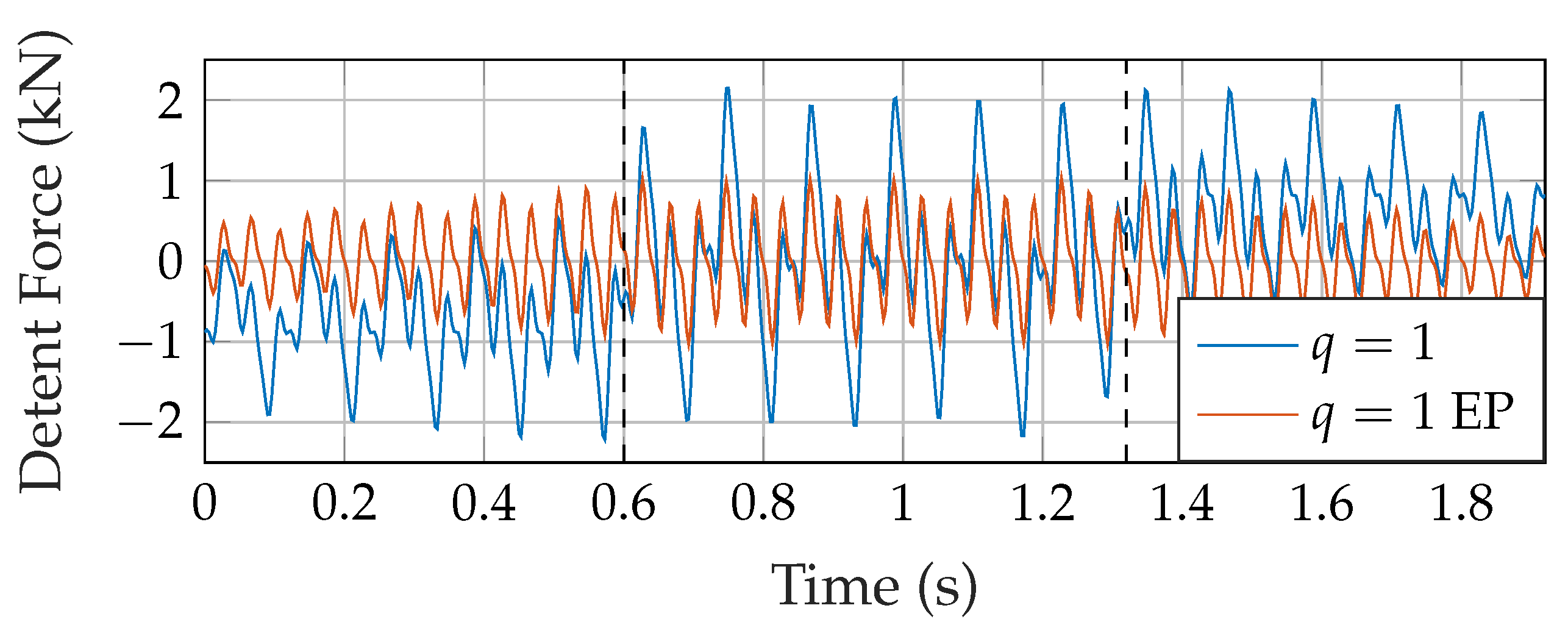
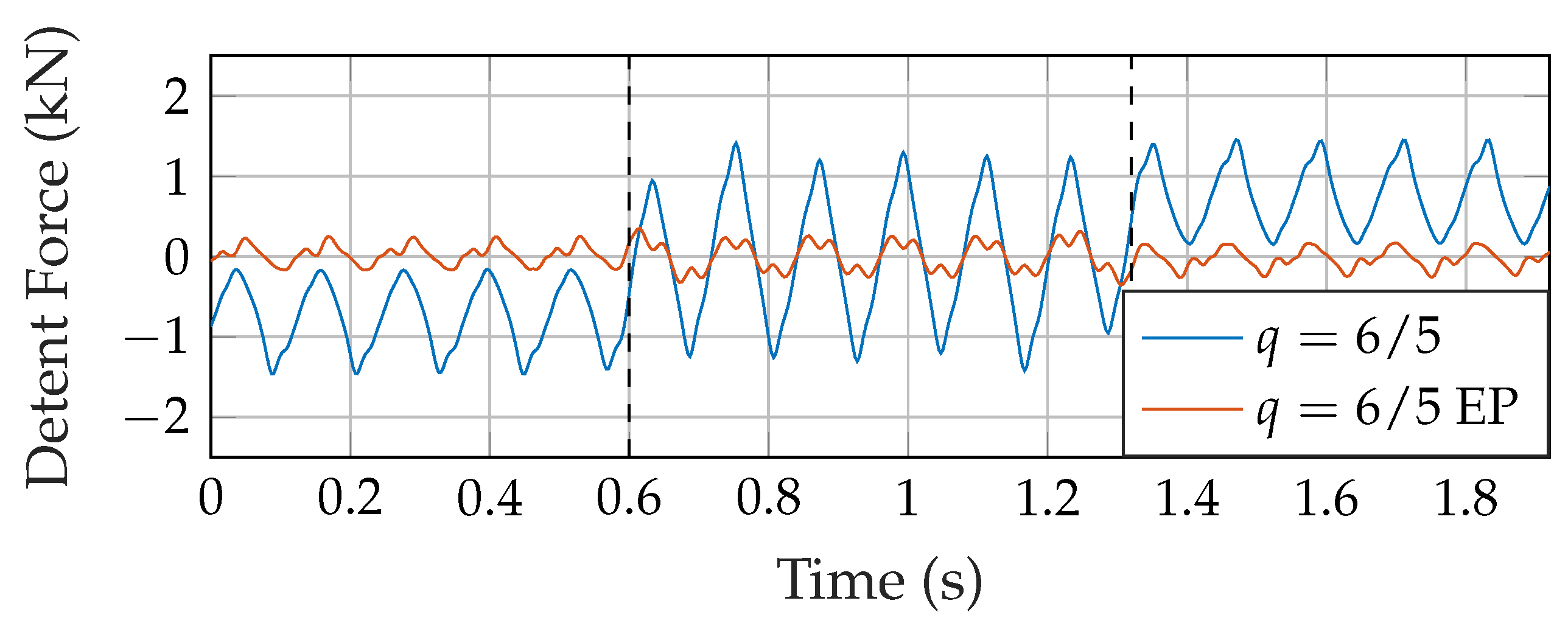
2.3. End Effect Compensation

Two methods are introduced in this study to reduce the impact of end effects for the buried topology.

The first method is to add soft magnetic material on the outer ends of the generator to keep the poles fully magnetized the entire stroke length. The magnetic material would, of course, have to be composed of thin lamination to minimize the eddy currents similar to the stator steel. An advantage to this is that there is little change in magnetization of the PMs during the whole stroke length and thus less end forces. The PMs are also thereby less subjected to irreversible demagnetization that otherwise is the case when they are surrounded by air. The added pieces, here denoted end plates (EP), are of the same width as the stator yoke.

The second method is to adjust the end regions of the stator with extended steel to coincide with the peak force of the poles leaving and entering the stator. This is, in some aspects, similar to [17], but here it is done for buried PMs in a finite element environment and a different method for the force calculation. This method is, in the paper, denoted extended stator (ES). In [4], the detent force is defined as

$$F_c\left(x\right)=a_0+b_{1}cos(2\pi \frac{1}{w_p}x+{\theta }_1)+b_{2}cos(2\pi \frac{3}{w_p}x+{\theta }_2),$$

(7)

where $a_0$ and $b_1$ are constant amplitudes while $b_2$ represents the cogging forces that increase in amplitude with active stator area. The introduction of extended stator ends would allow the splitting of ${\theta }_1$ in (7) into two components and separating those to ${180}^{\circ }$ to cancel out the force peaks. This is only possible during the full stator overlap.

The two end-force compensation methods are illustrated in Figure 4.

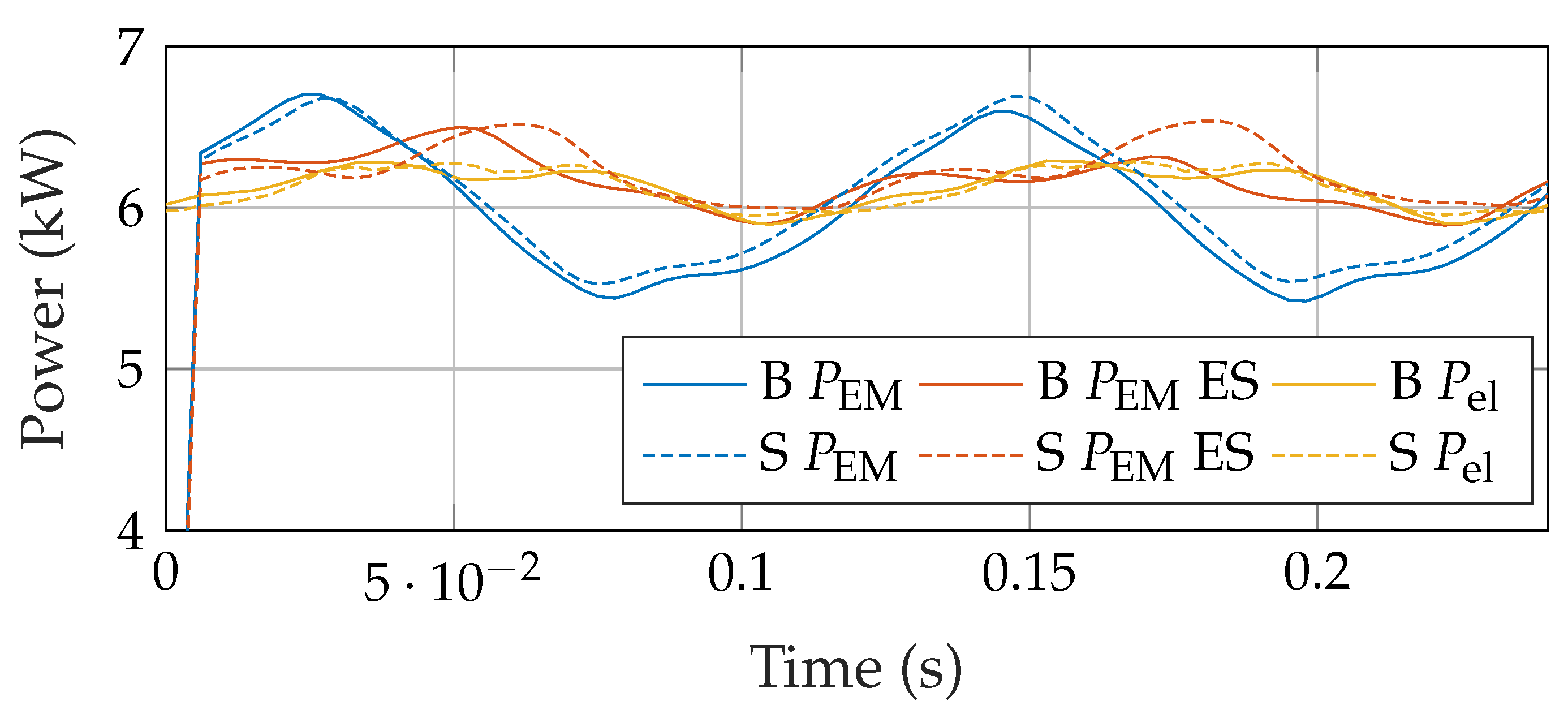
2.4. Comparison of Force Reduction between Buried and Surface Topology under No-Load and Load Conditionz

To further investigate how the alterations of the stator ends affect the end forces, a comparison is made between the buried and surface topologies. The hypothesis is that there is a difference in behavior because of the forced flux path through the surface-mounted PMs to the fluctuating proximity of the stator teeth, whereas the buried topology allows for a higher flux concentration at pole face regions closer to the stator teeth.

The dimensions of the surface-mounted translator are set in order to reach similar rms values of the no-load voltage at a time interval within the full active stator area. The same time interval is also used to investigate the impact of introduced currents in the stator windings. In this study, the introduced currents are in phase with the induced voltage. In practice, this kind of phase angle compensation can be accomplished by constant-torque-angle control [25]. As similar behavior of the end force reduction was apparent for both winding patterns, the winding patterns used for the comparison between the two topologies is $q=\frac{6}{5}$. As a way of further evaluating the force computations, the electrical power without resistive losses can be compared to the power associated with the magnetic forces. By having the currents in-phase with the induced voltage E, the load angle ($\delta$) equals the phase angle ($\theta$). The terminal voltage, expressed as $V=(E-RI)cos\left(\delta \right)$ is then used to determine the electrical power

$$P_{\mathrm{el}}=VIcos\left(\theta \right)=EI-R{I}^2.$$

(8)

The translator and stator dimensions can be seen in Table 1 and Table 2, respectively. The fill factor for the stator slots are 51%.

For the buried topology, the relative permeability is derived from (6). For the NdFeB magnets used in the surface-mounted topology, the relative pearmeability is set similar to other literature [21]. The difference in topology between surface-mounted and buried results in different flux paths in the translator. Due to the difference in flux path, the initial displacement of the surface-mounted PMs have to be adjusted to meet the same voltage phases. In other words, by adjusting the displacement, one can get the same phasors for the quadrature voltage component. Since the full active stator area is defined by the adjoining and leaving outer poles of the buried topology, the surface-mounted topology has a shorter full active stator area equal to half a pole-pitch on either side of the translator. This is visualized in Figure 5 and later evident especially in the results for the attraction forces. Despite covering the stator at $t=0.54$ s for surface-mounted PMs, it is not until $t=0.6$ s that it reaches a distribution that, ideally, covers the whole stator. For the two topologies, the stator overlap is therefore the same when the translator enters the stator and different when leaving the stator. The figure also reveals the varying flux in the translator yoke for the surface-mounted topology. The shorter coverage is the cause for a shorter interval of full active stator.

3. Results and Discussion

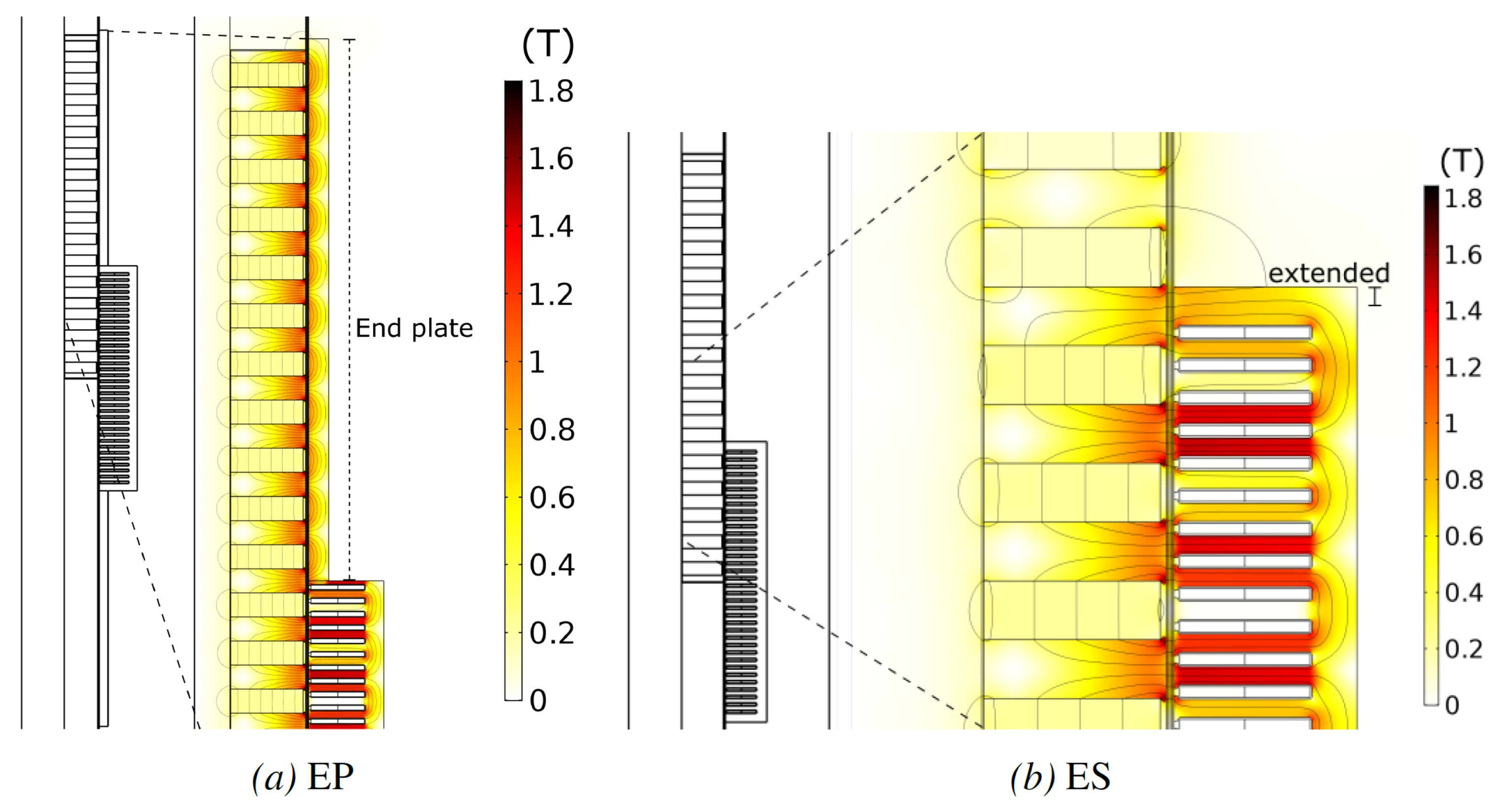
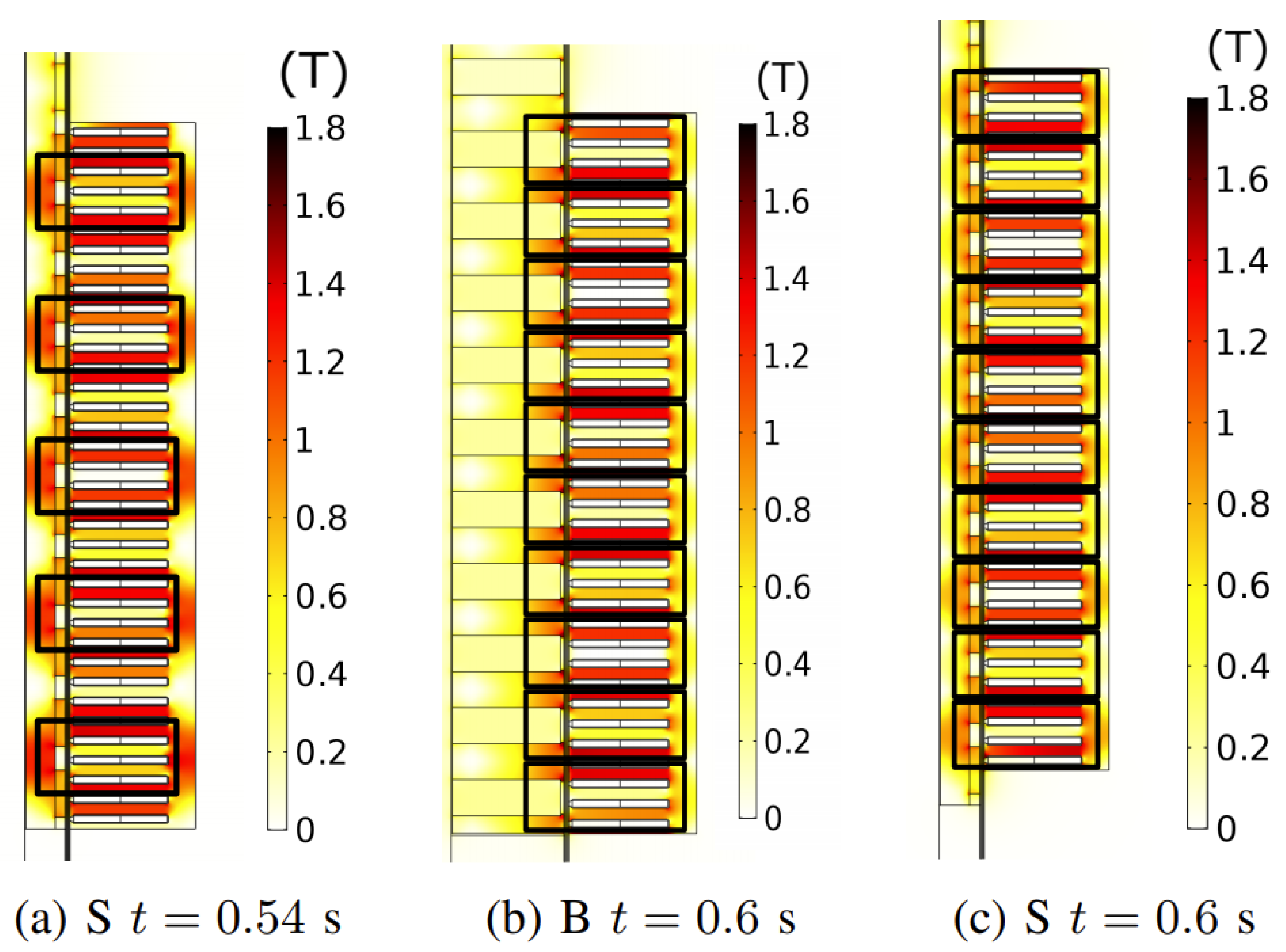
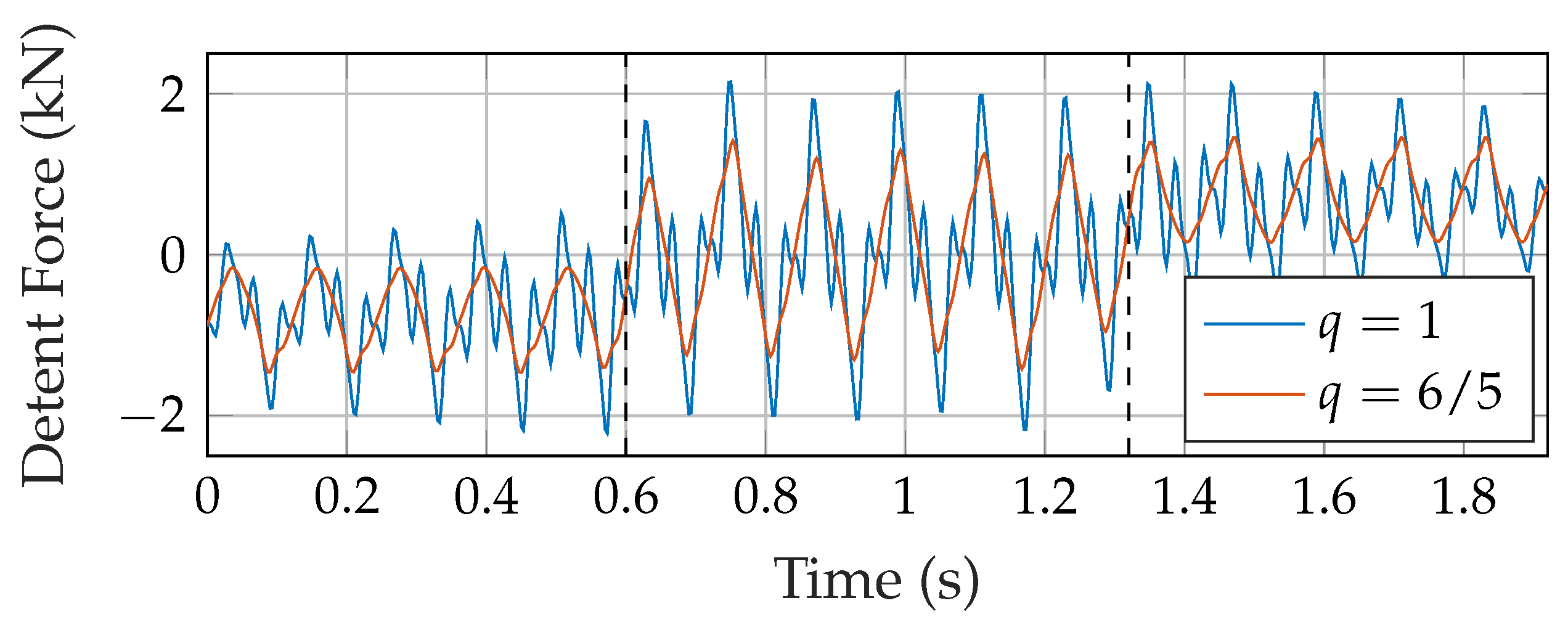
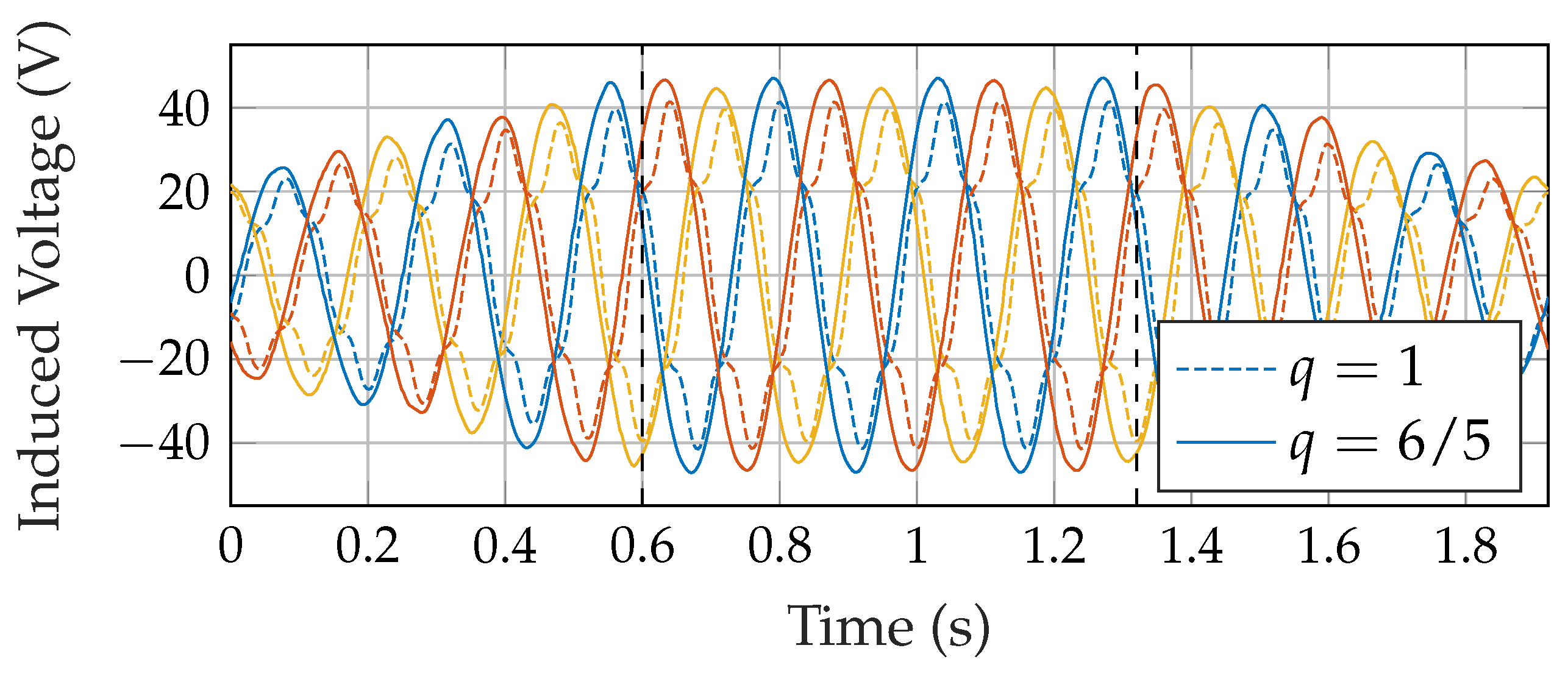
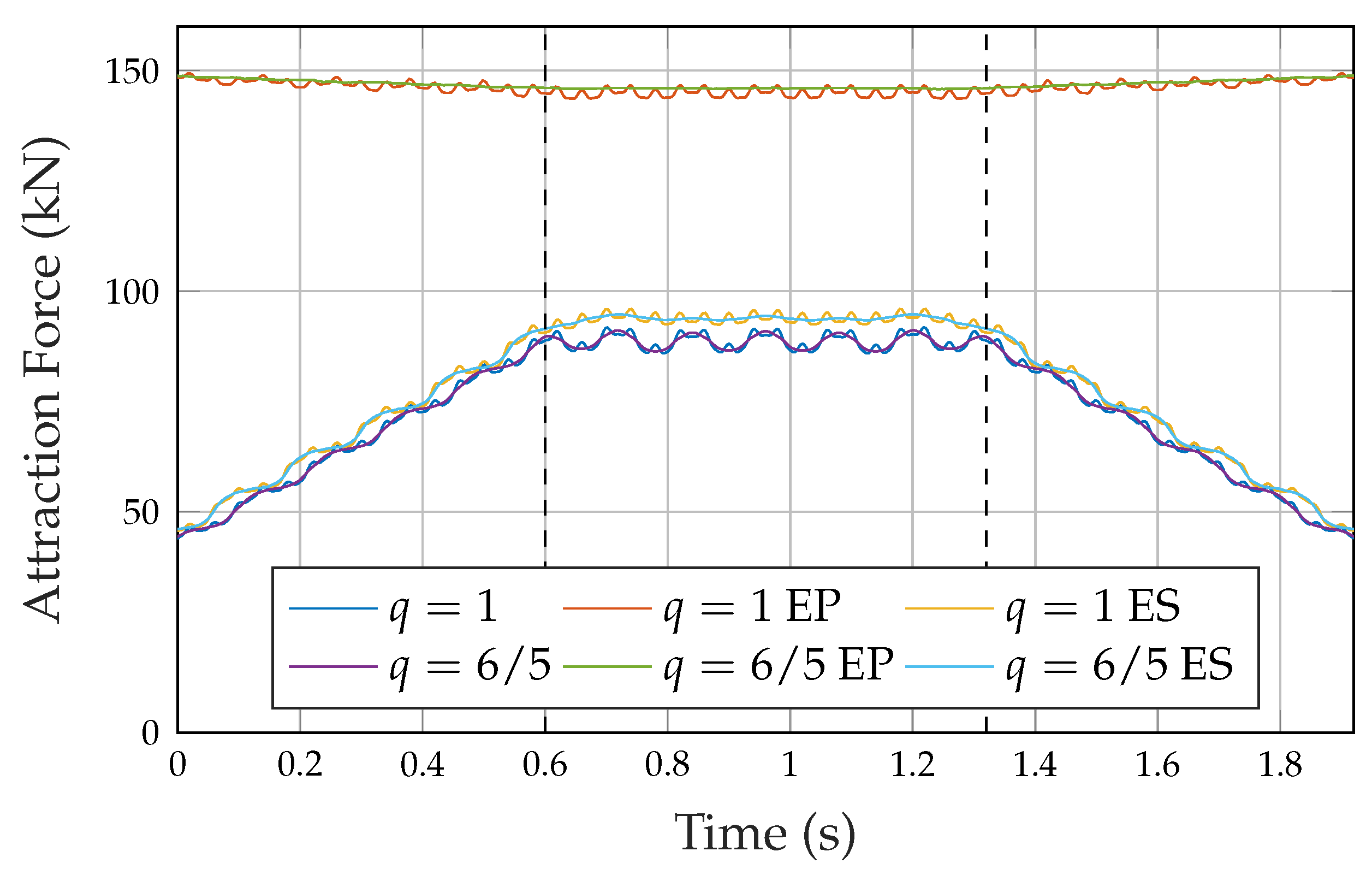
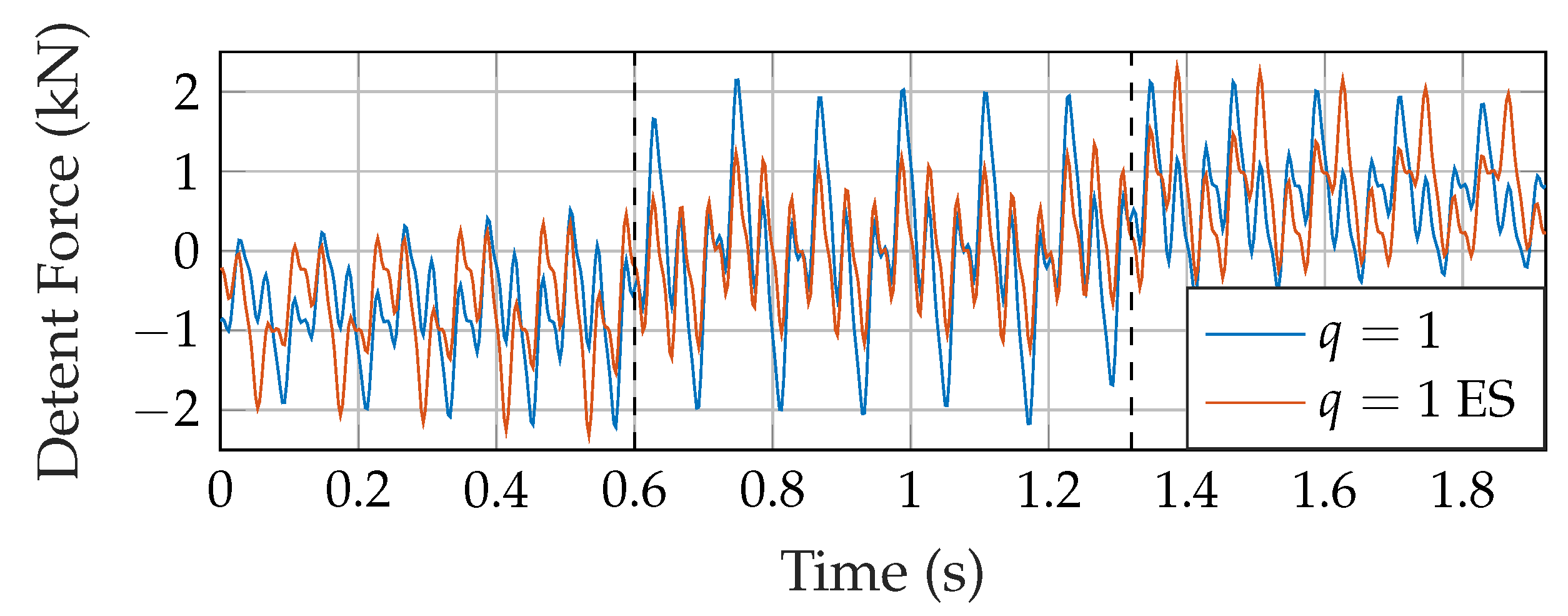
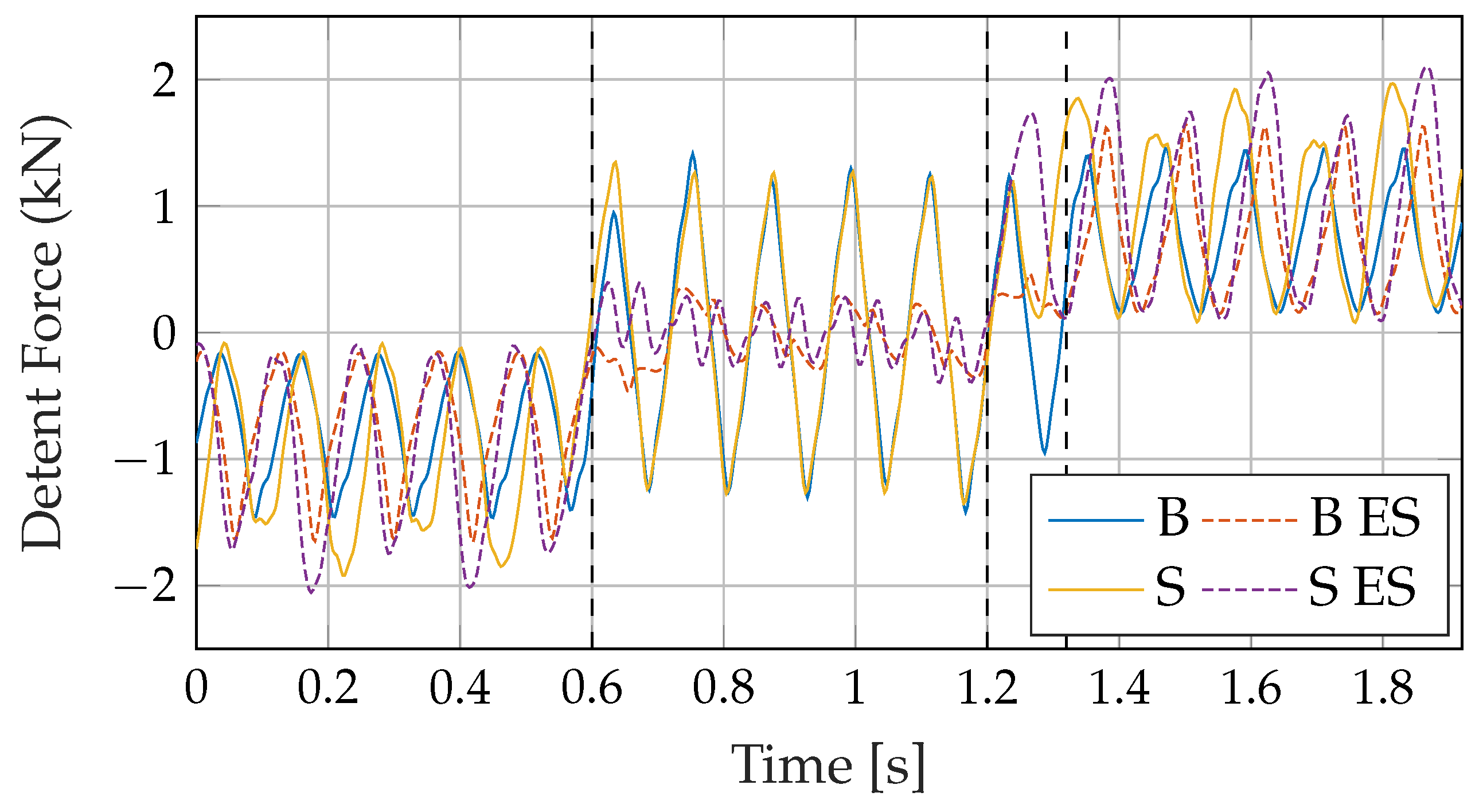
3.1. Buried Topology without End Region Alterations

Without any alterations to the end regions, the detent force is shown in Figure 6.

From the figure, it is evident that the peaks of the detent forces appear at the same instants. The end forces arise when the poles of the translator enter and leave the stator. When a pole enters the stator, the flux increases remarkably. The peaks of the average $B_y$ component for the outer stator tooth face perfectly align with the peak detent forces. This is in accordance with (2), where the time instant of maximum $B_y$ coincides with the time when the detent forces reach their maximum. Here, the maximum peak force is when the boundary between pole and PM passes the end of the stator iron.

The induced voltages for each phase can be seen in Figure 7. The induced voltage appears to be proportional to the stator overlap, as predicted in [6]. The induced phase voltages show slightly different magnitudes for a finite stator length. This is because of the different contributions along the stator windings for every phase. A resembling imbalance between phases was mentioned in [15].

This difference in magnitude between phases is more prominent when the ratio of the machine length over stroke length is low, as it is for this machine. Normally, the machine is longer where only the outer windings of the stator are subjected to a reduced flux linkage. The induced voltage still appears proportional to the active stator area. The end forces will also be of less significance compared to the cogging forces for a longer linear machine. In this paper, the end forces do, however, appear significant, and looking at ways to minimize the end forces can be of interest even for longer linear machines with partial overlap.

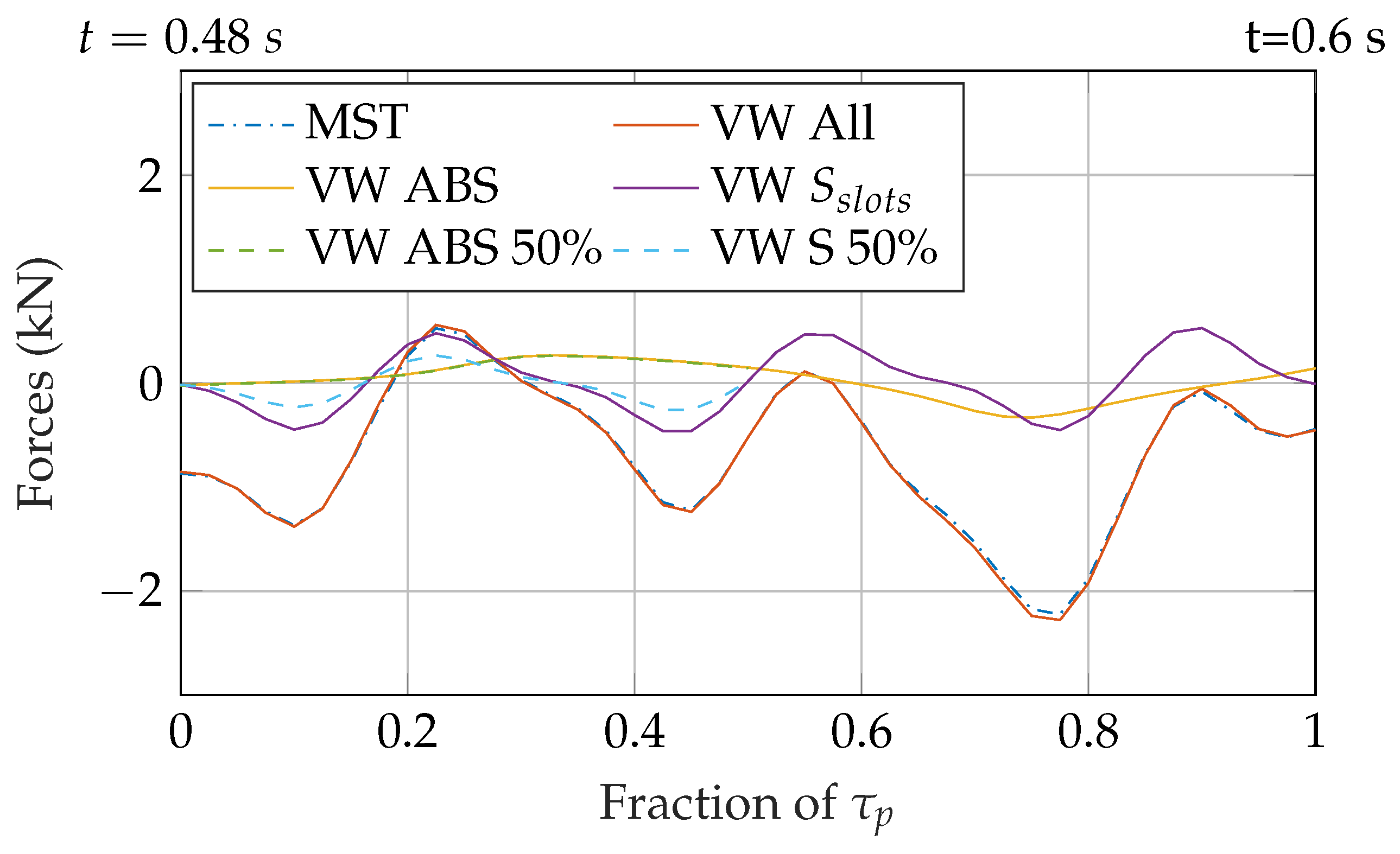
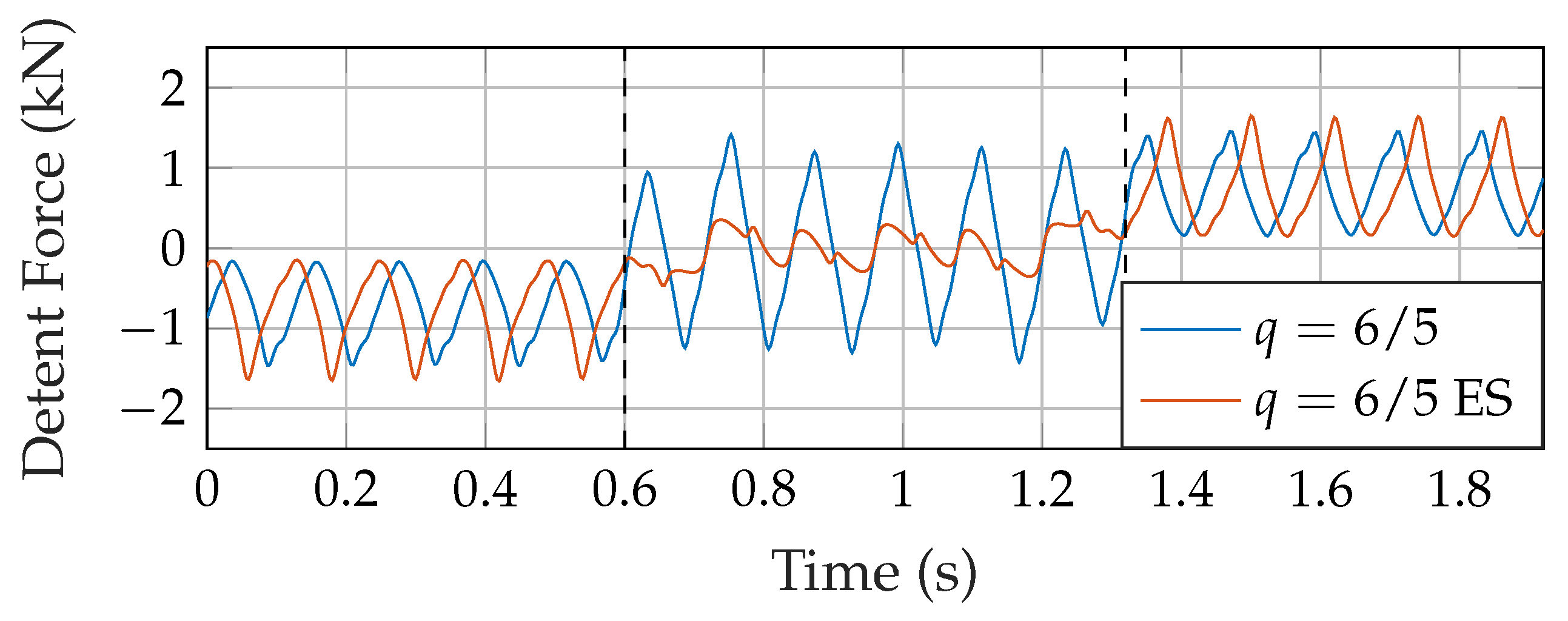
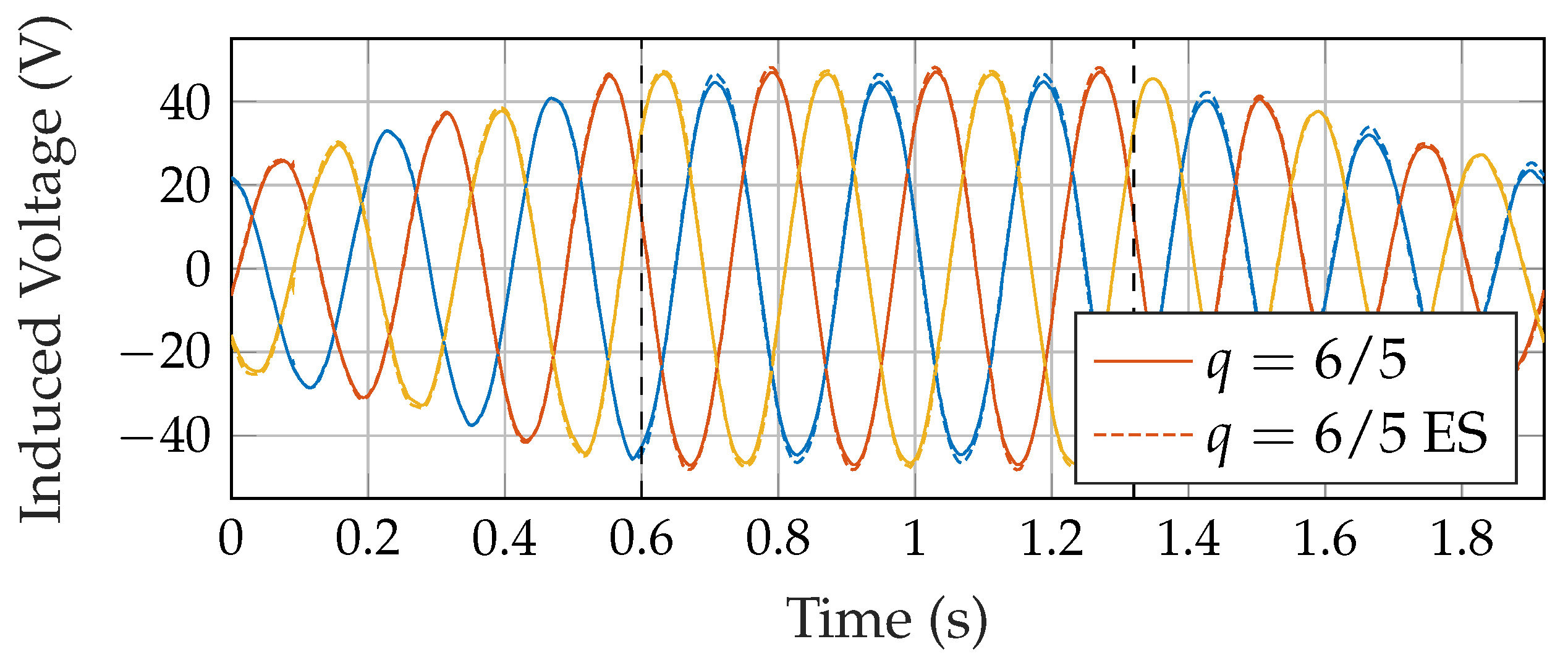
3.2. Force Reduction for Buried Topology with Different Winding Patterns

The flux distribution of a generator with added soft magnetic material on the stator is shown in Figure 4a, where the flux through each PM is of similar magnitude throughout the translator. The detent forces for $q=1$ and $q=\frac{6}{5}$ are shown in Figure 8 and Figure 9 with and without the added pieces, respectively.

Since the magnetic flux remains of the same magnitude for the whole stroke length, the end effects are efficiently reduced. What is then left of the detent forces is the cogging force that increases linearly with increasing stator overlap. It also shows that the cogging force of $q=1$ has a magnitude close to 50% at 50% stator overlap with an increased amplitude towards 100% stator overlap. This is in accordance with the increased amplitude of $b_2$ in [4] and is also indicated in Figure 1 for the slot component of the cogging force. A clear disadvantage is the increased attraction forces, as can be seen in Figure 10. The increased attraction force can increase the friction in the generator, which is a drawback.

The added end plates are of the same dimensions as the stator yoke. Still, one can observe from the attraction force that there is a slightly higher flux in the end plates than the stator yoke. This is because of the nonlinear BH curve of the iron and a flux density closer to saturation in the stator teeth.

The second way, having extended stator, is illustrated in Figure 4b and the detent force in Figure 11 for $q=1$ and in Figure 12 for $q=\frac{6}{5}$.

By adjusting the end lengths of the stator, one can change ${\theta }_1$ of (7) to counter the end forces from both ends. In the figures, it is shown that there is a large reduction in the detent force when the linear generator has a full active stator area. It is, however, slightly higher than its counterpart in Figure 8 and Figure 9. The new, but much lower, force peaks arise when one stator end is next to the mid pole and the other stator end is next to the mid PM. The detent force is slightly distorted for $q=\frac{6}{5}$ due to the new force peaks. The reduction is still visible, especially for $q=\frac{6}{5}$. Even with less saturation of the outer teeth, there is still a difference in magnitude between the phase voltages, as illustrated in Figure 13.

As earlier mentioned, this is because the winding patterns for the phases have different contributions in the end regions. The extended stator ends give little increase of the attraction forces, as shown in Figure 10.

3.3. Comparison in Force Reduction between Buried and Surface Topology and under Load Condition

The no-load voltage of the surface-mounted machine can be seen in comparison with the buried topology in Figure 14.

The dimensions of the surface-mounted topology is adjusted to match the rms values of the buried topology at full active stator area. The time interval starts from roughly $t=0.7$ s and is set when one of the phases intersects the 0 voltage line and continues for one electric period. A matlab script is used to calculate the interpolated value for the start. The difference in mean rms between the two topologies is less than 0.2 promille for the time interval. By not splitting the outer magnets of the surface-mounted PM, the voltage is slightly higher when there is no full active stator area compared to the buried topology. The lower phase voltages for the surface mounted on the right side in Figure 14 are due to the lower active stator area for the same time instant.

The values used for the extended stator of both topologies are derived from parametric sweeps at the full active stator area where the detent force is calculated. To get a more precise value for the stator end extensions, algorithmic optimization could be used with an increased number of allowed decimals. The parametric sweeps gave, however, optimal stator extensions of 15 mm and 20 mm for buried and surface topology, respectively. This equals half of the pole width for both topologies.

The detent force for both topologies with and without the extended stator (ES) is shown in Figure 15.

The range of full active stator area is, as mentioned earlier, different for the surface-mounted topology. This can be realized by the extra negative force peak of the buried topology at $t=1.287$ s. The figure shows similar behavior for both topologies when introducing the extended stator; a time shift of the force peak outside the full active stator area and a clear reduction in the forces within the full active stator area. The pair-wise connection of the surface-mounted PMs also introduces a difference in end forces when an even versus odd number of PMs overlap the stator. This phenomena has been known for quite some time [2]. One can also see in the figure that the detent force is slightly higher for the surface-mounted topology.

In Figure 16, the surface-mounted topology can be seen with and without extended stator at $t=0.756$ s. This is the time instant where a force peak arises without the extended stator.

Comparing the two topologies, one can see some clear similarities; the extended stator for the buried topology covers the outer edges of the poles, and the extended stator for the surface-mounted topology covers the outer edges of the permanent magnets; i.e., for either topology of this study, a significant reduction in end forces is achieved when the poles closest to the air gap is completely covered.

As for the attraction forces in Figure 17, one can see similar behavior in both topologies, with a smaller change in ripple for the surface topology.

Lastly, the behavior of the detent force is investigated when the machine is subjected to electrical loading in the stator windings. Each phase has a current density of $2{\mathrm{A}/\mathrm{mm}}^2$ RMS, taking the fill factor into account and is ramped up for the three phases before they reach their designated phase current. The electromagnetic (EM) power associated with the detent force and constant translator velocity, $P_{\mathrm{EM}}=F_{\mathrm{den}}v$ and the resistive-free electrical power with constant-torque-angle $P_{\mathrm{el}}=EI$ can be seen in Figure 18 for one electric period (or two pole-pitches). From the figure, one can see that the electrical power is of similar magnitude as the EM power. One can also see that the ripple is higher for both topologies without the extended stator. To further analyze the ripple, the detent force ripple for the second pole pitch can be seen in Figure 19. To give a fair comparison of the force ripple, they are all offset by their average number (i.e., the averaged value for each case is zero). The fraction of force ripple with and without extended stator $f_{\mathsf{\Delta },top,J}=\frac{rippleES}{ripple}$ for each topology (top) and current density (J) is; $f_{\mathsf{\Delta },S,0}=0.22$, $f_{\mathsf{\Delta },S,2}=0.45$, $f_{\mathsf{\Delta },B,0}=0.23$, $f_{\mathsf{\Delta },B,2}=0.36$. Since the velocity remains constant in the simulation, the same fraction is valid for both mechanical power ripple and force ripple. From these results, one can see that the extended stator reduces the force ripple of both topologies by similar factors at no-load. Under a load, however, the force ripple reduction due to the extended stator is less than under no load, with a better maintained reduction for the buried topology.

4. Conclusions

The electromagnetic forces were investigated for linear machines of buried and surface-mounted topologies, and means of reducing the end forces were included in a simulated FE environment. Initial investigation of the buried topology shows attraction forces and cogging forces that increase with active stator area. Meanwhile, the end forces did not increase in magnitude with an increased active stator area.

It was found that adding soft magnetic material for the whole stroke length reduced the detent force for the whole operating range but almost doubled the attraction forces, making it only viable for a linear machine where stroke length-to-machine length ratio is very low. If, instead, extending the stator ended slightly, the detent force was reduced for full active stator area by countering the end forces on opposite sides of the generator. This end effect compensation gave little increase to the attraction forces and was significant for both $q=1$ and $q=\frac{6}{5}$, with a higher reduction in detent force when q was a fractional number.

The detent force of the surface-mounted topology varied in magnitude, depending on whether the number of active poles was odd or even. At full active stator area, the extended stator reduced the detent force in a similar manner as the buried topology. Although the two topologies showed somewhat different behavior in how the detent force acts with the number of active poles, they showed some clear similarities with regards to end effect compensation: the optimal stator extension to reduce the end forces was achieved for both topologies when the poles closest to the air gap overlapped the extended stator on both ends.

Furthermore, during the load condition, it was shown that the extended stator reduced the force (or power) ripple for both topologies. The reduction was, however, lower under a load than under no load and with a slightly better result for the buried topology.

The results also indicate that the buried topology better utilizes the stator, as the surface-mounted topology has a lower full active stator area for the same stroke length, effectively reducing the average induced voltage for a stroke length with partial stator area. A partial translator overlap for the surface-mounted topology inherently introduces magnetic flux variations in the translator, which can be a source for induced eddy currents.

In a broader context, one can see that the end effects that are inherent for the longitudinal ends of linear machines depend on the soft magnetic material of the stator ends. By modifying the stator ends, one can influence the force peaks. The modifications presented in the paper can be done regardless of the winding pattern.